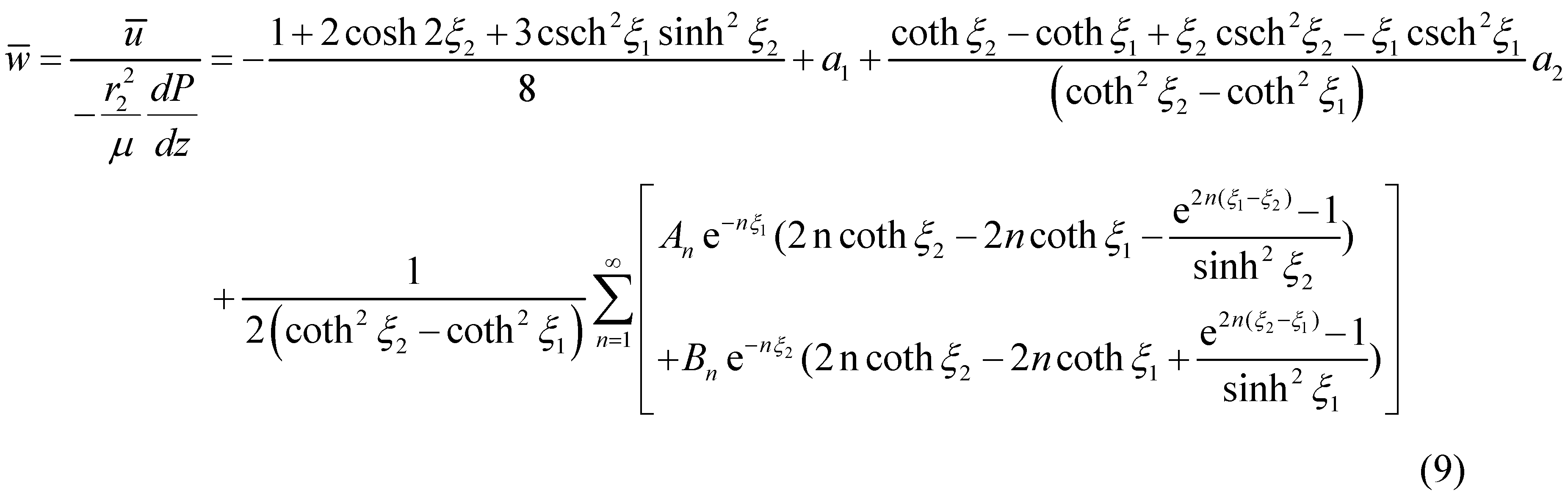Oscillation of a Liquid Column in an Eccentric Annulus

Preprint

Article

Oscillation of a Liquid Column in an Eccentric Annulus

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Rajai S Alassar^*

This version is not peer-reviewed

Submitted:

04 July 2024

Posted:

05 July 2024

You are already at the latest version

Alerts

Abstract

The velocity distribution of flow in an eccentric cylindrical annulus is determined in an attempt to investigate the vertical capillary rise in the channel. The radii ratio and the eccentricity at which a transition from monotone to oscillatory rise occurs, are determined. The results are shown to converge to the well-known limiting cases of concentric annuli and circular tubes.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

The study of capillary rise of liquids in thin tubes is important due to numerous applications. For example, a porous medium is modeled as a bundle of capillary tubes. Other applications that essentially require a thorough understanding of the interesting phenomenon include paper, ink, and textile industries.

The mathematical modeling of the capillary rise in a tube dates back to Ampt [1], Lucas [2], and Washburn [3]. Since then, the literature has been quite rich on all aspects of this phenomenon. The original celebrated Lucas-Washburn equation ignores gravity and kinetic effects. A model that includes both effects is given by Masoodi et al. [4], Szekely et al. [5], and Fries [6]. The model in abstract symbols reads as

y y' + y + ω d (y y') / d t = 1

with

ω

being a parameter that hosts the liquid and tube properties, and

y

is some dimensionless version of the height of the column. An interesting behavior is found near the equilibrium height of the rise. For some range of

ω

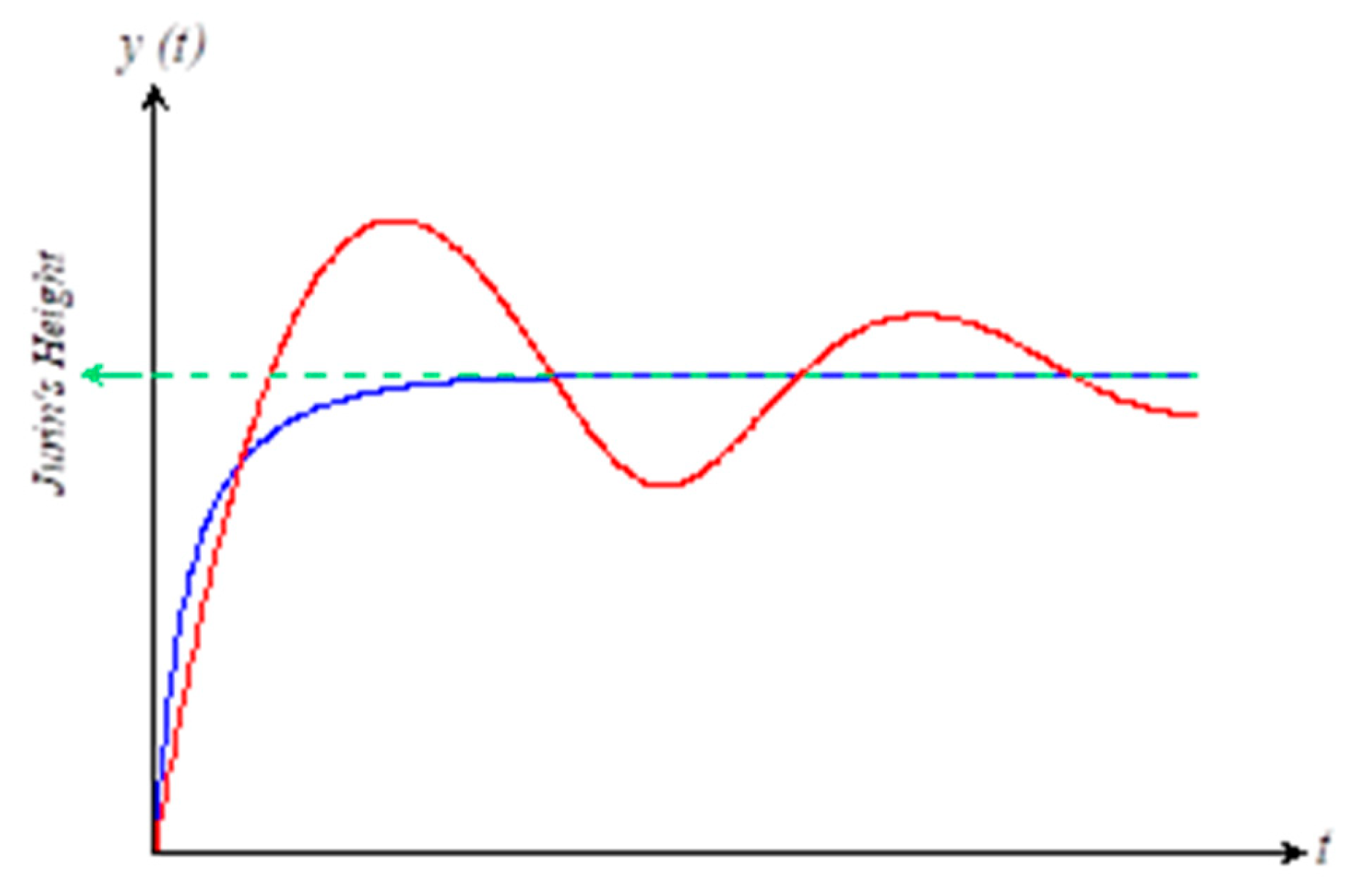
, the rise oscillates around its equilibrium destination, while for others the oscillations are completely dampened, Figure 1 (a gif-file is also attached).

Masoodi et al. [4] determined that the condition

ω > 1 / 4

leads to the onset of oscillations. The findings of this fundamental work was rigorously proved by Płociniczak and Świtała [7].

Numerous research has been done on the flow between two vertical plates (see for example [8,9,10,11,12]) and on the capillary rise in tubes. The bulk of research on capillary rise has been related to circular tubes. In this research, we investigate the capillary rise in an eccentric annulus from which a circular tube is a special case. The research is interesting from application point of view as many instruments involve capillary rise in the annulus of tubes. The annulus is not always, intentionally or unintentionally, perfectly centered. The eccentricity of the annulus can be of significant magnitude. Here, we determine the velocity distribution and investigate the effect of the radii ratio and the eccentricity on the transition from monotone to oscillatory rise. To the best of our knowledge, no such work has been carried out.

2. Velocity Profile

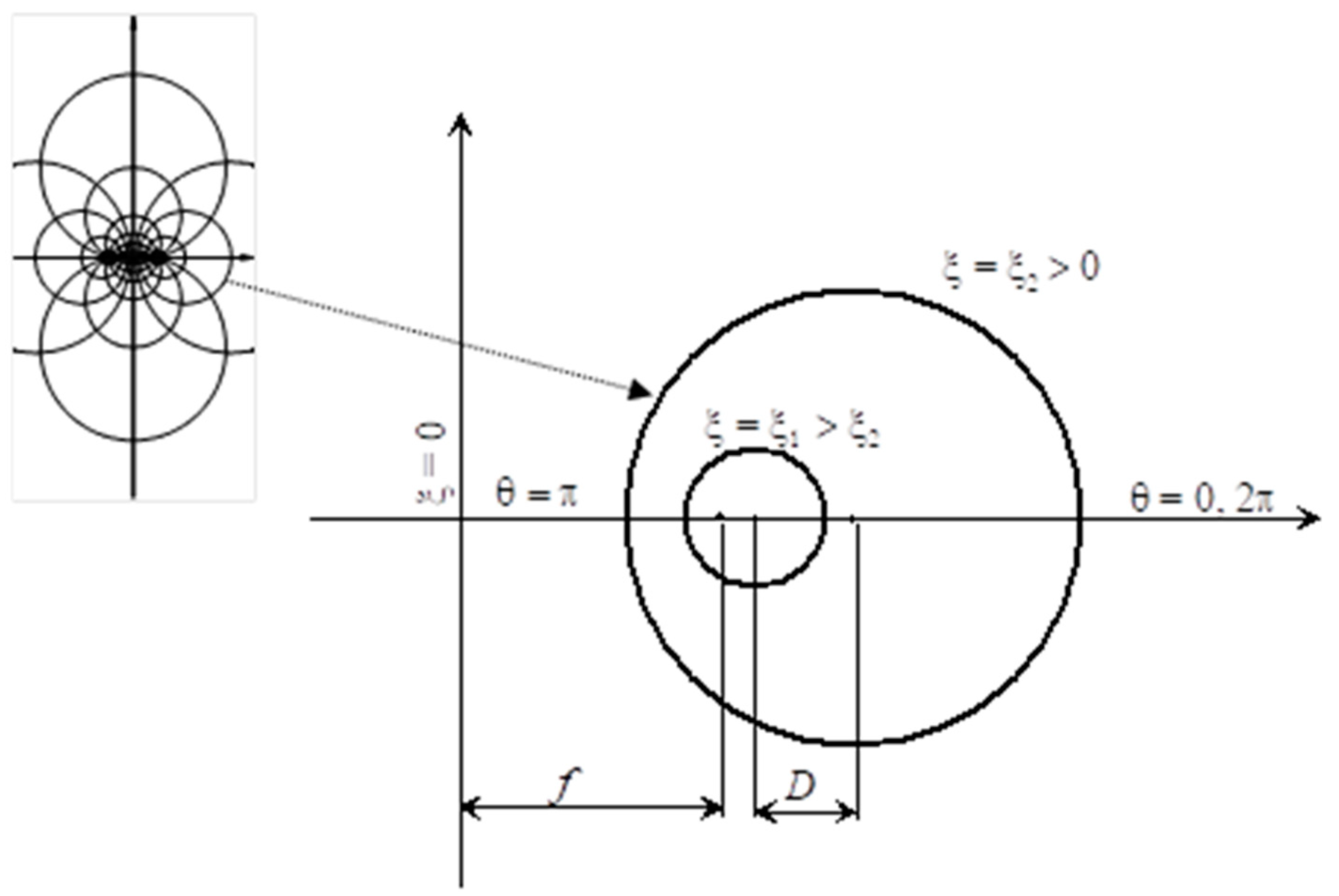
Consider an axial flow in an eccentric cylindrical annulus with inner radius

r_{1}

, outer radius

r_{2}

, and center-to-center distance

D

, Figure 2.

The steady developed flow in the annulus is assumed to obey Poiseuille equation

\nabla^{2} u = \frac{1}{μ} \frac{d P}{d z}

(1)

where

u

is the velocity in the axial direction

z

μ

is the viscosity, and

P

is the pressure.

The solution of (1), i.e. the velocity profile, can be obtained using the naturally-fit bipolar cylindrical coordinates system

(θ, ξ, z)

. This system is a three-dimensional orthogonal coordinates system whose projection on a plane perpendicular to the z-axis is composed of two sets of Apollonian circles, Figure 2. For more details on the coordinates system, the reader is referred to the work of Moon and Spencer [13], and Alassar and El-Gebeily [14]. The Cartesian coordinates system is related to the bipolar system by the relations:

x = \frac{a \sinh ξ}{\cosh ξ - \cos θ}, y = \frac{a \sin θ}{\cosh ξ - \cos θ}, z = z

(2)

with

0 \leq θ \leq 2 π

, and

- \infty < ξ < \infty

. The inner and the outer cylinders are identified, respectively, by

ξ_{1} = \sinh^{- 1} (f / r_{1})

and

ξ_{2} = \sinh^{- 1} (f / r_{2})

, where

f

is the focal length given by

f = \frac{\sqrt{(D - r_{1} - r_{2}) (D - r_{1} + r_{2}) (D + r_{1} - r_{2}) (D + r_{1} + r_{2})}}{2 D}

(3)

The bipolar coordinates system has the scale factors

h_{θ} = h_{ξ} = \frac{a}{\cosh ξ - \cos θ}, h_{z} = 1

(4)

It is of a standard procedure, Arfken [15], to cast equation (1) in any orthogonal coordinates system using the appropriate scale factors. In bipolar coordinates, equation (1) takes the form

\frac{\partial^{2} u}{\partial ξ^{2}} + \frac{\partial^{2} u}{\partial θ^{2}} = \frac{1}{μ} \frac{d P}{d z} \frac{f^{2}}{{(\cosh ξ - \cos θ)}^{2}}

(5)

At the surfaces of the cylinders, no-slip conditions (

u (θ, ξ_{1}) = u (θ, ξ_{2}) = 0

) are considered.

By inspection, one can notice that

\frac{f^{2}}{2 μ} \frac{d P}{d z} \frac{\cosh ξ}{\cosh ξ - \cos θ}

is a particular solution of (5). Considering the symmetry of the problem, we then assume a solution of the form

\frac{u}{- \frac{r_{2}^{2}}{μ} \frac{d P}{d z}} = \frac{- f^{2} \cosh ξ}{2 r_{2}^{2} (\cosh ξ - \cos θ)} + a_{1} + a_{2} ξ + \sum_{n = 1}^{\infty} [A_{n} \sinh n (ξ - ξ_{1}) + B_{n} \sinh n (ξ - ξ_{2})] \cos n θ

(6)

It is noted here that the velocity has been scaled by

- \frac{r_{2}^{2}}{μ} \frac{d P}{d z}

to make it dimensionless. The assumed solution (6) has the same form as that given by Alassar [16] for the flow in eccentric annuli but with slip. It can be shown, however, that the coefficients in (6) which were calculated numerically by Alassar [16] due to their coupled nature, decouples in the present no-slip case and can be obtained exactly in closed form. The coefficients are found to be

\begin{array}{l} a_{1} = - \frac{\sinh^{2} ξ_{2}}{2} \frac{ξ_{2} \coth ξ_{1} - ξ_{1} \coth ξ_{2}}{ξ_{1} - ξ_{2}}, a_{2} = - \frac{\sinh^{2} ξ_{2}}{2} \frac{\coth ξ_{2} - \coth ξ_{1}}{ξ_{1} - ξ_{2}} \\ A_{n} = \sinh^{2} ξ_{2} \frac{e^{- n ξ_{2}} \coth ξ_{2}}{\sinh n (ξ_{2} - ξ_{1})}, B_{n} = \sinh^{2} ξ_{2} \frac{e^{- n ξ_{1}} \coth ξ_{1}}{\sinh n (ξ_{1} - ξ_{2})} \end{array}

(7)

To obtain (7), one needs, in addition to the standard orthogonality relations of the trigonometric functions, the three special integrals

\begin{array}{l} \int_{0}^{2 π} \frac{\cos n θ}{\cosh ξ - \cos θ} d θ = \frac{2 π e^{- n ξ}}{\sinh ξ} \\ \int_{0}^{2 π} \frac{1}{{(\cosh ξ - \cos θ)}^{3}} d θ = \frac{π (2 + c o s h 2 ξ)}{\sinh^{5} ξ} \\ \int_{0}^{2 π} \frac{\cos n θ}{{(\cosh ξ - \cos θ)}^{2}} d θ = \frac{2 π (n + c o s h ξ) e^{- n ξ}}{\sinh^{2} ξ} \end{array}

(8)

The average dimensionless velocity,

\bar{w} = \bar{u} / (- \frac{r_{2}^{2}}{μ} \frac{d P}{d z})

, can now be calculated as

In summary, the velocity and the average velocity are completely determined if both the radii and the center-to-center distance are known. The center-to-center distance can be replaced by the eccentricity,

ε

ε = D / (r_{2} - r_{1}) = \frac{D / r_{2}}{1 - r_{1} / r_{2}}

(10)

The focal distance is then,

f = \frac{\sqrt{(1 - ε^{2}) ({(r_{2} + r_{1})}^{2} - ε^{2} {(r_{2} - r_{1})}^{2})}}{2 ε}

(11)

The two numbers representing the two surfaces of the cylinders,

ξ_{1}

and

ξ_{2}

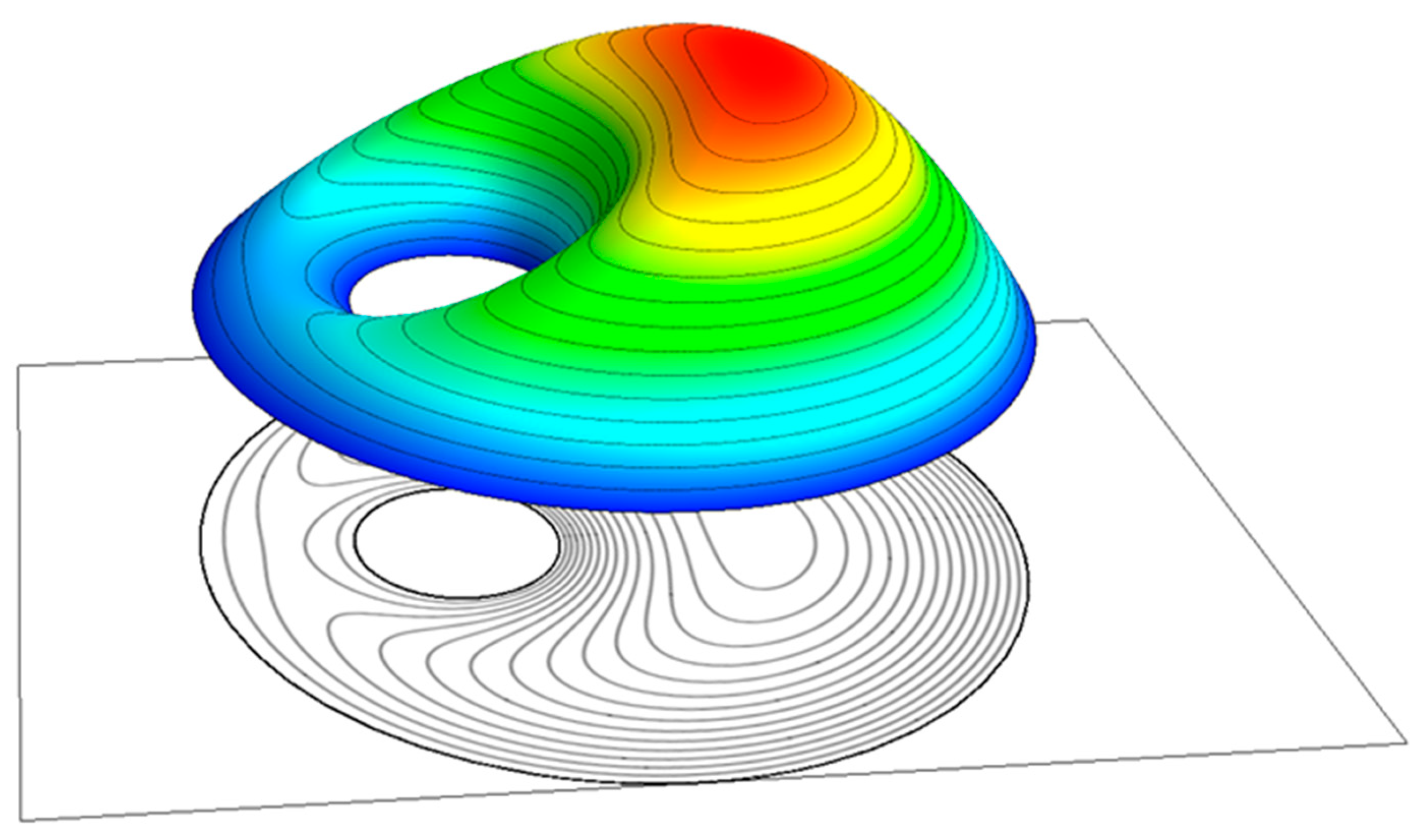
, are thus determined. Figure 3 shows a typical velocity profile (

r_{1} / r_{2} = 1 / 4

and

ε = 1 / 2

3. Capillary Rise

Consider a liquid of density

ρ

and viscosity

μ

rising in a vertical capillary channel of cross-sectional area

A

and perimeter

C

. The height of the liquid column,

h (t)

, is governed by Newton’s second law of motion,

\frac{d}{d t} (ρ A h \frac{d h}{d t}) = γ c o s θ C + Δ P A - ρ g h A

(12)

where

γ

is the surface tension,

θ

is the contact angle,

Δ P

is the pressure drop in the channel, and

g

is the gravitational acceleration, Masoodi et al. [4]. From (9), the pressure drop in a liquid column of height

L

, can be written as

Δ P = \frac{μ}{r_{2}^{2} \bar{w}} L \bar{u} = \frac{μ}{r_{2}^{2} \bar{w}} h \frac{d h}{d t}

(13)

There are several ways to cast (12) in dimensionless form, Fries and Dreyer [17]. Using

H = \frac{ρ g A}{γ C \cos θ} h

and

τ = \sqrt{\frac{ρ g^{2} A}{γ C \cos θ}} t

, equation (12) can be rewritten as

\frac{d}{d τ} (H \frac{d H}{d τ}) + \frac{{(1 - r_{1} / r_{2})}^{2}}{8 \bar{w}} \sqrt{\frac{128 \cos θ}{G a B o}} H \frac{d H}{d τ} + H = 1

(14)

where

G a = \frac{g R^{3} ρ^{2}}{μ^{2}}

is Galileo number,

B o = \frac{ρ g R^{2}}{γ}

is Bond number, and

R = \frac{2 A}{C} = r_{2} - r_{1}

is the hydraulic radius.

It has been shown that, under consistent boundary conditions (i.e.

H (0) = 0, H' (0) = 1

) and depending on the value of

\frac{{(1 - r_{1} / r_{2})}^{2}}{8 \bar{w}} \sqrt{\frac{128 \cos θ}{G a B o}}

( i.e. the coefficient of

H \frac{d H}{d τ}

in (14) ), the solution of equation (14) progresses in time either monotonically or oscillates about its equilibrium height. The equilibrium height, known as Jurin’s height, is usually used for the measurement of surface tension. It is obtained from (12) as

h_{e} = \frac{γ C \cos θ}{ρ g A} = \frac{2 γ \cos θ}{ρ g R}

or the dimensionless value

H_{e} = 1

According to Płociniczak and Świtała [7], the solution of (12) remains monotone as long as

\frac{{(1 - r_{1} / r_{2})}^{2}}{8 \bar{w}} \sqrt{\frac{128 \cos θ}{G a B o}} > 2

, or equivalently

\sqrt{\frac{128 \cos θ}{G a B o}} > \frac{16 \bar{w}}{{(1 - r_{1} / r_{2})}^{2}}

(15)

It is important to observe that, for a specific liquid and tube material, the condition (15) is purely geometric. We define the equality

\sqrt{\frac{128 \cos θ}{G a B o}} = \frac{16 \bar{w}}{{(1 - r_{1} / r_{2})}^{2}}

as the critical condition at which the rise changes from oscillatory to monotone or vice versa.

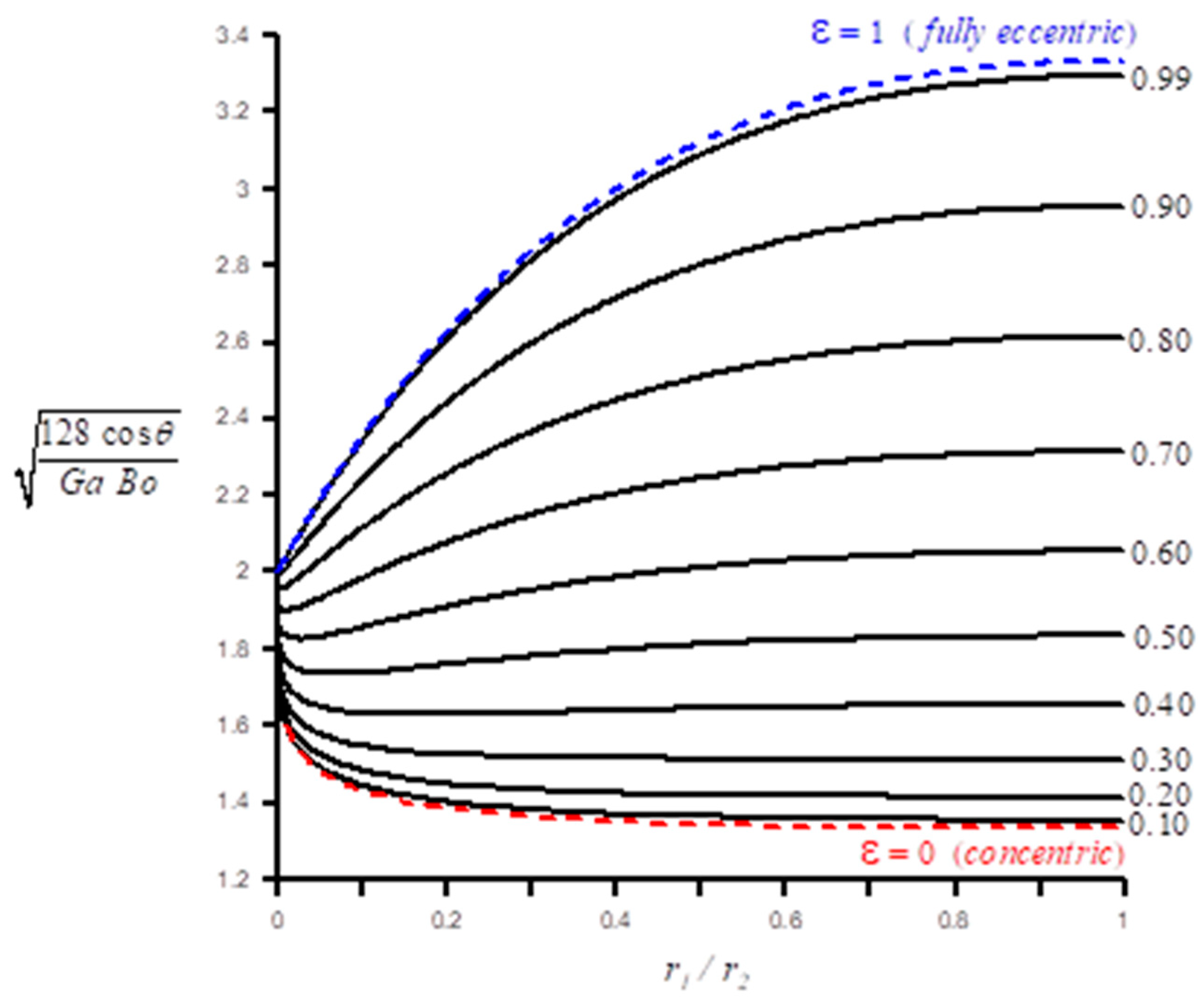
Figure 4 quantifies the expected effect of the radii ratio and the eccentricity on this critical value. As the eccentricity decreases, the rise becomes more oscillatory. In other words, eccentric annuli tend to dampen oscillations. The oscillations are also reduced when the radii ratio increases as a result of the annulus becoming narrower.

It is noted here that for a circular tube (i.e. as

r_{1} / r_{2} \to 0

), we get the well-known result

\bar{w} \to \frac{1}{8}

, and the limiting critical values is

\sqrt{\frac{128 \cos θ}{G a B o}} = 2

. The bottom and top curves in Figure 4 correspond to, respectively, the concentric (

ε = 0

) and the fully eccentric (

ε = 1

) cases. The critical values for these two limiting cases can be written, in order, as

{\sqrt{\frac{128 \cos θ}{G a B o}}|}_{c o n c e n t r i c} = 2 \frac{1 - {(r_{1} / r_{2})}^{4} + {[1 - {(r_{1} / r_{2})}^{2}]}^{2} / \ln (r_{1} / r_{2})}{{(1 - r_{1} / r_{2})}^{2} [1 - {(r_{1} / r_{2})}^{2}]}

(16)

{\sqrt{\frac{128 \cos θ}{G a B o}}|}_{e c c e n t r i c} = 2 \frac{1 - {(r_{1} / r_{2})}^{4} - 4 {(r_{1} / r_{2})}^{2} ψ_{1} (\frac{1}{1 - r_{1} / r_{2}})}{{(1 - r_{1} / r_{2})}^{2} [1 - {(r_{1} / r_{2})}^{2}]}

(17)

where

ψ_{1}

is the second Polygamma function. The condition in (17) is based on the velocity profile given by MacDonald [18]. For both cases, again,

\sqrt{\frac{128 \cos θ}{G a B o}} = 2

r_{1} / r_{2} \to 0

. As

r_{1} / r_{2} \to 1

, one can show, perhaps for only theoretical curiosity, that the critical value for the fully eccentric case

\sqrt{\frac{128 \cos θ}{G a B o}} \to \frac{10}{3}

, while for the concentric case

\sqrt{\frac{128 \cos θ}{G a B o}} \to \frac{4}{3}

Figure 4 is fundamental in determining the dimensions of a channel that supports monotone rise. The following paragraph explains the process.

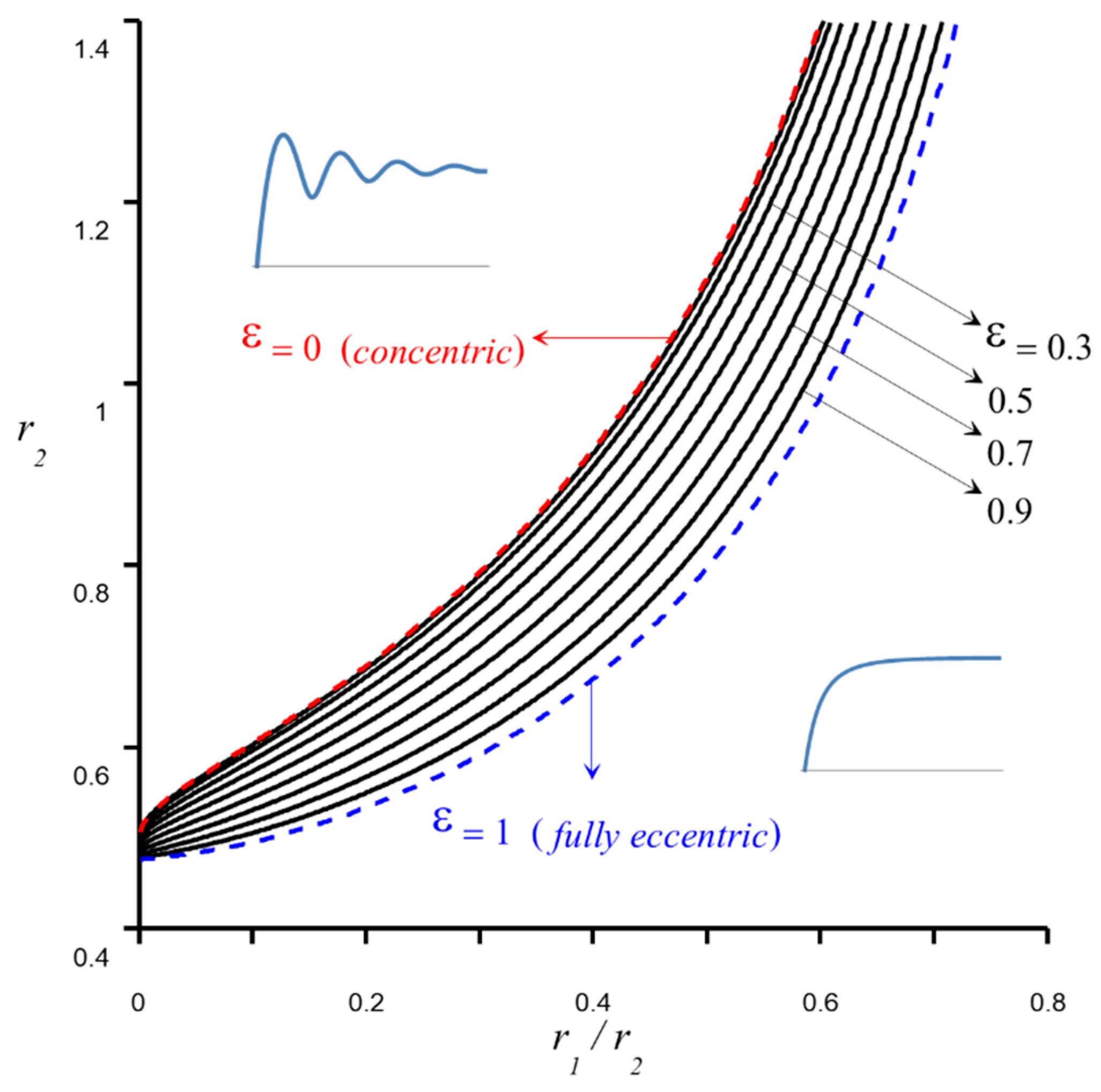
Given that

R = r_{2} - r_{1}

and

\sqrt{\frac{128 \cos θ}{G a B o}} = \sqrt{\frac{128 γ μ^{2} \cos θ}{ρ^{3} g^{2} R^{5}}}

, one can, for specific values of the radii ratio

r_{1} / r_{2}

, and the eccentricity

ε = \frac{D / r_{2}}{1 - r_{1} / r_{2}}

, find the maximum radius of the outer (equivalently the inner) cylinder that maintains monotone rise. The condition for maintaining monotone then reduces from (15) as

r_{2} < \sqrt[5]{\frac{γ μ^{2} \cos θ}{2 (1 - r_{1} / r_{2}) {\bar{w}}^{2} ρ^{3} g^{2}}}

(18)

In other words, the value

r_{2} = \sqrt[5]{\frac{γ μ^{2} \cos θ}{2 (1 - r_{1} / r_{2}) {\bar{w}}^{2} ρ^{3} g^{2}}}

is the largest outer radius before oscillations appear. As

r_{1} / r_{2} \to 0

, condition (18) reduces to

r_{2} < 2 \sqrt[5]{\frac{γ μ^{2} \cos θ}{ρ^{3} g^{2}}}

which is identical to that obtained by Masoodi et al. [4] for a circular tube.

Figure 5 shows the variation of the maximum value of

r_{2}

required to maintain monotonicity, with the radii ratio and the eccentricity for water at

20^{\circ}

C (

ρ = 998 . 23 kg {. m}^{- 3}

μ = 1 . 002 mPa . s

γ = 72 . 86 mN {. m}^{- 1}

, and

θ = 0^{\circ}

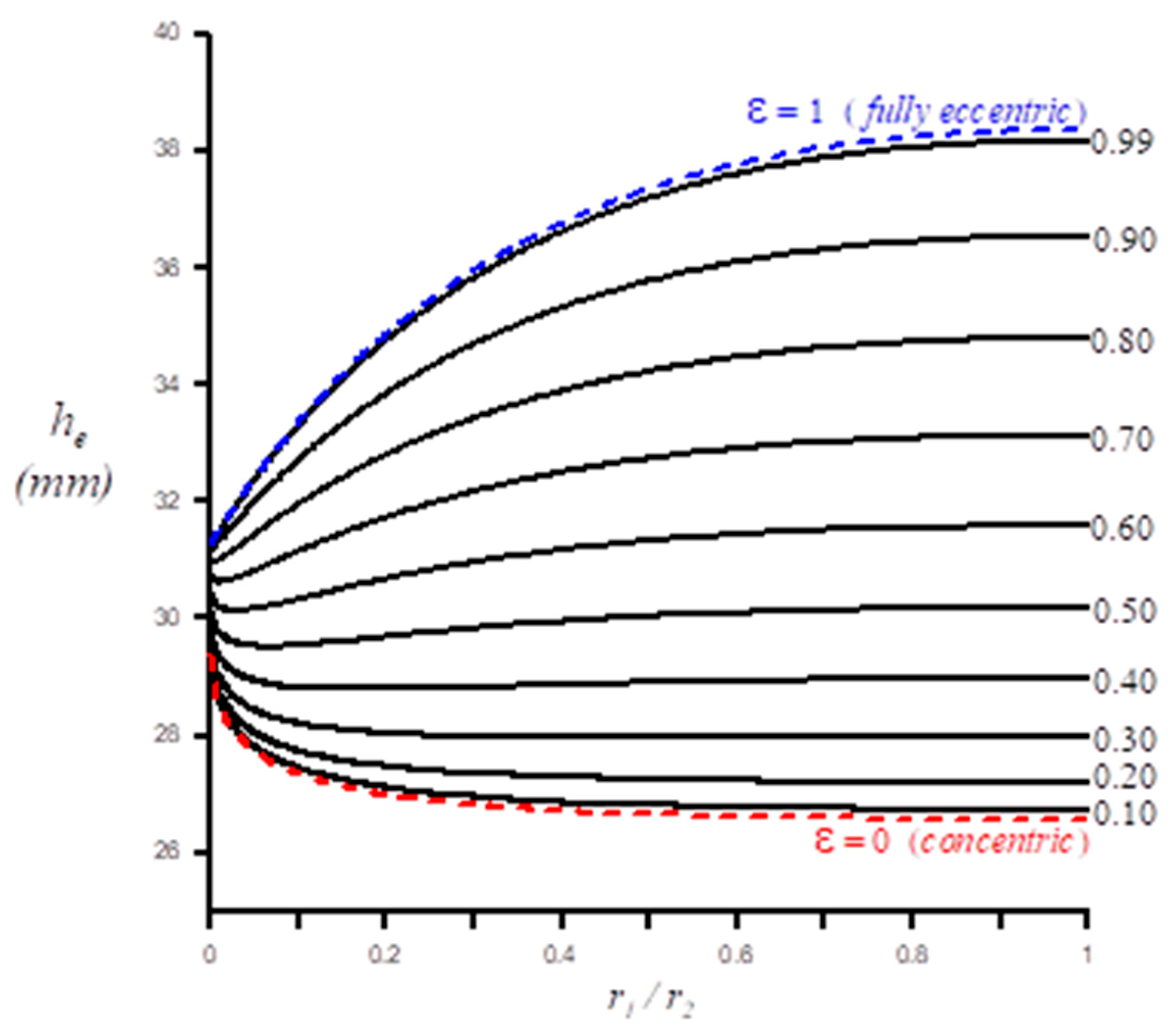
). The corresponding Jurin’s heights are also plotted in Figure 6. As

r_{1} / r_{2} \to 0

h_{e} \to \sqrt[5]{\frac{γ^{4} \cos^{4} θ}{ρ^{2} g^{3} μ^{2}}}

(

\sim

31.26 mm for water at

20^{\circ}

C). The calculations can be repeated easily for any other liquid.

4. Conclusions

The critical values of the radii ratio and the eccentricity at which the capillary rise in an eccentric annulus changes from oscillatory to monotone or vice versa have been determined. For a particular aspect ratio, the rise becomes monotonic as the eccentricity increases. The oscillations are also dampened as the annulus becomes thinner. These critical values, shown in Figure 4 and given explicitly by equations 15 and 18, depend on Galileo and Bond numbers as well as the contact angle. The results reduce to the limiting cases of concentric and fully eccentric annuli as given by equations 16 and 17. The critical values are also calculated for the special arrangements

r_{1} / r_{2} \to 1

, and

r_{1} / r_{2} \to 0

. The later limit is in perfect agreement of the condition found in the literature for the classical circular channel.

Funding

This study was funded by King Fahd University of Petroleum & Minerals under Grant No. SB201025.

Acknowledgments

The author would like to acknowledge King Fahd University of Petroleum & Minerals (KFUPM) for supporting this research under grant no. SB201025.

Conflicts of Interest

There is no conflict of interest to report.

Ethical approval

This article does not contain any studies with animals or human participants.

Availability of data and materials

Available upon request.

Authors’ contributions

Not Applicable.

Nomenclature

$r$ ( $m$ )	Radius of tube	$ρ$ $(k g / m^{3})$	Density
$P$ $(N / m^{2})$	Pressure	$C$ ( $m$ )	Perimeter
$u$ ( $m / s$ )	Axial velocity	$A$ $(m^{2})$	Cross-sectional area
$z$ ( $m$ )	Axial direction	$h$ $(m)$	Height of liquid column
$μ$ ( $\frac{N}{m^{2}} s$ )	Viscosity	$γ$ $(N / m)$	Surface tension
$(θ, ξ, z)$	Bipolar coordinate	$θ$	Contact angle
$f$ ( $m$ )	Focal length	$L$ ( $m$ )	Column height
$D$ ( $m$ )	Center to center distance	$g$ $(m / s^{2})$	Gravitational acceleration
$h_{θ}, h_{ξ}, h_{z}$	Scale factors	$G a = \frac{g R^{3} ρ^{2}}{μ^{2}}$	Galileo number
$\bar{u}$ ( $m / s$ )	Average Velocity	$B o = \frac{ρ g R^{2}}{γ}$	Bond number
$\bar{w}$	Dimensionless average velocity	$R$ ( $m$ )	Hydraulic radius
$ε$	Eccentricity	$H$	Dimensionless height
$h_{e}$ ( $m$ )	Equilibrium height	$H_{e}$	Dimensionless equilibrium height

References

W.H. Green, G.A. W.H. Green, G.A. Ampt, J. Agric. Sci. 4 (1911) 1–24. [CrossRef]
R. Lucas, Kollid Z. 23 (1918) 15–22. [CrossRef]
E.V. Washburn, Phys. Rev. 17 (1921) 273–283. [CrossRef]
Masoodi, R. , Languri, E., and Ostadhossein, A., 2013, “Dynamics of liquid rise in a vertical capillary tube,” Journal of Colloid and Interface Science, 389, p. 268–272. [CrossRef]
J. Szekely, A.W. Neumann, Y.K. Chuang, J. Colloid Interface Sci. 35 (2) (1971) 273–278.
N. Fries, Capillary Transport Processes in Porous Materials – Experiment and Model, Cuvillier Verlag Göttingen, 2010.
Płociniczak, Ł, and Świtała, M., 2018, “Monotonicity, oscillations and stability of a solution to a nonlinear equation modelling the capillary rise,” Physica D 362, p. 1–8.
Nehad Ali Shah, Abdelhalim Ebaid, Tosin Oreyeni & Se-Jin Yook (2023) MHD and porous effects on free convection flow of viscous fluid between vertical parallel plates: advance thermal analysis, Waves in Random and Complex Media. a. [CrossRef]
Zeeshan; Ahammad, N. A.; Shah, N.A.; Chung, J.D.; Attaullah; Rasheed, H.U. Analysis of Error and Stability of Nanofluid over Horizontal Channel with Heat/Mass Transfer and Nonlinear Thermal Conductivity. Mathematics 2023, 11, 690. [CrossRef]
Souhar, K. , Kriraa, M., Bammou, L., Alami, S., Bouchgl, J., Feddaoui, M., & Aniss, S. (2017). Convecting Threshold in Nanofluid Driven By Centrifugal Forces In A Rotating Annular Hele-Shaw. Computational Thermal Sciences: An International Journal, 9, 49-62. [CrossRef]
Yagoubi, M. , Aniss, S. Effect of vertical quasi-periodic vibrations on the stability of the free surface of a fluid layer. Eur. Phys. J. Plus 132, 226 (2017). [CrossRef]
Souhar, K. , Aniss, S. Effect of Coriolis force on the thermosolutal convection threshold in a rotating annular Hele-Shaw cell. Heat Mass Transfer 48, 175–182 (2012). [CrossRef]
Moon, P. , and Spencer, D. E., 1988, Field Theory Handbook, Including Coordinate Systems, Differential Equations and Their Solutions, 2nd ed., Springer Verlag, New York, pp. 1–48.
Alassar, R. S. , and El-Gebily, M. A., 2009, “Inviscid Flow Past two Cylinders,” ASME J. Fluids Eng., 131(5), p. 054501. [CrossRef]
Arfken, G. , Mathematical Methods for Physicists. Academic Press, London, 1970.
Alassar, R. S. , 2017, “Slip Flow in Eccentric Annuli,” ASME J. Fluids Eng., 139(4), p. 041201.
Fries, N. , and Dreyer, M., 2009, “Dimensionless scaling methods for capillary rise,” Journal of Colloid and Interface Science, 338, p. 514–518. [CrossRef]
MacDonald, D. A. , 1982, “Fully Developed Incompressible Flow Between Non-Coaxial Circular Cylinders,” J. Appl. Math. Phys. (ZAMP), 33(6), pp. 738–751. [CrossRef]

Figure 1. Oscillations of capillary rise.

Figure 2. Problem configuration.

Figure 3. Velocity profile for the case

r_{1} / r_{2} = 1 / 4

and

ε = 1 / 2

Figure 3. Velocity profile for the case

r_{1} / r_{2} = 1 / 4

and

ε = 1 / 2

Figure 4. Critical

\sqrt{\frac{128 \cos θ}{G a B o}}

for monotone rise.

Figure 4. Critical

\sqrt{\frac{128 \cos θ}{G a B o}}

for monotone rise.

Figure 5. Maximum

r_{2}

to maintain monotone rise for water at

20^{\circ}

Figure 5. Maximum

r_{2}

to maintain monotone rise for water at

20^{\circ}

Figure 6. Equilibrium heights at maximum

r_{2}

which maintain monotone rise for water at

20^{\circ}

Figure 6. Equilibrium heights at maximum

r_{2}

which maintain monotone rise for water at

20^{\circ}

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Oscillation of a Liquid Column in an Eccentric Annulus

Abstract

1. Introduction

2. Velocity Profile

3. Capillary Rise

4. Conclusions

Funding

Acknowledgments

Conflicts of Interest

Ethical approval

Availability of data and materials

Authors’ contributions

Nomenclature

References

MDPI Initiatives

Important Links

Subscribe