Prerpints.org logo
Preprint
Article

Task Dependent Comfort Zone, a Base Placement Strategy for Mobile Manipulators based on Manipulability Measures

Altmetrics

Downloads

333

Views

88

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

09 August 2024

Posted:

13 August 2024

You are already at the latest version

Alerts
Abstract
The present contribution introduces the task dependent comfort zone as a base placement strategy for mobile manipulators using different manipulability measures. Four different manipulability measures depending on end-effector velocities, forces, stiffness, and accelerations are considered. By evaluating a discrete subspace of the manipulator workspace with these manipulability measures and by using image processing algorithms, a suitable goal position for the autonomous mobile manipulator was defined within the comfort zone. This always ensures a certain manipulator manipulablity value with a lower limit in respect to the maximum possible manipulability in the discrete subspace. Results are shown for three different mobile manipulators using the velocity dependent manipulability measure in a simulation.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

Mobile manipulators, which combine a mobile base platform and a serial manipulator, are becoming increasingly popular in various applications due to their flexibility and adaptability when operating in diverse environments [1,2].
To ensure their efficient and reliable operation, it is crucial to choose movement algorithms that take into account the unique characteristics of both the mobile platform and the serial manipulator. While researchers work on combining base and manipulator movement [3], also physical limitations of mobile manipulators have to be considered. Mobile platform movement of wheeled mobile robots is imprecise in comparison to the movement of serial manipulators due to friction and slip between wheel and ground contact [4]. Furthermore, a safety-related reduction of velocity further highlights the need to study a division of a mobile manipulator into two subsystems. Combining their movements can lead to inaccurate positioning and potentially hazardous situations and much more complexity in the system. In this paper a simplified approach, as opposed to a holistic one, is used to find a suitable position for the mobile platform that allows for efficient and safe manipulation while ensuring optimal performance of the mobile platform and the manipulator. The combination of a mobile robot platform with a manipulator results often in a degree of freedom (DOF) greater than six and must be described as a robotic system with kinematic redundancy [5,6] for a certain task in three dimensional space where a DOF of six would be sufficient. However, the inherent complexities and uncertainties in these systems pose several challenges in realizing their full potential.
Different from conventional, stationary industrial robots which have often a DOF equal to six, redundant robots, as described above, can move while the position and orientation of the end-effector (EE) are fixed. Another advantage of such kinematically redundant systems is collision avoidance, while the EE follows a specific path [7]. Therefore, such systems can be used for technically difficult dexterity tasks, such as grasping inside a tube or picking between two walls. The workspace of a stationary industrial robot is not only limited by the arm length but also by the allowed joint torques. The placement of a robotic manipulator base has to be done adequate to the task which should be fulfilled by the robotic system. For mobile manipulators, this is even more challenging since the base of the robot manipulator can be moved. This also brings the possibility to change the manipulator base for each task in respect to the task constraints. A human worker knows by nature how to operate during different tasks. He utilizes his arm redundancy to take a comfortable arm position [8]. For example, soldering on a printed circuit board will be done with bent elbows in front of the body with a certain distance to ensure a good view. This position allows the worker optimal handling of tools. One could name this the ’human work comfort zone’ for this specific task. Modern mobile robots can be equipped with collaborative manipulators to fulfill different tasks as e.g. pick and place or transportation. This type of manipulator is specially designed to be used beside humans and to cooperate with human workers. However with some additional restrictions to speed, force and torque of these mobile platforms, they can be called collaborative mobile manipulators (see ISO15066 and ISO10218).
The selection of a suitable path and a suitable path goal for a mobile manipulator is a crucial aspect of its operation, as it directly affects the robot’s ability to perform tasks and its overall manipulability. In recent years, various approaches have been proposed in the literature to determine the optimal path for mobile manipulators.
For example [9,10,11] divides the problem and separates the mobile manipulator into two independent subsystems: the mobile base and the mounted serial manipulator. The authors of [12,13] use a different approach to combine the mobile base and the manipulator into one system with a higher number of DOF, well-known and often used sampling-based planners are used in multiple variations within this approach. Sampling based planners like the Rapidly-exploring Random Tree (RRT) [14], the Probabilisitic Road Map (PRM) [15] and the Expansive-Spaces Tree planner (EST) [16] or any of their variants (RRT-Connect, RRT-GoalBias, Informed RRT,...) have been used due to their ability to handle high-dimensional spaces. Those types of planners have been utilized for mobile manipulators where the entire system is treated as a single high DOF system during the planning process. Other types of planners minimize a certain cost function; Covariant Hamiltonian Optimization for Motion Planning (CHOMP) [17] and Stochastic trajectory optimization for Motion Planning (STOMP) [18] algorithms are often used in the robotics motion planning framework MoveIt [19]. Those planners use cost functions with various constraints like EE position and orientation as well as joint torques, joint limits and distance to obstacles (for collision avoidance).
As already mentioned by the authors before, finding an appropriate goal position for a mobile robot that satisfies a specific task is a challenging problem in robotics. The goal position has not only to be reachable by the robot, but must also meet limitations such as e.g. avoiding obstacles. To find an optimal solution, multiple factors such as the robot’s kinematic and dynamic properties, environment, and task requirements must be considered. In [20], Sandakalum et al. give a comprehensive review of the current state-of-the-art path planning of mobile manipulators as well as in determining the mobile base goal position in general. To find a suitable goal position of the mobile base and as well as a goal configuration of the mounted manipulator, two different approaches should be mentioned: Firstly, the concept of a reachability map [21] uses the reachable workspace of a mounted serial manipulator. Secondly, the so-called capability map by Zhang et al. [22,23]. This capability map uses the distribution of the manipulability, based on Yoshikawa [24], in Cartesian space to guide the base placement of manipulators [25].
In a previous work we defined the comfort zone as a region in the n-dimensional discrete joint space [26]. Each point in the so defined comfort zone represents a certain joint configuration and fulfills a multi-objective optimization including various manipulability measures (velocity, force, and stiffness dependent). Furthermore, these points are constrained with minimum/maximum velocities, forces, and stiffness. This was shown for a planar mobile robot with two translational and three rotational joints as used in Figure 1.
In this paper we propose a further method to determine a zone of possible base positions (task dependent comfort zone) for a mobile manipulator that can be used with various individual manipulability measures, such as velocity, force, acceleration, and stiffness. Using these manipulability measures, we are able to evaluate the specific demands of different tasks and determine a zone of base positions (on a plane in Cartesian space) that can accommodate these demands. The capability of staying within this task dependent comfort zone ensures that the mobile manipulator can perform tasks effectively and efficiently, while also taking into account the need for high-speed movements, large forces, high accelerations, or high stiffness. Our results provide a comprehensive evaluation of the robot’s ability to perform tasks and offer specific guidelines for selecting appropriate base placement strategies. This enables task dependent autonomous positioning of the mobile manipulator in a variety of applications. The proposed method will be shown within an example task using different types of mobile manipulators, including different serial manipulator configurations and DOF.
This paper is organized as follows: In Section 2 the Jacobian matrix is introduced and the various manipulability measures used to evaluate the robot’s performance for different tasks are described. The measures include velocity, force, acceleration, and stiffness dependent measures based on different already established approaches. Section 3 incorporates the manipulability measures into the proposed method to determine the task dependent comfort zone, which represents a zone of possible positions for the mobile on a plane in Cartesian space. Section 4 describes the evaluation of the proposed method using various mobile manipulators and arm configurations. Finally, the last section summarizes our findings and provides suggestions for future work.

2. Manipulability Measures

In this chapter, we focus on different concepts of manipulability measures. These measures are often related to fixed-mounted industrial robots. In literature different measures to characterize the movement capabilities of manipulators are discussed. Specifically, here we present an overview of manipulability measures, which are quantitative metrics used to evaluate the robot’s ability to perform a specific task, based on velocities, forces, stiffness, and acceleration. Those measures will be later used to define the task dependent comfort zone for mobile manipulators. The geometrical interpretation, so-called manipulability ellipsoids, of those measures used on force, velocity, stiffness, and dynamic manipulability measures can be seen in Figure 1. Here, for a two-dimensional case, a planar mobile robot with two translational and three rotational joints is used and results in this case in four manipulability ellipsis.

2.1. Jacobian Matrix

The Jacobian matrix is a fundamental tool in the analysis and control of serial manipulators, serving as a representation of the relationship between the joint velocities and the EE velocity. Furthermore, it has important properties that can be leveraged to develop the manipulability measures used in this paper. The kinematic relation between the joint velocities
q ˙ = d q d t = q ˙ 1 q ˙ 2 … q ˙ n T ∈ R n
and the EE velocities
ξ ˙ = d ξ d t = ξ ˙ 1 ξ ˙ 2 … ξ ˙ m T ∈ R m
is described by the manipulator Jacobian matrix J ( q ) ∈ R m × n with
ξ ˙ = ∂ ξ ∂ q ︸ J ( q ) ∂ q ∂ t = J ( q ) q ˙
and
J ( q ) = ∂ f 1 ∂ q 1 ∂ f 1 ∂ q 2 … ∂ f 1 ∂ q n ⋮ ⋮ ⋱ ⋮ ∂ f m ∂ q 1 ∂ f m ∂ q 2 … ∂ f m ∂ q n .
The EE velocity ξ ˙ includes linear and angular velocities, so the Jacobian matrix
J ( q ) = J T ( q ) J R ( q )
can be separated into a translational part J T , relating to the contribution of the joint velocities to the EE linear velocities, and a rotational part J R , relating to the contribution of the joint velocities to the EE angular velocities. Moreover, the Jacobian matrix is used to map EE forces to joint forces and torques [27]. Let τ q denote the vector of joint torques for revolute joints and forces for prismatic joints. The principle of virtual work can be described by
δ W τ q = τ q T δ q
for the configuration space and
δ W f EE = f EE T δ ξ = f EE T ∂ ξ ∂ q ∂ q ,
for the task space, with δ q being the virtual displacements of the robot’s joints and δ ξ being a virtual displacement of the EE. The virtual work in joint space and task space has to be equal,
δ W τ q = δ W f EE .
Thus Eq. (6) and Eq. (7) can be reformulated to
δ q T ( τ q − J T f EE ) = 0 .
Finally the mapping between joint torques and EE forces can be written as
τ q = J T f EE .

2.2. Velocity Manipulability Measure

Yoshikawa [24] uses the manipulator Jacobian to calculate a manipulability measure. This manipulability measure shows the ability for the robot’s end-effector to move with a velocity in a certain direction. The calculation of those measurements uses the idea of manipulability ellipsoids [28]. It also represents a distance to a singular joint configuration. If the joint rates satisfy | | q ˙ | | = 1 , this assumes a unit sphere in the n-dimensional joint-velocity space. This unit joint-velocity condition can be written as
q ˙ T q ˙ = 1 ,
and by the use of Eq. (3) we get
( J − 1 ξ ˙ ) T J − 1 ξ ˙ = ξ ˙ T J − T J − 1 ξ ˙ = ξ ˙ T ( J J T ) − 1 ξ ˙ = 1 .
If J has full rank, the matrix J J T is square, symmetric and positive definite.
For any symmetric and positive definite matrix J J T , the set of vectors ξ ˙ which satisfy Eq. (12), defines an ellipsoid in the m dimensional space. Furthermore, the volume of such an ellipsoid in the used EE task space [29] can be used as manipulability measure which further can be defined as
m v ( q ) = det ( J J T ) .
For the case m = n , which means J is a square matrix this relation simplifies to
m v ( q ) = ∥ det ( J ) ∥ ,
which will not further be considered. The velocity manipulability measure in Eq. (13) is proportional to the volume of the velocity ellipsoid [24,30], whose semi-axes correspond to the square roots of the eigenvalues of A v = J J T and are pointing into the direction of the eigenvectors of A v . Near a singular configuration, the velocity ellipsoid is increasingly compressed. In the singularity it collapses thereby the distance to a singularity can also be evaluated. For the two dimensional example in Figure 1 it becomes a line. The velocity ellipsoid shown gives a quantitative measure of the ability of the EE to move in any direction. Larger values of m v represent greater freedom for the movement of the EE in the specific configuration [7].

2.3. Force Manipulability Measure

Similarly, the attainable forces and moments of the EE can be represented by the so-called force ellipsoid [7,28,31]. If the joint torques satisfy | | τ q | | = 1 , this assumes a unit sphere in the n-dimensional joint-torque space. This unit joint-torque condition can be written as
τ q T τ q = 1 .
With the substitution of Eq. (10) in Eq. (15)
( J T f EE ) T J T f EE = 1 f EE T J J T f EE = 1
similar results as in the calculation of Eq. (13) can be obtained. With the resulting matrix A f = ( J J T ) − 1 the so called force ellipsoid can be calculated. The shape of this ellipsoid is defined by the eigenvalues and eigenvectors of A F = ( J J T ) − 1 . The eigenvectors pointing in the same direction as those of A v (the velocity ellipsoid) the Eigenvalues are reciprocal to those of the velocity ellipsoid. With the calculated quadratic matrix A f the force manipulability measure m f with
m f = det ( A f ) = det ( ( J J T ) − 1 )
can be calculated.

2.4. Stiffness Manipulability Measure

Ajoudani et al. [32] and Chen et al. [33] discuss the Cartesian stiffness of modern industrial manipulators depending on their joint configuration and the normal stiffness performance measure. Basics regarding stiffness calculations of articulated rigid-body systems can be found in the work of Kövecses [34]. For a discussion of joint stiffness identification, see Dumas et al. [35]. Since the stiffness (in general K ) or compliance C = K − 1 must also be taken into account when using collaborative manipulators, the following section uses a measure of the Cartesian stiffness K c of the EE. The joint stiffness k i with i = 1 , . . . , n of each joint is collected in a joint stiffness matrix
K q = k 1 0 0 0 ⋱ 0 0 0 k n .
Busson et al. [36] uses joint compliance and the theory of virtual work to describe the mapping between EE and joints. Sallsbury [37] shows how to calculate the Cartesian stiffness by the usage of the joint stiffness matrix K q and the manipulator Jacobian J ( q ) by following a generalization of the linear spring relationship F spring = k spring Δ x with Δ x describing a change in length of a linear spring element. Using the compliance, the virtual displacement and by substitution of
δ q = C q τ q ,
δ ξ = C x f EE
in
δ ξ = J δ q
results in
C x f EE = J C q τ q .
After the substitution of Eq. (10) in (22) one obtains
C x f EE = J C q J T f EE
and with the elimination of forces and by usage of the relation between stiffness and compliance, the Cartesian stiffness matrix can be calculated as
K x = ( J K q − 1 J T ) − 1 ,
which can be further reformulated as
K x = J − T K q J − 1 .
Here, additional terms depending on EE forces and torques will be neglected [35]. The Cartesian stiffness described in Eq. (24) can also be represented as an ellipsoid [32,38]. Eigenvalues λ of K x correspond to the length of the semi-axes and can be used to characterize the stiffness of the manipulator in a particular configuration. Here as a representation for the manipulator stiffness the smallest eigenvalue of the Cartesian stiffness matrix
m st ( q ) = min ( eig ( K x ) )
will be used as a stiffness measure.

2.5. Dynamic Manipulability Measure

The previous discussed manipulability measures only use system kinematics to evaluate the manipulability of the robotic system. The dynamic manipulability measure first defined by Yoshikawa [39] in 1985 was used by Chiacchio and Concilio [40] in 1998 to define a new dynamic manipulability ellipsoid for redundant manipulators. This new formulation of the manipulability ellipsoid is used to evaluate the manipulator capabilities in terms of task space acceleration and to define a dynamic manipulability measure. For a full overview we will present the calculations for this formulation in a short form in the following section. Differentiating Eq. (3) with respect to time leads to
ξ ¨ = a = J ( q ) q ¨ + J ˙ ( q ) q ˙ .
The manipulator dynamics can be written as
τ q = B ( q ) q ¨ + C ( q , q ˙ ) q ˙ + f fric + τ q COM + J f EE ,
where τ q ∈ R n is the vector of n joint torques, f EE ∈ R m is the vector of m EE forces, B ∈ R n × n is the inertia matrix, C ∈ R n × n includes the Coriolis and centrifugal terms and τ q COM is the vector of gravitational force terms. For a manipulator in a given configuration and without the EE interacting with its environment, we consider joint speed q ˙ = 0 , the friction force f fric = 0 and the external forces f EE = 0 . Using the proposed simplifications, and combining the robot dynamics with Eq. (27) and solving for ξ ¨ leads to
ξ ¨ = J B − 1 τ − J B − 1 τ q COM .
Using a scaling matrix T max with the maximum joint torques
T max = diag ( τ 1 max , ⋯ , τ n max ) and the inertia matrix B , the matrix
Q = ( T max − 1 B ) T T max − 1 B
can be introduced. Combining the results and using a pseudo inverse, the weighted Jacobian matrix is
J Q + = Q − 1 J T ( J Q − 1 J T ) − 1
and the dynamic manipulability ellipsoid can be defined as
( ξ ¨ + J B − 1 τ q COM ) T ( J Q + ) T Q J Q + ( ξ ¨ + J B − 1 τ q COM ) ≤ 1 .
By using the core of Eq. (32) this results in the definition of the dynamic acceleration matrix
N = ( J Q + ) T Q J Q + .
Calculating the eigenvalues of the matrix N , a dynamic manipulability measure can be defined as
m a ( q ) = min ( eig ( N ) ) ,
which represents the minimal eigenvalue of the dynamic acceleration matrix in the certain joint configuration.
In the next chapter, we use the manipulability measures ( m v , m f , m st , m a ), based on force, velocity, stiffness, and acceleration, discussed here and summarized in Table 1 to develop a method for defining the task dependent comfort zone of a mobile manipulator, taking into account different task requirements. The resulting task dependent comfort zone will provide more specific guidelines for selecting appropriate base placement strategies, ultimately improving the robot’s ability to perform tasks. Later, we define the term manipulability measure m x ( q ) with x ∈ { v , f , st , a } in general for any measure that can evaluate a particular manipulator joint configuration by a scalar value.

3. Task Dependent Comfort Zone

In our previous work the comfort zone was defined by combining the manipulability measures with help of a multi-objective optimization [26]. In this approach with a multi-objective optimization the problem rises that the used measures are related, and in some cases are inversely proportional. Here a different approach is considered to increase the variable usability of the proposed algorithm by choosing one measure at a time. However, care was taken to retain the possibility of performing a combination of the used measures.

3.1. Task Classification

In modern industrial environments the number and the need for human-robot interaction and thereby collaborative tasks continues to increase. Thus, tasks can be classified regarding requirements on the robotic system [41]. As humans we can classify tasks regarding forces to our body arising from interactions with the environment. This can be done due to our great and fast sensory capabilities and by learning how to interact with the environment [42]. To classify a robotic task, many different approaches are possible. For example, the motion constraints and the total force/torque acting on the system could be used [43]. In Table 2 we show a selection of tasks and try to classify them according to their velocity, force, stiffness, and acceleration requirements as to then choose the suitable manipulability measure for a certain task. Of course, these are just general examples and the specific requirements for each task will depend on the details of the task. It shows that our concept of task dependent comfort zone can be extended by using a different manipulability measure. Depending on the task, a directional manipulability measure [44] may be preferable as opposed to the more general approach discussed in Section 2.2.

3.2. Motivation

For any mobile manipulator, which is a combination of mobile robot platform and serial manipulator, the p + m joint variables can be separated as
q = [ q P , q M ] T = [ q P 1 , q P 2 , ⋯ , q P p , q M 1 , q M 2 , ⋯ , q M m ] T ,
where p is the number of joints of the mobile platform and m is the number of joints of the serial manipulator. Any pose of a mobile robot platform on a plane can be described with a three-dimensional vector
p = ( x P , y P , θ P ) ∈ R × R × [ 0 , 2 π ) ,
x P and y P are the coordinates and θ P is the rotation around the local z-axis of the mobile robot. The pose of the EE of a robot manipulator can be described with
ξ EE = [ x EE , ϕ EE ] T = [ x EE , y EE , z EE , ϕ x , EE , ϕ y , EE , ϕ z , EE ] T ,
with ϕ EE standing for the description of the orientation. We use Euler angles with rotation around ( x , y , z )-axis and x EE is the position of the EE. This can also be expressed by using the homogeneous transformation matrix T EE . The problem is now to find feasible placements for the mobile base P = ( p 1 , ⋯ , p n p ) with p i = ( x P , y P , θ P ) ∈ R × R × [ 0 , 2 π ) ∀ i ∈ 1 , 2 , 3 , ⋯ , n p where the EE can achieve the desired pose described by the homogeneous transformation matrix T des . The manipulation of an object located on a desk is used to motivate the used algorithm. The task focuses on a fast velocity of the EE. Thus in this description only the velocity dependent manipulability measure will be taken into account. This task can be seen in a lot of standard industrial applications as well as in the rules of the RoboCup@Work competition [45]. The schematic drawing shown in Figure 2a shows the principle of the task setup.
The pose of the object is described by the desired pose vector ξ EE , des = [ x EE , des , ϕ EE , des ] T and will further on be used as the starting point to calculate the task dependent comfort zone for a suitable mobile base placement. Note that the calculation of the manipulability measures does not include the joints of the mobile platform , because excluding the platform joints allows to reserve this degree of freedom for navigation within the designated comfort zone and the orientation of the platform is often influenced by external factors, such as spatial constraints.

3.3. Recommended Workspace

While using a serial link structured robotic manipulator with rotational joints, the values for the minimal and maximal EE ( x , y ) -coordinates,
x EE , min / max and y EE , min / max , are dependent of the desired z position. A subspace of the manipulators workspace where all positions and all orientations of the EE can be achieved is called recommended or dexterous workspace. To achieve all orientations ϕ EE , des of the EE, the desired position P EE , des = [ x EE , des , y EE , des , z EE , des ] T should be inside the recommended workspace of the robotic manipulator.
The workspace boundaries and workspace characterization of serial manipulators have been extensively researched [7,46,47,48]. Here, for simplification the outer limits of the recommended workspace for serial link manipulators are described by a triaxial ellipsoid as an approximation with
( x − x M , Base ) 2 a 2 + ( y − y M , Base ) 2 b 2 + ( z − z M , Base ) 2 c 2 = 1 ,
parameters a,b,c beeing the length of the three half axis which are specific to the used serial manipulator and the origin of the serial robot manipulator base frame is
P M , Base = [ x M , Base , y M , Base , z M , Base ] T .
Not reachable points within this simplified workspace are exclueded while calculating the proposed comfort zone.
By varying the ( x , y ) -positions of the mobile platform while holding the desired position of the EE fixed in the world frame, the configuration of the robotic manipulator can be changed. This set of configurations will be searched to find the comfort zone for the mobile manipulator. To find the inequality constraint equation for a point inside the recommended workspace, a plane is used to cut recommended workspace ellipsoid Eq. (38) at point P des with varying ( x , y ) -coordinates and a fixed z-coordinate. Therefore, this plane in its normal form is
x · n 0 = P EE , des · n 0
with n 0 = [ 0 , 0 , 1 ] T is said to be parallel to the ( x , y )-plane and results in
z = z EE , des .
Combining Eq. (38) and Eq. (41), an ellipse parallel to the ( x , y ) -plane, with its center at the point P M , Base
E EE ( x , y ) : = x 2 a 2 ( 1 − z EE , des 2 c 2 ) + y 2 b 2 ( 1 − z EE , des 2 c 2 ) = 1
and the axes lengths
a ^ = a 2 ( 1 − z EE , des 2 c 2 )
b ^ = b 2 ( 1 − z EE , des 2 c 2 )
can be found. Using the boundary condition
x 2 a ^ + y 2 b ^ ≤ 1
defined by the ellipse in Eq. (42), a set of points P EE ∈ R 2 can be calculated. This set includes all points which can be reached by the EE while the mobile base is placed at the point P M , Base and can be defined as
P EE = P EE ( x , y ) ∈ R 2 ∣ x 2 a ^ + y 2 b ^ ≤ 1 .
Using the desired EE position P EE , des and all points P EE ∈ P EE , a new set
P Base = P Base ∈ R 2 ∣ P Base ( x , y ) = P EE ( x , y ) + P EE , des ∀ P EE ( x , y )
of feasible base positions can be found. Assuming a planar movement in the ( x , y ) -plane of the mobile base and due to Eq. (41), z Base is set to be zero and will further be neglected. Each element in the new set P Base represents a suitable position of the mobile base to ensure the desired EE position P des using different manipulator joint configurations. By evaluation of the continuous set P Base with discrete values for x = x ^ and y = y ^ with
x ^ = [ x min , x min + Δ x , ⋯ , x max − Δ x , x max ]
and
y ^ = [ y min , y min + Δ x , ⋯ , y max − Δ x , y max ]
the discrete set
P ^ Base = P ^ Base , i ( x ^ , y ^ ) ∈ P Base
with n Base points can be found. Figure 2b shows an exemplary set of n Base = 460 feasible positions for a mobile base with a mounted serial manipulator. The discrete set of points P ^ Base is used to find a subset, defined as task dependent comfort zone (see Eq. (54)) for mobile manipulator placement. Thereby different manipulability measures m v ( q ) , m f ( q ) , m st ( q ) , m a ( q ) , as described in the previous sections are used to evaluate the corresponding joint configuration for each point in the discrete set.

3.4. Manipulability Measure Norm, Combination, and Constrains

In order to obtain equal weighting of the different measures and to set suitable boundary conditions the measures are normed with the help of the minimum and maximum values out of a set of possible points P ^ Base . The used manipulability measure m x can be normalized into a range 0 ≤ m ^ x ≤ 1 using f Norm ( m x ) = m ^ x with
f Norm ( m x , i ) = m x , i − m x , min m x , max − m x , min ,
m x , max is the maximum and m x , min is the minimum value out of the given set of manipulability measures. This is shown by an example in Figure 3a. Furthermore the measures can be combined using a weighted sum with
m ^ c , i = k v m ^ v , i + k f m ^ f , i + k st m ^ st , i + k a m ^ a , i , ∀ i ∈ 0 , 1 , ⋯ , n Base ,
where 0 ≤ k x ≤ 1 with x ∈ { v , f , st , a } and k v + k f + k st + k a = 1 to maintain normalization.

3.5. Comfort Zone Definition

The discrete set of points P Base can be constrained into a feasible zone by using constraints for the manipulability measure
m ^ x , low ≤ m ^ x , i ≤ m ^ x , up ,
where m ^ x , low and m ^ x , up are the lower and upper constraints for each individual measure ( m ^ v , m ^ f , m ^ st , m ^ a , m ^ c ). By using these constraints, a zone of possible base positions can be defined. The defined task dependent comfort zone A zone for mobile manipulators with
A zone = { P zone ( x , y ) ∈ R 2 ∣ P zone , i ( x , y ) ⊂ P ^ Base ∧ ( m ^ x , low ≤ m ^ x , i ≤ m ^ x , up ) ∀ i = [ 1 , ⋯ , n Base ] }
includes all points P zone such that the corresponding joint configuration and its manipulability measure fulfills the set constraints as shown in Figure 3b.

3.6. Comfort Zone Mesh Representation and Target Points

With the use of the discrete points defined by the comfort zone Eq. (54) a square mesh as shown in Figure 4a is built. For simplification and to avoid further computational effort with more precise discretization, the mean value out of 4 corner points for each square is used to interpolate the manipulability measure inside one square. We assume that in this square around each point no unfeasible solution in manipulator configuration will arise. The whole region is now used as a feasible goal for the mobile base.
Nevertheless, a defined point to aim for is needed and therefore we use the mesh representation and transform it into pixel coordinates where each square (center point) will be represented by an individual pixel. The resulting image, shown in Figure 4b will then be used for further investigations with image processing algorithms from scikit-image1, an image processing algorithm collection in Python [49] and OpenCV2, a library of Python bindings designed to solve computer vision problems. The following algorithms are used in three steps to determine a possible goal position inside the comfort zone: Firstly, the identification of possible disconnected areas by using the scikit-image function label [50]. Secondly, the comparison of the resulting areas with the scikit-image function regionprops [51] and, lastly, we use the OpenCV functions distanceTransform [52] and minMaxLoc for finding the centerpoint and radius of the largest possible inscribed circle, see Figure 5.
Figure 5 also shows that only the largest area found will be considered in further investigation. Therefore, other points which fulfill the manipulability constraints will be neglected even when the highest manipulability can be found outside the proposed comfort zone. Using the center of the largest possible inscribed circle in the comfort zone increases the robustness and enables to move around within this zone without a substantial loss of manipulability.

4. Comfort Zone Simulation Examples

We want to show the usage of the comfort zone for a given pick task and also that the approach can be applied to different types of mobile manipulators. All used mobile manipulators (the Stanford Robotics Platform, LeoBot, and Kairos) are equipped with a holonomic mobile base to achieve an omnidirectional movement. Each of these bases supports different types of serial manipulators. The results of this evaluation will provide insight into the practical usefulness of the proposed approach and its ability to offer specific guidelines for selecting appropriate base placements for different mobile manipulators. For the simulations a discrete workspace with a discretization of Δ x = Δ y = 0.05 m and Δ z = 0.01 m , is used. The region of interest is a subdomain of the manipulators workspace. Therefore, a cuboid with 1.6 × 1.6 × 0.4 m , as shown in Figure 6, is used. The simulation examples are using either a desired EE pose ξ EE , des = [ x EE , des , ϕ EE , des ] T , or a desired EE position x EE , des = [ x EE , des , y EE , des , z EE , des ] T where the orientation of the EE is not considered in the inverse kinematics calculation. For serial manipulators with a defined number of inverse kinematics solutions (UR5, PUMA) all feasible solutions (in terms of self-collision between manipulator and base) can be checked, for the Panda a numerical calculation of the inverse kinematics is used, so only one solution is checked. Also, within the shown results only either translational or rotational parts of the Jacobian matrix are considered while calculating the manipulability measures. Using the full Jacobian matrix would lead to problems as discussed in [53]. Thereby the usage of the full Jacobian matrix has been shown to have no physical consistency due to the fact that the rotational and translational part have different physical units. All the simulations and calculations are done using Python and the flexible multibody systems framework Exudyn [54] 3. In the simulation examples, the inverse kinematics algorithm ikine_LMS according to Levenberg-Marquadt with Sugihara´s tweak [55] from Peter Corke’s robotics toolbox [56] 4 was used.

4.1. Stanford Robotics Platform

The Stanford Robotics Platform, is a mobile manipulator with a Puma560 mounted on a base using four so-called powered caster modules [57]. In Figure 7b we show a 3D-CAD drawing as well as the kinematic chain. The Stanford Robotics Platformwas developed and built by the Stanford University Computer Science Department in year the 2000 [58] and combines a Unimate Puma560 manipulator with 6 rotational joints and Euler wrist configuration mounted on a Nomadic XR4000 holonomic mobile base. The Puma560 manipulator is widely used in research as an example for a classic 6 DOF serial manipulator. The kinematic chain and its parameter are well described in the literature [29,59,60]. The resulting system with 9 DOF is shown in Figure 7a including the mobile platform joints P 1 , P 2 , P 3 and the manipulator joints M 1 to M 6 .
In Figure 8 multiple possible placements for the mobile manipulator are shown. Both figures show the same results for pose and position while using the manipulability m v where only linear velocities are considered.
Figure 9 shows the results for m v based on only angular velocities whereby especially in Figure 9a the main purpose of the proposed comfort zone can be seen. Here the maximum value of the manipulability is outside the proposed comfort zone, therefore using this position leads to a lack of manipulability during operation for even a small movement of the mobile base. Using one of the proposed points (green), which are the centers of the maximum inscribed circles (light green), always leads to a manipulability of at least 65% of the maximum value.

4.2. Mobile Manipulator LeoBot

The mobile manipulator LeoBot [61], shown in Figure 10, uses Mecanum wheels for base motion with a mounted Franka Emika Panda 7 DOF serial manipulator. Figure 10a shows the kinematic chain of LeoBot which achieves in total 10 DOF, including the mobile platform joints P 1 , P 2 , P 3 and the manipulator joints M 1 to M 7 . The Franka Emika Panda is widely used in research and development and its parameters, including link masses, inertias and center of mass were recently investigated by researchers [62].
Figure 11 shows the results using m v based on linear velocities. Figure 11a shows that a mobile base placement at the proposed point (center of the maximal possible inscribed circle) gives the advantage to stay within a zone of minimum 30% manipulability even when the platform is moved. Also here the maximal manipulability is outside the comfort zone and a small movement there would lead to big loss in manipulability. The center points of all found inscribed circles would be feasible mobile platform goal positions with higher flexibility in base movement and ensures a solution for the inverse kinematics. A selection between them could be made by comparison of the individual manipulability of each point, but for all points here the manipulability is at least higher or equal than 30% of the maximum value.
Figure 12 shows the results using m v based on angular velocities. The mobile base placement at the proposed point (center of the maximal possible inscribed circle) gives a large zone of minimum 30% manipulability. The maximum value of manipulability is located outside of the comfort zone. So using that as a base goal position would quickly lead to a lack of manipulability.

4.3. Mobile Manipulator Kairos

The mobile manipulator Kairos from the company Robotnik5 combines a mobile base using Mecanum wheels with a mounted Universal Robot UR5 serial manipulator as shown in Figure 13. Figure 13a shows the kinematic chain of Kairos which achieves in total 9 DOF, including the mobile platform joints P 1 , P 2 , P 3 and the manipulator joints M 1 to M 6 . The Universal Robot UR5 manipulator is often used in medium sized companies as well as in research and development. Its parameters including link inertias can be found in [63,64].
Figure 14 shows the results using m v based on linear velocities. Figure 14a shows that a mobile base placement at the proposed point (center of the maximal possible inscribed circle) gives the advantage of staying within a zone of minimum 30% manipulability, even when the platform is moved. The maximum value of the manipulability is located outside the comfort zone. Hence, using this position, already a small movement of the mobile platform would lead to a manipulability lower than 30% of the maximal value and the same is also valid for Figure 14b.
Figure 15 shows the results using m v based on angular velocities. The mobile base placement at the proposed point (center of the maximal possible inscribed circle) gives a large zone of minimum 30% manipulability. In Figure 15b the maximum value of manipulability is located near the middle of the comfort zone. Here, a small area is excluded from the comfort zone, so a base movement into this area could lead to failure of the task- as the inverse kinematics could not find a solution for this example. The center points of all inscribed circles would be feasible mobile platform goal positions with higher flexibility in base movement and ensures a solution for the inverse kinematics. A selection between them could be made by comparison of the individual manipulability of each point, but for all points here the manipulability is at least higher or equal than 30% of the maximum value.
Figure 16 shows the mobile manipulator Kairos within a Python simulation. There, Exudyn (a C++ based Python framework for flexible multibody systems simulation) was used to simulate the mobile platform as well as the manipulator. The mobile platform and the manipulator links are represented by rigid bodies and the Mecanum wheels are modeled with a contact friction model based on the rolling disc as described in [4]. In Figure 16a the task starts and the comfort zone (possible mobile base goal placements) is drawn using red boxes. The height of each box corresponds to the used manipulability measure m v . Figure 16b shows the mobile manipulator within the pick task where the mobile base is already on its goal position.

5. Conclusions

In this work, we have presented a method to determine a zone of possible base positions, the so-called task dependent comfort zone, for mobile manipulators based on different manipulability measures. Our method takes into account the specific demands of different tasks, such as the need for high-speed movements, large forces, high accelerations, or heightened stiffness. To find a suitable goal position for a mobile manipulator we used discretization of the manipulator workspace and different image processing methods.
We evaluated our method in Python computation using different holonomic mobile manipulators. First, we used the Stanford Robotics Platform with a mounted Puma560 (6DOF, spherical wrist). Secondly, we used the mobile manipulator LeoBot with a mounted Franka Emika Panda (7DOF), and lastly, the mobile manipulator Kairos with a mounted Universal Robot UR5 (6DOF).
Our results showed that manipulability measures could be used to develop a task-dependent comfort zone for mobile manipulators, providing more specific guidelines for selecting appropriate mobile manipulator base placement strategies. In path planning algorithms, a fixed goal position for the mobile base is usually given, although in many cases the exact positioning of the platform is not as important as the goal of the manipulators end-effector.
Once, the task dependent comfort zone is calculated, it can help to find feasible mobile manipulator base positions in dynamically changing environments. Our study highlights the importance of considering manipulability measures when determining mobile manipulator base positions and shows the potential of our proposed method for use in practical applications. Future work could explore the use of our method within real-world scenarios to further evaluate its effectiveness. Thereby combining the concept of the task dependent comfort zone with a path planning algorithm to use it within the robot framework ROS should be considered. Especially a combination with the costmap2D algorithm [65] used in the ROS-Navigation stack. With help of this algorithm the proposed task dependent comfort zone could be included as an additional cost map layer to the ROS-Navigation stack [66].

Author Contributions

Conceptualization, M.S., P.M. and J.G.; methodology, M.S. and P.M.; software, M.S., P.M. and J.G.; validation, M.S.; formal analysis, M.S.; investigation, M.S.; resources, J.G.; writing—original draft preparation, M.S.; writing—review and editing, M.S., P.M. and J.G.; supervision, J.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding. We are grateful to all of those with whom we have had the pleasure to work with during this and other related projects. The RoboCup and LeoBot related work in this paper would not have been possible without the financial support of the

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Brandstötter, M.; Mirkovic, D.; Hofbaur, M. Mobile Manipulation – Eine altbekannte Technologie findet durch sensitive Robotertechnologie Einzug in die Industrie. C-AR2017 – Conference on Automation and Robotics, 2017, pp. 1–6.
  2. Sereinig, M.; Werth, W.; Faller, L.M. A review of the challenges in mobile manipulation: systems design and RoboCup challenges. e & i Elektrotechnik und Informationstechnik 2020. [CrossRef]
  3. Haviland, J.; Sünderhauf, N.; Corke, P. A Holistic Approach to Reactive Mobile Manipulation. IEEE Robotics and Automation Letters 2022, 7, 3122–3129. [CrossRef]
  4. Manzl, P.; Gerstmayr, J. An Improved Dynamic Model of the Mecanum Wheel for Multibody Simulations. Volume 9: 17th International Conference on Multibody Systems, Nonlinear Dynamics, and Control (MSNDC), 2021, International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. [CrossRef]
  5. Luca, A.D.; Oriolo, G.; Giordano, P.R. Kinematic modeling and redundancy resolution for nonholonomic mobile manipulators. Proceedings 2006 IEEE International Conference on Robotics and Automation, 2006. ICRA 2006., 2006, pp. 1867–1873. [CrossRef]
  6. Chiaverini, S. Singularity-robust task-priority redundancy resolution for real-time kinematic control of robot manipulators. IEEE Transactions on Robotics and Automation 1997, 13, 398–410. [CrossRef]
  7. Siciliano, B.; Khatib, O. Springer Handbook of Robotics; Springer Handbooks, Springer International Publishing, 2016.
  8. Zanchettin, A.M.; Rocco, P.; Bascetta, L.; Symeonidis, I.; Peldschus, S. Kinematic motion analysis of the human arm during a manipulation task. 2010, Vol. 2, pp. 1–6.
  9. Rastegarpanah, A.; Gonzalez, H.C.; Stolkin, R. Semi-Autonomous Behaviour Tree-Based Framework for Sorting Electric Vehicle Batteries Components. Robotics 2021, 10. [CrossRef]
  10. Saoji, S.; Rosell, J. Flexibly configuring task and motion planning problems for mobile manipulators. 2020 25th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), 2020, Vol. 1, pp. 1285–1288. [CrossRef]
  11. Castaman, N.; Pagello, E.; Menegatti, E.; Pretto, A. Receding Horizon Task and Motion Planning in Changing Environments. Robotics and Autonomous Systems 2021, 145, 103863. [CrossRef]
  12. Brock, O.; Kavraki, L. Decomposition-based motion planning: a framework for real-time motion planning in high-dimensional configuration spaces. Proceedings 2001 ICRA. IEEE International Conference on Robotics and Automation (Cat. No.01CH37164), 2001, Vol. 2, pp. 1469–1474 vol.2. [CrossRef]
  13. Su, J.; Xie, W. Motion Planning and Coordination for Robot Systems Based on Representation Space. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) 2011, 41, 248–259. [CrossRef]
  14. LaValle, S.M. Rapidly-exploring random trees : a new tool for path planning. The annual research report 1998.
  15. Kavraki, L.; Svestka, P.; Latombe, J.C.; Overmars, M. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Transactions on Robotics and Automation 1996, 12, 566–580. [CrossRef]
  16. Hsu, D.; Latombe, J.C.; Motwani, R. Path planning in expansive configuration spaces. Proceedings of International Conference on Robotics and Automation, 1997, Vol. 3, pp. 2719–2726 vol.3. [CrossRef]
  17. Ratliff, N.; Zucker, M.; Bagnell, J.A.; Srinivasa, S. CHOMP: Gradient optimization techniques for efficient motion planning. 2009 IEEE International Conference on Robotics and Automation, 2009, pp. 489–494. [CrossRef]
  18. Kalakrishnan, M.; Chitta, S.; Theodorou, E.; Pastor, P.; Schaal, S. STOMP: Stochastic trajectory optimization for motion planning. 2011 IEEE International Conference on Robotics and Automation, 2011, pp. 4569–4574. [CrossRef]
  19. Coleman, D.; Sucan, I.; Chitta, S.; Correll, N. Reducing the Barrier to Entry of Complex Robotic Software: a MoveIt! Case Study, 2014. [CrossRef]
  20. Sandakalum, T.; Ang, M.H. Motion Planning for Mobile ManipulatorsA Systematic Review. Machines 2022, 10. [CrossRef]
  21. Makhal, A.; Goins, A.K. Reuleaux: Robot Base Placement by Reachability Analysis. CoRR 2017, abs/1710.01328, [1710.01328].
  22. Zhang, H.; Sheng, Q.; Sun, Y.; Sheng, X.; Xiong, Z.; Zhu, X. A novel coordinated motion planner based on capability map for autonomous mobile manipulator. Robotics and Autonomous Systems 2020, 129, 103554. [CrossRef]
  23. Zhang, H.; Sheng, Q.; Hu, J.; Sheng, X.; Xiong, Z.; Zhu, X. Cooperative Transportation With Mobile Manipulator: A Capability Map-Based Framework for Physical Human–Robot Collaboration. IEEE/ASME Transactions on Mechatronics 2022, 27, 4396–4405. [CrossRef]
  24. Yoshikawa, T. Manipulability of Robotic Mechanisms. The International Journal of Robotics Research 1985, 4, 3–9.
  25. Zacharias, F.; Borst, C.; Hirzinger, G. Capturing robot workspace structure: representing robot capabilities. 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2007, pp. 3229–3236. [CrossRef]
  26. Sereinig, M.; Manzl, P.; Gerstmayr, J. Komfortzone mobiler Manipulatoren. Sechste IFToMM D-A-CH Konferenz 2020: 27./28. Februar 2020, Campus Technik Lienz; IFToMM D-A-CH., Ed., 2020, Vol. 2020. [CrossRef]
  27. Spong, M.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; Wiley, 2005.
  28. Lynch, K.M.; Park, F.C. Modern Robotics: Mechanics, Planning, and Control, 1st ed.; Cambridge University Press: USA, 2017.
  29. Corke, P. Robotics, Vision and Control: Fundamental Algorithms in MATLAB, 1st ed.; Springer Publishing Company, Incorporated, 2013.
  30. Jin-Oh Kim.; Khosla, K. Dexterity measures for design and control of manipulators. Proceedings IROS ’91:IEEE/RSJ International Workshop on Intelligent Robots and Systems, 1991, pp. 758–763 vol.2.
  31. Melchiorri, C. Force manipulability ellipsoids for general manipulation systems. IFAC Proceedings Volumes 1994, 27, 235 – 240. Fourth IFAC Symposium on Robot Control, Capri, Italy, September 19-21, . [CrossRef]
  32. Ajoudani, A.; Tsagarakis, N.G.; Bicchi, A. Choosing Poses for Force and Stiffness Control. IEEE Transactions on Robotics 2017, 33, 1483–1490.
  33. Chen, C.; Peng, F.; Yan, R.; Li, Y.; Wei, D.; Fan, Z.; Tang, X.; Zhu, Z. Stiffness performance index based posture and feed orientation optimization in robotic milling process. Robotics and Computer-Integrated Manufacturing 2019, 55, 29 – 40.
  34. Kövecses, J.; Angeles, J. The stiffness matrix in elastically articulated rigid-body systems. Multibody System Dynamics 2007, 18, 169–184.
  35. Dumas, C.; Caro, S.; Cherif, M.; Garnier, S.; Furet, B. Joint stiffness identification of industrial serial robots. Robotica 2012, 30, 649–659. [CrossRef]
  36. Busson, D.; Bearee, R.; Olabi, A. Task-oriented rigidity optimization for 7 DOF redundant manipulators. IFAC-PapersOnLine 2017, 50, 14588 – 14593. 20th IFAC World Congress, . [CrossRef]
  37. Salisbury, J.K. Active stiffness control of a manipulator in cartesian coordinates. 19th IEEE Conference on Decision and Control including the Symposium on Adaptive Processes, 1980, pp. 95–100.
  38. Guo, Y.; Dong, H.; Ke, Y. Stiffness-oriented posture optimization in robotic machining applications. Robotics and Computer-Integrated Manufacturing 2015, 35, 69 – 76.
  39. YOSHIKAWA, T. Dynamic Manipulability of Robot Manipulators. Transactions of the Society of Instrument and Control Engineers 1985, 21, 970–975. [CrossRef]
  40. Chiacchio, P.; Concilio, M. The dynamic manipulability ellipsoid for redundant manipulators. Proceedings. 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146) 1998, 1, 95–100 vol.1.
  41. El Makrini, I.; Merckaert, K.; De Winter, J.; Lefeber, D.; Vanderborght, B. Task allocation for improved ergonomics in Human-Robot Collaborative Assembly. Interaction Studies 2019, 20, 103–134. [CrossRef]
  42. Burdet, E.; Osu, R.; Franklin, D.W.; Milner, T.E.; Kawato, M. The central nervous system stabilizes unstable dynamics by learning optimal impedance. Nature 2001. [CrossRef]
  43. Khatib, O. A unified approach for motion and force control of robot manipulators: The operational space formulation. IEEE Journal on Robotics and Automation 1987, 3, 43–53. [CrossRef]
  44. Chen, H.; Lee, S.I.; Do, J.H.; Lee, J.M., Directional Manipulability to Improve Performance Index of Dual Arm Manipulator for Object Grasping. In Intelligent Autonomous Systems 12: Volume 1 Proceedings of the 12th International Conference IAS-12, held June 26-29, 2012, Jeju Island, Korea; Lee, S.; Cho, H.; Yoon, K.J.; Lee, J., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2013; pp. 595–602. [CrossRef]
  45. Kraetzschmar, G.K.; others. RoboCup@Work: Competing for the Factory of the Future. In RoboCup 2014: Robot World Cup XVIII; Springer International Publishing, 2015; pp. 171–182. [CrossRef]
  46. Abdel-Malek, K.; Yang, J. Workspace boundaries of serial manipulators using manifold stratification. The International Journal of Advanced Manufacturing Technology 2006, 28, 1211–1229. [CrossRef]
  47. Cao, Y.; Lu, K.; Li, X.; Zang, Y. Accurate Numerical Methods for Computing 2D and 3D Robot Workspace. International Journal of Advanced Robotic Systems 2011, 8, 76. [CrossRef]
  48. Patel, S.; Sobh, T. Task based synthesis of serial manipulators. Journal of Advanced Research 2015, 6, 479–492. [CrossRef]
  49. van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T.; the scikit-image contributors. scikit-image: image processing in Python. PeerJ 2014, 2, e453. [CrossRef]
  50. Fiorio, C.; Gustedt, J. Two linear time Union-Find strategies for image processing. Theoretical Computer Science 1996, 154, 165–181. [CrossRef]
  51. Jähne, B. Digital Image Processing 6th Edition; Springer Berlin, Heidelberg, 2005. [CrossRef]
  52. Felzenszwalb, P.; Huttenlocher, D. Distance Transforms of Sampled Functions. Theory of Computing 2004, 8. [CrossRef]
  53. Doty, K.L.; Melchiorri, C.; Schwartz, E.M.; Bonivento, C. Robot manipulability. IEEE Transactions on Robotics and Automation 1995, 11, 462–468.
  54. Gerstmayr, J. Exudyn – A C++ based Python package for flexible multibody systems. Multibody System Dynamics 2023. [CrossRef]
  55. Sugihara, T. Solvability-Unconcerned Inverse Kinematics by the Levenberg–Marquardt Method. IEEE Transactions on Robotics 2011, 27, 984–991. [CrossRef]
  56. Corke, P.; Haviland, J. Not your grandmother’s toolbox–the Robotics Toolbox reinvented for Python. 2021 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2021, pp. 11357–11363.
  57. Holmberg, R.; Khatib, O. Development and Control of a Holonomic Mobile Robot for Mobile Manipulation Tasks. The International Journal of Robotics Research 2000, 19, 1066–1074. [CrossRef]
  58. Chang, K.S.; Holmberg, R.; Khatib, O. The augmented object model: cooperative manipulation and parallel mechanism dynamics. Proceedings ICRA. IEEE International Conference on Robotics and Automation., 2000, Vol. 1, pp. 470 – 475 vol.1. [CrossRef]
  59. Corke, P.I. Visual Control of Robots: High-Performance Visual Serving; John Wiley amp Sons Inc.: USA, 1997.
  60. Kim, H.; Streit, D. Configuration dependent stiffness of the PUMA 560 manipulator: Analytical and experimental results. Mechanism and Machine Theory 1995, 30, 1269–1277. [CrossRef]
  61. Sereinig, M.; Manzl, P.; Hofmann, P.; Neurauter, R.; Pieber, M.; Gerstmayr, J. Omnidirectional Mobile Manipulator LeoBot for Industrial Environments, Developed for Research and Teaching. RoboCup 2022:; Eguchi, A.; Lau, N.; Paetzel-Prüsmann, M.; Wanichanon, T., Eds. Springer International Publishing, 2023, pp. 127–139. [CrossRef]
  62. Gaz, C.; Cognetti, M.; Oliva, A.; Robuffo Giordano, P.; De Luca, A. Dynamic Identification of the Franka Emika Panda Robot With Retrieval of Feasible Parameters Using Penalty-Based Optimization. IEEE Robotics and Automation Letters 2019, 4, 4147–4154. [CrossRef]
  63. Kebria, P.M.; Al-wais, S.; Abdi, H.; Nahavandi, S. Kinematic and dynamic modelling of UR5 manipulator. 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), 2016, pp. 004229–004234.
  64. Kovincic, N.; Müller, A.; Gattringer, H.; Weyrer, M.; Schlotzhauer, A.; Brandstötter, M. Dynamic parameter identification of the Universal Robots UR5. Proceedings of ARW & OAGM Workshop 2019. Verlag der Technischen Universität Graz, 2019, pp. 44–53. [CrossRef]
  65. Lu, D.V.; Hershberger, D.; Smart, W.D. Layered costmaps for context-sensitive navigation. 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2014, pp. 709–715. [CrossRef]
  66. Marder-Eppstein, E.; Berger, E.; Foote, T.; Gerkey, B.; Konolige, K. The Office Marathon: Robust navigation in an indoor office environment. 2010 IEEE International Conference on Robotics and Automation, 2010, pp. 300–307. [CrossRef]
1
https://scikit-image.org/ (accessed 03.08.2024)
2
https://docs.opencv.org/4.x/d6/d00/tutorial_py_root.html (accessed 03.08.2024)
3
https://github.com/jgerstmayr/exudyn (accessed 03.08.2024)
4
https://github.com/petercorke/robotics-toolbox-python (accessed 03.08.2024)
5
https://robotnik.eu/(accessed 03.08.2024)
Preprints 114790 g001
Figure 1. Geometrical representation of four different manipulability measures using a planar mobile manipulator with 5DOF.
Figure 1. Geometrical representation of four different manipulability measures using a planar mobile manipulator with 5DOF.
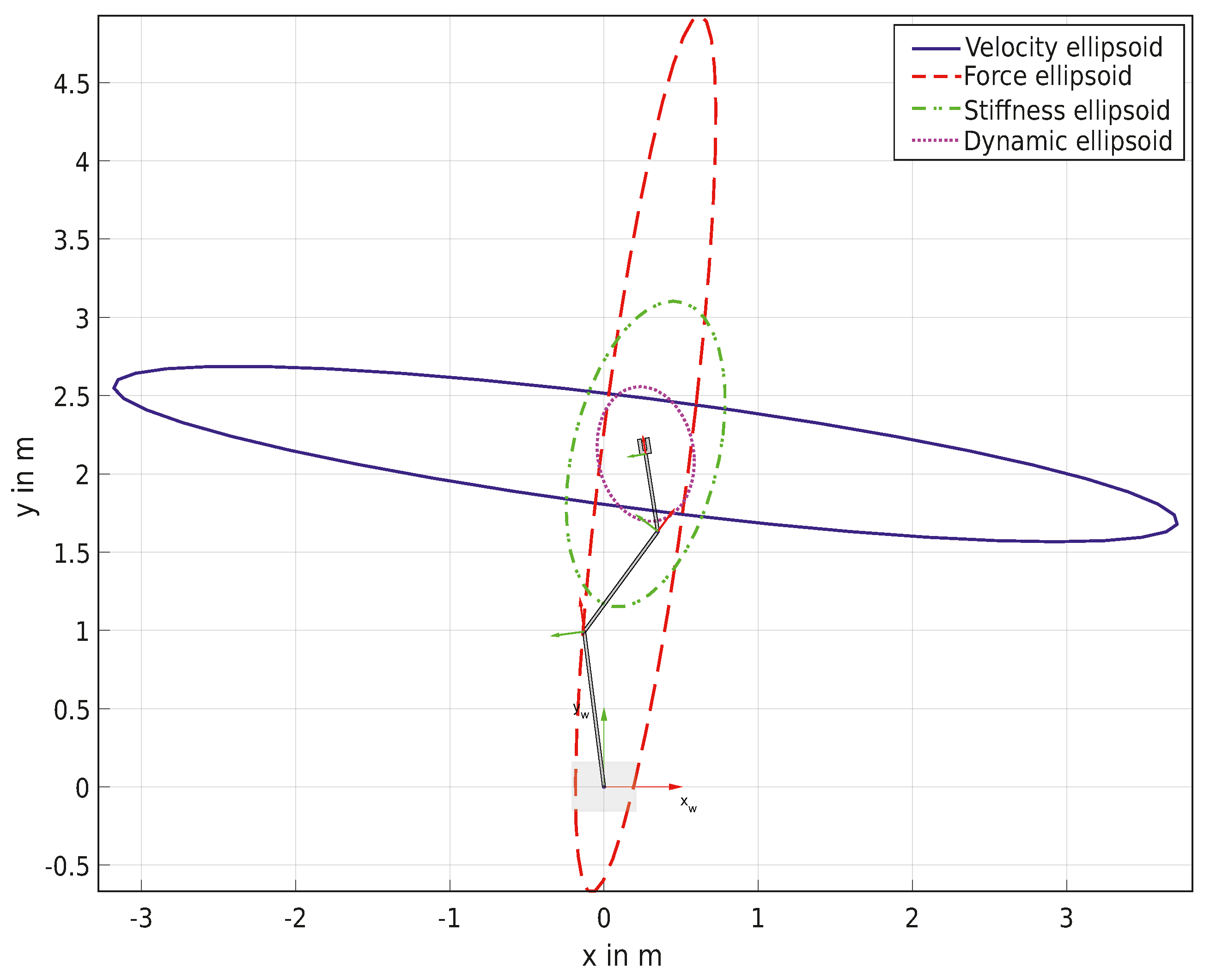
Preprints 114790 g001
Preprints 114790 g002
Figure 2. Schematic overview for a pick and place task (a). Feasible discrete base positions of a mobile manipulator (b).
Figure 2. Schematic overview for a pick and place task (a). Feasible discrete base positions of a mobile manipulator (b).
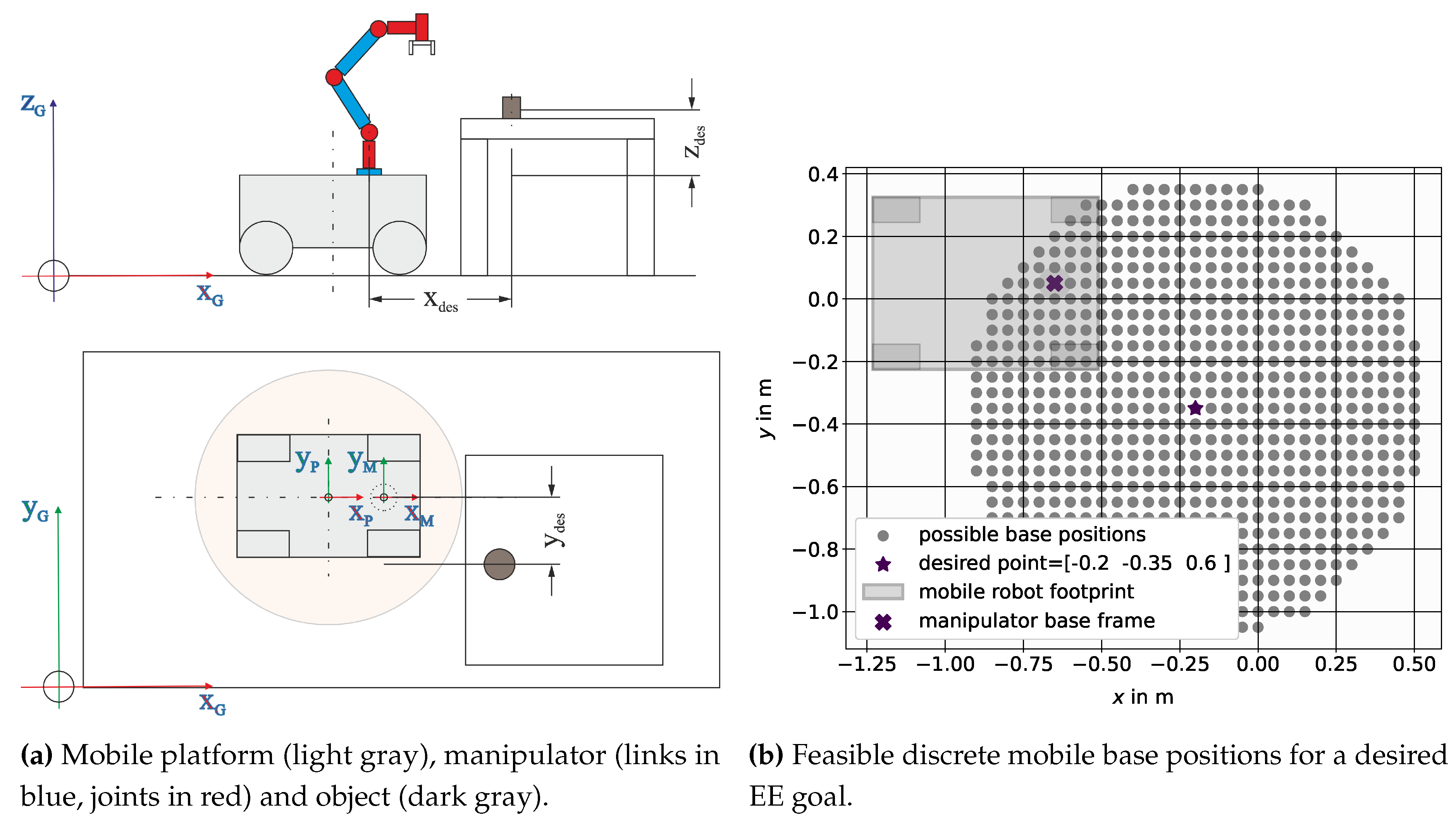
Preprints 114790 g002
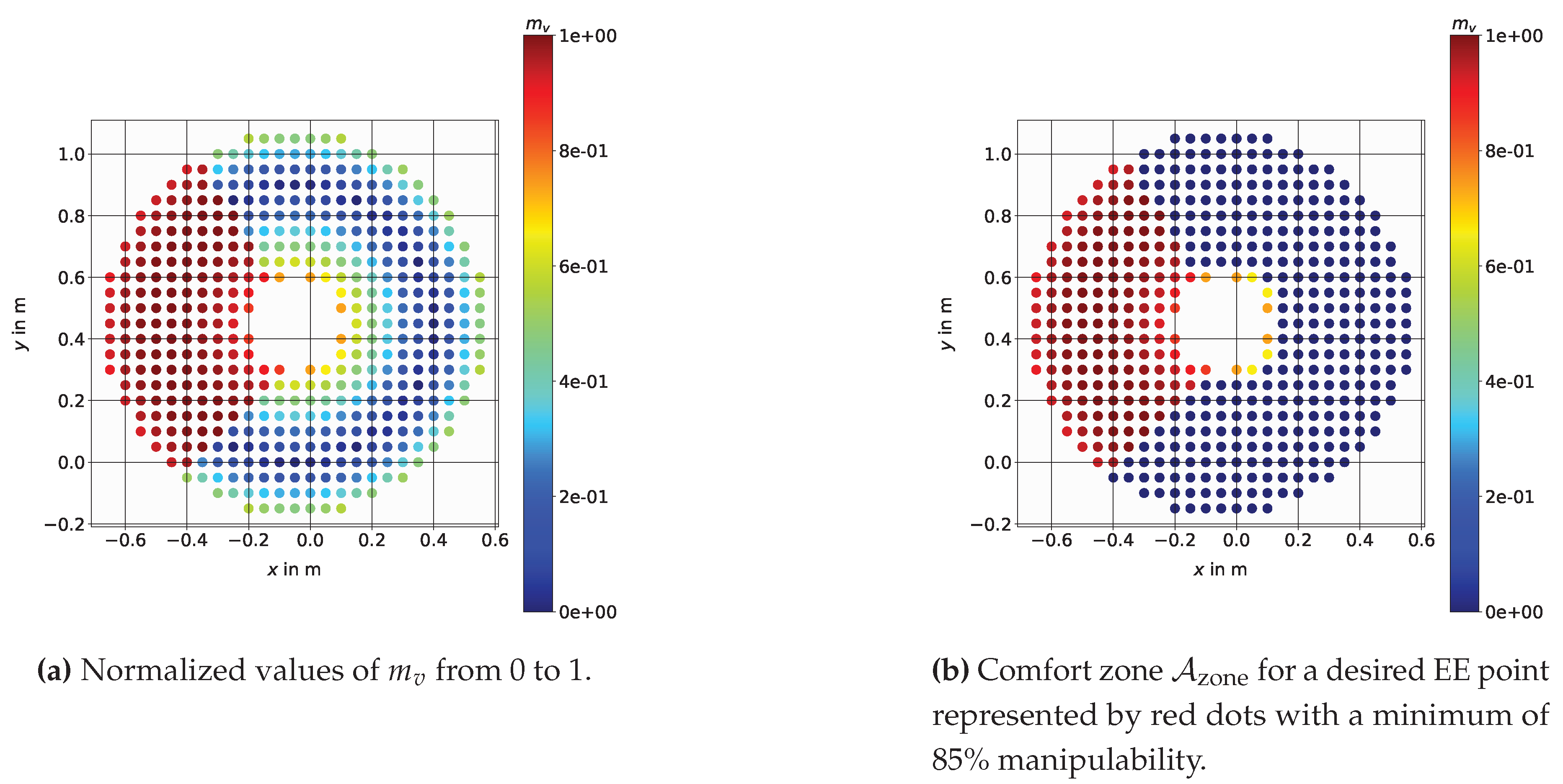
Preprints 114790 g003
Figure 3. Discrete point plot representation of feasible base position points for the Stanford Robotics Platform. Quality of points described by manipulability measure m v , red points have a high manipulability. Manipulability measure is dependent on the angular velocity of the EE for a desired EE pose ξ EE , des = [ − 0 . 05 , 0 . 45 , 0 . 65 , π 4 , 0 , − π 4 ] T .
Figure 3. Discrete point plot representation of feasible base position points for the Stanford Robotics Platform. Quality of points described by manipulability measure m v , red points have a high manipulability. Manipulability measure is dependent on the angular velocity of the EE for a desired EE pose ξ EE , des = [ − 0 . 05 , 0 . 45 , 0 . 65 , π 4 , 0 , − π 4 ] T .
Preprints 114790 g003
Preprints 114790 g004
Figure 4. Comfort zone example for the Stanford mobile manipulator, transformation to pixel representation. Each red/green square in (a) is transformed to a white pixel in (b) and represents a suitable mobile base position for the desired EE goal.
Figure 4. Comfort zone example for the Stanford mobile manipulator, transformation to pixel representation. Each red/green square in (a) is transformed to a white pixel in (b) and represents a suitable mobile base position for the desired EE goal.
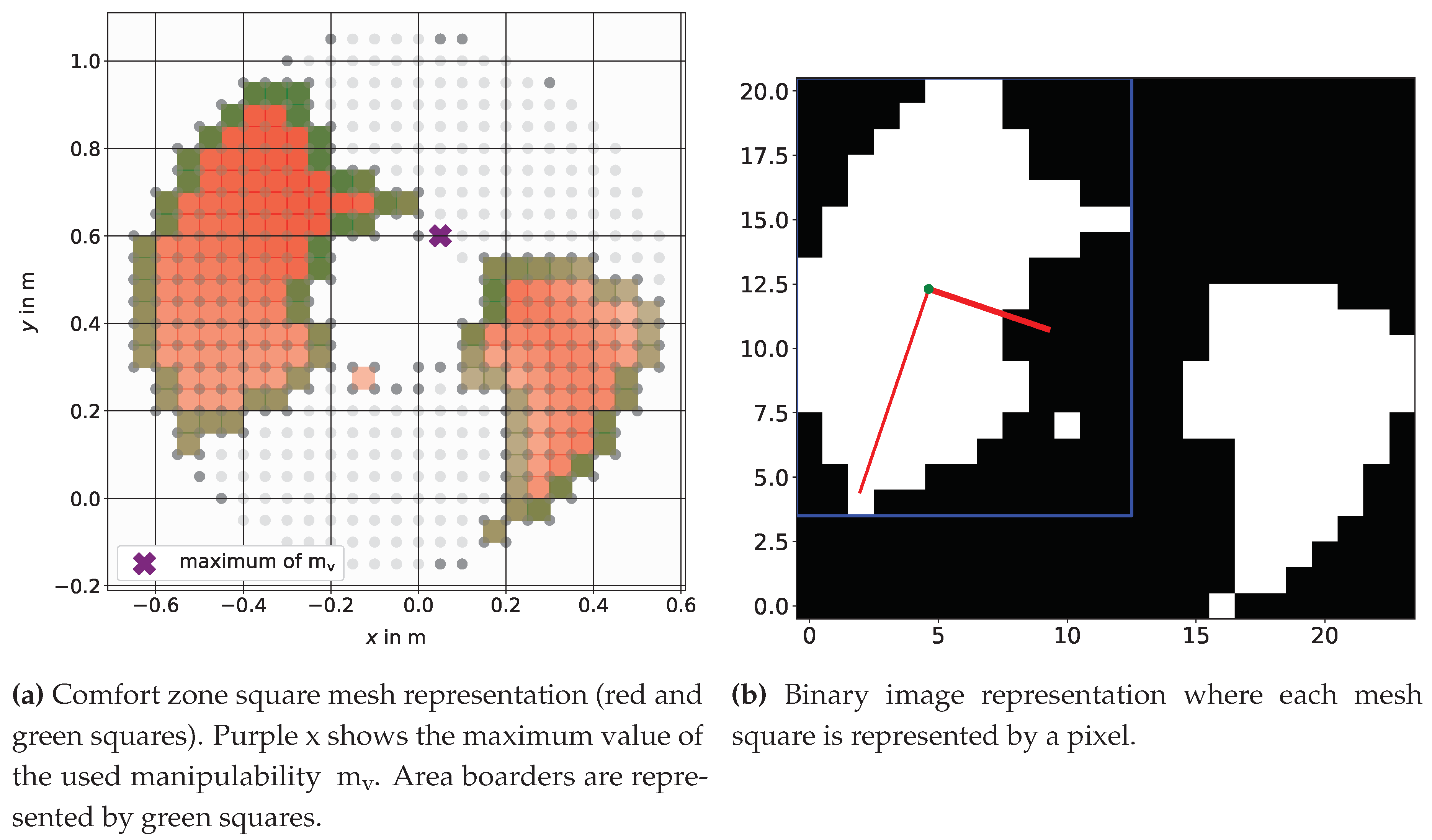
Preprints 114790 g004
Preprints 114790 g005
Figure 5. Comfort zone square mesh representation. Green circle represents the largest possible inscribed circle in the comfort zone with its center point marked in green. The maximum value of the used manipulability m v is marked in purple. Each red square represents a suitable mobile base position for the desired EE goal at z EE , des with at least 85% of the maximum manipulability.
Figure 5. Comfort zone square mesh representation. Green circle represents the largest possible inscribed circle in the comfort zone with its center point marked in green. The maximum value of the used manipulability m v is marked in purple. Each red square represents a suitable mobile base position for the desired EE goal at z EE , des with at least 85% of the maximum manipulability.
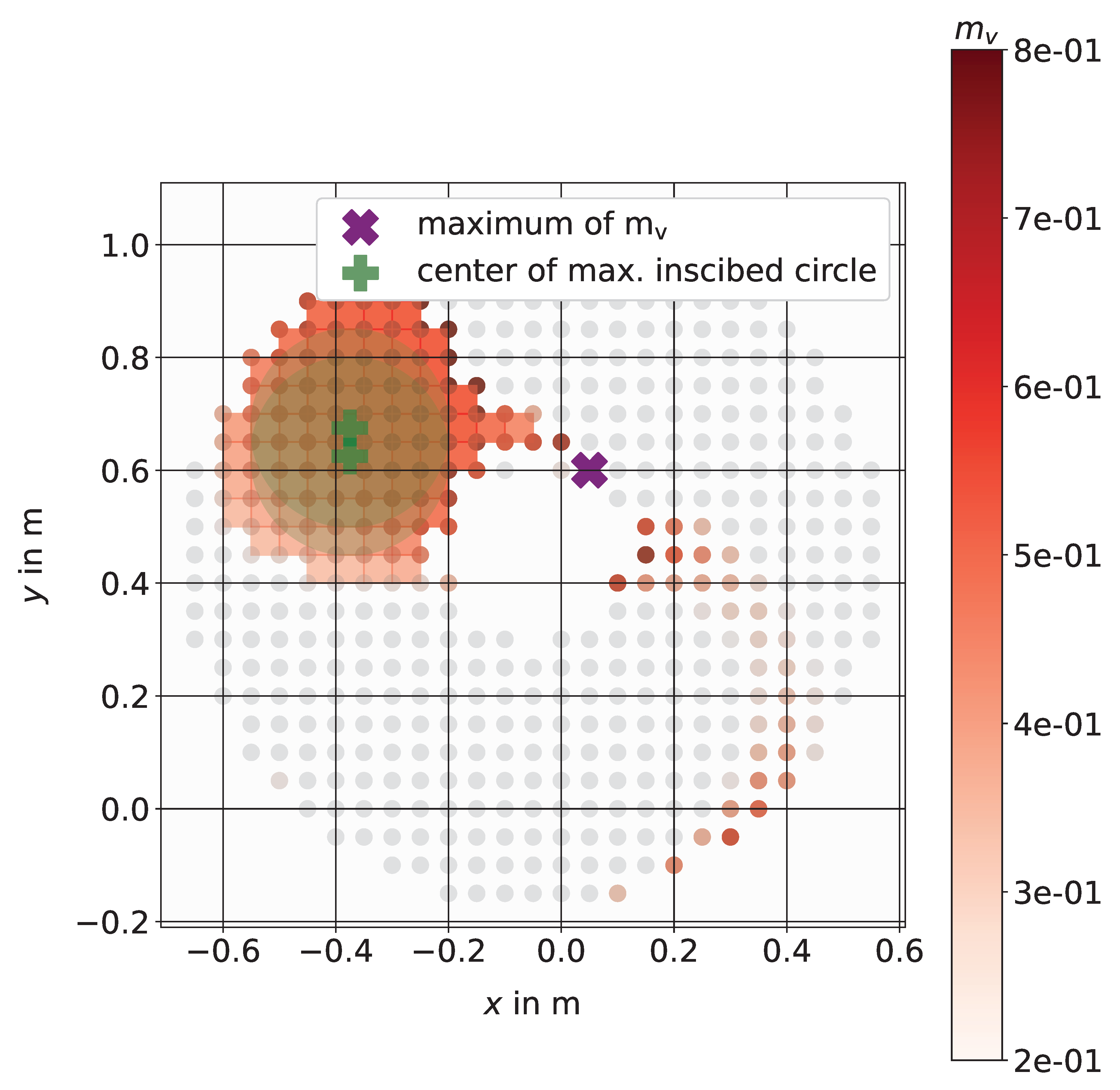
Preprints 114790 g005
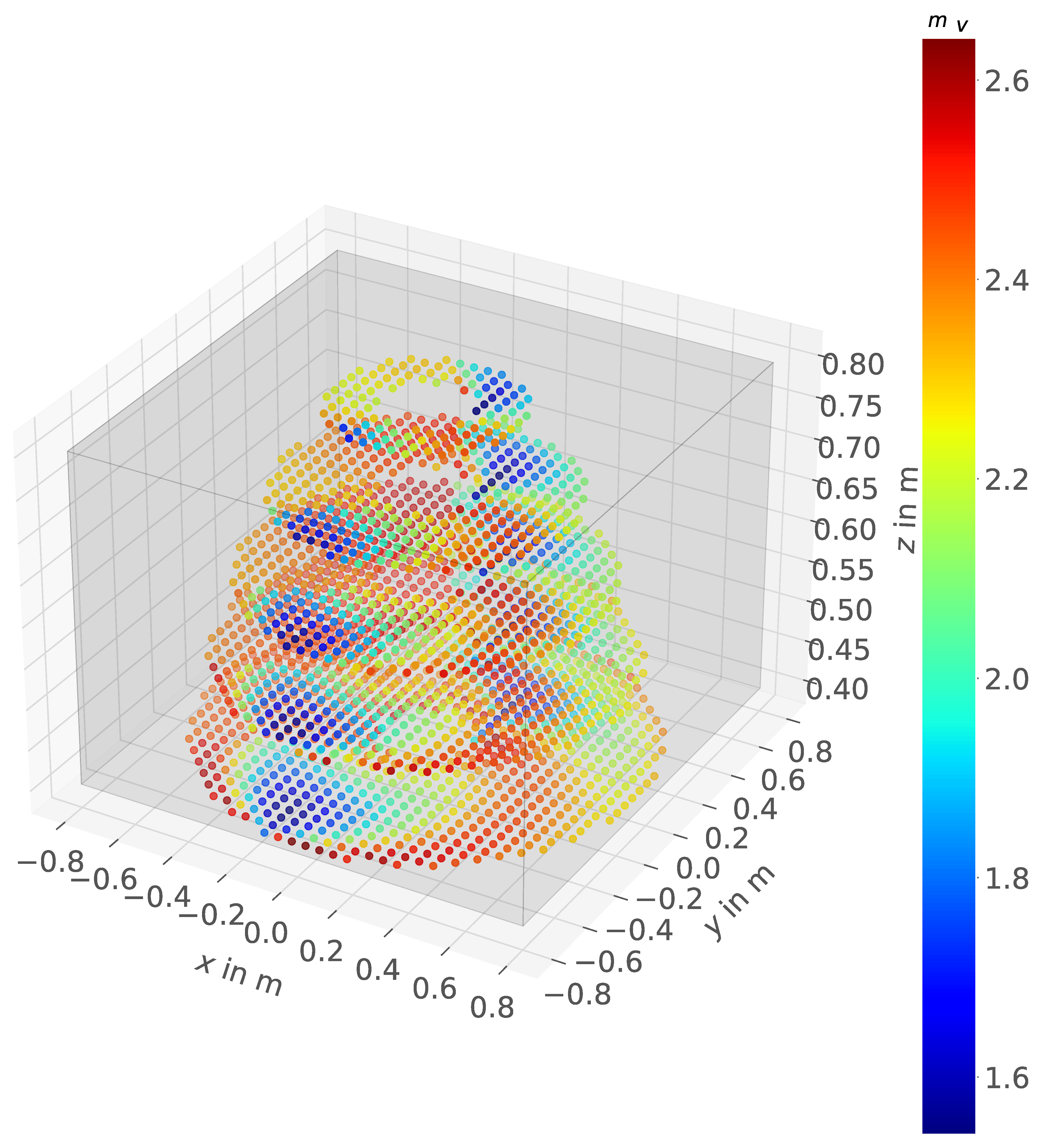
Preprints 114790 g006
Figure 6. Discrete subdomain of the Puma560 manipulator workspace shown as a grey cuboid. Evaluation of all discrete points regarding their manipulability m v (not normalized, Δ z = 0 . 05 ).
Figure 6. Discrete subdomain of the Puma560 manipulator workspace shown as a grey cuboid. Evaluation of all discrete points regarding their manipulability m v (not normalized, Δ z = 0 . 05 ).
Preprints 114790 g006
Preprints 114790 g007
Figure 7. Serial manipulator with 6 rotational joints mounted on a Nomadic XR4000 holonomic mobile base.
Figure 7. Serial manipulator with 6 rotational joints mounted on a Nomadic XR4000 holonomic mobile base.
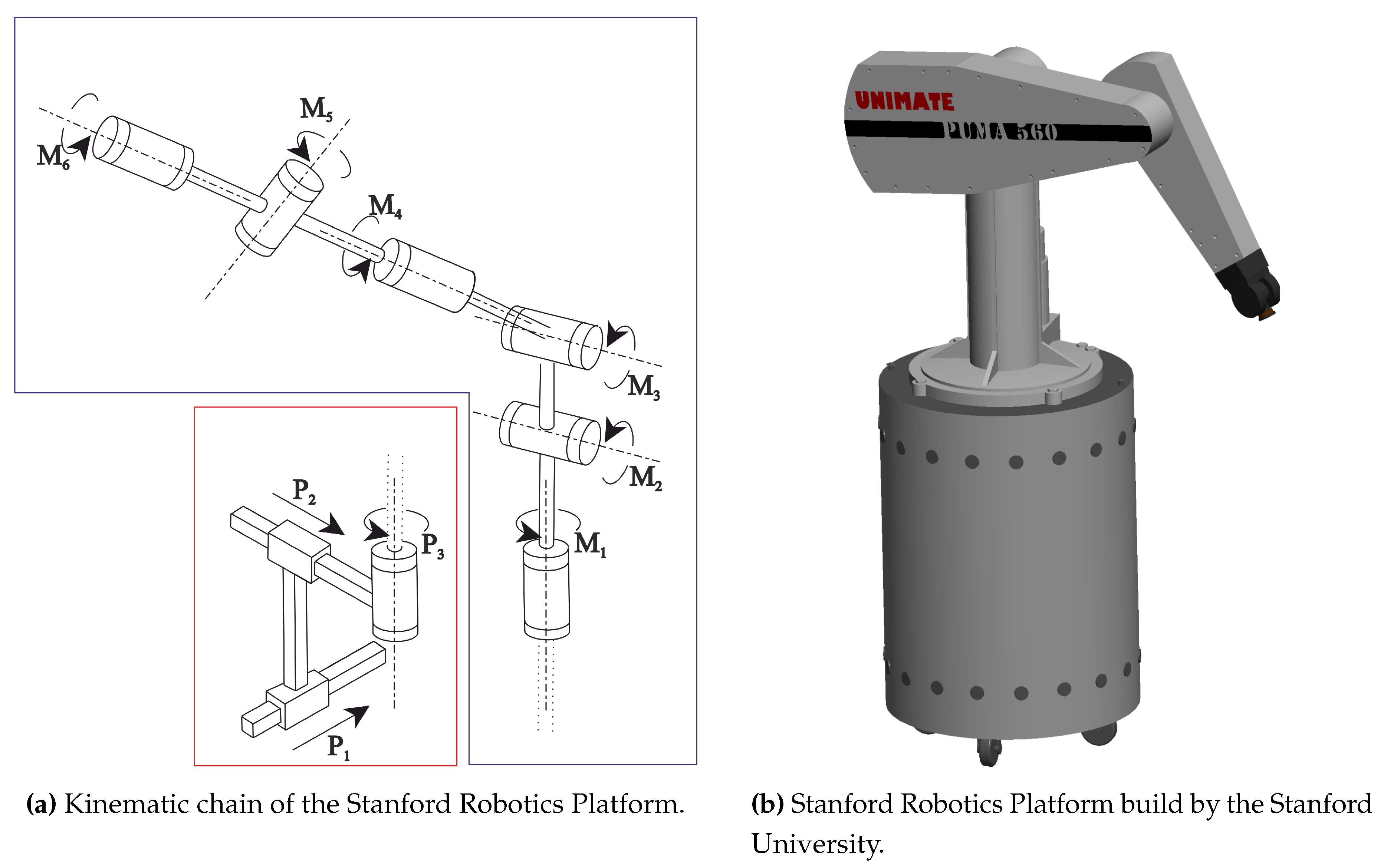
Preprints 114790 g007
Preprints 114790 g008
Figure 8. Comfort zone for the Stanford Robotics Platform using the linear velocity v dependent manipulability measure m v with a minimum of 65% manipulability for EE pose (a) and EE position (b).
Figure 8. Comfort zone for the Stanford Robotics Platform using the linear velocity v dependent manipulability measure m v with a minimum of 65% manipulability for EE pose (a) and EE position (b).
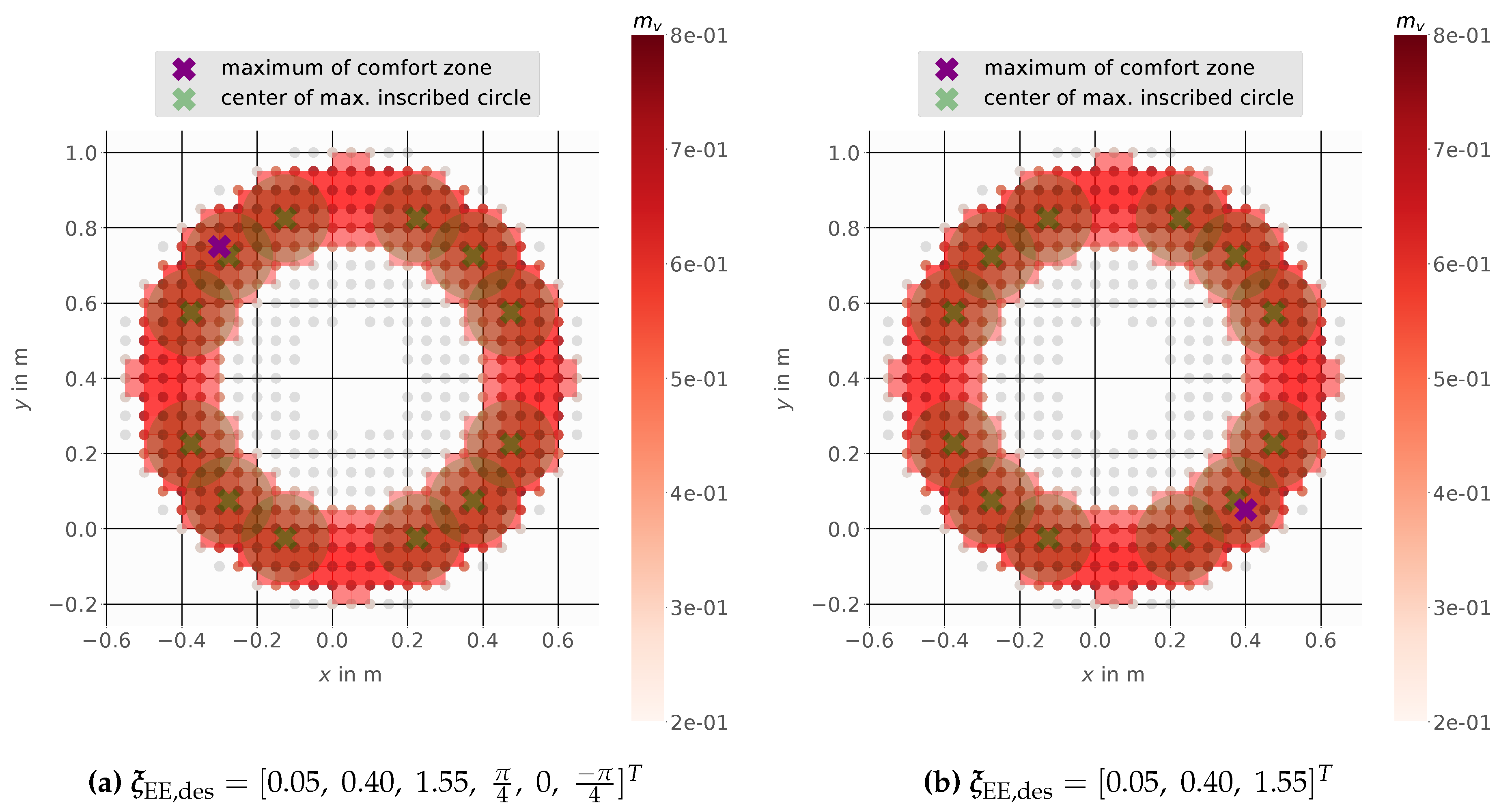
Preprints 114790 g008
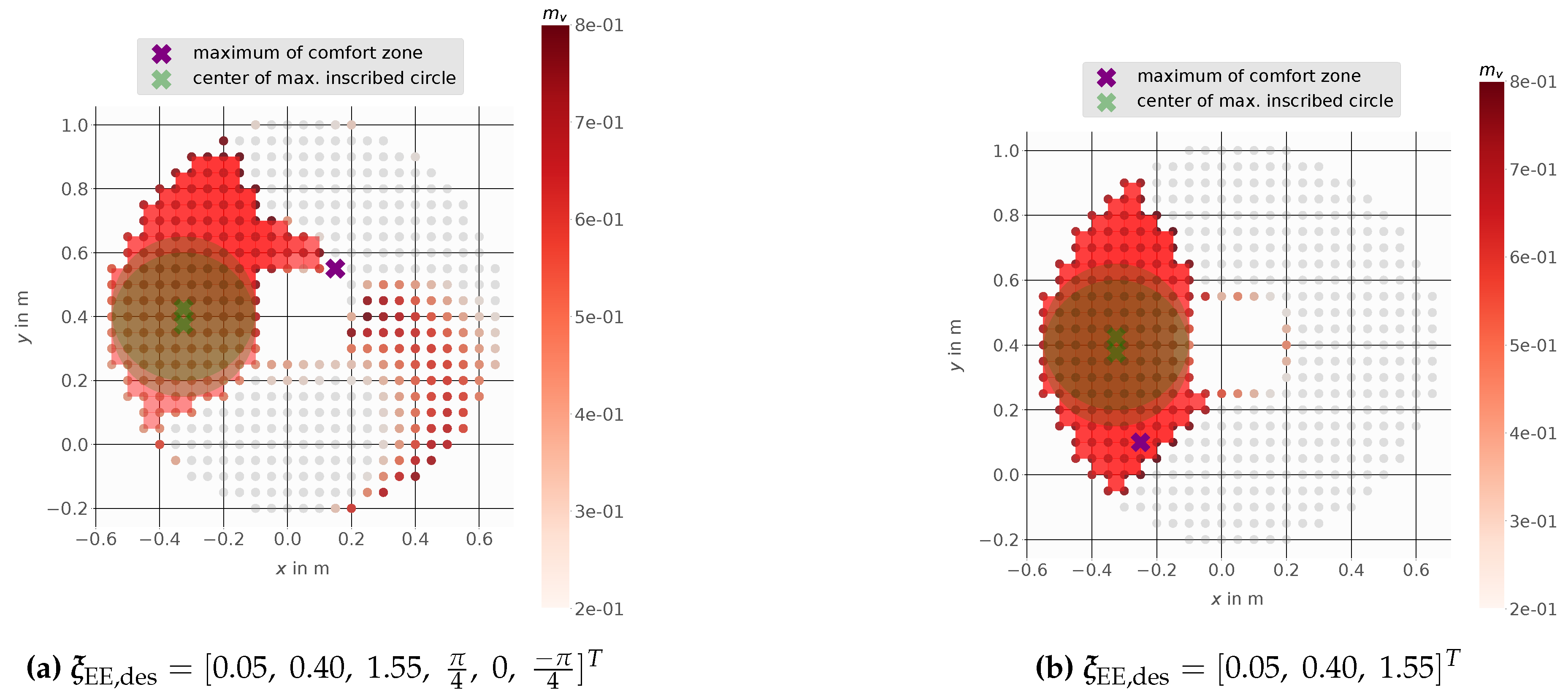
Preprints 114790 g009
Figure 9. Comfort zone for the Stanford Robotics Platform using the angular velocity ω dependent manipulability measure m v with a minimum of 65% manipulability for EE pose (a) and EE position (b).
Figure 9. Comfort zone for the Stanford Robotics Platform using the angular velocity ω dependent manipulability measure m v with a minimum of 65% manipulability for EE pose (a) and EE position (b).
Preprints 114790 g009
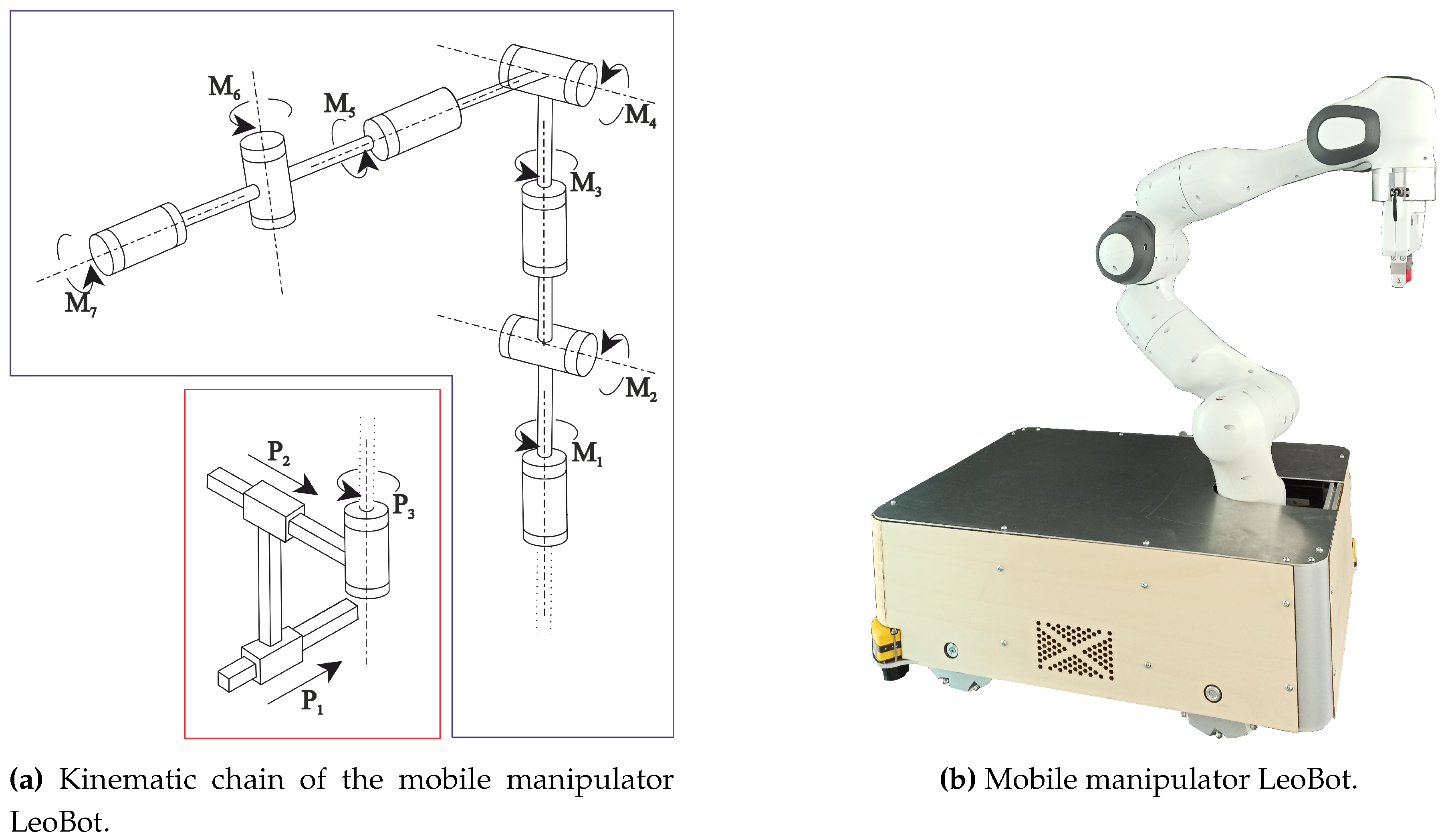
Preprints 114790 g010
Figure 10. LeoBot mobile manipulator developed and built by the Department of Mechatronics at the University of Innsbruck in year 2020. The mobile manipulator combines a Franka-Emika-Panda manipulator with 7 rotational joints mounted on a holonomic mobile base using Mecanum wheels.
Figure 10. LeoBot mobile manipulator developed and built by the Department of Mechatronics at the University of Innsbruck in year 2020. The mobile manipulator combines a Franka-Emika-Panda manipulator with 7 rotational joints mounted on a holonomic mobile base using Mecanum wheels.
Preprints 114790 g010
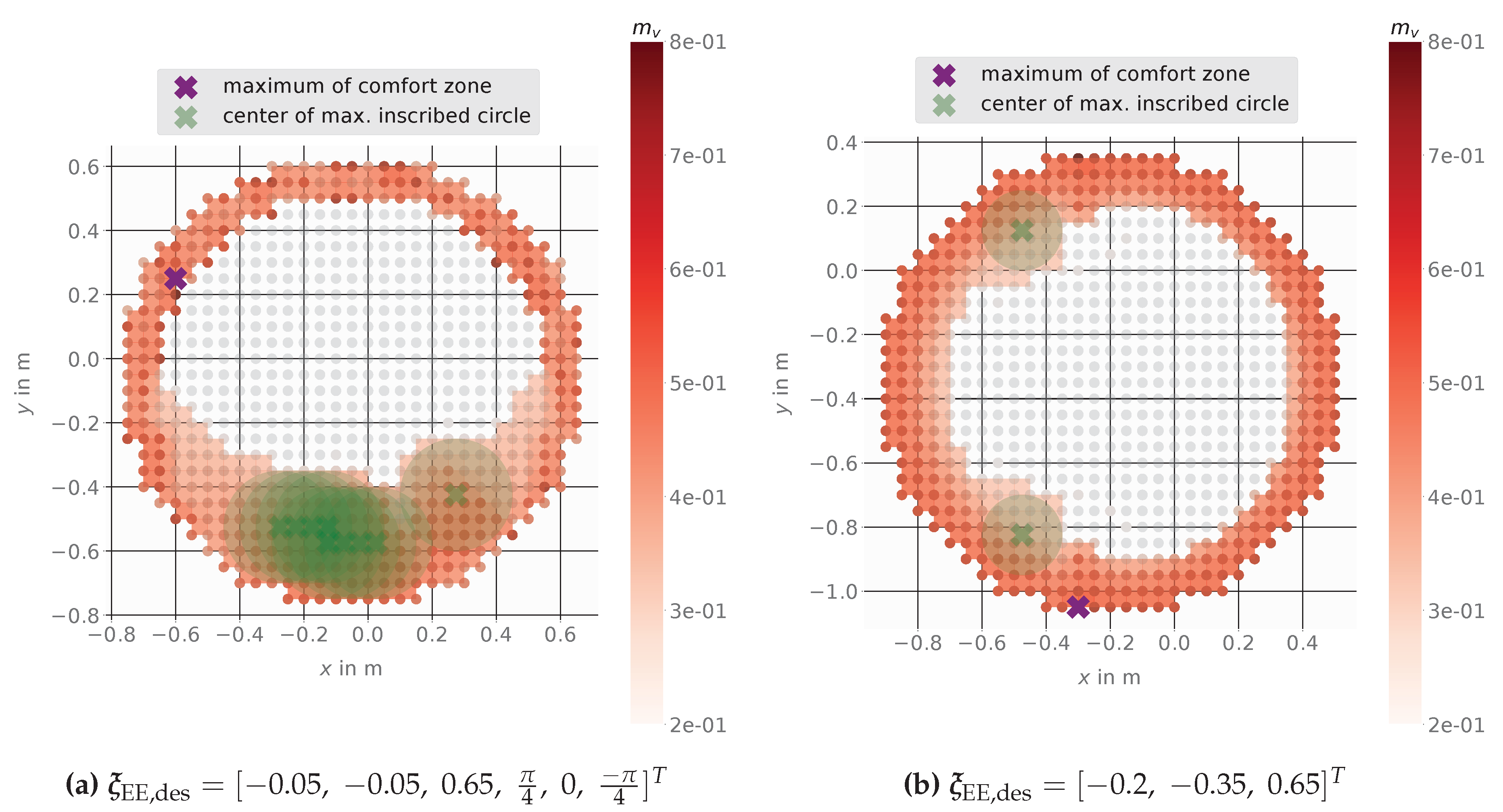
Preprints 114790 g011
Figure 11. Comfort Zone for the mobile manipulator LeoBot using the linear velocity v dependent manipulability measure m v with a minimum of 30% manipulability for EE pose (left) and EE position (right).
Figure 11. Comfort Zone for the mobile manipulator LeoBot using the linear velocity v dependent manipulability measure m v with a minimum of 30% manipulability for EE pose (left) and EE position (right).
Preprints 114790 g011
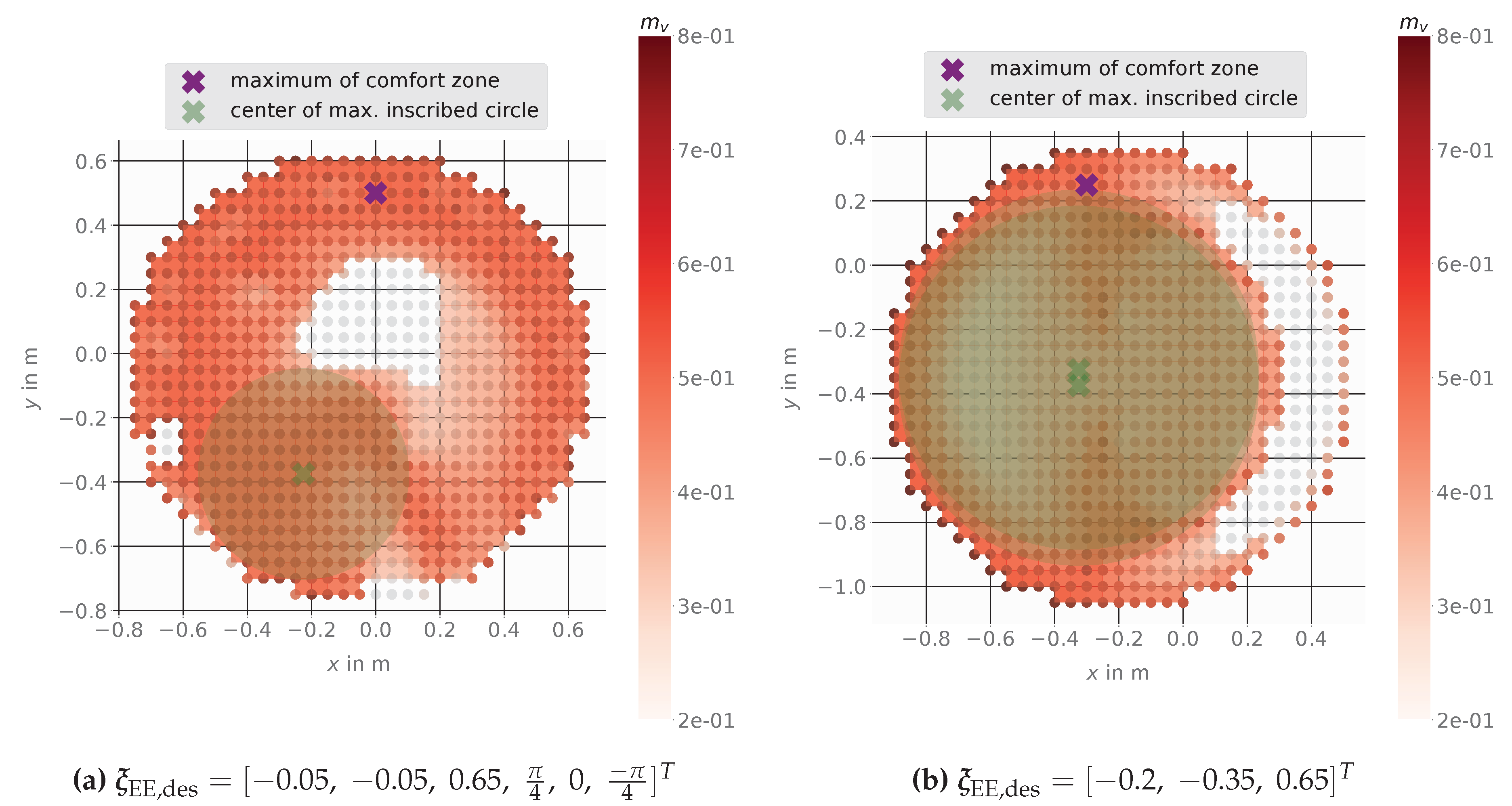
Preprints 114790 g012
Figure 12. Comfort Zone for the mobile manipulator LeoBot using the angular velocity ω dependent manipulability measure m v with a minimum of 30% manipulability for EE pose (a) and EE position (b).
Figure 12. Comfort Zone for the mobile manipulator LeoBot using the angular velocity ω dependent manipulability measure m v with a minimum of 30% manipulability for EE pose (a) and EE position (b).
Preprints 114790 g012
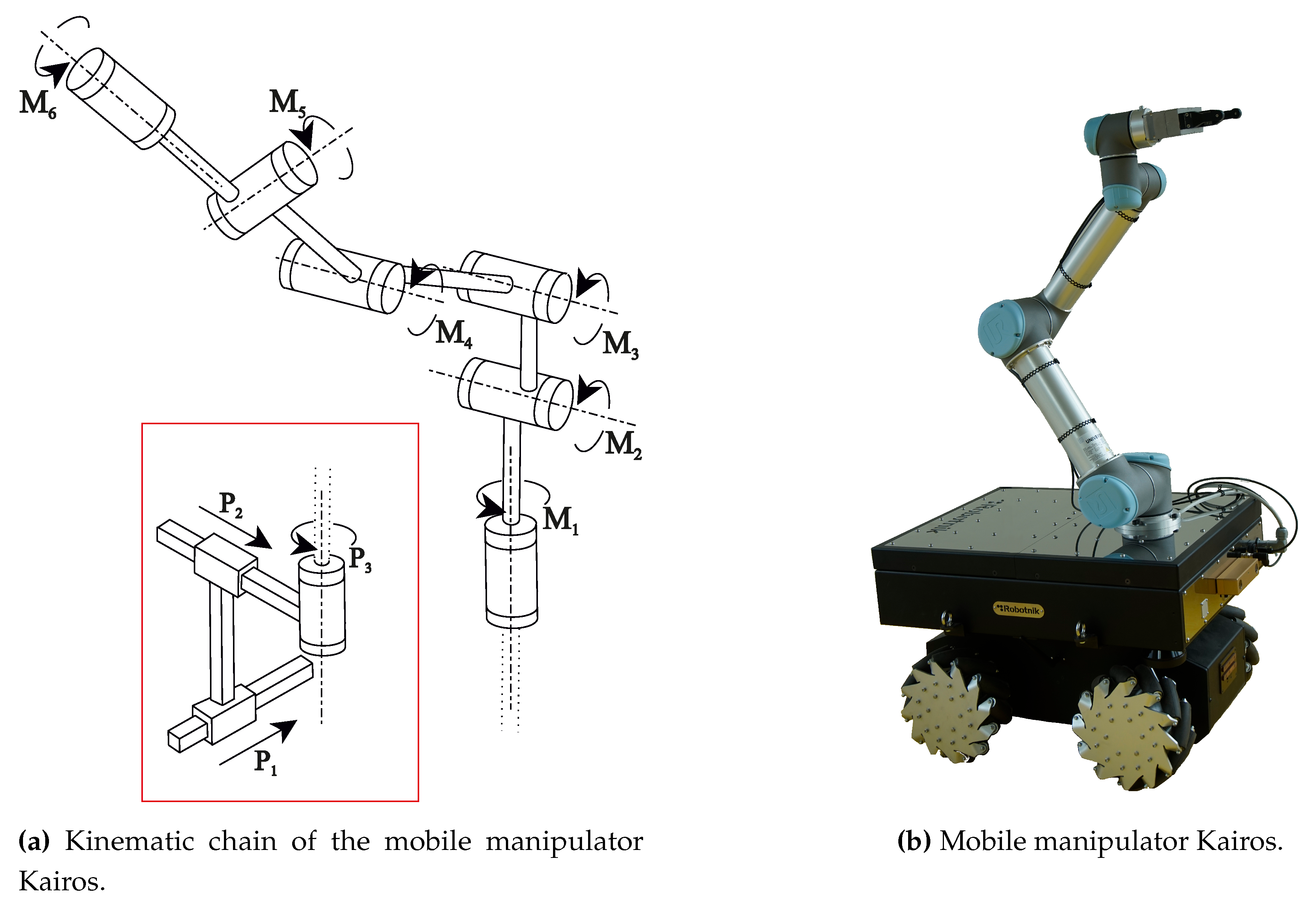
Preprints 114790 g013
Figure 13. Mobile manipulator Kairos developed and built by the company Robotnik. The mobile manipulator combines an Universal Robot UR5 manipulator with 6 rotational joints mounted on a holonomic mobile base using Mecanum wheels.
Figure 13. Mobile manipulator Kairos developed and built by the company Robotnik. The mobile manipulator combines an Universal Robot UR5 manipulator with 6 rotational joints mounted on a holonomic mobile base using Mecanum wheels.
Preprints 114790 g013
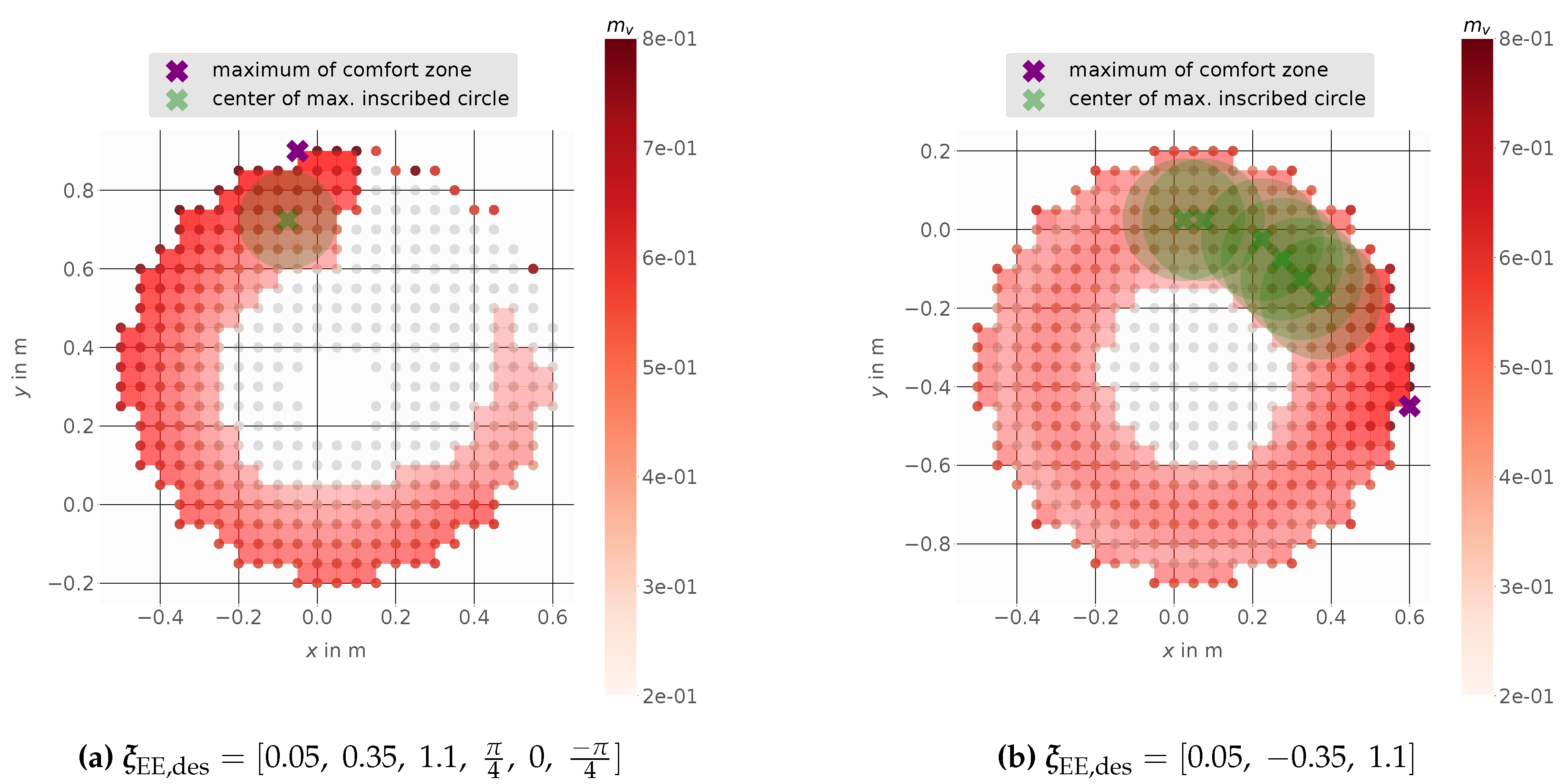
Preprints 114790 g014
Figure 14. Comfort Zone for the mobile manipulator Kairos using the linear velocity v dependent manipulability measure m v with a minimum of 30% manipulability for EE pose (a) and EE position (b).
Figure 14. Comfort Zone for the mobile manipulator Kairos using the linear velocity v dependent manipulability measure m v with a minimum of 30% manipulability for EE pose (a) and EE position (b).
Preprints 114790 g014
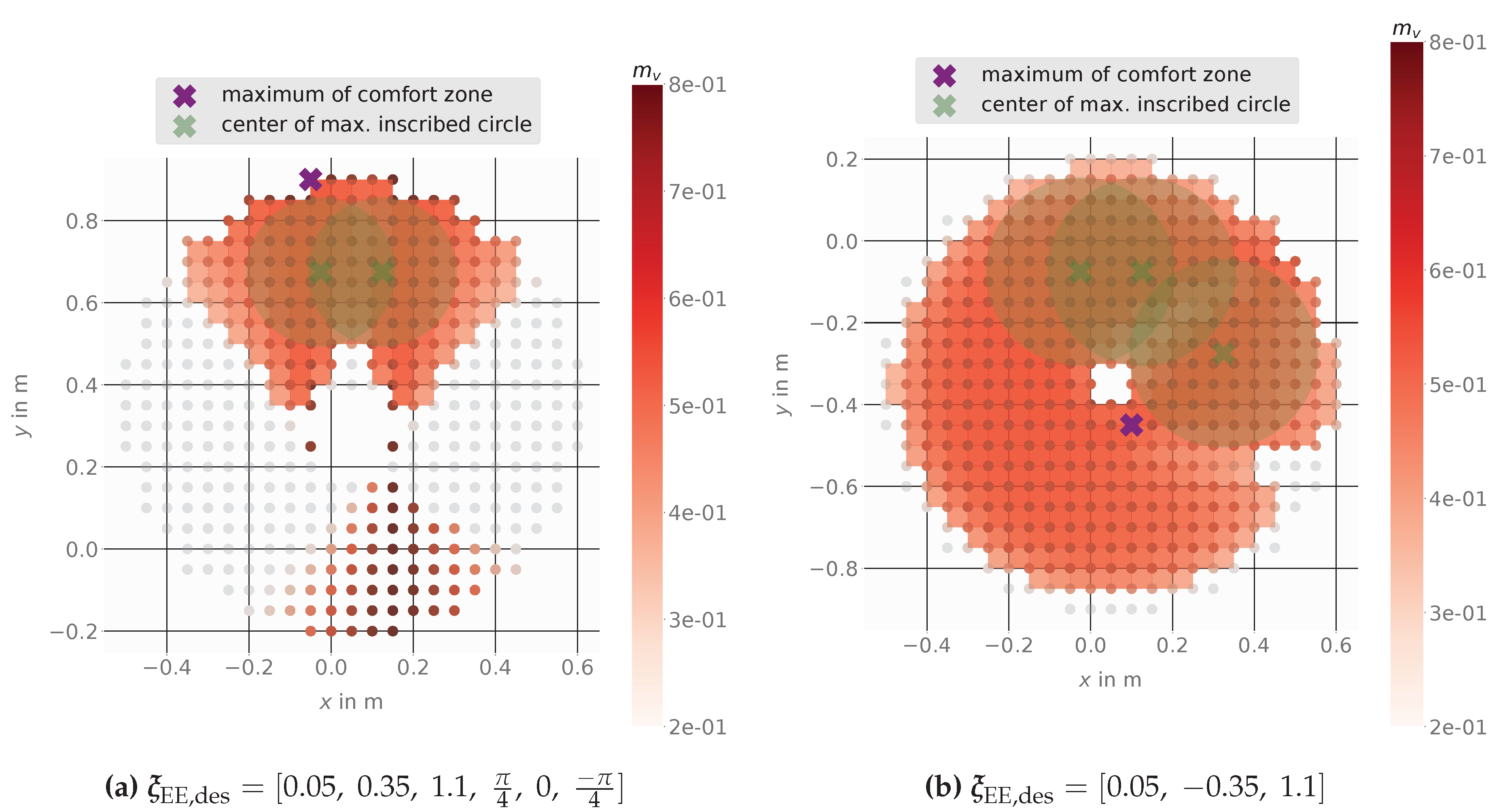
Preprints 114790 g015
Figure 15. Comfort Zone for the mobile manipulator Kairos using the angular velocity ω dependent manipulability measure m v with a minimum of 30% manipulability for EE pose (left) and EE position (right).
Figure 15. Comfort Zone for the mobile manipulator Kairos using the angular velocity ω dependent manipulability measure m v with a minimum of 30% manipulability for EE pose (left) and EE position (right).
Preprints 114790 g015
Preprints 114790 g016
Figure 16. Mobile manipulator Kairos approaching a target object by using the task dependent comfort zone (red boxes) for mobile manipulator base placement. Values as shown in Figure 14.
Figure 16. Mobile manipulator Kairos approaching a target object by using the task dependent comfort zone (red boxes) for mobile manipulator base placement. Values as shown in Figure 14.
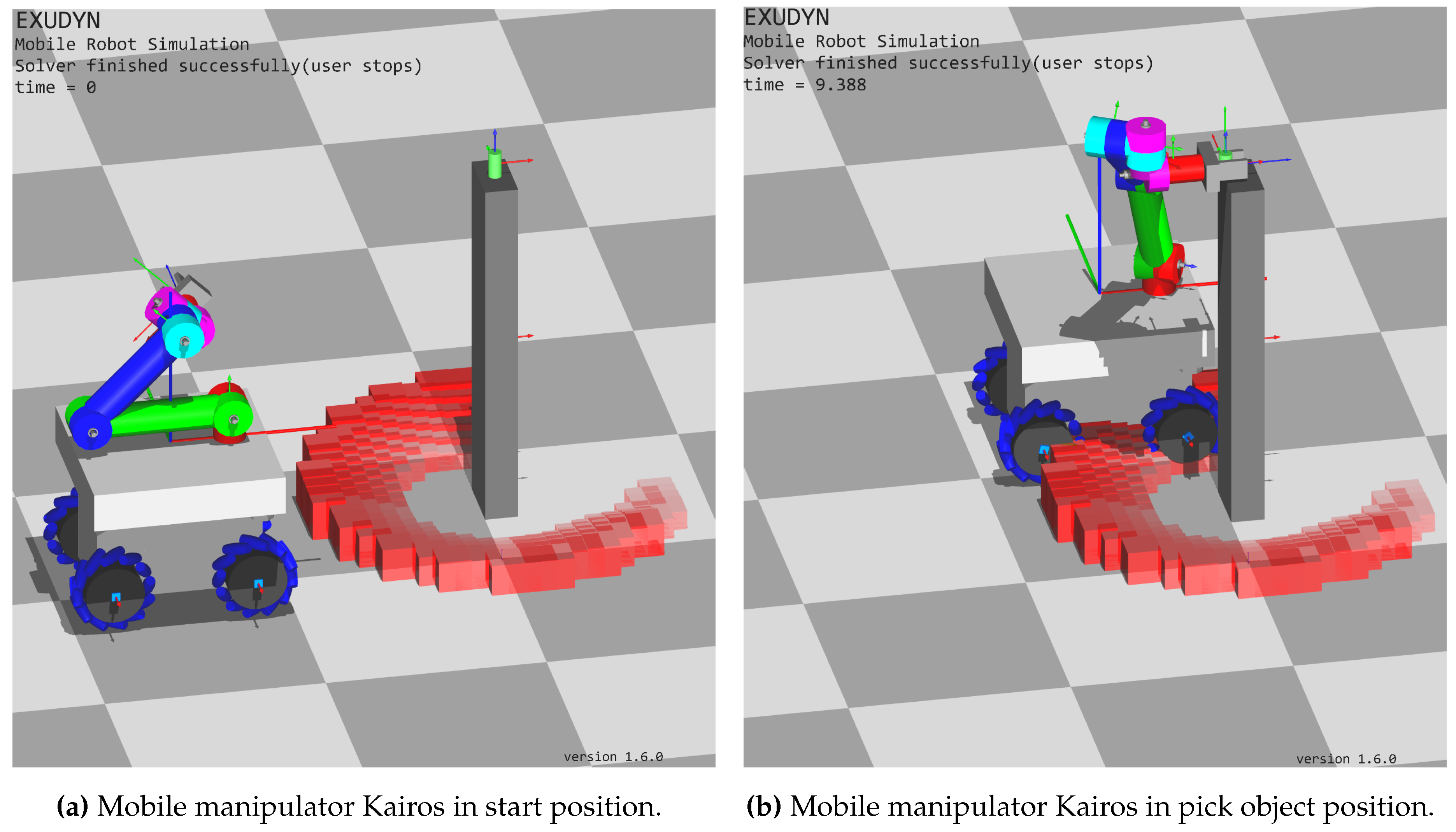
Preprints 114790 g016
Table 1. Summery of used manipulability measures.
Table 1. Summery of used manipulability measures.
Symbol Formula Description
m v Eq. (13) Proportional to the volume of the EE velocity ellipsoid, which represents the ability to move the EE with a certain velocity in all directions.
m f Eq. (17) Proportional to the volume of the EE force ellipsoid, which represents the ability to act with a certain force in all directions.
m a Eq. (26) Represents the minimum eigenvalue of the Cartesian stiffness matrix, which characterizes the smallest stiffness in a certain configuration.
m a Eq. (34) Represents the minimum eigenvalue of the weighted dynamic manipulability matrix, which characterizes the smallest acceleration in a certain direction.
Table 2. Possible classification of robotic tasks
Table 2. Possible classification of robotic tasks
Task Type Velocity Force Stiffness Acceleration
Pick and Place High Moderate Low High
Assembly Moderate High High Moderate
Painting Moderate Low Low Low
Milling Low High High Low
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated