Global Exponential Stability of Impulsive Delayed Neural Networks with Parameter Uncertainties and Reaction-Diffusion Terms

Preprint

Article

Global Exponential Stability of Impulsive Delayed Neural Networks with Parameter Uncertainties and Reaction-Diffusion Terms

Altmetrics

Downloads

103

Views

Comments

A peer-reviewed article of this preprint also exists.

Fei Luo,

Weiyi Hu^*,Enli Wu,Xiufang Yuan

Fei Luo,

Weiyi Hu^*,Enli Wu,Xiufang Yuan

This version is not peer-reviewed

Submitted:

05 July 2024

Posted:

05 July 2024

You are already at the latest version

Alerts

Abstract

In this paper we study a class of impulsive delayed neural networks with parameter uncertainties and reaction-diffusion terms. Using the properties of M-matrices and some inequality techniques, some sufficient conditions are derived to guarantee the global exponential stability of the given system. The results obtained are presented by simple algebraic inequalities, which are certainly more concise than previous methods. Finally, the validity and usefulness of our results are illustrated by arithmetic examples.

Keywords:

Subject: Computer Science and Mathematics - Computer Networks and Communications

MSC: 34D06; 34A37

1. Introduction

Cellular neural networks have been widely studied and applied in signal recognition, image processing, pattern classification and other fields since they were put forward in the 20th century [1]. It is well known that the global dynamic stable neural networks are the prerequisite for solving practical problems. Therefore, the studies on the stability of neural networks have received a lot of attention [2,3,4,5].

as we all know, time delays are unavoidable due to the limitations of signal transmission and limited switching speeds of amplifiers and the communication time. In addition, time delays are applied extensively in many aspects, such as biology and engineering [6,7,8]. In engineering applications, the system is suddenly affected by external factors, and the state of the system will suddenly change, that is impulsive effects. Although the duration of the impulses is very short, it can cause a sudden change for the state of the system, so it is harmful. At present, a quite hot topic is to stabilize the system with impulses. Therefore, it is particularly important to ensure the stability and good performance of the systems in the presence of time delays and impulses. This works on the stability of neural networks with time delays and impulses have been studied extensively, for example [9,10,11,12,13,14,15,16,17,18]. Among them, in [15], a novel exponential stability criterion in a form of linear matrix inequalities is firstly established. By applying the properties of M-matrices, Li et al. [16] investigated global exponential stability conditions for discrete-time BAM neural networks affected by impulses and time-varying delays. In [17], Rajchakit et al. investigated the global asymptotic stability problem for Clifford-valued neural network models with time-varying delays and impulsive effects. An auxiliary model-based nonsingular M-matrix approach is used to study the global exponential stability of neural networks with time-varying delays, connection weights and impulses in [18].

In particular, the neural networks generates diffusion phenomenon when electrons move in an asymmetric electromagnetic field, which means that the state of neurons changes not only with time, but also with space. This phenomenon can be modeled by introducing the diffusion term into the traditional neural network models. In order to better reflect the actual states of the neural networks, it is necessary to describe the reaction-diffusion of neurons in space by partial differential equations. The relevant investigations of stability of neural networks with diffusion terms expressed by partial differential equations are presented in [12,19,20,21,22,23,24,25,26,27,28,29,30,31] and the reference therein. Among them, global exponential stability of reaction-diffusion neural networks with time-varying was investigated in [12,19,20,22,27,28,29]. In [21], the stability of delay fuzzy cellular neural networks with reaction-diffusion was investigated by some new conditions. This conditions do not depend on the delay. Lu [24] studied a model with delayed reaction-diffusion and distributed delays and further discussed the robust global exponential stability and periodicity.

Moreover, parameter uncertainties are often encountered in engineering and biology systems due to the changes in the environment. In resent years, in order to solve the problems caused by parameter uncertainties, many scholars have done a lot of works on different uncertainties problems in this area and have obtained great progress, for example see [9,30,32,33,34,35,36]. In [32,33], the authors investigated the global exponential stability of neural networks by using the linear matrix inequality (LMI) methods. Here, time-delays correlation criterion was proposed to ensure robust stability of uncertain time-delays cellular neural networks. Hua et al. [34] investigated a uncertain stochastic neural network model and obtained a new results on robust exponential stability. Robust exponential stability of uncertain neural networks with time-varying was investigated by Balasubramaniam and Syed Ali in [35] and Zhang in [9]. An uncertain fuzzy cellular neural networks with time-varying delays and reaction diffusion terms was discussed in [30,31].

Despite the widespread works on stability analysis of neural networks, few attentions have been paid to the cases that the uncertain systems contains many complex terms, for example impulsive effect, time-varying and reaction terms. Motivated by the works above and the need for practical problems, we aim to study the global exponential stability of impulsive delayed neural networks with parameter uncertainties and reaction-diffusion terms.

Many authors have studied the global asymptotic stability of different types of uncertainty neural networks by using the linear matrix inequality (LMI) technique. It requires cumbersome conditions and yields tedious results. In this paper, a new differential inequality is established by using the properties of M-matrix and the technique of simple inequalities, which guarantees the global exponential stability of uncertain systems with time-varying delays and reaction-diffusion terms. All the results obtained are presented in a form of simple algebraic inequalities.

Our presentation is organized as follows. In Section 2, we describe the mathematical model of the system and give some preliminaries. The stability analysis of the given system is discussed in Section 3. In Section 4, two examples are given to verify the validity of the obtained results.

2. Model Description and Some Preliminaries

In this paper, we consider the following impulsive delayed neural network model with reaction-diffusion terms and parameter uncertainties:

\begin{matrix} \{\begin{matrix} \frac{\partial u_{p} (t, x)}{\partial t} = & \sum_{k = 1}^{m} \frac{\partial}{\partial x_{k}} (D_{p k} \frac{\partial u_{p} (t, x)}{\partial x_{k}}) - (a_{p} + Δ a_{p} (t)) u_{p} (t, x) + \sum_{q = 1}^{n} (b_{p q} + Δ b_{p q} (t)) f_{q} (u_{q} (t, x)) \\ + \sum_{q = 1}^{n} (c_{p q} + Δ c_{p q} (t)) g_{q} (u_{q} (t - τ_{p q} (t), x)) \\ + J_{p}, t \neq t_{l}, p = 1, 2, \dots, n, x \in Ξ, \\ u_{p} (t_{l}^{+}, x) = & I_{p l} (u_{p} (t_{l}^{-}, x)), p = 1, 2, \dots, n, x \in Ξ, l \in N ≜ {0, 1, 2, \dots}, \\ u_{p} (t, x) = & 0, t ⩾ 0, x \in \partial Ξ, \\ u_{p} (s, x) = & μ_{p} (s, x), s \in [- τ, 0], p = 1, 2, \dots, n, \end{matrix} \end{matrix}

(2.1)

where

u_{p} (t, x)

is the state of the pth neuron in space x and time t.

x = {(x_{1}, x_{2}, \dots, x_{m})}^{T} \in Ξ \subset R^{m}

Ξ = {x = {(x_{1}, x_{2}, \dots, x_{m})}^{T} | | x_{k} ∣ < L_{k}, k = 1, 2, \dots, m}

is a bounded compact set with smooth boundary

\partial Ξ

and mes

Ξ > 0

in space

R^{m} (L_{k}

is a positive constant).

u (t, x) = (u_{1} (t, x),

{u_{2} (t, x), \dots, u_{n} (t, x))}^{T} \in R^{n}

D_{p k} > 0

denotes diffusion coefficient.

a_{p} > 0

denotes the intensity of the pth element.

b_{p q}

and

c_{p q}

represent are elements of feedback and feedforward template.

Δ a_{p} (t), Δ b_{p q} (t), Δ c_{p q} (t)

represent bounded unstructured perturbations.

τ_{p q} (t) \in [0, τ]

represents the transmission delays from the pth element to the qth element;

f_{q} (\cdot) \in C (R, R)

and

g_{q} (\cdot) \in C (R, R)

represent the activation function with no delays and delays, respectively.

J_{p}

represents the external input.

I_{p k}

shows impulsive perturbation of the pth neuron.

Let

ω (s^{+}) = ω (s)

and

ω (s^{+}, x) = ω (s, x)

for all

s \in [- τ, 0]

ω (s^{-}) = ω (s)

and

ω (s^{-}, x) = ω (s, x)

for all but a finite number of points

s \in [- τ, 0]}

. Define

P C ≜ \{ω : [- τ, 0] \to R^{n} ∣ ω (s)

and

P C (Ξ) ≜ \{ω : [- τ, 0] \times Ξ \to R^{n} ∣ ω (s, x)

. It is easy to see that

P C

and

P C (Ξ)

are bounded on

[- τ, 0] \times Ξ

For any

ω (s, x) = {(ω_{1} (s, x), ω_{2} (s, x), \dots, ω_{n} (s, x))}^{T} \in P C (Ξ)

, the norm on

P C (Ξ)

is defined by

∥ ω ∥ = sup_{- τ ⩽ s ⩽ 0} \sum_{p = 1}^{n} {∥ω_{p} (s, x)∥}_{2} and {∥u_{p} (t, x)∥}_{2} = {[\int_{Ξ} {|u_{p} (t, x)|}^{2} d x]}^{\frac{1}{2}}, p = 1, 2, \dots, n .

For

C, D \in R^{m \times n},

we define the Schur product by

C \otimes D = {(c_{p q} d_{p q})}_{m \times n}

, in which

C ⩾ D (C > D)

means that the inequality

c_{p q} ⩾ b_{p q} (c_{p q} > d_{p q})

holds.

e = {(1, 1, \dots, 1)}^{T} \in R^{n}

and E is a n-dimensional identity matrix.

To complete the goal of this paper, we make the following assumptions:

(H1): There exist positive diagonal matrices F=diag $(F_{1}, F_{2}, \dots, F_{n})$ and G=diag $(G_{1}, G_{2}, \dots, G_{n})$ such that

$F_{p} = sup_{u \neq w} |\frac{f_{p} (u) - f_{p} (w)}{u - w}|, G_{p} = sup_{u \neq w} |\frac{g_{p} (u) - g_{p} (w)}{u - w}|,$

for all $u, w \in R (u \neq w), p = 1, 2 \dots n .$
(H2): There exists a positive diagonal matrix $I_{l} = diag (I_{1 l}, \dots, I_{n l})$ such that

$|I_{p l} (u) - I_{p l} (v)| ⩽ I_{p l} | u - v |$

for all $u, v \in R (u \neq v), p \in {1, 2, \dots, n}, l \in N .$
(H3): There exist some positive numbers $δ_{p 1}, δ_{p 2}$ and $δ_{p 3}$ , $p = 1, 2, \dots, n$ , such that $max | Δ a_{p} (t) | ⩽ δ_{p 1}, max | Δ b_{p q} (t) | ⩽ δ_{p 2}$ and $max | Δ c_{p q} (t) | ⩽ δ_{p 3}$ , $p, q = 1, 2, \dots, n$ , $\forall t ⩾ 0$ .

Remark 2.1.

In [9,32,33], the unstructured perturbations were dealt with through a relatively complex process. In real life, many perturbations are micro-perturbations, so we only assume that the unstructured perturbations are bounded shown in assumption (H3).

Definition 2.1.

If a function

u (t, x) : R \times Ξ \to R^{n}

satisfies the following conditions:

(1): $u (t, x)$ is a piecewise continuous function with the first kind of discontinuity point at $t_{l}$ for all $l \in N$ and $u (t, x)$ is right-continuous at each discontinuity point $t_{l}$ ;
(2): $u (t, x)$ satisfies system (1) for all $t ⩾ 0$ , and $u (t, x) = μ (t, x) (t \in [- τ, 0])$ ;

then

u (t, x)

is a particular solution that satisfies the initial conditions for system (1), and

u (t, μ, x)

represents the special solution of system (1) under initial condition

μ \in P C (Ξ)

Definition 2.2.

u (t, ω, x)

is a particular solution of the system (1) and satisfies the initial conditions

ω \in P C (Ξ)

. In the initial condition of

ϖ \in P C (Ξ)

u (t, ϖ, x)

is any solution of the system (1). If there is a positive number

λ > 0

and

M ⩾ 1

such that

∥u (t, ω, x) - u (t, ϖ, x)∥ ⩽ M ∥ω - ϖ∥ e^{- λ t} for all t ⩾ 0

then the system (1) is said to be globally exponentially stable.

Definition 2.3.

[37] A real matrix

D = {(d_{p q})}_{n \times n}

is said to be a nonsingular M-matrix if

d_{p q} ⩽ 0, p, q = 1, 2, \dots, n, p \neq q,

and all successive principal minors of D are positive.

Lemma 2.1.

[37] Let

D =

{(d_{p q})}_{n \times n}

with

d_{p q} ⩽ 0 (p \neq q),

then D is a nonsingular M-matrix if and only if the diagonal elements of D are all positive and there exists a positive vector d such that

D d > 0

D^{T} d > 0 .

Lemma 2.2.

[31] Let Ξ be a cube

|x_{k}| < L_{k}

(k = 1, 2, \dots, m)

and

h (x)

be a real-valued function belonging to

C^{1} (Ξ)

which vanish on the boundary an of

Ξ,

i.e.

{h (x)|}_{\partial Ξ} = 0

, then

\int_{Ξ} h^{2} (x) d x ⩽ L_{k}^{2} \int_{Ξ} {|\frac{\partial h}{\partial x_{k}}|}^{2} d x .

Lemma 2.3.

Let

τ > 0, a < b ⩽ + \infty

, suppose that

U (t) =

{(U_{1} (t), U_{2} (t), \dots, U_{n} (t))}^{T} \in C [[a, b), R^{n}]

satisfies the following differential inequality:

\{\begin{matrix} D^{+} U (t) ⩽ P U (t) + (Q \otimes \bar{U} (t)) e, & a ⩽ t < b, \\ U (a + s) \in P C, & - τ ⩽ s < 0, \end{matrix}

where

P = {({\tilde{p}}_{p q})}_{n \times n}

{\tilde{p}}_{p q} ⩾ 0

(p \neq q), Q = {({\tilde{q}}_{p q})}_{n \times n}

{\tilde{q}}_{p q} ⩾ 0

\bar{U} (t) = {(U (t - τ_{p q} (t)))}_{n \times n}

. If the initial condition satisfies

U (t) ⩽ κ ξ e^{- λ (t - a)}, κ ⩾ 0, ξ = {(ξ_{1}, ξ_{2}, \dots, ξ_{n})}^{T} > 0, t \in [a - τ, a],

where the value of λ is determined by the following inequality:

[λ E + P + Q \otimes ζ (λ)] ξ < 0, ζ (λ) = {(e^{λ τ_{p q} (t)})}_{n \times n},

then

U (t) ⩽ κ ξ e^{- λ (t - a)} for t \in [a, b)

Proof.

For

p \in {1, 2, \dots, n}

and arbitrary

ε > 0,

define

w_{p} (t) ≜

(κ + ε) ξ_{p} e^{- λ (t - a)}

. We prove that

\begin{matrix} U_{p} (t) ⩽ w_{p} (t) = (κ + ε) ξ_{p} e^{- λ (t - a)}, t \in [a, b), p = 1, 2, \dots, n . \end{matrix}

(2.2)

If this is not true, then there exist a number

t^{*} \in [a, b)

and some integer r such that

\begin{matrix} U_{r} (t^{*}) = w_{r} (t^{*}), D^{+} U_{r} (t^{*}) ⩾ {\dot{w}}_{r} (t^{*}), U_{p} (t) ⩽ w_{p} (t), t \in [a, t^{*}], p = 1, 2, \dots, n . \end{matrix}

(2.3)

From Lemma 2.3 and (2), we have

\begin{matrix} D^{+} U_{r} (t^{*}) & ⩽ & \sum_{q = 1}^{n} [{\tilde{p}}_{r q} U_{q} (t^{*}) + {\tilde{q}}_{r q} U_{q} (t^{*} - τ_{r q} (t^{*}))] \\ ⩽ & \sum_{q = 1}^{n} [{\tilde{p}}_{r q} (κ + ε) ξ_{q} e^{- λ (t^{*} - a)} + {\tilde{q}}_{r q} (κ + ε) ξ_{q} e^{- λ (t^{*} - τ_{r q} (t^{*}) - a)}] \\ = & \sum_{q = 1}^{n} [{\tilde{p}}_{r q} (κ + ε) ξ_{q} e^{- λ (t^{*} - a)} + {\tilde{q}}_{r q} e^{λ τ_{r q} (t^{*})} (κ + ε) ξ_{q} e^{- λ (t^{*} - a)}] \\ ⩽ & \sum_{q = 1}^{n} [{\tilde{p}}_{r q} + {\tilde{q}}_{r q} e^{λ τ_{r q} (t^{*})}] (κ + ε) ξ_{q} e^{- λ (t^{*} - a)} . \end{matrix}

(2.4)

Since

[λ E + P + Q \otimes ζ (λ)] ξ < 0, {\tilde{p}}_{p q} ⩾ 0,

{\tilde{q}}_{p q} ⩾ 0, (p \neq q)

and

e^{λ τ_{p q}} > 0,

it follows that

\sum_{q = 1}^{n} [{\tilde{p}}_{r q} + {\tilde{q}}_{r q} e^{λ τ_{r q} (t^{*})}] ξ_{q} < - λ ξ_{r} < 0,

From (4), one can obtain

D^{+} U_{r} (t^{*}) < - λ ξ_{r} (κ + ε) e^{- λ (t^{*} - l)} = {\dot{w}}_{r} (t^{*}) .

It is obvious that the result obtained is in contradiction with equation (2), so the inequality (7) holds. Let

ε \to 0

, one has

U_{p} (t) ⩽ κ ξ_{p} e^{- λ (t - a)}, p = 1, 2, \dots, n, t \in [a, b) .

The proof is completed. □

3. Global Exponential Stability Criteria

In this section, we obtain sufficient conditions for the global exponential stability of system (1).

Theorem 3.1.

Under assumption (H1)–(H3), then system (1) is globally exponentially stable if the following two conditions (C1) and (C2) hold:

(C1): There exist a vector $ξ = {(ξ_{1}, ξ_{2}, \dots, ξ_{n})}^{T} > 0$ and a constant $λ > 0$ such that

$[λ E - D + B F + C G \otimes ζ (λ)] ξ < 0, t ⩾ 0, ζ (λ) = e^{λ τ_{p q} (t)},$

where $D = diag (d_{1}, d_{2}, \dots, d_{n})$ with $d_{p} = a_{p} - δ_{p 1} + \sum_{k = 1}^{m} \frac{D_{p k}}{L_{k}^{2}}$ , $ζ (λ) = {(e^{λ τ_{p q} (t)})}_{n \times n}$ , $B = {(| b_{p q} + δ_{p 2} |)}_{n \times n}, C = {(| c_{p q} + δ_{p 3} |)}_{n \times n}$ , $F =$ diag $(F_{1}, F_{2}, \dots, F_{n})$ , $G =$ diag $(G_{1}, G_{2}, \dots, G_{n})$ , E is a n-dimensional identity matrix.
(C2): There is a positive number $γ > 0$ such that

$sup_{l \in N} \{\frac{ln γ_{l}}{t_{l} - t_{l - 1}}\} ⩽ γ < λ,$

where $γ_{l} = max_{1 ⩽ p ⩽ n} \{1, I_{p l}\}, l \in N$ .

Proof.

For

ω, ϖ \in P C (Ξ)

, the solutions of system (1) through

(0, ω)

and

(0, ϖ)

are denoted respectively as follows:

\begin{matrix} u (t, ω, x) & = & {(u_{1} (t, ω, x), u_{2} (t, ω, x), \dots, u_{n} (t, ω, x))}^{T}, \\ u (t, ϖ, x) & = & {(u_{1} (t, ϖ, x), u_{2} (t, ϖ, x), \dots, u_{n} (t, ϖ, x))}^{T} . \end{matrix}

Define

u_{t} (ω, x) = u (t + s, ω, x), u_{t} (ϖ, x) = u (t + s, ϖ, x), - τ < s ⩽ 0, t ⩾ 0,

then

u_{t} (ω, x)

u_{t} (ϖ, x) \in P C (Ξ)

for

t ⩾ 0 .

Let

U_{p} (t, ψ, x) =

u_{p} (t, ω, x) - u_{p} (t, ϖ, x), p = 1, 2, \dots, n, ψ = ω - ϖ

, we have

\begin{matrix} \frac{\partial U_{p} (t, ψ, x)}{\partial t} & = & \sum_{k = 1}^{m} \frac{\partial}{\partial x_{k}} (D_{p k} \frac{\partial U_{p} (t, ψ, x)}{\partial x_{k}}) - (a_{p} + Δ a_{p} (t)) U_{p} (t, ψ, x) \\ - \sum_{q = 1}^{n} (b_{p q} + Δ b_{p q} (t)) [f_{q} (u_{q} (t, ω, x)) - f_{q} (u_{q} (t, ϖ, x))] \\ - \sum_{q = 1}^{n} (c_{p q} + Δ c_{p q} (t)) [g_{q} (u_{q} (t - τ_{p q} (t), ω, x)) - g_{q} (u_{q} (t - τ_{p q} (t), ϖ, x))] \end{matrix}

(3.5)

for

t \neq t_{l}, x \in Ξ, p = 1, 2, \dots, n

Multiplying both sides of (5) by

U_{p} (t, ψ, x)

and integrate them, we have

\begin{matrix} \frac{d}{d t} \int_{Ξ} {(U_{p} (t, ψ, x))}^{2} d x & = & 2 \int_{Ξ} U_{p} (t, ψ, x) \sum_{k = 1}^{m} \frac{\partial}{\partial x_{k}} (D_{p k} \frac{\partial U_{p} (t, ψ, x)}{\partial x_{k}}) d x - g_{q} (u_{q} (t - τ_{p q} (t), ϖ, x))] d x \\ + 2 \sum_{q = 1}^{n} (b_{p q} + Δ b_{p q} (t)) \int_{Ξ} U_{p} (t, ψ, x) [f_{q} (u_{q} (t, ω, x)) - f_{q} (u_{q} (t, ϖ, x))] d x \\ + 2 \sum_{q = 1}^{n} (c_{p q} + Δ c_{p q} (t)) \int_{Ξ} U_{p} (t, ψ, x) [g_{q} (u_{q} (t - τ_{p q} (t), ω, x)) \\ - 2 \int_{Ξ} (a_{p} + Δ a_{p} (t)) U_{p}^{2} (t, ψ, x) d x . \end{matrix}

(3.6)

Applying the Dirichlet boundary conditions and Green’s formula, we can get

\begin{matrix} \int_{Ξ} U_{p} (t, ψ, x) \sum_{k = 1}^{m} \frac{\partial}{\partial x_{k}} (D_{p k} \frac{\partial U_{p} (t, ψ, x)}{\partial x_{k}}) d x = - \sum_{k = 1}^{m} \int_{Ξ} D_{p k} {(\frac{\partial (U_{p} (t, ψ, x))}{\partial x_{k}})}^{2} d x . \end{matrix}

By Lemma 2.2, we have

\begin{matrix} \int_{Ξ} U_{p} (t, ψ, x) \sum_{k = 1}^{m} \frac{\partial}{\partial x_{k}} (D_{p k} \frac{\partial U_{p} (t, ψ, x)}{\partial x_{k}}) d x & \leq & - \sum_{k = 1}^{m} \frac{D_{p k}}{L_{k}^{2}} \int_{Ξ} {(U_{p} (t, ψ, x))}^{2} d x \\ = & - \sum_{k = 1}^{m} \frac{D_{p k}}{L_{k}^{2}} {∥U_{p} (t, ψ, x)∥}_{2}^{2} . \end{matrix}

(3.7)

Applying the assumptions (H1)-(H3) and Holder inequality, it yields

\begin{matrix} \sum_{q = 1}^{n} (b_{p q} + Δ b_{p q} (t)) \int_{Ξ} U_{p} (t, ψ, x) [f_{q} (u_{q} (t, ω, x)) - f_{q} (u_{q} (t, ϖ, x))] d x \\ ⩽ & \sum_{q = 1}^{n} (b_{p q} + Δ b_{p q} (t)) \int_{Ξ} |U_{p} (t, ψ, x)| |f_{q} (u_{q} (t, ω, x)) - f_{q} (u_{q} (t, ϖ, x))| d x \\ ⩽ & \sum_{q = 1}^{n} (b_{p q} + δ_{p 2}) \int_{Ξ} |U_{p} (t, ψ, x)| |U_{q} (t, ψ, x)| F_{q} d x \\ ⩽ & \sum_{q = 1}^{n} |b_{p q} + δ_{p 2}| {∥U_{p} (t, ψ, x)∥}_{2} F_{q} {∥U_{q} (t, ψ, x)∥}_{2} . \end{matrix}

(3.8)

Similarly, we can get

\begin{matrix} \sum_{q = 1}^{n} (c_{p q} + Δ c_{p q} (t)) \int_{Ξ} U_{p} (t, ψ, x) [g_{q} (u_{q} (t - τ_{p q} (t), μ, x)) - g_{q} (u_{q} (t - τ_{p q} (t), ϖ, x))] d x \\ ⩽ & \sum_{q = 1}^{n} |c_{p q} + δ_{p 3}| {∥U_{q} (t - τ_{p q} (t), ψ, x)∥}_{2} G_{q} {∥U_{p} (t, ψ, x)∥}_{2} . \end{matrix}

(3.9)

Applying (6)–(9) to (5), we can obtain

\begin{matrix} \frac{1}{2} \frac{d}{d t} {∥U_{p} (t, ψ, x)∥}_{2}^{2} & \leq & - (a_{p} - δ_{p 1} + \sum_{k = 1}^{m} \frac{D_{p k}}{L_{k}^{2}}) {∥ U_{p} (t, ψ, x) ∥}_{2}^{2} \\ + \sum_{q = 1}^{n} |c_{p q} + δ_{p 3}| {∥U_{q} (t - τ_{p q} (t), ψ, x)∥}_{2} G_{q} {∥U_{p} (t, ψ, x)∥}_{2} \\ + \sum_{q = 1}^{n} | b_{p q} + δ_{p 2} | ∥ U_{p} {(t, ψ, x) ∥}_{2} F_{q} {∥ U_{q} (t, ψ, x) ∥}_{2}, \end{matrix}

i.e.,

\begin{matrix} D^{+} {∥U_{p} (t, ψ, x)∥}_{2} & \leq & - (a_{p} - δ_{p 1} + \sum_{k = 1}^{m} \frac{D_{p k}}{L_{k}^{2}}) {∥U_{p} (t, ψ, x)∥}_{2} + \sum_{q = 1}^{n} |b_{p q} + δ_{p 2}| F_{q} {∥U_{q} (t, ϑ, x)∥}_{2} \\ + \sum_{q = 1}^{n} |c_{p q} + δ_{p 3}| {∥U_{q} (t - τ_{p q} (t), ψ, x)∥}_{2} G_{q} . \end{matrix}

(3.10)

Let

U_{p} (t) = {∥U_{p} (t, ψ, x)∥}_{2}, U (t) = {(U_{1} (t), U_{2} (t), \dots, U_{n} (t))}^{T}, \bar{U} (t) = {(U_{p} (t - τ_{p q} (t)))}_{n \times n}, d_{p} = a_{p} - δ_{p 1} + \sum_{k = 1}^{m} (D_{p k} / L_{k}^{2}), p = 1, 2, \dots, n, D = diag (d_{1} d_{2}, \dots, d_{n})

B = {(| b_{p q} + δ_{p 2} |)}_{n \times n},

C = {(| c_{p q} + δ_{p 3} |)}_{n \times n}

P = - D + B F, Q = C G

. Then, (10) can be reduced to the following form:

\begin{matrix} D^{+} U (t) ⩽ P U (t) + (Q \otimes \bar{U} (t)) e . \end{matrix}

(3.11)

It means that there exist a vector

ξ = {(ξ_{1}, ξ_{2}, \dots, ξ_{n})}^{T} > 0

and a constant

λ > 0

such that

\begin{matrix} [λ E - D + B F + C G \otimes ζ (λ)] ξ < 0 . \end{matrix}

(3.12)

Take

κ = ∥ ψ ∥ / min_{1 ⩽ p ⩽ n} \{ξ_{p}\}

, it is easy to get

\begin{matrix} U (t) ⩽ κ ξ e^{- λ t}, t \in [- τ, t_{0}], t_{0} = 0 . \end{matrix}

(3.13)

By Lemma 2.3, we have

U (t) ⩽ κ ξ e^{- λ t}, t > 0 .

m ⩽ l

, the following inequality holds:

\begin{matrix} U (t) ⩽ κ γ_{0} \dots γ_{m - 1} ξ e^{- λ t}, t \in [t_{m - 1}, t_{m}), γ_{0} = 1 . \end{matrix}

(3.14)

When

m = l + 1,

we get

\begin{matrix} U (t_{l}) & = & {∥u (t_{l}, ω, x) - u (t_{l}, ϖ, x)∥}_{2} \\ = & ∥ I_{l} (u (t_{l}^{-}, ω, x)) - I_{l} (u (t_{l}^{-}, ϖ, x)) ∥_{2} \\ ⩽ & I_{l} {∥ U (t_{l}^{-}, ψ, x) ∥}_{2} \\ = & I_{l} U (t_{l}^{-}) \\ ⩽ & κ γ_{0} \dots γ_{l - 1} I_{l} ξ lim_{t \to t_{l}^{-}} e^{- λ t_{l}} \\ ⩽ & κ γ_{0} \dots γ_{l - 1} γ_{l} ξ e^{- λ t_{l}} . \end{matrix}

(3.15)

Combining (14), (15) and

γ_{l} ⩾ 1,

we have

\begin{matrix} U (t) ⩽ κ γ_{0} \dots γ_{l - 1} γ_{l} ξ e^{- λ t}, t_{l} - τ ⩽ t ⩽ t_{l} . \end{matrix}

(3.16)

By (12), (13), (16) and Lemma 2.3, we can obtain

\begin{matrix} U (t) ⩽ κ γ_{0} \dots γ_{l - 1} γ_{l} ξ e^{- λ t}, t_{l} ⩽ t < t_{l + 1} . \end{matrix}

(3.17)

By mathematical induction, we can get

\begin{matrix} U (t) ⩽ κ γ_{0} \dots γ_{l - 1} ξ e^{- λ t}, t_{l - 1} ⩽ t < t_{l}, l \in N . \end{matrix}

(3.18)

From condition

(C 2)

and (18), we have

\begin{matrix} U (t) \leq κ e^{γ t_{1}} e^{γ (t_{2} - t_{1})} \dots e^{γ (t_{l - 1} - t_{l - 2})} ξ e^{- λ t} \leq κ ξ e^{γ t} e^{- λ t} = κ ξ e^{- (λ - γ) t} \end{matrix}

(3.19)

for all

l \in N, t_{l - 1} ⩽ t < t_{l}

. It shows

\begin{matrix} ∥ u (t, ω, x) - u (t, ϖ, x) ∥ & = & \sum_{p = 1}^{n} {∥u_{p} (t, ω, x) - u_{p} (t, ϖ, x)∥}_{2} \\ = & \sum_{p = 1}^{n} U_{p} (t) \\ ⩽ & \sum_{p = 1}^{n} κ ξ_{p} e^{- λ t} \\ = & \frac{\sum_{p = 1}^{n} ξ_{p}}{min_{1 ⩽ p ⩽ n} \{ξ_{p}\}} ∥ ω - ϖ ∥ e^{- λ t} . \end{matrix}

That is

∥u_{t} (ω, x) - u_{t} (ϖ, x)∥ ⩽ M ∥ ω - ϖ ∥ e^{- λ t}, t ⩾ 0,

where

M = (\sum_{p = 1}^{n} ξ_{p} / min_{1 ⩽ p ⩽ n} \{ξ_{p}\})

. The proof is completed. □

Remark 3.1.

In Theorem 1, the condition (C1) ensures the global exponential stability of the uncertainty system (1), and the value of λ is taken with respect to the system parameters, the diffusion coefficient and the time delays. Condition (C2) describes the effect of impulse intensity and impulse spacing on the global exponential stability of system (1).

If impulsive operator

I_{p l} (u_{p}) = 0, p = 1, 2, \dots, n, l \in N

, system (1) will become a model of the following form:

\begin{matrix} \{\begin{matrix} \frac{\partial u_{p} (t, x)}{\partial t} = & \sum_{k = 1}^{m} \frac{\partial}{\partial x_{k}} (D_{p k} \frac{\partial u_{p} (t, x)}{\partial x_{k}}) - (a_{p} + Δ a_{p} (t)) u_{p} (t, x) + \sum_{q = 1}^{n} (b_{p q} + Δ b_{p q} (t)) f_{q} (u_{q} (t, x)) \\ + \sum_{q = 1}^{n} (c_{p q} + Δ c_{p q} (t)) g_{q} (u_{q} (t - τ_{p q} (t), x)) \\ + J_{p}, t \neq t_{l}, p = 1, 2, \dots, n, x \in Ξ, \\ u_{p} (t, x) = & 0, t ⩾ 0, x \in \partial Ξ, \\ u_{p} (s, x) = & μ_{p} (s, x), s \in [- τ, 0], p = 1, 2, \dots, n, \end{matrix} \end{matrix}

(3.20)

Theorem 3.2.

System (20) is globally exponentially stable if it satisfies the assumptions (H1) and (H3) and the following condition:

\begin{matrix} (a_{p} - δ_{p 1} + \sum_{k = 1}^{m} (\frac{D_{p k}}{L_{k}^{2}})) > \sum_{q = 1}^{n} [|b_{p q} + δ_{p 2}| F_{q} + |c_{p q} + δ_{p 3}| G_{q}], p, q = 1, 2, \dots, n . \end{matrix}

(3.21)

Proof.

Let

Θ = D - B F - C G

, then we know from condition (21) that all successive principal minors of

Θ

are positive because of diagonally dominant principle. It shows

Θ

is a nonsingular M-matrix by definition 2.3. From Lemma 2.1, there exists

ξ = {(ξ_{1}, ξ_{2}, \dots, ξ_{n})}^{T} > 0

such that

[D - B F - C G \otimes ζ (0)] ξ > 0, ζ (0) = 1 .

Since the continuity, there exists

λ > 0

satisfies:

\begin{matrix} [λ E - D + B F + C G \otimes ζ (λ)] ξ < 0, ζ (λ) = e^{λ τ_{p q} (t)}, \end{matrix}

(3.22)

where

D = diag (d_{1}, d_{2}, \dots, d_{n})

d_{p} = a_{p} - δ_{p 1} + \sum_{k = 1}^{m} \frac{D_{p k}}{L_{k}^{2}}

ζ (λ) = {(e^{λ τ_{p q} (t)})}_{n \times n}

B = {(| b_{p q} + δ_{p 2} |)}_{n \times n}, C = {(| c_{p q} + δ_{p 3} |)}_{n \times n}

F =

diag

(F_{1}, F_{2}, \dots, F_{n})

G =

diag

(G_{1}, G_{2}, \dots, G_{n})

. This shows that condition (C1) holds. □

Remark 3.2.

In Theorem 3.2, delays-independent stability criterion have been obtained when delays

τ_{p q} (t)

satisfies

0 ⩽ τ_{p q} (t) ⩽ τ, p, q = 1, 2, \dots, n .

Remark 3.3.

It is worth noting that the existing works on some uncertain neural networks become a special case of the system (1) constructed in this paper, for example [32,33]. In their works, the results obtained are independent of the impulse and reaction-diffusion. Compared to [32], it is easy to see that our standards have improved. However, it must be noted that comparing to LMI method in [33], none of our criteria is independent of the time delays when impulses and diffusion are not considered.

Remark 3.4.

Although the model considered in this paper is different from one in [30], the criteria we adopt have certain commonalities. And it is easy to see that all our criteria are presented in the form of simple algebraic inequalities, the obtained results are more concise.

Corollary 3.1.

τ_{p q} (t) = τ, p, q = 1, 2, \dots, n

, τ is a positive constant and system (20) satisfies Assumptions (H1),(H3) and (21), then system (20) is globally exponentially stable.

When

D_{p k} = 0

or the reaction diffusion can be neglected, the system (1) is rewritten as the following form:

\begin{matrix} \{\begin{matrix} \frac{\partial u_{p} (t, x)}{\partial t} = & - (a_{p} + Δ a_{p} (t)) u_{p} (t, x) + \sum_{q = 1}^{n} (b_{p q} + Δ b_{p q} (t)) f_{q} (u_{q} (t, x)) \\ + \sum_{q = 1}^{n} (c_{p q} + Δ c_{p q} (t)) g_{q} (u_{q} (t - τ_{p q} (t), x)) \\ + J_{p}, t \neq t_{l}, p = 1, 2, \dots, n, x \in Ξ, \\ u_{p} (t_{l}^{+}, x) = & I_{p l} (u_{p} (t_{l}^{-}, x)), p = 1, 2, \dots, n, x \in Ξ, l \in N ≜ {0, 1, 2, \dots}, \\ u_{p} (t, x) = & 0, t ⩾ 0, x \in \partial Ξ, \\ u_{p} (s, x) = & μ_{p} (s, x), s \in [- τ, 0], p = 1, 2, \dots, n, \end{matrix} \end{matrix}

(3.23)

Corollary 3.2.

Under assumption (H1)–(H3), then system (1) is globally exponentially stable if the following two conditions (D1) and (D2) hold:

(D1): There exist a vector $ξ = {(ξ_{1}, ξ_{2}, \dots, ξ_{n})}^{T} > 0$ and a constant $λ > 0$ such that

$[λ E - D^{*} + B F + C G \otimes ζ (λ)] ξ < 0, t ⩾ 0, ζ (λ) = e^{λ τ_{p q} (t)},$

where $D^{*} = diag (d_{1}, d_{2}, \dots, d_{n})$ , $d_{p} = a_{p} - δ_{p 1}$ , $ζ (λ) = {(e^{λ τ_{p q} (t)})}_{n \times n}$ , $B = {(| b_{p q} + δ_{p 2} |)}_{n \times n}, C = {(| c_{p q} + δ_{p 3} |)}_{n \times n}$ , $F =$ diag $(F_{1}, F_{2}, \dots, F_{n})$ , $G =$ diag $(G_{1}, G_{2}, \dots, G_{n})$ ;
(D2): There is a positive number $γ > 0$ such that

$sup_{l \in N} \{\frac{ln γ_{l}}{t_{l} - t_{l - 1}}\} ⩽ γ < λ,$

where $γ_{l} = max_{1 ⩽ p ⩽ n} \{1, I_{p l}\}, l \in N$ .

4. Illustrative Examples

In this section, we will verify the validity of the results obtained by two examples.

Example 4.1 Consider the uncertain impulsive system (1) with

n = m = 2, I_{p l} = 1.1, Ξ = [0, 1], t_{l} = 0.1 π l

max | Δ a_{p} (t) | ⩽ δ_{p 1} = 0.5, max | Δ b_{p q} (t) | ⩽ δ_{p 2} = 0.2, max | Δ c_{p q} (t) | ⩽ δ_{p 3} = 0.1

, where

p, q = 1, 2

. Let

f_{q} (u) = g_{q} (u) = \frac{| u + 1 | - | u - 1 |}{2} .

Based on the definition of the above parameters and functions, it is easy to see that the assumptions (H1)–(H3) are satisfied. Let

\begin{matrix} (D_{p 1}) = (\begin{matrix} 1 \\ 1 \end{matrix}), A = (\begin{matrix} 1 - δ_{11} & 0 \\ 0 & 1 - δ_{21} \end{matrix}), B = (\begin{matrix} 0.01 + δ_{12} & | - 0.2 + δ_{12} | \\ 0.3 + δ_{22} & | - 0.01 + δ_{22} | \end{matrix}) \end{matrix}

\begin{matrix} C = (\begin{matrix} 0.05 + δ_{13} & | - 0.1 + δ_{13} | \\ | - 0.2 + δ_{23} | & 0.08 + δ_{23} \end{matrix}), {(τ (t))}_{2 \times 2} = (\begin{matrix} | s i n t | & | s i n t | \\ | c o s t | & | c o s t | \end{matrix}) . \end{matrix}

then we get

\begin{matrix} ζ (λ) = (\begin{matrix} e^{λ | s i n t |} & e^{λ | s i n t |} \\ e^{λ | c o s t |} & e^{λ | c o s t |} \end{matrix}), D = (\begin{matrix} 1.1 & 0 \\ 0 & 1.1 \end{matrix}), F = G = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}), \end{matrix}

\begin{matrix} B = (\begin{matrix} 0.21 & 0 \\ 0.5 & 0.19 \end{matrix}), C = (\begin{matrix} 0.15 & 0 \\ 0.1 & 0.18 \end{matrix}), \end{matrix}

and

γ_{l} = max {1, 1.1} = 1.1 ⩾ 1, γ = sup_{l \in N} \frac{ln γ_{l}}{t_{l} - t_{l - 1}} = \frac{ln 1.1}{0.1 π} \approx 0.3033 .

Take

λ = 0.3946

and

ξ = (1, 1)

, then the condition (C1) in Theorem 3.1 are satisfied. Combined with the above equation, Theorem 3.1 holds. Therefore the system (1) is globally exponentially stable. Under the given parameters conditions above, the numerical simulation of system (1) is shown in Figure 1.

Example 4.2 Consider the uncertain impulsive system (1) with

n = m = 2, I_{p l} = 0, Ξ = [0, 1]

max | Δ a_{p} (t) | ⩽ δ_{p 1} = 0.2, max | Δ b_{p q} (t) | ⩽ δ_{p 2} = 0.5, max | Δ c_{p q} (t) | ⩽ δ_{p 3} = 0.2

, where

p, q = 1, 2

. Let

f_{q} (u) = g_{q} (u) = \frac{| u + 1 | - | u - 1 |}{2} .

By selecting the parameters and functions, it is easy to see that assumption (H1)–(H3) are satisfied. Let

\begin{matrix} (D_{p 1}) = (\begin{matrix} 1 \\ 1 \end{matrix}), A = (\begin{matrix} 1 - δ_{11} & 0 \\ 0 & 1 - δ_{21} \end{matrix}), B = (\begin{matrix} 0.02 + δ_{12} & | - 0.3 + δ_{12} | \\ 0.3 + δ_{22} & 0.02 + δ_{22} \end{matrix}) \end{matrix}

\begin{matrix} C = (\begin{matrix} 0.05 + δ_{13} & 0.2 + δ_{13} \\ | - 0.04 + δ_{23} | & 0.1 + δ_{23} \end{matrix}), {(τ (t))}_{2 \times 2} = (\begin{matrix} | s i n t | & | s i n t | \\ | c o s t | & | c o s t | \end{matrix}) . \end{matrix}

then we get

F_{1} = 1, F_{2} = 0, G_{1} = 0, G_{2} = 1

and

1.5 ⩽ (a_{p} - δ_{p 1} + \sum_{k = 1}^{1} (D_{p k} / L_{k}^{2})),

0 ⩽ \sum_{q = 1}^{2} [|b_{1 q} + δ_{12}| F_{q} + |c_{1 q} + δ_{13}| G_{q}] ⩽ 0.77,

0 ⩽ \sum_{q = 1}^{2} [|b_{2 q} + δ_{22}| F_{q} + |c_{2 q} + δ_{23}| G_{q}] ⩽ 0.82,

for

p, q = 1, 2

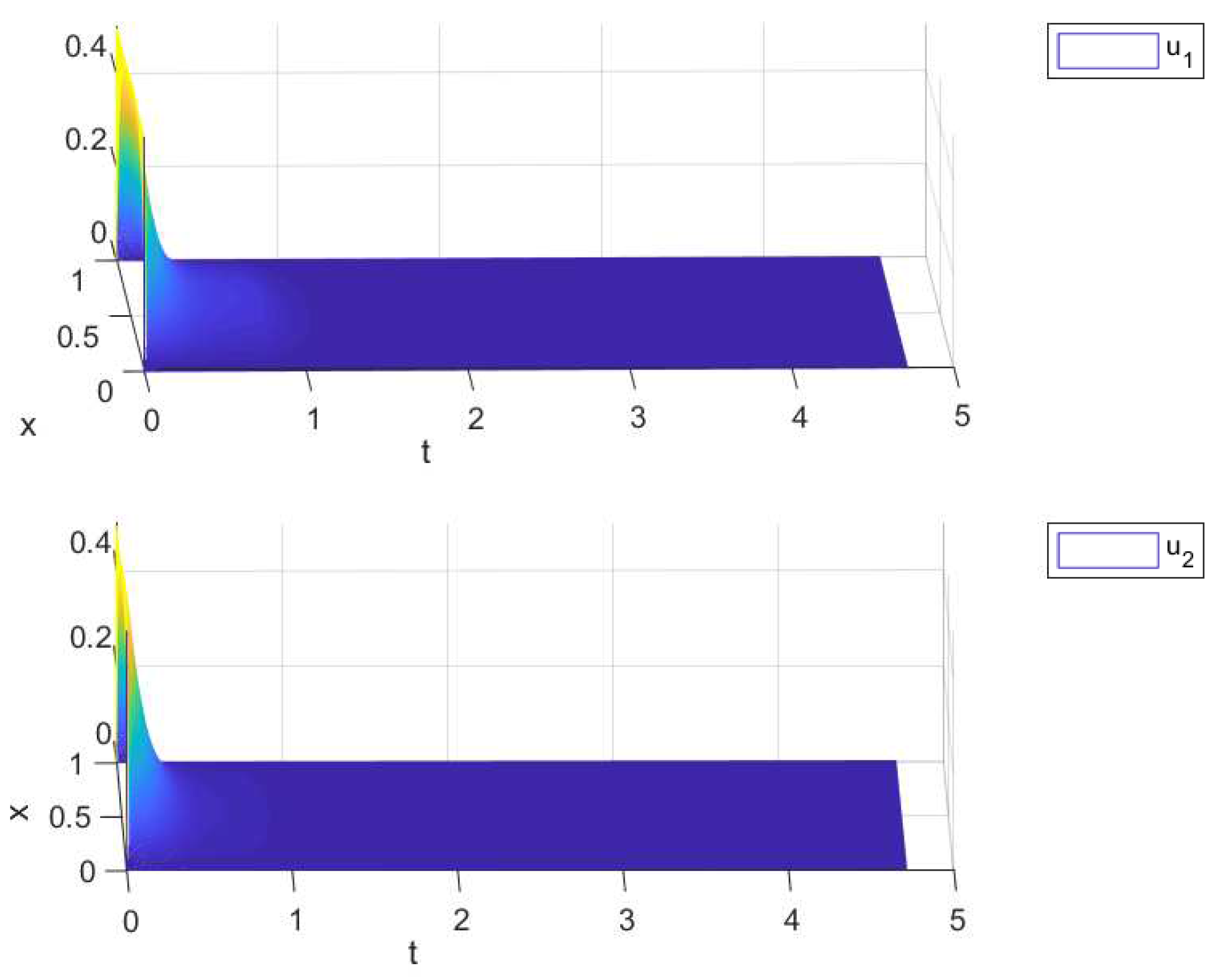
. It is obvious that the conditions (22) in Theorem 3.2 hold. Then the solution of system (1) under the given parameters conditions is globally exponentially stable, and the numerical simulation of system (1) is shown in Figure 2.

5. Conclusions

This paper investigates a class of impulsive delayed neural networks with parameter uncertainties and reaction-diffusion terms. By establishing a new differential inequality and combining the properties of M-matrices and some inequality tricks, several sufficient conditions are presented to guarantee the global exponential stability of the impulsive systems. And all results are given by a form of simple algebraic inequalities, which are certainly more concise than previous LMI methods. Finally the validity and generality of our results are illustrated with two arithmetic examples.

To reduce the computational difficulties, we mainly investigate stability of neural networks with impulse, in which the impulsive intensity is constant number. However, in engineering applications, the form of the impulsive intensity is rather complicated. Thus, in our future work, we plan to focus on investigating the stability of neural networks with random impulsive and reaction-diffusion terms. Therefore, it is important and interesting, but much more difficult.

Authorship Contribution

Fei Luo: Investigation, Methodology, Validation, Data curation, Software, Writing – original draft. Weiyi Hu: Conceptualization, Investigation, Methodology, Validation, Data curation, Software, Writing – reviewing and editing. Enli Wu: Conceptualization, Investigation, Methodology, Validation, Data curation, Software. Xiufang Yuan: Conceptualization, Investigation, Methodology, Software.

Funding

This work is supported by the National Natural Science Foundation of Sichuan (Grant No. 2024NSFSC1406), the Opening Project of Sichuan Province University Key Laboratory of Bridge Non-destruction Detecting and Engineering Computing (Grant No.2019QYY03, 2021QYJ03).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All data included in this study are available upon request by contact with the corresponding author.

Acknowledgments

The authors are very grateful to the associate editor and the anonymous referees for their careful reading and valuable suggestions.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

References

Chuan, L.O.; Yang, L. Cellular neural networks: theory, IEEE Trans. Circuits Syst. 1998, 35, 1257–1272. [Google Scholar]
Chen, W.; Zheng, W. Improved delay-dependent asymptotic stability criteria for delayed neural networks, IEEE Trans. Neural Netw., 2008, 19, 2154–2161.
Hua, C.; Yang, X.; Yan, J.; Guan, X. ; New exponential stability criteria for neural networks with time-varying delay, IEEE Trans. Circuits Syst. II: Exp. Briefs, 2011, 58, 931–935.
Liu, X.; Tang, M.; Wang, F. Improved exponential stability criterion for neural networks with time-varying delay, Neurocomputing, 2017, 234, 154–163.
Ji, M.; He, Y.; Zhang, C.; Wu, M. Novel stability criteria for recurrent neural networks with time-varying delay, Neurocomputing, 2014, 38, 383–391.
Cheng, J.; Park, J.H.; Wu, Z. Finite-time control of Markov jump Lur’e systems with singular perturbations, IEEE Trans. Autom. Control, 2023, 68, 6804–6811.
Xue, Y.; Liu, C.; Zhang, X. State bounding description and reachable set estimation for discrete-time genetic regulatory networks with time-varying delays and bounded disturbances, IEEE Trans. Syst. Man. Cybernet. Syst., 2022, 52, 6652–6661.
Zhang, X.; Han, Y.; Wu, L.; Wang, Y. State estimation for delayed genetic regulatory networks with reaction–diffusion terms, IEEE Trans. Neural Netw. Learn. Syst., 2018, 29, 299–309.
Zhang, Y. Robust exponential stability of uncertain impulsiv eneural networks with time-varying delays and delayed impulses, Neurocomputing, 2011, 74, 3268–3276.
Meng, F.; Li, K.; Zhao, Z.; Song, Q.; Liu, Y.; Alsaadi, F.E. Periodicity of impulsive Cohen–Grossberg–type fuzzy neural networks with hybrid delays, Neurocomputing, 2019, 368, 153–162.
Meng, F.; Li, K. ; Song Q; Liu Y.; Alsaadi F.E. Periodicity of Cohen–Grossberg–type fuzzy neural networks with impulses and time varying delays, Neurocomputing, 2019, 325, 254–259.
Hu, W.; Li, K. Global exponential stability and periodicity of nonautonomous impulsive neural networks with time-varying delays and reaction-diffusion terms, Complexity, 2021, Article ID 3495545.
Xu, C.; Liao, M.; Li, P.; Liu, Z.; Yuan, S. New results on pseudo almost periodic solutions of quaternion–valued fuzzy cellular neural networks with delays, Fuzzy Set. Syst., 2021, 411, 25–47.
Stamov, G.; Stamova, I.; Martynyuk, A.; Stamov, T. Almost periodic dynamics in a new class of impulsive reaction-diffusion neural networks with fractional-like derivatives, Chaos Soliton. Fract., 2021, 143, 110647.
Cong, E.; Han, X.; Zhang, X. Global exponential stabolity analysis of discrete-time BAM neural networks with delays: a mathematical induction approach, Neurcomputing, 2020, 379, 227–235.
Li, W.; Zhang, X.; Liu, C.; Yang, X. Global Exponential Stability Conditions for Discrete-Time BAM Neural Networks Affected by Impulses and Time-Varying Delays, Circ. Syst. Signal Pr., 2024.
Rajchakit, G.; Sriraman, R.; Vignesh, P.; Lim, C.P. Impulsive effects on Clifford-valued neural networks with time-varying delays: an asymptotic stability analysis, Appl. Math. Comput., 2021, 407, 126309.
Dong, Z. ; Zhang. X; Wang X. Global exponential stability of discrete-time higher-order Cohen-Grossberg neural networks with time-varying delays connection weights and impulses, J. Franklin Inst., 2021, 358, 5931–5950.
Liang, J.; Cao, J. Global exponential stability of reaction-diffusion recurrent neural networks with time-varying delays, Phys. Lett. A, 2003, 314, 434–442.
Wang, L.; Gao, Y. Global exponential robust stability of reaction-diffusion interval neural networks with time-varying delays, Phys. Lett. A, 2006, 350, 342–348.
Huang, T. Exponential stability of delayed fuzzy cellular neural networks with diffusion, Chaos Soliton. Fract., 2007, 31, 658–664.
Zhang, Z.; Yang, Y.; Huang, Y. Global exponential stability of interval general BAM neural networks with reaction-diffusion terms and multiple time-varying delays, Neural Netw., 2011, 24, 457–465.
Wang, Z.; Zhang, H. Global asymptotic stability of reaction-diffusion Cohen-Grossberg neural networks with continuously distributed delays, IEEE Trans. Neural Netw., 2010, 21, 39–49.
Lu, J. Robust global exponential stability for interval reaction-diffusion hopfield neural networks with distributed delays, IEEE Trans. Circuits Syst. II: Exp. Briefs, 2007, 54, 1115–1119.
Lu, J. Global exponential stability and periodicity of reaction-diffusion delayed recurrent neural networks with dirichlet boundary conditions, Chaos Soliton. Fract., 2008, 35, 116–125.
Lu, X.; Chen, W.; Ruan, Z.; Huang, T. A new method for global stability analysis of delayed reaction-diffusion neural networks, Neurocomputing, 2018, 317, 127–136.
Zhang, H.; Zeng, Z. stability and synchronization of nonautonomous reaction-diffusion neural networks with general time-varying delays, IEEE Trans. on neural netw. Learn. Syst., 2022, 33, 5804–5817.
Pan, J.; Zhong, S. Novel criteria on global robust exponential stability to a class of reaction-diffusion neural networks with delays, Discrete Dyn. Nat. Soc., 2009, 2009, 291594.
Rao, R. Delay-dependent exponential stability for nonlinear reaction-diffusion uncertain Cohen-Grossberg neural networks with partially known transition rates via Hardy-Poincar’e inequality, Chin. Ann. Math. Ser. B, 2014, 35, 575–598.
Balasubramaniam, P.; Syed Ali, M. Robust stability of uncertain fuzzy cellular neural networks with time-varying delays and reaction diffusion terms, Neurocomputing, 2010, 73, 439–446.
Wang, J.; Lu, J. Global exponential stability of fuzzy cellular neural networks with delays and reaction-diffusion terms, Chaos Soliton. Fract., 2008, 38, 878–885.
Chen, Y.; Bi, W. New robust exponential stability analysis for uncertain neural networks with time-varying delay, Int. J. Autom. and Comput., 2008, 5, 395–400.
Gau, R.S.; Lien, C.H.; Hsieh, J.G. Global exponential stability for uncertain cellular neural networks with multiple time-varying delays via LMI approach, Chaos Soliton. Fract., 2007, 32, 1258–1267.
Hua, M.; Liu, X.; Deng, F.; Fei, J. New results on robust exponential stability of uncertain stochastic neural networks with mixed time-varying delays, Neural Process. Lett., 2010, 32, 219–233.
Balasubramaniam, P.; Syed Ali, M. Robust exponential stability of uncertain fuzzy Cohen-Grossberg neural networks with time-varying delays, Fuzzy Set. Syst., 2010, 161, 608–618.
Cheng, C. Robust control of a class of neural networks with bounded uncertainties and time-varying delays, Comput. Math. Appl., 2008, 56, 1245–1254.
Berman, A.; Plemmons, R.J. Nonnegative Matrices in the Mathematical Science, Academic Press, Cambridge, MA, USA, 1979.

Figure 1. States response curves of the system in Example 1 with

Δ a_{p} (t) = 0.5, Δ b_{p q} (t) = 0.2

and

Δ c_{p q} (t) = 0.1, p, q = 1, 2

Figure 1. States response curves of the system in Example 1 with

Δ a_{p} (t) = 0.5, Δ b_{p q} (t) = 0.2

and

Δ c_{p q} (t) = 0.1, p, q = 1, 2

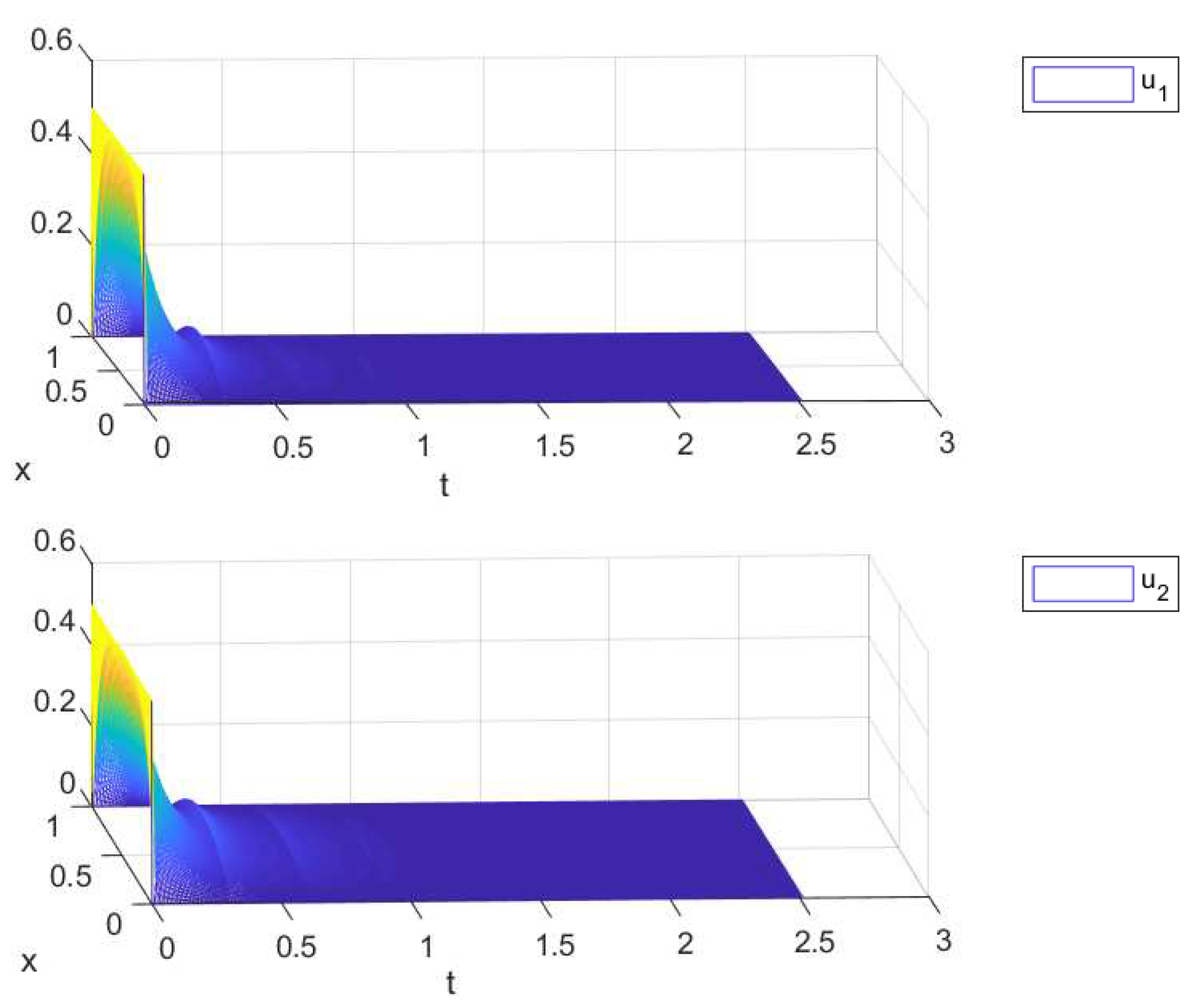
Figure 2. States response curves of the system in Example 2 with

Δ a_{p} (t) = 0.2, Δ b_{p q} (t) = 0.5

and

Δ c_{p q} (t) = 0.2, p, q = 1, 2

Figure 2. States response curves of the system in Example 2 with

Δ a_{p} (t) = 0.2, Δ b_{p q} (t) = 0.5

and

Δ c_{p q} (t) = 0.2, p, q = 1, 2

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Global Exponential Stability of Impulsive Delayed Neural Networks with Parameter Uncertainties and Reaction-Diffusion Terms

Abstract

1. Introduction

2. Model Description and Some Preliminaries

3. Global Exponential Stability Criteria

4. Illustrative Examples

5. Conclusions

Authorship Contribution

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe