On a Non‐Standard Atomic Model Developed in the Context of Bridge Electromagnetic Theory

Preprint

Article

On a Non‐Standard Atomic Model Developed in the Context of Bridge Electromagnetic Theory

Altmetrics

Downloads

174

Views

Comments

Massimo Auci^*

This version is not peer-reviewed

Submitted:

23 July 2024

Posted:

24 July 2024

Read the latest preprint version here

Alerts

Abstract

In the context of the Bridge Electromagnetic Theory, a quantum-relativistic theory based on Maxwellian electromagnetism, it has recently been shown that the characteristics of a hydrogen atom can be obtained through an electron-proton orbital capture process forming a non-radial emitting dipolar electromagnetic source. The model structurally different to the Bohr-Sommerfeld and Schrödinger models has now been deepened and completed by testing it on the properties of hydrogen and deuterium atoms and of helium and lithium in hydrogenoid form. These last two atoms are of cosmological interest as they are the heaviest elements produced by electron capture in the early universe. The theoretical results obtained regarding the atomic structure and spectra are in excellent agreement with the observational data by suggesting the implicit correctness of the model. It is also highlighted that the electron-nucleus interaction is influenced on an isotopic basis as a function of the value of the inertial mass of the nuclei considered.

Keywords:

Subject: Physical Sciences - Atomic and Molecular Physics

1. Introduction

Atomic ancient theory based on the Rutherford model has changed over the years both conceptually and formally. In spectroscopy, the current atomic model is fundamentally based on the Bohr-Sommerfeld theory [1], although the formulas for the determination of spectral lines and energy levels use the Rydberg-Ritz principle [2] which allows the calculation of the wavelengths of the emission spectra by means of ad hoc parameters identified on the basis of the atomic element considered. From the point of view of Quantum Mechanics, the Schrödinger model is used, to takes into account the dual wave-matter phenomenology of the atomic electrons giving a probabilistic description of their momentum and position in each single atomic level.

In this work, we propose a new approach to atomic model based on the bridge electromagnetic theory (BT) principles, which has its early foundations in Maxwellian electromagnetism^3-5. In this model, quantum and relativistic phenomena, as well as wave-matter dualism, emerge consistently from the theory used without forcing their introduction, in fact, it is known that quantum mechanics and relativity work well together even if their foundations are not compatible at all.

Bridge theory is a consistent and complete theory originating from the conjecture proposed in Ref. [3] on the role of the Transverse Component of the Poynting Vector (TCPV) of the Dipolar Electromagnetic Source (DEMS) formed during the direct interaction between two approaching charged particles of opposite sign (See also Ref. [4] and [5]). The TCPV is able to localize the amount of energy and momentum inside the DEMS in the quantum form

h c / λ

with a wavelength equal to the minimum distance of interaction achieved by the two interacting particles and with the theoretical value of the action constant

h

characterizing the electromagnetic interaction of the two particles. The value of the action constant calculated using the theory is in agreement with the standard value of Planck’s constant, thus demonstrating that quantization is not a principle but a phenomenon that derives from the particular way of interaction of a pair of charged particles.

The conjecture proposed in Ref. [3] on TCPV was subsequently proved in Ref. [4] and Ref. [5] by the calculation of Sommerfeld’s constant and consequently by the determination of the physical origin of Planck’s constant, subsequently allowing the development of an unconventional electromagnetic quantum theory presented in Ref. [6]. Later it was shown in Ref. [7] that relativistic phenomenology can also be explained using the same theoretical approach. Therefore, despite appearances, Maxwellian electromagnetism, Quantum Theory and Special Relativity are fully compatible theories and can therefore be used together in the form of an electromagnetic quantum-relativistic theory, the BT, whose formalism does not differ from that commonly used in QED, but offers new insights into interpreting the physical phenomena observed.

2. The Bridge Electromagnetic Theory: Brief Introduction

In BT, the interactions that produce quantum phenomena occur exclusively between pairs of charged particles of opposite signs that are defined as pairs of charge and anticharge, as the quantum behavior does not depend on the value of their original inertial mass, the mechanical nature of which has been studied separately in Ref. [8].

The crucial point in BT is the formation of DEMS, which bonds pairs of charges by producing an electromagnetic entanglement independent of the distance achieved by the two particles. This implies that a direct interaction in a pair of charges cannot be considered completely Coulombian because two interacting charges are always in motion with respect to each other, producing not only the Coulomb interaction but also an electromagnetic interaction that generates a non-point dipole source, i.e., the DEMS, which moving with respect to every other inertial observer, produces with each of them a different Doppler effect that gives rise to the relativistic phenomenology.

The electromagnetic field of the DEMS does not have, therefore, spherical symmetry as the Coulombian one but cylindrical symmetry with the symmetry axis coinciding with the dipole moment axis, so the Poynting vector is not everywhere radial and the emerging wave can be considered a composition of a spherical radial wave that describes the classical field with a plane transverse wave circulating around the virtual center of the DEMS that originates quantum effects. Each observer external to the direct interaction receives a superposition of both waves characterized by a Doppler⁷ the value of which defines the observed energy and momentum in full accordance with Special Relativity.

In the following sub-chapters, the fundamental elements of the theory necessary for the construction of the atomic model will be resumed.

2.1. Quantum Behavior: Poynting Vector, Action and Energy of a DEMS

The electric field of the dipole can be described by a local three-dimensional vector centered in the dipole having at each point

P

of the spacetime three unitary components

(\hat{l}, \hat{t}, \hat{r})

: lateral, transverse, and radial, of which the lateral component is always zero (Cf. Ref. [5] and [6]).

In Gaussian units, the electric field of the dipole is:

E = \frac{e}{r^{2}} (\begin{matrix} \begin{array}{l} 0 \end{array} \\ \frac{4 ρ \sin θ}{{(4 + ρ^{2} + 4 ρ c o s θ)}^{\frac{3}{2}}} + \frac{4 ρ \sin θ}{{(4 + ρ^{2} - 4 ρ c o s θ)}^{\frac{3}{2}}} \\ \frac{4 (2 + ρ c o s θ)}{{(4 + ρ^{2} + 4 ρ c o s θ)}^{\frac{3}{2}}} - \frac{4 (2 - ρ c o s θ)}{{(4 + ρ^{2} - 4 ρ c o s θ)}^{\frac{3}{2}}} \end{matrix})

(1)

whose only two non-null components are functions of the parameter

(ρ, θ)

. The first is the most important and is defined by the ratio

ρ = R / λ

, where

R

is the variable distance between the two interacting charges, corresponding to the length of the dipole moment for the unit of charge and the wavelength of the electromagnetic wave that will be emitted by the DEMS produced. The second is the polar angle between the radial vector pointing to a point

P

of spacetime and the dipole axis, whereas the magnetic field of the DEMS in the dipole wave zone is

B = (\begin{matrix} - |ε| \\ 0 \\ 0 \end{matrix})

(2)

consequently, the Poynting vector of the electromagnetic field

S = \frac{c}{4 π} ε \times B = (\begin{array}{l} 0 \\ S_{t} \\ S_{r} \end{array}) = \frac{c}{4 π} \frac{e^{2}}{r^{4}} (\begin{array}{l} 0 \\ f_{t} (ρ, θ) \\ f_{r} (ρ, θ) \end{array})

(3)

is characterized by a nonzero transverse component

S_{t}

that localizes within the wavefront of the DEMS, an amount of energy and momentum, and by a classical radial component

S_{r}

associated with the spherical radial wave.

For each interaction occurring between a pair of particles, the physical conditions change. Therefore, the value of the parameter

ρ

must be recalculated using a stochastic process defined by the constraints produced by the external forces acting on the DEMS. In the case of free interaction, when a pair of particles interacts without external constraints, the value of the ratio

ρ

was statistically accurately estimated (Cf. Ref. [5] and [6]), and the best value obtained is

\bar{ρ} = 1.2755578749164

. In this case, with reference to Equation (3), let

Θ_{t} (\bar{ρ}, θ) = |f_{t} (\bar{ρ}, θ)|

, the energy of the localized quantum is calculated by the expression

\begin{array}{l} E = (\frac{4 π}{3} \int_{0}^{π} Θ_{t} (\bar{ρ}, θ) d θ + \frac{1}{4 π {\bar{ρ}}^{2}}) \frac{e^{2}}{c} ω \\ = (σ_{e m} + σ_{e s}) \frac{e^{2}}{c} ω = ℏ ω \end{array}

(4)

where

ℏ = \begin{matrix} 1.05457266 10^{- 34} J H z^{- 1} \end{matrix}

is the theoretical value of Planck’s constant for free interactions described in Dirac form. Equation (4) describes the energy and momentum exchanged in the form of a photon by two interacting charges.

The energy, as shown in the second row of Equation (4), is described by two dimensionless contributions, one electrostatic (es) and one electromagnetic (em), which define and estimate the value of the total structure constant

σ = σ_{e m} + σ_{e s} = α^{- 1}

as a function of the mean value

\bar{ρ}

characterizing the DEMS.

Because the value of the structural constant during a free interaction is equal to the reciprocal value of Sommerfeld’s constant, the coupling constant

α

can be considered a universal constant with which it is possible to define the value of Planck’s constant.

For what has been written above, in BT the values of

σ

α

ℏ

are not true constants because they can vary, even if only slightly, as a function of the boundary conditions that define the physical reality in which the DEMS is formed, i.e., as a function of the forces acting on the interacting charges. In fact, for free interactions, Sommerfeld theoretical constant is in very good agreement with the one calculated experimentally, except for a very small difference due, in the case of theoretical calculation, to the lack of direct interaction of the DEMS with the observer. In other cases, the boundary conditions can significantly modify the value of

σ

and, consequently, the values of the coupling constant and action unit.

Considering an electron-proton interactions, the energy and momentum that characterize the DEMS are the energy and momentum associated with the initial reciprocal free motion of the particles before electron-proton capture takes place and represent the energy and momentum exchanged in the interaction in a limited time interval. In fact, contrary to what occurs in the strictly Coulombic interaction, the interaction associated with a DEMS has a finite duration and occupies a finite space (Cf. Ref. [6]).

During the electromagnetic interaction of a pair of particles, the start of the interaction corresponds to the zero-energy emission from the source, which is associated with an initial zero value of the radial Poynting vector. In agreement with BT, the value of the radial component of the Poynting vector increases over time by increasing the brightness of the source as the distance of the wavefront from the virtual center of the DEMS increases, reaching the maximum emission after a characteristic time

T / 2

equal to half of the total interaction time; then, the energy emission starts to decrease when the particles reach the minimum interaction distance, which is equal to the wavelength of the source, and begins to move away, increasing their interaction distance. Under these conditions, an electron and a proton forming a DEMS exchange a photon of energy and momentum (4) equal to that which the DEMS will gradually emit by means of the radial component of the Poynting vector; therefore, the DEMS cannot be a stable system.

As previously described, the Sommerfeld constant in the context of BT is calculated from the characteristics of the electromagnetic field structure of the DEMS in spacetime. Its value in the case of free interaction between pairs of particles or particles of different masses but with charge and anticharge corresponds to

α = 1 / 137.035989

, whose value is in agreement with the most recent value measured experimentally in Ref. [9].

The most recent theoretical value of Sommerfeld’s constant was calculated in the context of BT and is presented in Ref. [10] because of the formation of a hydrogen atom during the electron-proton capture process. The estimate obtained with the formation of the hydrogen atom gives an extremely precise and stable value of the coupling constant

α = 1 / 137.035950244954

, which differs from that obtained in the case of the free interaction of

2.1 10^{- 3}

ppm and from that obtained experimentally from

2.6 10^{- 3}

ppm (cf. Ref. [9]). The difference between the theoretical and experimental values was due to different physical contexts. In fact, the theoretical value of the fine-structure constant is obtained in the interaction process without the system interacting with external observers, and thus, is altered.

2.2. Relativistic Behavior: Energy and Momentum of a DEMS

Because the observation of a DEMS involves the measurement of the energy and momentum of each its component, in the simple case of a hydrogen atom formed by an electron and a proton, both are perceived by an external observer as two moving particles, each with its own energy and momentum, and with velocities referred to the Lab.

As proven in Ref. [7], an observer placed on one of the two particles in interaction feels the other as carrying all the energy and momentum that will form the DEMS. This has already been applied in Ref. [10] to simulate hydrogen formation with electron-proton capture, therefore, the total energy and momentum of hydrogen in formation correspond in according with the BT to those of a material particle with energy and momentum equal to those of the relativistic approaching particle:

\{\begin{matrix} E = γ ε \\ P = γ β \frac{ε}{c} \end{matrix}

(5)

From the point of view of the proton,

ε

is the resting mass energy of the electron in motion,

γ

and

β

are the Lorentz factor and the velocity of the electron divided by the light speed

c

at the time of the interaction, respectively.

2.3. An Atom Described by a DEMS with Zero Radial Emission

In general, when a DEMS is formed it emits a wave which propagate in all direction energy and momentum. To obtain the conditions under which the DEMS has null radial emission becoming a stable atomic system, it is necessary to examine the emissive conditions of the dipole.

Let us begin considering the local electromagnetic contribution to the radiated energy for a DEMS in a given direction (Cf. Ref. [6])

δ ε_{r a d} = \frac{1}{c} \int_{V_{δ Σ}} S d^{3} x

(6)

Equation (6) can be usefully analyzed by introducing the local brightness vector

Y

, defined as:

\nabla \cdot Y = \frac{1}{c} S = \frac{1}{4 π} |E \times B|

(7)

so that Equation (6) can be rewritten as

δ ε_{r a d} = \oint_{V_{δ Σ}} Y \cdot d a .

(8)

with

d a

infinitesimal element of the surface of the ideal sphere

Σ

, through which the luminosity is flowing.

By setting

|ε \times B| = R (r) Θ (θ)

, where

R (r)

and

Θ (θ) = |f (θ)|

describe the radial and angular behavior of the Poynting vector, respectively. To have a physically correct behavior for the emission of energy from the source with

q

arbitrary value of electric charge, it is necessary that

R (r) \approx \frac{q^{2}}{r^{4}} .

(9)

The length

S

of the Poynting vector in Equation (7), which transports the energy of the source, coincides with the radial component of the Poynting vector of the dipole.

S \equiv S_{r} ≅ \frac{c q^{2} Θ_{r} (θ)}{4 π r^{4}}

(10)

where

Θ_{r} (θ) = |f_{r} (θ)|

denotes the angular distribution of the radial part of the Poynting vector.

To analyze the radial emissions of a DEMS, Equation (7) can be written in polar coordinates as follows:

\frac{1}{r^{2}} \frac{\partial}{\partial r} r^{2} Y (r, θ) = \frac{q^{2} Θ_{r} (θ)}{4 π r^{4}} .

(11)

By setting the depth of field variable

z = k r

and neglecting the angular behavior, we define

y = \frac{4 π Y (r, θ)}{q^{2} Θ_{r} (θ) k^{3}}

(12)

and Equation (11) can be rewritten as

\frac{d y}{d z} + \frac{2}{z} y - \frac{1}{z^{4}} = 0

(13)

the general solution of which

y = \frac{1}{z^{3}} (ξ_{0} z - 1)

(14)

describes the behavior of the local brightness on the surface of the spherical shell

Σ_{z / k}

as a function of

z

For fixed wave number

k

and for

r \geq λ

, the wave converges to that emitted by an ideal point source; therefore, considering the asymptotic behavior of Equation (14), we obtain the luminosity on the surface

Σ_{z / k}

y_{i d} \approx \frac{ξ_{0}}{z^{2}} .

(15)

Comparing Equations (14) and (15), we can see that a DEMS emits less energy than a point source, and the difference in brightness is

Δ y = y_{i d} - y \approx \frac{1}{z^{3}} .

(16)

This implies that an amount of energy proportional to Equation (16) was retained within the surface

Σ_{z / k}

and was located in the volume around the DEMS. As the emission of energy from the source is continuous, there is a characteristic equilibrium spherical surface for which the energy emitted through the surface is equal to that not yet emitted. Because the wavelength characterizes the period of the wave, it is assumed that equilibrium is reached on the first wavefront of the DEMS for

r = λ

. Using Equations (15) and (16), we can then write the equilibrium condition as

Δ y = y,

(17)

whose solution gives

ξ_{0} = 1 / π

. Consequently, the brightness

Y

turns out to be

Y = \frac{q^{2}}{4 π r^{3}} (\frac{2 r}{λ} - 1) Θ_{r} (θ)

(18)

that it is equal to zero in

r_{0} = λ / 2

for each angular direction by reaching the maximum brightness for

r_{\max} = 3 λ / 4

. The extremes of the interval

[r_{0}, r_{\max}]

delimits the spherical crown defining the source zone (SZ) of the DEMS, so for

r < r_{0}

the radial emission of the DEMS is not active, and the DEMS absorbs energy and momentum from the impinging interacting particles and per

r > r_{\max}

the production of energy of the DEMS is ended.

Considering an atom formed by the mutual electron-nucleus capture of charges

(\begin{matrix} - e & + Z e \end{matrix})

, both associated with an inertial mass with a proper value of energy at rest, the total input energy described by Equation (5) can be used to power the rotational energy of the system around the center of mass of the source (Cf. Ref. [10]). When capture occurs and the electron orbits around the nucleus at a fixed orbital distance

λ_{o} = 2 r_{0}

, the round bracket in Equation (18) becomes null

(\frac{2 r_{0}}{λ_{o}} - 1) = 0

(19)

therefore, the dipole cannot emit radially and the brightness (18) becomes zero. In this case the electron and nucleus form a bound state in which the wave propagation occurs only with the transverse component of the Poynting vector along a circular path inside the spherical surface

Σ_{0}

delimiting the internal border of the SZ of radius

r_{0} = λ_{o} / 2

Remembering that the electron-nucleus interaction localizes fundamental energy and momentum

E = h c / λ_{o} = ℏ k_{1} c

with

k_{1} = 2 π / λ_{o}

, by generalizing the interaction energy at a multiple of the fundamental energy as

E_{n} = n E = ℏ k_{n} c

with

k_{n} = n k_{1}

, using the radial field depth variable

z = k_{n} r

, Equation (14) becomes

y = \frac{1}{z^{3}} (\frac{z}{π} - 1) .

(20)

that cancels for

z = π

. Therefore, the spherical shell

Σ_{π / k_{n}}

bounding the virtual center of the source is a surface with zero radial emission. A captured electron in motion on this surface maintains a constant distance

λ_{o}

from the nucleus, so that the DEMS does not emit radially. It follows that the surface

Σ_{π / k_{n}}

represents a sphere on which the radial component of the Poynting vector is everywhere zero and the transversal one propagates the electron as a local stationary wave of energy

E_{n}

. From the perspective of the nucleus, which has a higher mass than the electron, the captured electron forms a circular path centered on the nucleus with a radius

λ_{o}

. Under these conditions, the complete DEMS rotates around the nucleus taken as like a fixed point describing an electromagnetic field within a toroidal spacetime of extreme radius

λ_{o}

by defining the outer radius of the stable atom with energy equal to that of the n-th energy level with effective orbital radius

r_{n} \leq λ_{o}

In the ground state, the DEMS will emit radially only when the electron is stimulated by external fields to change the energy. In fact, during the transition between two different energy levels, a non-zero radial component of the Poynting vector is produced. After the emission of the excess of energy, the atom becomes stable again, returning to the ground state; if the system is destabilized by the transfer of more energy than that which characterizes the electron bond, the atom ionizes, returning the captured electron to the environment.

2.4. The Concepts of Electron Spin and Atomic Spin in BT for Two Fermions

In quantum mechanics, spin is a fundamental characteristic of the particles. It is considered a form of angular momentum that is intrinsic to particles and is independent of their motion or position. This phenomenon of quantum mechanics has no equivalent in classical physics.

Following BT, the spin is explained considering that each particle of charge

q

is entangled with all the anti-charges

\bar{q}

with which they are causally connected forming independent DEMS independently by their distance of interaction (Cf. Ref. [6] and [7]). For an atom of hydrogen, using the field vector

f

defined in Equation (3), the angular momenta associated with the hemispheric zones of a DEMS containing the positive or the negative interacting charges (IC) forming the DEMS, in units of

ℏ

, are defined as the field spin down and up of the IC:

L_{I C} = \frac{1}{ℏ} \int_{0}^{π} d ϕ \int_{- π / 2}^{π / 2} \frac{2}{3} \frac{e^{2}}{c} (\begin{matrix} f_{t} (θ) \\ {\tilde{f}}_{t} (θ) \end{matrix}) d θ ≅ (\begin{matrix} - \frac{1}{2} \\ + \frac{1}{2} \end{matrix})

(21)

where

f_{t} (θ)

is the transverse component of the vector

f

and

{\tilde{f}}_{t} (θ) = - f_{t} (θ)

is the same component for switched charges (Cf. Ref. [6]). Thus, the sign of the spin of the particles depends on the frame in which the interaction is observed.

Extending the calculation to the complete SZ and assuming the dipole axis as the axis of symmetry, by integrating the angular functions over all directions, we obtain a null total spin for both unswitched and switched charges:

L_{S Z} \equiv L_{p h}^{(0)} = \frac{1}{ℏ} \int_{0}^{π} d ϕ \int_{- π / 2}^{3 π / 2} \frac{2}{3} \frac{e^{2}}{c} (\begin{matrix} f_{t} (θ) \\ {\tilde{f}}_{t} (θ) \end{matrix}) d θ = (\begin{matrix} 0 \\ 0 \end{matrix}) .

(22)

In this case, the frame invariance provides the null spin values of the source as a unique effective component.

Considering the electromagnetic emission of the source, the directions of propagation of the photons are along the wave number

k

direction, which is normal to the dipole axis. Then, for an observer, the angular momentum can be naturally calculated using the propagation axis as the axis of symmetry around which the dipole moment spins during the interaction. By calling

φ ’

the angle measured around this axis, we obtain:

L_{p h}^{(1)} = \frac{1}{ℏ} \int_{0}^{2 π} d ϕ ’ \int_{- π / 2}^{π / 2} \frac{2}{3} \frac{e^{2}}{c} (\begin{matrix} f_{t} (θ) \\ {\tilde{f}}_{t} (θ) \end{matrix}) d θ = (\begin{matrix} - 1 \\ + 1 \end{matrix})

(23)

The two components of this vector are the spin components corresponding to the left and right circular polarizations of the wave, that is, of the emitted photons; however, in this case, an atom does not emit; therefore, the spin component (23) for an atom of hydrogen in stable conditions may not be considered.

Therefore, for an atom of hydrogen there are

Z = 1

DEMS components and it is possible to define three types of spins: atomic spin (22)

L_{S Z} = 0

for atoms in the fundamental state which is unobservable; electron spin (21)

L_{I C} = \pm 1 / 2

for the two particles forming the DEMS; and emission spin (23)

L_{p h} = \pm 1

for non-stable atoms. This spin value defines the orientation of the emission axis of DEMS. It is important to emphasize that the spin of a single particle continues to exist even when the particles have reached a great distance because the DEMS continue to exist also if the amount of localized energy is near to zero; therefore, spin is a property of the particle and indicates the existence of an interconnection with other particles. In this sense, the DEMS group all electromagnetically connected particles into pairs, creating a type of electromagnetic entanglement (Cf. Ref. [7]).

In summary, two interacting particles in pair can have spin

s = (- 1 / 2, + 1 / 2)

, whereas the DEMS formed using

L_{S Z}

and

L_{p h}

can have spin

L = (- 1, 0, + 1)

, where the null value always refers to the unobservable ground state of the hydrogen.

3. The Atomic Model: Kinetic Energy of the Orbiting System after Electronic Capture

In compliance with one of the fundamental principles of BT (Ref. [6]), the capture of one electron by the nucleus during the atom formation takes place in the form of a charge-anticharge interaction, forming a number Z of independent DEMS.

For simplification, we consider the atom of hydrogen in formation as an isolated system electron-proton, with the transverse component of the momentum of the electromagnetic field associated with the TCPV of the DEMS

p_{t} = \frac{1}{c^{2}} \int_{V_{Σ_{r}}} |S_{t}| d^{3} x,

(24)

from a mechanical point of view, the electron in motion along its trajectory has respect the proton total momentum

p = p_{r} + p_{t}

with angular momentum

L = r \times p = r p_{t} \hat{l}

(25)

Before capture when the electron is at a great distance from the proton

p_{t} ≅ 0

, therefore

L = 0

, for the conservation principle the time derivative of Equation (25) must be equal zero maintaining constant the original null angular momentum

|\frac{d L}{d t}| = r \frac{d p_{t}}{d t} + \frac{d r}{d t} p_{t} = 0

(26)

that implies that even after the formation of the atom, in the ground state the angular momentum (25) must be zero. In fact, the spin of a DEMS in Equation (22) returns as a value

l \equiv L_{S Z} = 0

As shown in Ref. [4] and [6], for a DEMS, the two addends in Equation (26) can be interpreted as the sum of two opposite energies. The first

T_{\exp} = r \frac{d p_{t}}{d t} < 0

is the expansion energy of the SZ due to the radial propagation of the electromagnetic field of the DEMS, while the second

T_{s p i n} = \frac{d r}{d t} p_{t} > 0

is the rotational energy associated with the spin of the field due to the circular propagation of the transverse component of the Poynting vector around the center of the DEMS.

From a mechanical point of view, during DEMS formation,

T_{s p i n}

is provided by a force acting radially on the electron-proton system. In fact, the strength of the radial force

F = \frac{d p_{t}}{d t} < 0

being less than zero is attractive in such a way that energy

T_{s p i n} = - T_{e x p} = - r F

is positive. Considering the DEMS point of view, the velocity of propagation of the electromagnetic field along the radial direction is

\frac{d r}{d t} = c

. From Equation (26) and from the definition of the force acting on the moving electron, we can write

d p_{t} = - \frac{1}{c} F d r > 0 .

(27)

During the capture process, the Coulombian interaction is always active; instead, the electromagnetic interaction mediated by the DEMS connecting the two particles is active only during a short period of time defined from the instant at which the source zone (SZ) of the DEMS starts at a reciprocal distance

3 λ_{o} / 2

until the SZ stops producing energy at the reciprocal minimum distance of interaction

λ_{o}

. Therefore, the total mechanical momentum acquired by the system at the end of the capture process is given by:

P = - \frac{1}{c} \int_{0}^{2 π} d φ \int_{λ_{0}}^{\infty} F \cdot d r > 0

(28)

that correspond to the conservation of the total transverse component of the momentum acquired by the electromagnetic field of the DEMS, therefore using Equations (24) and (27), the total momentum (28) associated with the field spin is obtained by integration in the form

P = \frac{1}{c^{2}} \int_{0}^{2 π} d φ \int_{V_{Σ_{r}}} |S_{t}| d^{3} x

(29)

In general, considering the Coulombian force active between electron and nucleus,

F = - \frac{Z e^{2}}{4 π ε_{0} r^{2}}

(30)

in SI units Equation (28) yields the total field spin energy

E_{s p i n} = P c

acquired by the system:

E_{s p i n} = \frac{Z e^{2}}{4 π ε_{0}} \int_{0}^{2 π} d φ \int_{λ_{o}}^{\infty} \frac{d r}{r^{2}} = \frac{Z e^{2}}{2 ε_{0} λ_{o}},

(31)

when the electron and nucleus reach a minimum interaction distance corresponding to the de Broglie wavelength

λ_{o} = λ_{e l} β^{- 1} γ^{- 1}

of the electron (Cf. Ref. [7] and [10]), the energy

E = P c = 2 π \frac{ℏ c}{λ_{o}}

(32)

of the quantum exchanged between the electron and the nucleus acquired by DEMS, propagates by the TCPV on the internal surface of the SZ of the DEMS keeping the energy of the atom stable.

In Equation (32) is used as the standard symbol of the Planck action in Dirac form

ℏ

, because in this case, the photon refers to a free interaction between charge pairs where the value of the action constant corresponds to Planck’s one, and in the case of the use of the Sommerfeld fine-structure constant the symbol is

α

, when necessary, the symbol for the different orbit levels will be diversified to avoid confusion.

Because the total energy (32) exchanged during the interaction cannot involve photons with energies greater than that which characterize the DEMS of a single electron-proton interaction given in Equation (32), the total energy exchanged in the process of electron capture can only be a multiple of this fundamental energy:

E_{c a p t} \equiv E_{n} = n E

(33)

Since the center of mass of the atom refers to an observer placed in the laboratory system, using Equations (31)–(33), in accordance with the four-momentum invariant (Cf. Ref. [10]), the total mass energy at rest calculated in the center of mass of the system is given by

ε = \sqrt{E_{c a p t}^{2} - E_{s p i n}^{2}}

(34)

Substituting in Equation (34) and the respective Equations (31)–(33), the rest energy of the atom gives

ε = E_{c a p t} \sqrt{1 - {(\frac{Z}{n} \frac{e^{2}}{4 π ε_{0} ℏ c})}^{2}}

(35)

with beta ratio of the electron

β_{n} = \frac{Z}{n} \frac{e^{2}}{4 π ε_{0} ℏ c} = \frac{Z}{n} α

(36)

and orbital Lorentz factor,

γ_{n} = 1 / \sqrt{1 - β_{n}^{2}}

. From Equations (31), (35), and (36), the capture energy (33) of the electron can be written as the identity

E_{n} = 2 π \frac{ℏ c}{λ_{n}} \equiv γ_{n} ε,

(37)

where the minimum interaction distance

λ_{n} = λ_{o} / n

is the de Broglie wavelength of the electron in the n-th energy level, that is, from the relativistic point of view,

λ_{n} = λ_{e l} β_{n}^{- 1} γ_{n}^{- 1}

gives

λ_{n} = λ_{e l} \sqrt{\frac{n^{2} σ^{2}}{Z^{2}} - 1}

(38)

with fundamental pseudo-orbit wavelength calculated as

λ_{o} = λ_{e l} n \sqrt{\frac{n^{2} σ^{2}}{Z^{2}} - 1} .

(39)

It is convenient to observe now that Equation (39) gives as the natural limit of the atomic number for the formation of a stable atom

Z \leq 137

. The existence of this limit in agreement with Chandrasekhar prediction¹² that normally has to do with the nucleus stability let us to suppose that the formation of the atom is more related of haw one can think to the nucleus formation.

The calculus of the orbital radius for the n-th energy level defined by the Equation (37), is given by the condition of coherence of the electromagnetic circulating wave, i.e., the effective length of the circumference of the orbit on which the wave propagates stably must be equal to a multiple of the de Broglie wavelength of the atomic system, because the electron cannot have a de Broglie wavelength different to the capture one defined by the Equation (32):

2 π r_{n} = n λ_{n} = λ_{o}

. By Equation (38), we obtain the radius of the pseudo-orbit which characterizes the n-th quantum state of the atom

r_{n} = ƛ_{o} = ƛ_{e l} n \sqrt{\frac{n^{2} σ^{2}}{Z^{2}} - 1} < λ_{o}

(40)

The pseudo-orbit is a circle of radius (40) on which the electron is described by a circulating electromagnetic wave. For atoms with

Z ≪ n σ

Equation (40) can be approximated in the form

r_{n} ≅ \frac{n^{2}}{Z} a_{0}

with

a_{0} = ƛ_{e l} σ

Bohr radius of the hydrogen.

Because the energy localized by the capture was completely transmitted to the system, Equation (37) can be rewritten using the reduced mass energy at rest of the electron-nucleus system rather than that of the electron, that is, one replaces at

ε_{e}

the reduced mass energy

ε_{μ} \equiv \frac{ε_{n u c} ε_{e}}{ε_{n u c} + ε_{e}},

(41)

therefore, following the founding principles of BT, to calculate the kinetic energy of the orbiting system is enough to subtract to the capture energy (37) relative to the orbiting system its energy at rest (41), therefore, in accordance with Special Relativity for the kinetic energy one obtains

K_{n} = ε_{μ} (γ_{n} - 1)

(42)

4. Effective Energy at Rest of a Nucleus

In Equation (41), it is necessary to estimate the value at rest of the mass energy

ε_{n u c}

of the nucleus; therefore, for a fixed atomic number

Z \geq 1

with a number

N

of neutrons, one can define

i = 1, 2, ..., N

the isotopic number. Considering that only the DEMS formed by electron-proton interactions contribute to the total energy of the atom, the presence of neutrons in the nucleus partially shields the positive charge by affecting the amount of energy available for the interaction. In fact, for a fixed value of

Z

, when the number of neutrons increase, neutrons and protons are arranged in such a way to maximize the stability of the nucleus. Therefore, the energy of the resting mass of the nucleus participating in the formation of the DEMS during the interaction with the orbital electrons cannot be higher than that of the protons forming the nucleus, therefore, it can be assumed that the mass of the nucleus participating in the reduced mass of the system is a fraction is lower than that of the nucleus and can be supposed to be proportional to the nucleus mass by a fraction

ζ = Z / (Z + N)

(43)

of the effective mass energy of the nucleus.

Considering an element

X

with its isotopes family, each with relative atomic mass

A_{r} ({}^{i}X)

with

i = 1, 2, ..., N

, and abundance

w ({}^{i}X)

, the average atomic mass of the mixing of the isotopes of the element gives

\bar{A} (X) = \sum_{i = 1}^{n} w ({}^{i}X) A_{r} ({}^{i}X)

(44)

which is equal to the sum of the atomic number

Z

, of the mean number of neutrons weighted as a function of their isotope abundance

\bar{N} = \sum_{i = 1}^{n} w ({}^{i}X) N_{i},

(45)

of the atomic electrons expressed in amu

z_{e} = Z ε_{e} / ε_{u}

(46)

and of the excess or defect of mass characteristic

Δ

of the considered nucleus, i.e.,

\bar{A} (X) = Z + \bar{N} + z_{e} + Δ .

(47)

Considering that for an element

X

, the resting mass energy associated with the effective nucleus, that is, the fraction of the average nuclear mass electrically active of a natural isotopic mix of the same element can be defined by considering the charge fraction (43) of the effective mass energy:

M (X) = \bar{A} (X) - z_{e} = Z + \bar{N} + Δ

(48)

by using the fraction (43) with the effective mass (48) one obtains

ε_{n u c} (X) = ζ M (X) ε_{u}

(49)

For an isotopic mix of the element

X

, Equation (49) becomes

ε_{n u c} (X) = \frac{Z}{Z + \bar{N}} (\bar{A} (X) - Z \frac{ε_{e}}{ε_{u}}) ε_{u}

(50)

Considering the natural mix of atoms formed by the fundamental isotopes of hydrogen

{}^{1}H

and

{}^{2}H

{}^{3}H

is neglectable, the resting mass energy (50) gives

ε_{n u c} (H) = 1.50327737 10^{- 10} J

instead of pure

{}^{1}H

and

ε_{n u c} ({}^{1}H) = 1.50327759 10^{- 10} J

. In both cases, the evaluations are lower than that of the remaining energy of the proton because of the use of the energy of an atomic mass unit:

ε_{u} = 1.49241808 10^{- 10} J

estimated for an atom of

{}^{12}C

, but in the case of the natural mix of hydrogen, the value is even lower because of the shielding effect due to the presence of neutrons in the nucleus of deuterium. In all cases, the differences in the model results were minimal, and Equation (50) is suitable for hydrogen and deuterium atoms, and can be extended to more heavy atoms as helium and lithium.

5. Quantum Numbers

Equation (33) is the energy acquired by the atomic system once after electron capture, stability is achieved. This value includes the mass energy at rest of the electron and the rotational kinetic energy provided during electron capture. The integer value

n

can be thought to consist of two components: a number

n_{r}

that defines the multiplicity of the action associated with the radial momentum and a number

n_{φ}

that defines the multiplicity of the action associated with the angular momentum supplied to the nucleus during the electron capture in such a way that

n = n_{r} + n_{φ}

with degenerate energy states associated with all their combinations without the orbit to be elliptical, as predicted by the Sommerfeld model, because this shape would produce a radial emission in the DEMS. To simplify, in accordance with the Bohr-Sommerfeld model, the principal quantum number

n_{r} \equiv n = 1, 2, 3...

and secondary quantum number

n_{φ} \equiv l = 0, 1, 2, ... n - 1

in such a way that

n = n + l

Because the spin of an atom in the fundamental state is always zero because the two particles forming each single DEMS have opposite spins, for excited atoms subject to external fields, the spatial orientation of the photon emission can be defined by a new number obtained as the product

m = l L

with values

m = (- l, ... 0, ... + l)

. This number is consistent with the role of the magnetic quantum number, and is in fact different from zero only if the atom is plunged in an external electromagnetic field, assuming a precise orientation up or down with rotational kinetic energy defined by the secondary quantum number. Therefore, it is possible to define the complete state of the electron and its atomic system using the spin

s = (- 1 / 2, + 1 / 2)

of the electron and the set of quantum numbers

(n, l, m)

defining the state of the atomic system in the environment.

6. The Wave Behavior of an Interacting Electron: Orbital Eigenvalues

As discussed in Ref. [11] and in the estimation of the Sommerfeld constant during the formation of a hydrogen atom by the electron-proton capture (Cf. Ref. [10]), an electron during its interaction with a positive charge as a nucleus gives up all of its energy at the DEMS, and its propagation is described by a wave described by the linear differential equation:

ℏ (\frac{1}{c} \frac{\partial}{\partial t} - \cos θ \frac{\partial}{\partial x} + i K) ψ = 0

(51a)

with solutions:

ψ = φ Ξ = \{\begin{matrix} e^{i (\frac{E}{ℏ} t + \frac{P}{ℏ} x - K c t)} t < 0^{-} \\ e^{- i K c t} 0^{-} \leq t \leq 0^{+} \\ e^{i (\frac{E}{ℏ} t - \frac{P}{ℏ} x - K c t)} t > 0^{+} \end{matrix}

(51b)

The first part of Equation (51b), defined as the wave function

φ = e^{- i K c t}

it is associated with the corpuscular characteristics of the captured electron, which carries the residual momentum of the electron corresponding to the momentum not yet transferred in time in other interactions, that is, the residual momentum

ℏ K_{n} = γ_{n} (1 - β_{n} \cos θ) ε / c

, whose value is always less than or equal to the Galilean momentum

m_{e} c

of the electron (Cf. Ref. [8]), and represents the total momentum transferred to the system during the capture process at time

t = 0

. The second part of Equation (51b) is a wave function

Ξ = e^{i (\frac{E}{ℏ} t \pm \frac{P}{ℏ} x)}

describing the system before and after the interaction by carrying information regarding the energy and momentum of the moving electron.

For an atom, the interaction between electron and nucleus is stable and is described over time as a DEMS formed in the time interval

0^{-} \leq t \leq 0^{+}

with action

ℏ

. In this case, we can consider the system electron nucleus, as described by the full wave function part

ψ = e^{- i K_{n} c t}

of Equation (51b), which describes the momentum exchange. In this case, the wave Equation (51a) can be rewritten in the reduced form as

(\hat{ℋ} + i c ℏ K_{n}) ψ = 0

, with

\hat{ℋ} = ℏ \frac{\partial}{\partial t}

, which can be considered the Hamiltonian operator of the stable system, variable only on time, with

c ℏ K_{n}

eigenvalues of the energy exchanged, corresponding to

E_{n}^{*} = γ_{n} (1 - β_{n} \cos θ) ε

that after electron capture with

\cos θ = 0

becomes the capture energy (33), that is,

E_{n}^{*} \equiv E_{n}

7. Electron Bond and Orbital Energy

The captured electron rotates with the nucleus around the common center of mass with a rotational kinetic energy equal to Equation (42), which balances the attractive force, such that the sum of the orbital relativistic kinetic energy with the binding energy is zero:

K_{n} + B_{n} = 0

. This condition implies that the energy that characterizes the capture of electrons in the n-th orbit of the ion must be opposed to the relativistic kinetic energy of the electron, using Equation (42) and using the values of the modified fine structure constants

α_{n}

expressed as a function of the first quantum number associated with the n-th capture level, computed using the recursive correction method examined in Ref. [10], the binding energy of the n-th orbit is given by

B ​_{n} = - K_{n} = ε (1 - \frac{1}{\sqrt{1 - {(\frac{α_{n}}{n})}^{2}}})

(52)

The values of

σ_{n}

and

α_{n}

for the atoms of hydrogen and deuterium are listed in Table 1. Figure 1 shows the orbital values of the orbital structure constant, that is,

σ_{n}

. Table 2 and Table 3 show the values of

σ_{n}

and

α_{n}

for helium and lithium atoms.

8. Atomic Energy Levels

To define the energy levels of the DEMS model of an atom, it is necessary to consider the difference in the binding energy (52) between the fundamental level with

n = 1

and another level

n > 1

, which is equivalent to the difference between the capture energy

E_{1}

for an electron bound to the bare atomic nucleus and the capture energy

E_{n}

at a level other than the principal quantum number. Using Equation (52), we can write:

\frac{1}{λ_{n}} = \frac{B_{n} - B_{1}}{h c} = \frac{E_{1} - E_{n}}{h c}

(53)

with

h

, standard value of the Planck constant obtained for an electron-proton free interaction during the transition between levels.

8.1. Hydrogen and Deuterium

The estimations of the energy levels for hydrogen in Table 4 and deuterium in Table 5 are presented. Using Equations (41), (52), and (53) and the orbital fine structure constant

α_{1}

shown in Table 1, the fundamental level of hydrogen, corresponding to the quantum number

(n = 1, l = 0)

, has a binding energy

B_{1}^{H} ​ = - 2.17877438 10^{- 18} J

equivalent to

|B_{1}^{H}| = 13 . 5988401 eV

. This value is only slightly lower than the Rydberg energy

E_{H} = 13.6057028 eV

of the atom; thus, of the kinetic energy of the electron

K_{e} = 13.6062462 eV

measured immediately before the capture process begins (see Ref. [10]). In fact, both values are greater than

|B_{1}^{H}|

because the effective resting energy of nucleus

{}^{1}H^{+}

is defined by Equation (49) with

\bar{A} (H) \equiv A_{r} ({}_{1}H) = 1.00782503223

being only slightly lower than the energy of proton

ε_{n u c} ({}^{1}H^{+}) = 1.50327759464 10^{- 10} J ≅ ε_{p}

; therefore, Equation (41) gives a reduced mass energy of the system

ε_{μ} < ε_{e}

only after the electron capture occurs, whereas before electron capture, the kinetic energy is that of the impinging electron, and the mass energy involved is independent of the mass of the proton because of the delay in the propagation of the electromagnetic field during the DEMS production. The proton can be considered not involved, that is, the proton is perceived as having an infinite mass by giving

ε_{μ} \to ε_{e}

. In this case, the relativistic kinetic energy of the electron was greater than that of

|B_{1}^{H}|

. In addition, in the case of Rydberg energy, the experimental value is measured during the process of ionization of the atom, that is, during a non-relativistic ejection of the electron in which the total energy is that of the resting mass energy

ε_{e}

The calculation for deuterium is similar to that performed for hydrogen, considering the effective resting energy of the deuterium nucleus defined by Equation (49) using

\bar{A} (H) \equiv A_{r} ({}_{2}H) = 2.01410177812

one obtains

ε ({}^{+}H^{2}) = 1 {. 50253160466 10}^{- 10} J < ε_{p}

. In this case, the fundamental energy level for deuterium (D) calculated using Equation (52) is given by

|B_{1}^{D}| = 13.5988364 eV

, with energy lower than that of hydrogen.

It is important to emphasize that the theoretical values calculated are exact values, that is, they refer to the atoms that are formed during the electron capture process according to the BT model. The energy level values in Table 2 and Table 3 were calculated using Equation (53).

8.2. Helium and Lithium

To extend the model to atoms with

Z > 1

, it is interesting to consider helium with

Z = 2

and lithium with

Z = 3

. These two atoms are interesting because they are the heaviest elements produced during non-stellar primordial nucleus synthesis. The procedure for calculating the energy levels was the same as that for hydrogen. The energy levels for helium and lithium are listed in Table 6 and Table 7, respectively.

9. Spectral Lines

To calculate the emission spectrum wavelengths for excited atoms, it is necessary to consider the change in energy of an atom or ion when the electron-nucleus system receives sufficient energy to change the energy state of one or more DEMS. If the energy received is sufficient to change the state of the system, the electron moves on the spherical shell, which corresponds to the energy absorbed at a wavelength

λ_{j} < λ_{i}

con

j > i

at a distance

r_{j} > r_{i}

from the nucleus, and then after a time

τ_{j i} = h / (E_{i} - E_{j})

returns to the original orbital emitting the surplus energy by means of a photon. Using the binding energy (52), since the excited final state

j

has a lower binding energy than the initial ground state

i

|B_{i}| > |B_{j}|

with

B_{j} - B_{i} = E_{i} - E_{j}

, for the return energy jump

j \to i

the use of the first part of Equation (37) yields the emission wavelength:

λ_{j \to i} = τ_{j i} c = \frac{h c}{E_{i} - E_{j}} = \frac{l_{0}}{γ_{i} - γ_{j}}

(54)

with

l_{0} = \frac{h c}{ε_{μ}} = (1 + \frac{ε_{e}}{ε_{n u c}}) \frac{h c}{ε_{e}} = λ_{e} + λ_{n u c}

(55)

and

γ_{i}

γ_{j}

Lorentz gamma factors are associated with the initial and final energy levels between which electron transitions occur.

From a phenomenological point of view, atoms emit only when they acquire enough energy to modify the pseudo-orbital of one or more electrons by transforming into emitting DEMS This process, called atomic excitation, consists of distributing an arbitrary amount of energy to the electrons of the atom starting from the outermost electrons that have a distance of interaction with the nucleus and an energy of greater bonding than the innermost electrons. In this way, in a power process, in which all the electrons of the atom acquire sufficient energy over time to move to higher energy levels, the atom behaves as a multi-dipole source (DEMS) by emitting chromatic photons associated with the excess energy acquired by the electron-nucleus system. The consequent effect is the return of the electrons to their original configuration. The process described involves each electron undergoing slippage during the level jump that involves the exit from the condition of atomic stability, inducing the transformation of the atom into a multi-dipole source with consequent chromatic emission of energy forming the characteristic spectrum. The orbital slippage causes the electron to move for a limited time on a noncircular trajectory, not necessarily elliptical, with respect to which the fine-structure constant differs from the exact value of the corresponding layer; therefore, a correction

χ_{i, j}

that takes into account the shift is necessary. Table 7 shows the correction ratios obtained empirically, considering the positive and negative orbital slippage of electrons during jumps between the energy levels. The corrections proposed are obtained by modifying the value of the fine structure constant of the outer layer such that the emitted spectral line corresponds to the experimental observation, which corresponds to a model that agrees exactly with the measured emission spectrum. In Table 8, Table 9 and Table 10 are tabulated the estimations of the principal transition lines of the Lyman, Balmer, and Paschen series for hydrogen and Table 11, Table 12 and Table 13 for deuterium. The correct values for the orbital slip are displayed in the third column.

λ_{j \to i} = \frac{l_{0}}{\frac{1}{\sqrt{1 - {(\frac{Z}{i} α_{i})}^{2}}} - \frac{1}{\sqrt{1 - {(\frac{Z}{j} χ_{i, j} α_{j})}^{2}}}}

(56)

Table 8. H I Emission Lines—Lyman Series (

Z = 1

N = 0

A_{r} ({}^{1}H) = 1.00782503223

Table 8. H I Emission Lines—Lyman Series (

Z = 1

N = 0

A_{r} ({}^{1}H) = 1.00782503223

$j \to i$	Theoretical Exact (nm)	Th. with slippage	Exp. ⁽¹⁾
10-1	92.09396771	92.0947	92.0947
9-1	92.31267996	92.3148	92.3148
8-1	92.62019267	92.6249	92.6249
7-1	93.07241725	93.0751	93.0751
6-1	93.77788760	93.7814	93.7814
5-1	94.97176049	94.9742	94.9742
4-1	97.25097237	97.2517	97.2517
3-1	102.56913342	102.5728	102.5728
2-1	121.56256576	121.5670	121.5670

⁽¹⁾ NIST ASD Spectra lines for Hydrogen—Lyman series.

Table 9. H I Emission Lines—Balmer Series (

Z = 1

N = 0

A_{r} ({}^{1}H) = 1.00782503223

Table 9. H I Emission Lines—Balmer Series (

Z = 1

N = 0

A_{r} ({}^{1}H) = 1.00782503223

$j \to i$	Theoretical Exact (nm)	Th. with slippage	Exp. ⁽⁶⁾
10-2	379.901988789	379.7909	379.7909
9-2	383.651625364	383.5397	383.5397
8-2	389.019526145	388.9064	388.9064
7-2	397.124003794	397.0075	397.0075
6-2	410.293779975	410.1734	410.1734
5-2	433.173044477	434.0472	434.0472
4-2	486.273257938	486.1350	486.1350
3-2	656.46728858	656.2790	656.2790

⁽¹⁾ NIST ASD Spectra lines for Hydrogen—Balmer series.

Table 10. H I Emission Lines—Paschen Series (

Z = 1

N = 0

A_{r} ({}^{1}H) = 1.00782503223

Table 10. H I Emission Lines—Paschen Series (

Z = 1

N = 0

A_{r} ({}^{1}H) = 1.00782503223

$j \to i$	Theoretical Exact (nm)	Th. with slippage	Exp. ⁽¹⁾
10-3	901.75169733	901.5300	901.5300
9-3	923.16819091	922.9700	922.9700
8-3	954.87279912	954.6200	954.6200
7-3	1005.22717686	1004.9800	1004.9800
6-3	1094.12441164	1093.8170	1093.8170
5-3	1282.17625443	1281.8072	1281.8072
4-3	1875.63856352	1875.1300	1875.1300

⁽¹⁾ NIST ASD Spectra lines for Hydrogen—Paschen series.

Table 11. H I—Correction Ratio.

	Lyman $χ_{1, j}$		Balmer $χ_{2, j}$		Paschen $χ_{3, j}$
1-2	1.000054838	-	-	-	-
1-3	1.000143000	2-3	0.99982067	-	-
1-4	1.000056150	2-4	0.99957331	3-4	0.99989454
1-5	1.000308300	2-5	0.99923863	3-5	0.99974404
1-6	1.000655400	2-6	0.99882536	3-6	0.99957835
1-7	1.000691800	2-7	0.99834800	3-7	0.99945350
1-8	1.001600000	2-8	0.99781600	3-8	0.99919060
1-9	1.000918500	2-9	0.99718730	3-9	0.99914100
1-10	1.000394000	2-10	0.99648380	3-10	0.99875600

Table 12. Hydrogen Atomic Constants.

Atomic Constants Electron Capture Model	Symbol—Equation	Theoretical Estimation (S.I.)
Mean square length	$ρ^{*}$	1.27555662
Structure constant	$σ$	137.035950
Bohr radius (+)	$a_{0} = ƛ_{e l} \sqrt{σ^{2} - 1} ≅ ƛ_{e l} σ$	5.29162744 10^-11m
Orbital radius	$r_{n} = n^{2} a_{0}$	-
Rydberg Constant (#)	$R_{H} = \frac{m_{e} c}{2 h σ^{2}}$	1.09737433 10⁷m^-1
Rydberg Energy (#)	$E_{H} = \frac{m_{e} c^{2}}{2 σ^{2}}$	13.6057028 eV

(+) Theoretical values calculated during capture process. (#) Refers to the electrons captured in the hydrogen atom being stabilized.

Table 13. He II—Emission Lines—Lyman Series (

Z = 2

\bar{A} (He) = 4.00260165

Table 13. He II—Emission Lines—Lyman Series (

Z = 2

\bar{A} (He) = 4.00260165

$j \to i$	Th. Exact (nm)	$χ_{1, j}$	Th. with slippage	Ritz ⁽¹⁾
6-1	23.4348924878197	0.99987710544	23.43472796	23.43472796
5-1	23.7332000516591	0.99994308262	23.73308751	23.73308751
4-1	24.3026966721836	0.99999722314	24.30268767	24.30268767
3-1	25.6315239693052	1.0000384430	25.63177027	25.63177027
2-1	30.3773027712290	1.0000631456	30.37858147	30.37858147

⁽¹⁾ NIST ASD Spectra lines for Hydrogen He II—Lyman series.

Table 14. Li III—Emission Lines—Lyman Series (

Z = 3

\bar{A} (Li) = 6 . 94093785

Table 14. Li III—Emission Lines—Lyman Series (

Z = 3

\bar{A} (Li) = 6 . 94093785

$j \to i$	Th. Exact (nm)	$χ_{i, j}$	Th. With slippage	Exp. ⁽¹⁾
8-1	10.2831914788377	1.02300	10.29	10.29
7-1	10.3333799366446	1.01600	10.34	10.34
6-1	10.4116739308196	0.99800	10.41	10.41
5-1	10.5441714594132	1.00800	10.55	10.55
4-1	10.7971212866958	1.00200	10.80	10.80
3-1	11.3873375502246	1.00100	11.39	11.39
2-1	13.4952527765271	1.00055	13.50	13.50

⁽¹⁾ NIST ASD Spectra lines for Lithium Li III—Lyman series.

10. The Bohr Model as First Order Approximation of the DEMS Atomic Model

Considering McLaurin’s development of the orbital gamma factor in Equation (37)

γ_{n} = \frac{1}{\sqrt{1 - β_{n}^{2}}} = 1 + \frac{1}{2} β_{n}^{2} + \frac{3}{8} β_{n}^{4} + ...

(57)

Equation (52) makes

B_{n} = - ε (\frac{1}{2} \frac{Z^{2}}{n^{2}} α_{n}^{2} + \frac{3}{8} \frac{Z^{4}}{n^{4}} α_{n}^{4} + ...)

(58)

using Equation (58), the difference in capture energy in the two levels

j \to i

given by

Δ E_{j \to i}

can be considered to be formed by a change in rotational energy and a change in the vibrational energy of the atom plus other terms that are negligible because they are not experimentally significant.

Δ E_{j \to i} ≅ δ E_{r o t} + δ E_{v i b} + ...

(59)

whereas the vibrational term is less than

10^{- 4}

times the rotational term, and because the shell-to-shell electron jumps change the rotational energy of the system, but not significantly the zitterbewegung of the nucleus, to simplify Equation (59) It is possible to assess the intensity of the energy transition spectral line by considering only the contribution to the rotational energy change in Equation (59). Thus, using Equations (52), (55), and (59), the reciprocal of the wavelength of the photon emitted by the atom during a transition is given by

\frac{1}{λ_{j \to i}} = \frac{Δ E_{j \to i}}{h c} ≅ \frac{Z^{2}}{2 l_{0}} (\frac{α_{i}^{2}}{i^{2}} - \frac{α_{j}^{2}}{j^{2}})

(60)

To simplify, considering that for orbits the values of the coupling constants are

α_{i} ≅ α_{j} ≅ α

, their value is replaced by that of the free value of the fine-structure constant

α

. Equation (60) becomes

{\frac{1}{λ}}_{j \to i} ≃ \frac{Z^{2} α^{2}}{2 l_{0}} (\frac{1}{i^{2}} - \frac{1}{j^{2}})

(61)

Equation (61) describes the emission line in the transition

j \to i

associated with the electron-nucleus system, and can be rewritten in the classical spectroscopic form:

{\frac{1}{λ}}_{j \to i} ≃ R (\frac{1}{i^{2}} - \frac{1}{j^{2}})

(62)

where using Equation (55) in (61), Rydberg’s constant in Equation (55) is given by:

R = \frac{ε_{0} ε_{e}}{e^{2} σ^{3}} \frac{Z^{2}}{(1 + \frac{ε_{e}}{ε_{n u c}})}

(63)

that for an atom of hydrogen, the value of the constant (63) with

Z = 1

R_{H} = 1.09675973 10^{7} m^{- 1}

; therefore, Equation (63) can be rewritten as

R = Z^{2} R_{H}

in agreement with classical spectroscopy.

This paragraph aims to prove that the DEMS atomic model is consistent in the first approximation to the Bohr model.

11. Effective Nuclear Mass

According to the Bridge theory (Cf. Ref. [8]), any electromagnetic interaction between electric charges in motion generates an inertial mass. By contrast, each inertial mass corresponds to an electromagnetic interaction that produces it.

The existence of a pair of interacting charges (e.g., electron-proton) leads to the creation of a DEMS of limited space-time extension that moves following a trajectory linked to the dynamic characteristics of the interacting particles. The overall energy and momentum of the DEMS correspond to the total energy and momentum of the observed system, in which the resting masses of a particles pre-exist the DEMS and represent the energy retained at the time of their formation starting from one or more events that generated them through a decay or assembly of other particles. At the present stage of BT development, it can be assumed that the phenomena that initiated the resting mass energies of particles are associated with the formation of space-time, but this topic is unrelated to this work.

During the direct interaction of the particles, all available energy is converted into electromagnetic energy of the DEMS, but only during the life of the source. In the case of a DEMS at zero-emission, i.e., an atom, the duration is indefinite, therefore, the total electromagnetic energy of the atom must correspond to the total inertial mass of the observed system. In particular, considering an atom from the point of view of the electron, the sum of all quantum jumps between the possible energy states must correspond to the available energy equivalent to the rest mass energy of the atom.

Let’s check it out. The energy relative to each possible orbit is considered. We define multiplicity as the number of times the reduced mass energy of the electron-nucleus system, very close in value to the resting energy of the orbiting electron, is contained in the resting energy of the atom

F = \frac{ε_{a t o m}}{ε_{μ}}

(64)

Equation (64) is equal to the maximum number of possible electron-nucleus orbital interactions, based on the available energy associated with the total resting mass of the nucleus. Using Equation (37) Each energy level corresponds to the capture of electrons whose energy is equivalent to a fraction of the total mass energy of the dipole system:

E_{n} = \frac{ε_{μ}}{\sqrt{1 - {(\frac{α_{n}}{n})}^{2}}}

(65)

Using the total capture energy (65) and summing the

F

possible quantum levels determined by the ratio (64), the total energy

E = \sum_{n = 1}^{F} E_{n} = \sum_{n = 1}^{F} \frac{ε_{μ}}{\sqrt{1 - {(\frac{α_{n}}{n})}^{2}}}

(66)

that can be engaged during all possible nucleus-electron interactions cannot exceed the total resting mass energy of the nucleus-electron system. The gamma factor in the McLaurin series was developed. The Equation (66) gives

E ≅ ε_{μ} (F + \frac{α^{2}}{2} \sum_{n = 1}^{F} \frac{1}{n^{2}} + ...) ≅ ε_{a t o m} (1 + \frac{π α^{2}}{12 F} + ...) ≃ ε_{a t o m}

(67)

In the case of a hydrogen atom with

F ≅ 1837

, Equation (65) provides the rest mass energy of the atom

ε_{a t o m} = (m_{p} + m_{e}) c^{2} ≅ m_{p} c^{2}

, showing that a fraction of its total mass energy is shared electromagnetically through the quantum levels that are formed during the interaction between the nucleus and the electron. In other words, the proton interacting with the electrons grants each quantum level a portion of its mass energy¹³. Consequently, generalizing, the sum of all capture energies associated with the quantum levels of an atom, is the effective rest mass energy of the nucleus-electrons system.

12. Discussion

In this work it has been proven that the atomic model based on the Bridge Theory is able to provide a perfect description of the atomic phenomenology, with the advantage, compared to the Bohr-Sommerfeld-Schrödinger models, of introducing quantum principles and Special Relativity in a way self-consistent with the Maxwellian electromagnetic theory, as both quantum and relativistic phenomenologies derive from the particular way of interacting in pairs of moving charged particles. This approach is completely theoretical without require the use of experimental or measured data and in this sense, it could be asserted that the consistency of the results obtained cannot be considered a coincidence at all. The adequate use of the principles of BT could therefore lead to a formal and phenomenological revision of QED in which the typical concepts of quantum indeterminism and wave-particle dualism disappear in favor of the principle of electromagnetic interaction in dipoles, which from a phenomenological point of view allows to replace the concept of Coulombian interaction with that of direct electromagnetic interaction, which transforms through DEMS all the energy of the interacting system into electromagnetic energy localized in the form of exchange photons and the atoms into DEMS with zero radial emission, simplifying the phenomenology of the elementary electromagnetic interactions of matter.

Considering the atoms examined, the good agreement shown by the calculation of the radii and energies of the atomic levels and of the spectral lines of the atoms H, D, He, Li, suggests how the orbital capture may be the only way to produce a large amount of monatomic hydrogen in a cooling universe in which electrons and protons can have been produced in perfect symmetry.

Although the model shows that the orbital motion of atomic electrons around the nucleus is relativistic, from a spectrometric point of view, the first-order approximation of the model leads back to Bohr’s model, thus demonstrating its substantial correctness in terms of first principles.

13. Conclusion

The theoretical results obtained were presented both in the exact form and in the modified form, necessary to match the theoretical data with the observational one. The corrections introduced are based on the principle of the orbital slippage of electrons due to the absorption of external energy, which produces the continuous passage of an electron from the fundamental orbit to a more energetic one. The proposed correction, although semi-empirical, is based on the principle that the fine-structure constant varies as a function of orbit because the dipole moment of the electron-nucleus system changes for each orbital motion.

Finally, it is shown that the electron-nucleus interaction changes on the basis of the nuclear isotopy due to the different inertia of the atomic nucleus and that only the mass energy of the charged fraction of the atomic nucleus can contribute to the binding energy of the system. Therefore, the sum of the energies of all the orbital levels is equal to the mass energy of the active atomic nucleus and its electrons.

Funding

This study is not supported by grant.

Data Availability Statement

No data associated in the manuscript.

Conflict of Interests

The authors declare that they have NO affiliations with or involvement in any organization or entity with any financial interest in the subject matter or materials discussed in this manuscript.

Ethical Compliance

In these studies, no procedures involved human participants.

References

M. Eckert. “How Sommerfeld extended Bohr’s model of the atom” (1913–1916). EPJ H 39, 141–156 (2014). [CrossRef]
M. A. El’yashevich et al. “Rydberg and the development of atomic spectroscopy”. Sov. Phys. Usp. 33 1047 (1990). [CrossRef]
M. Auci. “A conjecture on the physical meaning of the transversal component of the pointing vector”. Phys. Lett. A 135, 86 (1989). [CrossRef]
M. Auci. “A conjecture on the physical meaning of the transversal component of the Poynting vector. II. Bounds of a source zone and formal equivalence between the local energy and the photon.” Phys. Lett. A 148, 399 (1990). [CrossRef]
M. Auci. “A conjecture on the physical meaning of the transversal component of the Poynting vector. III. Conjecture, proof and physical nature of the fine structure constant”. Phys. Lett. A 150, 143 (1990). [CrossRef]
M. Auci, G. Dematteis. “An approach to unifying classical and quantum Electrodynamics”. Int. Journal of Modern Phys. B13, 1525 (1999). [CrossRef]
M. Auci. “Superluminality and Entanglement in an Electromagnetic Quantum-Relativistic Theory”. Journal of Modern Physics, 9, 2206-2222 (2018). [CrossRef]
M. Auci. “The Inertia in a Revised Mach’s Principle”. SSRG International Journal of Applied Physics vol 6, no.3, 57-65 (2019). Crossref. [CrossRef]
L. Morel, Z. Yao, P. Cladé et al. “Determination of the fine-structure constant with an accuracy of 81 parts per trillion”. Nature 588, 61–65 (2020). [CrossRef]
M. Auci. “Estimation of an absolute theoretical value of the Sommerfeld’s fine structure constant in the electron–proton capture process”. Eur. Phys. J. D 75, 253 (2021). [CrossRef]
M. Auci. “Relativistic Doppler Effect and Wave-Particle Duality”. SSRG International Journal of Applied Physics vol. 7, no 2, pp 7-15 (2020).
M. Goswami, S. Sahoo. “Ultimate Stable Element Z = 137” Indian Journal of Science and Thechnology, Vol. 2, No 3, pp 1-4 (2009). [CrossRef]
U. Fabbri. Private communication (2008).

Figure 1. Orbital Structure Constants for H and D. The orbital values in Table 1 of the structure constant

σ = α^{- 1}

are tabulated to show the asymptotical behavior towards the value of the constant without external constraints: 137.036669830443.

Figure 1. Orbital Structure Constants for H and D. The orbital values in Table 1 of the structure constant

σ = α^{- 1}

are tabulated to show the asymptotical behavior towards the value of the constant without external constraints: 137.036669830443.

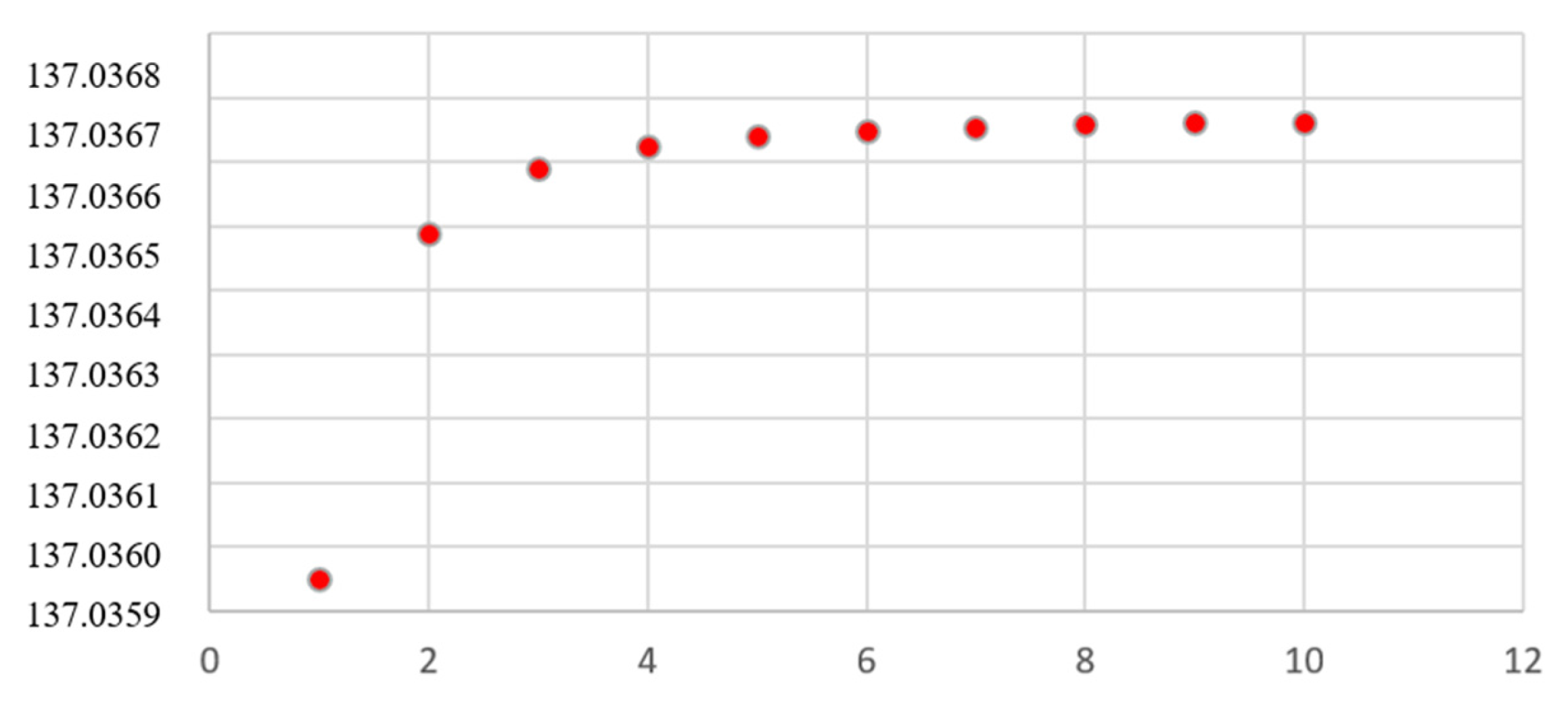
Table 1. Sommerfeld Orbital Constants for Z = 1 ^(*).

$n$	$σ_{n}$	$α_{n}$
1	137.035950244954	0.00729735517003008
2	137.036489933615	0.00729732643097056
3	137.036589876262	0.00729732110893124
4	137.036624856212	0.00729731924621806
5	137.036641046931	0.00729731838404832
6	137.036649841891	0.00729731791570920
7	137.036655144977	0.00729731763331538
8	137.036658586883	0.00729731745003099
9	137.036660946637	0.00729731732437210
10	137.036662634565	0.00729731723448852

(*) Values of the Sommerfeld constant for levels 1-10 were calculated for hydrogen using the recursive numerical method for electron capture presented in Ref. [10].

Table 2. Sommerfeld Orbital Constants for Z = 2 ^(*).

$n$	$σ_{n}$	$α_{n}$
1	137.034935840356	0.00729740918888733
2	137.036316427785	0.00729733567033653
3	137.036350014072	0.00729733388182998
4	137.036489934089	0.00729732643094532
5	137.036554696630	0.00729732298227863
6	137.036589876262	0.00729732110893124
7	137.036611088587	0.00729731997935612
8	137.036624856240	0.00729731924621657
9	137.036634295241	0.00729731874358161
10	137.036641046943	0.00729731838404768

(*) Values of the Sommerfeld constant for levels 1-10 were calculated for helium using the recursive numerical method for electron capture presented in Ref. [10].

Table 3. Sommerfeld Orbital Constants for Z = 3 ^(*).

$n$	$σ_{n}$	$α_{n}$
1	137.030194061221	0.00729766170770531
2	137.035050769958	0.00729740306864051
3	137.035950244954	0.00729735517003008
4	137.036265063006	0.00729733840556895
5	137.036410779106	0.00729733064602762
6	137.036489933615	0.00729732643097056
7	137.036537661315	0.00729732388942498
8	137.036568638438	0.00729732223986456
9	137.036589876262	0.00729732110893124
10	137.036605067546	0.00729732029998186

(*) Values of the Sommerfeld constant for levels 1-10 were calculated for lithium using the recursive numerical method for electron capture presented in Ref. [10].

Table 4. H I Energy Levels (

Z = 1

N = 0

A_{r} ({}^{1}H) = 1.00782503223

Table 4. H I Energy Levels (

Z = 1

N = 0

A_{r} ({}^{1}H) = 1.00782503223

n	Theoretical (cm^-1)	Experimental ⁽¹⁾ (cm^-1)	Th/Ex
1	0.0000	0.0000	-
2	82262.1663	82258.9544	1.00003905
3	97495.2178	97492.3040	1.00002989
4	102826.7354	102823.9040	1.00002754
5	105294.4575	105291.6570	1.00002660
6	106634.9462	106632.1681	1.00002605
7	107443.2178	107440.4508	1.00002575
8	107967.8168	107965.0568	1,00002556
9	108327.4801	108324.7253	1.00002543
10	108584.7450	108581.9945	1.00002533

⁽¹⁾ NIST ASD Energy levels for Hydrogen.

Table 5. D I Energy Levels (

Z = 1

N = 1

A_{r} ({}^{2}H) = 2.01410177812

Table 5. D I Energy Levels (

Z = 1

N = 1

A_{r} ({}^{2}H) = 2.01410177812

n	Theoretical (cm^-1)	Estimated ⁽¹⁾ (cm^-1)	Th/Es
1	0.0000	0.0000	-
2	82262.14406	82281.493	0.99976484
3	97495.19143	97518.836	0.99975754
4	102826.7076	102851.878	0.99975527
5	105294.4291	105320.308	0.99975428
6	106634.9174	106661.1812	0.99975376
7	107443.1888	107469.6848	0.99975346
8	107967.8169	107994.4344	0.99975326
9	108327.4800	108354.2009	0.99975312
10	108584.7156	108611.5396	0.99975308

⁽¹⁾ NIST ASD Energy levels for Deuterium.

Table 6. He II Energy Levels (

Z = 2

\bar{A} (He) = 4 . 00260165

Table 6. He II Energy Levels (

Z = 2

\bar{A} (He) = 4 . 00260165

n	Theoretical (cm^-1)	Estimated ⁽¹⁾ (cm^-1)	Th/Es
1	0.0000	0.0000	-
2	329193.15040	329179.76231	1.000041
3	390144.57400	390140.82497	1.000010
4	411476.97043	411477.18175	1.000000
5	421350.68083	421352.70920	0.999995
6	426714.14026	426717.15366	0.999993
7	429948.12435	429951.72607	0.999992
8	432047.09926	432051.07855	0.999991
9	433486.14721	433490.38252	0.999990
10	434515.48857	434519.90514	0.999990

⁽¹⁾ NIST ASD Energy levels for He II with relative abundance of ³He and ⁴He.

Table 7. Li III Energy Levels (

Z = 3

\bar{A} (Li) = 6 . 94093785

Table 7. Li III Energy Levels (

Z = 3

\bar{A} (Li) = 6 . 94093785

n	Theoretical (cm^-1)	Estimated ⁽¹⁾ (cm^-1)	Th/Es
1	0.0000	0.0000	-
2	741001.31102	740736.43390	1.000358
3	878168.40029	877919.74441	1.000283
4	926172.79499	925932.85143	1.000259
5	948391.25468	948155.58428	1.000249
6	960460.35118	960226.99032	1.000243
7	967737.57099	967505.57339	1.000240
8	972460.74048	972229.60574	1.000238
9	975698.91808	975468.36035	1.000236
10	978015.16155	977785.00701	1.000235

⁽¹⁾ NIST ASD Energy levels for Li III with relative abundances of ⁶Li and ⁷LI.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On a Non‐Standard Atomic Model Developed in the Context of Bridge Electromagnetic Theory

Abstract

1. Introduction

2. The Bridge Electromagnetic Theory: Brief Introduction

2.1. Quantum Behavior: Poynting Vector, Action and Energy of a DEMS

2.2. Relativistic Behavior: Energy and Momentum of a DEMS

2.3. An Atom Described by a DEMS with Zero Radial Emission

2.4. The Concepts of Electron Spin and Atomic Spin in BT for Two Fermions

3. The Atomic Model: Kinetic Energy of the Orbiting System after Electronic Capture

4. Effective Energy at Rest of a Nucleus

5. Quantum Numbers

6. The Wave Behavior of an Interacting Electron: Orbital Eigenvalues

7. Electron Bond and Orbital Energy

8. Atomic Energy Levels

8.1. Hydrogen and Deuterium

8.2. Helium and Lithium

9. Spectral Lines

10. The Bohr Model as First Order Approximation of the DEMS Atomic Model

11. Effective Nuclear Mass

12. Discussion

13. Conclusion

Funding

Data Availability Statement

Conflict of Interests

Ethical Compliance

References

MDPI Initiatives

Important Links

Subscribe