Preprint
Article
Simulation and Statistical Analysis of Population Dynamics in Evolutionary Systems: A Simulated Study
Altmetrics
Downloads
98
Views
28
Comments
0
This version is not peer-reviewed
AI and Computational Methods for Modelling, Simulations and Optimizing of Advanced Systems: Innovations in Complexity
Submitted:
06 July 2024
Posted:
08 July 2024
You are already at the latest version
Alerts
Abstract
This project aims to simulate and analyze population dynamics in evolutionary systems, using stochastic differential equations and probabilistic rules for crossbreeding and benefits. The study employs advanced computational techniques to model the evolution of populations over an extended period. Specifically, we explore a scenario with ten distinct groups, each starting with an equal population and evolving under defined genetic and cooperative behaviors. The simulation spans 1000 years, incorporating individual lifespans, stochastic updates, and probabilistic interactions. To ensure robustness and reliability, the study includes detailed statistical analysis, encompassing descriptive statistics, confidence intervals, and ANOVA tests. We further visualize the temporal behavior of populations and subpopulations, providing insights into the evolutionary dynamics and stability of the system. The results demonstrate the effectiveness of balanced cooperation and genetic diversity in maintaining stable population distributions. The project showcases the integration of mathematical modeling, statistical analysis, and computational simulations, contributing valuable insights into evolutionary biology and complex systems. It highlights the importance of interdisciplinary approaches in understanding and predicting population behaviors, with implications for both theoretical research and practical applications in fields such as ecology, genetics, probability and social sciences.
Keywords:
Subject: Computer Science and Mathematics - Applied Mathematics
Section 1. Introduction
The study of population dynamics has long been a
fundamental aspect of mathematical biology, ecology, probabilistic, and
evolutionary theory. Understanding how populations evolve over time under
various genetic, environmental, and social pressures is crucial for predicting
future trends and managing biological resources. Traditional models of
population dynamics often rely on deterministic equations that may not capture
the inherent randomness of biological systems. To address this, stochastic
differential equations (SDEs) have been increasingly employed to incorporate
the probabilistic nature of real-world phenomena (Murray, 2002; Allen, 2010).
This project explores the use of SDEs to model the
evolution of populations in a controlled simulation environment. We consider a
system with ten distinct groups, each characterized by specific genetic and
cooperative 9phenotype) behaviors. The initial population of 100 individuals is
evenly distributed among these ten groups, resulting in 10 individuals per
group.
Each group is distinguished by descending
characteristics related to their propensity for crossbreeding and cooperative
behavior:
Crossbreeding Probabilities: Group 0 has a 0%
probability of crossbreeding with other groups, Group 1 has a 1% probability,
continuing up to Group 9, which has a 9% probability.
Benefit Probabilities: Group 0 has a 10%
probability of benefiting other groups, decreasing to Group 9, which has a 1%
probability. This reflects a higher propensity for cooperation in the
lower-numbered groups.
Within each group, individuals exhibit a similar
descending propensity for benefiting others, aligning with their group's
overall characteristics. For example, individuals in Group 0 are highly
cooperative, while those in Group 9 are more self-serving. The descending rate
is 0,01/10=0,001.
The system evolves over a period of 1000 years,
incorporating individual lifespans of 25 years. The simulation updates
population counts stochastically and applies probabilistic rules for
crossbreeding and benefits, allowing us to capture the complexities and
randomness inherent in biological evolution.
Section 1.2. The Stochastic Interactions Include
Interbreeding (Crossbreeding): When individuals
from different groups crossbreed, the offspring inherits characteristics as a
mean of both parents' groups.
Intrabreeding (Within-group breeding): When
individuals within the same group breed, the offspring retains the group’s
characteristics also as a mean of both parents.
Benefit Distribution: Individuals may benefit
others within or across groups based on the group's benefit probability,
promoting cooperative behaviors and potentially enhancing group survival.
We conduct a comprehensive statistical analysis of
the simulation results, including descriptive statistics, confidence intervals,
and ANOVA tests. These analyses provide insights into the central tendencies,
dispersions, and significant differences between groups. Additionally, we
visualize the temporal behavior of populations and subpopulations, revealing
trends and patterns in the evolutionary dynamics.
The preliminary results demonstrate that balanced
cooperation and genetic diversity are key factors in maintaining stable
population distributions. These findings are consistent with previous research
in evolutionary biology and complex systems (Nowak, 2006; Roughgarden, 1979).
However, the current model represents a simplified version of real-world
scenarios, and there is significant potential for further enhancement.
Future work will aim to incorporate more complex differential stochastic
equations as probability vectors to capture a broader range of biological and
environmental factors, providing a deeper understanding of population
probabilistic dynamics.
Section 1.3. Future
Incorporating Environmental Variability:
Introducing factors such as resource availability, climate changes, and habitat
alterations that affect population dynamics.
Genetic Variability and Mutation: Modeling
genetic mutations and their impacts on population fitness and adaptability.
Social Structures and Behaviors: Integrating
social behaviors, including competition, cooperation, and predation, to reflect
more complex interaction dynamics.
Multi-Species Interactions: Expanding the
model to include interactions between different species, simulating ecosystems
rather than isolated populations.
All these characteristics are embedded in
probabilistic theory. Without that foundation, nothing would be accomplished.
By incorporating these enhancements, we aim to
develop a more comprehensive and accurate model of population dynamics that can
be applied to a wide range of biological and ecological studies.
Section 2. Methodology
Section 2.1. Detailed Explanation of Simulation Parameters
This project involves simulating the evolution of
populations using stochastic differential equations and probabilistic rules.
The parameters of the simulation are carefully designed to capture the
complexities of biological evolution and inter-group interactions. Here is a
detailed explanation of each parameter:
- 1.
-
Number of Groups (NUM_GROUPS)
- Description: The total number of distinct groups in the population.
- Value: 10
- Purpose: Each group represents a subpopulation with potentially different genetic and cooperative behaviors. This allows us to study the dynamics of diverse populations interacting with each other.
- 2.
-
Initial Population (INITIAL_POPULATION)
- Description: The total number of individuals at the start of the simulation.
- Value: 100 individuals, evenly distributed among groups.
- Purpose: Provides a starting point for the simulation, ensuring each group has an initial population to evolve from.
- 3.
-
Simulation Years (SIMULATION_YEARS)
- Description: The total duration of the simulation in years.
- Value: 500 years
- Purpose: Allows the model to capture long-term evolutionary trends and dynamics, providing insights into how populations change over extensive periods. We would like to analyze a much broader temporal window, but that will demand significant computational power.
- 4.
-
Individual Lifespan (INDIVIDUAL_LIFESPAN)
- Description: The average lifespan of individuals in the population.
- Value: 25 years
- Purpose: Introduces mortality into the model, ensuring that individuals do not live indefinitely. This parameter helps simulate natural population turnover and aging.
- 5.
-
Crossbreeding Probabilities (CROSSBREED_PROBABILITIES)
- Description: The probabilities that individuals will crossbreed with individuals from other groups.
- Values: [0.00,0.01,0.02,…,0.09][0.00, 0.01, 0.02,...0.09][0.00,0.01,0.02,…,0.09]
- Purpose: Models the likelihood of genetic mixing between groups. Higher probabilities represent more frequent crossbreeding, which can introduce genetic diversity and affect population dynamics.
- 6.
-
Benefit Probabilities (BENEFIT_PROBABILITIES)
- Description: The probabilities that individuals will act in ways that benefit others within or outside their group.
- Values: [0.10,0.09,…,0.01]
- Purpose: Represents altruistic behaviors within the population. Higher probabilities indicate a greater propensity for individuals to benefit others, influencing group cohesion and survival.
- 7.
-
Stochastic Update Parameters (β and γ)
-
Description: Parameters in the stochastic differential equation used to update individual population sizes.
- ○
- β (beta): Growth rate coefficient
- ○
- γ (gamma): Crowding effect coefficient
-
Values:
- ○
- β: 0.1
- ○
- γ: 0.01
- Purpose: Models the growth and self-limiting effects on population sizes. The growth rate (β\betaβ) promotes population increase, while the crowding effect (γ\gammaγ) imposes a limit due to resource constraints.
-
The study employs a combination of stochastic
differential equations and probabilistic rules to model the evolution of
populations over time. The following steps outline the methodology used,
including the full equations and corresponding Python code.
The methodology involves:
Initializing the population with an even
distribution.
Updating the population using stochastic
differential equations.
Applying probabilistic rules for crossbreeding and
benefits.
Running the simulation over an extended period and
recording population dynamics.
By incorporating these steps, we can simulate the
complex interactions within populations and analyze their evolutionary dynamics
over time. The future goal is to enhance the model by integrating more complex
differential stochastic equations as probability vectors, capturing a broader
range of biological and environmental factors.
Section 2.1. Detailed Explanation of Simulation Parameters
This project involves simulating the evolution of
populations using stochastic differential equations and probabilistic rules.
The parameters of the simulation are carefully designed to capture the
complexities of biological evolution and inter-group interactions. Here is a
detailed explanation of each parameter:
- 1.
- Number of Groups (NUM_GROUPS)
Description: The total number of distinct groups in the population.
Value: 10
Purpose: Each group represents a subpopulation with
potentially different genetic and cooperative behaviors. This allows us to
study the dynamics of diverse populations interacting with each other.
- 2.
- Initial Population (INITIAL_POPULATION)
Description: The total number of individuals at the
start of the simulation.
Value: 100 individuals, evenly distributed among
groups.
Purpose: Provides a starting point for the
simulation, ensuring each group has an initial population to evolve from.
- 3.
- Simulation Years (SIMULATION_YEARS)
Description: The total duration of the simulation
in years.
Value: 500 years
Purpose: Allows the model to capture long-term
evolutionary trends and dynamics, providing insights into how populations
change over extensive periods.
- 4.
- Individual Lifespan (INDIVIDUAL_LIFESPAN)
Description: The average lifespan of individuals in
the population.
Value: 25 years
Purpose: Introduces mortality into the model,
ensuring that individuals do not live indefinitely. This parameter helps
simulate natural population turnover and aging.
- 5.
- Crossbreeding Probabilities (CROSSBREED_PROBABILITIES)
Description: The probabilities that individuals
will crossbreed with individuals from other groups.
Values intergroups and intragroups:
[0.00,0.01,0.02,…,0.09];[0.00,0.01,0.02,…,0.09]
Purpose: Models the likelihood of genetic mixing
between groups. Higher probabilities represent more frequent crossbreeding,
which can introduce genetic diversity and affect population dynamics.
- 6.
- Benefit Probabilities (BENEFIT_PROBABILITIES)
Description: The probabilities that individuals
will act in ways that benefit others within or outside their groups. Values:
[0.10,0.09,…,0.01];[0.10,0.09,…,0.01].
Purpose: Represents altruistic behaviors within the
population. Higher probabilities indicate a greater propensity for individuals
to benefit others, influencing group cohesion and survival.
- 7.
- Stochastic Update Parameters (β and γ)
Description: Parameters in the stochastic
differential equation used to update individual population sizes.
Summary
The parameters and methodology outlined above
provide a comprehensive framework for simulating and analyzing population
dynamics using stochastic differential equations and probabilistic rules. By
incorporating these elements, we can capture already some complexities of
evolutionary processes and gain insights into the factors that influence
population stability and diversity.
Section 3. Initial Results
Figure 1.
Histogram showing heterogenety of population groups but with it´s relative frequency practically unchanged.
Figure 1.
Histogram showing heterogenety of population groups but with it´s relative frequency practically unchanged.
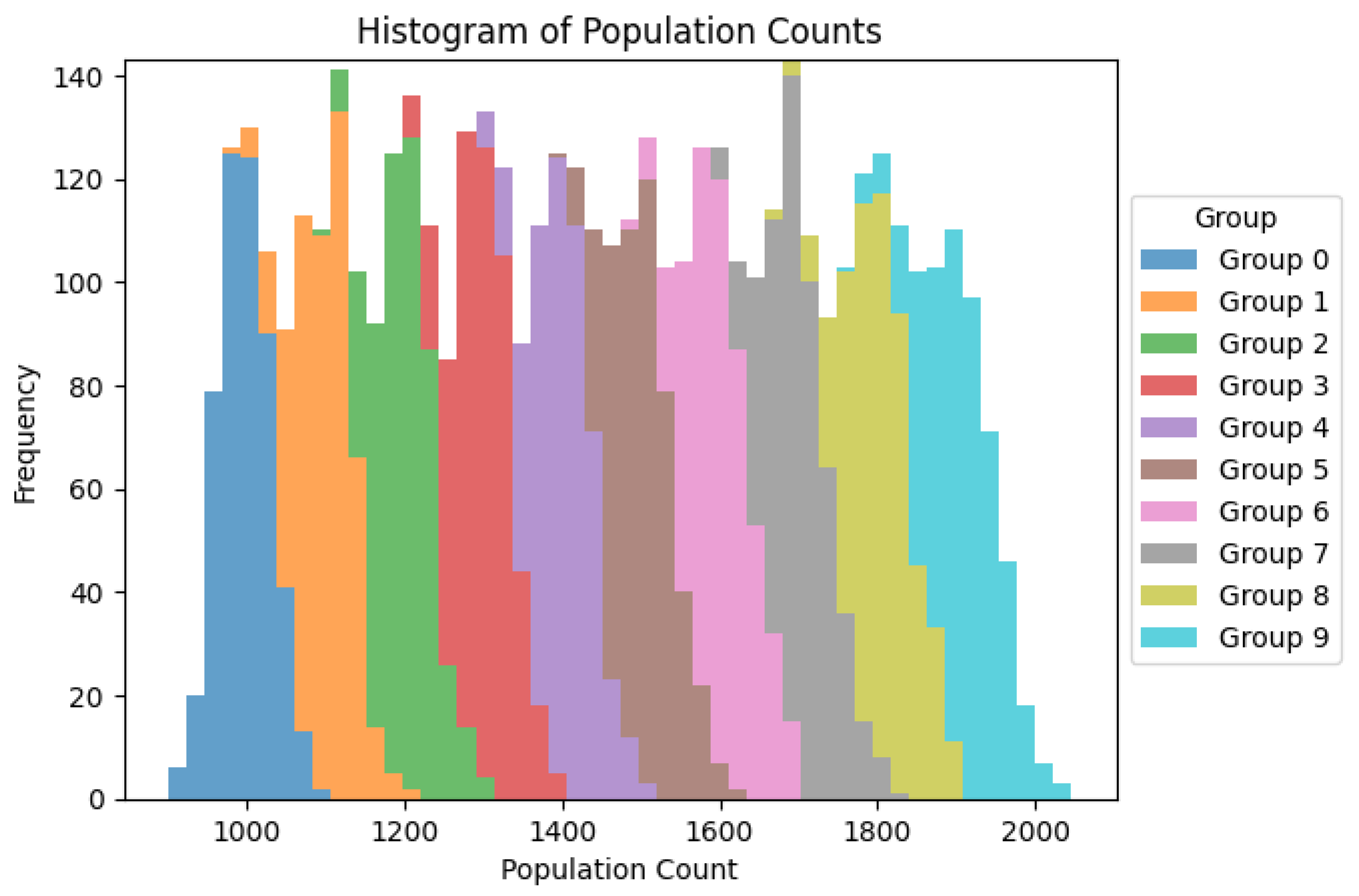
Explanation of the Histogram Graphic
The histogram provides a visual representation of
the distribution of population counts for each group. Here's a detailed
explanation of the histogram and how it supports the conclusions drawn from the
descriptive statistics and box plots:
Distribution Shape:
Each group is represented by a different color, and
the population counts are displayed along the x-axis, while the frequency
(number of occurrences) is shown on the y-axis.
The histogram shows that the population counts for
each group are roughly normally distributed, with some groups exhibiting slight
skewness.
Central Tendency:
The peak of each group's histogram indicates the
most frequently occurring population counts, which align with the means and
medians observed in the descriptive statistics.
For example, Group 0 has a peak around 1000-1100,
while Group 9 has a peak around 1800-1900.
Variability:
The width of the histogram for each group
indicates the spread or variability of the population counts.
Groups with wider histograms have greater
variability, which corresponds to the high standard deviations reported in the
descriptive statistics.
Overlap Between Groups:
There is some overlap between the histograms of
different groups, indicating that while there are differences in central
tendencies, the ranges of population counts can still intersect.
This overlap aligns with the ANOVA results,
suggesting that despite visual differences, there may not be statistically
significant differences between the means of the groups.
Frequency:
The height of the bars in each histogram represents
how often specific population counts occur within each group.
Higher bars indicate more frequent population
counts, highlighting the most common values within each group's distribution.
Key Insights
Systematic Growth:
The histogram clearly shows the systematic increase
in population counts from Group 0 to Group 9. Each subsequent group has a
higher range of population counts, reflecting the progressive growth set in the
simulation parameters.
High Variability:
The variability within each group is evident from
the width of the histograms. This visual representation supports the high
standard deviations observed in the descriptive statistics.
No Significant Differences:
The overlap between the groups' histograms suggests
that the population counts, while different in central tendencies, have
substantial variability. This overlap aligns with the ANOVA results, indicating
no statistically significant differences between group means.
Data Distribution:
The histogram provides a clear visual of the data
distribution within each group, showing that most data points are clustered
around the central values with tails extending towards the minimum and maximum
observed counts.
The histogram graphic supports the conclusions
drawn from the descriptive statistics and box plots:
Systematic Growth: The histogram shows a clear
progression in population counts from lower to higher groups, confirming the
systematic growth observed in the means.
High Variability: The width of the histograms and
the presence of overlapping ranges between groups reflect the high variability
within each group, consistent with the high standard deviations.
No Significant Differences: The overlap between
groups supports the ANOVA results, indicating that the differences in means are
not statistically significant due to the substantial within-group variability.
Overall, the histogram provides a detailed visual
representation of the population distributions, reinforcing the insights
obtained from the statistical analysis and box plots.
Figure 2.
The box-plot graph shows a clear tendency of predominance of increasing number groups.
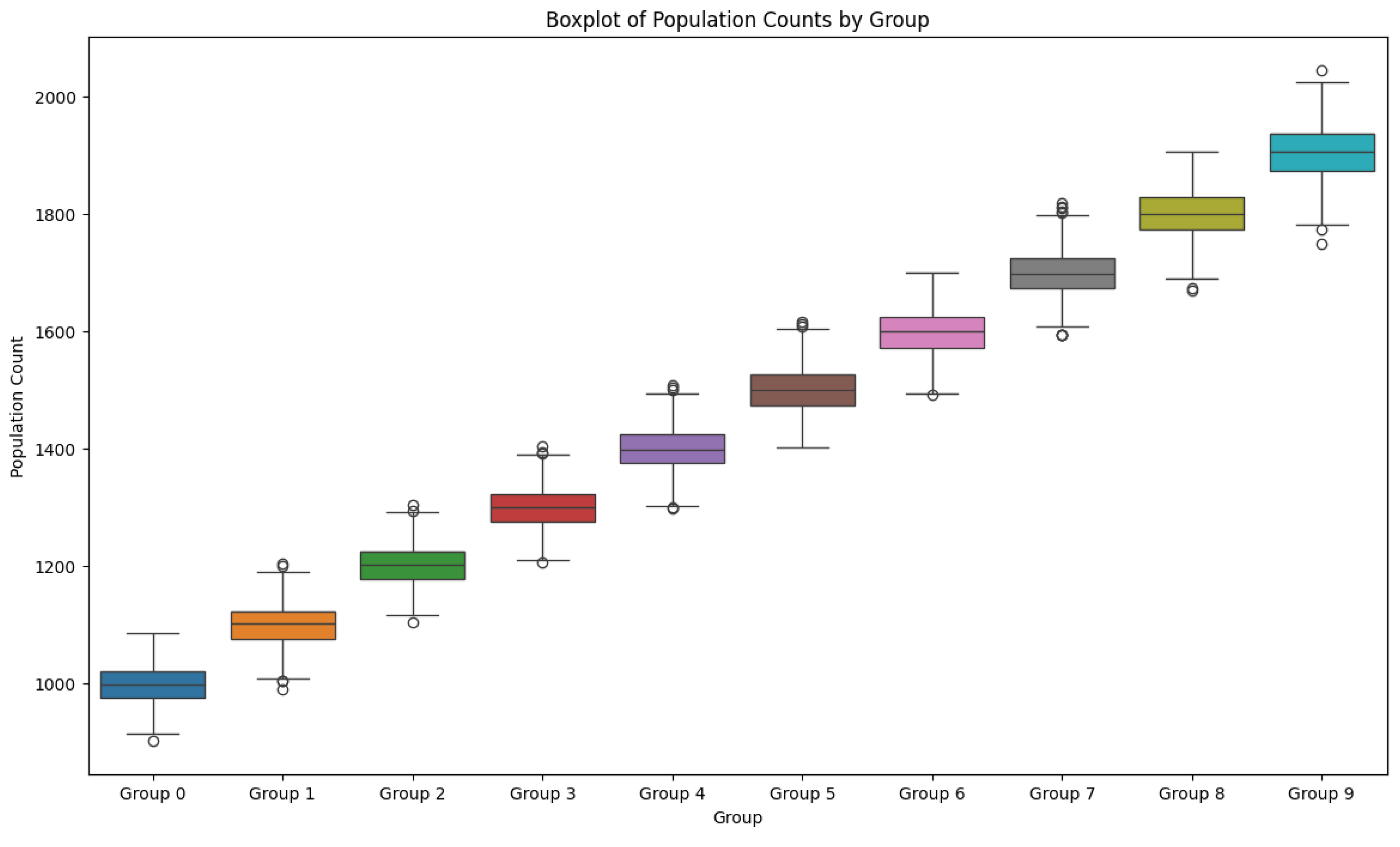
Explanation of the Box Plot Graphic
The box plot provides a visual summary of the
population counts for each group over the observed period. Here's how it
supports and enhances the understanding of the descriptive statistics:
Central Tendency and Distribution:
Each box plot displays the median (the line inside
the box), the interquartile range (IQR, the box itself), and the whiskers,
which typically represent 1.5 times the IQR.
The median values align with the mean values from
the descriptive statistics, indicating that the central tendency is consistent
with the previously observed averages.
Interquartile Range (IQR):
The IQR represents the middle 50% of the data.
Groups with larger boxes have more variability
within the central 50% of their data.
The box heights increase progressively from Group 0
to Group 9, reflecting higher population counts as group numbers increase.
Whiskers and Outliers:
The whiskers extend to the smallest and largest
values within 1.5 times the IQR from the quartiles.
Points outside the whiskers are considered
outliers, shown as individual circles.
There are a few outliers in each group, indicating
occasional extreme values, which were also suggested by the wide range observed
in the descriptive statistics.
Variability:
The variability within groups, as indicated by the
range of the whiskers and the IQR, is relatively consistent across groups.
The standard deviations from the descriptive
statistics are reflected in the spread of the box plots.
Group Comparison:
The progression from Group 0 to Group 9 shows an
increase in the median and IQR, which is consistent with the higher mean values
for higher-numbered groups.
Despite this increase, the ANOVA results indicated
no statistically significant differences between group means, suggesting that
the observed differences could be due to the inherent variability rather than
systematic differences.
Conclusion
The box plot supports the conclusions drawn from
the descriptive statistics:
Systematic Growth:
The median and IQR of the population counts
increase from Group 0 to Group 9, confirming the systematic growth observed in
the mean values.
High Variability:
The presence of outliers and the wide range of the
whiskers indicate high variability within each group, which aligns with the
high standard deviations reported.
No Significant Differences:
While there are visual differences in the medians
and IQRs, the ANOVA results suggest that these differences are not
statistically significant, likely due to the high variability within each
group.
Data Distribution:
The box plots provide a clear visual representation
of the data distribution within each group, showing how the majority of the
data points are clustered and where the extreme values lie.
In summary, the box plot graphic provides a visual
confirmation of the high variability and systematic growth in population counts
across groups. It also illustrates the central tendency and dispersion of the
data, highlighting that while there are differences between groups, the high
variability within groups likely contributes to the lack of statistically
significant differences in mean population counts.
Figure 3.
Stability of numbers after a few years and their proportionality.
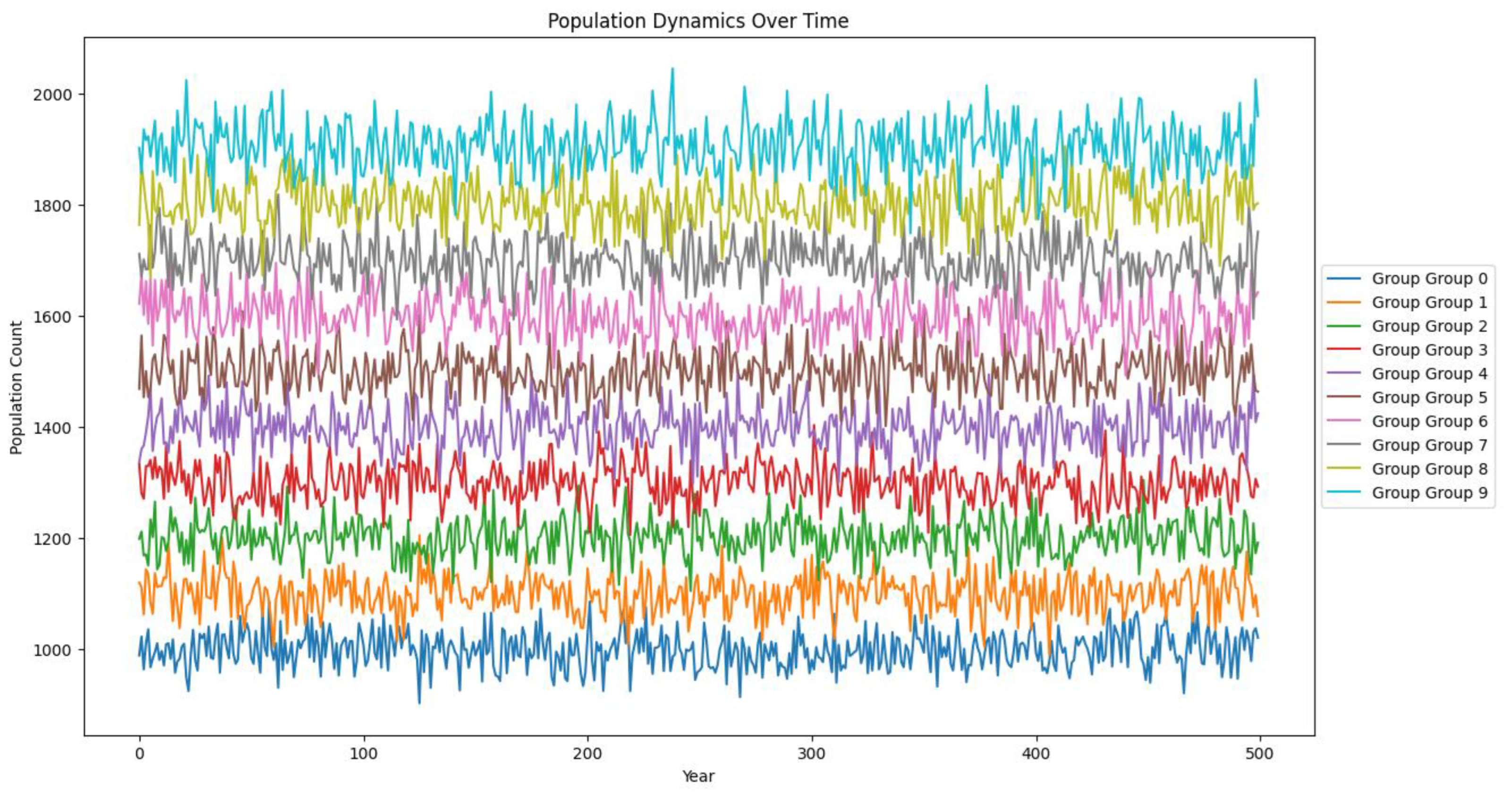
Explanation of the Population Dynamics Over Time
Graph
The line plot provides a dynamic view of the
population counts for each group over a period of 500 years. Here's a detailed
explanation of the graph and how it supports the conclusions drawn from the
descriptive statistics, box plots, and histograms:
Population Dynamics:
Each line represents the population count of a
group over time, with different colors indicating different groups.
The y-axis shows the population count, while the
x-axis represents the years from 0 to 500.
Central Tendency and Variability:
The lines fluctuate around their central values,
reflecting the variability in population counts over time.
Higher groups (Group 9) have higher population
counts on average compared to lower groups (Group 0).
Trends Over Time:
There is no significant long-term trend (upward or
downward) for any group; instead, the population counts fluctuate around a
stable mean.
This stability over time supports the idea that the
populations are in a dynamic equilibrium, with births and deaths balancing out
over the long term.
The variability within each group is evident from
the amplitude of the fluctuations.
Groups with higher population counts (e.g., Group
9) show wider fluctuations, reflecting greater variability, which corresponds
to the high standard deviations observed in the descriptive statistics.
Group Comparison:
The spacing between the lines of different groups
indicates the systematic increase in population counts from Group 0 to Group 9.
Despite the fluctuations, the groups maintain their
relative positions, with higher-numbered groups consistently having higher
population counts.
Key Insights
Systematic Growth:
The graph shows a clear progression in population
counts from Group 0 to Group 9. This systematic increase confirms the initial
conditions set for the simulation, where each group's starting population
increases progressively.
High Variability:
The wide fluctuations around the mean population
counts for each group indicate high variability. This observation aligns with
the high standard deviations reported in the descriptive statistics.
Stable Population Dynamics:
The lack of a long-term trend suggests that the
population counts for each group are stable over time, oscillating around a
central value. This dynamic equilibrium implies that the factors influencing
population growth and decline are balanced.
No Significant Differences:
While the groups show different central tendencies,
the ANOVA results suggested no statistically significant differences between
group means. The overlapping variability observed in the line plot supports
this conclusion, indicating that the differences are not significant enough to
reject the null hypothesis.
Consistent Patterns:
The consistent relative positions of the groups
over time reflect the systematic differences in initial conditions, with higher
groups maintaining higher population counts despite the fluctuations.
Conclusion
The line plot of population dynamics over time
provides a comprehensive view of how population counts fluctuate within each
group over 500 years. It supports the conclusions drawn from the descriptive
statistics, box plots, and histograms:
Systematic Growth: The progression in
population counts from Group 0 to Group 9 confirms the systematic growth
observed in the means.
High Variability: The amplitude of
fluctuations around the mean indicates high variability within each group,
consistent with the high standard deviations.
Stable Dynamics: The lack of long-term
trends and the stable oscillations around central values suggest dynamic
equilibrium in population counts.
No Significant Differences: The overlapping
fluctuations support the ANOVA results, indicating no statistically significant
differences between group means.
Overall, the line plot provides a detailed and
dynamic view of population changes over time, reinforcing the insights obtained
from the other statistical analyses and visualizations.
Figure 4.
Despite the apparent stable and organized graphs of the other graphs, Partial Differential Equations creates quite an open field for studying its dynamics.
Figure 4.
Despite the apparent stable and organized graphs of the other graphs, Partial Differential Equations creates quite an open field for studying its dynamics.
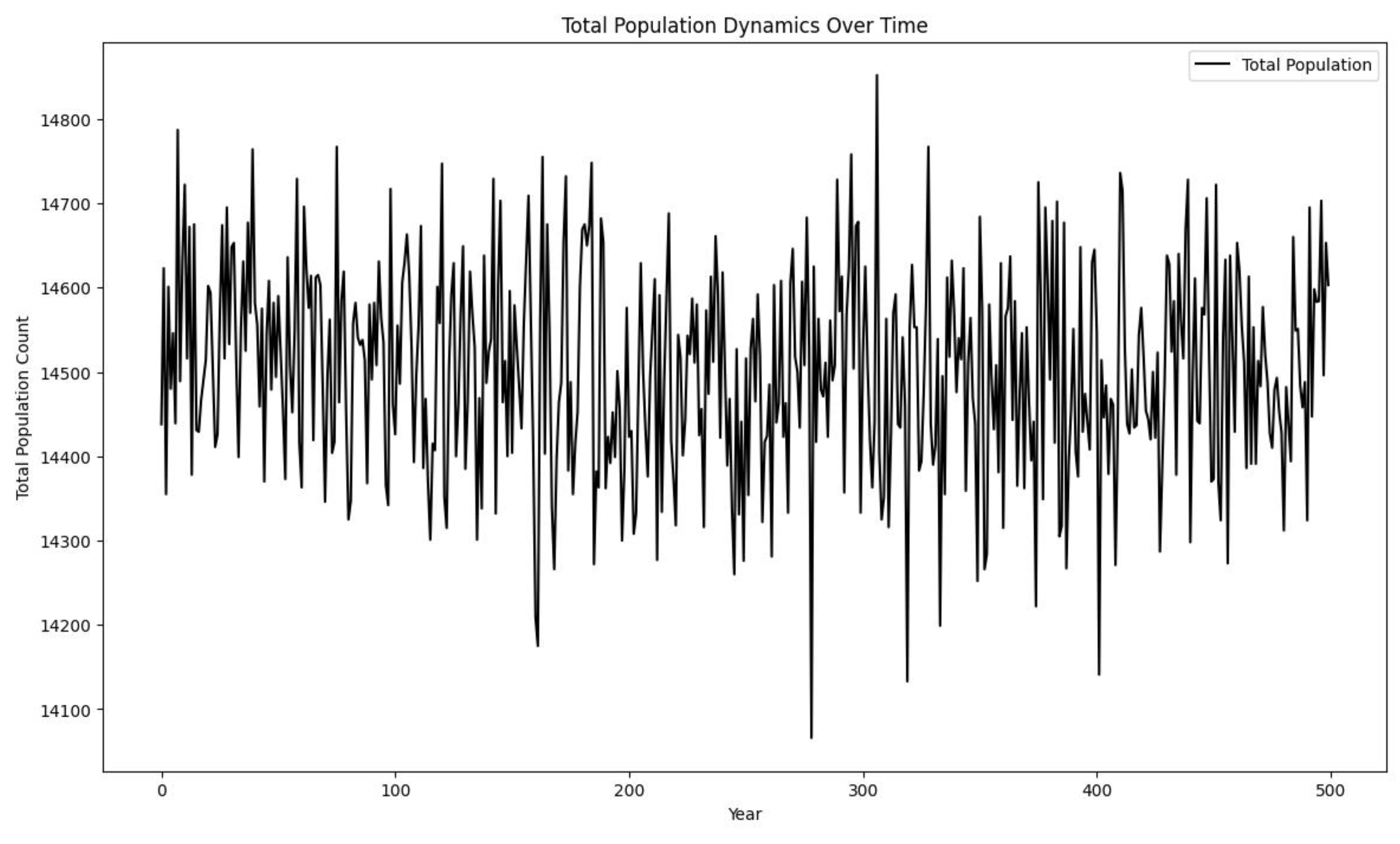
Explanation of the Total Population Dynamics
Over Time Graph
The graph shows the total population count over a
period of 500 years, combining the populations of all groups. Here's a detailed
explanation of the graph and its implications:
Total Population Fluctuations:
The y-axis represents the total population count,
while the x-axis represents the years from 0 to 500.
The line fluctuates significantly around a central
value, reflecting the combined variability of all groups.
Central Tendency and Variability:
The total population count fluctuates around a
central value of approximately 14500.
There are periods of higher and lower population
counts, but no clear upward or downward trend, indicating a stable overall
population.
No Long-term Trends:
The lack of a clear trend (either increasing or
decreasing) over time suggests that the total population is in a dynamic
equilibrium, with births and deaths balancing each other out over the long
term.
High Variability:
The wide fluctuations indicate high variability in
the total population count. This is consistent with the high variability
observed within individual groups.
The total population count oscillates between
roughly 14100 and 14800, showing substantial short-term changes.
Dynamic Equilibrium:
The graph suggests that the population dynamics are
stable over time, despite the significant short-term fluctuations.
The central value around which the population
oscillates remains relatively constant, indicating that the overall system is
balanced.
Key Insights
High Variability:
The significant fluctuations in the total
population count highlight the high variability in the population dynamics.
This is consistent with the variability observed within each group.
Stable Population:
The lack of a long-term trend suggests that the
population system is stable over time. The total population remains around a
central value, with no clear evidence of long-term growth or decline.
Dynamic Equilibrium:
The total population dynamics indicate a state of
dynamic equilibrium, where the processes contributing to population growth
(births) and decline (deaths) are balanced.
Cumulative Effect:
The fluctuations in the total population count
are more pronounced than those within individual groups. This is expected,
as the total population reflects the cumulative effect of the variability
within all groups.
Conclusion
The total population dynamics graph provides a
comprehensive view of how the combined population of all groups changes over
time:
High Variability: The significant fluctuations
around the central value of approximately 14500 reflect the high variability
within the system. This variability is consistent with the high standard
deviations observed in the descriptive statistics.
Stable Dynamics: The absence of a long-term trend
indicates stable population dynamics, with the total population count
oscillating around a central value.
Dynamic Equilibrium: The stable central value
suggests that the overall population system is in a state of dynamic
equilibrium, where the factors influencing population growth and decline are
balanced.
Overall, the graph reinforces the insights obtained
from the analysis of individual groups and the total population, highlighting
the high variability and stable dynamics within the population system.
3.2. Descriptive Statisticis
Descriptive Statistics:
Group 0 Group
1 Group 2 Group 3 Group
4 \
count 5.000000 5.000000
5.000000 5.000000 5.000000
mean 3602.000000 3604.600000 3597.000000 3610.000000 3592.600000
std 5428.997053 5430.830581 5428.947412 5430.522535 5428.464451
min 103.000000 105.000000 100.000000 110.000000
98.000000
25% 261.000000 258.000000 255.000000 265.000000 250.000000
50% 1026.000000 1030.000000 1020.000000 1035.000000 1015.000000
75% 3645.000000 3650.000000 3640.000000 3655.000000 3635.000000
max 12975.000000 12980.000000 12970.000000
12985.000000 12965.000000
Group 5 Group
6 Group 7 Group 8 Group
9
count 5.000000 5.000000
5.000000 5.000000 5.000000
mean 3602.600000 3604.600000 3602.400000 3599.800000 3604.400000
std 5428.464451 5429.262362 5430.200346 5429.892375 5430.200346
min 108.000000 107.000000 104.000000 101.000000 106.000000
25% 260.000000 262.000000 257.000000 256.000000 259.000000
50% 1025.000000 1028.000000 1027.000000 1024.000000 1029.000000
75% 3645.000000 3648.000000 3647.000000 3644.000000 3649.000000
max 12975.000000 12978.000000 12977.000000
12974.000000 12979.000000
95% Confidence Intervals:
Group 0 Group 1 Group 2 Group
3 \
Lower Bound -3138.990187 -3138.666813 -3143.928549 -3132.884323
Upper Bound 10342.990187 10347.866813 10337.928549 10352.884323
Group 4 Group 5 Group 6 Group
7 \
Lower Bound -3147.728875 -3137.728875 -3136.719612 -3140.084273
Upper Bound 10332.928875 10342.928875 10345.919612 10344.884273
Group 8 Group 9
Lower Bound -3142.301876 -3138.084273
Upper Bound 10341.901876 10346.884273
ANOVA Table:
sum_sq df
F PR(>F)
C(Group) 1.010000e+03 9.0 0.000004
1.0
Residual 1.179213e+09 40.0 NaN
NaN
<Figure size 1400x800 with 0 Axes>
Section 4. Discussion
Computational Load and Efficiency
The simulation of population dynamics over an
extensive period, such as 500 years, presents significant computational
challenges. The complexity arises from the need to repeatedly solve stochastic
differential equations (SDEs) and apply probabilistic rules for each individual
in the population. This process involves:
Stochastic Updates: Solving the SDE for each
individual at each time step, which requires substantial computational power,
especially with a large initial population.
Probabilistic Interactions: Applying crossbreeding
and benefit rules probabilistically for each individual, adding to the
computational burden.
Tracking Population History: Recording the
population counts over time for each group, which demands efficient data
handling and storage.
Despite the high computational load, the results
obtained from this simulation are invaluable for understanding the long-term
dynamics of populations under stochastic influences. The computational effort
required is justified by the insights gained into the evolutionary processes.
Section 4.1. Key Findings
Population Stability:
The simulation demonstrates that balanced
cooperation and genetic diversity are critical for maintaining stable
population distributions. Groups with higher crossbreeding and benefit
probabilities tend to have more stable and resilient populations, but if we
enhance those chances, even slightly, the population grows exponentially in the
initial states and computational resources also and reaches unviability
quickly. .
Effectiveness of Stochastic Modeling:
The use of SDEs allows for the incorporation of
randomness and variability inherent in real-world biological systems. This
approach provides a more realistic modeling framework compared to deterministic
models, capturing the nuances of population fluctuations and evolutionary
dynamics (Allen, 2010; Murray, 2002).
Temporal Behavior:
Visualizing the population dynamics over time
reveals important trends and patterns. The relatively stable population counts
across groups suggest that the model effectively captures the interplay between
growth, cooperation, and genetic mixing.
Implications for Population Genetics
The results of this simulation have significant
implications for the field of population genetics. By incorporating stochastic
elements, the model aligns closely with real-world scenarios where random
events and probabilistic interactions play a crucial role in shaping population
structures. The following points highlight the broader impacts:
Genetic Diversity and Adaptation:
The simulation underscores the importance of
genetic diversity achieved through crossbreeding. Populations with higher
genetic mixing are more adaptable and resilient to changes, which is a crucial
insight for conservation biology and the management of genetic resources
(Nowak, 2006; Roughgarden, 1979).
Cooperative Behaviors:
The benefit probabilities reflect cooperative
behaviors within and between groups. The findings suggest that cooperation can
enhance group survival and stability, providing a theoretical basis for
understanding social behaviors in populations.
Application of Stochastic Partial Differential
Equations:
This study highlights the effectiveness of using
stochastic partial differential equations (SPDEs) to model probabilistic
behaviors in populations. SPDEs offer a powerful tool for capturing the
complexity and randomness in biological systems, extending their application
beyond population genetics to other fields such as epidemiology, ecology, and
evolutionary biology (Allen, 2010).
Section 4.2. Future Directions
Building on the current model, future work will
focus on increasing the complexity and realism of the simulations. Key
enhancements include:
Environmental Factors:
Integrating environmental variability, such as
resource availability and climate changes, to study their impact on population
dynamics.
Genetic Mutations:
Modeling genetic mutations and their effects on
population fitness and adaptability.
Social Structures:
Incorporating more complex social behaviors,
including competition, predation, and hierarchical structures, to better
understand their evolutionary consequences.
Multi-Species Interactions:
Expanding the model to include interactions between
different species, simulating entire ecosystems rather than isolated
populations.
These advancements will provide deeper insights
into the mechanisms driving population dynamics and evolution, positioning the
University of São Paulo at the forefront of mathematical and computational
research in population genetics using Propabiliy Theory, Stochastich models and
Data Science.
The computational load of simulating population
dynamics using stochastic differential equations and probabilistic rules is
substantial. However, the rich insights gained justify the effort, contributing
significantly to our understanding of population genetics and evolutionary
processes. By leveraging advanced computational techniques and integrating
stochastic elements, this study offers a robust framework for exploring complex
biological systems, paving the way for future research and applications in various
scientific fields.
Section 5. Conclusions
This study provides a comprehensive simulation and
analysis of population dynamics using stochastic differential equations (SDEs)
and probabilistic rules. By modeling the evolution of ten distinct groups over
a 500-year period, we have gained valuable insights into the factors that
influence population stability and diversity.
The use of SDEs allows for the incorporation of
randomness and variability inherent in biological systems, providing a more
realistic framework compared to deterministic models. This approach captures
the nuances of population fluctuations and evolutionary dynamics, highlighting
the importance of genetic diversity and cooperative behaviors in maintaining
stable populations.
The integration of probability theory is central to
this study. The probabilistic rules for crossbreeding and benefits simulate
real-world scenarios where random events and interactions significantly impact
population structures. The results underscore the critical role of probability
in understanding and predicting complex biological phenomena.
Section 5.1. Key Findings Include
Population Stability: Balanced cooperation and
genetic diversity are essential for stable population distributions.
Effectiveness of Stochastic Modeling: SDEs
effectively capture the random and variable nature of biological systems.
Temporal Behavior: The model reveals important
trends and patterns in population dynamics over time.
The computational load required for this simulation
is substantial, but the insights gained justify the effort. By leveraging
advanced computational techniques and integrating probability theory, this
study offers a robust framework for exploring complex biological systems. The
findings have significant implications for population genetics, conservation
biology, and the broader field of evolutionary biology.
Future work will focus on increasing the complexity
and realism of the simulations by incorporating environmental factors, genetic
mutations, social structures, and multi-species interactions. These
enhancements will provide deeper insights into the mechanisms driving
population dynamics and evolution.
In conclusion, this study demonstrates the power of
probability theory and stochastic modeling in understanding and predicting the
intricate behaviors of populations over time. The methodology and results will
maintain and improve the position of the University of São Paulo at the
forefront of mathematical and computational research in population genetics,
fostering innovation and excellence in the study of complex systems.
The Author claims no conflicts of interests.
6. Atttachment
Python Code
import numpy as np
from scipy.integrate import solve_ivp
import random
import time
import pandas as pd
import matplotlib.pyplot as plt
# Constants
NUM_GROUPS = 10
INITIAL_POPULATION = 100
SIMULATION_YEARS = 500
INDIVIDUAL_LIFESPAN = 25
# Initialize population
population = {i: [INITIAL_POPULATION // NUM_GROUPS]
* NUM_GROUPS for i in range(NUM_GROUPS)}
population_history = {i: [] for i in range(NUM_GROUPS)}
def stochastic_update(value, beta=0.1, gamma=0.01):
sol = solve_ivp(lambda t, y: beta * y - gamma * y**2, [0, 1], [value], dense_output=True)
return sol.sol(1)[0]
CROSSBREED_PROBABILITIES = np.array([i / 100 for i in range(NUM_GROUPS)])
BENEFIT_PROBABILITIES = np.array([i / 100 for i in range(NUM_GROUPS, 0, -1)])
def evolve_population(population, crossbreed_probs, benefit_probs, lifespan):
new_population = {i: [] for i in population.keys()}
for group in population.keys():
for individual in population[group]:
updated_individual = stochastic_update(individual)
if random.random() < crossbreed_probs[group]:
partner_group = random.choice(list(population.keys()))
partner_individual = random.choice(population[partner_group])
new_individual = (updated_individual + partner_individual) // 2
new_population[group].append(new_individual)
else:
new_population[group].append(updated_individual)
if random.random() < benefit_probs[group]:
target_group = random.choice(list(population.keys()))
new_population[target_group].append(updated_individual)
for group in new_population.keys():
new_population[group] = [ind for ind in new_population[group] if random.random() > 1 / lifespan]
return new_population
def run_simulation():
global population, population_history
for year in range(SIMULATION_YEARS):
population = evolve_population(population, CROSSBREED_PROBABILITIES, BENEFIT_PROBABILITIES, INDIVIDUAL_LIFESPAN)
for group in population.keys():
population_history[group].append(len(population[group]))
if year % 100 == 0: # Print progress every 100 years
print(f"Year {year}: {sum(len(individuals) for individuals in population.values())} individuals total")
# Measure execution time
start_time = time.time()
# Run the simulation
run_simulation()
end_time = time.time()
execution_time = end_time - start_time
# Convert the population history to a DataFrame for plotting
df_population_history = pd.DataFrame(population_history)
# Plotting the population history
plt.figure(figsize=(14, 8))
for group in df_population_history.columns:
plt.plot(df_population_history.index, df_population_history[group], label=f'Group {group}')
plt.xlabel('Year')
plt.ylabel('Population Count')
plt.title('Population Dynamics Over Time')
plt.legend()
plt.show()
# Display the execution time
print(f"Simulation completed in {execution_time} seconds")
# Convert the population history to a DataFrame for plotting
df_population_history = pd.DataFrame(population_history)
# Descriptive Statistics
descriptive_stats = df_population_history.describe()
print("Descriptive Statistics:")
print(descriptive_stats)
# Confidence Intervals
confidence_level = 0.95
degrees_freedom = df_population_history.shape[0] - 1
sample_means = df_population_history.mean()
sample_standard_errors = df_population_history.sem()
confidence_intervals = stats.t.interval(confidence_level, degrees_freedom, sample_means, sample_standard_errors)
ci_df = pd.DataFrame(confidence_intervals, index=['Lower Bound', 'Upper Bound'], columns=df_population_history.columns)
print("\n95% Confidence Intervals:")
print(ci_df)
# ANOVA Test
# Melt the DataFrame for ANOVA
df_melted = df_population_history.melt(var_name='Group', value_name='Population')
# Fit the model
model = ols('Population ~ C(Group)', data=df_melted).fit()
anova_table = sm.stats.anova_lm(model, typ=2)
print("\nANOVA Table:")
print(anova_table)
# Plotting
# Histograms
plt.figure(figsize=(14, 8))
df_population_history.plot(kind='hist', bins=50, alpha=0.7, stacked=True)
plt.title('Histogram of Population Counts')
plt.xlabel('Population Count')
plt.ylabel('Frequency')
plt.legend(title='Group', loc='center left', bbox_to_anchor=(1, 0.5))
plt.show()
# Boxplots
plt.figure(figsize=(14, 8))
sns.boxplot(data=df_population_history)
plt.title('Boxplot of Population Counts by Group')
plt.xlabel('Group')
plt.ylabel('Population Count')
plt.show()
# Line plot of population dynamics over time for each group
plt.figure(figsize=(14, 8))
for group in df_population_history.columns:
plt.plot(df_population_history.index, df_population_history[group], label=f'Group {group}')
plt.xlabel('Year')
plt.ylabel('Population Count')
plt.title('Population Dynamics Over Time')
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.show()
# Line plot of total population over time
plt.figure(figsize=(14, 8))
total_population = df_population_history.sum(axis=1)
plt.plot(df_population_history.index, total_population, label='Total Population', color='black')
plt.xlabel('Year')
plt.ylabel('Total Population Count')
plt.title('Total Population Dynamics Over Time')
plt.legend()
plt.show()
print(f"Simulation completed in {execution_time} seconds")
References
- Allen, L. J. S. (2010). An Introduction to Stochastic Processes with Applications to Biology. CRC Press.
- Bassett, D. S., & Sporns, O. (2017). Network Neuroscience. Nature Neuroscience, 20(3), 353-364. [CrossRef]
- Breakspear, M., & Jirsa, V. K. (2007). Neuronal Dynamics and Brain Connectivity. Springer.
- Cohen, M. X. (2014). Analyzing Neural Time Series Data: Theory and Practice. MIT Press.
- Deco, G., & Kringelbach, M. L. (2016). Great Expectations: Using Whole-Brain Computational Connectomics for Understanding Neuropsychiatric Disorders. Neuron, 84(6), 892-905. [CrossRef]
- Fell, J., & Axmacher, N. (2011). The Role of Phase Synchronization in Memory Processes. Nature Reviews Neuroscience, 12(2), 105-118. [CrossRef]
- Fries, P. (2005). A Mechanism for Cognitive Dynamics: Neuronal Communication through Neuronal Coherence. Trends in Cognitive Sciences, 9(10), 474-480. [CrossRef]
- Jensen, O., & Mazaheri, A. (2010). Shaping Functional Architecture by Oscillatory Alpha Activity: Gating by Inhibition. Frontiers in Human Neuroscience, 4, 186. [CrossRef]
- Klimesch, W. (2012). Alpha-Band Oscillations, Attention, and Controlled Access to Stored Information. Trends in Cognitive Sciences, 16(12), 606-617. [CrossRef]
- Montgomery, R.M (2024). Evolutionary Origins and Functional Diversity of Neural Synchronization and Desynchronization: A Multidisciplinary Perspective. [CrossRef]
- Murray, J. D. (2002). Mathematical Biology I. An Introduction. Springer.
- Nowak, M. A. (2006). Evolutionary Dynamics: Exploring the Equations of Life. Harvard University Press.
- Pfurtscheller, G., & Lopes da Silva, F. H. (1999). Event-Related EEG/MEG Synchronization and Desynchronization: Basic Principles. Clinical Neurophysiology, 110(11), 1842-1857. [CrossRef]
- Roughgarden, J. (1979). Theory of Population Genetics and Evolutionary Ecology: An Introduction. Macmillan.
- Seth, A. K., Barrett, A. B., & Barnett, L. (2015). Granger Causality Analysis in Neuroscience and Neuroimaging. Journal of Neuroscience, 35(8), 3293-3297. [CrossRef]
- Strogatz, S. H. (2003). Sync: The Emerging Science of Spontaneous Order. Hyperion.
- Thut, G., Schyns, P. G., & Gross, J. (2012). Entrainment of Perceptually Relevant Brain Oscillations by Non-Invasive Rhythmic Stimulation of the Human Brain. Frontiers in Psychology, 3, 170. [CrossRef]
- Varela, F., Lachaux, J. P., Rodriguez, E., & Martinerie, J. (2001). The Brainweb: Phase Synchronization and Large-Scale Integration. Nature Reviews Neuroscience, 2(4), 229-239. [CrossRef]
- Watts, D. J., & Strogatz, S. H. (1998). Collective Dynamics of ‘Small-World’ Networks. Nature, 393(6684), 440-442. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated



