Submitted:
08 July 2024
Posted:
09 July 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
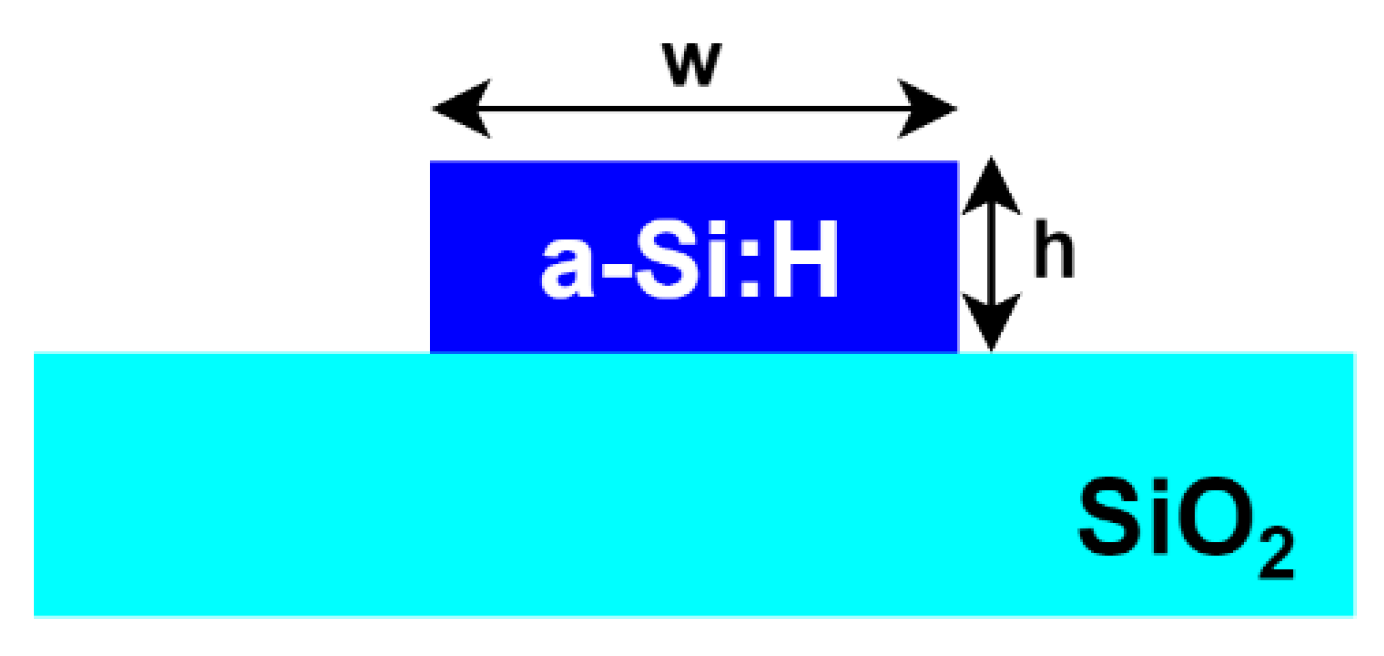
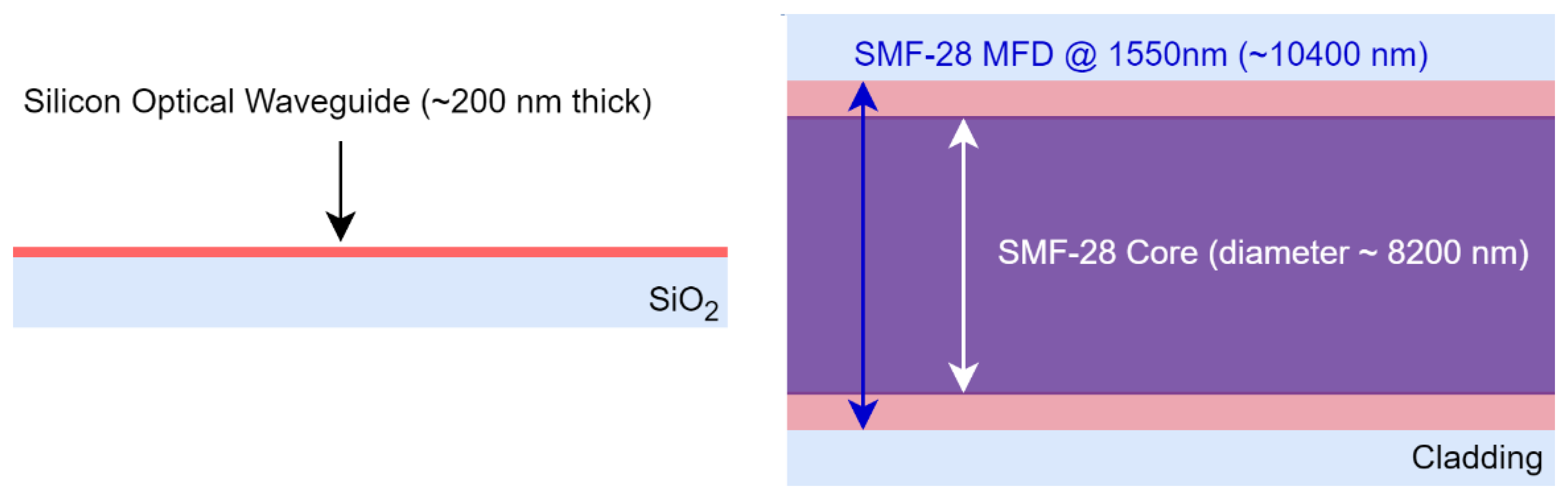
2.1. Single-Mode Optical Fiber
2.2. Single-Mode Waveguide
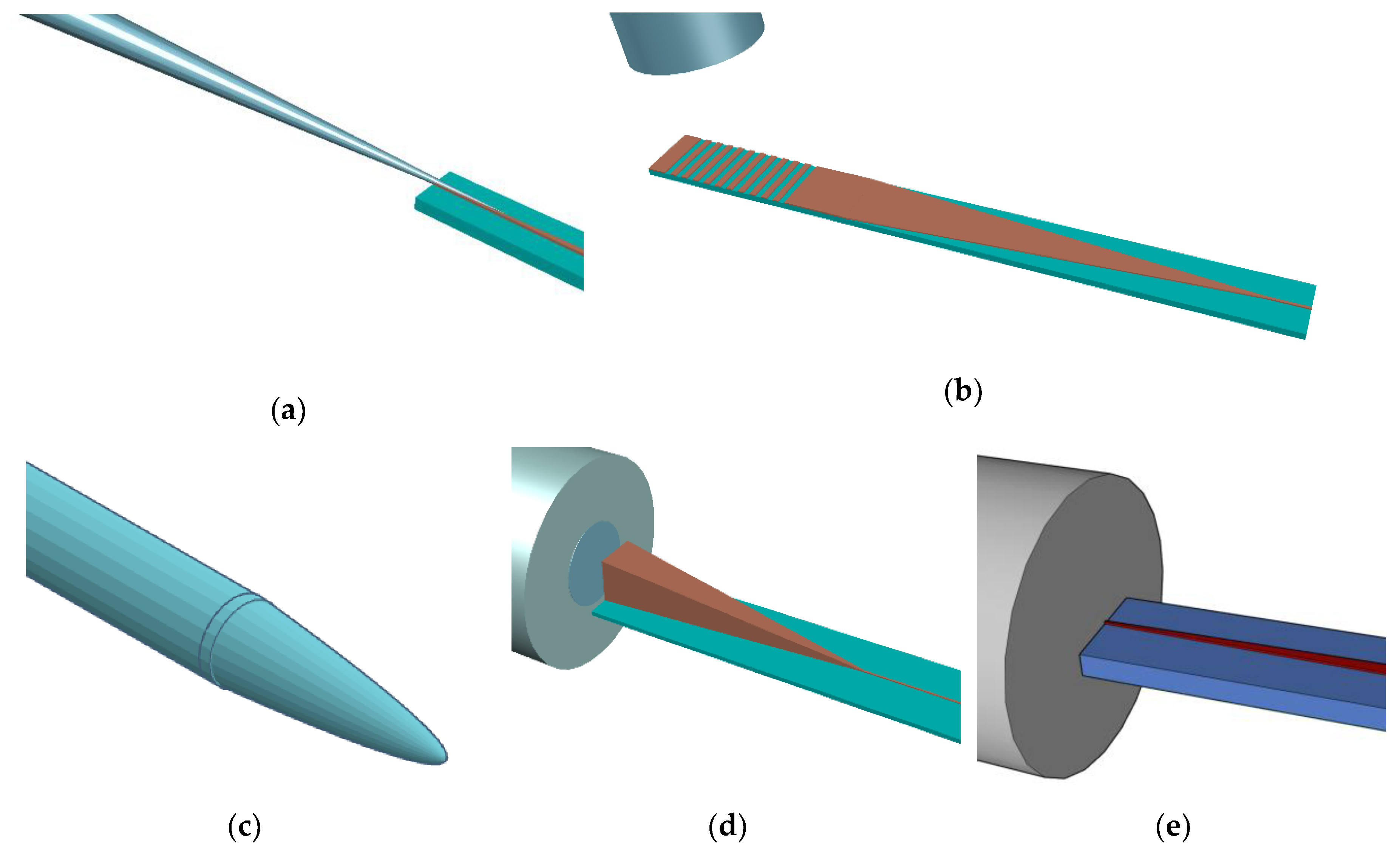
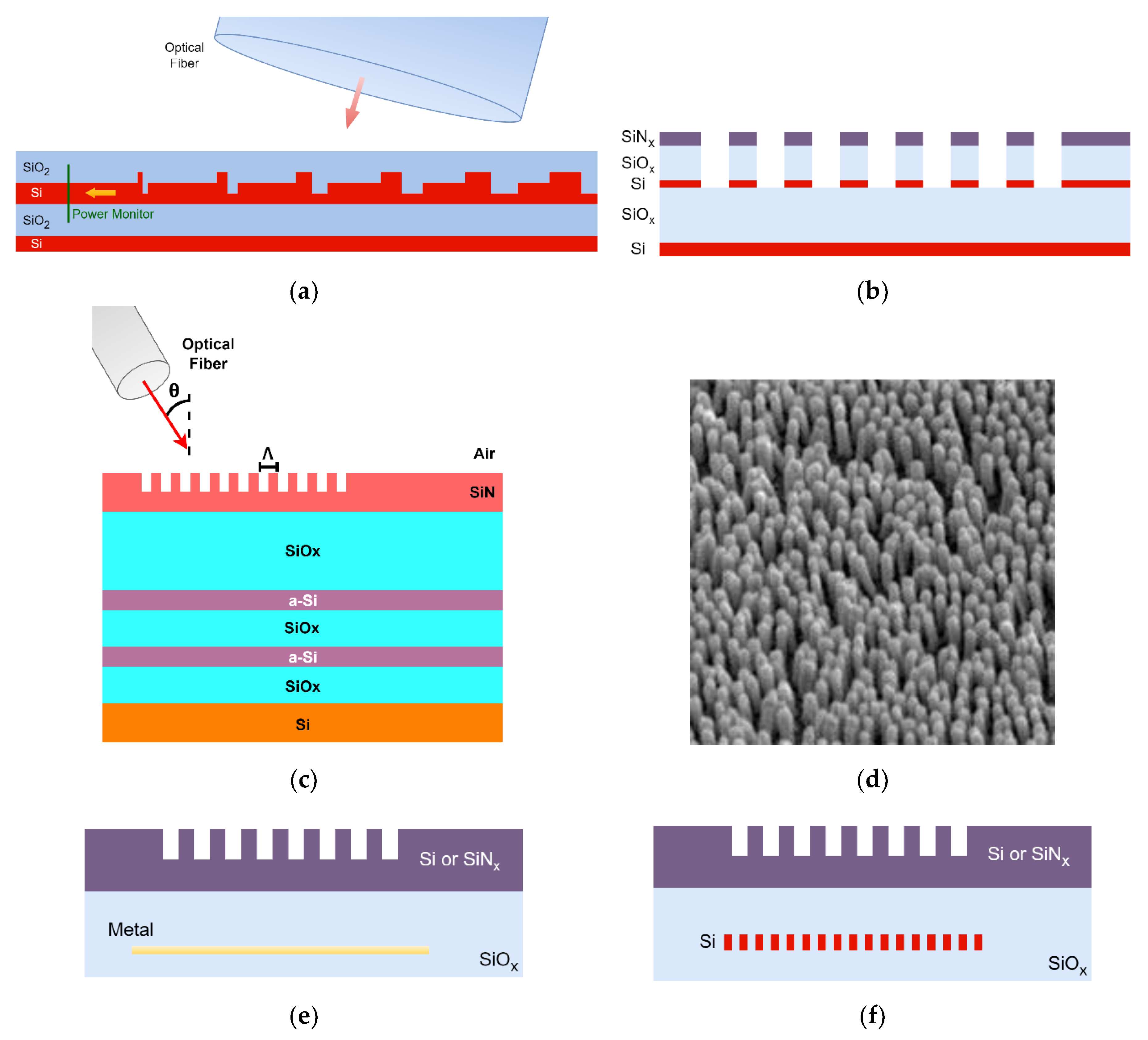
2.3. Light Coupler Design
- Lensed fibers [46];
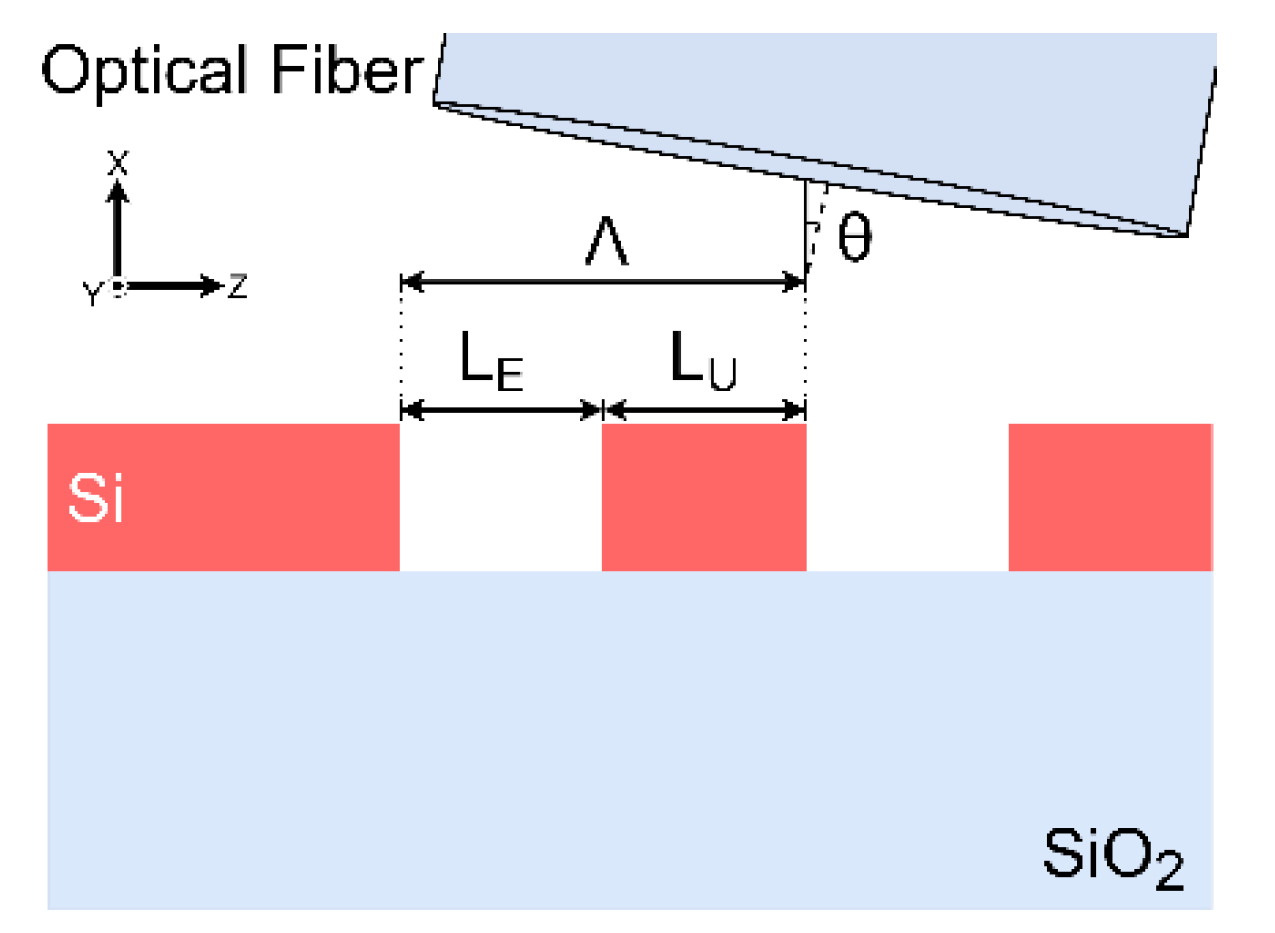
2.4. Grating Coupler Optimization
2.5. Linear Refractive Index Variation
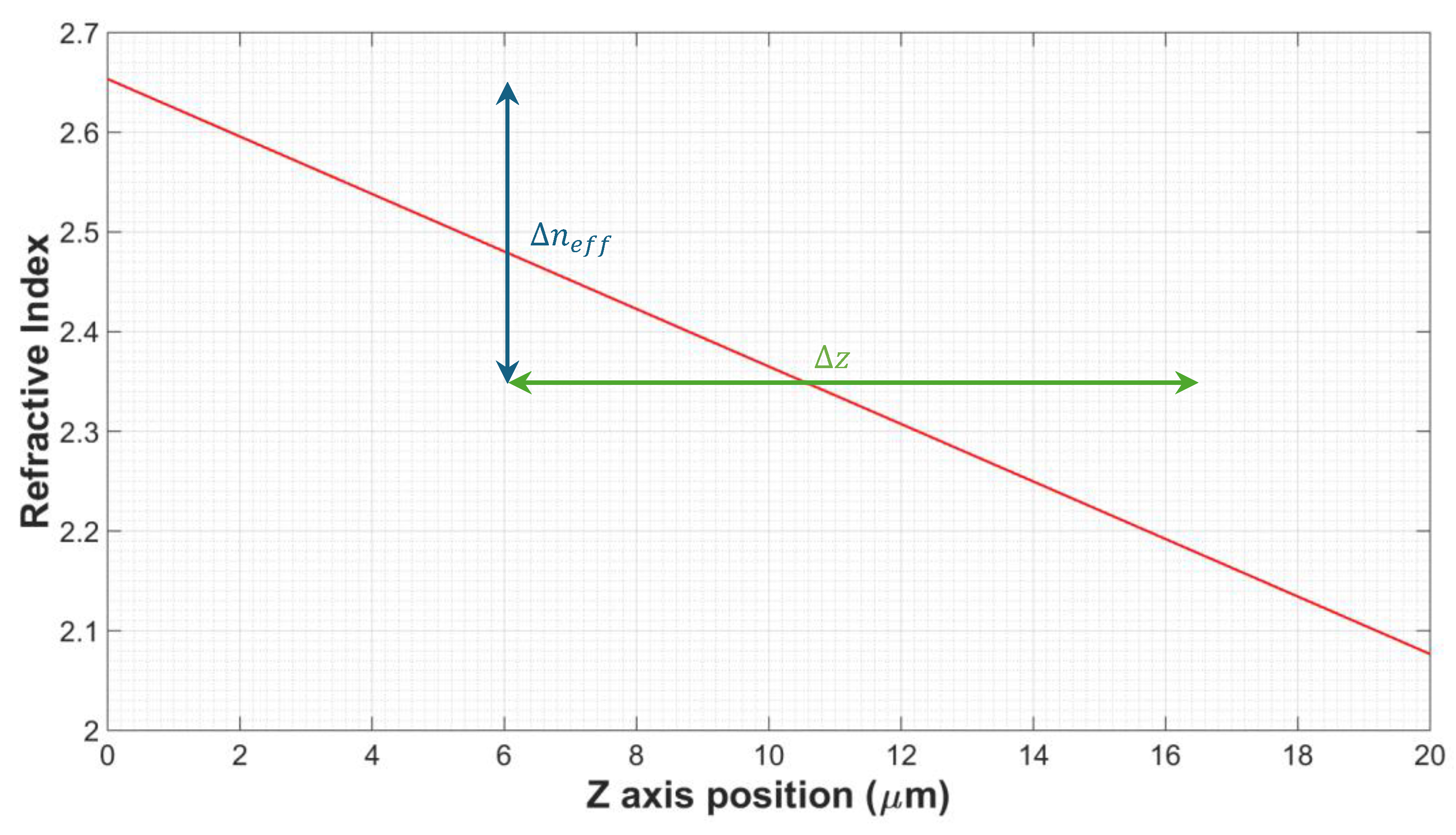
2.6. Quadratic Refractive Index Variation
2.7. Fill-Factor Greater than 50 %
2.8. Overlapped Grating Design
2.9. Random Distribution Overlapped Grating Design
3. Results
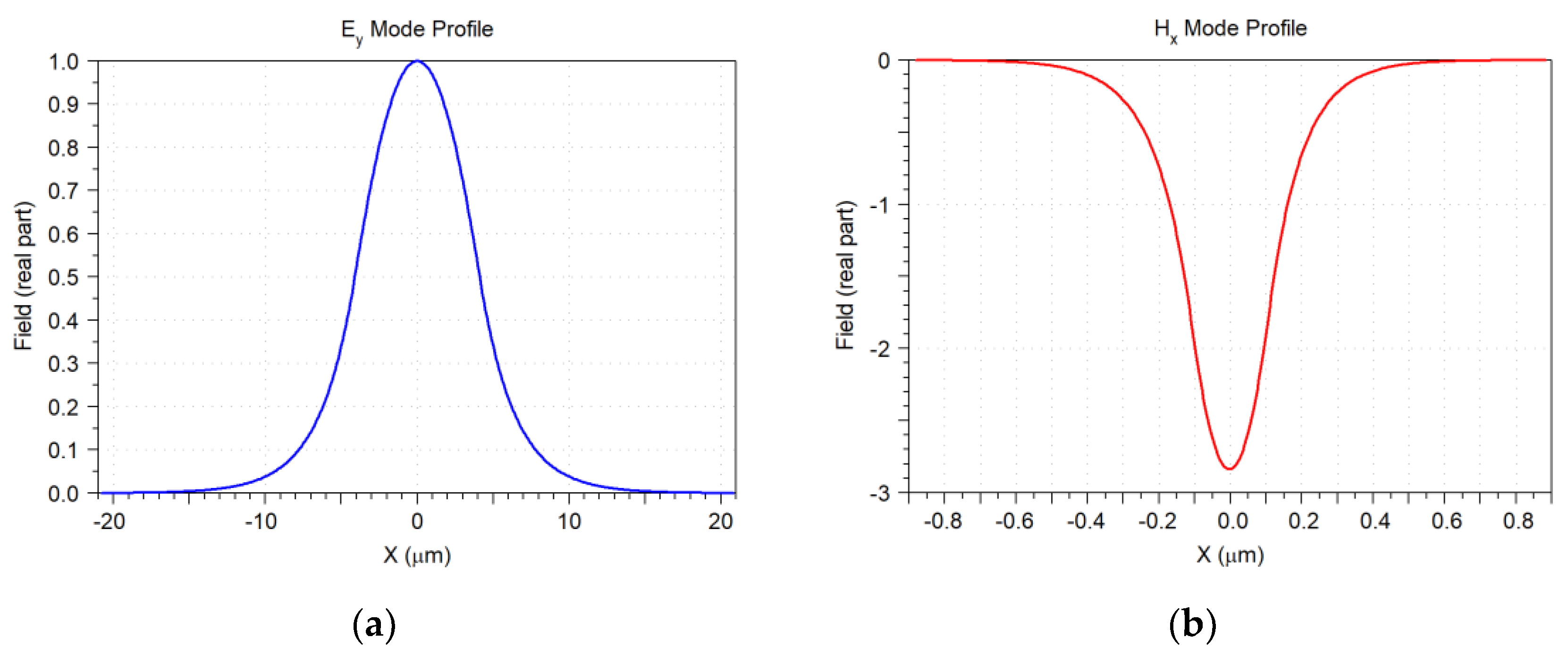
3.1. Fundamental Mode of the Waveguide
3.2. Simulated Single-Mode Fiber Fundamental Mode
3.3. Non-optimized Grating Coupler Performance
3.4. Constant Refractive Index and Fill-factor Greater Than 50 %
3.5. Linear Effective Refractive Index Variation
3.6. Quadratic Effective Refractive Index Variation
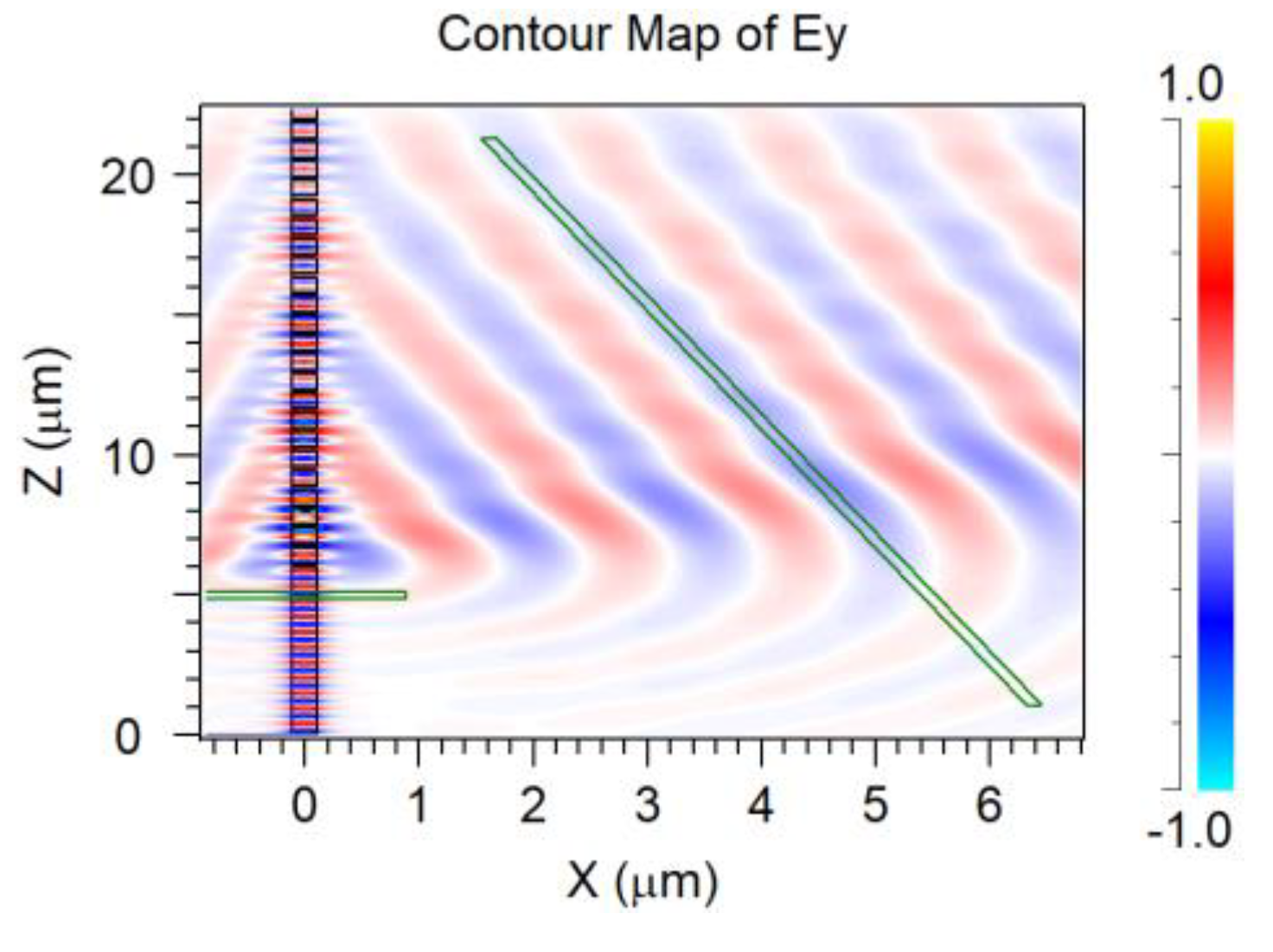
3.7. Overlapped Micrometric Design
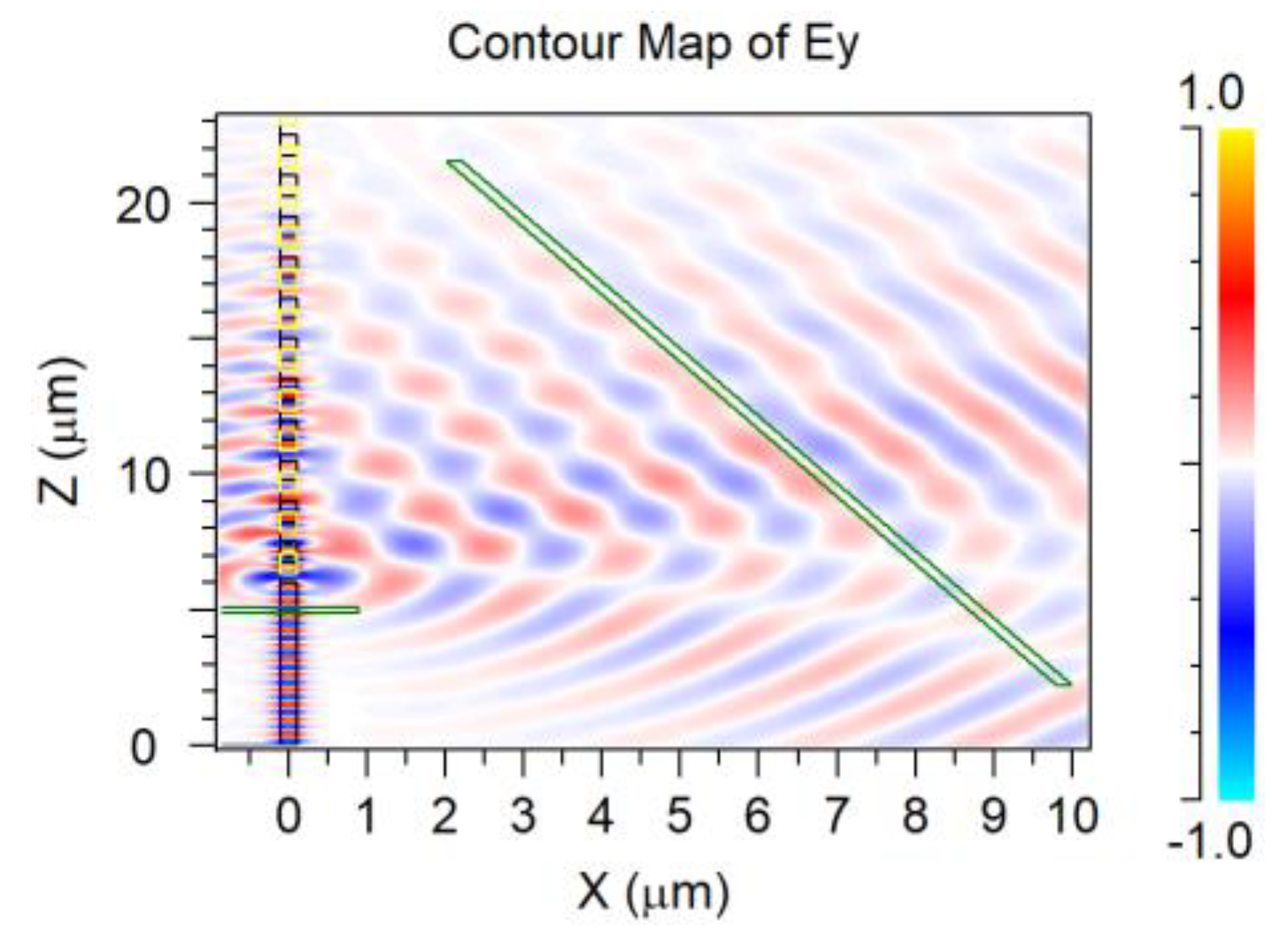
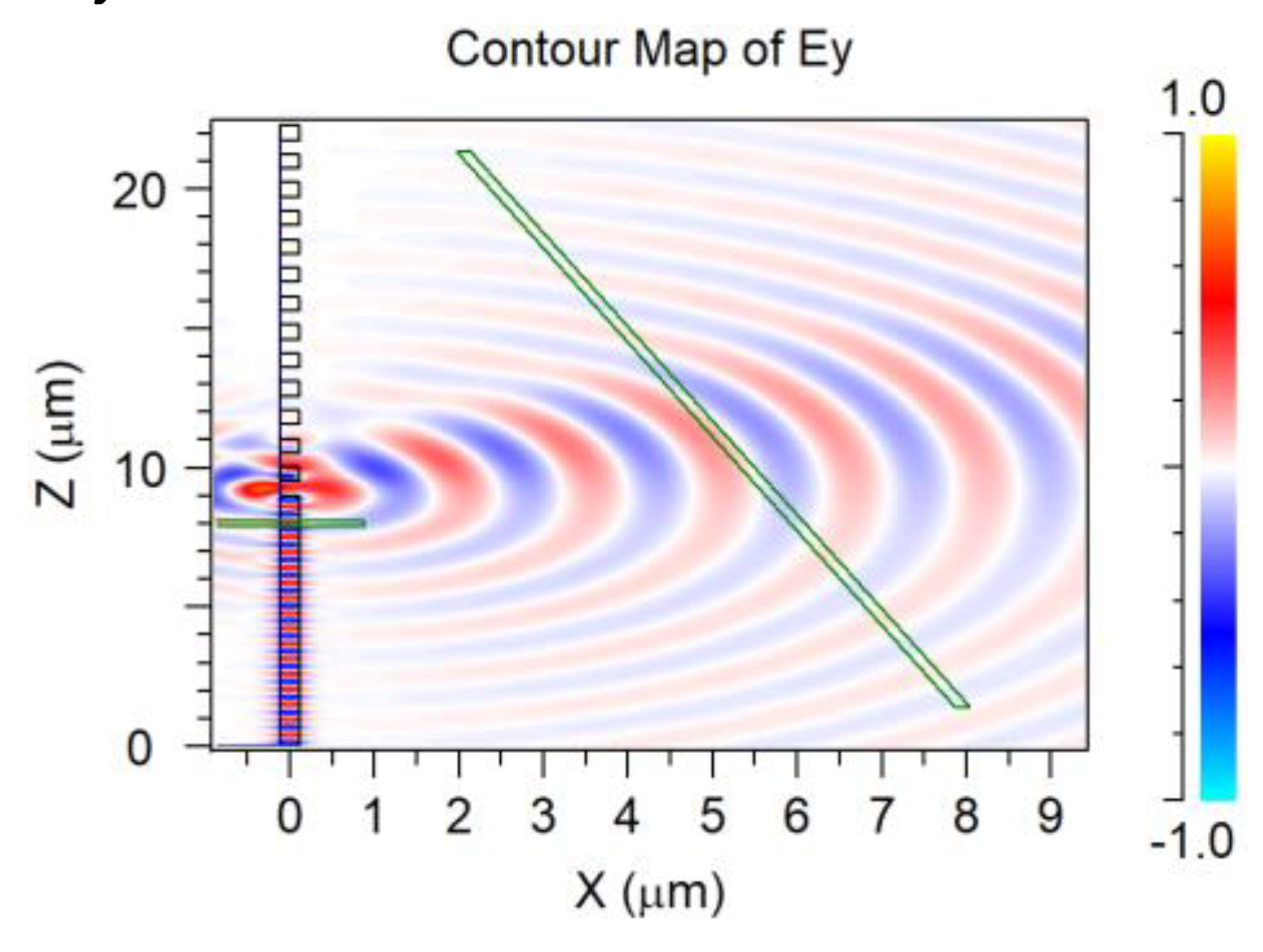
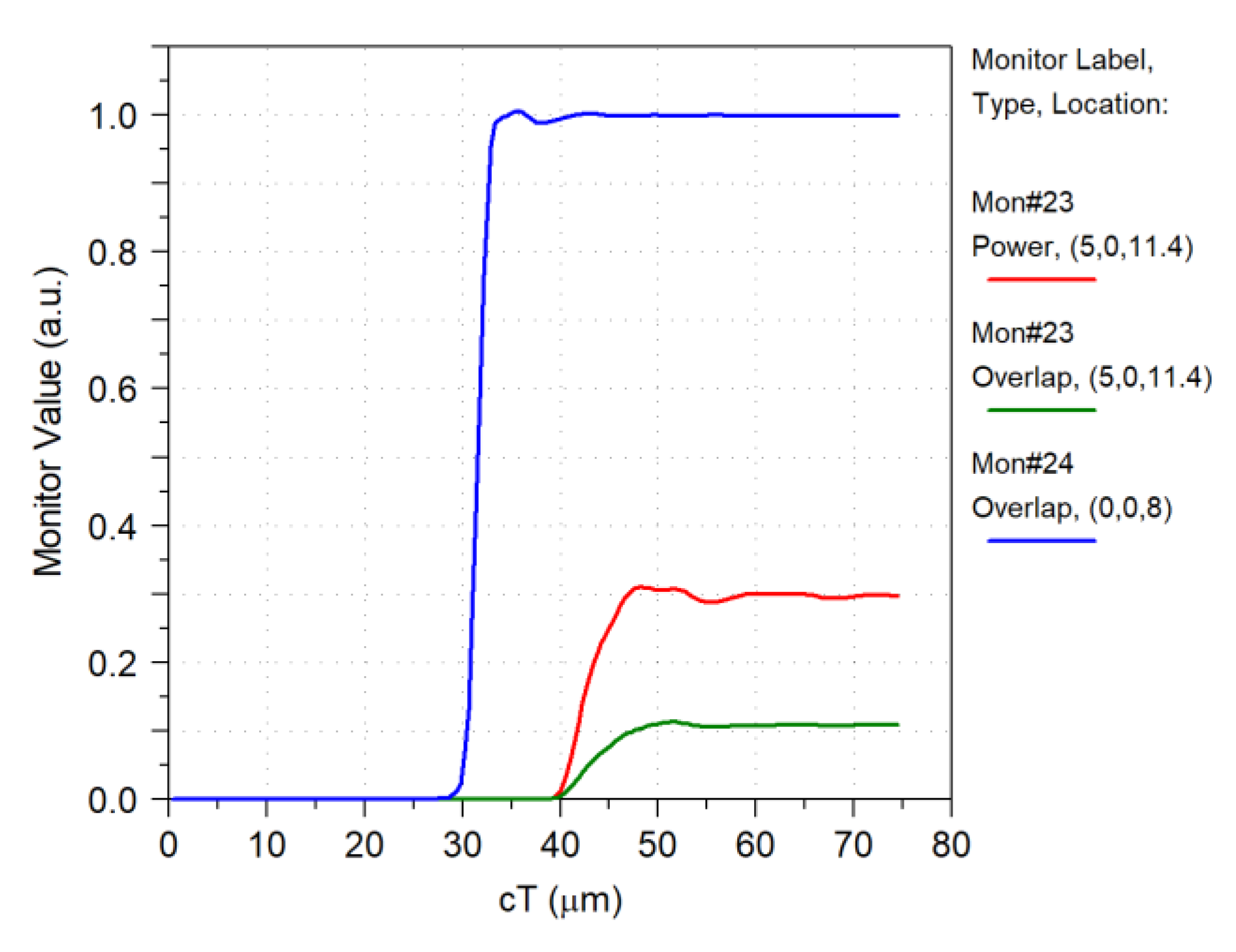
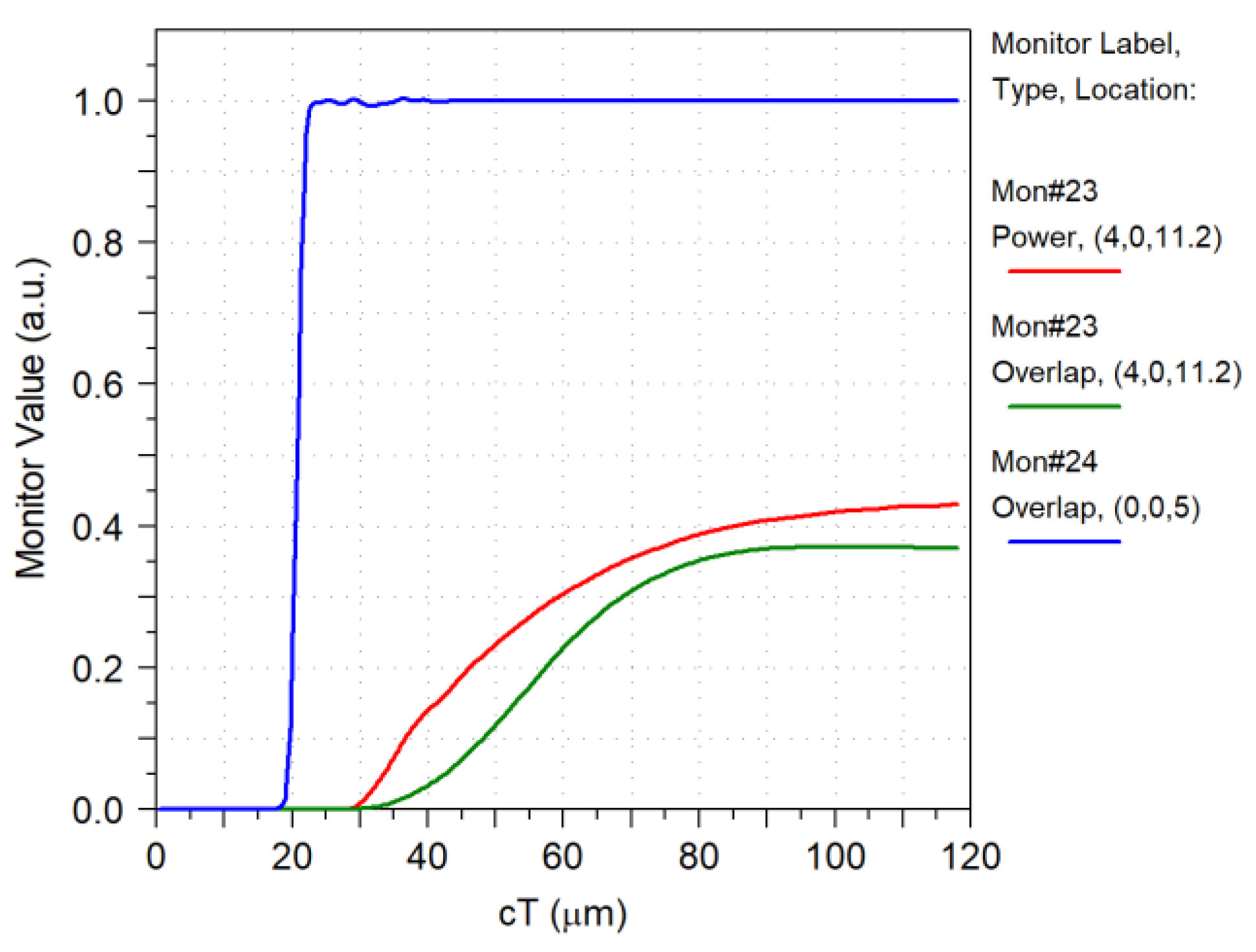
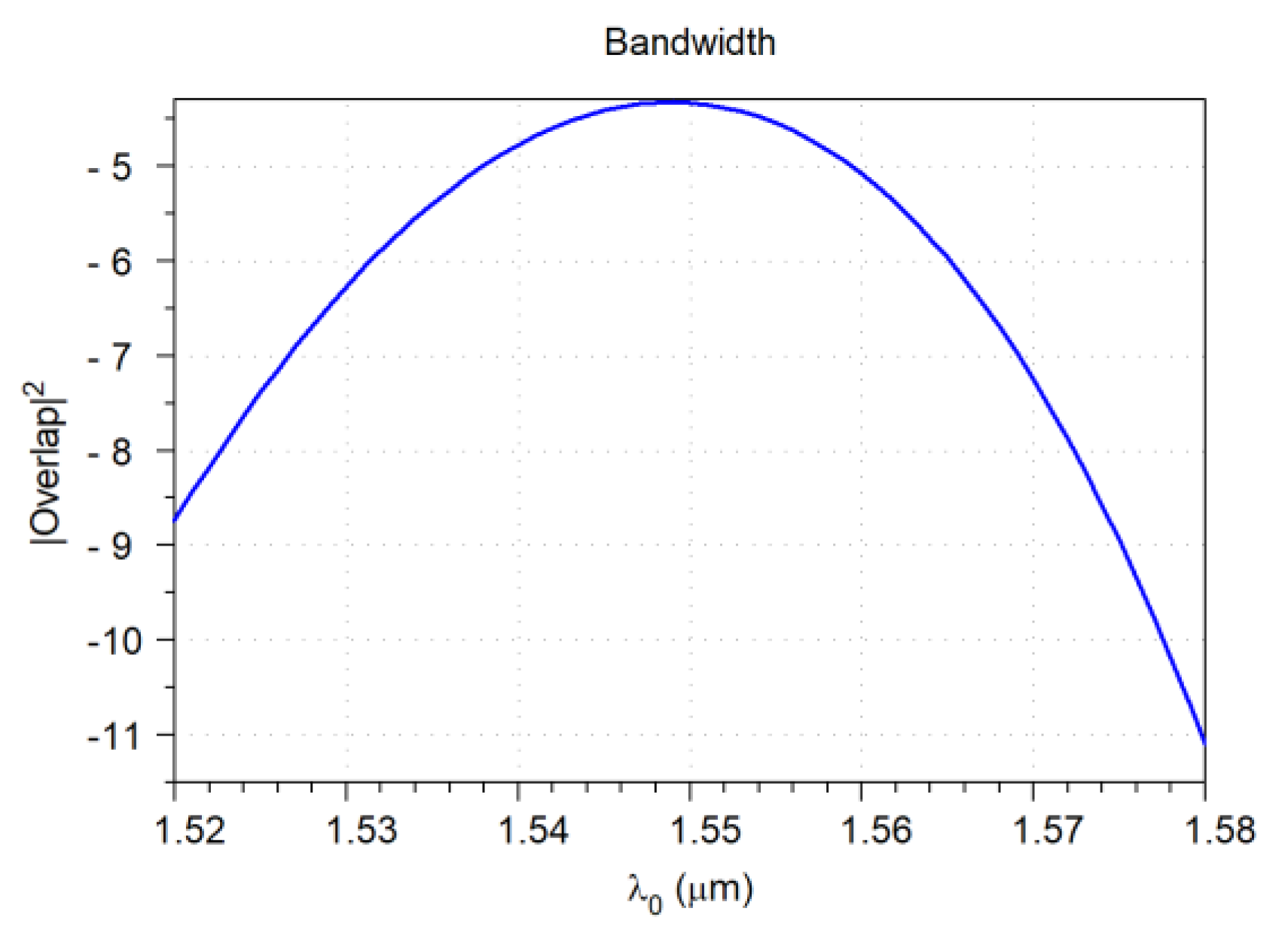
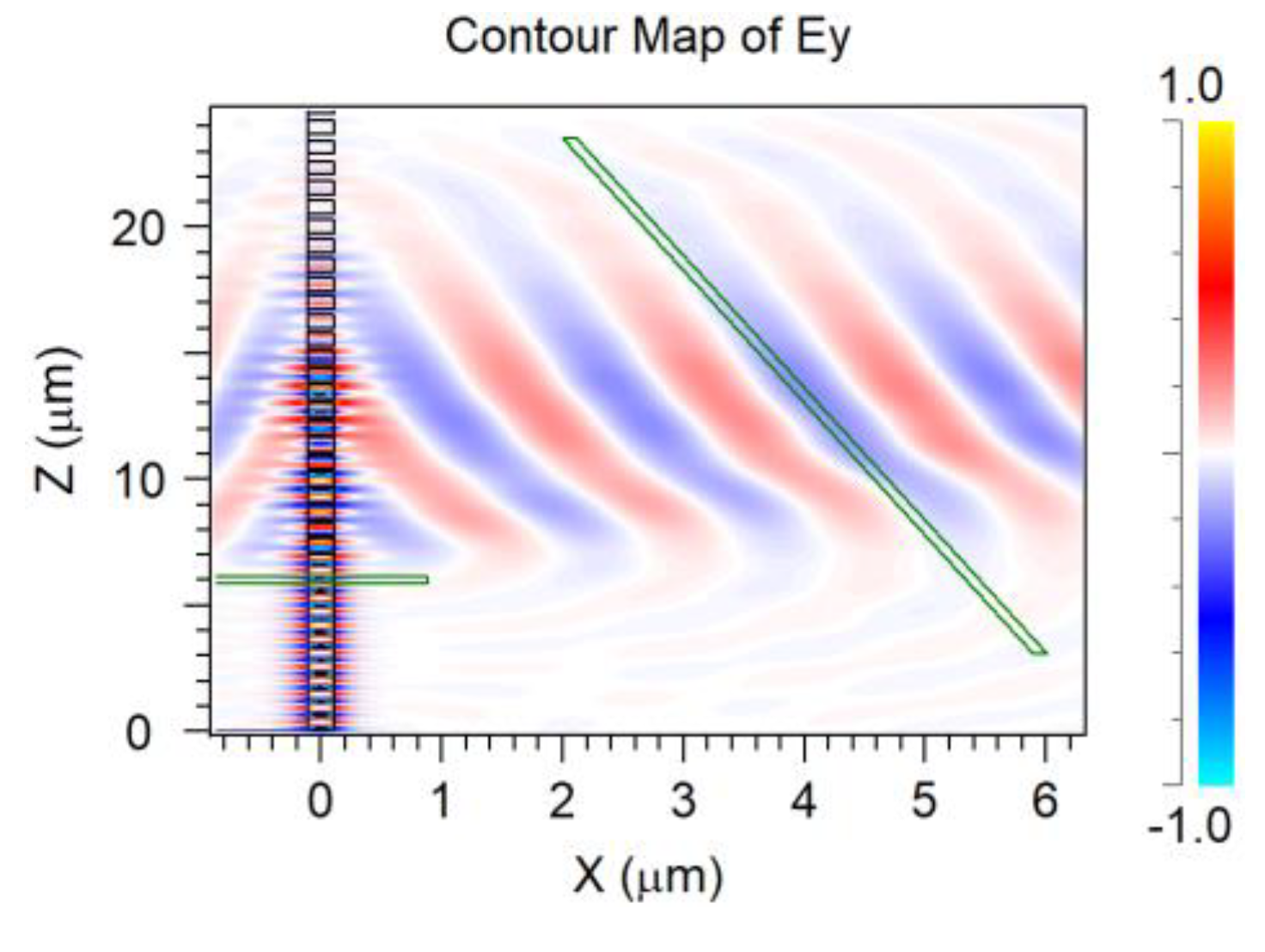
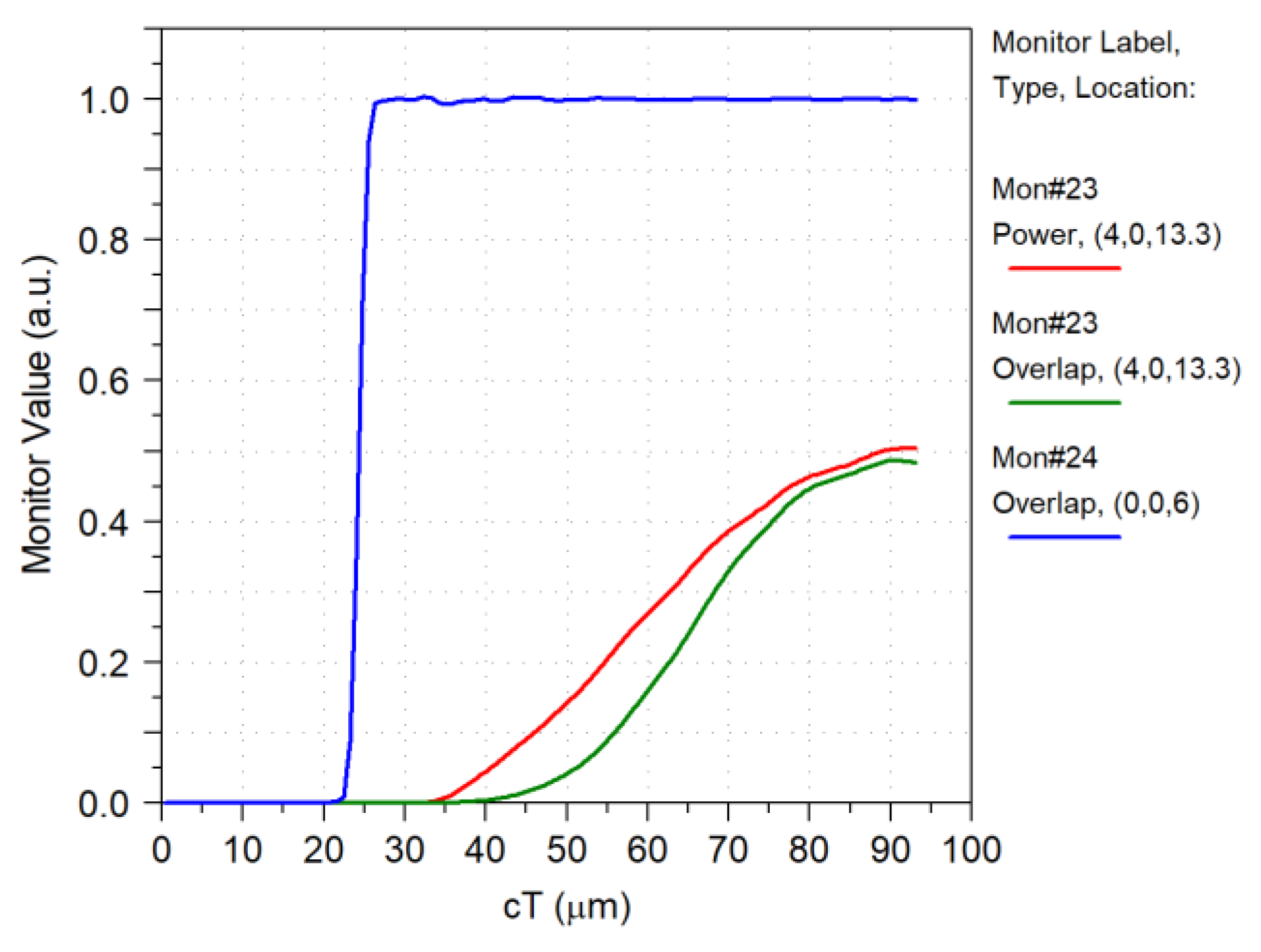
3.8. Random Distribution
4. Discussion
5. Conclusions
6. Future Work and Improvement
Author Contributions
Funding
Conflicts of Interest
Appendix A


Appendix B


References
- Sengupta, K., Nagatsuma, T., Mittleman, D.M.: Terahertz integrated electronic and hybrid electronic–photonic systems. Nat. Electron. 1, 622–635 (2018). [CrossRef]
- Thraskias, C.A., Lallas, E.N., Neumann, N., Schares, L., Offrein, B.J., Henker, R., Plettemeier, D., Ellinger, F., Leuthold, J., Tomkos, I.: Survey of photonic and plasmonic interconnect technologies for intra-datacenter and high-performance computing communications. IEEE Commun. Surv. Tutorials. 20, 2758–2783 (2018). [CrossRef]
- Pelucchi, E., Fagas, G., Aharonovich, I., Englund, D., Figueroa, E., Gong, Q., Hannes, H., Liu, J., Lu, C.Y., Matsuda, N., Pan, J.W., Schreck, F., Sciarrino, F., Silberhorn, C., Wang, J., Jöns, K.D.: The potential and global outlook of integrated photonics for quantum technologies. Nat. Rev. Phys. 4, 194–208 (2022). [CrossRef]
- Lukin, D.M., Guidry, M.A., Vučković, J.: Integrated Quantum Photonics with Silicon Carbide: Challenges and Prospects. PRX Quantum. 1, 1–19 (2020). [CrossRef]
- Pinske, J., Teuber, L., Scheel, S.: Highly degenerate photonic waveguide structures for holonomic computation. Phys. Rev. A. 101, (2020). [CrossRef]
- Huang, C., Sorger, V.J., Miscuglio, M., Al-Qadasi, M., Mukherjee, A., Lampe, L., Nichols, M., Tait, A.N., Ferreira de Lima, T., Marquez, B.A., Wang, J., Chrostowski, L., Fok, M.P., Brunner, D., Fan, S., Shekhar, S., Prucnal, P.R., Shastri, B.J.: Prospects and applications of photonic neural networks. Adv. Phys. X. 7, (2022). [CrossRef]
- Wu, C., Yu, H., Lee, S., Peng, R., Takeuchi, I., Li, M.: Programmable phase-change metasurfaces on waveguides for multimode photonic convolutional neural network. Nat. Commun. 12, 1–8 (2021). [CrossRef]
- Bai, B., Shu, H., Wang, X., Zou, W.: Towards silicon photonic neural networks for artificial intelligence. Sci. China Inf. Sci. 63, 1–14 (2020). [CrossRef]
- Moughames, J., Porte, X., Thiel, M., Ulliac, G., Larger, L., Jacquot, M., Kadic, M., Brunner, D.: Three-dimensional waveguide interconnects for scalable integration of photonic neural networks. Optica. 7, 640 (2020). [CrossRef]
- Torrijos-Morán, L., Lisboa, B.D., Soler, M., Lechuga, L.M., García-Rupérez, J.: Integrated optical bimodal waveguide biosensors: Principles and applications. Results Opt. (2022). [CrossRef]
- S, P.K., A, S.: Optimization of the Transverse Electric Photonic Strip Waveguide Biosensor for Detecting Diabetes Mellitus from Bulk Sensitivity. J. Healthc. Eng. 2021, 6081570 (2021). [CrossRef]
- Voronin, K. V., Stebunov, Y. V., Voronov, A.A., Arsenin, A. V., Volkov, V.S.: Vertically coupled plasmonic racetrack ring resonator for biosensor applications. Sensors (Switzerland). 20, 1–11 (2020). [CrossRef]
- Leuermann, J., Fernández-Gavela, A., Torres-Cubillo, A., Postigo, S., Sánchez-Postigo, A., Lechuga, L.M., Halir, R., Molina-Fernández, Í.: Optimizing the limit of detection of waveguide-based interferometric biosensor devices. Sensors (Switzerland). 19, 1–13 (2019). [CrossRef]
- Luan, E., Shoman, H., Ratner, D.M., Cheung, K.C., Chrostowski, L.: Silicon photonic biosensors using label-free detection. Sensors (Switzerland). 18, 1–42 (2018). [CrossRef]
- Niu, D., Zhang, D., Wang, L., Lian, T., Jiang, M., Sun, X., Li, Z., Wang, X.: High-resolution and fast-response optical waveguide temperature sensor using asymmetric Mach-Zehnder interferometer structure. Sensors Actuators, A Phys. 299, (2019). [CrossRef]
- Jin, T., Zhou, J., Lin, P.T.: Real-time and non-destructive hydrocarbon gas sensing using mid-infrared integrated photonic circuits. RSC Adv. 10, 7452–7459 (2020). [CrossRef]
- Hänsel, A., Heck, M.J.R.: Opportunities for photonic integrated circuits in optical gas sensors. JPhys Photonics. 2, (2020). [CrossRef]
- Consani, C., Ranacher, C., Tortschanoff, A., Grille, T., Irsigler, P., Jakoby, B.: Mid-infrared photonic gas sensing using a silicon waveguide and an integrated emitter. Sensors Actuators, B Chem. 274, 60–65 (2018). [CrossRef]
- Lipka, T., Moldenhauer, L., Müller, J., Trieu, H.K.: Photonic integrated circuit components based on amorphous silicon-on-insulator technology. Photonics Res. 4, 126 (2016). [CrossRef]
- Bucio, T.D., Lacava, C., Clementi, M., Faneca, J., Skandalos, I., Baldycheva, A., Galli, M., Debnath, K., Petropoulos, P., Gardes, F.: Silicon Nitride Photonics for the Near-Infrared. IEEE J. Sel. Top. Quantum Electron. 26, 1–12 (2020). [CrossRef]
- Wilmart, Q., El Dirani, H., Tyler, N., Fowler, D., Malhouitre, S., Garcia, S., Casale, M., Kerdiles, S., Hassan, K., Monat, C., Letartre, X., Kamel, A., Pu, M., Yvind, K., Oxenløwe, L.K., Rabaud, W., Sciancalepore, C., Szelag, B., Olivier, S.: A versatile silicon-silicon nitride photonics platform for enhanced functionalities and applications. Appl. Sci. 9, (2019). [CrossRef]
- Muñoz, P., Micó, G., Bru, L.A., Pastor, D., Pérez, D., Doménech, J.D., Fernández, J., Baños, R., Gargallo, B., Alemany, R., Sánchez, A.M., Cirera, J.M., Mas, R., Domínguez, C.: Silicon nitride photonic integration platforms for visible, near-infrared and mid-infrared applications. Sensors (Switzerland). 17, 1–25 (2017). [CrossRef]
- Porcel, M.A.G., Hinojosa, A., Jans, H., Stassen, A., Goyvaerts, J., Geuzebroek, D., Geiselmann, M., Dominguez, C., Artundo, I.: Silicon nitride photonic integration for visible light applications. Opt. Laser Technol. 112, 299–306 (2019). [CrossRef]
- Costa, J., Almeida, D., Fantoni, A., Lourenço, P., Vieira, M.: Silicon Nitride Interferometers for Optical Sensing with Multi-micron Dimensions. J. Phys. Conf. Ser. 2407, (2022). [CrossRef]
- Almeida, D., Costa, J., Fantoni, A., Vieira, M.: Rib Waveguide Plasmonic Sensor for Lab-on-Chip Technology. IFIP Adv. Inf. Commun. Technol. 649 IFIP, 187–196 (2022). [CrossRef]
- Costa, J., Fantoni, A., Lourenço, P., Vieira, M.: Optimisation of a plasmonic parallel waveguide sensor based on amorphous silicon compounds. 92 (2020). [CrossRef]
- Costa, J., Almeida, D., Fantoni, A., Lourenço, P.: Performance of an a-Si:H MMI multichannel beam splitter analyzed by computer simulation. Silicon Photonics XVI, SPIE. 1169106, (2021). [CrossRef]
- Domínguez Bucio, T., Tarazona, A., Khokhar, A.Z., Mashanovich, G.Z., Gardes, F.Y.: Low temperature silicon nitride waveguides for multilayer platforms. Silicon Photonics Photonic Integr. Circuits V. 9891, 335–341 (2016). [CrossRef]
- Suda, S., Tanizawa, K., Sakakibara, Y., Kamei, T., Nakanishi, K., Itoga, E., Ogasawara, T., Takei, R., Kawashima, H., Namiki, S., Mori, M., Hasama, T., Ishikawa, H.: Pattern-effect-free all-optical wavelength conversion using a hydrogenated amorphous silicon waveguide with ultra-fast carrier decay. Opt. Lett. 37, 1382–1384 (2012). [CrossRef]
- Takei, R., Manako, S., Omoda, E., Sakakibara, Y., Mori, M., Kamei, T.: Sub-1 dB/cm submicrometer-scale amorphous silicon waveguide for backend on-chip optical interconnect. Opt. Express. 22, 4779–4788 (2014). [CrossRef]
- Oo, S.Z., Tarazona, A., Khokhar, A.Z., Petra, R., Franz, Y., Mashanovich, G.Z., Reed, G.T., Peacock, A.C., Chong, H.M.H.: Hot-wire chemical vapor deposition low-loss hydrogenated amorphous silicon waveguides for silicon photonic devices. Photonics Res. 7, 193 (2019). [CrossRef]
- Marchetti, R., Lacava, C., Carroll, L., Gradkowski, K., Minzioni, P.: Coupling strategies for silicon photonics integrated chips [Invited]. Photonics Res. 7, 201 (2019). [CrossRef]
- Son, G., Han, S., Park, J., Kwon, K., Yu, K.: High-efficiency broadband light coupling between optical fibers and photonic integrated circuits. Nanophotonics. 7, 1845–1864 (2018). [CrossRef]
- Sethi, P., Kallega, R., Haldar, A., Selvaraja, S.K.: Compact broadband low-loss taper for coupling to a silicon nitride photonic wire. Opt. Lett. 43, 3433 (2018). [CrossRef]
- Tiecke, T.G., Nayak, K.P., Thompson, J.D., Peyronel, T., de Leon, N.P., Vuletić, V., Lukin, M.D.: Efficient fiber-optical interface for nanophotonic devices. Optica. 2, 70 (2015). [CrossRef]
- Fang, N., Yang, Z., Wu, A., Chen, J., Zhang, M., Zou, S., Wang, X.: Three-Dimensional Tapered Spot-Size Converter. 21, 820–822 (2009).
- Synopsys Inc.: RSoft Photonic Device Tools. https://www.synopsys.com/photonic-solutions/rsoft-photonic-device-tools/rsoft-products.html.
- Almeida, D., Rossi, M., Lourenço, P.J.P.S., Fantoni, A., Costa, J., Vieira, M.: Amorphous silicon grating couplers based on random and quadratic variation of the refractive index. In: Proc. SPIE 12880, Physics and Simulation of Optoelectronic Devices XXXII, 128800J (11 March 2024). p. 38 (2024).
- Saktioto, Zairmi, Y., Veriyanti, V., Candra, W., Syahputra, R.F., Soerbakti, Y., Asyana, V., Irawan, D., Okfalisa, Hairi, H., Hussein, N.A., Syamsudhuha, Anita, S.: Birefringence and Polarization Mode Dispersion Phenomena of Commercial Optical Fiber in Telecommunication Networks. J. Phys. Conf. Ser. 1655, (2020). [CrossRef]
- Corning Inc.: Corning®® SMF-28TM Optical Fiber. https://www.photonics.byu.edu/FiberOpticConnectors.parts/images/smf28.pdf.
- Fantoni, A., Lourenco, P., Vieira, M.: A model for the refractive index of amorphous silicon for FDTD simulation of photonics waveguides. Proc. Int. Conf. Numer. Simul. Optoelectron. Devices, NUSOD. 167–168 (2017). [CrossRef]
- Zhou, X., Tsang, H.K.: Photolithography Fabricated Sub-Decibel High-Efficiency Silicon Waveguide Grating Coupler. IEEE Photonics Technol. Lett. 35, 43–46 (2023). [CrossRef]
- Vitali, V., Domínguez Bucio, T., Lacava, C., Marchetti, R., Mastronardi, L., Rutirawut, T., Churchill, G., Faneca, J., Gates, J.C., Gardes, F., Petropoulos, P.: High-efficiency reflector-less dual-level silicon photonic grating coupler. Photonics Res. 11, 1275–1283 (2023). [CrossRef]
- Lourenço, P., Fantoni, A., Costa, J., Fernandes, M.: Design and optimization of a waveguide/fibre coupler in the visible range. Sensors Actuators A Phys. (2021). [CrossRef]
- Ong, E.W., Fahrenkopf, N.M., Coolbaugh, D.D.: SiN x bilayer grating coupler for photonic systems . OSA Contin. 1, 13 (2018). [CrossRef]
- Yoshida, T., Omoda, E., Atsumi, Y., Nishi, T., Tajima, S., Miura, N., Mori, M., Sakakibara, Y.: Vertically Curved Si Waveguide Coupler with Low Loss and Flat Wavelength Window. J. Light. Technol. 34, 1567–1571 (2016). [CrossRef]
- Mu, X., Wu, S., Cheng, L., Fu, H.Y.: Edge couplers in silicon photonic integrated circuits: A review. Appl. Sci. 10, (2020). [CrossRef]
- Sure, A., Dillon, T., Murakowski, J., Lin, C., Pustai, D., Prather, D.: Fabrication and characterization of three-dimensional silicon tapers. Opt. Express. 11, 3555 (2003). [CrossRef]
- Shiraishi, K., Yoda, H., Ohshima, A., Ikedo, H., Tsai, C.S.: A silicon-based spot-size converter between single-mode fibers and Si-wire waveguides using cascaded tapers. Appl. Phys. Lett. 91, (2007). [CrossRef]
- Fritze, M., Knecht, J., Bozler, C., Keast, C., Fijol, J., Jacobson, S., Keating, P., LeBlanc, J., Fike, E., Kessler, B., Frish, M., Manolatou, C.: Fabrication of three-dimensional mode converters for silicon-based integrated optics. J. Vac. Sci. Technol. B Microelectron. Nanom. Struct. 21, 2897 (2003). [CrossRef]
- Ong, E.W., Fahrenkopf, N.M., Coolbaugh, D.D.: SiNx bilayer grating coupler for photonic systems. OSA Contin. 1, 13 (2018). [CrossRef]
- Cheng, L., Mao, S., Li, Z., Han, Y., Fu, H.Y.: Grating Couplers on Silicon Photonics: Design Principles, Emerging Trends and Practical Issues. Micromachines. 13, (2022). [CrossRef]
- Xu, P., Zhang, Y., Shao, Z., Liu, L., Zhou, L., Yang, C., Chen, Y., Yu, S.: High-efficiency wideband SiN_x-on-SOI grating coupler with low fabrication complexity. Opt. Lett. 42, 3391 (2017). [CrossRef]
- Marchetti, R., Lacava, C., Khokhar, A., Chen, X., Cristiani, I., Richardson, D.J., Reed, G.T., Petropoulos, P., Minzioni, P.: High-efficiency grating-couplers: Demonstration of a new design strategy. Sci. Rep. 7, 1–8 (2017). [CrossRef]
- Zhao, Z., Fan, S.: Design Principles of Apodized Grating Couplers. J. Light. Technol. 38, 4435–4446 (2020). [CrossRef]
- Sacher, W.D., Huang, Y., Ding, L., Taylor, B.J.F., Jayatilleka, H., Lo, G.-Q., Poon, J.K.S.: Wide bandwidth and high coupling efficiency Si3N4-on-SOI dual-level grating coupler. Opt. Express. 22, 10938–10947 (2014). [CrossRef]
- Hong, J., Spring, A.M., Qiu, F., Yokoyama, S.: A high efficiency silicon nitride waveguide grating coupler with a multilayer bottom reflector. Sci. Rep. 9, 1–8 (2019). [CrossRef]
- Singh, R., Singh, R.R., Priye, V.: Parametric optimization of fiber to waveguide coupler using Bragg gratings. Opt. Quantum Electron. 51, 1–10 (2019). [CrossRef]
- Tan, H., Liu, W., Zhang, Y., Yin, S., Dai, D., Gao, S., Guan, X.: High-Efficiency Broadband Grating Couplers for Silicon Hybrid Plasmonic Waveguides. Photonics. 9, (2022). [CrossRef]
- Nambiar, S., Ranganath, P., Kallega, R., Selvaraja, S.K.: High efficiency DBR assisted grating chirp generators for silicon nitride fiber-chip coupling. Sci. Rep. 9, 1–9 (2019). [CrossRef]
- Ding, Y., Peucheret, C., Ou, H., Yvind, K.: Fully etched apodized grating coupler on the SOI platform with −0.58 dB coupling efficiency. Opt. Lett. 39, 5348 (2014). [CrossRef]
- Romero-García, S., Merget, F., Zhong, F., Finkelstein, H., Witzens, J.: Visible wavelength silicon nitride focusing grating coupler with AlCu/TiN reflector. Opt. Lett. 38, 2521 (2013). [CrossRef]
- Zhu, Y., Wang, J., Xie, W., Tian, B., Li, Y., Brainis, E., Jiao, Y., Van Thourhout, D.: Ultra-compact silicon nitride grating coupler for microscopy systems. Opt. Express. 25, 33297 (2017). [CrossRef]
- Jiang, Y., Krasavin, A. V., Nasir, M.E., Wang, P., Zayats, A. V.: Humidity-induced direct modification of the optical response of plasmonic nanorod metamaterials. Opt. Mater. Express. 12, 4574 (2022). [CrossRef]
- Lin, T., Yang, H., Li, L., Yun, B., Hu, G., Li, S., Yu, W., Ma, X., Liang, X., Cui, Y.: Ultra-broadband and highly efficient silicon nitride bi-layer grating couplers. Opt. Commun. 530, (2023). [CrossRef]
- Vitali, V., Lacava, C., Domínguez Bucio, T., Gardes, F.Y., Petropoulos, P.: Highly efficient dual-level grating couplers for silicon nitride photonics. Sci. Rep. 12, 1–12 (2022). [CrossRef]
- Zhang, Z., Shan, X., Huang, B., Zhang, Z., Cheng, C., Bai, B., Gao, T., Xu, X., Zhang, L., Chen, H.: Efficiency enhanced grating coupler for perfectly vertical fiber-to-chip coupling. Materials (Basel). 13, 1–11 (2020). [CrossRef]
- Fang, Y., He, Y.: Resolution technology of lithography machine. J. Phys. Conf. Ser. 2221, (2022). [CrossRef]
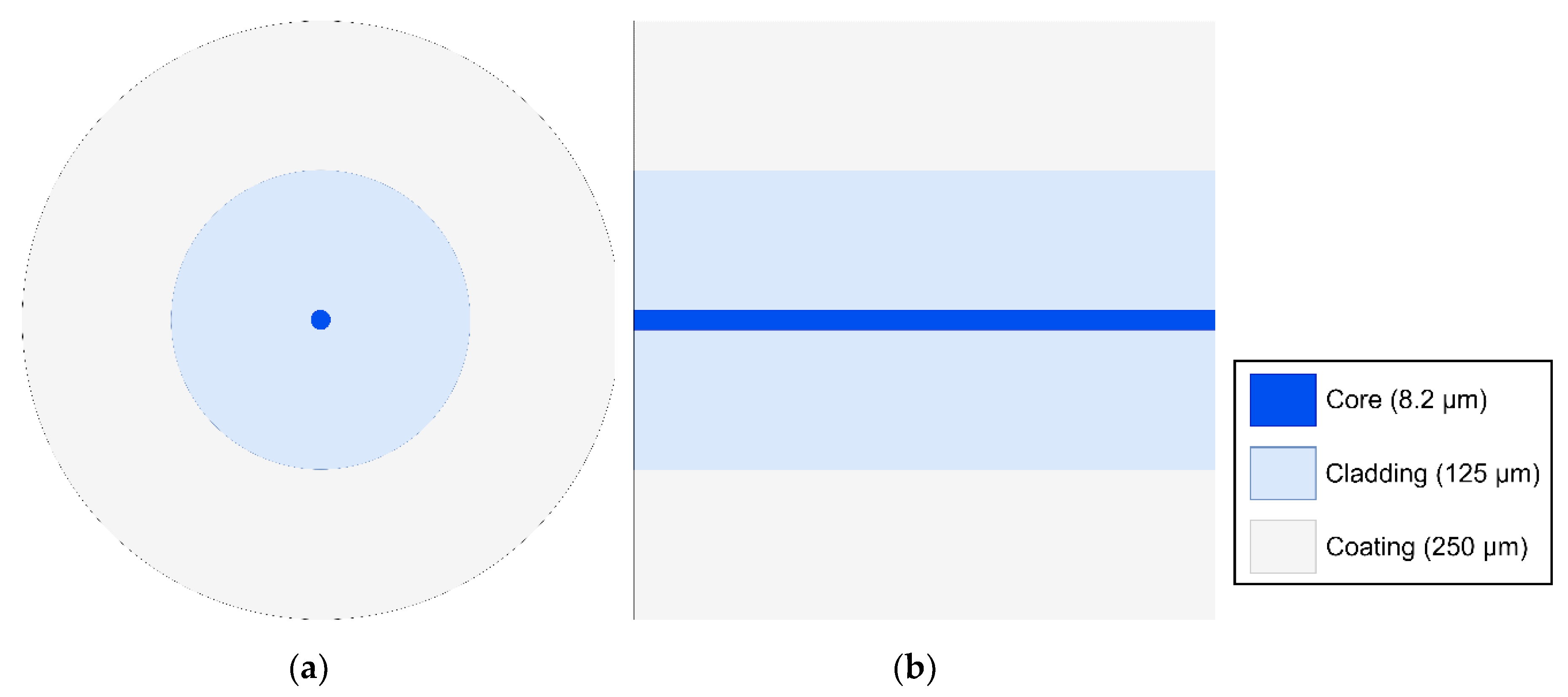
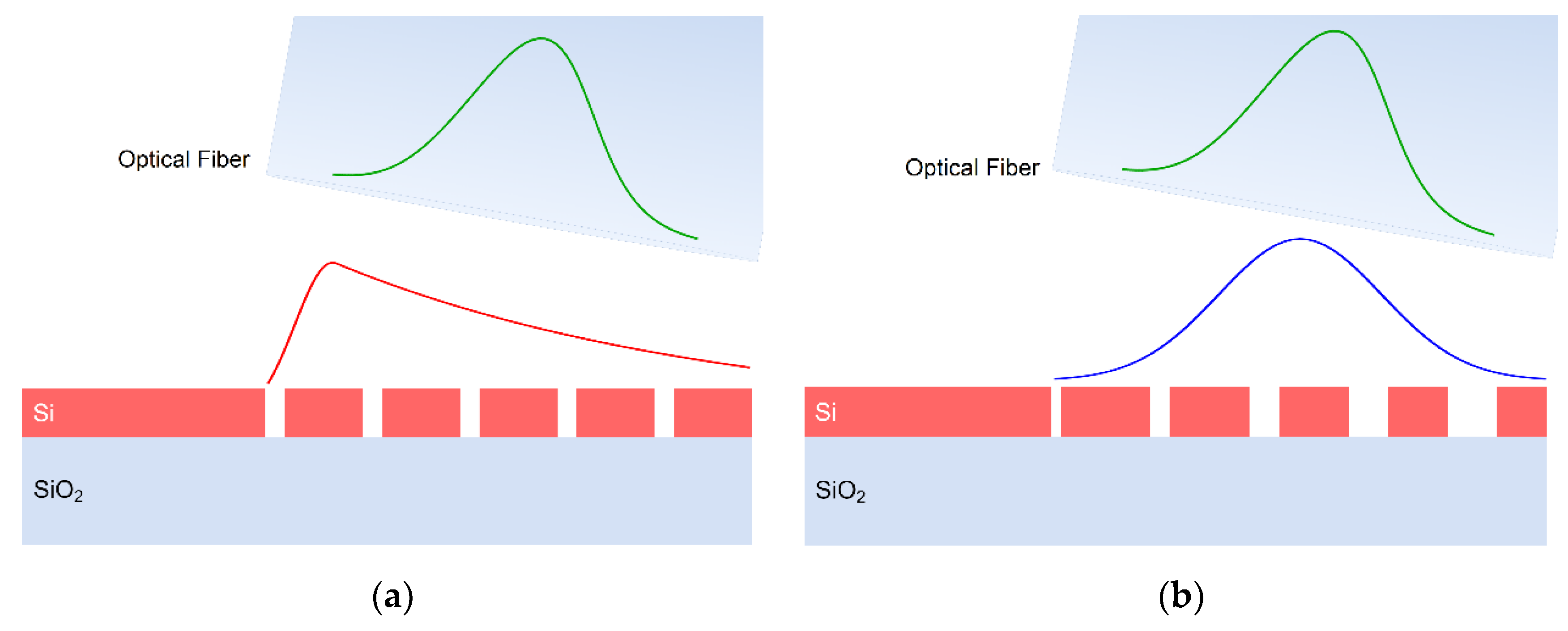
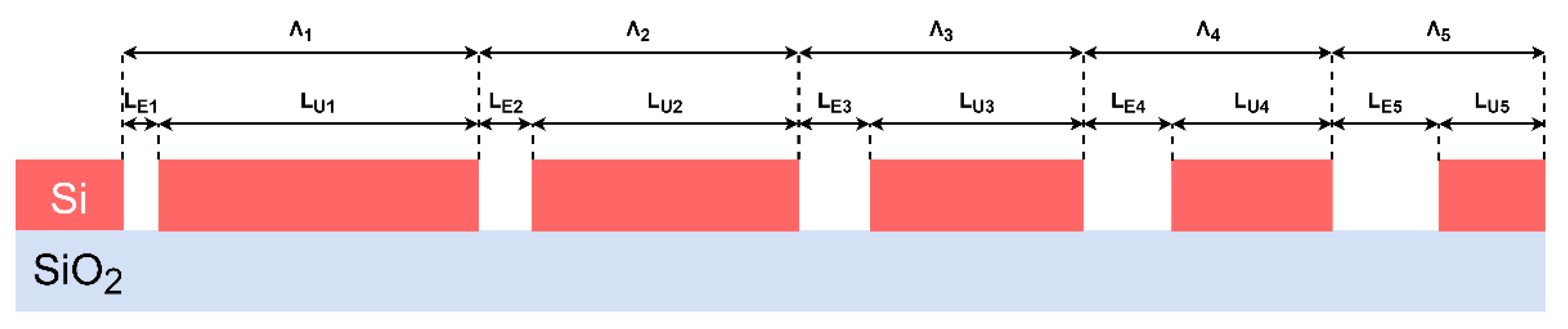

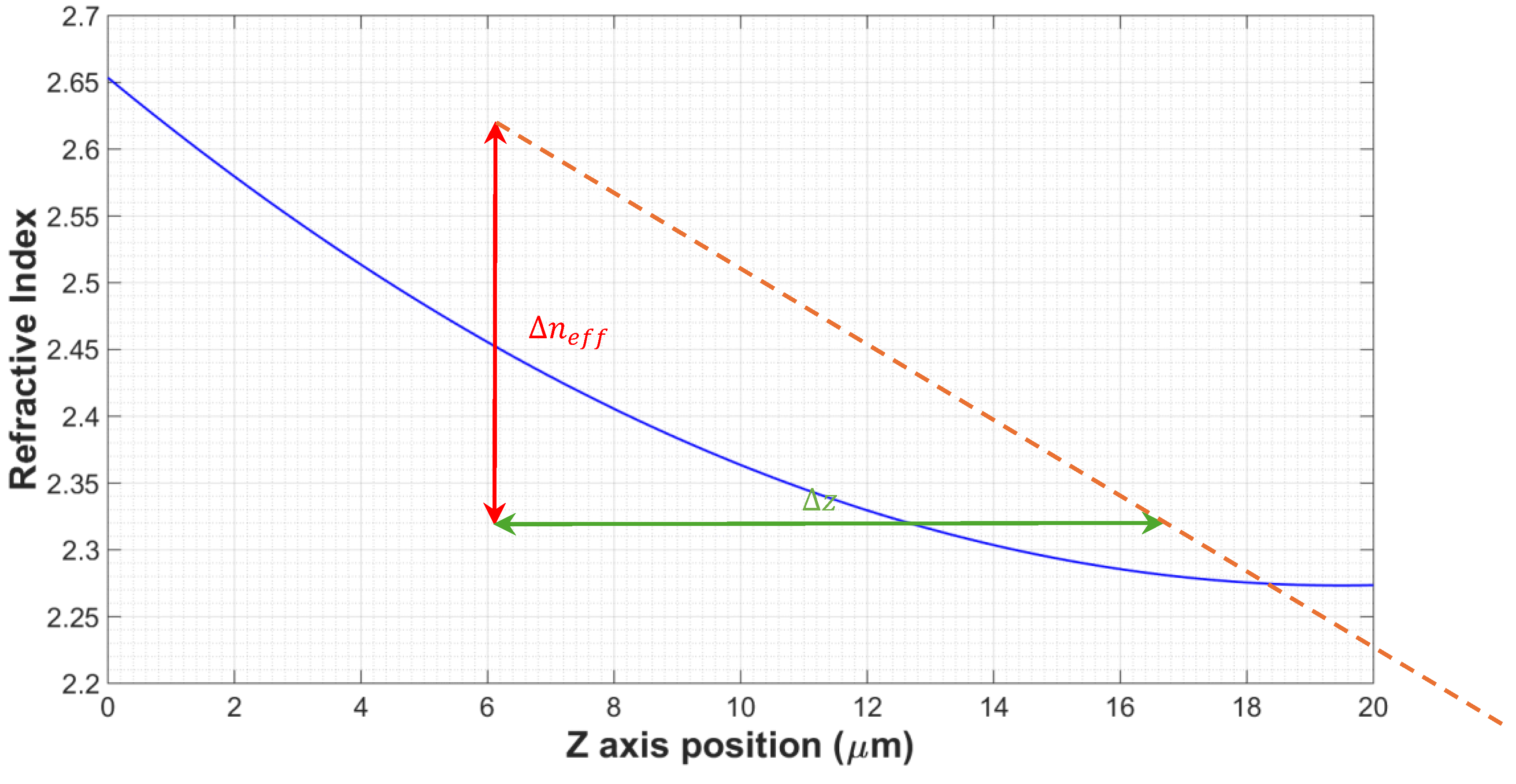




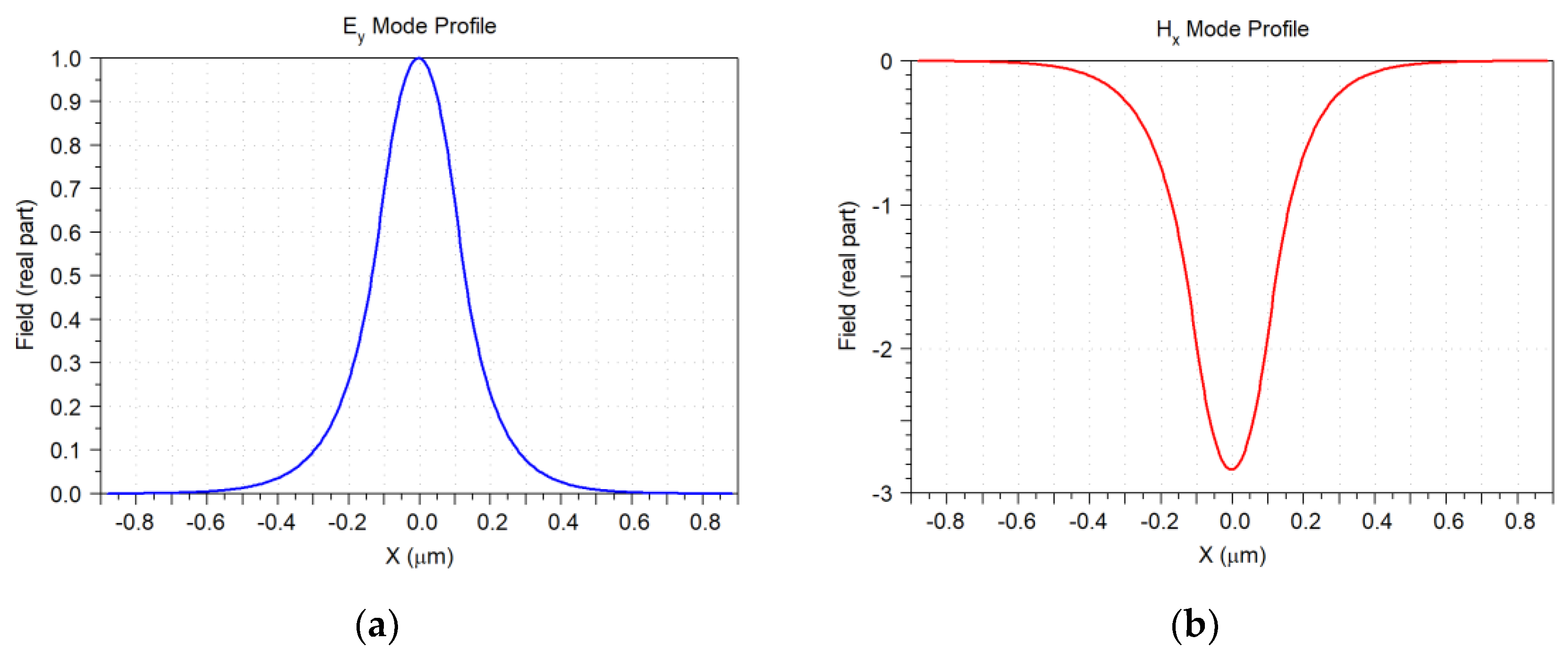
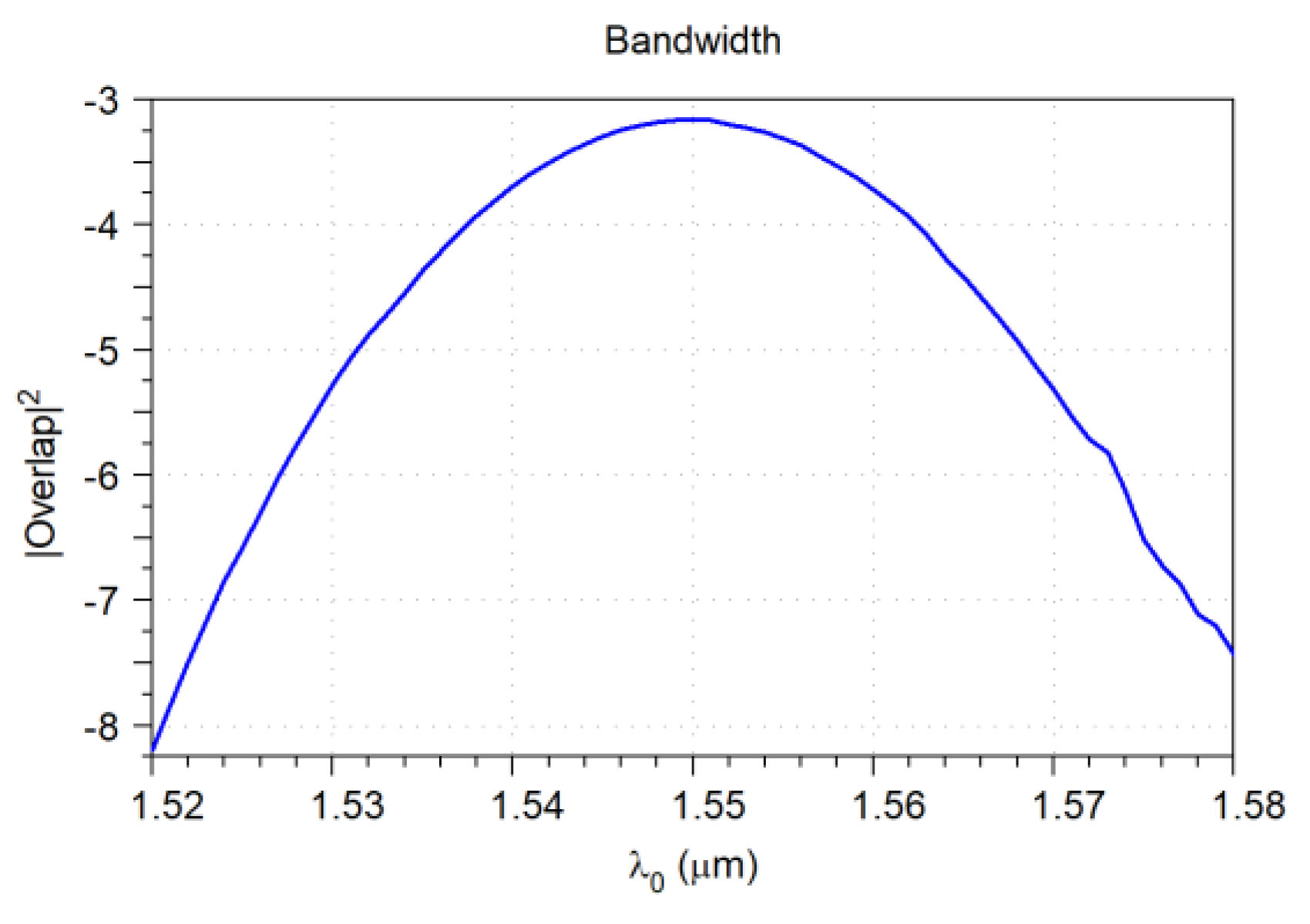
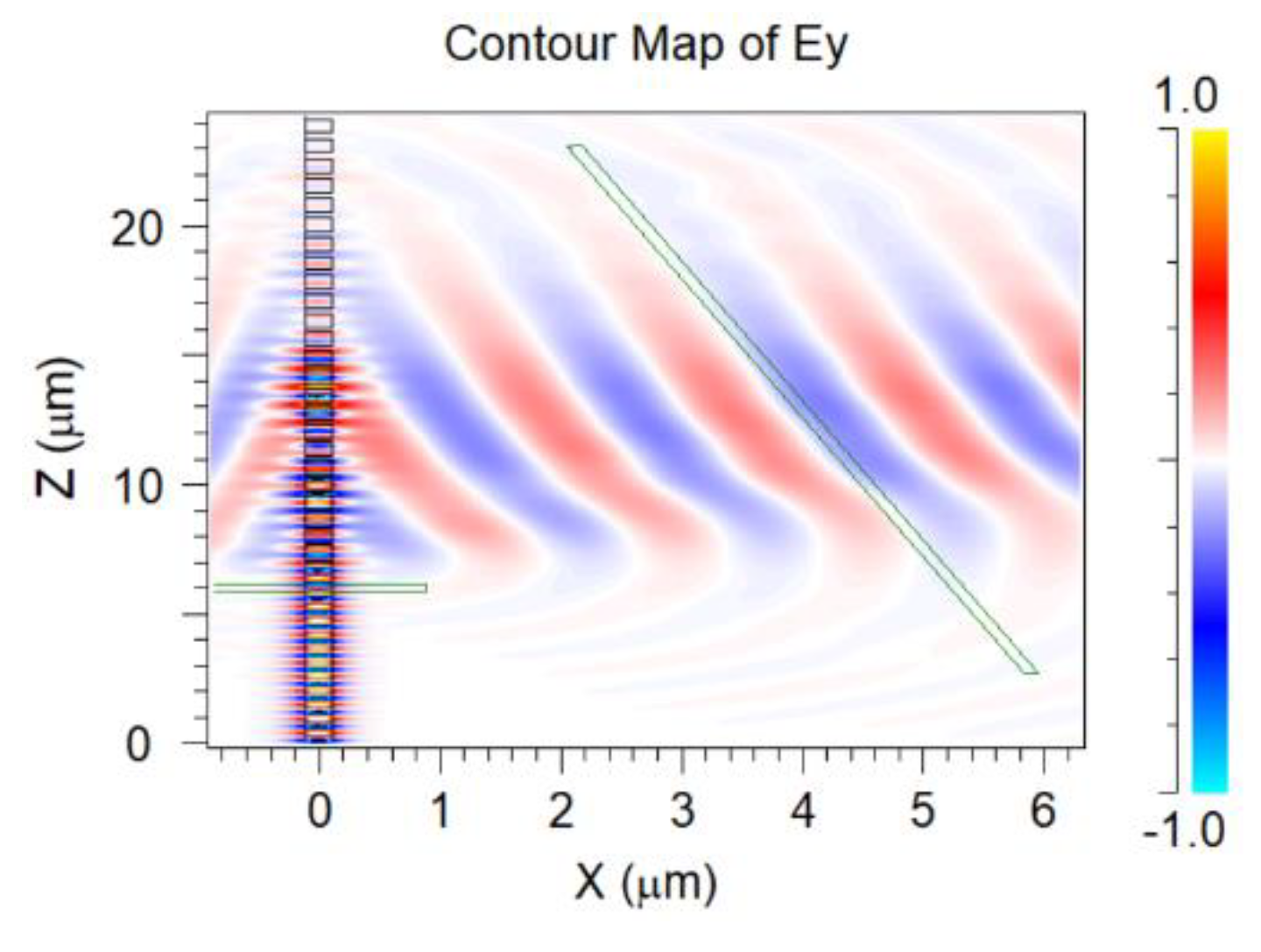
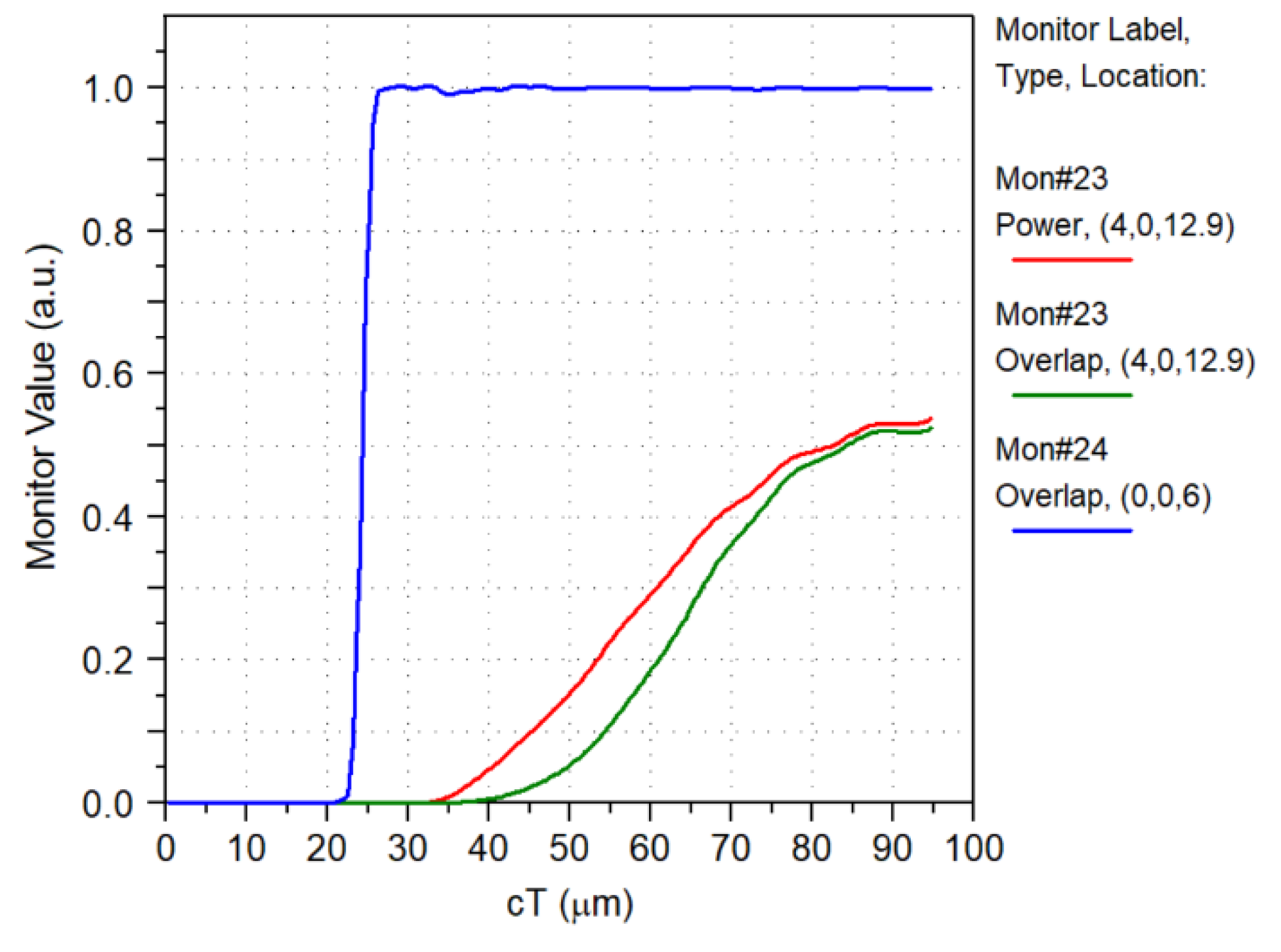
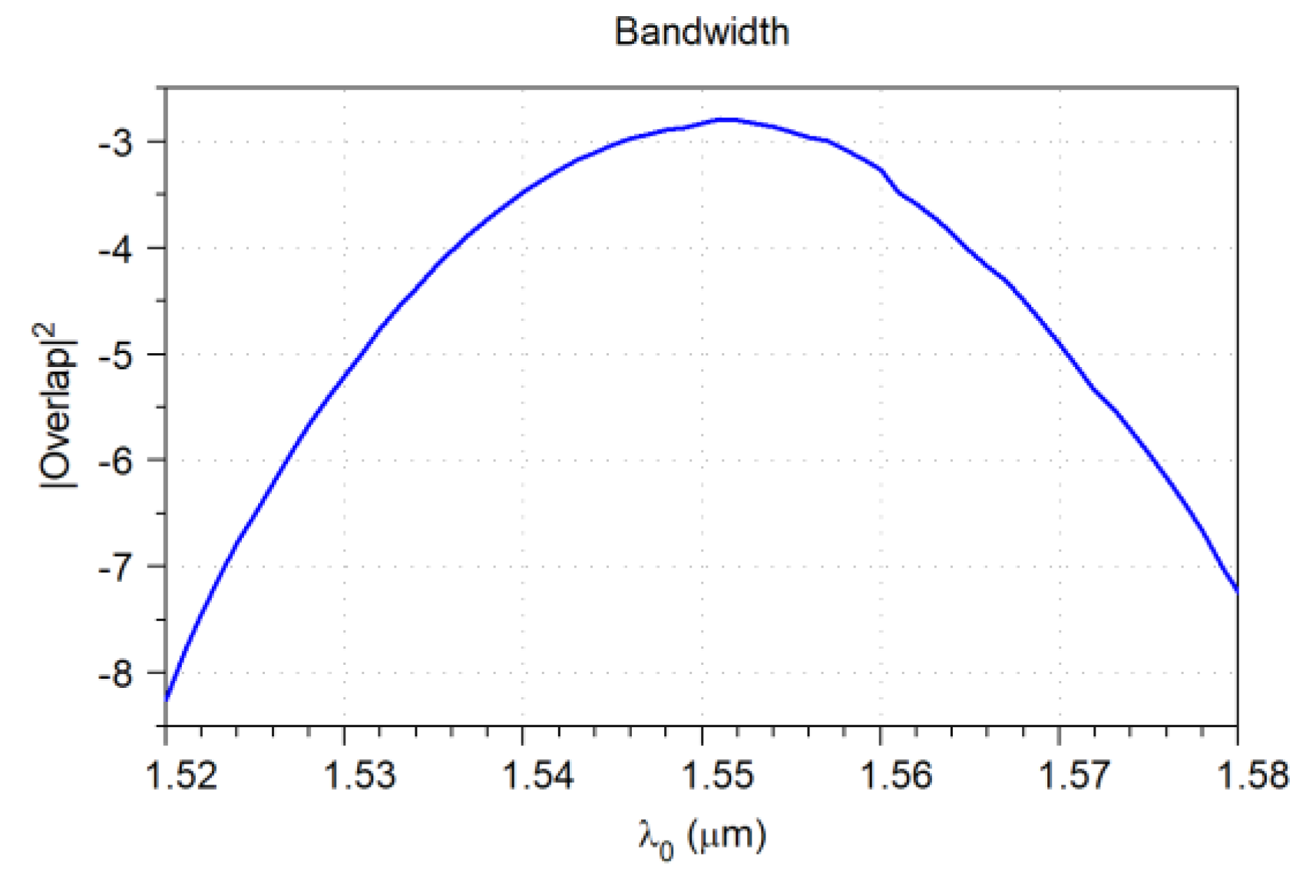
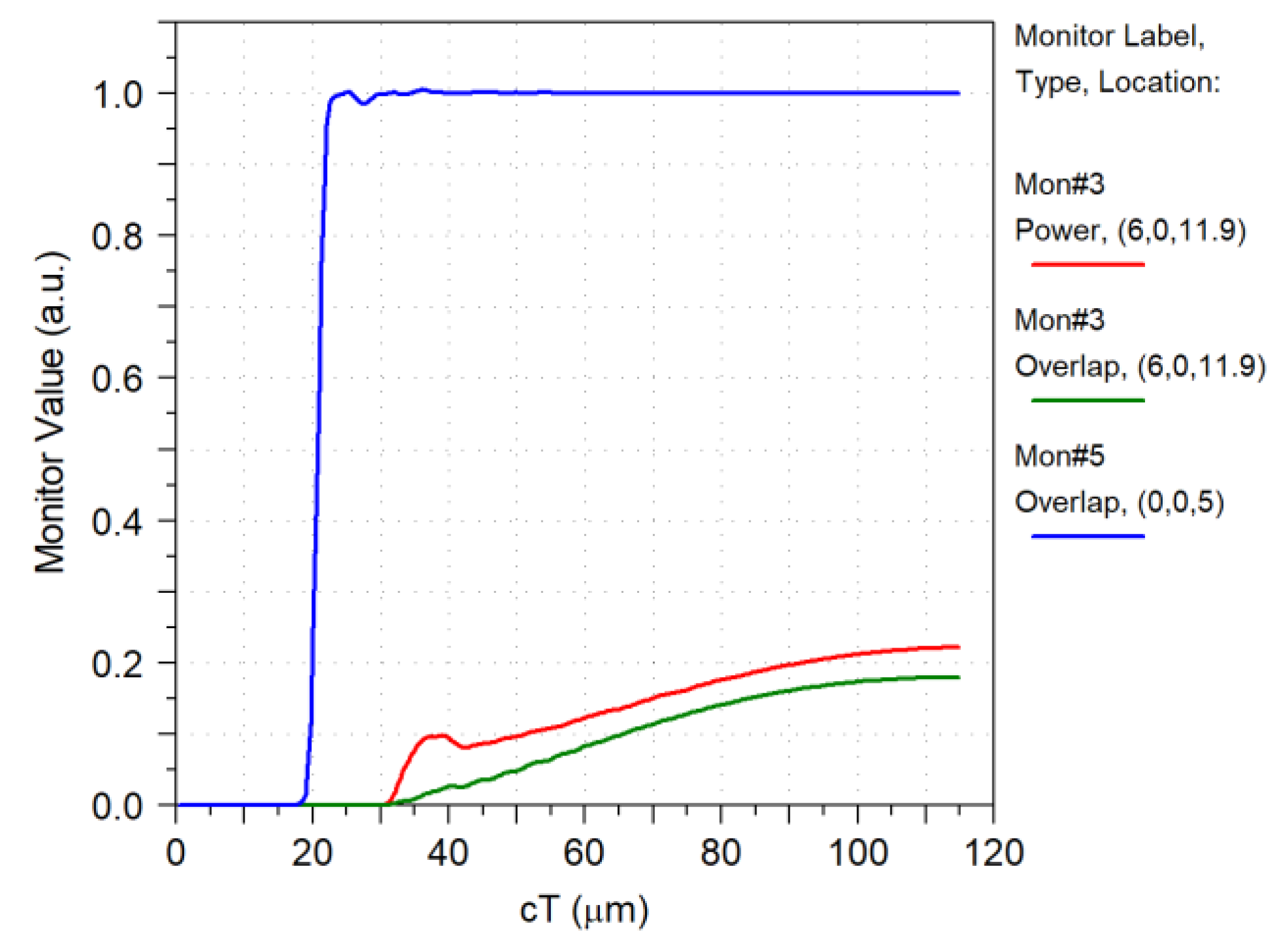
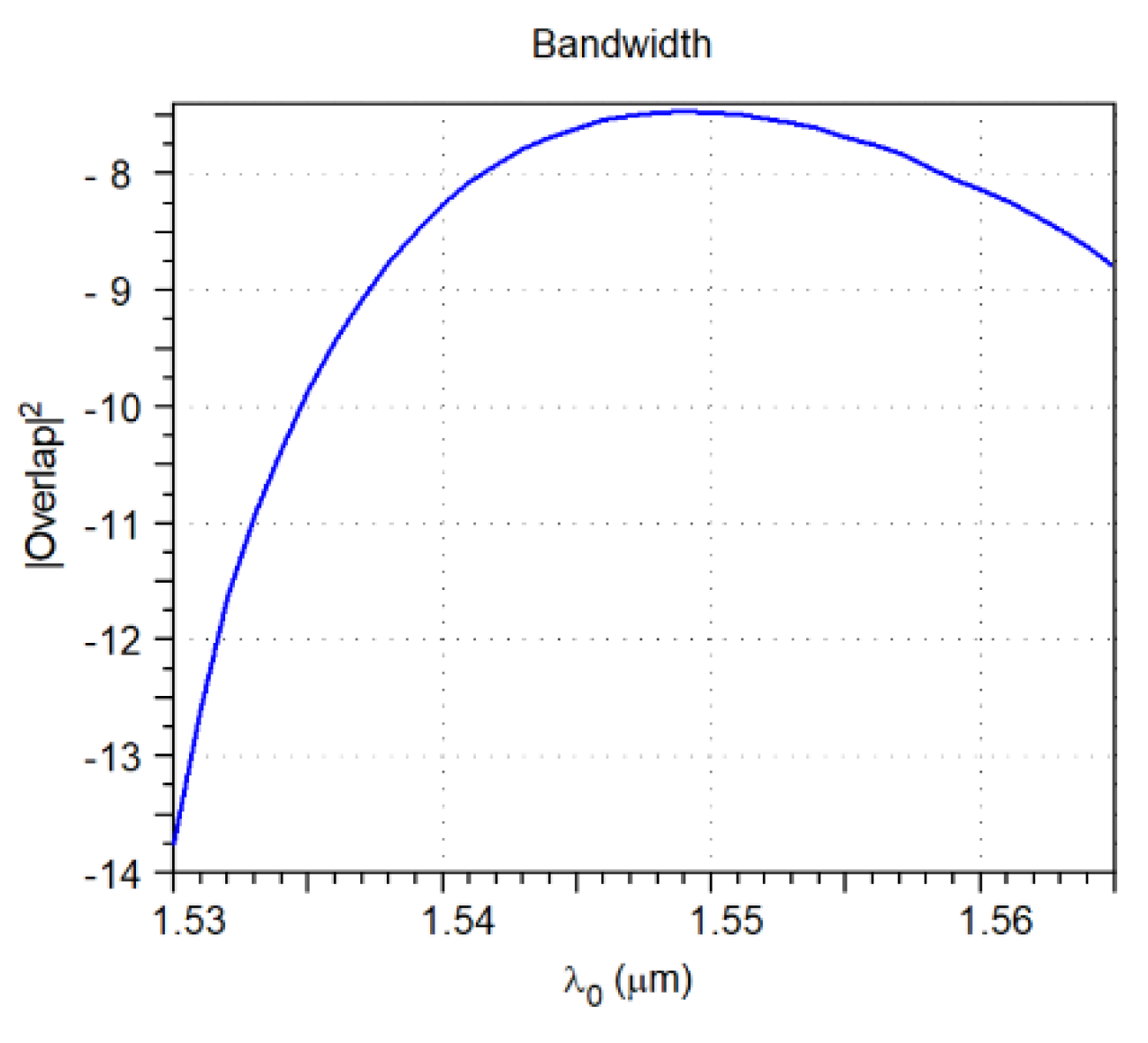
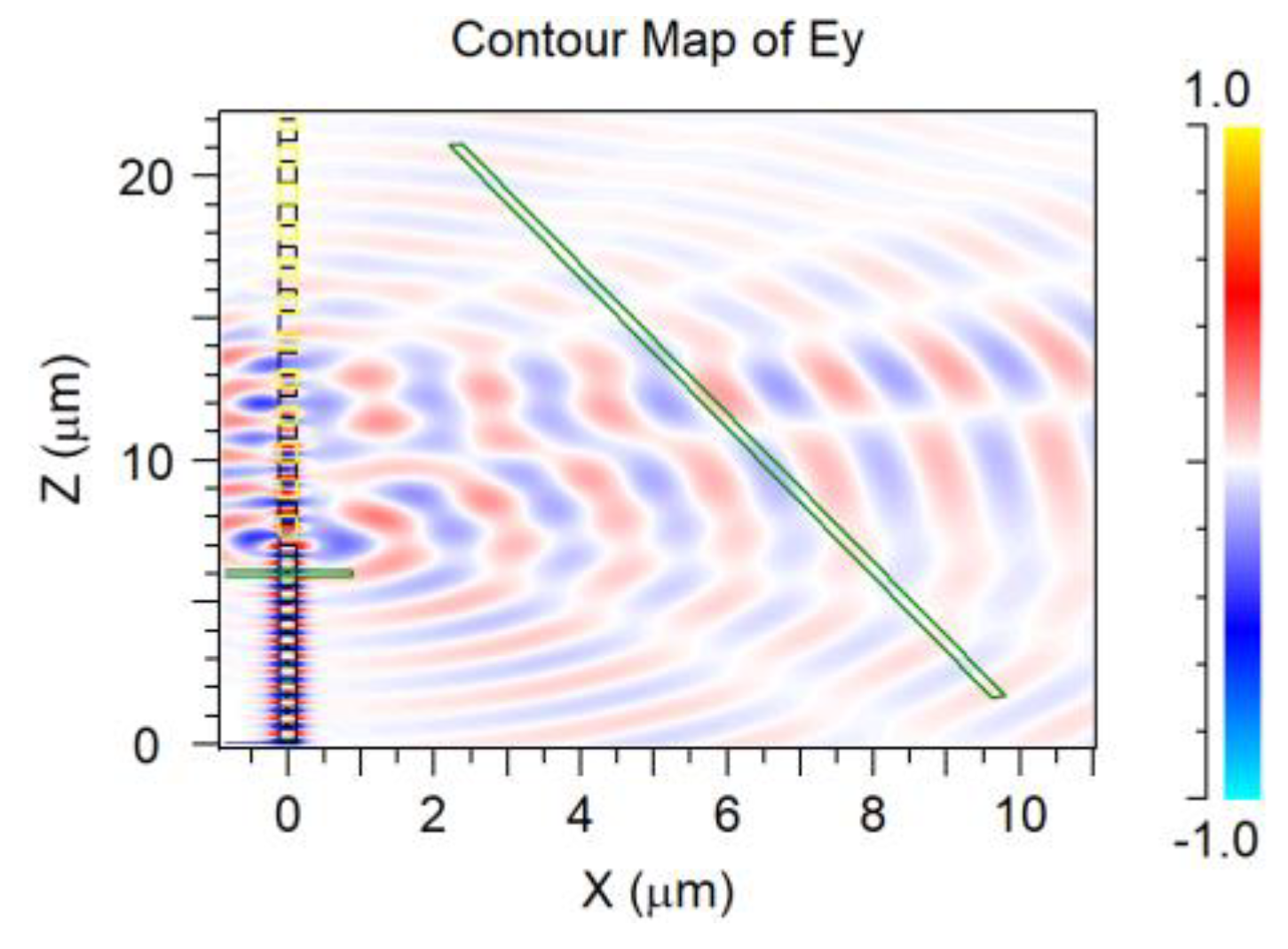
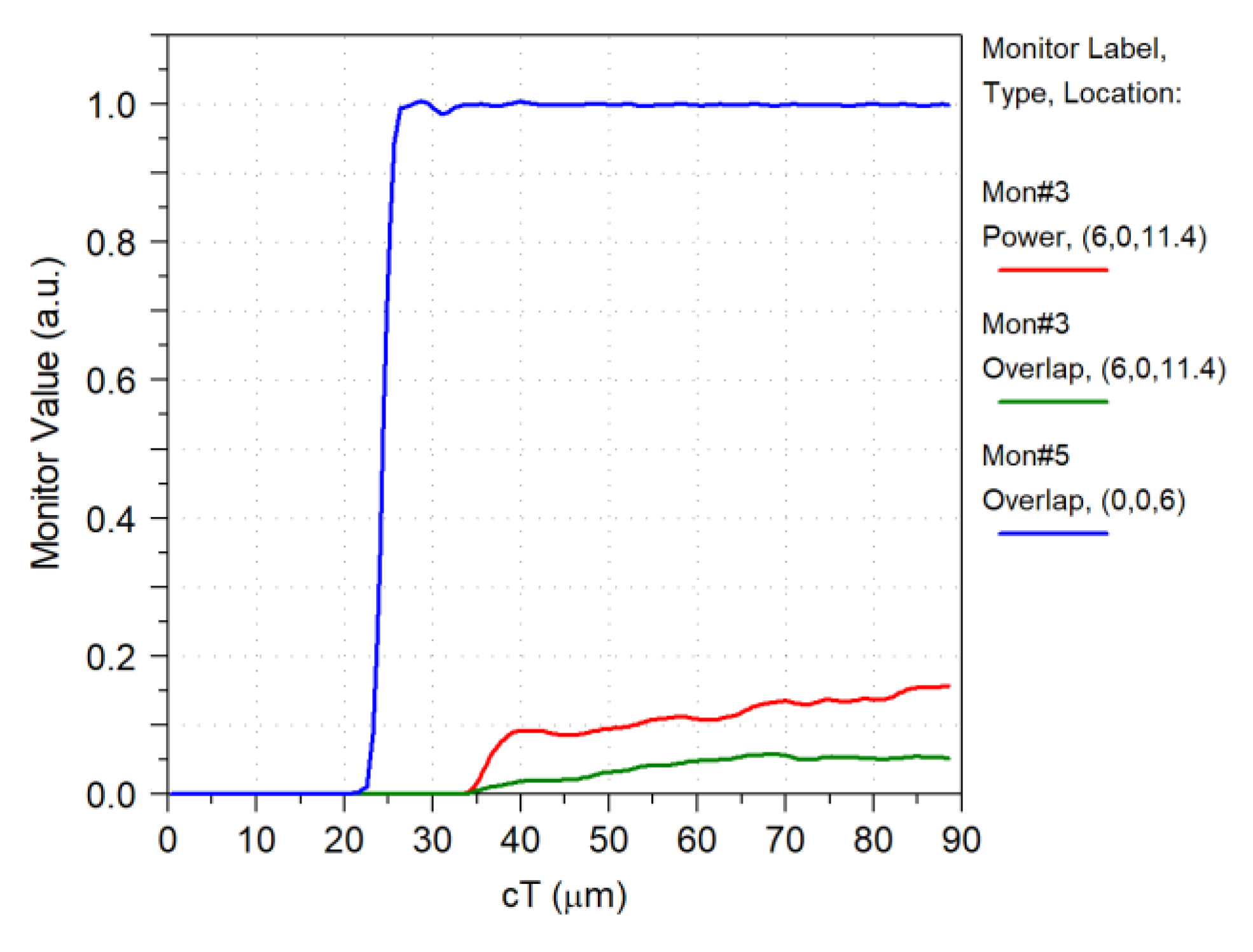
| Parameter | Value |
|---|---|
| Attenuation | ≤ 0.22 dB/km |
| Mode Field Diameter (MFD) | 10.4 ± 0.8 µm |
| Core Diameter | 8.2 µm |
| Cladding Diameter | 125 ± 0.7 µm |
| Coating Diameter | 245 ± 5 µm |
| Effective Refractive Index (Neff at rated MFD) | 1.4682 |
| Refractive Index Difference | 0.36 % |
| Segment Number | Λ [nm] | F (LE/Λ) | Segment Number | Λ [nm] | F (LE/Λ) |
|---|---|---|---|---|---|
| 1 | 647 | 0.900 | 15 | 732 | 0.750 |
| 2 | 652 | 0.890 | 16 | 739 | 0.738 |
| 3 | 658 | 0.880 | 17 | 747 | 0.727 |
| 4 | 663 | 0.869 | 18 | 754 | 0.715 |
| 5 | 668 | 0.859 | 19 | 763 | 0.703 |
| 6 | 674 | 0.848 | 20 | 771 | 0.691 |
| 7 | 680 | 0.838 | 21 | 779 | 0.679 |
| 8 | 686 | 0.827 | 22 | 788 | 0.667 |
| 9 | 692 | 0.816 | 23 | 798 | 0.654 |
| 10 | 698 | 0.805 | 24 | 807 | 0.642 |
| 11 | 704 | 0.795 | 25 | 817 | 0.629 |
| 12 | 711 | 0.783 | 26 | 827 | 0.616 |
| 13 | 718 | 0.772 | 27 | 838 | 0.603 |
| 14 | 725 | 0.761 | 28 | 849 | 0.590 |
| Segment Number | Λ [nm] | F (LE/Λ) | Segment Number | Λ [nm] | F (LE/Λ) |
|---|---|---|---|---|---|
| 1 | 647 | 0.900 | 15 | 734 | 0.746 |
| 2 | 654 | 0.886 | 16 | 739 | 0.738 |
| 3 | 661 | 0.873 | 17 | 744 | 0.731 |
| 4 | 668 | 0.860 | 18 | 748 | 0.725 |
| 5 | 674 | 0.848 | 19 | 752 | 0.719 |
| 6 | 681 | 0.836 | 20 | 755 | 0.713 |
| 7 | 687 | 0.824 | 21 | 759 | 0.709 |
| 8 | 694 | 0.813 | 22 | 761 | 0.705 |
| 9 | 700 | 0.802 | 23 | 764 | 0.701 |
| 10 | 706 | 0.791 | 24 | 766 | 0.698 |
| 11 | 712 | 0.781 | 25 | 767 | 0.696 |
| 12 | 718 | 0.772 | 26 | 769 | 0.694 |
| 13 | 724 | 0.763 | 27 | 769 | 0.693 |
| 14 | 729 | 0.754 | 28 | 769 | 0.693 |
| GC Design | GC Material | GC Feature Size* | Coupling Efficiency | -1 dB Bandwidth | Bottom Reflector | Required Masks** | Reference |
|---|---|---|---|---|---|---|---|
| Silicon Nitride Top Layer | Si | 266 nm | -1.7 dB | 64 nm | No | 3 | [67] |
| Fully Etched Apodized | Si | 100 nm | -0.6 dB | (71 nm, -3 dB) | Yes, Al layer | 1 | [61] |
| Shift-pattern Overlay | Si/Poly-Si | 171 nm | -0.9 dB | 35 nm | No | 3 | [42] |
| Dual-level GC | Si | 60 nm | -0.8 dB | 31.3 nm | No | 3 | [43] |
| Bilayer GC | Si3N4 | N/A | -1.0 dB | 117 nm | Yes, DBR | 2 | [65] |
| Dual-level GC | Si3N4/Si | 200 nm | -1.3 dB | 80 nm | Yes, GC | 2 | [56] |
| Chirped GC | Si | 26 nm | -0.1 dB | (35 nm, -3 dB) | Yes, DBR | 2 | [58] |
| Multilayer Bottom Reflector | SiNx | 86 nm | -1.8 dB | 52.5 nm | Yes, DBR | 1 | [57] |
| Bilayer GC | SiNx | N/A | -2.7 dB | 47.9 nm | No | 2 | [45] |
| Non optimized GC | a-Si:H | 510 nm | -9.7 dB | N/A | No | 1 | This work |
| Fill-factor > 50 % | a-Si:H | 120 nm | -4.3 dB | 25 nm | No | 1 | This work |
| Linear R.I. Variation | a-Si:H | 60 nm | -3.1 dB | 26 nm | No | 1 | This work |
| Quadratic R.I. Variation | a-Si:H | 60 nm | -2.8 dB | 25 nm | No | 1 | This work |
| Overlapped Micrometric | a-Si:H | 750 nm | -7.5 dB | 22 nm | No | 2 | This work |
| Random Distribution | a-Si:H | 650 nm | -12.8 dB | N/A | No | 2 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





