Prerpints.org logo
Preprint
Article

Thermal-Electrical-Mechanical Coupled Finite Element Models For Battery Electric Vehicle

Altmetrics

Downloads

131

Views

54

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

08 July 2024

Posted:

09 July 2024

You are already at the latest version

Alerts
Abstract
The safety of lithium-ion batteries is critical to the safety of battery electric vehicles (BEVs). The purpose of this work is to develop a method to predict battery thermal runaway in full electric vehicle crash simulation. The thermal-electrical-mechanical coupled finite element analysis is used to model an individual lithium-ion battery cell, a battery module, a battery pack, and a battery electric vehicle with 24 battery modules in a live circuit connection. The lithium-ion battery is modeled using a representative approach, with each battery internal component individually modeled to represent its geometric shape and realistic thermal, mechanical, and electrical properties. A resistance heating solver and Randles circuit model built with generalized voltage source are used to simulate the battery electrical behavior. The thermal simulation of the battery accounts for the heat capacity and thermal conductivity of various cell component materials, as well as heat conduction, radiation, and convection at their interfaces. The mechanical property of battery cell and battery module models is validated using spherical punch tests. The electrical property of the battery cell and battery module models is verified against CircuitLab simulation in an external short circuit test. The simulation result of battery module’s internal resistance agrees with the experimental data and the literature value. The multi-physics coupling phenomenon is demonstrated with a cylindrical compression simulation on the battery module. The multi-physics BEV model with 24 live battery modules is used to simulate the external short-circuit test and the side pole impact test. The simulations run time is less than 24 hours. The results demonstrated the feasibility of using representative battery model and multi-physics analysis to predict battery thermal runaway in full electric vehicle crash analysis.
Keywords: 
Subject: Engineering  -   Automotive Engineering

1. Introduction

With the increasing number of battery electric vehicles (BEV) on public roadways, there is a need to develop a finite element simulation method to fully understand the crash safety of BEVs and their lithium-ion batteries. Due to the relative low energy density of lithium-ion battery, BEVs are typically 125% heavier than their Internal Combustion Engine (ICE) equivalent [1,2]. This additional mass has negative effect on safety performance and fleet compatibility [3]. ICE vehicles and BEVs differ significantly in terms of mass distribution and structural arrangement, particularly concerning vehicle’s frontal, side, floor, and roof structures. These distinctions have a substantial impact on crashworthiness performance during frontal, side, and rollover collisions. Most importantly, the use of lithium-ion batteries in BEV is associated with a potential fire hazard [4]. Battery fire accident can be caused by various factors, including mechanical damage [5] , electric malfunction [6,7], expose to high heat or external fire [8,9], involvement in a crash [10], post-crash fire [11,12,13] or other unknown reasons [6].
Given that battery fires are a significant failure mode in electric vehicles, a simulation method capable of modeling battery thermal runaway is essential for the crash safety design and analysis of electric vehicles and their batteries. This method should address critical questions: whether the battery catches fire in specific crash scenarios, the root cause of any battery fires, and the vulnerable parts in the battery and vehicle design during thermal runaway events. Moreover, the method must be computationally efficient for practical industrial application.

A. Lithium-ion Battery Thermal Runaway Process

The lithium-ion battery catches fire in a mechanism called thermal-runaway [14]. Thermal runaway occurs in situations where an increase in battery temperature changes the battery conditions in a way that leads to further increase in temperature, often leading to fire or explosion. To fully understand the physics that leads to thermal runaway, the sequence of how the battery fire started should be understood first. The triggering event of the thermal runaway can be excessive current, overcharging, subjected to elevated temperatures, manufacturing defect, mechanical damage, or their combined effect (cf. Figure 1). High environmental temperature can directly heat up the battery. Overcharging and excessive current can increase the battery temperature through Joule heating. Mechanical damage or manufacturing defects can create internal short-circuits, further raising the temperature through localized Joule heating. Once the temperature reaches 80 degrees Celsius, the heat can cause permanent damage to the anode material. At 110 degrees Celsius, the organic electrode begins to break down, releasing heat and flammable gas. The polyethylene separator film melts at 135 degrees Celsius. After the separator fails, the direct contact between the cathode and anode material forms an internal short-circuit, releasing a large amount of heat and flammable gas, which often leads to fire or explosion [15]. By the time temperature reaches 200 degrees Celsius, the cathode will breakdown and release flammable gas. At this stage, a fire and explosion is likely to occur [16]. Battery thermal runaway typically starts in an individual cell and then propagates to neighboring cells and eventually the entire battery pack. Separator failure is a critical event in thermal runaway. If the separator remains intact, the temperature can decrease after the external circuit is cutoff or colling is applied. However, once the separator fails and the internal short-circuit forms, a large amount of heat is released, causing a larger area of the separator to melt. This, in turn, leads to more internal short-circuits and the release of more heat. This self-sustained chain reaction, known as the thermal runaway, will leads to smoke, fire, and explosion of the battery [17]. The thermal runaway point refers to the starting point of uncontrolled temperature escalation, thus it should be considered the failure point for battery safety analysis [15]. Separator failure most likely triggers a thermal runaway. Therefore, the point of separator failure should be recognized as the critical failure point for battery safety analysis. The purpose of battery simulation is to capture the phenomenon involving the coupling of multiple physics that leads to the starting point of battery thermal runaway. This allows us to predict whether a BEV will catch fire under specific crash scenarios. Phenomena occurring after the initiation of thermal runaway, such as the ignition and combustion processes, are beyond the scope of this study.

B. Selection of Battery Simulation Techniques

1) Finte Element Simulation Methods used in battery simulation are summarized here: The classical method for battery simulation uses mechanical-only finite element analysis, [18,19]; While computationally efficient, this method cannot predict thermal-runaway and battery fire, which are primary concerns for battery safety. It is noted that when a battery cell is mechanically damaged, internal short-circuit and thermal runaway could happens before the cell loses its mechanical strength [20]. In simpler terms, the battery may catch fire before it breaks. Mechanical-only simulation can only predict the structure failure point, leading to the impression that the battery is safer than its actual safety level. This could be dangerous because it may lead to the implementation of inadequate safety measures or the use of the battery in situations where it is not actually safe. Another battery simulation method involves electrical-chemical-thermal-mechanical finite element analysis. Solving electrochemical equations with heat generation significantly impacts the computational efficiency [21], making it impractical to model the entire BEV together with its battery cells in full vehicle crash simulations. Another alternative is electromagnetic-thermal-mechanicalfinite element analysis [22], which involves solving Maxwell’s equation. This method is computationally costly due to the complexity of Maxwell’s equations and their interactions with thermal and mechanical phenomena. Since the widely adopted Randles Circuit Model for battery equivalent circuit [23,24,25] uses only capacitors and resistors; the involvement of electromagnetism is unnecessary. The resistant heating solver is much more efficient for battery simulation. Thermal Electrical Mechanical Coupled Finite Analysis is previously used in lithium-ion battery simulation [26,27,28,29,30,31,32]. In this study, thermal-mechanical-electricalfinite element analysis features the use of thermal solver, electric resistant heating solver, and mechanical solver in a fully coupled LS-DYNA simulation. A user-defined voltage source was utilized to model the capacitor, so the Randles circuit can be modeled with the resistant heating solver [26]. This method to model Randle circuit is previously used to predict the thermal runaway of a single lithium-ion battery cell under normal and abusive conditions [33] [26]. This study demonstrates that the thermal-mechanical-electrical coupled simulation is suitable for modeling the crash safety of lithium-ion batteries integrated with BEVs.
2) Thermal Electrical Mechanical Coupling Formulation in LS-DYNA: The thermal-electrical-mechanical coupling formulation in LS-DYNA is summarized in literature [34,35,36,37]. The Multiphysics solvers are required to concurrently solve Maxwell’s equations, Joule’s Law, and Newton’s Law.
Electrical: the Maxwell equations are approximated using the Eddy-current approximation for conductors with low frequency varying field. It is assumed that ε ∂ E ∂ t ≪ σ E , where E is the electric field. ε is the permittivity of free space. σ is the electric conductivity. This approximation implies a divergence free current density and no free charge accumulation. The Maxwell equations become:
Faraday Law:
∇ × E = − ∂ B ∂ t
Amper Law:
∇ × B μ = j + ε ∂ E ∂ t
Gauss Law:
∇ ∙ B = 0
∇ ∙ ε E = 0
∇ ∙ j = 0
Ohm Law:
j = σ E + j s
where B is Magnetic flux density, j is Current density, j s is a divergence free source current density， μ is permeability, ε is permittivity. The divergence condition (3) allows B writing as:
B = ∇ × A
where A is the magnetic vector potential [38]. According to Equation (1), the electric field is:
E = − ∇ ϕ − ∂ A ∂ t
where ϕ is the electric scalar potential. The Gauge condition is used as:
∇ ∙ σ A = 0
which allows a separate the vector potential from the scalar potential in the equations, implying Equations (5), (6), (8), and (9)
∇ ∙ σ ∇ ϕ = 0
which implies Equations (2), (6), (7), and (8)
σ ∂ A ∂ t + ∇ × 1 μ ∇ × A + σ ∇ ϕ = j s
Equation (10), (11) is Maxwell equations in term of the 2 potentials. Let Ω be a set of multiply connected conducting regions. The surrounding insulator exterior regions is Ω e . The boundary between Ω and Ω e is Γ , and the artificial boundary on Ω at the end of the meshing region, where the conductors are connected to an external circuit, is called Γ c . In the following, let n be the outward normal to surfaces Γ or Γ c . In Ω e ,we have σ = 0 and μ = μ 0 .
n ∙ ∇ ϕ = 0 o n Γ
ϕ = ϕ c o n Γ c
n × ∇ × A = A e o n Γ
n × A = A c o n Γ c
Equation (13) and (15) allows the connection of the conductors to a voltage source and a current source, respectively. Once the potentials are computed, the electromagnetic fields are given by Equations and (6), (7), and (8).
Mechanical：After the EM fields are computed by solving Maxwell equations, the Lorentz force is evaluated at the nodes and added to the mechanical equation.
ρ D u D t = ∇ ∙ s + f + j × B
where u is the displacement. s is stress. f is the external force. ρ is mass density. Notice the extra Lorentz force term j × B represents the electric mechanical coupling.
Thermal: The thermal equation
D e D t = s : ε ˙ p l + D q D t + j 2 σ ρ e
where e is the internal energy. s is Stress tensor. ε ˙ p l is Plastic strain rate tensor. q is the external heat source. ρ e is electrical resistivity. The Joule heating term j 2 / σ ρ e is added to the thermal solver allowing to update the temperature.
Equation of State (EOS): The material’s mechanical properties are evaluated at Gauss point temperature. The conductivity also may vary with temperature change.
σ = σ ( T , ρ )
where T is temperature. ρ is the mass density.
3) Geometry Modeling of Battery Cell. The lithium-ion battery consists of numerous stacked layers of very thin membranes [39]. For porch cells, mechanical behavior in the thickness direction is particularly important for determining the strength of the cell in hemispherical punch test, radial bending test, and side crushing test [39,40]. Utilizing solid elements is crucial for realistically representing the strength of the battery cell in the through thickness direction. However, the small membrane thickness (0.01mm~0.06mm) [41,42] requires a very small element size and timestep in simulation, while the presence of a large number of stacked layers (>50 layers) leads to a very large model [43,44]. These factors make the simulation computationally impractical if the cell is modeled with realistic geometry. In this study, the battery cell is modeled with a representative battery model: Each cell component, including cathode current collector, cathode, separator, anode, anode current collector, is modeled separately with a representation geometry. Since the lithium-ion battery features a jelly roll structure of many thin layers. The thickness of the layers is proportionally scaled up, so a handful of thick layers can be used to represent many thin layers. Realistic material properties of each cell component, including density, Young’s module, Poisson’s ratio, stress-strain relation, porosity, thermal conductivity, specific heat capacity, electric resistivity, etc., were used in the FE model. The alternative method is the homogenized battery model: the entire battery cell is treated as one piece of material. The phenomenon-based material model is fitted by matching cell-level mechanical tests [19]. This material model represents the overall deformation pattern of the battery cell, but it does not represent any realistic material. The representative model is closer to true physics than the homogenized model because it incorporates the realistic mechanical, electrical, and thermal properties of each battery component. The battery cell comprises a loosely packed jelly roll structure with materials such as metal, polymer, graphite, each having very different material properties such as Young’s modulus, stress-strain curve, thermal conductivity, resistivity, melting point, and more. It is not feasible to model the mechanical, electrical, and thermal behavior of each cell component accurately if they are bundled together and treated as a single material. For instance, the melting point for each cell component is different. The polymer separator fails around 135 °C, some ceramic coated separators can withstand 200°C. The aluminum current collector sheet fails at 660 °C. Modeling these components together as a single material in the homogenized approach would overlook such critical distinction. Moreover, the phenomenon-based material model in the homogenized model lacks physical representation. The material model fitted to match one test may not match another test conducted on the same cell under different testing conditions. The homogenized model also struggles with electric modeling because it cannot accurately represent the internal battery circuit and resistivity variations among different cell parts. In contrast, the representative model can realistically predict internal resistance, voltage distribution, current flow, Ohmic heating power, and temperature distribution for each layer of the battery. Previous studies using a multi-physics single-cell representative model have shown its capability to match mechanical and electrical test results [26]. Following a similar methodology, the model employed in this study is calibrated using external short circuit tests and spherical punch tests. It can simulate the coupled physical phenomena that lead to battery thermal runaway.

C. Full Vehicle Finite Element Models for Crash Analysis

Finite element analysis has been widely used to study the crashworthiness of automobile and roadside hardware. [45,46,47,48]. The National Highway Traffic Safety Administration (NHTSA) has sponsored the development of public domain finite element models for more than two decades to promote automobile safety and support the rule making effort [49]. Center for Collision Safety and Analysis (CCSA) at George Mason university has developed or managed over 20 public domain vehicle crash analysis models based on the reverse engineering modeling protocol [50]. (cf. Figure 2) These finite element models are created by reverse engineering the vehicle on the market, and they are also calibrated with the full vehicle crash tests to ensure physical representation. These simulation models provide a powerful tool for research in vehicle crash safety, occupant safety, pedestrian safety, restraint system design, biomechanics, fleet compatibility, roadside hardware, accident reconstruction, and many other field. These models also serve as a modeling guideline for the state of the art of vehicle crash analysis. The typical procedure for developing a reverse-engineered crash analysis model is summarized as follows: The vehicle is tested for its weight, center of mass, and moment of inertia before disassembly. At the time of disassembly, the geometry and position of each part is laser scanned, the thickness and mass of each part are also measured. The material test coupons are cut from parts to determine the stress-strain relation for the material model. Finite element mesh is generated based on the part geometry, thickness, and mass following a strict quality control criterion. The mesh of different parts is then connected with spotwelds, constraint rigid body, beam element, rotatable joints and tied contact. The suspension, added mass, airbags and restraint system are defined next. The contact is then defined with penetration checked. The finite element model is verified to match mass, center of gravity, and moment of inertia of the vehicle. The developed finite element model is validated against multiple crash tests, including NCAP Frontal Impact, IIHS Offset Deformable Barrier Test, Pole Impact Test, Roof Crash Test, etc., The modeling is seen to provide satisfactory result [47,51,52]. The models feature accurate geometry, realistic material property, a soft interior, deployable airbags, and full restraint system, making it a close representation of the actual vehicle.
The classical crash safety simulation models are built in mechanical-only analysis for the ICE vehicle. The reverse engineering FE model for battery electric vehicles requires a proof-of-concept study, especially for the method to model battery. There are two decisions to be made regarding the technological path, with computational efficiency being the primary concern: 1. Electrical-Thermal-Mechanical Analysis vs. Mechanical-Only Analysis: it is seen that thermal-electrical-mechanical coupled analysis is necessary for capturing the battery thermal runaway. However, it was uncertain whether it was practical to simulate the entire BEV with all active connected battery cells in a multi-physics analysis. If this analysis takes too long to run on a typical cluster computer, then the mechanical-only model would be the only option. 2. Battery Homogenized model vs. Battery Representation Model: The battery homogenized model has the entire cell modeled with one chunk of material. The representation model has each cell parts modeled separately, so the physical material property can be used. The representation model is more accurate but can be more expensive in computational time. It was uncertain whether the representation battery model runs fast enough for a full EV simulation on a typical cluster computer. If the representation model takes too long to run. Then the homogenized model would be the only option.
This proof-of-concept study has demonstrated that the thermal-electrical-mechanical coupled analysis with representation battery model is able to simulate the crash safety for the entire EV along its battery cells. A typical multi-physics EV crash simulation can be completed within 24 hours using a cluster computer with 24 CPUs.

2. Methodology and Result

The thermal-electrical-mechanical coupled crash analysis model is built in three stages: 1. A single battery cell; 2. A multi-cell battery module; 3. A generic battery electric vehicle with 24 active cells. The exterior and interior features of the generic BEV model represent the first-generation Google Waymo BEV. The body in white referenced the Toyota Yaris crash analysis model [53]. The battery cell and module represent the system used in first-generation Nissan Leaf [54]. The battery cell modeling methodology is developed in previous study [26].
A.
Single Cell Model
The geometry of the single cell model represents the battery cell used by Nissan Leaf [54]. A repurposed Nissan leaf battery module (first generation) with 4 cells has been disassembled to the cell level. The model closely represents the exterior geometry of the cell. The cell dimension is 261 m m × 216 m m × 79 m m excludes the plastic wrapper, which has a thickness of 0.14 m m . The parts dimension inside battery cell is proportionally scaled from the cells in previous studies [26,43]. Five plates are used to represent the multi-layer sandwich structure, each representing one battery part (cf. Figure 3). In simulation, the cathode current collector has thickness of 0.857mm, the cathode layer has thickness of 1.745mm, the gap between cathode and separator is 0.266mm, the separator has a thickness of 0.932mm, the gap between separator and anode is 0.266mm, the anode layer has a thickness of 3.054mm, the anode current collector has a thickness of 0.779mm [43]. The thermal, electrical, and mechanical properties of each cell materials are summarized in previous study [26]. Two layers of solid elements are used on each plate to capture the strength of the cell in the thickness direction. The cathode and cathode current collector plate are connected by sharing nodes; and the same also applies to the anode and anode current collector. A gap is necessary to represent the mechanical strength of the loosely packed batteries layers [26]. The plate representing separator is modeled with some “wrinkles” to reflect the loosely packed sandwich structure (cf. Figure 3). Only certain parts of the separator touch the anode and cathode through frictional contact, without sharing nodes. This configuration creates a gap between the separator and the two electrodes while still maintaining structural integrity under gravity
The electric potential difference is defined between Node Set 1 (red) and Node Set 2 (blue) as shown in Figure 3. Only two node sets are defined for each battery cell. Node Set 1 contains all nodes with positive voltage, while Node Set 2 contains all nodes with zero voltage. Since the voltage difference on the same battery component is usually very small, it is more efficient to define only one Randles circuit for each battery cell [23].
The electric current starts from Node Set 1 on the side of the cathode layer closer to the separator. The current flows through the cathode, cathode current collector, and cathode current collector tab to the external circuit. The circuit returns from the anode current collector tab, through the anode current collector and anode, and finally back to Node Set 2, which is on the other side of the anode layer closer to the separator. The capacitor in the Randles circuit is analytically modeled by a generalized voltage source (Figure 4), enabling the use of a resistance heating solver to simulate the Randles circuit. The detailed methodology and source code for the generalized voltage source are presented in previous work [26].
The external short-circuit test (cf. Figure 4) is simulated using an FE battery cell model in LS-DYNA. The cell undergo normal discharging until an external short circuit is formed at 5 × 10 − 4 s . The predicted current from the LS-DYNA simulation is compared to the result from CircuitLab, an electric circuit simulation software [55]. It is seen that the FE battery cell model accurately captures the dynamic circuit behavior and predicts the temperature rise of the separator. The FE simulation also precisely captures the peak current and the steady state current.
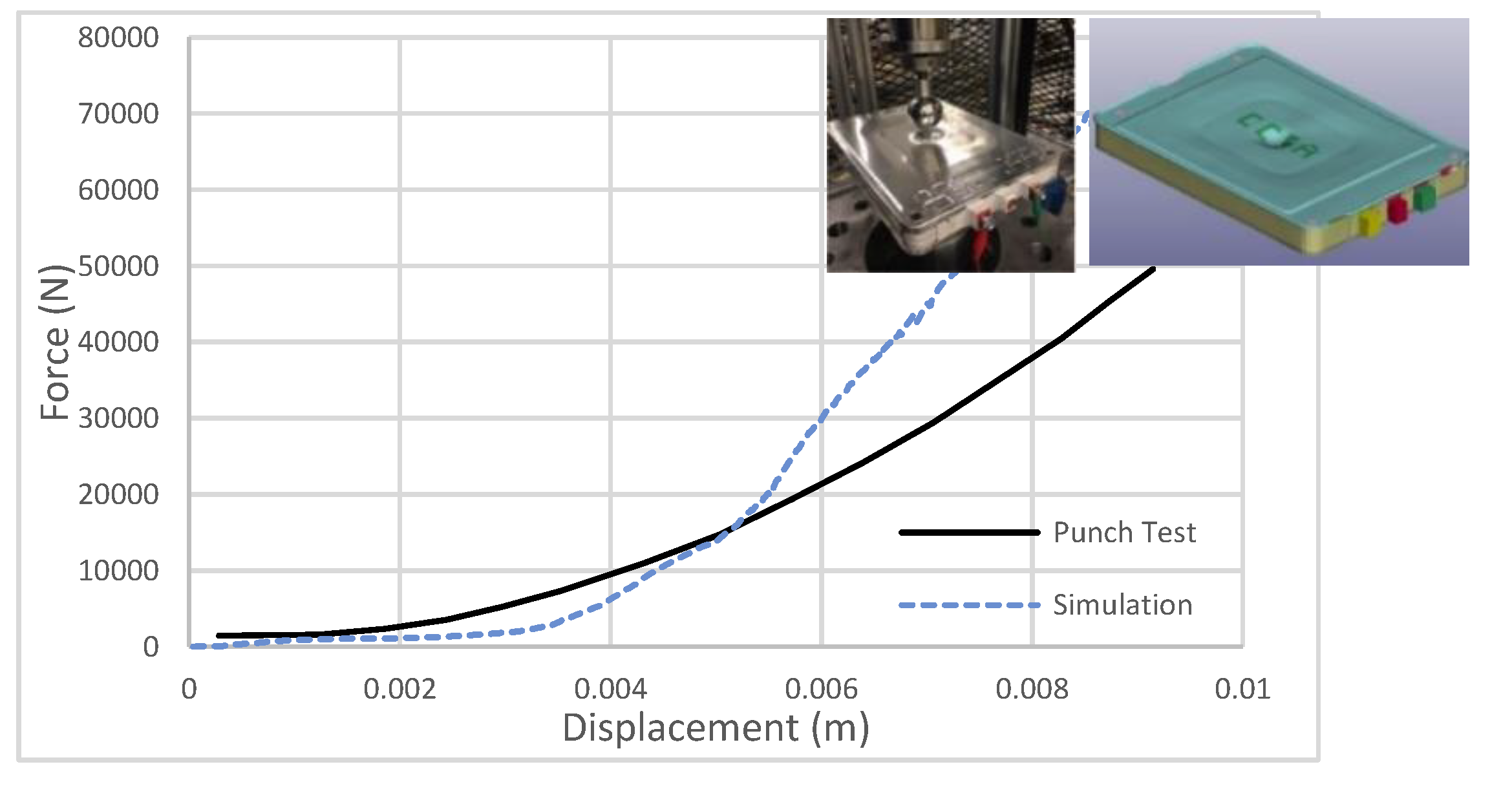
The mechanical property of the battery cell model is verified with spherical punch test. [56] A 1-inch diameter sphere indenter is used in the punch test. The LS-DYNA simulation result is compared with the test data in Figure 5. The results show that the battery cell FE model matches the mechanical property in general. It is noted that the porosity of the lithium material and graphite coating will influence the stiffness of the cell under deformation [26]. The Young’s material and plastic strain vs stress curve is scaled to 20% of the standard book value to reflect the porosity of the coated layers. Cell disassembly and detailed reverse engineering of the component part is necessary to further improve accuracy of the cell model.
Thermal contact within the battery cell is also incorporated into the model, as it is a cortical factor in predicting physical phenomenon that can lead to thermal runaway. The nonlinear transient thermal solver in LS-DYNA is used. A hybrid thermal contact model is used, considering the heat conduction, convection, and radiation. [57] The heat conductance between contact surfaces is calculated as
h = h 0 ,                                                                   0 ≤ l g a p ≤ l m i n h c o n d + h r a d ,             l m i n < l g a p ≤ l m a x 0 ,                                                                                   l g a p > l m a x ,
h c o n d = K l g a p
h r a d = f r a d ( T 1 + T 2 ) ( T 1 2 + T 2 2 )
f r a d = σ 1 ε 1 + 1 ε 2 − 1
l g a p is the gap between the two contact surfaces. h 0 is direct contact heat transfer conductance between two surfaces with a gap smaller than l m i n . h c o n d is the heat conductance of the fluid filling the gap fluid between the contact surfaces K is fluid’s thermal conductivity. K = 0.58 W / m and K = 0.024 W / m were adopted for thermal conductivity for the liquid electrolyte and air, respectively [58,59]. f r a d is the radiant heat transfer factor between contact surfaces. Stefan-Boltzmann constant σ = 5.6703 × 10 − 8 ( W / m 2 K 4 ) . ε 1 , ε 2 are the emissivity of two surfaces. The emissivity of black body ε 1 = ε 2 = 1 is assumed [57]. T 1 , T 2 are the absolute temperature of two contact surfaces, respectively. Inside the wrapper of the battery cell, the thermal conductivity of water ( K = 0.58 W / m ) is used to represent the liquid electrolyte between the battery layers. Outside the battery cell, the thermal conductivity of air K = 0.024 W / m is used for all other situations. Two different contact cards are set up separately to define the thermal contact within the battery cells and outside the battery cells. The same contact card also defines the mechanical contact between surfaces (cf. Figure 6,Figure 7) The surface-to-surface contact needs to be used for the combined thermal and mechanical contact. The dynamic friction coefficient, static fiction coefficient, and exponential decay coefficient are set to be 0.005 , 0.004 , and 0.001 , respectively [57].
B.
Battery Module Models
A Battery module consists of multiple individual battery cells assembled into a single unit. These cells are connected in serial or parallel to achieve the desired voltage and capacity. The module case offers structure integrity, housing the electric connection and protects the cells against external impact. Battery module is often the minimal replaceable part in an EV. The FE model of the battery module represents the system used in Nissan Leaf [54]. The battery module contains four lithium-ion battery cells in a 2s2p configuration, where two pairs of parallel-connected cells are connected in serial. The module exterior dimension is 303 × 223 × 55 mm, and the weight is 3.8kg [60]. In the simulation, the element size of the battery layers is 2mm in plain and 0.34~1mm in thickness. There are a total of 275,577 elements in this model. The cathode, cathode current collector, separator, anode, anode current collector, the module case and case cover are modeled with solid element (cf. Figure 8). The cushion and plastic wrap are modeled with shell element. The dimensions of the single cell model from the previous section has been slightly adjusted to fit into the case geometry of Nissan Leaf battery module. The material parameters for the battery module model are the same as those used in the single cell model [26]. Simulation of an event for 0.2 seconds in the battery module model takes approximately 3 hours. The electrical functions in this model operate as expected.”.
1)
Electric Verification
It is necessary to verify whether the use of user-defined voltage source to model the Randles circuit can be extended to multiple cells in electrical-thermal-mechanical simulation. Verification cases include two different battery cells connected in serial and parallel (Figure 9, Figure 10). Noted that the voltage and the capacitance for two battery cells are different. The result demonstrates that the electric simulation functions correctly for the two cells in live circuit connections. The method to model the Randles circuit with a generalized voltage source is described in the appendix of previous work [26]. It is important to ensure that each cell has a unique function name and ID for the generalized voltage source that are connected in circuit. Relative potentials must also be used in the user-defined voltage source, with only one ground defined with an absolute potential value for the entire circuit. The thermotical values from CircuitLab [61] are used to verify the electrical simulation in LS-DYNA. The results show that the dynamic effect of the circuit can be accurately captured in LS-DYNA’s multi-physics simulation. Therefore, the electric modeling method used for single cells can be extended to model multiple cells connected in circuit.
The simulation of an external short-circuit is used to verify the electrical behavior of the Leaf Battery module, which consists of 4 cells as shown in Figure 11. The result aligns well between the CircuitLab and LS-DYNA simulations. Notice the internal resistance of the cells (cf. R1, R2, R3, R4 in Figure 11) is determined through finite element analysis result and serves as input in the CircuitLab simulation. The LS-DYNA simulation calculates the internal resistant for each cell as 2.927 m Ω . Table 1 compares the internal resistant value from the finite element simulation with the value from battery module testing and literature sources. The battery module is tested for its DC internal resistant and AC impedance at 1kHz using an electrochemical workstation CHI660E. Additionally, AC impedance is tested with battery impedance tester YR1035+. The finite element simulation result of 2.927 m Ω closely match the literature value ranging from 1.1 m Ω to 6.0 m Ω in literature [62]. The measured AC impedance and DC internal resistance are higher than the literature value, possibly due to the fact that the test subject is repurposed electric vehicle battery module retired from EVs.
The current density contour shows the expected higher current accumulation near the tab area, indicating that the electrical stimulation works effectively in the battery module model with 4 cells connected in a live circuit.
2)
Mechanical Verification
We simulated the spherical indentation test conducted on the Leaf module by Oak Ridge National Laboratory, using a 2-inch diameter sphere as the punch head at a punching speed of 0.1 inch/min [20,56,63]. The result shows a general match in the force vs. displacement response. It should be noted that the module case serves as the primary load -bearing structure in the battery module design. A detailed reverse engineering process and material modeling of the battery module case and cushion pads are necessary to further increase the simulation accuracy.
Preprints 111601 g013
Figure 13. Experiment setup [20,63](Top Left), Simulation Model(top Middle) and Force vs. Displacement(Bottom) in Spherical indentation.
Figure 13. Experiment setup [20,63](Top Left), Simulation Model(top Middle) and Force vs. Displacement(Bottom) in Spherical indentation.
Preprints 111601 g013
3)
Thermal Verification
The resistive heat generation, heat conduction and thermal contact of the battery module model are verified in an external short-circuit simulation. The heat generated by Joule heating gradually propagates throughout the entire module (cf. Figure 14). The primary heating source is observed in the cathode layer. The area near the current collector tab has higher temperature due to the higher current passing through that location. The heat transfers from the cathode to the metal cathode current collector, then through the plastic wrapper, the cell cushion pad and finally to the aluminum module cover.
4)
Thermal-Mechanical- Electrical Verification
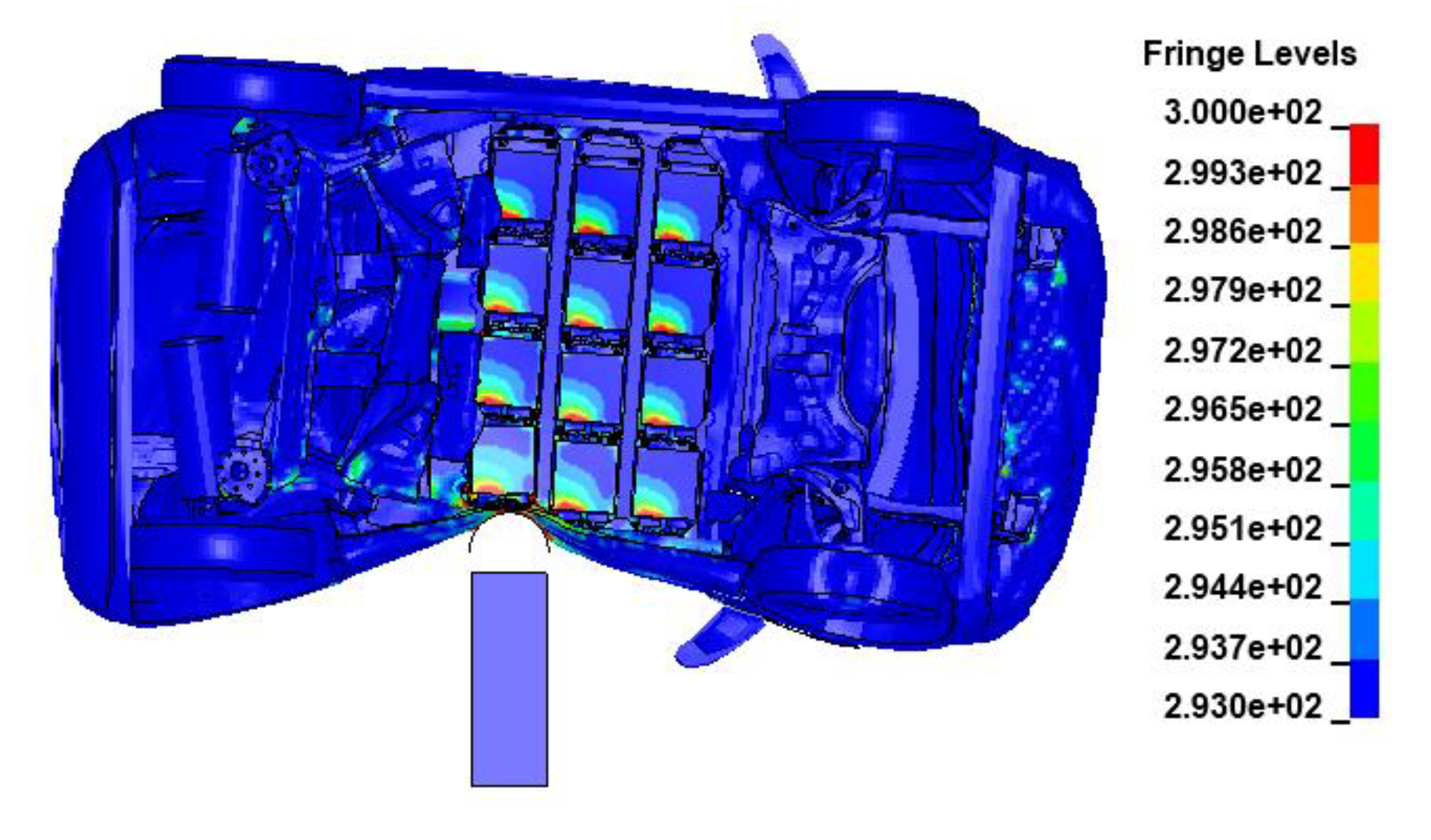
The thermal-mechanical-electrical coupling is verified in a side impact simulation. In the Nissan Leaf, battery modules are installed horizontally [64]. Besides Spherical indentation, side impacts are common collision directions. Battery module may deform similarity in frontal or side impact. The pole impact simulation is shown in Figure 15, with the pole having a radius of 50 mm and an impact speed of 1 m/s. The temperature increase in the impact area is primarily attributed to the mechanical work caused by plastic deformation.
5)
Coarse Battery Module Model
A coarse battery module model containing only one cell was also developed for use in full electric vehicle (EV) analyses. The goal is to reduce the CPU time to 24 hours for a complete EV crash simulation with active battery cells in a multi-physics analysis. (cf. Figure 16). This coarse model uses a single 7.4V cell to represent the battery module circuit shown in Figure 11.
A side pole impact was also conducted for the coarse module mode to verify the functionality of thermal-electrical-mechanical coupling. The temperature and Ohm heating power demonstrated that the battery module can accurately simulate heat generation during impact. (cf. Figure 17). Besides the heat generation though work hardening process. It was observed that cell deformation influence the internal resistance, leading to localized current increase, thereby locally raising Ohm heating power and temperature.
C.
Battery Electric Vehicle with 24 Active Cells.
A generic battery electric vehicle with 24 active battery modules has been developed. Body-in-White is based on Toyota Yaris, the exterior and interior features the first-generation Google Waymo battery electric vehicle. The battery cells and modules follow the same configuration as the Nissan Leaf. This generic battery electric vehicle model served as a proof-of-concept study for future EV crashworthiness models. The battery pack consist of 24 active battery cells connected in serial. The battery modules are packed and integrated into vehicle floor structure (cf. Figure 18)
1)
BEV in Normal Usage & External Short-Circuit
The case of BEV with a normal discharging battery pack is simulated. An external resistor of 1 Ω is connected to the battery pack to represent battery discharge under normal operating condition (cf. Figure 20). Recall that the BEV model consists of 24 battery modules in serial connection, with each module carrying a 7.4V Voltage. The simulation contour of electric potential confirms the serial connection of cells. The cell on upper left is connected to the ground and the cell on the lower right has the highest voltage of 177.6V (cf. Figure 19 left). All battery cells exhibit similar current density contours due to their serial connection, with higher densities observed near the current collector tab (cf. Figure 19 Right). Both the electric potential and current density contour suggest that the electrical simulation operates correctly. The temperature contour during normal discharged is shown in Figure 20.
For comparison, the case of external short-circuit is also simulated for the battery pack installed in the BEV. Due to the short-circuit, the voltage contour of the battery is almost zero (cf. Figure 21, Top Left). The current is over 30 times higher than the normal levels (cf. Figure 21, Top Right). These voltage and current results confirm the proper functionality of the electrical stimulation. The simulation results show a rapid temperature increase on the cathode, cathode current collector, and separator (cf. Figure 21, middle). The cathode is the primary heat source due to the high resistivity of cathode material. The heat generated at the cathode transfers to the adjacent cathode current collector and separator. The simulation shows the separators reach the melting point of 150 ℃ and failed at t=0.2s, suggesting that an external short-circuit of the battery pack could lead to nearly instantaneous battery thermal runaway (cf. Figure 22).
2)
BEV in FMVSS Pole Impact (20mph impact speed):
The side pole impact could potentially lead to intrusion on the battery compartment. The full vehicle pole impact simulation model (cf. Figure 23) was developed in accordance with Federal Motive Vehicle Safety Standard (FMVSS) No. 201 and 214 [65]. The rigid pole has a radius of 127.5 mm and an initial velocity of 20 mph upon impact. The pole impact simulation required 24 hours and 40 mins to simulate the event within 0.2s. The battery system undergoes normal discharge, representing a typical driving condition. The thermal and electric simulation performed as expected in Figure 24. It is seen that the heat generated by internal resistance is concentrated near the current collector tab on the cathode layer of the cells. The battery has a 20°C temperature rise due to normal discharge. (cf. Figure 26). In normal usage of BEV, the heat will be carried away by the battery active cooling system. However, the active colling system will most likely being shut down by battery management system during crash. For simplicity, this simple conceptual model does not model the active cooling system for the BEV. It is observed that the cells near the impact area exhibit a 4°C higher temperatures compared to the cell farther away (cf. Figure 26), which are largely uninfluenced by the impact and can be considered as the benchmark of normal discharge. Notice the time for cell plastic deformation is from 0.01s to 0.11s as shown in Figure 26 (Top). the abnormal temperature rise on the cathode layer is also from 0.01s to 0.11s as show in Figure 26(Bottom) Therefore, the temperature rise is primarily caused by plastic deformation. Notice the 4°C additional temperature rise is minimal (cf. Figure 24). Therefore, the simulation does not predict an immediate risk of thermal runaway. The cathode layer shows a 1.5% of plastic deformation (cf. Figure 26). The non-uniformity caused by permanent change of battery geometry is relatively small, so it is estimated the cell internal resistance will not be significantly influenced. The post-crash cell is still safe in future charging and discharging cycles. The plastic porch bag is seen to have a 70% plastic deformation (cf. Figure 28). If we assume the plastic cell wrapper used to make the porch bag fails at 100% of strain. The cell wrapper will remain intact after impact. The post-crash battery also has no thermal runaway risk caused by cell leakage.
2)
BEV in Pole Impact with 25mph impact speed:
Higher Pole impact speeds of 25 mph were examined to assess the thermal runaway risk. A moderate deformation is seen for the battery module closer to the impact area (cf. Figure 28 Middle. The maximum temperature contours for the 25mph case are presented in Figure 25. It is seen the cells near the impact area exhibit a 12°C temperatures raise compared to the cell far away from impact (cf. Figure 26). Notice the time for cell plastic deformation is from 0.04s to 0.08s. However, the significant temperature rise on the cathode layer is from 0.08s to 0.1s as show in Figure 26(Left). This temperature rise is primarily caused by the additional joule heating caused by cell internal resistance change, which is in turn caused by cell plastic deformation. Plastic work is the secondary effect that causes the cell temperature raise. Notie the cell far away from the impact area has a maximum temperature of 313K, which is identical to the 20mph case. (cf. Figure 26) This verified the assumption that the cell far away from impact area is largely uninfluenced, therefore can be treated as normal discharging cells for comparison purposes. This temperature rise of 12°C is not enough to cause a thermal runaway (cf. Figure 24). Therefore, the simulation does not predict an immediate risk of thermal runaway for pole impact at 25mph speed. However, the cathode layer shows a 15% of plastic deformation (cf. Figure 28). If this damaged cell is still used in normal charging and discharging cycles, the permanently deformed cathode layer will cause uneven change of local resistivity, which may lead to the accumulated heat and a risk of thermal runaway. The plastic cell wrapper is seen to have a 70% plastic deformation (cf. Figure 29). If we assume the plastic cell wrapper fails at 100% of strain. The cell wrapper will remain intact. The cell will not leak.
Preprints 111601 g025
Figure 25. Temperature Distribution at maximum intrusion moment in Pole Impact at 25mph impact speed.
Figure 25. Temperature Distribution at maximum intrusion moment in Pole Impact at 25mph impact speed.
Preprints 111601 g025
3)
BEV Pole Impact with 30mph impact speed:
The battery module undergoes severe deformation at this impact speed. The current collector tab is bent, the plastic porch has multiple failure points with plastic strain greater than 150% at the time of 0.04s (cf. Figure 28, Figure 29). The broken porch bag will cause the disintegration of the battery structure and exposure the flammable materials to the open air. The damaged porch bag is identified as the primary failure mode that may lead to thermal runaway under this speed. The severely damaged cell will also distort the finite element mesh to cause a stability problem in simulation. Immediate thermal runaway is predicted for BEV Pole impact with 30mph impact speed. Table 2 summarizes the simulation thermal runaway prediction for all 3 impact speeds.

5. Conclusions

The thermal-electrical-mechanical coupling FE Model with representative geometry is developed to model the battery cell, battery module, battery pack and battery electric vehicle. The result proves the feasibility of modeling the EV and battery cells in a multi-physics simulation for thermal runaway prediction. The multi-physics simulation captures various mechanical, electrical, thermal, phenomena and their coupling effects, so the thermal runaway and battery fire can be predicted. The simulation methodology is efficient, expecting a 24-hour turnaround for a typical EV crash simulation involving active cells. Future studies should emphasize utilizing more realistic material models in the simulation. The material model should come from material test of the battery component material, including electrical, mechanical, and thermal tests. Reverse engineering with laser-scanning should be used in the modeling of battery cells, battery modules, battery packs, and BEV.

Funding

This research received no external funding

Acknowledgments

Special thanks to Kevin Arellano-Moya, Rudolf Reichert, Chung-Kyu Park, Dan Brown, Pei Dong, Siyuan Wang, and Boshen Xu for their help and support of this work.

Conflicts of Interest

The authors declare no conflicts of interest

References

  1. F. Czerwinski, “Current Trends in Automotive Lightweighting Strategies and Materials,” Materials, vol. 14, no. 21, p. 6631, Nov. 2021. [CrossRef]
  2. J. A. Sanguesa, V. Torres-Sanz, P. Garrido, F. J. Martinez, and J. M. Marquez-Barja, “A Review on Electric Vehicles: Technologies and Challenges,” Smart Cities, vol. 4, no. 1, Art. no. 1, Mar. 2021. [CrossRef]
  3. R. Arbelaez, “As heavy EVs proliferate, their weight may be a drag on safety,” IIHS-HLDI crash testing and highway safety. Accessed: Jun. 06, 2023. [Online]. Available: https://www.iihsorg/news/detail/as-heavy-evs-proliferate-their-weight-may-be-a-drag-on-safety.
  4. A. Dorsz and, M. Lewandowski, “Analysis of Fire Hazards Associated with the Operation of Electric Vehicles in Enclosed Structures,” Energies, vol. 15, no. 1, Art. no. 1, Jan. 2022. [CrossRef]
  5. P. Valdes-Dapena, “Latest Tesla fire caused by running over a metal object,” CNNMoney. Accessed: Jun. 06, 2023. [Online]. Available: https://money.cnn.com/2013/11/08/autos/tesla-fire-details/index.html.
  6. P. Sun, R. P. Sun, R. Bisschop, H. Niu, and X. Huang, “A Review of Battery Fires in Electric Vehicles,” Fire Technol., vol. 56, no. 4, pp. 1361–1410, Jul. 2020. [CrossRef]
  7. “Kia Recall 23V218000: High Voltage Battery Pack Short Circuits Causing Fire Hazard,” RepairPal.com. Accessed: Jun. 07, 2023. [Online]. Available: https://repairpal. 2180.
  8. F. Larsson, P. F. Larsson, P. Andersson, P. Blomqvist, and B.-E. Mellander, “Toxic fluoride gas emissions from lithium-ion battery fires,” Sci. Rep., vol. 7, p. 10018, Aug. 2017. [CrossRef]
  9. J. Hynynen et al., “Electric Vehicle Fire Safety in Enclosed Spaces,” RISE Research Institutes of Sweden, RISE Report 2023:42.
  10. “UPDATE 5-Tesla reports third fire involving Model S electric car,” Reuters, Nov. 07, 2013. Accessed: Jun. 06, 2023. [Online]. Available: https://www.reuters.com/article/autos-tesla-fire-idUSL2N0IS0TL20131107. 2013.
  11. G. Gastelu, “NTSB: Tesla was going 116 mph at time of fatal Florida accident, battery pack reignited twice afterwards,” Fox News. Accessed: Jun. 06, 2023. [Online]. Available: https://www.foxnews.com/auto/ntsb-tesla-was-going-116-mph-at-time-of-fatal-florida-accident-battery-pack-reignited-twice-afterwards.
  12. Tessin – Tesla en feu sur l'A2: la batterie serait en cause | 24 heures.” Accessed: Jun. 06, 2023. [Online]. Available: https://www.24heures.ch/tesla-en-feu-sur-l-a2-la-batterie-serait-en-cause-373966884791.
  13. “NTSB to investigate fiery Tesla crash in Coral Gables that killed 2,” WSVN 7News | Miami News, Weather, Sports | Fort Lauderdale. Accessed: Jun. 06, 2023. [Online]. Available: https://wsvncom/news/local/miami-dade/ntsb-to-investigate-fiery-tesla-crash-in-coral-gables-that-killed-2/.
  14. L. Plaza, “Safety Risks to Emergency Responders from Lithium-Ion Battery Fires in Electric Vehicles”.
  15. Mauger and C., M. Julien, “Critical review on lithium-ion batteries: are they safe? Sustainable?,” Ionics, vol. 23, no. 8, pp. 1933–1947, Aug. 2017. [CrossRef]
  16. “Lithium Battery Failures.” Accessed: Aug. 06, 2020. [Online]. Available: https://www.mpoweruk.com/lithium_failures.htm.
  17. Dangerous, vs. Safe batteries, Explosion and fire test!, (Jan. 27, 2020). Accessed: Jul. 14, 2023. [Online Video]. Available: https://www.youtube.com/watch?v=Qzt9RZ0FQyM.
  18. L. Zhu, Y. Xia, Y. Liu, Y. Ge, L. Wang, and L. Zhang, “Extending a Homogenized Model for Characterizing Multidirectional Jellyroll Failure in Prismatic Lithium-Ion Batteries,” Energies, vol. 14, no. 12, Art. no. 12, Jan. 2021. [CrossRef]
  19. T. Werling, M. Sprenger, C. Ellersdorfer, and W. Sinz, “Experimental and Numerical Investigation of the Behavior of Automotive Battery Busbars under Varying Mechanical Loads,” Energies, vol. 13, no. 24, Art. no. 24, Jan. 2020. [CrossRef]
  20. S. Kalnaus et al., “Crashworthiness Models for Automotive Batteries,” ORNL/TM--2018/753, 1435250, Jan. 2018. [CrossRef]
  21. W. B. Gu and C. Y. Wang, “Thermal-Electrochemical Modeling of Battery Systems,” J. Electrochem. Soc., vol. 147, no. 8, p. 2910, Aug. 2000. [CrossRef]
  22. Q. Li, L. Q. Li, L. Zhu, and H. Ruan, “Electromagnetic–Thermo–Mechanical Coupling Behavior of Cu/Si Layered Thin Plate Under Pulsed Magnetic Field,” Acta Mech. Solida Sin., vol. 35, no. 1, pp. 90–100, Feb. 2022. [CrossRef]
  23. S. Bateau-Meyer, P. L’Eplattenier, J. Deng, M. Zhu, and C. Bae, “Randles Circuit Parameters Set Up for Battery Simulations in LS-DYNA®,” p. 15, 2018.
  24. P. L’Eplattenier et al., “A Distributed Randle Circuit Model for Battery Abuse Simulations Using LS-DYNA®,” p. 18, 2016.
  25. B.-M. Sarah, L. Pierre, D. Jie, M. Zhu, B. Chulheung, and M. Theodore, “Randles Circuit Parameters Setp Up for Batery Simulations in LS-DYNA,” 15th Int. -DYNA User Conf.
  26. L. Wang, C. Ling, C.-D. Kan, and C. Yang, “A coupled thermal–electrical–mechanical analysis for lithium-ion battery,” J. Micromechanics Mol. Phys., vol. 07, no. 01, pp. 61–70, Mar. 2022. [CrossRef]
  27. R. Zhao, J. Liu, and J. Gu, “The effects of electrode thickness on the electrochemical and thermal characteristics of lithium ion battery,” Appl. Energy, vol. 139, pp. 220–229, Feb. 2015. [CrossRef]
  28. W. Jiang, Q. Zhou, F. Lu, Y. Chen, and Z. Ma, “A thermal-electrochemical-mechanical coupled model based on non-equilibrium thermodynamics of Li-ion batteries,” J. Energy Storage, vol. 55, p. 105655, Nov. 2022. [CrossRef]
  29. X. Zhang et al., “An Electro-chemo-thermo-mechanical Coupled Three-dimensional Computational Framework for Lithium-ion Batteries,” J. Electrochem. Soc., vol. 167, no. 16, p. 160542, Dec. 2020. [CrossRef]
  30. K. Im, J. Lim, K.-J. Lee, Z.-C. Zhang, and G. Cook Jr., “Electrochemical-Thermal-Mechanical Coupling of Lithium-Ion Battery Model in LS-DYNA,” presented at the 16 th International LS-DYNA ® Users Conference, Jun. 2020.
  31. S. Kim, J. Wee, K. Peters, and H.-Y. S. Huang, “Multiphysics Coupling in Lithium-Ion Batteries with Reconstructed Porous Microstructures,” J. Phys. Chem. C, vol. 122, no. 10, pp. 5280–5290, Mar. 2018. [CrossRef]
  32. Fill, L. Bubeck, D. Knauer, J. Hemmerling, and K. P. Birke, “Multi-dimensional model for electrical, thermal and mechanical simulation of a Lithium-ion Cell,” in NEIS 2022; Conference on Sustainable Energy Supply and Energy Storage Systems, Sep. 2022, pp. 1–8.
  33. P. Kumar, G. Rankin, K. R. Pattipati, and B. Balasingam, “Model-Based Approach to Long Term Prediction of Battery Surface Temperature,” IEEE J. Emerg. Sel. Top. Ind. Electron., vol. 4, no. 1, pp. 389–399, Jan. 2023. [CrossRef]
  34. L. Sevgi, Electromagnetic modeling and simulation. in The IEEE Press series on electromagnetic wave theory. Piscataway, NJ: IEEE Press, 2014.
  35. P. L’Eplattenier and I. Çaldichoury, “Electromagnetism Module Presentation”.
  36. P. L’Eplattenier, G. Cook, C. Ashcraft, M. Burger, J. Imbert, and M. Worswick, “Introduction of an Electromagnetism Module in LS-DYNA for Coupled Mechanical-Thermal-Electromagnetic Simulations,” Met. Form., no. 5, p. 8, 2009.
  37. “Update On The Electromagnetism Module In LS-DYNA”.
  38. O. Biro and, K. Preis, “On the use of the magnetic vector potential in the finite-element analysis of three-dimensional eddy currents,” IEEE Trans. Magn., vol. 25, no. 4, pp. 3145–3159, Jul. 1989. [CrossRef]
  39. Y. Chen et al., “A review of lithium-ion battery safety concerns: The issues, strategies, and testing standards,” J. Energy Chem., vol. 59, pp. 83–99, Aug. 2021. [CrossRef]
  40. T. Kisters, E. Sahraei, and T. Wierzbicki, “Dynamic impact tests on lithium-ion cells,” Int. J. Impact Eng., vol. 108, pp. 205–216, Oct. 2017. [CrossRef]
  41. G. E. Blomgren, “The Development and Future of Lithium Ion Batteries,” J. Electrochem. Soc., vol. 164, no. 1, p. A5019, Dec. 2016. [CrossRef]
  42. X. Zhang, E. Sahraei, and K. Wang, “Deformation and failure characteristics of four types of lithium-ion battery separators,” J. Power Sources, vol. 327, pp. 693–701, Sep. 2016. [CrossRef]
  43. E. Sahraei, R. Hill, and T. Wierzbicki, “Calibration and finite element simulation of pouch lithium-ion batteries for mechanical integrity,” J. Power Sources, vol. 201, pp. 307–321, Mar. 2012. [CrossRef]
  44. “Time step size,” Welcome to the LS-DYNA support site. Accessed: Jul. 19, 2023. [Online]. Available: https://www.dynasupport.com/tutorial/ls-dyna-users-guide/time-step-size.
  45. R. M. Morgan, C. Cui, K. H. Digges, L. Cao, and C.-D. (Steve) Kan, “Impact and Injury Patterns in Between-Rails Frontal Crashes of Vehicles with Good Ratings for Frontal Crash Protection,” Ann. Adv. Automot. Med. Annu. Sci. Conf., vol. 56, pp. 255–265, Oct. 2012.
  46. C.-D. Kan, D. Marzougui, G. T. Bahouth, and N. E. Bedewi, “Crashworthiness Evaluation Using Integrated Vehicle and Occupant Finite Element Models,” Int. J. Crashworthiness, vol. 6, no. 3, pp. 387–398, Jan. 2001. [CrossRef]
  47. R. Reichert, P. Mohan, D. Marzougui, C.-D. Kan, and D. Brown, “Validation of a Toyota Camry Finite Element Model for Multiple Impact Configurations,” SAE International, Warrendale, PA, SAE Technical Paper 2016-01–1534, Apr. 2016. [CrossRef]
  48. A. Eskandarian, D. Marzougui, and N. E. Bedewi, “Finite element model and validation of a surrogate crash test vehicle for impacts with roadside objects,” Int. J. Crashworthiness, vol. 2, no. 3, pp. 239–258, Jan. 1997. [CrossRef]
  49. K. Opiela, S. Kan, and D. Marzougui, “NCAC Vehicle Model Development Update,” Art. no. NCAC 2007-T-006, Dec. 2007, Accessed: Jul. 18, 2023. [Online]. Available: https://trid.trb.org/view/926092. 9260.
  50. “Center for Collision Safety and Analysis – Finite Element Models.” Accessed: Jul. 18, 2023. [Online]. Available: https://www.ccsa.gmu..edu/models/.
  51. R. Powers et al., Roadside Barrier Designs near Bridge Rail Ends with Restricted Rights-of-Way: A Guide. Washington, D.C.: Transportation Research Board, 2022. [CrossRef]
  52. D. Marzougui et al., Evaluating the Performance of Longitudinal Barriers on Curved, Superelevated Roadway Sections. Washington, D.C.: Transportation Research Board, 2019. [CrossRef]
  53. “Center for Collision Safety and Analysis – 2010 Toyota Yaris.” Accessed: Jul. 19, 2023. [Online]. Available: https://www.ccsa.gmu.edu/models/2010-toyota-yaris/. 2010.
  54. “2024 Nissan LEAF | All-Electric Vehicle,” Nissan USA. Accessed: Jul. 19, 2023. [Online]. Available: https://www.nissanusa.com/vehicles/electric-cars/leaf.html.
  55. “Online circuit simulator & schematic editor,” CircuitLab. Accessed: Feb. 04, 2021. [Online]. Available: https://www.circuitlab.com/.
  56. S. Kalnaus et al., “Crashworthiness Models for Automotive Batteries - Report on Project 2088-A031-15 for DOT/NHTSA,” Oak Ridge National Lab. (ORNL), Oak Ridge, TN (United States), ORNL/TM-2016/435, Jul. 2016. [CrossRef]
  57. Livermore Software Technology, “LS-DYNA Manual Volume III Mutliphysics.
  58. “Air - Thermal Conductivity, vs. Temperature and Pressure.” Accessed: Jul. 21, 2023. [Online]. Available: https://www.engineeringtoolbox.com/air-properties-viscosity-conductivity-heat-capacity-d_1509.html.
  59. “Water - Thermal Conductivity, vs. Temperature.” Accessed: Jul. 21, 2023. [Online]. Available: https://www.engineeringtoolbox.com/water-liquid-gas-thermal-conductivity-temperature-pressure-d_2012.html.
  60. M. Ahmeid, M. M. Ahmeid, M. Muhammad, S. Lambert, P. S. Attidekou, and Z. Milojevic, “A rapid capacity evaluation of retired electric vehicle battery modules using partial discharge test,” J. Energy Storage, vol. 50, p. 104562, Jun. 2022. [CrossRef]
  61. “Online circuit simulator & schematic editor,” CircuitLab. Accessed: Jul. 21, 2023. [Online]. Available: https://www.circuitlab.com/.
  62. E. Braco, I. E. Braco, I. San Martín, P. Sanchis, and A. Ursúa, “Fast capacity and internal resistance estimation method for second-life batteries from electric vehicles,” Appl. Energy, vol. 329, p. 120235, Jan. 2023. [CrossRef]
  63. . A. Turner et al., “Crashworthiness Models for Automotive Batteries,” DOT HS 812 736, May 2019. Accessed: Jul. 14, 2023. [Online]. Available: https://rosap.ntl.bts.gov/view/dot/41005.
  64. “Qnovo | INSIDE THE BATTERY OF A NISSAN LEAF.” Accessed: May 23, 2022. [Online]. Available: https://www.qnovo.com/blogs/inside-the-battery-of-a-nissan-leaf. 23 May.
  65. J. Jones, “Laboratory Test Procedure for FMVSS No. 214, Dynamic Side Impact Protection Rigid Pole Side Impact Test Requirements.” Sep. 2012.
Preprints 111601 g001
Figure 1. Thermal-Runaway of Battery and EV.
Figure 1. Thermal-Runaway of Battery and EV.
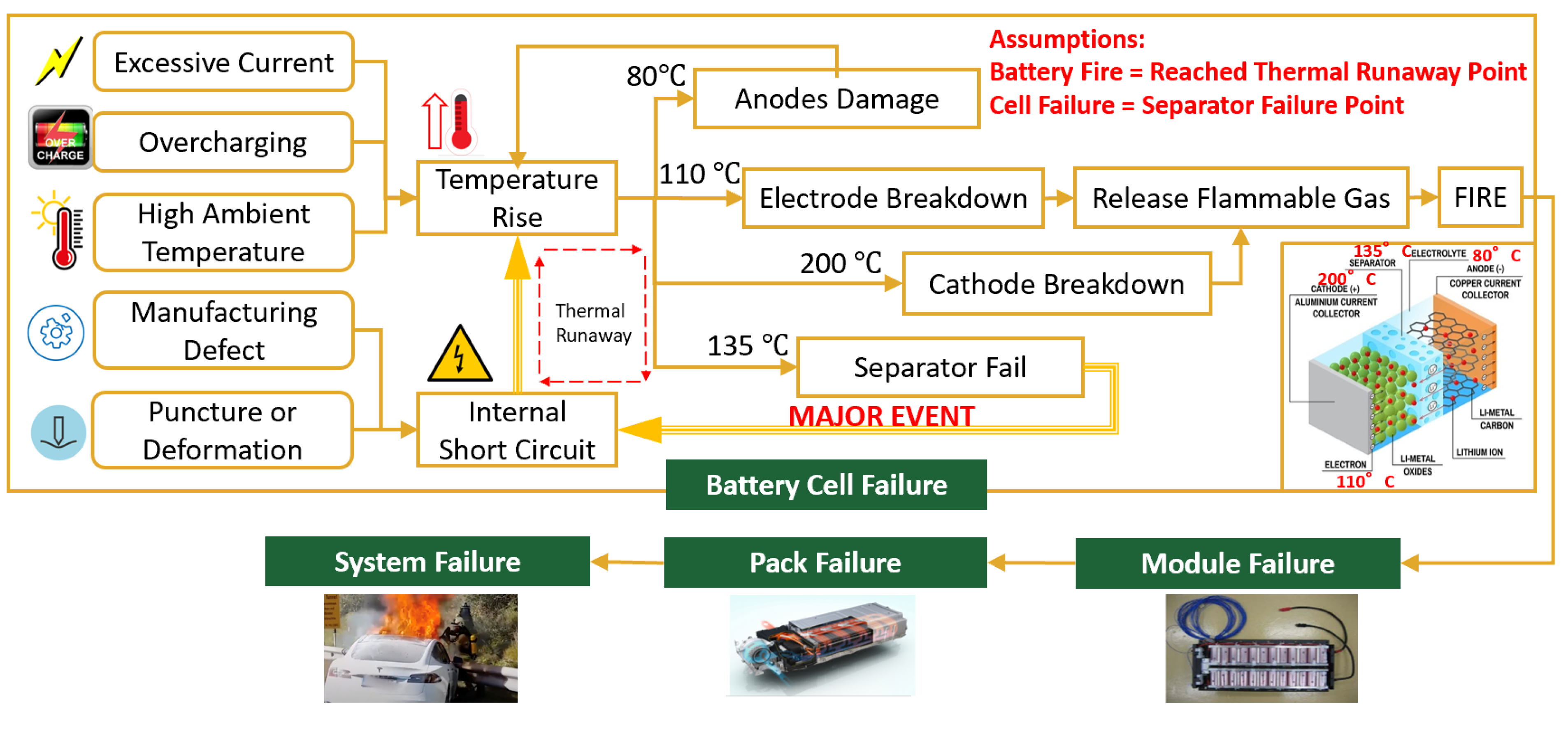
Preprints 111601 g001
Preprints 111601 g002
Figure 2. Vehicle Crash Safety FE Models Developed by the CCSA Team [50]. The models with* were created by others and improved by CCSA.
Figure 2. Vehicle Crash Safety FE Models Developed by the CCSA Team [50]. The models with* were created by others and improved by CCSA.
Preprints 111601 g002
Preprints 111601 g003
Figure 3. Representative Finite Element Model of Leaf Battery Cell (Top Left); Representative Separator is Modeled with “Wrinkles” (Top Right). Model Detail and Place to Define Electric Potential Difference (Bottom).
Figure 3. Representative Finite Element Model of Leaf Battery Cell (Top Left); Representative Separator is Modeled with “Wrinkles” (Top Right). Model Detail and Place to Define Electric Potential Difference (Bottom).
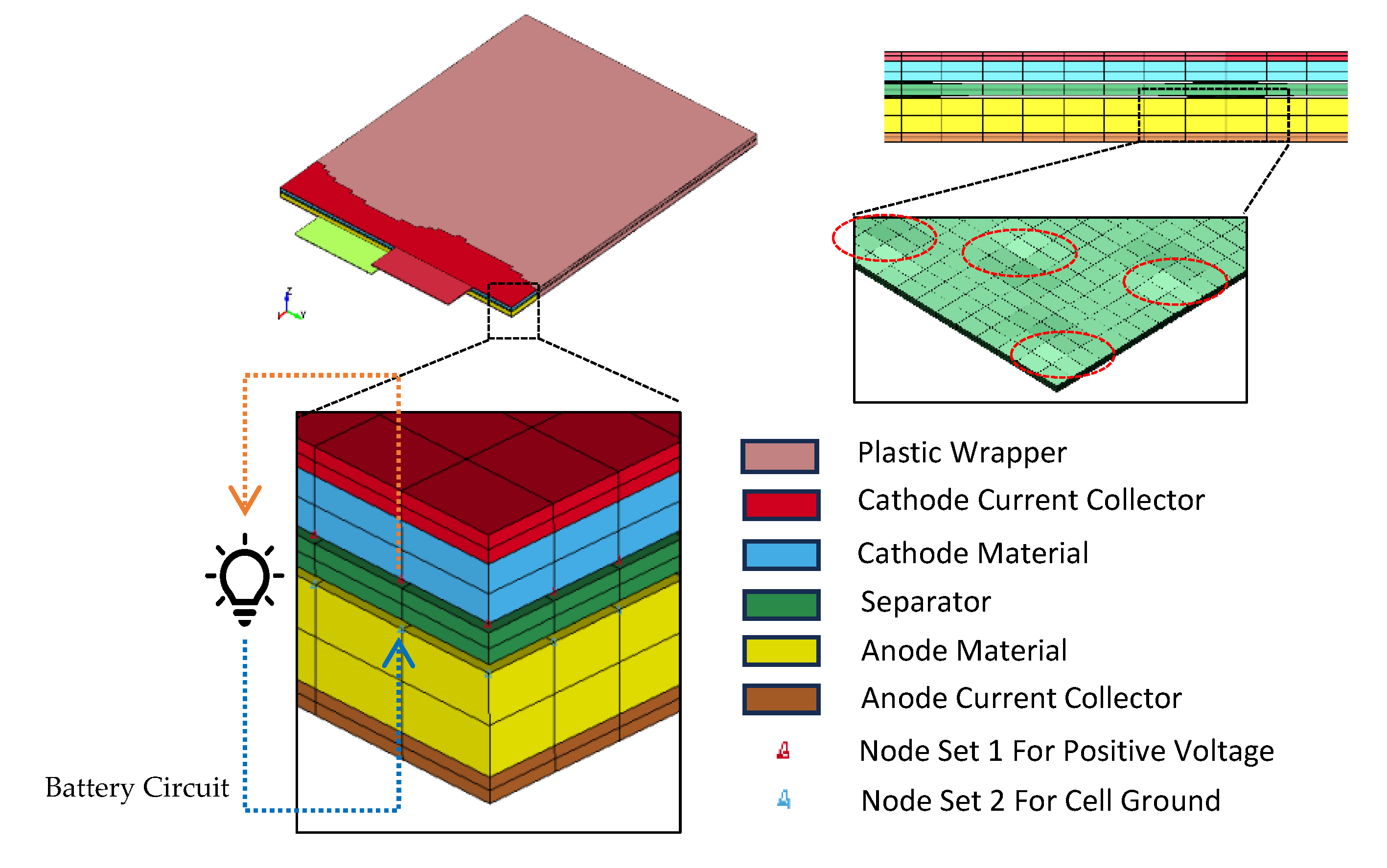
Preprints 111601 g003
Preprints 111601 g004
Figure 4. Electric Current at Ampere Meter “AM1” between LS-DYNA (Solid Line) and CircuitLab (Dash Line) (Left). Randles Circuit Model in CircuitLab in External Short-circuit (Right).
Figure 4. Electric Current at Ampere Meter “AM1” between LS-DYNA (Solid Line) and CircuitLab (Dash Line) (Left). Randles Circuit Model in CircuitLab in External Short-circuit (Right).
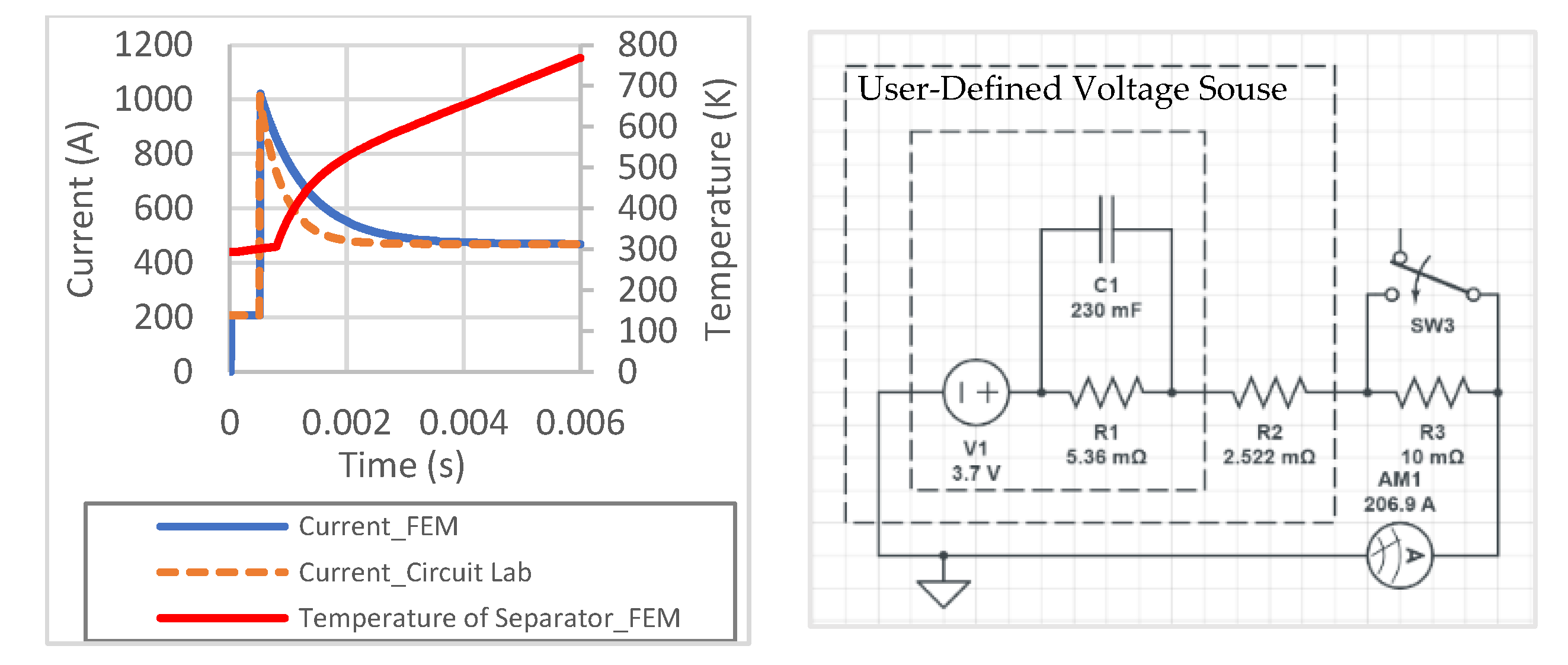
Preprints 111601 g004
Preprints 111601 g005
Figure 5. Nissan Leaf Cell Spherical Punch Test [56] vs. Simulation Result.
Figure 5. Nissan Leaf Cell Spherical Punch Test [56] vs. Simulation Result.
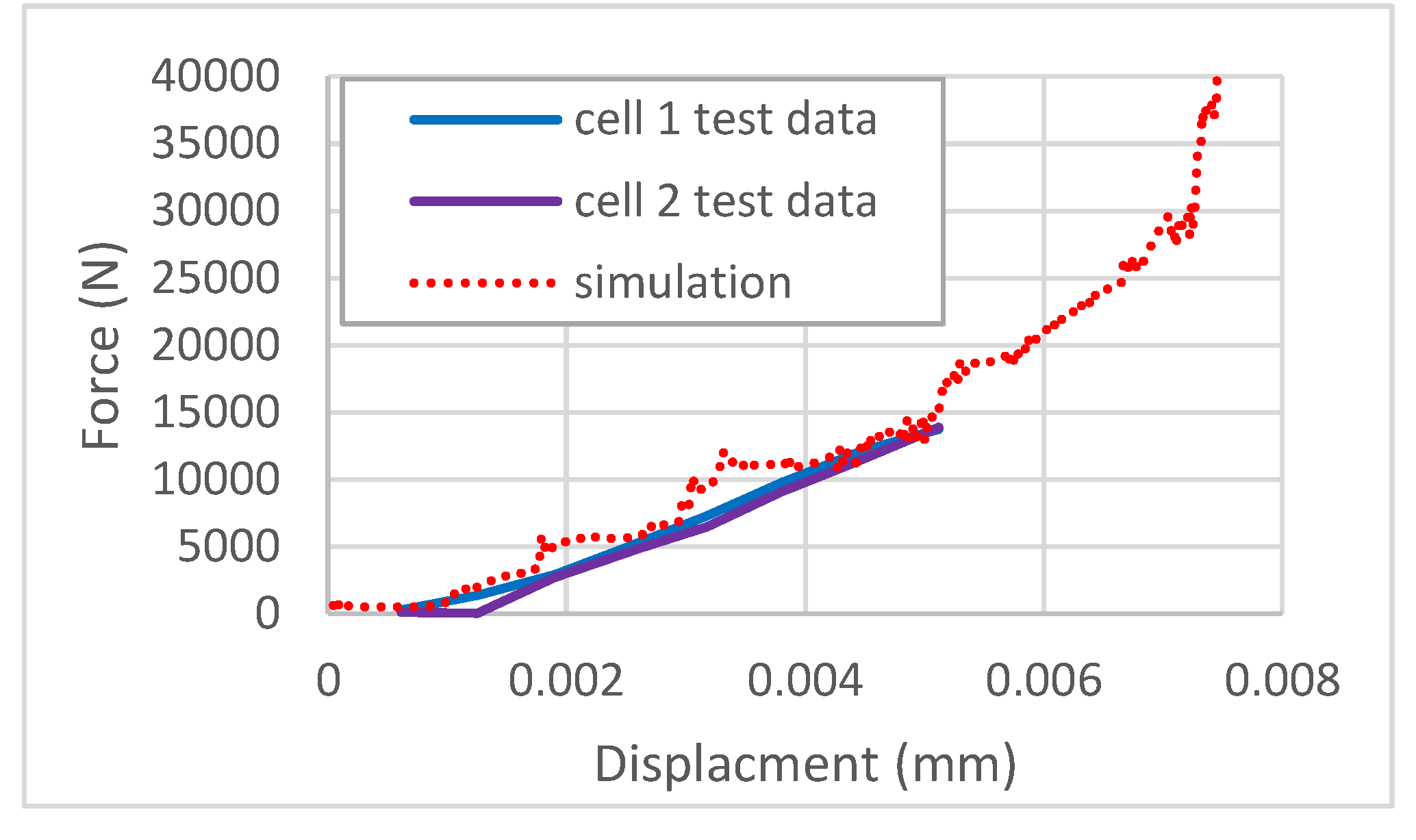
Preprints 111601 g005
Preprints 111601 g006
Figure 6. Sample Thermal-Mechanical Contact Card for Heat Transfer in Air. Kair= 0.024 W/m.
Figure 6. Sample Thermal-Mechanical Contact Card for Heat Transfer in Air. Kair= 0.024 W/m.
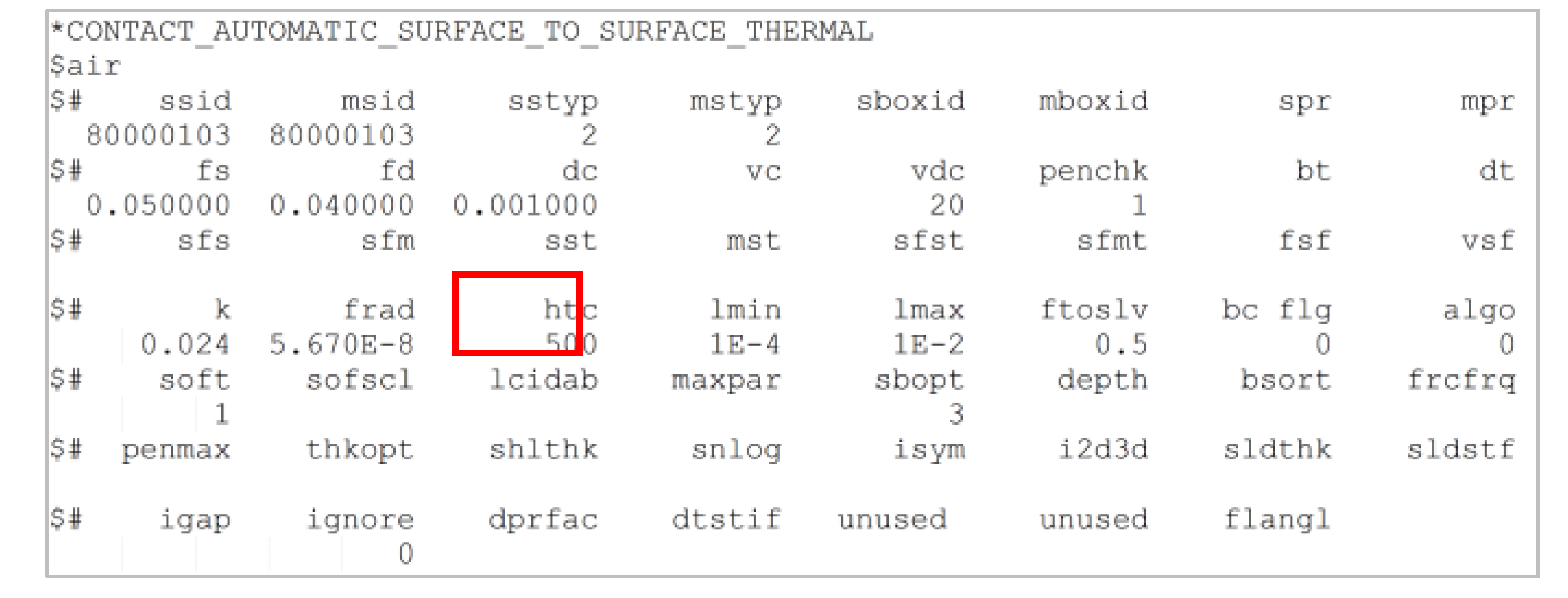
Preprints 111601 g006
Preprints 111601 g007
Figure 7. Sample Thermal-Mechanical Contact Card for Heat Transfer in Water. Kwater= 0.58 W/m.
Figure 7. Sample Thermal-Mechanical Contact Card for Heat Transfer in Water. Kwater= 0.58 W/m.
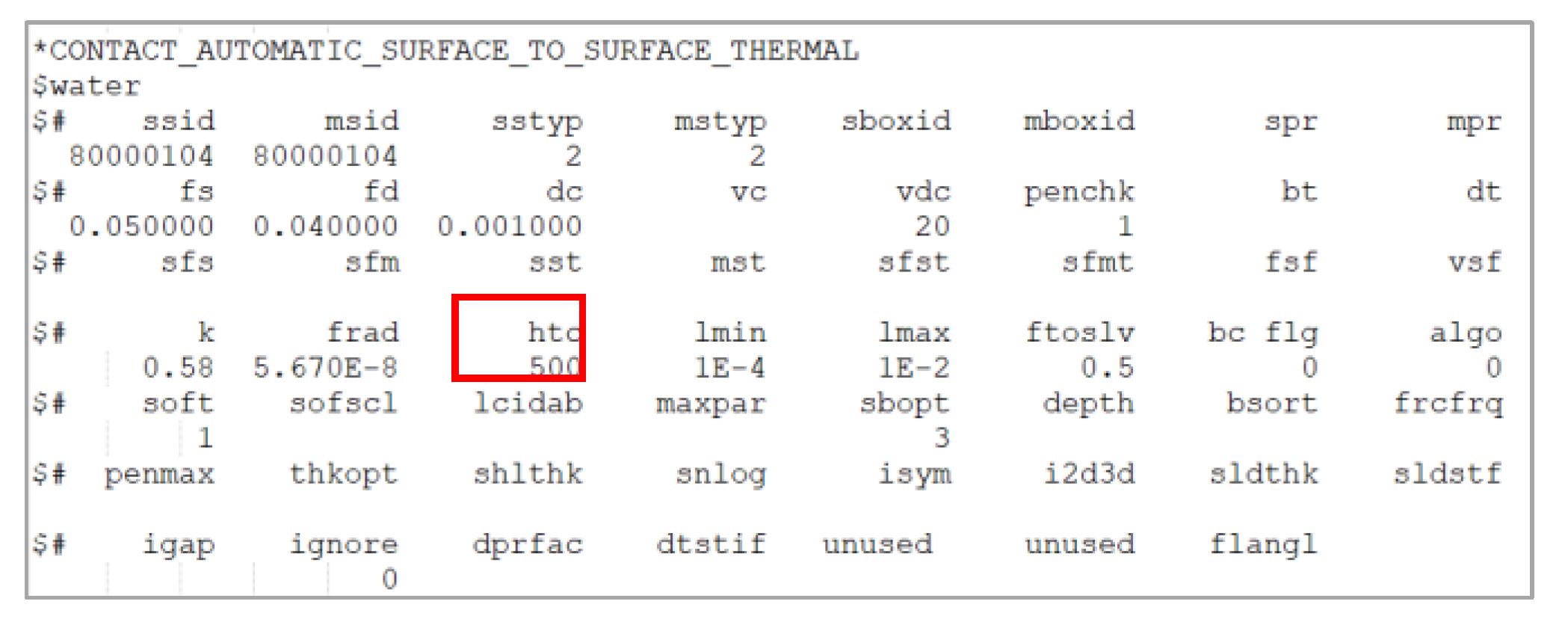
Preprints 111601 g007
Preprints 111601 g008
Figure 8. A thermal-mechanical-electrical coupled Representative FE Model for Nissan Leaf Module.
Figure 8. A thermal-mechanical-electrical coupled Representative FE Model for Nissan Leaf Module.
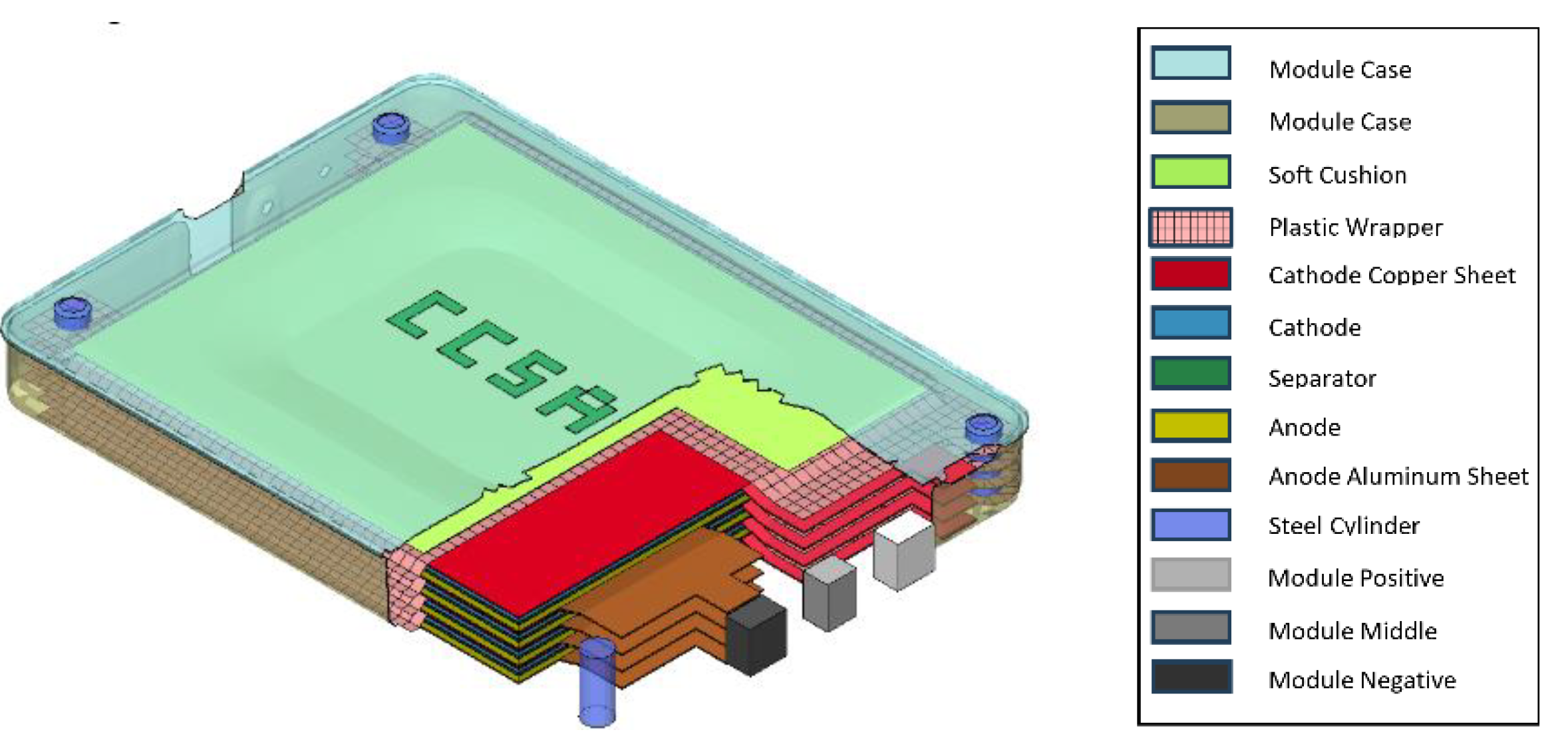
Preprints 111601 g008
Preprints 111601 g009
Figure 9. Two Different Battery Cells Connected in Serial. CircuitLab Simulation Diagram (Top); Time History of Current at Meter “AM1” of LS-DYNA and CircuitLab (Bottom Left); LS-DYNA Simulation Current Density Contour (Bottom Right).
Figure 9. Two Different Battery Cells Connected in Serial. CircuitLab Simulation Diagram (Top); Time History of Current at Meter “AM1” of LS-DYNA and CircuitLab (Bottom Left); LS-DYNA Simulation Current Density Contour (Bottom Right).
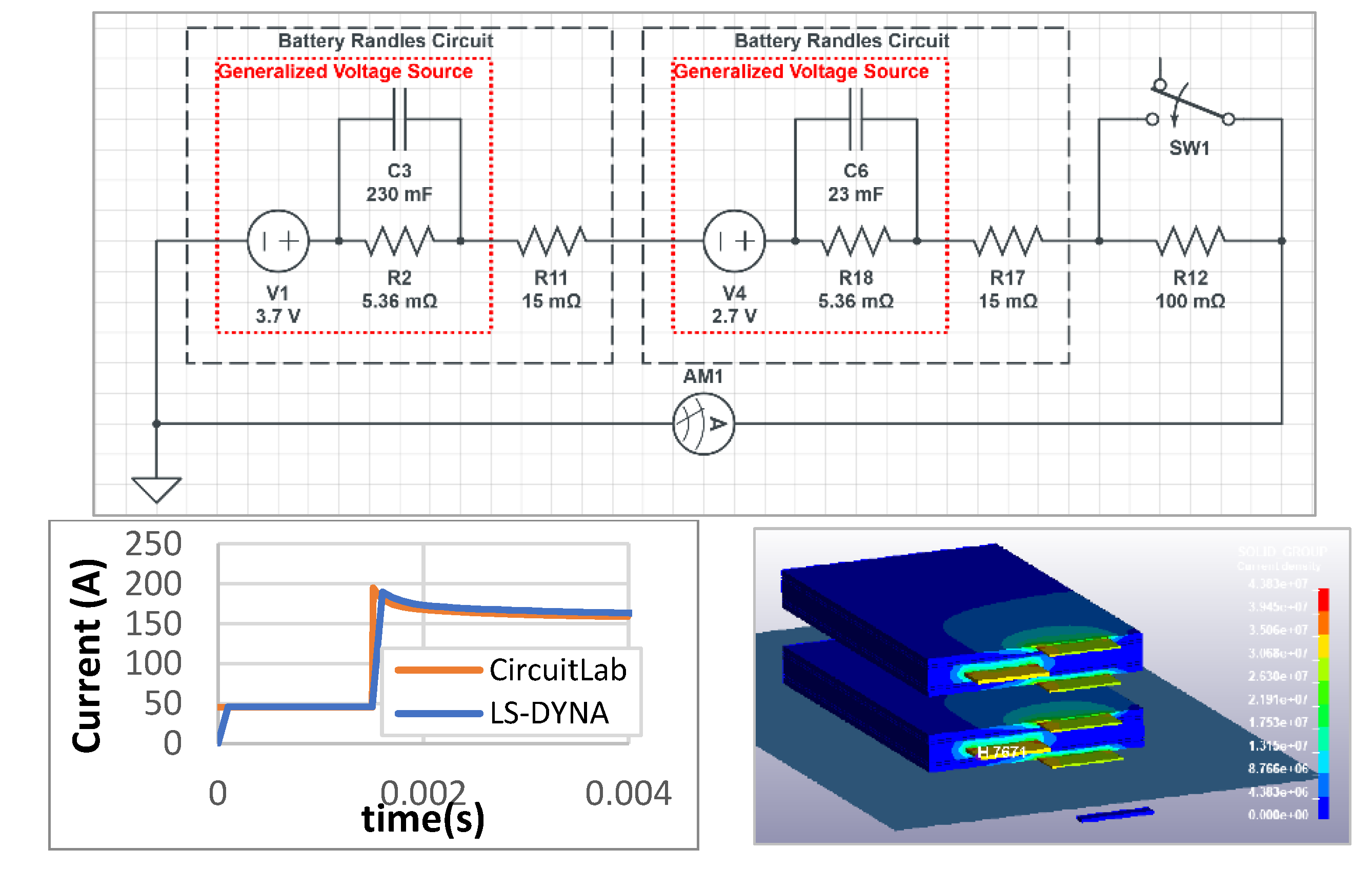
Preprints 111601 g009
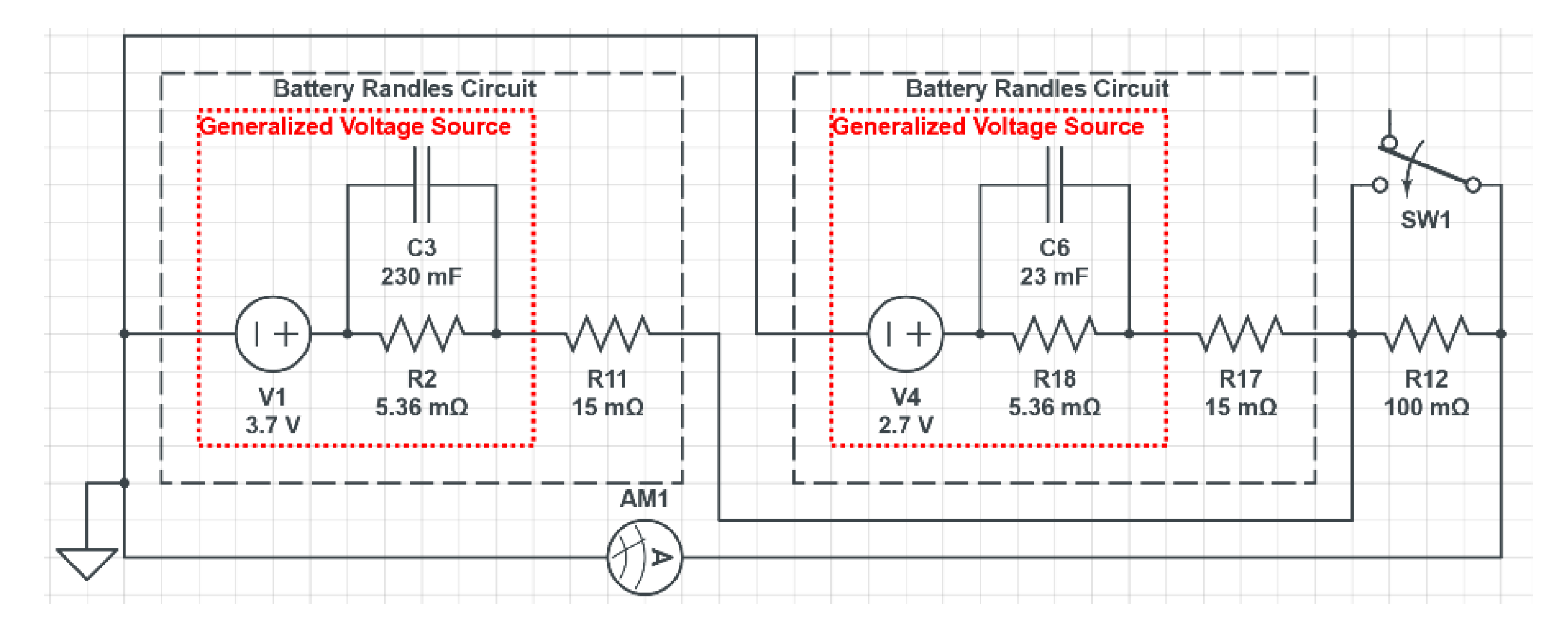
Preprints 111601 g010
Figure 10. Two Different Battery Cells in Parallel. Current Density (Top Left); CircuitLab Simulation Diagram (Top Right); Current at the “AM1” between LS-DYNA and CircuitLab (Bottom).
Figure 10. Two Different Battery Cells in Parallel. Current Density (Top Left); CircuitLab Simulation Diagram (Top Right); Current at the “AM1” between LS-DYNA and CircuitLab (Bottom).
Preprints 111601 g010
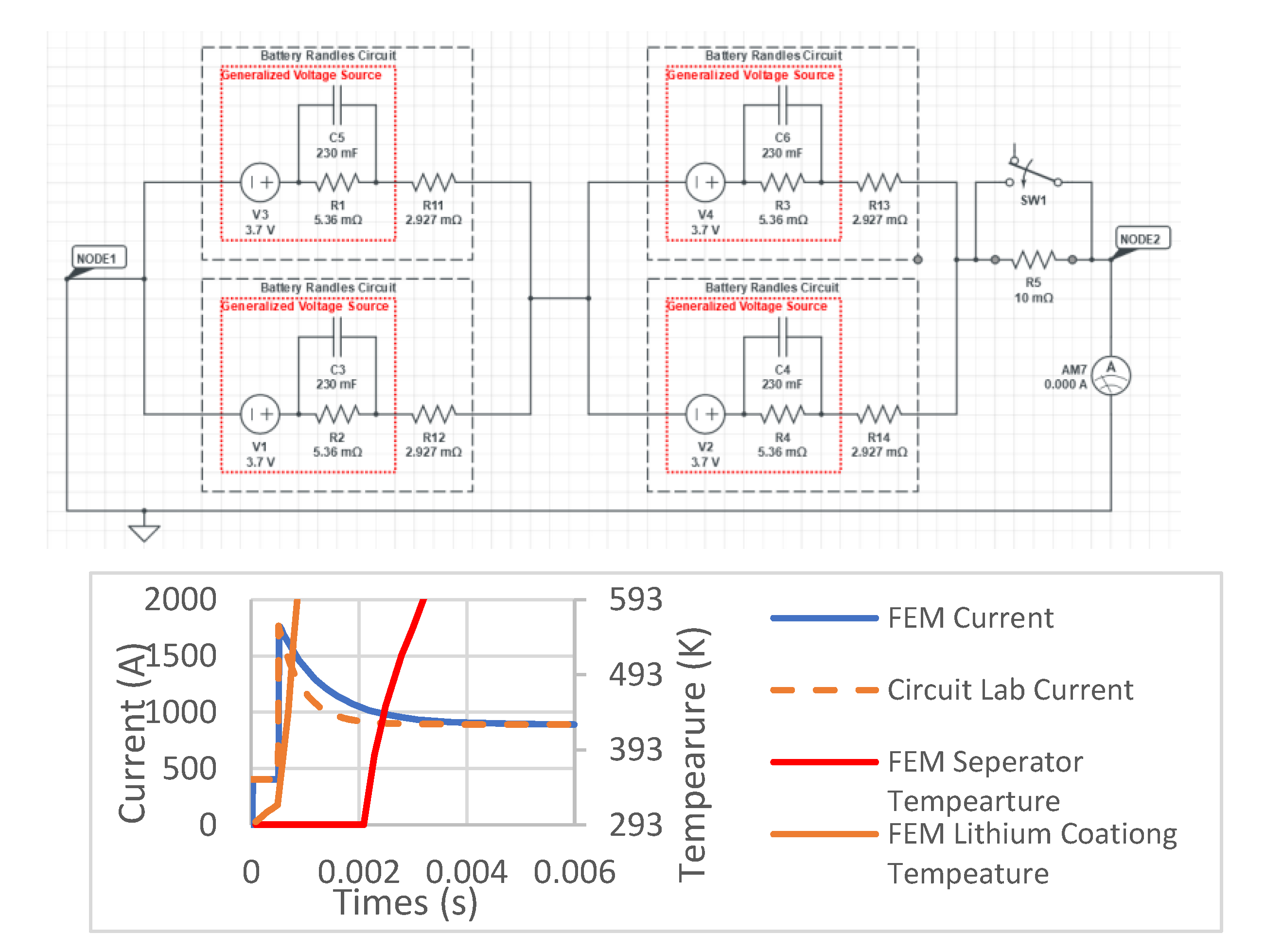
Preprints 111601 g011
Figure 11. Randles Circuit in CircuitLab (Top) and Electrical Calibration (Bottom). External Short is formed at 5E-4 second.
Figure 11. Randles Circuit in CircuitLab (Top) and Electrical Calibration (Bottom). External Short is formed at 5E-4 second.
Preprints 111601 g011
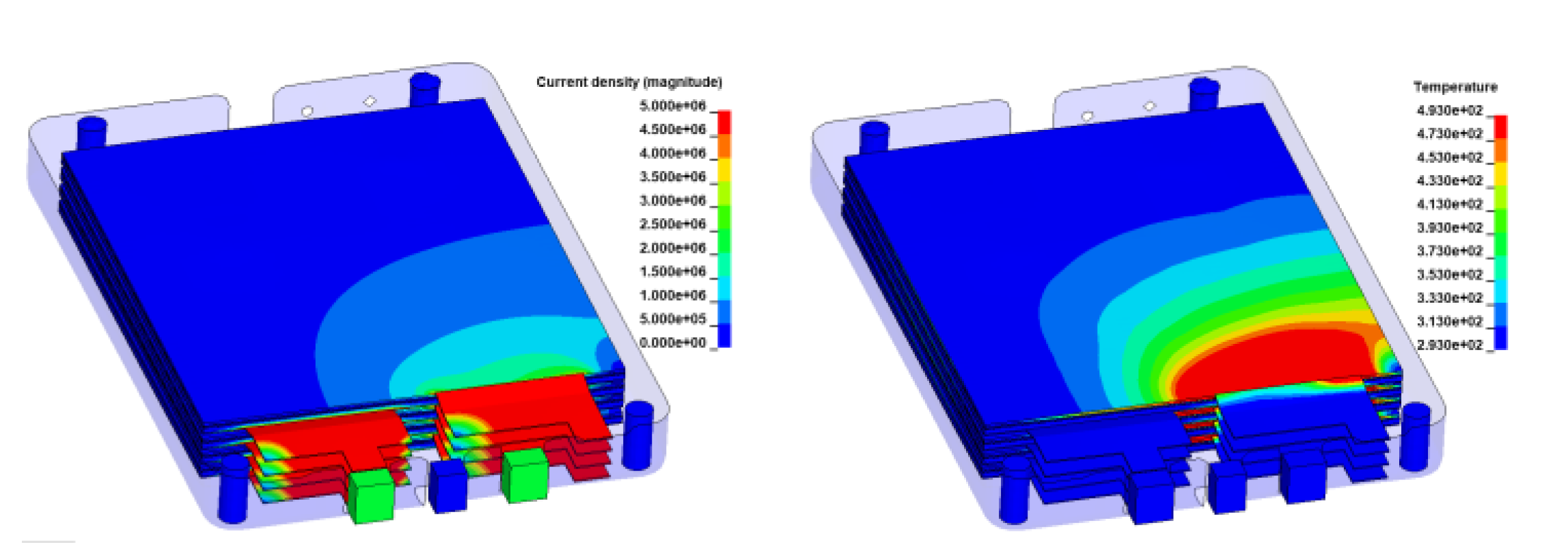
Preprints 111601 g012
Figure 12. Battery Module Current Density Distribution (Left) and Temperature Distribution in External Short Circuit Test.
Figure 12. Battery Module Current Density Distribution (Left) and Temperature Distribution in External Short Circuit Test.
Preprints 111601 g012
Preprints 111601 g014
Figure 14. Temperature Contour of Battery Module Simulation: Anode Aluminum Current Collector Sheet (A), Anode Graphite Coating (B), Separator (C), Cathode Lithium Material Coating (D). Cathode Copper Current Collector Sheet (E). Plastic Cell Wrapper (F). Soft Cushion (G). Module Case Cover (H).
Figure 14. Temperature Contour of Battery Module Simulation: Anode Aluminum Current Collector Sheet (A), Anode Graphite Coating (B), Separator (C), Cathode Lithium Material Coating (D). Cathode Copper Current Collector Sheet (E). Plastic Cell Wrapper (F). Soft Cushion (G). Module Case Cover (H).
Preprints 111601 g014
Preprints 111601 g015
Figure 15. Temperature Raise Caused by Side Pole Impact on a Battery Module with 4 cells. Exterior Temperature (Left). Interior in Critical Area (Right).
Figure 15. Temperature Raise Caused by Side Pole Impact on a Battery Module with 4 cells. Exterior Temperature (Left). Interior in Critical Area (Right).
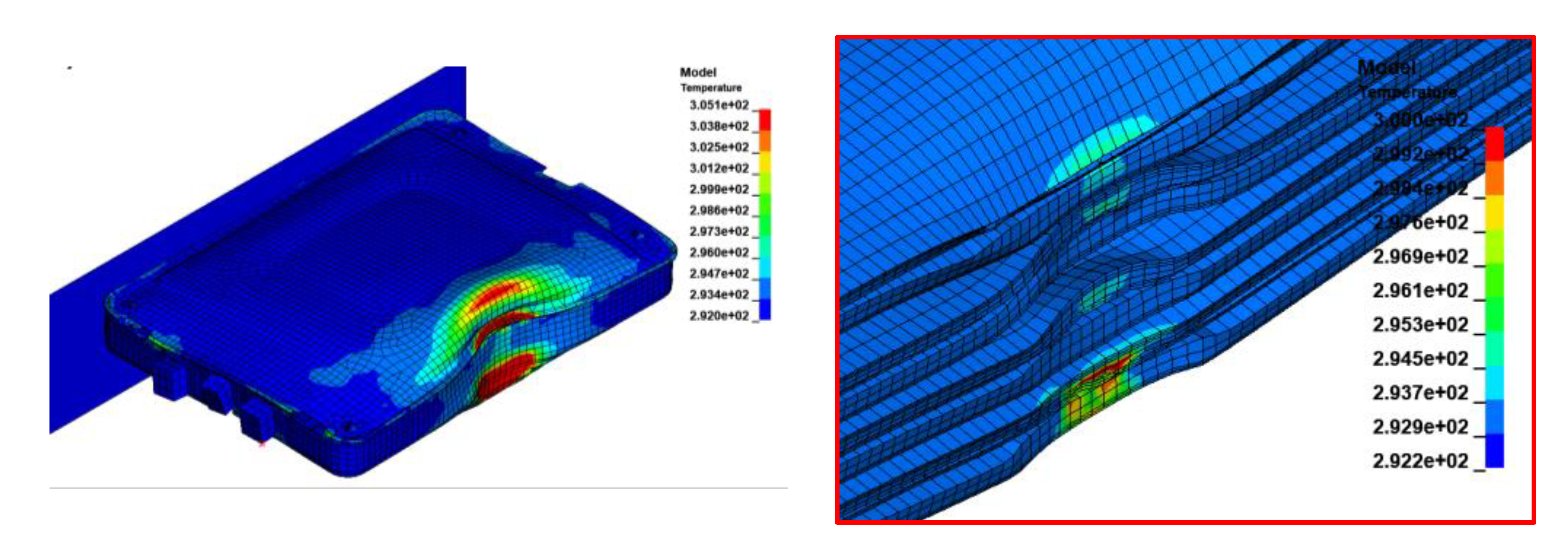
Preprints 111601 g015
Preprints 111601 g016
Figure 16. Battery Module Coarse model.
Figure 16. Battery Module Coarse model.
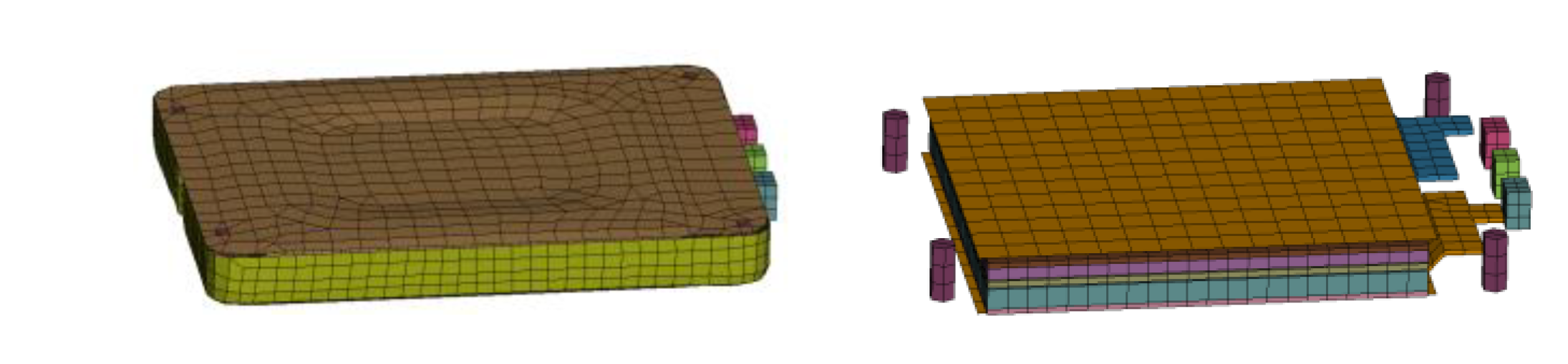
Preprints 111601 g016
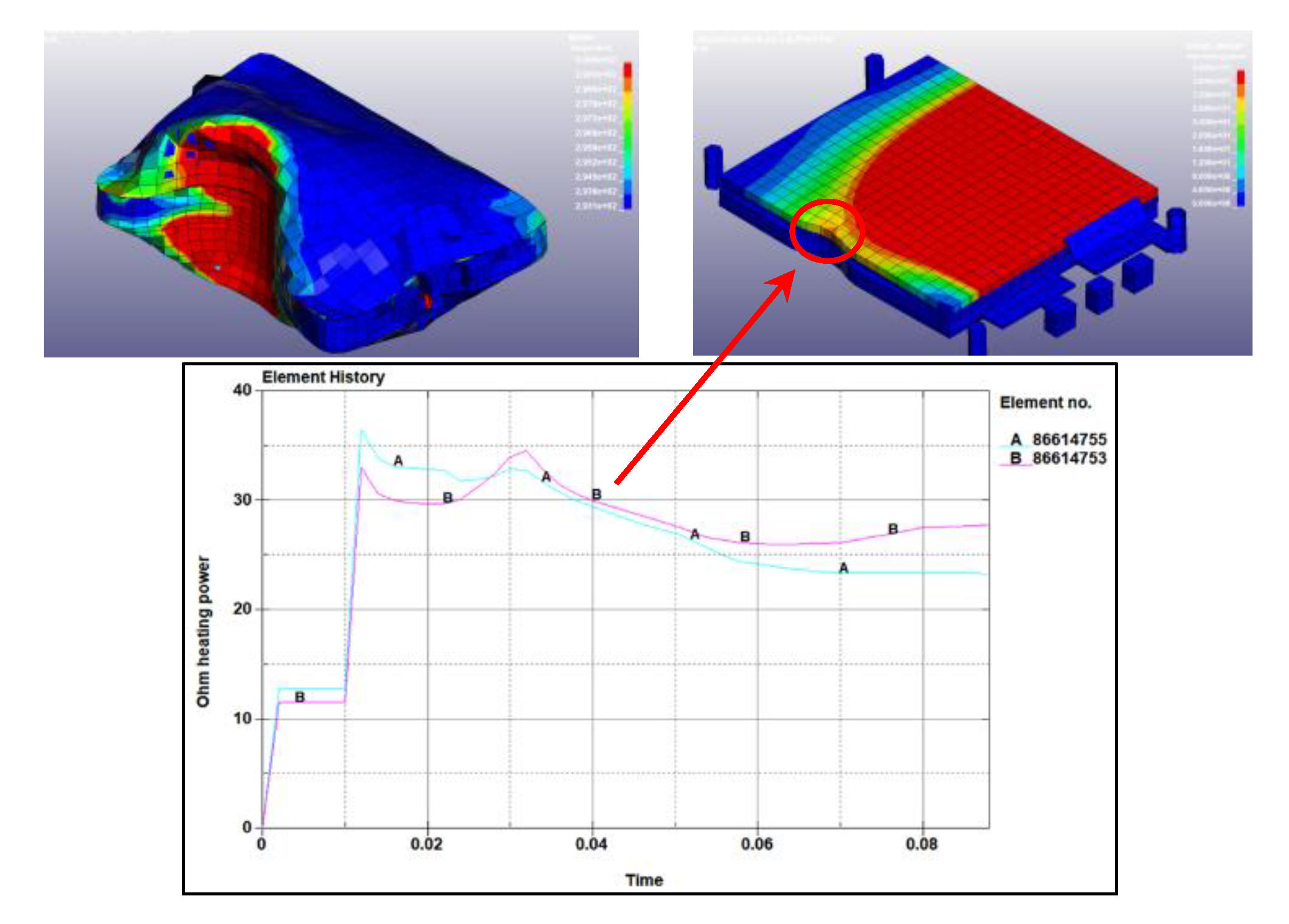
Preprints 111601 g017
Figure 17. Temperature in the Side Pole Impact (Top). Ohm Heating Power in the Side Pole Impact (Top Right). Ohm Heating Power in Impact Area (Bottom).
Figure 17. Temperature in the Side Pole Impact (Top). Ohm Heating Power in the Side Pole Impact (Top Right). Ohm Heating Power in Impact Area (Bottom).
Preprints 111601 g017
Preprints 111601 g018
Figure 18. EV Top View (Upper Left); Front View (Upper Right); Battery Pack Location (Lower Left); EV ISO View (Lower Right).
Figure 18. EV Top View (Upper Left); Front View (Upper Right); Battery Pack Location (Lower Left); EV ISO View (Lower Right).
Preprints 111601 g018
Preprints 111601 g019
Figure 19. EV Battery Pack Electric Potential (Left); Current Density of Battery pack (Right).
Figure 19. EV Battery Pack Electric Potential (Left); Current Density of Battery pack (Right).
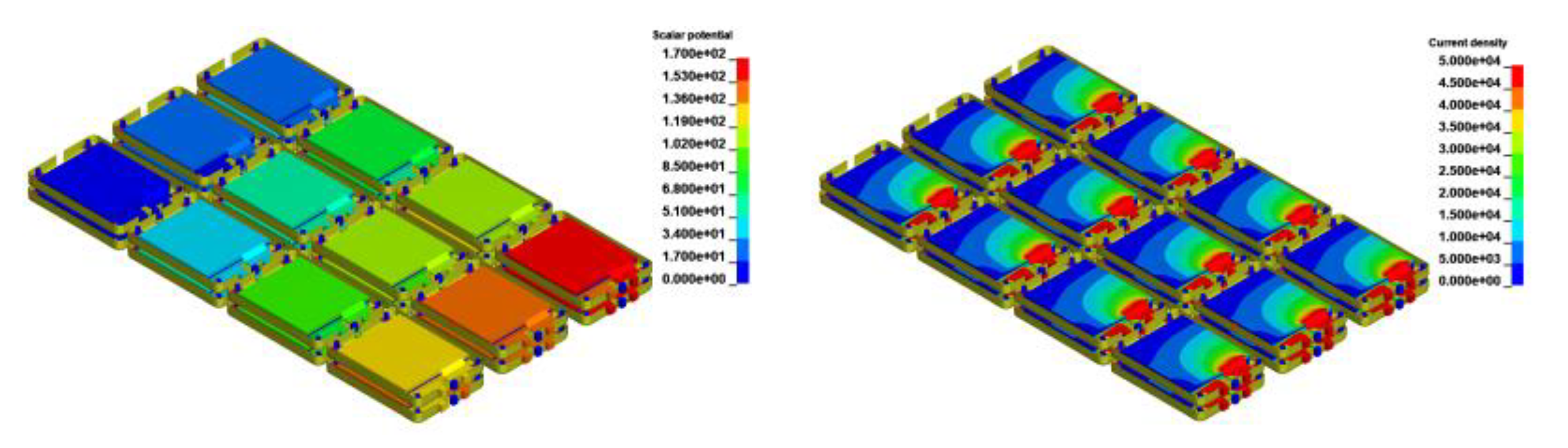
Preprints 111601 g019
Preprints 111601 g020
Figure 20. The Temperature Contour (Bottom) for a Normal Discharging Battery Pack in EV.
Figure 20. The Temperature Contour (Bottom) for a Normal Discharging Battery Pack in EV.
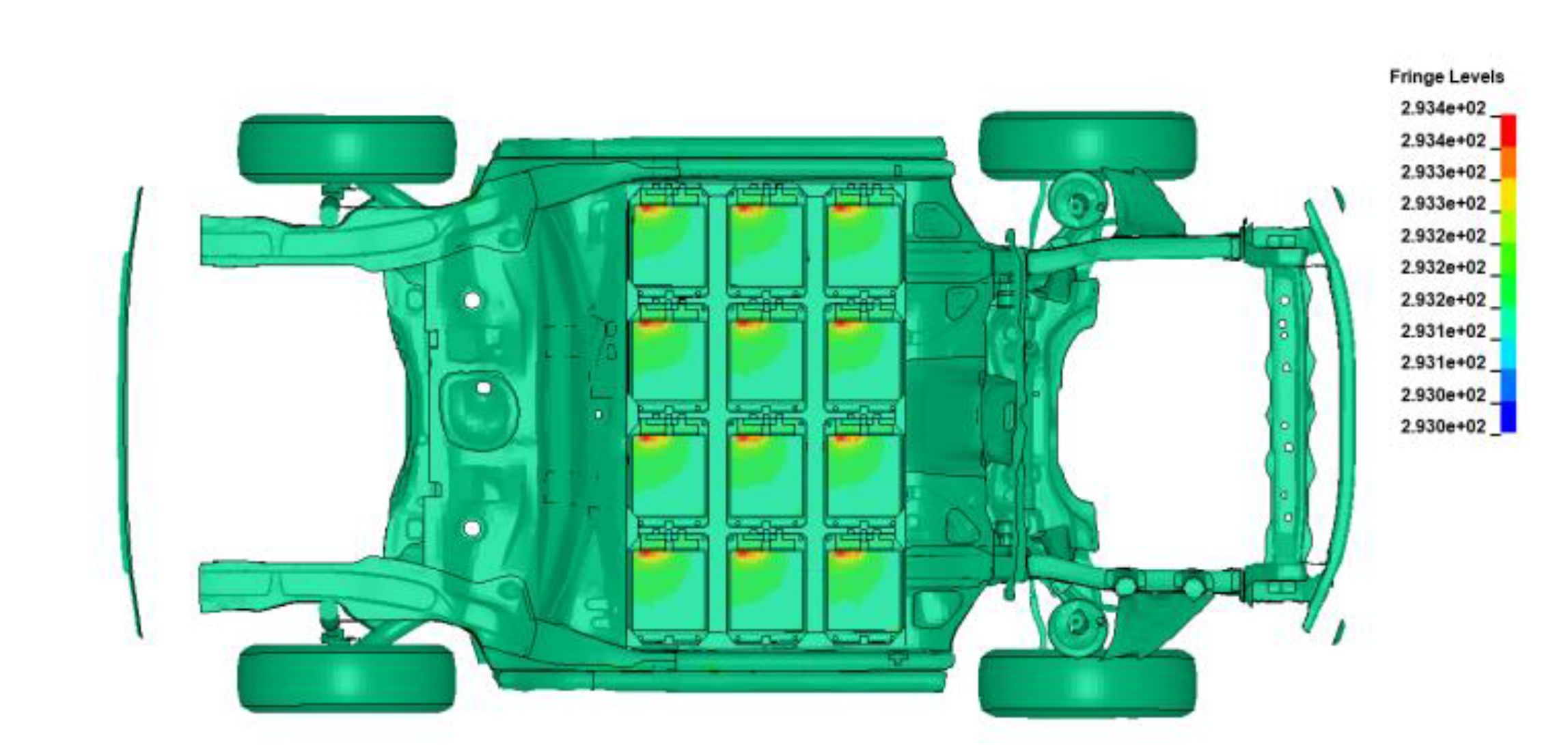
Preprints 111601 g020
Preprints 111601 g021
Figure 21. Voltage (Top Left), Current Density (Top Right) and Temperature (Bottom) of Battery pack in External Short.
Figure 21. Voltage (Top Left), Current Density (Top Right) and Temperature (Bottom) of Battery pack in External Short.
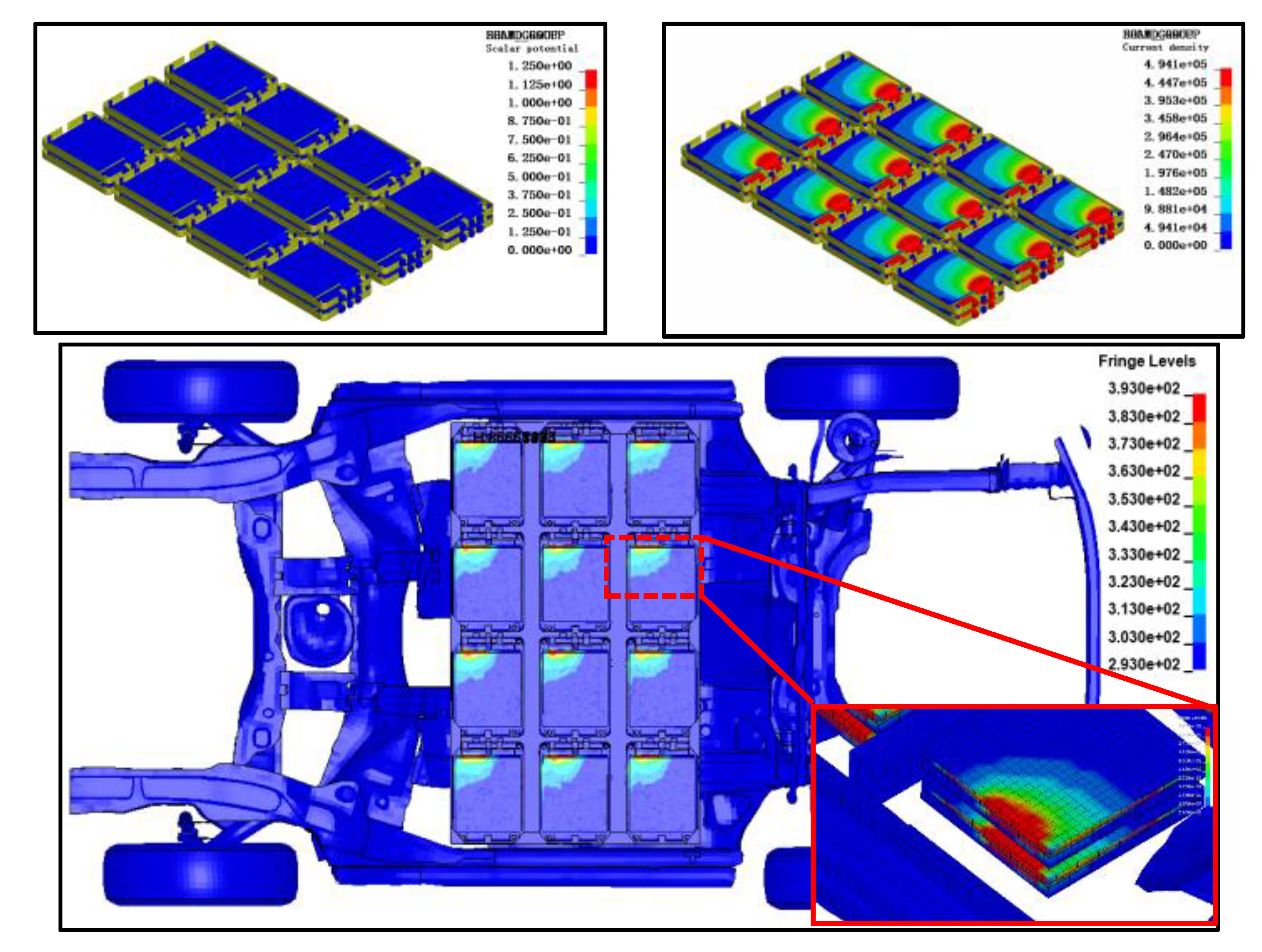
Preprints 111601 g021
Preprints 111601 g022
Figure 22. Maximum Temperature for Different Part of Battery Cell in External Short Circuit.
Figure 22. Maximum Temperature for Different Part of Battery Cell in External Short Circuit.
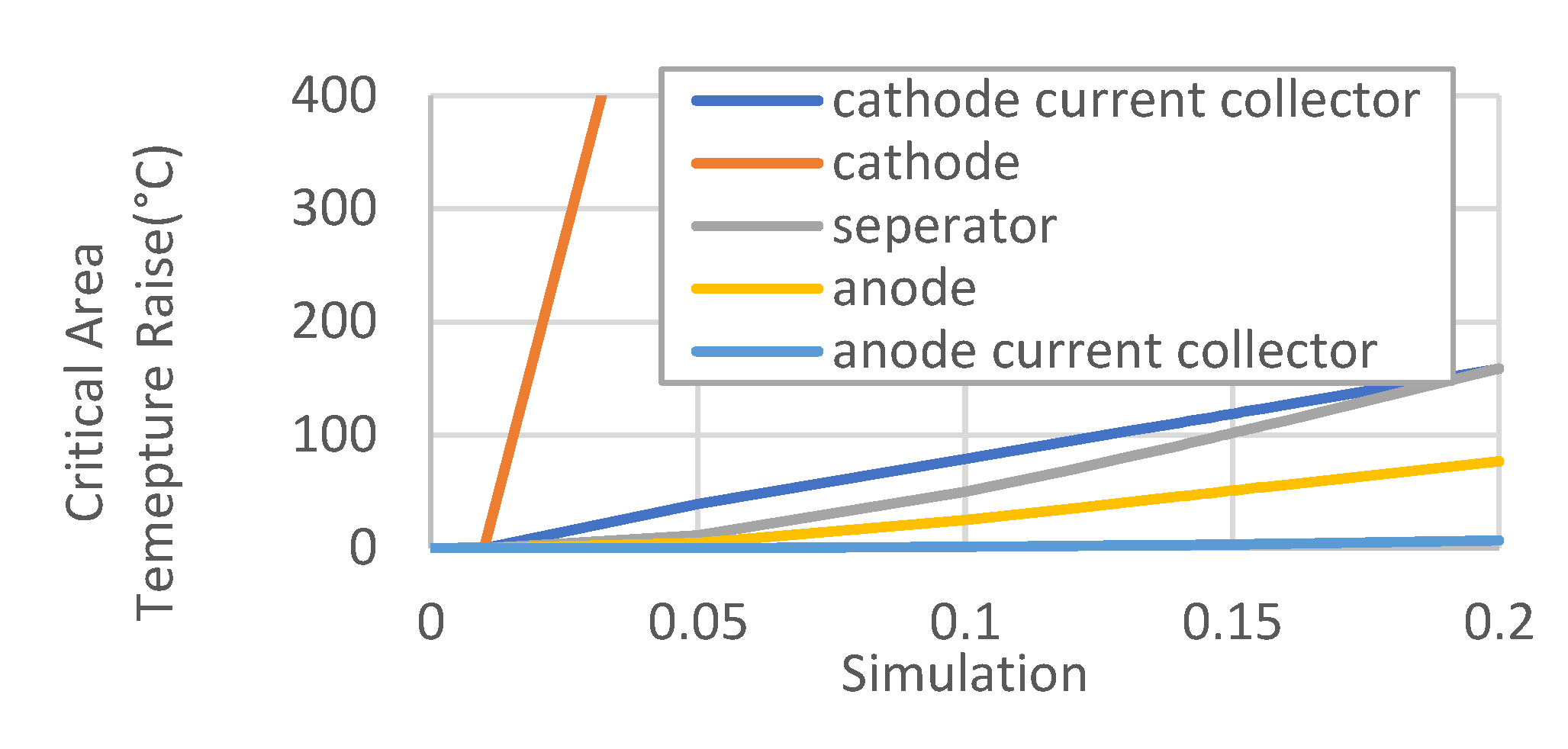
Preprints 111601 g022
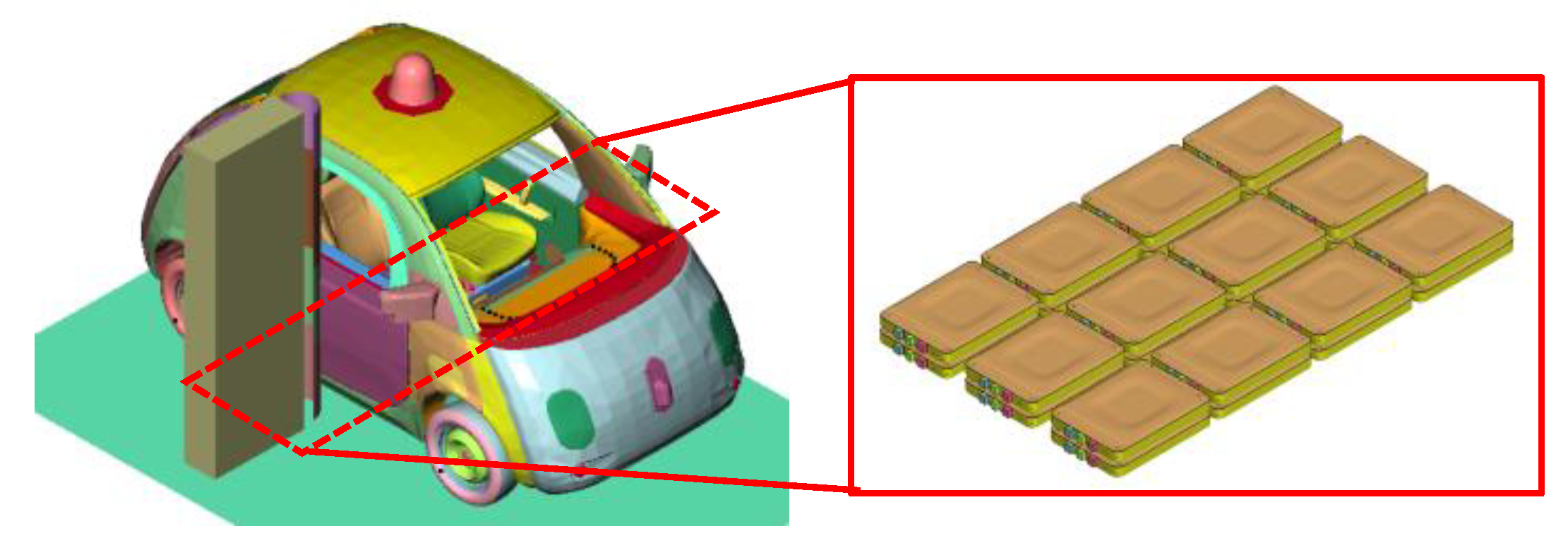
Preprints 111601 g023
Figure 23. A Generic EV model (Left) with 24 Active Cells (Right) in a Fully Coupled Electric-Thermal-Mechanical.
Figure 23. A Generic EV model (Left) with 24 Active Cells (Right) in a Fully Coupled Electric-Thermal-Mechanical.
Preprints 111601 g023
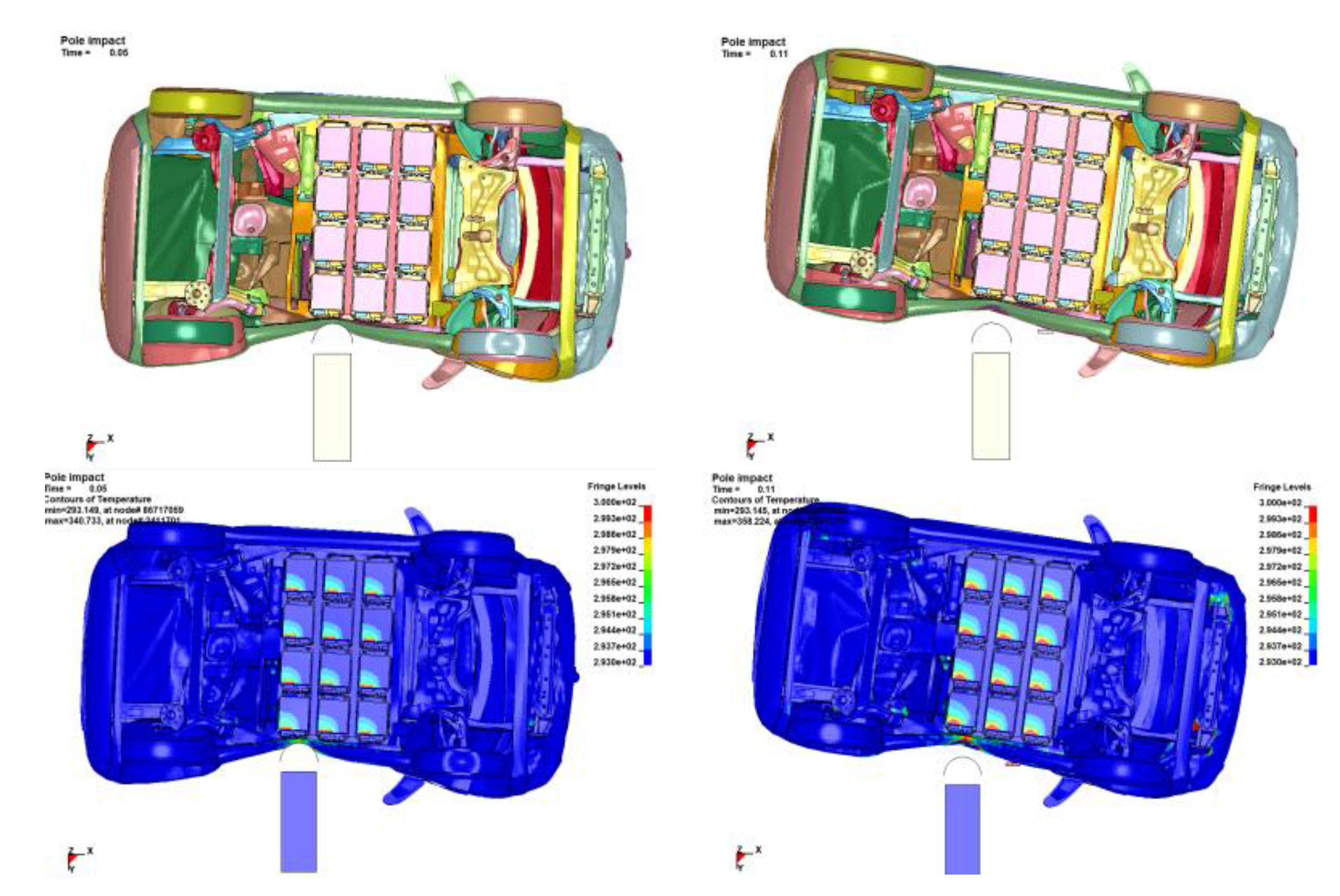
Preprints 111601 g024
Figure 24. Bottom View of EV Pole Impact at 20mph: Deformation at t=0.05s (Top Left). Deformation at t=0.12s (Top Right). Cathode Layers Temperature in Kelvin at t=0.05s (Bottom Left). Cathode Layers Temperature in Kelvin at t=0.12s (Bottom Right).
Figure 24. Bottom View of EV Pole Impact at 20mph: Deformation at t=0.05s (Top Left). Deformation at t=0.12s (Top Right). Cathode Layers Temperature in Kelvin at t=0.05s (Bottom Left). Cathode Layers Temperature in Kelvin at t=0.12s (Bottom Right).
Preprints 111601 g024
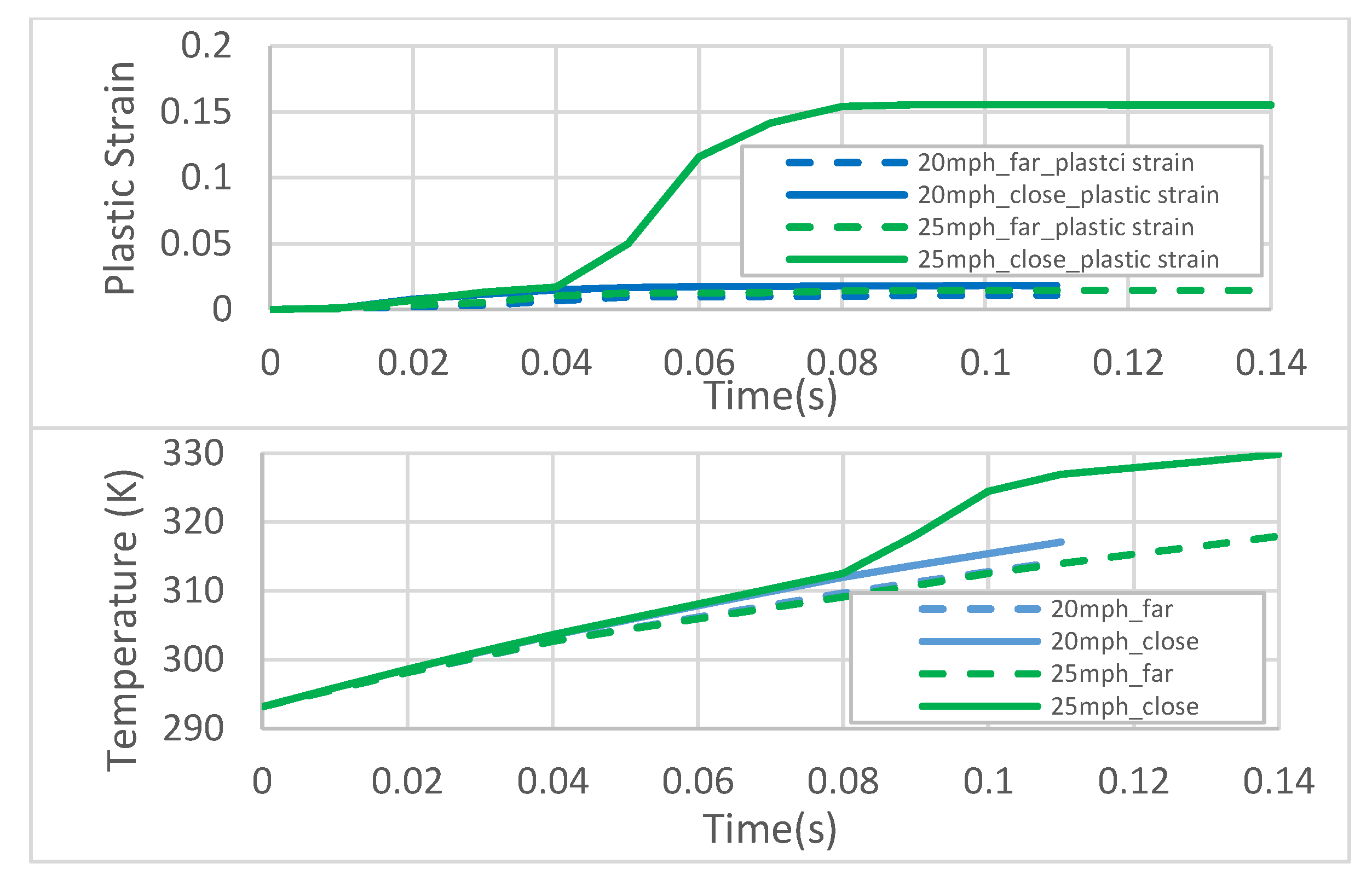
Preprints 111601 g026
Figure 26. Maximum Temperature (Left) and Maximum Plastic Strain at the Cathode Layer (Right) of EV cells under pole impact. Dash line represents the cell far away from the impact area. Solid line represents the cell close to the impact area.
Figure 26. Maximum Temperature (Left) and Maximum Plastic Strain at the Cathode Layer (Right) of EV cells under pole impact. Dash line represents the cell far away from the impact area. Solid line represents the cell close to the impact area.
Preprints 111601 g026
Preprints 111601 g027
Figure 27. Plastic Strain at Cathode Layer Indicate Permanent Damage to the Cell: Pole Impact Speed at 20mph (Left). Pole Impact Speed at 25mph (Right).
Figure 27. Plastic Strain at Cathode Layer Indicate Permanent Damage to the Cell: Pole Impact Speed at 20mph (Left). Pole Impact Speed at 25mph (Right).
Preprints 111601 g027
Preprints 111601 g028
Figure 28. Plastic Strain Contour of Cell Porch Bag at Impact Speed: 20Mph (Left); 25MPH (Middle); 30MPH(Right).
Figure 28. Plastic Strain Contour of Cell Porch Bag at Impact Speed: 20Mph (Left); 25MPH (Middle); 30MPH(Right).
Preprints 111601 g028
Preprints 111601 g029
Figure 29. Maximum Plastic Strain of Cell Porch Bag at Impact Speed: 20Mph (grey); 25MPH (orange);30MPH (blue).
Figure 29. Maximum Plastic Strain of Cell Porch Bag at Impact Speed: 20Mph (grey); 25MPH (orange);30MPH (blue).
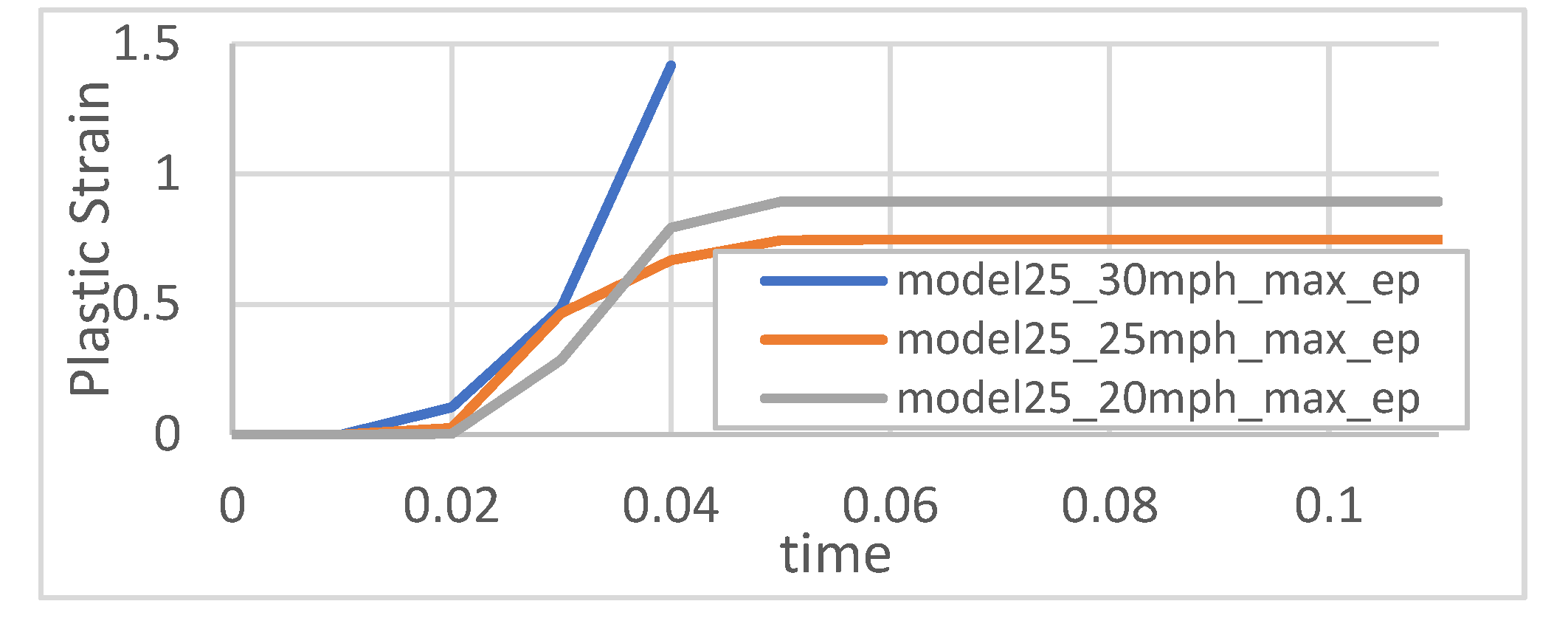
Preprints 111601 g029
Table 1. Impedance measurement of Leaf Battery Module.
Table 1. Impedance measurement of Leaf Battery Module.
AC Impedance at 1kHz DC Internal Resistant
“CHI660E” Test Data 5.61 mΩ 6.46 mΩ
“YR1035+” Test Data 4.89 mΩ N/A
Literature [62] 1.08-2.06 mΩ 2-6 mΩ
LS-DYNA simulation N/A 2.927 mΩ
Table 2. Battery Thermal Runaway Prediction for BEV Side Pole Impact with Different Impact Speed.
Table 2. Battery Thermal Runaway Prediction for BEV Side Pole Impact with Different Impact Speed.
Immediate Thermal Runaway Long Term Risk of Thermal Runaway Cell Leakage
20 Mph No No No
25 Mph No Yes No
30 Mph Yes N/A Yes
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated