Prerpints.org logo
Preprint
Article

Transitioning from Host-Pathogen Dynamics to Social Interactions: Assessing Vaccination Strategies through the IABM Model

Altmetrics

Downloads

92

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 July 2024

Posted:

09 July 2024

You are already at the latest version

Alerts
Abstract
This study presents extended Immunity Agent-Based Model (IABM) simulations to evaluate vaccination strategies in controlling the spread of infectious diseases. The application of IABM in the analysis of vaccination configurations is innovative, as a vaccinated individual can be infected depending on how their immune system acts against the invading pathogen, without a pre-established infection rate. Analysis at the microscopic level demonstrates the impact of vaccination on individual immune responses and infection outcomes, providing a more realistic representation of how the humoral response caused by vaccination affects the individual’s immune defense. At the macroscopic level, the effects of different population-wide vaccination strategies are explored, including random vaccination, targeted vaccination of specific demographic groups, and spatially focused vaccination. The results indicate that increased vaccination rates are correlated with decreased infection and mortality rates, highlighting the importance of achieving herd immunity. Furthermore, strategies focused on vulnerable populations or densely populated regions prove to be more effective in reducing disease transmission compared to randomly distributed vaccination. The results presented in this work show that vaccination strategies focused on highly crowded regions are more efficient in controlling epidemics and outbreaks. Results suggest that applying vaccination only in the densest region resulted in the suppression of infection in that region, with less intense viral spread in areas with lower population densities. Strategies focused on specific regions, in addition to being more efficient in reducing the number of infected and dead people, reduce costs related to transportation, storage, and distribution of doses compared to the random vaccination strategy. Considering that, despite scientific efforts to consolidate the use of mass vaccination, the accessibility, affordability, and acceptability of vaccines are problems that persist, investing in the study of strategies that mitigate such issues is crucial in the development and application of government policies that make immunization systems more efficient and robust.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematical and Computational Biology

1. Introduction

In century XVIII, Edward Jenner was responsible for conducting an experiment that would change society until nowadays, probably, forever. In 1796, Edward Jenner observed that people who lived with cows infected by cowpox did not get sick due to smallpox. After this observation, he inoculated a small dose of cowpox in an eight-year-old boy (James Phipps) who got sick and developed a mild form of the disease. After his recovery, Edward Jenner took a fatal dose of smallpox and introduced it to the kid. James Phipps became immune after the contact with cowpox and did not develop smallpox [1,2].
Smallpox vaccination paved the way for several other important vaccine development and application throughout history. The majority of developed vaccines work through the infusion of weakened pathogens into the organism, acting by destroying or weakening pathogens. The presence of these pathogens stimulates the immune system to produce antibodies that generate a preventive immunity response against a particular disease [3]. The last epidemiological events showed that the application of large quantities of vaccine doses requires a very efficient vaccination strategy. For instance, against Rubella, the vaccination of teenage girls in the United Kingdom from 1971 to 1988 emphasized the reduction of susceptible individuals, ensuring that the maximum amount of women who acquired previous immunity before the reproductive age. Another strategy promoted the vaccination of two-year-old boys and girls, leading to a decrease in the positive cases of Rubella [4].
More recently, the World population faced the pandemic of SARS-CoV-2, which caused profound changes in several aspects. Despite the virus’s fast spread and damage, the development of vaccines brought the hope of better days at record speed. During the COVID-19 pandemic, vaccine development and distribution have become crucial for limiting disease transmission [5]. Four months after the community spread of the virus was announced, a SARS-CoV-2 vaccine first generation was developed in silico. In July 2020, Moderna and Pfizer started large-scale phase II and III COVID-19 vaccine trials. In January 2021, just over a year after the first case of contamination by the new coronavirus, India approved the first DNA vaccine against SARS-CoV-2. In December 2022, there were 50 COVID-19 vaccine candidates approved by at least one country in the world [6]. Knowing that the world is increasingly connected and the global population growth, investing in immunization strategies is crucial. In this context, it is also essential to consider the population composition and the structure of social networks [7].
With science development, mathematical and computational models have been consolidated as efficient methods to estimate complex processes, such as infection dynamics [8,9,10] or interactions between the human immune system and a pathogen [11], for instance. One of these tools is Agent-based modeling (ABM), a powerful and very adaptable approach to exploring complex systems and reproducing the manifestations of emergent phenomena. Different empiric complex systems are studied using ABM [12,13,14], including in the development of models involving vaccination strategies. In a study using ABM and analysis of empirical data [15], authors studied scenarios with anti-vaccination (AV) movements considering contacts with medical practitioners and public vaccination campaigns, interpersonal communication, and the digital world’s influence. Another study merges genetic algorithm and ABM in a model that provides parameters for strategies of vaccination considering different population groups [16]. It is of the utmost importance to search for advanced models and techniques involving the vaccination process since challenges such as development, affordability, accessibility, and acceptability remain very current challenges [17,18].
The present work employs a recently introduced model, the IABM (Immunity Agent-Based Model) [19] to describe and analyze distinct vaccination scenarios, showing how infection curves vary in front of a vaccination process carried out before the occurrence of a new outbreak. The original IABM deals with the behavior of infection at the individual level (microscale), composed of innate and humoral immunological responses, and the social level (macroscale), which considers the community transmission of the pathogen. In this work, we add vaccinated individuals who exhibit a boost in their level of antibodies and study the dynamics between viral load, innate immune system response, and the work done by antibodies forming a microscopic dynamic within the model. Macroscopically, interpersonal interactions and epidemiological state transitions based on the SVEIR (Susceptible-Vaccinated-Exposed-Infected-Recovered) [21] model guide pathogen transmission between agents in the lattice.
The possibilities of reinfection were not considered in this study, since the reinfection rates of diseases such as COVID-19 and influenza, both diseases transmitted mainly by airways, are relatively low within a short period of time considering the circulation of the same variant of the virus [20,22,23]. We studied a type of vaccine that does not fully guarantee the individual’s immunity but reduces the chance of infection and the severity of symptoms.
The remainder of this paper is organized as follows. In Section 2, we provide a brief review of the main characteristics of the IABM. The methodology behind the model’s design is described in Section 3, while Section 4 presents the obtained results and an in-depth discussion of these findings. Finally, Section 5 encapsulates the conclusions drawn from our study.

2. The Immunity Agent-Based Model (IABM)

The Immunity Agent-Based Model (IABM), detailed in our previous publication [19], is a versatile tool for investigating airborne diseases caused by different pathogens. As in the previous work, here we study the spread of the virus, calibrating the model parameters considering COVID-19 characteristics (it is important to say that the calibration was carried out considering the original model, but the objective of this work is to provide analyses that support the definition of vaccination strategies that could be applied in immunization processes for different airborne diseases). The model stratifies the population by age, categorizing individuals into groups of 0–19, 20–49, 50–64, 65–74, 75–84, and older than 85, whose number of individuals in each range is based on the age pyramid of a real population [24], as seen in Figure 1. Additionally, 4 % [25] of the population represent the group of immunosuppressed individuals, whose innate and humoral response efficiencies are reduced in relation to an immunocompetent individual.
The model operates on two distinct levels: a microscopic level, focusing on interactions between immune system defense cells and invading pathogens, and a macroscopic level, where agents make social interactions, promoting airborne pathogen transmission. At this level, Epidemiological modeling of epidemiological state transitions is based on the SEIR (Susceptible-Exposed-Infected-Recovered) compartmental model. Our findings indicate the promising utility of the IABM, particularly in exploring vaccination scenarios. Unlike conventional models with predefined transition rates, the IABM captures the dynamic nature of transitions between epidemiological states, influenced by the intricate interplay between defense cells and pathogens. This feature results in a highly heterogeneous representation of real-world scenarios, enabling to simulate and analyze vaccination outcomes, for example.
In the IABM, the number of leukocytes [28] bases the innate response ( ψ ( t ) ) of each individual (agent) and immunocompromised individuals (individuals over 74 years of age and immunosuppressed individuals) present a reduction in the efficiency of the immune system about immunocompetent individuals. During the spread of the virus, individuals inhale a parcel of the virus particles expelled by infected individuals. After contact with the virus, the innate immune system reacts by capturing a viral particle with a scaled probability p = ( 1 − α ψ · I a g e ) · u , where u ∼ U [ a , b ] is a random variable uniformly distributed in the ranges [ a , b ] with α ψ = 4 . 5 · 10 − 3 , a = 10 − 3 and b = 6 · 10 − 2 . These probability and parameter values were defined in order to represent the senescence effect of the immune system, with its efficiency decreasing as the age ( I a g e ) of the individual increases, based on the probability of defense cells finding and destroying antigens [29].
A time τ η [30] was set a priori for each agent, and this time signals the production of antibodies beginning, triggering the humoral response. The temporal variation of antibodies is ( η ) t = ( 1 − δ η ) · ( η ) t − 1 + λ ϕ · ( ϕ ) t − 1 − λ η ( η ) t − 1 + α η ( ψ ) t − 1 . λ ϕ is the rate of antibodies production incited by the presence of the antigen in the body, forming the acute immune response. The long-last production of antibodies is made with a rate α η . The viral particle is eliminated by antibodies with a rate λ η , with the consequent antibodies amount reduction due to the opsonization process [31].

3. Methods

This section presents a resume of the methodology of designing the IABM [19] model and a description of the vaccination process modeling. We designed an Agent-Based Model (ABM) and performed extensive Monte Carlo simulations considering a square lattice with linear extension L=200 and periodic boundary conditions in both directions. Each site of the lattice has 10 m 2 of area and 2990 agents move across the lattice as random walkers or performing Lévy Flights [26]. The agents’s spatial distribution follows the Zipf law [27] and a greater statistical weight associated with the probability of displacement is assigned to sites with more occupancy, ensuring that agents are more likely to move to their vicinity if they are in sparsely occupied regions.

3.1. Modeling the Vaccination Process

The vaccination process is conducted a priori: Upon the initiation of virus transmission, a subset of individuals have already been vaccinated, thereby establishing a humoral response in these people. Vaccinated individuals start the dynamic process with a preexisting level of antibodies, whose production adheres to the circadian cycle (similar to the innate response [19]). Here, the humoral response generated by vaccination mirrors that provoked by natural infection, since the natural and vaccine-induced immunity are equivalent for the protection against SARS-CoV-2 [32].
We consider the strategies described in Table 1. In Strategy 2, we will focus on individuals who are at greater risk of dying if infected, that is, individuals over 74 years of age and immunosuppressed, constituting the group called immunocompromised. Strategies 3 and 4 deal with the spatial distribution of vaccinated individuals. Strategy 1 considers random vaccination with random distribution of doses.
The efficiency of the vaccine is linked to the capacity of antibodies to neutralize the viral particles. As previously said, the natural production of antibodies after natural infection depends on the innate response as ( η ) t → α η · ( ψ ) t − 1 . For a vaccinated individual, the induced production of antibodies is ( η ) t → α v a c · ( ψ ) t − 1 , with α v a c = α η . When a vaccinated individual becomes infected, the long-last production of antibodies is made with a rate α v a c + α η . The results presented here were obtained using α η = 1 . 0 . Notice that as α v a c is increased, the efficacy of the vaccine increases, and vice versa.

3.2. Epidemiological Modeling

Figure 2 shows a flowchart for the compartmental transitions based on the SVEIR model. The transitions are determined considering the viral load and how the organism fights the pathogen through innate and humoral immune responses. A susceptible (S) or vaccinated (V) individual becomes exposed (E) if its viral load ϕ is greater than or equal to β · ψ . If ϕ ≥ ϱ · ψ for at least 12 hours straight an exposed individual becomes infected, where β and ϱ are transition rates. The A s y m p t o m a t i c ( A x ) ↔ S y m p t o m a t i c ( S x ) transition was based on how the innate response is affected by viral activity, becoming symptomatic if ψ > Ω A S 1 or ψ < Ω A S 2 and becoming asymptomatic otherwise. Asymptomatic and Symptomatic individuals die with probability p d = exp ( − Δ / ( z · ( Φ / 2 − ψ ) ) ) or recover if its viral load ϕ is less than the threshold ϕ R . Δ is defined as the difference between viral load and innate response ( Δ = ϕ − ψ ) and z is a rescaled parameter.

4. Results and Discussion

In this section, we report and discuss the results of extended simulations of the IABM considering distinct vaccination strategies. Similar to the original work [19], the simulations start with three infected individuals with initial viral load following a normal distribution N ( μ , σ ) = N ( 80 . 0 , 1 . 0 ) . The parameters μ and σ were defined so that the dynamics begin with infected individuals whose viral load is close to their level of innate immune response.
We begin by analyzing the effects of the vaccination at the microscopic (individual) level. In Figure 3, we show the temporal variation of the innate response level ( ψ ( t ) ), viral load level ( ϕ ( t ) ), and humoral immunity level ( η ( t ) ) for three agents, to exemplify the typical behaviors observed for all recovered individuals. Figure 3(a) shows the typical variations for an unvaccinated individual that recovered after infection. Notice that the viral load of this individual reaches an impressive higher level when compared with a vaccinated individual (Figure 3(c)), leading this individual to present symptoms during the active phase of the disease (due to the increase in the innate immunity response, the cytokine storm [33]). In the second panel (Figure 3(b)), a vaccinated individual became sick after contact with the virus. It is observed a float down in the innate response in the acute phase of the infection, with a rise and fall dynamic between viral load and humoral immunity levels. After recovery, the individual presented a reinforced humoral response, as observed in some real cases of people infected with SARS-CoV-2 [34]. It is shown in Figure 3(c) a typical behavior of a vaccinated individual that, even after having contact with the virus, the vaccine-induced immunity is enough to prevent the individual from getting sick, destroying the viral particle and keep the individual uninfected. In this case, the presence of the virus was eradicated before the minimal impact on their organism due to viral activity, with no reinforcement of the humoral immunity due to natural infection.
Now, we turn our attention to the macroscopic (population) level. In this first analysis, we consider that a fraction of the population is vaccinated at random, regardless of its spatial location, age, or immunological capabilities. Our results are detailed in Figure 4. As expected, the number of infected individuals decreases when the fraction of vaccinated increases, resulting in a minor death rate, as shown in Figure 4(a-c). In particular, for the vaccine efficiency used, the number of dead individuals vanishes for vaccination rates above 70%. This is a consequence of the herd immunity effect, as can be seen from the data in Figure 4(d) where we observe an exponential reduction of infection of unvaccinated individuals while the number of vaccinated individuals increases. With 70% of the total individuals vaccinated, less than 2% of the unvaccinated group became infected, highlighting the indirect protection due to the vaccinated individuals in the lattice.
Until this point, we considered that vaccines are available to all individuals. However, for a new emerging disease, there may not exist a large number of doses available at hand due to the developing and manufacturing time and/or costs. In such cases, when only a small fraction of the population will be inoculated, an important question that arises is: which strategies, taking into account the heterogeneity of the population, will be more successful in reducing the number of infected and deaths? In the next subsection, we will apply the IABM to investigate three additional strategies.
The results obtained from the Strategy 2 are shown in Figure 5. Panel Figure 5(a) presents the difference between a scenario without vaccination and a scenario considering the vaccination of 100% of immunocompromised (Strategy 2). Without vaccination, 29 . 6 % of immunocompromised become infected, with the death of 0 . 59 % of the same group. Vaccinating 100 % of these individuals, the percentage of infected drops drastically to 0 . 18 % without deaths in this group. Now, considering the application of the same number of doses in each strategy, we show the time evolution of the fraction of infected individuals (Figure 5(b)) considering strategies 1 and 2. We observe that Strategy 2 is more efficient in reducing the number of infected and dead individuals. Looking in detail, we note that Strategy 2 reduced the number of infected people by 18 . 3 % and the number of deaths by 15 . 6 % compared to Strategy 1.
In Strategy 2, all immunocompromised individuals were vaccinated. Distributing and applying this same amount of doses randomly among individuals in the lattice (Strategy 1), 24.6% of immunocompromised people were infected, while the mortality rate was 0.5%. Thus, when we analyzed individuals in this group in a scenario in which doses were randomly distributed across the lattice, Strategy 2 showed a 99.3% reduction in the number of infected individuals and a 100% reduction in deaths compared to Strategy 1.
Now, we turn to the effects of the strategies that rely on the spatial distribution of the population. Figure 6((a-c)) illustrate how the vaccines were distributed: In Strategy 1, the doses were equally distributed across the lattice, whereas in Strategy 3, the doses were distributed only in the two denser sub-regions, and in Strategy 4, they are distributed solely in the denser sub-region. The snapshot in Figure 6((d-f)) depicts heatmaps with the sum of infected, dead, and recovered individuals as well as their spatial distribution 20 weeks after the start of viral spread. Comparing the three strategies, we can notice that Strategy 1 was a less effective strategy, with a higher concentration of infected individuals in the densest sub-region and with viruses reaching more regions of the lattice. The number of infected considering Strategy 3 and 4 is lower than in the first case, with the majority of cases concentrated in the second densest sub-region of the lattice when the doses are distributed only in the denser sub-region (Strategy 3). Strategy 4 emerges as the strategy for best controlling viral spread.
Comparing Strategies 1 and 3 ( Figure 7(a)), the process focusing on the vaccination of individuals initially located in the denser sub-region of the lattice (Strategy 3) reduced the number of infected in 8 % and the number of deaths in 11 % about Strategy 1. As shown in Figure 7(b), Strategy 4, focused on the individuals initially located in the two denser sub-regions of the lattice, reduced the number of infected in 27 . 8 % and the number of deaths in 33 . 3 % about Strategy 1. It shows us that vaccination strategies focused on denser regions are more effective than the random distribution (as proposed in Strategy 1). Furthermore, it is important to vaccinate individuals encountered in the denser sub-regions and also consider the neighboring sub-regions to obtain even more efficient results. Comparing Strategies 3 and 4, Strategy 4 reduced the number of infected and dead by 50% compared to Strategy 3, as seen in Figure 7(c) .
Let’s now delve deeper into the impact of vaccination on unvaccinated individuals as vaccination rates increase considering the spatial strategies. Figure 1 illustrates the exponential decrease in the percentage of unvaccinated infected individuals with the implementation of Strategies 3 and 4. The insets demonstrate a notable reduction in the number of immunocompromised individuals infected when these strategies are employed. Examining the distribution of doses in each strategy (numbers highlighted in the main graphs), it becomes clear that focusing vaccination efforts solely in the most densely populated region yields infection rates comparable to those observed in Strategy 4, particularly when doses are limited. This underscores the effectiveness of prioritizing vaccine distribution and administration in densely populated regions, especially in areas with constrained vaccine availability.
Although Strategies 3 and 4 proved to be more efficient in reducing the number of infected and dead individuals, random vaccination (Strategy 1) is also valuable. It also significantly decreased the number of infected individuals compared to a scenario without vaccines. Furthermore, we reinforce that adopting strategies focused on specific regions can reduce logistical costs and mitigate limitations related to the accessibility, affordability, and acceptability of vaccines, especially in scenarios of low vaccine availability (as occurred with COVID-19, for example).

5. Conclusions

We live in an increasingly interconnected society, where interpersonal interactions and our involvement with nature intensify every day. The increase in these interactions could bring humans into contact with previously unknown pathogens. This fierce social activity causes these same pathogens to evolve and acquire different characteristics, thanks to a process called biological pressure. In this sense, society must continue to develop technologies and innovations, developing and improving defense strategies against the actions of these microorganisms.
We saw that the application of the IABM model to study vaccination strategies allows us to analyze scenarios in which a previously vaccinated individual still has a chance of being infected, depending on the conditions imposed on them, as can be seen in Figure 3. The methods used in this model are unprecedented, as a vaccinated individual can become infected depending on the dynamics between their immune system and the invading pathogen. The robustness of the model and its credibility are clear in Figure 4, a scenario where different vaccination percentages are applied. We observed that by increasing the number of inoculated doses, the number of infected and dead people decreases drastically, with no viral spread when at least 70 % of the population is previously vaccinated. The Panel shown in Figure 4(d) shows the effect of herd immunity, with an exponential reduction in the number of unvaccinated infected people in relation to the increase in the vaccination rate, due to the indirect protection generated by those who receive the vaccine.
In order to analyze strategies considering an insufficient number of vaccines for the entire population, we carried out extensive simulations considering four vaccination strategies, as described in Table 1. Considering vaccination of immunocompromised people, we observed a drastic reduction in infection and mortality rates in this group, with a decrease of 18 . 3 % in the number of infected people and 15 . 6 % in the number of deaths over Strategy 1, that a random vaccination process applies to the general population, as seen in Figure 5.
Strategies targeting spatial disparities were also analyzed, comprising Strategies 3 and 4, whose dose distribution is illustrated in panels Figure 6(b,c). Observing the Figure 6(d–f), we see that strategies focused on denser regions are more efficient, generating less viral spread and, consequently, fewer infected and dead people. Drawing a parallel between Strategies 3 and 4 and comparing them with Strategy 1, as seen in Figure 7, we see that a vaccination strategy that includes the densest region and its neighborhood (Strategy 4) is more efficient than a strategy that focuses only on the densest region (Strategy 3), reducing the number of infected by 27 . 8 % and the number of deaths by 33 . 3 % , compared to a reduction of 8 % in the number of infected people and 11 % in deaths over Strategy 1. In a scenario considering a greater quantity of doses available, Strategy 4 reduced the number of infected and dead people by 50% when compared to Strategy 3. In another aspect, when the number of available doses is smaller, we observe in Figure 1 that the number of unvaccinated infected people and the infection rate of immunocompromised people are very close in both strategies, corroborating that, in a scenario of scarce doses, the most efficient strategy should focus on sub-regions with larger agglomerations. In addition to reducing the percentage of infected people observed in vaccination strategies focused on specific sub-regions, these strategies are also beneficial when considering logistical costs, storage and transportation of doses, and limitations related to the accessibility, affordability, and acceptability of vaccines.
Defining increasingly efficient public policies is extremely necessary. In an interconnected society, with complex challenges and the imminent occurrence of new outbreaks, epidemics, and pandemics, it is mandatory to invest in the development of robust models and techniques that provide knowledge and methods that make human life safer, to reduce deaths, economic costs, and losses expenses associated with logistics, and ensuring the survival of our society in the face of an active process of disease spread. In a more specific context, we must develop solid and efficient vaccination strategies, taking into account the indirect protection of those who, for some reason, cannot be vaccinated.

Author Contributions

Conceptualization, M.N. Gonzaga and A.P.F. Atman and M.M. de Oliveira; methodology, M.N. Gonzaga and A.P.F. Atman and M.M. de Oliveira; software, M.N. Gonzaga; validation, M.N. Gonzaga and A.P.F. Atman and M.M. de Oliveira.; formal analysis, M.N. Gonzaga and M.M. de Oliveira; investigation, M.N. Gonzaga and A.P.F. Atman and M.M. de Oliveira; resources, M.N. Gonzaga and A.P.F. Atman and M.M. de Oliveira; writing—original draft preparation, M.N. Gonzaga and A.P.F. Atman and M.M. de Oliveira; writing—review and editing, M.N. Gonzaga and A.P.F. Atman and M.M. de Oliveira; visualization, M.N. Gonzaga and A.P.F. Atman and M.M. de Oliveira; supervision, A.P.F. Atman and M.M. de Oliveira; project administration, A.P.F. Atman and M.M. de Oliveira. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Centro Federal de Educação Tecnológica de Minas Gerais, Brazil; and the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior, Brazil [grant number 001].

Data Availability Statement

No data was used for the research described in the article.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
ABM Agent-based Model
IABM Immunity Agent-Based Model
Ax Asymptomatic
Sx Symptomatic
SEIR Susceptible-Exposed-Infected-Recovered
SVEIR Susceptible-Vaccinated-Exposed-Infected-Recovered

References

  1. Jenner, E. On the Origin of the Vaccine Inoculation. Med Phys J. 1801, 06, 505–508.
  2. Boylston A. The origins of vaccination: myths and reality. Journal of the Royal Society of Medicine 2013, 351–354.
  3. Osamor V. C., Ikeakanam E., Bishung J. U. and et al. COVID-19 Vaccines: Computational tools and Development. Informatics in Medicine Unlocked 2023.
  4. Fine, P. E. Herd immunity: history, theory, practice. Epidemiol Rev. 1993, 265–302.
  5. Mohammed I., Nauman A., Paul P. and et al. The efficacy and effectiveness of the COVID-19 vaccines in reducing infection, severity, hospitalization, and mortality: a systematic review. Hum Vaccin Immunother. 2022.
  6. Chakraborty C., Bhattacharya M. and Dhama K. SARS-CoV-2 Vaccines, Vaccine Development Technologies, and Significant Efforts in Vaccine Development during the Pandemic: The Lessons Learned Might Help to Fight against the Next Pandemic. Vaccines. 2023, 1–19.
  7. Xue J.,Terano T., Deguchi H., Ichikawa M. Simulation analysis of immunization policy diffusion in social network with ABM approach. 2016 International Conference on Behavioral, Economic and Socio-cultural Computing (BESC). 2016.
  8. Béraud B. Mathematical models and vaccination strategies. Vaccine. 2018, 5366-5372.
  9. Wang, Z. and et al. Statistical physics of vaccination. Phys. Reports. 2016, 1–113.
  10. Jia F., Gu Z. and Yang L. Dynamic Analysis of an Epidemic Model Considering Personal Alert on a Complex Network. Entropy. 2024.
  11. Munteanu F. A Local Analysis of a Mathematical Pattern for Interactions between the Human Immune System and a Pathogenic Agent. Entropy. 2023.
  12. Kaszowska-Mojsa J., Włodarczyk P. and Szymańska A. Immunity in the ABM-DSGE Framework for Preventing and Controlling Epidemics—Validation of Results. Entropy. 2022.
  13. Zhou R.,Xiong X., Llacay B., and et al. Market Impact Analysis of Financial Literacy among A-Share Market Investors: An Agent-Based Model. Entropy. 2023.
  14. Schunck F., Wiedermann M., Heitzig J. and et al. A Dynamic Network Model of Societal Complexity and Resilience Inspired by Tainter’s Theory of Collapse. Entropy. 2024.
  15. Sobkowicz P. and Sobkowicz A. Agent Based Model of Anti-Vaccination Movements: Simulations and Comparison with Empirical Data. Vaccines. 2021.
  16. Sulis E. and Terna P. An Agent-based Decision Support for a Vaccination Campaign. Journal of Medical Systems. 2021, 1–7.
  17. Fine P. E. M. Herd Immunity: History, Theory, Practice. Epidemiologic Reviews. 1993, 1–38.
  18. Yarlagadda H. , Patel M. A. , Gupta V. and et al. COVID-19 Vaccine Challenges in Developing and Developed Countries. Cureus. 2022.
  19. Gonzaga, M. N., de Oliveira M. M. and Atman A. P. F. Immunity Agent-Based Model (IABM) for epidemiological systems. Chaos Solitons & Fractals. 2023, 1–10.
  20. Chen Y., Zhu W., Han X., et al. How does the SARS-CoV-2 reinfection rate change over time? The global evidence from systematic review and meta-analysis, 2024. BMC Infectious Diseases. 2024.
  21. Hajji M., Albargi A. H. A mathematical investigation of an "SVEIR" epidemic model for the measles transmission. Mathematical Biosciences and Engineering. 2024. 2853–2875.
  22. Tavakoli A., Lotfi F., Lotfi M., et al. COVID-19 Reinfection Rate and Related Risk Factors in Fars Province, Iran: A Retrospective Cohort Study, 2023. Iran J Med Sci. 2023. 302–312.
  23. Matthes K. L., Vu M. L., Bhattacharyya U., et al. Reinfections and Cross-Protection in the 1918/19 Influenza Pandemic: Revisiting a Survey Among Male and Female Factory Workers, 2023. International Journal of Public Health. 2023.
  24. Distribuição da população por sexo, segundo os grupos de idade (São Paulo - 2010). Available online: https://www.ibge.gov.br/censo2010/apps/sinopse/webservice/frm_piramide.php?codigo=35 (accessed on 02 02 2024).
  25. Harpaz R., Dahl R. M., Dooling K. L. Prevalence of Immunosuppression Among US Adults, 2013. JAMA. 2013. 2547–-2548.
  26. Baronchelli A. and Radicchi F. Lévy flights in human behavior and cognition. Chaos, Solitons & Fractals. 2013, 101–105.
  27. Zipf, G. K. Human behavior and the principle of least effort. Journal of Clinical Psychology. 1950.
  28. Haus E. and Smolensky M. H. Biologic rhythms in the immune system. Chronobiol Int. 1999, 581–622.
  29. Castiglione F., Deb D., Srivastava P.A., Liò P., Liso A. From Infection to Immunity: Understanding the Response to SARS-CoV2 Through In-Silico Modeling. Frontiers in Immunology. 2021.
  30. Khaire, N. S., Jindal N., Yaddanapudi L. N. and et al. Use of convalescent plasma for COVID-19 in India: A review & practical guidelines. Indian Journal of Medical Research. 2021, 64–85.
  31. Thau L., Asuka E. and Mahajan K. Physiology, Opsonization. StatPearls Publishing. 2022.
  32. Franchi M., Pellegrini G., Cereda D. and et al. Natural and vaccine-induced immunity are equivalent for the protection against SARS-CoV-2 infection. Journal of Infection and Public Health. 2023, 1137–1141.
  33. Castelli V., Cimini A. and Ferri C. Cytokine storm in COVID-19: “when you come out of the storm, you won’t be the same person who walked in”. Front Immunol. 2020.
  34. Bates T. A., McBride S. K., Leier H. C. and et al. Vaccination before or after SARS-CoV-2 infection leads to robust humoral response and antibodies that effectively neutralize variants. Science Immunology. 2022.
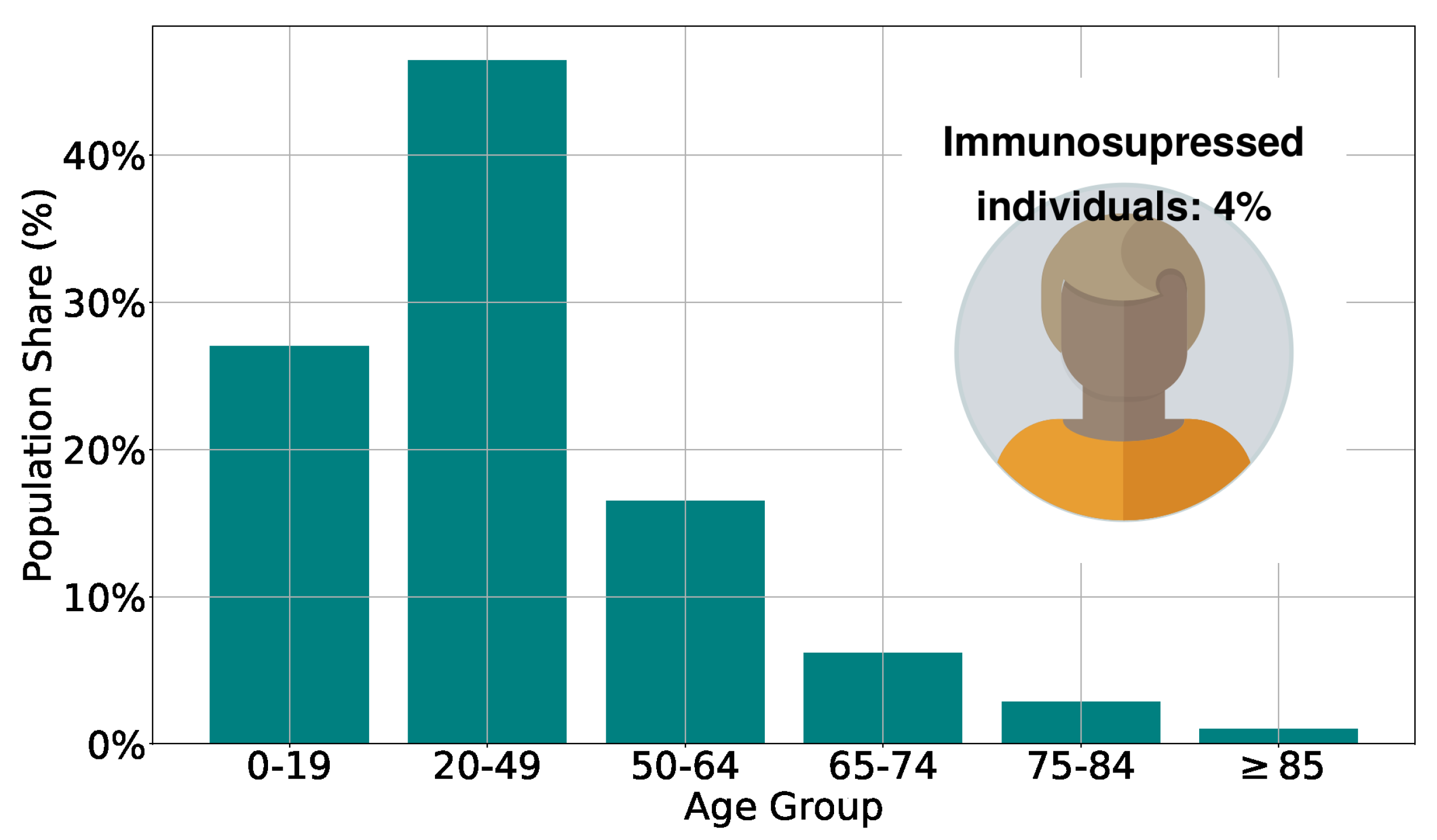
Preprints 111598 g001
Figure 1. Population age structure adopted in the model, based on an empiric population [24]. Immunosuppressed individuals represent 4 % [25] of the total population.
Figure 1. Population age structure adopted in the model, based on an empiric population [24]. Immunosuppressed individuals represent 4 % [25] of the total population.
Preprints 111598 g001
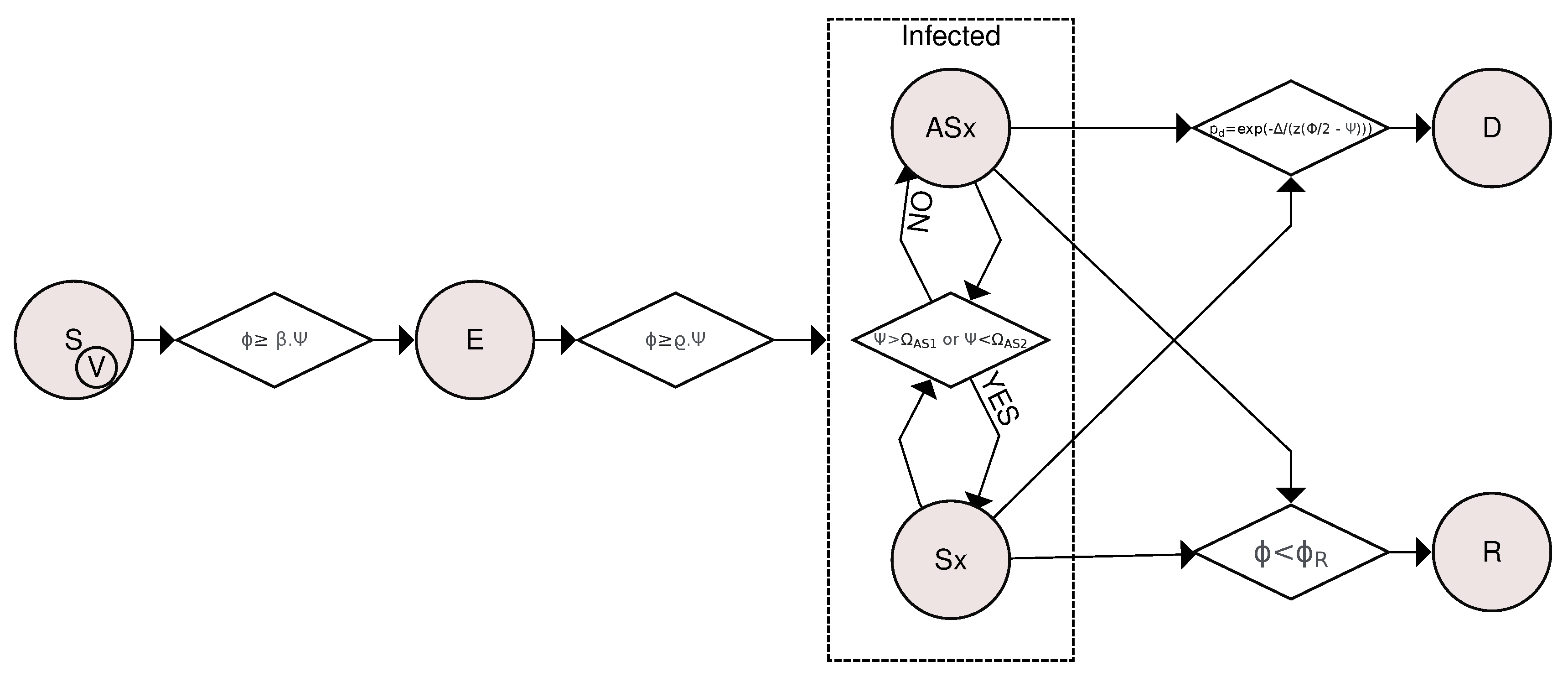
Preprints 111598 g002
Figure 2. Flowchart of compartmental transitions based on the SVEIR (Susceptible-Vaccinated-Exposed-Infected-Recovered) model. Transitions are determined by considering the viral load and how the organism fights the pathogen through innate and humoral immune responses. A susceptible or vaccinated individual is exposed if their viral load ϕ is greater than or equal to β · ψ , where β is a rate and ψ is the level of the individual’s innate response. If ϕ ≥ ϱ · ψ for at least 12 hours straight, an exposed individual becomes infected. The Asymptomatic⟷Symptomatic transition was based on how the innate response is affected by viral activity, becoming symptomatic if the immune response is exacerbated ( ψ > Ω A S 1 ) or if the immune system is weakened ( ψ < Ω A S 2 ). Otherwise, the individual is considered asymptomatic. Asymptomatic and symptomatic individuals are likely to die p d = exp ( − Δ / ( z · ( Φ / 2 − ψ ) ) ) or recover if their viral load ϕ is less than ϕ R .
Figure 2. Flowchart of compartmental transitions based on the SVEIR (Susceptible-Vaccinated-Exposed-Infected-Recovered) model. Transitions are determined by considering the viral load and how the organism fights the pathogen through innate and humoral immune responses. A susceptible or vaccinated individual is exposed if their viral load ϕ is greater than or equal to β · ψ , where β is a rate and ψ is the level of the individual’s innate response. If ϕ ≥ ϱ · ψ for at least 12 hours straight, an exposed individual becomes infected. The Asymptomatic⟷Symptomatic transition was based on how the innate response is affected by viral activity, becoming symptomatic if the immune response is exacerbated ( ψ > Ω A S 1 ) or if the immune system is weakened ( ψ < Ω A S 2 ). Otherwise, the individual is considered asymptomatic. Asymptomatic and symptomatic individuals are likely to die p d = exp ( − Δ / ( z · ( Φ / 2 − ψ ) ) ) or recover if their viral load ϕ is less than ϕ R .
Preprints 111598 g002
Preprints 111598 g003
Figure 3. Typical variation of Innate Response ( ψ ( t ) ), Viral Load ( ϕ ( t ) ) and Humoral Response ( η ( t ) ) for three distinct situations: (a) is an unvaccinated individual that recovered after infection, (b) is a vaccinated individual that got sick and recovered and (c) a vaccinated individual that not got sick. We see that, in (a), an unvaccinated individual can reach much higher viral load levels when compared to a vaccinated individual, leading to the appearance of symptoms. We observe in (b) a float down in the innate response in the acute phase of the infection, with a rise and fall dynamic between the viral load and the levels of humoral immunity of the vaccinated individual who ends up being infected by the virus. After recovery, the individual presented a reinforced humoral response, as observed in some real cases of people infected with SARS-CoV-2 [34]. In (c), we see the typical behavior of a vaccinated individual who, even after having contact with the virus, the immunity induced by the vaccine is sufficient to prevent him from becoming sick, destroying the viral particles and keeping the individual uninfected.
Figure 3. Typical variation of Innate Response ( ψ ( t ) ), Viral Load ( ϕ ( t ) ) and Humoral Response ( η ( t ) ) for three distinct situations: (a) is an unvaccinated individual that recovered after infection, (b) is a vaccinated individual that got sick and recovered and (c) a vaccinated individual that not got sick. We see that, in (a), an unvaccinated individual can reach much higher viral load levels when compared to a vaccinated individual, leading to the appearance of symptoms. We observe in (b) a float down in the innate response in the acute phase of the infection, with a rise and fall dynamic between the viral load and the levels of humoral immunity of the vaccinated individual who ends up being infected by the virus. After recovery, the individual presented a reinforced humoral response, as observed in some real cases of people infected with SARS-CoV-2 [34]. In (c), we see the typical behavior of a vaccinated individual who, even after having contact with the virus, the immunity induced by the vaccine is sufficient to prevent him from becoming sick, destroying the viral particles and keeping the individual uninfected.
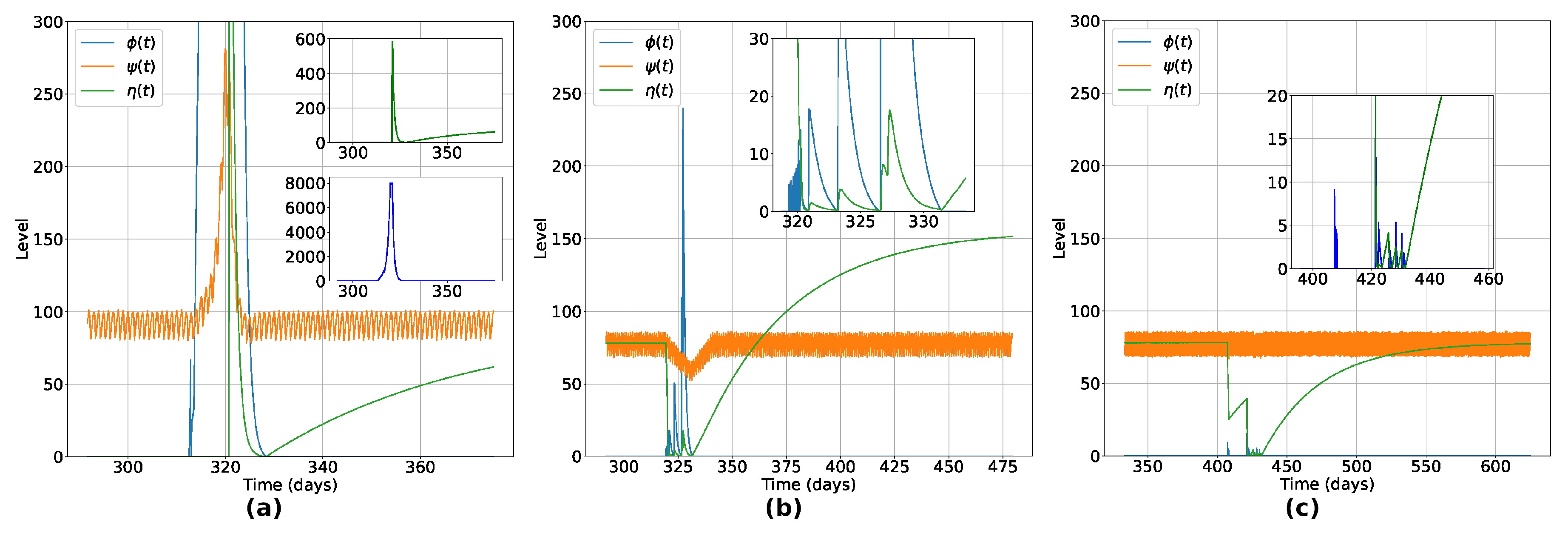
Preprints 111598 g003
Preprints 111598 g004
Figure 4. Percentage of infected ((a)), recovered ((b)) and dead ((c)) individuals considering Strategy 1. Panel (d) shows the variation in the percentage of unvaccinated individuals who become infected in relation to the increase in the number of vaccinated individuals. The number of doses is highlighted at each point of the graph. (a), (b) and (c) certify that the vaccination process inserting a non-zero level of humoral immunity induces the reduction of infected and dead individuals, vanishing the outbreak with rates of vaccination greater than 70%. Panel (d) shows the herd immunity effect, with exponential reduction of infection of unvaccinated individuals while the number of vaccinated individuals increases. In particular, for the vaccine efficiency used, with 70% of the total individuals vaccinated, less than 2% of the unvaccinated group became infected, highlighting the indirect protection due to the vaccinated individuals in the lattice.
Figure 4. Percentage of infected ((a)), recovered ((b)) and dead ((c)) individuals considering Strategy 1. Panel (d) shows the variation in the percentage of unvaccinated individuals who become infected in relation to the increase in the number of vaccinated individuals. The number of doses is highlighted at each point of the graph. (a), (b) and (c) certify that the vaccination process inserting a non-zero level of humoral immunity induces the reduction of infected and dead individuals, vanishing the outbreak with rates of vaccination greater than 70%. Panel (d) shows the herd immunity effect, with exponential reduction of infection of unvaccinated individuals while the number of vaccinated individuals increases. In particular, for the vaccine efficiency used, with 70% of the total individuals vaccinated, less than 2% of the unvaccinated group became infected, highlighting the indirect protection due to the vaccinated individuals in the lattice.
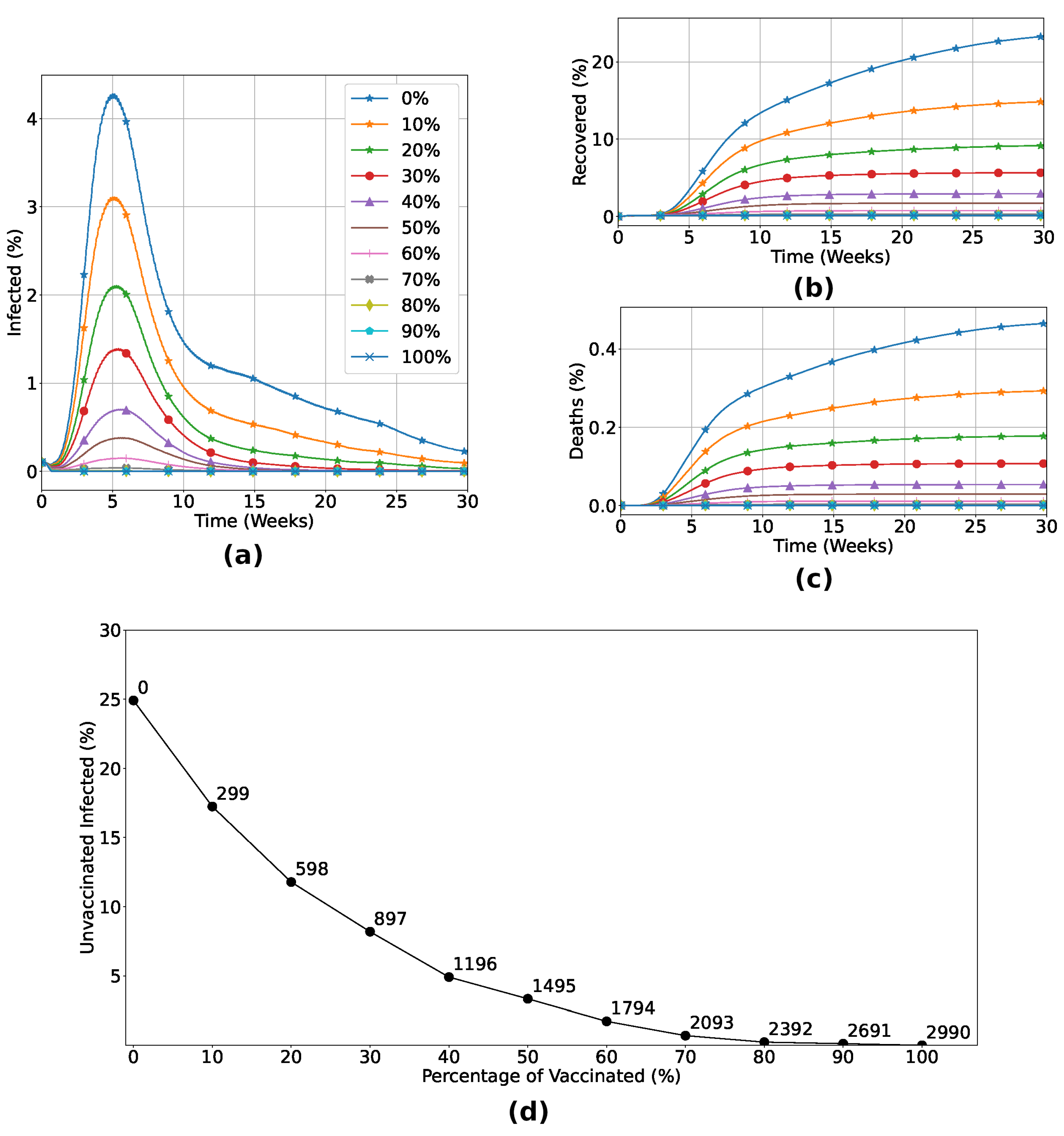
Preprints 111598 g004
Preprints 111598 g005
Figure 5. The bar chart shown in (a) presents the difference between a scenario without vaccination and a scenario considering the vaccination of 100% of immunocompromised individuals (Strategy 2). Without vaccination, 29 . 6 % of the immunocompromised became infected, with the death of 0 . 59 % of the same group. Vaccinating 100 % of these individuals, the percentage of infected drops drastically to 0 . 18 % without deaths in this group. Considering the application of the same number of doses, the curves of infected ((b)) considering Strategies 1 and 2 show that Strategy 2, focused on the immunocompromised individuals, was more efficient in reducing the number of infected and dead. Observing the inset, we notice that Strategy 2 reduced the number of infected in 18 . 3 % and the number of dead in 15 . 6 % about Strategy 1.
Figure 5. The bar chart shown in (a) presents the difference between a scenario without vaccination and a scenario considering the vaccination of 100% of immunocompromised individuals (Strategy 2). Without vaccination, 29 . 6 % of the immunocompromised became infected, with the death of 0 . 59 % of the same group. Vaccinating 100 % of these individuals, the percentage of infected drops drastically to 0 . 18 % without deaths in this group. Considering the application of the same number of doses, the curves of infected ((b)) considering Strategies 1 and 2 show that Strategy 2, focused on the immunocompromised individuals, was more efficient in reducing the number of infected and dead. Observing the inset, we notice that Strategy 2 reduced the number of infected in 18 . 3 % and the number of dead in 15 . 6 % about Strategy 1.
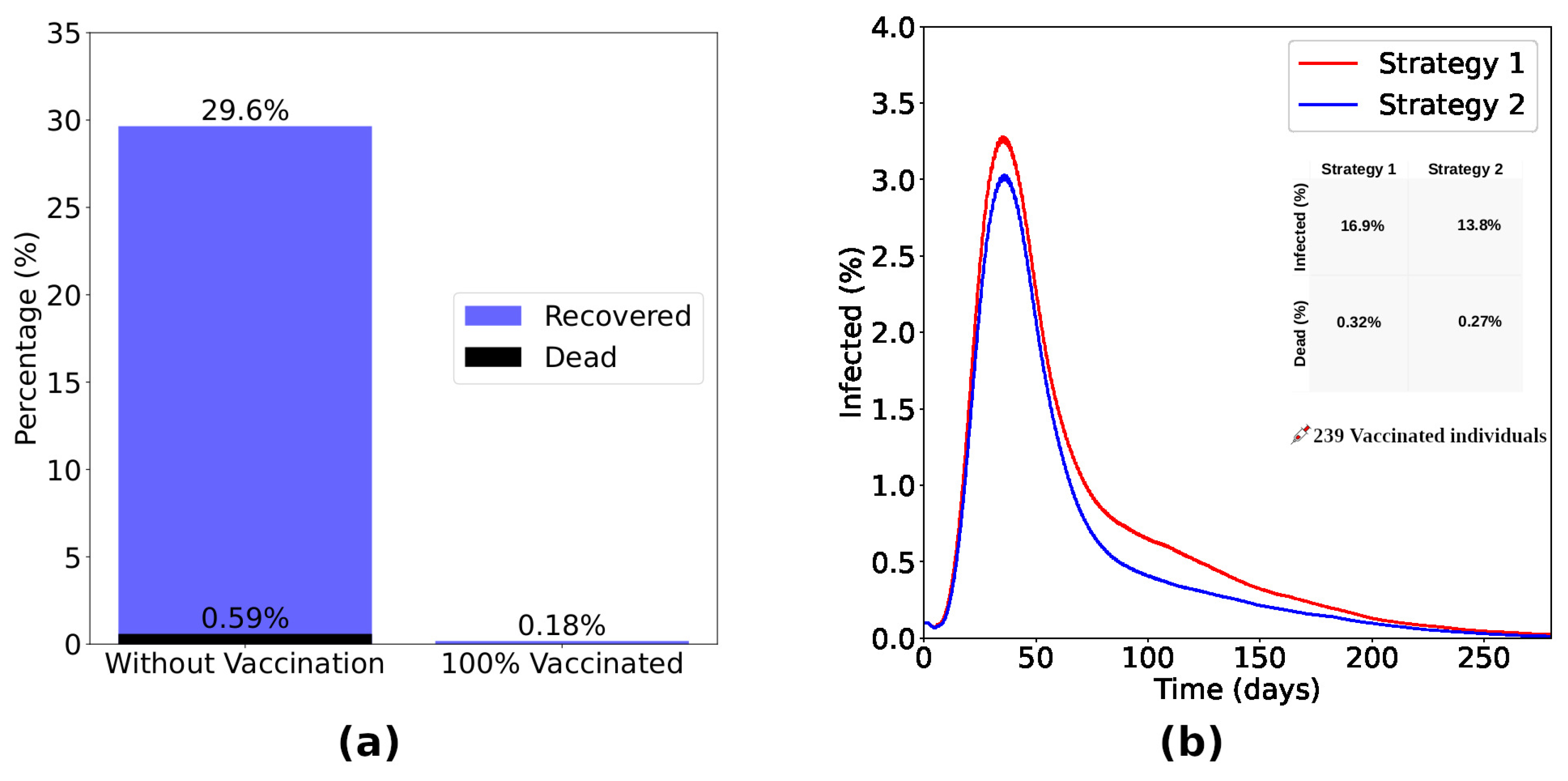
Preprints 111598 g005
Preprints 111598 g006
Figure 6. Panels ((a)-(c)) show the initial position of agents, differentiating vaccinated (blue points) from unvaccinated (gray points) individuals. The same amount of doses were applied in the three cases. Panels ((d)-(f)) present heatmaps with the position of each infected and the concentration of infected individuals per site 20 weeks after the viral spread has started, constructed by taking the average of 300 experiments. Comparing the three strategies, we can notice that Strategy 1 was less effective, with a higher concentration of infected individuals in the densest sub-region and the virus reaching further. The number of infected considering Strategy 3 and 4 is lower than in the first case, with the majority of cases concentrated in the second densest sub-region of the lattice when the doses are distributed only in the denser sub-region ((e)) and more effective control of viral spread in Strategy 4 ((f)). Rate of vaccination: 10%.
Figure 6. Panels ((a)-(c)) show the initial position of agents, differentiating vaccinated (blue points) from unvaccinated (gray points) individuals. The same amount of doses were applied in the three cases. Panels ((d)-(f)) present heatmaps with the position of each infected and the concentration of infected individuals per site 20 weeks after the viral spread has started, constructed by taking the average of 300 experiments. Comparing the three strategies, we can notice that Strategy 1 was less effective, with a higher concentration of infected individuals in the densest sub-region and the virus reaching further. The number of infected considering Strategy 3 and 4 is lower than in the first case, with the majority of cases concentrated in the second densest sub-region of the lattice when the doses are distributed only in the denser sub-region ((e)) and more effective control of viral spread in Strategy 4 ((f)). Rate of vaccination: 10%.
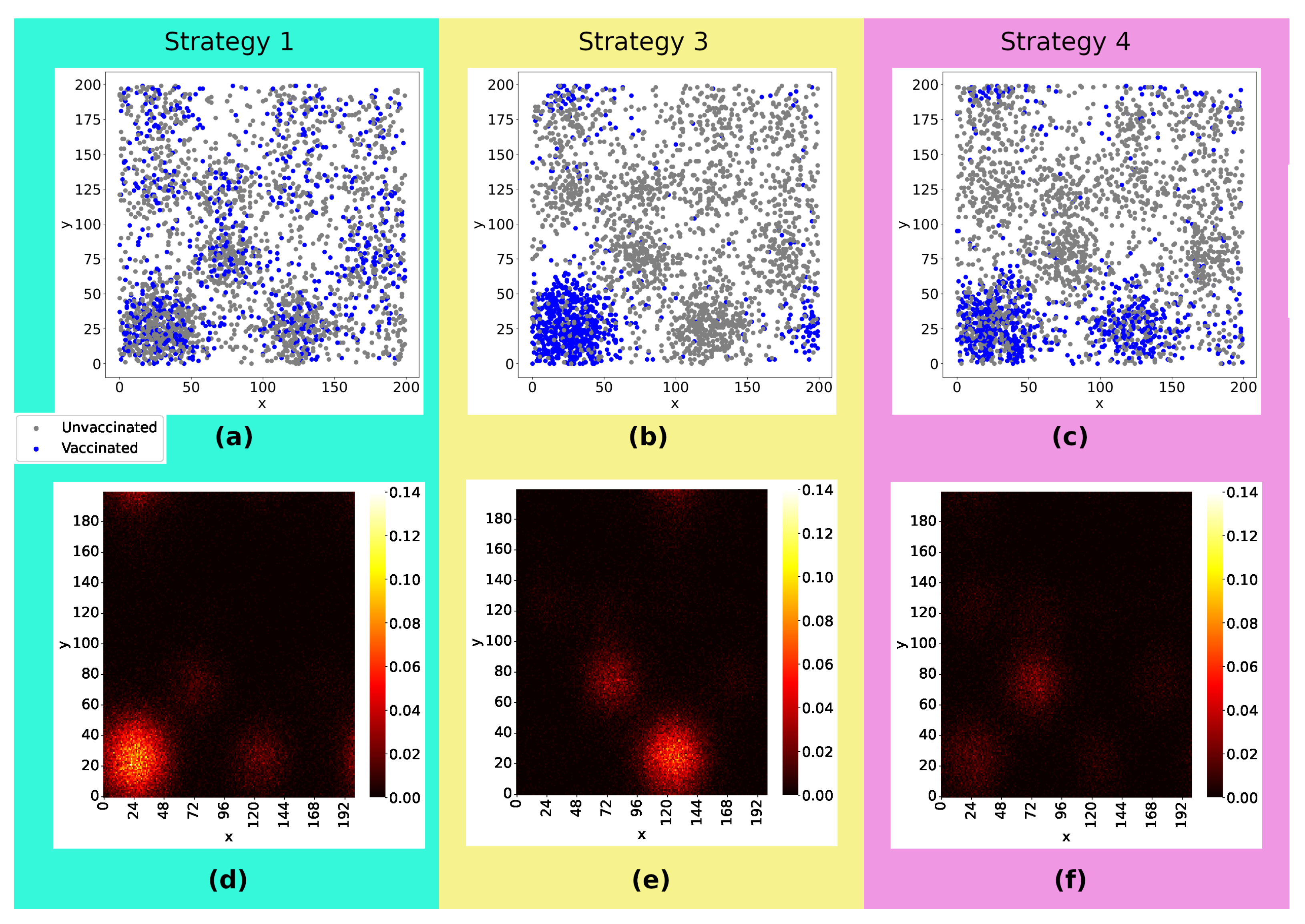
Preprints 111598 g006
Preprints 111598 g007
Figure 7. Comparing Strategies 1 and 3 ((a)), the process focusing on vaccinating individuals initially located in the denser sub-region of the lattice (Strategy 3) reduced the number of infected by 8 % and the number of deaths by 11 % about Strategy 1. As shown in (b), Strategy 4, focused on vaccinating individuals initially located in the two denser sub-regions of the lattice, reduced the number of infected by 27 . 8 % and the number of deaths by 33 . 3 % about Strategy 1. It shows us that Strategies of vaccinating focused in denser regions are more effective than random distribution (as proposed in Strategy 1). As seen in (c), it is important to vaccinate individuals encountered in the denser sub-regions, also considering the neighboring sub-regions to obtain even more efficient results. With the same number of doses, Strategy 4 reduced the number of infected and dead by 50% compared to Strategy 3.
Figure 7. Comparing Strategies 1 and 3 ((a)), the process focusing on vaccinating individuals initially located in the denser sub-region of the lattice (Strategy 3) reduced the number of infected by 8 % and the number of deaths by 11 % about Strategy 1. As shown in (b), Strategy 4, focused on vaccinating individuals initially located in the two denser sub-regions of the lattice, reduced the number of infected by 27 . 8 % and the number of deaths by 33 . 3 % about Strategy 1. It shows us that Strategies of vaccinating focused in denser regions are more effective than random distribution (as proposed in Strategy 1). As seen in (c), it is important to vaccinate individuals encountered in the denser sub-regions, also considering the neighboring sub-regions to obtain even more efficient results. With the same number of doses, Strategy 4 reduced the number of infected and dead by 50% compared to Strategy 3.
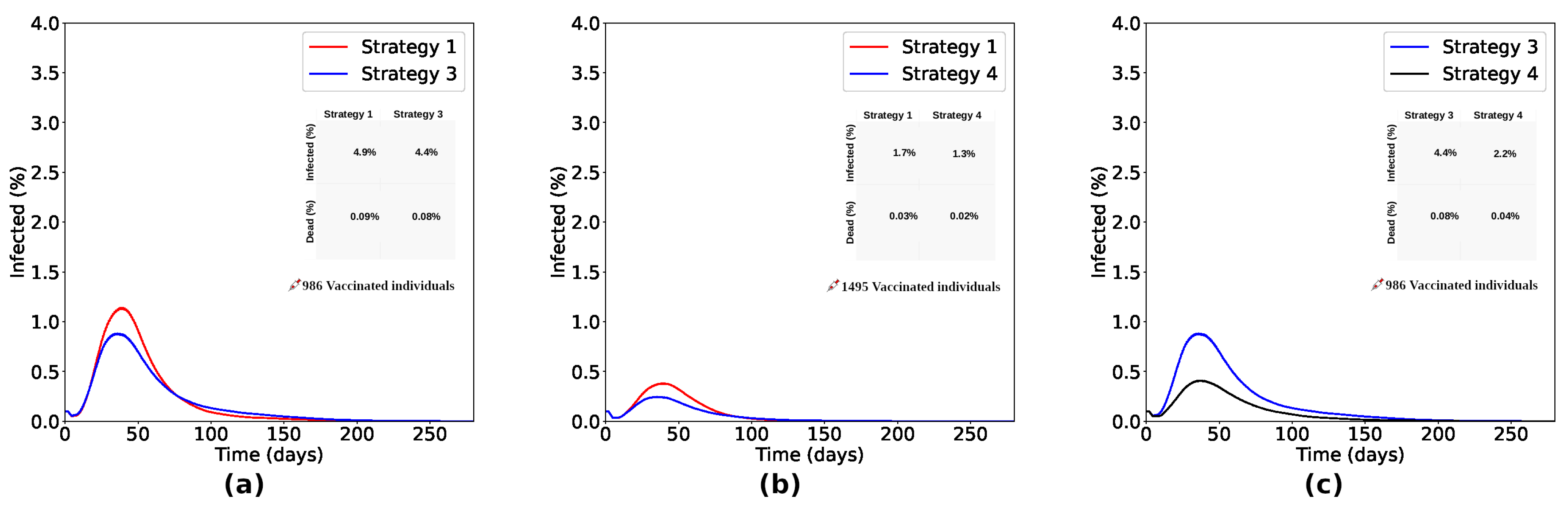
Preprints 111598 g007
Preprints 111598 g008
Figure 8. Variation in the percentage of unvaccinated infected given the increase in the vaccination rate considering Strategy 3 (Panel (a)) and Strategy 4 (Panel (b)). Analyzing the number of doses administered in each strategy (numbers highlighted at each point in the main graphs), we see that vaccinating only in the densest region resulted in infection rates for low vaccination percentages very similar to those observed in Strategy 4, given the same number of doses. This further corroborates that focusing on the distribution and administration of vaccines in the most crowded regions is the most efficient strategy in a scenario with few doses available. This is also reflected in the protection of immunocompromised individuals, as seen in the insets.
Figure 8. Variation in the percentage of unvaccinated infected given the increase in the vaccination rate considering Strategy 3 (Panel (a)) and Strategy 4 (Panel (b)). Analyzing the number of doses administered in each strategy (numbers highlighted at each point in the main graphs), we see that vaccinating only in the densest region resulted in infection rates for low vaccination percentages very similar to those observed in Strategy 4, given the same number of doses. This further corroborates that focusing on the distribution and administration of vaccines in the most crowded regions is the most efficient strategy in a scenario with few doses available. This is also reflected in the protection of immunocompromised individuals, as seen in the insets.
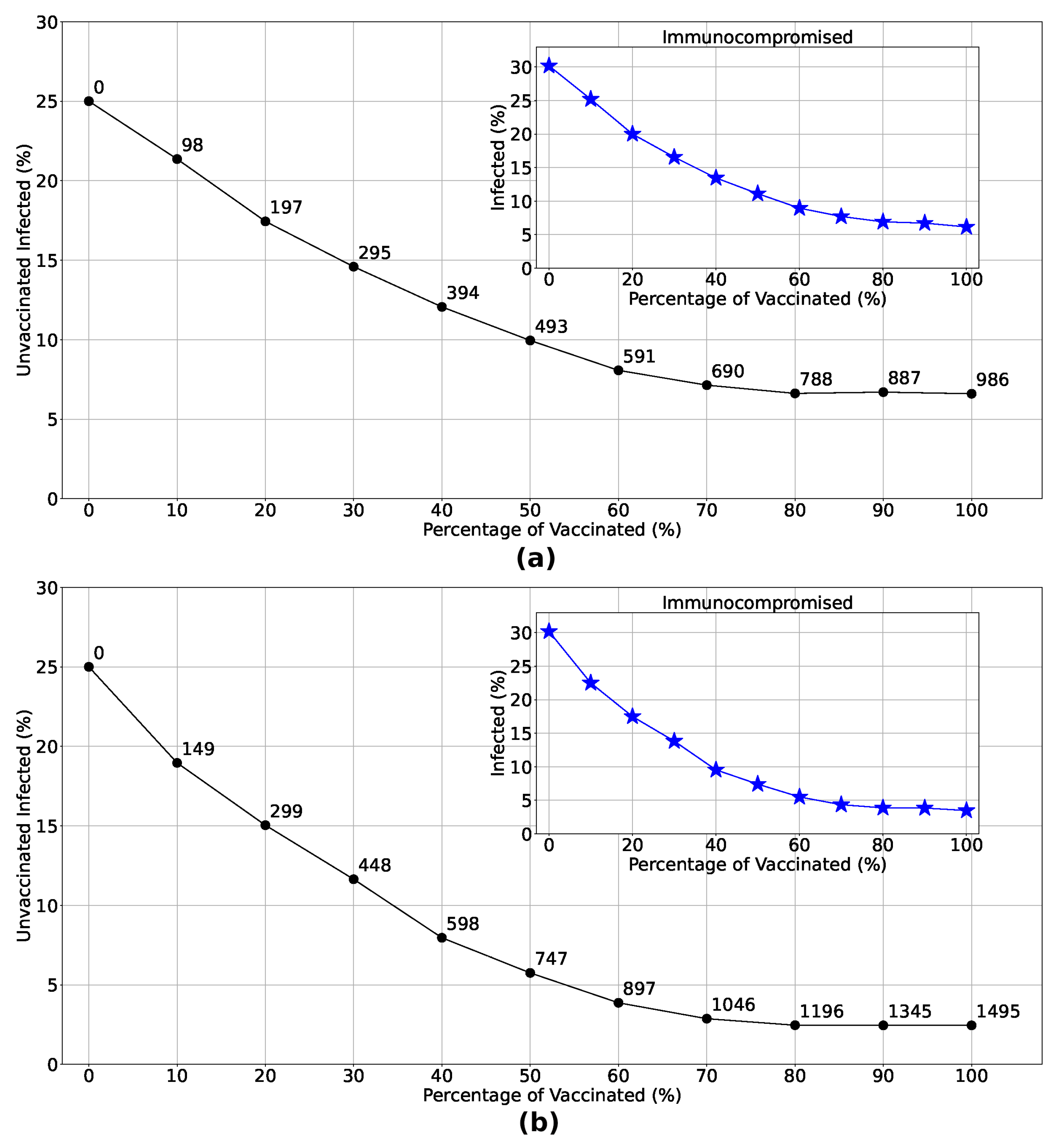
Preprints 111598 g008
Table 1. Description of the group(s) vaccinated in each vaccination strategy.
Table 1. Description of the group(s) vaccinated in each vaccination strategy.
Strategy Vaccinated group
Strategy 1 General population, not considering spatial and individual’s characteristics (random vaccination).
Strategy 2 Immunocompromised individuals.
Strategy 3 Individuals initially located in the denser sub-region of the lattice.
Strategy 4 Individuals initially located in the two denser sub-regions of the lattice.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated