Preprint
Article
Agricultural Decision-Making Concerning Crop Selection Using Analytic Hierarchy Process (AHP) in Trakya Region of Türkiye
Altmetrics
Downloads
87
Views
21
Comments
0
This version is not peer-reviewed
Submitted:
08 July 2024
Posted:
09 July 2024
You are already at the latest version
Alerts
Abstract
The Thrace region in Turkey is an important region where production suitable for irrigated agriculture such as sugar beet, paddy, sunflower and corn is widely carried out. Producers in the region have to decide on the product they will produce every year. A large number of factors that can affect decision-making in agricultural production can affect the outcome of the farmers. Therefore, it is necessary to have a decision-making process that can facilitate access to information and decision-making. Analytical Hierarchy Process (AHP) is a valuable decision-making methodology that can be applied not only in agricultural production but also in many other areas.
This study evaluates four products with the AHP method according to the criteria by surveying 271 producers in the area. The aim is to determine the most suitable products for planting in these areas. We found that rice is the product that provides the highest profit. The AHP model used in this study primarily serves to determine the importance levels of various criteria and demonstrates its effectiveness as a decision-making tool in product selection when the correct criteria are applied
Keywords:
Subject: Business, Economics and Management - Business and Management
I. Introduction
Choosing the crop to be grown in the upcoming
growing season is very important for farmers. Making this decision becomes
simpler when they can estimate the income that will be obtained from their
crops. However, due to environmental issues, this procedure is still full of
unknowns and this is a problem that farmers everywhere face, not only in
Turkey.
In Turkey, a developing country, farmers usually
choose crops that provide higher returns. They also prefer crops that are easy
to market, and public institutions sometimes intervene as buyers for such
products. Certain crops may also receive targeted support according to their
specific characteristics. However, farmers often base their planting decisions
on previous years' earnings rather than relying on scientific data. This
approach is in line with the classical Spider Web Theory that can be observed
in Turkey's agricultural sector. For example, this theory is clearly seen in
the price fluctuations of onions and potatoes, as stated in the SETA 2021
report[1].
The results of this study conducted in the Thrace
region are valid for many years. Wheat and sunflower cultivation are
particularly suitable for regions with inadequate irrigation systems due to
their adaptability to dry farming conditions. In addition, market demand for
these products reinforces their suitability. Turkey has an important public
institution dedicated to wheat-related products. The institution cooperates
with a producer association and sunflower oil factories to provide guidance to
farmers on production decisions. The aim is to manage the amounts of wheat and
sunflower produced by aiming for a harmonious balance. In regions where
irrigation is less than ideal, farmers are often limited to a narrow range of
crops, mainly wheat and sunflower. In regions with adequate irrigation, there
are competitive dynamics among four main crops, all of which offer significant
profitability: sunflower, corn, rice and sugar beet. Producers make cultivation
decisions based on a variety of factors, including government subsidies,
marketability and, predominantly, the income they have previously earned from
these crops. The main objective of this study is to evaluate the factors that
farmers in irrigated regions consider when choosing which crops to grow. To this
end, we use the Analytical Hierarchy Process (AHP), which uniquely combines
qualitative data and provides a mathematical approach to address multi-criteria
decision-making problems. Other multi-criteria decision-making methods, such as
goal programming, lack the ability to integrate qualitative data. Since
agricultural production choices represent a critical decision-making process,
the use of AHP allows the determination of the most advantageous crop choices
based on a comprehensive set of criteria.
The Analytical Hierarchy Process (AHP), developed
by Dr. Thomas L. Saaty, has a wide range of applications that demonstrate its
validity [2]. One of the main advantages of
AHP is that it allows decision makers to set priorities for the relative
importance of all factors involved by comparing the relative importance of each
factor with all other factors. Agriculture can benefit greatly from this
ability as it not only evaluates the importance of different factors but also
helps determine the optimum amount of crop to be grown each year. The
quantitative results obtained from AHP can significantly improve the quality of
decision-making.
AHP can be an effective decision support system for
shaping agricultural policies, especially in countries like Turkey. It can guide
the formulation of national agricultural production strategies. In this
particular case study, we found that the most important factor for growers is
the highest return on investment. By using AHP, policy makers can gain insight
into decision-making trends and create agricultural policies that better meet
economic goals and farmers’ needs.
2. Literature Summary
Introduced by mathematician Thomas L. Saaty in
1971, the Analytical Hierarchy Process (AHP) has evolved significantly since
its theoretical and practical applications began in 1973. Initially used to
develop a transportation system for agricultural exports in Sudan, the
versatility of the AHP was quickly recognized. Saaty and Bennett applied it to
predict the outcome of the US presidential election in 1976, demonstrating its
potential in socio-political areas. By 1982, Saaty and Vargas had expanded its
application to various sectors, including economic and technological
decision-making [2–10]. The widespread
adoption of the method was highlighted in a 2021 study by Fountzoula and
Aravossis, reflecting its robustness in various decision-making areas[11].
AHP has been significantly useful in agriculture.
Alphonce’s (1997) paper emphasized its role in agricultural decision-making in
developing countries, including the selection of optimal farm locations and
crop production technologies[12]. Guo and He
(1999) integrated AHP with Goal Programming to address grain losses and
production costs in developing countries [13].
This integration increased the effectiveness of AHP in agriculture by
demonstrating its ability to blend qualitative and quantitative criteria.
Furthermore, the adaptability of AHP to modern agricultural challenges is
demonstrated by its application in biofuel efficiency assessment by Acaroglu et
al. in 1999 and its continuing importance for sustainable agriculture as noted
by Kumar and Pant in 2023 [14,15]. The
practical utility of AHP in various organizational contexts has been further
highlighted by the development of decision support software such as Expert
Choice and Decision Lens.
3. Materials and Methods
3.1. Case Selection
The target audience of the research consists of
producers in irrigated agriculture villages in the Thrace Region. Since it is
impossible to examine all the producers in these villages, a sample was taken
to represent the main population. The following formula was used to determine
the sample volume [16].
n = Number of samples
= Confidence coefficient (for 90% confidence interval, this coefficient is taken as 1.645)
p = Probability of the unit being examined among the main population (Those who have a positive approach to irrigated agriculture)
q = 1-p (Proportion of those who have no knowledge about irrigated agriculture and have a negative opinion)
D = 5% (Error rate)
The probability (p) of the unit being examined within the population was taken as 0.50 in order to reach the highest sample that would represent the population. In other words, the rate of those who had a positive view of irrigated agriculture was accepted as 50%, and the rate of those who had no opinion and had a negative view was accepted as 50%. In this type of sampling, (p) = (q) = 0.5 is accepted. In this way, the largest possible sample volume is obtained. While the confidence level was accepted as 90% (z = 1.645), the sample size is calculated as 271. A review of the literature reveals that AHP has been employed in a diverse range of decision-making scenarios, as documented in Zahedi's 1986 study [17]. This breadth of application underscores the versatility and effectiveness of AHP in addressing complex decision-making problems.
3.2. The Analytic Hierarchy Process
Decision making is a fundamental aspect of both the personal and public spheres. When addressing decision-making challenges, a multitude of factors influence the optimum outcome, and various possible outcomes are prioritized based on these factors. It is crucial to organize these factors and outcomes in a way that clearly delineates their relationships with one another. A hierarchical structure proves extremely useful for this purpose.
The Analytical Hierarchy Process (AHP), described by Saaty and Vargas in 1987, does not impose predetermined factors on users. Instead, it offers the flexibility to identify and tailor a decision-making framework specific to the user’s needs. As Saaty noted in 1982, the first step in implementing the AHP involves comprehensively identifying all factors that affect the decision.
These identified factors are then systematically organized into a hierarchical order, typically consisting of the goal, criteria, subcriteria, and alternatives, as outlined by Zahir in 1991 [18]. This hierarchical setup should clearly represent the functional dependency relationships among the elements. Such an organized structure facilitates a comprehensive and systematic approach to complex decision-making scenarios, enabling clear and distinct judgments to be made about the various factors that influence the decision.
An example of a hierarchical structure is shown in Figure 1.
Once the hierarchical structure in the Analytical Hierarchy Process (AHP) is established, the next step involves creating pairwise comparison matrices. These matrices are crucial for determining the relative importance of criteria and sub-criteria within the hierarchy. In pairwise comparisons, the decision maker evaluates two factors simultaneously, using one as a reference and estimating how much more important the other is to a criterion when considering a goal or alternatives. The process of comparing each item to a large number of other items increases the accuracy and consistency of the decision-making process, as Saaty noted in 1980 [2].
A 1-9 scale based on Saaty's stimulus-response theory is used to make these pairwise comparisons. The validity of this scale has been established through various applications and theoretical comparisons with other scales, as discussed by Saaty and Vargas in 1991 [10]. The numbers on the scale are absolute, indicating the dominance of one item over another on a given factor, and are not convertible like numbers on ratio scales such as pounds to kilograms. Absolute numbers are invariant under identity transformation.
In scenarios involving multiple decision makers, different opinions on judgments may arise. Aczel and Saaty, in 1983, showed that the geometric mean should be used to aggregate the judgments of several individuals for each pair of comparisons [19]. The pair comparison matrix is supported by four main axioms that validate its theoretical basis, as detailed by Saaty in 1986 [4]. These axioms ensure that the matrix reliably reflects the relative importance and relationships between various factors in the decision-making process.
Once the pairwise comparison matrices are complete, the next step in the Analytical Hierarchy Process (AHP) is to derive priorities for the criteria, subcriteria, and alternatives. These priorities are derived from separate matrices for each category. The basic mathematical concept used in this step is the principal eigenvector, which corresponds to the principal eigenvalue of the matrix.
The principal eigenvector is important because it represents the relative weights or priorities of the elements being compared. The principal eigenvalue, on the other hand, is the largest eigenvalue of the matrix and is integral to the calculation of the principal eigenvector. This eigenvector essentially summarizes the information contained in the pairwise comparisons and provides a consistent ranking of the criteria, subcriteria, or alternatives based on the judgments made.
The use of the principal eigenvector in AHP is not arbitrary; it is theoretically justified as the most appropriate method for representing the derived priorities. By capturing the essence of the relative importance given to various factors in the decision-making process, it allows for a structured and quantitative approach to complex decisions.
If λmax is the principal eigenvalue, the priority vector W is obtained by solution of the homogeneous linear system of equations.
(A-λmaxI ) W = 0
In scenarios where computer access is limited or unavailable, an alternative, simpler method can be used for approximate calculations instead of solving the equation system (2). This method, proposed by Saaty (2000), involves normalizing the columns of the matrix and then calculating the mean [6]. To achieve this, each element in a column of the matrix is divided by the total sum of the elements of that column. Then, the sum of the elements in each row of the newly created matrix is divided by the number of elements in that row. The result of this operation provides an approximation of the priority vector.
The final weights of the alternatives are obtained by multiplying the priority of each alternative with respect to a given criterion by the weight of that criterion and then summing these values across all criteria. The alternative with the highest cumulative value is selected for the decision or a proportional combination based on the priorities is used.
At this stage, it is very important to assess whether the decision maker has made consistent comparisons between the factors. To assess this consistency, the consistency ratio (CR) of each comparison matrix is calculated. This calculation uses a Random Index based on the number of decision alternatives (n), as suggested by Saaty and Özdemir in 2003 [7].
A CR of 0 indicates “complete consistency in the decision maker’s judgments.” As the ratio approaches 1, it means that “the matrix reflects random judgments based on the decision maker’s evaluations.”
A consistency ratio of 0.1 or less means that “the result falls within acceptable limits of consistency.” If the consistency ratio exceeds 0.1, the comparison matrix needs to be reexamined.
If the consistency ratio does not meet the desired standard, the first step is to rank the activities according to weights derived from a simple line and then refine the second comparison matrix using this ranking information. This approach can lead to improved consistency [5].
4. Results and Discussion
4.1. The Determination of the Factors Affecting Crop Preference
As mentioned earlier, a critical step in solving decision-making problems using the Analytical Hierarchy Process (AHP) is to identify the factors that influence the decision. Accordingly, interviews were conducted with agricultural producers in the region and five experts specializing in product selection within the research area. The selection of these experts was based on their expertise on the subject, familiarity with the problem, and knowledge of the region. From the data collected, it was determined that product selections were made according to the following criteria:
- Income from the crop (I)
- Governmental support (GS)
- Guarantee of marketing (GM)
- Need of irrigation (NI )
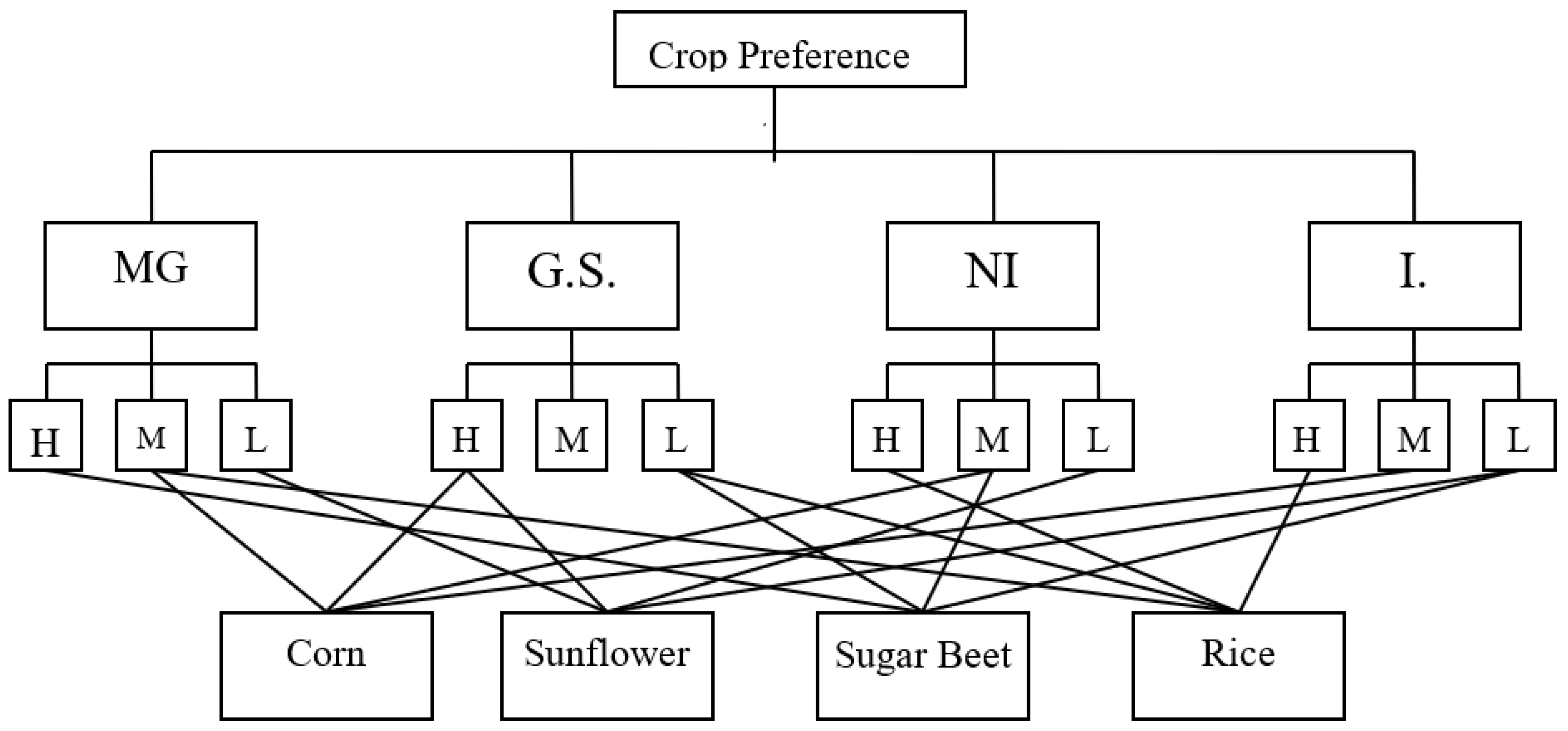
The aforementioned factors are categorized based on their impact levels: High (H), Medium (M), and Low (L). During the crop selection process, the favored crops identified were corn, sunflower, rice, and sugar beet. These selections were made considering the varying degrees of influence each factor has on the decision-making process.
a) Crop Income (I): The preferred crop should yield the highest income per unit area for the producer during the production period. The net profit, after deducting all costs from the revenue, should be at its maximum.
b) Governmental Support (GS): Agricultural support in Turkey is not considered sufficient. Support rates fluctuate annually, but government assistance is generally around 0.35-0.40% of GDP [20]. This support is provided according to the cultivated land area and agricultural inputs [21]. A significant benefit of this policy is the registration of all producers and increased transparency. In the past, public institutions guaranteed market prices, but this practice was discontinued, leading to a change in market dynamics. The government's participation in the market as a buyer has been shown to negatively affect competition. These support mechanisms are restricted by the WTO agricultural agreement.
The lack of additional policy instruments to complement these supports is a significant shortcoming. The primary problem for Turkish farms is their small size and low income. Due to their limited earnings, Turkish farmers often start a new production cycle in debt. A policy change in 2019 eliminated the role of the government as a market buyer, leading to a decrease in farmers' incomes. In addition, premium payments are made together with land support for certain products such as sunflower, soybean and corn, as their production is insufficient in Turkey. The aim of this policy is to increase the production of these products [22].
c) Guarantee of Marketing (GM): A critical concern for producers is finding buyers after harvest, given that agricultural products are produced seasonally but consumed throughout the year. It is vital for producers to receive payment for their crops promptly in order to sustain their livelihoods. A major challenge arises from the necessity to sell the entire harvest at once, which requires injecting significant amounts of money into the market at once. As a result, buyers often prefer to purchase crops in stages, resulting in additional storage costs for producers. To alleviate this problem, public institutions occasionally step in to purchase unsold produce. For some products, marketing is not a problem because they serve as raw materials for existing industries, thus providing automatic market guarantees.
d) Need for Irrigation (NI): Water is a key element that increases the yield of agricultural crops. Different crops have different water requirements. Meeting these needs adequately can significantly increase productivity. Regional governments invest in irrigation infrastructure such as dams and canals to support crop irrigation requirements. Increased yields through improved irrigation directly contribute to the country’s overall agricultural production.
A general overview of the crops examined in this study and their salient features are provided below:
Sunflower: Sunflower is usually selected as a rotation crop grown every two years in dry farming areas. In such areas, sunflower yield is approximately 1500 kg per hectare [23]. Producers may choose not to grow sunflower after overproduction of other crops in previous years. However, not rotating crops can lead to problems such as wheat crop maggots and Eurygaster ssp. With irrigation, as in the studied areas, sunflower yield can reach 3000-3500 kg per hectare and increase producer income. Market prices and government premium payments become more important than in previous years. There may be delays in these payments due to Turkey's balance of payments problems. In such cases, income from other products becomes important. There are many sunflower processing plants in the region and a cooperative union consisting of 40,000 producers. Despite being an important crop, Turkey's sunflower production is insufficient for domestic needs, which facilitates producers' access to the market. However, low export earnings lead to a preference for sunflower imports, causing marketing problems for domestic production. The irrigation requirement of sunflower is lower compared to the other crops studied.
Corn: Another important product that has a production deficit in Turkey, corn, was imported for 3.5 billion tons in 2023 [20]. There is a constant demand for corn from animal feed factories in the region. The government provides market guarantees and price support for corn production through the Soil Products Office, but production remains insufficient. The government also offers premiums to encourage corn production. Despite these efforts, corn production in the region and throughout Turkey cannot meet demand. Producer income generally remains at the levels determined by the government. Corn production tends to decrease after years of low prices declared by the government. While corn yield in the region is 3000-3500 kg per hectare without irrigation, it increases to 6000-6500 kg with irrigation.
Sugar Beet: Sugar beet production has exceeded domestic needs despite quota applications. The state has been promoting sugar beet farming since the 1930s, leading to unexpected increases in planting. To control production, the state has limited purchasing guarantees and has stopped providing incentives since 2019. State support is limited to agricultural input subsidies. However, sugar beet remains a preferred crop in irrigated agricultural areas due to its high yields and low irrigation needs.
Rice: Turkey imports 40% of its rice. Rice is highly appreciated by Turkish consumers, with per capita consumption increasing from 3 kg in 1980 to 7 kg in 2022 [20]. Rice provides the highest income to producers. The state intervenes minimally, but a large number of specialized rice mills alleviate marketing problems. State incentives for rice are limited to agricultural inputs and a small, stagnant subsidy per kilogram. Rice requires more water than other crops, requiring river and dam water resources in rice-growing areas.
4.2. Formulation and Solution of a Hierarchical Model for the Problem
After identifying the factors and alternatives that affect the decision, we structured these elements hierarchically. The hierarchy extends from the main objective (Product Preference) to the criteria, sub-criteria, and alternatives. This resulted in a four-level hierarchical model as shown in Figure 2.
The hierarchy usually consists of several levels and increases in number with the complexity of the decision. The Analytical Hierarchy Process (AHP) offers flexibility in formulating the decision hierarchy. A logically modeled hierarchy helps in understanding the problem and serves as a valuable guide in assessing the relative importance of the criteria in the decision process.
The hierarchy usually consists of several levels and increases in number with the complexity of the decision. The Analytical Hierarchy Process (AHP) offers flexibility in formulating the decision hierarchy. A logically modeled hierarchy helps in understanding the problem and serves as a valuable guide in assessing the relative importance of the criteria in the decision process.
The top level of this four-level hierarchy represents our primary objective, “Crop preference.” The second level covers the criteria that influence crop choice as determined by experts. The third level shows the extent to which each criterion is met, and the fourth level lists the alternatives.
First, the hierarchical structure was formulated, then step-by-step comparisons were made along the hierarchy, starting from the objective.
Initially, crop preference was considered as the main objective. The second level below this objective includes the factors that influence crop choice, which are compared in pairs. This approach allows the evaluator to remain unaffected by other factors and focus only on the two factors being compared. This pairwise comparison method is advantageous because of its sensitivity. Inconsistencies in the responses are flagged by the computer program, highlighting the judgments that need the most adjustment to increase consistency. This feature is another advantage of using AHP.
The producers and experts who participated in the survey compared two criteria according to their contribution to the objective. These judgments were converted into numerical data using a comparison scale, and a comparison matrix was created. Table 2 presents the results of the hierarchical structure assessments including geometric means and five experts’ opinions from the data collected from the surveyed producers. The consistency ratio for each matrix is shown below the matrix, with all matrices showing a consistency ratio below 0.10.
Table 1.
The AHP Pairwise Comparison Scale.
| The level of importance | DEFINITION | EXPLANATION |
| 1 | Equal importance of both elements | Two elements contribute equally to the property |
| 3 | Weak importance of one element over there | Experience and judgment slightly favor one element over another |
| 5 | Essential or strong importance of one element over another | Experience and judgment strongly favor one element over another |
| 7 | Demonstrated importance of one element over another | An element is strongly favored and its dominance is demonstrated in practice |
| 9 | Absolute importance of one element over another | The evidence favoring one element over another is of the highest possible order of affirmation |
| 2,4,6,8 | Intermediate values between two adjacent judgments | Compromise is needed between two judgments |
Table 2.
Dual Comparison Matrix of Criteria.
| GM | GS | NI | I | Priorities | |
| GM | 1 | 3,22 | 5,48 | 0,21 | 0.218 |
| GS | 0,31 | 1 | 4,23 | 0,15 | 0.114 |
| NI | 0,18 | 0,24 | 1 | 0,11 | 0,045 |
| I | 4,73 | 6,74 | 8,74 | 1 | 0,622 |
CR= 0,097.
Table 3.
Dual Comparison Matrix Guarantee of Marketing Governmental Support According to Sub Criteria.
Table 3.
Dual Comparison Matrix Guarantee of Marketing Governmental Support According to Sub Criteria.
| GM | H | M | L | Priorities |
| H | 1 | 4.73 | 7.74 | 0.72 |
| M | 0.21 | 1 | 3.72 | 0.21 |
| L | 0.13 | 0.27 | 1 | 0.07 |
| CR=0.07 | ||||
Table 4.
Dual Comparison Matrix of According to Sub Criteria.
| GS | H | M | L | Priorities |
| H | 1 | 4.73 | 9 | 0.75 |
| M | 0.21 | 1 | 2.71 | 0.18 |
| L | 0.11 | 0.37 | 1 | 0.07 |
| CR=0.01 | ||||
Table 5.
Dual Comparison Matrix of Need of Irragation Income from the Crop According to Sub Criteria.
Table 5.
Dual Comparison Matrix of Need of Irragation Income from the Crop According to Sub Criteria.
| NI | H | M | L | Priorities |
| H | 1 | 0.22 | 0.11 | 0.06 |
| M | 4.47 | 1 | 0.21 | 0.21 |
| L | 8.74 | 4.93 | 1 | 0.72 |
| CR=0.08 | ||||
Table 6.
Dual Comparison Matrix of According to Sub Criteria.
| I. | H | M | L | Priorities |
| H | 1 | 7.24 | 9 | 0.78 |
| M | 0.14 | 1 | 3.22 | 0.16 |
| L | 0.11 | 0.31 | 1 | 0.07 |
| CR=0.09 | ||||
Paired comparisons as inputs to the AHP were used to calculate the comparative priority and weights of each alternative. The priorities column in a comparison matrix shows the normalized weights of the factors compared within the matrix. According to these priorities, farmers’ product preferences are as follows: Income from the product (63%), Marketing guarantee (22%), Government support (11%), Irrigation requirement (4%).
Producers and experts determined that the most important factor in the decision-making process is 63% of the income from the unit of land. Therefore, irrigation was considered by the respondents as a less important factor in product selection. However, experts acknowledged the specific irrigation needs of each product.
The producers then gave their opinions on the intensity levels of the above-mentioned attributes or criteria.
At the fourth level of the hierarchy, four products were selected as alternatives by experts. Experts compared these products according to each factor determined at the second level of the hierarchy. The following tables show the pairwise comparisons. As can be seen from the priorities (Table 7), the product with the highest marketing guarantee is sugar beet. This is attributed to the various agricultural inputs provided by the sugar factories in the region and purchase guarantees similar to contract farming. The low marketing guarantee for sunflower is explained by Turkey's foreign trade policy. Due to insufficient local production, Turkey imports sunflower, the main reason for this is the higher cost of local production compared to imported sunflower. This situation leads to producers being hesitant to grow sunflower despite the existence of oil factories that can provide market guarantee. However, these factories generally prefer imported sunflower due to its cost advantages. The state support criterion rates for corn and sunflower are similar (Table 8), since production is carried out in a uniform manner with the support provided to registered producers. While many products receive support per kg to increase production, other products such as sugar beet and corn do not receive such support.
Producers and experts stated that rice has the highest irrigation needs due to being a water-intensive product (Table 9).
Rice also brings the highest profit (Table 10). Local rice is preferred by consumers in Turkey and leads to higher market prices during harvest periods, thus providing higher profits to producers. This scenario is not repeated for sunflower, which faces a production deficit. Imported sunflower, which is cheaper, is preferred by the sector over domestic production.
After weighting and summing, the overall product priorities are as shown in Table 11. Rice emerges as the most preferred product with a priority rate of 49%.
In this study, the criteria and alternatives were limited to those considered important by the experts. However, other criteria not considered in this study may affect the production decision. The solution may change with changes in the criteria and alternatives that form the hierarchical structure. Therefore, it is important to note that the solution is based on the alternatives and criteria selected in this particular application.
5. Conclusions
In countries where agricultural policy makers do not control the market, there are no contractual agreements between buyers and sellers, and farmers decide independently on crop production, farmers are presented with a wide range of options. This scenario is particularly important in Turkey, where agricultural support is distributed almost equally across all crop types. In such environments where production decisions are left to farmers, farmers have the authority to base their choices on various criteria. This study conducted an analysis of crop preferences in irrigated lands in the Thrace region of Turkey using the Analytical Hierarchy Process (AHP) to examine four criteria that influence production decisions.
Globally and in the study region, farmers tend to prefer crops that yield higher profits as they seek significant returns for their efforts.
This study identified rice as the crop that offers the highest profit levels. This conclusion, theoretically supported by the AHP, is confirmed by the fact that rice yields the highest profits in the study area. Furthermore, producers tend to grow rice even in areas with limited irrigation facilities and resort to the use of costly groundwater resources. The AHP model used in this study primarily serves to determine the importance levels of various criteria and demonstrates its effectiveness as a decision-making tool in product selection when the right set of criteria is applied. Policy makers guiding national agricultural policies can use AHP for production planning and direction. They can direct production potential and focus by determining production criteria and weights for a region according to annual values. A critical issue here is the nature of government support tailored to the characteristics of each product. Different forms of government support can change the perception and preference for certain products. This study demonstrates such a phenomenon: Sunflower is the least preferred product despite receiving support per land area and per kg. While government support has remained constant over the years, rice emerges as the most preferred product due to its high profitability and significant market opportunities. It is clear that current policies for sunflower cultivation are not well received by farmers. In order to increase the attractiveness of sunflower, the value obtained from this product must be at the same or equivalent level with the support provided by the state.
References
- SETA. (2021), Food Inflation in Turkey is an Indicator of Problems from Farm to Fork, Politics, Economy And Social Research Foundation, Num:85, Ankara.
- SAATY, T.L. (1980), The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation, Mc Grawhill, Newyork.
- SAATY, T.L. (1982), Decision Making for Leaders, Wadsworth Inc., p.15.
- SAATY, T.L. (1986), “Axiomatic Foundation of Analytic Hierarchy Process”, Management Science, 32, pp 841-855.
- SAATY, T.L. (1988), Mathematical Methods of Operations Research, Dover Publications New York, p 427.
- SAATY, T.L. (2000), Fundamentals of Decision Making and Priority Theory. RWS Publications, Pittsburgh,USA.
- SAATY, T.L. and OZDEMIR, M.S. (2003), “Why the Magic Number Seven Plus or Minus Two”, Mathematical and Computer Modeling, 38, pp 233-244.
- SAATY, T.L. and VARGAS, L.G. (1982), The Logic of Priorities, Applications in Business, Energy, Health, Transportation, Kluwer-Nijhoff Publishing, Boston.
- SAATY, T. L. and VARGAS, L.G., (1987) ”Uncertainty and Rank Order in the AHP”, European J. of Operational Research, 32, pp 107-117.
- SAATY, T.L., VARGAS, L.G. (1991), Prediction, Projection and Forecasting, Kluwer, Academic, Boston.
- FOUNTZOULA, C. , & Aravossis, K. (2021). Analytic hierarchy process and its applications in the public sector: a review. Academy of Accounting and Financial Studies Journal, 25(6), pp 1-15.
- ALPHONCE, B.C.(1997), “Application of Analytic Hierarchy Process in Agriculture in Developing Countries”, Agricultural System, 53, pp 97-112.
- GUO, L.S. and HE, Y. S. (1999), “Integrated Multi-Criteria Decision Model: A Case Study for the Allocation of Facilities in Chinese Agriculture”, J. Agric.Eng. Res., 73, pp 87-94.
- ACAROGLU, M. and OGUT, H. And OGUZ, H. (1999), 7.International Congress on Agricultural Mechanization and Energy 26-27 May, Adana, Turkey, pp 302-307.
- KUMAR, A. and Pant, S. (2023), Analytical hierarchy process for sustainable agriculture:An overview, MethodsX, 10, 1-10.
- COCHRAN, W.G. 1977. Sampling Techniques. 3rd ed. New York: John Wiley & Sons.
- ZAHEDI, F. (1986), “The Analytic Hierarchy Process: A Survey of Method and Its Applications”, Interfaces, 16, pp 96-108.
- ZAHIR, M.S. (1991),”Incorporating The Uncertainty of Decision Judgments in The Analytic Hierarchy Process”, European J.of Operational Research 53, pp 206-216.
- ACZEL, J. and SAATY, T.L.(1983), “Procedure for Synthesizing Ratio Judgments”, Journal of Mathematical Psychology, 27, pp 93-102.
- TUIK Turkish Statistical Institute (2022). www.tuik.gov.tr.
- Turkish Ministry of Agriculture and Forestry (2023). https://www.tarimorman.gov.tr/.
- İNAN, H. , (2016), “Agricultural Economics and Management”, Ideal Culture Publications, Istanbul.
- TRAKYABIRLIK. (2022), “Trakya Oilseeds Sales Cooperatives Union Records”, Edirne.
Figure 1.
Hierarchical Organization Example.
Figure 2.
Crop Preference Hierarchy.
Table 7.
Dual Comparison of Products According to Guarantee of Marketing.
| GM | |||||
| Corn | Sunflower | Sugar beet | Rice | Priorities | |
| Corn | 1 | 1.68 | 0.21 | 0.66 | 0.13 |
| Sunflower | 0.59 | 1 | 0.16 | 0.24 | 0.07 |
| Sugar beet | 4.73 | 6.24 | 1 | 3.22 | 0.58 |
| Rice | 1.52 | 4.23 | 0.31 | 1 | 0.22 |
| CR=0.02 |
Table 8.
Dual Comparison of Crops According to Governmental Support.
| G.S | |||||
| Corn | Sunflower | Sugar beet | Rice | Priorities | |
| Corn | 1 | 1.41 | 8.74 | 8.24 | 0.49 |
| Sunflower | 0.71 | 1 | 8.49 | 8.49 | 0.41 |
| Sugar beet | 0.11 | 0.12 | 1 | 1.19 | 0.05 |
| Rice | 0.12 | 0.11 | 0.84 | 1 | 0.05 |
| CR=0.01 |
Table 9.
Dual Comparison of Products According to Need of Irrigation.
| NI | |||||
| Corn | Sunflower | Sugar beet | Rice | Priorities | |
| Corn | 1 | 3.22 | 0.24 | 0.15 | 0.10 |
| Sunflower | 0.31 | 1 | 0.21 | 0.11 | 0.05 |
| Sugar beet | 4.23 | 4.73 | 1 | 0.25 | 0.24 |
| Rice | 6.74 | 8.74 | 4 | 1 | 0.61 |
| CR=0.08 |
Table 10.
Dual Comparison of Products According to Income.
| IC | |||||
| Corn | Sunflower | Sugar beet | Rice | Priorities | |
| Corn | 1 | 4.73 | 3.22 | 0.19 | 0.20 |
| Sunflower | 0.21 | 1 | 0.29 | 0.11 | 0.05 |
| Sugar beet | 0.31 | 3.46 | 1 | 0.13 | 0.10 |
| Rice | 5.23 | 9.00 | 7.48 | 1 | 0.65 |
| CR=0.09 |
Table 11.
AHP Result Matrix.
| PRODUCT | Priorities |
| CORN | 0.214 |
| SUNFLOWER | 0.092 |
| SUGAR BEET | 0.200 |
| RICE | 0.493 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated