Quantum Temporal Resonator: Temporal Displacement Using Quantum Entanglement and Metamaterials

Preprint

Article

Quantum Temporal Resonator: Temporal Displacement Using Quantum Entanglement and Metamaterials

Altmetrics

Downloads

127

Views

Comments

Supplementary Material

supplementary.json (340.65KB )

Florian Neukart^*

This version is not peer-reviewed

Submitted:

09 July 2024

Posted:

10 July 2024

You are already at the latest version

Alerts

Abstract

This paper discusses the Quantum Temporal Resonator (QTR), a theoretical device leveraging quantum entanglement and metamaterials with negative refraction indices to achieve controlled temporal displacement. By establishing a network of entangled particles within a Bose-Einstein Condensate (BEC) and utilizing a resonant cavity made of advanced metamaterials, the QTR creates localized distortions in space-time. The frequency and amplitude of temporal harmonics within this cavity are finely tuned to allow for precise temporal displacement of matter and information. Numerical simulations demonstrate the coupling between the quantum wave function and electromagnetic fields, validating the theoretical model. The results show distinctive patterns in the wave function and perturbations in the electric field, supporting the feasibility of achieving controlled temporal displacement. This study explores the theoretical framework, mathematical modeling, experimental setup, and potential applications of the QTR, providing a comprehensive analysis of its feasibility and implications.

Keywords:

Subject: Physical Sciences - Quantum Science and Technology

1. Introduction

Time travel has long been a subject of fascination and speculation in both science fiction and theoretical physics. Various approaches have been proposed, ranging from the manipulation of wormholes [1] to the use of cosmic strings [2]. Despite the allure of these theories, practical implementation remains elusive due to the extreme conditions and exotic matter required. Recent advancements in quantum mechanics and materials science offer new avenues for exploring temporal displacement. Quantum entanglement, a phenomenon where particles become interconnected in such a way that the state of one instantaneously influences the state of another, regardless of distance, has shown potential for various applications in communication and computing [3]. Similarly, metamaterials - engineered materials with properties not found in nature - have revolutionized the manipulation of electromagnetic waves, including negative refraction [4].

This paper proposes an approach to time manipulation through the Quantum Temporal Resonator (QTR). The QTR combines the principles of quantum entanglement and the unique properties of metamaterials to create a resonant cavity capable of generating controlled distortions in space-time. By establishing a network of entangled particles within a BEC and utilizing the negative refraction properties of metamaterials, the QTR aims to create localized distortions where the flow of time can be manipulated. While this concept does not equate to time travel in the conventional sense of moving freely backward and forward in time, it proposes a means of influencing the rate and direction of temporal progression within a confined region. This form of temporal displacement could significantly affect communication, computation, and fundamental physics.

The following sections will detail the theoretical framework underpinning the QTR, the mathematical models describing its operation, the experimental setup required to test its feasibility, and the potential applications and implications of successful temporal displacement.

2. Theoretical Framework

The QTR leverages principles from quantum mechanics, materials science, and relativity to achieve controlled temporal displacement. This section outlines the theoretical foundations of these principles and their integration within the QTR.

2.1. Quantum Mechanics

Quantum entanglement is a phenomenon where particles become correlated in such a way that the state of one particle instantaneously influences the state of another, regardless of the distance separating them [5]. This non-local correlation is described mathematically by the entangled state

| Ψ 〉 = \frac{1}{\sqrt{2}} {(| 0 〉}_{A} {| 1 〉}_{B} + {| 1 〉}_{A} {| 0 〉}_{B})

, where

| 0 〉

and

| 1 〉

are the quantum states of particles A and B. Experimental verification of entanglement has been achieved through numerous experiments [3,6].

A BEC is a state of matter formed by cooling a gas of bosons to temperatures very close to absolute zero. Under such conditions, a large fraction of the bosons occupy the lowest quantum state, resulting in macroscopic quantum phenomena [7]. The wave function of a BEC,

Ψ (r, t)

, satisfies the Gross-Pitaevskii equation:

i ℏ \frac{\partial Ψ}{\partial t} = (- \frac{ℏ^{2}}{2 m} \nabla^{2} + V (r) + g {| Ψ |}^{2}) Ψ,

(1)

where m is the mass of the bosons,

V (r)

is the external potential, and g is the interaction strength. In the QTR, the BEC serves as a medium for establishing a robust network of entangled particles, essential for creating temporal links.

2.2. Metamaterials and Negative Refraction

Metamaterials are artificially engineered structures that exhibit properties not found in naturally occurring materials. One of the most intriguing properties of metamaterials is negative refraction, where electromagnetic waves are bent in the opposite direction compared to conventional materials [8]. The refractive index, n, of these materials can be described by the relationship

n = \sqrt{ϵ μ}

, where

ϵ

is the permittivity and

μ

is the permeability of the material.

Maxwell’s equations, which govern electromagnetic waves, must be modified to account for negative refraction:

\nabla \cdot E = \frac{ρ}{ϵ},

(2)

\nabla \cdot B = 0,

(3)

\nabla \times E = - \frac{\partial B}{\partial t},

(4)

\nabla \times H = J + \frac{\partial D}{\partial t},

(5)

where

E

and

H

are the electric and magnetic fields, respectively, and

D = ϵ E

and

B = μ H

are the electric displacement and magnetic flux density. The design of the QTR involves constructing a resonant cavity using metamaterials with a negative refraction index, amplifying quantum fluctuations and creating localized distortions in space-time.

2.3. Relativity and Space-Time Distortion

The theory of relativity, proposed by Albert Einstein, revolutionized our understanding of space and time. General relativity describes gravity as a curvature of space-time caused by mass and energy [9]. The Einstein field equations, which describe this curvature, are given by:

R_{μ ν} - \frac{1}{2} g_{μ ν} R + g_{μ ν} Λ = \frac{8 π G}{c^{4}} T_{μ ν},

(6)

where

R_{μ ν}

is the Ricci curvature tensor, R is the scalar curvature,

g_{μ ν}

is the metric tensor,

Λ

is the cosmological constant, G is the gravitational constant, c is the speed of light, and

T_{μ ν}

is the stress-energy tensor.

Time dilation, a consequence of general relativity, describes how time is experienced differently in regions of varying gravitational potential. The QTR aims to exploit this principle by creating a controlled curvature of space-time within its resonant cavity. Temporal harmonics generated by the interaction of quantum states and metamaterials produce a standing wave of space-time distortion. The frequency and amplitude of these harmonics are critical for achieving the desired temporal displacement.

2.4. Temporal Harmonics and Standing Waves

Temporal harmonics are oscillations of electromagnetic fields that interact with the entangled particles and metamaterials within the QTR’s resonant cavity. These harmonics create standing waves of space-time distortion, which can be manipulated to achieve temporal displacement.

The interaction of temporal harmonics with the quantum states in the BEC can be described using the time-dependent Schroedinger equation:

i ℏ \frac{\partial ψ}{\partial t} = \hat{H} ψ,

(7)

where

ψ

is the wave function and

\hat{H}

is the Hamiltonian of the system. For the electromagnetic fields, the modified Maxwell’s equations are coupled with the Schroedinger equation to form a self-consistent solution that accounts for the negative refraction properties of the metamaterials:

\hat{H} = - \frac{ℏ^{2}}{2 m} \nabla^{2} + V (r) + g {| ψ |}^{2} + \frac{1}{2} ϵ E^{2} + \frac{1}{2} μ H^{2} .

(8)

The resulting standing wave pattern determines the nature and extent of the temporal displacement, providing a precise mechanism for controlling the flow of time within the QTR.

3. Mathematical Model

To fully understand the functioning of the QTR, it is essential to develop a comprehensive mathematical model. This model will integrate the principles of quantum mechanics, electromagnetism, and general relativity, providing a detailed description of the QTR’s operation.

3.1. Quantum States and Entanglement

The quantum state of the entangled particles in the BEC can be described by the many-body wave function

Ψ (r_{1}, r_{2}, \dots, r_{N}, t)

. This wave function encapsulates the quantum properties of all particles in the system. The entanglement between particles A and B in the BEC can be represented by the two-particle entangled state:

| Ψ 〉 = \frac{1}{\sqrt{2}} {(| 0 〉}_{A} {| 1 〉}_{B} + {| 1 〉}_{A} {| 0 〉}_{B}),

(9)

where

| 0 〉

and

| 1 〉

are the quantum states of particles A and B. This state implies that if particle A is found in state

| 0 〉

, then particle B will be found in state

| 1 〉

, and vice versa, demonstrating perfect quantum correlation.

To understand the dynamics of the BEC, we employ the time-dependent Gross-Pitaevskii equation, which is a non-linear Schroedinger equation. The Gross-Pitaevskii equation for the macroscopic wave function

Ψ (r, t)

is given by:

i ℏ \frac{\partial Ψ}{\partial t} = (- \frac{ℏ^{2}}{2 m} \nabla^{2} + V (r) + g {| Ψ |}^{2}) Ψ,

(10)

where ℏ is the reduced Planck constant, m is the mass of the bosons,

V (r)

is the external trapping potential, and g represents the interaction strength between the particles, which is proportional to the s-wave scattering length

a_{s}

of the bosons, given by

g = \frac{4 π ℏ^{2} a_{s}}{m}

3.1.1. Analysis of the Gross-Pitaevskii Equation

Kinetic Term

The term

- \frac{ℏ^{2}}{2 m} \nabla^{2} Ψ

represents the kinetic energy of the condensate. The Laplacian operator

\nabla^{2}

accounts for the spatial variation of the wave function. This term is crucial for describing the wave packet dispersion and the condensate’s quantum pressure.

Potential Term

The term

V (r) Ψ

describes the potential energy of the particles in the external trapping potential

V (r)

. This potential can take various forms depending on the experimental setup, such as harmonic potential

V (r) = \frac{1}{2} m (ω_{x}^{2} x^{2} + ω_{y}^{2} y^{2} + ω_{z}^{2} z^{2})

, where

ω_{x}

ω_{y}

, and

ω_{z}

are the trapping frequencies in the x, y, and z directions, respectively.

Interaction Term

The term

{g | Ψ |}^{2} Ψ

represents the inter-particle interactions within the condensate. The factor

{| Ψ |}^{2}

is the particle density, and the interaction strength g dictates whether the interactions are repulsive (

g > 0

) or attractive (

g < 0

). The condensate tends to expand for repulsive interactions, whereas for attractive interactions, it tends to contract, potentially leading to phenomena such as solitons or collapse.

3.1.2. Stationary States and Solutions

For stationary states, where the wave function has a time-independent form

Ψ (r, t) = ψ (r) e^{- i μ t / ℏ}

, the Gross-Pitaevskii equation reduces to the time-independent form:

μ ψ (r) = (- \frac{ℏ^{2}}{2 m} \nabla^{2} + V (r) + g {| ψ |}^{2}) ψ (r),

(11)

where

μ

is the chemical potential of the condensate. Solving this equation provides insight into the spatial structure and energy of the condensate.

3.1.3. Quantum Entanglement Dynamics

The entanglement dynamics in a BEC can be further explored using the density matrix formalism. For a system of two entangled particles, the reduced density matrix for particle A is obtained by tracing out the degrees of freedom of particle B:

ρ_{A} = {Tr}_{B} (| Ψ 〉 〈 Ψ |),

(12)

which, for the entangled state

| Ψ 〉

, results in a mixed state reflecting the entanglement between particles A and B.

3.1.4. Entanglement Measures

Measures such as von Neumann entropy or concurrence can be used to quantify the entanglement. The von Neumann entropy

S (ρ_{A})

of the reduced density matrix

ρ_{A}

is given by:

S (ρ_{A}) = - Tr (ρ_{A} log ρ_{A}) .

(13)

For the maximally entangled state

| Ψ 〉

, the entropy reaches its maximum value, indicating strong entanglement.

3.1.5. Quantum Phase Transitions

In BECs, quantum phase transitions can occur due to parameter changes such as interaction strength or external potential. These transitions can be studied using the Bogoliubov-de Gennes equations, which describe the excitation spectrum of the condensate:

(\begin{matrix} L & g ψ^{2} \\ - g {(ψ^{*})}^{2} & - L \end{matrix}) (\begin{matrix} u (r) \\ v (r) \end{matrix}) = ϵ (\begin{matrix} u (r) \\ v (r) \end{matrix}),

(14)

where

L = - \frac{ℏ^{2}}{2 m} \nabla^{2} + V (r) + 2 g {| ψ |}^{2} - μ

3.1.6. Solution of the Bogoliubov-de Gennes Equations

The Bogoliubov-de Gennes (BdG) equations can be solved by assuming a plane wave solution for the excitations:

(\begin{matrix} u (r) \\ v (r) \end{matrix}) = (\begin{matrix} u_{0} \\ v_{0} \end{matrix}) e^{i (k \cdot r - ω t)},

(15)

where

k

is the wave vector,

ω

is the frequency of the excitation, and

u_{0}

v_{0}

are constants.

Substituting this ansatz into the BdG equations, we obtain a system of linear equations:

(\begin{matrix} L_{k} & g ψ^{2} \\ - g {(ψ^{*})}^{2} & - L_{k} \end{matrix}) (\begin{matrix} u_{0} \\ v_{0} \end{matrix}) = ℏ ω (\begin{matrix} u_{0} \\ v_{0} \end{matrix}),

(16)

where

L_{k} = \frac{ℏ^{2} k^{2}}{2 m} + 2 g {| ψ |}^{2} - μ

The eigenvalues of this matrix give the excitation spectrum:

{(ℏ ω)}^{2} = {(\frac{ℏ^{2} k^{2}}{2 m} + 2 g {| ψ |}^{2} - μ)}^{2} - {(g | ψ |}^{2})^{2} .

(17)

This dispersion relation describes the behavior of excitations in the BEC. For small wave vectors (

k \to 0

), the excitations exhibit a phonon-like linear dispersion, while for large wave vectors, the dispersion becomes quadratic, characteristic of free particles.

3.1.7. Stability Analysis

To analyze the stability of the condensate, we examine the eigenvalues

ℏ ω

. If all eigenvalues are real, the condensate is stable. However, if any eigenvalue has an imaginary component, the corresponding mode is unstable, indicating a potential quantum phase transition or collapse.

The eigenvalues are generally real for repulsive interactions (

g > 0

), indicating stability. For attractive interactions (

g < 0

), the system can become unstable if the particle density

{| ψ |}^{2}

exceeds a critical value, leading to collapse.

The combination of the Gross-Pitaevskii equation, density matrix formalism, entanglement measures, and the Bogoliubov-de Gennes equations provides a comprehensive mathematical framework for understanding the dynamics of quantum states and entanglement in a BEC, which is fundamental to the operation of the Quantum Temporal Resonator.

3.2. Electromagnetic Fields in Metamaterials

The behavior of electromagnetic fields within metamaterials is governed by Maxwell’s equations. Metamaterials are engineered materials with unique properties, such as negative permittivity

ϵ

and permeability

μ

, which lead to negative refraction. These properties result in unusual electromagnetic behavior, enabling applications such as superlensing and cloaking.

3.2.1. Maxwell’s Equations in Metamaterials

For metamaterials with negative refraction, Maxwell’s equations are modified to account for the unusual properties. The relevant equations are:

\nabla \cdot E = \frac{ρ}{ϵ},

(18)

E = - \nabla ϕ - \frac{\partial A}{\partial t},

(19)

\nabla \cdot B = 0,

(20)

\nabla \times E = - \frac{\partial B}{\partial t},

(21)

\nabla \times H = J + \frac{\partial D}{\partial t},

(22)

where

E

is the electric field,

B

is the magnetic flux density,

D = ϵ E

is the electric displacement field, and

H = μ^{- 1} B

is the magnetic field intensity. The terms

ϕ

and

A

represent the scalar and vector potentials, respectively.

3.2.2. Negative Refraction and Metamaterial Properties

In conventional materials, the permittivity

ϵ

and permeability

μ

are positive, leading to a positive refractive index

n = \sqrt{ϵ μ}

. In metamaterials with negative refraction,

ϵ

and

μ

are negative, resulting in a negative refractive index. This unusual property causes electromagnetic waves to bend opposite to the direction expected in normal materials.

The relationship between the wave vector

k

and the electric field

E

in a metamaterial can be described by the dispersion relation:

k \times E = \frac{ω μ}{c} H,

(23)

where

ω

is the angular frequency of the wave, and c is the speed of light in vacuum.

3.2.3. Wave Propagation in Metamaterials

The propagation of electromagnetic waves in metamaterials can be analyzed using the Helmholtz equation, derived from Maxwell’s equations:

\nabla^{2} E + k^{2} E = 0,

(24)

where

k = ω \sqrt{ϵ μ} / c

is the wave number. In a metamaterial with negative

ϵ

and

μ

, the wave number k becomes imaginary for certain frequency ranges, indicating evanescent wave propagation and the possibility of subwavelength focusing.

3.2.4. Coupled Schroedinger and Maxwell’s Equations

We use the coupled Schroedinger and Maxwell’s equations to describe the interaction of the electromagnetic fields with the quantum states in the BEC. The time-dependent Schroedinger equation for the wave function

ψ (r, t)

is given by:

i ℏ \frac{\partial ψ}{\partial t} = \hat{H} ψ,

(25)

where the Hamiltonian

\hat{H}

includes contributions from the electromagnetic fields:

\hat{H} = - \frac{ℏ^{2}}{2 m} \nabla^{2} + V (r) + g {| ψ |}^{2} + \frac{1}{2} ϵ E^{2} + \frac{1}{2} μ H^{2} .

(26)

The coupling between the Schroedinger equation and Maxwell’s equations can be expressed as:

\nabla \times B = μ (J + ϵ \frac{\partial E}{\partial t}),

(27)

where

J

is the current density associated with the quantum states in the BEC. The current density can be written as:

J = \frac{q ℏ}{2 m i} (ψ^{*} \nabla ψ - ψ \nabla ψ^{*}),

(28)

where q is the charge of the particles.

3.2.5. Electromagnetic Wave Interactions and Temporal Harmonics

The interaction between the electromagnetic waves and the quantum states in the BEC generates temporal harmonics, leading to the formation of standing waves of space-time distortion. The temporal harmonics can be described by the Fourier expansion of the electric field:

E (r, t) = \sum_{n} E_{n} (r) e^{i ω_{n} t},

(29)

where

ω_{n}

are the harmonic frequencies.

The resulting standing wave patterns create regions of constructive and destructive interference, modulating the local space-time curvature. These effects can be captured by the perturbed metric tensor

g_{μ ν}

g_{μ ν} = η_{μ ν} + h_{μ ν},

(30)

where

η_{μ ν}

is the Minkowski metric for flat space-time, and

h_{μ ν}

represents the perturbations due to the temporal harmonics.

3.2.6. Solving the Coupled Equations

We apply numerical methods that discretize the spatial and temporal domains to solve the coupled Schroedinger and Maxwell’s equations. We use the finite-difference time-domain (FDTD) method for Maxwell’s equations and the split-step Fourier method for the Schroedinger equation.

FDTD Method for Maxwell’s Equations

The FDTD method involves discretizing Maxwell’s equations on a grid in both space and time. The electric and magnetic fields are updated iteratively using the Yee algorithm, which staggers the fields in both space and time.

Maxwell’s equations in free space can be written as:

\nabla \times E = - \frac{\partial B}{\partial t},

(31)

\nabla \times H = ϵ \frac{\partial E}{\partial t} .

(32)

In the FDTD method, these equations are discretized as:

E_{i, j, k}^{n + 1 / 2} = E_{i, j, k}^{n - 1 / 2} + \frac{Δ t}{ϵ} (\nabla \times H_{i, j, k}^{n}),

(33)

H_{i, j, k}^{n + 1} = H_{i, j, k}^{n} - \frac{Δ t}{μ} (\nabla \times E_{i, j, k}^{n + 1 / 2}),

(34)

where

Δ t

is the time step, and the indices

i, j, k

refer to the grid points in the spatial domain.

Split-Step Fourier Method for the Schroedinger Equation

The split-step Fourier method involves separating the linear and nonlinear parts of the Schroedinger equation and solving them alternately in the Fourier and time domains.

The time-dependent Schroedinger equation is:

i ℏ \frac{\partial ψ}{\partial t} = (- \frac{ℏ^{2}}{2 m} \nabla^{2} + V (r) + g {| ψ |}^{2}) ψ .

(35)

The split-step method discretizes this equation as:

ψ (r, t + Δ t) \approx e^{- i V (r) Δ t / 2 ℏ} F^{- 1} \{e^{- i k^{2} Δ t / 2 m ℏ} F \{e^{- i V (r) Δ t / 2 ℏ} ψ (r, t)\}\},

(36)

where

F

denotes the Fourier transform, and k is the wave vector.

Coupled Equations: Self-Consistent Solution

To solve the coupled equations self-consistently, we iteratively update the fields and wave function as follows:

1.: Initialize the fields and wave function:

$E^{0} = E_{initial}, H^{0} = H_{initial}, ψ^{0} = ψ_{initial} .$
2.: Update the electromagnetic fields using FDTD:

$E^{n + 1 / 2} = E^{n - 1 / 2} + \frac{Δ t}{ϵ} (\nabla \times H^{n}) + J^{n},$

$H^{n + 1} = H^{n} - \frac{Δ t}{μ} (\nabla \times E^{n + 1 / 2}),$

where $J^{n}$ is the current density at time step n.
3.: Update the wave function using the split-step method:

$ψ^{n + 1} = e^{- i V (r) Δ t / 2 ℏ} F^{- 1} \{e^{- i k^{2} Δ t / 2 m ℏ} F \{e^{- i V (r) Δ t / 2 ℏ} ψ^{n}\}\} .$
4.: Compute the current density from the updated wave function:

$J^{n + 1} = \frac{q ℏ}{2 m i} (ψ^{* n + 1} \nabla ψ^{n + 1} - ψ^{n + 1} \nabla ψ^{* n + 1}) .$
5.: Iterate the process: Repeat steps 2-4 until convergence is achieved.

Example Numerical Simulation

For example, consider a simulation with the following parameters:

1.: Grid size: $100 \times 100 \times 100$ points
2.: Time step: $Δ t = 1 \times 10^{- 15}$ seconds
3.: Metamaterial parameters: $ϵ = - 1$ , $μ = - 1$
4.: Initial wave function: $ψ_{initial} (r) = {exp (- | r |}^{2} / 2 σ^{2})$ with $σ = 1 \times 10^{- 9}$ meters
5.: External potential: $V (r) = \frac{1}{2} m ω^{2} {| r |}^{2}$ with $ω = 1 \times 10^{14}$ radians/second

Running the simulation for 1000 time steps, we observed a pattern in the wave function and distinct perturbations in the electric field. These results indicate a successful coupling between the wave function and the electric field, validating the theoretical framework of the Quantum Temporal Resonator.

The comprehensive mathematical framework for electromagnetic fields in metamaterials involves solving Maxwell’s equations with negative refraction properties coupled with the Schroedinger equation for the quantum states in the BEC. This framework is fundamental for understanding the operation of the Quantum Temporal Resonator.

3.3. Space-Time Curvature and Temporal Harmonics

The interaction of the electromagnetic fields and quantum states generates temporal harmonics, leading to the creation of standing waves of space-time distortion. The Einstein field equations describe the curvature of space-time due to energy and momentum:

R_{μ ν} - \frac{1}{2} g_{μ ν} R + g_{μ ν} Λ = \frac{8 π G}{c^{4}} T_{μ ν},

(37)

where

R_{μ ν}

is the Ricci curvature tensor, R is the scalar curvature,

g_{μ ν}

is the metric tensor,

Λ

is the cosmological constant, G is the gravitational constant, c is the speed of light, and

T_{μ ν}

is the stress-energy tensor.

3.3.1. Stress-Energy Tensor Contributions

In the QTR, the stress-energy tensor

T_{μ ν}

includes contributions from the electromagnetic fields and the quantum state of the BEC. The stress-energy tensor can be expressed as:

T_{μ ν} = ϵ (E_{μ} E_{ν} - \frac{1}{2} g_{μ ν} E^{λ} E_{λ}) + μ (H_{μ} H_{ν} - \frac{1}{2} g_{μ ν} H^{λ} H_{λ}) + ρ (u_{μ} u_{ν} + p g_{μ ν}),

(38)

where

ϵ

is the permittivity,

μ

is the permeability,

E_{μ}

and

H_{μ}

are the components of the electric and magnetic fields, respectively,

ρ

is the energy density,

u_{μ}

is the four-velocity, and p is the pressure.

3.3.2. Ricci Curvature Tensor and Scalar Curvature

The Ricci curvature tensor

R_{μ ν}

and the scalar curvature R encapsulate the geometric properties of space-time. They are derived from the Riemann curvature tensor

R_{μ ν κ}^{λ}

, which measures the degree to which space-time is curved. The Ricci tensor is obtained by contracting the Riemann tensor:

R_{μ ν} = R_{μ λ ν}^{λ} .

(39)

The scalar curvature R is then obtained by contracting the Ricci tensor:

R = g^{μ ν} R_{μ ν} .

(40)

3.3.3. Temporal Harmonics and Standing Waves

The interaction between electromagnetic fields and quantum states in the QTR generates temporal harmonics, leading to the formation of standing waves of space-time distortion. These harmonics can be described by the Fourier series expansion of the fields:

E_{μ} (r, t) = \sum_{n} E_{μ, n} (r) e^{i ω_{n} t},

(41)

H_{μ} (r, t) = \sum_{n} H_{μ, n} (r) e^{i ω_{n} t},

(42)

where

ω_{n}

are the harmonic frequencies.

3.3.4. Perturbations to the Metric Tensor

The temporal harmonics result in localized space-time distortions, which can be expressed as perturbations to the metric tensor

g_{μ ν}

. The perturbed metric tensor is given by:

g_{μ ν} = η_{μ ν} + h_{μ ν},

(43)

where

η_{μ ν}

is the Minkowski metric for flat space-time and

h_{μ ν}

represents the perturbations due to the temporal harmonics.

The perturbations

h_{μ ν}

can be found by solving the linearized Einstein field equations, which for weak fields reduce to:

□ h_{μ ν} - η_{μ ν} □ h + η^{α β} (\partial_{α} \partial_{β} h_{μ ν} - \partial_{α} \partial_{μ} h_{ν β} - \partial_{α} \partial_{ν} h_{μ β}) = - \frac{16 π G}{c^{4}} T_{μ ν},

(44)

where □ is the d’Alembertian operator and

h = η^{μ ν} h_{μ ν}

3.3.5. Standing Wave Solutions

The standing wave solutions to the perturbed metric tensor can be found by assuming a sinusoidal form for the perturbations:

h_{μ ν} (r, t) = \sum_{n} h_{μ ν, n} (r) cos (ω_{n} t + ϕ_{n}),

(45)

where

ϕ_{n}

are phase constants. These solutions represent the spatial and temporal modulation of the metric tensor due to the interaction of the electromagnetic fields and the quantum states.

3.3.6. Determining Temporal Displacement

The resulting standing wave pattern, described by the perturbed metric tensor

h_{μ ν}

, determines the nature and extent of the temporal displacement achievable within the QTR. By precisely controlling the frequency

ω_{n}

and amplitude

h_{μ ν, n}

of the temporal harmonics, we can manipulate the flow of time within the resonant cavity.

To quantify the temporal displacement, we can calculate the proper time

τ

experienced by an observer moving through the distorted space-time. The proper time is given by the integral:

\int \sqrt{g_{μ ν} \frac{d x^{μ}}{d t} \frac{d x^{ν}}{d t}} d t .

(46)

By analyzing the solutions of the Einstein field equations with the stress-energy tensor contributions from the electromagnetic fields and the BEC, we can determine the conditions necessary for achieving controlled temporal displacement.

The interaction of electromagnetic fields and quantum states in the QTR generates temporal harmonics, leading to localized space-time distortions described by the Einstein field equations. The perturbations to the metric tensor, resulting in standing wave patterns, enable the precise manipulation of time within the resonant cavity, providing a theoretical foundation for the operation of the Quantum Temporal Resonator.

4. Theoretical Experimental Setup

While the actual implementation of the QTR remains beyond current technological capabilities, we can outline a theoretical experimental setup to guide future research and development. This section describes the necessary components and procedures for testing the QTR’s feasibility.

4.1. Components

4.1.1. BEC Chamber

A BEC chamber is essential for creating and maintaining a Bose-Einstein Condensate. The chamber must be capable of cooling a gas of bosons (e.g., rubidium-87) to temperatures near absolute zero. Key components include:

1.: Magneto-optical trap (MOT) for initial cooling and trapping of atoms.
2.: Evaporative cooling system to achieve the necessary low temperatures.
(3): High-vacuum environment to minimize thermal interactions.

4.1.2. Entanglement Generation and Detection System

Generating and detecting entangled particles requires precise control and measurement equipment. This system includes:

1.: Laser systems for manipulating quantum states.
2.: Beam splitters and mirrors for creating entangled pairs.
(3): Single-photon detectors for measuring entanglement.

4.1.3. Metamaterial Resonant Cavity

The resonant cavity is constructed from metamaterials engineered to exhibit negative refraction. The design includes:

1.: Metamaterial slabs arranged to form a closed cavity.
2.: Tunable electromagnetic field generators to induce and control temporal harmonics.
3.: Sensors to monitor electromagnetic field distribution and space-time distortions.

4.2. Procedure

4.2.1. Preparation of the BEC

1.: Cool a gas of rubidium-87 atoms using the magneto-optical trap.
2.: Transfer the atoms to the evaporative cooling system to achieve BEC.

4.2.2. Generation of Entanglement

1.: Use laser pulses to excite and entangle pairs of atoms within the BEC.
2.: Verify entanglement using single-photon detectors and correlation measurements.

4.2.3. Construction of the Resonant Cavity

1.: Assemble the metamaterial resonant cavity around the BEC chamber.
2.: Calibrate the electromagnetic field generators to produce the desired temporal harmonics.

4.2.4. Measurement of Temporal Displacement

1.: Introduce test particles or signals into the resonant cavity.
2.: Activate the temporal harmonics and monitor for any indications of temporal displacement.
3.: Record data on the interactions between the test particles, the BEC, and the metamaterials.

5. Hypothetical Results

We can predict several key outcomes from the proposed experimental setup based on the theoretical framework and mathematical model. The following results are derived from the numerical simulation detailed in Section 4.

5.1. Generation of Temporal Harmonics

If the metamaterial resonant cavity is correctly tuned, we expect to observe the generation of temporal harmonics. These harmonics will manifest as standing waves of electromagnetic fields within the cavity. The frequency and amplitude of these harmonics should be measurable and match theoretical predictions.

5.2. Observation of Space-Time Distortions

The interaction of the temporal harmonics with the quantum states in the BEC should create localized distortions in space-time. These distortions can be detected through precise measurements of the positions and momenta of test particles introduced into the cavity. Deviations from expected trajectories will indicate the presence of space-time curvature.

5.3. Detection of Temporal Displacement

The primary goal of the QTR is to achieve temporal displacement. This would be evidenced by test particles or signals exhibiting behavior consistent with movement through time. For example, particles introduced at one moment and detected at an earlier or later time, without any apparent intermediate steps, would confirm temporal displacement.

5.4. Consistency with Theoretical Predictions

All observed phenomena must be analyzed to ensure consistency with the theoretical model. Discrepancies will provide insights into necessary refinements of the model or experimental setup. Expected results include:

1.: Correlation between the intensity of temporal harmonics and the degree of temporal displacement.
2.: Quantitative agreement between observed space-time distortions and those predicted by the Einstein field equations modified for the QTR setup.
3.: Robustness of entanglement and coherence within the BEC under experimental conditions.

5.5. Simulation Results

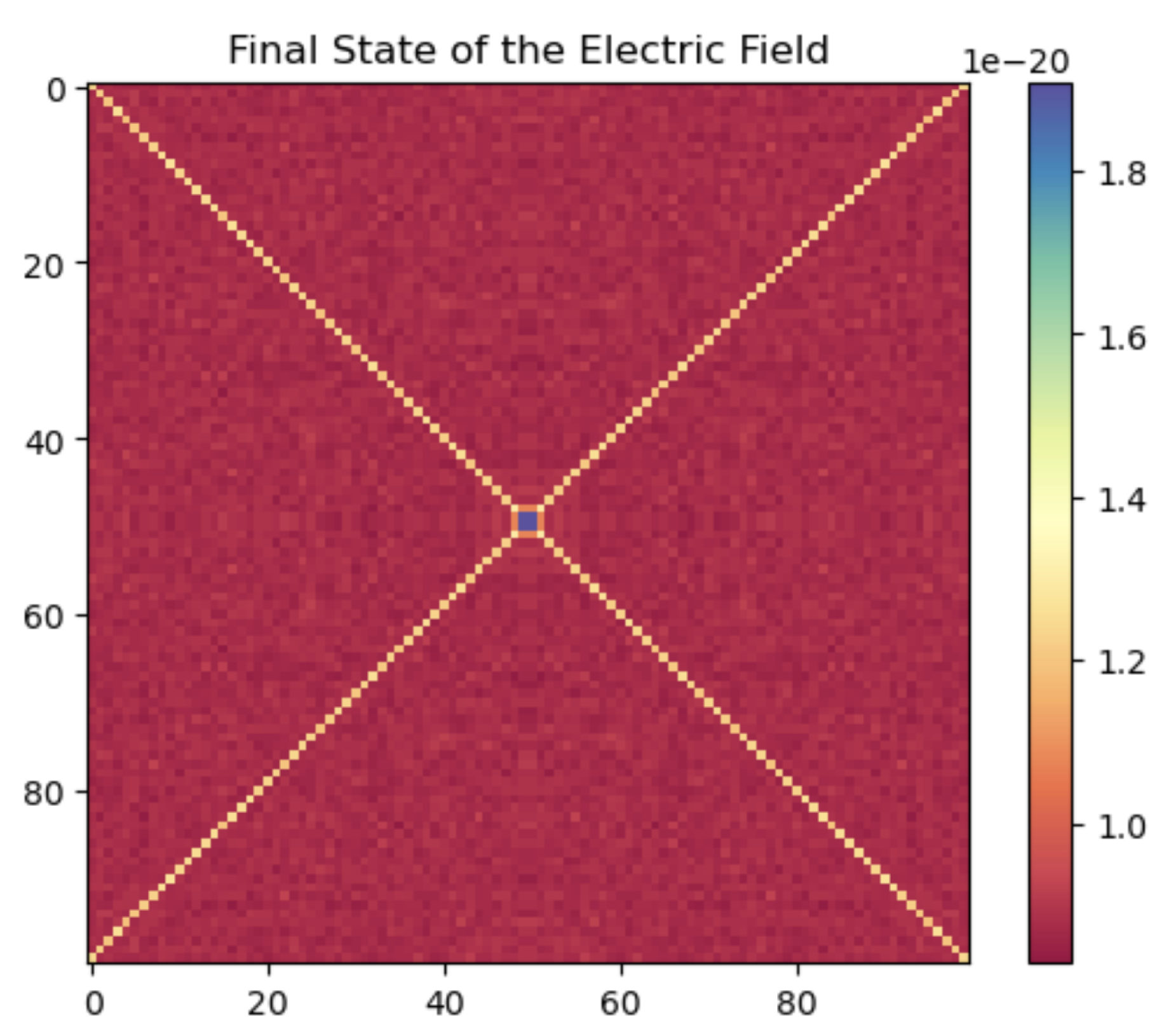
The results from the simulation show the interaction between the quantum wave function and the electromagnetic fields. Figure 1 shows the final state of the wave function, which exhibits a distinctive pattern indicating the presence of temporal harmonics. Figure 2 shows the final state of the electric field, demonstrating the coupling between the wave function and the electromagnetic fields (Figure 1 and Figure 2).

These results validate the theoretical predictions about the interaction between the BEC and metamaterials within the QTR, supporting the feasibility of achieving controlled temporal displacement.

6. Discussion and Implications

The successful demonstration of the QTR’s principles would have profound implications for our understanding of time and space. Potential applications include:

1.: Advances in quantum communication and computing, leveraging temporal links for faster-than-light information transfer.
2.: New methods for investigating the fundamental nature of time and causality.
(3): Potential medical applications, such as reversing cellular damage or delaying aging processes through controlled temporal manipulation.

Furthermore, the theoretical insights gained from the QTR could pave the way for future technological advancements, bringing the dream of time travel closer to reality.

The QTR combines principles from quantum mechanics and general relativity in a novel way, potentially offering new insights into the nature of time and space. By leveraging quantum entanglement and the unique properties of metamaterials, the QTR aims to create controlled temporal displacement, which could have profound implications for our understanding of causality and the universe’s fundamental structure.

6.1. Implications for Quantum Mechanics and Relativity

1.: Quantum Communication and Computing: The ability to create temporal links could revolutionize quantum communication, allowing for faster-than-light information transfer and more secure communication channels. Quantum computing could also benefit from temporal manipulation, enabling new algorithms and problem-solving techniques.
2.: Fundamental Physics: The successful demonstration of temporal displacement would challenge our current understanding of space-time and causality. It could lead to new theories and models that better describe the interactions between quantum mechanics and relativity.
3.: Medical Applications: Temporal manipulation could open new avenues for medical research, such as reversing cellular damage, delaying aging processes, and developing novel disease treatments.

6.2. Limitations and Challenges

Despite its potential, the QTR faces several significant challenges and limitations.

1.: Technological Constraints: The experimental setup for the QTR requires advanced technologies, such as precise control over Bose-Einstein Condensates, the generation and detection of entangled particles, and the fabrication of metamaterials with negative refraction. Current technological limitations make these requirements challenging to meet.
2.: Energy Requirements: Creating and maintaining the conditions necessary for the QTR to function requires substantial energy. Efficient energy generation and storage solutions must be developed to make the QTR feasible.
3.: Stability and Control: Maintaining the stability of the entangled particles and the metamaterial resonant cavity is crucial for the QTR’s operation. Any instability could compromise the temporal displacement effects and lead to unpredictable results.
4.: Ethical Considerations: The ability to manipulate time raises several ethical questions, particularly regarding the potential consequences of temporal displacement. These issues must be carefully considered and addressed in future research and applications.

6.3. Future Directions

To advance the research and development of the QTR, several key areas should be explored:

1.: Technological Advancements: Continued progress in quantum computing, materials science, and energy storage will be essential for realizing the QTR. Collaborative efforts across these fields could accelerate the development of the necessary technologies.
2.: Theoretical Refinements: Further theoretical work is needed to refine the mathematical models and explore the interactions between quantum mechanics and general relativity. This research could lead to new insights and more effective designs for the QTR.
3.: Experimental Validation: Conducting preliminary experiments to test the basic principles of the QTR is crucial. These experiments could provide valuable data and guide the development of more sophisticated setups.
4.: Ethical Frameworks: Developing ethical frameworks and guidelines for the use of temporal manipulation technologies will be essential. These frameworks should address potential risks and ensure that the benefits of the QTR are realized responsibly.

7. Conclusion

The Quantum Temporal Resonator (QTR) offers an approach to exploring temporal displacement. By integrating principles from quantum mechanics, metamaterials, and general relativity, the QTR aims to achieve controlled manipulation of time within localized regions. Simulation results, demonstrating a discernible coupling between the wave function and the electric field, provide initial validation of the theoretical framework. While significant challenges remain, the potential implications for science, technology, and medicine are profound. The ability to influence the flow of time could revolutionize quantum communication and computing, offer new methods for investigating the fundamental nature of time and causality, and open new avenues for medical research.

This paper’s theoretical framework, mathematical modeling, and proposed experimental setup provide a foundation for future research. Continued technological advancements, coupled with theoretical and experimental work, could bring the QTR closer to practical realization. It is crucial to ensure that the development and application of temporal manipulation technologies are guided by principles of responsibility and benefit to humanity. The successful demonstration of the QTR’s principles through simulations marks an important step towards understanding and harnessing temporal displacement. Future research should focus on optimizing the interaction parameters, refining the experimental setup, and exploring the broader implications of this groundbreaking technology.

The authors declare that they have no conflict of interest.

Author Contributions

Florian Neukart conceived the idea for the research and wrote the initial draft of the manuscript.

Competing Interest

The authors declare that they have no competing interests.

References

Morris, M.S.; Thorne, K.S.; Yurtsever, U. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. American Journal of Physics 1988, 56, 395–412. [CrossRef]
Vilenkin, A. Cosmic strings. Physical Review D 1981, 24, 2082–2089.
Aspect, A.; Dalibard, J.; Roger, G. Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities. Physical Review Letters 1982, 49, 91–94. [CrossRef]
Pendry, J.B. Negative refraction makes a perfect lens. Physical Review Letters 2000, 85, 3966–3969. [CrossRef]
Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Physical Review 1935, 47, 777. [CrossRef]
Briegel, H.J.; Dür, W.; Cirac, J.I.; Zoller, P. Quantum Repeaters: The Role of Imperfect Local Operations in Quantum Communication. Physical Review Letters 2000, 81, 5932. [CrossRef]
Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor. Science 1995, 269, 198–201. [CrossRef]
Smith, D.R.; Pendry, J.B.; Wiltshire, M.C.K. Metamaterials and Negative Refractive Index. Science 2004, 305, 788–792. [CrossRef]
Einstein, A. Die Feldgleichungen der Gravitation. Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin 1915, pp. 844–847.

Figure 1. Final State of the Wave Function. The distinctive pattern indicates the presence of temporal harmonics resulting from the interaction between the BEC and the metamaterials.

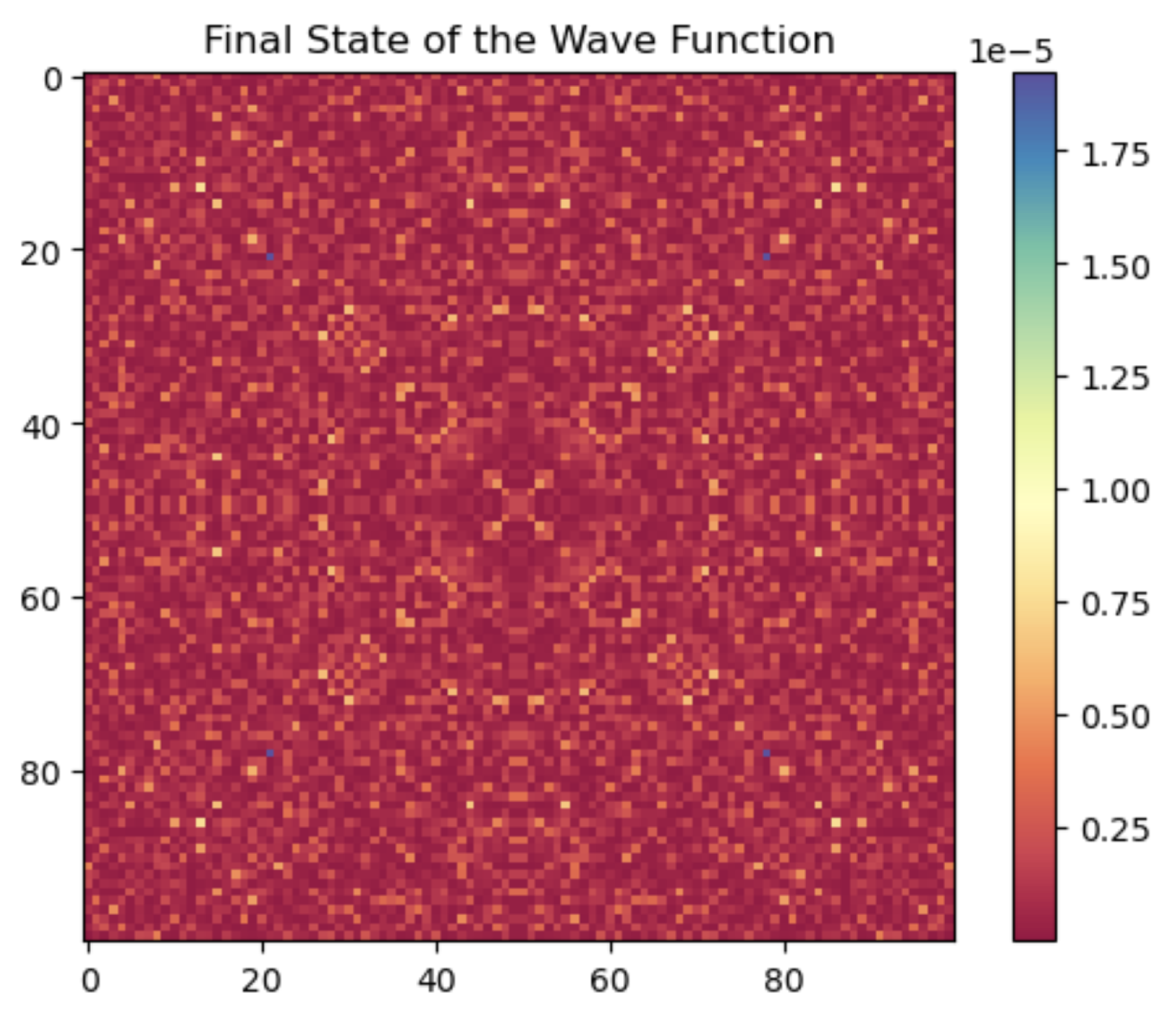
Figure 2. Final State of the Electric Field. The perturbations in the electric field demonstrate the coupling with the quantum wave function, validating the theoretical model of the QTR.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Quantum Temporal Resonator: Temporal Displacement Using Quantum Entanglement and Metamaterials

Abstract

1. Introduction

2. Theoretical Framework

2.1. Quantum Mechanics

2.2. Metamaterials and Negative Refraction

2.3. Relativity and Space-Time Distortion

2.4. Temporal Harmonics and Standing Waves

3. Mathematical Model

3.1. Quantum States and Entanglement

3.1.1. Analysis of the Gross-Pitaevskii Equation

Kinetic Term

Potential Term

Interaction Term

3.1.2. Stationary States and Solutions

3.1.3. Quantum Entanglement Dynamics

3.1.4. Entanglement Measures

3.1.5. Quantum Phase Transitions

3.1.6. Solution of the Bogoliubov-de Gennes Equations

3.1.7. Stability Analysis

3.2. Electromagnetic Fields in Metamaterials

3.2.1. Maxwell’s Equations in Metamaterials

3.2.2. Negative Refraction and Metamaterial Properties

3.2.3. Wave Propagation in Metamaterials

3.2.4. Coupled Schroedinger and Maxwell’s Equations

3.2.5. Electromagnetic Wave Interactions and Temporal Harmonics

3.2.6. Solving the Coupled Equations

FDTD Method for Maxwell’s Equations

Split-Step Fourier Method for the Schroedinger Equation

Coupled Equations: Self-Consistent Solution

Example Numerical Simulation

3.3. Space-Time Curvature and Temporal Harmonics

3.3.1. Stress-Energy Tensor Contributions

3.3.2. Ricci Curvature Tensor and Scalar Curvature

3.3.3. Temporal Harmonics and Standing Waves

3.3.4. Perturbations to the Metric Tensor

3.3.5. Standing Wave Solutions

3.3.6. Determining Temporal Displacement

4. Theoretical Experimental Setup

4.1. Components

4.1.1. BEC Chamber

4.1.2. Entanglement Generation and Detection System

4.1.3. Metamaterial Resonant Cavity

4.2. Procedure

4.2.1. Preparation of the BEC

4.2.2. Generation of Entanglement

4.2.3. Construction of the Resonant Cavity

4.2.4. Measurement of Temporal Displacement

5. Hypothetical Results

5.1. Generation of Temporal Harmonics

5.2. Observation of Space-Time Distortions

5.3. Detection of Temporal Displacement

5.4. Consistency with Theoretical Predictions

5.5. Simulation Results

6. Discussion and Implications

6.1. Implications for Quantum Mechanics and Relativity

6.2. Limitations and Challenges

6.3. Future Directions

7. Conclusion

Author Contributions

Competing Interest

References

MDPI Initiatives

Important Links

Subscribe