Prerpints.org logo
Preprint
Article

A Hybrid Forecasting Structure Based On Arima And Artificial Neural Network Models

Altmetrics

Downloads

80

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

09 July 2024

Posted:

10 July 2024

You are already at the latest version

Alerts
Abstract
This study involves the development of a hybrid forecasting framework that integrates two different models in a framework to improve prediction capability. Although the concept of hybridization is not a new issue in forecasting, our approach presents a new structure that combines two standard simple forecasting models uniquely for superior performance. Hybridization is significant for complex data sets with multiple patterns. Such data sets do not respond well to simple models, and hybrid models based on the integration of various forecasting tools often lead to better forecasting performance. The proposed architecture includes serially connected ARIMA and ANN models. The original data set is first processed by ARIMA. The error (i.e., residuals) of the ARIMA is sent to the ANN for secondary processing. Between these two models, there is a classification mechanism where the raw output of the ARIMA is categorized into three groups before they are sent to the secondary model. The algorithm is tested on well-known forecasting cases from the literature. The proposed model performs better than existing methods in most cases.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

A time series is a set of records collected over time. To be called a time series, the data should be ordered chronologically, with equal distance between observation points. A weekly sale of a particular item in a store would comprise a time series. Depending on circumstances, data may be collected hourly, daily, weekly, monthly, etc. Time-indexed data could be the subject matter of a diverse spectrum of research areas, including science, engineering, and finance. Such broad interest from different fields has led to developing an assorted set of forecasting approaches.
Developing forecast models for time series can be challenging from several perspectives. In many instances, there is no insight into the underlying mechanism that generates data, hindering the development of a valid mathematical model. Empirical data is a product of a complex real-world mechanism (e.g., daily change in stock prices); standard statistical procedures may be inadequate to reveal the underlying relationships.
That built-up complexity in the data may exhibit itself as noise or be observed as nonstationary or nonlinear behavior. Noise is a natural phenomenon because many undetected variables impact the controlled variable. For effective modeling, the noise has to be appropriately identified and excluded by the model. Nonstationarity refers to the dynamic nature of the data. The underlying process that generates the data changes over time, and the model has to be capable of determining these changes. In the long run, almost all data series become nonstationary because of the dynamic nature of the underlying processes. This brings the issue of determining the length of usable history, which is a challenging task. To further aggravate the issue, noise in the series may vary with time. Nonlinearity is also another interesting issue. Most of the time, models are based on the assumption that the underlying relationship is linear, which may not be valid for all instances. There are many examples where it has been shown that the nonlinear model serves as a better fit for the data [1].
Inherent difficulties in time series modeling led researchers to look for creative alternatives. One popular method is to combine different forecasting models in a framework to enhance forecasting capability. This process is better known as hybridization, based on the following premise. Each modeling methodology has its superior aspects but may be weak in others, and it is possible to combine them in a framework to maximize the overall benefit. Efforts to combine multiple forecasting models can be traced back to the pioneering work of Bates and Granger [2], in which two separate forecasts generated by different approaches are combined into one to minimize the variance. Many researchers followed the path opened by Bates and Granger [2] to develop creative hybrid models. With more accurate and reliable forecasts, hybrid models ranked top in prominent forecasting competitions. In a recent M4 competition, where each entrant had to generate forecasts for thousands of data sets, a hybrid model that combined exponential smoothing and recurrent neural networks came first by a solid margin [3]. Our research contributes to this field with its unique structure of combining two standard forecasting methods.

2. Literature Review

Because of the broad nature of time series forecasting, the literature review is confined to previous works related directly to our proposed approach. The subject of hybridization, which covers umbrella structures combining different forecasting methods, can be divided into two broad categories. In the first category, each model runs independently and generates a separate forecast. These forecasts are then consolidated into a final number. The pioneering work of Bates and Granger [2] falls into this category. Their method involves generating two separate forecasts and then averaging them into a single number. In the second category, models are connected in series. Figure 1 shows a simple, serially connected model, where the output of the first model is directly fed into the second one. In this serial combination, the underlying implicit assumption is that the series can be decomposed into distinct sub-categories. Once the series is decomposed, we can handle each sub-category with a different model.
For the serial combination of models, the earliest arrangement is proposed by Zhang [4] where ARIMA (autoregressive integrated moving average) and ANN are connected in series as basic and secondary models. Following this work, various serially connected models utilizing both linear and nonlinear methods have been proposed. Additionally, the original approach was fine-tuned for better performance [5].
The accumulated work in serially-connected hybrid models can be further divided into two broad categories. The first category includes studies that propose a new forecasting method for basic or secondary models. The "new" methodology does not necessarily refer to an original approach, but it is something new within the context of serial hybridization. Here, the emphasis is on the novelty of the method used, and model verification and validation are often done by using popular data sets from the literature. The second category of research is about applications of hybrid models. This work aims to generate the most accurate forecast and often involves trial and error of multiple hybrid alternatives.
One caveat is that the categorization schema presented above is not clear-cut, and some works can claim novelty in terms of both methodology and data sets involved. Within the framework of this broad division, the list of recent works for each category is listed below. For methodology-oriented research: Autoregressive moving average (MARMA) and exogenous multi-variable input [6], ARIMAX (ARIMA with explanatory variables), Holt-winter, ANN [7], SARIMAX (seasonal ARIMA with explanatory variables), LSSVM (least-squares support-vector machine) [8], ARMAX, ANN [9] , ARIMA and ANN [10,11,12]. For application-oriented research: Wind speed forecasting [7,13], oil prices [12], tourist arrivals [14], monthly rainfall [8], computer network traffic [15], and dengue epidemics [11].
Two interesting serial-model studies deserve special mention, as they are related directly to our work. In both studies, the output of the first model is not sent directly to the secondary model. Instead, the residuals, the difference between actual and fitted values, are analyzed and then sent to the second model according to a preset algorithm. The first approach proposed by Khashei et al. [5] combines ARIMA with PNN (probabilistic neural networks) as first and secondary models. The PNN utilizes the error output of the ARIMA. Error values coming out of ARIMA are categorized, and each category is treated differently by PNN. The second study, by Babu and Reddy [16], also uses the ARIMA and ANN combination, and it has a similar error classification mechanism between the first and second models. The error output of the first model is classified according to spread around the mean. For this purpose, the mean value for the error output of the first model and the accompanying deviation for each observation are calculated. Based on the magnitude of the deviation, observations are categorized as high- and low-volatility groups, and each group is treated differently by the ANN model.

3. Methodology

The proposed hybrid model has two components that are connected sequentially. The first one is called the basic model, and includes ARIMA forecasting to capture the linear relationship of the input data. The output of the ARIMA is fed into the second component. A neural network model capable of capturing both linear and nonlinear patterns is used in the second component. As most data sets are composed of linear and nonlinear elements, two separate models that work in tandem will be more effective in capturing different portions of the data. Before moving into details of the hybrid model, brief descriptions of ARIMA and ANN models are given below.

3.1. ARIMA Models

ARIMA is a popular forecasting tool used in time series forecasting. In this approach, the forecast is based on the linear combination of past values and random errors. The general formula for an ARIMA (p,d,q) model is given in Equation 1. Two primary components of ARIMA are autoregressive (AR) and moving average (MA) functions. The p and q parameters in Equation 1 represent the order of AR and MA functions, respectively. The third parameter, d, gives the number of differencing performed on the series to make it stationary.
1 − ϕ 1 B − ϕ 2 B 2 − . . . − ϕ p B p 1 − B d Y = 1 − θ 1 B − θ 2 B 2 − . . . − θ q B q e t t
where Y t and e t represent the actual value and the error (offset between the actual and the fitted value). Parameter sets ϕ i (i= 1,2,…,p) and θ j (j= 0,1,2,…,q) represent AR and MA sections of the ARIMA. The term (1-B)d serves as a difference operator.

3.2. Artificial Neural Networks (ANN)

ANN are computational systems based on the operational structure of a biological brain. ANN architecture consists of units (i.e., neurons) that are organized in layers. In addition to input and output layers, there are hidden layers between the input and the output. ANN is a nonparametric approach that can extract nonlinear dynamics present in the data. Because of the limitations of statistical tools, ANN has long been regarded as an alternative route to deal with nonlinear problems in various fields. There are various architectures used in ANN, some of which mimic the function of the brain, but others are mathematical representations constructed according to the problem requirements. Among these varieties, MLP (multi-layer perceptron) has long been used for nonlinear regression problems.

3.3. Forecast Accuracy Metrics

The accuracy of a forecast can be assessed in several different ways. In this study, three standard metrics, MAD, MSE, and MAPE, are used to compare the performance of different forecasting methods. The MAD and MSE are scale-dependent metrics, and the magnitude of the error varies with the magnitude of the underlying series. On the other hand, the MAPE is a relative-error metric ranging between 0 and 1. The scale-independent nature of MAPE makes it a convenient assessment tool in a one-to-one comparison of time series with varying magnitudes. The formulation for each error metric is given in Equations 2, 3, and 4.
  • Mean Absolute Deviation (MAD)
M A D = 1 n ∑ t = 1 n Y t − F t
  • Mean Squared Error (MSE)
M S E = 1 n ∑ t = 1 n Y t − F t 2
  • Mean Absolute Percent Error (MAPE):
M A P E = 1 n ∑ t = 1 n Y t − F t Y t * 100
where Y t and F t represent the actual and the forecast. As we propose a new forecasting approach in this study, our primary focus is to compare the performance of the proposed method with respect to previous work. For a one-to-one comparison of different models, each model has to be tested on the same data set. In test runs, we used MAD and MSE to evaluate forecast accuracy. These two metrics are easy to compute and understand [17,18].

3.4. Hybrid Model

The proposed hybrid arrangement combines ARIMA and ANN models in series. As given in Equation 5, the original time series is considered as the sum of two components. First, a multi-period lagged ARIMA model (Mt) captures the underlying linear relationship in the data. The second component (Nt) is built on the leftover error of the first model. Whatever cannot be explained by ARIMA is fed into the ANN.
Y t = M t + N t
Processes involved in hybrid modeling can be divided into six sub-tasks performed in sequential order: (1) The routine starts with the basic model; (2) The error output of the basic model is processed in the classification; (3) Based on the classification, the input lists are prepared for the second model; (4) The secondary model runs on each list separately; (5) Output of the second model is consolidated in hybridization; (6) In the final stage, projections are generated with the hybrid model. Figure 2 shows tasks and relationships graphically.
Step 1. The Basic Model
The modeling process starts with the division of the original time series into training and test series. Next, the basic model is developed using only the training data, which includes the first portion of the data set (i.e., the chronologically older). In terms of size, the training data is typically several times larger than the test portion. In selecting the split point, we followed the guidelines used in previous studies on the same data sets. It should be noted that the number of observations in the training data is further reduced because of the lag effect in the data. The formula for the basic model is given in Equation 6.
Y t = M t + e t
where Y t and M t represent the actual and forecast values at point t. The offset between the two is the error ( e t ) , and it is used as a basis to construct a new time series for the second component.
e t = Y t − M t
Step 2. Classification
In the second stage, the error output of the first component (Equation 7) is classified into three distinct groups. The classification is done according to a priori selected threshold value. Over-shooters include non-negative errors that are greater than the threshold. Under-shooters are negative errors that are smaller than the negative value of the threshold limit. Anything that falls between these two limits is categorized as neutral. This type of categorization was first proposed by Khashei et al. [19], where the threshold limits are defined as the desired level of error (DLE). The value of this parameter could be set by the user based on the analysis of the error coming from the basic model. In particular, the distribution of error coming from the basic model can provide insight regarding when or how the basic model over- or under-estimates. If there is no insight into the performance of the basic model, it could be set to a fixed value. For example, the DLE is set to 5% in experimental runs by Khashei et al. [19]. The error output of the basic model is categorized into three groups as A, B, and C, with the following definitions:
  • e i | e i > D L E , Category A
  • e i | e i < − D L E , Category B
  • | e i | ≤ D L E , Category C
Step 3. Input Lists for the Second Model
Based on the categorization of the second step, three separate data lists are constructed from the original error output in Equation 7. To explain the process, let us assume that the output of the basic model is stored in a list, E, with n members, E = { e 1 , e 2 , e 3 , … , e n } . Three separate lists, A, B, and C, are generated from list E. While lists A and B represent underestimated and overestimated values of E, list C holds neutral error values. The content of E is directly copied to A, B, and C to initialize the lists. Then, with the guidelines given in Equation 8, adjustments are made to each list. In list A, which represents underestimated values, all category A values are kept as they are, but everything else is set to zero. Similarly, list B, representing overestimated errors (i.e., category B), retains its original values, but overwrites everything else with zero. For list C, all elements with over- and underestimated values are set to zero.
Underestimation list: A = i f e i ∈ c a t e g o r y A ⇒ e i = e i e l s e e i = 0
Overestimation   list : B = i f e i ∈ c a t e g o r y B ⇒ e i = e i e l s e e i = 0
Neutral list: C = i f e i ∉ c a t e g . A A N D e i ∉ c a t e g o r y B ⇒ e i = e i e l s e e i = 0 Step 4. The Second Model
The second model performs a complementary function. It uses leftover error values of the basic model to extract additional explanatory information. As explained in the previous step, the error output is categorized into three separate lists. The lists A and B represent under- and overestimated values, and they are the inputs for the second model. List C contains error values that remain below the threshold (i.e., DLE), and are excluded from the run. The second model includes an artificial neural network (ANN) to identify nonlinear patterns and any high-order linear relationships that the basic model missed. In the original approach proposed by Zhang [20], the primary and secondary models are assigned specific tasks. While the primary model deals with the linear component of the data, the leftover error is assumed to be the nonlinear component. This type of classification of the domain may not be applicable in every situation, and the residual error of the primary model cannot be presupposed as a nonlinear component. It is likely that leftover error values are a combination of linear and nonlinear error values.
The ANN model is run separately on A and B lists to generate two sets of forecasts, representing the under- and overestimation portions of the model. As stated in Equations 9 and 10, the ANN uses n period lagged values from t to t-n to generate the forecast for t+1.
N A ( t + 1 ) = e A ( t + 1 ) = f A ( e A t , e A ( t − 1 ) , e A ( t − 2 ) , . . . , e A ( t − n ) ) + ε A ( t + 1 )
N B ( t + 1 ) = e B ( t + 1 ) = f B ( e B t , e B ( t − 1 ) , e B ( t − 2 ) , . . . , e B ( t − n ) ) + ε B ( t + 1 )
where f A and f B represent functions used by ANN. The terms ε A ( t + 1 ) and ε B ( t + 1 ) are random errors.
Step 5. Hybridization
Hybridization involves integrating basic and secondary models in a schema to produce a single (i.e., hybrid) forecast. In the proposed schema, the hybrid forecast for t+1 is the sum of outputs generated by M t and N t .
Y ^ A ( t + 1 ) = M t + 1 + N A ( t + 1 )
Y ^ B ( t + 1 ) = M t + 1 + N B ( t + 1 )
Forecasts given in 11 and 12 can be considered as a modified version of the basic model forecast. The Y ^ A ( t + 1 ) in 11 is the corrected version when the basic model underestimates the true value. Underestimation produces positive errors in the basic model. When positive values are fed into the secondary model, the secondary model, in turn, is likely to produce positive-valued forecasts. This could be considered as compensation for the underestimation of the basic model. A reverse mechanism works in 12. When the basic model overestimates, errors are likely to be negative. To compensate, the second model will produce negative-valued forecasts ( Y ^ B ( t + 1 ) ).
In addition to these two forecasts, the basic model's direct output can be considered as a third forecast. The second model is bypassed, and the output of the basic model is the final forecast: Y ^ C ( t + 1 ) = M t + 1 . The Y ^ C ( t + 1 ) can be considered as category C, and it represents the mid-value of three forecasts. While category C determines the midpoint, forecasts for A and B are upper and lower estimates. Among three candidate forecast points (i.e., Y ^ A ( t + 1 ) Y ^ A ( t + 1 ) Y ^ A ( t + 1 ) ), one must be selected as the final forecast. The selection is based on the error metrics discussed in (3.3). The combination with the lowest score is chosen as the final hybrid model.
Step 6. Projection
The hybrid model selected in the previous step is used for projection. Model selection is based on the performance of the training data, which is exclusively used for model development. Once the model is finalized, its forecasting performance is evaluated on the test data. This data set is a continuation of the training data and is used for model validation only.
In terms of platform and software, we used IBM's SPSS statistical software to build ARIMA models. MATLAB Toolbox is used for ANN models. Development and test runs were conducted on a Windows-based laptop with Intel Core i5-7200U CPU @ 2.50GHz. For both ARIMA and ANN models, the run times were trivial.

4. Results

To test the performance of the proposed approach, we used several well-known data sets from the literature. Our analysis also includes a local data set for Turkish wheat yield, which was the primary motivation to undertake this study. Data sets from the literature include the following series: annual sunspot observations [20], Canadian Lynx counts [21], airline passenger data [22], and hourly electricity rates from New South Wales [23]. Lastly, a new data set of Turkish wheat yields is part of this study. The series for monthly yields from 1938 onwards is available at the Turkish Grain Board [24].
Selected data sets are used in evaluating the performance of the proposed approach. The evaluation is based on a one-to-one comparison of our model with the ones reported in the literature. For this reason, we have tried to use the same error metric of the original benchmark study for performance comparison. A brief explanation of the error metrics can be found in section (3.3).

4.1. Sunspot Data

The number of darker spots on the sun's surface has long been a subject of curiosity for humanity, so we have a solid history of records going back several hundred years. An observatory in Belgium keeps records of current sunspot activity and has an archive of historical numbers [20]. The sunspot series is often referred to as Wolf's sunspot data because Rudolf Wolf first compiled the time series [25]. Because of its crucial influence on various fields, from climate to telecommunications, statisticians have studied sunspot data extensively. However, identifying a functional relationship in the sunspot series has been challenging because of the nonlinear, nonstationary, and non-Gaussian nature of the series [26,27]. In addition, a high level of complexity in the series has made sunspot data a yardstick in evaluating forecasting models.
The sunspot series used in this study comprises 288 annual observations, covering 1700 to 1987. The data set was split into two parts for training and testing purposes. The test data includes 221 observations from 1700 to 1920, and the remaining portion, from 1921 to 1987 (67 data points), is used for testing. In parallel with previous studies on this series, we followed a two-step hybrid model approach to model the series [19,28,29].
An autoregressive model of order nine, AR(9), and an ANN architecture of 4x4x1 are used in basic and secondary models. The decision to select these models is based on the previous research work done on the problem [29,30,31].
Figure 3 shows the forecast and actual data over the test period. For most of the observations, the difference between the forecast and the actual remains small. Table 1 compares the performance of various methods in terms of MAD (mean absolute deviation). The list indicates that the proposed method performs better than previous models.

4.2. Canadian Lynx Trapping

This series includes Canadian lynx trapped in Northwest Canada from 1821 to 1934. The lynx population has a cyclical behavior with a period of 10 years. It is reported that this interesting cycle is observable for other animal populations in North Canada [21]. The cyclical behavior has tall peaks and deep bottoms, making it a challenging series for forecasting. The first 100 observations, data from 1821 to 1920, are used as the training set. The test section covers observations from 1921 to 1934, with 14 data points. Based on previous research on this problem, an AR(12) model is used in the basic model. An ANN architecture of 7x5x1 is selected for the secondary model.
Figure 4 shows the fitted values versus the actual data. The forecast performance in comparison to other models is presented in Table 2. Although the proposed model performed better than Zhang's, the performance is slightly lower, or on par, compared to the others.

4.3. Hourly Electricity Rates

This data set includes hourly electricity prices in the New South Wales State of Australia. The price data is kept by the Australian Energy Market Operator (AEMO), a semi-official organization in charge of Australia's national electricity and gas markets [32]. Price statistics for March 2013 are analyzed in this study. In the original data set, the price is recorded at half-hour intervals. First, the data set is converted to hourly rates with 24 records per day, totaling 744 (31x24) data points for the entire month (i.e., March 2013). While the first 30 days of data are used for development, the last day of the month is reserved as test data. ARIMA (1,0,1) and a multi-layer perceptron type of ANN architecture of 7x6x1 are used in basic and secondary models. Figure 5 shows the fitted versus actuals for the 24-hour period of March 31, 2013. Table 3 includes MSE and MAD comparisons. Error statistics suggest that the proposed approach performed relatively better than benchmarks in terms of both metrics.

4.4. Airline Passenger Data

This is a popular time-series data, including monthly international passenger counts from 1949 to 1960. Since its introduction by Brown [22], this series has been the subject of many studies, and it is a popular benchmark for forecasting models. The series is readily available in data repositories and statistical software libraries [33]. There is a clear seasonality and an upward trend in the data, making it an exemplary test case for any time series modeling (Figure 6). The twelve-year monthly series has 144 observations. In our analysis, the first 11 years of the data (1949 to 1959) are used as a training set, while the remaining 12 observations of 1960 are used for testing.
For this data set, we used SARIMA(0,1,1) x (0,1,1)12 in the basic model. This representation was first used by Box et al. [34]. Because of the exponential upward trend, a logarithmic transformation is applied beforehand. The model originally proposed by Box et al. [34] is also confirmed by later studies [35,36]. For ANN in the secondary model, the input includes three nodes with lags 1, 2, and 12. There are two nodes in the hidden layer and a single output. Our basic model is based on the SARIMA (i.e., seasonal ARIMA) architecture, as proposed by [36].
The output of the hybrid model on the test data covering 12 months of 1960 is shown in Figure 7. In addition, the performance comparison with respect to two previous studies is presented in Table 4. Although the model performed significantly better than one of the comparisons [35] in MSE metrics, its performance was slightly worse in the second one [36]. It is worth mentioning that our model performed marginally better in MDA metrics.

4.5. Wheat Yield in Turkey

This data is about wheat yield in Turkey. The yield refers to the dry grain of the harvested crop, and it is often expressed in terms of either kilogram per decare or tons per hectare. The yield data is in annual series, covering the period from 1938 to 2013. Turkey is a major wheat producer, and a leading trader of cereals, including wheat. Because of the strategic importance of the crop, speculations regarding wheat yield are a great concern for many parties, particularly those involved in commodities trading. Although wheat is considered a strategic agricultural commodity in Turkey, the output has been flat for years. The decline in land dedicated to wheat agriculture has been partially compensated by an increase in yields, which kept the output at a level of 20 million tons per year [37]. For agricultural commodities such as wheat, yield is defined in terms of kilograms of seeds harvested per decare (1,000 m2). As a first step in the model development, the available data set was split into development and test sections, with 80% and 20% ratios. Yield data from 1938 to 1998 was used for model development, and the remaining portion, data from 1999 to 2013, was used for testing.
Historical change in yields from 1938 to 2013 is given in Figure 8. As the graph shows, the wheat yield in Turkey has been rising in recent years, but it is still well below the major wheat producers of Europe, such as Germany or France [38,39]. The yield data has an upward trend with random fluctuations. It does not exhibit any seasonal or periodic variations. For basic and secondary models, ARIMA (0,1,0) time series and ANN architecture of 7x7x1 are selected as final models after testing various combinations.
The graph of fitted values versus actuals for the test data (from 1999 to 2013) shows that the model captures the recent upward trend with reasonable accuracy (Figure 9). Performance statistics (MSE, MAD, MAPE) for the hybrid model are given in Table 5. This table includes statistics for two more models. Two sub-components of the hybrid approach, the ARIMA model in the basic model and the ANN model of the secondary models, are run separately on the yield data. The performance of each model is recorded, and relevant error metrics are included in Table 5.

5. Conclusion

Previous research has shown that combining different forecasting methods in a framework generates superior results to the stand-alone models based on a single methodology. The last case (i.e., yield forecasting) presented in the "Experimental Results" section clearly illustrates this phenomenon. For that case, we first run ARIMA and ANN models separately. Then, we run the hybrid model that combines ARIMA and ANN in a unique framework. Accuracy metrics in Table 5 show that the hybrid model's performance is far superior to stand-alone ARIMA or stand-alone ANN. Combining different forecasting methods in a framework has been previously studied by many researchers, and different approaches have been proposed. Our approach is an improvement along this line of research. As we detailed in the previous section, the performance in terms of forecast accuracy has been better than, or on par with, similar approaches.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Tsay, R.S.; Chen, R. Nonlinear Time Series Analysis; John Wiley & Sons, 2018; ISBN 978-1-119-26405-7.
  2. Bates, J.M.; Granger, C.W.J. The Combination of Forecasts. Operational Research Quarterly 1969, 20, 19. [Google Scholar] [CrossRef]
  3. Smyl, S. A Hybrid Method of Exponential Smoothing and Recurrent Neural Networks for Time Series Forecasting. International Journal of Forecasting 2020, 36, 75–85. [Google Scholar] [CrossRef]
  4. Zhang, G.P. Time Series Forecasting Using a Hybrid ARIMA and Neural Network Model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
  5. Khashei, M.; Bijari, M. An Artificial Neural Network (p,d,q) Model for Timeseries Forecasting. Expert Systems with Applications 2010, 37, 479–489. [Google Scholar] [CrossRef]
  6. Banihabib, M.E.; Ahmadian, A.; Valipour, M. Hybrid MARMA-NARX Model for Flow Forecasting Based on the Large-Scale Climate Signals, Sea-Surface Temperatures, and Rainfall. Hydrology Research 2018, 49, 1788–1803. [Google Scholar] [CrossRef]
  7. Camelo, H. do N.; Lucio, P.S.; Leal Junior, J.B.V.; Carvalho, de P.C.M.; Santos, dos D. von G. Innovative Hybrid Models for Forecasting Time Series Applied in Wind Generation Based on the Combination of Time Series Models with Artificial Neural Networks. Energy 2018, 151, 347–357. [Google Scholar] [CrossRef]
  8. Farajzadeh, J.; Alizadeh, F. A Hybrid Linear-Nonlinear Approach to Predict the Monthly Rainfall over the Urmia Lake Watershed Using Wavelet-SARIMAX-LSSVM Conjugated Model. Journal of Hydroinformatics 2018, 20, 246–262. [Google Scholar] [CrossRef]
  9. Moeeni, H.; Bonakdari, H. Impact of Normalization and Input on ARMAX-ANN Model Performance in Suspended Sediment Load Prediction. Water Resources Management 2018, 32, 845–863. [Google Scholar] [CrossRef]
  10. Buyuksahin, U.C.; Ertekina, S. Improving Forecasting Accuracy of Time Series Data Using a New ARIMA-ANN Hybrid Method and Empirical Mode Decomposition. Neurocomputing 2019, 361, 151–163. [Google Scholar] [CrossRef]
  11. Chakraborty, T.; Chattopadhyay, S.; Ghosh, I. Forecasting Dengue Epidemics Using a Hybrid Methodology. Physica a-Statistical Mechanics and Its Applications 2019, 527, 121266. [Google Scholar] [CrossRef]
  12. Safari, A.; Davallou, M. Oil Price Forecasting Using a Hybrid Model. Energy 2018, 148, 49–58. [Google Scholar] [CrossRef]
  13. Aasim; Singh, S. N.; Mohapatra, A. Repeated Wavelet Transform Based ARIMA Model for Very Short-Term Wind Speed Forecasting. Renewable Energy 2019, 136, 758–768. [Google Scholar] [CrossRef]
  14. Liu, H.-H.; Chang, L.-C.; Li, C.-W.; Yang, C.-H. Particle Swarm Optimization-Based Support Vector Regression for Tourist Arrivals Forecasting. Computational Intelligence and Neuroscience 2018, 2018, 6076475. [Google Scholar] [CrossRef] [PubMed]
  15. Madan, R.; Mangipudi, P.S. Predicting Computer Network Traffic: A Time Series Forecasting Approach Using DWT, ARIMA and RNN. In 2018 Eleventh International Conference on Contemporary Computing (ic3); Aluru, S., Kalyanaraman, A., Bera, D., Kothapalli, K., Abramson, D., Altintas, I., Bhowmick, S., Govindaraju, M., Sarangi, S.R., Prasad, S., Bogaerts, S., Saxena, V., Goel, S., Eds.; Ieee: New York, 2018; ISBN 978-1-5386-6835-1. [Google Scholar]
  16. Babu, C.N.; Reddy, B.E. A Moving-Average Filter Based Hybrid ARIMA–ANN Model for Forecasting Time Series Data. Applied Soft Computing 2014, 23, 27–38. [Google Scholar] [CrossRef]
  17. Hyndman, R.J.; Koehler, A.B. Another Look at Measures of Forecast Accuracy. International Journal of Forecasting 2006, 22, 679–688. [Google Scholar] [CrossRef]
  18. Makridakis, S.G.; Wheelwright, S.C.; Hyndman, R.J. Forecasting: Methods and Applications; Wiley, 1998; ISBN 978-0-471-53233-0.
  19. Khashei, M.; Bijari, M.; Raissi Ardali, G.A. Hybridization of Autoregressive Integrated Moving Average (ARIMA) with Probabilistic Neural Networks (PNNs). Computers & Industrial Engineering 2012, 63, 37–45. [Google Scholar] [CrossRef]
  20. Sunspot Number | SILSO Available online:. Available online: http://www.sidc.be/silso/datafiles (accessed on 10 March 2021).
  21. Bulmer, M.G. A Statistical Analysis of the 10-Year Cycle in Canada. Journal of Animal Ecology 1974, 43, 701–718. [Google Scholar] [CrossRef]
  22. Brown, R.G. Smoothing, Forecasting and Prediction of Discrete Time Series; Prentice Hall: Englewood Cliffs, NJ, 1962. [Google Scholar]
  23. Babu, C.N.; Reddy, B.E. A Moving-Average Filter Based Hybrid ARIMA–ANN Model for Forecasting Time Series Data. Applied Soft Computing 2014, 23, 27–38. [Google Scholar] [CrossRef]
  24. Turkish Grain Board TMO - Turkish Grain Board Statistics Available online:. Available online: https://www.tmo.gov.tr/bilgi-merkezi/tablolar (accessed on 5 June 2021).
  25. The Sun -- History Available online:. Available online: https://pwg.gsfc.nasa.gov/Education/whsun.html (accessed on 10 March 2021).
  26. Izenman, A.J. J. R. Wolf and H. A. Wolfer: An Historical Note on the Zurich Sunspot Relative Numbers. Journal of the Royal Statistical Society. Series A (General) 1983, 146, 311–318. [Google Scholar] [CrossRef]
  27. Suyal, V.; Prasad, A.; Singh, H.P. Nonlinear Time Series Analysis of Sunspot Data. Sol Phys 2009, 260, 441–449. [Google Scholar] [CrossRef]
  28. Khashei, M.; Bijari, M. An Artificial Neural Network (p,d,q) Model for Timeseries Forecasting. Expert Systems with Applications 2010, 37, 479–489. [Google Scholar] [CrossRef]
  29. Zhang, G.P. Time Series Forecasting Using a Hybrid ARIMA and Neural Network Model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
  30. Cottrell, M.; Girard, B.; Girard, Y.; Mangeas, M.; Muller, C. Neural Modeling for Time Series: A Statistical Stepwise Method for Weight Elimination. IEEE Transactions on Neural Networks 1995, 6, 1355–1364. [Google Scholar] [CrossRef] [PubMed]
  31. Rao, T.S.; Gabr, M.M. An Introduction to Bispectral Analysis and Bilinear Time Series Models; Springer Science & Business Media, 2012; ISBN 978-1-4684-6318-7.
  32. Australian Energy Market Operator Available online:. Available online: https://aemo.com.au/ (accessed on 13 June 2024).
  33. R-manual R: Monthly Airline Passenger Numbers 1949-1960 Available online:. Available online: https://stat.ethz.ch/R-manual/R-patched/library/datasets/html/AirPassengers.html (accessed on 25 March 2021).
  34. Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; 5th edition.; Wiley: Hoboken, New Jersey, 2015; ISBN 978-1-118-67502-1. [Google Scholar]
  35. Faraway, J.; Chatfield, C. Time Series Forecasting with Neural Networks: A Comparative Study Using the Air Line Data. Journal of the Royal Statistical Society: Series C (Applied Statistics) 1998, 47, 231–250. [Google Scholar] [CrossRef]
  36. Hamzaçebi, C. Improving Artificial Neural Networks’ Performance in Seasonal Time Series Forecasting. Inf. Sci. 2008, 178, 4550–4559. [Google Scholar] [CrossRef]
  37. Dunya, Economic Daily Decline in land use for startegic commodity, wheat. Available online: https://www.dunya.com/sehirler/stratejik-urun-bugday-ekim-alanlari-daraliyor-haberi-470018 (accessed on 3 May 2021).
  38. World Bank Cereal Production (Metric Tons) | Data Available online:. Available online: https://data.worldbank.org/indicator/AG.PRD.CREL.MT (accessed on 22 March 2021).
  39. Tiryaki̇oglu, M.; Demi̇rtas, B.; Tutar, H. Comparison of Wheat Yield in Turkey: Hatay and Şanlıurfa Study Case. Süleyman Demirel Universitesi Ziraat Fakültesi Dergisi 2017, 12, 56–67. [Google Scholar]
Preprints 111651 g001
Figure 1. A serially connected hybrid model
Figure 1. A serially connected hybrid model
Preprints 111651 g001
Preprints 111651 g002
Figure 2. Proposed hybrid structure.
Figure 2. Proposed hybrid structure.
Preprints 111651 g002
Preprints 111651 g003
Figure 3. Hybrid forecast vs. actual data over the test data (Sunspot data—67 observations)
Figure 3. Hybrid forecast vs. actual data over the test data (Sunspot data—67 observations)
Preprints 111651 g003
Preprints 111651 g004
Figure 4. Hybrid forecast vs. actual data over the test data (Canadian lynx—14 observations)
Figure 4. Hybrid forecast vs. actual data over the test data (Canadian lynx—14 observations)
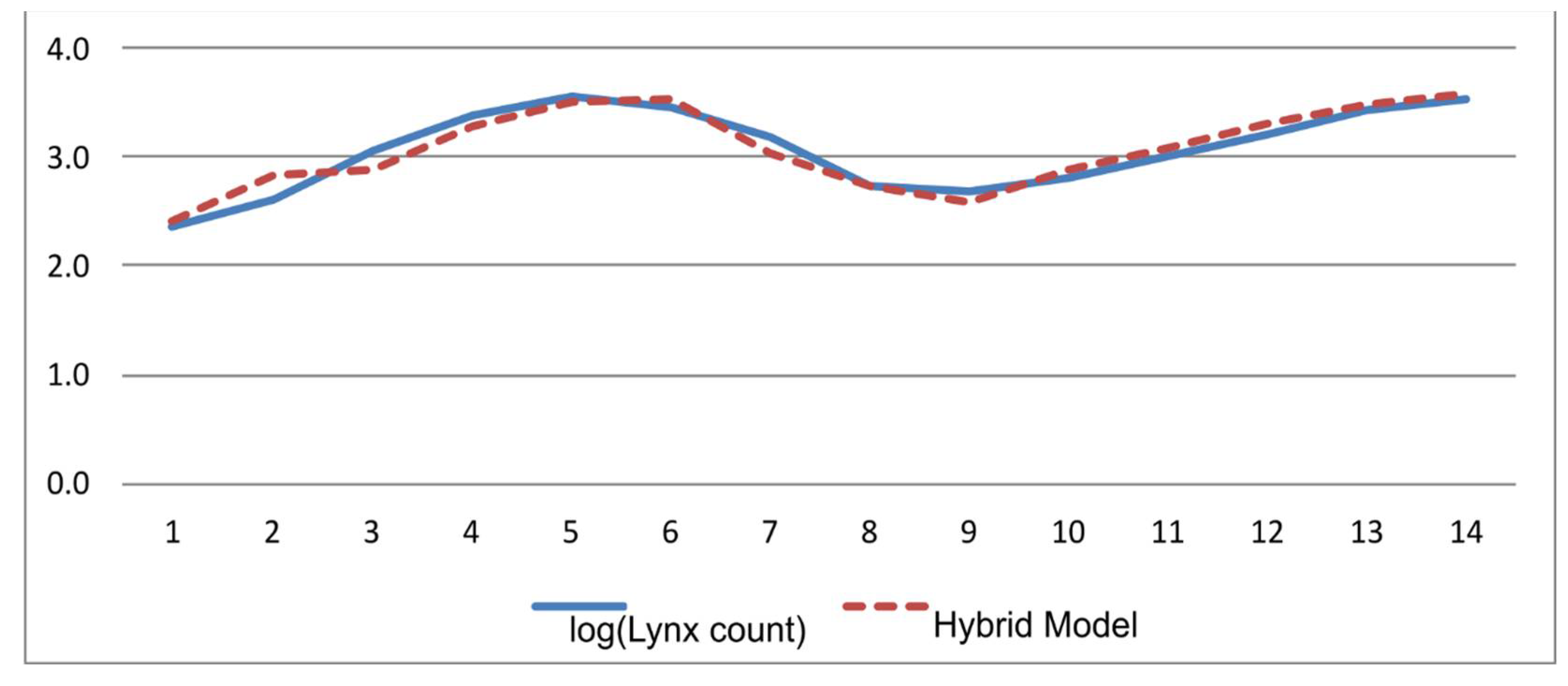
Preprints 111651 g004
Preprints 111651 g005
Figure 5. Hybrid forecast vs. actual data over the test data (Hourly electricity rates—24 observations).
Figure 5. Hybrid forecast vs. actual data over the test data (Hourly electricity rates—24 observations).
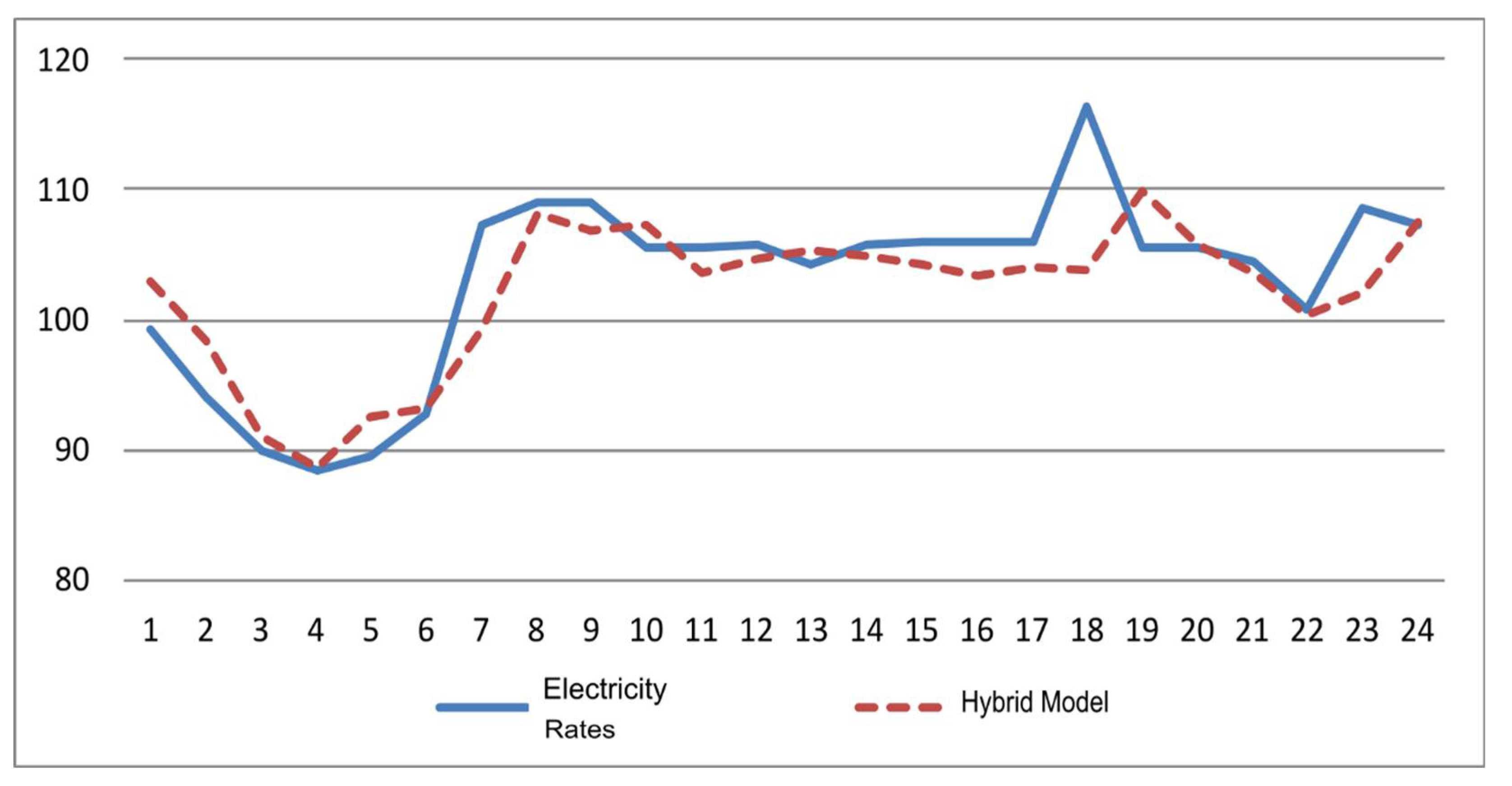
Preprints 111651 g005
Preprints 111651 g006
Figure 6. Monthly airline passenger data
Figure 6. Monthly airline passenger data
Preprints 111651 g006
Preprints 111651 g007
Figure 7. Hybrid forecast vs. actual data over the test data (Airline passenger data)
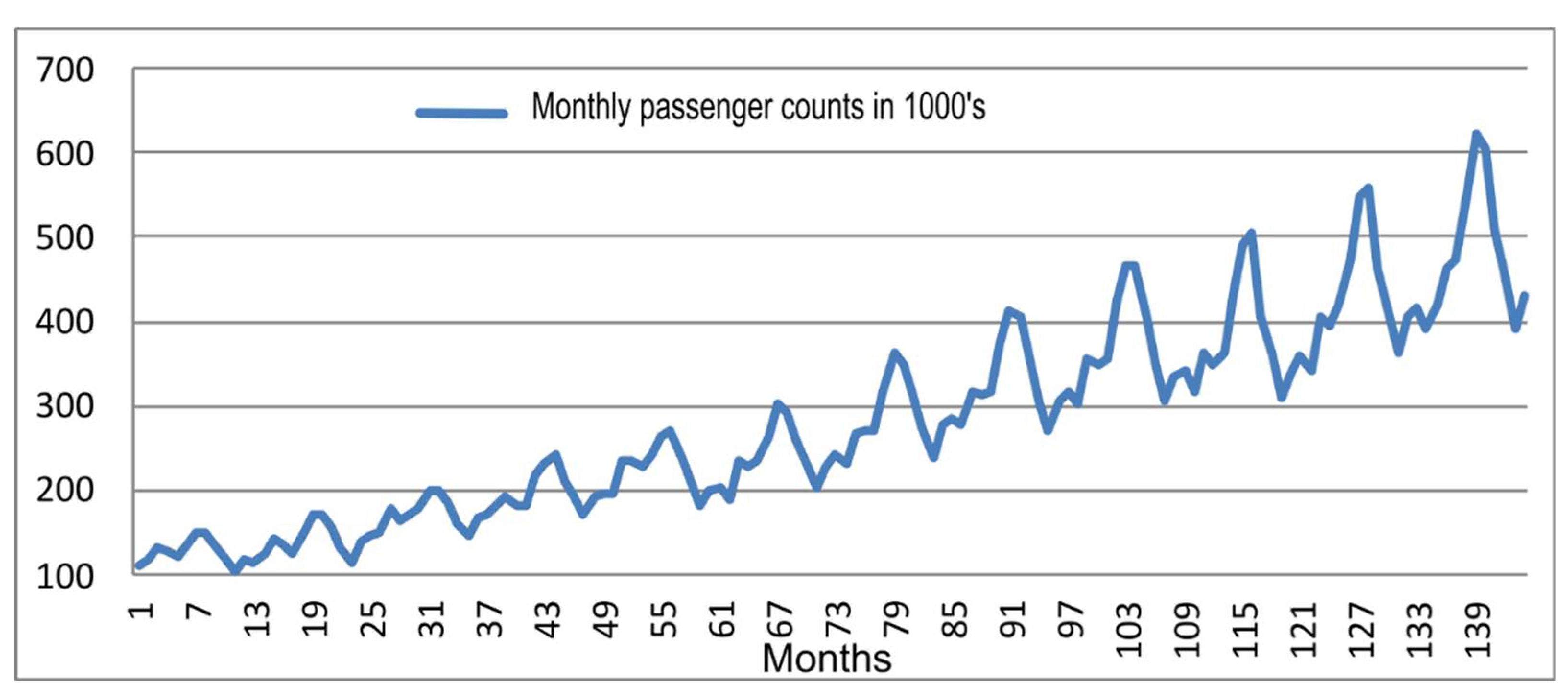
Figure 7. Hybrid forecast vs. actual data over the test data (Airline passenger data)
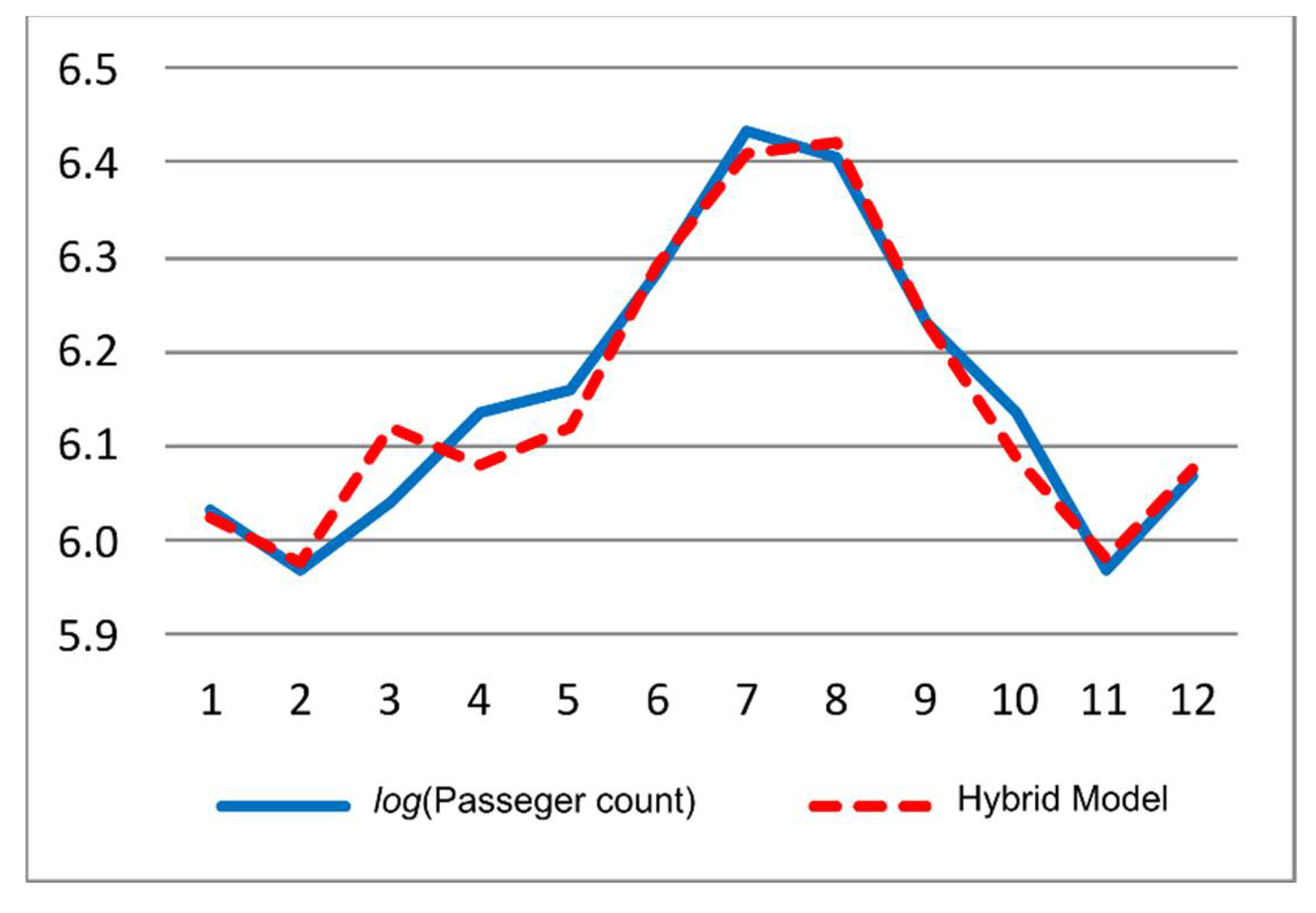
Preprints 111651 g007
Preprints 111651 g008
Figure 8. Historical wheat yield in Turkey
Figure 8. Historical wheat yield in Turkey
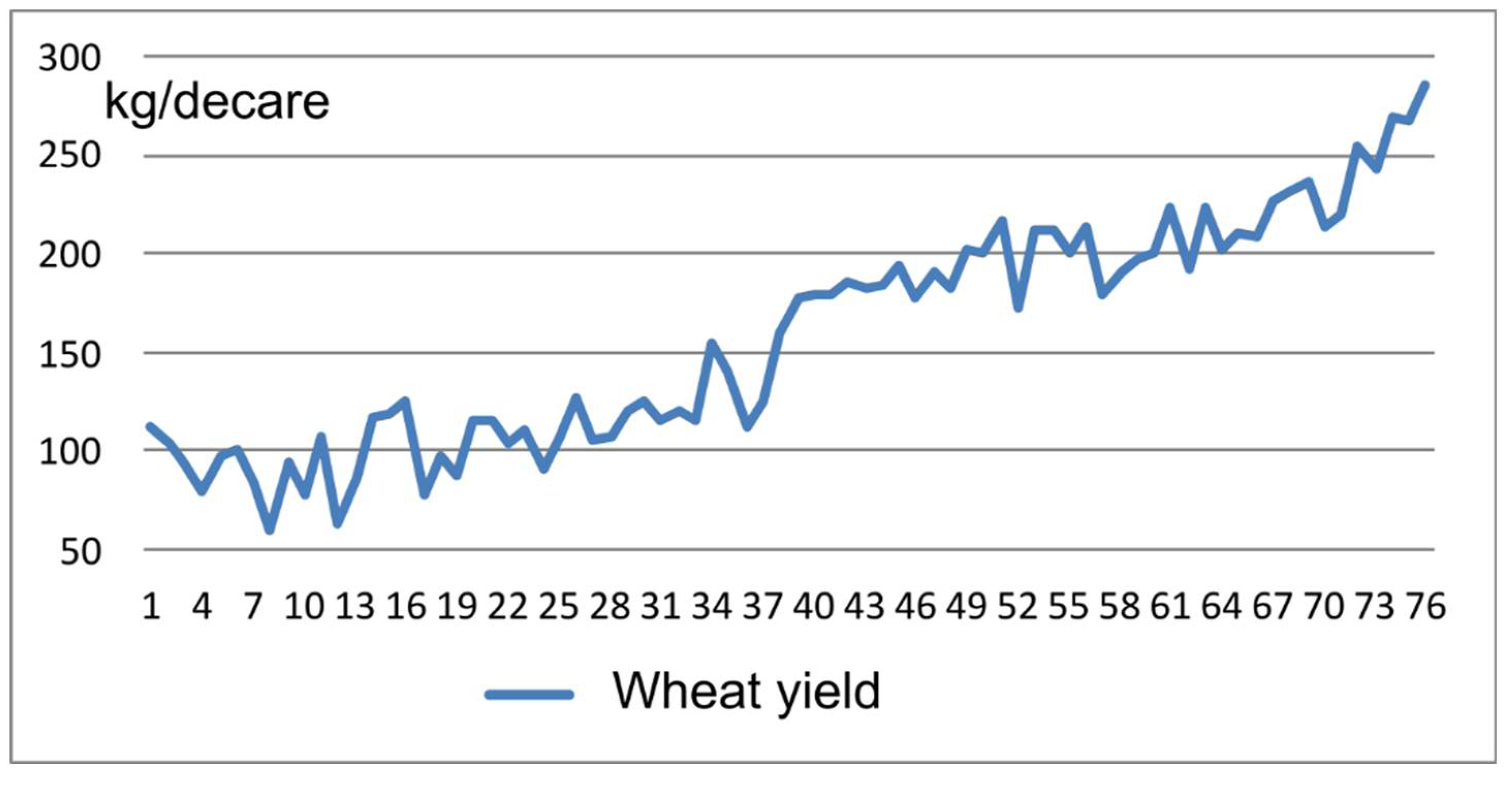
Preprints 111651 g008
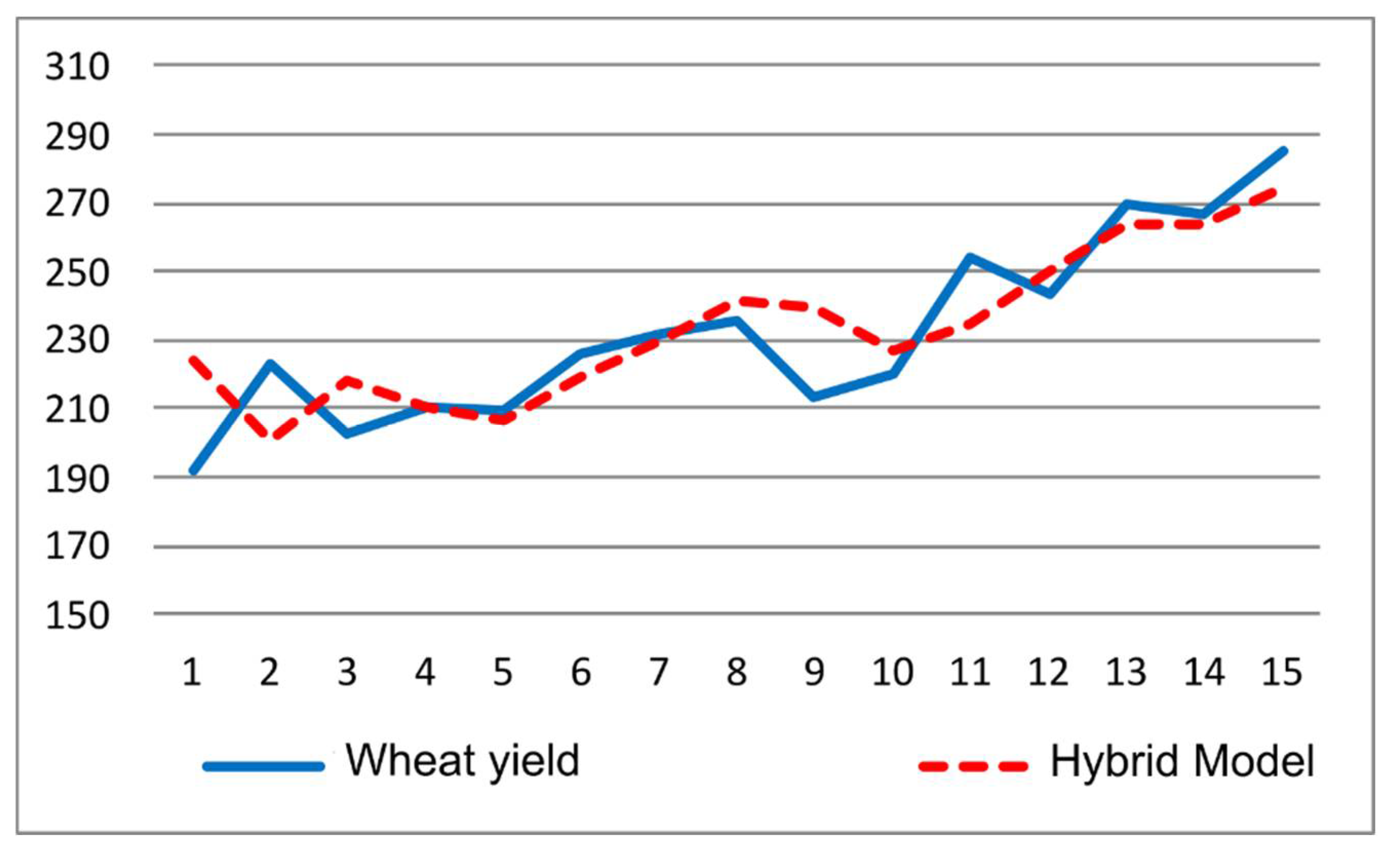
Preprints 111651 g009
Figure 9. Hybrid forecast vs. actual data over the test data (wheat yield).
Figure 9. Hybrid forecast vs. actual data over the test data (wheat yield).
Preprints 111651 g009
Table 1. Comparison of forecast performance over test data.
Table 1. Comparison of forecast performance over test data.
MODEL MSE MAD
Zhang Hibrit AR(9)-MLP 280.160 12.780
Khashei, Bijari AR(9)-MLP I 234.206 12.117
Khashei, Bijari AR(9)-MLP II 218.642 11.447
Khashei, Bijari, Ardali AR(9)-PNN 234.775 11.549
Proposed Hybrid AR(9)-MLP 240.896 11.416
Table 2. Comparison of forecast performance over test data
Table 2. Comparison of forecast performance over test data
MODEL MSE MAD
Zhang Hibrit AR(12)-MLP [2] 0.0172 0.1040
Khashei, Bijari AR(12)-MLP I [3] 0.0136 0.0896
Khashei, Bijari AR(12)-MLP II [31] 0.0100 0.0851
Khashei, Bijari, Ardali AR(12)-PNN [17] 0.0115 0.0844
Proposed Hybrid AR(12)-MLP* 0.0129 0.0986
Table 3. Comparison of forecast performance over test data (Hourly electricity rates)
Table 3. Comparison of forecast performance over test data (Hourly electricity rates)
MODEL MSE MAD
Babu, Reddy ANN 22.4304 3.7374
Zhang Hibrit ARIMA(1,0,1)-MLP 27.0377 3.9204
Khashei, Bijari ARIMA(1,0,1)-MLP 26.1396 3.8346
Babu, Reddy ARIMA(1,1,1)-MLP 18.2793 3.2342
Proposed Hybrid ARIMA(1,0,1)-MLP 14.7566 2.5634
Table 4. Comparison of forecast performance over test data (Airline passenger data).
Table 4. Comparison of forecast performance over test data (Airline passenger data).
MODEL MSE MAD
Faraway, Chatfield ANN 0.024167 -
Hamzacebi Seasonal-ANN 0.001083 0.0280
Proposed Hybrid SARIMA-MLP 0.001133 0.0242
Table 5. Comparison of forecast performance over test data (Wheat yield data)
Table 5. Comparison of forecast performance over test data (Wheat yield data)
MODEL MSE MAD MAPE (%)
ARIMA (0,1,0) – stand-alone 375.33 16.00 6.99
ANN – stand-alone 348.39 16.29 6.81
Proposed hybrid model, ARIMA-MLP 212.24 11.09 5.00
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated