Prerpints.org logo
Preprint
Article

Knowledge-Based Fuzzy Control System for Automatic Transmission with Human-Sensitive Inputs

Altmetrics

Downloads

146

Views

62

Comments

0

Submitted:

22 August 2024

Posted:

23 August 2024

You are already at the latest version

Alerts
Abstract
With the increasing use of automatic transmissions in passenger vehicles, there is a growing need for improved gear shifting control strategies that aim to enhance performance and fuel efficiency. This paper introduces a knowledge-based fuzzy control system designed specifically for automatic transmissions in light vehicles. The proposed system utilizes a fuzzy inference system as the controller, enabling the emulation of the driver’s perceptions during the gear shifting process. Consequently, the input signal consists of variables that are either sensitive to or observable by the driver, while the output represents the selected gear. The paper evaluates three distinct control strategies, each based on different inputs. These inputs include the longitudinal velocity of the vehicle, the angular velocity of the engine, or a combination of both, along with the time-derivative of the throttle valve opening. Through the evaluation, it is observed that the combination of inputs yields significantly improved performance. Therefore, the methodology presented in this paper demonstrates that the combined input approach is more effective for gear shifting control.
Keywords: 
Subject: Engineering  -   Automotive Engineering

1. Introduction

In the present era, automatic transmissions have become widely utilized in both light and heavy vehicles. With the increasing need for enhanced performance and reduced fuel consumption, there is a greater demand for precise control algorithms. However, the decision-making process for gear shifting is often complex due to the multitude of available input variables. These variables include the output velocity of the gearbox, oil brake pressure, current-gear indicator, clutch parameters, and others, as described by [1,2], and [3].
Several authors have focused on selecting specific clutch parameters for control purposes, considering either kinematics or dynamics. [4], for instance, emphasize the significance of shift quality in automatic transmissions (AT). To optimize fuel economy, they propose the utilization of a proportional solenoid valve for clutch pressure control, with the speed difference of the clutch chosen as the control input. Similarly, [5] employ Takashi-Sugeno (T-S) fuzzy control and PID during various phases of the starting shift control process. They analyze the turbine speed in the automatic transmission and achieve satisfactory results in terms of shift quality. On the other hand, [6] focus on enhancing shift quality by employing adaptive fuzzy control for the filling process in wet clutches. They do not specifically work with kinematic parameters but share the same goal of improving shift quality, as also explored by [7] for an adaptive control strategy.
In their study, [8] explore an unconventional moving-off mechanism known as the Hydraulic Mechanical Power Reflux Transmission (HMPRT) and aim also to determine the optimal control strategy for the gear shifting process, specifically in a wheel loader. To define the gear ratio, they consider both the vehicle speed and throttle opening. Additionally, certain factors from the HMPRT are necessary for the decision-making process.
As observed in the works of numerous authors, it is commonplace to employ multi-objective optimization techniques for automatic transmissions. These techniques involve the consideration of independent parameters that measure various aspects such as performance, comfort, and fuel economy. [9] investigate a specific aspect known as double-transition downshift (DTS) in automatic transmissions. Their objective is to achieve a balance between shift comfort and performance. To validate their control strategies, they utilize a Pareto frontier approach for a 10-speed gearbox, examining different types of DTS.
Many researchers have utilized meta-heuristic optimization algorithms in the context of automatic transmissions. [10] propose a method that combines planetary gear sets with parallel-axis gear pairs to enhance both fuel consumption and driving performance. To achieve this, they employ a Genetic Algorithm to optimize gear ratios, with the goal of achieving a wider gear ratio spread. The parameters evaluated during the optimization process include power flow, efficiency, and clutching sequence. Similarly, [11] employ a Genetic Algorithm for multi-objective optimization in a dual-clutch transmission. The authors aim to find the most suitable gear shift map by considering factors such as C O 2 emissions, driveability, and gearbox durability, among others. Likewise, [12] utilize a Genetic Algorithm aiming at the minimization of fuel consumption, exhaust emissions and gearbox power losses.
As observed, previous studies on control strategies for light vehicle transmissions have not extensively examined the performance analysis when altering only driver-sensitive inputs, nor have they explored the application of knowledge-based fuzzy control. These areas of investigation offer the opportunity to approximate the gear shifting process to the human decision-making method, according to [13]. By focusing on these subjects, a deeper understanding of the relationship between driver perception and gear shifting can be achieved, leading to more effective control strategies in light vehicle transmissions.
[14] present a comprehensive work in this field, introducing a straightforward method for applying fuzzy logic to control automatic transmissions, considering kinematic inputs, differential force, and slipping. Their approach is applicable in a generic context, making it versatile and widely applicable. Similarly, [15] and [16] investigate the use of both human and non-human sensitive parameters in traditional automatic transmissions, employing fuzzy control techniques. In another related study, [17] propose a fuzzy system for predicting driver’s intentions and subsequently employ it as a control algorithm for gear shifting in an automated transmission.
Furthermore, [18] and [19] have investigated the impact of external factors on automatic transmission control, including variables such as ramp angle, traffic conditions, and road conditions. In their studies, a fuzzy logic system is employed to simulate the gear shift process, taking into account these external factors. In a different approach, [20] focus on utilizing a neuro-fuzzy logic model for automated manual transmission considering only two key inputs, namely wheel angular velocity and throttle valve opening angle.
[21] focus solely on fuzzy modeling as they develop a control system for an automatic transmission based solely on longitudinal velocity. However, their ultimate objective is to compare the simulation accuracy of different membership functions, namely triangular, trapezoidal, and Gaussian. Moreover,[22,23], and [24] establish the fundamental concepts of fuzzy logic, laying the groundwork for various model constructions. They demonstrate that this logic enables computational manipulation of the imprecise nature of human thought, leveraging natural human intelligence without reliance on explicit models. Additionally, by utilizing a parametric structure, it becomes more convenient to work with knowledge-based models and effectively control systems with multiple inputs and multiple outputs (MIMO). Furthermore, the subsequent implementation of adaptive control is also made easier through this approach.
[25] further demonstrate the advantages of knowledge-based fuzzy inference systems (FIS) by achieving significant improvements in real-time collision systems. Taking a different perspective, [26] emphasize the importance of human knowledge and explore methods for its more effective filtering.[27] propose an extrapolation-enhanced approach for modeling travel decision making, leveraging knowledge-based theory. This theory even finds applications in Computer-Aided Design (CAD) and Finite Element Analysis (FEA), as investigated by [28], providing a unified model representation.
Hence, by narrowing down the scope to a particular domain, this research paper strives to accomplish two objectives: firstly, to develop a knowledge-based fuzzy control system, and secondly, to propose a control system that solely incorporates driver-sensitive inputs. The primary contribution of this study lies in introducing a methodology for defining fuzzy control strategies for automatic transmissions. This approach relies on leveraging the knowledge of experienced drivers to design membership functions, eliminating the need for additional sensor measurements. The anticipated outcomes of this proposed control methodology include efficiency, minimal computational burden, and relative simplicity in implementation. In this manner, the effectiveness of the research can be demonstrated by comparing the obtained results with real-world data extracted from [3].
So, first of all, in Section Theoretical Study, we begin by examining fundamental concepts pertaining to control strategies and fuzzy control. To facilitate this study, we utilize the mathematical model introduced by [29] for the powertrain, constructed using the bond graphs technique and implemented in MATLAB®. Moving on to Section Development of Control Strategies, we present the proposed control strategies, outlining the potential inputs that can be considered within the fuzzy inference system. In Section Simulations and Results, we present the performance evaluation of a light vehicle, analyzing the longitudinal dynamics for various combinations of control inputs. This assessment allows us to compare the impact of each input on the vehicle’s behavior. Finally, in Section Conclusions, we assess these results in relation to relevant technical data, while also suggesting potential avenues for future research that can be pursued based on the findings of this study.

2. Theoretical Study

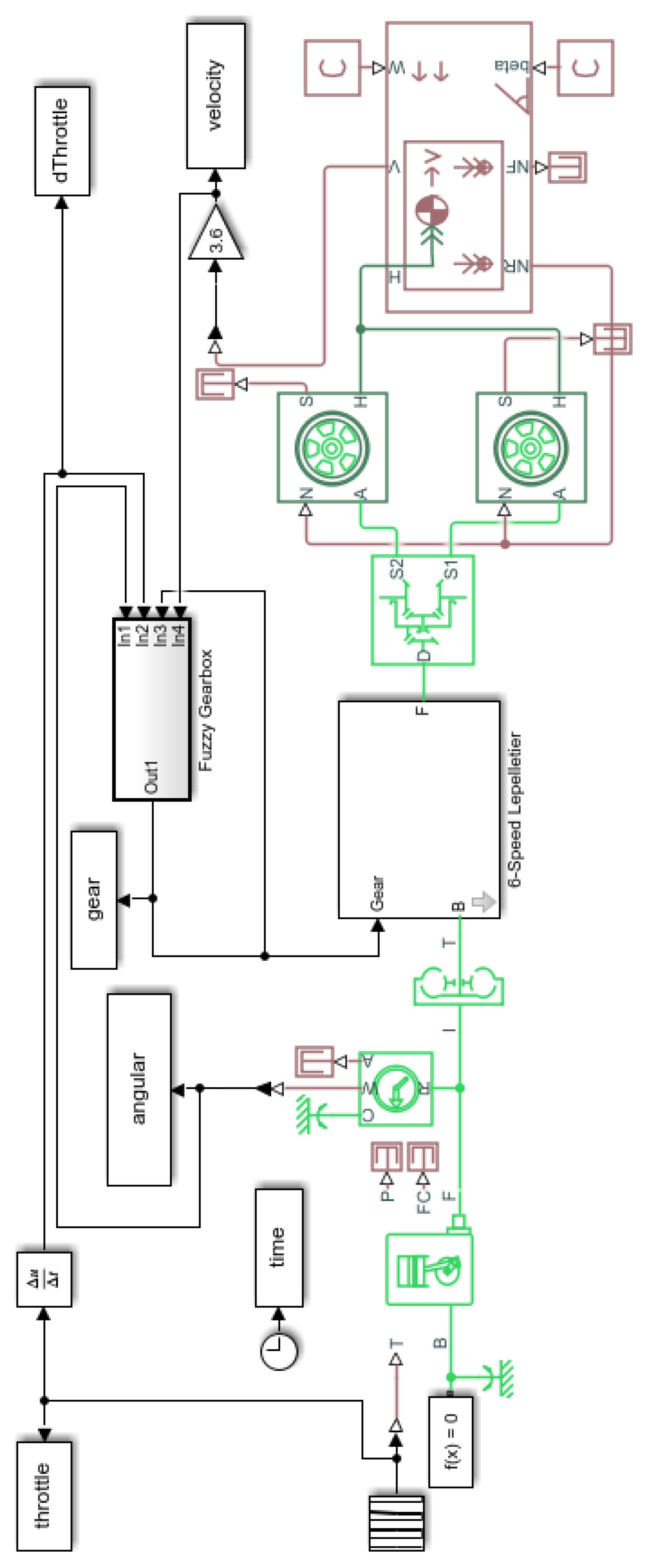
The computational modeling utilized for the vehicle with an automatic transmission has been previously introduced and validated in studies by [30] and [29]. The model is based on data obtained from [31]. Specifically, the powertrain model encompasses the engine, torque converter, automatic gearbox, differential, and tires, as depicted in Figure 1.
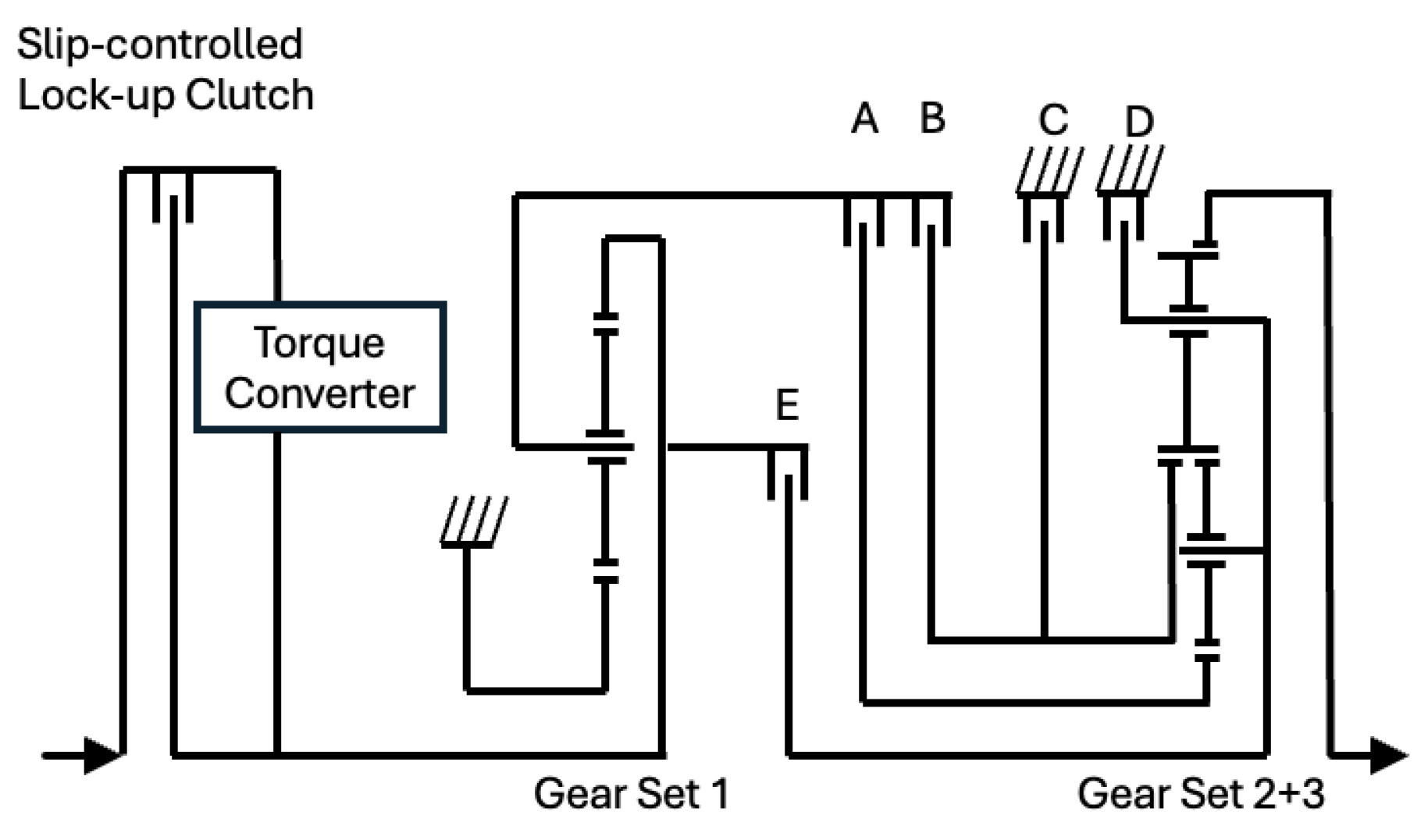
The selected gearbox for the study is a Lepelletier 6-velocities gearbox, which consists of a typical planetary gear set and a Ravigneaux gear set. The composition of this gearbox configuration is illustrated in Figure 2. This specific gearbox design is extensively utilized by numerous manufacturers of automatic transmissions, including contemporary ones. The trend toward incorporating more gears introduces significant challenges, such as the need for more complex software control and an increased calibration workload, as highlighted by [7]. 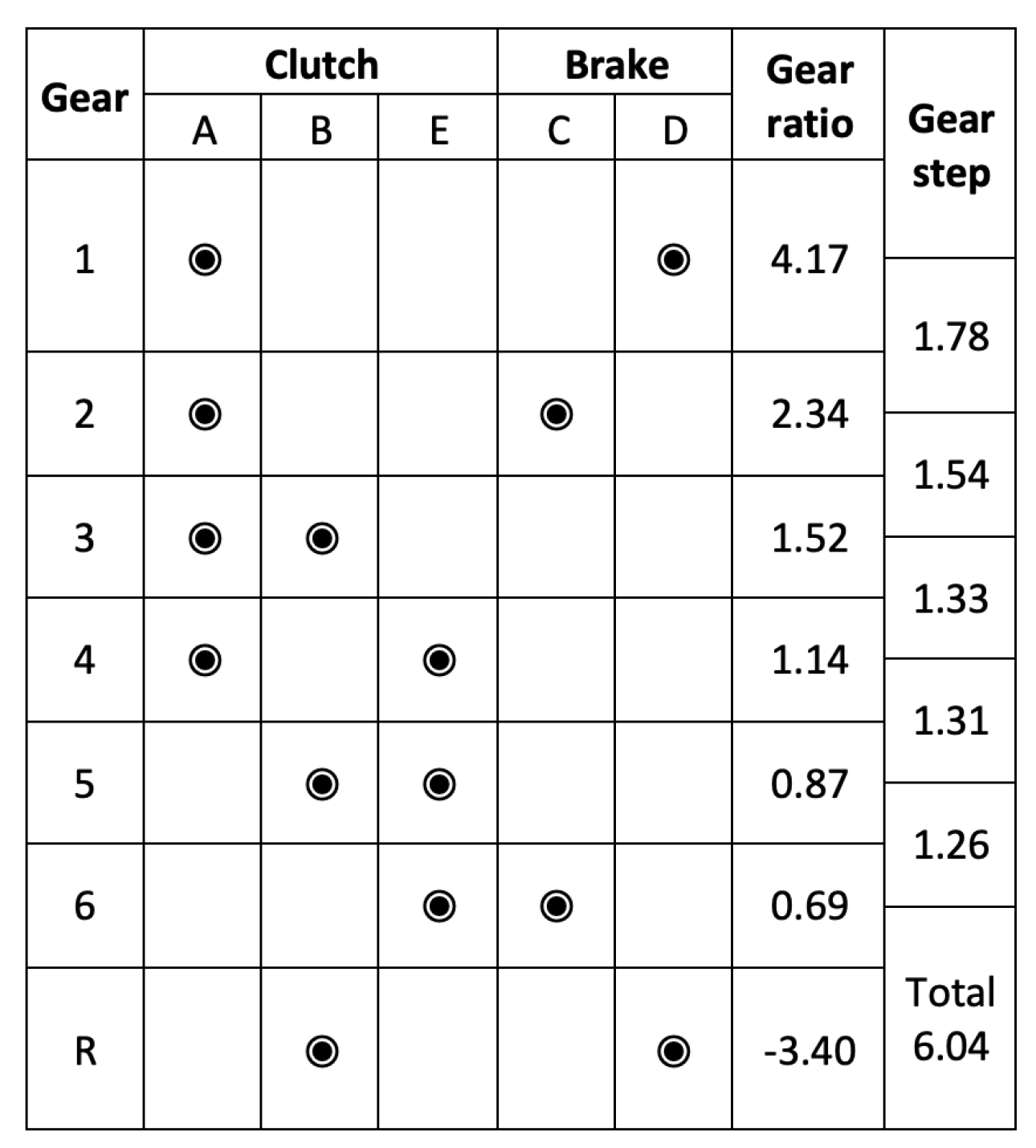Additionally, Figure 3 displays the gear ratio values for each gear as well as the corresponding connected clutches and brakes.

2.1. Control Strategy

As described by [33], the primary objective of the control strategies is to determine the optimal gear selection based on the prevailing driving conditions.
In the case of modern automatic transmission vehicles, there exist distinct primary objectives for this process. [1] outline two options: fuel economy and comfort. However, certain vehicles are equipped with a switch key that allows the driver to toggle between these two options.
In general, as stated by [1], several inputs need to be provided to the Transmission Control Unit (TCU). These inputs may include:
  • Speed selector position (Parking, Reverse, Neutral or Drive)
  • Position buttons to use the gearbox sequentially
  • Engine speed
  • Throttle position
  • Turbine velocity for the torque converter
  • Oil pressure for brakes
  • Door state (open or closed)
Likewise, the TCU generates various outputs through the utilization of actuators such as electrovalves and proportional valves. These outputs play a crucial role in executing the control strategy and can vary depending on the specific case and system dynamics. The mentioned factors serve as illustrative examples to elucidate the dynamics of the control strategy, which can exhibit variations in different scenarios.

2.2. Fuzzy Inference Systems

Fuzzy Logic finds extensive application when there is a need to convert human perceptions into precisely defined numerical values. As elucidated by [22], Fuzzy Logic operates on the principle of multivalence, encompassing various degrees between the states of being and not being. Within the realm of control systems, Fuzzy Logic is commonly employed in the form of Fuzzy Inference Systems (FIS), which can be delineated into four distinct steps:
  • Fuzzyfication
  • Knowledge set
  • Decision-making process
  • Defuzzyfication
Firstly, discrete values are transformed into fuzzy numbers, which represent variables defined by intervals. This conversion process enables the transition from objective analysis to a subjective perspective.
Secondly, the control model is constructed, encompassing all membership functions and control strategies. During the development of the knowledge base, it is advisable to consider the characteristics of the process being controlled or gather data on how a human operator would manually perform the given task, as advocated by [24]. In general, as outlined by [22], several best practices are crucial for determining these functions, including:
  • Opt for selecting 5 to 7 membership functions for each parameter.
  • The commonly utilized shapes include trapezoids and triangles.
  • The degree of overlap between the membership functions should range from 25% to 75%.
Thirdly, the control actions are derived through the combination of steps 1 and 2, requiring the use of an inference system. In this paper, a parametric structure known as the Sugeno Model is employed due to its precision and the flexibility it offers in terms of data requirements, as highlighted by [22]. As a zero-order Sugeno model is utilized, the representative rule for this model, considering a constant output, can be expressed as Equation (1).
I F s = S i T H E N v O U T = a 0 i
Here, s represents the input variable, S i denotes its value for the case i, v O U T represents the output variable, and a 0 i signifies its constant value for the case i.
Fourthly, and lastly, fuzzy values are converted back into discrete numbers, enabling computational manipulation. As described by [23], in the case of Sugeno Models, this step is relatively straightforward, and the defuzzification process involves calculating a weighted average that takes into account the membership values of all sets involved. This process will be further elucidated in the subsequent section.

3. Development of Control Strategies

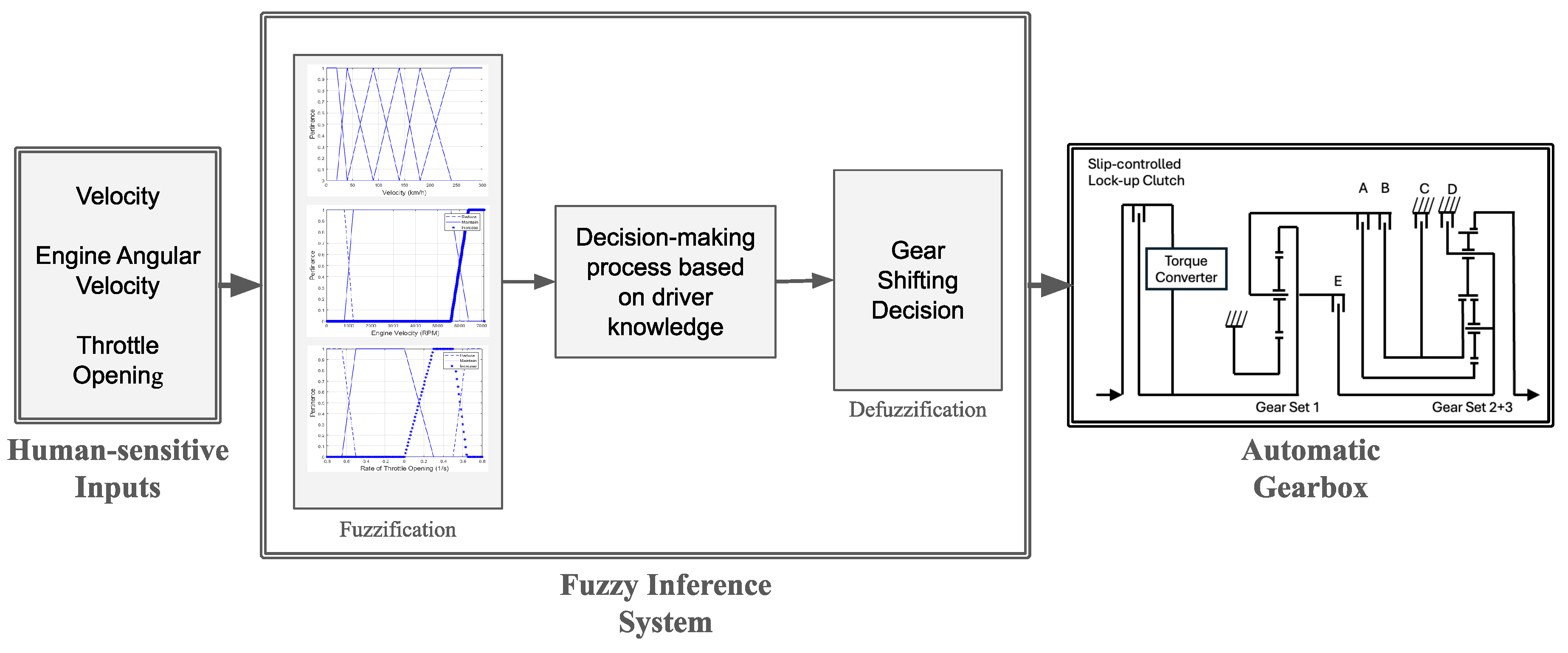
The proposed controller utilizes input parameters of the vehicle, which are obtained through sensors, and employs fuzzy logic for the decision-making process. It is crucial to emphasize that all inputs for the Fuzzy Gearbox (Figure 1) are driver-sensitive, meaning that they can be observed or perceived by the driver, in order to eliminate the need for additional sensor measurements. Furthermore, the desired output of the controller is the current gear selection.
A block diagram, as depicted in Figure 1, is employed to illustrate the bond graph modeling within the Simulink® environment. The structure of this diagram is based on a standard automatic transmission system featuring the Trilok torque converter, as described in previous works by [30] and [29].
Furthermore, in accordance with established literature, such as [33] and [32], a Lepelletier gearbox is commonly employed in numerous light vehicles equipped with a 6-speed automatic transmission. Thus, for the purpose of this paper, the Lepelletier gearbox type is adopted, as the focus is not on comparing various types of transmissions.

3.1. Selection of Driver Sensitive Inputs

When a driver is making a decision regarding the appropriate gear selection, they rely on sensory inputs that can be rapidly felt, seen, or heard. As emphasized by [17], the driver can be perceived as an adaptive intelligent sensor, as they utilize their senses and cognitive abilities to gather information and make informed decisions.
Novice drivers often tend to focus solely on the speedometer or tachometer displayed on the dashboard, primarily due to their limited sensitivity and experience. Conversely, experienced and skilled drivers typically rely on multiple sensory inputs. They listen to the engine’s angular velocity and feel the acceleration generated by the pressure applied to the accelerator pedal. This enables them to simultaneously monitor the longitudinal velocity of the vehicle. As a result, they effectively utilize the engine speed range and convey the need for additional power to the vehicle’s system.
Commencing this study, the analysis begins by employing the longitudinal velocity as the sole input parameter, as outlined in Subsection Case 1: FIS with Longitudinal Velocity as Input. Subsequently, the investigation proceeds to incorporate the engine angular velocity as an additional input, as described in Subsection Case 2: FIS with Engine Angular Velocity as Input. Finally, the study combines the previously mentioned inputs with the throttle opening rate in Subsection Case 3: FIS with Multiple Input Parameters, facilitating a comparison of the three approaches in terms of performance, specifically the maximum velocity achieved.
In all cases, the current gear is also considered as a factor in the analysis, thereby simulating the human decision-making process.

3.2. Case 1: FIS with Longitudinal Velocity as Input

Each notable point is carefully selected based on the experience of drivers and tailored to passenger vehicles, aiming to approximate the computational approach to the human decision-making process. Given the subjective nature of this process, interviews were conducted with experienced drivers from diverse social groups. It is acknowledged that the chosen top velocities for each gear may appear excessively high; however, it is essential to consider that this selection reflects a scenario focused on maximum performance. Moreover, it is crucial to emphasize that specific throttle openings are defined for each gear to prevent excessively high longitudinal slip values. A detailed explanation of this process is provided in Section Simulations and Results.
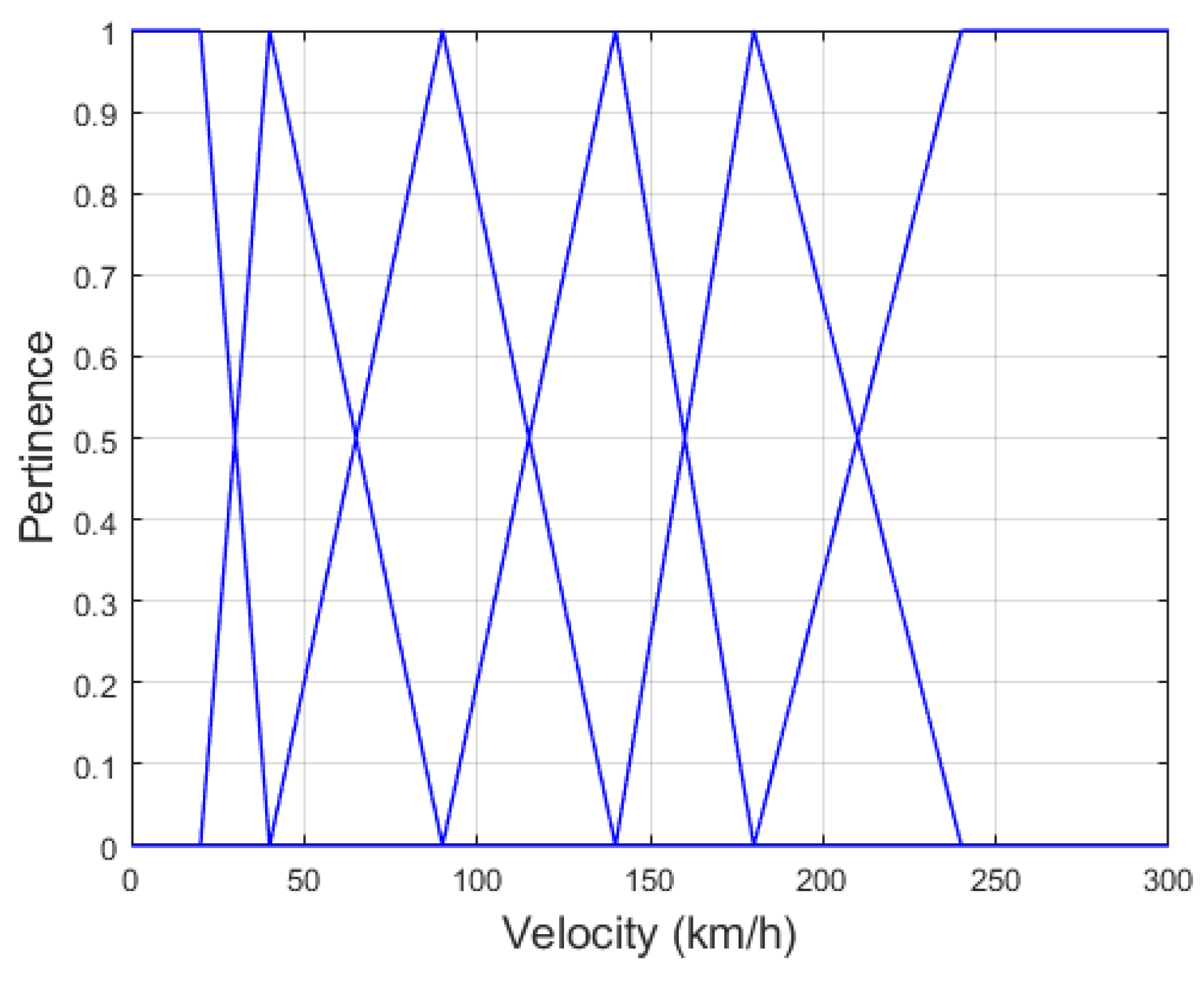
In the case where the sole determining factor for the FIS is the longitudinal velocity, the membership function set depicted in Figure 4 is employed. For every velocity value, a 6-column vector of pertinence can be derived, corresponding to the 6 membership functions illustrated in the figure.
Assuming v represents the longitudinal velocity, the inference model adheres to the following rules:
If v is extremely low, then the current gear = 1
If v is low, then the current gear = 2
If v is moderate, then the current gear = 3
If v is slightly high, then the current gear = 4
If v is high, then the current gear = 5
If v is significantly high, then the current gear = 6
Finally, employing a T-S defuzzification process, the outputs are derived by calculating the weighted average of all gear numbers, with membership values serving as weights. The nearest integer is then selected to determine the current gear.

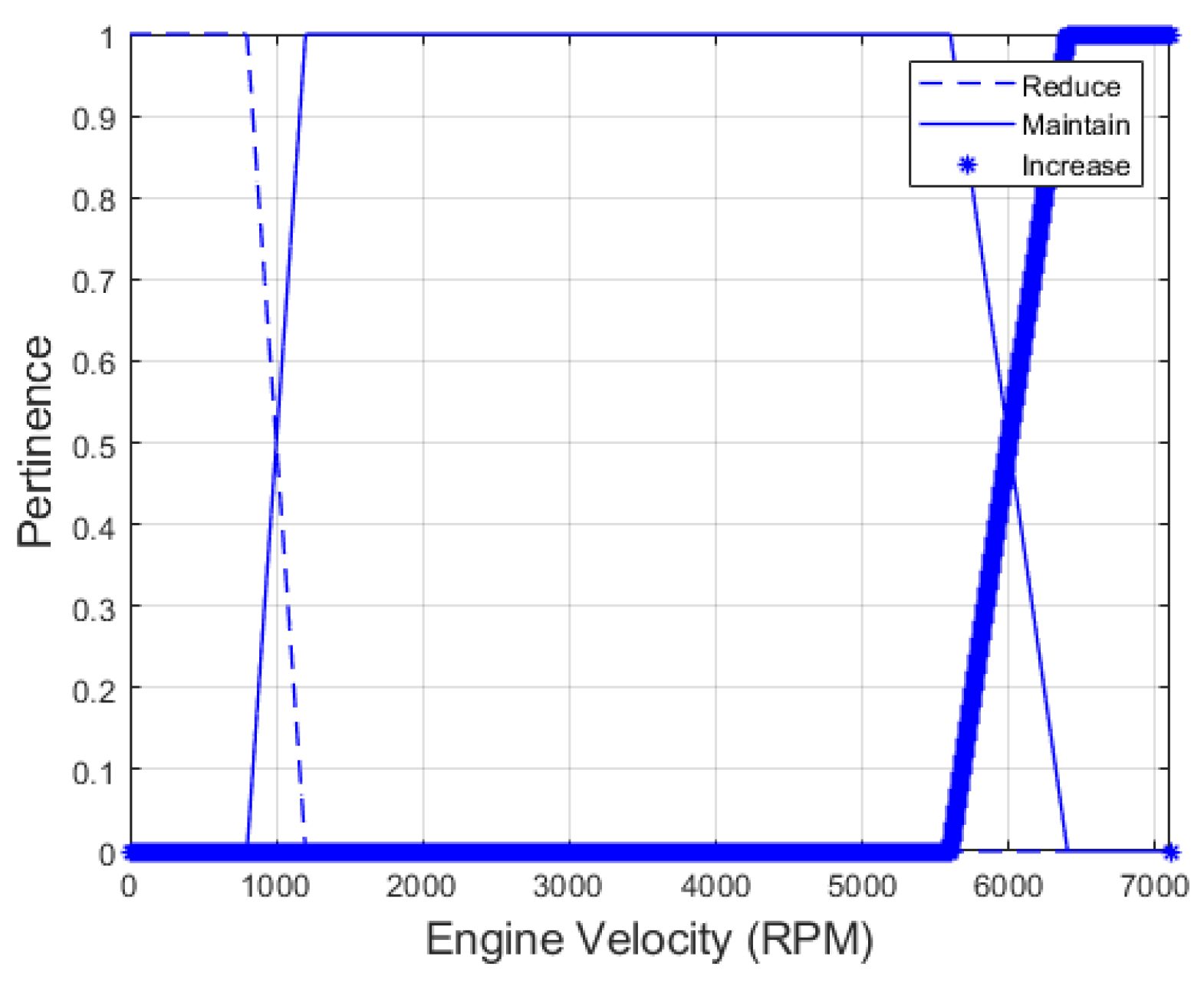
3.3. Case 2: FIS with Engine Angular Velocity as Input

In this scenario, it is possible to output a single unitary change in the gear number by adding or subtracting it from the current value. However, as observed in Section Simulations and Results, it is necessary to evaluate the outcomes for different throttle openings, thereby creating distinct cases. In all of these cases, the same membership function set, illustrated in Figure 5, is employed.
Furthermore, assuming ω represents the engine velocity in revolutions per minute (rpm), a 3-column vector of pertinence can be obtained for each engine velocity value, corresponding to the three membership functions (reduce, maintain, and increase) denoted as ω r , ω m , and ω i , respectively. The rule base for this inference is as follows:
If ω is low, then Δgear = -1 (Reduce)
If ω is moderate, then Δgear = 0 (Maintain)
If ω is high, then Δgear = 1 (Increase)
Similar to Case 1, the notable points for the membership functions are selected based on the experience of drivers using typical passenger cars, taking into account the lower and upper limits of engine rotation. Due to the subjective nature of this process, interviews were conducted with experienced drivers from various social backgrounds. In the employed model, the engine necessitates a lower gear when it reaches angular velocities below 1000 RPM, which is close to the stall point. Similarly, it requires a higher gear when it reaches 6000 RPM. This model can be adapted for different vehicles equipped with automatic transmission.
As a zero-order Sugeno model is utilized, the output y corresponds to the weighted average of each possible variation in the gear number, with the corresponding membership values serving as weights. Therefore, the representative equation can be expressed as Equation (2).
y = w r w m w i − 1 0 1

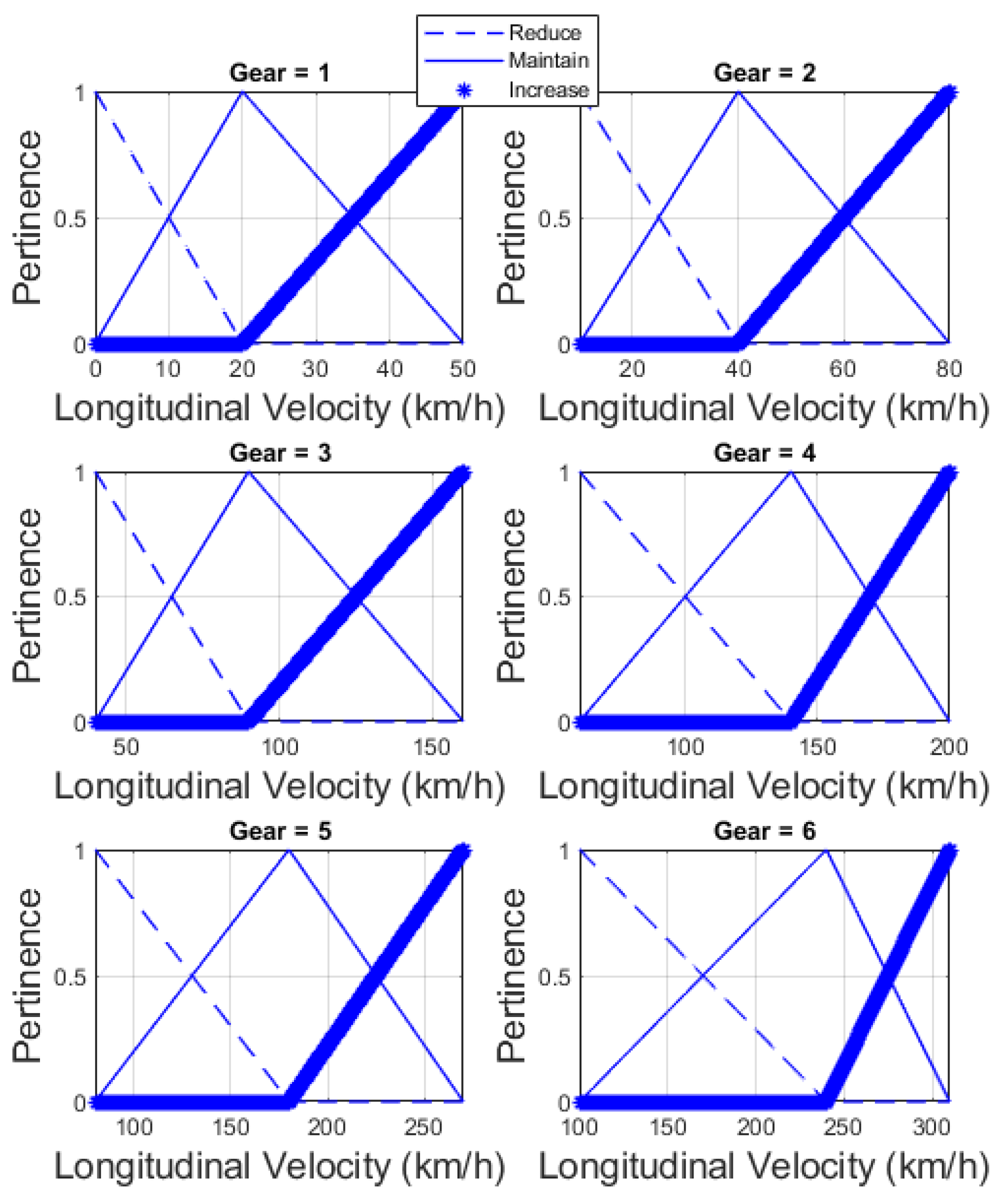
3.4. Case 3: FIS with Multiple Input Parameters

To harness the full benefits of fuzzy logic and achieve optimal design, it is more appropriate to incorporate multiple parameters for the decision-making process in automatic transmission shifting problems. This approach enhances the performance of this artificial intelligence technique. Therefore, in this scenario, three input variables are taken into account:
  • Longitudinal Velocity
  • Engine Velocity
  • Rate of Throttle Opening
The first two variables, longitudinal velocity and engine velocity, have been previously explained and modeled in the previous sections. However, an adaptation is required for the membership functions of the longitudinal velocity (v), in order to obtain the gear number variation as the output. Therefore, the current gear number (n) is used as an input solely as an initial condition. The resulting membership functions are depicted in Figure 6, where the analysis is divided into six cases, with three rules in each case, as illustrated below:
If v is low, then Δgear = -1 (Reduce)
If v is moderate, then Δgear = 0 (Maintain)
If v is high, then Δgear = 1 (Increase)
Moreover, a 3-column vector of pertinence can be determined for every longitudinal velocity value in a particular gear, corresponding to the three membership functions (reduce, maintain, and increase) denoted as v r , v m , and v i , respectively.
Each significant point is chosen based on the experience of drivers operating passenger cars. Due to the subjective nature of this process, interviews were conducted with experienced drivers from diverse social groups. For each gear, there exists a specific range of velocities that is considered more suitable.
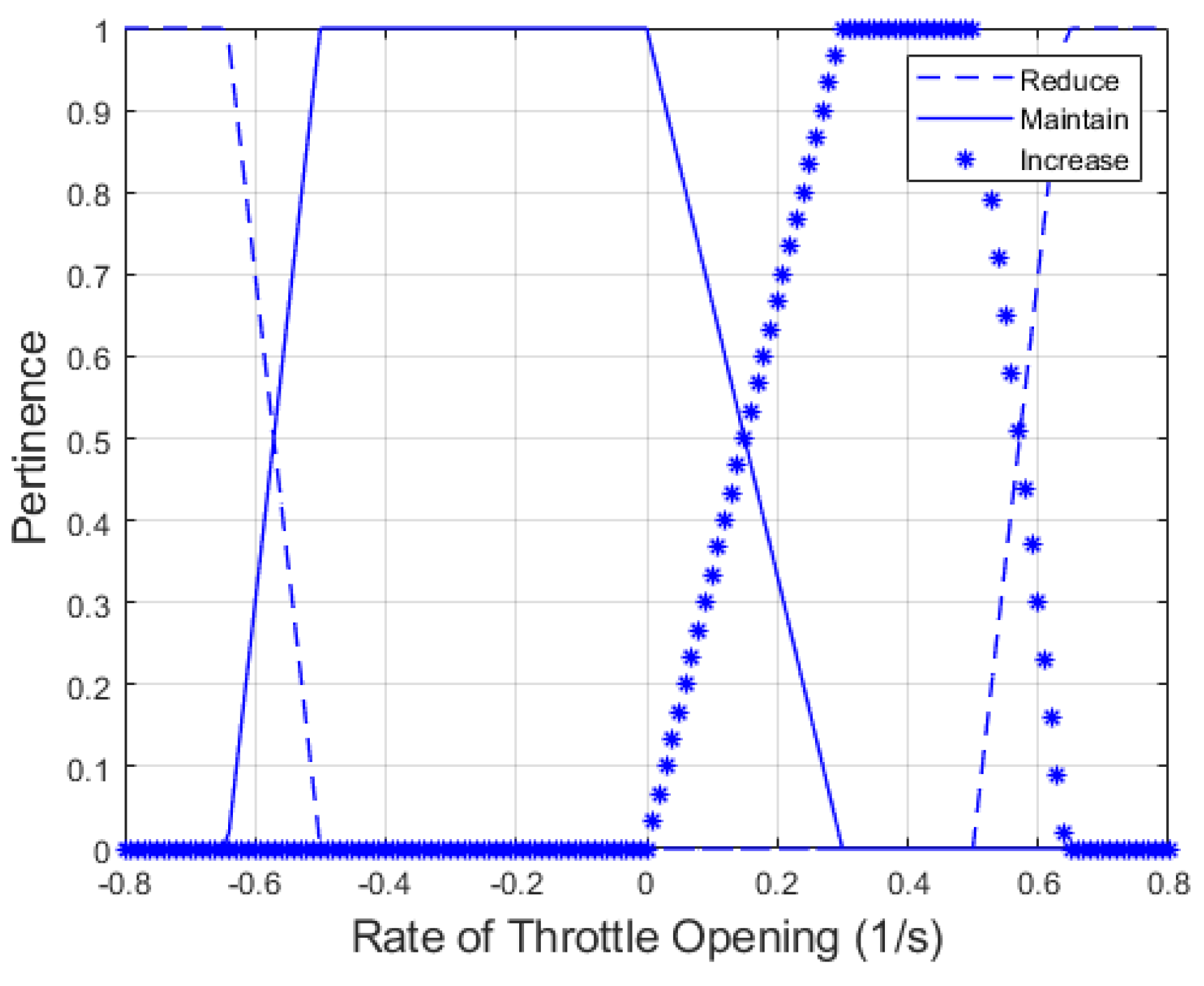
Regarding the rate of throttle opening ( Δ t T . O . ), the membership functions are presented in Figure 7. In this case, this variable is driver-sensitive and is controlled by the accelerator pedal. For each value of the rate of throttle opening, a 3-column vector of pertinence can be determined, corresponding to the three membership functions (reduce, maintain, and increase) denoted as b r , b m , and b i respectively. The rules of inference are defined as follows:
If Δ t T . O . is high, then Δgear = -1 (Reduce)
If Δ t T . O . is moderate, then Δgear = 0 (Maintain)
If Δ t T . O . is low, then Δgear = 1 (Increase)
For the throttle membership functions, the values are also determined based on experience. Due to the subjective nature of this process, interviews were conducted with experienced drivers from diverse social groups. A variation of 0.4 within 0.7 seconds is considered abrupt or high, while a variation of 0.3 within 2 seconds is deemed progressive or low.
Additionally, weights (fuzzy constants) are assigned to each decision aspect, denoted as c 1 , c 2 , and c 3 respectively. Therefore, the resulting equation incorporating all the parameters is given by Equation (3).
y = c 1 v r v m v i − 1 0 1 + c 2 w r w m w i − 1 0 1 + c 3 b r b m b i − 1 0 1
In this case, the constants c 1 , c 2 , and c 3 are selected through a trial and error process, as explained in Section sec:results.
In summary, the proposed methodology is illustrated in Figure 8, where it is possible to note the selected inputs and the Fuzzy Inference System used on this research.

4. Simulations and Results

As per the findings discussed in the preceding section, the results can be classified into three distinct categories, elaborated as follows:

4.1. Case 1

In this particular scenario, if a throttle opening (TO) value of 1 were maintained throughout the entire duration, it would result in excessive tire slip. However, through a trial and error approach, increasing values of TO are utilized for each gear (as indicated in Table 1). This adjustment enables optimal adherence and enhances overall performance in this specific case.
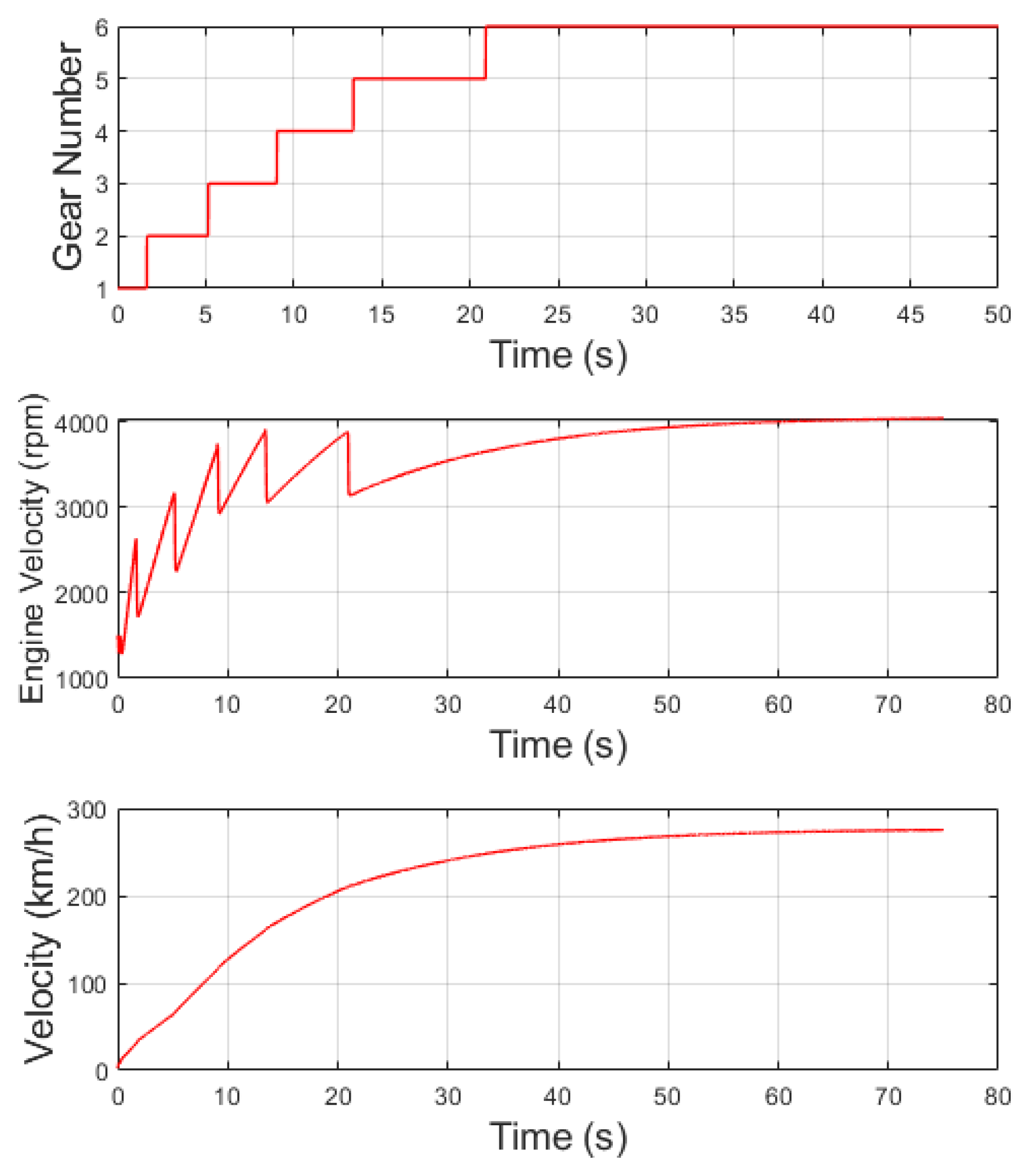
The obtained results are presented as a sequence in Figure 9.
One noticeable aspect is the initial lack of smoothness observed in the velocity graph. This behavior can be attributed to the Trilok torque converter transitioning through the lock-up point.
Moreover, towards the end of the graph, a stabilization is observed, which is attributed to the equilibrium between resisting forces and traction force. The maximum velocity achieved, approximately 270 km/h, aligns with the values reported in [31] and is supported by [30]. Additionally, when considering the 0-100 km/h test, the performance displayed in the graph aligns with the references mentioned earlier.
As a consequence of relying solely on longitudinal velocity for control purposes, it is not possible to fully utilize the entire engine capacity, even with the application of fuzzy logic. This can be observed in the gear number graph, where the more powerful gears are engaged for a shorter duration, resulting in a maximum velocity below the maximum power velocity (6100 rpm), as depicted in the engine angular velocity graph. This limitation is further emphasized by the requirement for low throttle opening at the beginning of the process.

4.2. Case 2

In contrast to the previous section, in this case, the fuzzy output represents the gear number variation, as illustrated in Section Case 2: FIS with Engine Angular Velocity as Input. To conduct a comprehensive evaluation, it is essential to simulate various scenarios with different throttle openings and determine the optimal case through a trial and error approach.
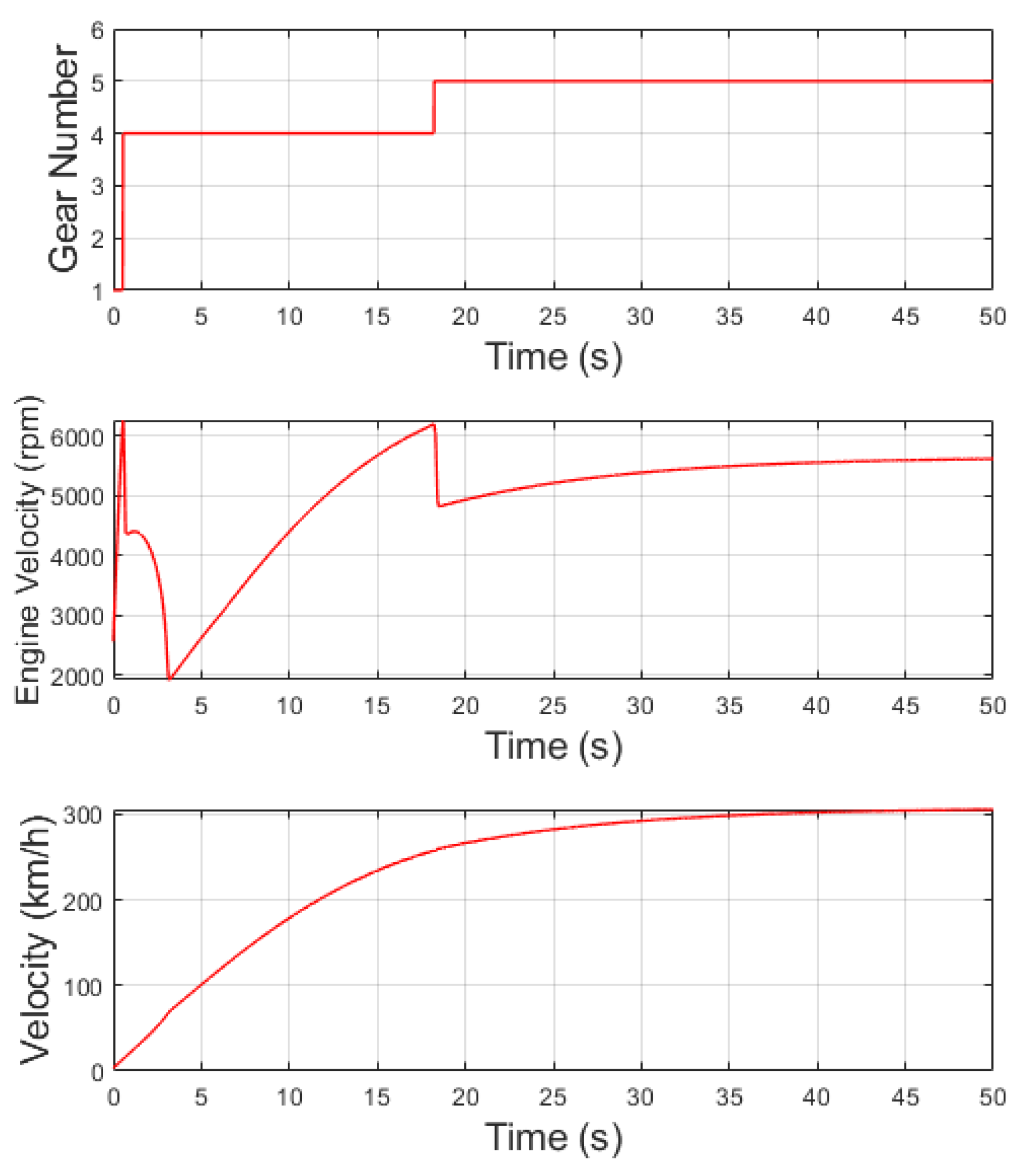
When considering a throttle opening equal to 1 (wide open throttle or WOT), the results are depicted in Figure 10.
Given the high engine power (298 kW) combined with maximum throttle opening throughout the entire process, the engine reaches an excessive angular velocity in results of Figure 10. In this scenario, the Fuzzy logic system interprets that it is feasible to initiate vehicle movement and subsequently shift to gear number 4. As a consequence, the vehicle experiences a gradual acceleration and attains a top speed of 300 km/h, which is better than the data of reference in [31]. However, it is advisable to reduce the throttle opening during the initial moments, which supports the idea presented in Case 1.
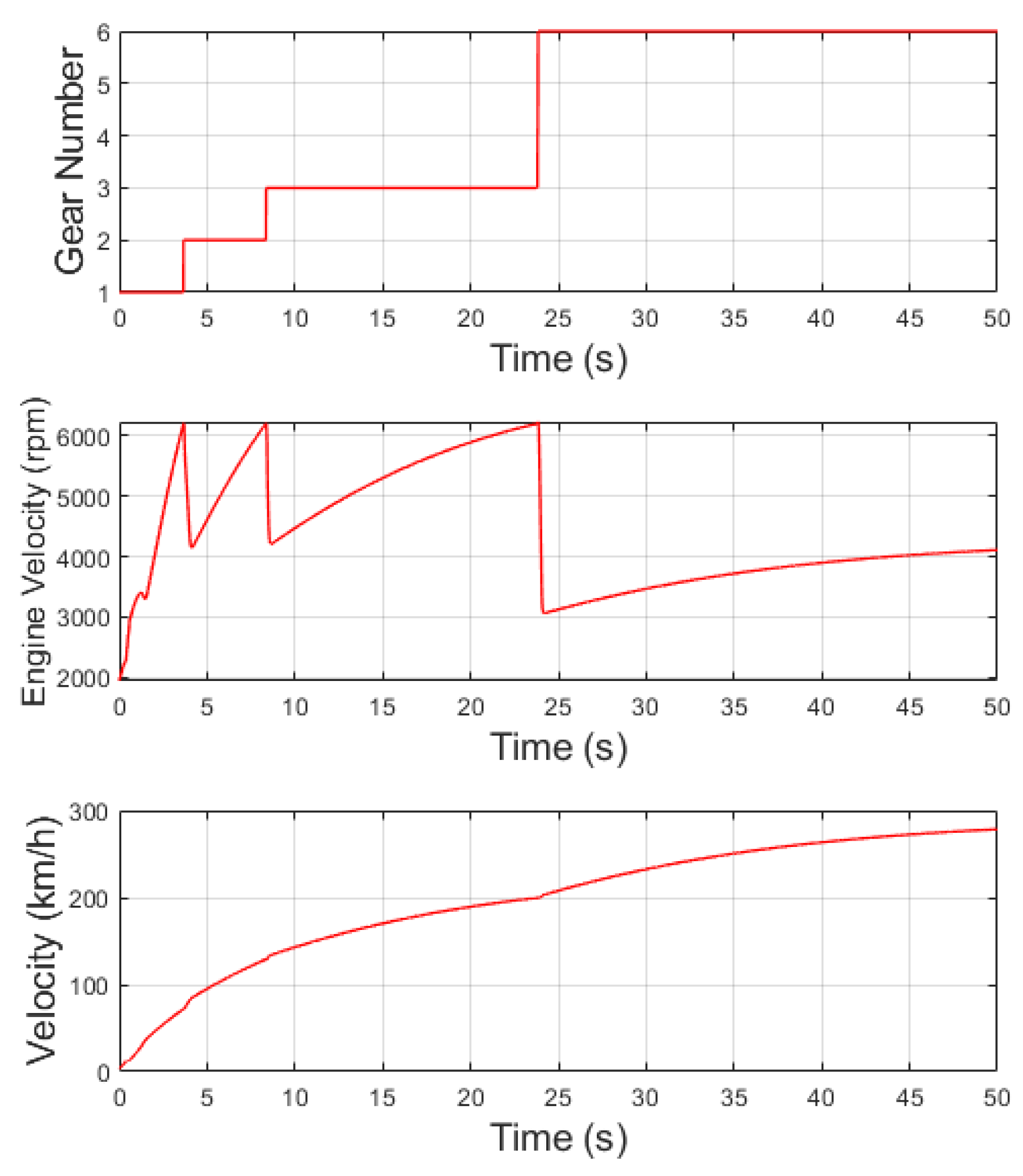
When considering a throttle opening equal to 0.4 in gears n = [1, 2, 3, 4] and equal to 1 in gears n = [5, 6], the results are illustrated in Figure 11.
In this case, the utilization of a low throttle opening for most of the time results in a lower acceleration rate. Consequently, the vehicle gets stuck in gear n = 4 , leading to a lower maximum velocity when compared to the previous simulation, but coherent with the data of reference in [31]. Notably, the engine angular velocity remains almost constant during the final moments, limiting the vehicle’s top speed.
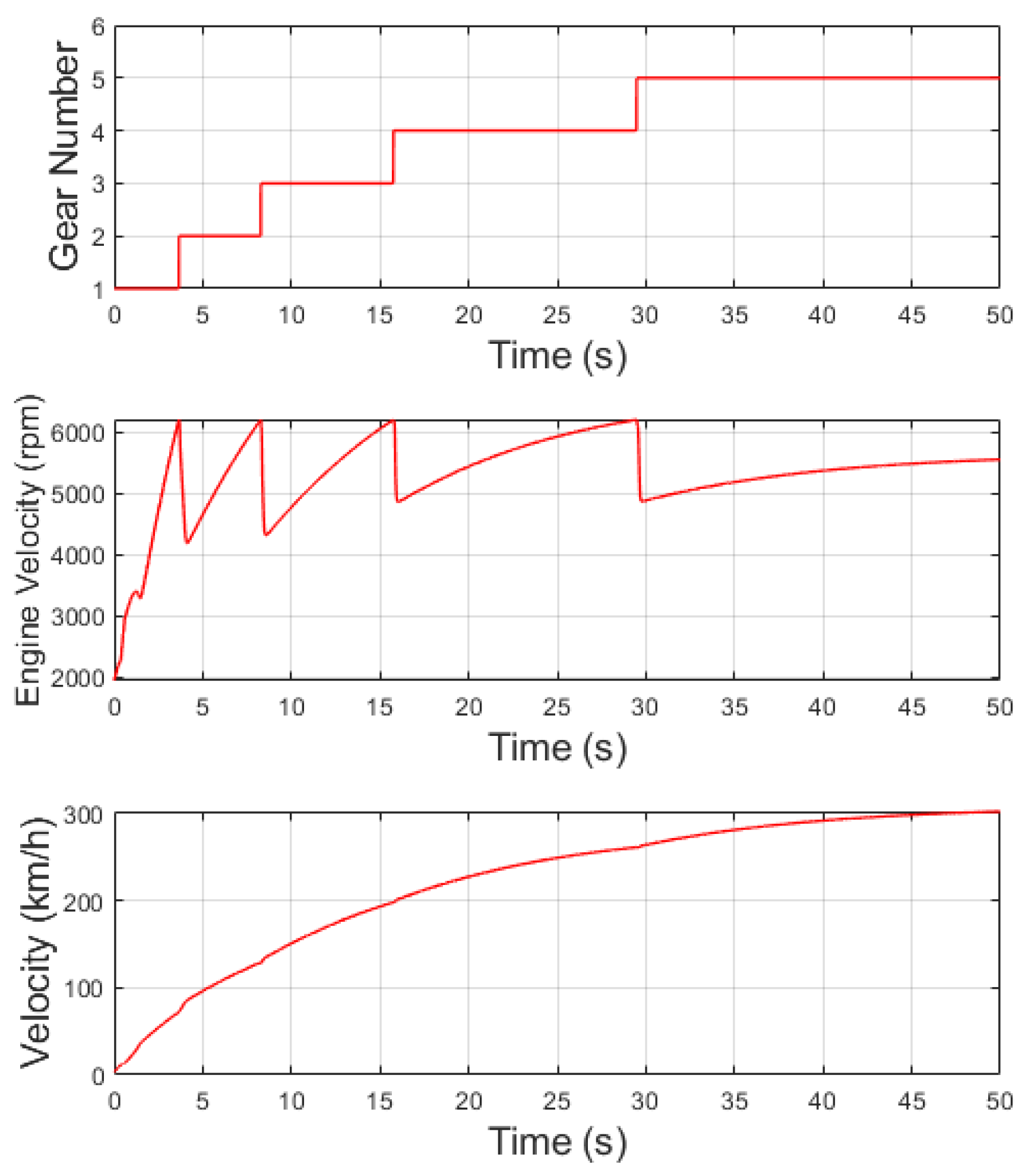
Finally, the best performance is achieved and reflected in Figure 12. The corresponding throttle opening values for each gear are presented in Table 2.
After evaluating the previous cases, the optimal result is obtained, where 5 out of 6 gears are utilized, enabling the engine to reach its maximum angular velocity in each gear. As a result, the vehicle attains a top speed of approximately 300 km/h, even without utilizing the last gear ( n = 6 ), which represents an unequivocally better result compared to that obtained in the reference data of [31]. This is evident in the velocity graph.
Based on these results, it is evident that the throttle opening (or a function thereof) has a significant influence on automatic transmission control.

4.3. Case 3

As a final step, it is possible to obtain the results for a system based on multiple parameters. In this case, for each set of fuzzy constants, there are two distinct situations, which can be summarized as follows:
  • Performance Test: The throttle opening starts at 0 and gradually increases to 1 over a period of 2 seconds, after which it remains constant.
  • Fuzzy Response Test: The throttle opening starts at 0, gradually increases to 1 over a period of 2 seconds, remains constant for a while, then suddenly drops to 0, and finally, rises to 1 again within a specified time frame.
The first case aims to evaluate the performance by considering the top speed achieved by the vehicle and comparing it with the results obtained in previous cases.
The second case complements the results by evaluating the fuzzy response under different throttle openings and varying rates of throttle opening, while considering a ramp angle of 10º. This evaluation demonstrates the system’s capability to handle adverse situations and respond effectively to changing throttle inputs and challenging driving conditions.
Unlike the previous cases, in this situation, it is not necessary to adjust the throttle opening based on the current gear to achieve optimal performance. This is due to the fact that the fuzzy constants employed in the system are responsible for that.
In each case, the throttle opening as a function of time is depicted, as it is the sole input for the entire block diagram. This input is independent of the modeling process, as represented in Figure 1. Additionally, the input parameters for the Fuzzy logic block are plotted to evaluate their behavior throughout the simulation time. This enables the observation of the performance of the fuzzy control system.
By employing a trial and error methodology, the optimal fuzzy constants for the model were determined to be c 1 = 1.0 , c 2 = 0.9 , and c 3 = 0.7 . As a result, the corresponding outcomes for each gear are illustrated in Figure 13 through Figure 18.
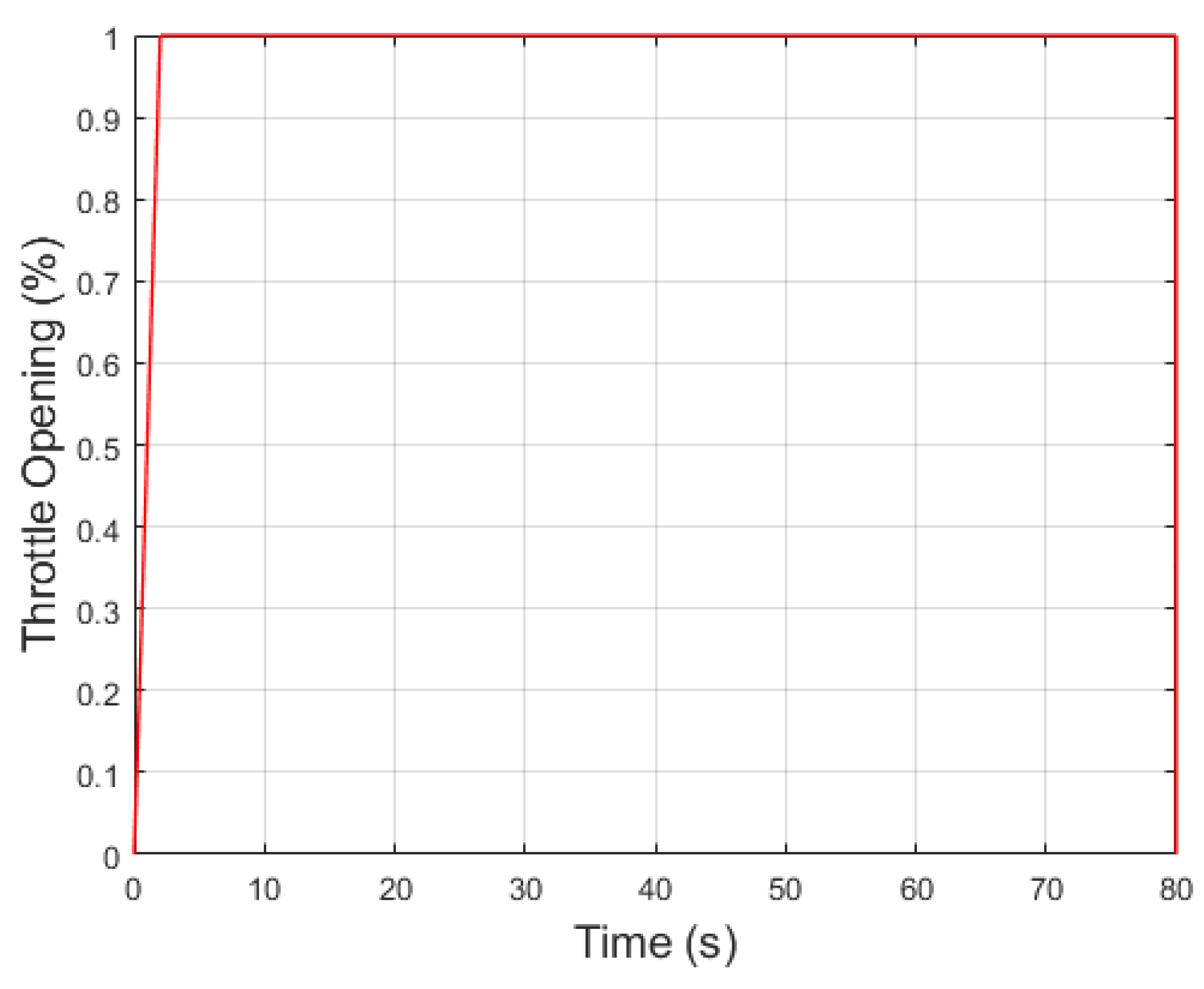
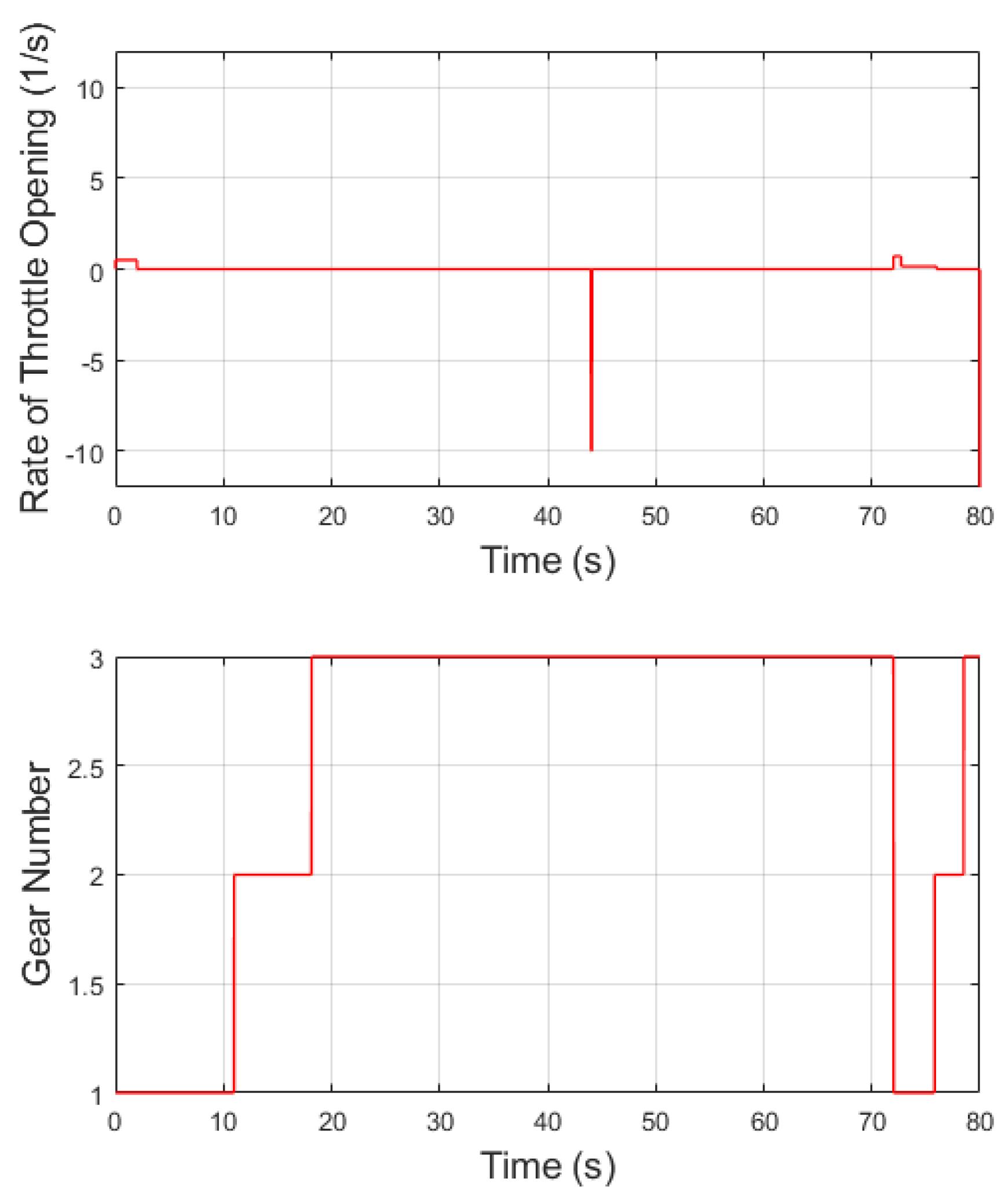
Figure 13 illustrates a progressive acceleration, albeit rapid, over a period of 2 seconds. The goal of this representation is not to simulate an aggressive stepping on the accelerator pedal, but rather to mimic a real-world scenario where power is required from a stationary position. This behavior is designed to ensure that tire slip is minimized, as a sudden and aggressive throttle input would lead to increased tire slip, compromising initial traction and prolonging the system’s time response.
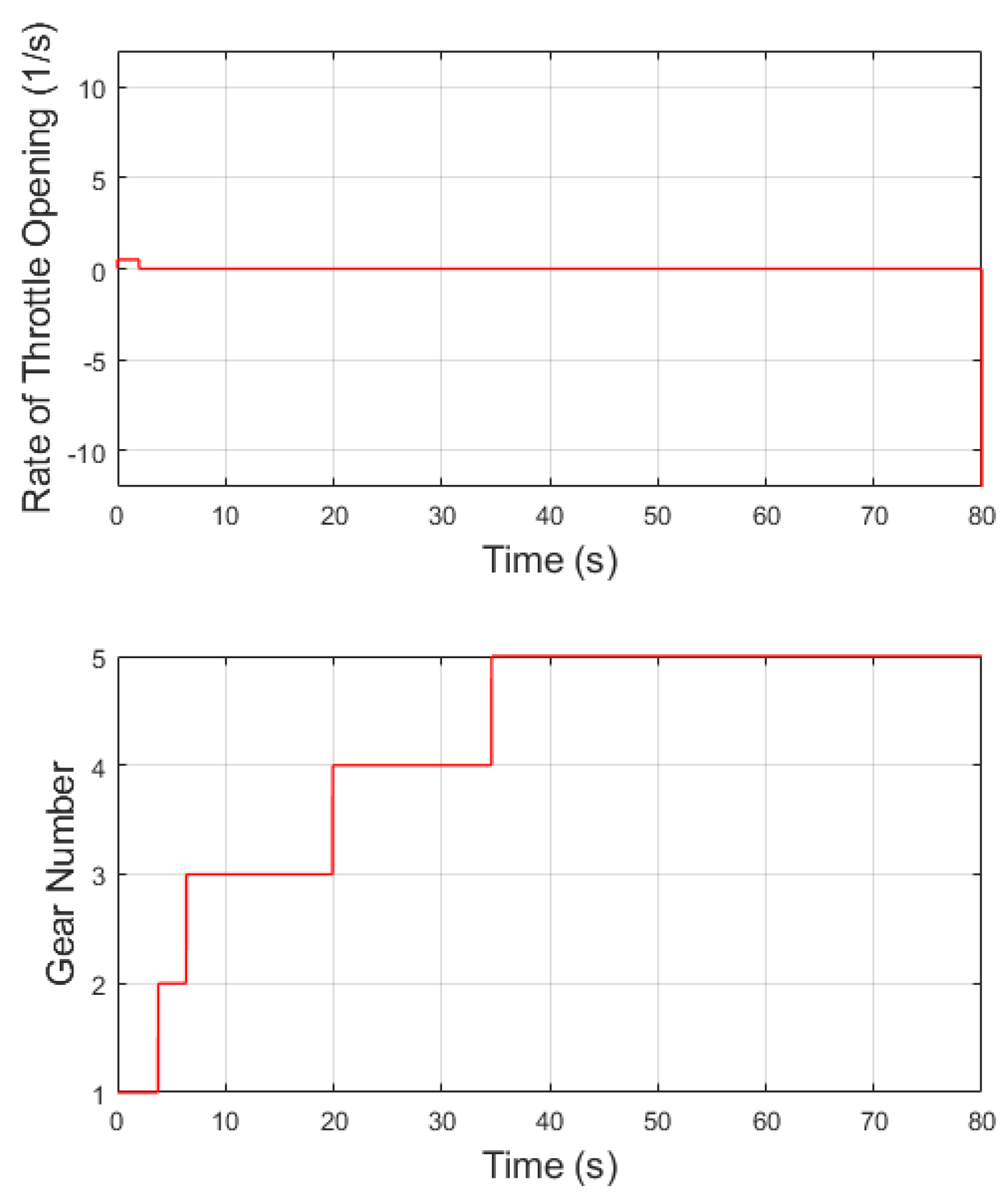
As anticipated, the rate of throttle opening is only nonzero during the initial moments, as depicted in Figure 14. Due to the simultaneous influence of three factors, a progressive gear shift is evident, even though the vehicle remains in second gear for only a brief period. This observation highlights one of the advantages of fuzzy logic based on multiple parameters, as it allows for a smooth gear transition without the need to reduce the throttle opening.
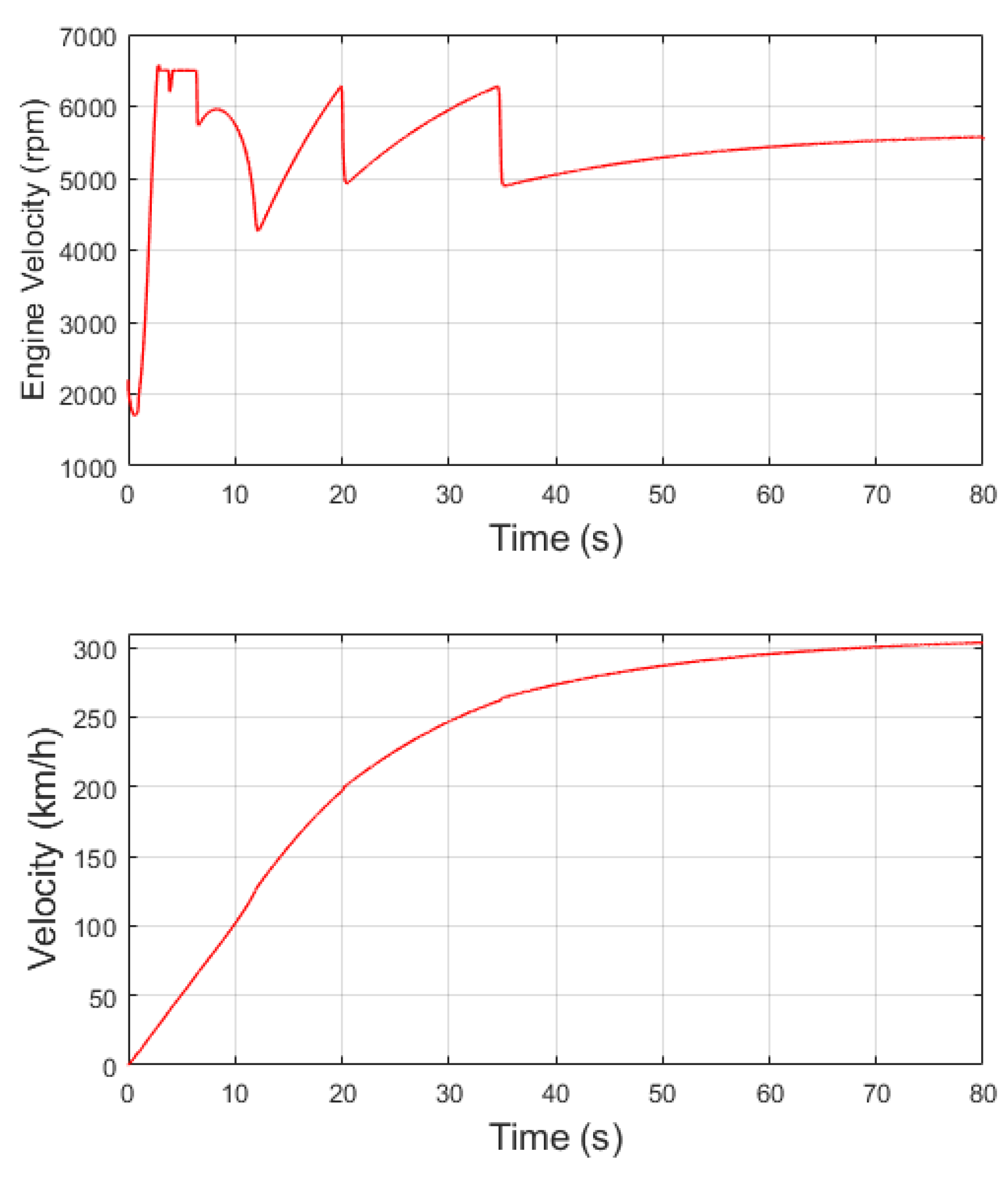
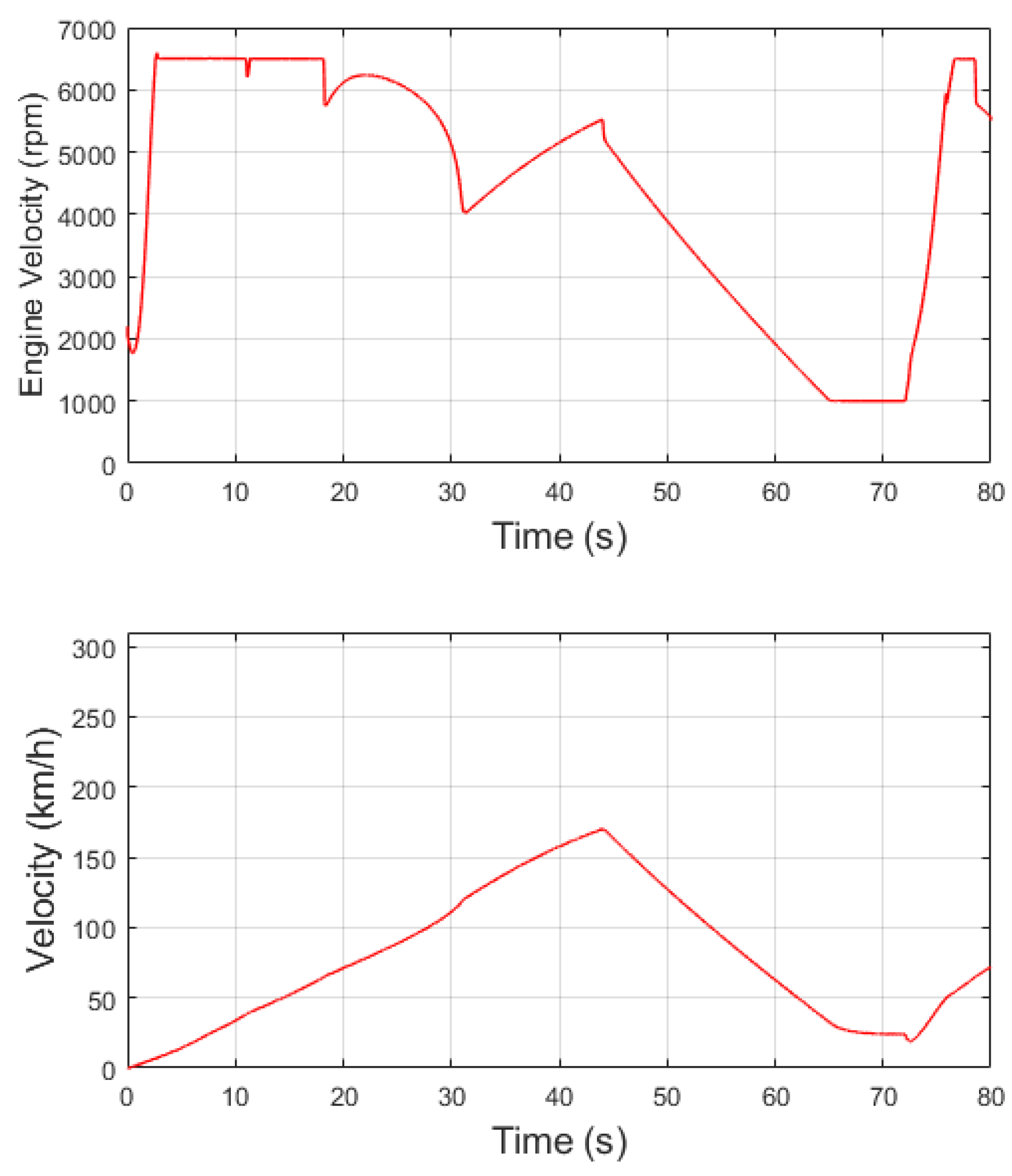
In terms of performance, the vehicle maintains its top speed of 300 km/h with a clear tendency to increase, as demonstrated in Figure 15. Additionally, when observing the engine velocity, there are successive drops between the fifth and tenth seconds of the simulation, resulting in power losses and increasing the system’s response time.
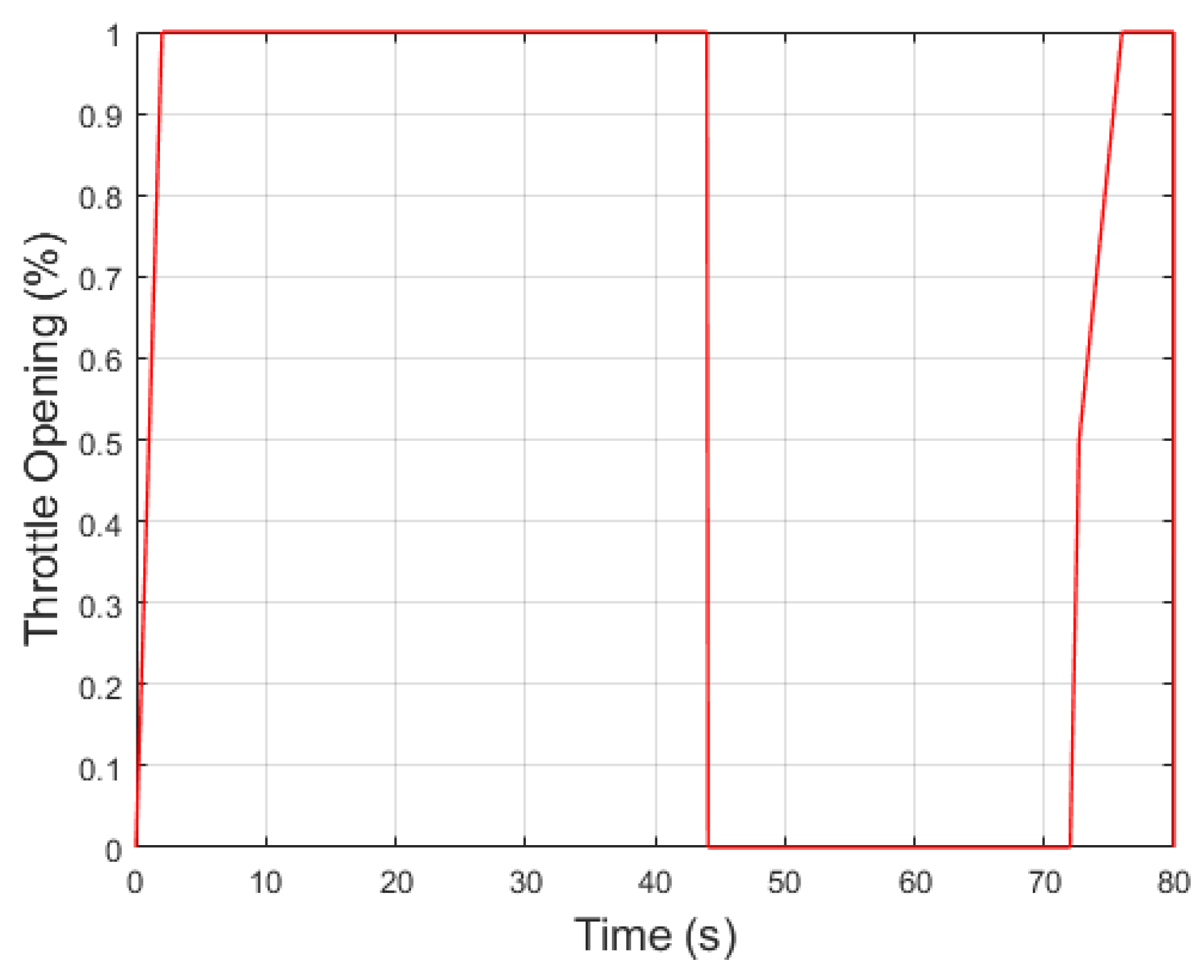
In Figure 16, the simulation starts similarly to the previous case, but with a release of the pedal between t = 40 s and t = 50 s to observe the adaptability of the fuzzy control system. During this interval, the throttle opening is changed from 1 to 0 in 0.1 s . Subsequently, the vehicle experiences a sudden acceleration, with the throttle opening changing from 0 to 0.5 in 0.7 s . This rate of change is determined based on prior experience.
As expected from Figure 16, the throttle opening rate is equal to 10 between t = 40 s and t = 50 s , as illustrated in Figure 17. Towards the end of the simulation, a much lower throttle opening rate is observed. In response to the first situation described, the gear number remains constant due to the high engine velocity depicted in Figure 18, which prevents downshifting. However, in the second situation, there is no such constraint, allowing for a reduction in gear by two levels as more power is required. The presence of a ramp angle of 10 further complicates this last scenario.
A notable observation in Figure 18 is the equilibrium reached by the vehicle on the ramp, indicated by the constant engine velocity at 1000 rpm, resulting in a steady vehicle velocity. This equilibrium point, achieved using the third gear, is only possible due to the high engine capacity. It is also noteworthy that, in the final moments of the simulation, there is a prolonged period of remaining in the second gear, which differs from the subsequent corresponding situation.

4.4. Discussion

Upon observing the previously presented results, it is evident that utilizing only velocity as an input parameter yields significant performance improvements and closely aligns with human decision-making, as individuals often rely on velocity to determine when to shift gears. However, in adverse situations, relying solely on velocity as an input is inadequate. Additionally, considering the inconsistency of maximum engine speed in each gear, power losses occur, impacting overall performance.
By utilizing only the engine velocity as an input, which is also observed by the driver, it becomes possible to achieve maximum engine utilization and attain optimal performance by selecting appropriate throttle openings. However, in this approach, there is no direct consideration of the vehicle velocity as a variable. While the focus is on maximizing engine performance, the lack of vehicle velocity information may limit the ability to make informed decisions based on the vehicle’s speed and dynamic behavior. Therefore, although this approach optimizes engine utilization, it may not provide a complete understanding of the vehicle’s overall performance and speed characteristics.
Finally, by considering both the longitudinal velocity and engine velocity as input parameters, all the advantages of each approach can be combined. When coupled with the adaptability provided by the rate of throttle opening as an input, the system can achieve a progressive gear shift, enabling the attainment of maximum achievable velocity, considerable better than in the data of reference of [31], and ensuring suitable behavior in scenarios such as ramp situations. Additionally, the system can effectively respond to sudden changes in throttle opening, allowing for smooth adjustments in power delivery.
Considering the aforementioned points, it is evident that the approach of combining longitudinal velocity, engine velocity, and rate of throttle opening as input parameters offers a better balance between achieving satisfactory results and maintaining a less complex computational model. This approach proves to be advantageous when compared to similar previous and more complex works, such as [7,12,13,14,15,17,18].

5. Conclusions

In conclusion, the proposed methodology for designing a Fuzzy Inference System (FIS) based controller for automatic transmission gear shifting has been demonstrated to be efficient. The successful application of this methodology has been observed in the simulation environment, specifically for passenger vehicles.
The car model utilized in this paper is well-suited for the application at hand, primarily due to its versatility and modularity. While the focus of this study is on employing a Fuzzy Inference System (FIS) for controlling the automatic transmission, it is important to note that the same model can be adapted and utilized for the application and evaluation of other Electronic Control Unit (ECU) algorithms as well.
Throughout the development of this research, it became apparent that fuzzy logic enables the construction of effective knowledge-based control algorithms with relatively low computational effort, as also demonstrated by [17]. In parallel, the proposed strategy heavily relies on the careful selection of input parameters that are inherently sensitive to human driving behavior. The chosen inputs are particularly appropriate for gear-shifting control algorithms, as they align with the key factors considered by human drivers when making shifting decisions. This highlights the effectiveness of a human knowledge-based strategy, as emphasized in the contributions of this paper.
For future research, it is recommended to compare the presented methodology with the application of optimization methods to determine the fuzzy membership function parameters ( c 1 , c 2 , and c 3 ). This could involve defining an objective function related to maximum performance, comfort, minimum fuel consumption, higher traction forces, or a combination of these factors through multi-objective optimization. The lateral and the vertical dynamics could be also integrated to the proposed model in future works.
Additionally, the concepts and methodology discussed in this paper can be extended to gearbox controllers in Unmanned Ground Vehicles (UGVs) and electric vehicles. The flexibility and adaptability of the model make it suitable for a wide range of vehicle types, beyond just passenger cars.

Funding

This research was funded by the National Council for Scientific and Technological Development of Brazilian Government.

Acknowledgments

We would like to acknowledge the financial support of the National Council for Scientific and Technological Development of Brazilian Government (CNPq, in Portuguese).

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Genta, G.; Morello, L. The Automotive Chassis; Vol. 1, Springer, 2009.
  2. Bosch. Manual de Tecnologia Automotiva. Edgar Blücher, São Paulo, 25th ed., 2005.
  3. Altrok, C.V. Fuzzy Logic in Automotive Engineering. Circuit Cellar INK: the Computer Applications Journal, 1997.
  4. Meng, F.; Tao, G.; Zhang, T.; Hu, Y.; Geng, P. Optimal shifting control strategy in inertia phase of an automatic transmission for automotive applications. Mechanical Systems and Signal Processing: Elsevier 2015, 60–61, 742–752. [Google Scholar] [CrossRef]
  5. Li, C.; Meng, F.; Xi, J.; Zhai, Y. Starting shift control of heavy-duty automatic transmissions based on the optimal trajectory of turbine speed. Mechanical Systems and Signal Processing: Elsevier 2019, 126, 490–504. [Google Scholar] [CrossRef]
  6. Wang, S.; Liu, Y.; Wang, Z.; Dong, P.; Cheng, Y.; Xu, X.; Tenberge, P. Adaptive fuzzy iterative control strategy for the wet-clutch filling of automatic transmission. Mechanical Systems and Signal Processing: Elsevier 2019, 130, 164–182. [Google Scholar] [CrossRef]
  7. Zou, W.; Wang, Y.; Zhong, C.; Song, Z.; Li, S. Research on shifting process control of automatic transmission. Scientific Reports 2022, 12, 13054. [Google Scholar] [CrossRef] [PubMed]
  8. You, Y.; Sun, D.; Qin, D. Shift strategy of a new continuously variable transmission based wheel loader. Mechanism and Machine Theory: Elsevier 2018, 130, 313–329. [Google Scholar] [CrossRef]
  9. Ranogajec, V.; Deur, J.; Ivanović, V.; Tseng, H.E. Multi-objective parameter optimization of control profiles for automatic transmission double-transition shifts. Control Engineering Practice: Elsevier 2019, 93, 104–183. [Google Scholar] [CrossRef]
  10. Dong, P.; Liu, Y.; Tenbergec, P.; Xu, X. Design and analysis of a novel multi-speed automatic transmission with four degrees-of-freedom. Mechanism and Machine Theory: Elsevier 2017, 108, 83–96. [Google Scholar] [CrossRef]
  11. Fofana, A.; Haas, O.; Ersanilli, V.; Burnham, K.; Mahtani, J.; Woolley, C.; Vithanage, K. Multi-Objective Genetic Algorithm for an automatic transmission gear shift map. IFAC - Papers OnLine 2016, 49-3, 123–128. [Google Scholar] [CrossRef]
  12. Eckert, J.J.; da Silva, S.F.; Santiciolli, F.M.; de Carvalho, Á.C.; Dedini, F.G. Multi-speed gearbox design and shifting control optimization to minimize fuel consumption, exhaust emissions and drivetrain mechanical losses. Mechanism and Machine Theory 2022, 169, 104644. [Google Scholar] [CrossRef]
  13. Qin, G.; Ge, A.; Lee, J.J. Knowledge-based gear-position decision. IEEE transactions on intelligent transportation systems 2004, 5, 121–125. [Google Scholar] [CrossRef]
  14. Graf, F.; Probst, G.; Weil, H.G. Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility. United States Patent: Siemens, 2007.
  15. Bastian, A. Fuzzy Logic in Automatic Transmission Control. Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility 1995, 24, 389–400. [Google Scholar] [CrossRef]
  16. Yamaguchi, H.; Narita, Y.; Takahashi, H.; Katou, Y. Automatic Transmission Shift Schedule Control Using Fuzzy Logic. SAE Technical Paper Series 1993, 24. [Google Scholar]
  17. Zhang, L.; Zhang, X.; Han, Z.; Chen, J.; Liu, J. A novel multi-parameter coordinated shift control strategy for an automated manual transmission based on fuzzy inference. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering 2017, 231, 684–699. [Google Scholar] [CrossRef]
  18. Mehta, S.; Soundararajan, K.; Eranna, U.; SH, B. Fuzzy Logic Based Controller For Automated Gear Control in Vehicles. IPASJ International Journal of Computer Science (IIJCS) 2014, 2. [Google Scholar]
  19. Takahashi, H.; Yasuoka, M.; Matsumura, T. Intelligent Controlled Automatic Transmission. IFAC 12th Triennial World Congress 1993.
  20. El-Ashwah, M.M.M.; Abbas, W.; Farid, T.M.; Atia, M.R.A. Modeling and Simulation of Gear-Shift Controller for Automated Manual Gearbox Based on Neuro Fuzzy Control Logic. Middle East Journal of Applied Sciences 2014, 4, 1000–1006. [Google Scholar]
  21. Ahmad, H.; Basiran, S.N.A. Fuzzy Logic Based Vehicle Speed Control Performance Considering Different Membership Types. ARPN Journal of Engineering and Applied Sciences 2015, 10. [Google Scholar]
  22. Simões, M.G.; Shaw, I.S. Controle e Modelagem Fuzzy, 2nd ed.; Blücher, 2007.
  23. Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing; Prentice-Hall, 1997.
  24. Kosko, B. Fuzzy Engineering; Springer, 1997.
  25. Hu, Y.; Meng, X.; Zhang, Q.; Park, G.K. A real-time collision avoidance system for autonomous surface vessel using fuzzy logic. IEEE Access 2020, 8, 108835–108846. [Google Scholar] [CrossRef]
  26. Leake, D.; Maguitman, A.; Reichherzer, T. Experience-based support for human-centered knowledge modeling. Knowledge-based systems 2014, 68, 77–87. [Google Scholar] [CrossRef]
  27. Gao, K.; Yang, Y.; Zhang, T.; Li, A.; Qu, X. An extrapolation-enhanced approach for modeling travel decision making: Integrating ensemble machine learning with knowledge-based decision-making theory. Knowledge-Based Systems 2021, p. 106882.
  28. Chapman, C.B.; Pinfold, M. Design engineering—a need to rethink the solution using knowledge based engineering. Knowledge-based systems 1999, 12, 257–267. [Google Scholar] [CrossRef]
  29. Reinaldo, I.L.; Lopes, E.D.R.; Rodrigues, G.S.; da Costa Neto, R.T. Simulação da dinâmica longitudinal de veículos leves automáticos com diferentes acoplamentos hidrodinâmicos. Revista Militar de Ciência e Tecnologia 2020, 37. [Google Scholar]
  30. da Costa Neto, R.T.; Lopes, E.D.R.; Reinaldo, I.L. Modelagem e Simulação da Dinâmica Longitudinal de um Veículo Leve com Transmissão Automática. SAE Technical Paper Series 2018, 1. [Google Scholar]
  31. Automobile-Catalog. : the complete catalog of cars since 1945, 2020.
  32. Naunheimer, H.; Bertsche, B.; Ryborz, J.; Novak, W. Automotive Transmissions: Fundamentals, Selection, Design and Application, 2nd ed.; Springer, 2011.
  33. Fischer, R.; Küçükay, F.; Jürgens, G.; Najork, R.; Pollak, B. The Automotive Transmission Book; Springer, 2015.
Preprints 116023 g001
Figure 1. Block Diagram representing the powertrain model
Figure 1. Block Diagram representing the powertrain model
Preprints 116023 g001
Preprints 116023 g002
Figure 2. Lepelletier Gearbox Scheme adapted from [32]
Figure 2. Lepelletier Gearbox Scheme adapted from [32]
Preprints 116023 g002
Preprints 116023 g003
Figure 3. Clutches and Brakes Configuration for Lepelletier Gearbox. Data from [32]
Figure 3. Clutches and Brakes Configuration for Lepelletier Gearbox. Data from [32]
Preprints 116023 g003
Preprints 116023 g004
Figure 4. Membership Functions for Velocity
Figure 4. Membership Functions for Velocity
Preprints 116023 g004
Preprints 116023 g005
Figure 5. Membership Functions for Engine
Figure 5. Membership Functions for Engine
Preprints 116023 g005
Preprints 116023 g006
Figure 6. New Membership Functions for Velocity
Figure 6. New Membership Functions for Velocity
Preprints 116023 g006
Preprints 116023 g007
Figure 7. Membership Functions for Throttle
Figure 7. Membership Functions for Throttle
Preprints 116023 g007
Preprints 116023 g008
Figure 8. Flowchart of the proposed methodology
Figure 8. Flowchart of the proposed methodology
Preprints 116023 g008
Preprints 116023 g009
Figure 9. Results based on longitudinal velocity
Figure 9. Results based on longitudinal velocity
Preprints 116023 g009
Preprints 116023 g010
Figure 10. Results based on Engine Angular Velocity in WOT
Figure 10. Results based on Engine Angular Velocity in WOT
Preprints 116023 g010
Preprints 116023 g011
Figure 11. Results based on Engine Angular Velocity in Partial Load case 1
Figure 11. Results based on Engine Angular Velocity in Partial Load case 1
Preprints 116023 g011
Preprints 116023 g012
Figure 12. Results based on Engine Angular Velocity in Partial Load - Case 2
Figure 12. Results based on Engine Angular Velocity in Partial Load - Case 2
Preprints 116023 g012
Preprints 116023 g013
Figure 13. Throttle opening for the first constant set and performance test
Figure 13. Throttle opening for the first constant set and performance test
Preprints 116023 g013
Preprints 116023 g014
Figure 14. Results for the first constant set and performance test
Figure 14. Results for the first constant set and performance test
Preprints 116023 g014
Preprints 116023 g015
Figure 15. Results for the first constant set and performance test
Figure 15. Results for the first constant set and performance test
Preprints 116023 g015
Preprints 116023 g016
Figure 16. Throttle opening for the first constant set and fuzzy response test
Figure 16. Throttle opening for the first constant set and fuzzy response test
Preprints 116023 g016
Preprints 116023 g017
Figure 17. Results for the first constant set and fuzzy response test
Figure 17. Results for the first constant set and fuzzy response test
Preprints 116023 g017
Preprints 116023 g018
Figure 18. Results for the first constant set and fuzzy response test
Figure 18. Results for the first constant set and fuzzy response test
Preprints 116023 g018
Table 1. Parameters of the Model.
Table 1. Parameters of the Model.
Gear Throttle Opening
1 0.3
2 0.3
3 0.6
4 0.7
5 0.8
6 0.9
Table 2. Parameters of the Model.
Table 2. Parameters of the Model.
Gear Throttle Opening
1 0.4
2 0.4
3 0.6
4 0.75
5 1
6 1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated