Preprint
Article
Complexity and Regime Transitions in Simple Master Equations
Altmetrics
Downloads
84
Views
24
Comments
0
This version is not peer-reviewed
Submitted:
10 July 2024
Posted:
11 July 2024
You are already at the latest version
Alerts
Abstract
We investigated the dynamics of a simple master equation describing the evolution of a probability distribution between two states, \( p_1 \) and \( p_2 \) (with \( p_1 + p_2 = 1 \)). Our focus is on the behavior of the entropy \( S \), the distance \( D \) from the uniform distribution (\( p_1 = p_2 = 1/2 \)), and the free energy \( F \). We define two ratios, \( \eta_S = \frac{dS/dt}{dF/dt} \) and \( \eta_D = \frac{dD/dt}{dF/dt} \), and find that both diverge to plus-minus infinity as the system evolves towards the uniform distribution. This divergence marks a critical transition point where the master equation temporarily loses physical meaning. However, after this divergence, the system settles into a new, well-behaved regime where the solutions stabilize at finite values, representing a new equilibrium or steady state. This two-regime behavior underscores the intricate dynamics of simple probabilistic systems as they approach and surpass equilibrium, providing insights into the complex interplay of entropy, distance, and free energy in statistical mechanics.
Keywords:
Subject: Physical Sciences - Thermodynamics
1. Preliminaries
A master equation is a phenomenological set of first-order differential equations specifying the temporal evolution of the probability of a given (let us call it A) system to occupy each one of a discrete set of states. The variable is the time t. We speak of an equation of motion for the occupation probabilities of A with the underlying supposition that A interacts with a usually much larger system B.
Entropy, in addition to many other facets, is a common synonym from disorder. Since about 25 years ago the rather novel notion of disequilibrium D [1-3], to be discussed below, has come to represent for many people (after reference [1]) the degree of order (of course, there exist many alternative measures).
We wish here to discuss the order-disorder contrast as playing a protagonist role in the workings of a simple master equation. One of the simplest master equation contemplates two states with probabilities P with components and and energies and . We wish here to study a master equation whose final stationary state is a Gibbs’ canonical one at the inverse temperature . Some interesting insight will be gained. In this respect an interesting order-indicator is the disequilibrium D (advanced in [1]), which, in probability space, represents the Euclidean distance between P and the uniform distribution with . This uniform distribution is associated with maximum disorder [1-3]. The larger the distance between P and , the larger the degree of order, according to references [1–8].
1.1. Motivation
Understanding the intricate dynamics of probabilistic systems as they approach equilibrium is fundamental in statistical mechanics. For such reason, we wish here to study a simple master equation governing the evolution of a probability distribution between two states, and , constrained by . Despite its simplicity, this model exhibits rich and complex behavior near equilibrium. By examining the entropy S, the distance D from the uniform distribution, and the free energy F, we identify critical phenomena that arise in the system’s temporal evolution. Specifically, we define and analyze two key ratios, and , which diverge to infinity as the system approaches the uniform state. This divergence points to non-linear dynamics, critical slowing down, and the interdependence of variables, highlighting the emergent complexity even in seemingly simple probabilistic frameworks. Our investigation provides new insights into the mechanisms driving such complexity and underscores the importance of these dynamics in broader thermodynamic contexts.
1.2. Master Equations
Investigating master equations is of significant importance in the fields of quantum mechanics, quantum optics, quantum information theory, and various other areas of physics and science. Below we list several key reasons regarding why the study of master equations is important:
1) Modeling quantum and complex classical systems: Master equations allow scientists to describe how a system evolves over time when it is interacting with its environment. This is crucial for understanding and predicting the behavior of complex quantum systems.
2) Master equations deal with the evolution of (discrete or continuous) probability distributions and not with the dynamics of microscopical degrees of freedom.
3) Decoherence [9] and Dissipation: Understanding how quantum coherence is lost due to interactions with the environment (decoherence) and how energy dissipates in quantum systems is crucial for quantum technologies. Master equations allow researchers to quantify these processes, which is useful for designing and maintaining quantum devices.
4) Quantum Information and Quantum Computing [9]: In the field of quantum information theory, Master equations are fundamental for understanding and mitigating errors in quantum computation and communication. Master equations help researchers develop error-correction codes and quantum error-correcting schemes.
5) Quantum Optics and Photonics: In quantum optics and photonics, Master equations are used to study the behavior of light and quantum states of light in various physical systems. This has applications in quantum communication, quantum cryptography, and quantum sensing.
1.3. Usefulness of This Work
We insist on the fact that studying a very simple master equation with all parameters having analytic expressions, as we will do here, can be relevant and beneficial in several ways:
- Pedagogical Purposes: Simple master equations with analytic solutions are excellent for educational purposes. They help students and researchers to gain understanding of key concepts in quantum mechanics and open quantum systems without the complexity of numerical or approximate methods.
- Theoretical Foundations: Simple master equations serve as building blocks for more complex models. By starting with analytic solutions, you can develop a solid theoretical foundation for understanding quantum systems. This can be particularly valuable when working with complex systems, as one uses insights gained from the simple case to understand more complex ones.
- Benchmarking: Simple models can be used as benchmarks for numerical or approximate methods. By comparing the results of more sophisticated numerical techniques to the exact analytical solutions of a simple master equation, one verifies the accuracy of the computational methods and identifies potential of error.
- Intuition and Insight: Analytic solutions provide deep insight into the behavior of quantum systems. They allow for a clear and intuitive understanding of how different parameters affect the system’s dynamics.
- Generalizations: Simple models can serve as a starting point for more generalized models. Once you understand the basic dynamics of a simple system, the knowledge can be extended to more complex problems.
- Exploration of Fundamental Principles: Simple models can be used to explore fundamental principles in quantum mechanics and open quantum systems. This can lead to new insights and discoveries, even if the model itself is highly idealized.
- Thus, studying a simple master equation with analytic solutions is a valuable starting point in quantum mechanics and open quantum systems. It can provide fundamental knowledge, benchmarking capabilities, and a clear understanding of how important parameters affect the system’s behavior. This understanding can then be applied to more complex and realistic scenarios, making it a relevant and useful exercise in various research and educational contexts.
2. Master Equation and Disorder Quantifiers
2.1. Order-Disorder Contraposition
Analyzing the order-disorder contrast is important in various scientific disciplines, including physics, chemistry, material science, and even in broader contexts like philosophy and social sciences. Here are several reasons why analyzing the order-disorder disjunction is significant. 1) Understanding the transition between ordered and disordered states is central to thermodynamics. It plays a crucial role in understanding phase transitions, like the transition between solid, liquid, and gas phases. The study of order-disorder transitions is essential for predicting and controlling these transitions. 2) In material science, the arrangement of atoms and molecules in a material can profoundly impact its properties. Analyzing the order-disorder disjunction is vital for the development of new materials with tailored properties, including semiconductors, superconductors, and advanced polymers. 3) In the realm of statistical mechanics, the order-disorder disjunction is a key consideration. This field provides a framework for understanding how macroscopic properties emerge from the behavior of individual particles. Understanding order and disorder at the microscale is vital in statistical mechanics. 4) Biological systems are rife with examples of the order-disorder disjunction. For instance, the folding of proteins into specific, ordered structures is crucial for their function. Understanding how biological systems maintain order and manage disorder is essential in fields like biochemistry and molecular biology. 5) In information theory and coding, error correction codes and data compression techniques rely on managing the trade-off between order and disorder in data transmission and storage. Analyzing this disjunction is critical for reliable communication and data storage. 6) The emergence of order from disorder and vice versa is a topic of interest in understanding emergent properties in complex systems. Emergence is a basic concept in many fields, including philosophy, physics, and biology.
2.2. Entropy, Disequilibrium, and Our Master Equation
Entropy is a common synonym from disorder. On the other hand, for almost three decades the notion of disequilibrium, to be explained below, has come to represent the degree of order. We wish here to analyze using a simple master equation the order-disorder question.
Possibly the simplest master equation faces two states with (1) probabilities (P) components and and (2) energies and . We will here study a master equation whose final stationary state is a Gibbs’ canonical one at the inverse temperature . Some valuable insight will be gained. In this respect an interesting order-indicator is the disequilibrium D, which, in probability space, represents the Euclidean distance between P and the uniform distribution with This uniform distribution is associated with maximum disorder. The larger the distance between P and , the larger the degree of order, according to references [1,2,3,4,5,6,7,8].
The master equation describing the time evolution of the probabilities and can be written as [10,11]:
or more simply,
The transitions between the states can be governed by rates (rate of transition from to ) and (rate of transition from to ). These rates could be functions of time, external fields, or other environmental factors.
To satisfy detailed balance, the ratio of the transition rates should match the ratio of the Boltzmann factors of the states’ energies [10]: .
Accordingly, we set
and . is the inverse temperature . We set Boltzmann’s constant equal to unity.
Detailed balance is a condition that ensures the system’s microscopic reversibility and is fundamental to the consistency of statistical mechanics. A master equation should obey detailed balance to ensure that the system it describes can reach and maintain thermodynamic equilibrium. Detailed balance guarantees microscopic reversibility, consistency with the Boltzmann distribution, and adherence to fundamental principles of statistical mechanics and thermodynamics. It is essential for the physical validity of models and simulations, ensuring they accurately reflect the behavior of real-world systems in equilibrium.
The exact solution of the system is
where
is an appropriate constant. It depends on the initial conditions at . For any other t one has .
The stationary solution for large t has the form
Revisit now Eqs. (3). We clearly see that a canonical Gibbs’ distribution is eventually attained with our p’s. We must also speak of the detailed balance condition, that is a specific symmetry property demanding that the transition rates in the master equation must satisfy for the system to reach detailed equilibrium. In detailed equilibrium, the probabilities of transitions between pairs of states must be balanced in such a way that there is no net flow of probability between those states over time. in other words: , so that detailed balance holds at the stationary stage.
Let
- P be an n-vector whose components are the probabilities and
- an matrix.
- The master equation is then the matrix equationwhere is defined though equations (1) and (2), that is, , , and .
Note that, in general, this master equation represents a process that is not stationary. This implies that there are ongoing changes in the system. For example, the system’s properties may be changing with time, or there may be gradients in temperature, pressure, or other thermodynamic variables within the system. Such a system is not in thermodynamic equilibrium. However, the we will use here leads eventually to stationarity.
3. Time Evolution of Our Quantifiers
In analyzing our master equation, time is measured always in arbitrary units. We start by looking at the time evolution of our two probabilities in Figure 1. We see that they eventually cross each other, which anticipates an interesting thermodynamics.
We begin with and . Figure 1 depicts the behavior of our two probabilities for the initial conditions and versus time in arbitrary units. They cross at a time . Here we have , , , and . Note that stationarity is eventually reached.
We compute next the entropy S, Helmholtz free energy F, and mean energy U from their definitions and then plot the first two of them in Figure 2. We have [12]
Remind that the lower the free energy of a system, the more stable it tends to be since spontaneous changes involve a decrease in F. Results are given in Figure 2. Notice that the system reaches a minimum value for F (color black, maximum stability) at a certain time . However, the master equation mechanism takes the system away from the minimum till it reaches stationarity. We discover that our master equation mechanism prefers stationarity over stability. Not surprisingly, the system reaches maximum entropy S (color orange, disorder) at a time close to (see above).
It seems that our master equation describes a process of initially growing of the entropy and the useful available energy followed by one of equilibration at higher values of both S and F.
The following graph, Figure 3, depicts
- the mean energy difference ,
- the difference of the free energy ,
- the disequilibrium ,
- the purity (degree of mixing in the quantum sense) where , with for a pure state,
- the entropy S, and
- the sum .
Remark that is almost constant as we approach the stationary zone, which reinforces our assertions above about D-representing order. Thus, we note that the sum of order plus disorder indicators approaches a constant value as we get near stationarity.
The entropic and free energy behaviors are those displayed in Figure 2 above. The disequilibrium (order indicator) attains its minimum when S gets maximal, as expected. The purity starts being maximal at , descends first afterwards, and then slightly increased till it reaches stationarity. Thus, our master equation transforms a pure state into a stationary mixed one. The master equation is able to yield useful free energy only for a very short time in which it creates disorder.
We pass now to plot in Figure 4, versus final time , the derivatives , , .
4. Regime Transitions
We reach interesting insights at this stage. Consider now the novel quantities
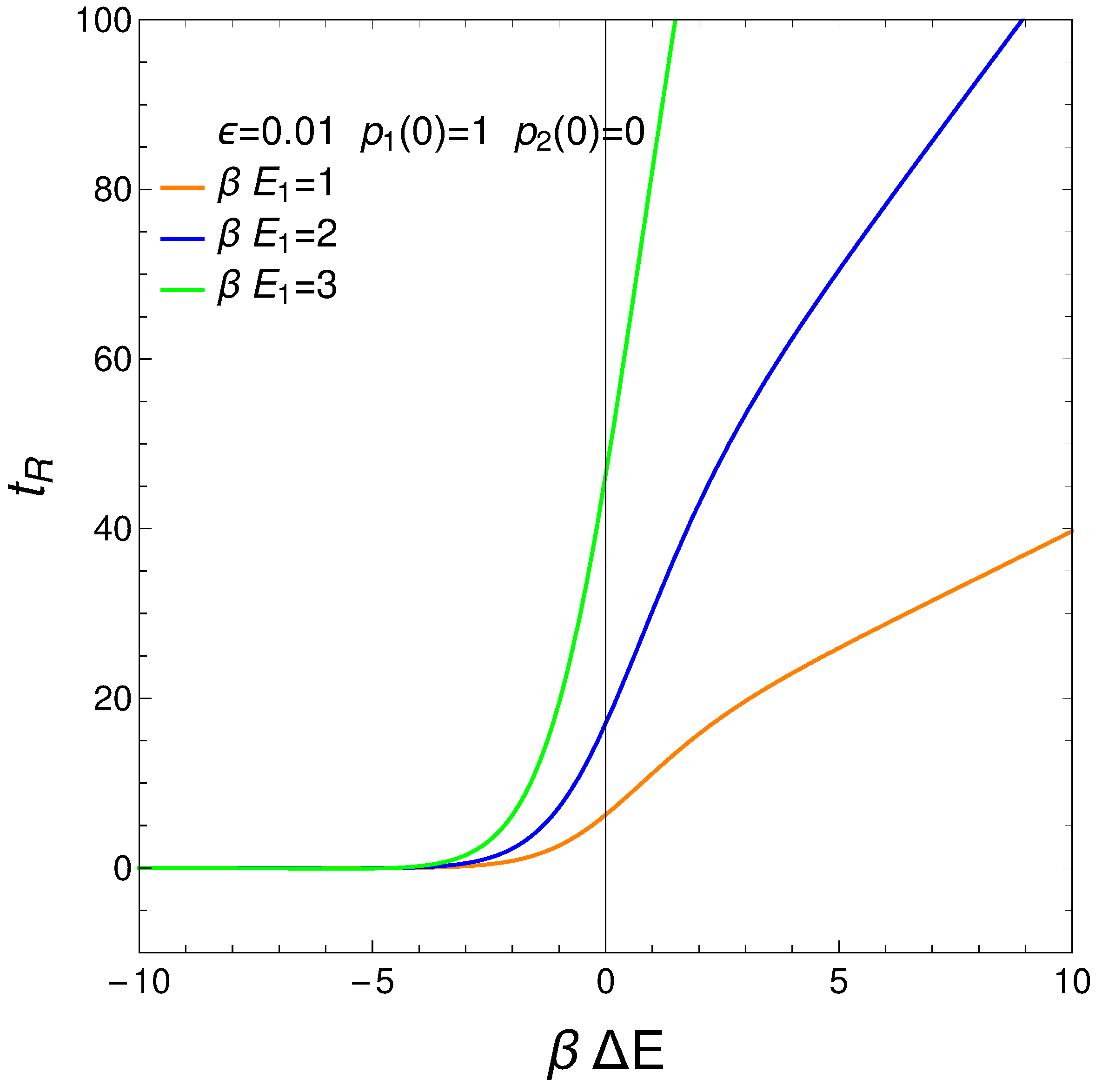
that determine how much free energy is expended or received so as to change either the disequilibrium or the entropy. Our ’s behavior is rather surprising, as can be seen in Figure 5. The free energies required to effect our changes diverge at the time at which where the entropy is a maximum, that we called . The divergence at this time indicate a temporary singularity.
4.1. Two Regimes for Our Master Equation
One can describe the behavior of the master equation as representing two distinct regimes, with a temporary loss of physical sense at the divergence time . This is, the master equation shows different behaviors before and after a critical divergence time, . Initially, the system evolves according to the master equation, but as it approaches a uniform distribution (), certain ratios ( and ) diverge. This divergence indicates a point where the current form of the master equation temporarily loses its physical meaning. Pre-Divergence: From the initial state up to . the system evolves according to the master equation, with well-defined changes in entropy, distance, and free energy. The master equation provides a physically meaningful description of the system’s dynamics, which is governed by linear or weakly non-linear interactions, and the ratios and behave regularly. Post-Divergence: from onward, the system settles into a new, well-behaved regime where the solutions of the master equation stabilize at finite values. This represents a new equilibrium or steady state. The dynamics are again well-described by the master equation, and the physical quantities stabilize, indicating a return to physical sense.
At time we face a temporary loss of physical meaning: the ratios and diverge, suggesting a temporary breakdown in the physical interpretation provided by the master equation. This time marks a critical transition in the system’s behavior, potentially indicating complex dynamics such as critical slowing down or a phase transition.
Summing up, the master equation describes two distinct regimes in the system’s dynamics. In the first regime, from the initial state up to a critical divergence time , the system evolves predictably and the master equation retains physical meaning. At , the system experiences a temporary divergence in key ratios, indicating a loss of physical sense. However, beyond this point, the system settles into a new, well-behaved regime where the master equation’s solutions stabilize at finite values, representing a new equilibrium or steady state. Thus, the master equation temporarily loses physical meaning only at the divergence time , but remains valid in describing both pre- and post-divergence regimes. This framing highlights the temporary nature of the breakdown at and acknowledges the master equation’s validity in describing the system’s dynamics in both regimes.
4.2. Statistical Complexity
- The fact that the ratios diverge as the system approaches equilibrium suggests that the dynamics of the system are non-linear. Near equilibrium, small changes in one quantity (like free energy) can lead to disproportionately large changes in others (like entropy and distance in probability space). This non-linearity is a hallmark of complex systems, where the relationships between variables are not straightforward.
- The divergence of these ratios is related to a phenomenon known as critical slowing down, where the rate of change of a system’s state variables becomes very slow near equilibrium (or near a critical point in phase transitions). As the free energy change rate approaches zero, the system’s response to external perturbations also slows down, indicating that the system is in a state of heightened sensitivity and complexity.
- The ratios involve the rates of change of entropy, distance, and free energy, showing that these variables are interdependent. This interdependence means that changes in one variable can have complex effects on the others. Such interdependence and feedback loops are characteristic of complex systems, where the behavior of the whole system cannot be easily inferred from the behavior of individual parts.
- As the system approaches the uniform distribution, small differences in initial conditions can lead to significantly different trajectories in the state space. This sensitivity is another hallmark of complexity, often observed in chaotic systems.
- The divergence to plus-minus infinity of the ratios suggests emergent behavior, where the macroscopic properties (like the ratios and ) exhibit behaviors that are not straightforwardly predictable from the microscopic rules (the master equation governing the probabilities and ). Emergence is a key feature of complex systems.
- The described behavior indicates a high level of complexity in the system’s approach to equilibrium. This complexity arises from non-linear dynamics, critical slowing down, interdependence of state variables, sensitivity to initial conditions, and emergent behavior, all of which are characteristic of complex systems in statistical mechanics and thermodynamics.
Our master equation displays a picturesque regime’s transition in our novel quantities when the entropy attains a maximum.
4.3. The Lope-Ruiz, Mancini, Calvet Form for the Statistical Complexity C
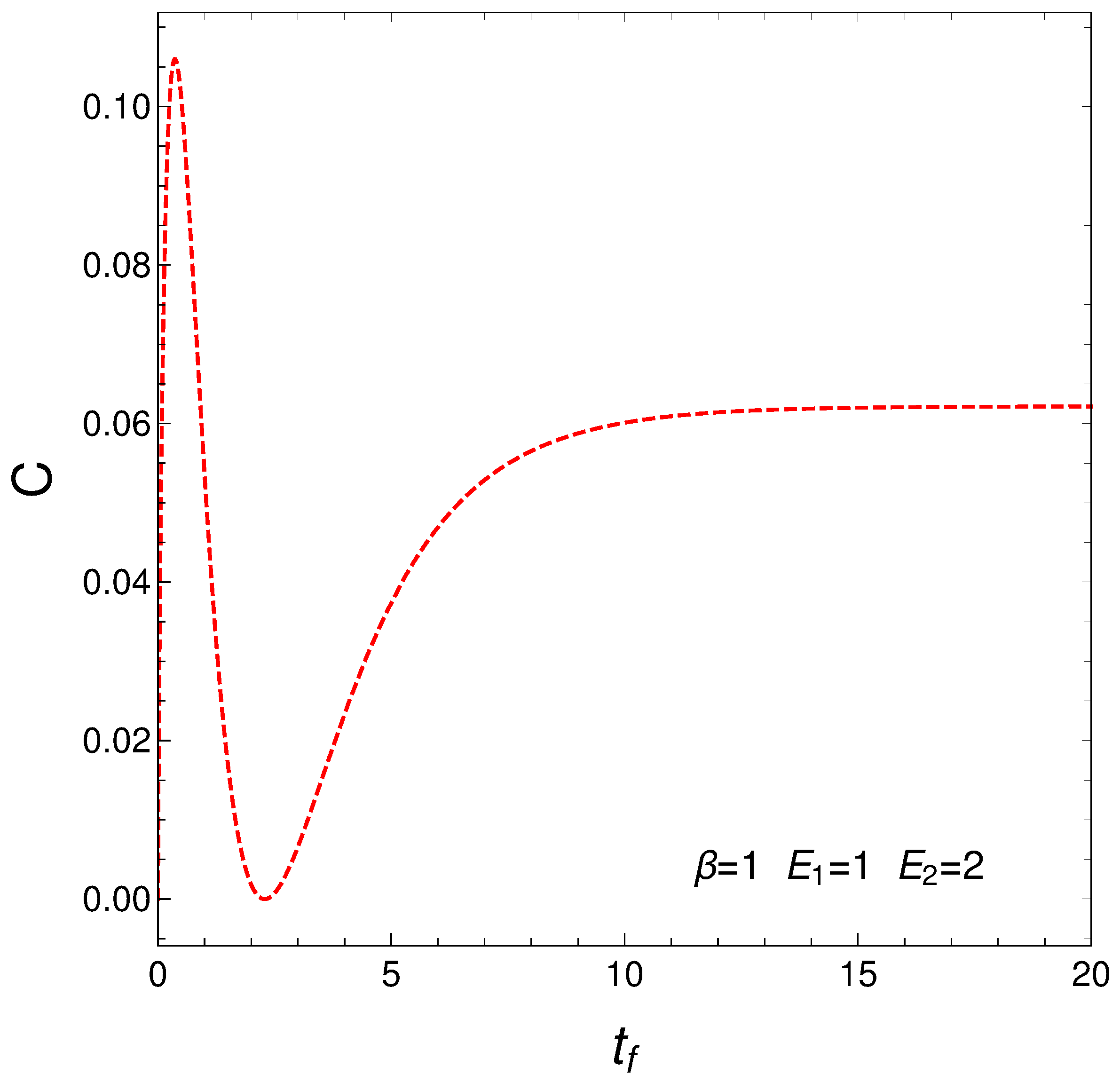
This measure of the statistical complexity was originated about 25 years ago and has become quite popular, being used for variegated purposes. We just cite here [3,4,5,6,7]. We depict now C versus time in the context of our master equation. We clearly see that our two regimes exhibit different complexity.
Figure 6.
Statistical complexity evolution with time. Two different regimes emerge. As before one sets , , , and IC y .
Figure 6.
Statistical complexity evolution with time. Two different regimes emerge. As before one sets , , , and IC y .
5. Initial Conditions of Maximum Entropy
Given its great importance, consider in more detail the solutions of our master equation for at . The results for these maximum entropy initial conditions (MSIC) are plotted below. The entropy, of course, descends and the remaining quantifiers increase till reaching stationarity.
Figure 7.
MSIC. Thermal quantities versus time. One sets , and . The entropy diminishes. The remaining quaifiers incresae. Stationarity is reached.
Figure 7.
MSIC. Thermal quantities versus time. One sets , and . The entropy diminishes. The remaining quaifiers incresae. Stationarity is reached.
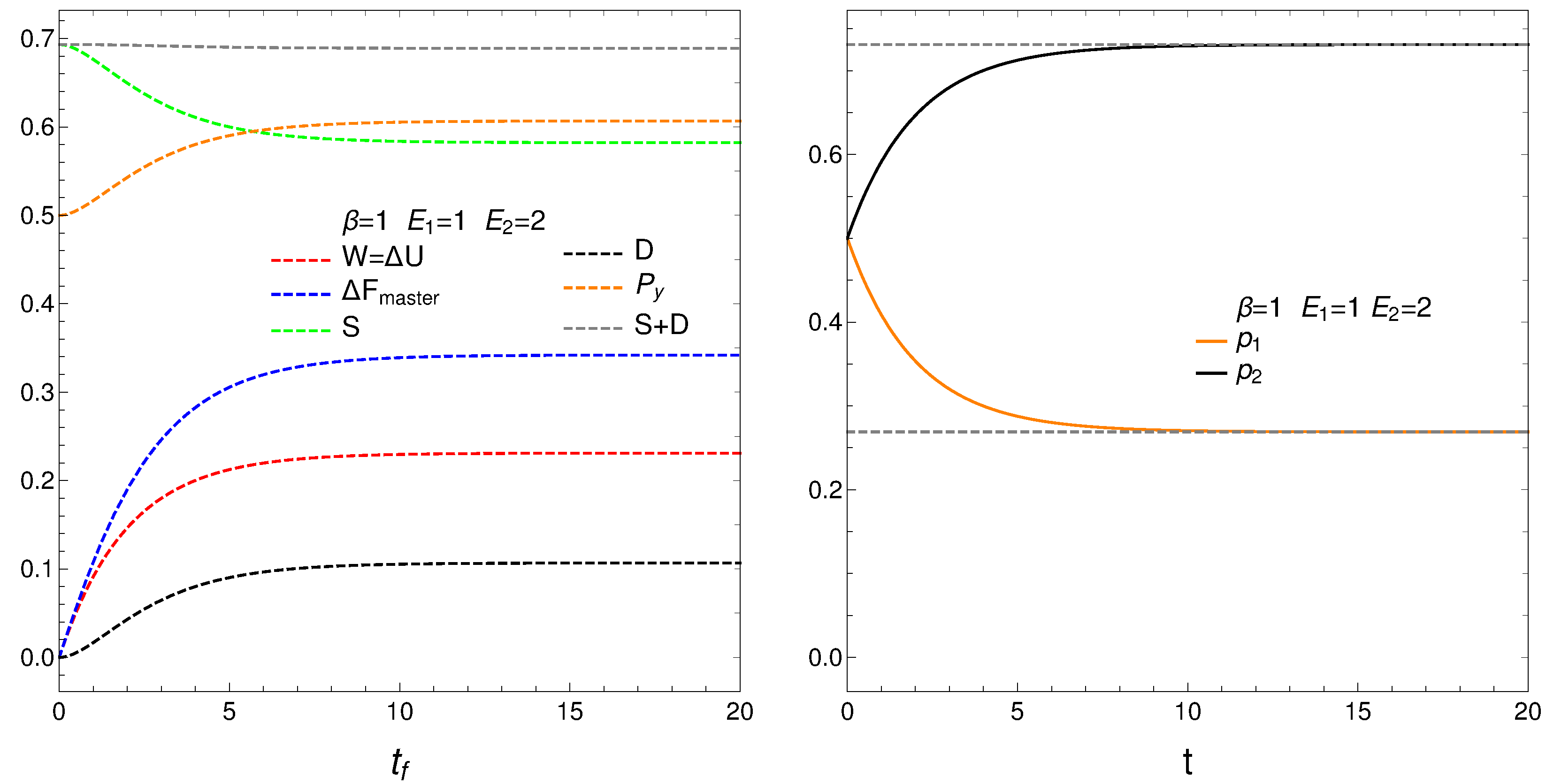
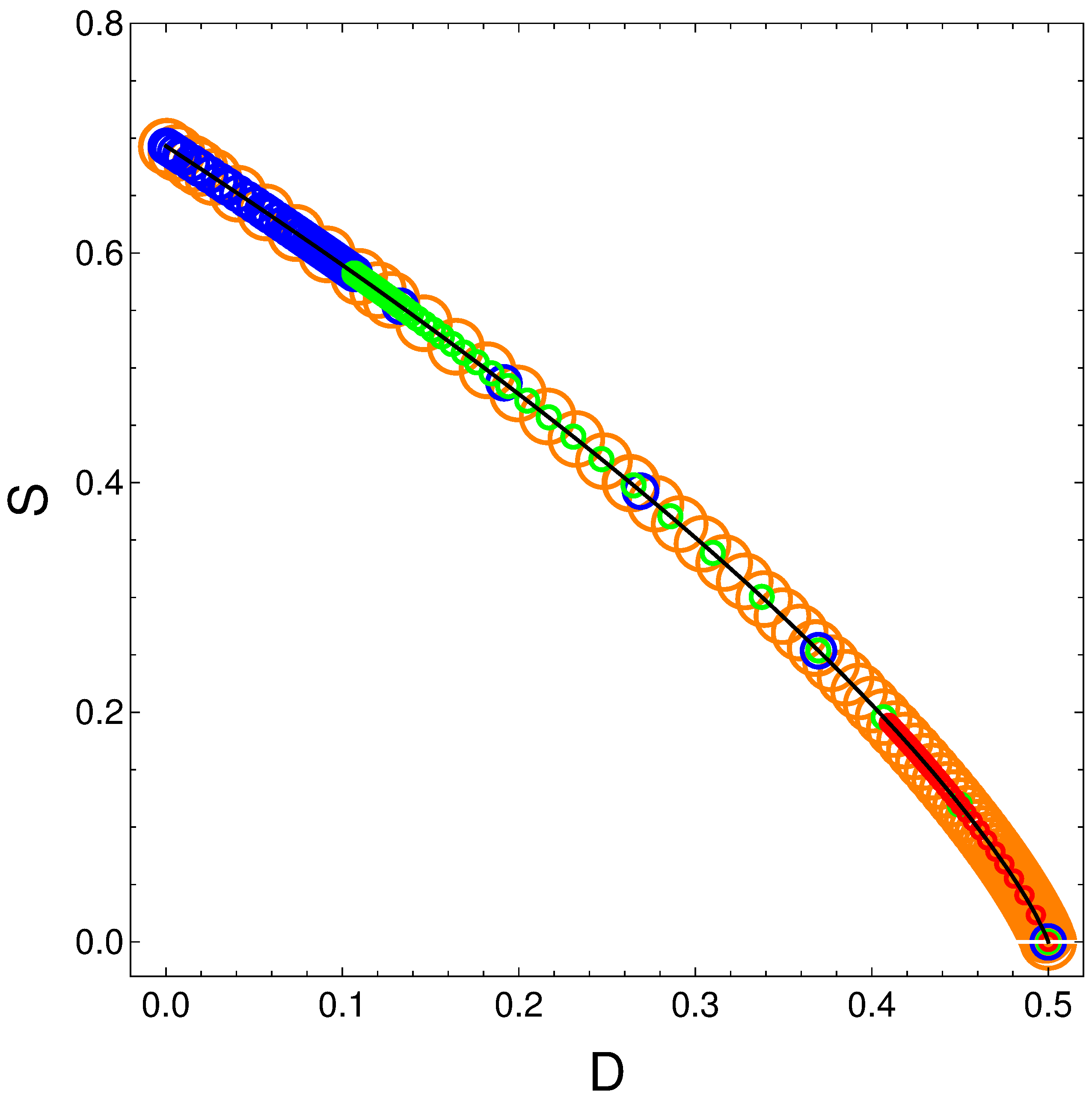
6. The Order(D)-Disorder(S) Equation Generated by the Master Equation
From its definition and from the relation , we gather that and , with
From the entropic definition one then finds SvsD which turns out to be, for any values of , , and the rather beautiful expression that gives the entropy solely in terms of the order quantifier:
The above relation is independent of the and of . We plot versus with the time as parameter. The solid curve represents the above equation . Of course, if the order is maximal the entropy vanishes. The circles represent specific parameters’ values of the energies in the following fashion:
- orange: ;
- blue: ;
- green: ;
- red: .
It is clear that S decreases as D grows. But this does not happen neither linearly nor in complex manner.
Figure 8.
SvsD for variegated selection of the parameters that is detailed in the text. Also, and . Black line underling represents Equation (20).
Figure 8.
SvsD for variegated selection of the parameters that is detailed in the text. Also, and . Black line underling represents Equation (20).
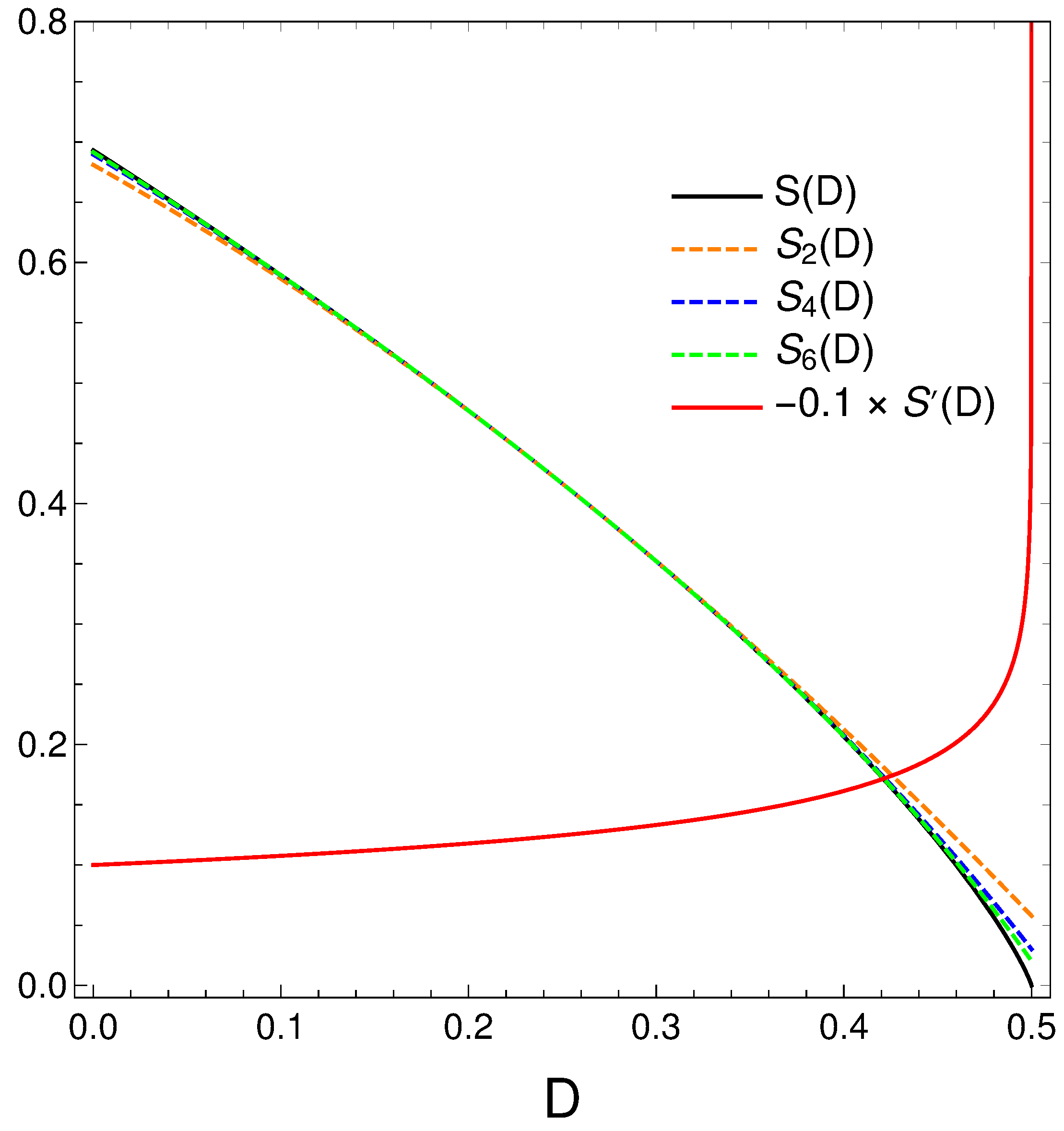
6.1. Polynomial Approximations for the Relation S versus D
We pay now a closer look to the order-disorder relation that our master equation displays. We proceed thus to make a Taylor expansion of around and obtain
We plot below (black) and minus its derivative (red) [in fact, )]. Orange, blue, and green dashed curves represent, respectively, approximations to of degree two, four, and six. Note that the relation disorder versus order looks quasi linear in some region, but not quite of course. When the order-degree gets near its maximum value of one half, the disorder diminishes in a quite rapid fashion, as the derivative plot illustrates. Summing up, the order-disorder relation for our master equation displays some quirky traits.
Figure 9.
Polynomial approximations to the relation of orders two, four, and six in different colors. The exact is given in black. We also depict in orange.
Figure 9.
Polynomial approximations to the relation of orders two, four, and six in different colors. The exact is given in black. We also depict in orange.
7. Relaxation Time
We define our system’s relaxation as the time-interval needed to reach stationarity so that the no longer display significant changes. We can require, for instance, that , with . Thus, from Eqs. (3) and (4), we gather that
where . The relation is displayed next for different values of the pre factor . The initial conditions are . For a considerable range of the relaxation time is independent of this quantity.
Figure 10.
vs for . is the approximation’s degree (see text). Save for very small (negative) values of the relaxation time is constant. If g becomes small augments. This fact is of interest for high temperatures, of course. It makes sense that for such temperatures it should become more difficult to reach equilibration. Positive values of make little sense in the context of our master equation.
Figure 10.
vs for . is the approximation’s degree (see text). Save for very small (negative) values of the relaxation time is constant. If g becomes small augments. This fact is of interest for high temperatures, of course. It makes sense that for such temperatures it should become more difficult to reach equilibration. Positive values of make little sense in the context of our master equation.
8. Relating the Derivatives and
From our formalism we immediately obtain the important relation
This relation between the rates of change of order and disorder is illustrated next. These rates are positively correlated, as one intuitively expects. We consider two situations: a) , and b) . No important differences ensue between a) and b).
Figure 11.
versus for and - . Left: and . Right: and .
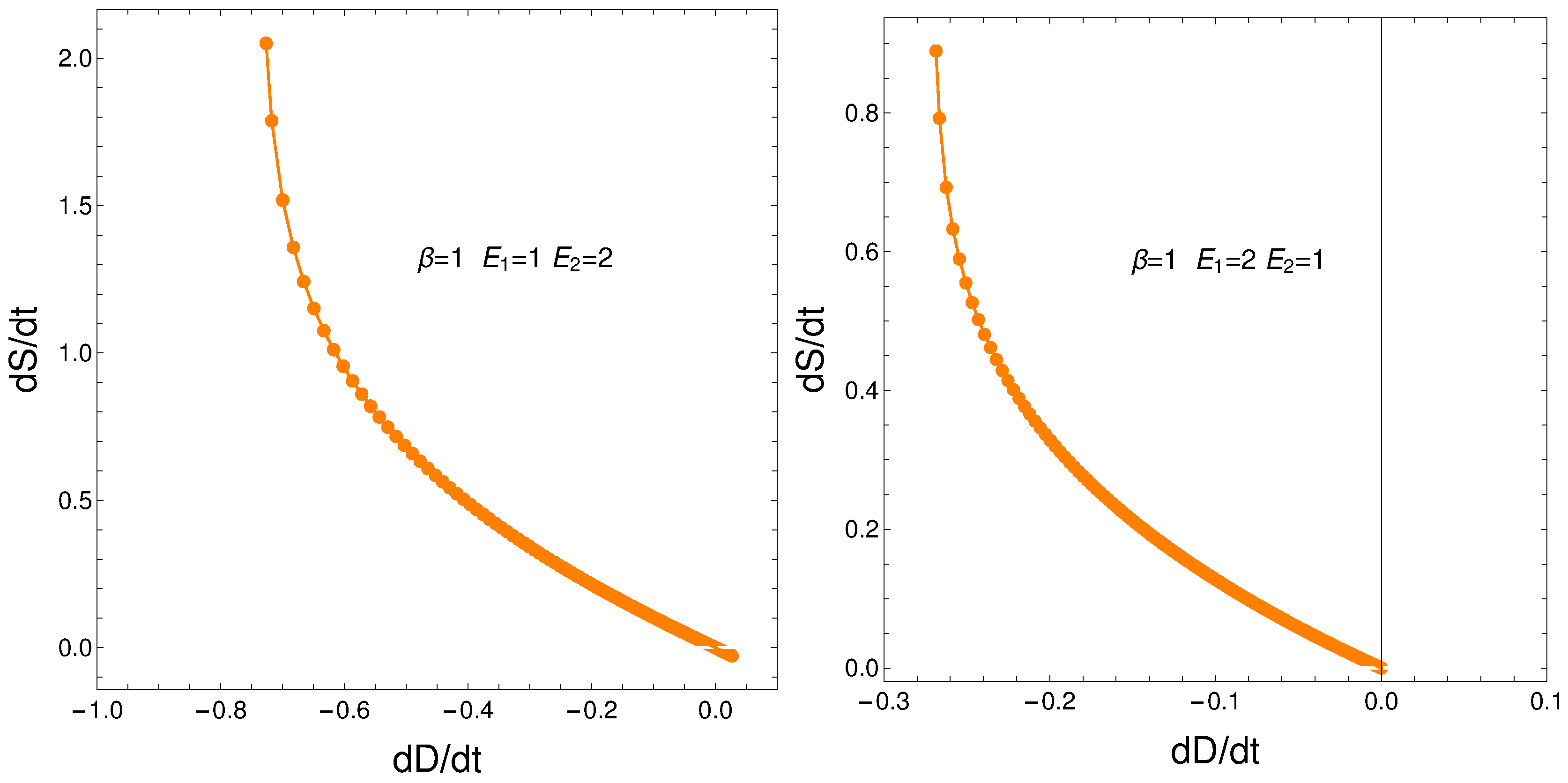
9. Conclusions
We have studied in detail a very simple master equation that displays a complex physics, as the divergences depicted in Figure 5 illustrate. Our present master equation hides a powerful mechanism that is able to produce two different regimes with a quite sharp transition between them signaled by a specific quantifier. The transition is associated to a regime-change implying a considerable energetic cost. This master equation’s simplicity allows for easy access to recondite facts of the pertinent process. Our master equation describes a process of initial growth of both the entropy and the useful available energy followed by one of equilibration at higher values of both S and F. Note that near the stationary stage order balances disorder.
We represent the notion of order by the disequilibrium D and (of course) disorder by the entropy S. Surprisingly enough we find that their sum tends to be a constant for much of the time under a variety of conditions. Since the meaning of S has been established more than a century ago, or results give new validity to the newer notion of disequilibrium. Note that Figure 8 shows that the degree of disorder greatly accelerates itself as D tends towards its maximum possible value. For smaller D values the rate of S growth is rather uniform.
Simple exactly solvable models are often used as starting points for understanding more complex systems. Our discovery of regime-transitions (RT) here can serve as a model system to investigate the nature of RT and their scaling behavior. This knowledge might be applied to more intricate systems in the future. Discovering phase transitions in an elementary exactly solvable master equation can also have methodological importance. It demonstrates that our analytical and modeling techniques are capable of capturing non-trivial collective behaviors and can be applied to other systems.
The existence of two regimes in the master equation is a sign of complexity due to the following reasons:
- The transition between two regimes often indicates non-linear behavior in the system. Non-linear dynamics are a hallmark of complex systems, where small changes in initial conditions or parameters can lead to vastly different outcomes.
- The divergence at the critical transition point is indicative of phenomena such as critical slowing down, where the system’s response to perturbations becomes significantly slower near equilibrium. Such critical points are often associated with phase transitions in complex systems.
- In complex systems, variables are often interdependent in non-trivial ways. The fact that the ratios and diverge suggests intricate interdependencies between entropy, distance, and free energy, contributing to the system’s overall complexity.
- The existence of multiple regimes with distinct stable states (pre- and post-divergence) suggests that the system can settle into different configurations depending on its initial conditions and evolution. This multiplicity of stable states is a characteristic feature of complex systems.
- The transition between regimes highlights the system’s sensitivity to initial conditions. Complex systems often exhibit such sensitivity, where initial conditions or slight perturbations can lead to entirely different behaviors and outcomes.
- The stabilization into a new regime after the divergence indicates emergent behavior, where the system self-organizes into a new equilibrium or steady state. Emergent behavior is a key aspect of complexity, where the whole is more than the sum of its parts.
- Summing up, the existence of two regimes in the master equation is a sign of complexity because it reflects non-linear dynamics, critical transitions, interdependencies between variables, multiple stable states, sensitivity to initial conditions, and emergent behavior. These factors collectively contribute to the intricate and often unpredictable nature of complex systems.
References
- R. López-Ruiz, H. R. López-Ruiz, H. Mancini, X. Calbet, A statistical measure of complexity. Phys. Lett. A 209 (1995) 321-326. [CrossRef]
- R. López-Ruiz, Complexity in some physical systems, International Journal of Bifurcation and Chaos 11 (2001) 2669-2673. [CrossRef]
- M.T. Martin, A. Plastino, O.A. Rosso, Statistical complexity and disequilibrium, Phys. Lett. A 311 (2003) 126-132. [CrossRef]
- L. Rudnicki, I.V. L. Rudnicki, I.V. Toranzo, P. Sánchez-Moreno, J.S. Dehesa, Monotone measures of statistical complexity, Phys. Lett. A 380 (2016) 377-380. [CrossRef]
- R. López-Ruiz, A Statistical Measure of Complexity in Concepts and recent advances in generalized infpormation measures and statistics, A. Kowalski, R. Rossignoli, E.M.C. Curado (Eds.), Bentham Science Books, pp. 147-168, New York, 2013.
- K.D. Sen (Editor), Statistical Complexity, Applications in elctronic structure, Springer, Berlin 2011.
- M.T. Martin, A. Plastino, O.A. Rosso, Generalized statistical complexity measures: Geometrical and analytical properties, Physica A 369 (2006) 439-462. [CrossRef]
- C. Anteneodo, A.R. Plastino, Some features of the López-Ruiz-Mancini-Calbet (LMC) statistical measure of complexity, Phys. Lett. A 223 (1996) 348-354. [CrossRef]
- S. Yong, C. Yu, Annals of Physics, Operational resource theory of total quantum coherence, 388 (2018) 305. [CrossRef]
- Kryszewski, S. and Czechowska-Kryszk, J. (2008) Master Equation—Tutorial Approach.
- Takada, A. Conradt, R. and Richet, P. (2013) Journal of Non-Crystalline Solids, 360, 13; ; Angel Ricardo Plastino1, Gustavo Luis Ferri, Angelo Plastino, Journal of Modern Physics 11 (2020) 1312-1325. [CrossRef]
- R.K. Pathria, Statistical Mechanics, 2nd., Butterworth-Heinemann, Oxford, UK, 1996.
Figure 1.
and vs.t (arbitrary units), with , , , and initial conditions - .
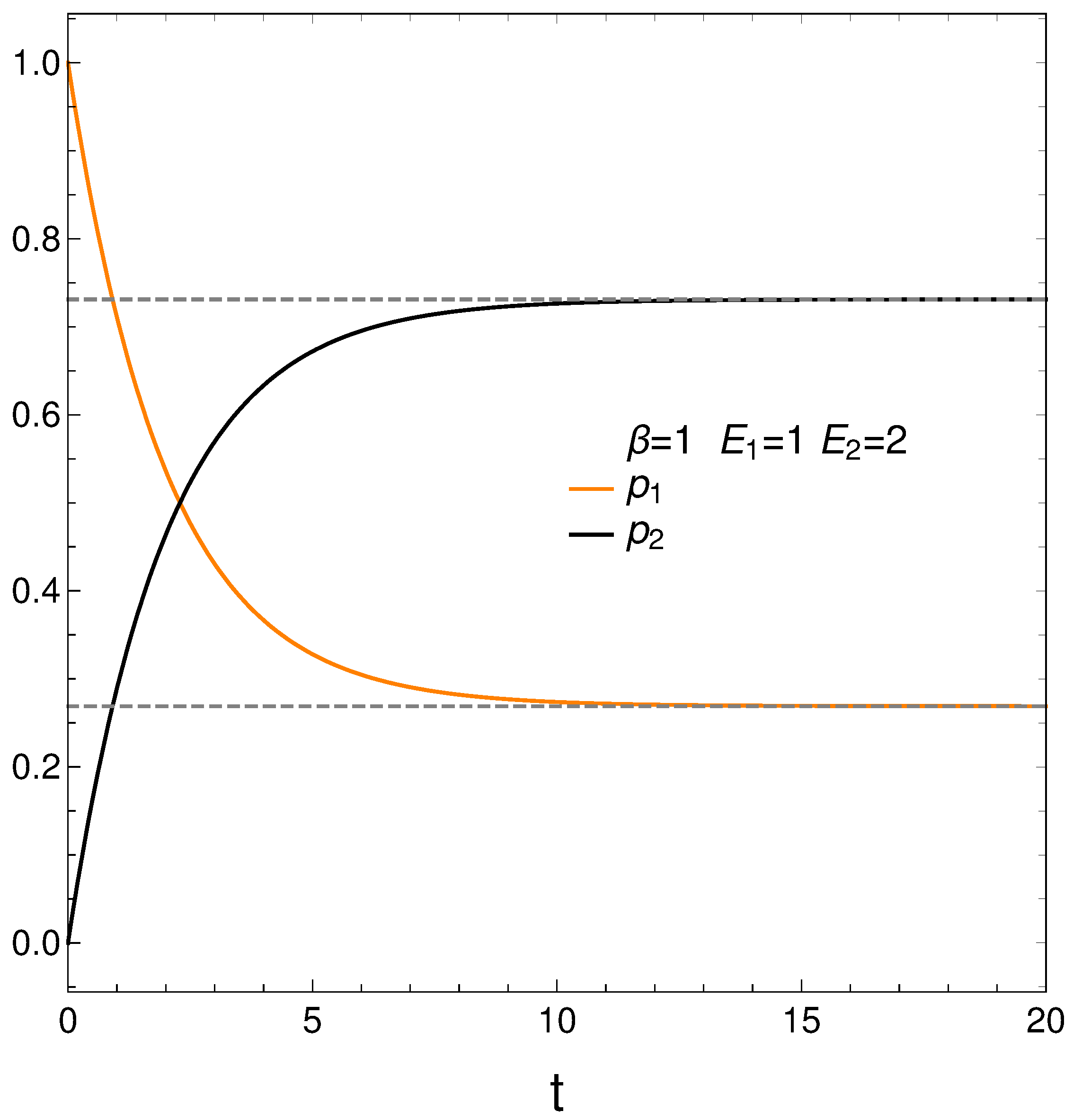
Figure 2.
S (orange) and F (black) vs. time t, with , , , and . Notice that the system reaches a minimum value for F (maximum stability) at a time . However, the master equation mechanism takes the system away from the minimum till it reaches stationarity. We discover that our master equation mechanism prefers stationarity over stability. Not surprisingly, the system reaches maximum entropy (disorder) almost at the time .
Figure 2.
S (orange) and F (black) vs. time t, with , , , and . Notice that the system reaches a minimum value for F (maximum stability) at a time . However, the master equation mechanism takes the system away from the minimum till it reaches stationarity. We discover that our master equation mechanism prefers stationarity over stability. Not surprisingly, the system reaches maximum entropy (disorder) almost at the time .
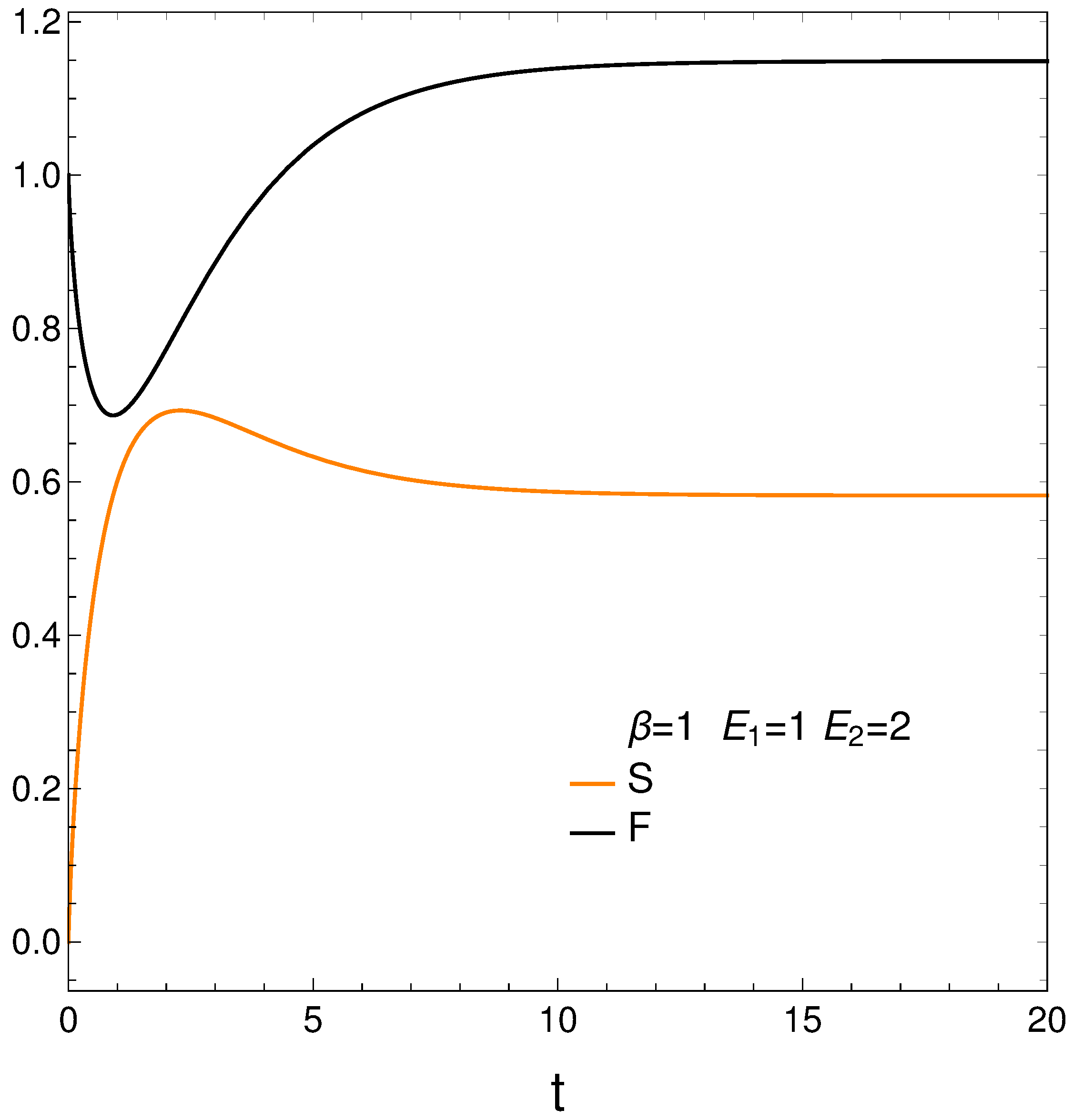
Figure 3.
This graph is intended as a complement of Figure 2. The horizontal axis displays the final time . The plot depicts the mean energy difference . In similar fashion, also , the disequilibrium D, purity , and entropy S versus , with , , , and initial conditions and . What we learned from Figure 2 is reinforced here using different quantities. Note that near stationarity order again balance’s disorder.
Figure 3.
This graph is intended as a complement of Figure 2. The horizontal axis displays the final time . The plot depicts the mean energy difference . In similar fashion, also , the disequilibrium D, purity , and entropy S versus , with , , , and initial conditions and . What we learned from Figure 2 is reinforced here using different quantities. Note that near stationarity order again balance’s disorder.
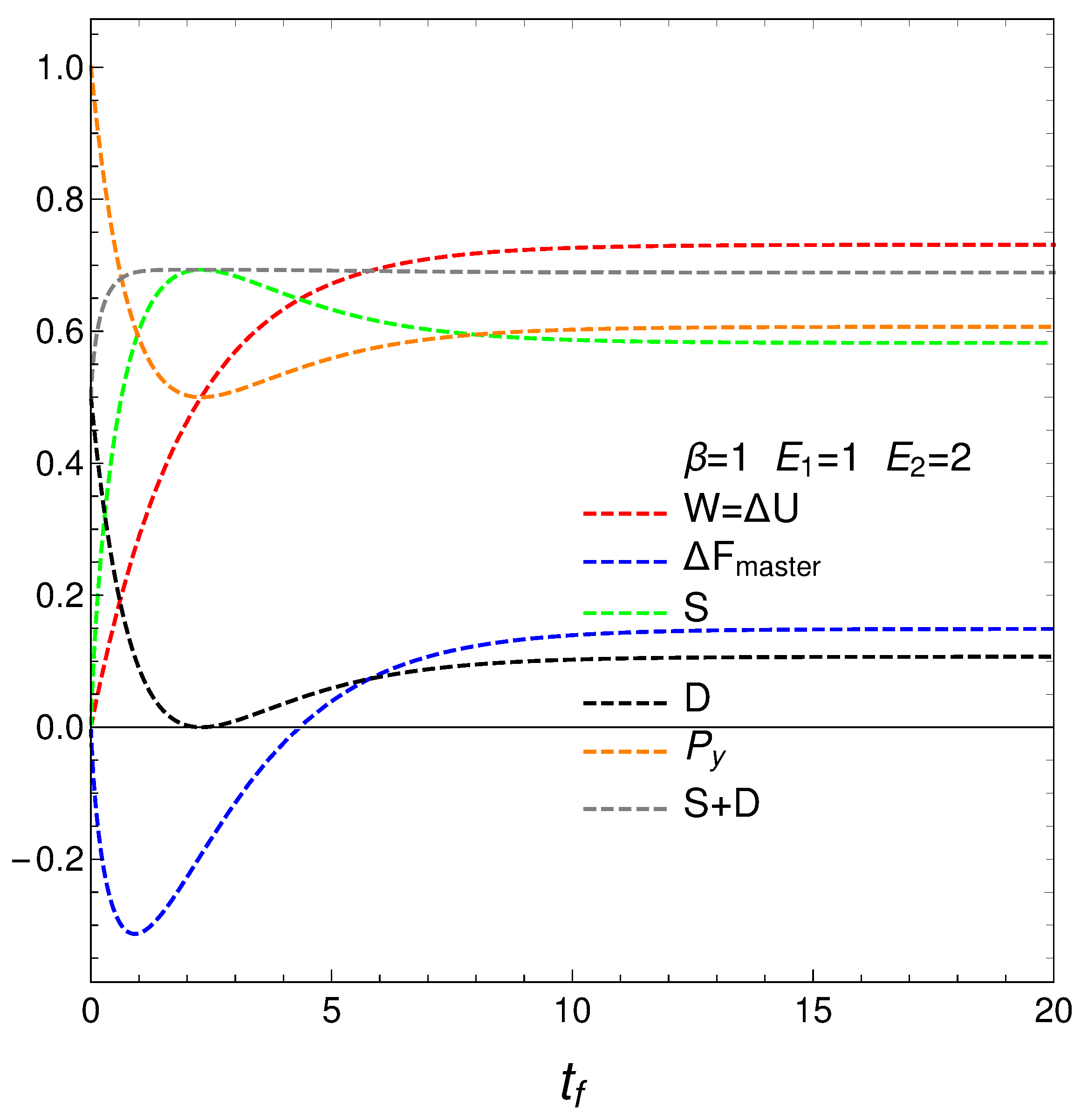
Figure 4.
, , , and vs.. One sets , , , and initial conditions (IC) - . This graph is still another complement to Figure 2, using different quantities from those of Figure 2 and 3. Maxima and minima are found at the right of and are also . Their message is thus reinforced here.
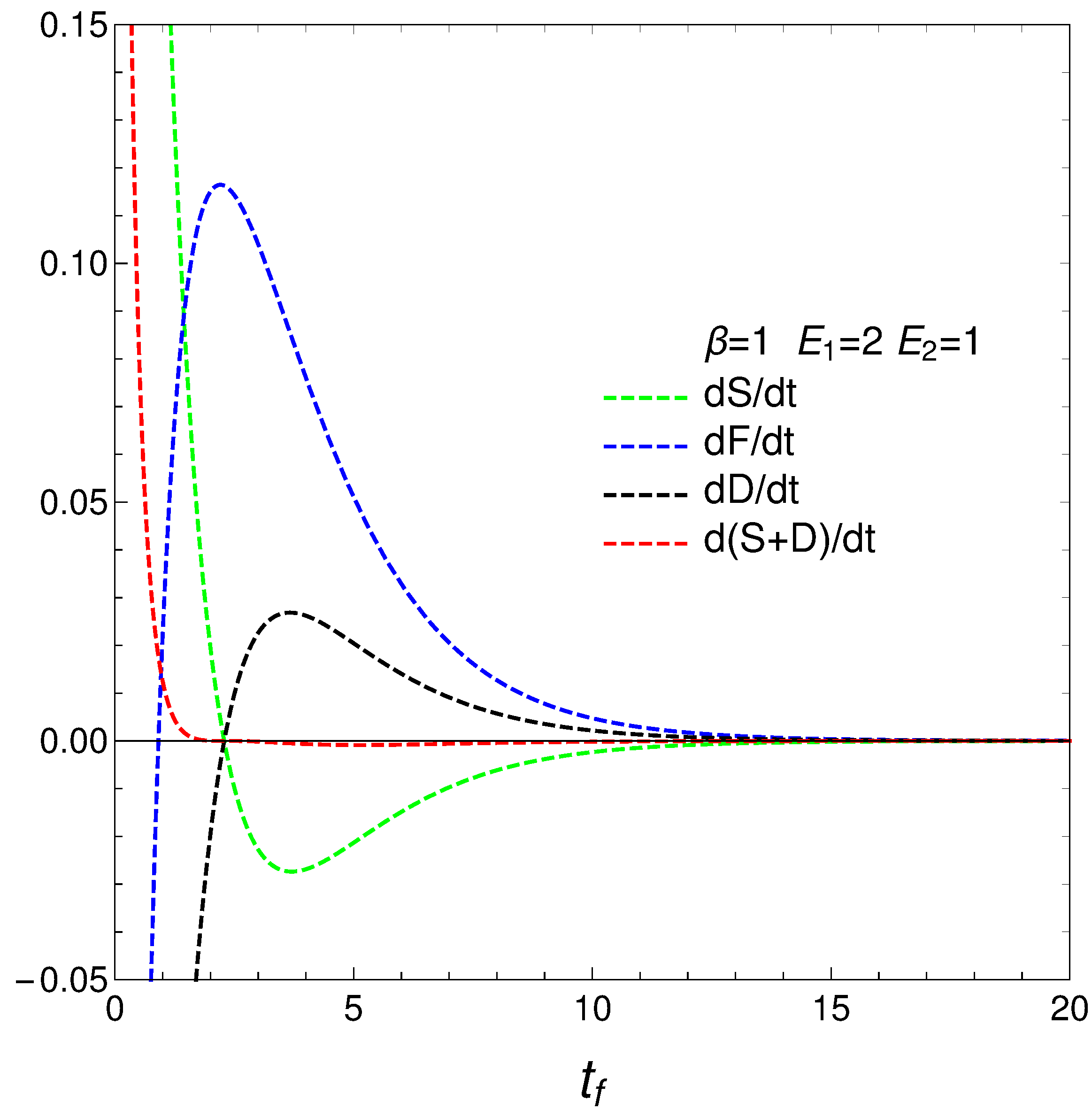
Figure 5.
and vs.. One sets , , , and IC y . Also the value corresponding to is shown. The three quantities diverge (regime-transition) at the time for which . Our very simple system exhibits divergence there.
Figure 5.
and vs.. One sets , , , and IC y . Also the value corresponding to is shown. The three quantities diverge (regime-transition) at the time for which . Our very simple system exhibits divergence there.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





