Prerpints.org logo
Preprint
Article

The Various Radii Circle Packing Problem in a Triangle

Altmetrics

Downloads

98

Views

18

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 July 2024

Posted:

12 July 2024

You are already at the latest version

Alerts
Abstract
In the extended malfatti problem, the numbers of circles in the triangle are triangle numbers, because the tangency properties among the internal circles and 3 sides of the triangle have special type of structure. That is, the corner circle tangent to two sides of the triangle and two boundary circles, the boundary circles tangent to one side of the triangle and 4 other circles, and the inner circles always tangent to 6 other circles. The circles we find in extended general Malfatti’s problem has the property that the smallest radius and the largest radius for the circle has big difference. In this paper, we proposed algorithms to solve the problem that the tangency properties among circles and sides of triangle is not fixed, so that the number of circles in the triangle is not necessary a triangle numbers. The purpose of this change is try to find the radii of the circles in the triangle is within a small range.
Keywords: 
Subject: Computer Science and Mathematics  -   Computational Mathematics

1. Introduction

Before we explain the problem, we introduce the related material such as Malfatti’s problem and extended Malfatti’s problem.

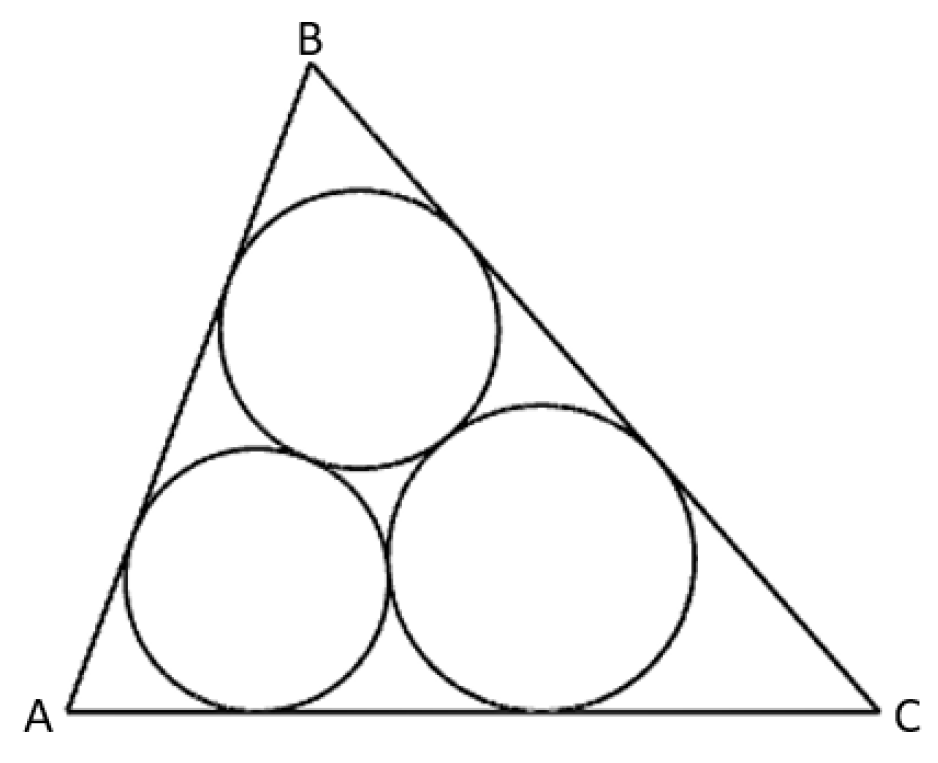
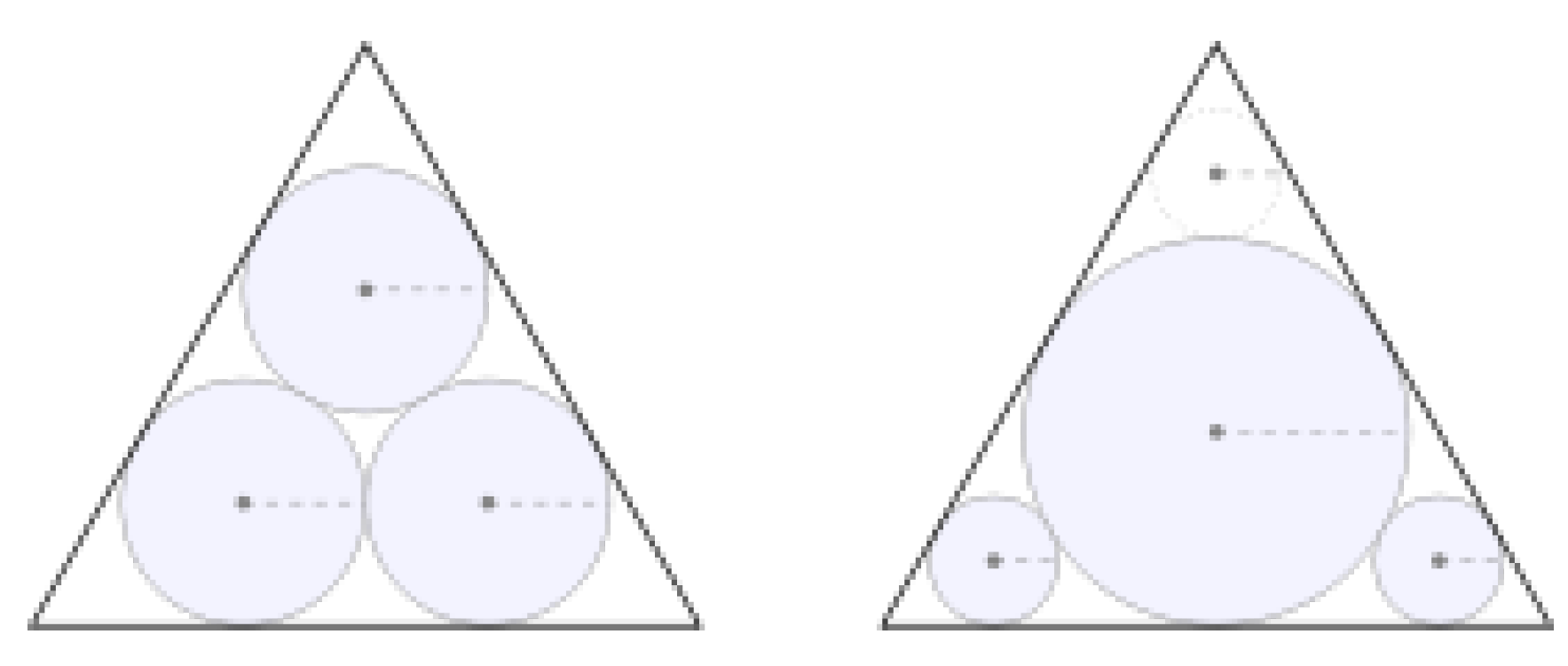
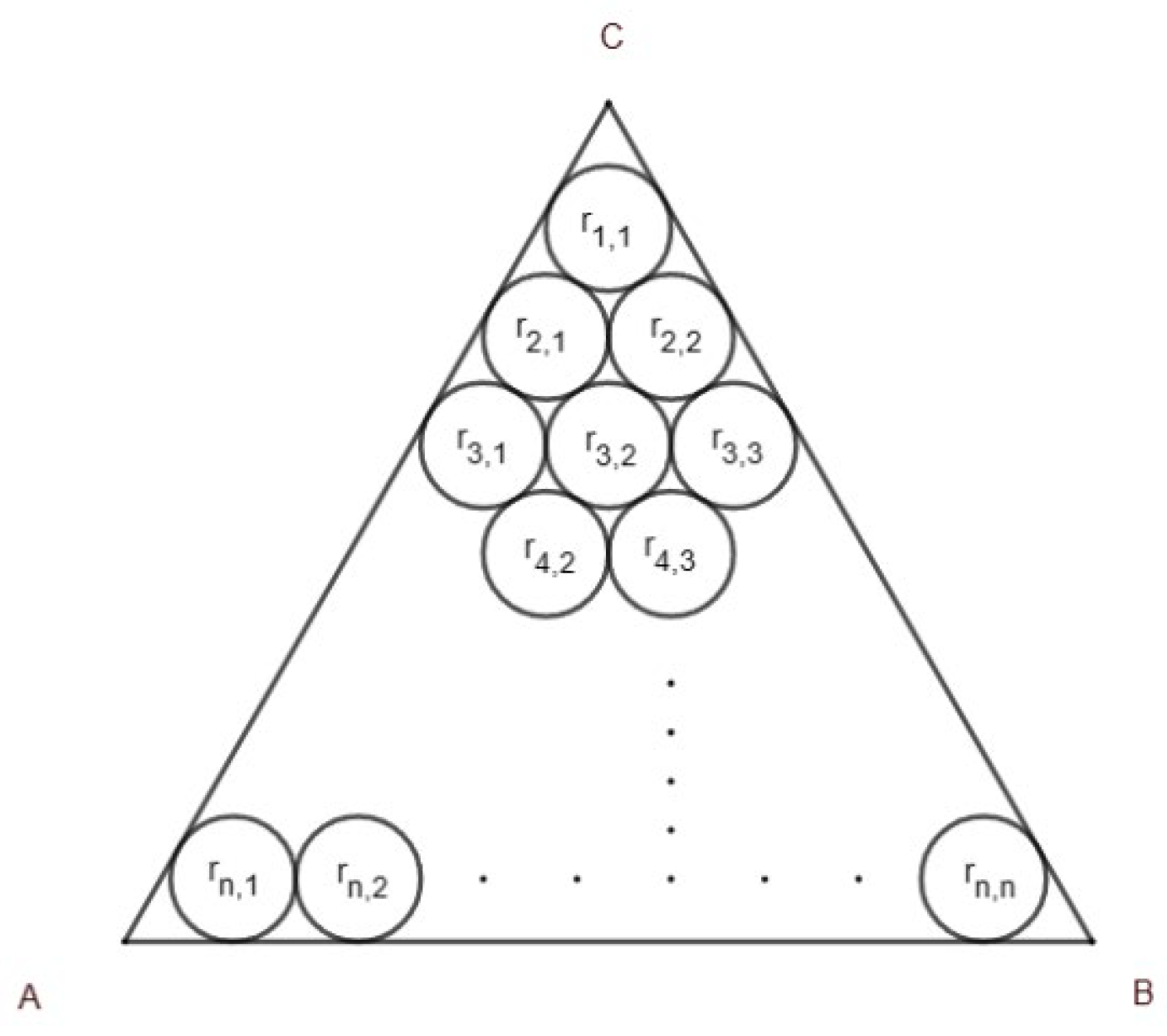
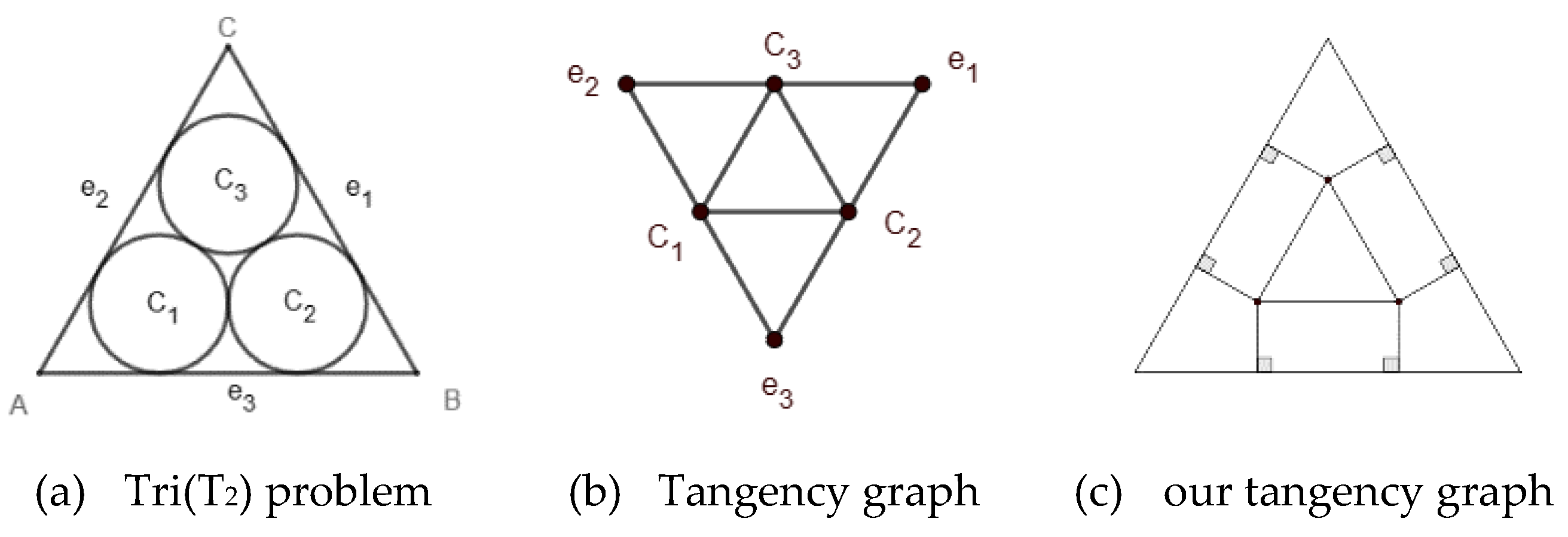
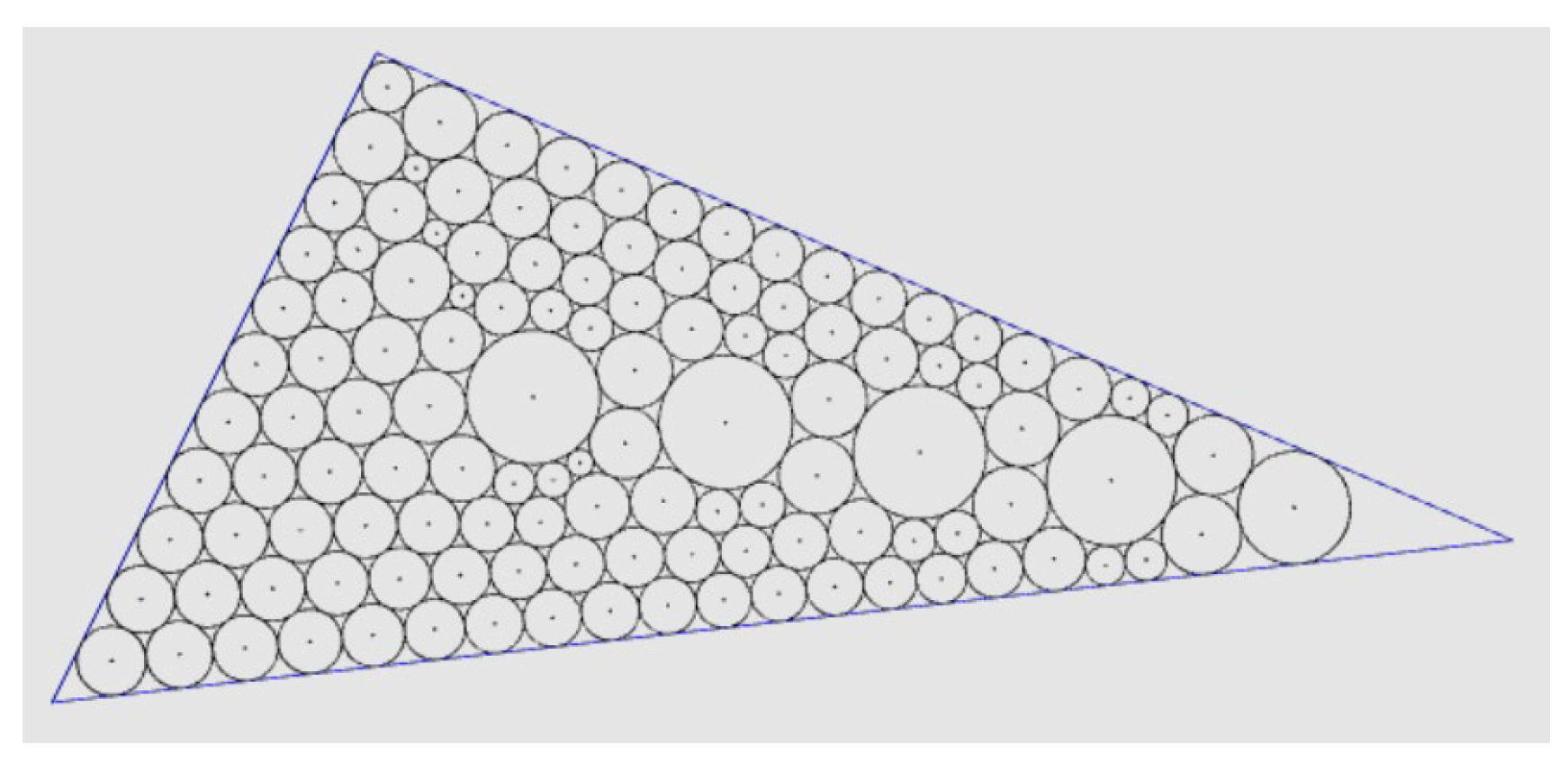
1.1. Malfatti’s Problem and Extended General Malfatti’s Problem

In 1803, Gian Francesco Malfatti [1] proposed the problem: how to find the maximum total volume of three cylindrical columns out of a triangular prism of marble.
Identically, the problem can be recognized as to find three circles to fit in specific triangle and make sure the total area is maximum. Malfatti thought the solution is to make three circles tangent to each other and each circle tangent to two sides of the triangle. A case is shown as Figure 1 [2].
In fact, Malfatti’s thought is not correct. In 1930, Lob and Richmond [3] found that a way to get a larger area of some triangles by using greedy algorithm that inscribes a single circle of maximal radius within the triangle, inscribes a second circle within one of the three remaining corners of the triangle, the one with the smallest angle, and inscribes a third circle within the largest of the five remaining pieces. The difference in area for an equilateral triangle is just about over 1% (as shown in Figure 2), [4] but as Howard Eves (1946) mentioned, for an isosceles triangle with a very sharp apex, the optimal solution has nearly twice the area of the Malfatti circles. (as shown in Figure 3) [5] In 1960s, later proven firmly, Lob-Richmond procedure always gives the largest area and solved the problem. In the literature, the Malfatti’s thought has become understood as the Malfatti’s problem.
There are several known solutions to Malfatti's problem. Fukagawa and Pedoe [6] mentioned that Chokuen Ajima actually formulated and solved the Malfatti's problem. For a detailed history of the problem and explanations of various solutions and generalizations, interested readers are referred to [7,8,9].
The Extended Malfatti problem [10] aims to determine Tn circles that can be inscribed inside a triangle while maintaining tangency among the circles and the triangle's sides. When considering the problem with Tn= ∑ 1 n i circles, it is referred to as the Tri(Tn) n problem (as shown in Figure 4). Notably, when n=1, the problem seeks to find the inscribed circle of a triangle, and when n=2, it is precisely the Malfatti's problem.
There are closed forms for finding inscribed circle and malfatti’s circles. So, when n=1 or n=2, it is easy to propose a constant time algorithm to solve these problems. Chiang [10] proposed algorithms to solve the Tri(Tn) problem when n>2.
The main idea of the algorithm [10] is to calculate total surrounding angles for each circle and change the circle’s size depends on the sum of angles. (shown in Figure 5). There are three kinds of circles, which is corner circle, edge circle, inner circle. (from left to right in Figure 5). Circles are surround by other circles and sides of the triangle. Every circle is surround by a series of object (other circles and sides of the triangle), and correspond angle between center of this circle to two objects, center of other circle of the nearest points on the sides of the triangle) can computed. If the total surrounding angles is greater than 2π, the radius of the circle should be enlarged. Otherwise, the radius of the circle should be redused. There are different ways to compute the surrounding angles for corner circles, edge circles [10], and inner circles [12]. With these constraints is not enough to find one solution. Consider Tri(T2) problem, there are only corner circles in this problem (See Figure 5a, assume these three circles has radii r1, r2, and r3. When we multiply these radii by a constant k, the angle computation (in Figure 5a) for α1, α2, α3, α4 have the same result. It means that there are infinitely many solutions in this case. It need one more constraint to find one solution only. The constant k can be computed by the comparison of the length in one side of the triangle with correspond side of triangle bounded these three circles, as shown in Figure 6. This constant k is called the change ratio for the current solution and the real solution.
So, the algorithm Chiang [10] proposed is:
  • Input the coordinate of 3 vertices A, B, C; Calculate the angle A, B, C, and the edge length c.
  • Set a tolerance variable eps = 0.01
  • Initial radius list r= [ri,j |where 1≤i≤n, 1≤j≤i.]
  • Calculate the surrounding angle list for all circles Ci,j (whose associated radius is ri,j), call them θi,j.
  • While one of | θi,j-2π|>eps:
    5.1
    Modify the radius list, all radii value is computed by current radii, and assign to new radius list in the meantime.
    5.2
    Calculate the surrounding angle list for all circles Ci,j(using new radii), call them θi,j.
    5.3
    From the radius list, calculate the change ratio, and modify the radius list from the change ratio.
  • Display the result.
The result for Tri(Tn) problem, n=2,3,4,8,31, using Chiang’s algorithm [10] is shown in Figure 7.

1.2. Problem Statement

We would like to modify Chiang’s Algorithm, so that the radii of these circles have small range. Consider the result in Figure 7, the smallest angle of triangle is corresponding to the biggest circle. On the other hand, the largest angle is corresponding to the smallest circle, especially for the acute angle. In the circle packing area, some problem fixed the radius of the circles, or at least similar size of circles inside the specified region. So, we propose new algorithm to modify Chiang’s algorithm, so that the circles radii have small range of the radii.
There are four sections in this paper, the first section illustrates the Malfatti’s problem and extended Malfatti problem. The second section define some terms, derived theories and proposed algorithms for the new problem. The third section describe the implementing details. The conclusion is at the final section.

2. Term, Theories and Algorithms

We want to find circles inside a triangle, and there are specified tangency constraints among these circles and 3 sides of the triangle. We use the tangency graph to show the tangency constraints. Consider a graph G (V, E), V is the vertices which represents the circles or sides of triangles, and E represents the edge connecting vertices. When an edge connects two vertices, it means that these two geometric object tangent to each other. That is, circle externally tangent to circle if these two geometric objects are circles, or circle tangent to side of triangle. When a circle is tangent to two, one, or zero sides of a triangle, we call it a corner circles, edge circle or inner circle respectively.
We use Tri(T2) as an example (see Figure 8a), its tangency graph G(V, E) where V={c1, c2, c3, e1, e2, e3} and E={(c1, c2),(c1, c3),(c2,c3),(c1,e2),(c1,e3),(c2,e1),(c2,e3),(c3,e1),(c3,e2)}, as shown in Figure 8b. To see more clearly for the edge circle or corner circle tangent to side of triangle, we draw the tangency graph as in Figure 8c.
The main idea of the new proposed algorithm is to generate the tangency graph, find solution radii for all circles satisfied the constraints specify by the tangency graph, and then display. The purpose of this algorithm is to find circles with small range of radii. In the very beginning, we need to set a value r, so that all circle we generate to pack inside the triangle has radius near r.
So, the main idea of the proposed algorithm is:
1.
Input the coordinate of 3 vertices A, B, C; Calculate the angle A, B, C, and the edge length c.
2.
Set a tolerance variable eps = 0.0001, epsr=0.3. Set a value r. set i=1.
3.
Generate the r-offset of the triangle. Call it Ti.
3.1
Generate the vertices on Ti.
3.2
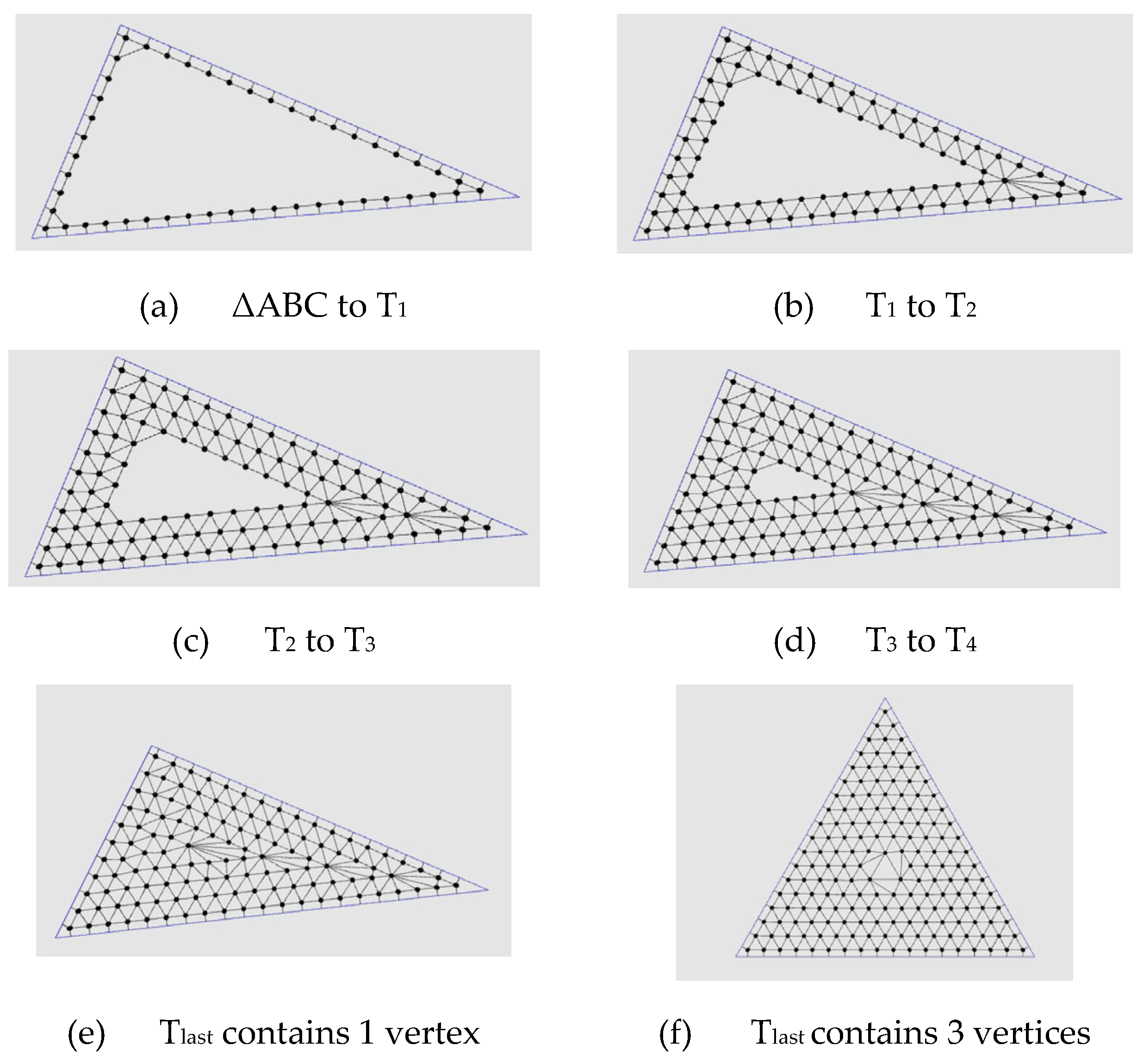
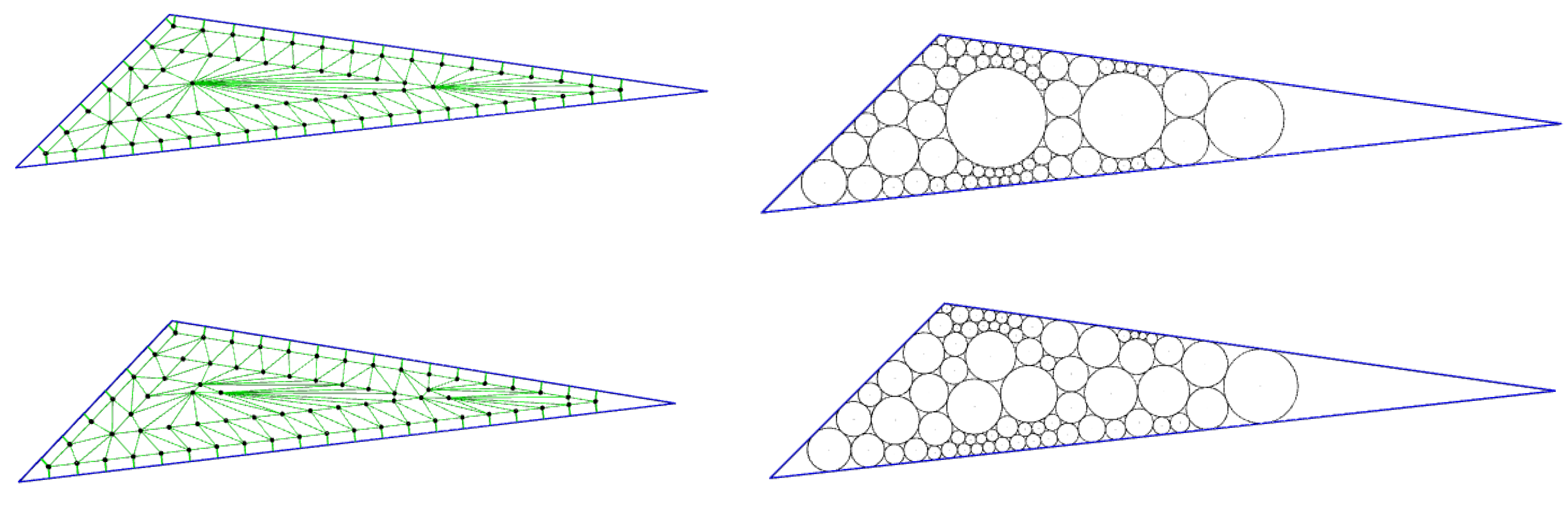
Generate the edges for vertices on Ti, including the edges connecting 2 neighbors of vertices A, B, C. (See Figure 13a).
3.3
Generate edges for vertices on Ti to the side of the triangle A B ¯ , B C ¯ , C A ¯ . (See Figure 13a).
4
While Ti did not satisfy some conditions:
4.1
Generate the 3 r-offset of the triangle Ti, call it Ti+1.
4.2
Generate the vertices and edges on Ti+1, as we do on step 3.1 and 3.2.
4.3
Generate the edge connect vertices on Ti to vertices on Ti+1. (See Figure 13b–f)
4.4
i=i+1
5.
Decide whether the last triangle contains only one vertex(circle) or 3 vertices(circles) (See Figure 13e,f. Call the last triangle Tlast.
6.
Establish the edge of graph to connect Ti-1 and Tlast. (See Figure 13e,f)
7.
Using Chiang’s algorithm with tolerance eps to find the solution.
8.
Display the result.
We will describe the above algorithm more detail, including the answer of the following 4 questions:
  • How to find the r-offset of a triangle in step 3
  • How to construct the tangency graph (vertices and edges) for the same layer?
  • How to construct the tangency (vertices and edges) for two consecutive layers?
  • How the while loop stops in step 4.
The above 4 questions will be described in section 2.1 to section 2.4.

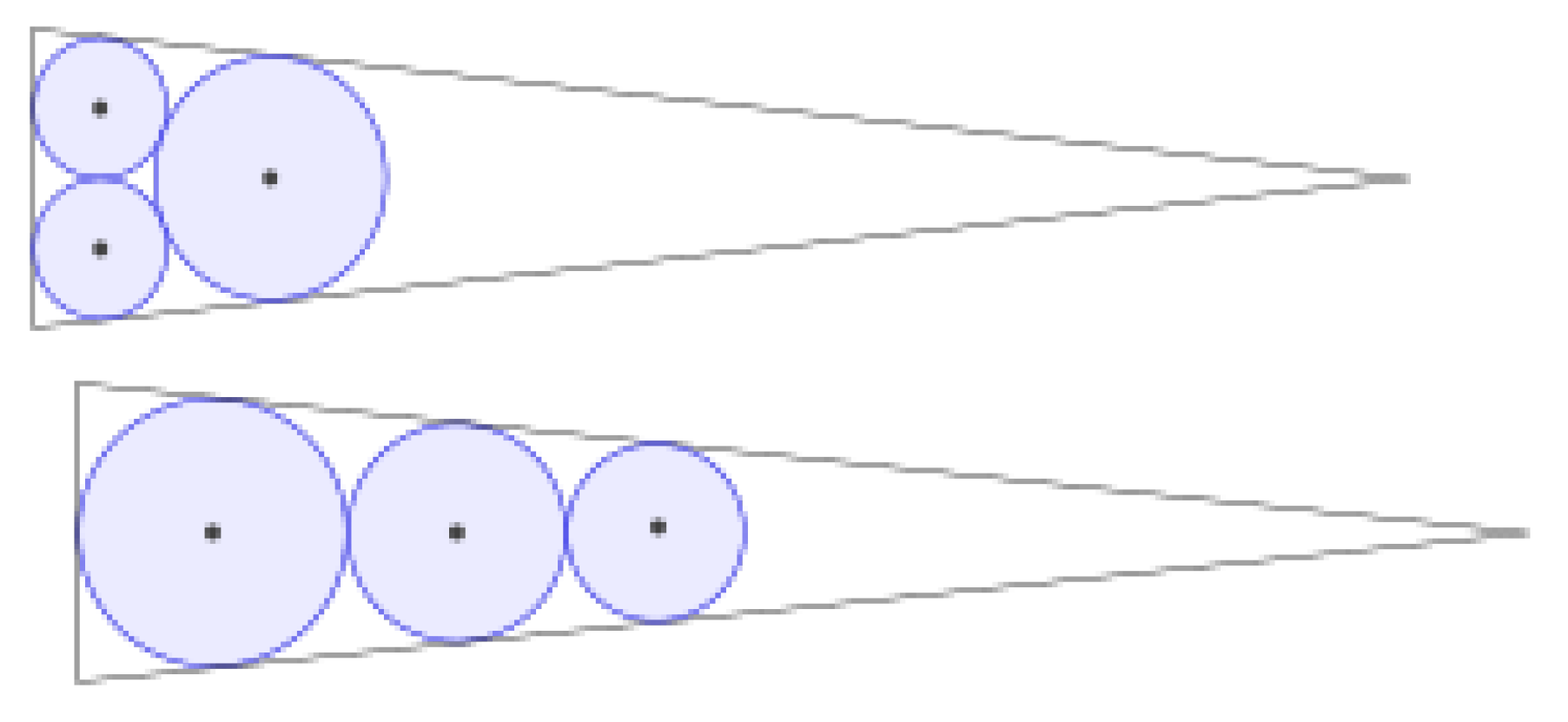
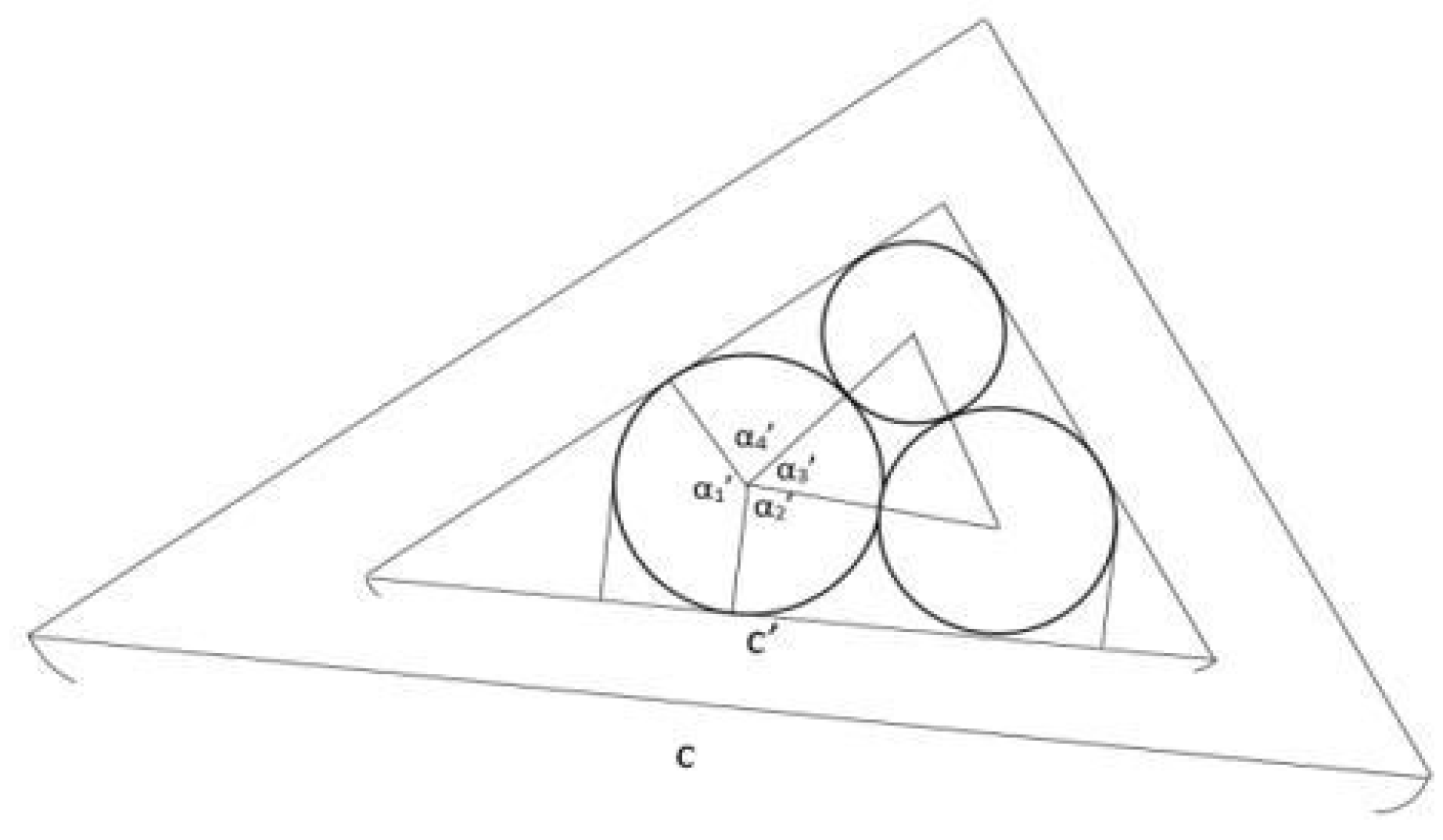
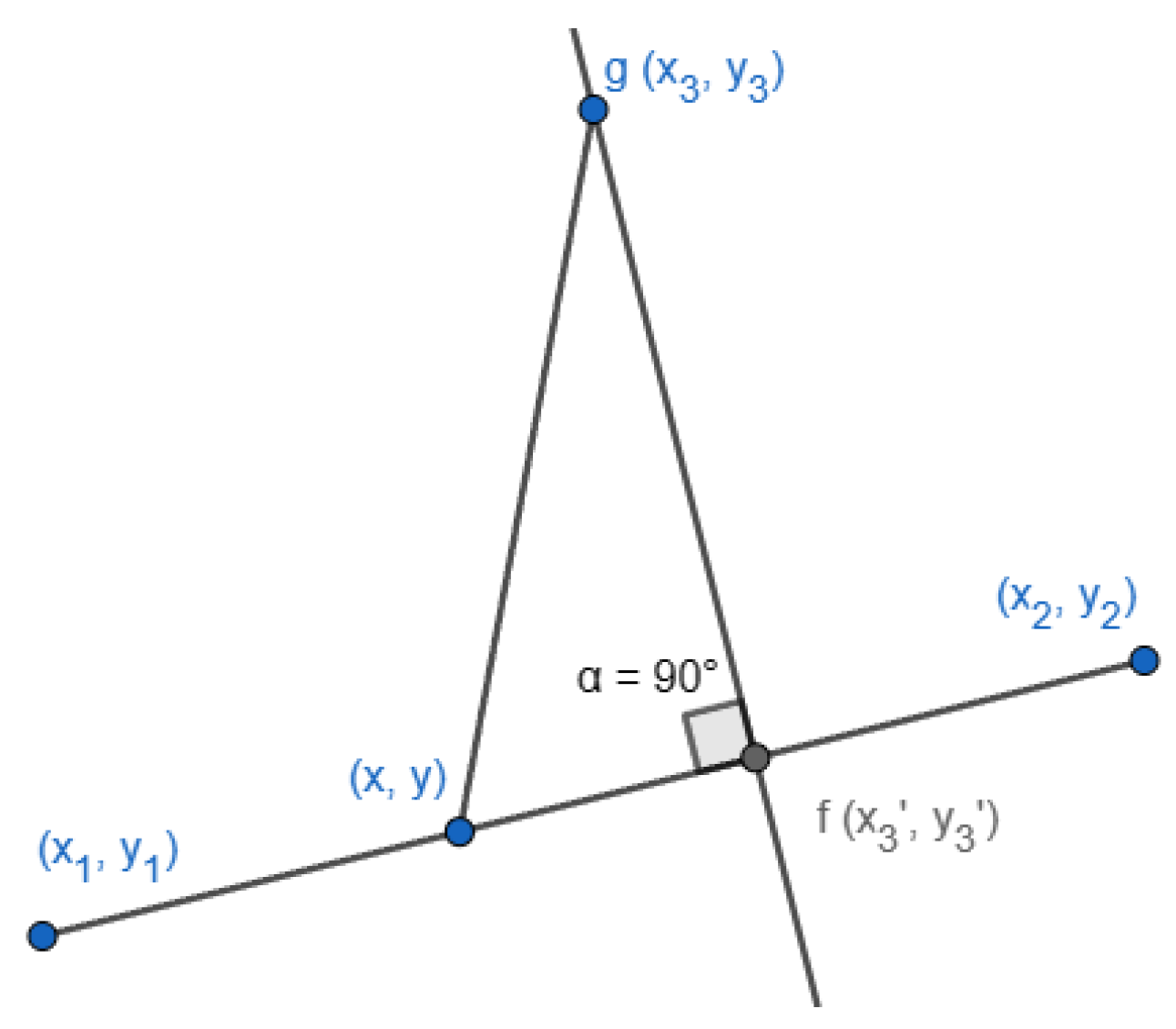
2.1. Offset a Triangle

Consider three different terms, line, ray and line segment. There is no end point for line, and one end points for ray, and two end points for line segment. Consider the parametric form for a line, ray, and line segment passing through two points P1 and P2, they have the same parametric form (1-t)P1+tP2 with different range of the parameter. It is a line, ray, line segment when t∈R, t≥0 , 0≤t≤1 respectively. Notice that the ray has P1 as its end point, denote Ray(P1, P2) and with the orientation of Ray(P1, P2), we may define the left side and right side of Ray(P1, P2). Let L= Ray (P1, P2), we denotes the point P1′ is the point moving P1 to the left side of Ray(P1, P2) r distance, denotes P1′ =Move(P1, L, r). The Ray(P1′, P2′), also denote Rayr(P1, P2), is called the r-offset of Ray(P1,P2).
Before the more detail description for proposed algorithm, we have the following theorem:
Theorem 1. 
r-offset of a ray. Given Ray(P1, P2), where P1 = (x1, y1), P2=(x2, y2), the parametric form for Rayr(P1, P2) is (1-t)P1+tP2+r×nL, 0 ≤ t , where nL= 1 ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 ( y 1 − y 2 ,   x 2 − x 1 ). The implicit form for the line cover Rayr(P1, P2) is a′x+b′y+c′=0 where a′ = (y2-y1), b′ = (x1-x2), and c′= − x 1 y 1 x 2 y 2 − r × − x 2 − x 1 2 + y 2 − y 1 2
Proof of Theorem 1. 
The direction of the ray is P2-P1= ( x 2 − x 1 , y 2 − y 1 ) . The two vectors nL = 1 ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 ( y 1 − y 2 , x 2 − x 1 ) and nR = 1 ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 ( y 2 − y 1 , x 1 − x 2 ) are perpendicular to P2-P1. This two vectors points to its left (nL) and its right(nR). We can move points on Ray(P1, P2) along nL direction r distance, so the parametric form for Rayr (P1, P2) is (1-t)P1+tP2+r×nL. Consider two points P1′, P2′, which is the points P1, P2, move to its left. That is Pi′=(xi′,yi′)=Pi+r×nL, i=1,2. The implicit form for Ray(P1, P2) is: ax + by + c = 0, where a = y2 - y1, b = x1 – x2, c = − x 1 y 1 x 2 y 2 . Let the r-offset of Ray(P1, P2) denote as Rayr = a′x + b′y + c′ = 0, where a'=y2′-y1′=a, b′=x1′–x2′=b, c′= − x 1 ′ y 1 ′ x 2 ′ y 2 ′ = c + r * x 2 − x 1 2 + y 2 − y 1 2 . So, the implicit form of Rayr is (y2-y1)x + (x1-x2)y - x 1 y 1 x 2 y 2 + x 2 − x 1 2 + y 2 − y 1 2 × r = 0.
Example 1. 
Given two points P1=(1,1), P2=(5,2). Let L= Ray1 (P1, P2), the points P1′= Move(P1, L, 1) =(0.757,1.970) and P2′= Move(P2, L, 1) =(4.757,2.970). In Figure 9, the L is shown in blue with implicit form x+4y+3=0. Furthermore, the Ray1(P1,P2) = Ray(P1′,P2′) is shown in orange with implicit form x+4y+7.123=0.
We call Ray(P1′,P2′) is the r-offset of Ray(P1,P2).
The following theorem is directly from [11].
Theorem 2: 
Intersection of two lines from 4 points [11]. Given 4 points P1(x1, y1), P2(x2, y2), P3 (x3, y3), P4(x4, y4). Two lines L1, L2, where L1 passing through P1, P2 and L2 passing through P3, P4. Then: If  x 1 − x 2 y 1 − y 2 x 3 − x 4 ( y 3 − y 4 ) = 0 , L1, L2 are parallel to each other. Otherwise, these two lines intersect each other at (x,y) where, x = x 1 y 1 x 2 y 2 x 3 y 3 x 4 y 4 x 1 − x 2 ( x 3 − x 4 ) x 1 − x 2 y 1 − y 2 x 3 − x 4 ( y 3 − y 4 ) ,   y = x 1 y 1 x 2 y 2 x 3 y 3 x 4 y 4 y 1 − y 2 ( y 3 − y 4 ) x 1 − x 2 y 1 − y 2 x 3 − x 4 ( y 3 − y 4 )
Theorem 3: 
Intersection of two r-offset rays from 3 points. Given Ray(P1, P2), Ray(P2, P3), where Pi=(xi,yi), i=1,2,3. The intersection of Rayr(P1, P2), Rayr(P2, P3) is (x, y) = ( ∆ x ∆ , ∆ y ∆ ) if  ∆ ≠0 where
∆ = x 1 − x 2 y 1 − y 2 x 2 − x 3 ( y 2 − y 3 )
∆ x = x 1 y 1 − r x 2 y 2 − r n 12 x n 12 y 1 x 2 y 2 − r x 3 y 3 − r n 23 x n 23 y 1 x 1 − x 2 ( x 2 − x 3 )
∆ y = x 1 y 1 − r x 2 y 2 − r n 12 x n 12 y 1 x 2 y 2 − r x 3 y 3 − r n 23 x n 23 y 1 y 1 − y 2 ( y 2 − y 3 )
n 12 = ( n 12 x , n 12 y ) = 1 ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 ( y 1 − y 2 , x 2 − x 1 )
n 23 = ( n 23 x , n 23 y ) = 1 ( x 3 − x 2 ) 2 + ( y 3 − y 2 ) 2 ( y 2 − y 3 , x 3 − x 2 )
Proof of Theorem 3. 
Let L1=Ray(P1,P2), L2=Ray(P2, P3), L3=Rayr(P1, P2), L4=Rayr(P2, P3). Let P1′=Move(P1, L1, r), P2′=Move(P2,L1,r), P3′=Move(P2,L2,r) and P4′=Move(P3,L2,r), then: P1′ = P1 + r×n12, P2′ = P2+ r×n12, P3′ = P2+ r×n23, P4′= P3 + r×n23, where n12 = 1 ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 ( y 1 − y 2 , x 2 − x 1 ) and n23 = 1 ( x 3 − x 2 ) 2 + ( y 3 − y 2 ) 2 ( y 2 − y 3 , x 3 − x 2 ) . The proof can be easily derived by using theorem 2 with these 4 points P1′, P2′ ,P3′, P4′.
Denote
∆ = x 1 ′ − x 2 ′ y 1 ′ − y 2 ′ x 3 ′ − x 4 ′ y 3 ′ − y 4 ′ = x 1 − x 2 y 1 − y 2 x 2 − x 3 ( y 2 − y 3 )
∆ x = x 1 y 1 − r x 2 y 2 − r n 12 x n 12 y 1 x 2 y 2 − r x 3 y 3 − r n 23 x n 23 y 1 x 1 − x 2 ( x 2 − x 3 )
∆ y = x 1 y 1 − r x 2 y 2 − r n 12 x n 12 y 1 x 2 y 2 − r x 3 y 3 − r n 23 x n 23 y 1 y 1 − y 2 ( y 2 − y 3 )
The intersection P (x, y) = ( ∆ x ∆ , ∆ y ∆ ), when ∆   ≠ 0
Example 2. 
Given 3 points P1=(1,1), P2=(10,2), P3=(3,5), then P1′=(0.889,1.993), P2′=(9.889, 2.993), P3′=(9.606, 1.080) and P4′=(2.606,4.080). The intersection points P for Ray1(P1,P2) and Ray1(P2,P3) is at (6.119, 2.575), As shown in Figure 10.
We denote P=Ray1(P1,P2)∩Ray1(P2,P3).
From △ABC, we can find 3 points B′=Rayr(A,B) ∩Rayr(B,C), C′=Rayr(B,C)∩Rayr(C,A) and A′=Rayr(C,A) ∩Rayr(A,B). We call △A′B′C′ is the r-offset triangle for △ABC.
Example 3. 
Given A=(1,1), B=(10,2), C=(3,5), the 1-offset triangle for △ABC is a triangle with vertices A′=(2.716, 2.196), B′=(6.119,2.575) and C′=(3.472, 3.709), see Figure 11.

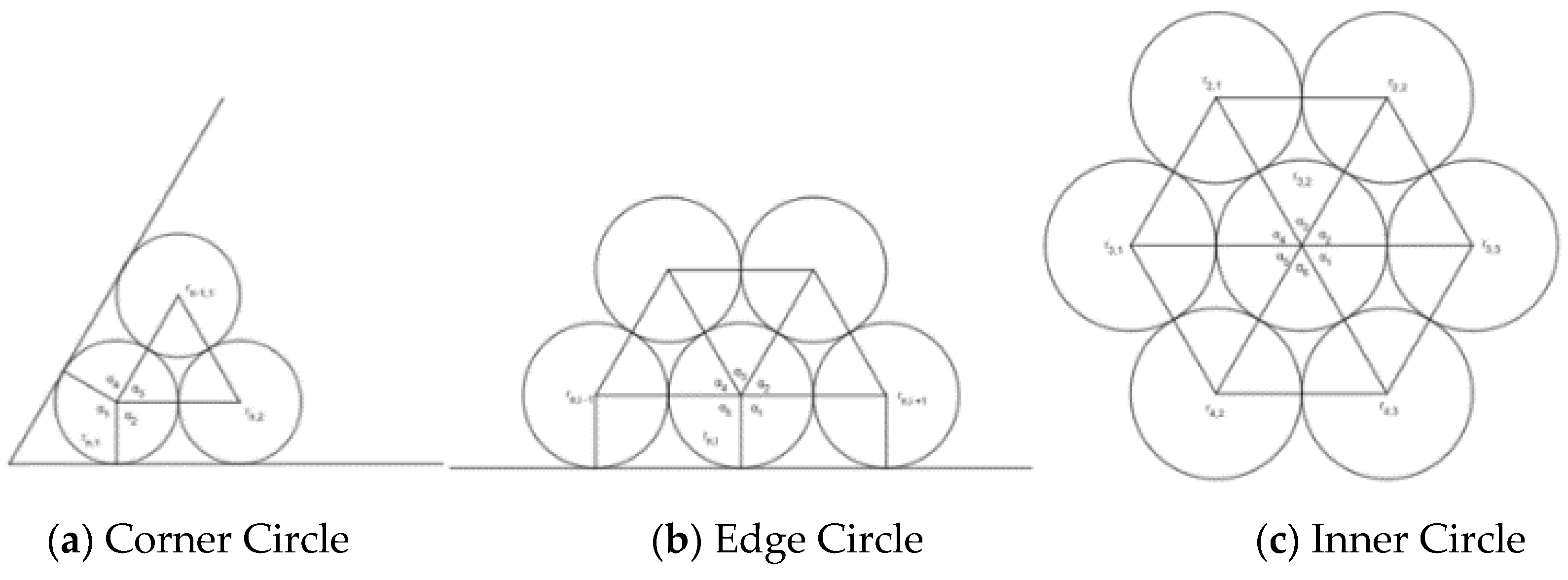
2.2. How to Construct Vertices and Edges on the Same Layer

The main task for the proposed algorithm is to generate the tangency graphic G (V, E) so that circles in the triangle has small range of radii. So, we need to generate vertices, and edges connect vertices. We generate vertices layer by layer, and generate edges for the same layer and edges connect two consecutive layers. Given a triangle △ABC and circles with radius r, where r is much less than the least length of 3 sides of the triangle. Given △A′B′C′ is the r-offset of △ABC. Then, the circles centered at the sides of △A′B′C′ with radius r tangent to △ABC. We want to find the vertices on sides of △A′B′C′ with the following approach (see Figure 12):
1.
The vertices of △A′B′C′ belongs to V.
2.
For 3 sides of △A′B′C′:
2.1
Find the a value r′ and integer n, so that |r-r′| is minimum, and 2(r+n*r′) is equal to the length of this side of the △A′B′C′.
2.2
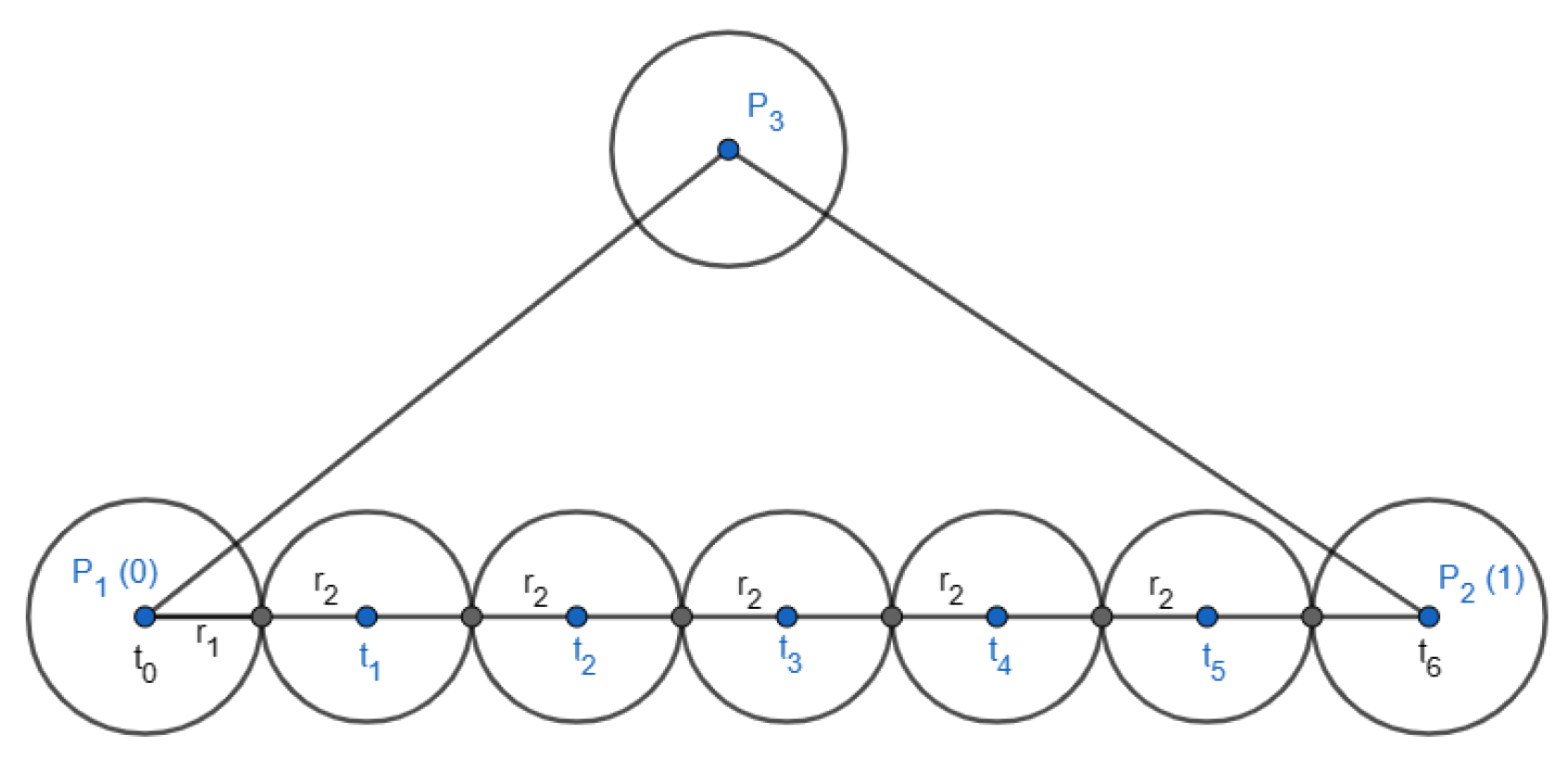
From this r′, find associated vertices, which are center of a series of circles shown in Figure 12, in this side of triangle.
2.3
Connect two consecutive vertices to establish edge of the graph.
3.
Connect two neighbors of the vertices of △A′B′C′.
4.
Connect edges from A ′ B ′ ¯ to A B ¯ , from B ′ C ′ ¯ to B C ¯ , and from C ′ A ′ ¯ to C A ¯ (described in the section 2.3)
Using this approach, start from the △ABC, the r-offset of △ABC is T1(△A′B′C′), the vertices and edges for T1 is shown in Figure 13a. Notice that the 3 vertices of triangle T1 has the properties that a circle center at these 3 vertices with radius r tangent to △ABC.
Now, consider the triangle T2 which is 3 r-offset of T1. The way to generate vertices and edges for T2 is the same as the way to generate vertices and edges for T1. After we generate edges for vertices in T1 to vertices in T2(will described in the next section), the tangency graph is shown in Figure 13b.

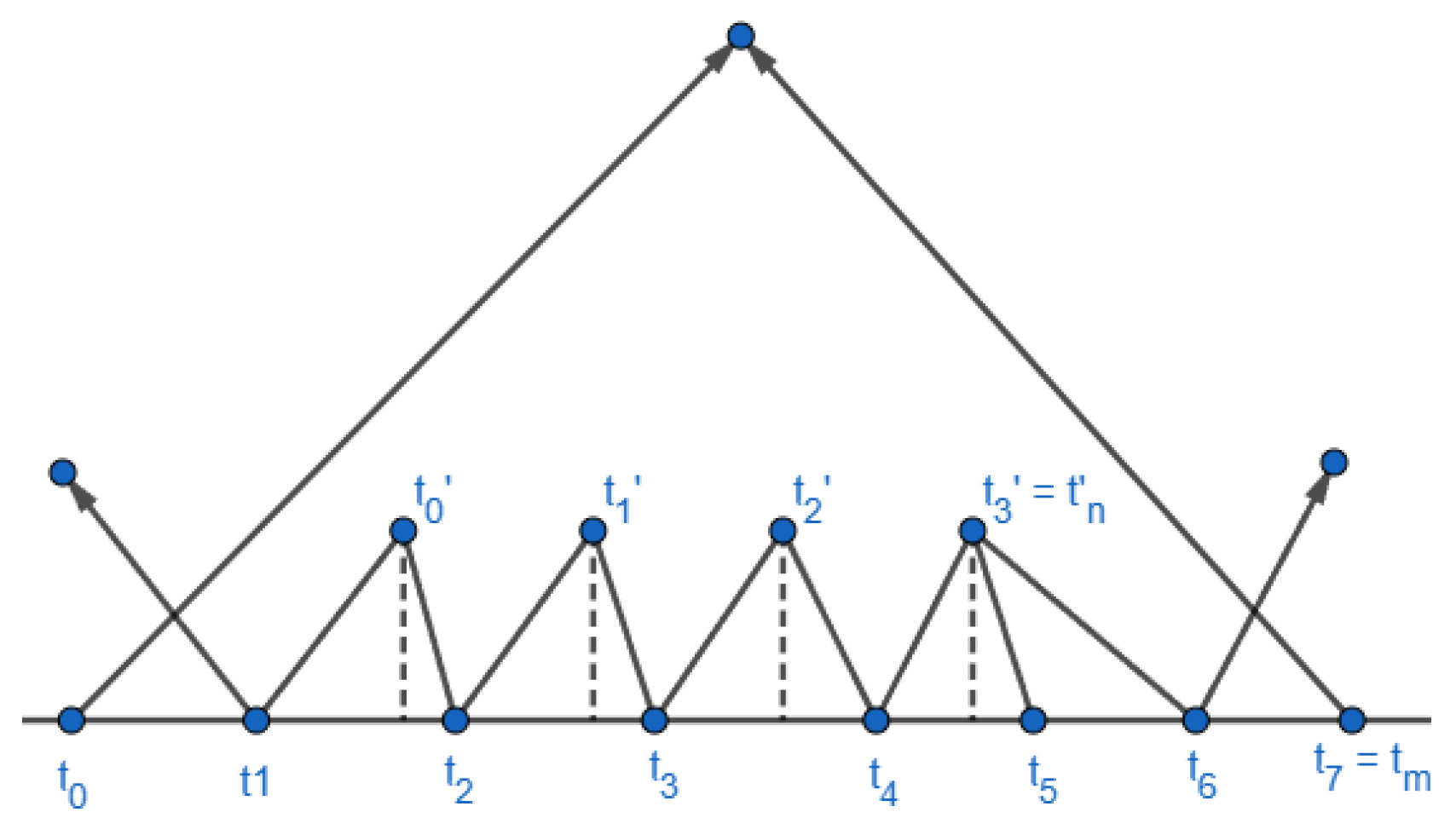
2.3. How to Construct Edges on Two Consecutive Layer

Now is the time to generate edges between vertices on T1 and vertices on T2. Before we explain our strategy to connect vertices on these two triangles, we have the following theorem:
Theorem 4. 
Find foot point of a point onto a line. Given a point g (x3, y3) and a line L(g∉L) passing through two points (x1, y1), (x2, y2). The nearest points, also called the footpoint, of g onto L is at  ( x , y ) = 1 − t x 1 , y 1 + t x 2 , y 2 .     w h e r e   t = ( x 3 − x 1 ) ( x 2 − x 1 ) + ( y 3 − y 1 ) ( y 2 − y 1 ) x 2 − x 1 2 + y 2 − y 1 2 (Shown as Figure 14)
Proof of Theorem 4. 
A point (x,y) on L, we can generate the square of the distance function from (x,y) to point g: f(t) = ( x − x 3 ) 2 + ( y − y 3 ) 2 = [ 1 − t x 1 + t x 2 − x 3 ] 2 + [ 1 − t y 1 + t y 2 − y 3 ] 2 . We want to find the value t, so that f(x) is minimum. That is, d d t f ( t ) = 0 , the parameter value t can be computed from d d t f ( t ) = 0 .
Consider the correspondence edge A ′ B ′ ¯ on T1 and A ″ B ″ ¯ on T2. Assume the parameter values for the vertices on A ′ B ′ are t0, t1, …, tm and the parameter values for the footpoints of vertices on A ″ B ″ ¯ onto A ′ B ′ ¯   are t0′, t1′, …, tn′. We explain the details with m=7 and n=3, as shown in Figure 15. To simplify our description, we use the parameter values as its vertex name from now on. The vertex t0 and t7 are the vertices on A ′ B ′ ¯ , it did not connect any vertices on A ″ B ″ ¯ (T2) yet. When we construct edges for △A′B′C′, we construct one edge from t1 to the last vertex on C ′ A ′ ¯ ., and t6 to the first vertex on B ′ C ′ ¯ . Now, we need to construct the edges for ti, i=1...,6 and tj′, j=0,3. We use the following approach to connect edges between vertices generate on T1 and T2. Notice that we try to connect vertices in A ″ B ″ ¯ to the vertices near it in A ′ B ′ ¯ . We did the same process for vertices in B ″ C ″ ¯ to the vertices near it in B ′ C ′ ¯ and for vertices in C ″ A ″ ¯ to the vertices near it in C ′ A ′ ¯ .
We define floor and ceiling for the vertices  t i ′ as the following:
t i ′ = max ⁡ t j t j < t i ′ } ; t j ′ = min ⁡ t j t j > t i ′ } , Where   t n ′ = t m − 1   t − 1 ′ = t 1 , With the above definition, we connect vertices t i ′ to all vertices from t i − 1 ′ t o t i ′ ∀ i = 0, .., n. So, in Figure 15, t 0 ′ connect vertices from t − 1 ′ =t1 to t 0 ′ =t2, and t 3 ′ connect vertices from t 2 ′ =t4 to t 3 ′ =t6. So, vertex with parameter t 3 ′   i n   A ″ B ″ has 3 edges connect vertices on A ′ B ′ ¯ .
After connecting edges between T1 and T2, the result is shown on Figure 13b. Continue to generate vertices on T3= 3 r-offset(T2), T4= 3 r-offset(T3), and generate vertices and edges for the tangency graph G(V,E), increase vertices on V, and edges connecting vertices on the same layer and previous layer, see Figure 13c,d, it is time to think how to stop the process.

2.4. How to Stop the While Loop

We know any triangles has an inscribed circle and 3 malfatti’s circles. The criterion to stop the algorithm depends on the radius of the inscribed circle and the minimum radius of the 3 malfatti’s circles.
This process specified the tangency properties among circles, representing vertices on G(V,E). Let r1 be the radius of the inscribed circle for Tlast, and r2 be the minimum radius of the 3 malfatti’s circles for Tlast. One of this two radii is less than (1+epsR)r, eqpR is a small value we set, we stop the process and go out of the loop. If r1 is close to r, we use one vertex for Tlast(See Figure 13e), otherwise we use 3 vertices for Tlast(See Figure 13f). The last thing for constructing tangency graph is to connect edges for vertices of Tlast with the previous layer triangle (See Figure 13e,f).

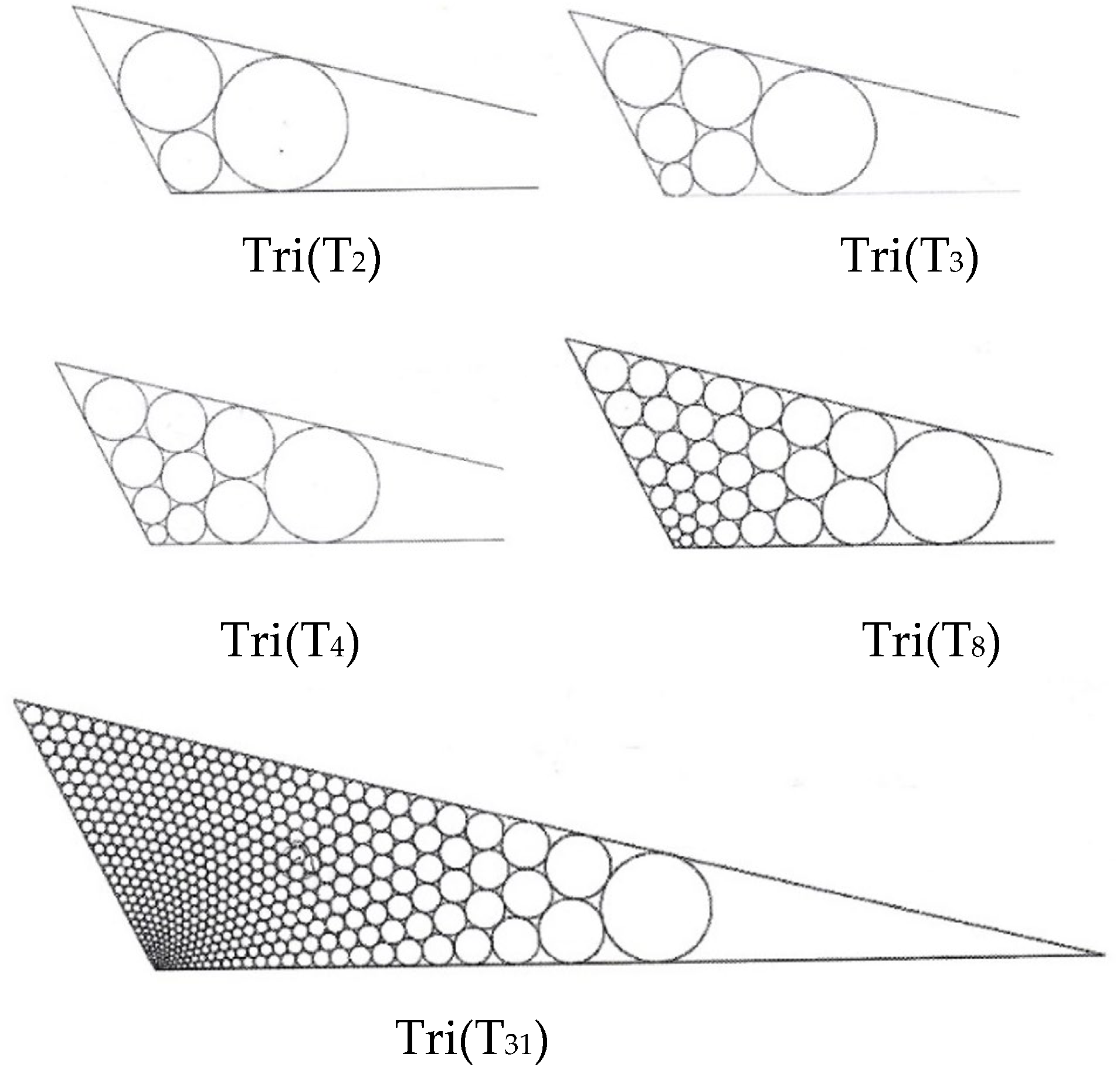
3. Examples

We use Intel(R) Core(TM) i7-10750H CPU, 16G Ram, and Anaconda 23.5.2 with Python 3.11.3 to implement the algorithm. We give two examples as the following:
Example 4. 
Given a triangle with vertices at A=(10,10), B=(100,20) and C=(30,50), and initial r=2. Set epsR=0.3, eps=0.0001, the tangency graph it generates is shown in Figure 13a–e, and after the angle computation for every circles, including vertices circle, boundary circles and inner circles, the result figure is shown in Figure 16. It takes 144.9, 6.140, and 0.288 seconds to construct tangency graph, find the radii for all circles, and display the result respectively. All the circles generated has the radii range (0.829, 4.129), which is (0.415r, 2.065r).
In this case, at the last layer, the radius of the inscribed circle is 2.22, which is less than (1+epsR)r=2.6, and the radii of the malfatti’s circles are 1.432, 1.099, 1.766, the minimum of them is 1.099. The value 2.22 is closed to r=2, compare to the difference of 2 and 1.099. So we generate the last layer has one vertex only. The output is shown in Figure 16.
Notice that there are 4 circles in Figure 16 has larger inner circles. We find that when a circle has large number of surround circle, it has large chance that its radius is large. So, if we add more circle near by, is it possible to reduce the range of the radii for the problem? So, after constructing the tangency graph, we check the degree of each vertex, if the degree is larger than 15 or between 12 and 15, we constructing two vertices/circles or one new vertex/circle with this vertex. With this approach, we have the following example.
Example 5. 
Given a triangle with vertices at A=(10,10), B=(100,20) and C=(30,30), and initial r=1.9. Set epsR=0.3, eps=0.0001. The tangency graph this algorithm construct is shown in Figure 17a, its associated tangency circles in triangle is shown in Figure 17b. Notice that two vertices have more than 15 vertices, so we add two more vertices for each of these two vertex, as shown in Figure 17c and its associated tangency circles in triangle is shown in Figure 17d. Notice that the range of the radii for Figure 17d is smaller than the range of the radii for Figure 17b.
Example 6. 
Given a triangle with vertices at A=(0,0), B=(37.5,64.952) and C=(75,0). Set r=2, epsR=0.4, eps=0.0001, the tangency graph it generates is similar to the last example, except the final step, shown in Figure 13f. After the angle computation for every circles, including vertices circle, boundary circles and inner circles, the result figure is shown in figure 17. It takes 127.106, 1.430, and 0.130 seconds to construct tangency graph, find the radii for all circles, and display the result respectively. All the circles generated has the radii range (1.506, 2.194), which is (0.753r, 1.097r).
In this case, at the last layer, the radius of the inscribed circle is 4.330, and the minimum radius of the malfatti’s circles is 2.745. Because 4.330>2.8 and 2.745<2.8, we generate the last layer has three vertices, and connect these 3 vertices to the vertices in the previous layer triangle. The output is shown in Figure 17.
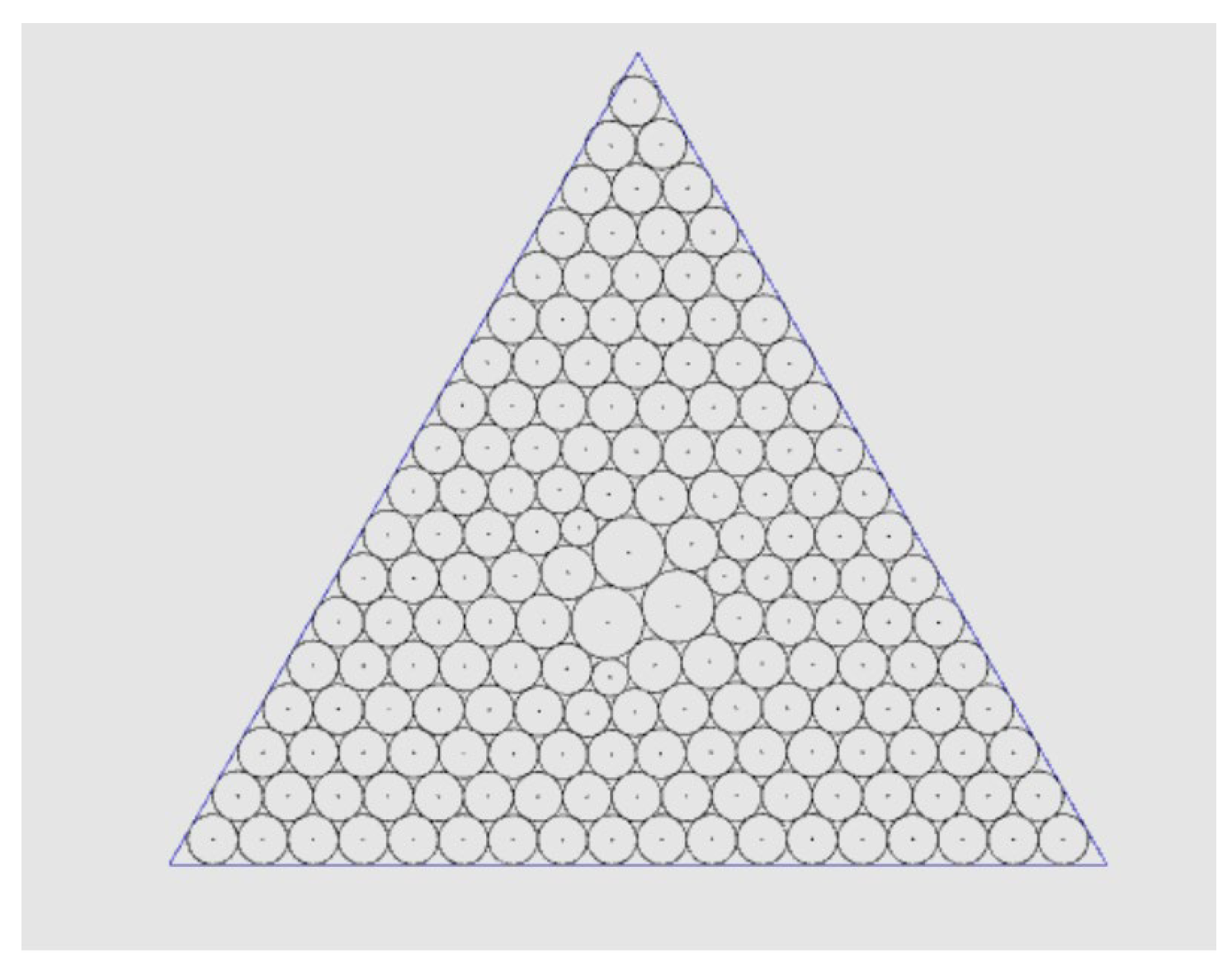
Preprints 111866 g018
Figure 18. Output Display for Example 6.
Figure 18. Output Display for Example 6.
Preprints 111866 g018

4. Conclusions

We proposed an algorithm to generate the tangency graph to specify the tangency relationship among all circles and triangle boundary. The purpose of this proposed algorithm is to reduce the range of the radii among all circles. The process to generate tangency graph, takes more CPU time, compare to the time spend on construct circle and display circles.

Acknowledgments

This research is support NSTC-112-221-E-031-003. We extend our heartfelt gratitude to Guan Wen Wang and Hsi Wen Wang for their invaluable contributions to the programming aspect of this research.

References

  1. Malfatti, G. Memoria sopra un problema stereotomico. Memorie di Matematica e di Fisica della Società Italiana delle Scienze 1803, 10, 235–244. [Google Scholar]
  2. Chiang, C. S.; Hoffmann, C. M.; Rosen, P. A gereralized Malfatti’s Problem. Computational Geometry 2012, 45, 425–435. [Google Scholar] [CrossRef]
  3. Lob, H.; Richmond, H. W. On the Solutions of Malfatti's Problem for a Triangle. Proceedings of the London Mathematical Society 1930, s2-30, 287–304. [Google Scholar] [CrossRef]
  4. Wells, D. Malfatti's problem. In The Penguin Dictionary of Curious and Interesting Geometry; Penguin Books: New York, 1991; pp. 145–146. ISBN 978-0-14-011813-1. [Google Scholar]
  5. Ogilvy, C. S. Malfatti's problem. In Excursions in Geometry; Dover, 1990; pp. 145–147. ISBN 978-0-486-26530-8. [Google Scholar]
  6. Fukagawa, H. and Pedoe, D. "The Malfatti Problem." Japanese Temple Geometry Problems (San Gaku). Winnipeg: The Charles Babbage Research Centre, pp. 28 and 103-106, 1989.
  7. Bottema. The Malfatti Problem. Forum Geometricorum 2000, 1, 43–50. [Google Scholar]
  8. Stefanović, M. Triangle centers associated with the Malfatti circles. Forum Geometricorum 2003, 3, 83–93. [Google Scholar]
  9. Wolfram Math World. “Malfatti Circles,” Available online: http://mathworld.wolfram.com/MalfattiCircles.html.
  10. Ching-Shoei Chiang, Hung Chieh Li, Min-Hsuan Hsiung, and Fan-Ming Chiu. Extended General Malfatti’s Problem, The 19th International Conference on Scientific Computing, 2021/7/26-29.
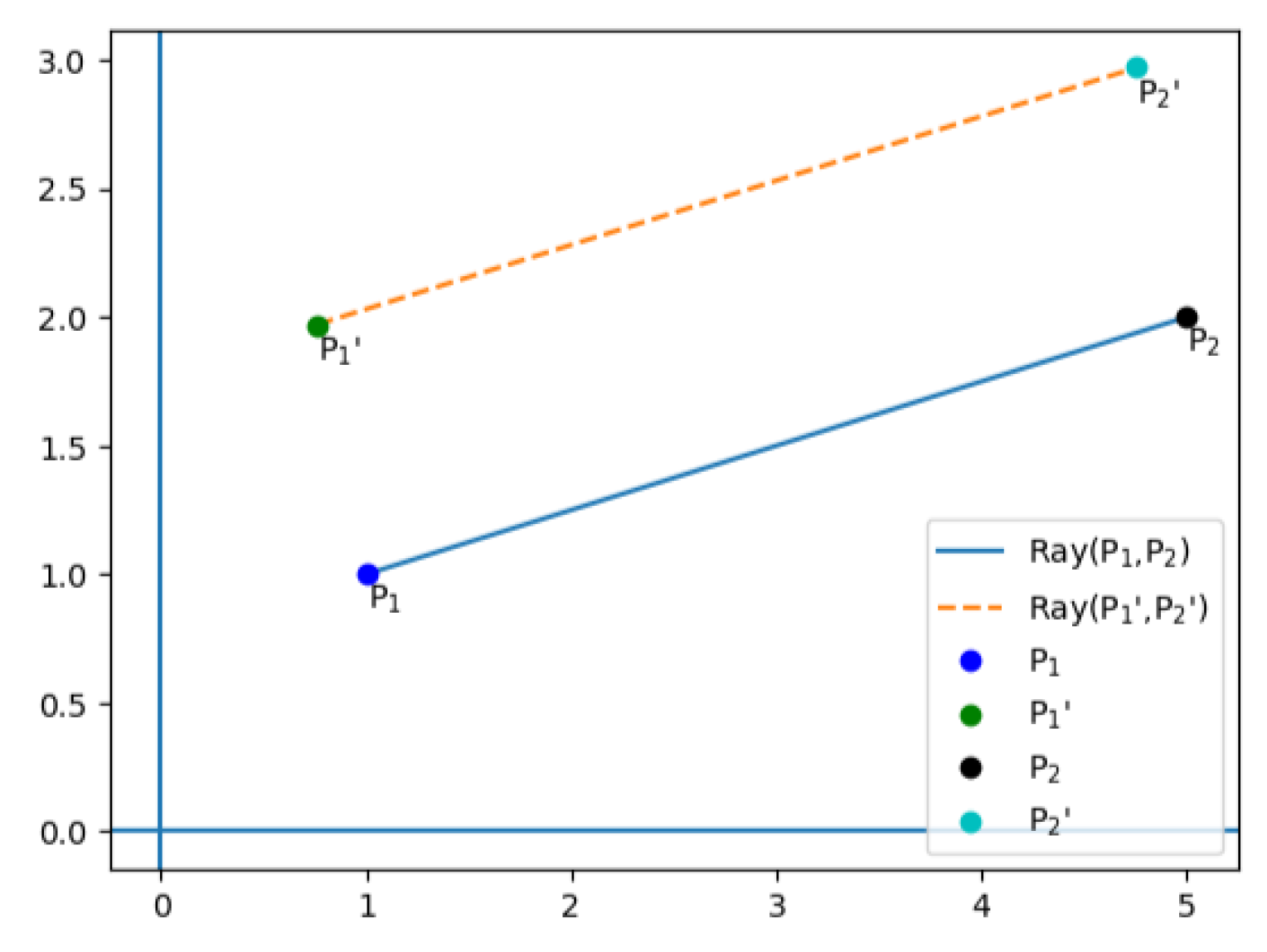
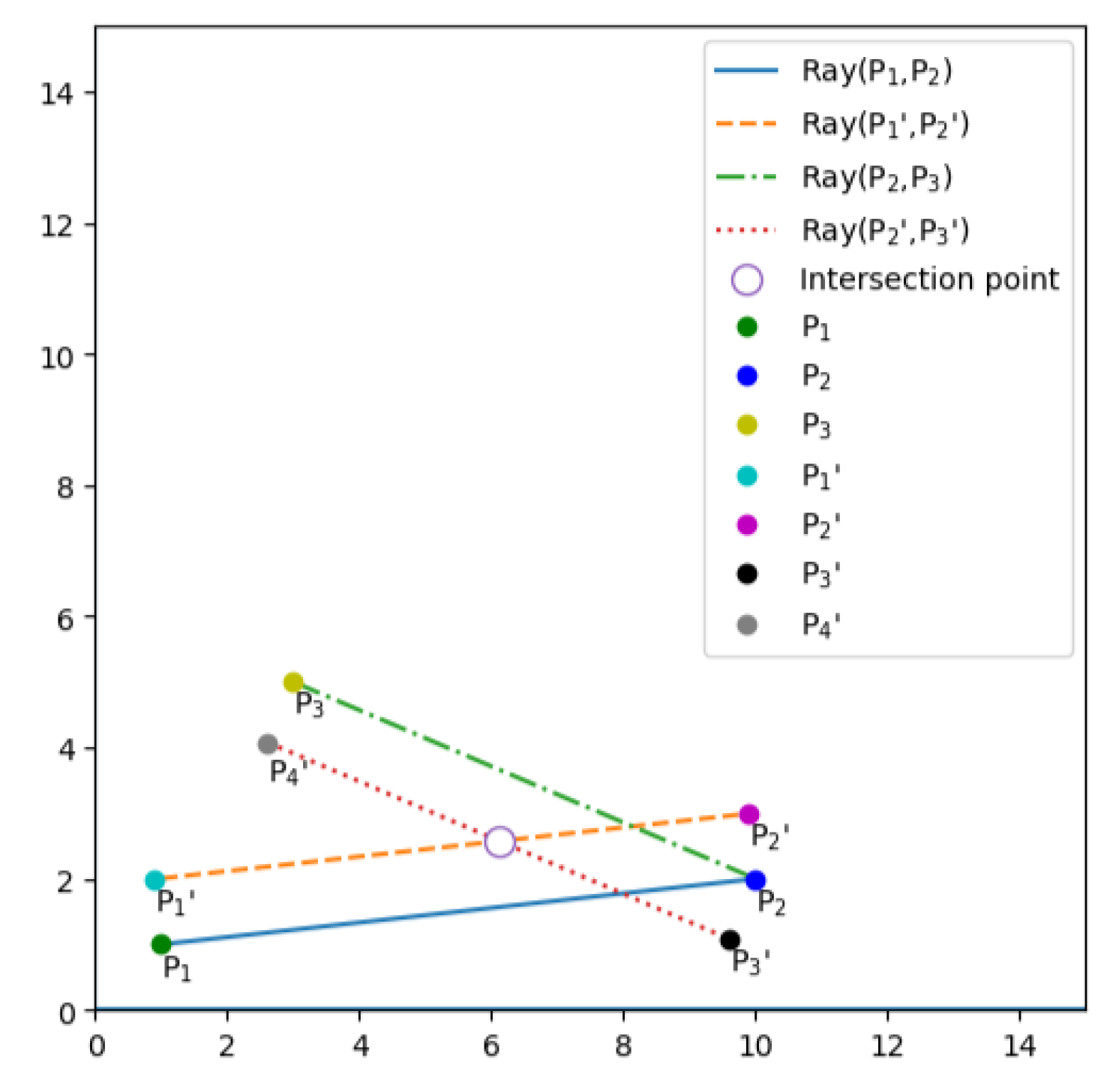
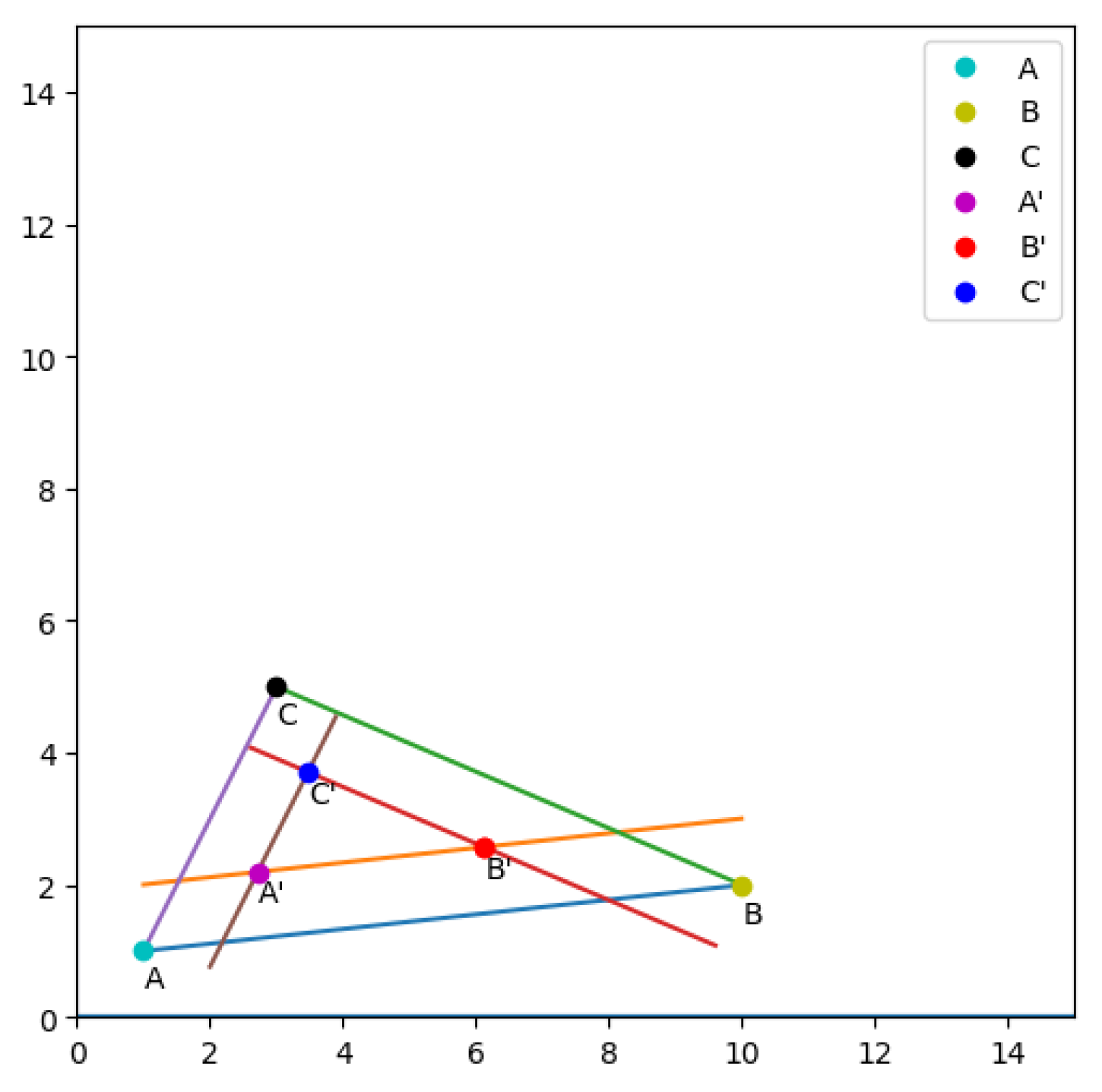
  11. Weisstein, Eric W. "Line-Line Intersection." From MathWorld--A Wolfram Web Resource. Available online:. https://mathworld.wolfram.com/Line-LineIntersection.html.
  12. Collins, C. R.; Stephenson, K. A circle packing algorithm. Computational Geometry 2003, 25, 233–256. [Google Scholar] [CrossRef]
Preprints 111866 g001
Figure 1. Malfatti’s problem.
Figure 1. Malfatti’s problem.
Preprints 111866 g001
Preprints 111866 g002
Figure 2. In an equilateral triangle.
Figure 2. In an equilateral triangle.
Preprints 111866 g002
Preprints 111866 g003
Figure 3. Malfatti’s problem and max-area problem.
Figure 3. Malfatti’s problem and max-area problem.
Preprints 111866 g003
Preprints 111866 g004
Figure 4. The tangency property for Tri(Tn) problem.
Figure 4. The tangency property for Tri(Tn) problem.
Preprints 111866 g004
Preprints 111866 g005
Figure 5. Calculating total surrounding angles for 3 kinds of circles.
Figure 5. Calculating total surrounding angles for 3 kinds of circles.
Preprints 111866 g005
Preprints 111866 g006
Figure 6. Tri(T2) problem, change ratio = c′/c.
Figure 6. Tri(T2) problem, change ratio = c′/c.
Preprints 111866 g006
Preprints 111866 g007
Figure 7. Tri(Tn) Problem, where n=2, 3, 4, 8, 31.
Figure 7. Tri(Tn) Problem, where n=2, 3, 4, 8, 31.
Preprints 111866 g007
Preprints 111866 g008
Figure 8. Tangency graph.
Figure 8. Tangency graph.
Preprints 111866 g008
Preprints 111866 g009
Figure 9. r-offset of a ray.
Figure 9. r-offset of a ray.
Preprints 111866 g009
Preprints 111866 g010
Figure 10. Intersection of two r-offset rays from 3 points.
Figure 10. Intersection of two r-offset rays from 3 points.
Preprints 111866 g010
Preprints 111866 g011
Figure 11. The result of r-offset triangle.
Figure 11. The result of r-offset triangle.
Preprints 111866 g011
Preprints 111866 g012
Figure 12. vertices setup for one side of triangle.
Figure 12. vertices setup for one side of triangle.
Preprints 111866 g012
Preprints 111866 g013
Figure 13. Generating the tangency tree for triangle.
Figure 13. Generating the tangency tree for triangle.
Preprints 111866 g013
Preprints 111866 g014
Figure 14. Find out the foot point f of point g.
Figure 14. Find out the foot point f of point g.
Preprints 111866 g014
Preprints 111866 g015
Figure 15. relation between vertices.
Figure 15. relation between vertices.
Preprints 111866 g015
Preprints 111866 g016
Figure 16. Output Display for Example 4.
Figure 16. Output Display for Example 4.
Preprints 111866 g016
Preprints 111866 g017
Figure 17. Add more vertices in Example 5.
Figure 17. Add more vertices in Example 5.
Preprints 111866 g017
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated