Prerpints.org logo
Preprint
Article

IDENTIFICATION OF DOMINANT PARAMETERS IN THE PREDICTION OF STATUS OF PEDIATRIC CONGENITAL HEART DISEASES ICU PATIENTS

Altmetrics

Downloads

99

Views

55

Comments

0

Submitted:

09 July 2024

Posted:

11 July 2024

You are already at the latest version

Alerts
Abstract
Background: The key objective of this research was to identify the dominant parameters and determine the patient status of pediatric patients with congenital heart disease in the ICU. The data we collected from the Congenital Heart Disease (CHD) Surgery Unit (ICU) in the National Heart Foundation Hospital and Research Institute, Dhaka, Bangladesh. Data from 300 ICU patients was collected and analyzed. We choose patients who are less than 12 years old at the time of ICU admission and whose ICU stay is longer than 24 hours. (2) Methods: According to the doctor’s advice, the dependent and independent variables are selected. The relationship between these parameters in the ICU was selected by linear modeling, which is associated with mortality risk. These parameters are used in the linear regression model and the ARIMA model for prediction. The prediction model is used for pediatric congenital heart disease patients in the ICU. (3) Results: The relation between CVP and BP (95% CI=0.2113,0.353 r=0.2841249), PEEP, and FiO2 (95% CI=0.6992,0.770 r=0.7367744) is statistically significant (p value<0.001). pH and PO2 were statistically significant, but there were correlations (95% CI=0.161,0.308 r=0.2362575). The statistically significant (p < 0.001) parameters were selected for prediction. In this study, BP, FiO2, and PO2 parameters were used in the linear regression model and the ARIMA model for prediction. We predict the next-hour patient’s status. The ARIMA model was found to have less error than the linear regression model. (4) Conclusions: This study helps identify the important parameters that are measured in the ICU to monitor patient status and predict the future value of those parameters, with the ultimate goal of providing physicians with an early signal of future patient conditions.
Keywords: 
Subject: Computer Science and Mathematics  -   Analysis

1. Introduction

Pediatric ICU patients generally fall within the age group of 0–12 years, having complications mostly from congenital heart diseases (CHD) from birth. Now we see a rise in neonatal admissions in the pediatric cardiac ICU. An Indian study shows a 30-50% increase in admission of child patients due to cardiac diseases [1]. Another study shows that 32000 children are affected by CHD, of which 25% require invasive treatment in the USA [2,3]. Birth defect-induced CHD causes a 30-40% mortality among infants and children [4]. In recent years, though several advanced interventional and surgical techniques have been devised, heart disease in infants and children remains a major cause of morbidity and mortality [5]. Winter admissions further increase the number of pediatric patients per unit on mortality [6]. On the other hand, the number of required pediatric ICUs is not adequate globally, and most low- and middle-income countries even do not have a designated ICU with adequately trained staff. They are further characterized by a critically low nurse-to-patient ratio [7].
Prediction of ICU patient status can effectively contribute toward a better quality of treatment in at least three ways. First, it will help the doctors plan better treatment based on the prediction of the future status of the patient. Second, better treatment will reduce the length of stay in hospitals, which will enable them to handle more patients with limited resources, which will reduce the treatment cost. Third, doctors and families will be more prepared by knowing the status of their patients.
Several studies have been reported that employ a time series model for sensing or predicting the clinical status of patients. Kennedy and Turley [8] outlined the processes required to construct predictive models employing time series clinical data as well as prediction models from nonclinical domains that use time series data. Using the specific example of developing a prediction model for cardiac arrest in a pediatric intensive care unit, this paper demonstrates the methodology. Muge Capan et al [9] predict the hospital census for neonatal ICU patients. They have shown that the time series model predicts the census with less error compared to the fixed average census approach, though the inputs were static variables. Yixian Xu1 et al [10] proposed a model to predict ICU mortality in rheumatic heart disease. A framework based on machine learning was published in [11] to forecast cardiac arrests in a pediatric intensive care unit. To assess predictability, this study takes advantage of causally related changes in signals such as heart rate, respiration rate, systolic blood pressure, and peripheral cutaneous oxygen saturation. Meanwhile, M. Pishgar et al [12] predict unplanned 30-day readmission of ICU patients with heart failure. Demographic information and severity scores were used for this prediction. Some papers analyze early prediction of critical events for infants. A machine learning model was employed by Bongjin Lee et al [13] to forecast fatal outcomes during the initial stages of intensive care unit admission. Victor M. Ruiz et al [14] focused on the early prediction of critical events for infants. None of these methods, however, offers a comprehensive framework for expertly enhanced causal graph construction with a focused clinical application. However, the identification of dominant parameters for prediction may decrease the mortality rate. So, in this paper, we provide a cause-and-effect relationship between ICU parameters. Here, we use the Pearson correlation model to find the statistically significant predictors. Then we predict the patient status using the ARIMA model and the simple linear regression(LR) model and analyze the performance between the two models.
With the ultimate goal of giving doctors an early warning of a patient’s future condition and enabling better healthcare services by enhancing patient information, the study aims to identify the critical parameters that are measured in the intensive care unit to monitor the status of the patient and predict the future value of those parameters.

2. Materials and Methods

2.1. Data Collection and Preprocessing

This study included 300 postoperative congenital heart disease pediatric patients. They were admitted to the ICU at the National Heart Foundation Hospital and Research Institute in Dhaka, Bangladesh, between 2017 and 2018. Among them, 156 (52% ) were female patients, and 144 (48% ) were male patients. In this data set, approximately 3 (1 % ) were neonate(> 1 month), 32 ( 10.6 % ) of the participants were infants (> 1 year), 211(70 % ) were young children and 57( 19 % ) were older children ( > = 18 years).
This study included patients with congenital cardiac disease who were between the ages of one day to twelve. Patients who were >12 years and suffered from other diseases were excluded from this study. Here, 12 patients were excluded from this study.
The patient is always under observation by medical assistants in the intensive care unit. They are holding a piece of paper with 42 parameters on it. They track 42 parameters while observing patients. Each patient’s data is gathered every hour. One patient typically remains in the ICU for two to seven days. Each day, a massive data-sheet is created. We select ICU stays for patients that must be greater than 24 hours. Patient variables that were collected included demographic variables like age, sex, weight, date of ICU admission, and total ICU stay. The physiological data collected in this dataset include respiratory, arterial blood pressure (ABP), central venous pressure (CVP), pulmonary arterial pressure (PAP), body and peripheral temperature, and peripheral capillary oxygen saturation (SpO2). Ventilation data included in this study were the mode of vent, vent rate, tidal volume (TV), peak inspiratory pressure (PIP), positive end-expiratory pressure (PEEP), mean airway pressure (MAP), fraction of inspired oxygen (FiO2), and arterial and venous blood gas references (Ph, pCO2, and bicarbonate). Laboratory findings included calcium, potassium, chloride, sodium, urine, and anion gap. The primary drugs included in our dataset were dobutamine, norepinephrine, milrinone, amiodarone, and Lasix. The dataset has many inaccurate items because of noise, missing values, or wrong records. As a result, we must recognize and deal with these conflicting or inaccurate records. First, we noticed that several variables’ measurement units varied. For instance, the peripheral temperature is expressed in Celsius. Secondly, some parameter values have been collected as errors or are missing entirely. Third, some variables are recorded with multiple values simultaneously. We perform forward and backward imputation if the record is occasionally missing within 24 hours. Second, if there is no such data for 24 hours, we take all patients’ average values of that variable. Then We randomly select one value from more than one in an hour. We represent all data in Fahrenheit measurements to solve the problem of conflicting values in body temperature records.
This study’s protocols and procedures followed the ethical rules and principles of the Declaration of Helsinki. Ethical approval was obtained from the National Heart Foundation Hospital and Research Institute Ethics Committee (Decision No. 4/14-7/AD-2230/2022).

2.2. Cause Effect Relation

Cause-and-effect statements demonstrate a distinct, direct connection between events. They demonstrate how one action or occurrence sets off another [15,16,17]. By working with the clinical domain expert, a critical care physician, we created the causal graph using our knowledge of the clinical domain. Three operations are involved in the causal relationship: If the edge is supported by the domain knowledge, preserve it; if not, modify the direction or orientation of the edge if the domain information supports it; and if not, remove the edge. Statistical analyses were performed using the R programming language. The Pearson Correlation test was used to conduct correlation analysis. The threshold for statistical significance was set at p < 0.01.

2.3. Linear Model and ARIMA Model

A predictive, quantifiable technique for showing a relationship between a dependent variable and a certain configuration of independent elements is called linear regression. It is an easy method to deal with showing how one dependent variable and one or more independent variables are related. It is referred to as simple linear regression when there is just one independent variable present. The process is known as multiple linear regressions when there are numerous independent factors. Linear regression has been used in this study to forecast patient status [18].
The linear condition that adds special information literacy, particular arrangement x, to the linear regression description is described as follows: its response is the predicted return y of the data, particular arrangement (y). Each information value is provided by the linear condition, or a portion of a scale factor known as the coefficient (represented by the Greek letter beta β ). Adding more coefficients in the same manner gives the line more degrees of freedom and is frequently referred to as the intercept or offset coefficient. For a simple regression problem, the model type would be:
Y i = β 0 + β 1 x
where β 0 is the intercept, β 1 is the coefficient, x is the independent variable, and y is the dependent variable [18,19].
Auto regressive integrated moving averages are limited to being linear functions of prior data and exhibit linearity in their projections of future values [20]. ARIMA stands for autoregressive integrated moving average, which is a statistical technique used to analyze time series data. An autoregressive (AR), an integrated (I), and a moving average (MA) process are the three main components of an ARIMA. The most popular method for predicting future value in time series forecasting is the ARIMA model, sometimes known as the Box Jenkins model [21]. According to [22], Equation 5 is used to compute the future value of the variable by summing the values from the past.
X t = b 0 + a 1 X t − 1 + ⋯ + a p X t − p + e t − b 1 e t − 1 + ⋯ + b q e t − q
In this case, the error is denoted by e subscript t, the number of moving averages is q, the number of autoregressive terms is p, and the real value at t is represented by X subscript t.
The MSE, mean absolute error (MAE), RMSE were used as indices to evaluate the performance of the model. The absolute form of the MAE is the measurement of error compared to the actual and expected value. The root-mean-square error (RMSE) is the difference between the actual and anticipated values squared. The functions are based on the following equations. [23,24]:
M A E = ∑ 1 N | y − y ^ |
R M S E = 1 N ∑ ( y − y ^ ) 2
The MAE and RMSE are represented by equations 3 and 4, respectively. The real value in this example is y, but the predicted value is y ^ .

3. Results

This study included 300 post operative CHD pediatric patients. In health studies, variables typically fall into two categories. We anticipate that independent variables ( N o d e f r o m ) will have an impact on dependent variables ( N o d e t o ) (predictors). What occurs as a consequence of the independent variable is known as a dependent variable, or predictor. The dependent and independent variables are selected according to the doctor’s advice. The procedure for using the advice of the domain expert is shown in Table 1 . N o d e f r o m to N o d e t o means N o d e f r o m causes N o d e t o . After consulting a physician, we evaluate the graph to ensure it is acyclic. 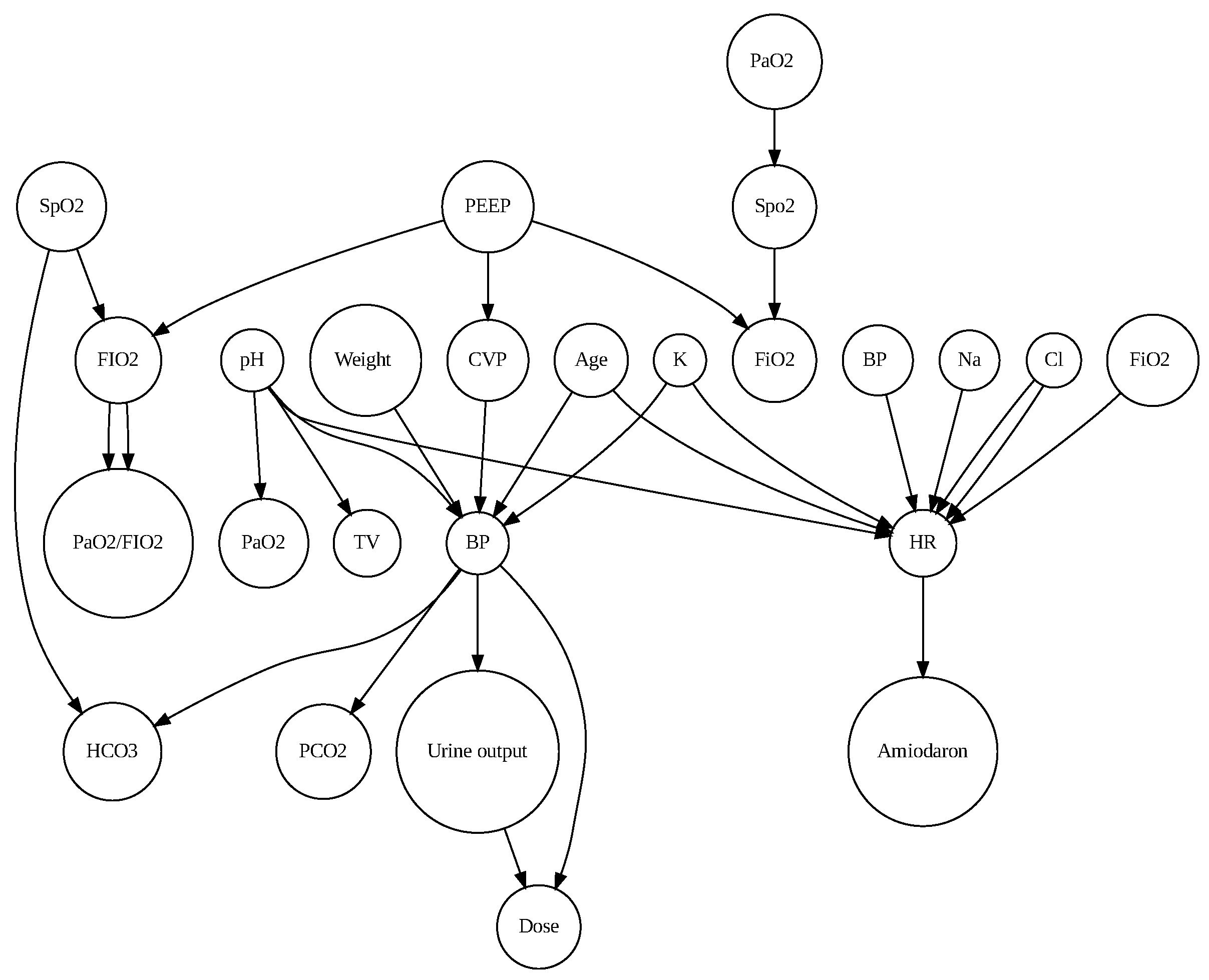Figure 1 shows the cause effect relation between parameters.
According to expert knowledge, weight and BP are confounding variables that can influence other independent and dependent variables. So, we eliminate these weight-BP correlations. Table 2 demonstrates that BP and urine output were significant (r = 0.151079, p<0.001), pH and PO2 were significant (r = 0.2362, p<0.001), Peep and FiO2 had a high correlation (r = 0.7367744) and were significant. So, for forecasting patient status, this study used three parameters: BP (mmHg), PO2 (mmHg), and FiO2(%). To predict patient status, the LR and ARIMA models were used. 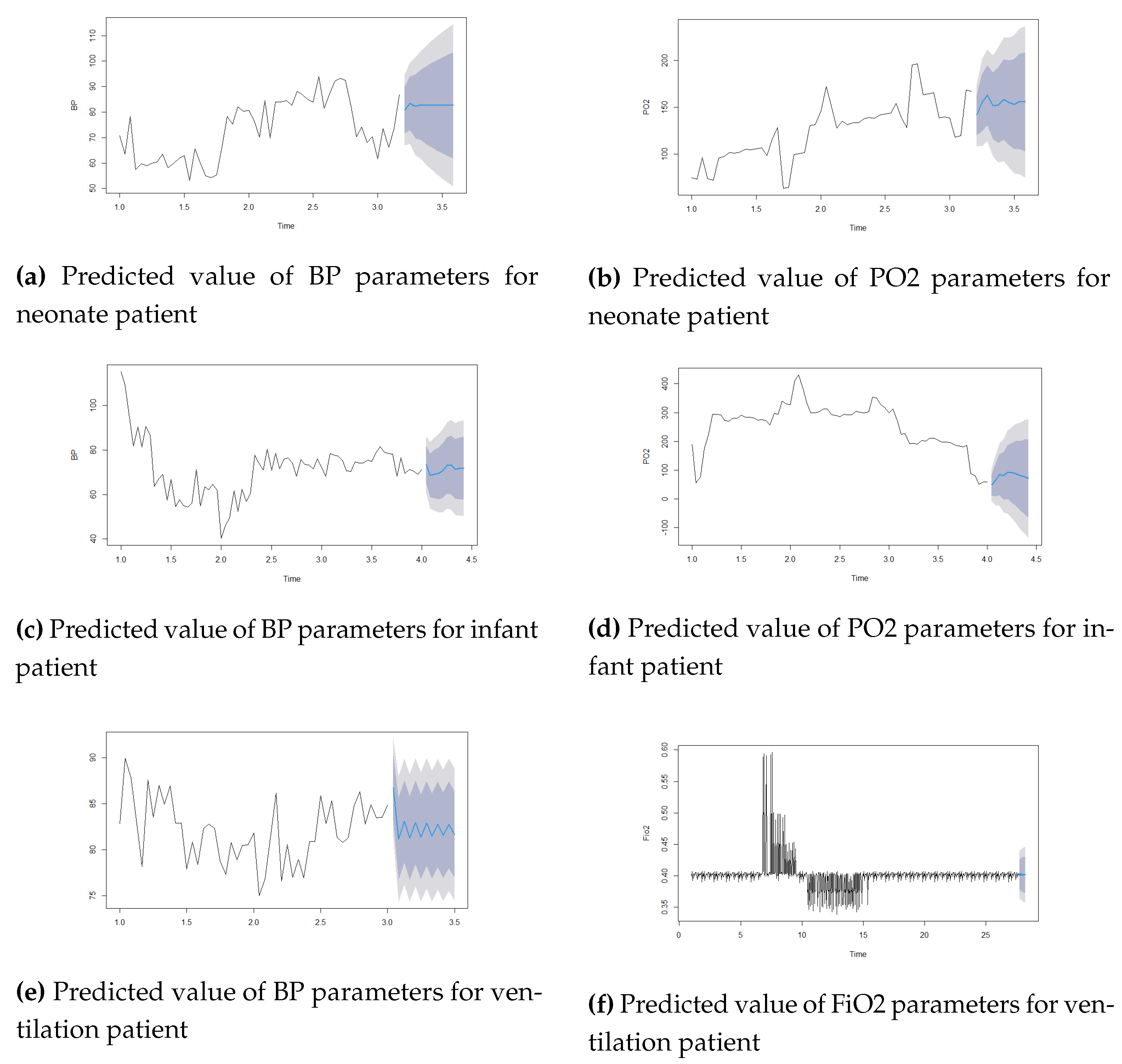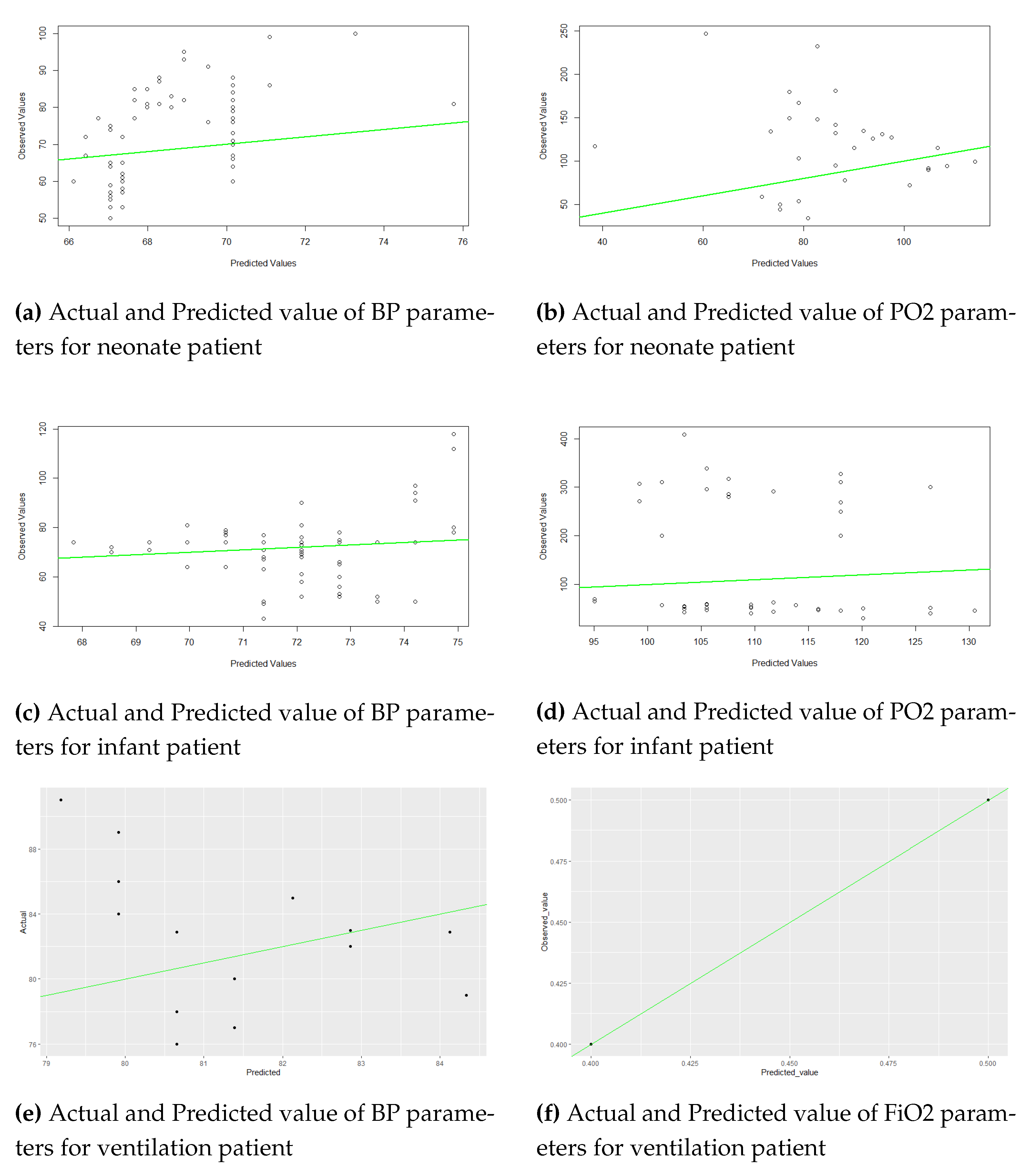Figure 2 and 3 show the actual and predicted values of parameters BP, PO2, and Fio2 using the LR model and the Arima model. For the ARIMA model, the autoarima function is used in R and R Studio version 2.1.1. For Neonate patients, the best ARIMA (2,1,1), infant patients ARIMA (1,1,0), and ventilation patients ARIMA (1,0,2) models were selected for the prediction. This study used the first 48 hours of time series data for prediction. The univariate time series data set was used for this analysis. The lowest errors in both forecast accuracies are shown in Table 3. The study showed minimal errors in MAE (BP=2.17, FiO2=0.009) for ventilation patient, for neonate patient MAE=5.2274, RMSE=7.001 for BP parameters, MAE=10.83, RMSE=16.04 for PO2 parameters in ARIMA model.
Table 2. Relationship between independent variable and dependent variable.
Table 2. Relationship between independent variable and dependent variable.
Independent variables Predictors p value correlation t test
BP HR 0.7631 0.01191929 0.30156
CVP BP < 0.001 * 0.2841249 7.4968
BP Urine output 0.0001217* 0.151079 3.8664
Urine output Dose 0.4037 0.03301339 0.83564
BP PCO2 0.7896 -0.0105502 -0.26692
BP HCO3 0.5382 -0.02433762 -0.61588
Na HR 0.07837 0.0695229 1.7631
Cl HR 0.1415 0.05808523 1.4719
PEEP FiO2 < 0.001 * 0.7367744 27.567
Spo2 FiO2 0.7339 0.01344123 0.34007
FiO2 PaO2/FiO2 0.0002411* -0.1444255 -3.6924
K BP 0.5047 -0.02637669 -0.66752
K HR 0.1022 -0.06456345 -1.6368
PH PO2 < 0.001 * 0.2362575 6.151
pH TV 0.01845 0.09298063 2.3625
PH HR 0.725 -0.01390998 -0.35193
pH BP 0.002025* -0.1216032 -3.0993
PO2 Spo2 0.5347 0.2362575 0.62112
Here * indicates p <0.01.
Table 3. The performance evaluation metrics.
Table 3. The performance evaluation metrics.
Model Neonat Patient Infant Patient Ventilation Patient
MAE RMSE MAE RMSE MAE RMSE
LR MODEL(BP) 5.973879 8.0574 2.795142 6.707442 4.47021 4.974626
LR Model(PO2) 38.5670 49.01 81.72645 99.54716 - -
LR Model(FiO2) - - - - 0.0122449 01503418
ARIMA Model(BP) 5.2724 7.0011 4.435455 6.362786 2.176254 2.618761
ARIMA Model(PO2) 10.8366 16.0403 16.065 27.812 - -
ARIMA Model(FiO2) - - - - 0.0095 0.01941237
Grey box indicates lowest errors. Here, LR=linear regression model. ARIMA=Autoregressive integrated moving average.

4. Discussion

Every year, CHD causes many morbidities and deaths in children. Despite significant advancements in the medical and surgical treatment of newborns, CHD, a severe form of the disease still accounts for the majority of deaths from congenital abnormalities and are linked with significant mortality and morbidity. Studying the dominant parameters after surgery and identifying the model to predict the patient’s condition is necessary.
Our study presents a cause-and-effect relationship from observational data using expert knowledge. Nowadays, the ability to determine the causal consequences of medical therapies through data analysis makes causal inference an essential topic in the medical industry [29]. However, potential outcome guidelines (Rubin CausalModel) [30,31] and structural causal models (SCM) [32] are thought to be the foundation of causal models because they consistently incorporate prior causal knowledge, assumptions, and estimates. Using expert information from clinicians or previously published literature, structure learning algorithms must be used to create a graphical representation of the causal link between variables of interest in this approach [33]. However, a variety of algorithms exist that can determine the graphical structure from data under various presumptions. As a result, depending on the underlying assumptions, the resulting causal graph may differ significantly [34]. Although there exist additional clinical applications of SCM, the majority of the literature mainly utilized domain expertise to create the causal graph [35]. In our study, we provided the casual graph using clinical expertise knowledge in Figure 1. A significant association between parameters is shown in Table 2. We found significant correlations between CVP-BP (r = 0.284), PH-PO2 (r = 0.23), and PEEP-FiO2 (r = 0.734).
The limitations of this study include that, for cause-and–and-effect relations, dobutamine drugs are used for dose calculation. We should include other drugs. Confounding parameters should be considered for casual relations in this study. This study also used a simple linear regression model and an ARIMA model for predicting patient conditions in the ICU. The prediction of patient outcomes in the Intensive Care Unit (ICU) setting is a critical challenge that has garnered significant research attention. While traditional statistical models such as linear regression and ARIMA (Autoregressive Integrated Moving Average) have been applied to this task, they often fall short of capturing the complex and nonlinear relationships inherent in ICU patient data. One of the key challenges in using ARIMA models for ICU patient data is the limited availability of historical data. Typically, ARIMA models require a relatively long time series of data to accurately capture the underlying patterns and trends [36,37]. In the context of ICU patient data, the duration of stay and the rapid changes in the patient’s condition can lead to short and irregularly spaced time series, making it difficult for ARIMA models to perform accurate forecasts [38].
Moreover, ICU patient data often exhibit complex and nonlinear relationships that may not be adequately captured by the linear structure of ARIMA models [39]. Patients’ disease risk and mortality are influenced by a multitude of factors, including clinical characteristics, demographic information, and treatment interventions, which can introduce significant heterogeneity and nonlinearity in the data [40].
To address these limitations, our future work will explore the use of more advanced machine learning techniques, which have demonstrated improved performance in predicting ICU patient outcomes.

5. Conclusions

Prediction of the ICU data set is a big problem in health sciences. Even if different techniques exist in this area, analyzing noisy, irregular time series data sets in the ICU is difficult. This article proposes to identify the important parameters that are measured in the ICU to monitor patient status and predict the future value of those parameters, with the ultimate goal of providing physicians with an early signal of future patient conditions and therefore facilitating better health care services by augmenting the information of patients. We also predict what the patient’s condition will be in the next hour of intensive care. To solve this problem, we applied two models, simple LR and ARIMA, and analyzed their efficiency.

Author Contributions

All authors have contributed equally to this manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

The hospital’s institutional review board and the ethics committee of National Heart Foundation Hospital and Research Institute approved this study (Approval number: 4/14-7/AD-2230/2022). All procedures followed in our study were in accordance with the ethical standards of the hospital’s institutional review board and the university’s ethics committee, as well as with the principles of the Declaration of Helsinki.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request for privacy reasons.

Acknowledgments

The authors would like to thank the National Heart Foundation Hospital and Research Institute authority in Dhaka, Bangladesh for providing hospital patients with access to information. Authors also thank Bangladesh’s Ministry of Information and Communication Technology for their financial support for the PhD fellowship..

Conflicts of Interest

The authors declare no conflicts of interests.

References

  1. Iyer, P.U. Management issues in intensive care units for infants and children with heart disease. The Indian Journal of Pediatrics 2015, 82, 1164–1171. [Google Scholar] [CrossRef] [PubMed]
  2. Roger, V.L.; Go, A.S.; Lloyd-Jones, D.M.; Adams, R.J.; Berry, J.D.; Brown, T.M.; Carnethon, M.R.; Dai, S.; De Simone, G.; Ford, E.S.; others. Heart disease and stroke statistics—2011 update: a report from the American Heart Association. Circulation 2011, 123, e18–e209. [Google Scholar] [CrossRef] [PubMed]
  3. Gundogdu, Z.; Babaoglu, K.; Deveci, M.; Tugral, O.; Uyan, Z. A study of mortality in cardiac patients in a pediatric intensive care unit. Cureus 2019, 11. [Google Scholar] [CrossRef] [PubMed]
  4. Gilboa, S.M.; Salemi, J.L.; Nembhard, W.N.; Fixler, D.E.; Correa, A. Mortality resulting from congenital heart disease among children and adults in the United States, 1999 to 2006. Circulation 2010, 122, 2254–2263. [Google Scholar] [CrossRef] [PubMed]
  5. Kula, S.; Cevik, A.; Olguntürk, F.R.; Tunaoğlu, F.S.; Oğuz, A.D.; İlhan, M.N. Distribution of congenital heart disease in Turkey. Turkish Journal of Medical Sciences 2011, 41, 889–893. [Google Scholar] [CrossRef]
  6. McShane, P.; Draper, E.S.; McKinney, P.A.; McFadzean, J.; Parslow, R.C.; Network, P.I.C.A. Effects of out-of-hours and winter admissions and number of patients per unit on mortality in pediatric intensive care. The Journal of Pediatrics 2013, 163, 1039–1044. [Google Scholar] [CrossRef] [PubMed]
  7. Murthy, S.; Leligdowicz, A.; Adhikari, N.K. Intensive care unit capacity in low-income countries: a systematic review. PloS one 2015, 10, e0116949. [Google Scholar] [CrossRef] [PubMed]
  8. Kennedy, C.E.; Turley, J.P. Time series analysis as input for clinical predictive modeling: Modeling cardiac arrest in a pediatric ICU. Theoretical Biology and Medical Modelling 2011, 8, 1–25. [Google Scholar] [CrossRef]
  9. Capan, M.; Hoover, S.; Jackson, E.V.; Paul, D.; Locke, R. Time series analysis for forecasting hospital census: Application to the neonatal intensive care unit. Applied clinical informatics 2016, 7, 275–289. [Google Scholar]
  10. Xu, Y.; Han, D.; Huang, T.; Zhang, X.; Lu, H.; Shen, S.; Lyu, J.; Wang, H. Predicting ICU Mortality in Rheumatic Heart Disease: Comparison of XGBoost and Logistic Regression. Frontiers in Cardiovascular Medicine 2022, 9. [Google Scholar] [CrossRef]
  11. Matam, B.; Duncan, H.; Lowe, D. Machine learning based framework to predict cardiac arrests in a paediatric intensive care unit. Journal of clinical monitoring and computing 2019, 33, 713–724. [Google Scholar] [CrossRef] [PubMed]
  12. Pishgar, M.; Theis, J.; Del Rios, M.; Ardati, A.; Anahideh, H.; Darabi, H. Prediction of unplanned 30-day readmission for ICU patients with heart failure. BMC Medical Informatics and Decision Making 2022, 22, 1–12. [Google Scholar] [CrossRef] [PubMed]
  13. Lee, B.; Kim, K.; Hwang, H.; Kim, Y.S.; Chung, E.H.; Yoon, J.S.; Cho, H.J.; Park, J.D. Development of a machine learning model for predicting pediatric mortality in the early stages of intensive care unit admission. Scientific reports 2021, 11, 1–7. [Google Scholar] [CrossRef] [PubMed]
  14. Ruiz, V.M.; Saenz, L.; Lopez-Magallon, A.; Shields, A.; Ogoe, H.A.; Suresh, S.; Munoz, R.; Tsui, F.R. Early prediction of critical events for infants with single-ventricle physiology in critical care using routinely collected data. The Journal of thoracic and cardiovascular surgery 2019, 158, 234–243. [Google Scholar] [CrossRef] [PubMed]
  15. Rubin, D.B. Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of educational Psychology 1974, 66, 688. [Google Scholar] [CrossRef]
  16. Robins, J. A new approach to causal inference in mortality studies with a sustained exposure period—application to control of the healthy worker survivor effect. Mathematical modelling 1986, 7, 1393–1512. [Google Scholar] [CrossRef]
  17. Nordon, G.; Koren, G.; Shalev, V.; Kimelfeld, B.; Shalit, U.; Radinsky, K. Building causal graphs from medical literature and electronic medical records. Proceedings of the AAAI Conference on Artificial Intelligence, 2019, Vol. 33, pp. 1102–1109.
  18. Linear-Regression Description. https://www.machinelearningplus.com/machine-learning/complete-introduction-linear-regression-r/. Accessed: 2018-07-23.
  19. Nathans, L.L.; Oswald, F.L.; Nimon, K. Interpreting multiple linear regression: A guidebook of variable importance. Practical Assessment, Research, and Evaluation 2012, 17, 9. [Google Scholar]
  20. Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
  21. Mehrmolaei, S.; Keyvanpourr, M.R. A Brief Survey on Event Prediction Methods in Time Series. In Artificial Intelligence Perspectives and Applications; Springer, 2015; pp. 235–246.
  22. Mehrmolaei, S.; Keyvanpour, M.R. Time series forecasting using improved ARIMA. 2016 Artificial Intelligence and Robotics (IRANOPEN), 2016, pp. 92–97. [CrossRef]
  23. Patterson, J.; Gibson, A. Deep Learning: A Practitioner’s Approach; O’Reilly Media, 2017.
  24. Aggarwal, C. Neural Networks and Deep Learning: A Textbook; Springer International Publishing, 2018.
  25. Sinha, A.; Bagga, A. Pediatric Nephrology: Update for Clinicians, 2020.
  26. Abbott, M.B.; Vlasses, C.H. Nelson textbook of pediatrics. Jama 2011, 306, 2387–2388. [Google Scholar] [CrossRef]
  27. Pacheco, L.D.; Saad, A.F. Ventilator management in critical illness. Critical care obstetrics 2024, 233–266. [Google Scholar]
  28. Tài, P.; Laurent, J.; Arthur, S. Mechanical ventilation: state of the art. Mayo foundation for medical education and research. Mayo Clin Proc, 2017.
  29. Wu, X.; Peng, S.; Li, J.; Zhang, J.; Sun, Q.; Li, W.; Qian, Q.; Liu, Y.; Guo, Y. Causal inference in the medical domain: a survey. Applied Intelligence 2024, 1–24. [Google Scholar] [CrossRef]
  30. Keller, B.; Branson, Z. Defining, identifying, and estimating effects with the rubin causal model: A review for education research 2023.
  31. Imbens, G.W.; Rubin, D.B. Rubin causal model. In Microeconometrics; Springer, 2010; pp. 229–241.
  32. Imbens, G.W.; Rubin, D.B. Causal inference in statistics, social, and biomedical sciences; Cambridge university press, 2015.
  33. Lederer, D.J.; Bell, S.C.; Branson, R.D.; Chalmers, J.D.; Marshall, R.; Maslove, D.M.; Ost, D.E.; Punjabi, N.M.; Schatz, M.; Smyth, A.R.; others. Control of confounding and reporting of results in causal inference studies. Guidance for authors from editors of respiratory, sleep, and critical care journals. Annals of the American Thoracic Society 2019, 16, 22–28. [Google Scholar] [CrossRef] [PubMed]
  34. Raghu, V.K.; Poon, A.; Benos, P.V. Evaluation of causal structure learning methods on mixed data types. Proceedings of 2018 ACM SIGKDD Workshop on Causal Discovery. PMLR, 2018, pp. 48–65.
  35. Adegunsoye, A.; Oldham, J.M.; Bellam, S.K.; Montner, S.; Churpek, M.M.; Noth, I.; Vij, R.; Strek, M.E.; Chung, J.H. Computed tomography honeycombing identifies a progressive fibrotic phenotype with increased mortality across diverse interstitial lung diseases. Annals of the American Thoracic Society 2019, 16, 580–588. [Google Scholar] [CrossRef] [PubMed]
  36. Zhu, T.; Luo, L.; Zhang, X.; Shi, Y.; Shen, W. Time-series approaches for forecasting the number of hospital daily discharged inpatients. IEEE journal of biomedical and health informatics 2015, 21, 515–526. [Google Scholar] [CrossRef] [PubMed]
  37. Liu, J. Navigating the Financial Landscape: The Power and Limitations of the ARIMA Model. Highlights in Science, Engineering and Technology 2024, 88, 747–752. [Google Scholar] [CrossRef]
  38. Jones, S.S.; Thomas, A.; Evans, R.S.; Welch, S.J.; Haug, P.J.; Snow, G.L. Forecasting daily patient volumes in the emergency department. Academic Emergency Medicine 2008, 15, 159–170. [Google Scholar] [CrossRef] [PubMed]
  39. Ridwan, M.; Sadik, K.; Afendi, F.M. Comparison of ARIMA and GRU Models for High-Frequency Time Series Forecasting. Scientific Journal of Informatics 2023, 10, 389–400. [Google Scholar]
  40. Singh, D.; Kumar, V.; Qiu, R.G. Patients’ disease risk predictive modeling using MIMIC data. Procedia Computer Science 2020, 168, 112–117. [Google Scholar] [CrossRef]
Preprints 111714 g001
Figure 1. Causal Graph after expert evaluations were utilized to include domain knowledge. Here Dose is the treatment variable which include dobutamine, Norepinephrine, milrinone. Amiodaron is a medication that prevents and treats an irregular heartbeat .
Figure 1. Causal Graph after expert evaluations were utilized to include domain knowledge. Here Dose is the treatment variable which include dobutamine, Norepinephrine, milrinone. Amiodaron is a medication that prevents and treats an irregular heartbeat .
Preprints 111714 g001
Preprints 111714 g002
Figure 2. Forecast next hour patient’s condition using ARIMA model.
Figure 2. Forecast next hour patient’s condition using ARIMA model.
Preprints 111714 g002
Preprints 111714 g003
Figure 3. Forecast next hour patient’s condition using Linear Regression model.
Figure 3. Forecast next hour patient’s condition using Linear Regression model.
Preprints 111714 g003
Table 1. Expert knowledge in the casual relation.
Table 1. Expert knowledge in the casual relation.
N o d e f r o m N o d e t o Evidence
Weight BP Domain Expert [25]
BP HR Domain Expert [25]
CVP BP Domain Expert [26]
BP Urine output Domain Expert [25]
Urine output Dose Domain Expert [25]
Age HR Domain Expert
Age BP Domain Expert [25]
BP PCO2 Domain Expert
BP HCO3 Domain Expert
Na HR Domain Expert
Cl HR Domain Expert
PEEP FIO2 Domain Expert [27]
Spo2 FIO2 Domain Expert
FiO2 PaO2/FiO2 Domain Expert [28]
HR Amiodaron Domain Expert
K BP Domain Expert
K HR Domain Expert
PH PaO2 Domain Expert
pH TV Domain Expert
PH HR Domain Expert
PH BP Domain Expert
PaO2 Spo2 Domain Expert [28]
1 Here, BP-blood pressure, CVP-Central venous pressure, HR-heart rate, PCO2-partial pressure of carbon dioxide, HCO3-Bicarbonate, SpO2-Oxygen saturation, Na-sodium, Cl-chloride, k-potassium, PEEP-Positive end-expiratory pressure, FIO2- fraction of inspired oxygen, PaO2-Partial pressure of oxygen, TV-Tidal volume, PaO2/FiO2-the ratio of arterial oxygen partial pressure to fractional inspired oxygen.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated