Prerpints.org logo
Preprint
Article

Research on Acid Aging and Damage Pattern Recognition of GFRP Oil-Gas Gathering Pipeline Based on Acoustic Emission

Altmetrics

Downloads

101

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

11 July 2024

Posted:

12 July 2024

You are already at the latest version

Alerts
Abstract
Pipelines extend thousands of kilometers to transport and distribute oil and gas. Given the challenges often faced with corrosion, fatigue, and other issues on steel pipes, the demand for glass fiber reinforced plastics (GFRP) pipes is increasing in the oil and gas gathering and transmission systems. However, the medium transported through these pipelines contains multiple acid gases such as CO2 and H2S, as well as ions including Cl-、Ca2+、Mg2+、SO42-、CO32- and HCO3-. These substances can cause a series of problems, such as aging, debonding, delamination, and fracture. In this study, a series of aging damage experiments were conducted on V-shaped GFRP pipes with depths of 2mm and 5mm. The aging and failure of GFRP were studied under the combined effects of external force and acidic solution using acoustic emission (AE) techniques. It was found that the acidic aging solution promoted matrix damage, fiber/matrix desorption, and delamination damage in GFRP pipes over a short period. However, the overall aging effect was relatively weak. Based on the experimental data, the SSA-LSSVM algorithm was proposed and applied to the damage pattern recognition of GFRP. An average recognition rate of up to 90% was achieved, indicating that this method is highly suitable for analyzing AE signals related to GFRP damage.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

With the persistent challenges of corrosion, fatigue, and other issues on steel pipes, the demand for glass fiber reinforced plastics (GFRP) pipes has increased in the oil and gas gathering and transmission systems [1,2,3]. However, under the conditions of pressure loading and aging of the transmission medium, GFRP pipelines also experience damage and failure issues, such as delamination and matrix cracking [4,5,6], which can easily lead to pipeline safety accidents.
Numerous scholars have studied the mechanical properties of GFRP pipes during long-term aging [7,8,9]. Solis et al. [10] designed a stress corrosion cracking (SCC) four-point bend self-loaded fixture to study the performance of aged glass-reinforced polymer composite materials and found that the residual bending strength and rigidity of the materials had been reduced. However, there is limited research on the damage to GFRP materials under external load and aging conditions simultaneously. André et al. [11] used acoustic emission technology to reveal different corrosion modes of glass fibers in HCl solution, demonstrating the high efficiency of AE technology for active corrosion detection of glass fibers.
In recent years, clustering analysis methods have been increasingly used in the classification of acoustic emission (AE) data. Numerous international experts and scholars have conducted extensive studies on the damage mechanisms and failure modes of GFRP composite materials using AE technology [12,13,14]. They have determined that parameters such as amplitude, ringing count, energy, and duration effectively reflect material damage. The K-means clustering algorithm is commonly applied to classify AE signals. For instance, Seif [15] extracted frequency characteristics of three-point bending damage signals from unidirectional glass fiber reinforced polymer composite samples using the Hilbert-Huang Transform (HHT). He classified matrix cracking, fiber/matrix debonding, fiber fracture, and delamination signals based on the K-means clustering algorithm, demonstrating the robustness of AE data classification using HHT. Pashmforoush et al. [16] combined the K-means algorithm with a genetic algorithm to cluster AE signals of I-type delamination damage in sandwich composite materials. They verified the effectiveness of this clustering method using scanning electron microscopy and identified four frequency bands (30-80 kHz, 100-150 kHz, 160-250 kHz, and 250-500 kHz) corresponding to core material cracking, panel-core material debonding, matrix cracking, and fiber fracture damage. Momon et al. [17] used clustering analysis to derive the damage modes of C/SiC composites at high temperatures. Monti et al. [18] investigated the mechanical properties of composites made of glass fiber reinforced thermoplastic matrices under uniaxial tensile loading using AE techniques. They post-processed AE signals using a K-means clustering recognition algorithm to clarify the correlation between AE event categories and observed damage mechanisms.
At present, AE technology is widely used in the petrochemical industry, aerospace, transportation, construction, power, and other fields. It involves the detection of metal materials, non-metallic materials, and composite materials such as GFRP [19,20,21,22,23,24,25]. Research on GFRP primarily focuses on aging experiments based on morphological analysis and stress damage experiments using acoustic emission. However, there are relatively few studies investigating the damage and aging processes of glass fiber materials under the coupling of aging and stress using AE technology.
In this study, GFRP pipes were used as experimental materials, and a four-point bending experimental device was designed. AE technology was employed to detect the real-time damage of GFRP under aging solution and external load. The K-means clustering algorithm was utilized to accurately classify the damage and aging signals of GFRP materials. This allowed for the analysis and study of the characteristics of AE signals and the types of material damage. Additionally, the SSA-LSSVM algorithm was applied to identify the damage modes of GFRP materials.

2. Experimental Procedures

2.1. Experimental Materials and Treatment

In this experiment, GFRP pipes used in the oilfield are selected as the experimental materials, as shown in Figure 1. The GFRP pipe is divided into three main layers: the inner layer, the inner winding layer, and the outer winding layer. The inner winding layer consists of three sub-layers, each with a thickness of 1mm. Specific parameters of the GFRP pipe are detailed in Table 1.
Cut the GFRP pipe into specimens measuring 250 × 40 × 7.5 mm using an NC machine tool. Create V-shaped defects with depths of 2 mm and 5 mm, and an included angle of 60° at the center of the specimens. Figure 2 illustrates the V-shaped defect specimens. Place the treated specimens in the aging device for 10 days. To isolate the aging solution, wrap one end of the specimen (the isolation area) with tin foil and fix it. The specific procedure is as follows: pour an appropriate amount of purified water into the magnetic stirrer, place a beaker containing the aging solution into the water, and vertically immerse the GFRP specimen into the aging solution. Ensure that both the isolation area and the aging area of the specimen are in contact with the aging solution. Conduct the aging pre-treatment for 10 days with the aging solution maintained at a temperature of 70°C and a pH of 5.0. Figure 3 shows the aging device used for the GFRP specimens.

2.2. Experimental Aging Solution

Through investigating the components of field-produced fluids and the water formation in oilfields, it has been observed that the medium is predominantly acidic and contains Cl-, HCO3-, Na+, Ca2+, and Mg2+. Therefore, for this experiment, the aging solution is prepared using NaCl, NaHCO3, CaCl2, MgSO4·7H2O, and CH3COOH to adjust the pH value to 5.0. The specific composition of the prepared aging solution is detailed in Table 2.

2.3. Experimental Device

Based on the Standard Test Method for Flexural Properties of Polymer Matrix Composite Materials, a four-point loading configuration is utilized as depicted in Figure 4. In this configuration, the GFRP specimen is supported at two points and loaded at two points, each equidistant from the adjacent support point. The load span is half the distance between the support points.
During the experiment, the GFRP specimen is positioned such that the middle defect at the bottom is submerged in the aging solution. An AE (acoustic emission) sensor is securely affixed to the upper surface of the specimen and connected to the AE system. The experiment involves measuring and recording the force applied to the GFRP specimen and the resulting deflection at the center of the span until failure occurs on either outer surface.
This setup allows for the study of the damage characteristics and aging mechanism of GFRP under acidic aging conditions and a specific loading configuration using AE technology.

2.4. Experimental Process

This study utilized a four-point bending device to apply stress to pre-damaged specimens with a 2 mm depth V-shaped defect until they reached a significant matrix cracking state. Stress was applied to pre-damaged GFRP specimens with a 5 mm depth V-shaped defect until they exhibited a macroscopic delamination state. A 72-hour acid aging experiment was conducted on the damaged part of the specimens, and the acoustic emission signal characteristics of the specimens’ damage and aging process were collected in real-time using an acoustic emission instrument. The specific specimen design is shown in Table 3.

3. Results and Discussion

3.1. Microscopic Morphology Analysis

The loading stress primarily induces visible damage morphology on the specimen after aging, while the aging solution does not visibly alter the material’s surface morphology over a short period. As depicted in Figure 5, the post-experiment damage morphology of the specimen reveals two perspectives: (1) surface damage morphology and (2) side damage morphology. For A1 specimens, surface observations reveal matrix cracking and fiber fracture damage, with slight delamination damage visible on the side. However, A2 specimens exhibit more severe damage. Clear matrix cracks and fiber fractures are prominently visible at the central V-shaped pre-treated area, accompanied by distinct delamination characteristics along the specimen’s side.

3.2. AE Parameter Analysis

Before the acid aging test, the specimen underwent loading to various degrees of damage, during which acoustic emission (AE) signals were collected. It was observed that the AE hits decreased significantly after approximately 18 hours. Subsequently, the collected AE signals predominantly reflected the aging effects of the acid solution. Therefore, the entire procedure was divided into two stages: the stress damage stage and the aging stage. Signals collected from stage 2 to stage 5 were categorized as aging AE signals.
Figure 6 illustrates the AE hits of the GFRP specimens at different aging stages over time. It is evident that there is no significant variation in the number of AE hits for GFRP specimens across the four stages. The AE hits consistently remain at a relatively low level, consistently below 20. This observation reaffirms the accelerating effect of the acidic solution during the aging stage.
In Figure 7, the time-amplitude relationship of the AE signal reveals the progression of specimen damage during the initial loading stage, where high signal amplitudes peak at 99 dB. During the first stage, AE signals indicating GFRP damage gradually diminish as mechanical stress-induced damage subsides within an hour. Concurrently, the aging effect of the acid solution on the GFRP specimen begins to manifest, characterized by AE signal amplitudes ranging mainly from 40 to 80 dB. Subsequently, AE signals during the aging stages (from stage 2 to stage 5) stabilize, with amplitudes consistently falling within the range of 40 to 70 dB. This pattern suggests a relatively stable state of aging-induced AE signals in the materials as the acid solution continues to exert its effects over time.
As shown in Figure 8, the time-peak frequency relationship of the signal reveals that the peak frequency of the A1 specimen signal is distributed within the range of 70-180 kHz, primarily concentrated between 70-120 kHz and 140-180 kHz, with most signals falling within the 70-120 kHz range. Additionally, the peak frequency of the damage signal during the stress loading period is also distributed in the 200-380 kHz range. Based on the analysis of extensive data accumulated previously, this part of the signal corresponds to the fiber fracture damage of the material.
A2 is the pipe specimen treated with a 5mm deep pre-damage. The bending section under pressure has reduced matrix resin and glass fiber content. Stress primarily induces delamination as the main damage pattern. The amplitude ranges mainly between 40~70 dB. Compared to the A1 specimen, signals above 70 dB are less frequent. From stage 2 to stage 5, signal amplitudes are predominantly distributed between 40~75 dB. Although the aging signal is reduced compared to the A1 specimen, the overall amplitude remains higher. Specific amplitude distribution is depicted in Figure 9.
As shown in Figure10, the time-peak frequency distribution characteristics of the aging signal of the A2 specimen are pronounced. Initially, during Phase 1, the peak frequency ranges predominantly between 75~120 kHz and 140~200 kHz, with a notable concentration in the 140~200 kHz range. Subsequently, from the 2nd stage to the 5th stage, frequencies above 150 kHz prevail, although the number of hits diminishes significantly. This suggests that the acidic solution with pH=5.0 enhances debonding and delamination damage in GFRP pipes to a certain extent, whereas the aging effects on the A1 specimen, characterized by matrix crack damage, are more pronounced.

3.3. Cluster Analysis

From the time-amplitude and time-peak frequency analyses of the specimens mentioned earlier, it is evident that the acidic solution exerts varying effects on the aging of GFRP materials under different damage conditions. To further verify the damage types of the A1 and A2 specimens after stress loading, the AE signals from the specimens within the first 10 minutes of loading were intercepted and analyzed using K-means clustering analysis.
Through correlation analysis of the data, the parameters of amplitude, peak frequency, energy, count, and duration of the GFRP pipe specimens were selected. To reduce the complexity of the calculations, principal component analysis (PCA) was employed to reduce the dimensionality of these high-dimensional characteristic parameters. PCA is a powerful algorithm for data dimension reduction, converting a group of correlated data into several linearly independent variables through orthogonal transformation. These linearly independent variables are known as principal components [26]. Using PCA, two principal components, F1 and F2, were obtained for both specimens. The sampling suitability of the KMO (Kaiser-Meyer-Olkin) measure was greater than 0.6, with values of 0.742, 0.796, 0.716, and 0.774, respectively. The cumulative contribution rate was above 80%, indicating that the data was suitable for principal component analysis [27].
The damage signals of each specimen can be categorized into four types using the principal components that yield the best effect. These types are named type 1, type 2, type 3, and type 4. Based on the characteristics of these damage signals, the damage evolution process of specimens under stress loading, and microscopic morphology observations, it is found that the four signal types correspond to matrix damage, debonding, delamination, and fiber fracture of GFRP materials. The clustering effect is displayed in two dimensions, and the damage signals are classified on the peak frequency-amplitude scale, as shown in Figure 11. The number of AE hits on the 2 mm deep V-shaped pre-damaged specimen (A1 specimen) within 10 minutes is significantly greater than that on the 5 mm deep V-shaped pre-damaged specimen (A2 specimen).
As the loading stress gradually increases, the specimen initially exhibits bending deformation. Subsequently, the stress concentration at the V-shaped defect leads to matrix damage and partial fiber fracture. Delamination damage then begins to occur at the layer where the tip of the V-shaped defect is located, extending to one or both sides. Based on Table 4, it is evident that the damage in the A1 specimen is primarily characterized by matrix cracking and debonding. In contrast, in the A2 specimen, matrix damage is no longer the predominant type, and the proportion of delamination damage has significantly increased.
Similarly, cluster analysis was conducted on the aging signal data of two GFRP materials from Phase 2 to Phase 5 to study the damage types and aging signal characteristics promoted by the acidic aging solution. K-means clustering analysis was performed on the aging signals of the A1 and A2 specimens by selecting amplitude, peak frequency, duration, and center frequency as parameters. It was found that the clustering effect was optimal when the signals were divided into three types. The clustering results are shown in Figure 12.
The amplitude of the aging signal is concentrated between 40 and 80 dB, while the peak frequency values are concentrated between 70 and 180 kHz. Specifically, Class 1 signals are low-frequency, low-amplitude signals with peak frequencies between 70 and 110 kHz, corresponding to matrix crack damage. Class 2 signals are intermediate-frequency, low-amplitude signals with peak frequencies between 140 and 180 kHz, corresponding to fiber/matrix debonding damage. Class 3 signals are medium-to-low-frequency, high-amplitude signals with peak frequencies between 70 and 170 kHz, corresponding to delamination damage.
The cluster analysis reveals distinct damage characteristics between the A1 and A2 specimens during the stress loading stage. For the A1 specimen, the damage is primarily characterized by matrix cracking and delamination. At this damage level, the aging signals are mainly due to matrix aging, with additional contributions from debonding and delamination. Conversely, for the A2 specimen, the damage is predominantly due to debonding and delamination. At this more severe damage level, the aging signals are primarily due to delamination, with debonding as a secondary contributor, and matrix aging being the least significant.
As shown in Table 5, the number of fiber/matrix debonding signals is greater for the pre-damaged specimens with a 5 mm deep V-shaped defect compared to those with a 2 mm deep V-shaped defect. This can be attributed to two main factors. First, the larger pretreatment depth of the 5 mm groove increases the contact surface area between the aging solution and the interior of the material. Second, due to the severe delamination damage, the aging solution penetrates and diffuses into the material through multiple channels, such as the delaminated areas, which reduces the mechanical properties and accelerates the aging process.

3.4. Least Squares Support Vector Machine Algorithm for Classified Prediction

The Least Squares Support Vector Machine (LSSVM) algorithm, proposed by Su, is an enhancement of the traditional support vector machine (SVM) algorithm. While the SVM algorithm yields good prediction results in classification modeling, it suffers from complex models, large computational requirements, and low efficiency in solving convex quadratic programming problems [28]. LSSVM retains the powerful learning and generalization capabilities of the SVM algorithm but improves efficiency by converting the convex quadratic programming problem into a linear solution problem. This is achieved by defining the Lagrange function and employing a least squares algorithm, thereby reducing model complexity and calculation time [29].
Assuming the data set S = x , i y i | i = 1 , 2 , 3 , … , n , where y i represents the output data, the calculation process for high-dimensional mapping of feature data is:
y i = w T ϕ ( x i ) + b + e i , i = 1 , 2 , 3 , … n
where w is a normal vector, ϕ ( ⋅ ) is the nonlinear mapping function, b is the amount of displacement and e i is relaxation variables.
Equation (1) is the constraint condition under which LSSVM controls all samples and errors. The optimization problem is:
min w , b , e J ( w , e ) = 1 2 w T w + 1 2 γ ′ ∑ i = 1 n e i 2
where γ ′ is a regularization parameter, J ( w , e ) is an optimization function.
Therefore, for the above optimization problem, the Lagrange function set by LSSVM is:
L ( ω , b , e , α ) = J ( w , e ) − ∑ i = 1 n α i w T ϕ ( x i ) + b + e i − y i = 1 2 w T w + 1 2 γ ′ ∑ i = 1 n e i 2 − ∑ i = 1 n α i w T ϕ ( x i ) + b + e i − y i
where α i is Lagrange multiplier. Respectively solve partial derivative for ω , b , e , α and eliminate ω , e to obtain a linear equation set:
0 D T D Q i , j + 1 γ ′ I b a = 0 y
where y = y 1 , y 2 , y 3 … y n , α = α 1 , α 2 , α 3 , … α n , T , D = 1 , 1 , 1 , … 1 n T According to the Mercer condition,
Q i , j = y i y j φ ( x i ) T φ ( x j ) = y i y j K ( x i , x j )
It can be obtained through formulas (3) and (5),
y ( x ) = ∑ i = 1 n α i K ( x i , x j ) + b
Based on the above analysis, the LSSVM model calculation is straightforward. In this paper, the Gaussian kernel function is selected for model calculation.
The LSSVM model requires the determination of the kernel function and the normalized parameter C. Both the normalized parameter and the penalty factor serve similar roles, balancing the error size of training results against the complexity of the model. The kernel function choice influences the number of support vectors; an excessively large value can lead to model simplicity, resulting in under-fitting and reduced prediction accuracy. Before modeling, it is crucial to select appropriate kernel functions and normalized parameter C values, as these parameters significantly impact the accuracy of model training. Intelligent algorithms are increasingly employed to find optimal parameters. In this study, a swarm intelligence optimization technique is proposed which called sparrow search algorithm (SSA). The SSA is utilized to identify optimal penalty factors and kernel function parameters. Introduced by Xue in 2020 [30], the SSA is a group-based intelligent optimization algorithm known for its rapid convergence and robust local search capabilities. SSA has found applications in various domains including logistics site selection, rolling bearing fault diagnosis, and agricultural network detection.
In the sparrow search algorithm, the population can be represented by X, which represents n sparrows in the d-dimension space.
X = x 1 1 x 1 2 … x 1 d x 2 1 x 2 2 … x 2 d … … … … x n 1 x n 2 … x n d
Population fitness can be expressed as F, which is the individual fitness value of sparrows:
F = f ( [ x 1 1 x 1 2 … x 1 d ] ) f ( [ x 2 1 x 2 2 … x 2 d ] ) ⋮ f ( [ x n 1 x n 2 … x n d ] )
The finder usually finds the food with the highest fitness value, accounting for about 20% of the population. Its location iterative formula is shown in (9). When R 2 ＜ S T , it means that no danger is detected within the population, and individuals within the population can update their positions; When R 2 ≥ S T , it indicates the presence of danger such as predators within the population, prompting the birds to migrate for self-preservation.
X i , j t + 1 = X i , j t ⋅ exp 1 i α ⋅ T R 2 < S T X i , j t + Q ⋅ L R 2 ≥ S T
where t is iteration, X i , j t is Position of the ith individual of the jth dimension at iteration t, α is a constant between 0 , 1 , R 2 is Pre-Alarm value between 0 , 1 , T is maximum iteration times, S T is safety value between 0.5 , 1 , L is 1×d matrix with all elements equal to 1.
The sparrow assigned the role of follower within the population can continually monitor the location of the finder. When the finder discovers better food, the follower promptly seizes the opportunity. The iterative formula governing the follower’s position is as follows, highlighting that if the fitness of the ith follower is low, it must relocate to another location:
X i , j t + 1 = Q ⋅ exp X w o r s t − X i , j t i 2 ， i > n 2 X p t + 1 + | X i , j t − X p t + 1 | A + ⋅ L
where X w o r s t is the worst-case global location, X p t + 1 is the best position for the finder at iteration t+1, A is a 1 × d matrix with random elements of 1 or – 1, A+=AT(AAT)-1.
The sparrow designated as the scout within the population, responsible for detecting danger and issuing warnings, operates according to the following location iterative formula:
X i , j t + 1 = X b e s t t + β ⋅ | X i , j t − X b e s t t | , f i > f g X i , j t + K ⋅ | X i , j t − X w o r s t t | ( f i − f w ) + ε , f i = f g
where X b e s t is the global optimum location, β , K is the step control parameter, ε is a constant to guarantee that the molecule is not 0, f i is the fitness value of the current individual, and f g , f w is the global optimum and worst fitness value.
The detailed process of optimizing the LSSVM algorithm using the SSA includes the following steps: (1) Establishing tagged stress damage-oriented data sample sets and aging-oriented data sample sets. (2) Normalizing the sample data and selecting a training set and a test set. (3) Determining penalty factors and kernel function parameters of the SSA optimization algorithm using the training samples. (4) Evaluating the accuracy of the LSSVM algorithm modeling and model recognition.
To summarize, this paper adopts the SSA-LSSVM algorithm for modeling and predicting data classification. The specific algorithm flow is illustrated in Figure 13.
Taking the A1 specimen as an example, the AE signal is segmented into two parts: stress damage and aging. A prediction model is established using the LSSVM. For the stress damage part: Training Set: 100 signals of matrix cracking, debonding, and delamination after clustering, along with 50 signals of fiber fracture. Test Set: 30 signals of matrix cracking, debonding, and delamination, along with 20 signals of fiber fracture after clustering. For the aging failure part: Training Set: 60 matrix crack signals after clustering, 20 debonding signals, and 20 delamination signals. Test Set: 30 matrix crack signals, 10 debonding signals, and 10 delamination signals after clustering. The composition and quantity of acoustic emission data samples used for model training and testing are detailed in Table 6.
Furthermore, characteristic parameters such as amplitude, peak frequency, energy, count, duration, and center frequency are selected as input features for the LSSVM. SVM characteristic parameters are initialized, and both damage signal samples and aging signal samples are trained and classified using these parameters. The prediction results are illustrated in Figure 14.

4. Conclusions

This paper investigates the stress aging behavior of GFRP pipe specimens exhibiting matrix cracking and delamination damage in an acidic solution with pH=5.0. The experiments are divided into two stages: the stress damage stage and the aging stage. Different types of damage in GFRP materials are identified through cluster analysis, and the aging promotion effect of the acidic solution on various specimens is analyzed. The SSA-LSSVM algorithm is utilized for pattern recognition of damage and aging signals. The main conclusions are as follows:
(1) The acid aging solution accelerates matrix damage, fiber/matrix debonding, and delamination of GFRP pipes in the short term, yet its overall aging effect is mild. This underscores that GFRP pipes, as alternatives to steel pipes in oil and gas fields, exhibit robust corrosion resistance and significant advantages.
(2) The matrix aging signal in GFRP manifests as a low-frequency, low-amplitude signal peaking between 70 to 110 kHz. In contrast, the fiber/matrix debonding signal appears as a high-frequency, medium-to-low-amplitude signal with a peak frequency of 140 to 180 kHz. Signals indicative of layered damage show overlapping frequencies ranging mainly from 70 to 170 kHz, characterized by high amplitudes.
(3) This paper employs the SSA-LSSVM algorithm to develop a predictive model with excellent identification capabilities. The model achieves high identification accuracies of 96% for the stress damage stage and 94% for the aging stage.

Author Contributions

Conceptualization, Haisheng Bi and Haoran Cheng; methodology, Yuhong Zhang; software, Chen Zhang; validation, Chunxun Ma., Jiaxu Miao and Yuxiang Li; formal analysis, Guang Wang; investigation, Haisheng Bi; resources, Haoran Cheng; data curation, Yuhong Zhang; writing—original draft preparation, Yuhong Zhang; writing—review and editing, Haisheng Bi; visualization, Chunxun Ma; supervision, Jiaxu Miao; project administration, Haoran Cheng; funding acquisition, Haisheng Bi, Haoran Cheng.

Funding

This research was funded by the National Key R&D Program of China (2021YFB3401400), the National Natural Science Foundation of China (52104028), the Opening fund of Shandong Key Laboratory of Oil & Gas Storage and Transportation Safety, and the Fundamental Research Funds for Central Universities (19CX05007A), the Young Taishan Scholars Program of Shandong Province, China (No. tsqn202312208).

Acknowledgments

This study is supported by the National Key R&D Program of China (2021YFB3401400), the National Natural Science Foundation of China (52104028), the Opening fund of Shandong Key Laboratory of Oil & Gas Storage and Transportation Safety, and the Fundamental Research Funds for Central Universities (19CX05007A), the Young Taishan Scholars Program of Shandong Province, China (No. tsqn202312208).

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Salibi, Z. Performance of reinforced thermosetting resin pipe systems in desalination applications: a long-term solution to corrosion — the Arabian Gulf example. Desalination 2001, 138, 379–384. [Google Scholar] [CrossRef]
  2. M. H N, Guihua H. Vinylester-glass fiber composite for water pipe: Processing and effect of fiber direction. Egyptian Journal of Petroleum 2023, 32, 24–30. [Google Scholar] [CrossRef]
  3. D. T L, Hassan K, Wayne H. Design of reinforced thermoplastic pipelines for hydrogen transport. Procedia Structural Integrity 2023, 45, 109–116. [Google Scholar] [CrossRef]
  4. Rodríguez, E.S.; Alvarez, V.A.; Montemartini, P.E. Failure analysis of a GFRP pipe for oil transport. Engineering Failure Analysis 2013, 28, 16–24. [Google Scholar] [CrossRef]
  5. Dandan, L.; Biao, H.; Jie, L.; et al. Failure analysis of glass fiber reinforced composite pipe for high pressure sewage transport. Engineering Failure Analysis 2023, 144. [Google Scholar]
  6. ZHANG Xuemin, LI Houbu, QI Dongtao, et al. Failure analysis of anticorrosion plastic alloy composite pipe used for oilfield gathering and transportation. Engineering Failure Analysis 2013, 32, 35–43. [Google Scholar] [CrossRef]
  7. W. B. Liau, F. P. Tseng. The effect of long-term ultraviolet light irradiation on polymer matrix composites. Polymer Composites, 1998; 440–445.
  8. L Monney, C Dubois, D Perreux, et al. Mechanical behaviour of an epoxy-glass composite under photo-oxidation. Polymer Degradation and Stability 1999, 63, 219–224. [Google Scholar] [CrossRef]
  9. Dionysis, E. Mouzakis, Helen Zoga, Costas Galiotis. Accelerated environmental ageing study of polyester/glass fiber reinforced composites (GFRPCs). Composites Part B 2006, 39, 467–475. [Google Scholar]
  10. Solis-Ramos, E.; Kumosa, M. Synergistic effects in stress corrosion cracking of glass reinforced polymer composites. Polymer Degradation and Stability 2016, 136, 146–157. [Google Scholar] [CrossRef]
  11. André, M.; Siguret, D.; Foulon, A.; et al. Corrosion evaluation of glass fiber reinforced plastic (gfrp) Tanks pressure vessels using acoustic emission technology. Synthèse: Revue des Sciences et de la Technologie 2019, 25, 129. [Google Scholar]
  12. Arumugam, V.; Kumar, C.S.; Santulli, C.; et al. Identification of Failure Modes in Composites from Clustered Acoustic Emission Data Using Pattern Recognition and Wavelet Transformation. Arabian Journal Forence & Engineering 2013, 38, 1087–1102. [Google Scholar]
  13. Wang, X.M.; Zhu, C.M.; Mao, H.L.; et al. Wavelet packet analysis for the propagation of acoustic emission signals across turbine runners. NDT&E International 2009, 42, 42–46. [Google Scholar]
  14. Dijck, G.V.; Hulle, M.V. Genetic algorithm for informative basis function selection from the wavelet packet decomposition with application to corrosion identification using acoustic emission. Chemometrics and Intelligent Laboratory System 2011, 107, 318–332. [Google Scholar] [CrossRef]
  15. Seif, E.H.; Alain, L.D.; Laurent, S.; et al. Acoustic emission pattern recognition approach based on Hilbert-Huang transform for structural health monitoring in polymer-composite materials. Applied Acoustics 2013, 74, 746–757. [Google Scholar]
  16. Pashmforoush, F.; Khamedi, R.; Fotouhi, M.; et al. Damage classification of sandwich composites using acoustic emission technique and k-means genetic algorithm. Journal of Technology & Science, 2014; 481. [Google Scholar]
  17. Momon, S.; Godin, N.; Reynaud, P. Unsupervised and supervised classification of AE data collected during fatigue test on CMC at high temperature. Compositespart A 2012, 43, 254–260. [Google Scholar] [CrossRef]
  18. Monti, A.; Mahi, E.A.; Jendli, Z.; et al. Mechanical behaviour and damage mechanisms analysis of a flax-fibre reinforced composite by acoustic emission. Composites Part A 2016, 90, 100–110. [Google Scholar] [CrossRef]
  19. Rolando, C.S.R.; Takenobu, S.; Shuichi, W. Analyzing the Sound of Materials: Application of Acoustic Emission Technique for Monitoring Material Behavior. Materials Science Forum 2024, 7136111–117. [Google Scholar]
  20. Claudia, B.; Caterina, C.; Giovanni, P.; et al. Laplacian score and K-means data clustering for damage characterization of adhesively bonded CFRP composites by means of acoustic emission technique. Applied Acoustics 2022, 185. [Google Scholar]
  21. Álvaro Carrasco, Franco Méndez, Félix Leaman, et al. Short Review of the Use of Acoustic Emissions for Detection and Monitoring of Cracks. Acoustics Australia 2021, 49, 1–8. [Google Scholar]
  22. Luigi, C.; Edoardo, P. A Review on the Applications of Acoustic Emission Technique in the Study of Stress Corrosion Cracking. Corrosion and Materials Degradation 2020, 2, 1–30. [Google Scholar]
  23. Zhang, Z.; Feng, H.; Zhao, W.; et al. Application of acoustic emission technology in hydraulic pressure test of nuclear power plant. IOP Conference Series: Earth and Environmental Science 2020, 514, 042039. [Google Scholar] [CrossRef]
  24. Zubova, M.E.; Tretyakova, V.T.; Wildemann, E.V. Application the acoustic emission technique to investigation of damage initiation in composites. Procedia Structural Integrity 2019, 18843–848. [Google Scholar] [CrossRef]
  25. Jing, N.J.; Dong, H.L.; Wang, D.H.; et al. Application of Acoustic Emission Technology for Quantitative Characterization of Plasma-Sprayed Coatings Subjected to Bending Fatigue Tests. Journal of Thermal Spray Technology 2018, 27, 1090–1102. [Google Scholar] [CrossRef]
  26. Tayfur, S.; Alver, N.; Abdi, S.; et al. Characterization of concrete matrix/steel fiber de-bonding in an SFRC beam: Principal component analysis and k -mean algorithm for clustering AE data. Engineering Fracture Mechanics 2018, 19473–85. [Google Scholar] [CrossRef]
  27. Shenglan, M.; Shurong, R.; Zhining, C.; et al. Wooden beam damage evaluation under bending loading based on the integration of acoustic emission and principal component analysis. Measurement 2023, 222. [Google Scholar]
  28. Suykens, J.A.K.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Processing Letters 1999, 9, 293–300. [Google Scholar] [CrossRef]
  29. Xi, P.; Zhao, Y.; Wang, P.; et al. Least squares support vector machine for class imbalance learning and their applications to fault detection of aircraft engine. Aerospace Science and Technology 2019, 8456–74. [Google Scholar] [CrossRef]
  30. Jiankai Xue. Research and Application of A Novel Swarm Intelligence Optimization Technique: Sparrow Search Algorithm. Master’s Degree, Donghua University, Shanghai, 2020.
Preprints 111874 g001
Figure 1. Experimental materials.
Figure 1. Experimental materials.
Preprints 111874 g001
Preprints 111874 g002
Figure 2. GFRP specimens.
Figure 2. GFRP specimens.
Preprints 111874 g002
Preprints 111874 g003
Figure 3. The Aging Device of GFRP Specimens.
Figure 3. The Aging Device of GFRP Specimens.
Preprints 111874 g003
Preprints 111874 g004
Figure 4. Loading diagram of experimental device.
Figure 4. Loading diagram of experimental device.
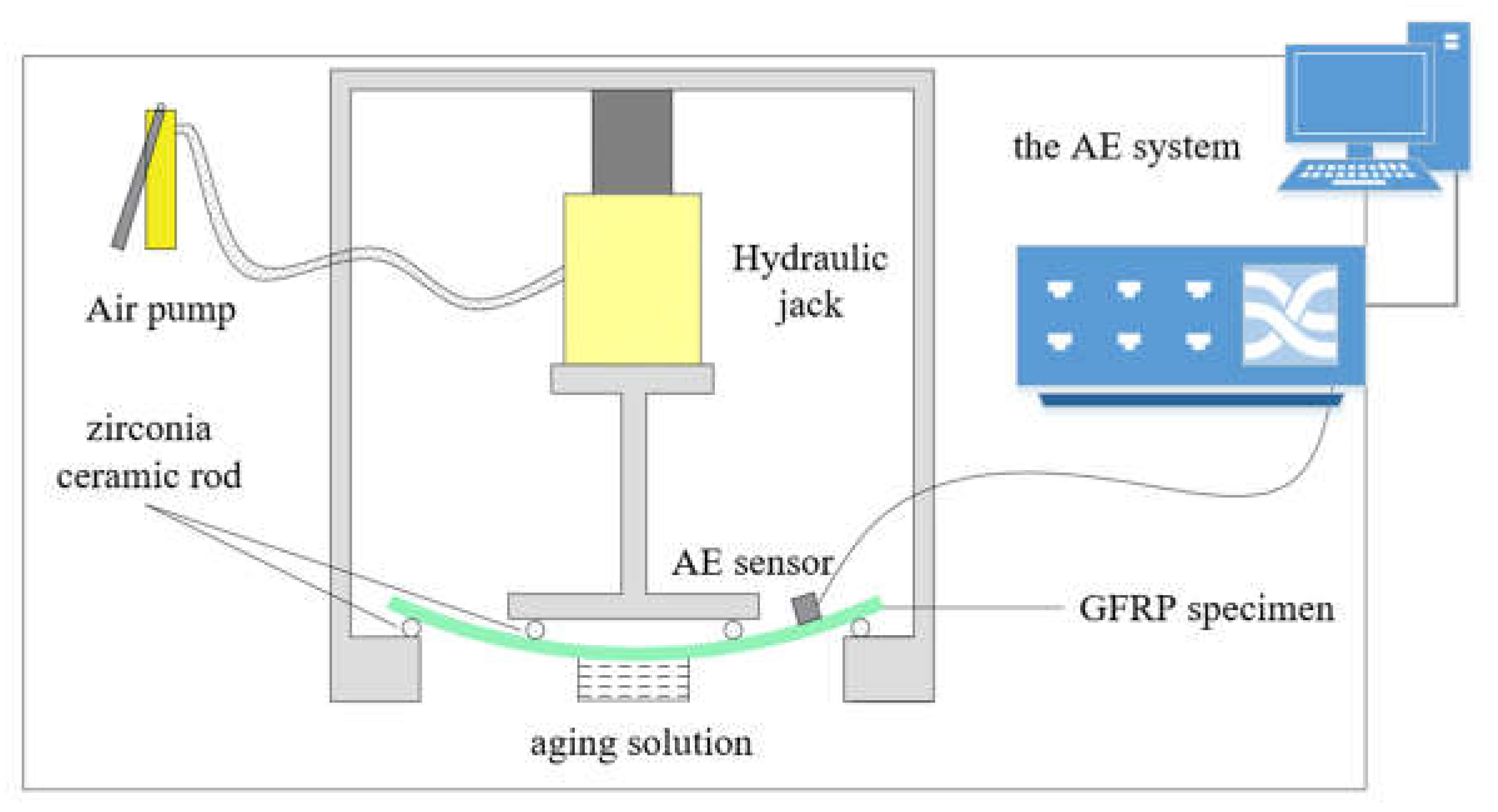
Preprints 111874 g004
Preprints 111874 g005
Figure 5. Microscopic observation of specimen. (a) A1 specimen; (b)A2 specimen.
Figure 5. Microscopic observation of specimen. (a) A1 specimen; (b)A2 specimen.
Preprints 111874 g005
Preprints 111874 g006
Figure 6. Hits distribution of aging signal for GFRP pipe. (a) A1 specimen; (b) A2 specimen.
Figure 6. Hits distribution of aging signal for GFRP pipe. (a) A1 specimen; (b) A2 specimen.
Preprints 111874 g006
Preprints 111874 g007
Figure 7. Time-amplitude distribution of damage AE signal in A1 specimen. (a) Phase 1; (b)Phase 2; (c)Phase 3; (d) Phase 4; (e) Phase 5.
Figure 7. Time-amplitude distribution of damage AE signal in A1 specimen. (a) Phase 1; (b)Phase 2; (c)Phase 3; (d) Phase 4; (e) Phase 5.
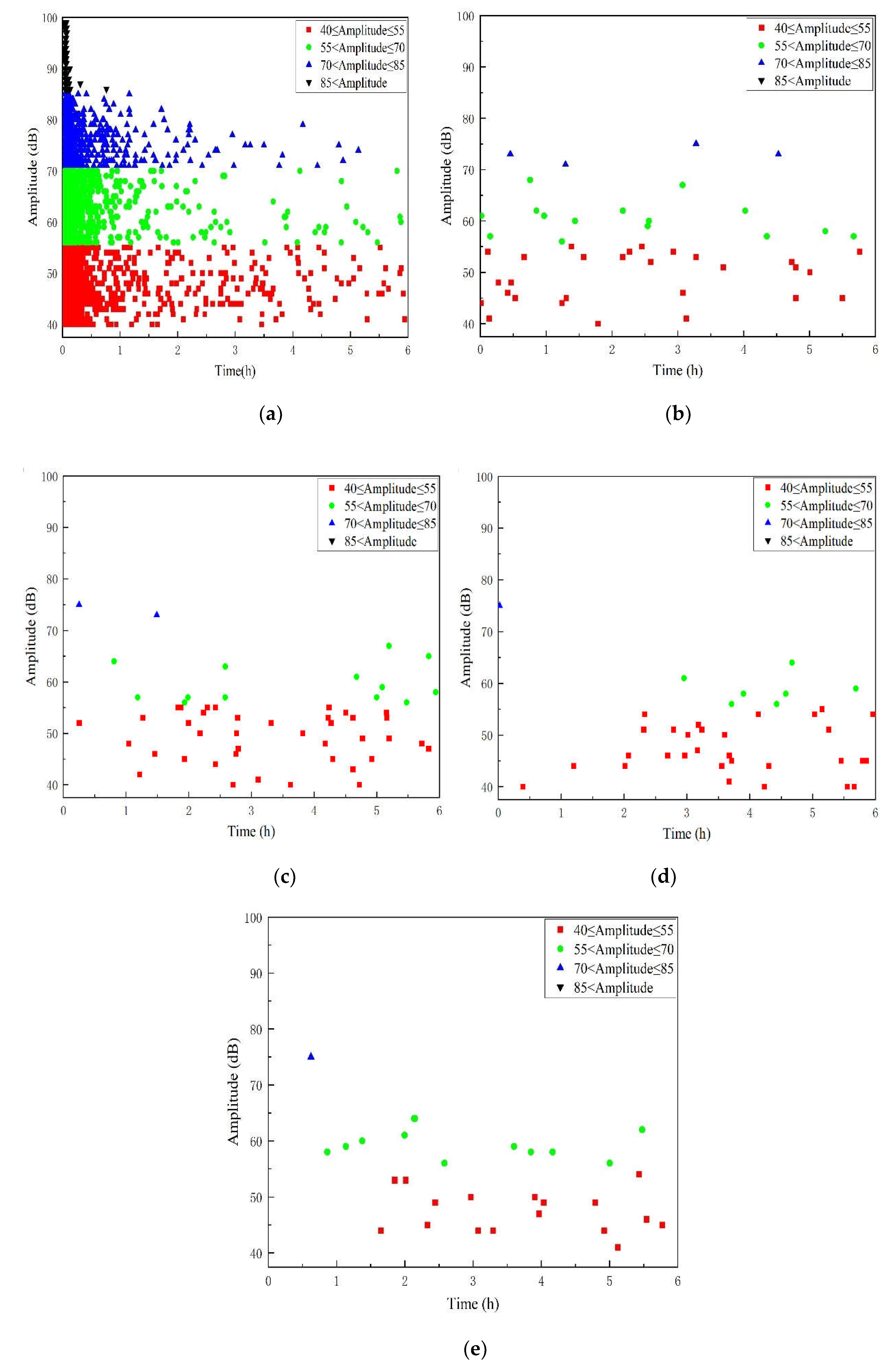
Preprints 111874 g007
Preprints 111874 g008
Figure 8. Time-peak frequency distribution of AE signal in specimen A1. (a) Phase 1; (b)Phase 2; (c)Phase 3; (d) Phase 4; (e) Phase 5.
Figure 8. Time-peak frequency distribution of AE signal in specimen A1. (a) Phase 1; (b)Phase 2; (c)Phase 3; (d) Phase 4; (e) Phase 5.
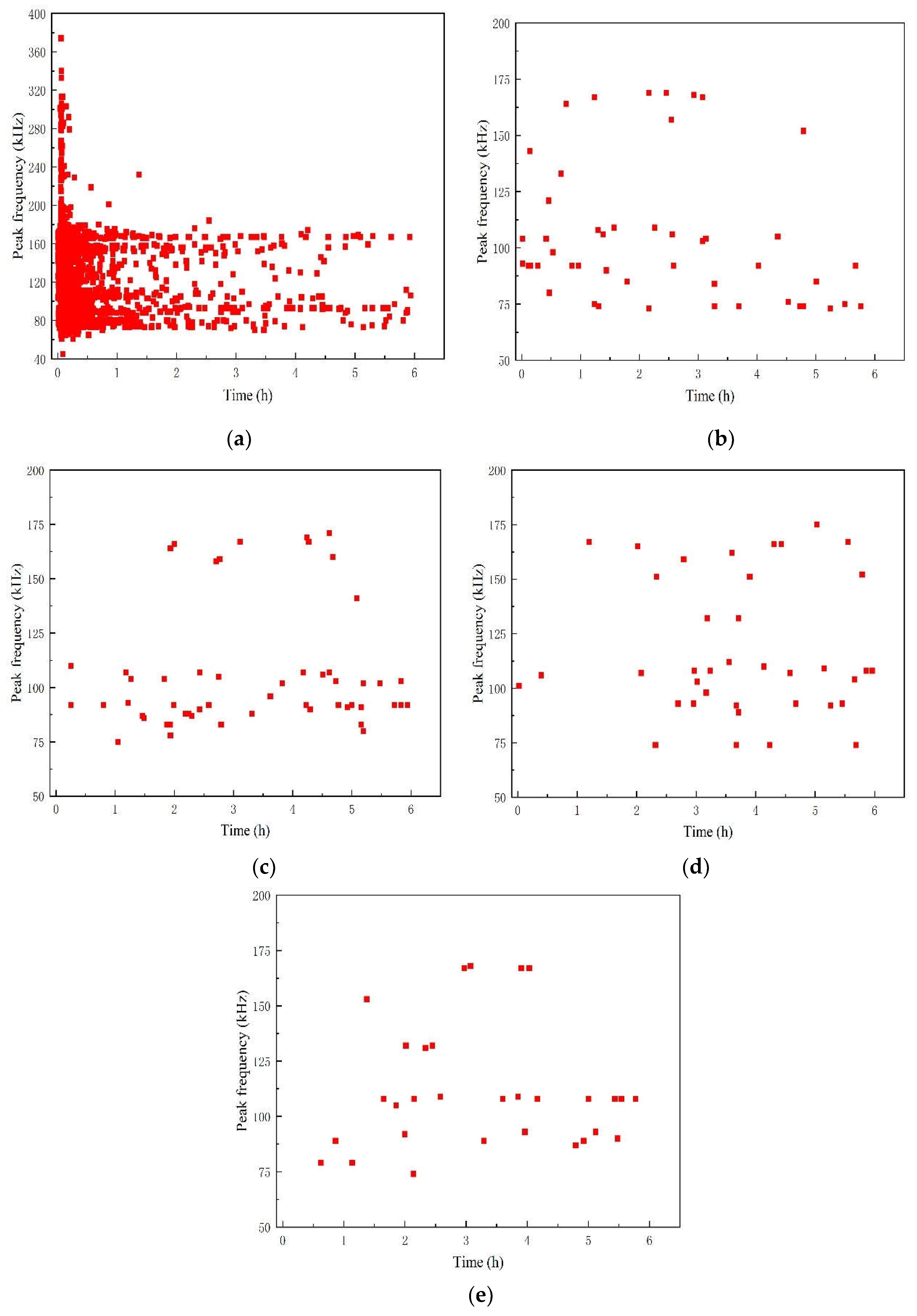
Preprints 111874 g008
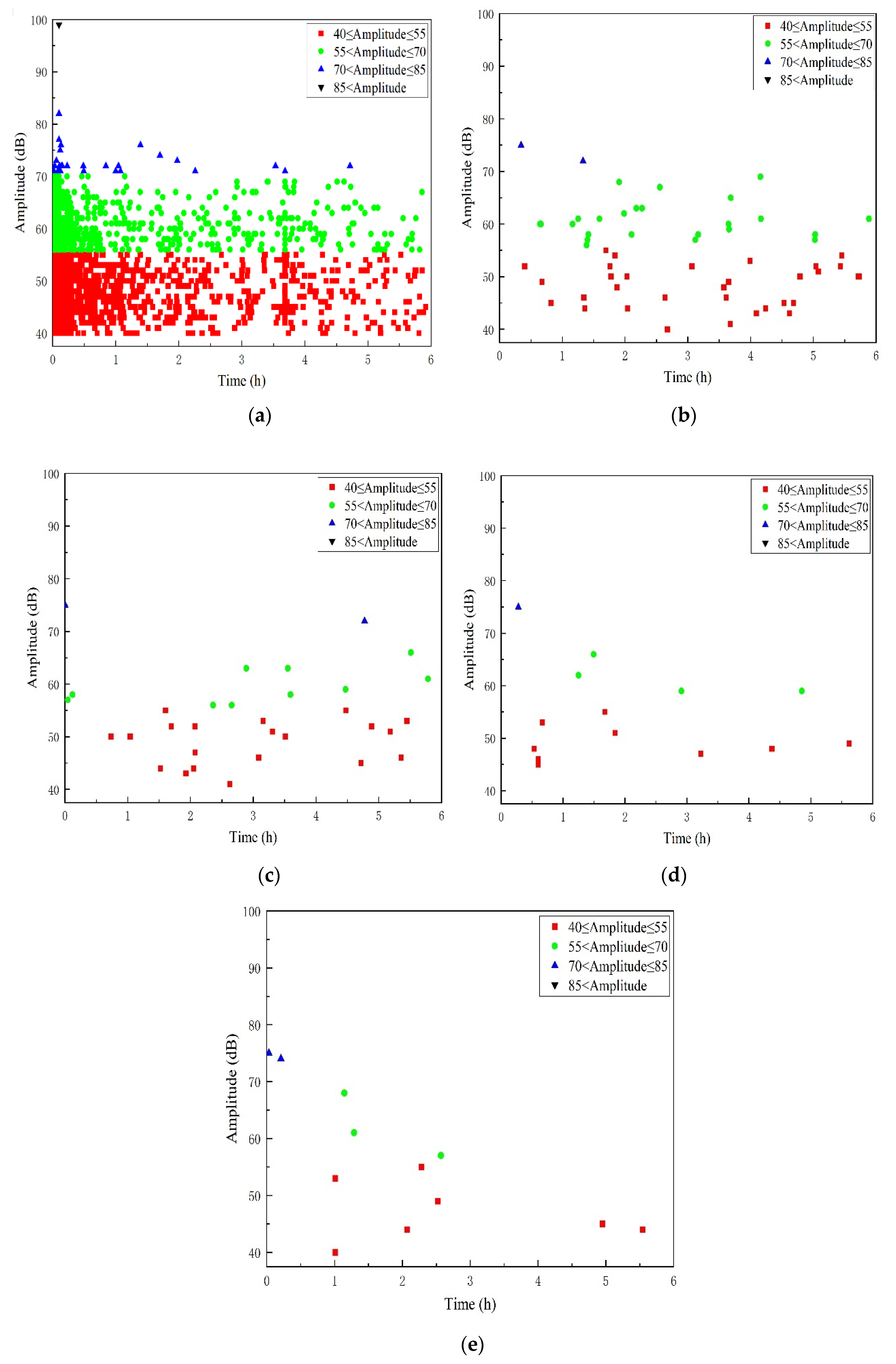
Preprints 111874 g009
Figure 9. Time-amplitude distribution of AE signal in A2 specimen. (a) Phase 1; (b)Phase 2; (c)Phase 3; (d) Phase 4; (e) Phase 5.
Figure 9. Time-amplitude distribution of AE signal in A2 specimen. (a) Phase 1; (b)Phase 2; (c)Phase 3; (d) Phase 4; (e) Phase 5.
Preprints 111874 g009
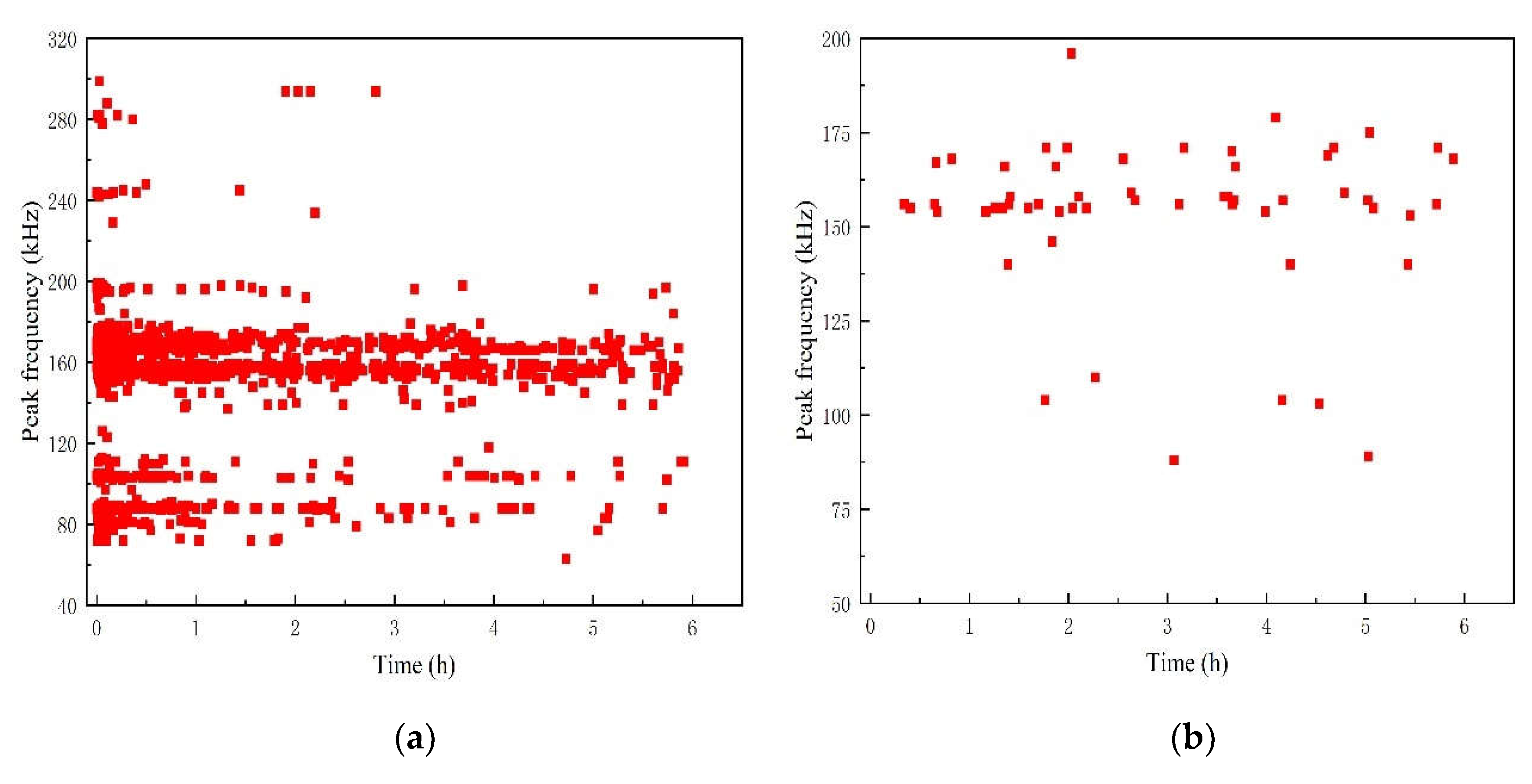
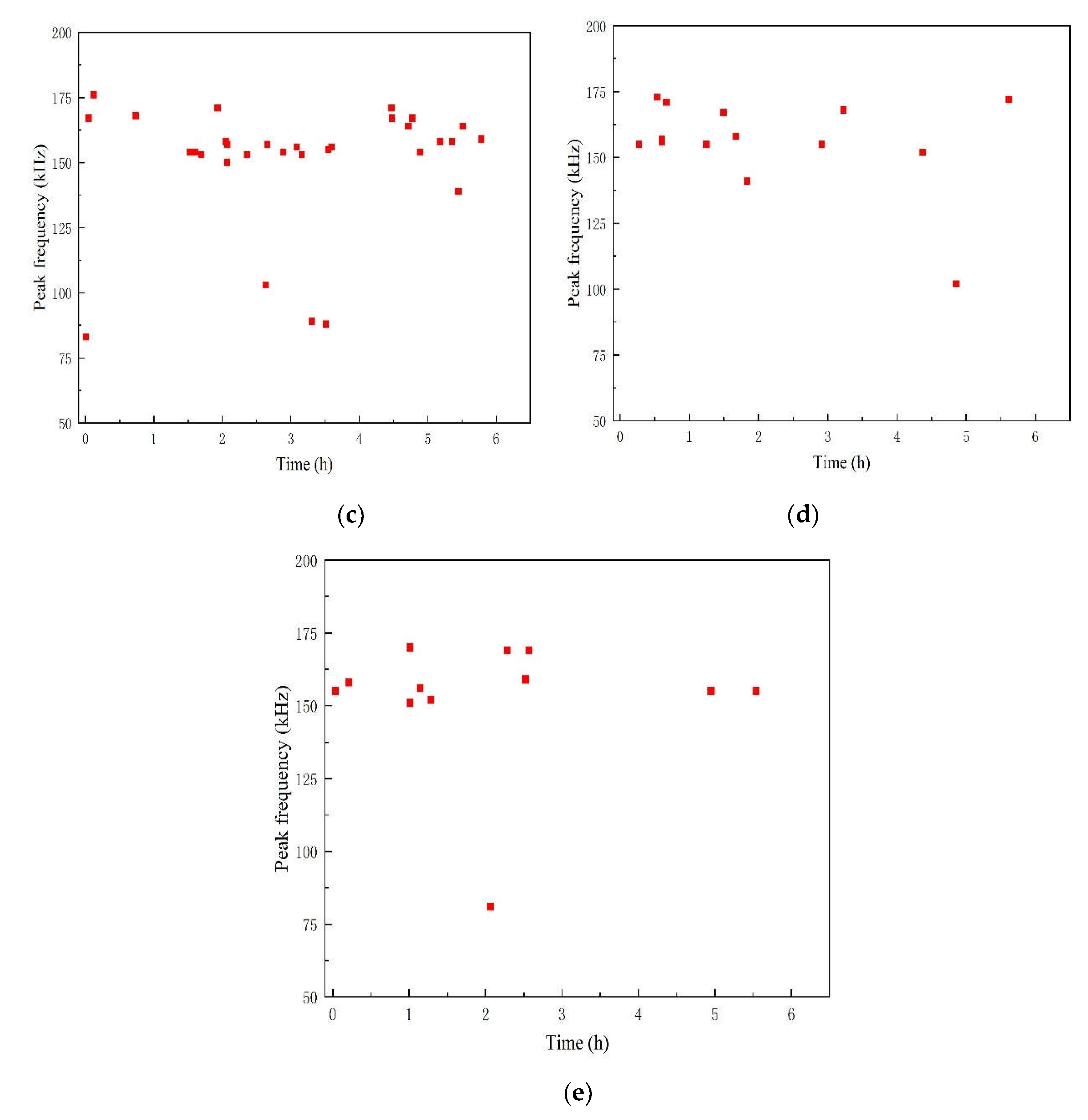
Preprints 111874 g010aPreprints 111874 g010b
Figure 10. Time-peak frequency distribution of AE signal in A2 specimen. (a) Phase 1; (b)Phase 2; (c)Phase 3; (d) Phase 4; (e) Phase 5.
Figure 10. Time-peak frequency distribution of AE signal in A2 specimen. (a) Phase 1; (b)Phase 2; (c)Phase 3; (d) Phase 4; (e) Phase 5.
Preprints 111874 g010aPreprints 111874 g010b
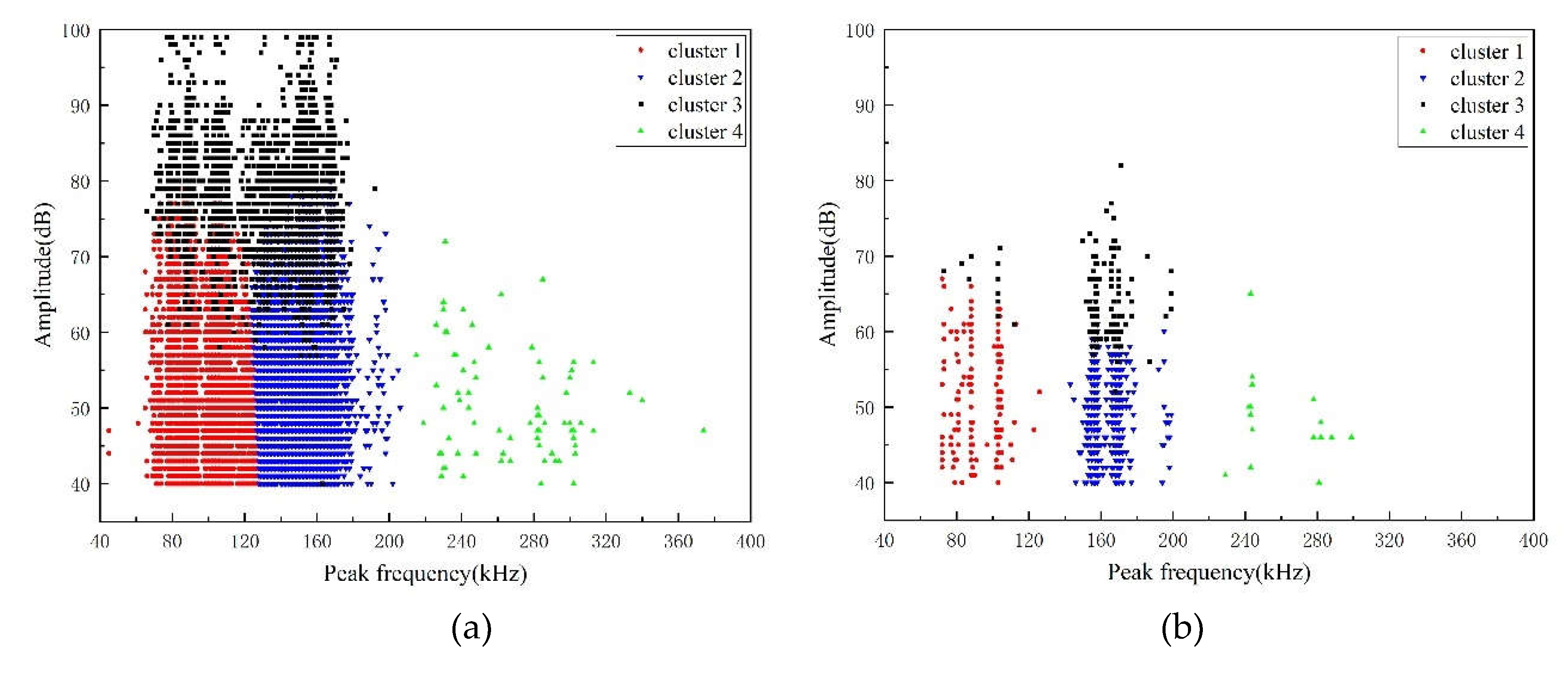
Preprints 111874 g011
Figure 11. Cluster result. (a) A1 specimen; (b) A2 specimen.
Figure 11. Cluster result. (a) A1 specimen; (b) A2 specimen.
Preprints 111874 g011
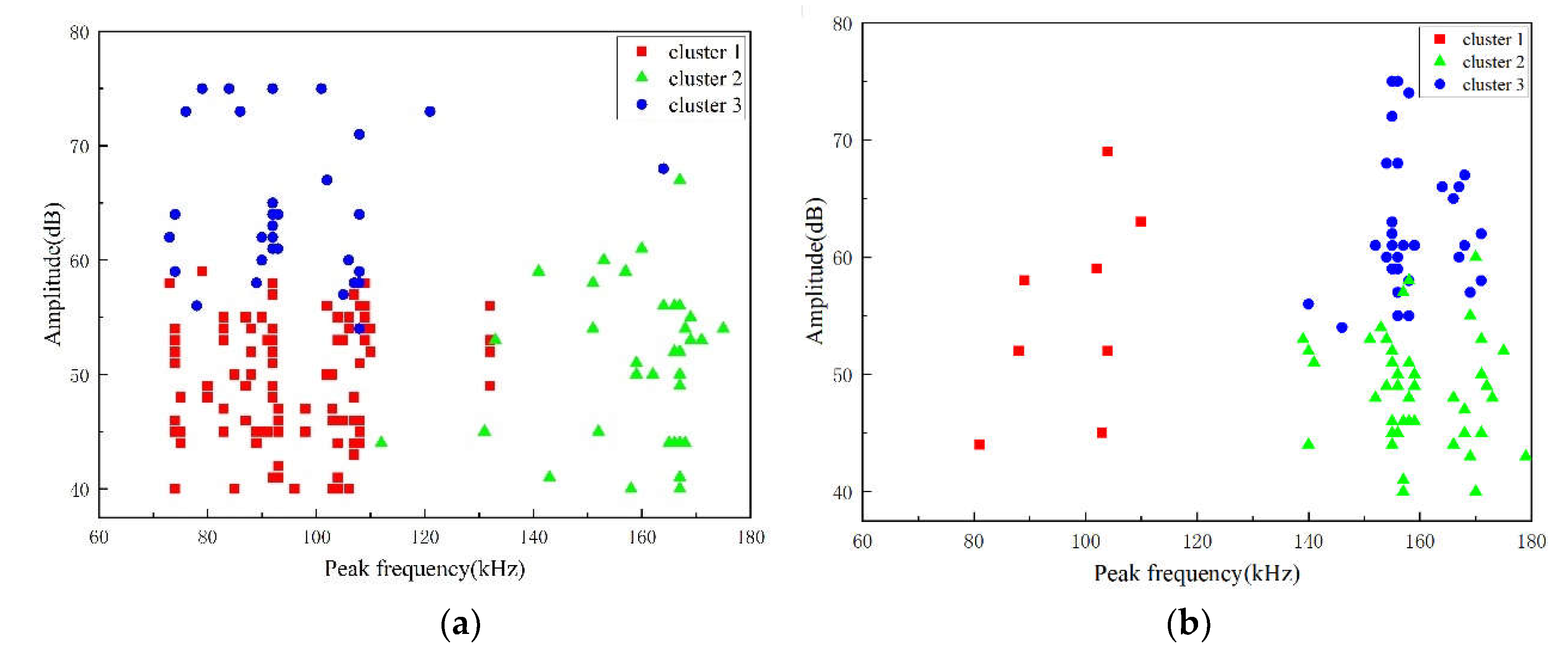
Preprints 111874 g012
Figure 12. Clustering results of aging signals. (a) A1 specimen; (b) A2 specimen.
Figure 12. Clustering results of aging signals. (a) A1 specimen; (b) A2 specimen.
Preprints 111874 g012
Preprints 111874 g013
Figure 13. Process of the SSA-LSSVM algorithm.
Figure 13. Process of the SSA-LSSVM algorithm.
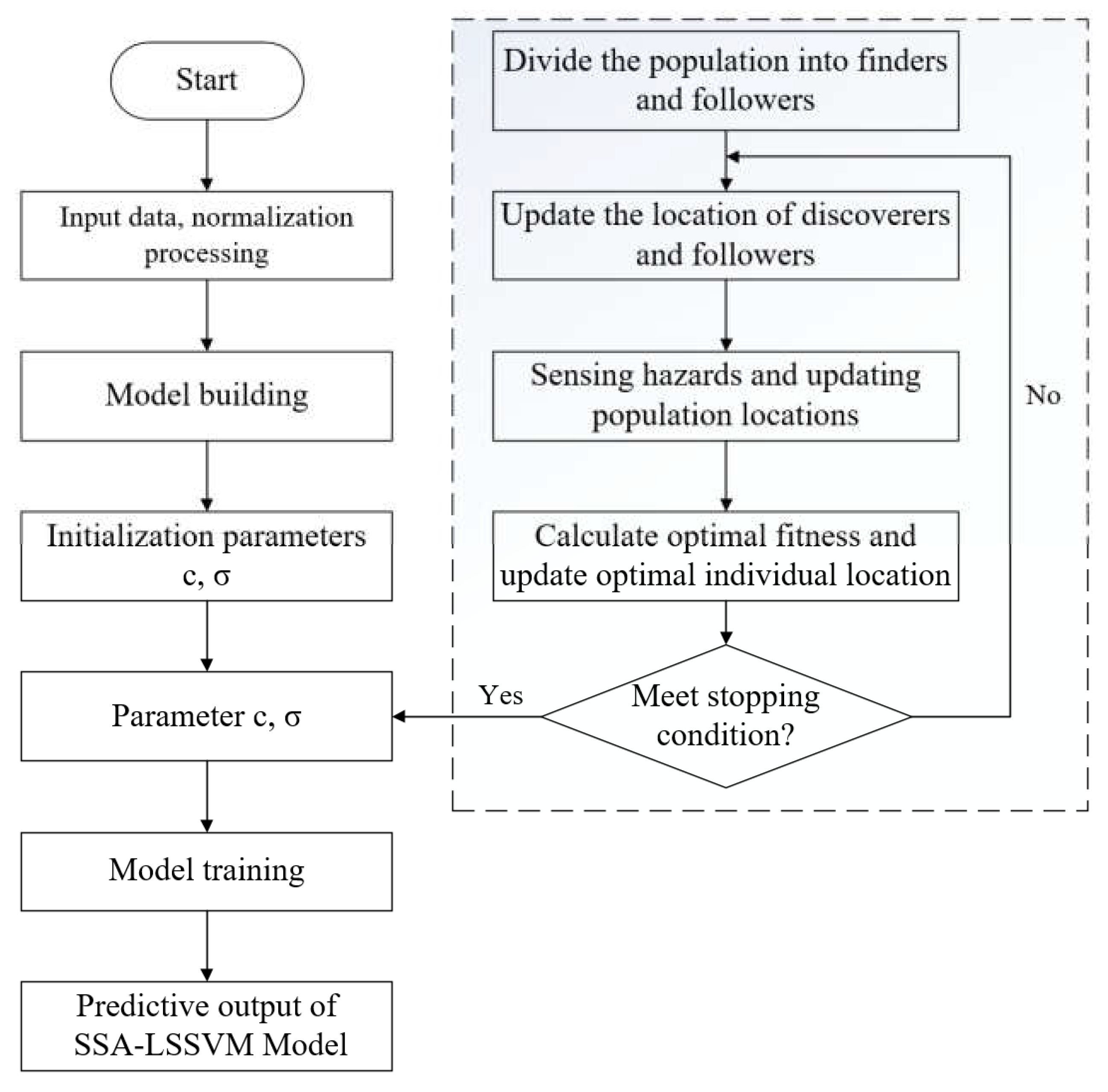
Preprints 111874 g013
Preprints 111874 g014
Figure 14. Prediction results. (a) Stress damage stage; (b) Aging stage.
Figure 14. Prediction results. (a) Stress damage stage; (b) Aging stage.
Preprints 111874 g014
Table 1. Parameters of the GFRP pipe.
Table 1. Parameters of the GFRP pipe.
angle thickness
winding angle inner liner inner winding layer outer winding layer
54.75° 3mm 3mm 1.5mm
Table 2. Composition of aging solution.
Table 2. Composition of aging solution.
ion Cl- HCO3- Ca2+ Mg2+
concentration (g/L) 15 0.8 0.8 0.8
Table 3. Design of specimen.
Table 3. Design of specimen.
preprocessed specimens Specimen number Degree of damage
2mm A1 Matrix crack
5mm A2 Obvious delamination
Table 4. Hits during the damage process of various specimens.
Table 4. Hits during the damage process of various specimens.
damage type Hits
matrix cracking debonding delamination fiber fracture
A1 9676 21621 2863 77
A2 162 457 170 17
Table 5. Hits during the aging process of various specimen.
Table 5. Hits during the aging process of various specimen.
damage type Hits
matrix crack debonding delamination
A1 99 37 34
34
A2 8 47
Table 6. Model components.
Table 6. Model components.
Model Experimental stage Sample number of training set Sample number of the testing set
Model 1 Stress damage stage 350 110
Model 2 Aging stage 100 50
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated