Preprint
Article
Periodic and Quasi periodic Orbits in the Collinear Four-Body Problem: A Variational Analysis
Altmetrics
Downloads
165
Views
110
Comments
0
This version is not peer-reviewed
Submitted:
11 July 2024
Posted:
12 July 2024
You are already at the latest version
Alerts
Abstract
This paper investigates the periodic and quasi-periodic orbits in the symmetric collinear four-body problem through a variational approach. In Section 3, we analyze the conditions under which homographic solutions minimize the action functional. We demonstrate that these solutions for four equal masses arranged in a linear configuration are indeed the minimizers of the action functional and compute the minimum value of the action functional for these solutions. Additionally, we employ numerical experiments using Poincaré sections to explore the existence and stability of periodic and quasi-periodic solutions within this dynamical system. Our results provide a deeper understanding of the variational principles in celestial mechanics and reveal complex dynamical behaviors that are crucial for further studies in multi-body problems. The findings have significant implications for theoretical research and practical applications in astrodynamics and space mission planning.
Keywords:
Subject: Computer Science and Mathematics - Mathematics
1. Introduction
Let be four point masses moving in in accordance with Newton’s Second Law, that is to say,
where denotes the position, and the mass of the ith particle [1,2,3,4]. With configuration , the force function (negative of the potential energy) is defined as
The Kinetic energy is defined as
while the Hamiltonian governing the equations of motion is
For this problem, we define the action functional to be of the form:
where the Lagrangian is defined as
In [5] Gordon has demonstrated that the elliptic Keplerian orbit minimize the Lagrangian action of the two body problems with periodic boundary conditions. The minimum value he has obtained of the Keplerian action functional was computed as
The authors in [6,7] have demonstrated that the Lagrangian and Eulerian elliptical solutions for the planar three-body problem are the variational minimizers of the Lagrangian action functional. In [8], it was shown that the homographic solutions to the rhombus four-body problem are the variational minimizers of the action functional restricted to a rhombus loop space. Additionally, the authors in [9,10] identified the minimizers of the classical action functional restricted to the homographic solutions of the kite and trapezoidal four-body problems as the Keplerian elliptical solutions. Chen [11] discovered a new periodic solution family for the planar four-body problem with equal masses, minimizing solutions over a quarter of the period using numerical integration. Furthermore, the authors in [12] extended Chen’s solutions to include minimization over the entire period without relying on numerical techniques.
This paper advances the understanding of the collinear four-body problem by demonstrating that homographic solutions for this symmetric configuration minimize the action function without the need for numerical integration. By analyzing the conditions for action minimization in Section 3 and employing numerical experiments with Poincaré sections, we provide a comprehensive exploration of periodic and quasi-periodic solutions. These findings enhance the theoretical framework for studying the stability and instability properties of homographic solutions in the symmetric collinear four-body problem, offering significant implications for both theoretical research and practical applications in celestial mechanics.
2. Symmetric Collinear Equilibrium Configurations
In this section, we are following the discussion in [16], for collinear configuration of a symmetric four-body problem.
Define the two mass ratios as
where m and M are the two unequal masses, and is the total mass of the system. For the symmetrical arrangement of the two pairs of masses there are two possible cases. In one case the pair with masses m lie in the middle of the collinear arrangement and in the second case their position is swapped. Both cases are symmetric about the center of mass Let
The equations of motion for and are
where
For the equilibrium solutions to exist we must have . Therefore
where
We know from equation (2) that Therefore
Lemma:
For and when
Proof.
It is trivial to show that and when . To show that for , we need to show that
or
Equivalently
It is easy to show that for k Therefore is an increasing function for k Also and therefore there exists only one root, . For . Hence for □
3. Action Minimizing Orbits
This section introduces the analytical discussion of a family of periodic solutions in the collinear four-body problem using variational techniques. We focus on solutions called the homographic solutions of the form where is smooth, and .The following theorem proves that these solutions are the variational minimizers of the action function and the minimum value is also computed.
Theorem:
The Keplerian elliptical solutions are the minimal regular solutions to the symmetric collinear four-body problem with two pairs of equal masses, with the minimum action equal to
Proof.
We aim to restrict the action functional to homographic solutions of the above-mentioned form.
Let , and the total mass , then the kinetic energy is equal to
The potential is given by
Using , we get
Multiplying and dividing by we obtain
The action restricted to this class of homographic solutions can be computed as below:
Let
and
Then
The infimum of is
We use Gordon’s result [5] to calculate the following infimum
Then
Let
The function attains its infimum at if and only if attains its infimum at . To show that is convex we need to show that For this purpose we rewrite as and
where , and are given in the appendix. After some subtle simplifications we obtain as below.
where
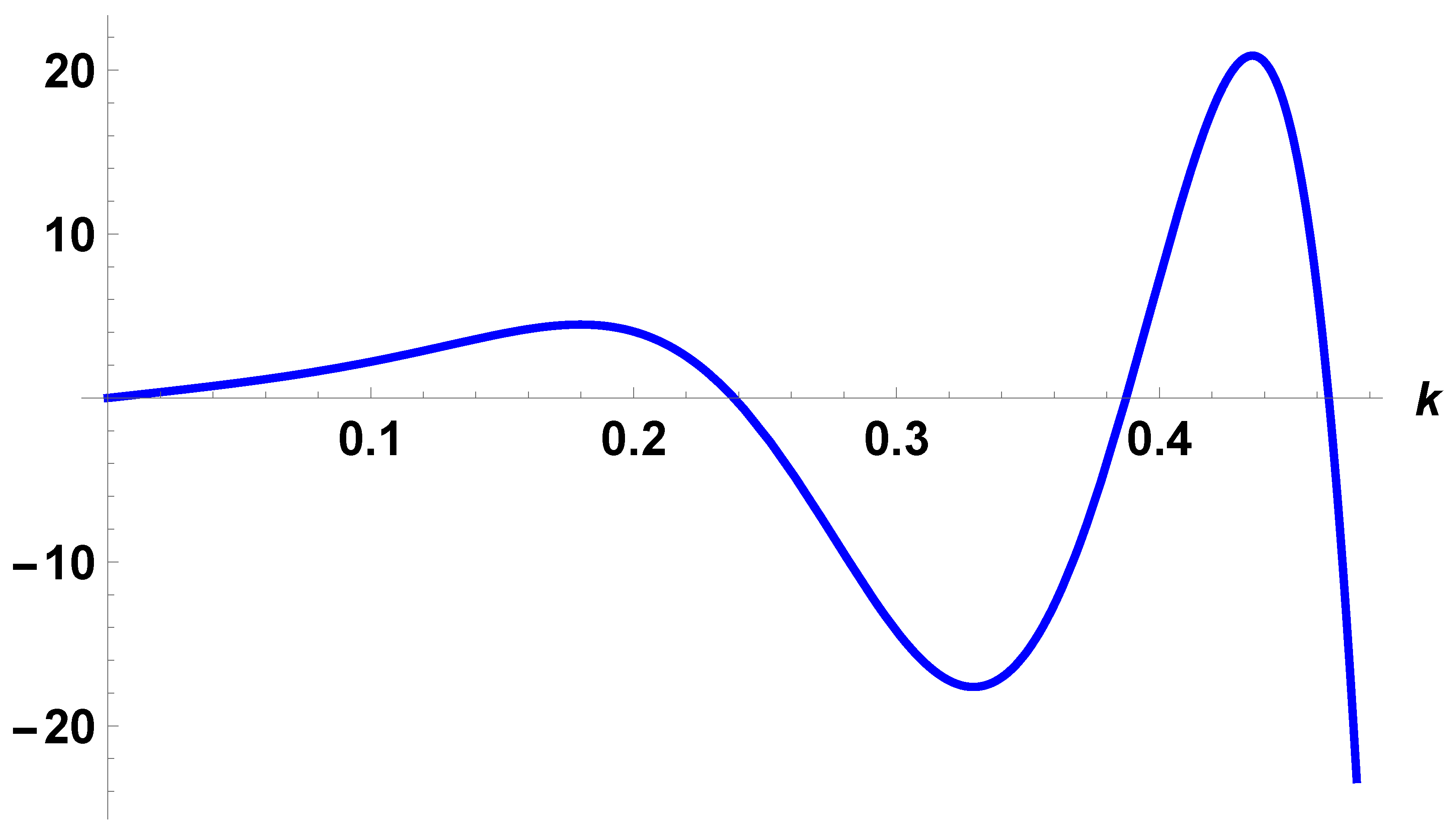
We note that the factor is negative when . The factor has only one positive real root at and is negative when and positive when The last factor, which is a polynomial of degree 39 has only 2 real positive roots and . The polynomial is positive when and is negative when see Figure (1). Therefore is positive when see Figure (2).This proves that the function is convex when .
For coercivity, we see that is continuous for all positive values of k, as and when , tends to ∞, which implies is coercive. Hence, attains at unique positive and satisfies . □
Figure 1.
The polynomial is positive when and is negative when
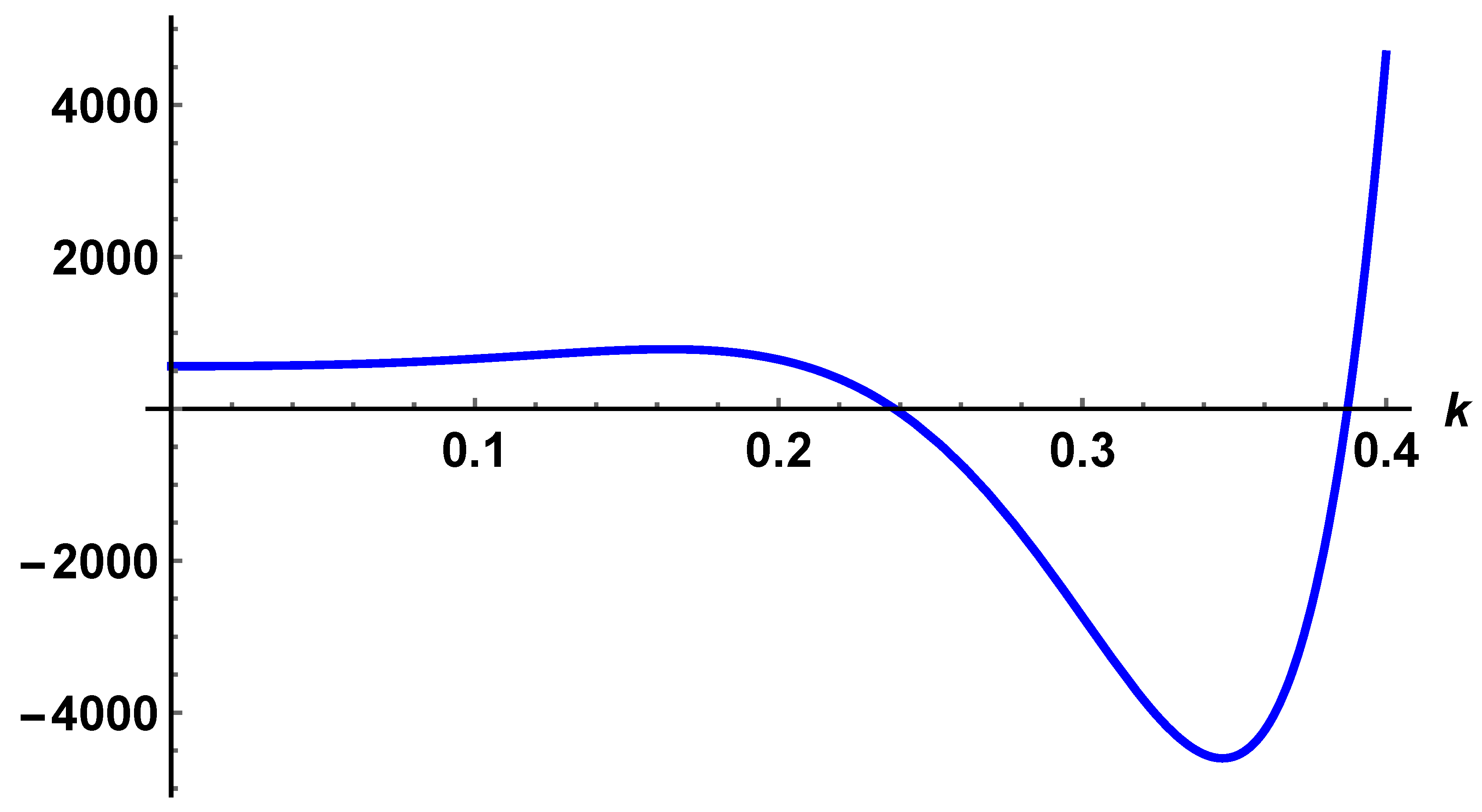
Figure 2.
The function is convex when
4. Numerical Examples
Recent investigations show that the four-star system, particularly two binaries (i.e., two pairs of twin stars that revolve around each other at great distances), is more common in the universe than previously thought. By studying the orbits of stars, we can obtain information about the formation processes and evolution of multiple star systems. The orbits of stars preserve information about these formation processes. Thus, by analytically and numerically investigating the collinear four-body problems, we can better understand the dynamic behavior of such quadruple-star systems.
We focus on the symmetric collinear four-body (SC4BP) central configurations presented in Section 2.
Figure 3.
Configuration of the symmetric collinear four-body (SC4BP) problem.
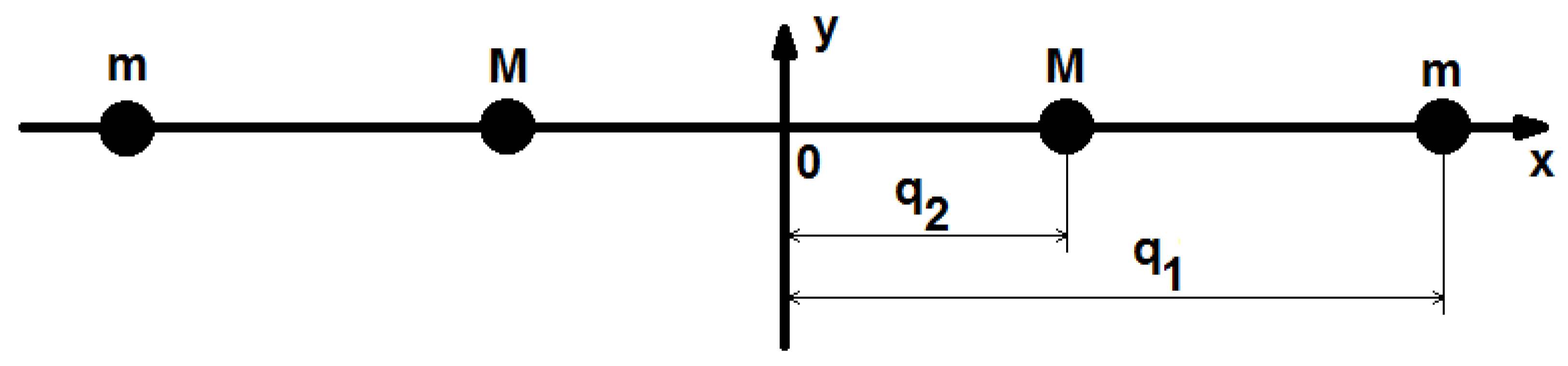
Let us consider the case of four point masses, where , lying collinearly on the x-axis and symmetrical to the y-axis at the origin, as introduced in Section 2 (see Figure 3). Using the position coordinates from Section 2, we obtain the following reduced Hamiltonian of the symmetric collinear four-body problem:
where are generalized coordinates and are generalized momenta.
Explicitly, the equations of motion are the following:
We aim to find some stable regions in special cases and analyze their stability over time. The dynamical parameters of our system are studied with phase portraits and Poincaré maps, which contain all the information necessary to characterize the dynamics of a system.
For the investigation of the reduced Hamiltonian equations of motion, we have tested two cases with different masses: and . In these situations, we studied the quasiperiodic orbits implemented using the Poincaré surface of section technique by selecting the phase element [13,14].
In Figure 4 and Figure 5, with , and for energy levels we found some interesting surface of sections.
At the energy level , the inner part is empty, the outer part is very close to instability, and the middle part of the figure contains some invariant curves, but no stable region.
At in the inner part is also empty space, and the outer part is chaotic, without any stable behaviors.
In Figure 5, at , it seems that the chaotic outer part surrounds the inner part with small invariant curves.
All three surfaces of the sections show instability, but the small invariant curves lead to further research.
Consequently, for proper study of the motion of SC4BP, we need to regularize the equations [15]. We make canonical changes of variables and time. Let us introduce the polar coordinates:
where , and , , . For the case , the Hamiltonian in Equation (7) becomes:
and we obtain the following equations of motion:
We remark the total collision is at the manifold , but still have discontinuities when or , where .
Firstly, we remove the singularity (), introducing the following variables: .
The system (11) becomes
We mention that is the first integral of the system in these new variables.
Consequently, we specify the following time variables , and we note with , and the system (12) becomes
Furthermore, to regularize the discontinuities we introduce the variable:
We note that w is regular in the Hill region, and the system becomes:
Now, we introduce the time variable s as the second time transformation:
and we note with , and we obtain the following new system:
In the new variable we can write the following part using Equation (14) and the first integral of the system:
and to study the periodic orbits of Equation (17) for a fixed energy level H, and mass m, we introduce the solution of , namely the critical value .
For negative energy the left part of relation (18) becomes less than or equal to 1, which depicts in variables the intersection between the total collision and the section .
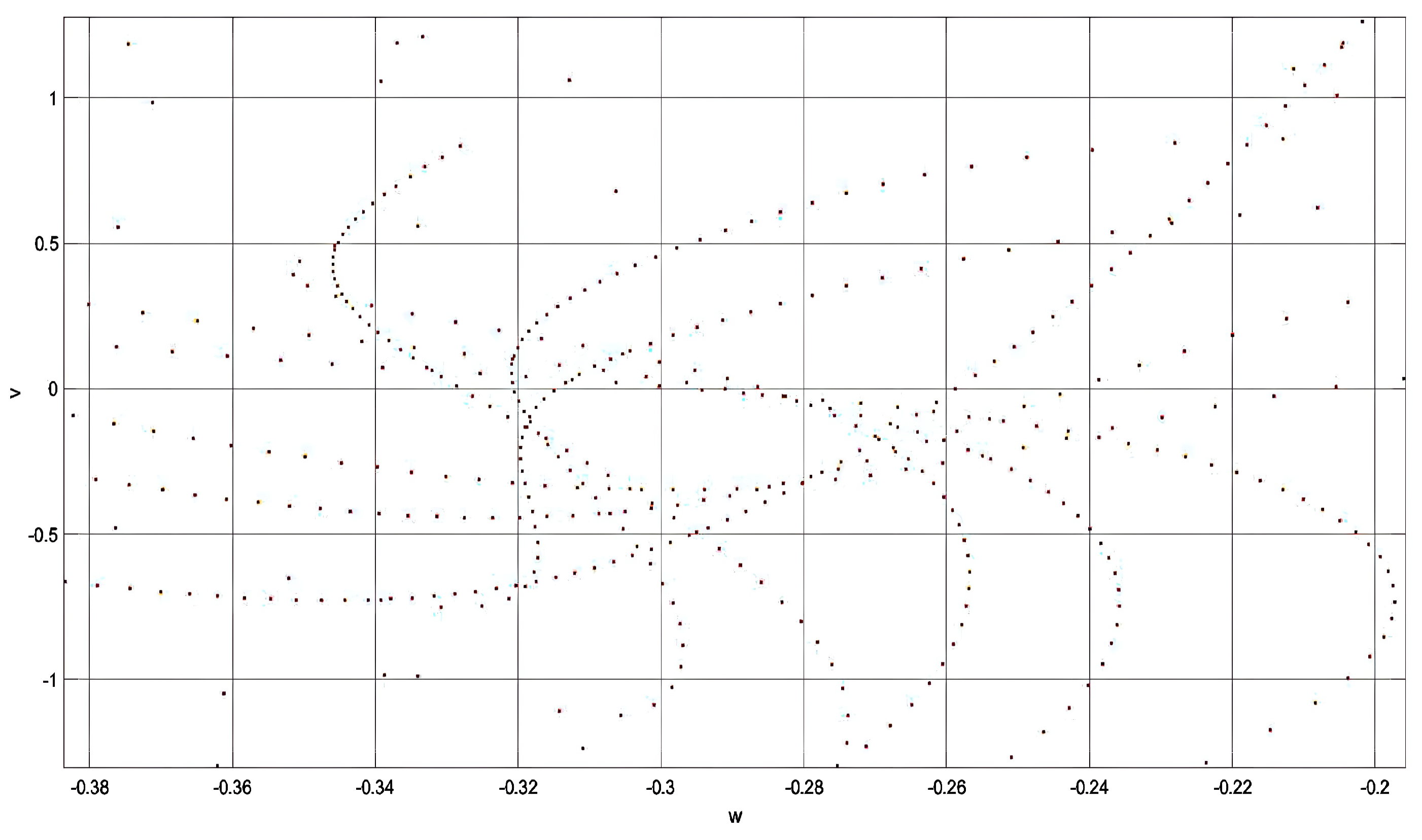
For this critical section, where we took and , we plot the Poincaré surface of sections (Figure 6), which gives an inside look at how the given system acts.
We can observe a quasiperiodic region as a vent in the center of Figure 6, and there were twisted lines on a chaotic backdrop. These results show how much the stability of the collinear four-body problem depends on the initial conditions. The quasiperiodic region could denote a stable manifold, and the outer part is an unstable manifold with unstable orbits.
5. Conclusions
In this study, we have investigated the periodic and quasi-periodic orbits in the symmetric collinear four-body problem using variational methods. Our primary findings demonstrate that the homographic solutions for this problem with equal masses indeed minimize the action functional. We have also computed the minimum value of the action functional specifically for these solutions. Furthermore, through numerical experiments employing Poincaré sections, we have explored the existence and stability of periodic and quasi-periodic solutions within the broader dynamics of the symmetric collinear four-body problem.
These results have significant implications for the understanding of celestial mechanics and the stability of multi-body systems. By confirming that homographic solutions minimize the action, we provide a foundation for future stability analyses of such solutions in the collinear four-body problem. The numerical techniques used in this study, particularly the Poincaré sections, offer valuable insights into the complex dynamical behaviors and can be extended to study more general configurations and other types of symmetry in multi-body problems.
Future research could extend these methods to non-symmetric configurations and explore the implications of mass variations among the bodies. Additionally, investigating the application of these variational techniques to three-dimensional multi-body problems could provide a more comprehensive understanding of celestial dynamics. The use of advanced numerical methods and computational power can further refine the solutions and contribute to the broader field of astrodynamics and space mission planning.
In summary, our findings contribute to the theoretical understanding of action-minimizing orbits in the collinear four-body problem, opening avenues for further research in both theoretical and applied celestial mechanics.
Appendix A
References
- Meyer, K.R.; Offin, D.C. Introduction to Hamiltonian systems and the N-body problem, Springer: New-York, 2017.
- Shoaib, M.; Kashif, A.R.; Szücs-Csillik, I. On the planar central configurations of rhomboidal and triangular four- and five-body problems, Astrophysics and Space Science 2017, 362(10), Article Nr. 182. [CrossRef]
- Sweetman W. L. The symmetrical one-dimensional Newtonian four-body problem: A numerical investigation, Kluwer Academic Publishers, 2002.
- Sweatman, W.L. Symmetrical one-dimensional four-body problem, Celest. Mech. Dynam. Astron. 2002, 82: 179-201. [CrossRef]
- Gordon, W.B. A minimizing property of Keplerian orbits, Amer. J. Math. 1970, 99(5), 961-971. [CrossRef]
- Zhang, S.Q.; Zhou, Q. A minimizing property of Eulerian solutions, Celestial Mechanics and Dynamical Astronomy 2004, 90, 239-243. [CrossRef]
- Zhang, S.Q.; Zhou, Q. A minimizing property of Lagrangian solutions, Acta Mathematica Sinica, English Series 2001, 17(3), 497-500. [CrossRef]
- Mansur, A.; Offin. D.; Lewis, L. Instability for a Family of Homographic Periodic Solutions in the Parallelogram Four Body Problem, Qualitative Theory of Dynamical Systems 2017, 16(3), 671-688. [CrossRef]
- Benhammouda, B.; Mansur, A.; Shoaib, M.; Szücs-Csillik, I.; Offin, D. Central configurations and action minimizing orbits in kite four-body problem, Advances in Astronomy 2020, Article ID 5263750. [CrossRef]
- Mansur, A.; Shoaib, M.; Szücs-Csillik, I.; Offin, D.; Brimberg, J. Action minimizing orbits in the trapezoidal four-body problem, AIMS Mathematics 2023, 8(8), 17650-17665. [CrossRef]
- Chen, K.C. Action minimizing orbits in the parallelogram four-body problem with equal masses, Arch. Rational Mech. Anal. 2021, 158, 293-318. [CrossRef]
- Mansur, A.; Offin, D.; Arsie, A. Extensions to Chen’s Minimizing Equal Mass Parallelogram Solutions, Taiwanese Journal of Mathematics 2017, 21(6), 1437-1453. [CrossRef]
- Szücs-Csillik, I. On the study of surfaces of section in the restricted trapezoidal four-body problem, Romanian Astronomical Journal 2021, 31(1), 9-20.
- Cheb-Terrab, E.S. and de Oliveira, H.P. Poincaré sections of Hamiltonian systems. Comp. Phys. Comm. 1996, 2-3, 171–189. [CrossRef]
- Mioc, V.; Csillik, I. The two-body problem in the point mass approximation field. IV. Symmetries, Rom. Astron. J. 2002, 12(2), 167-177.
- Shoaib, M.; Faye, I. Collinear equilibrium solutions of four-body problem, Journal of Astrophysics and Astronomy 2001, 32(3), 411-423. [CrossRef]
Figure 4.
Examples of Poincaré surface of sections in case for energy levels and .
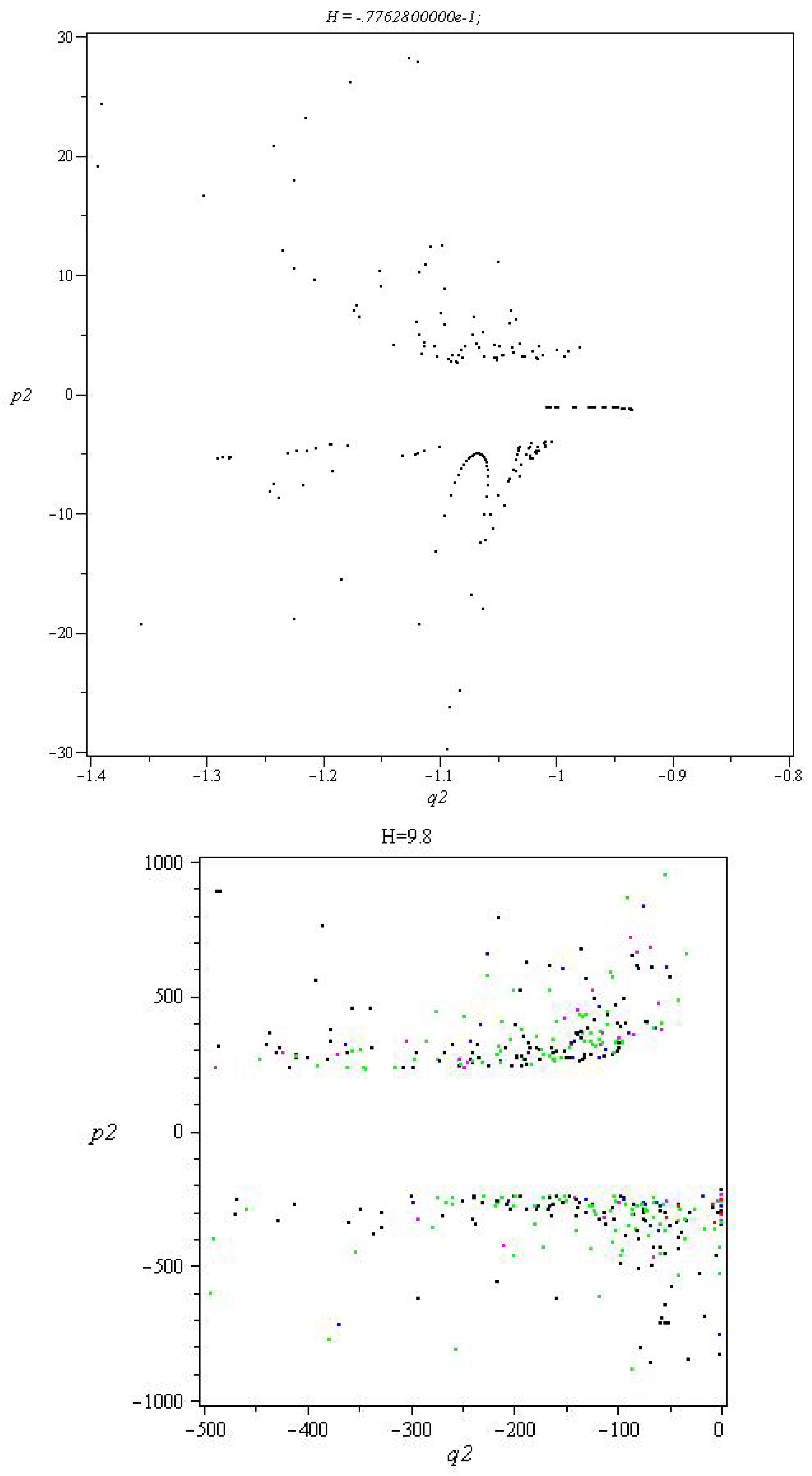
Figure 5.
Poincaré surface of sections in case for energy level 15.

Figure 6.
Poincaré surface of section for energy level .
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





