Impact of Oil Viscosity on Emissions and Fuel Efficiency at High Altitudes: An RSM Analysis

Preprint

Article

Impact of Oil Viscosity on Emissions and Fuel Efficiency at High Altitudes: An RSM Analysis

Altmetrics

Downloads

104

Views

Comments

A peer-reviewed article of this preprint also exists.

Milton Garcia Tobar^*

,Oscar Cabrera Ojeda,Fredy Crespo Montaño

Milton Garcia Tobar^*

,Oscar Cabrera Ojeda,Fredy Crespo Montaño

This version is not peer-reviewed

Submitted:

12 July 2024

Posted:

12 July 2024

You are already at the latest version

Alerts

Abstract

This study investigates the effect of oil viscosity on pollutant emissions and fuel consumption of an internal combustion engine (ICE) in high-altitude using Response Surface Methodology (RSM). A Chevrolet Corsa Evolution 1.5 SOHC gasoline engine was used in Cuenca, Ecuador (2560 meters above sea level), testing three lubricating oils with kinematic viscosities of 9.66, 14.08, and 18.5 cSt under various engine speeds and loads. Key findings include: hydrocarbon (HC) emissions were minimized to 7.25 ppm with low viscosity and load; carbon dioxide (CO2) emissions peaked at 15.2% vol with high viscosity and load; carbon monoxide (CO) ranged from 0.04% to 3.74% depending on viscosity and load; nitrogen oxides (NOx) were significantly influenced by viscosity, RPM, and load, indicating a need for model refinement; and fuel consumption was significantly affected by load and viscosity. RSM-based optimization identified optimal operational conditions with a viscosity of 13 sCt, 1473 rpm, and a load of 78%, resulting in 52.35 ppm of HC, 13.97% vol of CO2, 1.2% vol of CO, 0 ppm of NOx, and a fuel consumption of 6.66 l/h. These conditions demonstrate the ability to adjust operational variables to maximize fuel efficiency and minimize emissions. This study underscores the critical role of optimizing lubricant viscosity and operational conditions to mitigate environmental impact and enhance engine performance in high-altitude environments.

Keywords:

Subject: Engineering - Automotive Engineering

1. Introduction

The exponential growth of the vehicle fleet in recent decades has generated a significant increase in polluting emissions, becoming one of the leading environmental challenges at a global level [1]. Road vehicle growth in developed and developing countries is projected to increase by 45% by 2025, affecting traffic, traffic density, and emissions [2]. In 2023, the EU approved a series of Commission suggestions to align the EU's climate, energy, transport, and taxation policies to reduce net greenhouse gas emissions by at least 55% by 2030, compared to 1990 levels. This initiative aims to make the EU the first climate-neutral continent by 2050 [3]. Therefore, reducing environmental pollutant emissions from internal combustion engines (ICEs) requires the development of more efficient engines in terms of fuel consumption, emission generation, and power density [4]. Harmful components of engine exhaust gases include nitrous oxides (NOx), carbon dioxide (CO₂), carbon monoxide (CO), hydrocarbons (HC), and particulate matter (PM) [5] which have a direct impact on air quality and are a significant risk factor for human health, contributing to global warming and acid rains [6].

ICEs are complex systems involving various components: lubrication, friction, charge cycles, supercharging, mixture formation, ignition, combustion systems, electronics and mechanics for engine management, transmission shift control, powertrain, sensors, actuators, cooling, exhaust emissions, operating fluids, filtration, etc., providing alternatives to optimize its performance [7]. One of these alternatives to reduce fuel consumption and, therefore, minimize the emission of polluting gases into the environment is based on lowering mechanical losses and increasing engine efficiency [8]. In this regard, strategies have been developed to reduce these losses in the ICEs [9,10,11,12,13].

Hybrid surface modification techniques, such as coatings, textures, and nanoparticles, can improve the tribological performance of engine components [14]. Improving surface coatings through micro-reliefs on the inner surface of cylinder liners can reduce mechanical losses in internal combustion engines by an average of 10.8% and increase mechanical efficiency by 4.0% [10,15]. Hazar et al. propose coating engine components with MgO-ZrO₂ and ZrO₂ which provides a thermal barrier, increasing engine power and reducing fuel consumption while improving pollutant emissions [16].

On the other hand, downsizing internal combustion engines can improve fuel utilization, reduce emissions, and increase efficiency by reducing the weight of moving parts such as pistons and crankshafts [17,18] which can reduce CO₂ emissions by about 18% in warm engine conditions for mid-class vehicles [19]. Podrigalo et al. conclude that a rational reduction in effective engine capacity can lead to a 9.5% reduction in fuel consumption while maintaining the specified maximum speed and dynamic properties of cars [20]. Likewise, reducing the gap between compression rings and increasing the twist angle can help reduce leakage flows by 37% and contribute to minimizing global emissions [21].

Similarly, the use of low-viscosity oils (LVO) is adopted to reduce mechanical losses in ICEs due to the ease of implementation costs versus the advantages of reducing pollutant emissions and fuel consumption [12,22,23,24]. These oils reduce frictional power loss and wear load on compression ring surfaces, leading to maximum fuel economy in internal combustion engines [25]. LVO can reduce fuel consumption by around 2% in light-duty diesel engines [22], and 5% in urban transport buses [26] depending on the test conditions, offering a cost-effective way to increase engine efficiency and reduce CO₂ emissions. Hawley et al. determine up to 3.5% fuel economy improvement in engines using lower-viscosity lubricants, compared to current production lubricants [27]. In the same way, Ishizaki et al. conclude that ultra-low viscosity engine oils can reduce CO₂ emissions by 0.6% in 1.5-1.8 L gasoline engines in New European Driving Cycles (NEDC) mode and improve fuel efficiency in passenger vehicles, but their cost-effectiveness depends on both viscosity reduction and oil drain interval extension [28]. However, the use of low-viscosity oils in ICE results in magnified wear due to thinner oil films and requires additional wear protection additives for effective performance [29,30].

Another factor that significantly affects fuel consumption and pollutant emissions is altitude. These altitude changes have a direct impact on the performance, fuel consumption, and emissions of ICEs [31]. Diesel vehicles, in particular, have higher CO₂, CO, and NOx emission factors than gasoline vehicles. These emissions increase with altitude because there is lower atmospheric pressure, temperature, and oxygen concentration, resulting in reduced combustion efficiency in automotive engines with atmospheric pressure being the primary environmental factor affecting emissions [32] by lengthening the ignition delay, increasing energy release, and prolonging the late combustion period, leading to reduced thermal and combustion efficiency [33]. Wan et al. declare that as altitude increases from 0 to 2000 meters, engine torque drops by 2.9%, BSFC increases by 2.6%, NOx emissions reduce by 11.8%, and opacity smoke increases by 26.2% [34], while He et al. state that high altitude increases diesel engine emissions of HC, CO, and smoke, with average increases of 30%, 34%, and 35% at 1000 meters [35]. NOx emissions vary with engine types and working conditions [36].

2. Materials and Methods

2.1. Description of the Experimental Setup

For the present study, a data acquisition protocol is established through an experimental design using Response Surface Methodology (RSM), which will allow visual analysis of the average result for a particular area of the levels of the input factors or variables such as lubricant viscosity, engine speed, and applied load, thus evaluating the sensitivity of the output variables (emissions and fuel consumption) to such changes in operating conditions.

In this study, the experiments were performed on a Chevrolet Corsa Evolution 1.5 SOHC, four cylinders, four-stroke, and SI (spark ignition) gasoline engine in the city of Cuenca, Ecuador, which is located 2,560 meters above sea level. The engine specification is given in Table 1.

This vehicle is mounted on a dynamometer MAHA LPS 3000, which is composed of eddy current dynamometer brakes, which, in addition to measuring traction and power at the same time, can also generate loads with revolutions within a range of 0 – 10,000 rpm, speed from 0 to 260 km/h and constant tractive force from 0 - 6 KN, as shown in Figure 1. The dynamometer is also equipped with an AIC 5008 fuel flow meter capable of measuring volumetric flow rate from 0 to 120 l/h with a sensitivity of 0.01.

Exhaust gases were measured using a Brain Bee AGS-688 analyzer, which can determine the different concentrations of HC, CO, CO₂, O_2, and NOx emitted in the experimental unit vehicle, as shown in Table 2.

The levels of the input variable, oil viscosity, are characterized by the kinematic viscosity measured in cSt @ 100 °C of three lubricating oils with similar compounds, whose technical specifications are shown in Table 3.

2.2. Response Surface Methodology

The Response Surface Methodology (RSM) is based on several mathematical and statistical methodologies that are used to develop a suitable functional relationship between a factor of interest

(y)

, and certain control (input) variables denoted by

x_{1}, x_{2}, \dots ., x_{k}

. This relationship is not commonly known, but can be approximated by a polynomial model of lower degree as expressed in Equation (1):

y = f' (x) β + ε

(1)

where

{x = (x}_{1}, x_{2}, \dots ., x_{k})'

f (x)

represents a p-element vector function consisting of powers and cross products of powers of

x_{1}, x_{2}, \dots ., x_{k}

until reaching a certain degree denoted by

d (> 1)

β

is a vector of p coefficients which are constant, and unknown being denoted as parameters, and

ε

is the random experimental error, assumed to have zero mean. This is conditional on the idea that the model in Equation (1) provides an adequate representation of the response. In this case, the quantity

f' (x) β

represents the mean response, i.e., the expected value of y, and is denoted by

μ (x)

. Typically, the response surface methodology uses two important models. These are special cases of the model presented in Equation (1). Equation (2) presents the first-degree polynomial model

(d = 1)

y = β_{0} + \sum_{i = 1}^{k} β_{i} X_{i} + ε

(2)

Equation (3), states the second-degree model

(d = 2)

y = β_{0} + \sum_{i = 1}^{k} β_{i} x_{i} + \sum_{i = 1}^{k} \sum_{j \geq 1}^{k} β_{i j} x_{i} x_{j} + \sum_{j = 1}^{k} β_{i i} {x_{i}}^{2} + ε

(3)

where

k

is the number of variables, for this study

(k = 3)

;

x_{i}

x_{j}

{x_{i}}^{2}

represent these variables.

β_{0}

are the constant terms,

β_{i}

the coefficients of the linear terms

x_{i}

β_{i i}

the coefficients of quadratic terms

{x_{i}}^{2}

and

β_{i j}

the coefficients of the interaction of the terms

x_{i j}

.Finally

ε

is the residual associated with the experiment. Table 4 shows the input variables and levels.

Figure 2 shows a schematic illustration of the experimental setup. The test vehicle is mounted on the dynamometer (a), on which the speed and load are monitored (b). Inference variables such as coolant temperature, wheels, and lubricant are monitored through the dynamometer's sensor console (c). During data acquisition, fuel flow (d) and pollutant emissions (e) are recorded to finally analyze the data obtained in the experiment through specific software (f).

3. Results

3.1. Model for HC.

The ANOVA results and fit statistics for HC are presented in Table 5. The ANOVA analysis of the quadratic model indicates that the model is significant, with an F-value of 6.36 and a p-value of 0.0117, suggesting a statistically significant impact of the studied factors on the HC response. Among the individual terms, load (C) emerges as the most influential factor, with an F-value of 27.61 and a p-value of 0.0012, highlighting its critical importance in the model. The quadratic term of load (C²) is also significant, with an F-value of 16.38 and a p-value of 0.0049, indicating a robust nonlinear relationship between load and the response. In contrast, viscosity (A) and the interactions between factors (AB, AC) were not significant (p > 0.78). While the interaction BC and the quadratic term of RPM (B²) showed trends towards significance (p ≈ 0.06 and p ≈ 0.12, respectively), they did not meet the critical threshold. The model’s R² value is 0.8910 (refer to Table 6), indicating that it explains 89.10% of the variability in the data, while the adjusted R² is 0.7509, reflecting a decrease in explanatory power when accounting for the number of terms in the model. However, the predicted R² is -0.7362, implying poor predictive performance, suggesting that the overall mean might be a better predictor than the current model. The significant lack of fit, with an F-value of 278.41 and an extremely low p-value (p < 0.0001), indicates that the model does not fully capture the observed variations, underscoring the need to explore more complex models or consider additional factors. The actual regression equation for HC is given in Equation (4).

HC [ppm] = 240.451001208 − 39.284156753547 * Viscosity + 0.067123768964599*RPM − 2.3811266968326 * Load + 0.00079850944902852 * Viscosity * RPM − 0.020361990950226 * Viscosity * Load + 0.00082352941176471 * RPM * Load + 1.3743576093856 * Viscosity² − 2.9273356401384e-05 * RPM² + 0.02474 * Load²

(4)

The contour plot (see Figure 3a) shows the interrelation of variables, with viscosity ranging from 9.66 to 18.5 sCt and load spanning from 0% to 100%. Notable predictions include an HC emission of 150.223 ppm at maximum load (100%) and viscosity (18.5 sCt), represented in reddish tones, suggesting a significant increase in emissions under these conditions. Conversely, at a minimal load of 5% and viscosity of 9.66 sCt, HC emissions decrease to 7.25303 ppm, indicated in bluish tones, showing a marked reduction. The surface plot of Figure 3b corroborates these findings, illustrating a pronounced curvature indicative of a non-linear relationship between the independent variables and HC emissions. The 3D plot reveals that a low viscosity of 9.66 sCt combined with a low load of 5% results in HC emissions of 7.25303 ppm, while a viscosity of 18.5 sCt and a load of 100% produce 150.223 ppm of HC. This analysis underscores the critical need to optimize lubrication parameters to mitigate environmental impact, emphasizing the influence of lubricant viscosity and operational load on emissions.

3.2. Model for CO₂

Presented in Table 7 are the ANOVA results and fit statistics for CO₂. The model is significant, as evidenced by the F-value of 4.59 and a p-value of 0.0285. Additionally, terms C and C² (C-Load) are individually significant, suggesting their influence on the response variable. However, a considerable lack of fit is observed, as indicated by the high lack of fit F-value of 397.92 and an extremely low p-value. Regarding the fit statistics (refer to Table 8), the coefficient of determination R² indicates that the model explains approximately 85.5% of the total variability in the data. At the same time, the adjusted R², at 0.6687, reflects a corrected measure considering the number of terms in the model. Despite the model's high capability to explain variability, the lack of fit underscores the need for improved predictive accuracy. The regression equation for CO₂ is provided in Equation (5).

CO₂ [% vol] = 8.79847 + 0.818029 * Viscosity − 0.000233 * RPM + 0.036257 * Load − 0.000053 * Viscosity * RPM − 0.000113 * Viscosity * Load − 0.000015 * RPM * Load − 0.024825 * Viscosity² + 4.35986E-07 * RPM² − 0.000304 * Load²

(5)

The contour plot of Figure 4a illustrates the response surface predictions with various levels ranging from 14.2 to 15.2 % vol. The critical design points marked in red indicate significant regions where the response variable peaks or valleys are observed. For instance, the contour lines show that the response value is approximately 14.4 near the design points, increasing to around 15.2 at the lower edge of the plot. This gradient highlights a clear response trend as one moves through the design space, indicating regions of high and low responses.

The surface plot of Figure 4b reveals the response surface's three-dimensional aspects, visually representing how the response variable changes across the design space. The surface's curvature suggests a non-linear relationship between the independent variables and the response. Specific predictions at notable points, such as 14.4312, 14.1647, and 15.1471, are highlighted, indicating areas where the response variable exhibits significant changes. The upper surface portion shows a prediction value of 14.7036, demonstrating a peak in the response.

3.3. Model for CO

Table 9 outlines the ANOVA results and fit statistics for CO. The analysis of the evaluated quadratic model reveals significant results and provides a detailed view of the influence of various variables on the studied response. The primary factors evaluated include viscosity (A), RPM (B), and load (C). The model, as a whole, is significant (p = 0.0107), indicating that, in general, the variables included in the model have a relevant impact on the response. Among the individual factors, the variable load (C) shows considerable significance (p = 0.0009), suggesting that the load has a notable effect on the response. On the other hand, the variables viscosity (A) and RPM (B) do not exhibit individual statistical significance (p = 0.9569 and p = 0.1232, respectively). Interactions between variables, such as AB and AC, also do not show significance, indicating that there are no relevant synergistic effects between these factors within the model. The coefficient of determination (R²) of 0.8941 suggests that the model explains 89.41% of the observed variability in the data, which is relatively high, as shown in Table 10. However, the adjusted R² is significantly lower (0.7579), suggesting that some variables may not be contributing efficiently to explaining the variability. The model's adequate precision is 8.2728, indicating a good signal-to-noise ratio, essential for the reliability of predictions. The regression equation for CO is detailed in Equation (6).

CO [% vol] = 4.73817 − 0.834030 * Viscosity + 0.002036 * RPM − 0.073847 * Load + 1.13095E-18 * Viscosity * RPM + 0.000192 *Viscosity * Load + 0.000024 * RPM * Load + 0.029407 * Viscosity² − 7.96540E-07 * RPM² + 0.000637 * Load²

(6)

The contour graph for CO (see Figure 5a) displays a significant variation in CO concentration depending on the levels of viscosity and load, with values ranging from a minimum of 0.0418921 in areas of low viscosity and load to a maximum of 3.74443 under conditions of high viscosity and increased load. In this graph, a color gradient transitions from blue (low CO concentration) to yellow (high CO concentration), highlighting the impact of the interactions between viscosity and load on CO production. For instance, the CO value is 0.0716529 at a point with intermediate viscosity and load, escalating dramatically to 3.10733 and 3.74443 in regions where both variables reach higher levels. This pattern suggests that an increase in viscosity, possibly in conjunction with higher load, elevates CO concentration, indicating a strong correlation between these variables.

The surface plot of Figure 5b provides a three-dimensional representation of these effects, showing how the response surface rises with increases in viscosity and load. The curvature of this surface clearly illustrates how specific adjustments in these input variables can lead to the maximization or minimization of CO production.

3.4. Model for NOx

Table 11 provides the ANOVA results and fit statistics for NOx. The analysis shows the model is significant, with a Model F-value of 12.96. This high F-value corresponds to a probability of only 0.14% that such a result could occur due to random noise, affirming the model's statistical significance. Significant model terms are identified by p-values less than 0.0500. In this case, the terms B, C, BC, A², and B² are significant, indicating their substantial impact on the NOx response. Conversely, terms with p-values greater than 0.1000 are considered insignificant and may warrant removal for model simplification. However, a notable concern is the discrepancy between the Predicted R² of 0.0941 and the Adjusted R² of 0.8706 (Table 12). This significant difference, exceeding 0.2, suggests potential issues with the model or data, such as a large block effect, the presence of outliers, or other anomalies. Exploring model reduction, response transformation, and the identification of outliers is recommended to address this discrepancy. Moreover, conducting confirmation runs is essential to validate the empirical model. The Adequate Precision ratio of 10.719 exceeds the desirable threshold of 4, indicating a strong signal-to-noise ratio. This high ratio suggests that the model is reliable and can effectively navigate the design space for the NOx response. Despite the model's overall significance and adequate signal strength, the substantial gap between the Predicted and Adjusted R² values necessitates further refinement and validation to ensure the model's robustness and accuracy. In conclusion, while the NOx response model shows strong potential with significant terms and an adequate signal, addressing the underlying issues indicated by the R² discrepancy is crucial for enhancing model reliability and predictive performance. The regression equation for NOx is provided in Equation (7).

NOx [ppm] = 1264.7614990479 − 124.39715095923 * Viscosity − 0.63473249933458 * RPM - 5.2812556561086 * Load − 0.0036598349747138 * Viscosity * RPM + 0.25565610859728 * Viscosity * Load + 0.0022176470588235 * RPM * Load + 4.5044122765709 * Viscosity² + 0.00023148788927336 * RPM² − 0.0012 * Load²

(7)

In the contour graph of Figure 6a, NOx concentration exhibits a broad range, with a notable minimum of 0.250162 located near the center of the lower edge, indicative of moderate load and high viscosity conditions. An intermediate value of 118.617 at the graph's center reflects a moderate NOx response under median viscosity and load conditions. The observed maximum of 250.689 in the top right corner reveals that a combination of high viscosity and high load leads to the highest production of NOx, highlighting a strong interaction between these two variables. The surface plot offers a three-dimensional perspective, demonstrating how NOx levels escalate in response to increments in both variables. The surface of Figure 6b illustrates a gradual increase in NOx from the center towards the top right corner, indicating that the highest concentrations are achieved under extreme conditions of both variables.

3.5. Model for Consumption

Table 13 displays the ANOVA results and fit statistics for consumption. The model is significant, with an F-value of 11.05. This high F-value suggests that there is only a 0.01% chance that such a result could occur due to random noise, confirming the model's statistical significance. Significant model terms are identified by p-values less than 0.0500; in this case, the terms C, A², B², and C² are significant, demonstrating their considerable impact on the consumption response. Conversely, terms with p-values more significant than 0.1000 are considered insignificant and may be candidates for model reduction to improve efficiency. However, the Lack of Fit F-value of 5.60 indicates a significant lack of fit. This is problematic, as we desire the model to fit well to the data, and there is only a 0.34% chance that this high Lack of Fit F-value is due to noise. A significant lack of fit suggests that the model does not adequately capture the observed variability in the data. Regarding the fit statistics, the standard deviation is 0.8548, and the R² is 0.7397, indicating that the model explains 73.97% of the variability in the data. However, the adjusted R² is 0.6728, and the predicted R² is negative (-0.6143), suggesting that the overall mean might better predict the response than the current model (see Table 14). In such cases, a higher-order model may also predict better. The adequate precision, with a signal-to-noise ratio of 16.958, exceeds the desirable threshold of 4, indicating a strong signal and confirming that the model can navigate the design space effectively. The regression equation for consumption is detailed in Equation (8).

Consumption [l/h] = 14.502664936873 − 2.141698743542 * Viscosity + 0.0075285799840298 * RPM − 0.036325253667901 * Load − 0.00011977641735427 * Viscosity * RPM + 0.0011538461538462 * Viscosity * Load − 1.6294117647059e-05 * RPM * Load + 0.081245001560413 * Viscosity² − 1.6059033238964e-06 * RPM² + 0.00080389393939394 * Load²

(8)

The contour and surface plots presented in Figure 7 provide an in-depth analysis of how input variables, viscosity (x-axis) and load (y-axis), influence fuel consumption in a controlled experimental setting. These graphs depict significant variations in fuel consumption based on these variables. In the contour graph (Figure 7a), fuel consumption values range from 5.53313 to 10.3842, illustrating a distinct trend where consumption increases with load and viscosity. The lower consumption values, such as 5.53313 and 5.37454, are found in the central region, suggesting moderate conditions of load and viscosity. Conversely, the highest consumption values, reaching up to 10.3842, are located in the upper right corner of the graph, indicating high load and viscosity conditions.

The surface plot of Figure 7b presents a three-dimensional representation of these effects, showing how fuel consumption escalates with increases in viscosity and load. The surface's curvature clearly demonstrates a direct relationship between increased load and viscosity and higher fuel consumption.

This analysis is essential for developing effective fuel management strategies. It enables the identification of operational configurations that minimize consumption and enhance energy efficiency in internal combustion engines. Understanding the interplay between viscosity and load in relation to fuel consumption provides valuable opportunities for resource optimization and operational sustainability.

4. RSM Based Optimization

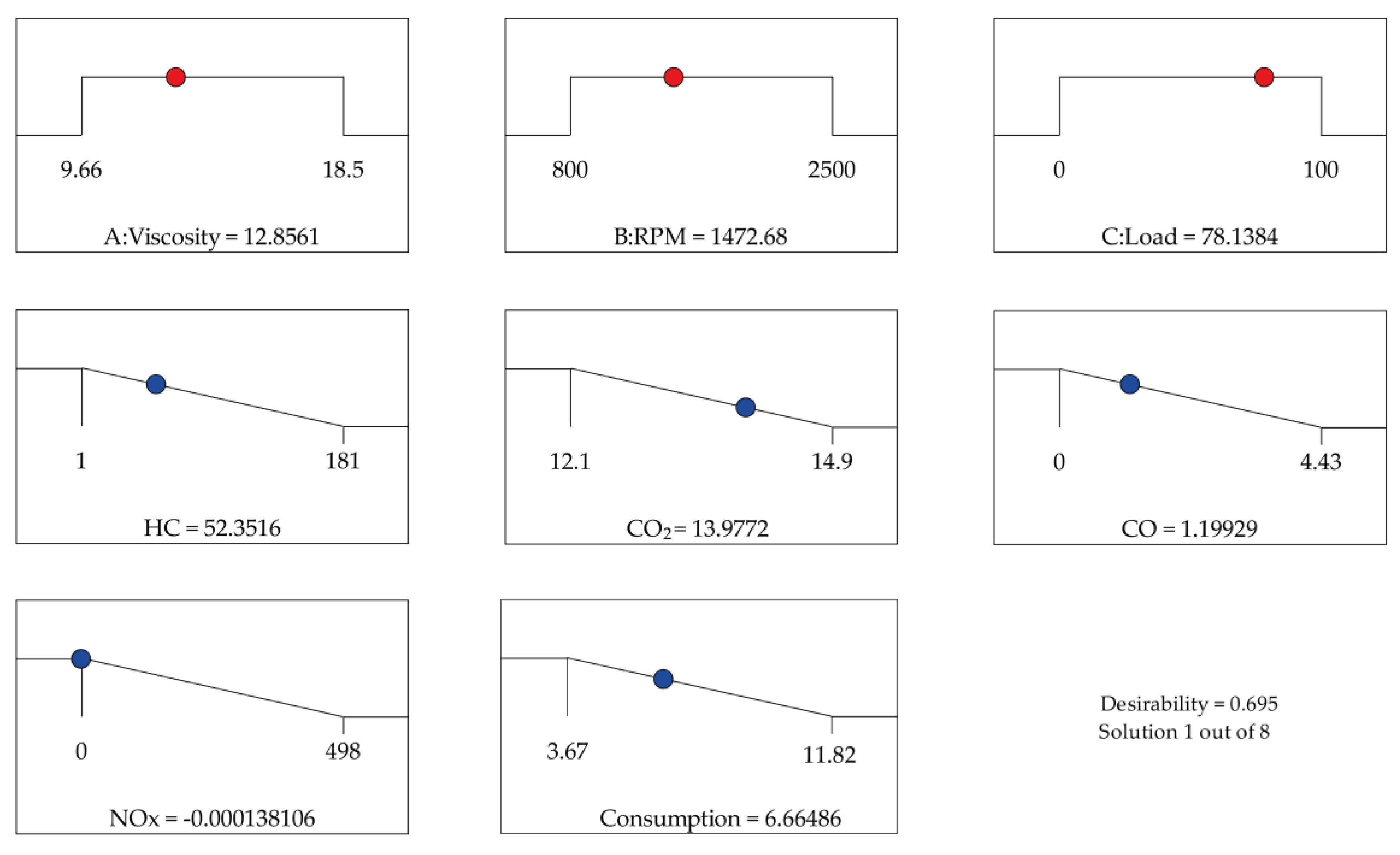
An RSM-based optimization is a method to explore the shape and location of the maximum or minimum of a surface that mathematically represents the relationship between one or more responses and the influencing factors. In the current work, the emissions and fuel consumption of the engine are optimized. In this setup, shown in Table 15, the goal of minimum criteria was selected. Moreover, the default in the range criterion for study factors was selected.

The engine operating conditions identified by optimization were 13 sCt for viscosity, 1473 rpm, and 78% engine load, rounded to the nearest whole number. The response variables, corresponding to optimized operating conditions, were 52.35 ppm of HC, 13.97 % Vol of CO₂, 1.2 % Vol of CO, 0 ppm for NOx, and 6.66 l/h for consumption. The optimum gained values of study factors and response variables are shown by the red and blue dots in Figure 8.

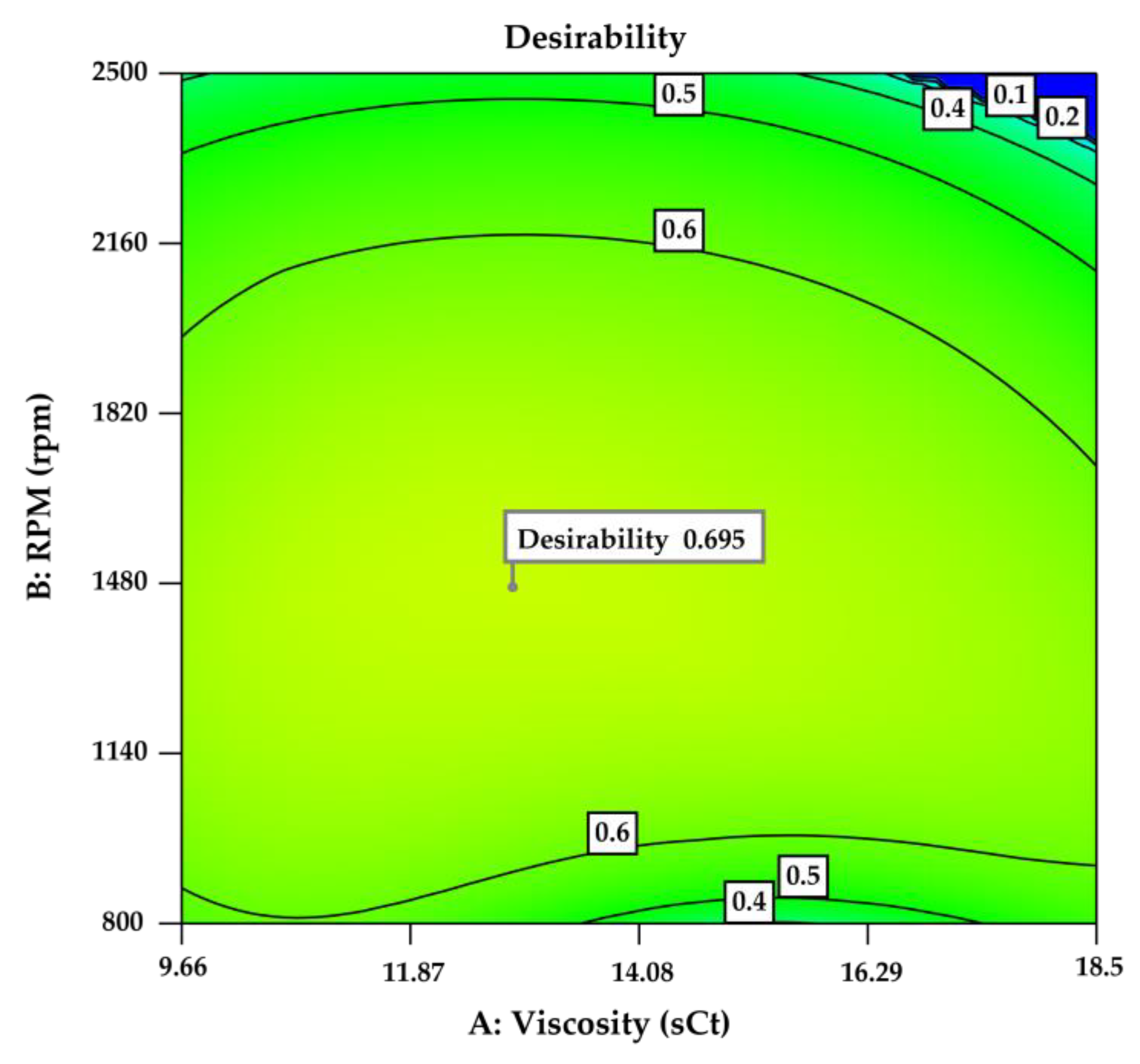
The statistical analysis of optimization and its impact on overall responses was examined using composite desirability (D). This metric, which ranges from 0 to 1, assigns a value of 1 to the best outcomes and 0 to the worst. In this study, the composite desirability achieved a value of 0.695, indicating that the optimization settings yielded positive results for all responses. Figure 9 displays the contour plot of desirability.

5. Discussion

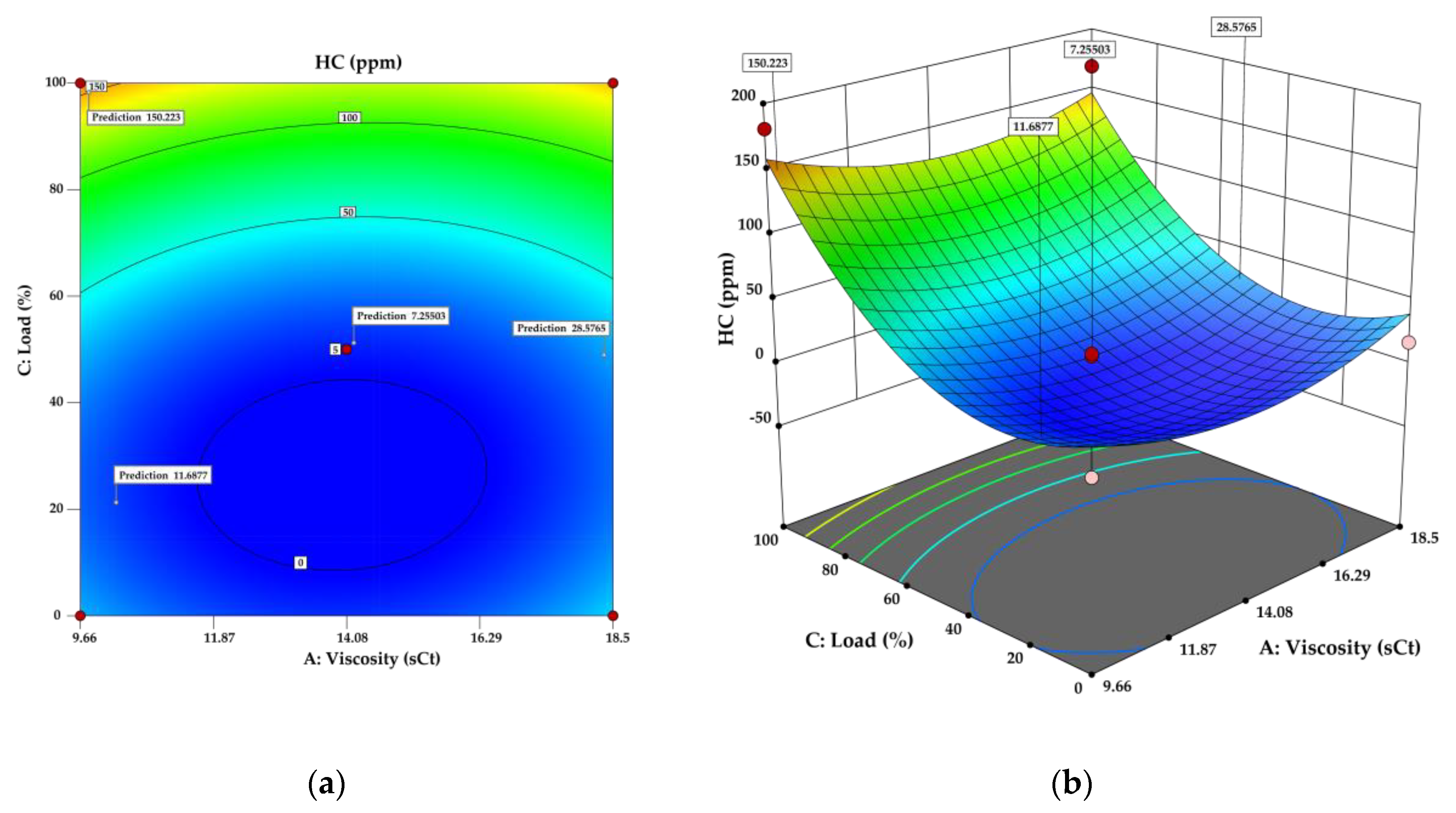
The findings of this study underscore the significant influence of oil viscosity on pollutant emissions and fuel consumption in internal combustion engines at high altitudes, as evidenced by ANOVA analyses. Reducing HC emissions to 7.25 ppm with low-viscosity oils and reduced load highlights that appropriate lubricant selection could be an effective strategy to meet stricter environmental regulations without compromising engine performance. These results are consistent with previous studies, which demonstrated that lower-viscosity lubricants can reduce internal engine friction, thus decreasing pollutant emissions.

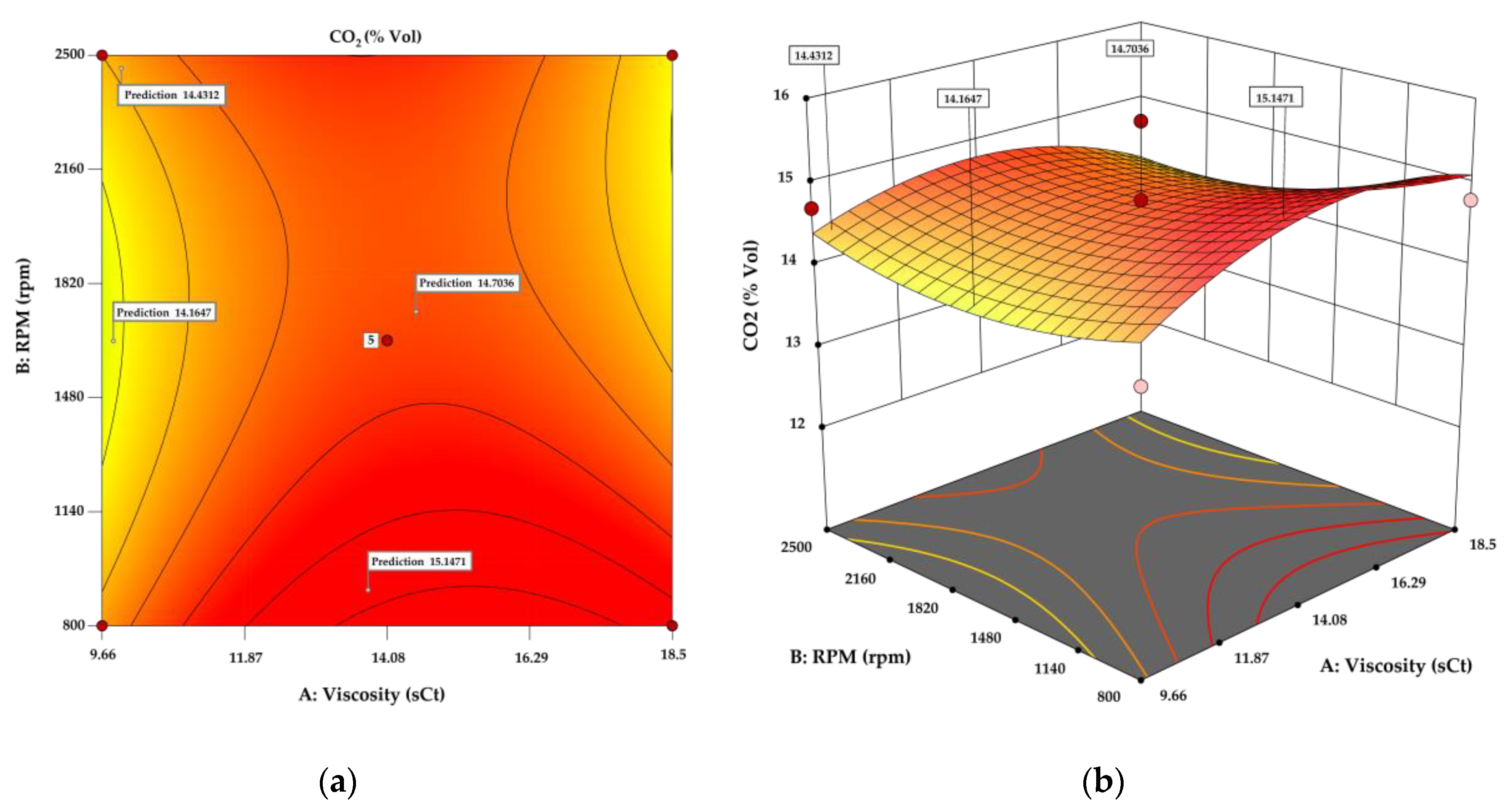
Moreover, the peak in CO₂ emissions observed with high-viscosity oils under heavy loads underscores the direct relationship between engine operating conditions and the production of greenhouse gases. This outcome, reinforced by significant ANOVA results, supports the hypothesis that interventions in lubricant formulation and engine operating conditions can play a critical role in mitigating climate change, aligning with global initiatives for carbon reduction.

RSM-based optimization revealed that adjusting the oil viscosity to 13 cSt, along with specific speed and load settings, optimally reduces emissions while maintaining fuel efficiency. This approach provides a robust framework for future research and encourages the exploration of different types of oils and engine design modifications that could further improve performance and environmental sustainability.

Future research could benefit from expanding the range of tested environmental and operational conditions, including different types of fuels and engine configurations, as suggested by the ANOVA models' interaction terms. Additionally, incorporating life cycle analysis to assess the environmental impacts of lubricant production and disposal could provide a more comprehensive understanding of the total ecological footprint.

Further investigation into developing new lubricant compounds that operate effectively across a broader range of temperatures and pressures, mainly designed for high-altitude conditions, would be valuable. Exploring the interaction between these lubricants and hybrid or electric engine technologies could also lead to integrated strategies that maximize energy efficiency and minimize emissions across the entire vehicular system.

Author Contributions

Conceptualization, M.G.T., O.C.O. and F.C.M.; methodology, M.G.T.; investigation, O.C.O. and F.C.M.; writing—original draft preparation, M.G.T., O.C.O. and F.C.M.; writing—review and editing, M.G.T.; supervision, M.G.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Pischinger, S. Current and Future Challenges for Automotive Catalysis: Engine Technology Trends and Their Impact. Top Catal 2016, 59, 834–844. [Google Scholar] [CrossRef]
Dargay, J. Road Vehicles: Future Growth in Developed and Developing Countries. Proceedings of the Institution of Civil Engineers - Municipal Engineer 2002, 151, 3–11. [Google Scholar] [CrossRef]
2030 Climate Targets - European Commission. Available online: https://climate.ec.europa.eu/eu-action/climate-strategies-targets/2030-climate-targets_en (accessed on 15 May 2024).
Beles, H.; Tusinean, A.; Mitran, T.; Scurt, F.B. Research Regarding the Development of the Combustion Chamber of Internal Combustion Engines with Opposite Pistons. Machines 2023, 11, 309. [Google Scholar] [CrossRef]
Khoa, N.X.; Lim, O. A Review of the External and Internal Residual Exhaust Gas in the Internal Combustion Engine. Energies (Basel) 2022, 15, 1208. [Google Scholar] [CrossRef]
Morgunov, B.; Chashchin, V.; Gudkov, A.; Chashchin, M.; Popova, O.; Nikanov, A.; Thomassen, Y. Health Risk Factors of Emissions from Internal Combustion Engine Vehicles: An Up-to-Date Status of the Problem. ЗДОРОВЬЕ НАСЕЛЕНИЯ И СРЕДА ОБИТАНИЯ - ЗНиСО / PUBLIC HEALTH AND LIFE ENVIRONMENT 2022, 7–14. [CrossRef]
Basshuysen, R. Van; Schaefer, F. Internal Combustion Engine Handbook Basics, Components, Systems, and Perspectives; SAE International: Warrendale, PA, 2004; ISBN 978-0-7680-1139-5. [Google Scholar]
Payri González, F.; Desantes Fernández, J.M. Motores de Combustión Interna Alternativos; Editorial Universitat politécnica de valencia, 2011; ISBN 8483637057.
Posmyk, A. Influence of Material Properties on the Wear of Composite Coatings. Wear 2003, 254, 399–407. [Google Scholar] [CrossRef]
Etsion, I.; Sher, E. Improving Fuel Efficiency with Laser Surface Textured Piston Rings. Tribol Int 2009, 42, 542–547. [Google Scholar] [CrossRef]
Silva, C.; Ross, M.; Farias, T. Analysis and Simulation of “Low-Cost” Strategies to Reduce Fuel Consumption and Emissions in Conventional Gasoline Light-Duty Vehicles. Energy Convers Manag 2009, 50, 215–222. [Google Scholar] [CrossRef]
Fontaras, G.; Vouitsis, E.; Samaras, Z. Experimental Evaluation of the Fuel Consumption and Emissions Reduction Potential of Low Viscosity Lubricants.; June 15 2009.
Macián, V.; Tormos, B.; Bermúdez, V.; Ramírez, L. Assessment of the Effect of Low Viscosity Oils Usage on a Light Duty Diesel Engine Fuel Consumption in Stationary and Transient Conditions. Tribol Int 2014, 79, 132–139. [Google Scholar] [CrossRef]
Murari, G.; Nahak, B.; Pratap, T. Hybrid Surface Modification for Improved Tribological Performance of IC Engine Components – a Review. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering 2023, 095440892211507. [Google Scholar] [CrossRef]
Ha Hiep, N.; Cong Doan, N.; Quoc Quan, N.; Van Duong, N. Structural Modifications of the Inner Surface of Cylinder Liners for Decreasing Mechanical Losses in High-Speed Diesel Engines.; April 27 2023.
Hazar, H. Effects of Biodiesel on a Low Heat Loss Diesel Engine. Renew Energy 2009, 34, 1533–1537. [Google Scholar] [CrossRef]
Balaji, M.; Sarfas, M.; Vishaal, G.S.B.; Madhusudhan, G.V.; Gupta, S.; Kanchan, S. Scope for Improving the Efficiency and Environmental Impact of Internal Combustion Engines Using Engine Downsizing Approach: A Comprehensive Case Study. IOP Conf Ser Mater Sci Eng 2021, 1116, 012070. [Google Scholar] [CrossRef]
Menon, S.; Cadou, C. Scaling of Losses in Small IC Aero Engines with Engine Size. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit; American Institute of Aeronautics and Astronautics:, Reston, Virigina, 5 January 2004. [Google Scholar]
Leduc, P.; Dubar, B.; Ranini, A.; Monnier, G. Downsizing of Gasoline Engine: An Efficient Way to Reduce CO₂ Emissions. Oil & Gas Science and Technology 2003, 58, 115–127. [Google Scholar] [CrossRef]
Podrigalo, M.; Tarasov, Y.; Kholodov, M.; Shein, V.; Tkachenko, A.; Kasianenko, O. Assessment of Increased Energy Efficiency of Vehicles with a Rational Reduction of Engine Capacity. Automobile transport 2022, 26–34. [Google Scholar] [CrossRef]
Hernández-Comas, B.; Maestre-Cambronel, D.; Pardo-García, C.; Fonseca-Vigoya, M.D.S.; Pabón-León, J. Influence of Compression Rings on the Dynamic Characteristics and Sealing Capacity of the Combustion Chamber in Diesel Engines. Lubricants 2021, 9, 25. [Google Scholar] [CrossRef]
Macián, V.; Tormos, B.; Bermúdez, V.; Ramírez, L. Assessment of the Effect of Low Viscosity Oils Usage on a Light Duty Diesel Engine Fuel Consumption in Stationary and Transient Conditions. Tribol Int 2014, 79, 132–139. [Google Scholar] [CrossRef]
Fan, Q.; Wang, Y.; Xiao, J.; Wang, Z.; Li, W.; Jia, T.; Zheng, B.; Taylor, R. Effect of Oil Viscosity and Driving Mode on Oil Dilution and Transient Emissions Including Particle Number in Plug-In Hybrid Electric Vehicle.; April 14 2020.
Taylor, R.I.; Coy, R.C. Improved Fuel Efficiency by Lubricant Design: A Review. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology 2000, 214, 1–15. [Google Scholar] [CrossRef]
Hei, D.; Zheng, M.; Liu, C.; Jiang, L.; Zhang, Y.; Zhao, X. Study on the Frictional Properties of the Top Ring-Liner Conjunction for Different-Viscosity Lubricant. Advances in Mechanical Engineering 2023, 15, 168781322311550. [Google Scholar] [CrossRef]
Macián, V.; Tormos, B.; Ramírez, L.; Pérez, T.; Martínez, J. CO ₂ Emissions Reduction by Using Low Viscosity Oils in Public Urban Bus Fleets.; June 2 2015; pp. 255–266.
Hawley, J.G.; Bannister, C.D.; Brace, C.J.; Akehurst, S.; Pegg, I.; Avery, M.R. The Effect of Engine and Transmission Oil Viscometrics on Vehicle Fuel Consumption. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering 2010, 224, 1213–1228. [Google Scholar] [CrossRef]
Ishizaki, K.; Nakano, M. Reduction of CO₂ Emissions and Cost Analysis of Ultra-Low Viscosity Engine Oil. Lubricants 2018, 6. [Google Scholar] [CrossRef]
Minami, I.; Murakami, H.; Nanao, H.; Mori, S. Additive Effect for Environmental Lubricants—Decreased Phosphorus Contents in Low Viscosity Base Oils for Antiwear Performance—. Journal of the Japan Petroleum Institute 2006, 49, 268–273. [Google Scholar] [CrossRef]
Taylor, C.M. Engine Tribology; Elsevier, 1993; Vol. 26; ISBN 0080875904.
Ceballos, J.J.; Melgar, A.; Tinaut, F.V. Influence of Environmental Changes Due to Altitude on Performance, Fuel Consumption and Emissions of a Naturally Aspirated Diesel Engine. Energies (Basel) 2021, 14, 5346. [Google Scholar] [CrossRef]
Qi, Z.; Gu, M.; Cao, J.; Zhang, Z.; You, C.; Zhan, Y.; Ma, Z.; Huang, W. The Effects of Varying Altitudes on the Rates of Emissions from Diesel and Gasoline Vehicles Using a Portable Emission Measurement System. Atmosphere (Basel) 2023, 14, 1739. [Google Scholar] [CrossRef]
Liu, Z.; Liu, J. Investigation of the Effect of Simulated Atmospheric Conditions at Different Altitudes on the Combustion Process in a Heavy-Duty Diesel Engine Based on Zero-Dimensional Modeling. J Eng Gas Turbine Power 2022, 144. [Google Scholar] [CrossRef]
Wan, M.; Huang, F.; Shen, L.; Lei, J. Experimental Investigation on Effects of Fuel Injection and Intake Parameters on Combustion and Performance of a Turbocharged Diesel Engine at Different Altitudes. Front Energy Res 2023, 10. [Google Scholar] [CrossRef]
He, C.; Ge, Y.; Ma, C.; Tan, J.; Liu, Z.; Wang, C.; Yu, L.; Ding, Y. Emission Characteristics of a Heavy-Duty Diesel Engine at Simulated High Altitudes. Science of The Total Environment 2011, 409, 3138–3143. [Google Scholar] [CrossRef]
Zheng, Y.M.; Xie, L.B.; Liu, D.Y.; Ji, J.L.; Li, S.F.; Zhao, L.L.; Zen, X.H. Emission Characteristics of Heavy-Duty Vehicle Diesel Engines at High Altitudes. Journal of Applied Fluid Mechanics 2023, 16, 2329–2343. [Google Scholar] [CrossRef]

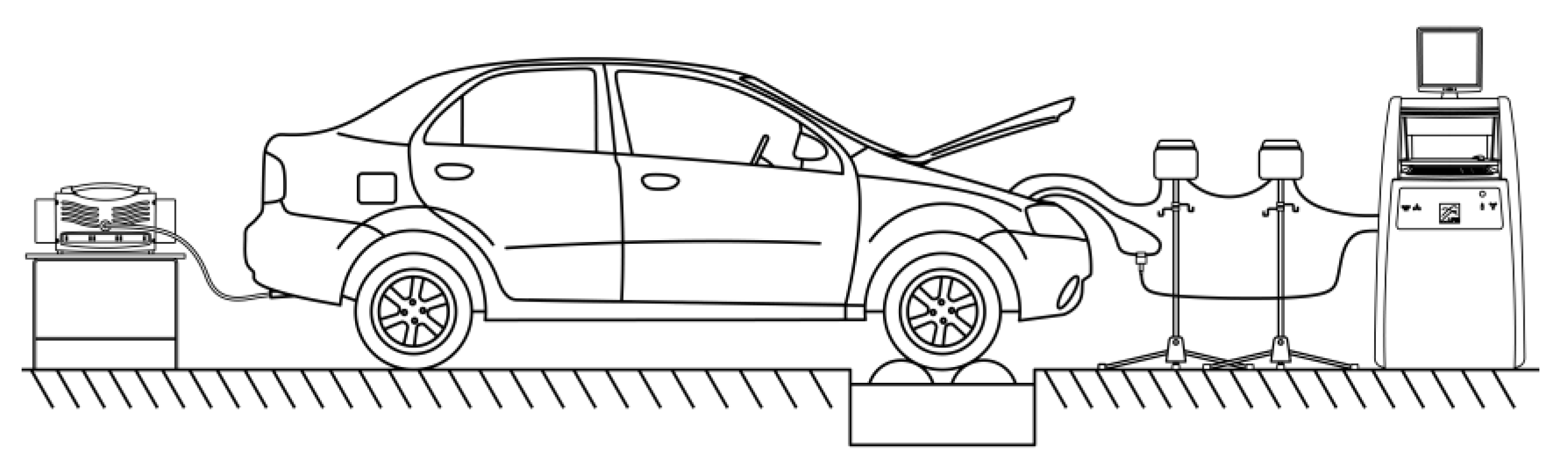
Figure 1. Experimental unit.

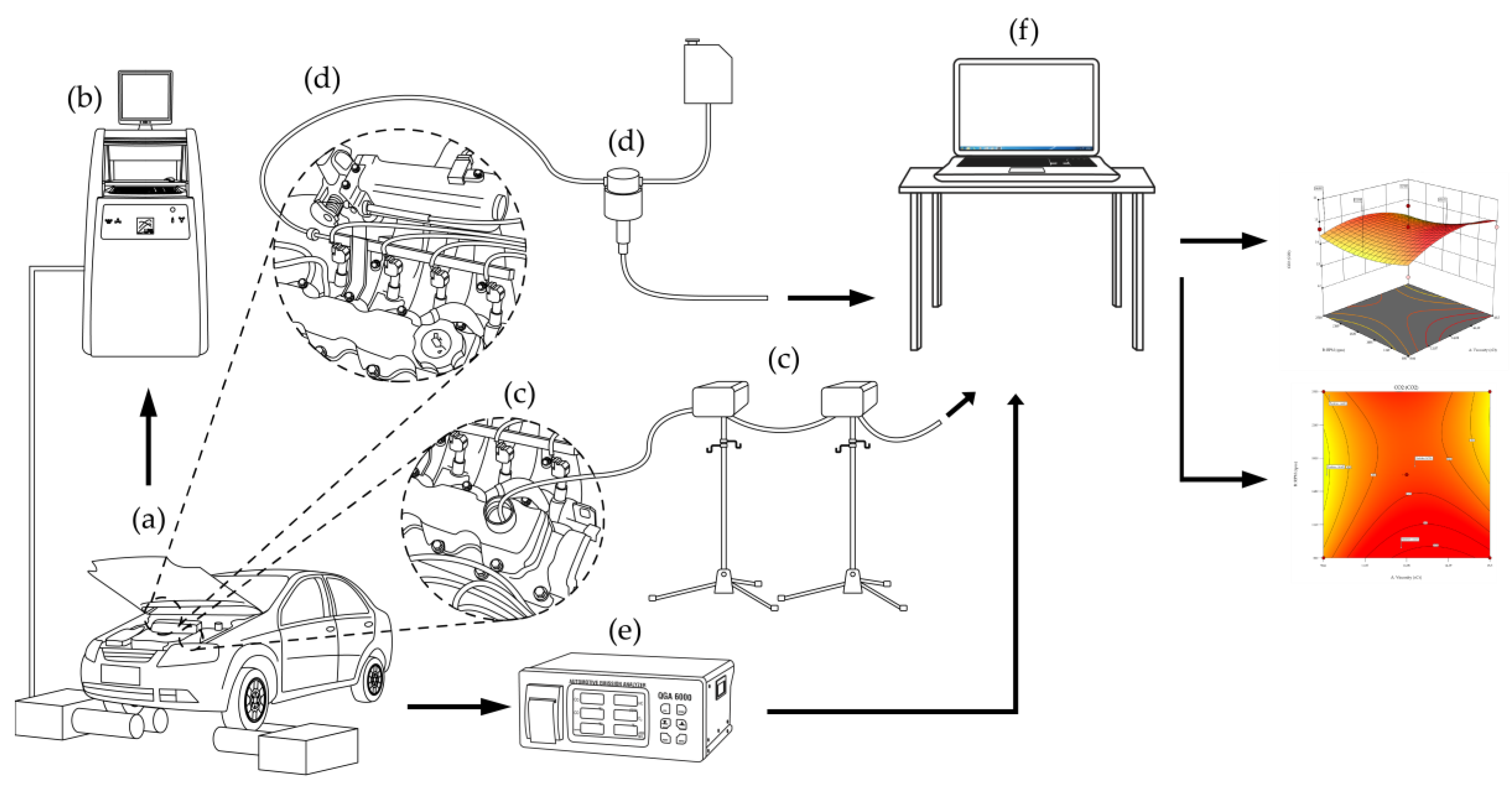
Figure 2. Schematic of the experimental setup.

Figure 3. (a) Contour plot and (b) Response surface for HC.

Figure 4. (a) Contour plot and (b) Response surface for CO_2.

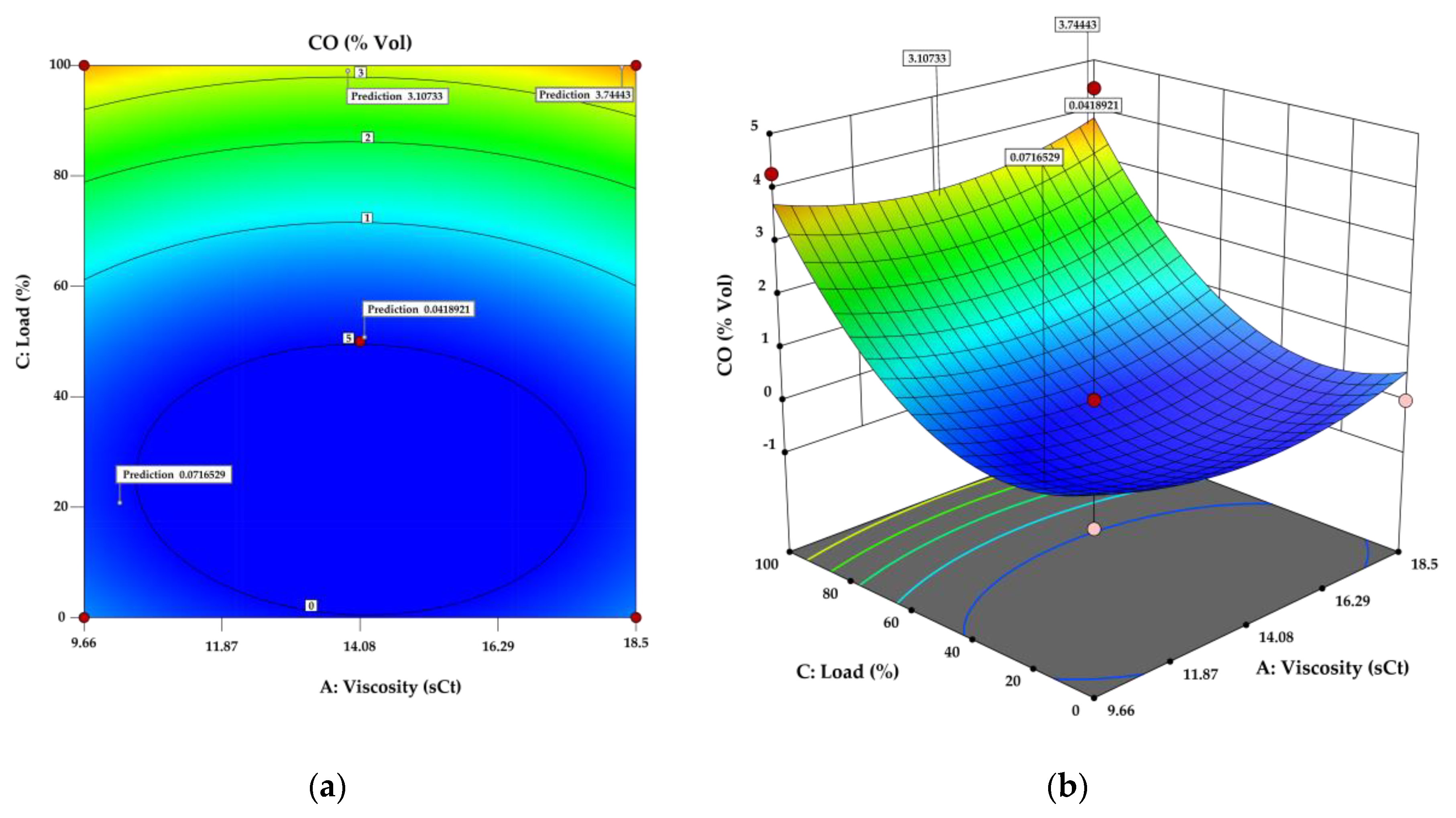
Figure 5. (a) Contour plot and (b) Response surface for CO

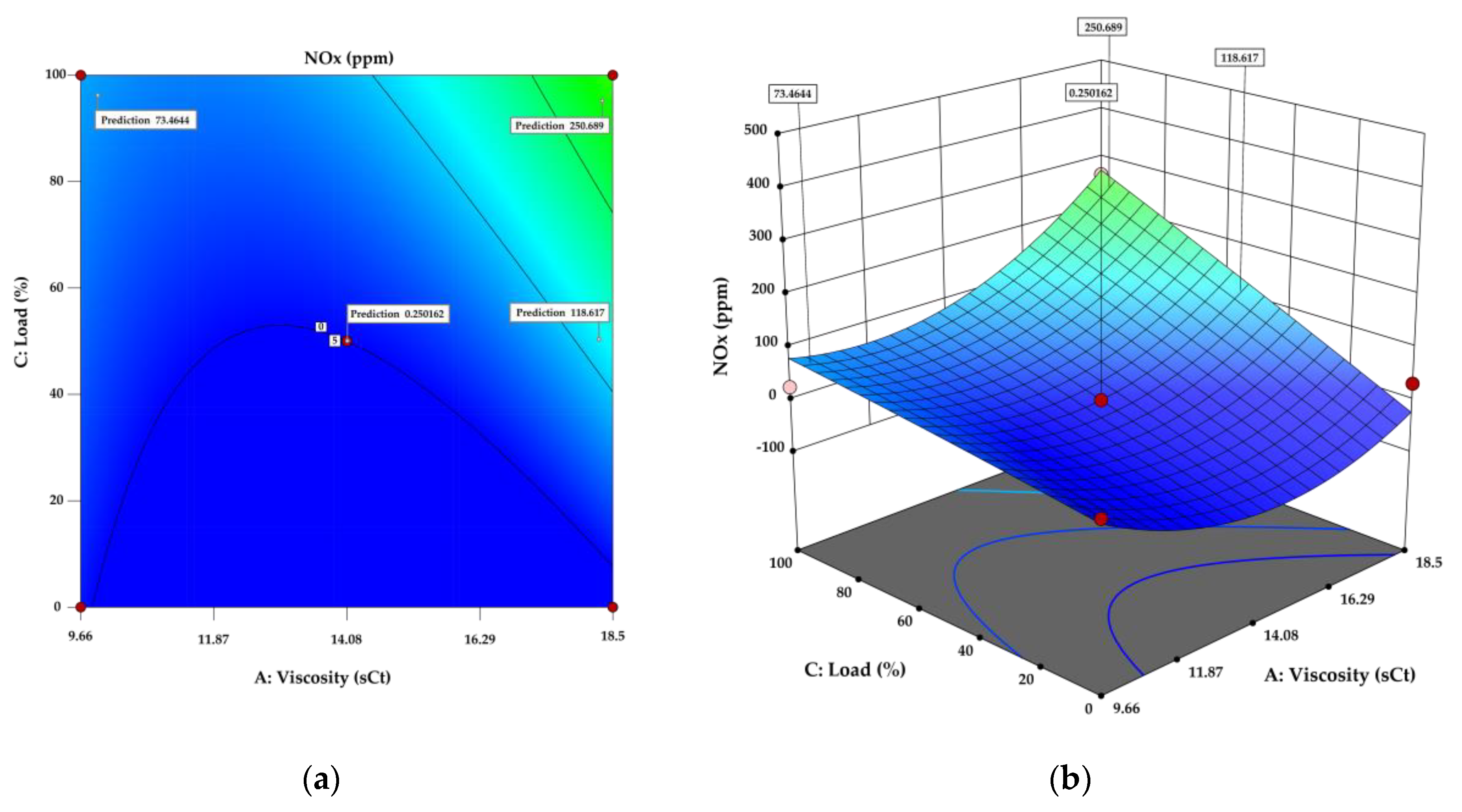
Figure 6. Contour plot and (b) Response surface for NOx

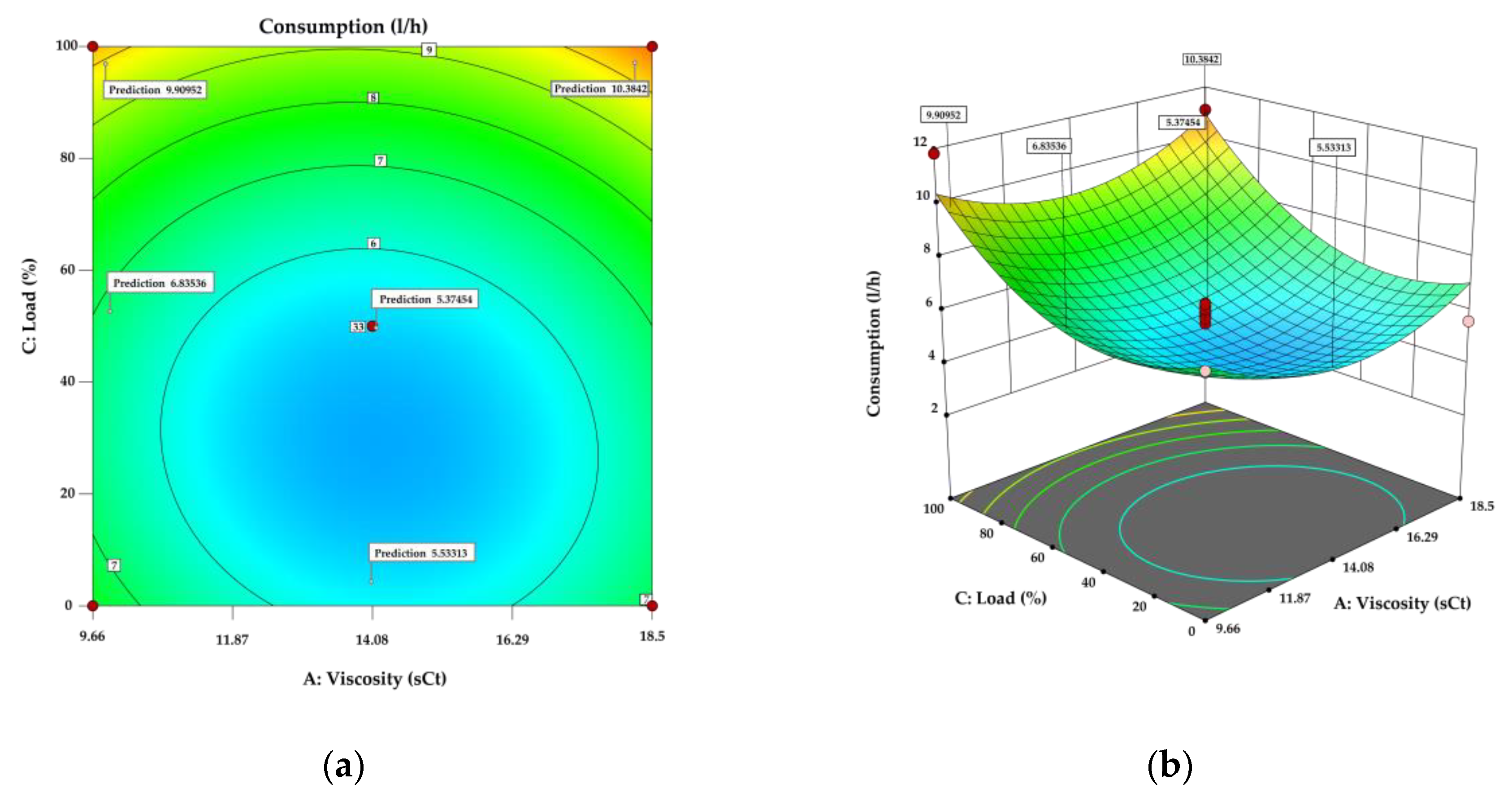
Figure 7. (a) Contour plot and (b) Response surface of Consumption

Figure 8. Identified optimum point.

Figure 9. Contour plot of desirability.

Table 1. Main characteristics of the test engine.

Technical specifications
Engine	1.5 L SOHC
Valves	8
Number of cylinders	4
Power (hp @ rpm)	83 @ 5600
Torque (Nm @ rpm)	128 @ 3000
Fuel supply	MPFI
Compression ratio	9.5
Final Ratio	3.944
Gross vehicle weight	1,365 Kg
Load Capacity	325 Kg

Table 2. Technical specifications of the gas analyzer.

Measuring fields	Range	Unit	Resolution
CO	0 – 9,99	% vol	0.01
CO₂	0 – 19,9	% vol	0.1
HC hexane	0 – 9,999	ppm vol	1
O₂	0 – 25	% vol	0.01
NOx	0 – 5,000	ppm vol	1
Lambda	0.5 – 5		0.001
Revolutions Inductance/capacitance	300 – 9,990	rpm	10
Oil temperature	20 – 150	°C	1

Table 3. Technical specifications of the oils used in the study.

SAE grade	5w30	10w30	20w50
Specific Gravity @ 60°F	0.861	0.866	0.881
Density, lbs/gal @ 60°F	7.17	7.21	7.33
Color, ASTM D1500	3.0	3.0	3.0
Flash Point (COC), °C (°F)	216 (421)	229 (444)	230 (446)
Pour Point, °C (°F)	-39 (-38)	-39 (-38)	-30 (-22)
Kinematic Viscosity @ cSt @ 40°C	66.2	65.7	176
Kinematic Viscosity @ cSt @ 100°C	9.66	14.08	18.5
Viscosity Index	158	148	128
Cold Cranking Viscosity, cP @ (°C)	6,150 (-30)	4,550 (-25)	7,200 (-15)
High-Temp/High-Shear Viscosity, cP @ 150°C	3.1	3.0	4.9

Table 4. Input variables and levels of the experiment.

Factor	Unit	Lower level	Middle level	Upper level
Viscosity	sCt	9.66	14.08	18.5
Engine speed	rpm	800	1650	2500
Load	%	0	50	10

Table 5. ANOVA results for HC.

Source	Sum of Squares	Df	Mean Square	F-value	p-value
Model	56264.32	9	6251.59	6.36	0.0117	significant
A-Viscosity	12.50	1	12.50	0.0127	0.9134
B-RPM	3042.00	1	3042.00	3.09	0.1220
C-Load	27144.50	1	27144.50	27.61	0.0012
AB	36.00	1	36.00	0.0366	0.8537
AC	81.00	1	81.00	0.0824	0.7824
BC	4900.00	1	4900.00	4.98	0.0607
A²	3035.46	1	3035.46	3.09	0.1223
B²	1883.46	1	1883.46	1.92	0.2088
C²	16107.04	1	16107.04	16.38	0.0049
Residual	6881.80	7	983.11
Lack of Fit	6849.00	3	2283.00	278.41	< 0.0001	significant
Pure Error	32.80	4	8.20
Cor Total	63146.12	16

Table 6. Coefficient of determination for HC.

Coefficient of determination	Value
R²	0.8910
Adjusted R²	0.7509
Predicted R²	-0.7362

Table 7. ANOVA results for CO₂.

Source	Sum of Squares	Df	Mean Square	F-value	p-value
Model	14.13	9	1.57	4.59	0.0285	significant
A-Viscosity	0.1013	1	0.1013	0.2959	0.6034
B-RPM	0.4513	1	0.4513	1.32	0.2886
C-Load	8.00	1	8.00	23.38	0.0019
AB	0.1600	1	0.1600	0.4675	0.5161
AC	0.0025	1	0.0025	0.0073	0.9343
BC	1.56	1	1.56	4.57	0.0700
A²	0.9904	1	0.9904	2.89	0.1327
B²	0.4178	1	0.4178	1.22	0.3057
C²	2.43	1	2.43	7.11	0.0322
Residual	2.40	7	0.3422
Lack of Fit	2.39	3	0.7958	397.92	< 0.0001	significant
Pure Error	0.0080	4	0.0020
Cor Total	16.52	16

Table 8. Coefficient of determination for CO₂.

Coefficient of determination	Value
R²	0.8550
Adjusted R²	0.6687
Predicted R²	-1.3124

Table 9. ANOVA results for CO.

Source	Sum of Squares	Df	Mean Square	F-value	p-value
Model	39.85	9	4.43	6.57	0.0107	significant
A-Viscosity	0.0021	1	0.0021	0.0031	0.9569
B-RPM	2.07	1	2.07	3.07	0.1232
C-Load	20.29	1	20.29	30.09	0.0009
AB	0	1	0	0	10.000
AC	0.0072	1	0.0072	0.0107	0.9205
BC	4.1	1	4.1	6.08	0.0431
A²	1.39	1	1.39	2.06	0.1942
B²	1.39	1	1.39	2.07	0.1936
C²	10.67	1	10.67	15.83	0.0053
Residual	4.72	7	0.6742
Lack of Fit	4.72	3	1.57	12100.58	< 0.0001	significant
Pure Error	0.0005	4	0.0001
Cor Total	44.57	16

Table 10. Coefficient of determination for CO.

Coefficient of determination	Value
R²	0.8941
Adjusted R²	0.7579
Predicted R²	-0.6943

Table 11. ANOVA results for NOx.

Source	Sum of Squares	Df	Mean Square	F-value	p-value
Model	4.95E+05	9	54953.48	12.96	0.0014	significant
A-Viscosity	13203.13	1	13203.13	3.11	0.121
B-RPM	2.05E+05	1	2.05E+05	48.45	0.0002
C-Load	69006.13	1	69006.13	16.27	0.005
AB	756.25	1	756.25	0.1783	0.6855
AC	12769	1	12769	3.01	0.1263
BC	35532.25	1	35532.25	8.38	0.0232
A²	32606.32	1	32606.32	7.69	0.0276
B²	1.18E+05	1	1.18E+05	27.77	0.0012
C²	37.89	1	37.89	0.0089	0.9273
Residual	29684.25	7	4240.61
Lack of Fit	29684.25	3	9894.75			significant
Pure Error	0	4	0
Cor Total	5.24E+05	16

Table 12. Coefficient of determination for NOx.

Coefficient of determination	Value
R²	0.9434
Adjusted R²	0.8706
Predicted R²	0.0941

Table 13. ANOVA results for Consumption.

Source	Sum of Squares	Df	Mean Square	F-value	p-value
Model	72.69	9	8.08	11.05	< 0.0001	significant
A-Viscosity	0.0061	1	0.0061	0.0083	0.928
B-RPM	0.4278	1	0.4278	0.5855	0.4493
C-Load	22.34	1	22.34	30.58	< 0.0001
AB	0.81	1	0.81	1.11	0.2996
AC	0.2601	1	0.2601	0.3559	0.5546
BC	1.92	1	1.92	2.63	0.1142
A²	12.91	1	12.91	17.67	0.0002
B²	6.9	1	6.9	9.44	0.0041
C²	20.7	1	20.7	28.33	< 0.0001
Residual	25.58	35	0.7307
Lack of Fit	8.8	3	2.93	5.6	0.0034	significant
Pure Error	16.78	32	0.5242
Cor Total	98.27	44

Table 14. Coefficient of determination for Consumption.

Coefficient of determination	Value
R²	0.7397
Adjusted R²	0.6728
Predicted R²	-0.6143

Table 15. Optimization Setup.

Name	Goal	Lower Limit	Upper Limit	Lower Weight	Upper Weight	Importance
A: Viscosity (sCt)	is in range	9.66	18.5	1	1	3
B: RPM (rpm)	is in range	800	2500	1	1	3
C: Load (%)	is in range	0	100	1	1	3
HC (ppm)	minimize	1	181	1	1	3
CO₂ (% Vol)	minimize	12.1	14.9	1	1	3
CO (% Vol)	minimize	0	4.43	1	1	3
NOx (ppm)	minimize	0	498	1	1	3
Consumption (l/h)	minimize	3.67	11.82	1	1	3

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Impact of Oil Viscosity on Emissions and Fuel Efficiency at High Altitudes: An RSM Analysis

Abstract

1. Introduction

2. Materials and Methods

2.1. Description of the Experimental Setup

2.2. Response Surface Methodology

3. Results

3.1. Model for HC.

3.2. Model for CO2

3.3. Model for CO

3.4. Model for NOx

3.5. Model for Consumption

4. RSM Based Optimization

5. Discussion

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3.2. Model for CO₂