Preprint
Article
Hydrogen Bond Strengthens Acceptor Group: The Curious Case of The C-H...O=C Bond
Altmetrics
Downloads
83
Views
34
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.pdf (7.30MB )
This version is not peer-reviewed
Submitted:
04 July 2024
Posted:
12 July 2024
You are already at the latest version
Alerts
Abstract
An H-bond involves the sharing of a hydrogen atom between an electronegative atom to which it is covalently bound (the donor) and another electronegative atom serving as an electron acceptor. Such bonds represent a critically important geometrical force in biological macromolecules and, as such, have been characterized extensively. H-bond formation invariably leads to a weakening within the acceptor moiety due to the pulling exerted by the donor hydrogen. This phenomenon can be compared to a spring connecting two masses; pulling one mass stretches the spring, similarly affecting the bond between the two masses. Herein, we describe the opposite phenomenon when investigating the energetics of the C-H...O=C bond. This bond underpins the most prevalent protein transmembrane dimerization motif (GxxxG) in which a glycine C-H on one helix forms a hydrogen bond with a carbonyl in a nearby helix. We use isotope-edited FT-IR spectroscopy and corroborating computational approaches to demonstrate a surprising strengthening of the acceptor C=O bond upon binding with the glycine C-H. We show that electronic factors associated with the C-H bond strengthen the C=O oscillator by increasing the s-character of the -bond, lowering the hyperconjugative disruption of the -bond. In addition, a reduction of the acceptor C=O bond’s polarity is observed upon the formation of the C-H...O=C bond. Our findings challenge the conventional understanding of H-bond dynamics and provide new insights into the structural stability of inter-helical protein interactions.
Keywords:
Subject: Biology and Life Sciences - Biophysics
1. Introduction
Hydrogen bonding is one of the most important forces governing molecular integrity in the physical and biological worlds. It describes the sharing of a hydrogen that is covalently bound to an electronegative Donor atom, with another electronegative Acceptor atom that has a lone pair of electrons: D−H···A.
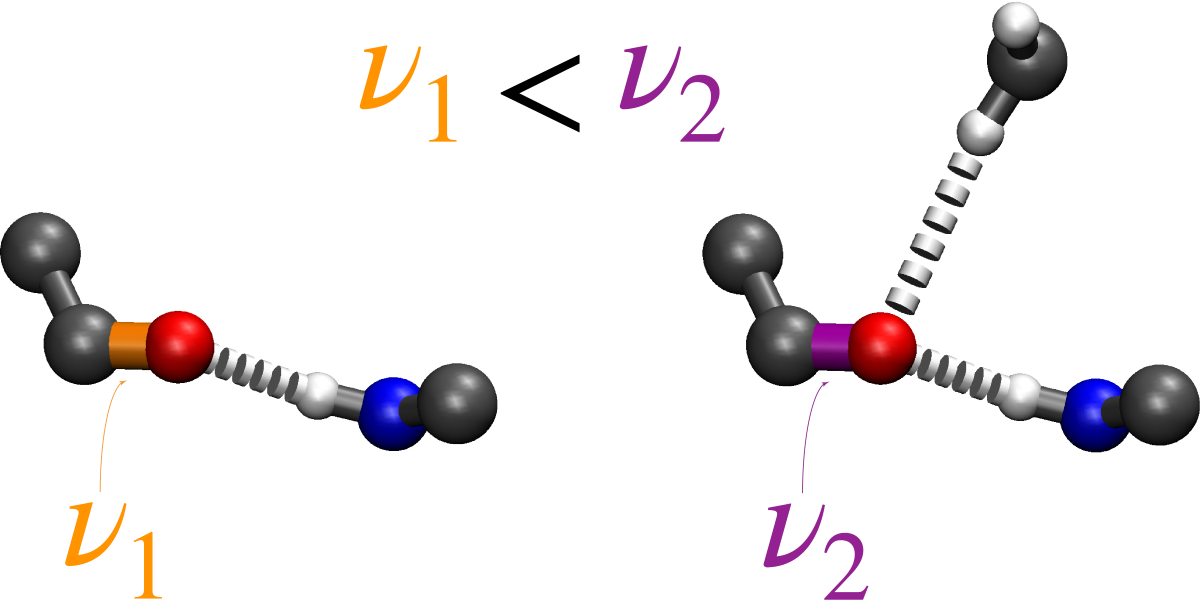
In the biological world, the acceptor group is often composed of nitrogen or oxygen bound to a carbon. Upon H-bonding, the C−O or C−N bonds are weakened due to the pulling exerted on the electronegative atom by the hydrogen. In the current study, we identified the opposite effect, wherein the acceptor of an H-bond is surprisingly strengthened upon H-bonding. Consequently, by looking into the governing factors of H-bond formation, we aimed to examine the roots of this unexpected and intriguing observation.
Theoretical and experimental findings describe the formation of hydrogen bonds due to several energy components: electrostatic attraction, electron delocalization, charge transfer, dispersive interactions, cooperative effects, steric effects, and secondary interactions [1].
H-bonds in proteins exhibit variations in these energy components, tailored to fulfill the specific physiological role of the molecule [2]. The nature of H-bonds in proteins is further influenced by the molecular makeup of the donor and acceptor, the protein backbone, and the side chain [3,4].
One can classify protein and peptide H-bonds as canonical or noncanonical. Canonical or conventional H-bonds are formed by regular and predictable H-bonding interactions, like the i to H-bonds formed between the C=O and N−H groups in -helices [5]. Noncanonical H-bonds exhibit a significantly larger variation of donor and acceptor groups and a multiplicity of partners. For example, an over-coordinated system entails several donors bonded to a single acceptor, while multifurcation involves a single donor with multiple acceptors. Experimental and computational analyses have shown that some of these noncanonical bonds are highly important for protein structure [6,7].
An important class of noncanonical H-bonds in proteins are those formed between the a C hydrogen and a carbonyl oxygen [8,9,10,11,12,13,14,15]. X-ray and neutron crystallography have confirmed the identity of C−H···O=C hydrogen bonds within the protein environment in the presence of a solvent, other proteins, and ligands [16,17], suggesting an essential role in catalytic activity [18]. These important hydrogen bonding schemes necessitate detailed analyses to provide a quantitative understanding of their role in macromolecules.
The C−H···O=C hydrogen bond in a transmembrane helical dimerization interface, was first identified in glycophorin A [19]. The interface has a GxxxG motif, one of the most prevalent oligomerization factors in transmembrane helices [20,21]. In the GxxxG motif of glycophorin A, the C−Hs of glycines 79 and 83 form H-bonds with the carbonyls of isoleucine 76 and valine 80 in the opposing helix, respectively. Such bonds form the basis of the GxxxG dimerization motif [13].
Previous attempts to measure the energetics of the C−H···O=C H-bonds resulted in varying estimates. Using a mutagenesis cycle analysis, Bowie and coworkers found that such bonds are not stabilizing [22], while an empirical FTIR-based approach indicated a bond enthalpy of 0.88 kcal/mol [23].
Considering the prevalence of the C−H···O=C interaction and its contested contribution to protein stability, we decided to examine the energetics of C−H···O=C hydrogen bonds using a combination of experimental and computational methods. Experimentally, we employed vibrational spectroscopy, an exquisitely sensitive tool to measure H-bond strength. Computationally, we use Molecular Dynamic Simulations and DFT calculations that can yield detailed energetics and vibrational shifts that can be verified with experiments. Specifically, we targeted the frequency change of the C=O acceptor upon H-bond formation, made possible by isotopic labelling to resolve the specific carbonyl group [24,25]. This combined approach enabled us to both measure the strength of this interaction and explain the source of its curious spectroscopic behavior.
2. Results and Discussion
Glycophorin A is the first membrane protein to have its sequence determined [26] and is the archetypical GxxxG containing transmembrane domain dimer [13,19,27]. The GxxxG motif enables close positing of the two helices with minimal steric hindrance due to the small size of the glycine hydrogen side-chain that H-bonds to a carbonyl residue in the other helix. Figure 1 depicts the bond between the C−H of Gly83 and the carbonyl acceptor of Val80. Note that the acceptor is also involved in a canonical H-bond with the backbone amide donor hydrogen Val84. Hence, Val80’s carbonyl group participates in an over-coordinated H-bonding interaction.
We spectroscopically isolated the C−H···O=C bond in Glycophorin A by editing of Val80’s carbonyl group with 13C and 18O. Due to the fact that the amide I mode is composed mainly of the C=O stretch [28], such labeling baseline resolves the isotope-edited mode from the unlabelled amide groups by shifting it more than 60 cm−1, enabling detailed site-specific analysis of the labeled peak separately from the unlabeled peak. [25]. Accordingly, as shown in Figure 2, the 13C=18O amide I mode of Val80 within glycophorin A is shifted to 1599.4 cm−1, which is 62 cm−1 from the main amide-I envelope of the protein. The entire spectra of both peptides, in which all other vibrational modes arising from the lipid and protein can be observed, are presented in Figure S1.
The peptide encompasses the transmembrane domain of wild-type glycophorin A, a strongly dimeric species [27,29,30] in which the C−H···O=C hydrogen bond exists [13,19]. Therefore, to determine the impact of the Gly83–Val80 inter-helical H-bond, we measured the spectrum obtained from a peptide containing the Gly79Leu monomerizing mutation which separates the helices and so the bond does not exist [27].
In the monomeric protein that does not contain the noncanonical H-bond, the isotope-labeled amide I mode resonates at 1596.8 cm−1, which is lower than the H-bonded dimeric species by 1.7 cm−1 (Figure 2). These results appear surprising since H-bond formation is expected to reduce the vibrational energy of the acceptor carbonyl and thus shift the isotope-edited carbonyl peak to lower frequencies when it is involved in a hydrogen bond.
We note that previous studies report a blue shifting of an H-bond donor. For example, using computational tools, Schlegel and colleagues have elucidated the electrostatic origin of this shift [31]. However, to the best of our knowledge, we are reporting for the first time the blue shift of the stretching frequency of an H-bond acceptor C=O in proteins.
To understand the root of the surprising frequency shift, we employed DFT-based computational tools that detail the characteristics of such H-bonds [32]. The size of a transmembrane helix system is beyond the current capabilities of detailed quantum calculations. Therefore, two mimetic systems that capture the specific H-bonding interactions were analyzed and compared (see supplementary Figure S4):
- Monomer (single H-bond):
- The canonical -helical H-bond between the carbonyl of valine 80 and the amide H of glycine 84 was mimicked by two N-methylacetamides.
- Dimer (two H-bonds):
- The inter-helical H-bonding system contained the canonical H-bond described above, with an additional non-canonical inter-helical hydrogen bond. The C−H of glycine 83 from the opposing helix is bonded to the same carbonyl of valine 80 that is also involved in the canonical hydrogen bond. This system was mimicked by two N-methylacetamides forming the canonical H-bond to which an acetylglycinemethylamide is hydrogen bonded.
To ensure that the calculations replicate the experimental system accurately, we sought to superimpose the coordinates of the atoms on the corresponding groups of the transmembrane protein. However, only the structure of the wild-type, dimeric glycophorin A, has been solved experimentally [19,33]. Moreover, the structures were elucidated in micelles or bicelles but not in a lipid bilayer, the native environment of the protein and the one in which the FTIR spectra were obtained. Therefore, we used molecular dynamics (MD) simulations in hydrated 1,2-dimyristoyl-sn-glycero-3-phosphocholine bilayers to determine the atom positions in the wild-type, dimeric glycophorin A and a monomeric glycophorin A peptide that contains the G79I mutations. In both instances, the experimentally determined structure in bicelles was used as a starting point [33]. The results of the MD simulation can be seen in supporting information, Figure S2, depicting structures of both monomer and dimer species and Figure S3 showing the root mean square deviation for each species.
We extended the utility of the MD simulations beyond creating mimetic systems for density functional theory (DFT) calculations, applying them also to geometric analyses of bond parameters. The geometry of a bond, and in particular its distance and angle influences its energetics and, consequently, the vibrational frequency. Previous research, has highlighted the variability of H-bond distances along helical peptides, discussing a trend of bond shortening at helix midpoints due to the cooperative effect of H-bonding along the length of the helix [34]. Similarly, Tan et al. have shown how the strength of an H-bond is dependent on the donor-acceptor angle, introducing the concept of an `antecedent angle’, which varies across protein secondary structures [35].
We calculated hydrogen bond distances and angles within our simulated systems. Specifically, we found the average O···N distance between Val80’s C=O and Val84’s N−H along the same helix to be Å in the dimeric species of glycophorin A, compared to Å in the monomeric variant. On the other hand, the C−O···N bond angle was in the dimer and in the monomer.
Hydrogen bonding interactions between donor and acceptor moieties can be both dipolar and electronic. An electronic interaction is possible when the donor N-H anti-bonding orbital overlaps the C=O oxygen nonbonding orbital. Electronic interactions are optimal when the C−O···N angle is near 120 [36], facilitating maximal overlap of these orbitals. But in protein systems, there are typically geometric constraints that restrict such bond angles to around 155 [35,37].
In the the dimeric model, with the additional inter-helical H-bond, a 3 wider C−O···N bond angle is observed relative to the monomeric model. This finding points to a reduced C=O to N−H canonical hydrogen bond strength. On the other hand, the canonical H-bond distance upon dimer formation was shortened by 0.09 Å , potentially increasing orbital overlap and thus increasing the canonical C=O···H−N interaction strength. Given the competing influences observed, MD simulations alone do not provide a definitive conclusion on the dominant effect on if the canonical hydrogen bonding strength should increase or decrease in the dimer system versus the monomer system. Such ambiguity is perhaps not unexpected due to the simplicity of the point charge model of the MD force field). Therefore, we proceeded to conduct quantum mechanical calculations for each system in which the C=O oscillator strength and other parameters can be estimated with greater accuracy, and the hydrogen bond strength directly inferred.
We calculated the frequencies of the amide I stretching modes (C=0) of both the monomeric and dimeric systems. We chose several points of time from the MD simulation trajectory to make model systems for DFT calculations and expressed the results as a time average form. (see Experimental section) The average Val80 C=0 value for the dimeric glycophorin A is cm−1, whereas for the monomeric species (with the G79I mutation) the frequency is cm−1. Notably, there is a 3.7 cm−1 increase in the C=O stretching upon dimer formation which corresponds with the FTIR experimental C=0 shift upon dimer formation. Hence, the surprising C=O bond strengthening is obtained both experimentally and computationally. The observed shift is independent of isotopic substitution. The 12C=16O variant of the construct produced a shift of 4.1 cm−1 comparable to the 13C=18O analog that yielded an average shift of 4.2 cm−1, arising from the stretching frequencies cm−1 for dimer and cm−1 for monomer.
In a typical H-bond, the acceptor (C=O in this instance) transfers electrons to the donor anti-bonding orbital, reducing the double bond character of the C=O, reflected as a decrease in C=0. The H-bond of a C=O···H−D undergoes a hyperconjugative C+−O−H···D− type interaction (analogous to charge transfer) that in turn lowers the double bond character of C=O. [38]
To explore the electronic basis of the observed acceptor vibrational mode strengthening of the dimer system (upon over-coordination with the additional inter-helical hydrogen bond), we employed Natural Bonding Orbital (NBO) calculations to analyze the estimated electron distributions and atomic orbitals in a localized way. Local hybrid orbitals can be extracted using the NBO approach, which can correlate with classical qualitative bonding theories [39]. Alabugin et al. have shown how imperfect H-bonds can be analyzed by the NBO approach by showing the hyperconjugation effects [38].
According to valence bond theory, a C=O bond should be formed by the overlap of two sp2-orbitals from the C and O atoms to form a -bond, and two p-orbitals from the C and O atoms to form a -bond. Yet in reality, this picture changes depending on the electronegativity of each participating atom, as explained by Bent’s Rule [40]. However, for an ideal situation of a double bond, a -bond (like in the Val84 amide C=O) should project an sp2 hybrid orbital to the other atom (O in this instance) present in the covalent bond, making the bond % s and % p. A deviation from these percentages will weaken the bond. In contrast, the -bond should be formed by two unhybridized 100% p-orbitals with no s-character.
Upon taking the hyperconjugative effect into account, the C=O bond should lose some of its double bond character due to the presence of a C+−O−H species and the localized orbitals will be far from an ideal sp2 overlap that we would expect in the bond.
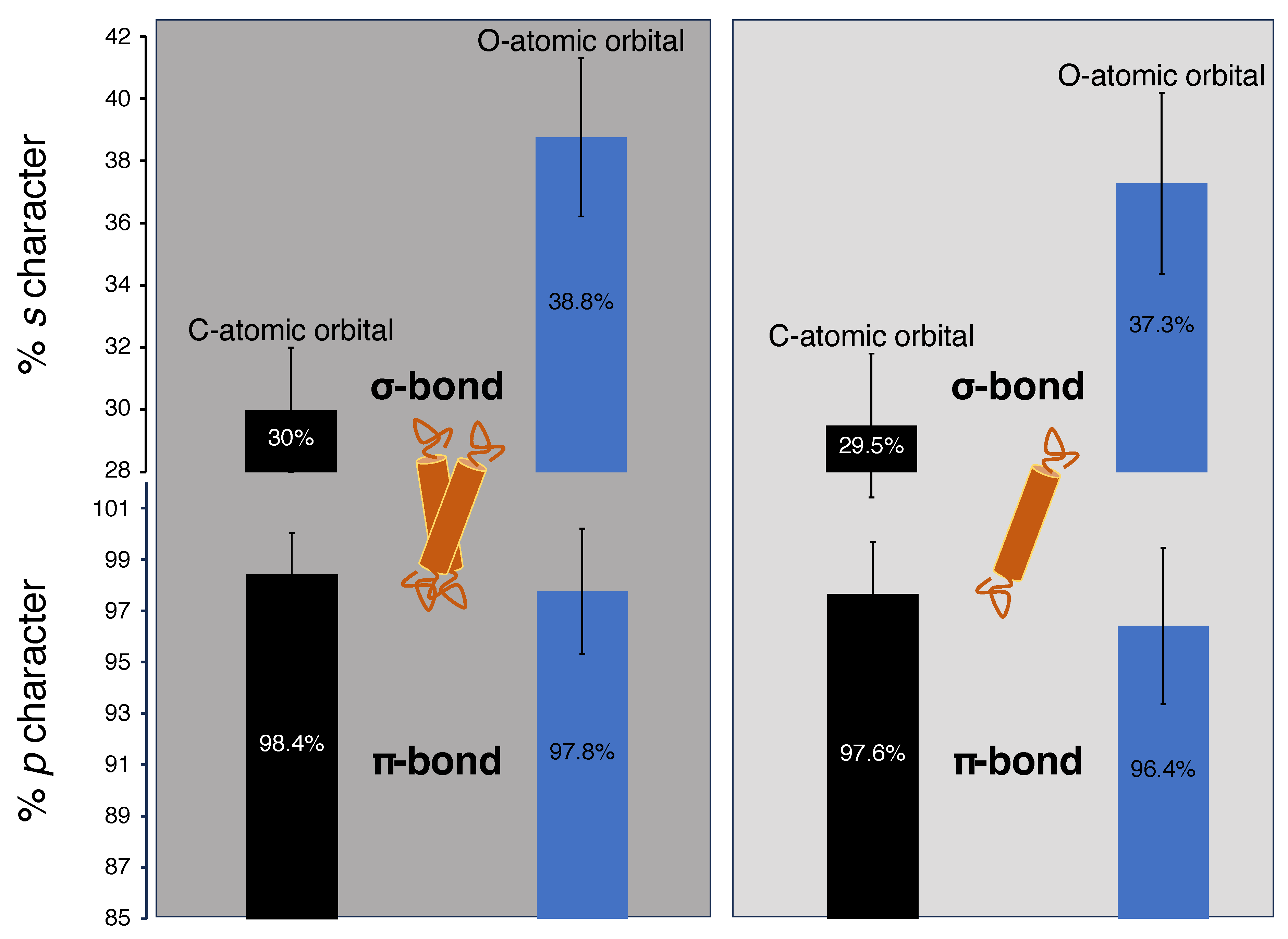
We ran NBO calculations on the energy-optimized DFT structures collected from MD-simulation trajectories and extracted the values of the s-character of the C and O atomic orbitals of the C=O bonding interactions. The results of the calculations, shown in Figure 3, indicate that both the monomeric and dimeric species experience a deviation in the s-character of the and -bonds from the ideal, % and 100% s and p-characters, respectively.
The dimeric form has a higher s-character in the -bond and a higher p-character in the -bond compared to the monomeric form. The average s-character of the atomic orbitals contributing to bond of C=O are shown in Figure 3, upper panels. It can be seen that the C and O hybrid orbitals posses a slight but definite higher s-character than the corresponding monomeric species. The monomer has a 29.5% and 37.3% s-character in its C and O hybrid orbitals, respectively. On the other hand, the dimeric species has a 30% and 38.8% of s-character in the respective orbitals. Therefore, upon dimerization and formation of the additional C−H···O bond, the C−O bond becomes stronger due to its higher s-character which can be a major contributing factor for the increased C=0 stretching frequency. This kind of s-character enhancement has been previously encountered and has been accounted as the main factor for bond strengthening of the H-donor [38].
On the other hand, the -bonding C and O atomic orbitals in the dimer are 98.4% and 97.8% of p, respectively, whereas for the monomer they are 97.6% and 96.4% of p, respectively (Figure 3). So the C=Odimer has more p-character in the sidewise overlapping orbitals than in the C=Omonomer, suggesting reduced hyperconjugation, which should theoretically enhance the oscillator strength of the C=O bond, supporting the observed frequency increase [38]. Finally, we note that indistinguishable results were obtained upon using a dispersion correction (D3_BJ) [41] method with a larger basis set (cc-pVTZ) [42].
These computational results suggest that the C=O bond strength increases upon dimerization, and the formation of the second H-bonding C−H group, due to the increased s-character of the bond and a simultaneous increase in the p-character of the bond which reduces hyperconjugation. Altogether, this leaves the C=O bond more double bonded in nature as observed in the later dispersion-corrected calculation.
We followed by analyzing how H-bonding impacts the charges of Val80’s carbonyl group. When the C=O···H−C interaction is absent, either in the monomeric system or in a separated dimeric assembly (Figure S6), a polar distribution is obtained: C+0.45=O-0.71 or C+0.60=O-0.65, respectively. In contrast, when the C=O···H−C is present (dimeric assembly) a markedly different charge distribution is obtained: C-0.21=O+0.09.
Lowering the C=O bond’s polarity should increase its covalent character. This factor, together with reduced hyperconjugation, potentially contributes to a stronger C=O bond.
It is worth mentioning that less hyperconjugation and a reduction in bond polarity do not imply that the C−H···O H-bond is energetically unfavorable. H-bonding involves both electronic and polar counterparts. Electronic interactions involve the transfer of electrons and the formation of charge-transfer species, whereas dipolar interactions are solely electrostatic in nature. An analysis of the energy terms associated with the canonical and noncanonical H-bonds in both monomer and dimer species reveals this complexity.
There is a small destabilization in the canonical H-bond of the dimer compared to the monomer, with the dimer having a canonical H bond energy value of kcal/mol compared to that of the monomer at kcal/mol. Hence, both bonds impact one another and are consequently not orthogonal in nature [43]. On the other hand, the noncanonical C−H···O H-bond in the dimer has a bond energy of kcal/mol which indicates an overall stabilization of the dimer species due to the incorporation of two H-bonds. In other words, the additional H-bond from the glycine C−H strengthens the interaction between the two helices. Finally, the value of this additional noncanonical C−H···O H-bond is similar to previous measurements [23].
3. Conclusions
Taken together, we examined the C−H···O=C H-bond at the atomic level, using a synergistic combination of experiment and computation focusing on the carbonyl acceptor group. To our surprise, both lines of investigation show a blue shift of the acceptor stretching frequency indicative of a strengthening of the C=O bond, despite previous studies that have shown that proton acceptor groups often have reduced internal bonds upon increased hydrogen bonding. Molecular dynamic simulations followed by DFT calculations reveal that the C-H group cannot undergo effective hyperconjugation thereby increasing the C=O oscillator strength.
4. Materials and Methods
4.1. Sample Preparation
4.1.1. Isotopic Label Synthesis
Isotopic labeling was conducted as described previously [44]. Briefly, 4.52 mmol of 3,5-dimethylpyridine hydrobromide (Sigma-Aldrich; Rehovot, Israel) in 2 mL of anhydrous N,N-dimethylformamide (Sigma-Aldrich) was mixed with 2.24 mmol of N-(3-(dimethylamino)propyl)-N’-ethylcaerbodiimide hydrochloride (EDC·HCl) (Sigma-Aldrich) and with 11.3 mmol of H218O (Sigma-Aldrich) under N2 atmosphere. 225 µmol of 1−13C−N−FMOC L-valine (Cambridge Isotope Laboratories, Inc; Andover, MA, USA), dissolved in 3 mL of anhydrous N,N-dimethylformamide, was added into the above-stated mixture. Subsequently, the reaction vessel was kept at room temperature and stirred overnight. After allowing the reaction to proceed overnight, another portion of 2.24 mmol EDC·HCl was added in the morning, followed by a third addition of 2.24 mmol EDC·HCl after approximately seven hours, and the reaction was allowed to continue overnight. Afterward, approximately 30 mL of ethyl acetate (Gadot-group; Netanya, Israel) was added. The mixture was transferred to a separatory funnel and washed three times with 0.1 M citric acid, and then once with brine. Ethyl acetate was then added to the combined citric acid and brine portions and separated. The combined portions of ethyl acetate, containing the labeled amino acid, were dried over anhydrous sodium sulfate (Da-sit Group; Milan, Italy) and filtered to remove any extra water. The ethyl acetate was removed by rotary evaporation, creating an azeotrope with methylene chloride (Gadot-group).
4.1.2. Peptide Synthesis and Purification
The labeled valine (see above), was incorporated into two different peptides corresponding to the transmembrane domain of glycophorin A [29]. Two peptides included the native sequence with Valines 80 labeled as well as an G79I [27] mutant with Valines 80 labeled in boldface (sequence starts at residue 70):
EPEITLIIFGVMAGVIGTILLISYGIRRL
EPEITLIIFIVMAGVIGTILLISYGIRRL
Both of the peptides were synthesized separately with N-(9-fluorenylmethoxycarbonyl) solid-phase chemistry. Each peptide sample was purified with high performance liquid chromatography on a 20 mL Jupiter 300 Å C4 5 µm high-performance liquid chromatography column (Phenomenex; Torrance, CA, USA). The column was pre-equilibrated with 80:8:12 (by volume) water:acetonitrile:isopropanol, where all solvents contained 0.1% trifluoroacetic acid (TFA) (Merck; Darmstadt, Germany). Approximately 2 mg of protein sample was dissolved in 2 mL of TFA and injected into the column. The solvent gradient was linearly altered with the VWR Hitachi Chromaster 5160 Pump (Tokyo, Japan) to remove all water composition while retaining the acetonitrile:isopropanol ratio at 40%:60% with 0.1% TFA. Peptide elution was monitored at 280 nm using the VWR Hitachi Chromaster 5410 UV detector.
4.1.3. Peptide Reconstitution
All experimental measurements were performed on peptides in lipid vesicles. We used organic solvent co-solubilization in order to reconstitute each peptide in a membrane bilayer. Approximately 1 mg of purified protein and 10 mg of 1,2-dimyristoyl-sn-glycero-3-phosphocholine (Avanti Polar Lipids; Alabaster, AL, USA) were dissolved in 1 mL of 1,1,1,3,3,3-hexafluoro-2-propanol (HFIP) (Merck, Darmstadt, Germany). The mixture was rotary evaporated at 37C until all the HFIP evaporated. One milliliter of water was added, and the mixture was rotated at 37C to spontaneously form vesicles. The sample was then sonicated to ensure uniformly sized vesicles and no aggregation.
4.2. FTIR Spectroscopy
For each of the two samples of peptides in a membrane vesicle, separate FTIR spectra were collected. First, 200 µL of sample was deposited on a germanium trapezoid ATR plate ( mm) with a 45 face angle (Wilmad; Vineland, NJ, USA). Following removal of bulk solvent, the crystal was incorporated into a 25 reflection variable angle ATR unit (Specac; Orpington, UK), which reflects the incoming FTIR beam 25 times before its exit from the crystal. The ATR unit was incorporated within a Nicolet iS10 FTIR spectrometer, with a mercury cadmium telluride detector (Thermo Scientific; Waltham, MA, USA), cooled with liquid nitrogen. The FTIR spectrometer was purged with water- and CO2-depleted air, and spectra were collected at room temperature.
For each sample, 1000 scans were sampled and averaged at a data spacing of 0.241 cm−1 with two levels of zero filling, N-B strong apodization, and Mertz phase correction. For each of the two samples of peptides in a membrane vesicle, separate FTIR spectra were collected at room temperature. Prior to deposition of the sample on the germanium ATR plate, background spectra were collected with an empty germanium ATR plate and used to subtract background IR absorption.
4.3. Computational Details
4.3.1. Molecular Dynamic Simulations
PDB structure of the dimeric glycophorin A dimer (2KPF) was downloaded from RCSB PDB. The monomer was created by stripping out chain B from the dimeric structure and mutating G79 to I79 using Swiss-PDBeditor [45]. Both of the structures were then fitted into a pre-equilibrated 1,2-dimyristoyl-sn-glycero-3-phosphocholine bilayer obtained from supporting data of the study by Poger & Mark [46] to satisfy and mimic the experimental conditions. The fitting was done in such a way that the helical bundle(s) remain perpendicular to the bilayer plane. The bilayer contains 228 lipid molecules with 4166 water molecules. After initial structural alignment, lipid molecules that coalesced with protein coordinates were removed using InflateGro methodology developed by Tieleman and co-workers [47]. In this method an automatic running algorithm deletes molecules within 2 Å range. Position restraints (100,00 kcal mol-1 Å-2) on heavy atoms of protein molecules were imposed to make sure that the protein molecules do not change positions during the energy minimization process. Energy minimization was done with steepest descent minimization algorithm with a tolerance of 500 kj mol-1 nm-1.
Molecular Dynamic (MD) Simulations of the monomeric and dimeric protein were done for 200 ns using Gromacs version 2022.3 [48,49,50,51,52] using an extended version of GROMOS96 53A6 force field [53]. The length and angles of H-atoms were restrained with the LINCS algorithm allowing an integration time step of 2 fs [54]. Atomic coordinates were saved every 1000 ps. Reference temperatures were kept at 323 K and solvent, lipids, and proteins were separately coupled to a Nosé-Hoover temperature bath [54,55] with a coupling constant value = 0.5 ps. Pressure coupling was done with a Parrinello-Rahman barostat with = 2 ps [56,57]. A 1.2 nm distance was set as cut-off for van der Waals interactions. At every 10 fs the neighbor list was updated. 4th order Particle Mesh Ewald (PME) long-range electrostatics was used to calculate electrostatic parameters [58].
The final simulation box had 225 lipid molecules. Hydration with FLEXSPC model [59] water molecules and addition of Na+ and Cl- as counter ions led to a number of atoms of 25598 and 37365 for the monomer and dimer protein systems, respectively.
4.3.2. Quantum Mechanical Calculations
The protein H-bonding system was modeled with smaller molecular mimics. Our focus is the Val80 residue which is the proton acceptor in the C−H···O bond while simultaneously participating in a canonical H-bond with its H-bond- donating Val84 counterpart from the same helix. We represent this canonical H-bond between Val80 and Val84 with two N-methylacetamide molecules. The noncanonical H-bond-donating glycine moiety from the neighboring helix was modeled with an acetylglycinemethylamide. Schematic representations of the chemical formulae are shown in Figure S4.
Besides atoms in the capping CH3 groups, all other atoms of the three molecules are derived from the original protein. Coordinates were chosen from the structure of glycophorin A and its monomer from different frames of MD simulations trajectory based on minimal RMSD values. The C atoms of the capping CH3 groups were positioned where the C and C atoms were located in the PDB structures. Atom coordinates were selected from chains A and B of the structure, and the terminal C atoms of the N-methylacetamides and glycine were fixed during minimization. The α-carbon of the glycine mimicking molecule was similarly fixed.
While determining H-bonding energy, we required breaking the C−H···O H-bond. Breaking was accomplished by moving the glycine residue 30 Å apart from the original position, shown schematically in Figure S6. The 13C=18O system of Val80 was achieved by using 13C and 18O isotopes in the carbonyl group of the Val80-mimicking N-methylacetamide residue.
The computation was done using a Q-chem [60] set up at the B3LYP level of theory [61,62,63,64] using the “aug-cc-pvdz” basis set [65]. Such large basis sets reduce the chance of basis set superposition error. Moreover, the basis set superposition error was corrected using the DFT-C method available in the Q-chem package [66]. Furthermore, no difference was obtained upon repeating the computational analyses at the same level of theory (B3LYP), using a dispersion correction (D3_BJ) [41] method and with a larger basis set (cc-pVTZ) [42] to further minimize the effects of basis set superposition error.
The dielectric constant was fixed at 4 to mimic the membrane environment. Section 1 of supporting information shows the detailed methodology of the computational procedure. The structures of the model molecular assembly before and after energy minimization can be seen in Figures S4 and S6 in supporting information.
Q-chem package provides a Natural Bonding Orbital (NBO) calculation tool for measuring natural bonding orbital contributions involved in the chemical bondings. NBO outputs were extracted from the Q-chem output as percent orbital contributions. NBO output also involves Natural Population Analysis (NPA) for each construct which was also extracted.
5. Patents
This section is not mandatory, but may be added if there are patents resulting from the work reported in this manuscript.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org.
Acknowledgments
This work was supported in part by grants from the binational science foundation (2013618), the Israeli minstry of science, and the Israeli science foundation (948/19). The authors thank Prof. I. Schapiro from the Hebrew University for helpful discussion. I.T.A. is the Arthur Lejwa Professor of Structural Biochemistry at the Hebrew University of Jerusalem.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
References
- van der Lubbe, S.C.; Fonseca Guerra, C. The Nature of Hydrogen Bonds: A Delineation of the Role of Different Energy Components on Hydrogen Bond Strengths and Lengths. Chemistry–An Asian Journal 2019, 14, 2760–2769. [Google Scholar] [CrossRef] [PubMed]
- Sheu, S.Y.; Yang, D.Y.; Selzle, H.L.; Schlag, E.W. Energetics of Hydrogen Bonds in Peptides. Proc Natl Acad Sci U S A 2003, 100, 12683–7. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S.; Kar, T.; Pattanayak, J. Comparison of Various Types of Hydrogen Bonds Involving Aromatic Amino Acids. J. Am. Chem. Soc. 2002, 124, 13257–13264. [Google Scholar] [CrossRef] [PubMed]
- Escobedo, A.; Topal, B.; Kunze, M.B.A.; Aranda, J.; Chiesa, G.; Mungianu, D.; Bernardo-Seisdedos, G.; Eftekharzadeh, B.; Gairi, M.; Pierattelli, R.; et al. Side Chain to Main Chain Hydrogen Bonds Stabilize a Polyglutamine Helix in a Transcription Factor. Nat. Commun. 2019, 10. [Google Scholar] [CrossRef] [PubMed]
- Pauling, L.; Corey, R.B.; Branson, H.R. The Structure of Proteins; Two Hydrogen-Bonded Helical Configurations of the Polypeptide Chain. Proc Natl Acad Sci U S A 1951, 37, 205–11. [Google Scholar] [CrossRef] [PubMed]
- Brielle, E.S.; Arkin, I.T. Quantitative Analysis of Multiplex H-Bonds. J. Am. Chem. Soc. 2020, 142, 14150–14157. [Google Scholar] [CrossRef] [PubMed]
- Feldblum, E.S.; Arkin, I.T. Strength of a Bifurcated H Bond. Proc. Natl. Acad. Sci. U. S. A. 2014, 111, 4085–4090. [Google Scholar] [CrossRef] [PubMed]
- Manikandan, K.; Ramakumar, S. The Occurrence of C−H···O Hydrogen Bonds in -Helices and Helix Termini in Globular Proteins. Proteins 2004, 56, 768–81. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.M.; Chang, H.C.; Jiang, J.C.; Chen, J.C.C.; Kao, H.E.; Lin, S.H.; Lin, I.J.B. C−H···O Hydrogen Bonds in -Sheetlike Networks: Combined X-Ray Crystallography and High-Pressure Infrared Study. J Am Chem Soc 2003, 125, 12358–64. [Google Scholar] [CrossRef] [PubMed]
- Fabiola, G.F.; Krishnaswamy, S.; Nagarajan, V.; Pattabhi, V. C−H···O Hydrogen Bonds in Beta-Sheets. Acta Crystallogr D Biol Crystallogr 1997, 53, 316–20. [Google Scholar] [CrossRef] [PubMed]
- Bella, J.; Berman, H.M. Crystallographic Evidence for C−H···O=C Hydrogen Bonds in a Collagen Triple Helix. J. Mol. Biol. 1996, 264, 734–742. [Google Scholar] [CrossRef] [PubMed]
- Derewenda, Z.S.; Lee, L.; Derewenda, U. The Occurrence of C−H···O Hydrogen Bonds in Proteins. J Mol Biol 1995, 252, 248–62. [Google Scholar] [CrossRef] [PubMed]
- Senes, A.; Ubarretxena-Belandia, I.; Engelman, D.M. The C−H···O=C Hydrogen Bond: A Determinant of Stability and Specificity in Transmembrane Helix Interactions. Proc. Natl. Acad. Sci. U. S. A. 2001, 98, 9056–9061. [Google Scholar] [CrossRef] [PubMed]
- Horowitz, S.; Trievel, R.C. Carbon-Oxygen Hydrogen Bonding in Biological Structure and Function. J. Biol. Chem. 2012, 287, 41576–41582. [Google Scholar] [CrossRef] [PubMed]
- Derewenda, Z.S. CH groups as donors in hydrogen bonds: a historical overview and occurrence in proteins and nucleic acids. International Journal of Molecular Sciences 2023, 24, 13165. [Google Scholar] [CrossRef] [PubMed]
- Panigrahi, S.K.; Desiraju, G.R. Strong and Weak Hydrogen Bonds in the Protein-Ligand Interface. Proteins 2007, 67, 128–141. [Google Scholar] [CrossRef] [PubMed]
- Blakeley, M.P.; Langan, P.; Niimura, N.; Podjarny, A. Neutron Crystallography: Opportunities, Challenges, and Limitations. Curr Opin Struct Biol 2008, 18, 593–600. [Google Scholar] [CrossRef] [PubMed]
- Derewenda, Z.S.; Derewenda, U.; Kobos, P.M. (His)C−H···O=C < Hydrogen Bond in the Active Sites of Serine Hydrolases. J Mol Biol 1994, 241, 83–93. [Google Scholar] [CrossRef]
- MacKenzie, K.R.; Prestegard, J.H.; Engelman, D.M. A Transmembrane Helix Dimer: Structure and Implications. Science 1997, 276, 131–3. [Google Scholar] [CrossRef] [PubMed]
- Teese, M.G.; Langosch, D. Role of GxxxG Motifs in Transmembrane Domain Interactions. Biochemistry 2015, 54, 5125–5135. [Google Scholar] [CrossRef] [PubMed]
- Arkin, I.T.; Brunger, A.T. Statistical Analysis of Predicted Transmembrane Alpha-Helices. Biochim Biophys Acta 1998, 1429, 113–28. [Google Scholar] [CrossRef] [PubMed]
- Yohannan, S.; Faham, S.; Yang, D.; Grosfeld, D.; Chamberlain, A.K.; Bowie, J.U. A C−H···O=C Hydrogen Bond in a Membrane Protein Is Not Stabilizing. J Am Chem Soc 2004, 126, 2284–5. [Google Scholar] [CrossRef] [PubMed]
- Arbely, E.; Arkin, I.T. Experimental Measurement of the Strength of a C−H···O=C Bond in a Lipid Bilayer. J. Am. Chem. Soc. 2004, 126, 5362–5363. [Google Scholar] [CrossRef] [PubMed]
- Tadesse, L.; Nazarbaghi, R.; Walters, L. Isotopically Enhanced Infrared-Spectroscopy - a Novel Method for Examining Secondary Structure at Specific Sites in Conformationally Heterogeneous Peptides. J. Am. Chem. Soc. 1991, 113, 7036–7037. [Google Scholar] [CrossRef]
- Torres, J.; Kukol, A.; Goodman, J.M.; Arkin, I.T. Site-Specific Examination of Secondary Structure and Orientation Determination in Membrane Proteins: The Peptidic (13)C=(18)O Group as a Novel Infrared Probe. Biopolymers 2001, 59, 396–401. [Google Scholar] [CrossRef] [PubMed]
- Tomita, M.; Marchesi, V.T. Amino-acid sequence and oligosaccharide attachment sites of human erythrocyte glycophorin. Proc Natl Acad Sci U S A 1975, 72, 2964–8. [Google Scholar] [CrossRef] [PubMed]
- Lemmon, M.A.; Flanagan, J.M.; Hunt, J.F.; Adair, B.D.; Bormann, B.J.; Dempsey, C.E.; Engelman, D.M. Glycophorin a Dimerization Is Driven by Specific Interactions Between Transmembrane Alpha-Helices. J Biol Chem 1992, 267, 7683–9. [Google Scholar] [CrossRef] [PubMed]
- Krimm, S.; Bandekar, J. Vibrational Spectroscopy and Conformation of Peptides, Polypeptides, and Proteins. Adv Protein Chem 1986, 38, 181–364. [Google Scholar] [CrossRef] [PubMed]
- Bormann, B.J.; Knowles, W.J.; Marchesi, V.T. Synthetic Peptides Mimic the Assembly of Transmembrane Glycoproteins. J Biol Chem 1989, 264, 4033–7. [Google Scholar] [CrossRef] [PubMed]
- Bormann, B.J.; Engelman, D.M. Intramembrane Helix-Helix Association in Oligomerization and Transmembrane Signaling. Annu Rev Biophys Biomol Struct 1992, 21, 223–42. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Liu, L.; Schlegel, H.B. On the Physical Origin of Blue-Shifted Hydrogen Bonds. J Am Chem Soc 2002, 124, 9639–47. [Google Scholar] [CrossRef] [PubMed]
- Boese, A.D. Density Functional Theory and Hydrogen Bonds: Are We There Yet? ChemPhysChem 2015, 16, 978–985. [Google Scholar] [CrossRef] [PubMed]
- Mineev, K.S.; Bocharov, E.V.; Volynsky, P.E.; Goncharuk, M.V.; Tkach, E.N.; Ermolyuk, Y.S.; Schulga, A.A.; Chupin, V.V.; Maslennikov, I.V.; Efremov, R.G.; et al. Dimeric Structure of the Transmembrane Domain of Glycophorin a in Lipidic and Detergent Environments. Acta Naturae 2011, 3, 90–98. [Google Scholar] [CrossRef] [PubMed]
- Wieczorek, R.; Dannenberg, J.J. H-bonding cooperativity and energetics of alpha-helix formation of five 17-amino acid peptides. J Am Chem Soc 2003, 125, 8124–9. [Google Scholar] [CrossRef] [PubMed]
- Tan, K.P.; Singh, K.; Hazra, A.; Madhusudhan, M.S. Peptide bond planarity constrains hydrogen bond geometry and influences secondary structure conformations. Curr Res Struct Biol 2021, 3, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Morozov, A.V.; Kortemme, T. Potential functions for hydrogen bonds in protein structure prediction and design. Advances in protein chemistry 2005, 72, 1–38. [Google Scholar] [PubMed]
- Mandala, V.S.; McKay, M.J.; Shcherbakov, A.A.; Dregni, A.J.; Kolocouris, A.; Hong, M. Structure and drug binding of the SARS-CoV-2 envelope protein transmembrane domain in lipid bilayers. Nat Struct Mol Biol 2020, 27, 1202–1208. [Google Scholar] [CrossRef] [PubMed]
- Alabugin, I.V.; Manoharan, M.; Peabody, S.; Weinhold, F. Electronic basis of improper hydrogen bonding: a subtle balance of hyperconjugation and rehybridization. Journal of the American Chemical Society 2003, 125, 5973–5987. [Google Scholar] [CrossRef] [PubMed]
- Alabugin, I.V.; Bresch, S.; Gomes, G.d.P. Orbital Hybridization: a Key Electronic Factor in Control of Structure and Reactivity. J. Phys. Org. Chem. 2015, 28, 147–162. [Google Scholar] [CrossRef]
- Bent, H.A. An Appraisal of Valence-bond Structures and Hybridization in Compounds of the First-row elements. Chemical Reviews 1961, 61, 275–311. [Google Scholar] [CrossRef]
- Grimme, S. Density functional theory with London dispersion corrections. Wiley Interdisciplinary Reviews: Computational Molecular Science 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Dunning Jr, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. The Journal of chemical physics 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Voth, A.R.; Khuu, P.; Oishi, K.; Ho, P.S. Halogen bonds as orthogonal molecular interactions to hydrogen bonds. Nat Chem 2009, 1, 74–9. [Google Scholar] [CrossRef] [PubMed]
- Seyfried, M.S.; Lauber, B.S.; Luedtke, N.W. Multiple-Turnover Isotopic Labeling of Fmoc- and Boc-Protected Amino Acids With Oxygen Isotopes. Organic Letters 2010, 12, 104–106. [Google Scholar] [CrossRef] [PubMed]
- Guex, N.; Peitsch, M.C. SWISS-MODEL and the Swiss-Pdb Viewer: an environment for comparative protein modeling. electrophoresis 1997, 18, 2714–2723. [Google Scholar] [CrossRef] [PubMed]
- Poger, D.; Mark, A.E. On the validation of molecular dynamics simulations of saturated and cis-monounsaturated phosphatidylcholine lipid bilayers: a comparison with experiment. Journal of Chemical Theory and Computation 2010, 6, 325–336. [Google Scholar] [CrossRef] [PubMed]
- Kandt, C.; Ash, W.L.; Tieleman, D.P. Setting up and running molecular dynamics simulations of membrane proteins. Methods 2007, 41, 475–488. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Bekker, H.; Berendsen, H.; Dijkstra, E.; Achterop, S.; Vondrumen, R.v.; Vanderspoel, D.; Sijbers, A.; Keegstra, H.; Renardus, M. Gromacs-a parallel computer for molecular-dynamics simulations. In Proceedings of the 4th international conference on computational physics (PC 92). World Scientific Publishing; 1993; pp. 252–256. [Google Scholar]
- Berendsen, H.J.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Computer physics communications 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Lindahl, E.; Hess, B.; Van Der Spoel, D. GROMACS 3.0: a package for molecular simulation and trajectory analysis. Molecular modeling annual 2001, 7, 306–317. [Google Scholar] [CrossRef]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; Van Der Spoel, D.; et al. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef] [PubMed]
- Oostenbrink, C.; Villa, A.; Mark, A.E.; Van Gunsteren, W.F. A biomolecular force field based on the free enthalpy of hydration and solvation: the GROMOS force-field parameter sets 53A5 and 53A6. Journal of computational chemistry 2004, 25, 1656–1676. [Google Scholar] [CrossRef] [PubMed]
- Hess, B.; Bekker, H.; Berendsen, H.J.; Fraaije, J.G. LINCS: A linear constraint solver for molecular simulations. Journal of computational chemistry 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Physical review A 1985, 31, 1695. [Google Scholar] [CrossRef] [PubMed]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. Journal of Applied physics 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Nosé, S.; Klein, M. Constant pressure molecular dynamics for molecular systems. Molecular Physics 1983, 50, 1055–1076. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N · log (N) method for Ewald sums in large systems. The Journal of chemical physics 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Berendsen, H.J.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. Journal of Physical Chemistry 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Shao, Y.; Gan, Z.; Epifanovsky, E.; Gilbert, A.T.; Wormit, M.; Kussmann, J.; Lange, A.W.; Behn, A.; Deng, J.; Feng, X.; et al. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Molecular Physics 2015, 113, 184–215. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. I. The effect of the exchange-only gradient correction. The Journal of chemical physics 1992, 96, 2155–2160. [Google Scholar] [CrossRef]
- Lee, C.Y.; Parr, W. RG Phys. Rev. B 1988, 37, 785–789. b) Becke, AD. Physical Review A 1988, 38, 3098–3100. [Google Scholar]
- Vosko, S.; Wilk, L.; Nusair, M. Development of the Colle–Salvetti correlation–energy formula into a functional of the electron density. Can J Phys 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. The Journal of physical chemistry 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Woon, D.; Dunning Jr, T. Electron Affinities of the First-Row Atoms Revisited. Systematic Basis Sets and Wave Functions. Journal of Chemical Physics 1993, 98, 1358. [Google Scholar] [CrossRef]
- Witte, J.; Neaton, J.B.; Head-Gordon, M. Effective Empirical Corrections for Basis Set Superposition Error in the def2-SVPD Basis: gCP and DFT-C. J Chem Phys 2017, 146, 234105. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Graphical representation of the homo dimer (left) and monomer (right) species showing the presence or absence of the noncanonical C−H···O bond, respectively. The impact on the C=O bond and its corresponding vibration frequency is shown in green.
Figure 1.
Graphical representation of the homo dimer (left) and monomer (right) species showing the presence or absence of the noncanonical C−H···O bond, respectively. The impact on the C=O bond and its corresponding vibration frequency is shown in green.
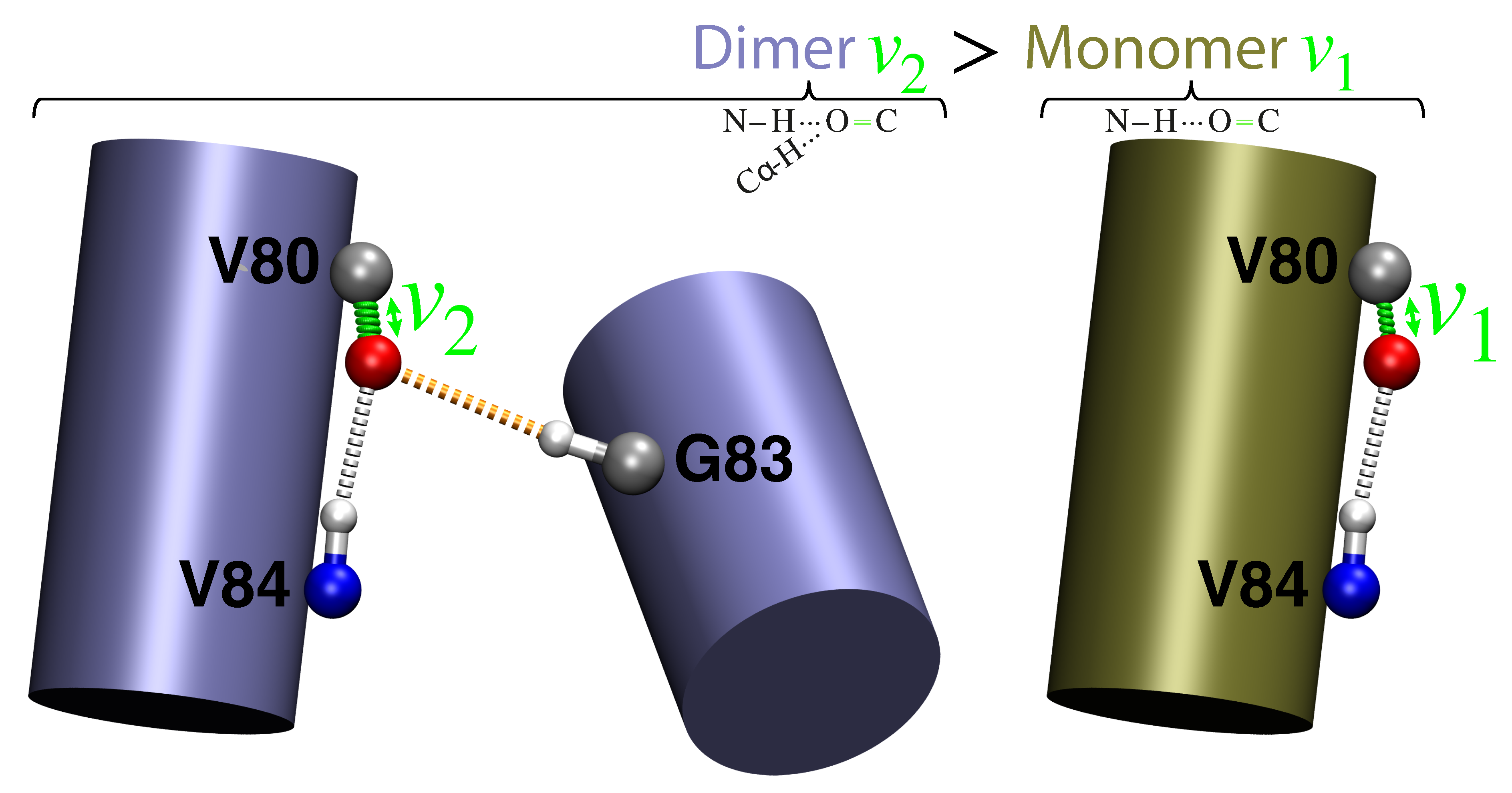
Figure 2.
Amide I stretch of Val80 13C=18O isotopically labeled dimeric (with C−H···O H-bond) and monomeric (without H-bond) species, depicted in blue and brown, respectively. The spectrum of a peptide without isotopic labels is shown in red. Top: sequences of the dimeric (blue) and monomeric (brown) peptides used in the study, indicating the position of the13C=18O label at Val80 in green.
Figure 2.
Amide I stretch of Val80 13C=18O isotopically labeled dimeric (with C−H···O H-bond) and monomeric (without H-bond) species, depicted in blue and brown, respectively. The spectrum of a peptide without isotopic labels is shown in red. Top: sequences of the dimeric (blue) and monomeric (brown) peptides used in the study, indicating the position of the13C=18O label at Val80 in green.
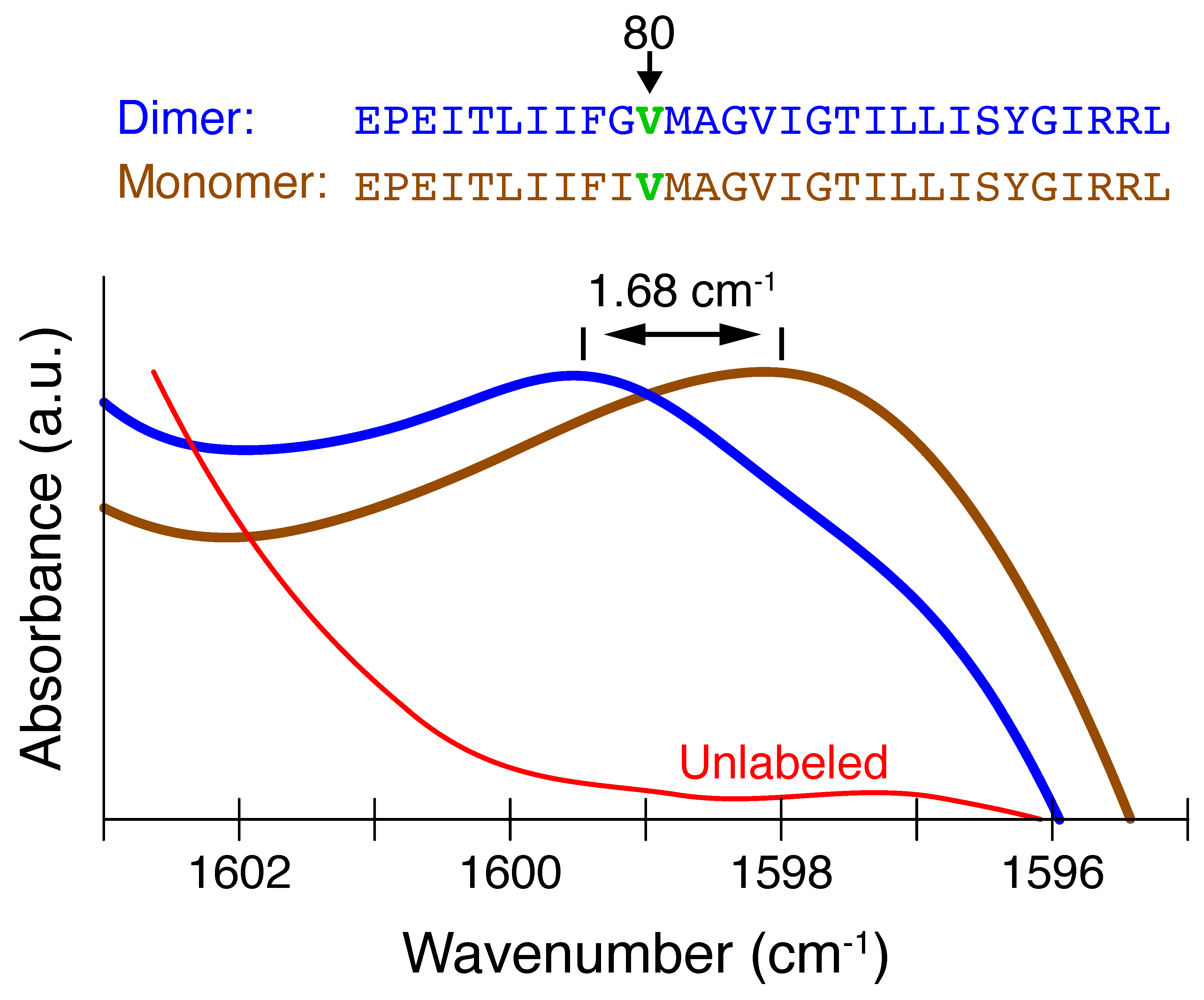
Figure 3.
Graphical representation of calculated orbital s/p-character. The left panel shows calculations on dimeric glycophorin A and the right panel shows monomeric G79I mutated glycophorin A.
Figure 3.
Graphical representation of calculated orbital s/p-character. The left panel shows calculations on dimeric glycophorin A and the right panel shows monomeric G79I mutated glycophorin A.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







