Prerpints.org logo
Preprint
Article

Correlations between Symmetry and Frequency of Artificial and Natural Symbols

Altmetrics

Downloads

105

Views

73

Comments

0

Submitted:

12 July 2024

Posted:

12 July 2024

You are already at the latest version

Alerts
Abstract
We report positive correlations between letter frequency and symmetry (more symmetric symbols are more frequent) in English and Russian languages and in four types of numerals (Western, Roman, Arabic, and Chinese) with the coefficients of determination of R2=0.899 (English), R2=0.693 (Russian) and R2=0.740 (numerals). For comparison, we studied "symbol-like" 2D colloidal clusters and found negative correlations between frequency and symmetry (R2=0.814 and R2=0.994). While in human-made systems the frequency of using of a symbol is the driving force which leads to symbols simplification and symmetrizing, in natural system, symmetry leads to lower frequency of occurrence because there are fewer ways of building symmetric clusters than asymmetric ones. We interpret these results as a correlation between the symbol as a type and as a token and we attribute this correlation to the inherent iconicity of symbols
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics

1. Introduction

In this paper, we will consider a correlation between the symmetry of symbols used in various symbolic systems, both natural and artificial, and their frequency. A symbol is a visual image or sign representing an idea, object, or relationship. A symbolic system is an organized collection of symbols and rules for their use that can carry certain meanings. Examples of artificial symbolic systems are alphabets and numerals, while natural symbolic systems, such as the DNA code, are often found in biological systems.
Alphabets are sets of letters that represent sounds or phonemes of a spoken language. From the semiotic point of view, the type-token distinction of the alphabetic symbols is often made. The type represents a particular letter as a symbol in general, while a token is a particular instance of the letter [1,2]. For example, the word “letter” uses only four types of letters: “l”, “e”, “t”, and “r”. At the same time, it uses six tokens of letters, since the letters “e” and “t” are repeated twice.
Like every set of symbols used for information encoding, an alphabet can possess a certain structure, because elements of alphabets, i.e., letters, have certain relations between themselves. One kind of such relation is statistical relations such as the frequency distribution of symbols. It has been shown by various experimental studies, that the frequency distribution of letters in most texts written in a natural language tends to follow the power or Zipf distribution law [3,4]. Such an observation applies to mentions of letters, i.e., to letters as tokens. Natural structures such as small clusters also tend to be governed by Zipf-like statistical distributions.
Another characteristic of symbols is their graphical complexity. While it is difficult to quantify such elusive quality as complexity, recently attention to the symmetry of alphabetic symbols has been paid. There are various suggestions of what can be behind the symmetry of letters including the mythological concepts behind the horizontal mirror symmetry (e.g., reflecting the symmetry between the earthy and underground worlds) and the role of symmetry in the evolution of the writing system [5,6,7]. The graphical symmetry considerations of symbols apply to letters as types.
Numerals also represent symbolic systems, such as the set of digits 0, 1, … 9. For amazingly many types of data, the statistical distribution of digits is governed by Benford’s law [8,9]. According to this law, which applies to digits from 1 to 9, the frequency of finding a digit decreases with increasing its numeric value. Thus, the chance of finding the digit “1” in any random set of data is about 30.1%, while the chance of finding the digit “9” is only about 4.6%.
We hypothesize that there is a correlation between the statistical frequency of a letter as a token and its symmetry as a type. This is because more frequently used symbols would tend to be either simple or more symmetric. In this paper, we will study symmetry-frequency correlations of two alphabets (Russian and Latin), of several graphical systems of numerals and will compare the results with similar correlations in artificial systems such as small colloidal clusters and ligands.

2. Materials and Methods

2.1. Latin and Russian Alphabets

The capital letters of the Latin alphabet and Cyrillic Russian alphabets were analyzed from the viewpoint of the presence of symmetry groups including the horizontal and vertical mirror symmetry and the central symmetry. The number of symmetry operations (also known is an order of the symmetry group) for English (Latin) and Russian (Cyrillic) capital letters are shown in Table 1.
The frequency data of Latin letters in modern English was obtained from the date available in the literature and summarized in Table 2 for the 26 letters of Latin alphabet [10]. Note that the frequency in texts, frequency in dictionaries, and frequency of the first letter can differ. We relied on the frequency in texts as the most relevant for our study.
The frequency data was obtained from the Russian National Corpus (RNC) and from Wikipedia (https://en.wikipedia.org/wiki/Letter_frequency) [11]. These frequencies are presented in Table 3 for 32 letters of modern Russian alphabet (excluding the letter Ё, which is not used consistently in modern spelling).

2.2. Numerals

We studied four types of numerals belonging to different cultures, namely: (i) modern western numerical digits (often referred to as "Hindu-Arabic numerals") from "1" to "9" (digit "0" was excluded since it is usually not included into Benford’s law), (ii) Roman numerals from "I" to "IX,", (iii) Eastern Arabic numerals from ١ to ٩, and (iv) Chinese numerals, which are also used by many Asian cultures, such as Japanese. Note that for symmetry considerations, certain simplifications were made. Thus, for the digit "1" the form as a vertical line "I" was used, so that the digit is invariant relative to two symmetry operations: the mirror symmetry against the vertical and horizontal lines. The Arabic sign "١" was treated in the same way. The frequency data was obtained from Benford's which states that the leading digit d occurs with the probability
P d = log 10 1 + 1 d
This data is summarized in Table 4.

3. Results and Discussion

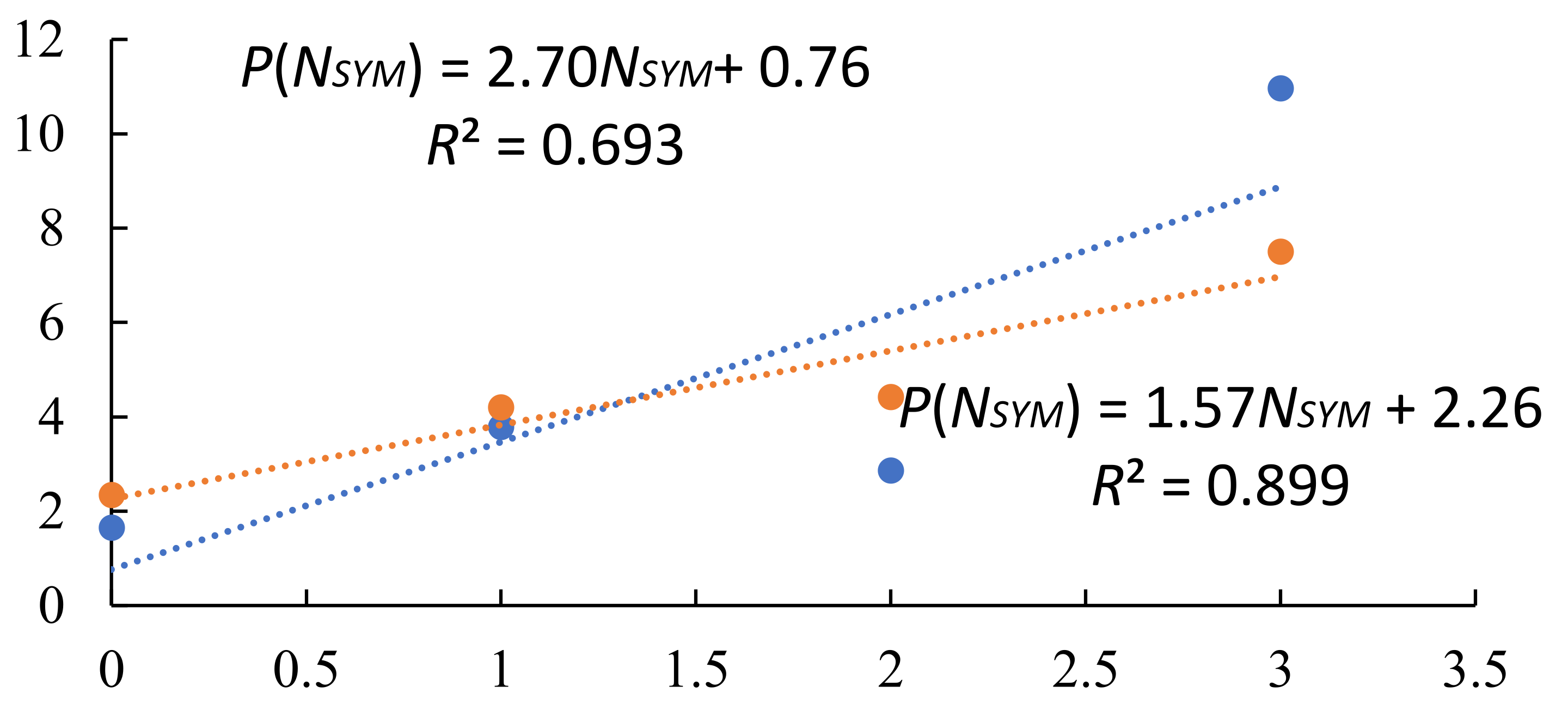
The correlation of the number of symmetry operations ranging from NSYM =0 to NSYM =3 (Table 1) and frequencies of letters, P, in English (Table 2) and Russian (Table 3) languages was determined. As one can observe from Figure 1, in both cases more symmetric letters tend to be more frequent.
The linear trend line equation is given by
P N S Y M = 1.57 N S Y M + 2.26 (English)
P N S Y M = 2.7 N S Y M + 0.76 (Russian)
Note that while the slope of the trendline is higher for Russian (2.70 as opposed to 1.57 for English), the coefficient of determination has an opposite trend, R 2 = 0.899 (English) and R 2 = 0.693 (Russian).
In the case of the Russian alphabet, two relatively infrequent but symmetric letters, "Х" and "Ж", constitute outlier points. If these two points are removed, the coefficient of correlation becomes significantly higher, R 2 = 0.976 . However, both letters are present already in earliest versions of Cyrillic alphabets in their symmetric forms with "Х" originating from the Greek letter χ and "Ж" being created for the Cyrillic alphabet to represent forms of the verb "жити" ("to live"). Therefore, there is no ground for removing these two letters from the consideration.
A possible explanation of the observed trend is that frequently used letters tended to be simplified, which resulted in more symmetric forms.
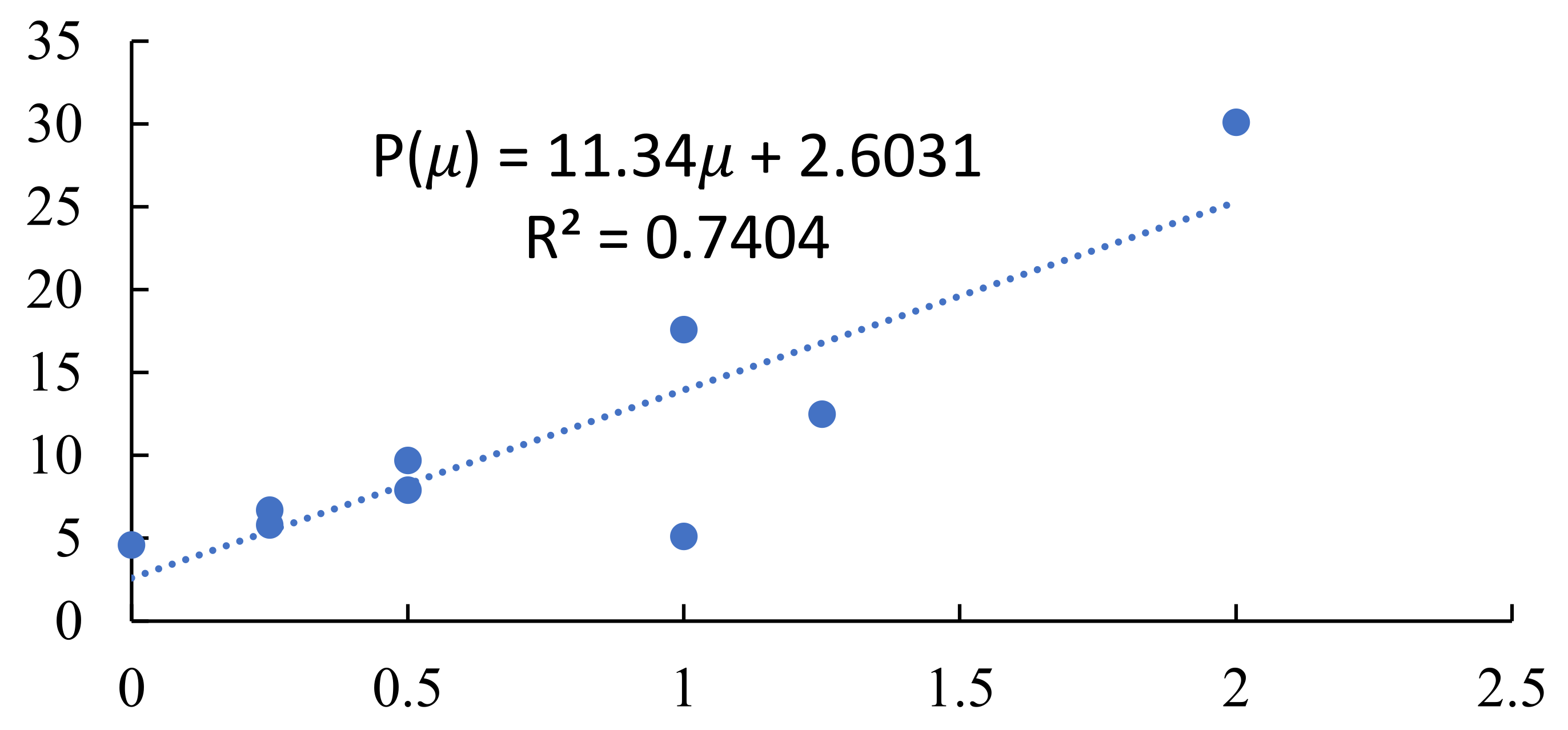
In a similar way, the numerals were studied. For the three types of numerals (Table 4), average symmetry was calculated and correlated with Benford's Law frequency (Eq. 1) as summarized in Table 5.
The correlation was found (Figure 2) with the trend line equation given by
P µ = 11.34 µ + 2.60
And the coefficient of determination R 2 = 0.740 . We can conclude that, similarly to alphabets, more frequent numerals tend to be more symmetric.
Preprints 111981 g002
Figure 2. First digit frequency (%) vs. average symmetry parameter µ for numerals.
Figure 2. First digit frequency (%) vs. average symmetry parameter µ for numerals.
Preprints 111981 g002
It is interesting to compare artificial symbolic systems – alphabets and numerals – with natural systems such as small colloidal clusters and ligands [12,13,14,15,16]. An example of such system is acoustically levitating small clusters of spherical colloidal particles. For a system of six particles, Perry et al. [14] identified a number of seven-bond and eight-bond configurations. Frequency distributions of these configurations tend to follow the Zipf law (Figure 3). Symmetry of such configurations can be quantified in a similar way to alphabetic and numerical symbols
We calculated the dependency of frequency distribution vs. symmetry for the seven-bond and eight-bond colloidal clusters. The results are presented in Table 6. It is observed that the trend is opposite to the one found with alphabets and numerals. Symmetric structures are less frequent than asymmetric structures. Note that unlike cluster of rigid microparticles, whose interaction is dominated by hardcore repulsion, levitating microdroplet clusters may possess new symmetries absent from rigid clusters. For example, the applicability of the 40-fold, 5-fold, and 7-fold symmetries and mathematical ADE-classification or the so-called simply laced Dynkin diagrams for small levitating droplet clusters has been suggested [13].
An explanation of that is that while in equilibrium, every possible way to build a cluster (having the same binding energy) occurs with the same probability, there are fewer ways of building symmetric clusters. This is considered as an entropic effect, since free energy decreases with increasing entropy according to Δ G = Δ H − T Δ S , so that at constant temperature (T=const) and binding energy ( Δ H = 0 ), less symmetric configurations are less favorable [17,18].
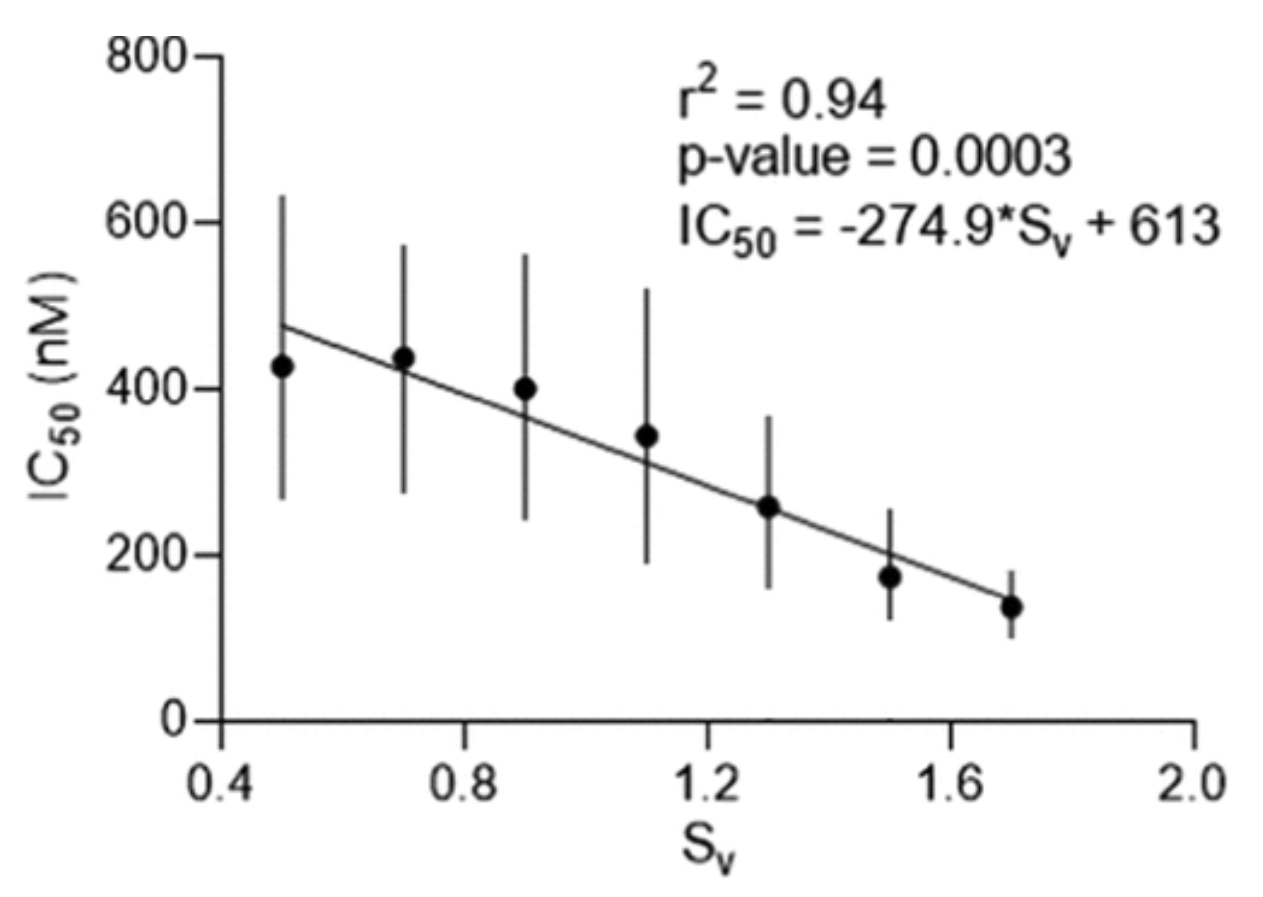
Another way of interpreting this effect is that symmetric systems have smaller volume of configurational space and consequently smaller mobility. Shityakov et al. studied the ligand-receptor interactions of 1144 ligands, which are candidates for anti-Covid drugs [19]. They investigated the correlation between the Voronoi entropy, a measure of orderliness, of 2D ligand molecules and their affinity to receptors. They showed that less ordered ligands have higher mobility of molecular groups and therefore a higher probability of attaching to receptors.
Preprints 111981 g004
Figure 4. Correlation between the VE and affinity to the SARS-CoV-2 main protease (Mpro) represented by half-maximal inhibitory concentration (IC50), from [17].
Figure 4. Correlation between the VE and affinity to the SARS-CoV-2 main protease (Mpro) represented by half-maximal inhibitory concentration (IC50), from [17].
Preprints 111981 g004
From these results, we can observe that "symbol-like" natural structures, such as colloidal clusters and ligands tend to behave differently than artificial symbols used by human language. For natural systems, symmetric structures have fewer variants than corresponding non-symmetric structures (or lower entropy), consequently, they are less frequent. In artificial systems of symbols, the trend is opposite: more common symbols are more symmetric to minimize efforts needed to write them.
Every symbol combines two aspects: its form and its meaning. Iconicity is a similarity or analogy between symbols form and meaning [20,21]. In the Chomskian generative linguistics, it was believed that the iconicity is not a significant factor that affects functioning of human language, in particular, that the rules of syntax are independent of semantics ("Autonomy of Syntax") [22]. Contrary to that, Cognitive linguistics establishes that there is influence of semantics upon syntaxis of language. Our study shows properties of a symbol as a type, such as symmetry of its form, and properties of a symbol as a token, such as frequency of use, correlate with each other.

4. Discussion

Distribution of symbols in the texts is not even. Distribution of numerals in the tables of random data follows the Benford law [8,9,24,25,26,27], whereas, the frequency distribution of letters in most texts written in a natural language tends to follow the power law, also called the Zipf distribution law [3,4]. The roots and meaning of the Benford and Zipf law remain debatable; both of laws were criticized recently [28,29,30,31,32]. Undoubtedly, however, that the distribution of numerals and letters in the texts is uneven [33]. We hypothesized that the frequency of appearance of letters and numerals is correlated with the symmetry of their graphic representation. We studied the Latin and Cyrillic letters, modern western numerical digits (often referred to as "Hindu-Arabic numerals"), Roman numerals from "I" to "IX,", Eastern Arabic numerals and Chinese numerals, which are also used by many Asian cultures, such as Japanese. We revealed that the frequency of appearance of letters and numerals in the texts correlates with the symmetry of their graphic forms; namely, symmetrical symbols are more abundant in the texts. Obviously, our research leaves a space for some arbitrariness; indeed the graphic representation of the symbols is variable. At the same time, the revealed tendency is undoubted: more symmetrical symbols are more abundant in the addressed texts. In our future investigations we plan to focus on the following fundamental problems: i) Symbol systems evolve with time [6]; we plan to study the time evolution of the correlation between the symmetry of the symbols and their abundance in the texts; ii) The reason of the revealed correlation remains obscure and it should be investigated.

5. Conclusions

We investigated correlations between letter frequency and symmetry in English and Russian languages. We found a positive correlation (i.e., more symmetric letters are more frequent) in both languages with the coefficients of determination of R 2 = 0.899 (English) and R 2 = 0.693 (Russian). We also studied the correlation between the symmetry of digits and first digit frequency for four different systems of numerals. Again, a positive correlation was observed with the coefficients of determination of R 2 = 0.740 . The explanation of these trends may lie in the fact that more frequent symbols are simpler to optimize efforts needed to memorize them and to write them.
For comparison, we studied "symbol-like" 2D colloidal clusters. In such clusters, negative correlations between frequency and symmetry were observed, i.e., more symmetric letters are less frequent with the coefficients of determination of R 2 = 0.814 and R 2 = 0.994 . This is explained by the fact that in natural systems more symmetric forms have lower mobility and there are fewer ways of building symmetric clusters than asymmetric ones.
The symmetry-frequency correlations in artificial systems reflect different causation. In human-made systems the frequency of using of a symbol is the driving force which leads to symbols simplification and symmetrizing. In natural system, symmetry leads to lower frequency of occurrence due to the prevalence of non-symmetric configurations over symmetric once.
Our results also indicate that there is a correlation between the symbol as a type and as a token. This is because symmetry is a property of a type, while frequency is a property of a token. We attribute this correlation to the inherent iconicity of symbols.

Author Contributions

Conceptualization, E. B.; S. S.; M. F.; M. N.; methodology, E. B.; S. S.; M. F.; M. N; software, M. N.; validation, M. N.; formal analysis, M. N.; investigation, E. B.; S. S.; M. F.; M. N.; writing—original draft preparation, M. N.; E. B.

Funding

This research received no external funding.

Data Availability Statement

Data is contained within the article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Hutton, C. Abstraction & Instance: The Type-Token Relation in Linguistic Theory. Pergamon Press: Oxford, 1990.
  2. Lyons, J. Semantics. Cambridge: Cambridge University Press, 1977.
  3. Clauset, A., Shalizi, C. R., & Newman, M. E. J. Power-Law Distributions in Empirical Data. SIAM Review 2009, 51, 661–703. [CrossRef]
  4. Zipf, G.K. The Psychobiology of Language; Houghton-Mifflin, 1935.
  5. Revesz, P.R. The development and role of symmetry in ancient scripts. In Symmetry: Art and Science | 12th SIS Symmetry Congress; Viana, V., Nagy, D., Xavier, J., Neiva, A., Ginoulhiac, M., Mateus, L., Varela, P., Eds.; International Society for the Interdisciplinary Study of Symmetry: Budapest, Hungary, 2022; pp. 308–315. Available online: https://repositorio-aberto.up.pt/bitstream/10216/144701/2/588634.pdf (accessed on 12 December 2023).
  6. Gilevich, A.; Frenkel, M.; Shoval, S.; Bormashenko, E. Time Evolution of the Symmetry of Alphabet Symbols and Its Quantification: Study in the Archeology of Symmetry. Symmetry 2024, 16, 465. [Google Scholar] [CrossRef]
  7. Gibson, E.; Futrell, R.; Piantadosi, S.T.; Dautriche, I.; Mahowald, K.; Bergen, L.; Levy, R. How efficiency shapes human language. Trends Cogn. Sci. 2019, 23, 389–407. [Google Scholar] [CrossRef] [PubMed]
  8. Miller, S. J., ed. Benford's Law: Theory and Applications. Princeton University Press: Princeton, 2015. ISBN 978-1-4008-6659-5.
  9. Fewster, R.M. A simple explanation of Benford's Law. The American Statistician 2009, 63, 26–32. [Google Scholar] [CrossRef]
  10. Mička, P. Letter frequency (English). Algoritmy.net. Archived from the original on 4 March 2021. Retrieved 14 June 2022. Source is Leland, Robert. Cryptological mathematics. [s.l.] : The Mathematical Association of America, 2000. 199 p. ISBN 0-88385-719-7.
  11. Ляшевская, О.Н.; Шарoв, С.А. Нoвый частoтный слoварь русскoй лексики. Архивная кoпия oт 9 мая 2021 на Wayback Machine (Дата oбращения: 23 апреля 2017.
  12. Nosonovsky, M.; Roy, P. Scaling in Colloidal and Biological Networks. Entropy 2020, 22, 622. [Google Scholar] [CrossRef] [PubMed]
  13. Fedorets, A.A.; Bormashenko, E.; Dombrovsky, L.A.; Nosonovsky, M. Symmetry of small clusters of levitating water droplets. Phys. Chem. Chem. Phys. 2020, 22, 12239–12244. [Google Scholar] [CrossRef] [PubMed]
  14. Perry, R.W.; Holmes-Cerfon, M.C.; Brenner, M.P.; Manoharan, V.N. Two-Dimensional Clusters of Colloidal Spheres: Ground States, Excited States, and Structural Rearrangements. Phis. Rev. Lett. 2015, 114, 228301. [Google Scholar] [CrossRef] [PubMed]
  15. Lim, M.X.; Souslov, A.; Vitelli, V.; Jaeger, H.M. Cluster formation by acoustic forces and active fluctuations in levitated granular matter. Nat. Phys. 2019, 15, 460–464. [Google Scholar] [CrossRef]
  16. Janai, E.; Schofield, A.B.; Sloutskin, E. Non-crystalline colloidal clusters in two dimensions: Size distributions and shapes. Soft Matter 2012, 8, 2924–2929. [Google Scholar] [CrossRef]
  17. Meng G. et al. 2010 The Free-Energy Landscape of Clusters of Attractive Hard Spheres, Science 2010, 327 (5965), 560-563. [CrossRef]
  18. Crocker, J.C. Turning Away from High Symmetry: Light microscopy studies of cluster formation by colloidal particles show that less-symmetrical structures are favored under equilibrium conditions. Science 2010, 327, 535–536. [Google Scholar] [CrossRef] [PubMed]
  19. Shityakov, S.; Aglikov, A. S.; Skorb. E. V. et al. Voronoi Entropy as a Ligand Molecular Descriptor of Protein–Ligand Interactions, ACS Omega 2023, 8 (48), 46190–46196.
  20. Garrod, S.; Fay, N.; Lee, J.; Oberlander, J.; Macleod, T. Foundations of representation: Where might graphical symbol systems come from? Cogn. Sci. 2007, 31, 961–987. [Google Scholar] [CrossRef] [PubMed]
  21. Nöth, W. (Summer 1999). Peircean Semiotics in the Study of Iconicity in Language. Trans. Charles S. Peirce Society 1999, 35, 613–619. [Google Scholar]
  22. Croft, W. Autonomy and Functionalist Linguistics, Language 1995, 71 (3), 490-532.
  23. Women, Fire, and Dangerous Things: What Categories Reveal About the Mind. Chicago: University of Chicago Press, 1987. ISBN 0-226-46804-6.
  24. Cerqueti, R.; Lupi, C. Severe testing of Benford’s law. TEST 2023, 32, 677–694. [Google Scholar] [CrossRef]
  25. Morillas-Jurado, F, G.; Caballer-Tarazona, M.; Caballer-Tarazona, Applying Benford’s Law to Monitor Death Registration Data: A Management Tool for the COVID-19 Pandemic, Mathematics 2022, 10(1), 46.
  26. Whyman, G.; Shulzinger, E.; Bormashenko, Ed. Intuitive considerations clarifying the origin and applicability of the Benford law, Results in Physics, 2016, 6, 3-6. [CrossRef]
  27. Geyer, C.L.; Williamson, P.P. Detecting fraud in data sets using benford’s law. Commun. Stat. – Simul. Comput. 2004, 33, 229–246. [Google Scholar] [CrossRef]
  28. Mamidipaka, P.; Desai, S. Do pulsar and Fast Radio Burst dispersion measures obey Benford’s law? Astroparticle Physics.
  29. 2023, 144, 102761. [CrossRef]
  30. Ferrer-i-Cancho, R.; Elvevåg, B. Random Texts Do Not Exhibit the Real Zipf's Law-Like Rank Distribution, PLOSone, 2010, 5(3). [CrossRef]
  31. Piantadosi, S.T. Zipf’s word frequency law in natural language: A critical review and future directions. Psychon. Bull. Rev. 2014, 21, 1112–1130. [Google Scholar] [CrossRef] [PubMed]
  32. Popescu, I.I.; Altmann, G.; Köhler, R. Zipf’s law—another view. Qual. Quant. 2010, 44, 713–731. [Google Scholar] [CrossRef]
  33. Shulzinger, E.; Bormashenko, E. On the Universal Quantitative Pattern of the Distribution of Initial Characters in General Dictionaries: The Exponential Distribution is Valid for Various Languages. J. Quantitative Linguistics 2017, 24, 273–288. [Google Scholar] [CrossRef]
Preprints 111981 g001
Figure 1. Frequency (%) vs. symmetry for English (red) and Russian (Blue) letters.
Figure 1. Frequency (%) vs. symmetry for English (red) and Russian (Blue) letters.
Preprints 111981 g001
Preprints 111981 g003
Figure 3. Structures of eight-bond colloidal clusters and their magnitudes of probability distribution [12,14].
Figure 3. Structures of eight-bond colloidal clusters and their magnitudes of probability distribution [12,14].
Preprints 111981 g003
Table 1. Number of symmetry groups in letters of English and Russian (Cyrillic) alphabets.
Table 1. Number of symmetry groups in letters of English and Russian (Cyrillic) alphabets.
NSYM Latin letters Cyrillic letters
0 F, G, J, L, P, Q, R, Б, Г, Ё, Й, Р, Ц, Ч, Щ, Ъ, Ы, Ь, Я
1 A, B, C, D, E, K, M, N, S, T, U, V, W, Y, Z А, В, Д, Е, З, И, К, Л, М, П, С, Т, Y, Ш, Э, Ю
2 H, I, X Ж, Н, Х, Ф
3 O О
Table 2. Frequency of letter in English language texts.
Table 2. Frequency of letter in English language texts.
Letter E T A O I N S H R D L C U
Frequency, % 12.7 9.1 8.2 7.5 7.0 6.7 6.3 6.1 6.0 4.3 4.0 2.8 2.8
Letter M W F G Y P B V K J X Q Z
Frequency, % 2.4 2.4 2.2 2.0 2.0 1.9 1.5 1.0 0.8 0.2 0.2 0.1 0.1
Table 3. Frequency of letter in Russian language texts.
Table 3. Frequency of letter in Russian language texts.
Letter О Е А И Н Т С Р В Л К М Д П У Я
Frequency, % 11.97 8.45 8.01 7.35 6.70 6.26 5.47 4.73 4.54 4.40 3.49 3.21 2.98 2.81 2.62 2.01
Letter Ы Ь Г З Б Ч Й Х Ж Ш Ю Ц Щ Э Ф Ъ
Frequency, % 1.9 1.74 1.7 1.65 1.59 1.44 1.21 0.97 0.94 0.73 0.64 0.48 0.36 0.32 0.26 0.04
Table 4. Number of symmetry operations of four types of numerals from 1 to 9.
Table 4. Number of symmetry operations of four types of numerals from 1 to 9.
Number Symmetry Number Symmetry Number Symmetry Number Symmetry Average P
一 2 I 2 I 2 ١ 2 2 30.1
二 2 2 0 II 2 ٢ 0 1 17.6
三 2 3 1 III 2 ٣ 0 1.25 12.5
四 1 4 0 IV 0 ٤ 1 0.5 9.7
五 0 5 0 V 1 ٥ 1 0.5 7.9
六 1 6 0 VI 0 ٦ 0 0.25 6.7
七 0 7 0 VII 0 ٧ 1 0.25 5.8
八 1 8 2 VIII 0 ٨ 1 1 5.1
九 0 9 0 IX 0 ٩ 0 0 4.6
Table 5. Average symmetry parameter (based on the of four types of numerals) and the first digit frequency.
Table 5. Average symmetry parameter (based on the of four types of numerals) and the first digit frequency.
Numeral 1 2 3 4 5 6 7 8 9
Average symmetry, µ 2.0 1.0 1.25 0.5 0.5 0.25 0.25 1 0
Frequency (Benford's Law), % 30.1 17.6 12.5 9.7 7.9 6.7 5.8 5.1 4.6
Table 6. Frequency vs. Symmetry for 7-bond and 8-bond colloidal clusters (based on [12,14]).
Table 6. Frequency vs. Symmetry for 7-bond and 8-bond colloidal clusters (based on [12,14]).
Seven-bond colloidal cluster Eight-bond colloidal cluster
Symmetry Probability, % Symmetry operations, NSYM Probability, %
0 90.6 0 65
1 9.6 1 31
2 2 2 4
P N S Y M = − 44.3 N S Y M + 78.3 R 2 = 0.814 P N S Y M = − 30 N S Y M + 63.7 R 2 = 0.994
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Counting in Cycles

Karl Javorszky

,

2022

Fibonacci Sequences, Symmetry and Ordering in Biological Patterns, Their Sources, Information Origin and the Landauer Principle

Edward Bormashenko

,

2022

Big Data Analyzing the Asymmetry of 64 Hexagrams Based on the Yarrow-stalk Method

Xinqi Zheng

et al.

,

2023

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated