Introduction

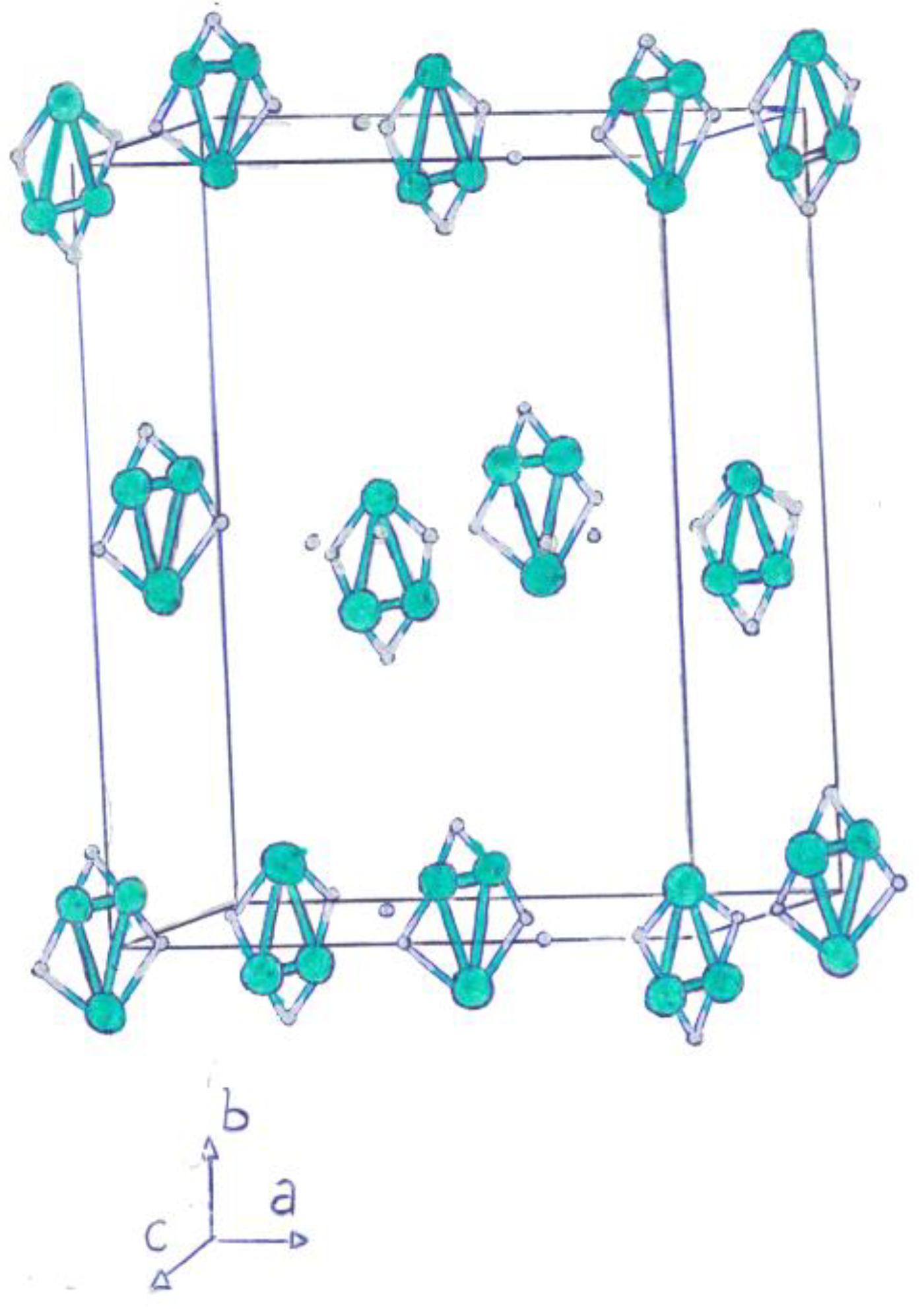
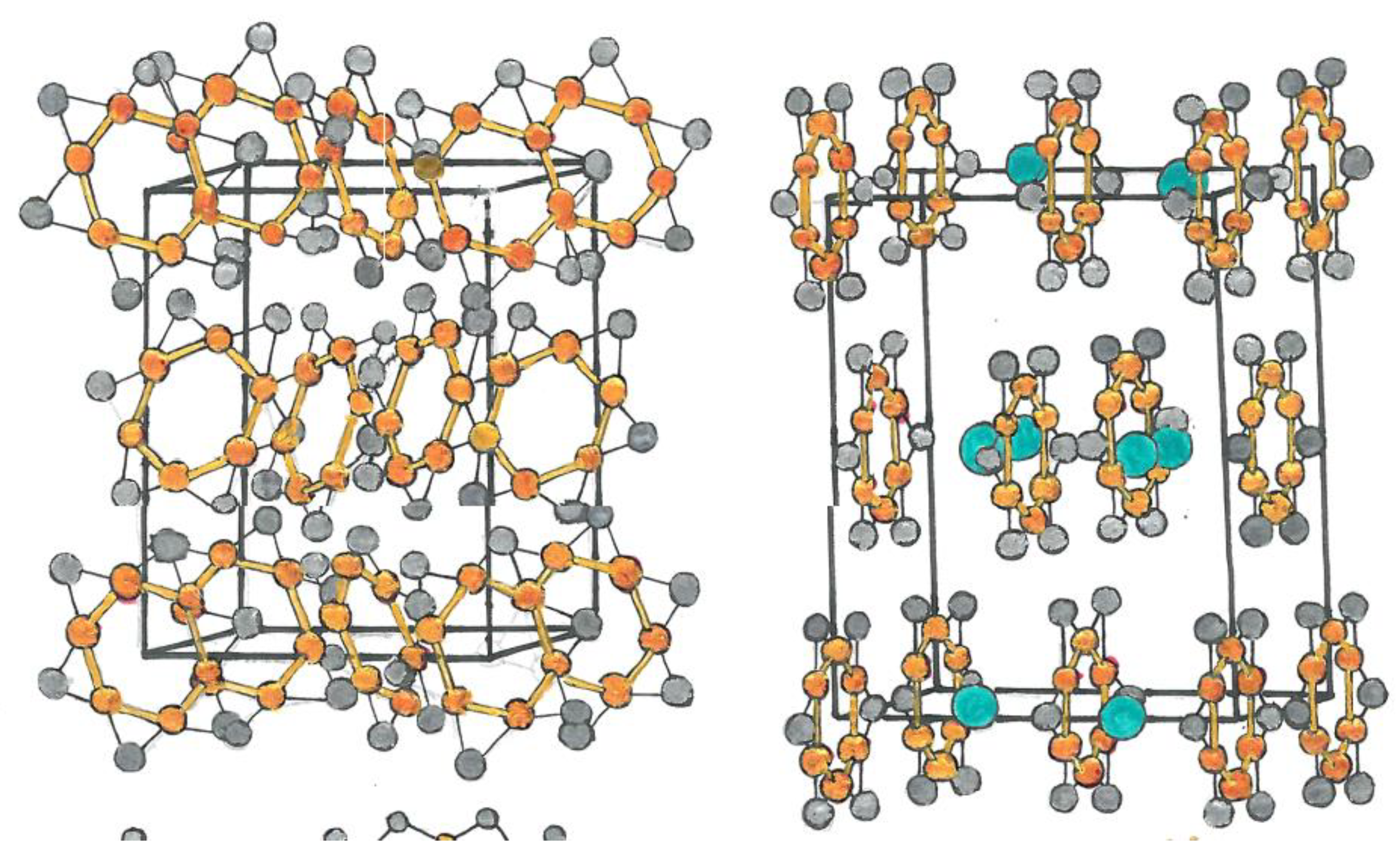
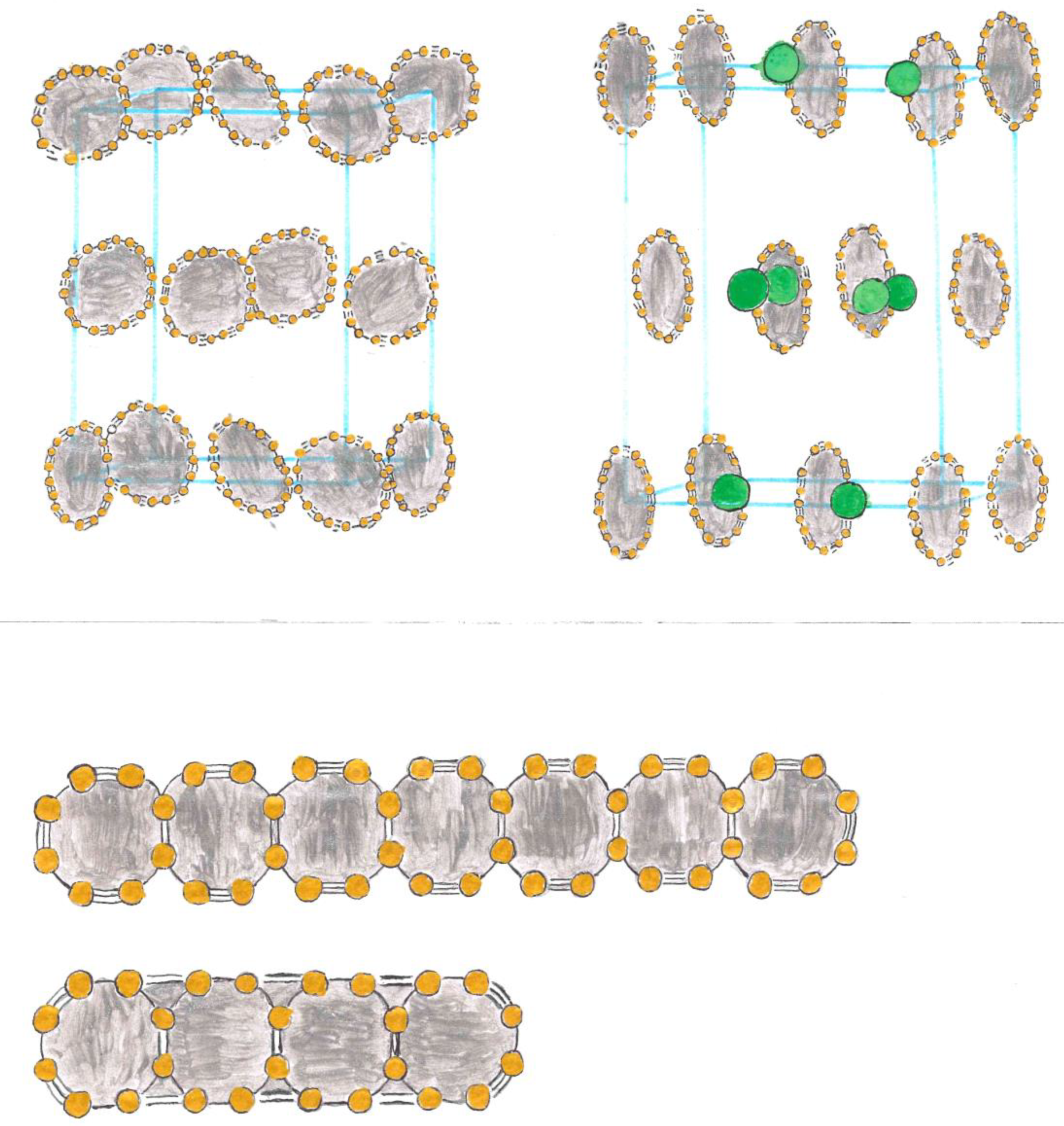
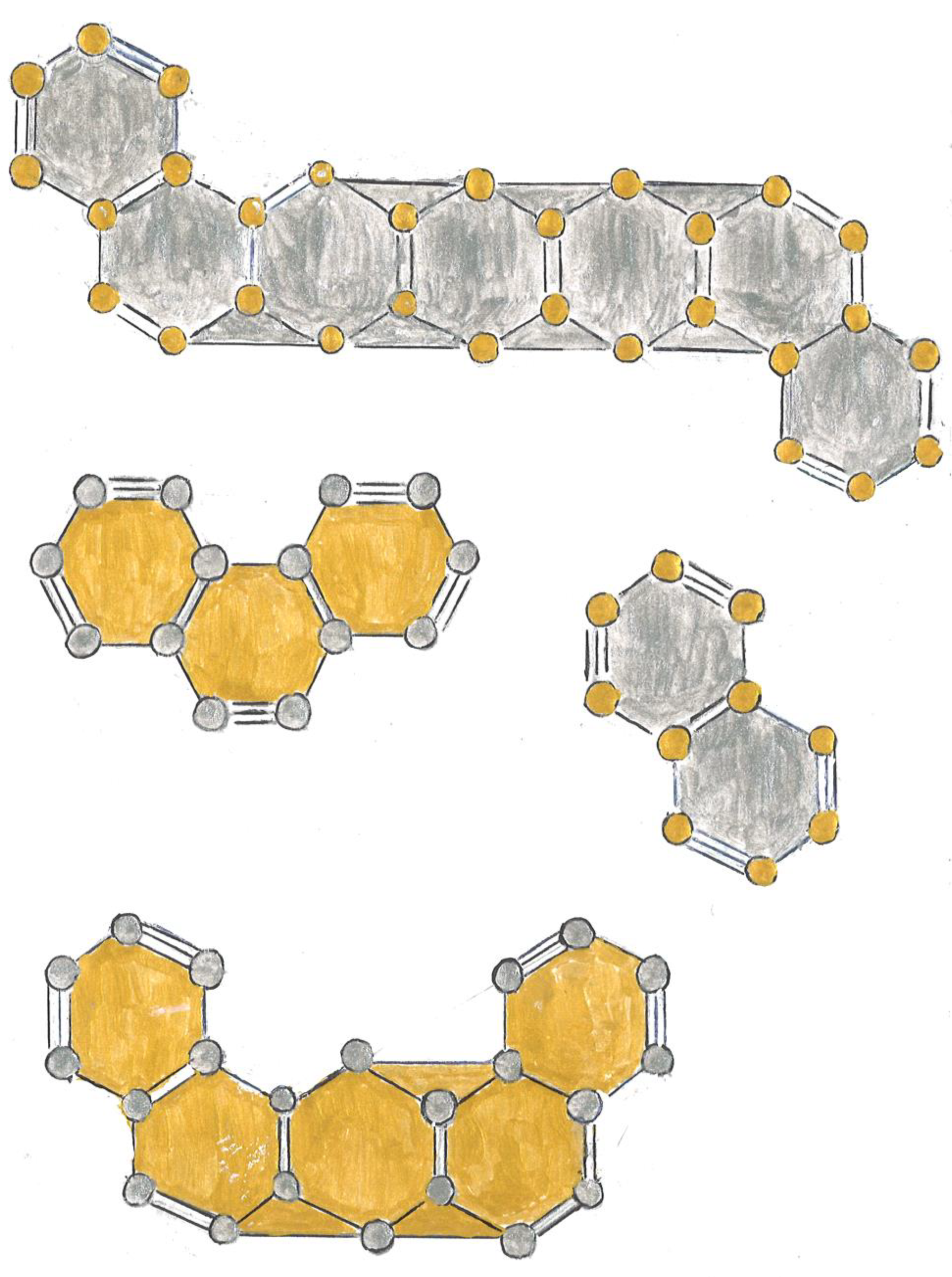
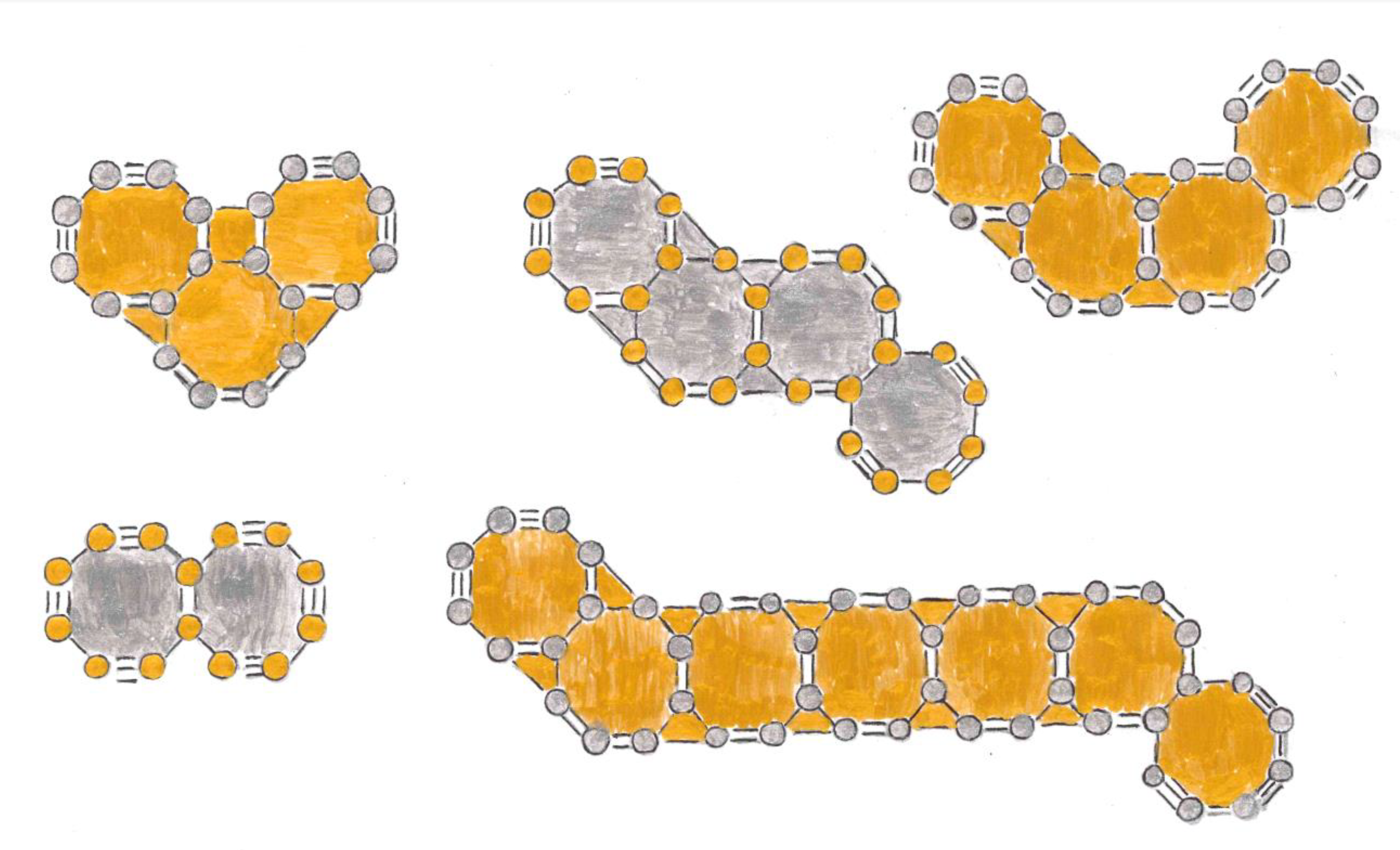
Exposition

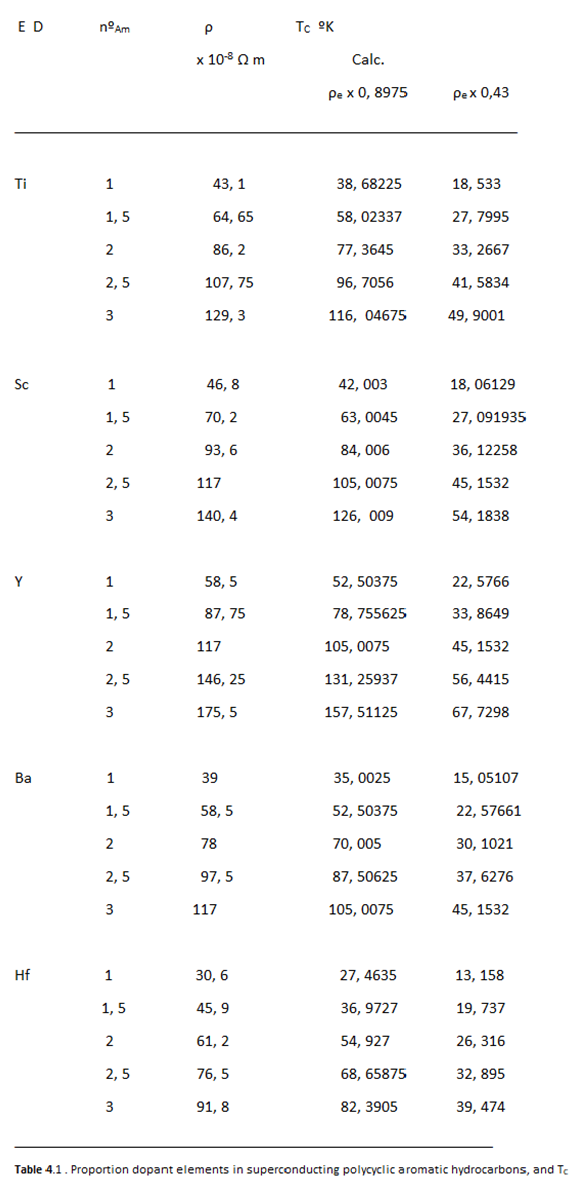
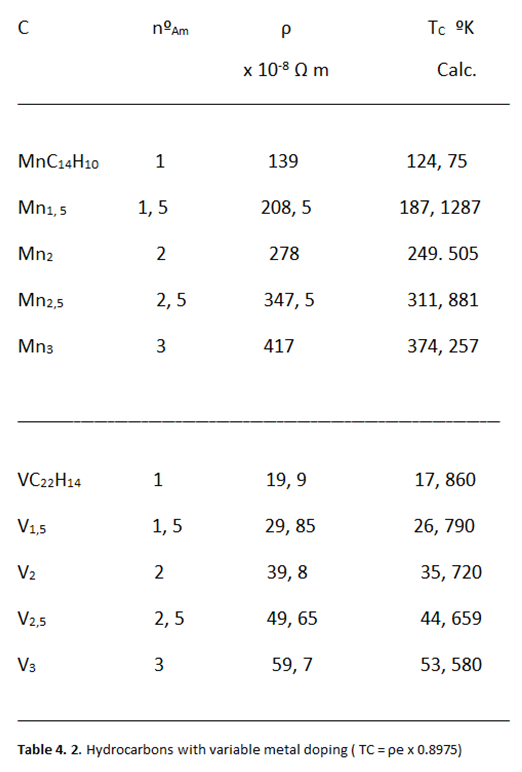
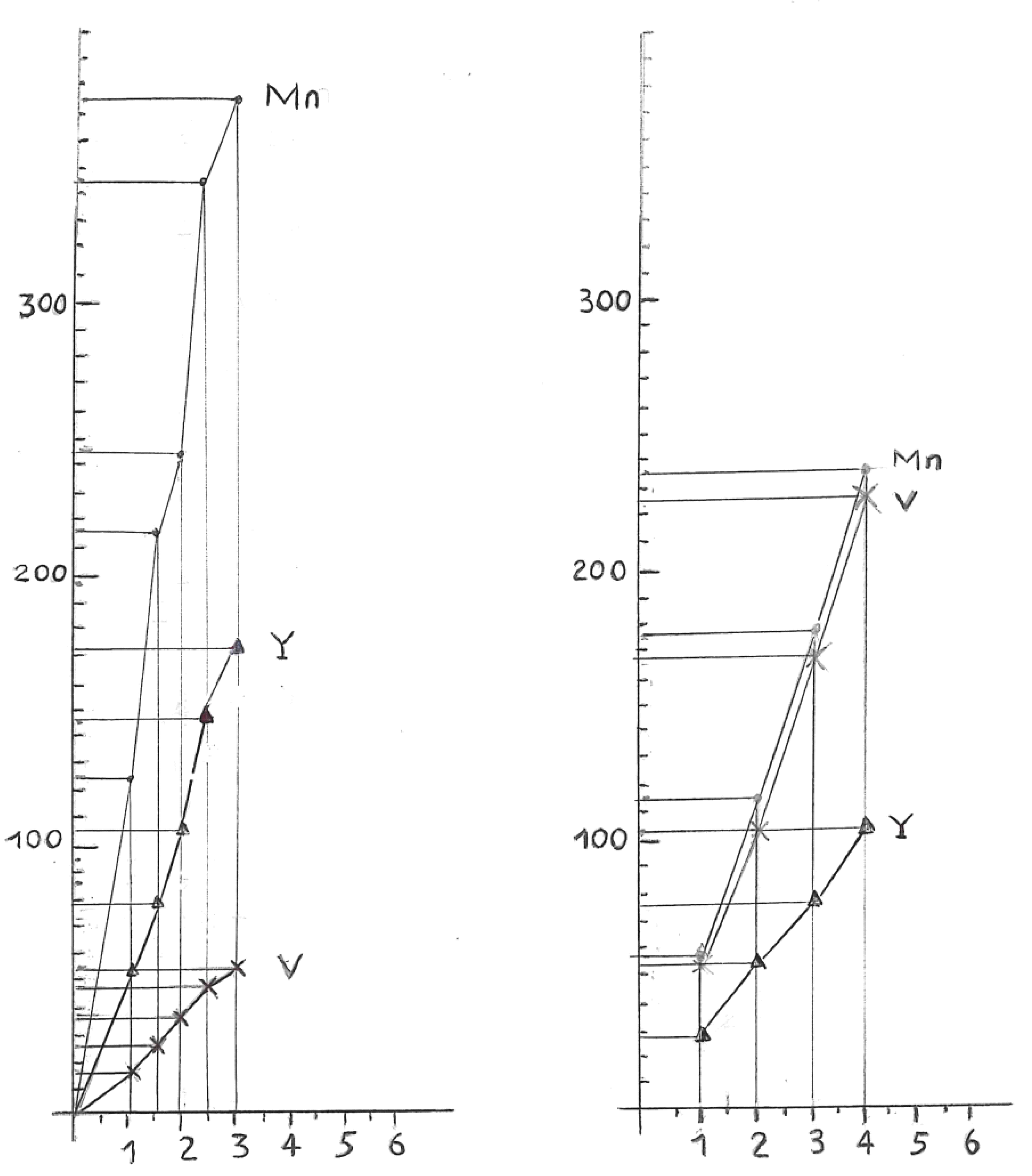
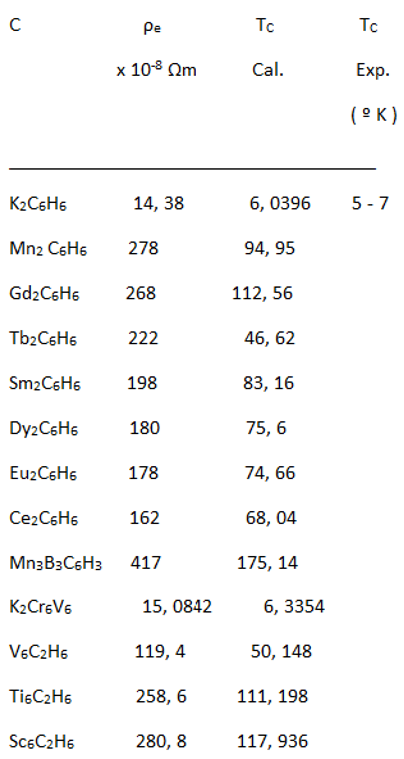
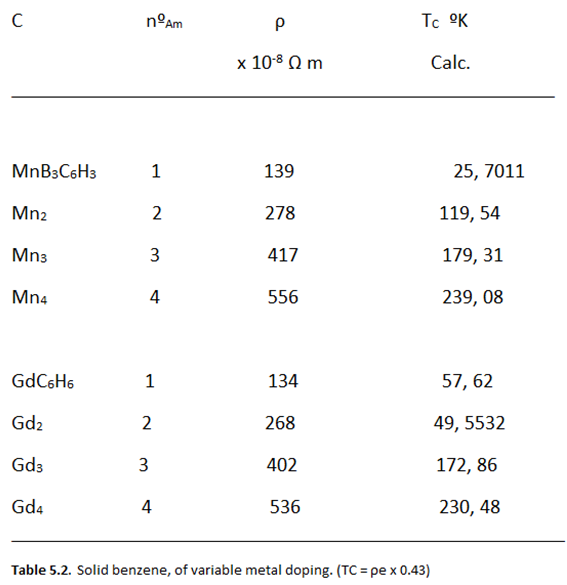
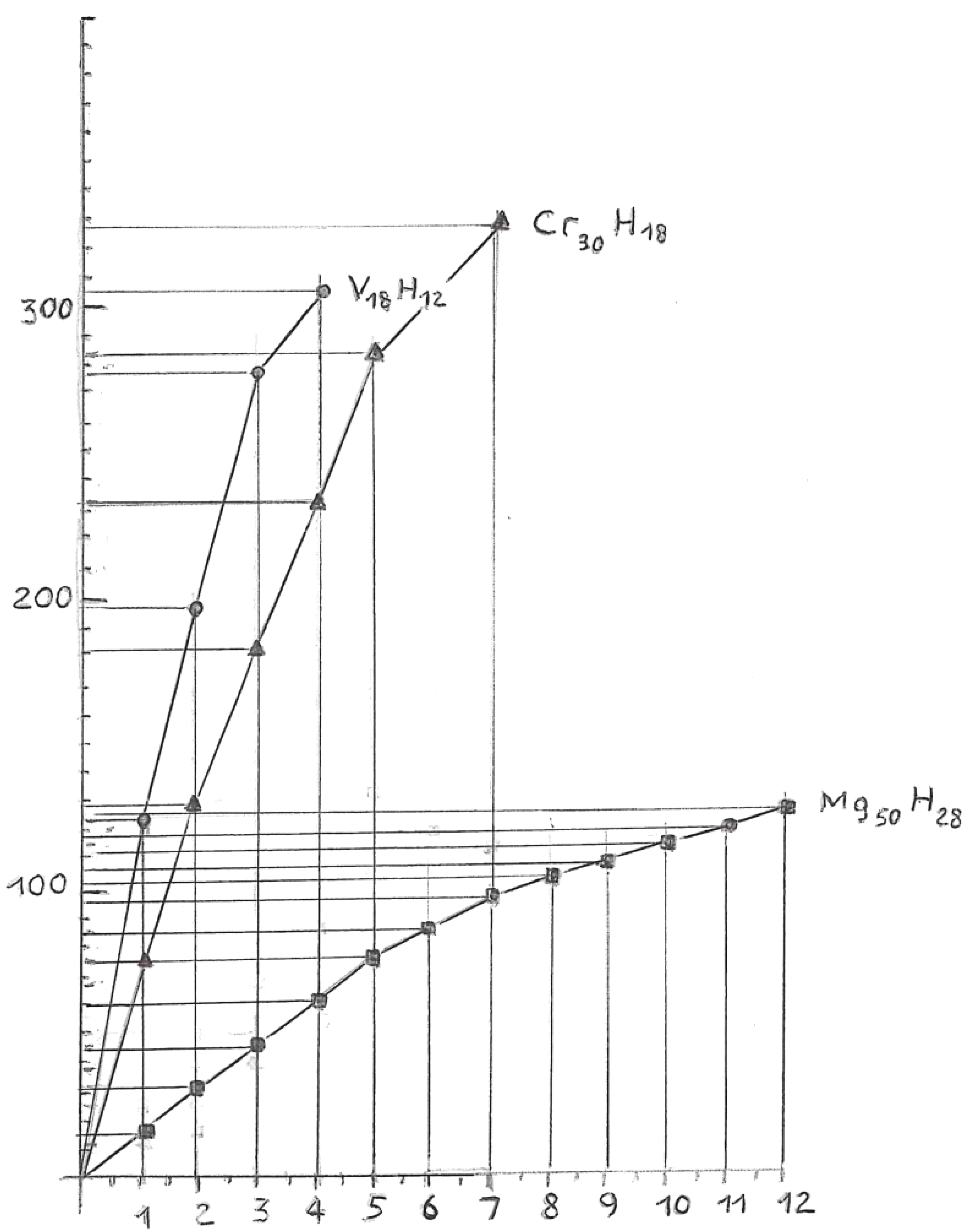
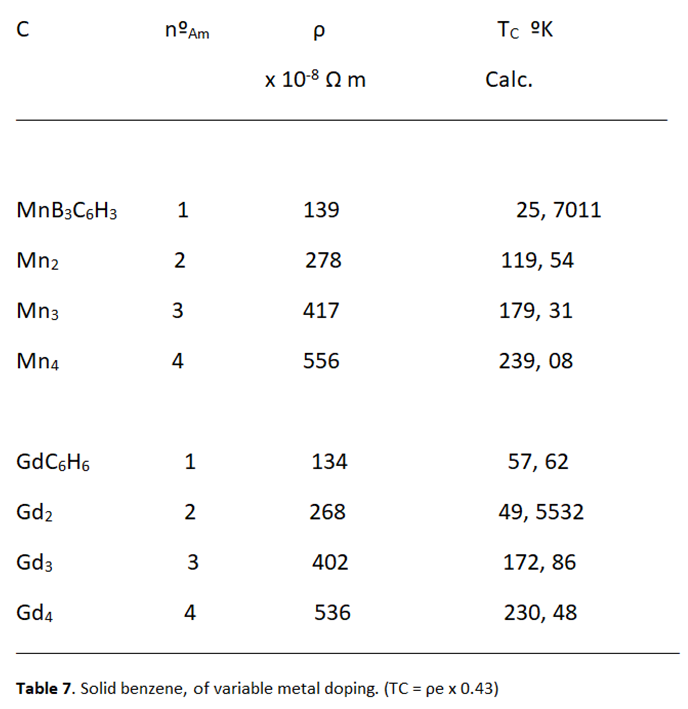
Relationship between Resistivity and Superconductivity

Minjae Kim, Hong Chul Choi, and other authors conclude in their study that superconductivity in solid polycyclic hydrocarbons doped with metals is of the conventional BCS type, mediated by phonons; instead of other more exotic mechanisms [6]. In this line, a relationship can be established between the electronic resistivity and the superconducting Tc; that relates the interatomic distance and the intensity of the free electron - phonon coupling; this intensifying, at a smaller distance between atoms in the crystal lattice.

The electronic resistivity is defined by some parameters of previous calculation, for its determination. We first have its mass density:

, where m, is the mass; and V is the volume of the unit cell. Then we have the density, or concentration of free electrons, in the solid [7].

In this expression, we have N_A, as Avogadro's number ( 6.02214 x 1023 mol-1 ); Z is the electronic valence number of the atom; A is the atomic mass number; and ρm , as we have already seen, in its previous expression, is the mass density.

Per unit cell, this equation simplifies to:

Being nº_A , the number of atoms that make up the unit cell; which is what we will use here.

The mean free path between collisions of the free electrons with the ions is defined by the equation [7]:

Where the number of ions ( nºion ) is directly proportional to their radius ( rion ); and inversely proportional to that of the mean free path ( ℓ ). Finally, we arrive at the final expression, for the electrical resistivity [7]:

K_B, is the Boltzman constant ( 8.61733 × 10-5 eV K−1 ), and the temperature ( T ), comes in absolute degrees or Kelvin.

The electron´s effective or dynamic máss, came difinited by the math formula [8]:

According to Kittel and G. T. Meaden [9,10,11], only metals compute electronic resistivity, excluding semi-metallic and non-metallic elements.

Table 1. Electrical resistivity of K and Ba, , not computing non-metallic.

Table 1. Electrical resistivity of K and Ba, , not computing non-metallic.

For the calculation of the superconducting TC, in the case of having only one metallic element (in this case, dopant metallic atoms), in a molecular solid, as is the case; we have found the relation:

, for Ba - anthracene and K - picene, is a fairly good approximation, for superconducting T_C.

Table 2. Intercalated reference compounds for this study. Ba - anthracene ( TC = 35ºK ) and K - picene ( TC = 22ºK ), in their experimental record. ( TC, calculated with the equation, 7 ).

Table 2. Intercalated reference compounds for this study. Ba - anthracene ( TC = 35ºK ) and K - picene ( TC = 22ºK ), in their experimental record. ( TC, calculated with the equation, 7 ).

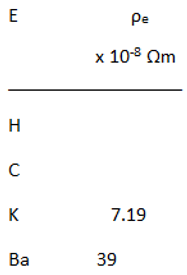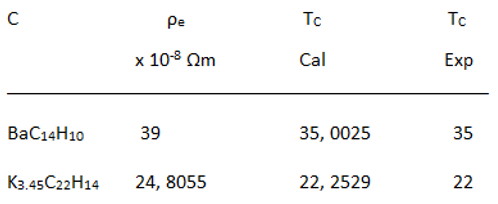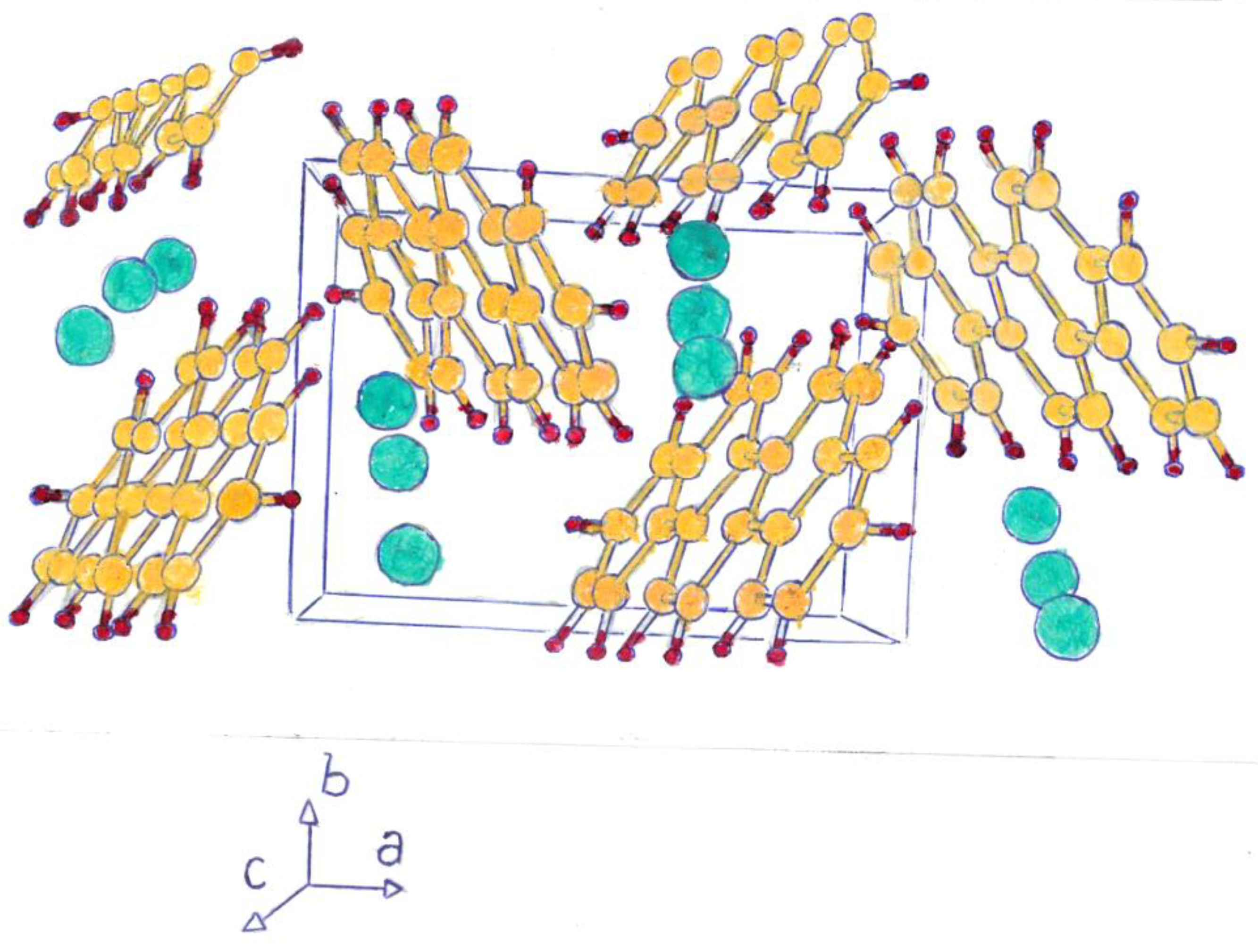
High Electrical Resistivity, among Metals

Some of the most resistive elements among the metals in the periodic table are:

Table 3. Some of most resistive metals of the periodic table.

Table 3. Some of most resistive metals of the periodic table.

Figure 1. Mn₃C₂₂H₁₄ , in his unit cell.

Figure 1. Mn₃C₂₂H₁₄ , in his unit cell.

Table 4. Polyciclic Aromatic Hydrocarbons doped with metals, of high resistivity.

Table 4. Polyciclic Aromatic Hydrocarbons doped with metals, of high resistivity.

Scheme 1. Relationship, between T_C superconductivity and number of metallic atoms doping component, in polycyclic aromatic hydrocarbons ( PAH ).

Scheme 1. Relationship, between T_C superconductivity and number of metallic atoms doping component, in polycyclic aromatic hydrocarbons ( PAH ).

For solids composed of simple or discrete molecules, of the solid benzene type, equation number 7 changes to:

When we have two components that form the star ring, such as Cr₆V₆, we can use the same equation that we used to calculate the reduced mass [11].

If we have the formula A _m B _n C _o and the resistivities ρ _{e, m}; ρ _{e, n} and ρ _{e, o} :

Figure 2. Mn₃B₃ C₆H_3.

Figure 2. Mn₃B₃ C₆H_3.

Figure 3. Cr ₆ V ₆ and K ₂ Cr ₆ V _6.

Figure 3. Cr ₆ V ₆ and K ₂ Cr ₆ V _6.

Table 5. Aromatic ring hydrocarbon doped whit high resistivity metals.

Table 5. Aromatic ring hydrocarbon doped whit high resistivity metals.

Scheme 2. Critical temperature of three metal doped polyciclic aromatic hydrocarbon.

Scheme 2. Critical temperature of three metal doped polyciclic aromatic hydrocarbon.

Figure 4. Different lengths of polycyclic aromatic hydrocarbon chains; formed by n cycles ( n = 2 to 12).

Figure 4. Different lengths of polycyclic aromatic hydrocarbon chains; formed by n cycles ( n = 2 to 12).

Table 6. Electrical resistivity as a function of the number of rings, and its relationship with the T_C, of superconducting.

Table 6. Electrical resistivity as a function of the number of rings, and its relationship with the T_C, of superconducting.

Figure 5. Cyclic hydrocarbons of the benzene type, composed of 18 atoms, with single and triple bonds; in its pure state, undoped (top left), and doped with metal atoms (top right).

Figure 5. Cyclic hydrocarbons of the benzene type, composed of 18 atoms, with single and triple bonds; in its pure state, undoped (top left), and doped with metal atoms (top right).

Below, different lengths of chains, formed by cycles of 8 atoms, formed by single and triple bonds.

Figure 6. Non-aromatic (non-toxic) polycyclic chains, formed by joined carbon and silicon hexagons.

Figure 6. Non-aromatic (non-toxic) polycyclic chains, formed by joined carbon and silicon hexagons.

Figure 7. Nonlinear chains, formed by cycles [18] carbon and silicon.

Figure 7. Nonlinear chains, formed by cycles [18] carbon and silicon.

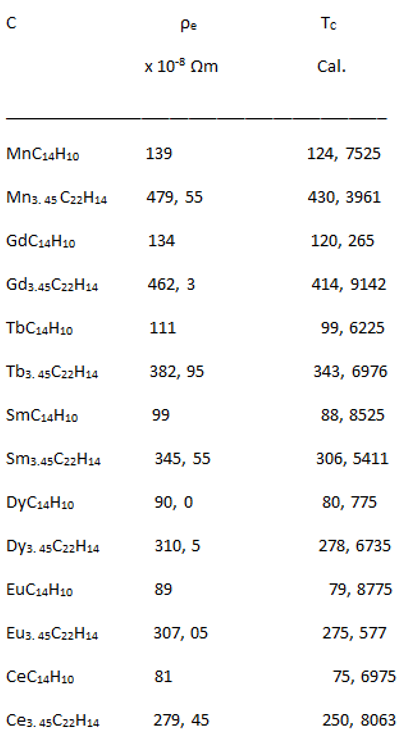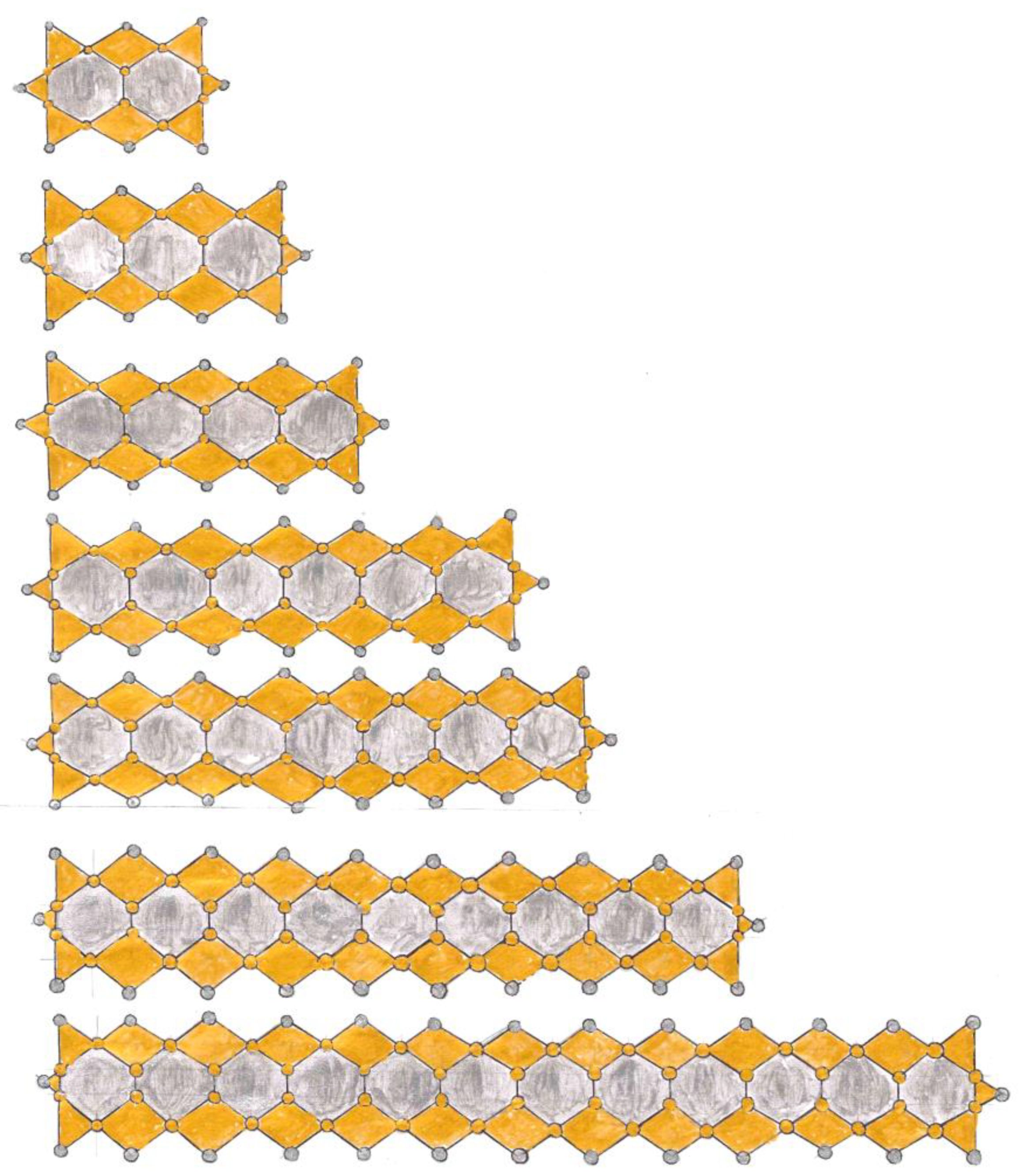
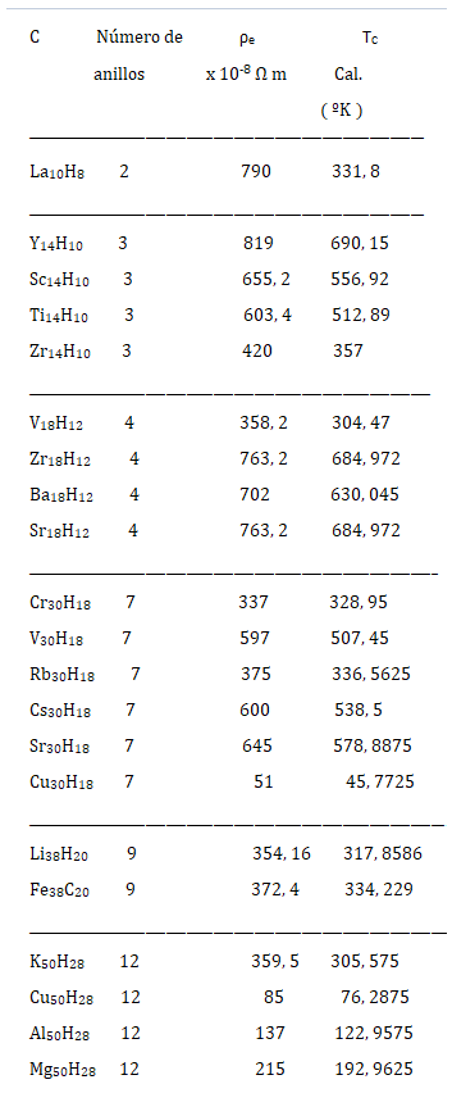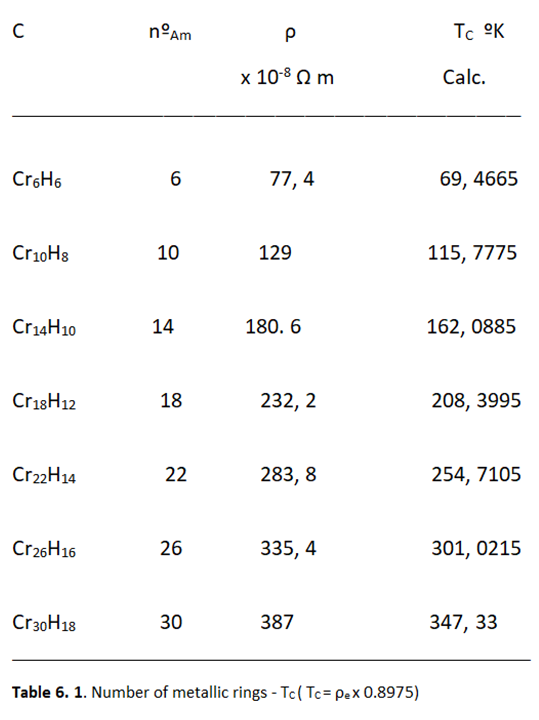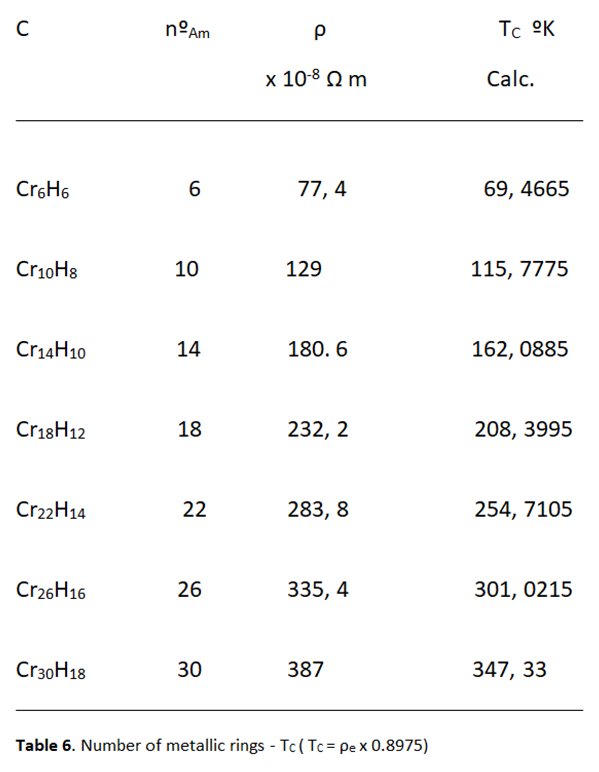Conclusions

References

1. Superconductivity in aromatic hydrocarbons. Yoshihiro Kubozono, Hidenori Goto, Taihei Jabuchi, Takayoshi Yokoya, Takashi Kambe, Yusuke Sakai, Masanari Izumi, Lu Zheng, Shino Hamao, Huyen L. T. Nguyen, Masafumi Sakata,Tomoko Kagayama and Katsuya Shimizu https://www.sciencedirect.com/science/article/am/pii/S0921453415000428.
2. Materiales derivados de hidrocarbuuros aromáticos policíclicos intercalados con metales alcalinos. Manuel Carrera Fernández https://rua.ua.es/dspace/bitstream/10045/86012/1/tesis_manuel_carrera_fernandez.pdf.
3. Synthesis and characterization of alkali-metal reduced polycyclic aromatic hydrocarbon based materials. A. Štefančič ( Table2-1, pag 35. ) http://etheses.dur.ac.uk/12339/1/Ales_Stefancic_PhD_Thesis.pdf?DDD7+.
4. Superconductivity in transition metals. Daniel R. Slocombe, Vladimir L. Kuznetsov, Wojciech Grochala, Robert J. P. Williams and Peter P. Edwards https://royalsocietypublishing.org/doi/10.1098/rsta.2014.0476.
5. D. Hillesheim, K. Gofryk, and A. S. Sefat. On the nature of filamentary superconductivity inmetal-doped hydrocarbon organic materials. DeGruyter Open Access https://www.degruyter.com/document/doi/10.1515/nsm-2015-0001/html.
6. Correlated electronic structures and the phase diagram of hydrocarbon-based superconductors. https://arxiv.org/abs/1304.1613.
7. vol-1-tipler-mosca-solucionary. Chapter 38.Solids and the Theory of Conduction. Page 2786.
8. Combined theoretical and experimental characterizations of semiconductors for photoelectrocatalytic applications. Tangui Le Bahers and Kazuhiro Takanabe. ( Page 38 ).
9. http://hyperphysics.phy-astr.gsu.edu/hbasees/Tables/elecon.html.
10. Kittel, Introduction to Solid State Physics, 7th Ed. Chapter 6 Free Electron Fermi Gas.
11. G. T. Meaden, Electrical resistance of metals, Plenum, 1965.
12. INVESTIGATION OF EMPIRICAL LAWS FOR SUPERCONDUCTIVITY OF ALLOY AND COMPOUND SUPERCONDUCTORS. Liu Long-Jian and Zhang Zhuan-Jian. Chinese Physic, 2001.