Prerpints.org logo
Preprint
Article

Formation of Vibration Fields for a Mechatronic Platform Driven by Dual Asynchronous Motors

Altmetrics

Downloads

82

Views

29

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

12 July 2024

Posted:

15 July 2024

You are already at the latest version

Alerts
Abstract
This paper delves into the challenge of controlling the multiple synchronizations in mechatronic vibration machines featuring a duo of unbalanced rotors. Its primary aim is to not only attain specific rotation speeds but also to ensure the desired phase shift between these rotors. To tackle this issue, the paper employs a control law integrating cross-couplings. It conducts an analysis of the dynamics of a simplified linearized system, showcasing the robustness of the control system across varying plant parameters. Additionally, the paper outlines experimental findings from a multi-resonance vibrational laboratory setup. These findings effectively demonstrate the effectiveness of the proposed approach and highlight its potential applications. Crucially, the paper provides experimental evidence illustrating the capability to control vibration fields on the operational platform, a vital aspect pertinent to vibration transportation and bulk material mixing processes.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Vibration machines and technologies play a crucial role across various industries, including manufacturing and agriculture. It’s challenging to envision conducting tasks such as material separation, vibratory transportation, grinding, rolling, mixing, compaction, pile driving, and more without the aid of vibration machines and associated devices [1]. Their utilization not only yields significant technical and economic benefits but also contributes to enhancing working conditions.
Among the primary sources for inducing oscillations in vibration machines, unbalanced actuators stand out as the most commonly employed [1,2,3,4,5]. These actuators find application in various technologies such as vibratory conveyors, lifters, screens, and rammers, where circular, elliptical, or directional vibrations are necessary. Circular vibrations are typically produced by an unbalanced rotor, or two unbalanced rotors, revolving in phase in the same direction, or anti-phase – in the opposite directions. When there exists a phase discrepancy between the driving forces of two-shaft vibration actuators, elliptical oscillations manifest themselves.
In the advancement of vibratory machines for tasks like screening, crushing, and bulk material transportation, enhancing productivity often hinges on maintaining a stable synchronous rotation mode of unbalanced rotors (vibration actuators). The foundational theories of vibration machine synchronization were established in the 1960s by I.I. Blekhman [3,6,7,8,9,10]. These theories laid the groundwork for synchronization mechanisms in traditional rigid transmissions, or flexible transmissions, gradually giving way to vibration synchronization equipment powered by two or more actuators. Such systems enable the vibrating system to produce various trajectories through a synchronization phenomenon, see [5]. When developing a control system for a vibratory machine (VM), all these considerations come into play, see [4,11,12,13,14,15,16]. The versatility of multiple synchronization modes is rooted in the phenomenon of self-synchronization, wherein vibration actuators rotate at average angular velocities that are multiples of each other. This mode facilitates more efficient vibration displacement, especially in challenging tasks such as transporting dusty, sticky, or wet goods.
The investigation into the flow field variation in twin-roll strip casting processes induced by oscillating rollers has been addressed in [17]. This study emphasizes achieving a homogeneous distribution of strip impurities, reducing grain size, and thereby enhancing strip quality through the adoption of vibrating casting technology proposed therein.
Electro-hydraulic vibration equipment finds extensive application in various vibration environment simulation tests. Liu et al. [18] addresses challenges pertaining to bandwidth, waveform distortion control, stability, offset control, and complex waveform generation in high-frequency vibration conditions.
In a different vein, Shi et al. [19] concentrated on the vibration synchronization of mechanical structures propelled by two vibrators. It introduces a synchronization mechanism combining space and plane patterns driven by two vibrators through the extension of vibrator installation to arbitrary directions in spatial axes. Gouskov et al. [20], Panovko et al. [21] examined variations in the arrangement of technological loads on the machine’s working body. It elucidates how shifts in load center from the machine’s constructive axis of symmetry lead to changes in resonant frequencies and mutual phasing of unbalances, discussing the feasibility of controlling resonant vibration machines by adjusting vibro-actuator power frequencies to compensate for uncontrolled load shifts.
In the realm of dual-mass vibrating systems, Liu et al. [22] investigated vibratory synchronization phenomena driven by two actuators. It employs averaging methods to deduce synchronization and stability criteria in synchronous states, quantitatively analyzing parameters such as actuator rotational speeds, phase differences, and responses in sub-resonant and super-resonant states, accompanied by an engineering example. Using asymptotic and average methods, Zhang et al. [23], derived theoretical conditions for implementing multiple synchronization and stability, with particular focus on analyzing synchronization for four actuators. Leniowska and Sierze [24] studied the controlled vibration damping of a round plate utilizing a controller with phase shift adjustment in the feedback loop. A novel controller is proposed, combining regulator structures with positive position feedback and strain rate feedback. Experimental studies involve measuring plate vibrations using a laser vibrometer, with a control signal applied to the plate via a Macro Fiber Composite (MFC) disk affixed to its center. The findings demonstrate the feasibility of employing this solution to mitigate plate vibration effectively.
The phenomenon of transporting solid and granular bodies over oscillating rough surfaces has found numerous technical applications. Vibrational movement arises from an average directed motion of material particles relative to horizontally oscillating uniformly rough surfaces, stemming from the asymmetry of surface oscillation shapes, as expressed in the inequality of time intervals between consecutive extrema of surface acceleration oscillations [25,26,27]. Theoretical investigations by Blekhman et al. [27] focused on the oscillatory transportation of solid particles over flat surfaces under non-translational vibrations. The study reveals that the existing theory, with additional parameters introduced, can effectively determine the speed of vibrational transportation, with experimental validation conducted on a vibration platform. While previous works primarily analyze particle behavior during transportation, advancements towards intelligent technological systems involve employing mechatronics principles, particularly computer-controlled vibration setups with feedback mechanisms [27].
The introduction of feedback control in vibration field manipulation has been addressed by Tomchina [28], Fradkov et al. [29], initially focusing on simple synchronization cases. However, the advent of multiple synchronous modes introduces asymmetry, enhancing vibration movement efficacy by creating complex trajectories for rotors and carrier bodies. Nevertheless, the stability of multiple synchronous operation remains a challenge, necessitating further exploration into controlling vibration fields under conditions of multiple synchronization of vibroactuators.
The chaotization of platform vibrations by means of the phase-shift control was recently demonstrated in [14]. Coupling effects of support stiffness on geometric scaling factor powers of rotor-bearing systems and vibration characteristics are studied in [30].
This paper investigates the vibrational system controlled by the method proposed by Andrievsky and Boikov [31] from the perspective of creating the various vibration fields for the operational platform, driven by unbalanced rotors. Experimental validation conducted at the Multi-resonance Mechatronic Laboratory Setup confirms the approach’s efficacy, demonstrating its practical applicability in controlling the type of vibration fields of the working platform, crucial for bulk material transportation processes.
The subsequent sections are structured as follows: Section 2 briefly outlines the Mechatronic Setup SV-2M utilized for experiments. Section 3 presents the bidirectional control law for multiple synchronization of the unebalanced rotors. The experimental results along with the data processing algorithm are presented in Section 4. Concluding remarks and future work intentions are outlined in Section 5.

2. Description of Experimental Mechatronic Setup

The Multiresonance Mechatronic Laboratory Setup (MMLS) SV-2M of the IPME RAS, used in this work for experimental investigations has broad research capabilities, see [14,29,32,33,34] for details.
A vibration complex SV-2M is a nonlinear electromechanical system equipped by two induction motors (IM) with unbalanced rotors [32,33]. The self-synchronization mode is not always sufficiently stable due to random variations in motor and system parameters, and structural oscillations. Instability in the self-synchronization mode can lead to significant deviations in the phase difference between the rotors from the desired values. The desired rotations phasing can also become unstable. This raises the challenge of controlling the synchronization of the electric motors, which requires measuring the rotor rotation angles and acting on the relative phase shift.
Optical motion sensors DFRobot Smart Grayscale Sensors are installed for obtaining information about the linear and angular coordinates of 6 degrees of freedom platform. The location of linear displacement sensors on the main platform is shown schematically in Figure 1. Sensors S   1 – S   3 measure the position of the main platform in the vertical plane, and sensors S   4 – S   6 measure its position in the horizontal plane; sensors S   4 and S   5 measure displacement along the X axis, sensor S   6 measures displacement along the Y axis. In Figure 1, the numbers #1 ...#4 indicate the points of interest for the following study of the platform vibrations.Optical motion sensors DFRobotSmart Grayscale Sensors are installed for obtaining information about the linear and angular coordinates of 6 degrees of freedom platform. The location of linear displacement sensors on the main platform is shown schematically in Figure 1. Sensors S   1 – S   3 measure the position of the main platform in the vertical plane, and sensors S   4 – S   6 measure its position in the horizontal plane; sensors S   4 and S   5 measure displacement along the X axis, sensor S   6 measures displacement along the Y axis. In Figure 1, numbers #1 ...#4 indicate the points of interest for the succeeding study of the platform vibrations.

3. Bidirectional Control Law for Multiple Synchronization of Unbalanced Rotors

In [29,31,34] the problem of controlled synchronization for unbalanced rotors phase shift was considered. The control law peoposed in [31] for multiple synchronization of unbalanced rotors has the following form:
ω r * = κ − 1 ω l * ,
e ω l = ω l * − ω l , e ω r = ω r * − ω r ,
σ ˙ ω l = e ω l , u ω l = K i ω l σ ω l + K p ω l e ω l ,
σ ˙ ω r = e ω r , u ω r = K i ω r σ ω r + K p e ω r ,
ψ = κ φ r − φ l ,
e ψ = ψ * − ψ ,
σ ˙ ψ = e ψ , u ψ = − K i , ψ σ ψ + K p , ψ e ψ ,
u l = u ω l + u ψ , u r = u ω r − u ψ ,
where ω r * , ω l * are the reference motors’ velocities, κ is the normalization coefficient; e ω l , e ω r are the motor velocity errors; PI-controllers for velocities of the left and right motors are described by (), (), respectively, where K i ω l , K i ω r are for the integral, and K p ω l , K p ω r are for the proportional controller gains; in (), φ r and φ l are the phase angles of the rotors, ψ denotes the normalized phase shift between the rotors; the phase shift error is denoted by e ψ , where ψ * is the prescribed phase shift between the rotors; u l and u r in () denote the control signals applied to the left and right drive systems produced by the corresponding PI-controllers.

4. Experimental Results

The experimental study of the multiple synchronization by means of the control law (1)–() has been performed on the MMLS SV-2M and the results for various frequencies ω l * and of normalization coefficient κ and demanded normalized phase shift ψ * are presented in [31].
In the present paper these results are extendend to studying the corresponding vivration platform deflections and summarized in the form of the spectral dencetients of selected points of platform deflections and the “vibration fields” of the platform.
The main aim of this study is to demonstrate the vibration fields by the example of moving the platform sections #1–#4 (see Figure 1).

4.1. Data Processing Algorithm and its Software Implementation

The following processing algorithm is implemented to obtain the type of vibration fields based on experimental data.
Platform position sensor data are acquired at a selected sampling interval T s and saved to a file for further offline processing. Given the range of platform motion frequencies, an interval of T s = 0.002 s seconds was chosen, corresponding to a Nyquist frequency ω N ≈ 3100 rad/s. At the end of the experiment, the data array was saved to the hard disk drive (HDD) for subsequent processing.
Data acquisition from the sensors is performed using Simulink Desktop Real-Time toolbox, which includes Simulink I/O driver blocks enabling closed-loop control of physical systems from a desktop computer, allowing connections to sensors, actuators, and other devices. Data Type Conversion blocks are used to convert the measurements to MATLAB double type data for further processing. Simulink blocks “To Workspace” are used to save the data to the workspace. After the experiment, using the MATLAB save routine, the data obtained are saved on the HDD in the form of a MATLAB mat-file.
Since the measurement characteristics of optical sensors S 1 , ⋯ , S 6 , given by L i = f i ( l i ) , i = 1 , ⋯ , 6 , are close to the inversely proportional mappings presented in Figure 2 (cf. [34]), the displacements L i ( t k ) , at times t k = k T s , k = 1 , 2 , ⋯ of the corresponding platform points S 1 , ⋯ , S 6 are restored based on the sensor readings. Before the experiments, the position optical sensors had been calibrated to obtain their real measurement characteristics and the results were tabulated in 20 points inside the working range. Sensor measurements sometimes include random spikes, which are erroneous readings outside the normal range. Therefore, these anomalies were removed before further processing. For this purpose, each sensor’s entire array of measurements was subjected to statistical analysis using the MATLAB procedure histcounts with M = 1000 bins. Next, values that occur in the measurement array less than the specified threshold value n min are selected ( n min = 10 was set) and are replaced by the arithmetic mean of the measurement array. To recover displacement values L i ( t k ) from sensor signals l i ( t k ) , a standard MATLAB procedure interp1 in the option `spline’ was used on the every data processing step k = 0 , 1 , ⋯ .
For the obtained data arrays, spectrograms of the displacement processes of the sensor positions are constructed and displayed to the user. To do this, using the mean function, their time-average values are found, and the Discrete Fourier Transform (DFT), implemented by the fft MATLAB procedure, is applied to the resulting centered processes L ¯ i ( k ) . The resulting complex-valued array of images Y is converted into the array of spectral densities S i ( ω ) by calculating the squared Y modulus, normalized by the number of points. Sensor measurements were cleaned using the DFT concerning L ¯ i ( k ) . The resulting arrays Y i ( ω ) were processed as follows. Based on the obtained spectral densities S i ( ω ) , frequencies ω j , j = 1 , 2 , 3 , were selected where S i ( ω ) bursts were observed. Next, the set of frequencies Ω in the vicinities of ω j were found as: Ω = ⋃ j = 1 3 | ω − ω j | ≤ Δ ω , where Δ ω > 0 is a certain bandwidth relative to the peak frequencies ω j . New complex-valued arrays Y ˜ i ( ω ) were formed by zeroing the values of Y i ( ω ) except those that correspond to the frequencies from Ω , which values are copied from Y ˜ i ( ω ) , and their spectral densities S ˜ i ( ω ) were found. The Inverse Discrete Fourier Transform (IDFT), implemented by MATLAB routine ifft is applyied to Y ˜ i ( ω ) and, finally, the filtered centered platform displacements D ˜ i ( k ) were calculated as L ˜ i ( k ) = real ( L i ( k ) ) ∥ S i ( ω ) ∥ / ∥ S ˜ i ( ω ) ∥ , where L i ( k ) denote complex-valued inverse Fourier transforms to Y ˜ i ( ω ) , and real ( · ) denotes the real part of L i ( k ) (standard MATLAB routine real); ∥ · ∥ stands for the Euclidean norm of the complex-valued vector argument (routine norm).
As an example of the application of the described procedure, consider the case of filtering data of L 2 ( t ) , L 5 ( t ) , obtained for ω l = 80 rad/s, ω r = 40 rad/s, ψ = π / 2 , taking ω j ∈ { 20.5 , 40 , 80 } rad/s, Δ ω = 5 rad/s. The resulting time histories for L i ( t k ) , i ∈ { 2 , 5 } along with L ˜ i ( t k ) are depicted in Figure 3.
After L ˜ i ( t k ) are found, the platform points of interest #1–#4 (see Figure 1) displacements Δ x j , Δ y j , j = 1 , ⋯ , 4 on the vertical plane O X Y are calculated as follows:
Δ x 1 ( t k ) = L ˜ 4 ( t k ) + L ˜ 5 ( t k ) / 2 , Δ y 1 ( t k ) = L ˜ 1 ( t k ) + L ˜ 2 ( t k ) + L ˜ 3 ( t k ) / 3 , Δ x 2 ( t k ) = L ˜ 4 ( t k ) + L ˜ 5 ( t k ) / 2 , Δ y 2 ( t k ) = L ˜ 2 ( t k ) + L ˜ 3 ( t k ) / 2 , Δ x 3 ( t k ) = L ˜ 5 ( t k ) , Δ y 3 ( t k ) = L ˜ 3 ( t k ) , Δ x 4 ( t k ) = L ˜ 5 ( t k ) , Δ y 4 ( t k ) = L ˜ 4 ( t k ) .
The experimental results for various revolving speeds of rotors and phase shifts are presented below. For legibility of the graphs, the trajectories are displayed only in the final section of the experiment t ∈ [ t a , t b ] with a duration of t b − t a about two characteristic periods of oscillation.

4.2. Case of Identical Rotation Velocities

At first, consider the case when both rotors revolve with the same desired frequency. Namely, let ω l * = ω r * = 80 rad/s be taken (i.e. in (1) – () parameter κ = 1 be set). The desired phase shift between the rotors ψ * is set to zero. The spectral densities for displacements of sensors # 2, # 3 are pictured in Figure 4. As is seen from the plot, the “outstanding” peak on frequency close to 20.5 rad/s appears. It corresponds to the low-frequency resonant mode of the platform.
The motion of the various points of the platform on the vertical plane O X Y (where O X stands for the horizon axis, O Y denotes the vertical one), are plotted in Figure 5. The time interval for plotting the curves is taken as t ∈ 27 + [ 0.1726 , 0.6438 ] s. This interval corresponds 6 periods of motion with a frequency 80 rad/s.
The upper plots series correspond zero phase shift ( ψ * = 0 ) between the rotors. Respectively, the lower plot is related to phase shift ψ * = π . It is seen that the vibration field, having, in general, a similar shape that in the case of ψ * = 0 , changes its inclination. This property can be used for control of the vibrational transportation speed and direction.

4.3. Case of Different Rotation Velocities

Secondly, the similar experiments were performed for the case of different rotation frequencies of rotors. Namely, ω l * = 90 rad/s and ω r * = 45 rad/s were taken (i.e. in (1) – () parameter κ = 2 was set). The desired phase shift between the rotors ψ * is set to zero. The corresponding spectral densities for displacements of sensors # 2, # 3 are pictured in Figure 6. As is seen from the plot, the spectrograms have three peaks: on the frequencies of 45 rad/s, 90 rad/s, corresponding the rotation velocities of the drives, and the peak on 20 rad/s appears related to the natural oscillating of the platform.
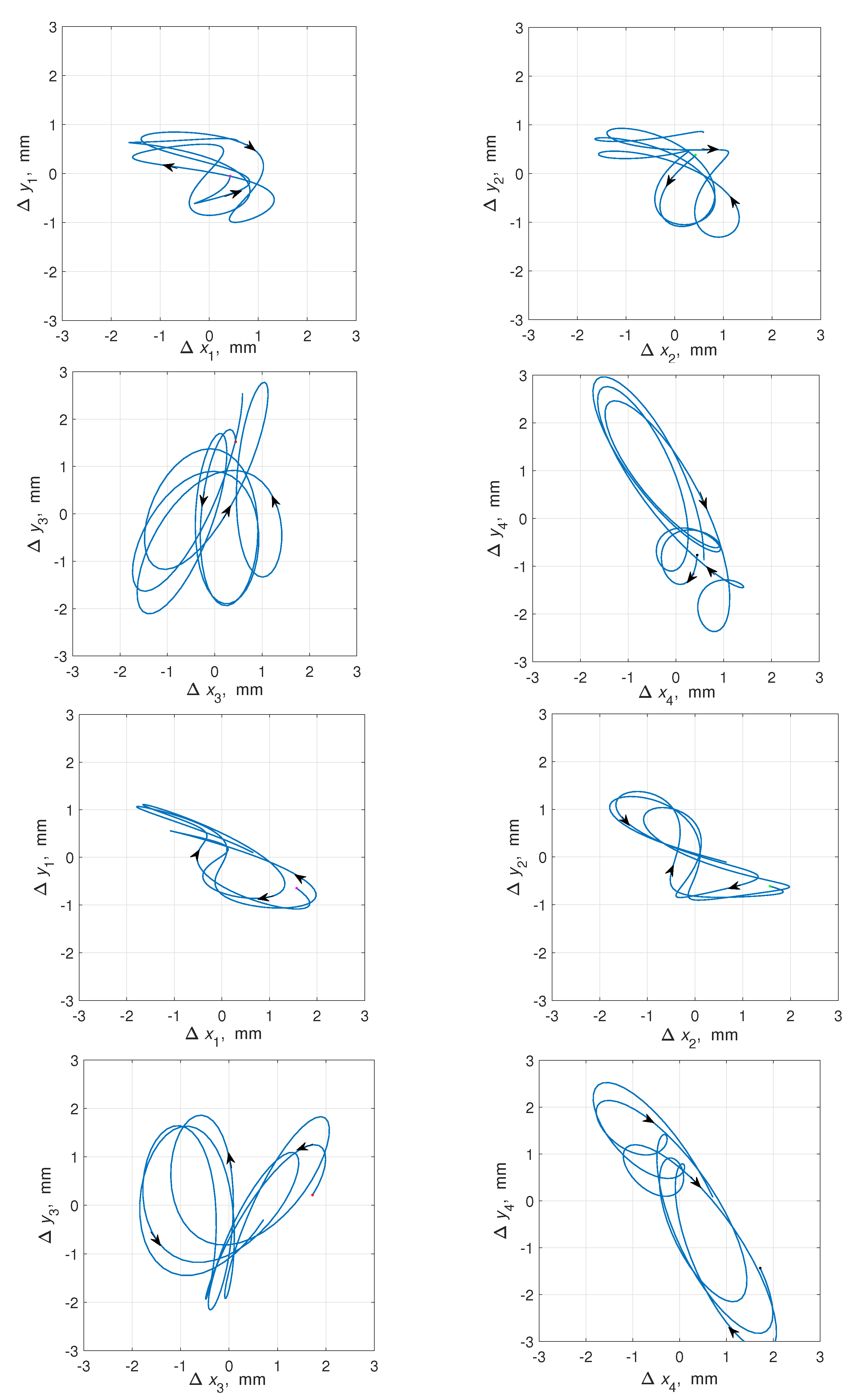
The corresponding vibration fields of the platform sections #1–#4 on the vertical plane O X Y are plotted in Figure 7. The time interval for plotting the curves is taken as t ∈ 27 + [ 0.4867 , 0.9056 ] s. This interval corresponds 6 periods of motion with a frequency 90 rad/s. The platform motion is for the considered multiple case in more complex compared with the single-frequency one due to interference both from the slow oscillations with the natural frequency of the platform (20 rad/s) and two rotation speeds of the drives with the different values (90 and 45 rad/s).
The upper plots in Figure 7 correspond zero phase shift ( ψ * = 0 ) between the rotors, while the lower plot is related to phase shift ψ * = π . It is seen that the vibration field is more complex than in the single-frequency case and also is varying with the phase shift, set between the rotors. This gives additional flexibility in control of the platform vibration fields and can be used in developing smart vibrational technologies.

5. Conclusions

The paper demonstrates the possibility of using controlled multiple synchronization of unbalanced rotors driven by induction motors to form vibration fields in the working platform of a vibration mechatronic setup. The experimental results obtained at the MMLS SV-2M of the IPME RAS are presented, demonstrating the efficacy of the proposed approach.
Expanding the capabilities of controlled synchronization can be gained by employing unidirectional (master-slave synchronization) and alternative control methods. These methods include adaptive control, variable-structure sliding-mode control, speed gradient techniques, Neural Networks, and nonlinear correction methods, which represent promising areas for further research.

Author Contributions

Conceptualization, O.T.; data curation, I.Z.; formal analysis, A.F. and B.A.; funding acquisition, A.F.; investigation, I.Z.; methodology, B.A.; project administration, A.F.; software, I.Z.; supervision, B.A.; writing—original draft, A.F. and B.A.; writing—review and editing, B.A. and O.T. All authors have read and agreed to the published version of the manuscript.

Funding

The research was supported by the Ministry of Science and Higher Education of the Russian Federation (project no. 124041500008-1).

Data Availability Statement

Not applicable.

Acknowledgments

The Authors are grateful to V. I. Boikov for his invaluable work in creating the electronic and computer facilities of the MMLS SV-2M.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
AC Alternating Current
DFT Discrete Fourier Transform
DoF Degrees of Freedom
IDFT Inverse Discrete Fourier Transform
IM Induction Motor
HDD Hard Disk Drive
MFC Macro Fiber Composite
MMLS Multiresonance Mechatronic Laboratory Setup
VM Vibratory Machine

References

  1. Blekhman, I.I. Vibrational Mechanics; World Scientific: Singapore, 2000. [Google Scholar]
  2. Braun, S.; Ewins, D.; Rao, S. Encyclopedia of Vibration; Academic Press: San Diego, 2002. [Google Scholar]
  3. Blekhman, I.I.; Vaisberg, L.A. Self-Synchronization as a Self-Organization Phenomenon and a Basis for Development of Energy-Efficient Technologies. In Proceedings of the 10th Biennial International Conference on Vibration Problems (ICOVP); Segla, S. Tuma, J., Petrikova, I., Eds.; 2011; pp. 365–370. [Google Scholar]
  4. Fradkov, A.; Gorlatov, D.; Tomchina, O.; Tomchin, D. Control of oscillations in vibration machines: Start up and passage through resonance. Chaos 2016, 26, 116310. [Google Scholar] [CrossRef] [PubMed]
  5. Li, L.; Chen, X. Multi-frequency Vibration Synchronization and Stability of the Nonlinear Screening System. IEEE Access 2019, 7, 171032–171045. [Google Scholar] [CrossRef]
  6. Blekhman, I.I.; Landa, P.S.; Rosenblum, M.G. Synchronization and chaotization in interacting dynamical systems. Applied Mechanics Reviews 1995, 48, 733–752. [Google Scholar] [CrossRef]
  7. Blekhman, I.I.; Fradkov, A.L.; Nijmeijer, H.; Pogromsky, A.Y. On self-synchronization and controlled synchronization of dynamical systems. Systems & Control Letters 1997, 31, 299–306. [Google Scholar]
  8. Blekhman, I.I.; Fradkov, A.L.; Tomchina, O.P.; Bogdanov, D.E. Self-Synchronization and Controlled Synchronization: General Definition and Example Design. Mathematics and Computers in Simulation 2002, 58, 367–384. [Google Scholar] [CrossRef]
  9. Blekhman, I.; Fradkov, A. On general definitions of synchronization. In Selected Topics in Vibrational Mechanics; Blekhman, I.I., Ed.; World Scientific: Singapore, 2004; pp. 179–188. [Google Scholar]
  10. Blekhman, I.I.; Yaroshevich, N.P. Extension of the domain of applicability of the integral stability criterion (extremum property) in synchronization problems. J. Applied Mathematics and Mechanics 2004, 68. [Google Scholar] [CrossRef]
  11. Fradkov, A.; Tomchina, O.; Galitskaya, V.; Gorlatov, D. Multiple Controlled Synchronization for 3-Rotor Vibration Unit with Varying Payload. IFAC-PapersOnLine 2013, 46, 5–10. [Google Scholar] [CrossRef]
  12. Andrievsky, B.; Boikov, V.I.; Fradkov, A.L.; Seifullaev, R.E. Mechatronic Laboratory Setup For Study of Controlled Nonlinear Vibrations. IFAC-PapersOnLine 2016, 49, 1–6. [Google Scholar] [CrossRef]
  13. Zaitceva, I.; Andrievsky, B. Real-time Reinforcement Learning of Vibration Machine PI-controller. In Proceedings of the 6th Scientific School "Dynamics of Complex Networks and their Applications (DCNA 2022); 2022; pp. 307–311. [Google Scholar]
  14. Andrievsky, B.; Zaitceva, I. Symmetrical Control Law for Chaotization of Platform Vibrations. Symmetry 2022, 14. [Google Scholar] [CrossRef]
  15. Zaitceva, I.; Kuznetsov, N.V.; Andrievsky, B. Approach to Identifying Areas of Uncontrolled Oscillations in Human-Machine Systems. In Proceedings of the 2023 International Russian Smart Industry Conference (SmartIndustryCon); 2023; pp. 196–201. [Google Scholar] [CrossRef]
  16. Andrievsky, B.; Zaitceva, I.; Barkana, I. Passification-Based Robust Phase-Shift Control for Two-Rotor Vibration Machine. Electronics 2023, 12. [Google Scholar] [CrossRef]
  17. Xu, Z.Q.; Meng, Z.R.; Xue, S.H.; Zhang, D.Q.; Du, F.S. Effect of Oscillation Parameters to Flow Field in the Pool during the Oscillating Twin-Roll Strip Casting Process. Chinese Journal of Mechanical Engineering (English Edition) 2018, 31. [Google Scholar] [CrossRef]
  18. Liu, Y.; Wang, T.; Gong, G.; Gao, R. Present Status and Prospect of High-Frequency Electro-hydraulic Vibration Control Technology. Chinese Journal of Mechanical Engineering (English Edition) 2019, 32. [Google Scholar] [CrossRef]
  19. Shi, S.; Hou, Y.; Fang, P.; Hou, D.; Peng, H. Synchronization investigation on space vibration system driven by two vibrators with arbitrary direction axes. Applied Mathematical Modelling 2023, 120, 199–216. [Google Scholar] [CrossRef]
  20. Gouskov, A.; Panovko, G.; Shokhin, A. To the issue of control resonant oscillations of a vibrating machine with two self-synchronizing inertial exciters. Lecture Notes in Mechanical Engineering 2021, 58, 515–526. [Google Scholar] [CrossRef]
  21. Panovko, G.; Shokhin, A.; Eremeikin, S. The control of the resonant mode of a vibrating machine that is driven by an asynchronous electro motor. J. Machinery Manufacture and Reliability 2015, 44, 109–113. [Google Scholar] [CrossRef]
  22. Liu, Y.; Zhang, X.; Gu, D.; Jia, L.; Wen, B. Synchronization of a Dual-Mass Vibrating System with Two Exciters. Shock and Vibration 2020, 2020, 1–12. [Google Scholar] [CrossRef]
  23. Zhang, X.; Zhang, X.; Zhang, C.; Wang, Z.; Wen, B.C. Multiple-frequency synchronization of the four exciters in a far super-resonant vibrating system with an isolation frame. J. Low Frequency Noise, Vibration and Active Control 2021. [Google Scholar] [CrossRef]
  24. Leniowska, L.; Sierże, M. Vibration control of a circular plate using parametric controller with phase shift adjustment. Mechatronics 2019, 58, 39–46. [Google Scholar] [CrossRef]
  25. Blekhman, I.I.; Dzhanelidze, G.Y. Vibrational Movement [Vibratsionnoye peremeshcheniye]; Nauka: M, 1964. [Google Scholar]
  26. Lyan, I.; Panovko, G. Modelling the granular medium dynamics on rough vibrating plane using method of large particles. IOP Conf. Series: Materials Science and Engineering 2019, 489. [Google Scholar] [CrossRef]
  27. Blekhman, I.I.; Vasil’kov, V.B.; Semenov, Y.A. Vibrotransporting of Bodies on a Surface with Non-Translational Rotational Oscillations. J. Machinery Manufacture and Reliability 2020, 49, 280–286. [Google Scholar] [CrossRef]
  28. Tomchina, O. Control of vibrational field in a cyber-physical vibration unit. Cybernetics and Physics 2018, 7, 144–151. [Google Scholar] [CrossRef]
  29. Fradkov, A.L.; Tomchina, O.P.; Andrievsky, B.; Boikov, V.I. Control of Phase Shift in Two-Rotor Vibration Units. IEEE Trans. Control Syst. Technol. 2021, 29, 1316–1323. [Google Scholar] [CrossRef]
  30. Zhang, W.; Luo, Z.; Li, Y.; Zhu, Y. A novel method to determine the coupling scaling laws of vibration characteristics for rotor-bearing systems. JVC/Journal of Vibration and Control 2021, 27, 2630–2641. [Google Scholar] [CrossRef]
  31. Andrievsky, B.; Boikov, V.I. Bidirectional controlled multiple synchronization of unbalanced rotors and its experimental evaluation. Cybernetics And Physics 2021, 10, 63–74. [Google Scholar] [CrossRef]
  32. Andrievskii, B.R.; Blekhman, I.I.; Blekhman, L.I.; Boikov, V.I.; Vasil’kov, V.B.; Fradkov, A.L. Education and Research Mechatronic Complex for Studying Vibration Devices and Processes. J. Mach. Manuf. Reliab. 2016, 45, 369–374. [Google Scholar] [CrossRef]
  33. Boikov, V.I.; Andrievsky, B.; Shiegin, V.V. Experimental study of unbalanced rotors synchronization of the mechatronic vibration setup. Cybernetics and Physics 2016, 5, 5–11. [Google Scholar]
  34. Andrievsky, B.; Fradkov, A.L.; Tomchina, O.P.; Boikov, V.I. Angular velocity and phase shift control of mechatronic vibrational setup. IFAC-PapersOnLine 2019, 52, 436–441. [Google Scholar] [CrossRef]
Preprints 112011 g001
Figure 1. Schematic diagram of the setup (top view) and location of sensors S   1 – S   6 on the main platform
Figure 1. Schematic diagram of the setup (top view) and location of sensors S   1 – S   6 on the main platform
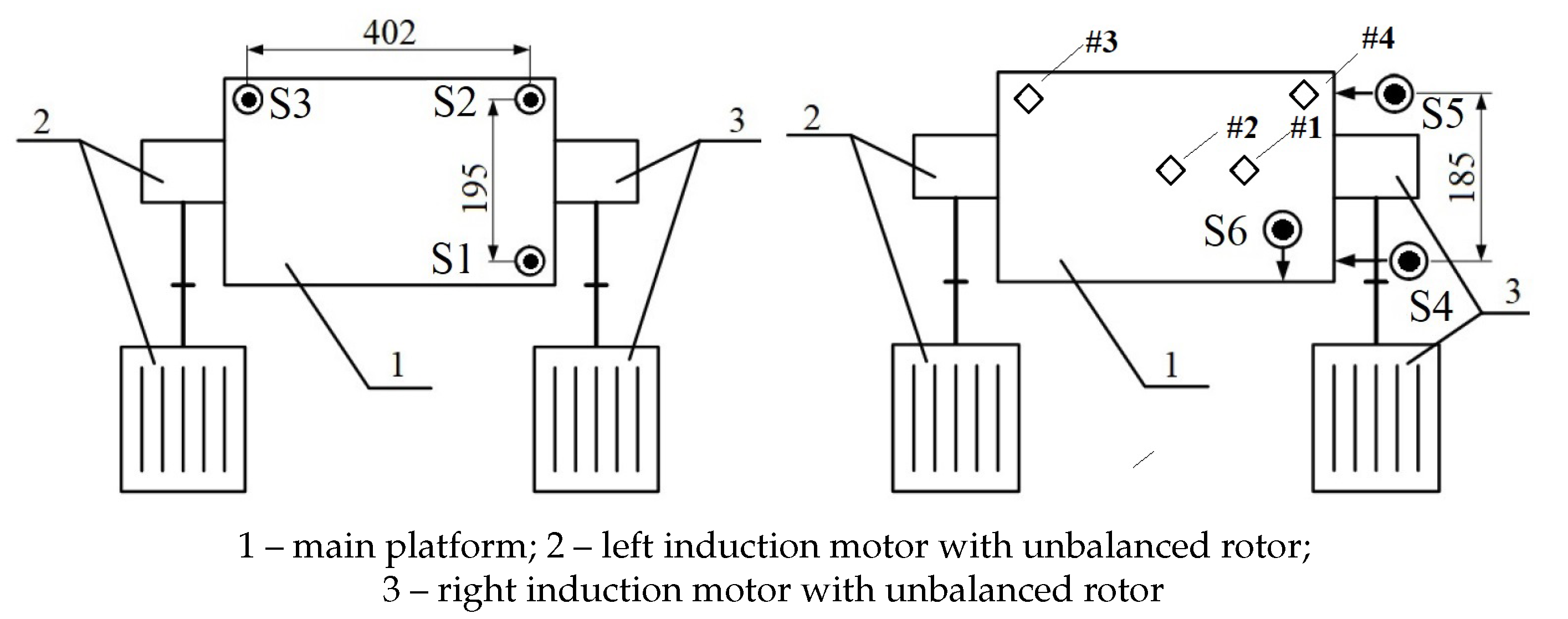
Preprints 112011 g001
Preprints 112011 g002
Figure 2. Measuring characteristics of sensors S   1 – S   6 (as in [34])
Figure 2. Measuring characteristics of sensors S   1 – S   6 (as in [34])
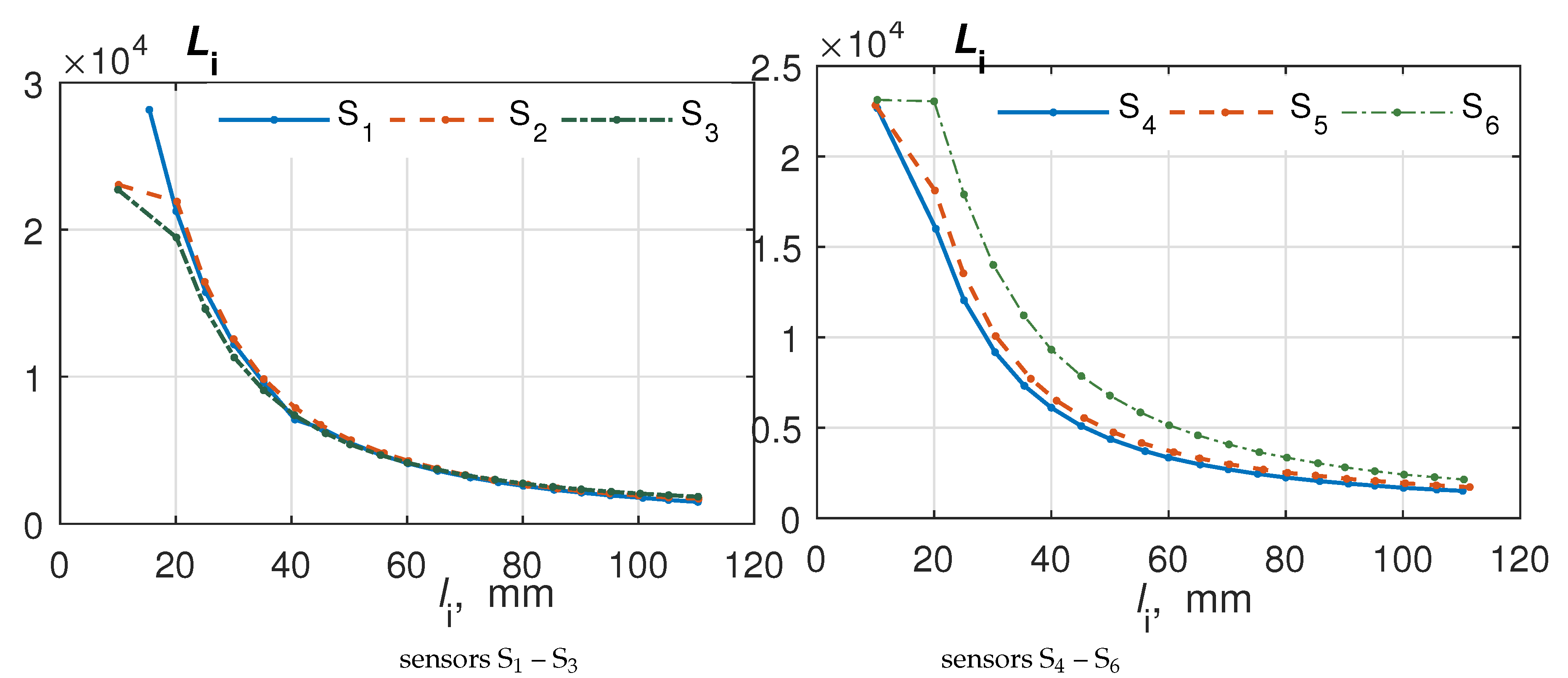
Preprints 112011 g002
Preprints 112011 g003
Figure 3. Time histories of measured (dash-dot line) and filtered (solid line) platform positions L 2 ( t ) , L 5 ( t ) , t ∈ [ 29 , 30 ] s, for the case of ω l = 80 rad/s, ω r = 40 rad/s, ψ = π / 2 ; ω j ∈ { 20.5 , 40 , 80 } rad/s, Δ ω = 5 rad/s.
Figure 3. Time histories of measured (dash-dot line) and filtered (solid line) platform positions L 2 ( t ) , L 5 ( t ) , t ∈ [ 29 , 30 ] s, for the case of ω l = 80 rad/s, ω r = 40 rad/s, ψ = π / 2 ; ω j ∈ { 20.5 , 40 , 80 } rad/s, Δ ω = 5 rad/s.
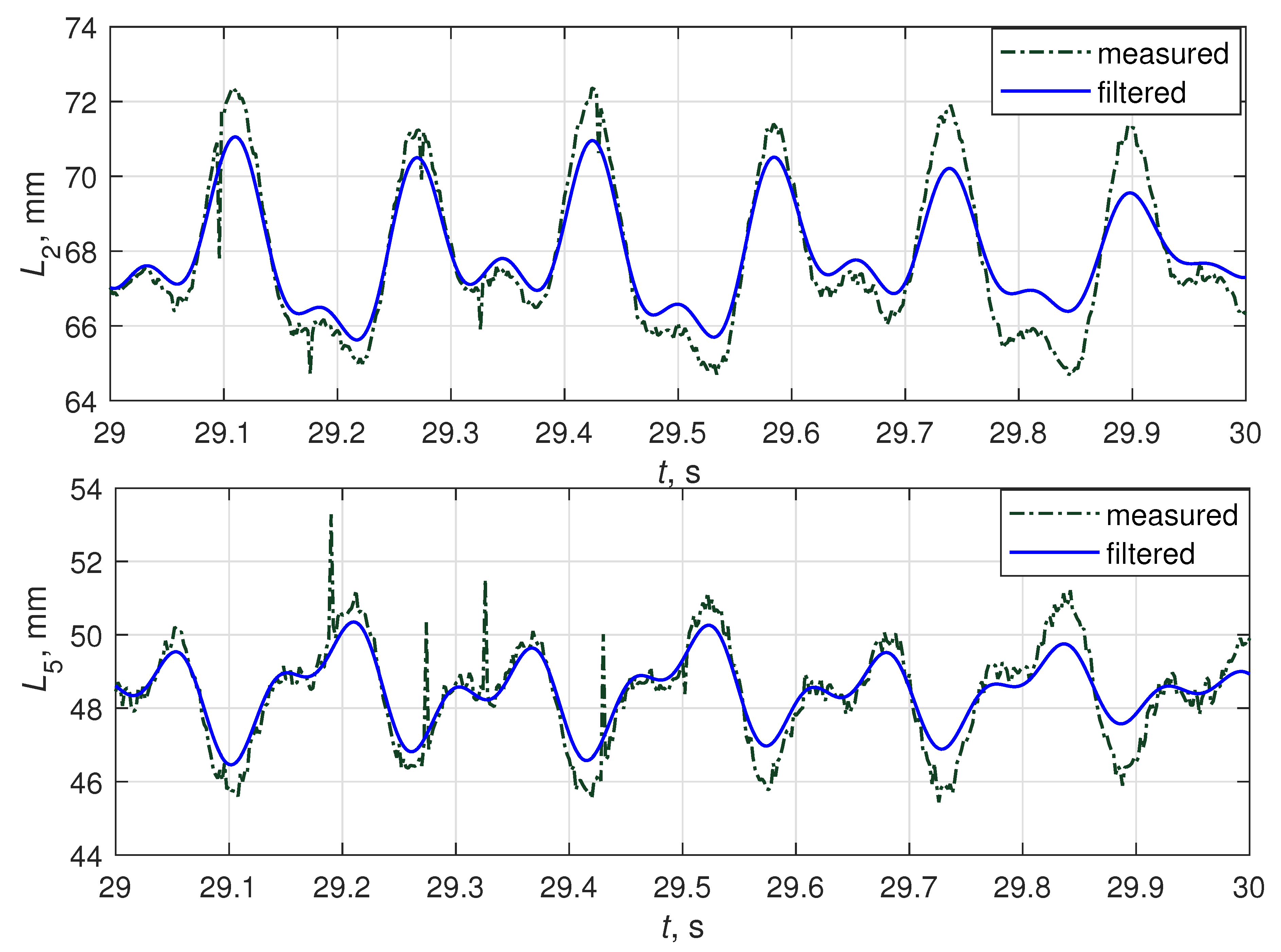
Preprints 112011 g003
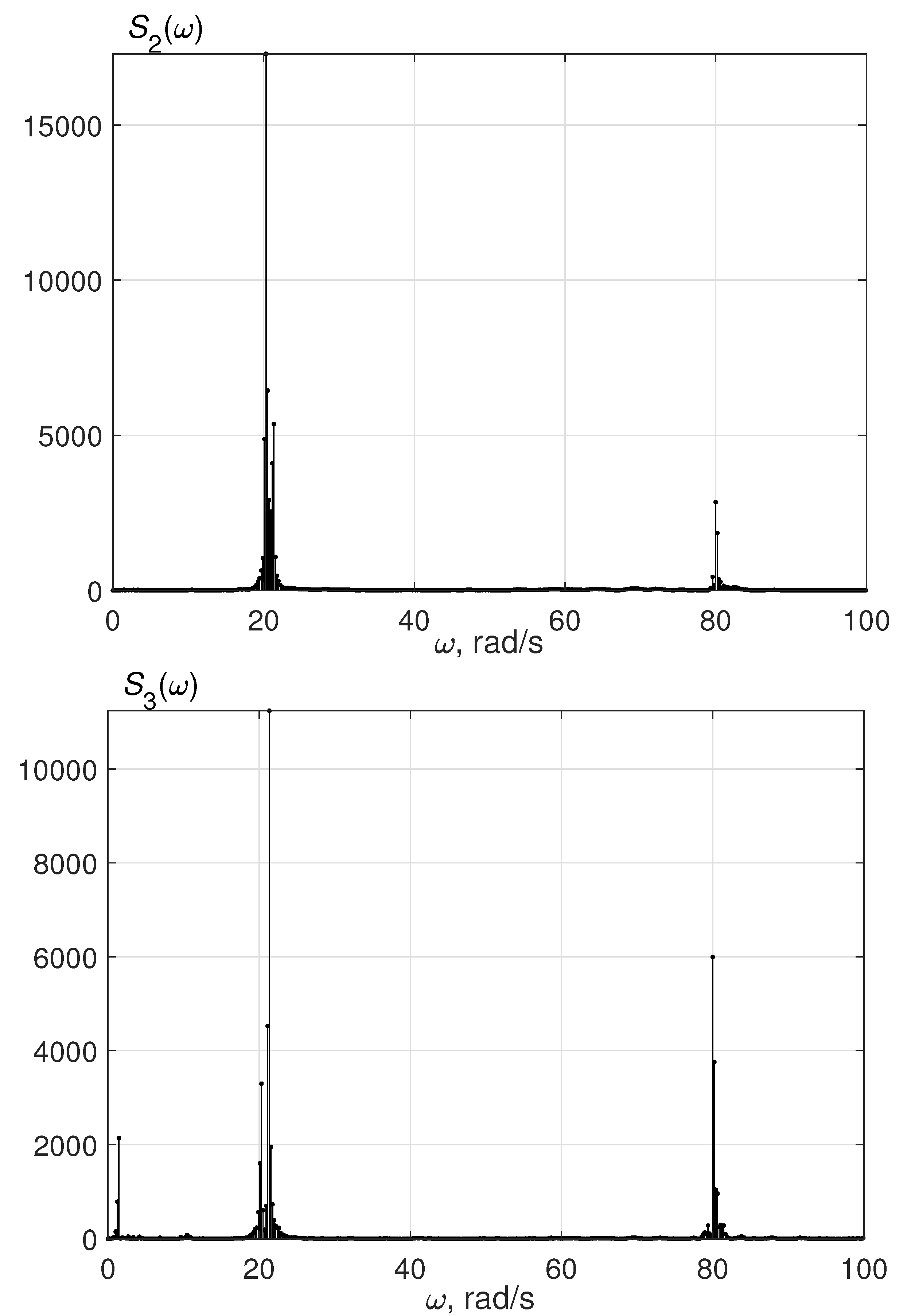
Preprints 112011 g004
Figure 4. Spectral densities for sensors # 2, 3 displacements (in mm). ω l = ω r = 80 rad/s, ψ = 0 .
Figure 4. Spectral densities for sensors # 2, 3 displacements (in mm). ω l = ω r = 80 rad/s, ψ = 0 .
Preprints 112011 g004
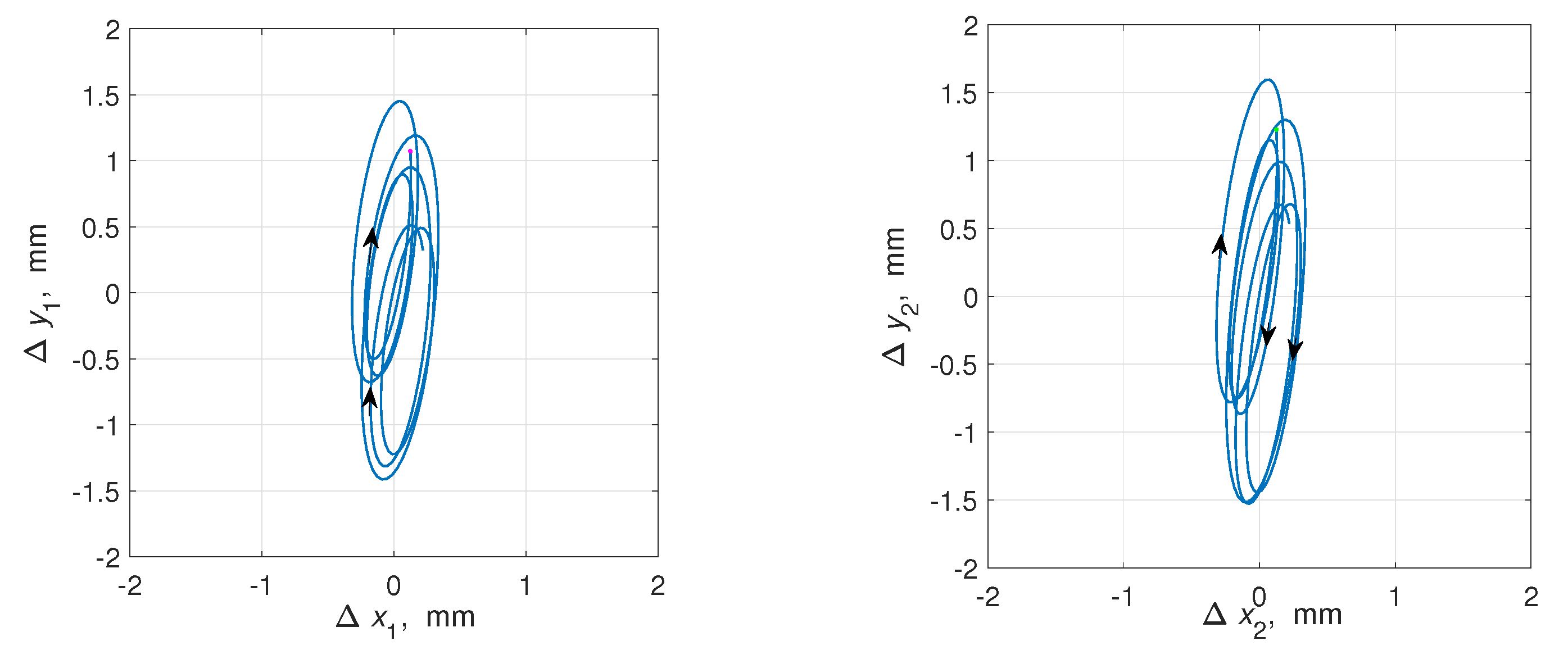
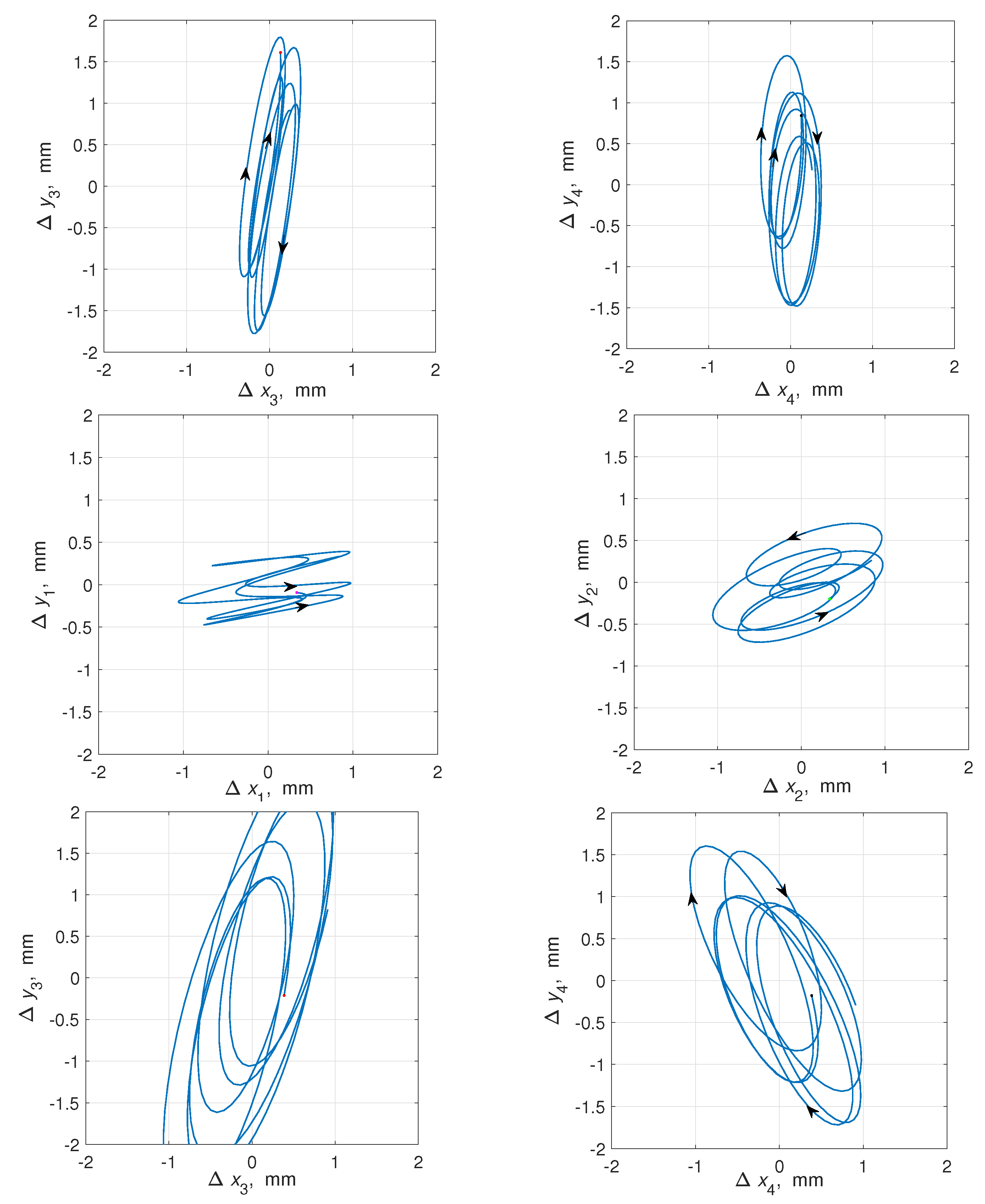
Preprints 112011 g005aPreprints 112011 g005b
Figure 5. Vibration fields in the platform sections #1–#4. ω l = ω r = 80 rad/s. Upper plot: ψ = 0 . Lower plot: ψ = π rad.
Figure 5. Vibration fields in the platform sections #1–#4. ω l = ω r = 80 rad/s. Upper plot: ψ = 0 . Lower plot: ψ = π rad.
Preprints 112011 g005aPreprints 112011 g005b
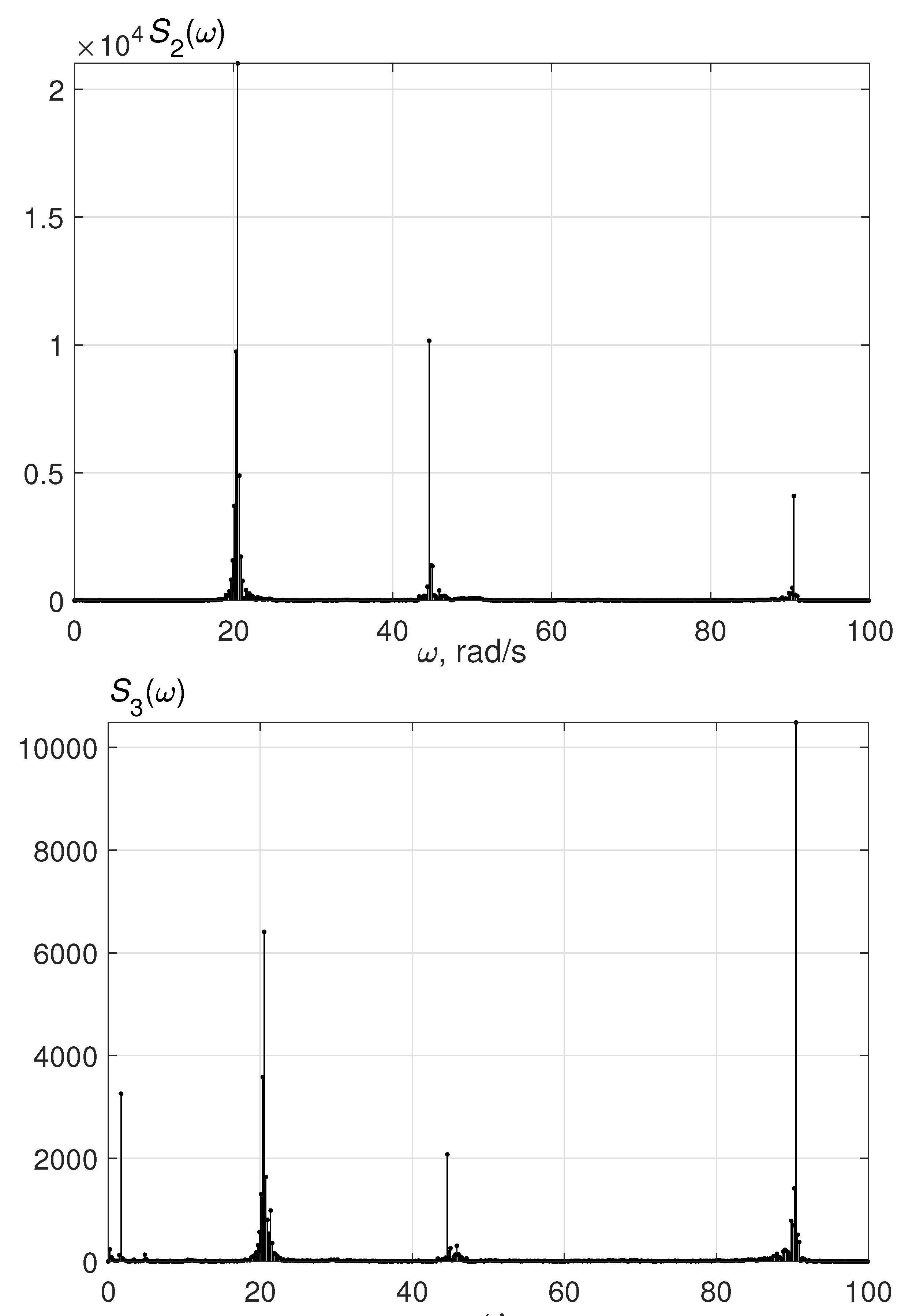
Preprints 112011 g006
Figure 6. Spectral densities for sensors # 2, 3 displacements (in mm). ω l = 90 rad/s, ω r = 45 rad/s, ψ = 0 .
Figure 6. Spectral densities for sensors # 2, 3 displacements (in mm). ω l = 90 rad/s, ω r = 45 rad/s, ψ = 0 .
Preprints 112011 g006
Preprints 112011 g007
Figure 7. Vibration fields in the platform sections #1–#4. ω l = 90 rad/s, ω r = 45 rad/s. Upper plot: ψ = 0 . Lower plot: ψ = π rad.
Figure 7. Vibration fields in the platform sections #1–#4. ω l = 90 rad/s, ω r = 45 rad/s. Upper plot: ψ = 0 . Lower plot: ψ = π rad.
Preprints 112011 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated