Prerpints.org logo
Preprint
Article

Creation of a Spatio-Temporal Algorithm & Application to COVID-19 Data

Altmetrics

Downloads

115

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Preprints on COVID-19 and SARS-CoV-2

Submitted:

15 July 2024

Posted:

15 July 2024

You are already at the latest version

Alerts
Abstract
This study offers an in-depth analysis of the COVID-19 pandemic’s trajectory in several member countries of the European Union (EU) to assess similarities in their crisis experiences. We also examine data from the United States to facilitate a larger comparison across continents. We introduce our new approach, which uses a spatio-temporal algorithm to identify five distinct and recurring phases that each country undergoes at different times during the pandemic. These stages include a Comfort Period characterized by minimal COVID-19 activity and limited impacts. The Preventive Situation demonstrates the implementation of proactive measures, with relatively low numbers of cases, deaths, and Intensive Care Unit (ICU) admissions. The Worrying Situation is defined by high levels of concern and preparation as deaths and cases begin to rise and reach substantial levels. The Panic Situation is marked by a high number of deaths relative to the number of cases and a rise in ICU admissions, denoting a critical and alarming period of the pandemic. Finally, the Epidemic Control Situation distinguishes itself by limiting COVID-19 deaths despite a high number of new cases. By examining these phases, we identify the various waves of the pandemic, indicating periods where the health crisis has a significant impact. This comparative analysis highlights the time lags between countries as they transition through these different critical stages and navigate the waves of COVID-19.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction

Since its declaration as a pandemic on March 11, 2020, by the World Health Organization (WHO), COVID-19 is the subject of ongoing research. Notably, a study presented in [1] uses hierarchical clustering to predict COVID-19 waves. Originating in Wuhan, China, in December 2019, COVID-19 spreads quickly across continents, experiencing fluctuations in infection rates and fatalities. However, the pandemic’s effects vary across nations, prompting the need for a clustering model to track its evolution accurately. Thus, our paper introduces an algorithm designed for this purpose and applies it to data from various European Union (EU) countries and the United States.
The COVID-19 pandemic represents a major challenge to global public health, revealing the need for advanced analytical techniques to understand and manage its spread during the crisis and to learn lessons from it afterward. Spatio-temporal analysis is particularly important, as it allows researchers to discover patterns and the evolution of the pandemic in different regions and time periods. This knowledge is vital for improving future responses to pandemics by optimizing prevention strategies and understanding the advantages and disadvantages of each country compared to others in terms of health systems and disaster management. For instance, Huang et al. (2021) utilize space-time aggregation and spatial statistics to analyze the global spatio-temporal evolution of COVID-19, revealing significant understandings into the spatial autocorrelation of confirmed cases and geographic centroid migrations across continents [2]. Similarly, Sebastiani and Palù (2021) apply hierarchical clustering and mathematical morphology to COVID-19 incidence data in Italy, identifying distinct clusters of infection and providing a robust methodology for reducing image noise and accurately modeling spatial distributions [3]. Furthermore, Li et al. (2021) explore the spatial dependency of COVID-19 within and between cities in China using a dynamic spatial autoregressive model, highlighting the impact of inter-city mobility restrictions on controlling disease transmission [4]. These studies underscore the importance of spatio-temporal approaches in understanding the pandemic’s dynamics and guiding effective public health interventions.
Comparing the progression of the COVID-19 pandemic within different EU countries is essential due to their diverse experiences. Despite the EU’s principle of free movement, each nation adopts unique strategies to curb virus transmission, reflecting their geographical, demographic, economic, and political diversity. For example, countries with older populations face greater challenges, while those with robust healthcare systems mitigate the spread more effectively. The European Union shows significant variability in COVID-19 responses. Countries like Italy and Spain, which have older populations, are severely impacted early in the pandemic, highlighting the challenges faced by nations with vulnerable demographics [5]. In contrast, Germany’s robust healthcare system and effective testing strategy enable it to manage the virus efficiently, resulting in lower mortality rates during the initial waves [6]. Additionally, the EU exhibits varying degrees of stringency in public health measures. For example, while Italy implements strict lockdowns, Sweden opts for a more relaxed approach, focusing on herd immunity. This leads to differences in infection rates and public health outcomes, emphasizing the impact of policy decisions on pandemic progression [7,8]. The disparity in policy and healthcare infrastructure across the EU underscores the need for coordinated efforts and shared strategies to effectively manage such pandemics [9].
Understanding the different trajectories of the COVID-19 pandemic in Europe and the United States is crucial due to significant differences in geography, healthcare infrastructure, public health policies, and response strategies. In the United States, vast geography and varied population densities lead to different transmission rates in urban versus rural areas. A CDC (Centers for Disease Control and Prevention) report indicates that during the early phase of the pandemic, dense urban centers like New York City experience rapid virus spread, while rural areas see slower transmission rates. From mid-March to mid-May 2020, COVID-19 incidence is highest in large metropolitan areas, but begins to decline in mid-April before increasing uniformly across all regions [10]. In Europe, the smaller geographical size and higher population densities lead to quick virus transmission. Standardized case reporting and efficient contact tracing are used to manage the situation [11,12]. The differences in healthcare infrastructure affect the handling of COVID-19 in Europe and the United States. In general, European countries have robust public healthcare systems that support effective testing, contact tracing, and treatment. In contrast, the U.S. has an employment-based insurance system with fragmented coverage [13,14,15]. Public health policies differ between Europe and the United States. The European Union generally adopts uniform measures, while the U.S. experiences varied efforts due to its decentralized governance [16,17,18].
Essentially, when we compare the impact of COVID-19 on EU countries, we’re looking into nations that share numerous similarities. Conversely, when we compare the pandemic’s situation between Europe and the United States, we’re contrasting regions marked by greater differences. These two perspectives complement each other and enrich our results and the interpretations that can be drawn. Thus, the findings presented here provide deeper realizations into how the variations and commonalities among different countries, as well as between Europe and the United States, shape the health landscape and the progression of the pandemic.
In clustering, the nature of the data we are confronted with is always very important and determining in the choice of the best methodology to use in order to obtain homogeneous and meaningful clusters. One type of data that is central to various clustering topics nowadays is that of time-dependent data. Several studies with this type of data have been carried out, particularly in ecology and environmental applications, looking for example on the temperature or the constitution of the air for different populations at disparate times, as seen in [19,20,21,22,23]. Similarly, in political and socio-economic studies, spatio-temporal data plays a very important role in visualizing how situations change over time, see e.g [24] among others. Time-dependent data is also prevalent in criminology and epidemiology, as evidenced by [25,26] among others. It is in this last area that the subject treated in this paper lies, which is about following the evolution of the COVID situation in different countries over time while grouping them together whenever they have similar COVID situations. However, it is important to note that the clustering methodology introduced in our work can also be applied to other fields. When the temporal dimension of a data is taken into account, it is interesting to graphically visualize the evolution of the obtained clusters over time. For instance, in [27], a graphic showing the evolution of mortality over time is proposed while in [28], an observation of the evolution and projection of life expectancy over time is exposed.
Thus, in this paper, we build a clustering method to group spatio-temporal data and to graphically visualize the evolution of these different groups over time. Generally, some studies have been conducted on creating an algorithm suitable for spatio-temporal data. An example is in [29,30], in which the self-organizing map algorithm is modified to fit spatio-temporal data. In our work, we extend these methodologies by considering the data as being able to present similarities in their characteristics for different spaces over periods of time which are not necessarily consecutive. Examining the necessity of developing such a clustering method is essential. When temporal continuity is ignored, comparing clusters obtained at different time points becomes problematic, as there is no temporal linkage between them. Indeed, the classes obtained for different time periods do not have similar characteristics. Conversely, applying classic clustering methods directly to the entire dataset without temporal segmentation introduces bias, as historical events are treated equally to current ones. Hence, our objective is to compare individuals for each fixed period while considering the temporal evolution of the data.
Moreover, when comparing the status of different populations over time, temporal misalignment (time lag) among similar statuses is a common occurrence. This underscores the importance of comparing population similarities at different times without limiting the analysis to successive periods, while emphasizing the need to understand the dynamics within separate populations during the same period. Our method addresses this by acknowledging the significance of weighting both temporal and spatial dimensions in cluster formation. This nuanced approach enables a more comprehensive analysis, ensuring that the clustering algorithm effectively accounts for both temporal and spatial dynamics.
Before presenting the method developed in this article, we provide a brief overview of two classic clustering methods: K-means and Self-Organizing Map (SOM). As explained in [31], K-means is a popular clustering algorithm that classifies data objects into K different clusters through iterations. The algorithm begins by randomly selecting K centers, or centroids, from the dataset. It then alternates between two main steps until convergence: first, assigning each data object to its nearest center, typically based on the Euclidean distance; second, recalculating the cluster averages and reassigning them to their respective centroids. While K-means is simple and easy to understand, it struggles with identifying groups with complex shapes and its final representation is difficult to visualize in a convenient 2-D format. This is where the Self-Organizing Maps (SOM) method becomes relevant. Proposed by Kohonen in 1982, SOMs, detailed in [32], offer a solution by projecting multi-dimensional data onto a lower-dimensional grid while preserving topological ordering. This process involves competitive learning, where neurons interact laterally to form a semantic map, grouping similar patterns closer together. After initialization, the SOM algorithm progresses through three phases as elaborated in [33]: Competition, Cooperation, and Adaptation. During the Competition phase, the algorithm identifies the neuron most similar to each input pattern, termed the Best Matching Unit (BMU). In the Cooperation phase, the winning neuron determines the spatial location of a topological neighborhood, with its size controlled by a chosen radius. Finally, during the Adaptation phase, neurons adjust their values based on input patterns, converging towards the selected example. These phases ensure a gradual convergence towards meaningful clusters.
The method developed in this paper draws inspiration from the ideas of the two methodologies described above, with a focus on incorporating temporal considerations. Our aim is to create clusters that can handle complex structures and allow for detailed examination of variables within each cluster to enhance interpretation. Overall, our method involves representing groupings in a multidimensional space, utilizing the concept of neighborhood, and implementing a gradually decreasing learning rate during iterations. The mathematical formulations are influenced by the work cited in [34]. Our algorithm presents enhanced flexibility and adaptability, allowing for the selection of features, dimensionality reduction parameters, and neighborhood functions.
The paper is structured as follows: Section 2 outlines the algorithm designed for spatio-temporal datasets. In Section 3, we implement this algorithm on the COVID-19 dataset and present the findings. Lastly, the conclusion provides avenues for future research.

2. Spatio-Temporal Data Analysis and Clustering

When the data has two dimensions: spatial and temporal, the clustering methods must adapt to them in order to be able to create groups that make sense on each of these dimensions. The idea of the constructed method is to ensure that each point in the database looks at the path followed by other points in order to choose its most appropriate group. It is essential to give more importance to what is happening at the same time in the different populations than to what is happening at different times, without however forgetting that there is continuity between what is happening at a given time, what happened before, and what will happen later. In this paper, we use similar notations as in [34] which are in line with common practice for clustering algorithms.

2.1. Training Algorithm for Spatio-Temporal Data

Let M be the number of study periods, and S be the number of populations considered. In our application in Section 3, populations refer to different countries, and periods represent months. We define set D as a collection of N data objects, where each D is characterized by ( s , m ) for 1 to N. Here, s denotes a population chosen from S populations, and m denotes a period selected from M periods in the study. Notably, N is the product of M and S, and D comprises the data objects central to clustering and analysis. Each D is associated with a vector of variables, X = ( x 1 , … , x v ) , where x j ∈ R and v denotes the number of variables considered. The collection of these variable vectors is denoted as X. Additionally, let K represent the desired number of groups, and let P denote the set of K clusters. Using an ascending hierarchical method, we identify the ultimate superclasses represented by P f , a subset of P, where N f is the number of final groups obtained.
The ascending hierarchical classification, as described in [31], is a statistical technique employed to divide a given population into distinct groups or subgroups. Its fundamental objective is to maximize the intra-class homogeneity, that is, to ensure that individuals grouped together within the same class are as similar as possible, while at the same time maximizing the inter-class heterogeneity, meaning that the classes themselves are the most dissimilar. This method operates based on a criterion of resemblance, typically represented as a distance matrix denoted as d, where d i j quantifies the dissimilarity or distance between individuals i and j. For instance, two identical observations give zero distance, and the distance increases as the difference between the two observations increases. Ascending hierarchical classification combines individuals iteratively, resulting in the construction of a dendrogram or classification tree. It starts with individual observations as the initial classes and proceeds hierarchically, creating larger classes or groups that may include subgroups nested within them. The final partition of the population is obtained by strategically defining a cut in the hierarchical tree at a chosen height h. This process is often represented as:
C = cut ( T , h ) ,
where C represents the final partition, T is the hierarchical tree, and h is the chosen height at which the tree is cut. The hierarchical method provides a systematic approach to explore the structure within a population while providing the flexibility to accommodate different levels of detail in the final groupings.
Once the primary groups are obtained with the constructed method explained below, the ascending hierarchical method is applied to the centers of these clusters (called neurons) to group the nearest centers together. We can apply this methodology for each fixed time, but that eliminates the work done in the constructed method, which allows grouping very similar data points even if they do not necessarily belong to the same time period. To preserve the spirit in which the first clusters are created, we choose to apply the ascending hierarchical method to all the centers without fixing the time.
Given the unique nature of data characterized by both temporal and spatial dimensions, distinct from traditional statistical data, we propose to incorporate the temporal dimension into our analysis. Initially, we select a subset of E populations from the total S populations, ensuring that their product with M yields K. Each selected population, along with its corresponding time, constitutes a point in our dataset D. Subsequently, we extract variable value vectors from X corresponding to these selected points in D. We then label the extracted variable value vectors as W k = ( w k 1 , … , w k v ) for k ranging from 1 to K, organized in ascending order based on the means of the variables within each fixed population. This ordering strategy primarily aids in organizing the initial centers of the clusters. The ordering changes during the clustering process; therefore, this choice does not significantly affect the final clustering results. Each element w k j is a real number in R . These W k vectors act as prototypes or reference models for the clusters we aim to construct. They represent the central points of the clusters, and their values are iteratively adjusted to minimize the distance from the points in the dataset, thereby refining the cluster centers. Altering the prototype vector for a specific k impacts the adjustments in neighboring prototype vectors, creating a connection among points K. This interconnected behavior leads us to designate these K points as "neurons." The choice of the term "neurons" reflects their collective adaptability, drawing a parallel with how neurons communicate in our brains. This naming decision illustrates the collaborative nature of these points and their role in shaping the system’s overall behavior.
After randomly selecting a data point from the dataset D, we determine its associated time. Subsequently, we search among the neurons with the same time for the prototype vector closest to the variable vector X, representative of the selected data point. This neuron is termed the Best Matching Unit (BMU) or winning neuron. We then adjust the prototype vectors of the BMU and its neighboring neurons to minimize their distance from the selected data point, based on their proximity to the BMU. To incorporate both temporal and spatial aspects, we construct separate neighborhood functions ( h BMU , k p and h BMU , k s ) for each dimension. These functions govern the intensity with which neurons approach the selected data point, depending on their temporal and spatial distance from the BMU. Neurons sharing the same time as the selected data point approach it with greater intensity compared to those with different times, reflecting the emphasis on contemporaneous events. This approach retains the principle of temporal continuity within populations while allowing comparison across different times, with a focus on fixed periods. It’s essential to consider temporal evolution, especially for data exhibiting temporal disparities across populations. Mathematically, we represent intensity through the notion of radius incorporated into the neighborhood functions. Thus, a temporal radius σ p and a spatial radius σ s are employed, ensuring greater intensity of change for neurons with the same time as the BMU compared to those with different times.
The temporal radius is exclusively used in the temporal neighborhood function for neurons with different times than the Best Matching Unit (BMU), while the spatial radius is only present in the spatial neighborhood function for neurons with the same period as the BMU. This differentiation emphasizes the need to handle spatial and temporal iterations distinctly within the algorithm. For each fixed spatial iteration denoted as t s , the temporal iteration t p increases until the temporal radius approaches zero. At this point, a new data point is drawn from D, leading to an increment in spatial iteration by one unit, a reduction in spatial radius, and a reset of the temporal radius using the updated spatial radius value. Consequently, the total number of iterations equals the product of the total spatial iterations ( T s ) and the total temporal iterations ( T p ).
To ensure the algorithm’s convergence while avoiding excessive data clustering, it is important to introduce a learning rate ( α ). This learning rate represents the percentage by which the algorithm learns during each iteration, driving the modification of prototype vectors for neurons without distinguishing between temporal and spatial dimensions. As the iterations progress, the learning rate gradually decreases, resulting in a diminishing influence over time. Typically, in practical applications, this hyperparameter is fine-tuned starting with an initial value of 70%. The subsequent section details the procedural aspects of identifying the Best Matching Unit and outlines the steps involved in updating the prototype vectors of neurons. Additionally, it elaborates on the neighborhood weighting functions and the mechanisms used to reduce radii and adjust the learning rate.

2.2. Key Parameters of the Developed Algorithm

In Table 1, we give a detailed description of the parameters used in our clustering approach for spatio-temporal data. These variables are essential in determining how the algorithm behaves and produces results. Each parameter is accompanied by a description of its relevance as well as its involvement in the clustering procedure. Our method and its application to datasets, including the study of temporal and geographical patterns in COVID-19 data, need an understanding of these parameters.
The notation with an exponent ( t s ) indicates the relevance of the parameter or operation within the spatial iteration of the clustering process, while the exponent ( t p ) highlights its significance during the temporal iteration. Additionally, parameters marked with the exponent p represent temporal considerations, while those marked with the exponent s denote their spatial counterparts.

2.3. Best Matching Unit and Prototype Vectors

Our clustering technique begins with the selection of a data point from the dataset. Subsequently, we seek the nearest prototype vector, denoted as W k , from the existing pool of prototypes, W. This step is pivotal in assigning the data point to a specific class. To achieve this, we employ the Euclidean distance metric, d ( . , . ) , which quantifies dissimilarity between vectors, to compute the Euclidean distance between each prototype vector W k and the selected data point X. This computation allows us to identify the prototype vector W k that exhibits the closest match to X.
The Euclidean distance computation is defined as:
d ( X , W k ) = ∑ j = 1 v ( x j − w k j ) 2 ,
To identify the neuron with the closest prototype vector, referred to as the Best Matching Unit (BMU), we utilize the expression:
BMU ( t s ) = arg min k = 1 , … , K d X ( t s ) , W k ( t s ) .
Here, we aim to find the BMU for the data vector X ( t s ) , where ( t s ) represents the specific spatial iteration. The BMU is selected from the set of prototype vectors W k ( t s ) for k = 1 to K, based on the Euclidean distance metric d between each W k ( t s ) and X ( t s ) . Ensuring temporal alignment, this computation facilitates the identification of the neuron that best captures the properties of X ( t s ) . The prototype vector of the Best Matching Unit (BMU) is denoted as W BMU . During the updating process for each prototype vector W k (where k = 1 , … , K ), the incorporation of both spatial and temporal neighborhood functions is crucial. This integration is represented by the following formula, which applies to the specific data point chosen from the dataset:
W k ( t p + 1 ) = W k ( t p ) + α h BMU , k s , ( t p ) [ X ( t p ) − W k ( t p ) ] + h BMU , k t , ( t p ) [ X ( t p ) − W k ( t p ) ] .
This equation incorporates three key components: the temporal iteration t p , the learning rate at the t p -th time iteration α ( t p ) , and the spatial and temporal neighborhood functions h BMU , k s , ( t p ) and h BMU , k t , ( t p ) . It adjusts each prototype vector based on its proximity to the BMU and the associated data point at the time t p .
The neighborhood functions h BMU , k s and h BMU , k p play a pivotal role in this adaptation process. h BMU , k s ensures alignment between the temporal characteristics of neuron k, the BMU, and X by serving as a Gaussian neighborhood function around the BMU. Conversely, h BMU , k p guarantees that neuron k has a distinct temporal characteristic from the BMU and X, thereby maintaining temporal diversity.
Mathematically, these neighborhood functions are defined as:
h BMU , k i = exp − d 2 ( W BMU , W k ) 2 σ i 2 ,
where i = s , t .
By considering both spatial and temporal factors throughout the adaptation process, the neighborhood functions determine the extent to which each neuron’s prototype vector is influenced by the data point X and the BMU. In our spatio-temporal clustering algorithm, the use of Gaussian functions is important for controlling the evolution of values within neurons. This process relies on specific radii, σ s for spatial neighborhood and σ p for temporal neighborhood at each Best Matching Unit (BMU) during iteration t p . These radii essentially determine the intensity with which neurons at the same time as the selected data point are affected, as well as neurons at different times.
Gaussian functions assign values to neurons based on their proximity to the central BMU. Neurons farther from the BMU receive lower values in the neighborhood function, reflecting their greater distance from the central point. It’s noteworthy that the BMU’s own spatial neighborhood function is set to 1 while its temporal neighborhood function is set to 0, ensuring that the BMU has no effect on its neighbors.
As the algorithm progresses, both the spatial and temporal neighborhood radii gradually decrease. The spatial neighborhood radius, starting at σ i s and ending at approximately σ f s = 0 , decreases with each spatial iteration t s . Similarly, for a given spatial radius σ s , the size of the temporal neighborhood decreases from σ s to nearly σ f p = 0 throughout temporal iterations t p .
To achieve convergence, we introduce a decreasing learning rate α . At the end of each temporal iteration t p , the learning rate α gradually decreases from its initial value α i , ensuring a gradual slowdown of the learning process.
The spatial radius, denoted as σ s , gradually diminishes over iterations following the equation:
σ s = σ i s + t s T s σ f s − σ i s .
Similarly, the temporal radius, denoted as σ p , undergoes a reduction across iterations based on the formula:
σ p = σ i p + t p T p σ f p − σ i p .
Additionally, the learning rate, represented by α ( t p ) , steadily decreases throughout the training process according to:
α ( t p ) = α i 1 − t p T p .
These formulas define how the spatial and temporal radii, as well as the learning rate, evolve over time facilitating the convergence of the algorithm towards an optimal solution. In the final iterations, where both temporal and spatial radii approach 0, the spatial neighborhood function h BMU , k s assigns a value of 1 to the BMU, while the temporal neighborhood function h BMU , k p remains constantly equal to 0 for all neurons.
Finally, the clustering process ends with the grouping of data points sharing the same nearest neuron among the K considered neurons, using the Euclidean distance metric.
Our developed spatio-temporal algorithm is summarized as follows: Preprints 112172 i001

3. Application to COVID-19 Dataset and Results

3.1. COVID-19 Dataset

The dataset D, related to the COVID-19 pandemic, is sourced from the Our World in Data website in May 2022. It includes a comprehensive collection of COVID-19 data dating back to the onset of the pandemic, gathered from various reputable sources including the World Health Organization (WHO) and local health agencies. This dataset provides a vital understanding of the dynamic progression of COVID-19 across different countries and through various stages of the pandemic.
The study considers essential factors for understanding the COVID-19 pandemic. Firstly, it includes the Incidence Rate, which measures the rate of new COVID-19 cases per one million people, indicating the virus’s spread. Secondly, it incorporates the Mortality Rate, representing the number of COVID-19-related deaths per one million individuals, reflecting the pandemic’s severity. Thirdly, it involves the Intensive Care Admission Rate, indicating the frequency of COVID-19 patients requiring intensive medical care, providing information about healthcare system strain. Lastly, the study integrates the Government Stringency Index, quantifying the rigor of government measures aimed at controlling the pandemic. Together, these factors enable a comprehensive understanding of the pandemic’s impact and government responses.
With a Pearson correlation coefficient of approximately 80%, we observe a strong correlation between the number of new deaths due to COVID-19 per million people and the number of intensive care patients admitted because of COVID-19 per million people. Therefore, our focus for explanations and interpretations primarily centers on the number of new deaths per million people. The evolution of these four variables with time are analyzed for 15 countries: Austria (AUT), Belgium (BEL), Bulgaria (BGR), Switzerland (CHE), Cyprus (CYP), Germany (DEU), Spain (ESP), Estonia (EST), France (FRA), United Kingdom (GBR), Italy (ITA), Luxembourg (LUX), Slovakia (SVK), Sweden (SWE), and the United States of America (USA).
The study intends to observe and compare the COVID-19 situations in various European countries and the USA throughout the health crisis from February 2020 to April 2022. It is particularly interesting to analyze the temporal delays between the peaks of the considered variables reached by each country. For countries in the European Union, which share many common conditions and laws, this analysis allows us to see how the measures taken and factors directly related to COVID-19 influence the trajectory of the virus. Furthermore, comparing the COVID-19 trajectories between Europe and the United States provides a wider perspective on how additional conditions, such as geographical location, healthcare systems, and political laws, affect the pandemic’s progression

3.2. Clustering Results and Discussion

3.2.1. Construction and Composition of the Different Classes

After a meticulous refinement process through iterative adjustments, and following the application of the ascending hierarchical clustering method, the convergence of our algorithm allows us to identify five final superclasses. This convergence is of capital importance in ensuring the consistency of the algorithm and is guaranteed by the design of our parameters, configured to decrease over the iterations. The number of iterations needed for convergence is carefully selected by exploring different parameter setups and monitoring the graphic evolution of points, ensuring the choice of an optimal number for stable and meaningful superclasses.
Thus, the final five superclasses encapsulate a wide range of unique attributes and interrelationships within the dataset, thereby offering valuable perspectives on various aspects of the COVID-19 pandemic.
To clarify the characteristics of these superclasses, we adopt a dual-view approach, as illustrated in Figure 1 and Figure 2, thereby providing a detailed exploration of the complex patterns and relationships revealed by our clustering analysis. Presenting the data in separate views aims to provide an exhaustive understanding of the underlying dynamics that leads to the formation of each superclass.
Additionally, in Figure 3, we introduce an alternative visualization technique – a joint 2D PCA projection – providing a broader overview of the dataset. This method facilitates comparative analyses and identification of trends across all superclasses. Including bubble size as an indicator of the severity index adds additional understanding into the severity of COVID-19 measures implemented in different scenarios.
By exploiting multiple visualization techniques, we improve the interpretability and comprehensiveness of our analysis. While Figure 1 and Figure 2 explore specific characteristics and relationships within each superclass, Figure 3 provides a larger perspective, contributing to a complete understanding of the complex dynamics and implications of the COVID-19 pandemic.
Aiming to provide valuable information regarding the trajectory of the COVID-19 pandemic in different countries, we identify five key categories that illustrate different aspects of the pandemic’s effects. Firstly, the comforting situation (Cf1 - blue) depicts a reassuring scenario with minimal new cases, deaths, and intensive care cases per million people, alongside a low severity index. Secondly, the epidemic control situation (Cf2 - green) represents a state of epidemic control, characterized by a high incidence of new cases per million people, while the number of deaths remains relatively low. Thirdly, the panic situation (Cf3 - red) signifies a scenario inducing panic, marked by a significant increase in deaths and intensive care cases relative to new cases. Next, the preventive situation (Cf4 - purple) portrays a proactive approach to combating COVID-19, with low counts of new cases, deaths, and intensive care cases per million people, despite a high severity index. Lastly, the worrying situation (Cf5 - yellow) indicates a transition to concern, with a high number of deaths and intensive care cases relative to new cases, despite the latter being low. The severity index is substantial, reflecting significant measures in place.
In addition to the findings from Figure 1, Figure 2, and Figure 3, Figure 4 serves as a complementary visualization, shedding further light on the distinct characteristics of each identified class. By examining the average values of pertinent variables within each class, we gain a deeper understanding of the nuanced differences among them. Upon closer inspection, these average values reaffirm the distinctive traits attributed to each class. For instance, the blue class continues to exemplify a state of relative comfort amidst the pandemic, with consistently low averages across all variables. Conversely, the green class signifies a phase of epidemic control, as evidenced by a notably higher average number of new cases in comparison to new deaths, suggesting effective management measures. Moving forward, the red class embodies a concerning scenario marked by a stark contrast between the average number of new deaths and new cases, indicative of a potential healthcare crisis. Meanwhile, the purple class portrays a proactive stance against the spread of COVID-19, characterized by a relatively high average stringency index alongside low averages for other variables, signaling stringent preventive measures. Lastly, the yellow class denotes a transitioning phase towards heightened concern, where the average number of new deaths slightly surpasses that of new cases, coupled with a sustained adherence to significant measures reflected in the stringency index. By looking into these nuanced averages, we enrich our understanding of the diverse COVID-19 scenarios encapsulated within each class, thereby facilitating more informed decision-making and targeted interventions.
In Figure 5 and Figure 6, we present the results obtained by applying our proposed algorithm to the COVID-19 dataset. Each box on the graphs corresponds to the stringency index of a specific country at a particular point in time. The horizontal axis represents the timeline in months, spanning from February 2020 to April 2022. Meanwhile, the vertical axis displays the 15 countries included in the study. In the context of studying the COVID-19 pandemic, "waves" refer to distinct and often recurring periods of increased COVID-19 cases, hospitalizations, and/or deaths within a given region or population. These waves characterize surges in the number of individuals testing positive for COVID-19 or experiencing severe illness and may correspond to the rapid spread of new variants of the virus. The concept of waves describes the fluctuating patterns of COVID-19 transmission over time. Typically, a wave involves a significant increase in cases, reaches a peak, and then shows a decrease in cases. The reasons for these waves vary and may include factors such as changes in public health measures (e.g., lockdowns, mask mandates), the emergence of new variants, vaccination campaigns, and public behavior. It is important to note that the terminology and criteria for defining COVID-19 waves vary between regions and among researchers. Waves are often analyzed to understand the dynamics of the pandemic, assess the effectiveness of public health interventions, and plan for healthcare system capacity. In summary, COVID-19 waves represent recurring surges in cases or outbreaks of the virus, playing a key role in shaping the trajectory and impact of the pandemic.
In our analysis of the COVID-19 pandemic, we focus in Figure 6 on identifying and observing distinct waves of the virus within the data. To do this effectively, we focus our attention on specific classes, namely the "Worrying situation," "Epidemic control situation," and "Panic situation." The rationale behind this approach lies in the unique characteristics and severity of these classes. These particular classes represent critical phases of the pandemic, where the impact of COVID-19 on a given country or region is most pronounced. In the "Worrying situation" class, the population is deeply affected, either due to a substantial number of new deaths in proportion to new cases or due to a massive spread of the virus with effective control over the number of deaths. Similarly, the "Epidemic control situation" class indicates a situation where there is a significant number of new cases but relatively fewer deaths, signifying effective measures to mitigate the impact. The "Panic situation" class reflects a scenario where there is a substantial number of deaths and patients in intensive care, often exceeding the number of new cases. This situation results from the time delay between COVID-19 infection and mortality, highlighting the urgency of addressing the pandemic’s impact. By focusing on these three classes over time, we trace the trajectory of the pandemic’s waves. These classes encapsulate the periods when the COVID-19 situation is most critical and when waves, characterized by surges in cases and their consequences, are most evident. Our approach enables us to discern and analyze the dynamics of the pandemic with a sharper focus on these impactful phases, providing a clearer perspective on the virus’s behavior and its response to various factors such as public health measures, vaccination efforts, and emerging variants.
For the first wave, the countries divide into two groups: the yellow class and the red class, representing respectively situations of concern and panic where the number of new deaths is high compared to the number of new cases. Additionally, only a small number of countries considered in the study are deeply affected by this first wave, which lasts only about three months, from March 2020 to May 2020. Each of the countries that is part of this first wave stays there for up to two consecutive months, except Belgium and Sweden, which stay there for three months. It appears that during this wave, Switzerland and Luxembourg do not reach the extreme situation, the situation of panic. It is noteworthy that Italy is the only country among the considered countries that is in the most critical class from the start and remains there for two months without transitioning through a worrying class. Moreover, despite their absence during the first three months of the COVID-19 wave, the United States experiences a later first wave, during the months of July and August 2020 when all the European countries considered are in a rest period between the first and the second wave.
In the second wave, the most common group is the red class, indicating the peak in terms of new COVID-19 deaths since the beginning of this crisis. This represents the most critical situation as the number of new deaths is very high and often exceeds the number of new cases. This period spans approximately eight months from October 2020 to May 2021. During this wave, all the considered countries are affected over more or less similar periods, particularly during the first four months. In the United States, Spain, France, and Belgium, the second wave of COVID-19 begins with a number of new cases that is not yet very high. Then, the majority of the countries in this study move directly during November 2020 and December 2020 to a very large number of new deaths compared to new cases, the panic situation. Cyprus is the country least affected by this wave.
For the third and last wave observed on this graph, we observe the emergence of a new cluster, the green group, which is prevalent from January 2022 until March 2022 and indicates good control of deaths due to COVID-19. During this wave, despite a very high number of new cases, the number of deaths remains considerably low. This situation results from the impact of the vaccination against COVID-19, which starts in January 2021, in addition to the possibility of acquisition of global immunity around the world. It is also possible that the variant of COVID-19 present at this time is less severe than the previous forms. During this wave, all the considered countries are affected, and it is especially in January 2022 that the number of new cases peaks in all countries. This period follows the end-of-year celebrations, which could explain this observation. This last wave lasts about nine months, from August 2021 to April 2022. Almost absent from the first and second waves of COVID-19 so far, Cyprus now starts the third wave in July 2021. This wave spreads to Spain, France, and the United States in August 2021. Five months later, in January 2022, this wave of COVID-19 encompasses all the considered countries without exception. An interesting point to note is that France and Spain are at the beginning of each wave and are therefore always among the first countries to feel the effect of a new wave of COVID-19. Another surprising observation is that during this wave, despite the explosion in the number of new cases, the measures taken are quite weak, and this does not affect the small number of deaths.
As for the other periods, we notice that the first period of calm between the first and second waves lasts about four months, from June 2020 to September 2020, while the second period of rest between the second and third waves lasts about one to two months. This situation results from the fact that during the first period of COVID-19, the measures taken concerning quarantine are quite severe and, at a certain point, COVID-19 stops spreading as fast as before. In contrast, especially after the vaccination and the control of the number of new deaths, there is a relaxation of the considered measures.

3.2.2. Evolution of COVID-19 in France, Italy, Sweden, and the United States

Thanks to the results obtained, we can follow the transition of countries from one cluster to another over time. From fig3 and fig4, we notice that France often starts the waves, Italy is one of the first European countries to enter the worst COVID-19 situation, Sweden very rarely, almost never takes severe measures according to the values seen in the boxes, and the United States experiences a delay in its COVID-19 situation compared to Europe. For these reasons, we are interested in observing the evolution of the COVID-19 situations for these three European countries: France, Italy, and Sweden, and comparing them with the United States’ COVID-19 situation. We examine these COVID-19 trajectories in fig5. The colors used represent the same clusters with the same characteristics mentioned earlier in this paper. The curve drawn above each list of colored boxes represents the wave of COVID-19 that the specific country is experiencing. It is drawn according to the following benchmark: if the country passes through a comforting or preventive situation (blue or purple), the curve takes the value 0; if the country is in a worrying situation (yellow), the curve takes the value 0.5; for a passage through an epidemic control situation (green), the curve takes the value 1; and for the panic situation (red), the curve takes the value 2.
In the United States, during the months of February and March 2020, the COVID-19 pandemic does not start yet. In April 2020, the USA moves to the preventive class during which the government establishes several measures and precautions even though the numbers of new cases and new deaths are still very low. The United States remains in this class for three months until June 2020. In July 2020, the health situation in the United States becomes critical and concerning with a significant number of new deaths despite a small number of new cases. This situation remains stable for two months, then the United States sees its number of new deaths and new cases become low but maintains fairly significant measures in September 2020. In October 2020, the number of new deaths increases and the USA returns to the critical class where the number of deaths is high compared to a low number of new cases. In November 2020, the pandemic reaches the panic situation for the first time with a very high number of new deaths compared to the number of new cases, which itself is quite large. It remains there for four months in a row, therefore until February 2021. In March 2021, the number of new cases decreases but the number of new deaths remains quite high compared to the number of new cases until June 2021. In June 2021, the situation becomes less worrying as the United States moves to the preventive cluster (purple) and to a situation where the undertaken measures remain quite significant with a low number of new cases and new deaths. Then, in July 2021, the United States moves to a comforting situation with even weaker measures. Just after July 2021, in August 2021, the United States returns to a worrying class and then remains for two months in the red group, the panic class with a very high number of new deaths compared to the number of new cases. The USA remains in the worrying class for two months then reaches a new peak of panic for two months and finally in April 2022, the USA witnesses an easing of the COVID-19 situation with its entry into a preventive situation with a low number of new cases and new deaths while the stringency index is high. Generally, for the United States, it is noted that the crisis only really begins in July 2020. It is also noted that there are few blue and purple classes since the outbreak of this crisis, meaning that the situations of rest between a wave and another wave are very short or that the situation has never been calm enough until April 2022. The absence of a green class, which constitutes the control situation class where the number of new deaths is limited according to the number of new cases, is also noted.
As for Sweden, during the first two months of February and March 2020, the epidemic does not arrive yet. In April 2020, Sweden moves directly into the red class, the panic class, where the number of new deaths exceeds the number of new cases. Sweden remains in this class for two months and transitions to the yellow class in June 2020, representing a class that is still quite critical but where the number of new cases has decreased. From July 2020, Sweden shifts to the purple group where significant prevention measures are established, but the numbers of new cases and new deaths are quite low. Sweden stays in this cluster for four months until November 2020 when it returns to the yellow class with quite low new cases but a significant number of new deaths. Then, in December 2020 and January 2021, Sweden is in the red group, the panic class, until February 2021 when it moves to the class where the panic is less intense with a smaller number of new cases. Sweden then moves to the purple class, the preventive class, in March 2021, and to the yellow, the worrying class, in April 2021. In May 2021, Sweden is in the preventive situation. After that, there seems to be an eradication of the epidemic in this country as Sweden mainly remains in the blue class until April 2022. Indeed, the only class change from June 2021 occurs in January 2022, when Sweden makes a brief passage through the green cluster which characterizes the control of the number of new deaths compared to the number of new cases, which is quite high. Thus, even when there is a high level of contamination and therefore a large number of new cases of COVID-19, Sweden manages the crisis and limits the damages. What characterizes the evolution of the epidemic in Sweden is that this country quickly limits the damages caused by COVID. From June 2021, the situation concerning COVID-19 is quite calm and the undertaken measures are no longer severe. Even when the number of new cases in January 2022 becomes very large, the number of new deaths remains quite low, indicating that the epidemic is well under control.
Unlike Sweden and the United States, Italy sees the epidemic break out from the second month considered, i.e., March 2020. Italy quickly moves to the red class, the panic class, with a very high number of new deaths compared to the very high number of new cases. Italy remains in this situation for the two months of March and April 2020. In May 2020, the precautions taken are significant, but the numbers of new cases and new deaths weaken, and therefore Italy enters the preventive class and stays there for about six months, until October 2020. In November 2020, Italy reverts to the red group, the panic class, and stays there for three months: November 2020, December 2020, and January 2021. In February 2021, Italy enters the worrying class, the yellow class, with a considerably high number of new deaths compared to the new cases, which are still low. The situation worsens in March and April 2021, with Italy entering the panic situation with a higher number of new deaths than the number of new cases, which is significant. In May 2021, Italy is in the yellow worrying class, i.e., the class where the number of new deaths is high despite the number of new cases being low. Then, the number of new deaths decreases in May 2021, allowing Italy to move in June 2021 to the purple preventive situation where the stringency index is quite high, but the numbers of new cases and new deaths are quite low. Italy stays in this group until December 2021 and then moves to the green class in January 2022 with the very low number of deaths compared to the number of new cases, which is very high. In February and March 2022, Italy returns to the preventive situation where the undertaken measures remain important while the number of new cases and new deaths are low. Finally, in April 2022, Italy moves to the yellow class where the situation starts to be a little worrying again. The particularity of Italy is that it quickly enters into a panic situation from the second month of the crisis: March 2020. Additionally, the measures taken remain quite significant throughout the entire COVID-19 period until April 2022. Since the beginning of the crisis in Italy, there are no comforting situations (blue); the calmest groups are the preventive situations (purple) with significant importance for the conditions and measures taken. We conclude that even during periods of rest, the undertaken measures in Italy remain quite rigid. We also notice that even after passing through a control class in January 2022 where the number of new deaths is limited compared to the number of new cases that is very high, it appears that the number of new deaths starts again to be considerably large compared to the number of new cases in April 2022.
For France, as for Italy, the epidemic becomes visible from March 2020. However, in France, the arrival in the panic situation is gradual as there is a passage through the worrying class in yellow in March 2020. In April 2020, France enters a situation of panic with a very high number of new deaths compared to the number of new cases. In May and June 2020, France controls the situation and is in a preventive situation where the measures taken are significant but the numbers of new cases and new deaths are quite low. In July, August, and September 2020, France remains in a calm, comforting situation where even the measures are relaxed. In October 2020, France returns to the yellow cluster where the number of new deaths is quite high compared to the number of new cases which remains quite low. In November 2020, France reaches the panic situation and stays in this situation for six months in a row until April 2021. The number of new cases then decreases, allowing France to switch to the yellow class during May 2021 and then to the blue class in July 2021 with a comfortable situation where even the measures are weakened. This peaceful situation does not last very long and in August 2021, France returns to the yellow class, a worrying class. However, the situation is quickly taken care of, and France returns to the purple group of prevention with the presence of measures with quite low numbers of new cases and new deaths. France stays in this purple group until November 2021 and then moves into the worrying yellow cluster in December 2021 with a number of new deaths which is considerably large compared to the number of new cases which is quite low. In January 2022, we see the emergence of the green class which indicates a situation of control of the number of new deaths compared to the number of new cases, so even if the number of new cases becomes very important, the number of new deaths remains weak. In February and March 2022, France is in the worrying yellow class but returns to a light blue comforting group in April 2022 where even the measures are abandoned. The evolution of COVID-19 in France from February 2020 to April 2022 is characterized by a long period in a situation of panic which extends from November 2020 until April 2021. During this period, the number of new deaths is very high compared to the number of new cases. In addition, we see that after each yellow period and therefore after each period where the number of new cases is considerably low, France goes directly to a light blue class where the conditions and measures taken are abandoned. We can then say that, unlike Italy which remains vigilant by constantly implementing measures throughout the pandemic, France lifts the conditions as soon as the health situation seems to improve.
By making a general comparison of the evolution of COVID-19 between the countries of Europe and the United States, we see that over the last year considered, from April 2021 to April 2022, the three European countries considered do not enter the panic situation (red) at all times. This red cluster indicates the worst COVID-19 situation with more new deaths than new cases. For Italy and France, even after entering the yellow class, a worrying class, these countries quickly master the COVID-19 situation. However, looking at the evolution of COVID-19 in the United States for the period from April 2021 to April 2022, we notice that the USA remains in the most serious panic situation for four months (September 2021, October 2021, January 2022, February 2022) and in general, after each worrying situation (yellow), there is a transition to the panic group (red), which represents the most serious case. Also, as noted earlier, the United States never enters the epidemic control situation that indicates good control of the number of new deaths relative to the number of new cases. There also appears to be a lag of about three to four months between the start of the COVID-19 pandemic in Europe and the start of the crisis in the United States, which could partly explain the occurrence of serious situations in the USA until April 2022, unlike in Europe.

4. Conclusion

As highlighted by Gaber et al. (2010) [35], spatio-temporal data integrates spatial (geographic) and temporal (time-based) information, offering a comprehensive approach to analyzing patterns and trends over time and space. This combination enables more effective decision-making and planning across various domains. Clustering methods, a fundamental aspect of machine learning and data mining, are instrumental in revealing hidden structures within data, facilitating the identification of patterns that may not be immediately evident at the individual data point level. These methods enable the organization of large datasets into meaningful clusters based on inherent similarities [36].
In this paper, we introduce a novel clustering algorithm tailored for spatio-temporal data analysis. Unlike traditional methods, our approach offers enhanced flexibility, adaptability, and interpretability by integrating techniques for feature selection, dimensionality reduction, and algorithmic customization. Additionally, our algorithm allows for the assignment of weights to both temporal and spatial dimensions, enabling the prioritization of their importance in cluster formation, thus providing a more nuanced analysis.
The immediate application of our algorithm to COVID-19 data underlines its relevance in pandemic contexts. Analyzing COVID-19 data from various countries provides valuable perspectives on the progression of the pandemic, facilitating the identification of trends, patterns, and influential factors. This understanding is critical for evaluating the effectiveness of implemented strategies and informing future preparedness efforts for public health crises.
Understanding the evolution of COVID-19 in the European Union and the United States is of paramount importance due to the significant impact of the pandemic on these regions. By analyzing COVID-19 data from different countries within these regions, we can gain valuable understanding of the effectiveness of various containment measures, vaccination campaigns, and healthcare systems’ responses. Comparing trends and patterns between the European Union and the United States allows for the identification of successful strategies and best practices, fostering cross-border collaboration and learning. Moreover, studying the evolution of the pandemic in these regions provides crucial information for evaluating the global response to COVID-19 and informing future preparedness efforts for similar public health crises. These findings reflect the complex interplay between public health infrastructure, governmental policy, and demographic factors in shaping the pandemic’s trajectory within each country. They highlight the importance of tailored public health strategies that consider the unique characteristics and capabilities of each country to effectively manage future health crises.
Future work will focus on refining the algorithm to address challenges related to variable correlation in clustering and streamlining implementation for scenarios with a large number of variables. Our algorithm’s adaptability extends its applicability to challenges beyond COVID-19, including public health, urban planning, and environmental monitoring.
In conclusion, our clustering algorithm represents a significant advancement in spatio-temporal data analysis. Its flexibility and interpretability make it a powerful tool for uncovering hidden structures and extracting practical information from complex datasets. By navigating the complexities of spatio-temporal data, our algorithm contributes to informed decision-making processes essential for addressing current and future societal challenges.

References

  1. Rios, R.A.; Nogueira, T.; Coimbra, D.B.; Lopes, T.J.S.; Abraham, A.; de Mello, R.F. Country Transition Index Based on Hierarchical Clustering to Predict Next COVID-19 Waves. Sci. Rep. 2021, 11, 15271. [Google Scholar] [CrossRef] [PubMed]
  2. Huang, Z. Spatiotemporal Evolution Patterns of the COVID-19 Pandemic Using Space-Time Aggregation and Spatial Statistics: A Global Perspective. ISPRS Int. J. Geo-Inf. 2021, 10, 519. [Google Scholar] [CrossRef]
  3. Spassiani, I.; Sebastiani, G.; Palù, G. Spatiotemporal Analysis of COVID-19 Incidence Data. Viruses 2021, 13, 463. [Google Scholar] [CrossRef] [PubMed]
  4. Yu, H.; Li, J.; Bardin, S.; Gu, H.; Fan, C. Spatiotemporal Dynamic of COVID-19 Diffusion in China: A Dynamic Spatial Autoregressive Model Analysis. ISPRS Int. J. Geo-Inf. 2021, 10, 510. [Google Scholar] [CrossRef]
  5. Signorelli, C.; Odone, A.; Gianfredi, V.; Bossi, E.; Bucci, D.; Oradini-Alacreu, A.; Frascella, B. et al. The Spread of COVID-19 in Six Western Metropolitan Regions: A False Myth on the Excess of Mortality in Lombardy and the Defense of the City of Milan. Acta Bio Med. Atenei Parm. 2020, 91, 23. [Google Scholar]
  6. Wieler, L.H.; Rexroth, U.; Gottschalk, R. Emerging COVID-19 Success Story: Germany’s Push to Maintain Progress. 2021.
  7. Usuelli, M. The Lombardy Region of Italy Launches the First Investigative COVID-19 Commission. Lancet 2020, 396, e86–e87. [Google Scholar] [CrossRef] [PubMed]
  8. Korhonen, J.; Granberg, B. Sweden Backcasting, Now?—Strategic Planning for COVID-19 Mitigation in a Liberal Democracy. Sustainability 2020, 12, 4138. [Google Scholar] [CrossRef]
  9. Rozanova, L.; Temerev, A.; Flahault, A. Comparing the Scope and Efficacy of COVID-19 Response Strategies in 16 Countries: An Overview. Int. J. Environ. Res. Public Health 2020, 17, 9421. [Google Scholar] [CrossRef] [PubMed]
  10. Centers for Disease Control and Prevention. COVID-19 Incidence, by Urban-Rural Classification — United States, January 22–October 31, 2020. Morb. Mortal. Wkly. Rep. 2020, 69, 1753–1757. [Google Scholar]
  11. Velicu, M.A.; Furlanetti, L.; Jung, J.; Ashkan, K. Epidemiological Trends in COVID-19 Pandemic: Prospective Critical Appraisal of Observations from Six Countries in Europe and the USA. BMJ Open 2021, 11, e045782. [Google Scholar] [CrossRef]
  12. Cascini, F.; Failla, G.; Gobbi, C.; Pallini, E.; Luxi, J.H.; Villani, L.; Quentin, W.; Boccia, S.; Ricciardi, W. A Cross-Country Comparison of COVID-19 Containment Measures and Their Effects on the Epidemic Curves. BMC Public Health 2022, 22, 1765. [Google Scholar] [CrossRef] [PubMed]
  13. Ndayishimiye, C.; Sowada, C.; Dyjach, P.; Stasiak, A.; Middleton, J.; Lopes, H.; Dubas-Jakóbczyk, K. Associations between the COVID-19 Pandemic and Hospital Infrastructure Adaptation and Planning—A Scoping Review. Int. J. Environ. Res. Public Health 2022, 19, 8195. [Google Scholar] [CrossRef] [PubMed]
  14. Ciulla, M.; Marinelli, L.; Di Biase, G.; Cacciatore, I.; Santoleri, F.; Costantini, A.; Dimmito, M.P.; Di Stefano, A. Healthcare Systems across Europe and the US: The Managed Entry Agreements Experience. Healthcare 2023, 11, 447. [Google Scholar] [CrossRef] [PubMed]
  15. Lau, Y.-Y.; Dulebenets, M.A.; Yip, H.-T.; Tang, Y.-M. Healthcare Supply Chain Management under COVID-19 Settings: The Existing Practices in Hong Kong and the United States. Healthcare 2022, 10, 1549. [Google Scholar] [CrossRef] [PubMed]
  16. Primc, K.; Slabe-Erker, R. The Success of Public Health Measures in Europe during the COVID-19 Pandemic. Sustainability 2020, 12, 4321. [Google Scholar] [CrossRef]
  17. Liu, S.; Ermolieva, T.; Cao, G.; Chen, G.; Zheng, X. Analyzing the Effectiveness of COVID-19 Lockdown Policies Using the Time-Dependent Reproduction Number and the Regression Discontinuity Framework: Comparison between Countries. Eng. Proc. 2021, 5, 8. [Google Scholar] [CrossRef]
  18. Wang, W.; Gurgone, A.; Martínez, H.; Góes, M.C.B.; Gallo, E.; Kerényi, Á.; Turco, E.M.; Coburger, C.; Andrade, P.D.S. COVID-19 Mortality and Economic Losses: The Role of Policies and Structural Conditions. J. Risk Financ. Manag. 2022, 15, 354. [Google Scholar] [CrossRef]
  19. Cheam, A.S.M.; Marbac, M.; McNicholas, P.D. Model-Based Clustering for Spatiotemporal Data on Air Quality Monitoring. Environmetrics 2017, 28, e2437. [Google Scholar] [CrossRef]
  20. Wu, X.; Zurita-Milla, R.; Kraak, M.-J.; Izquierdo-Verdiguier, E. Clustering-Based Approaches to the Exploration of Spatio-Temporal Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 1387–1391. [Google Scholar] [CrossRef]
  21. Deng, M.; Liu, Q.; Wang, J.; Shi, Y. A General Method of Spatio-Temporal Clustering Analysis. Sci. China Inf. Sci. 2013, 56, 1–14. [Google Scholar] [CrossRef]
  22. Izakian, H.; Pedrycz, W.; Jamal, I. Clustering Spatiotemporal Data: An Augmented Fuzzy C-Means. IEEE Trans. Fuzzy Syst. 2012, 21, 855–868. [Google Scholar] [CrossRef]
  23. Hoffman, F.M.; Hargrove, W.W.; Mills, R.T.; Mahajan, S.; Erickson, D.J.; Oglesby, R.J. Multivariate Spatio-Temporal Clustering (MSTC) as a Data Mining Tool for Environmental Applications. 2008.
  24. Hagenauer, J.; Helbich, M. Hierarchical Self-Organizing Maps for Clustering Spatiotemporal Data. Int. J. Geogr. Inf. Sci. 2013, 27, 2026–2042. [Google Scholar] [CrossRef]
  25. Win, K.N.; Chen, J.; Chen, Y.; Fournier-Viger, P. PCPD: A Parallel Crime Pattern Discovery System for Large-Scale Spatiotemporal Data Based on Fuzzy Clustering. Int. J. Fuzzy Syst. 2019, 21, 1961–1974. [Google Scholar] [CrossRef]
  26. Tuite, A.R.; Guthrie, J.L.; Alexander, D.C.; Whelan, M.S.; Lee, B.; Lam, K.; Ma, J.; Fisman, D.N.; Jamieson, F.B. Epidemiological Evaluation of Spatiotemporal and Genotypic Clustering of Mycobacterium Tuberculosis in Ontario, Canada. Int. J. Tuberc. Lung Dis. 2013, 17, 1322–1327. [Google Scholar] [CrossRef]
  27. Léger, A.-E.; Mazzuco, S. What Can We Learn from the Functional Clustering of Mortality Data? An Application to the Human Mortality Database. Eur. J. Popul. 2021, 37, 769–798. [Google Scholar] [CrossRef]
  28. Levantesi, S.; Nigri, A.; Piscopo, G. Clustering-Based Simultaneous Forecasting of Life Expectancy Time Series through Long-Short Term Memory Neural Networks. Int. J. Approx. Reason. 2022, 140, 282–297. [Google Scholar] [CrossRef]
  29. Aaron, C.; Perraudin, C.; Rynkiewicz, J. Curves Based Kohonen Map and Adaptative Classification: An Application to the Convergence of the European Union Countries. In Proceedings of the Conference WSOM; 2003; pp. 324–330. [Google Scholar]
  30. Aaron, C.; Perraudin, C.; Rynkiewicz, J. Adaptation de l’algorithme SOM à l’analyse de données temporelles et spatiales: Application à l’étude de l’évolution des performances en matière d’emploi. In Proceedings of the ASMDA 2005; 2005; pp. 480–488. [Google Scholar]
  31. Na, S.; Xumin, L.; Yong, G. Research on K-means Clustering Algorithm: An Improved K-means Clustering Algorithm. In Proceedings of the 2010 Third International Symposium on Intelligent Information Technology and Security Informatics; 2010; pp. 63–67. [Google Scholar]
  32. Miljković, D. Brief Review of Self-Organizing Maps. In Proceedings of the 2017 40th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), 2017; pp. 1061-1066.
  33. Bullinaria, J.A. Self Organizing Maps: Fundamentals. Introduction to Neural 2004, 15. [Google Scholar]
  34. Natita, W.; Wiboonsak, W.; Dusadee, S. Appropriate Learning Rate and Neighborhood Function of Self-Organizing Map (SOM) for Specific Humidity Pattern Classification over Southern Thailand. Int. J. Model. Optim. 2016, 6, 61. [Google Scholar] [CrossRef]
  35. Gaber, M.M.; Vatsavai, R.R.; Omitaomu, O.A.; Gama, J.; Chawla, N.V.; Ganguly, A.R. Knowledge Discovery from Sensor Data: Second International Workshop, Sensor-KDD 2008, Las Vegas, NV, USA, August 24-27, 2008, Revised Selected Papers; Springer: Berlin/Heidelberg, Germany, 2010; Volume 5840. [Google Scholar]
  36. Pitafi, S.; Anwar, T.; Sharif, Z. A Taxonomy of Machine Learning Clustering Algorithms, Challenges, and Future Realms. Appl. Sci. 2023, 13, 3529. [Google Scholar] [CrossRef]
Preprints 112172 g001
Figure 1. Class Characteristics Based on COVID-19 Cases and Deaths per Million.
Figure 1. Class Characteristics Based on COVID-19 Cases and Deaths per Million.
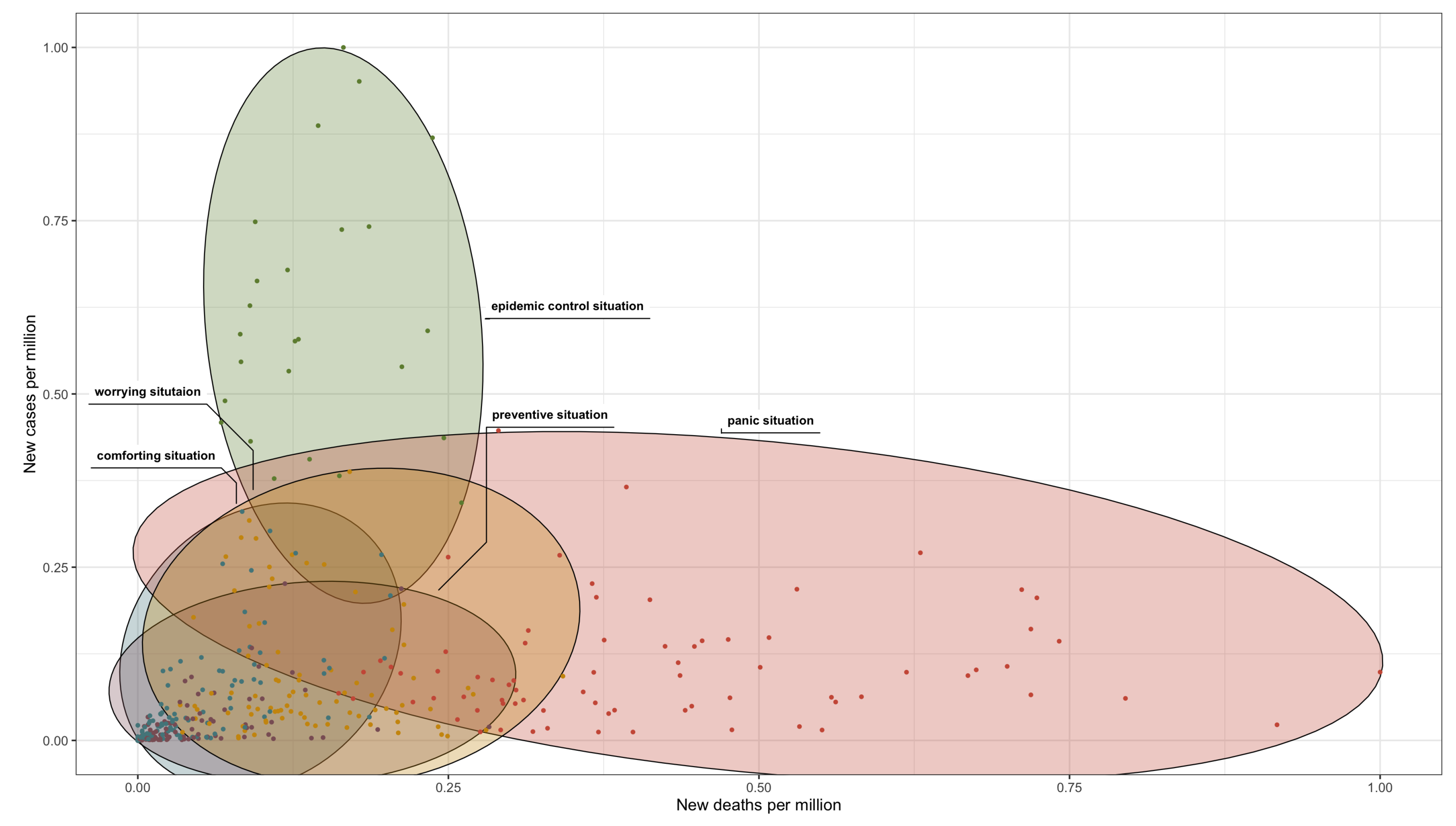
Preprints 112172 g001
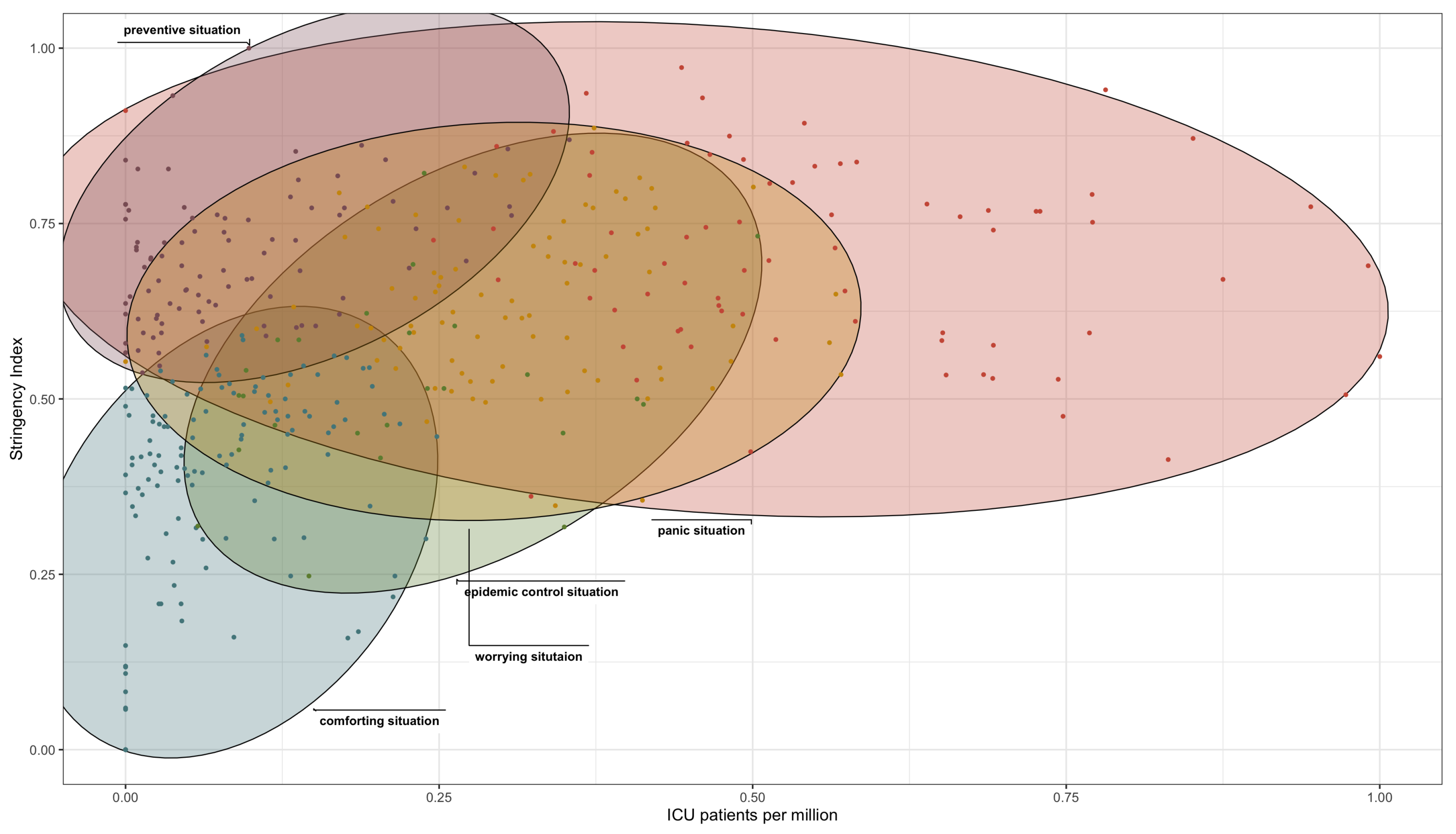
Preprints 112172 g002
Figure 2. Class Characteristics Based on ICU Admissions and Stringency Index.
Figure 2. Class Characteristics Based on ICU Admissions and Stringency Index.
Preprints 112172 g002
Preprints 112172 g003
Figure 3. Overview of Cluster Attributes in COVID-19 Data Analysis.
Figure 3. Overview of Cluster Attributes in COVID-19 Data Analysis.
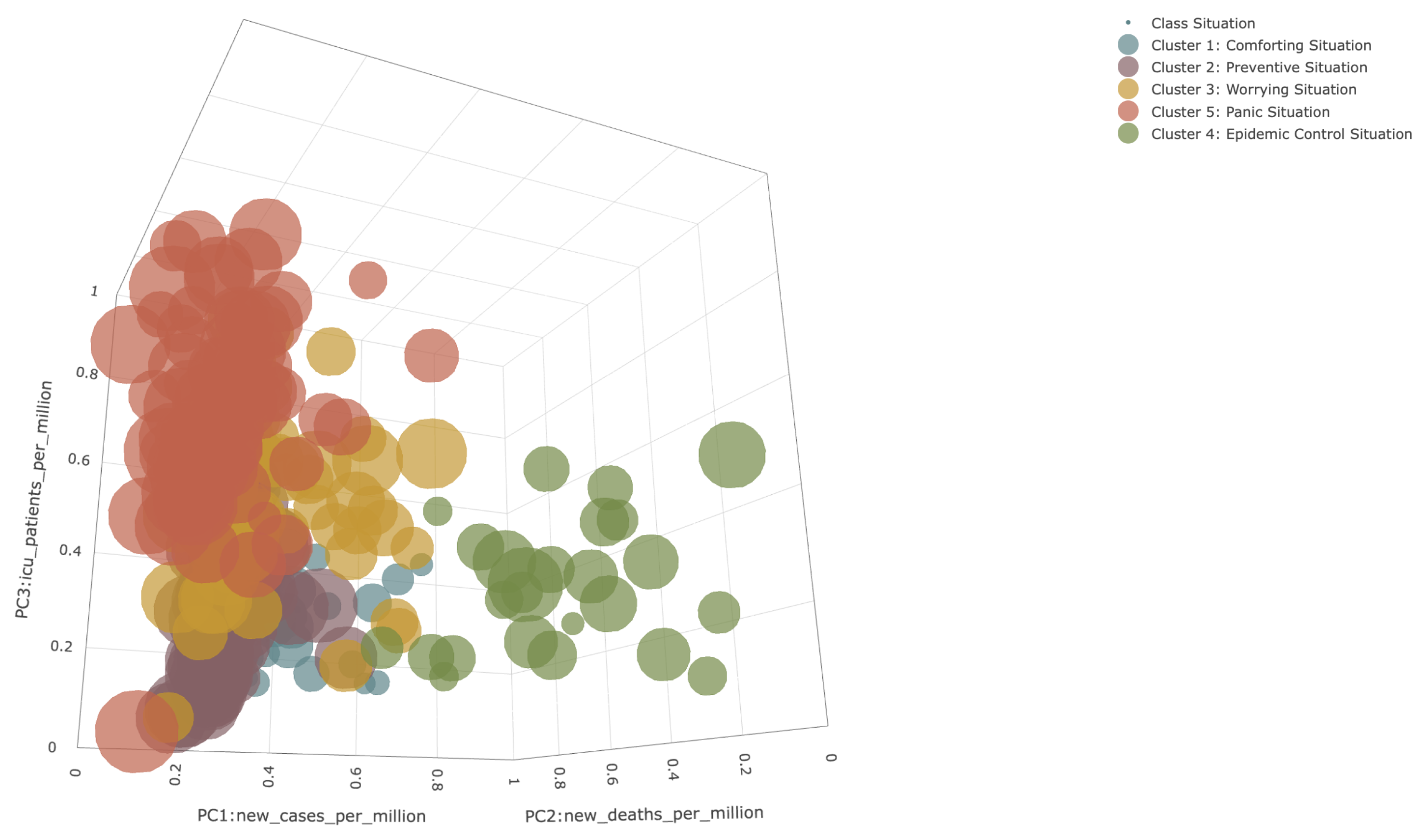
Preprints 112172 g003
Preprints 112172 g004
Figure 4. Comparative Analysis of COVID-19 Means by Class: Cases, Deaths, ICU Admissions, and Stringency Index.
Figure 4. Comparative Analysis of COVID-19 Means by Class: Cases, Deaths, ICU Admissions, and Stringency Index.
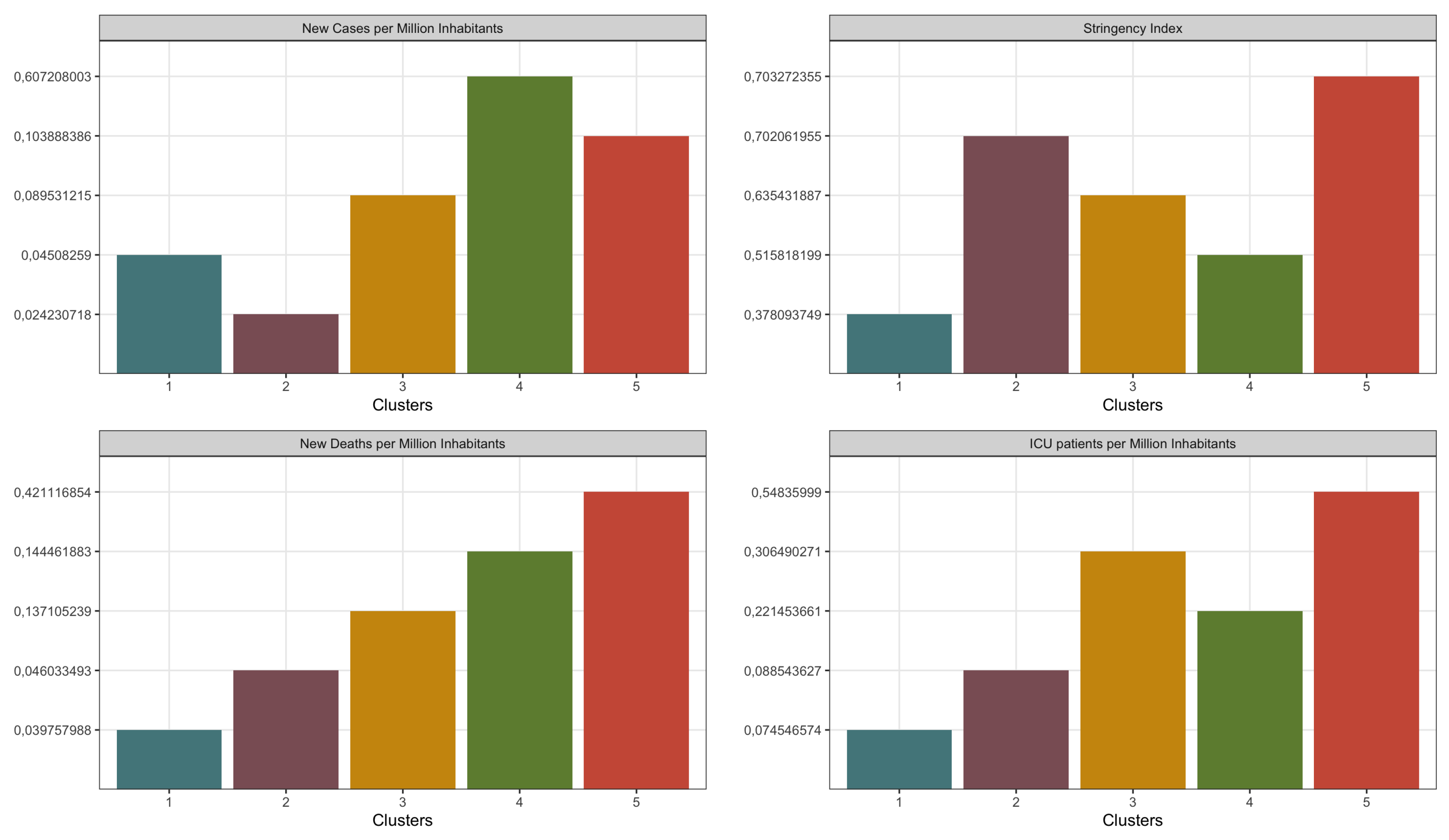
Preprints 112172 g004
Preprints 112172 g005
Figure 5. Pandemic Progression Timeline: A Comparative View of Europe and the United States (Feb 2020 - Apr 2022).
Figure 5. Pandemic Progression Timeline: A Comparative View of Europe and the United States (Feb 2020 - Apr 2022).
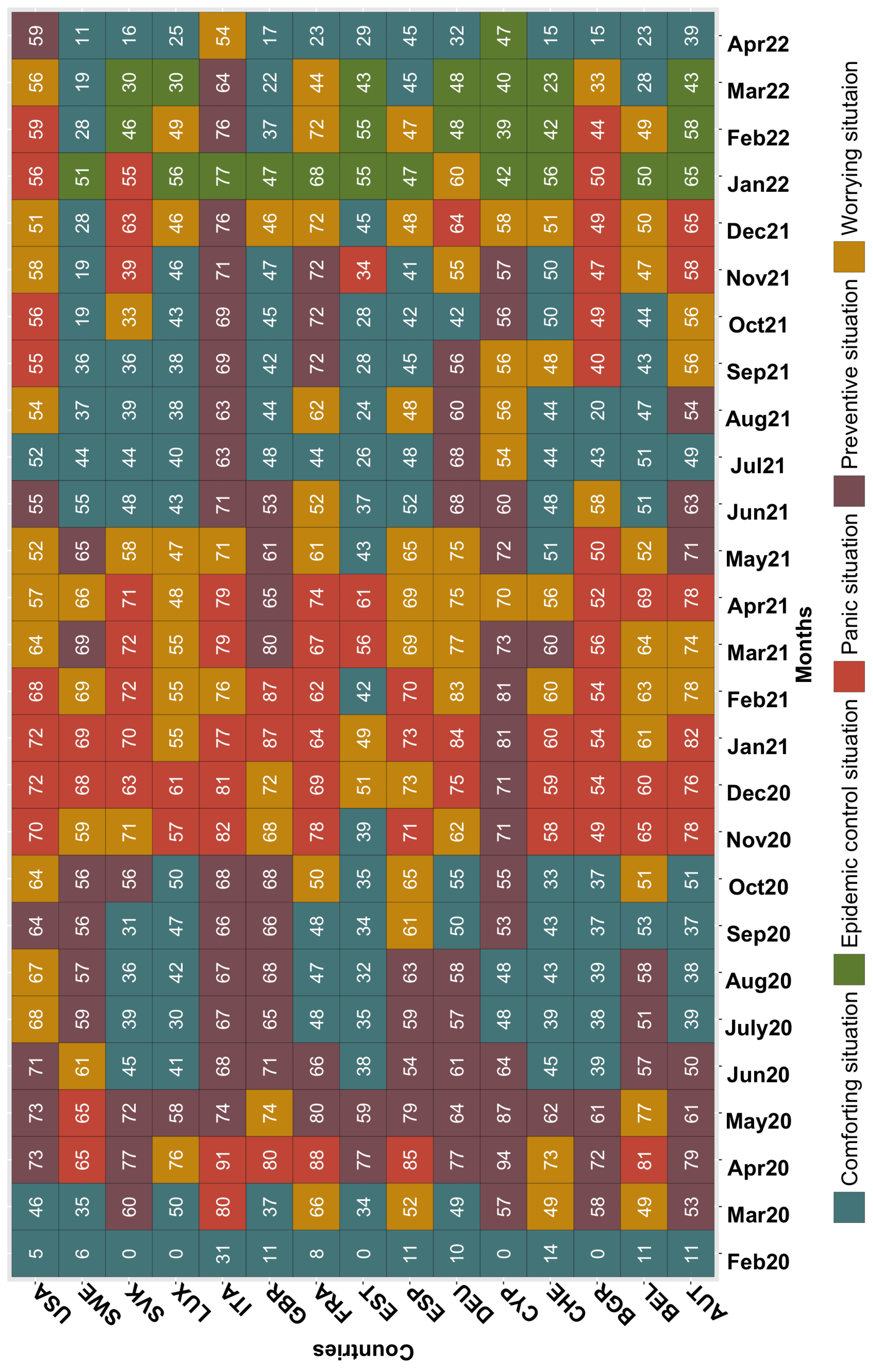
Preprints 112172 g005
Preprints 112172 g006
Figure 6. COVID-19 Pandemic Waves: Comparative Analysis Across Europe and the United States (Feb 2020 - Apr 2022).
Figure 6. COVID-19 Pandemic Waves: Comparative Analysis Across Europe and the United States (Feb 2020 - Apr 2022).
Preprints 112172 g006
Preprints 112172 g007
Figure 7. COVID-19 Class Transitions in France, Italy, Sweden, and the USA (Feb 2020 - Apr 2022).
Figure 7. COVID-19 Class Transitions in France, Italy, Sweden, and the USA (Feb 2020 - Apr 2022).
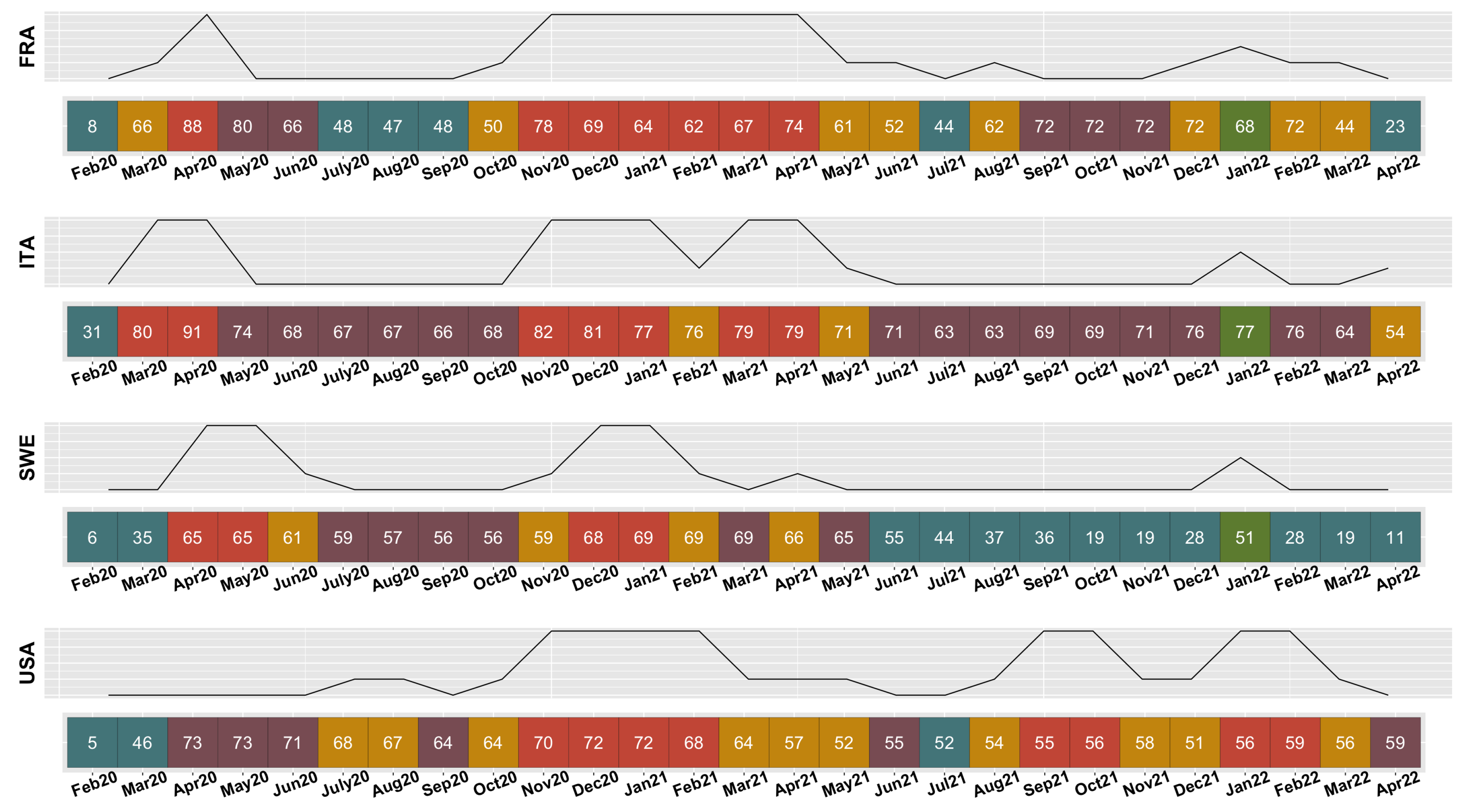
Preprints 112172 g007
Table 1. Parameter Explanations.
Table 1. Parameter Explanations.
Parameter Explanation
M Number of study periods. Represents the number of distinct temporal periods considered in the analysis.
S Number of populations. Represents the number of distinct populations (e.g., countries) considered in the analysis.
D Data Set. Collection of N data objects characterized by ( s , m ) , where s denotes a population and m denotes a period.
X Data Representation. Vector of variables associated with each data point in D, enabling comparisons and similarity calculations.
K Desired number of groups. Represents the desired final number of clusters or prototypes aimed to be formed within the data.
P f Ultimate Superclasses. Subset of P obtained using ascending hierarchical method, representing the final groups.
α Learning Rate. Percentage by which the algorithm learns during each iteration, influencing modification of prototype vectors.
h B M U , k p Temporal Neighborhood Function. Governs intensity with which neurons having different times than BMU approach a data point.
h B M U , k s Spatial Neighborhood Function. Determines intensity with which neurons with same period as BMU approach a data point.
σ p Temporal Radius. Defines extent of temporal influence, allowing adjustments in temporal neighborhood function.
σ s Spatial Radius. Controls spatial influence on clustering, impacting spatial neighborhood function.
T s Total Spatial Iterations. Represents total number of spatial iterations, influencing cluster evolution over space.
T p Total Temporal Iterations. Represents total temporal iterations within each spatial iteration, allowing exploration of temporal patterns.
K desired Clustering Target. Desired final number of clusters or prototypes aimed to be formed within the data.
σ i s Initial Spatial Radius. Initial spatial radius for neighborhood functions.
σ f s Final Spatial Radius. Final spatial radius for neighborhood functions.
σ i p Initial Temporal Radius. Initial temporal radius for neighborhood functions.
σ f p Final Temporal Radius. Final temporal radius for neighborhood functions.
E Number of Randomly Selected Populations. Represents number of randomly selected populations from the dataset.
W k Prototype Vector. Serves as the prototype vector associated with neuron k, evolving during clustering to capture cluster characteristics.
BMU Best Matching Unit. Identifies the neuron with the prototype vector closest to the data point, pivotal in clustering.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated