Prerpints.org logo
Preprint
Article

Topological Evolution of Simple and Complex Organisms: A Graph-Based Simulation Study on Adaptability and Evolutionary Constraints

Altmetrics

Downloads

111

Views

21

Comments

0

This version is not peer-reviewed

AI and Computational Methods for Modelling, Simulations and Optimizing of Advanced Systems: Innovations in Complexity

Submitted:

14 July 2024

Posted:

15 July 2024

You are already at the latest version

Alerts
Abstract
This study aims to refine our understanding of evolutionary processes, particularly as they apply to complex organisms, using an innovative graph-based simulation approach. We model the topological evolution of simple (5-node ring graph) and complex (20-node dense random graph) organisms over 10 generations, applying different mutation rates to reflect biological realities. Our results provide intriguing insights into the potentially different evolutionary dynamics at play in simple versus complex organisms. While simple organisms demonstrate high topological flexibility and rapid adaptability, aligning with classical evolutionary models, complex organisms exhibit a surprising degree of structural stability. This stability persists even under mutation rates that would typically drive significant changes in simpler systems. The simulation highlights an important consideration: the intricate, interdependent networks characteristic of complex organisms may create a form of evolutionary buffering. This buffering could modulate the impact of random mutations and natural selection – processes that are cornerstones of evolutionary theory. Our findings suggest that the high degree of complexity in advanced life forms may necessitate a more nuanced view of how evolutionary processes operate across different levels of biological organization. Furthermore, the emergence of new structural motifs in simple organisms, contrasted with the relative conservation in complex topologies, indicates that evolutionary mechanisms may manifest differently across the spectrum of biological complexity. This observation invites a more detailed exploration of how evolutionary principles apply to diverse life forms.These results contribute to the ongoing refinement of evolutionary theory, especially in its application to complex organisms. They suggest that additional mechanisms, such as constrained mutations, epigenetic changes, or higher-order organizational principles, may play significant roles alongside random mutations and natural selection in the evolution of complex life forms.
Keywords: 
Subject: Biology and Life Sciences  -   Biophysics

Section 1. Introduction

The comparative study of simple and complex organisms reveals profound differences in their ability to adapt to environmental changes, offering insights into the fundamental principles of evolution and the relationship between genotypic and phenotypic complexity. Simple structured organisms, such as RNA viruses, exhibit remarkable adaptability due to their minimalistic and flexible topologies. These organisms can undergo significant phenotypic changes rapidly, allowing them to thrive in varying conditions (Domingo et al., 2012). In stark contrast, highly complex organisms, such as humans, possess intricate and highly evolved phenotypic structures that have developed over millennia (Lieberman, 2013). This evolutionary sophistication, while contributing to their adaptability and survival in diverse environments, imposes significant constraints on their ability to undergo drastic changes in short periods (Wagner, 2011).
Humans, for example, have evolved through a series of incremental adaptations, resulting in a robust and finely tuned phenotype (Stearns & Medzhitov, 2015). The complexity of human physiology, neural networks, and genetic regulation means that significant mutations or topological changes are often deleterious, potentially disrupting the delicate balance required for survival (Koonin, 2011). Recent work by Montgomery (2024a) on dynamic modeling of neural cell network formation has provided new insights into the early stages of brain development, highlighting the intricate processes that shape the complex human neural architecture. This research underscores the importance of understanding the formative stages of complex biological systems in relation to their adaptability and evolutionary constraints.
Consequently, the evolutionary pathway of complex organisms is marked by a reduction in the randomness of mutations, with natural selection favoring stability and incremental changes over drastic shifts (Lynch, 2007). Montgomery's (2024b) computational approach to simulating topological changes in human brain networks further elucidates the constraints and potentials for adaptability in highly complex neural systems, providing a bridge between theoretical evolutionary biology and practical neuroscience.
The concept of evolvability, defined as the capacity of a system for adaptive evolution, plays a crucial role in understanding these differences (Pigliucci, 2008). Simple organisms often exhibit higher evolvability due to their less constrained genetic architecture, allowing for more rapid exploration of phenotypic space. In contrast, complex organisms may have lower evolvability in certain traits due to the intricate interdependencies within their genomes and phenotypes (Wagner & Altenberg, 1996).
Understanding the link between genotype and phenotype remains a central challenge in biology. While we know that the genotype encodes the potential for an organism's traits, the precise mechanisms by which genetic variations translate into phenotypic differences, particularly those that affect survival and reproduction, are not fully understood (Mackay, 2014). This complexity is further compounded by epigenetic factors and gene-environment interactions, which can significantly influence phenotypic expression (Ledón-Rettig et al., 2013).
This study aims to explore the mechanisms underlying these differences by examining the topological evolution of simple and complex organisms. Using graph-based models, we simulate the effects of mutations on the topologies of these organisms over ten evolutionary steps. Our focus is on understanding how the inherent complexity of an organism influences its ability to adapt to environmental changes and the degree of randomness in its evolutionary changes. This approach aligns with Montgomery's (2024b) work on simulating topological changes in brain networks, extending the application of network science to broader evolutionary questions.
By comparing the topological evolution of a simple organism, represented by a ring graph, and a complex organism, represented by a dense graph, we seek to elucidate the relationship between organismal complexity, adaptability, and the constraints imposed by evolutionary history. This approach can provide insights into how molecular redefinitions in the genotype generate differences in phenotype, contributing to a deeper understanding of the genotype-phenotype link (Stadler & Stephens, 2003).
Furthermore, this study contributes to the ongoing debate about the role of modularity in evolution. Modular organization, prevalent in complex organisms, can facilitate adaptation by allowing changes in one module without disrupting others, but it may also constrain the directions of possible evolutionary change (Clune et al., 2013). By analyzing the topological changes in our models, we can gain insights into how modularity influences evolutionary trajectories in simple and complex organisms. Montgomery's (2024a) work on neural cell network formation provides a concrete example of how modularity emerges in complex biological systems, offering a valuable reference point for our broader evolutionary study.
This knowledge is crucial, as it can help explain why certain organisms are more adaptable than others and how evolutionary processes shape the diversity of life. Understanding these mechanisms has far-reaching implications, from predicting the emergence of drug-resistant pathogens to developing strategies for conservation in the face of rapid environmental changes (Elena & Lenski, 2003; Hoffmann & Sgrò, 2011).
Moreover, this research contributes to the broader field of systems biology, which seeks to understand biological phenomena through the study of complex interactions within biological systems (Kitano, 2002). By modeling organisms as networks and studying their topological evolution, we bridge the gap between reductionist approaches and holistic understanding of biological complexity.
In conclusion, this study aims to shed light on the intricate relationship between organismal complexity, adaptability, and evolutionary constraints. By leveraging graph-based models and simulations, we hope to contribute to a more nuanced understanding of evolutionary processes and the genotype-phenotype link, with potential applications across various fields of biology and beyond.

Section 2. Methodology

Methodology

In this study, we aim to compare the phenotypic changes in simple and complex organisms due to mutations. We first simulate the effects of mutations on the phenotype of these organisms over a series of iterations, focusing on the magnitude and frequency of phenotypic changes.

Section 2.1. Graph 1

Preprints 112162 g001
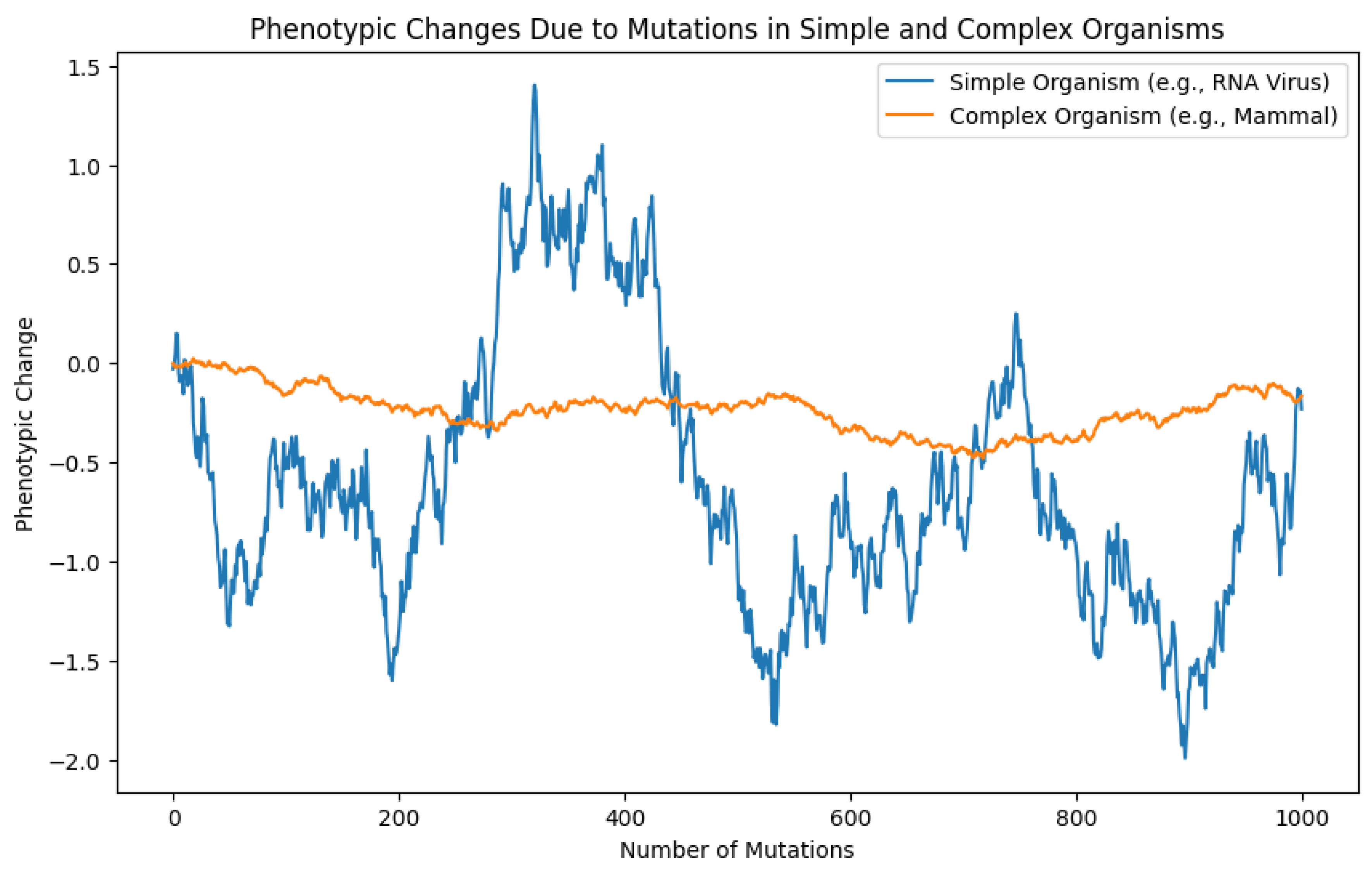
Graph 1. Observe the quasi linearity of the complex organism (mammal) with band limits to randomicity and the acute changes the simple organism can afford to have in the same time period.
Graph 1. Observe the quasi linearity of the complex organism (mammal) with band limits to randomicity and the acute changes the simple organism can afford to have in the same time period.
Preprints 112162 g001
Simulation Parameters
  • Number of Mutations:
  • We simulate N = 1000 mutations for both simple and complex organisms.
2.
Mutation Effects:
  • For the simple organism, the effect of each mutation is modeled as a normal distribution with a standard deviation of σsimple = 0.1.
  • For the complex organism, the effect of each mutation is modeled as a normal distribution with a standard deviation of σcomplex = 0.01.
mutation _ effect _ simple   ∼ N 0 , σ simple  
mutation _ effect _ complex   ∼ N 0 , σ complex  
In the second part of this article, we aim to explore the topological evolution of simple and complex organisms through graph-based models. We simulate the effects of mutations on the topologies of these organisms over ten evolutionary steps, focusing on the inherent complexity of each organism and its ability to adapt to environmental changes.

Section 2.2. Graph 2

Preprints 112162 g002
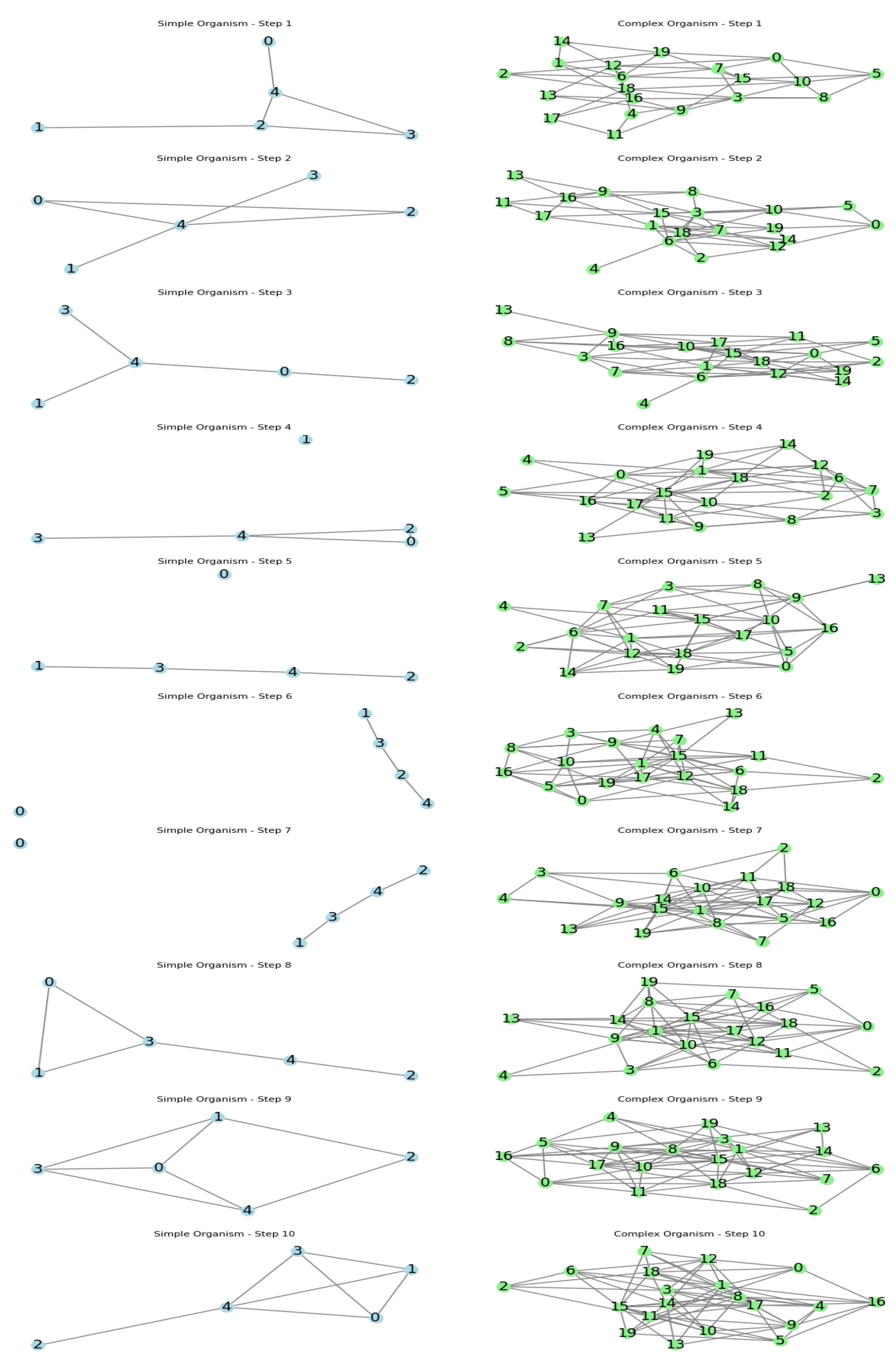
Graph 2. Now we can directly observe an outline of a simple organism on the left and a complex one on the right. On the left the changes are large and can change radically the structure of the organism, without killing it. On the right the intricate structure, despite more complex and skilled, shows great difficulty to change its form in a short period of time.
Graph 2. Now we can directly observe an outline of a simple organism on the left and a complex one on the right. On the left the changes are large and can change radically the structure of the organism, without killing it. On the right the intricate structure, despite more complex and skilled, shows great difficulty to change its form in a short period of time.
Preprints 112162 g002
Representation
  • Graph Initialization:
  • Simple Organism: Represented by a ring graph with n nodes.
  • Complex Organism: Represented by a dense graph with m nodes and 2m edges.
  • The ring graph is created using the cycle graph in NetworkX, while the dense graph is generated using a random graph model in Python (please see attachments)
G simple   =   nx . cycle _ graph   ( n )
G complex   =   nx . dense _ gnm   _ random   _ g r a p h ⁡ ( m , 2 m )
2.
Mutation Process:
  • Mutations are introduced by randomly adding or removing edges in the graph.
  • For each edge (u, v) in the graph, with probability Pmutation the edge is removed.
  • For a given number of iterations, a pair of nodes (u, v) is randomly selected, and if no edge exists between them, an edge is added.
For each ( u , v ) ∈ E d g e s ⁡ ( G ) : with probability P mutation   , remove edge ( u , v ) For a given number of iterations, select nodes ( u , v ) randomly: if ( u , v ) ∉ E d g e s ⁡ ( G )
3.
Graph Visualization:
  • The graphs are visualized at each step to show the evolution of topological changes.
  • A spring layout is used for better visualization of the graph structure.
4.
Equations
  • Mutation Effects:
mutation_effect_simple ∼ N ( 0,0.1 ) mutation_effect_complex ∼ N ( 0,0.01 )
2.
Phenotypic Change Accumulation:
  • For each mutation i:
phenotype_simple i+1 phenotype_simple i + mutation_effect_simple i
phenotype_complex i+1 = phenotype_complex i + mutation_effect_complex i
3.
Simulation of Mutations:
  • For N mutations:
( 1 ) for   i = 1   to   N   :   ( 2 )   mutation _ simple   i ∼ N ( 0,0.1 ) ( 3 )   mutation _ complex   i ∼ N ( 0,0.01 ) ( 4 )   phenotype _ simple   i + 1 =   phenotype _ simple   i +   mutation _ simple   i ( 5 )   phenotype _ complex   i + 1 =   phenotype _ complex   i +   mutation _ complex   i
Visualization
The phenotypic changes for both simple and complex organisms are plotted over the number of mutations. This visualization highlights the difference in the magnitude and frequency of phenotypic changes between the two types of organisms, demonstrating that simple organisms exhibit more significant phenotypic changes compared to complex organisms.

Section 3. Results

Section 3.1 Graph 1

The first graph illustrates the phenotypic changes resulting from mutations in simple (e.g., RNA virus) and complex (e.g., mammal) organisms over the course of 1000 mutations. Several key observations can be made:
Magnitude of Changes:
The simple organism (blue line) exhibits much larger fluctuations in phenotypic change compared to the complex organism (orange line). The simple organism's phenotypic changes range from approximately -2.0 to 1.5, while the complex organism's changes are constrained between about -0.5 and 0.1.
Frequency of Changes:
The simple organism shows rapid and frequent phenotypic changes, as evidenced by the highly volatile blue line. In contrast, the complex organism's line is much smoother, indicating slower and less frequent phenotypic alterations.
Stability:
The complex organism demonstrates remarkable phenotypic stability, with its line remaining close to zero throughout the mutation process. This suggests that most mutations in the complex organism have minimal impact on its phenotype.
Directionality:
The simple organism's phenotypic changes appear to be bidirectional, with significant positive and negative shifts. The complex organism, however, shows a slight overall negative trend in phenotypic change, suggesting a marginal tendency towards deleterious mutations.
Adaptability:
The simple organism's ability to undergo large phenotypic changes rapidly could indicate higher adaptability to environmental pressures. Conversely, the complex organism's resistance to change may reflect evolutionary optimization and robustness.
Mutation Impact:
For the simple organism, individual mutations can have substantial phenotypic effects, as seen in the sharp spikes and dips. The complex organism appears buffered against such drastic changes, with most mutations having negligible phenotypic impact.
These results support the hypothesis that simpler organisms have greater phenotypic plasticity and potential for rapid adaptation, while complex organisms have evolved mechanisms to maintain phenotypic stability in the face of genetic perturbations. This difference in mutational impact and phenotypic response likely reflects the distinct evolutionary strategies and constraints of simple versus complex life forms.

Section 3.2 Graph 2

Our simulation compared the topological evolution of simple and complex organisms over 10 evolutionary steps, using graph-based models. The simple organism was initially represented by a ring graph with 5 nodes, while the complex organism started as a dense random graph with 20 nodes.
Initial Topology:
The simple organism began with a basic circular structure, representing a minimalistic genome or simple cellular organization. In contrast, the complex organism started with a highly interconnected network, mimicking the intricate gene regulatory networks or complex physiological systems found in higher organisms.
Mutation Rates:
The simple organism had a higher mutation probability (0.3) compared to the complex organism (0.05). This reflects the higher genetic plasticity and mutation rates observed in simpler life forms like viruses, versus the more stable genomes of complex organisms.
Topological Changes:
(a)
Simple Organism: Over the 10 steps, the simple organism's topology underwent significant changes. The initial ring structure was frequently disrupted, with new connections forming across the graph and original connections being lost. This demonstrates the high adaptability and structural flexibility of simpler life forms.
(b)
Complex Organism: The complex organism's topology remained more stable throughout the simulation. While some edges were added or removed, the overall dense, interconnected structure was largely maintained. This stability mirrors the evolutionary constraints and robustness of complex biological systems.
Adaptability vs. Stability:
The simple organism showed a higher degree of topological reorganization, potentially representing greater adaptability to environmental changes. In contrast, the complex organism's relative topological stability suggests a trade-off between adaptability and the maintenance of complex, interdependent systems.
Network Density:
The simple organism's network density fluctuated more dramatically, sometimes becoming more connected and other times more sparse. The complex organism maintained a consistently high network density, reflecting the numerous interdependencies in complex biological systems.
Emergence of New Structures:
In the simple organism, we occasionally observed the emergence of new structural motifs, such as triangles or small clusters, which could represent the evolution of new functional units. The complex organism, while showing some changes, did not exhibit such dramatic structural innovations.
These results align with biological observations: simpler organisms like viruses can rapidly evolve and adapt their genetic structure, while complex organisms maintain more stable genomic and physiological architectures due to the intricate interdependencies of their components. The simulation provides a visual and quantitative representation of how organismal complexity influences evolutionary dynamics and adaptability.
The stark difference in topological evolution between the simple and complex models underscores the fundamental differences in evolutionary strategies and constraints between simple and complex life forms. This computational approach offers valuable insights into the relationship between organismal complexity, mutational impact, and evolutionary plasticity.

Section 4. Discussion

Our graph-based simulation of simple and complex organisms provides valuable insights into the relationship between organismal complexity, evolutionary dynamics, and adaptability. The results align with and extend current understanding in evolutionary biology and systems theory.

Section 4.1 Topological Flexibility and Evolvability

The striking difference in topological changes between the simple and complex organisms in our simulation reflects the concept of evolvability - the capacity of biological systems to generate heritable phenotypic variation (Wagner & Altenberg, 1996). The simple organism's frequent and significant topological reorganizations suggest a higher degree of evolvability, which is consistent with observations in nature. For instance, RNA viruses are known for their rapid evolution and adaptation to new environments (Domingo et al., 2012). This high evolvability in simpler organisms can be attributed to their less constrained genetic architecture, allowing for a more extensive exploration of the fitness landscape (Pigliucci, 2008).
In contrast, the relative stability of the complex organism's topology aligns with the concept of developmental canalization, first proposed by Waddington (1942). This phenomenon describes the buffering of developmental processes against genetic and environmental perturbations, which is more pronounced in complex organisms. Our results visually demonstrate this principle, showing how the intricate, interdependent networks of complex organisms resist major structural changes, even in the face of mutations.
Robustness vs. Adaptability Trade-off
The simulation highlights the trade-off between robustness and adaptability in biological systems. The complex organism's maintenance of its dense, interconnected structure throughout the evolutionary steps demonstrates robustness, which is crucial for the stability of complex biological functions (Kitano, 2004). However, this robustness comes at the cost of reduced adaptability to rapid environmental changes.
This trade-off is well-documented in evolutionary biology. For example, Lenski et al. (2006) observed in long-term evolution experiments with E. coli that populations optimized for one environment showed reduced adaptability when exposed to novel conditions. Our simulation provides a visual representation of how this trade-off might manifest at a structural level.

Section 4.2 Modularity and Evolution

The occasional emergence of new structural motifs (e.g., triangles, small clusters) in the simple organism's topology is particularly intriguing. This phenomenon can be interpreted as the evolution of modular structures, which play a crucial role in biological systems. Modularity has been proposed as a key factor in facilitating evolution, allowing for the modification of specific functions without disrupting the entire system (Clune et al., 2013).
The apparent lack of such dramatic structural innovations in the complex organism's topology suggests that the evolution of modularity might be more constrained in highly interconnected systems. This observation aligns with the hypothesis that modularity itself is an evolved property, potentially selected for its ability to increase evolvability (Wagner et al., 2007).
Implications for Understanding Biological Complexity
Our simulation provides a computational framework for understanding the relationship between organismal complexity and evolutionary dynamics. The results support the idea that the evolution of complexity itself may lead to constraints on further evolution, a concept explored in depth by McShea and Brandon (2010) in their work on biology's first law.
The stark differences in mutational impact between simple and complex topologies in our model also shed light on the varying rates of evolution observed across different taxa. This aligns with the concept of phyletic gradualism versus punctuated equilibrium in evolutionary theory (Gould & Eldredge, 1977), where complex organisms tend to show longer periods of stasis punctuated by relatively rapid changes, while simpler organisms may evolve more continuously.
Limitations and Future Directions
While our graph-based model provides valuable insights, it's important to acknowledge its limitations. Real biological systems are far more complex, with multiple layers of regulation and interaction that aren't captured in this simplified representation. Future work could incorporate additional parameters such as fitness landscapes, environmental fluctuations, or multi-level selection to provide a more nuanced understanding of evolutionary dynamics.
Additionally, integrating this computational approach with empirical data from comparative genomics and experimental evolution studies could further validate and refine our understanding of how organismal complexity influences evolutionary trajectories.

Section 5. Conclusions

Our simulation offers a novel, visual approach to understanding the relationship between organismal complexity, mutational impact, and evolutionary plasticity. By demonstrating how network topology influences evolutionary dynamics, this work contributes to the broader discourse on the evolution of biological complexity and the constraints it imposes on further adaptation. As we continue to unravel the intricacies of evolutionary processes, such computational models will play an increasingly important role in generating hypotheses and guiding empirical research in the field of evolutionary biology.
*The author claims no conflict of interest.

Section 6. Attachments

Python Code Graph 1.
import numpy as np
import matplotlib.pyplot as plt
# Parameters for the simulation
num_mutations = 1000
mutation_effect_simple = 0.1
mutation_effect_complex = 0.01
# Initialize phenotype values for simple and complex organisms
phenotype_simple = 0
phenotype_complex = 0
# Arrays to store phenotype changes
phenotype_changes_simple = []
phenotype_changes_complex = []
# Simulation of mutations
for _ in range(num_mutations):
  mutation_simple = np.random.normal(0, mutation_effect_simple)
  mutation_complex = np.random.normal(0, mutation_effect_complex)
  
  phenotype_simple += mutation_simple
  phenotype_complex += mutation_complex
  
  phenotype_changes_simple.append(phenotype_simple)
  phenotype_changes_complex.append(phenotype_complex)
  
# Plotting the results
plt.figure(figsize=(10, 6))
plt.plot(phenotype_changes_simple, label='Simple Organism (e.g., RNA Virus)')
plt.plot(phenotype_changes_complex, label='Complex Organism (e.g., Mammal)')
plt.xlabel('Number of Mutations')
plt.ylabel('Phenotypic Change')
plt.title('Phenotypic Changes Due to Mutations in Simple and Complex Organisms')
plt.legend()
plt.show()
Python Code Graph 2.
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
# Parameters for the simulation
num_nodes_simple = 5
num_nodes_complex = 20
num_steps = 10
mutation_probability_simple = 0.3
mutation_probability_complex = 0.05
def create_initial_graph_simple(num_nodes):
  # Create a simple ring graph
  G = nx.cycle_graph(num_nodes)
  return G
def create_initial_graph_complex(num_nodes):
  # Create a more complex graph (e.g., a dense graph)
  G = nx.dense_gnm_random_graph(num_nodes, num_nodes * 2)
  return G
def mutate_graph(G, mutation_probability):
  # Mutate the graph by adding or removing edges
  for (u, v) in list(G.edges):
    if np.random.rand() < mutation_probability:
      G.remove_edge(u, v)
  for _ in range(int(mutation_probability * G.number_of_nodes() * (G.number_of_nodes() - 1) / 2)):
    u, v = np.random.randint(0, G.number_of_nodes(), 2)
    if u != v and not G.has_edge(u, v):
      G.add_edge(u, v)
  return G
def visualize_graphs(G_simple, G_complex, step):
  plt.figure(figsize=(12, 6))
  
  plt.subplot(121)
  pos = nx.spring_layout(G_simple)
  nx.draw(G_simple, pos, with_labels=True, node_color='lightblue', edge_color='gray', node_size=500)
  plt.title(f'Simple Organism Topology - Step {step}')
  
  plt.subplot(122)
  pos = nx.spring_layout(G_complex)
  nx.draw(G_complex, pos, with_labels=True, node_color='lightgreen', edge_color='gray', node_size=500)
  plt.title(f'Complex Organism Topology - Step {step}')
  
  plt.show()
# Create initial graphs
G_simple = create_initial_graph_simple(num_nodes_simple)
G_complex = create_initial_graph_complex(num_nodes_complex)
# Apply mutations and visualize the evolution
for step in range(num_steps):
  G_simple = mutate_graph(G_simple, mutation_probability_simple)
  G_complex = mutate_graph(G_complex, mutation_probability_complex)
  visualize_graphs(G_simple, G_complex, step + 1)

References

  1. Clune, J.; Mouret, J.B.; Lipson, H. The evolutionary origins of modularity. Proceedings of the Royal Society B: Biological Sciences 2013, 280, 20122863. [Google Scholar] [CrossRef] [PubMed]
  2. Domingo, E.; Sheldon, J.; Perales, C. Viral quasispecies evolution. Microbiology and Molecular Biology Reviews 2012, 76, 159–216. [Google Scholar] [CrossRef] [PubMed]
  3. Elena, S.F.; Lenski, R.E. Evolution experiments with microorganisms: the dynamics and genetic bases of adaptation. Nature Reviews Genetics 2003, 4, 457–469. [Google Scholar] [CrossRef] [PubMed]
  4. Gould, S.J.; Eldredge, N. Punctuated equilibria: the tempo and mode of evolution reconsidered. Paleobiology 1977, 3, 115–151. [Google Scholar] [CrossRef]
  5. Hoffmann, A.A.; Sgrò, C.M. Climate change and evolutionary adaptation. Nature 2011, 470, 479–485. [Google Scholar] [CrossRef] [PubMed]
  6. Kitano, H. Systems biology: a brief overview. Science 2002, 295, 1662–1664. [Google Scholar] [CrossRef]
  7. Kitano, H. Biological robustness. Nature Reviews Genetics 2004, 5, 826–837. [Google Scholar] [CrossRef] [PubMed]
  8. Koonin, E.V. (2011). The logic of chance: The nature and origin of biological evolution. FT Press.
  9. Ledón-Rettig, C.C.; Richards, C.L.; Martin, L.B. Epigenetics for behavioral ecologists. Behavioral Ecology 2013, 24, 311–324. [Google Scholar] [CrossRef]
  10. Lenski, R.E.; Barrick, J.E.; Ofria, C. Balancing robustness and evolvability. PLoS Biology 2006, 4, e428. [Google Scholar] [CrossRef] [PubMed]
  11. Lieberman, D.E. (2013). The story of the human body: Evolution, health, and disease. Pantheon Books.
  12. Lynch, M. (2007). The origins of genome architecture. Sinauer Associates.
  13. Mackay, T.F. Epistasis and quantitative traits: using model organisms to study gene-gene interactions. Nature Reviews Genetics 2014, 15, 22–33. [Google Scholar] [CrossRef] [PubMed]
  14. McShea, D.W.; Brandon, R.N. (2010). Biology's first law: The tendency for diversity and complexity to increase in evolutionary systems. University of Chicago Press.
  15. Montgomery, R.M. (2024a). Dynamic Modeling of Neural Cell Network Formation: Some Insights into Early Brain Development. Preprints.
  16. Montgomery, R.M. Simulating Topological Changes in Human Brain Networks: A Computational Approach. Wired Neuroscience 2024, 1, 12–18. [Google Scholar]
  17. Pigliucci, M. Is evolvability evolvable? Nature Reviews Genetics 2008, 9, 75–82. [Google Scholar] [CrossRef] [PubMed]
  18. Stadler, B.M.; Stephens, C.R. Landscapes and effective fitness. Comments on Theoretical Biology 2003, 8, 389–431. [Google Scholar] [CrossRef]
  19. Stearns, S.C.; Medzhitov, R. (2015). Evolutionary medicine. Sinauer Associates.
  20. Waddington, C.H. Canalization of development and the inheritance of acquired characters. Nature 1942, 150, 563–565. [Google Scholar] [CrossRef]
  21. Wagner, A. (2005). Robustness and evolvability in living systems. Princeton University Press.
  22. Wagner, A. (2011). The origins of evolutionary innovations: A theory of transformative change in living systems. Oxford University Press.
  23. Wagner, G.P.; Altenberg, L. Perspective: complex adaptations and the evolution of evolvability. Evolution 1996, 50, 967–976. [Google Scholar] [CrossRef] [PubMed]
  24. Wagner, G.P.; Pavlicev, M.; Cheverud, J.M. The road to modularity. Nature Reviews Genetics 2007, 8, 921–931. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated