Prerpints.org logo
Preprint
Article

Modeling the Stress-Strain State of a Filled Human Bladder

Altmetrics

Downloads

124

Views

46

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 July 2024

Posted:

16 July 2024

You are already at the latest version

Alerts
Abstract
The problems of modeling the human bladder and its stress-strain state under external static influence were considered. A method for identification of the anisotropic biomechanical characteristics of bladder tissue was proposed. A FEM model was created, which accepts into regard that the bladder is surrounded by fiber and affected by surrounding organs, and partially protected by pelvic bones. The model considered the presence of constant hydrostatic pressure on the walls of the bladder when it is full. It has been shown that isotropic mechanical characteristics of biological tissue can be used for studying the deformed state of a filled bladder if the filled bladder 300 ml is considered as initial non-deformed stage. This was shown by modeling and verification the effect of the external static force on the bladder. Numerical experiments were conducted based on the constructed model. To validate the results obtained, a series of natural experiments on the effect of external pressure on the bladder under ultrasound control was conducted. In the future, it is planned to use the constructed model to study rupture deformations of the bladder under the influence of static and dynamic loads.
Keywords: 
Subject: Physical Sciences  -   Biophysics

1. Introduction

Trauma to the bladder leads to violations of the integrity of the organ wall. Usually, such injuries are caused by mechanical damage. At the same time, the mechanism of damage depends on different factors [1]. For example, with a blunt blow to the hypo-gastrium, intravesical pressure increases sharply and the load on the bladder wall growing. Also, the incident of a hydrodynamic effect contributes to the intraperitoneal rupture of the organ around the least developed muscles (near the tip on the back wall of the bladder) [2,3,4]. With a lower force of mechanical effect, the impact causes closed damage (bruises, hemorrhages). Also, this pathogenesis is characteristic in the presence of urological diseases with a decrease in urine passage. A significant displacement of the bladder in case of mechanical injuries leads to a sharp tension of the supporting lateral and vesico-prostatic ligaments with an extraperitoneal rupture of the soft-elastic wall of the organ [5]. A strong blow can cause rupture of ligaments, as well as urinary blood vessels.
The criteria for systematization of traumatic injuries are severity, connection with the environment, location of the rupture relative to the peritoneum and combination with damage to other organs. In this regard it is important to know how the human bladder is deformed under effect of a blunt blow to the pelvic region. Knowledge of deformations of the bladder walls will allow us to predict the course of pathological processes and complications. In this regard, it will be possible to choose the optimal patient management tactics [6,7].
The problems of mathematical and numerical modeling of the stress-strain state of internal organs are of interest to researchers. So, in the study [8], a finite element model of the human thorax and abdomen was developed based on computed tomography images from the Visible Human Project [9] for the research of blunt trauma. In [10], the effect of blunt abdominal trauma on liver rupture was studied using a finite element model. For the model, the authors used a detailed geometry of the liver obtained by tomography. Also, a simplified model of the torso was used. The verification of the model was carried out by comparing the curves of liver displacement at a certain load. The authors [11] showed the mechanism of damage to the spleen because of blunt force trauma based on finite element analysis. Stress distribution and damage to the spleen were considered by simulating a knuckle effect with a certain velocity in the spleen area on a THUMS human body model [12]. The results obtained using the model were compared with clinical cases of spleen injury. The authors concluded that the damage to the spleen was caused by a direct kick to the protuberance, compression of neighborhood tissues and organs. In [13], a finite element model of the eye was constructed for dynamic modeling of blunt force trauma. After constructing the model, an analysis of the potential causes of damage to the optic nerve was carried out by evaluating the stress-strain state.
Currently, there are not enough works devoted to the study of deformation of the bladder under any influence. Most of the works related to the modeling of the bladder is most often associated with the study of fluid dynamics and the behavior of the walls of the bladder during its filling and emptying [14]. For example, in [15], the relationship between changes in the basic size of the bladder and an increase in the volume of the bladder during filling was investigated. The results of finite element modeling showed that the size of the bladder increases linearly with its volume during filling. In another study [16], a three-dimensional finite element model was used to study communication of the bladder with the pelvic organs caused only by changes in the volume of the bladder.
Most of the works related to the study of the bladder are devoted to the study of mechanical properties using various methods. Similar studies began in the 70s and one of the first works [17] confirmed that the bladder has viscoelastic properties. Thus, in [18], using step-by-step cytometry, the viscoelastic properties of the bladder wall tissue were analyzed. During the study, the authors obtained modulus of elasticity and viscosity. Because the pig’s bladder is similar in characteristics to a human’s bladder, most studies conduct experiments on it. In [19], the viscoelastic properties of pig bladder tissue were studied using experiments on uniaxial stretching, ball burst and DMA. The researchers received differing information and concluded that using the results of all three methods in combination could be useful for other studies. The authors [20] investigated the quasi-static uniaxial mechanical properties of the bladder walls. The study revealed a significant directional anisotropy of the mechanical properties of the bladder. The authors item out that the data obtained can be used to develop the most realistic computer modeling for predicting deformations in various conditions. There are also studies that have investigated the mechanical conduct of the human bladder. For example, the article [21] investigated the biomechanical properties of women’s bladders by uniaxial tensile. Tissue samples were obtained from cadavers without impaired pelvic floor functions. The obtained characteristics show that age can influence the mechanical conduct of the bladder.
Thus, there are not enough publications dedicated to modeling the stress-strain state of the human bladder, considering the surrounding tissues. Therefore, the objective of the work is to create a model of the human bladder and study stress-strain state under the influence of a blunt blow to the suprapubic region. When creating the model, it was considered that the bladder is surrounded by fiber. It was also considered that the bladder is exposed to the surrounding organs and is partially protected by the pelvic bones. Of course, it was considered that it was initially in a tense state due to the fullness by fluid.
The remainder of this paper is organized as follows. The assumptions and limitations, biomechanical properties and finite elements model of bladder are described in Section 2. The research results are stated in Section 3. The validation of the suggested approach is in Section 4. Finally, Section 5 discusses the study’s findings, results, and the main conclusion of the work.

2. Materials and Methods

2.1. Assumptions and Limitations

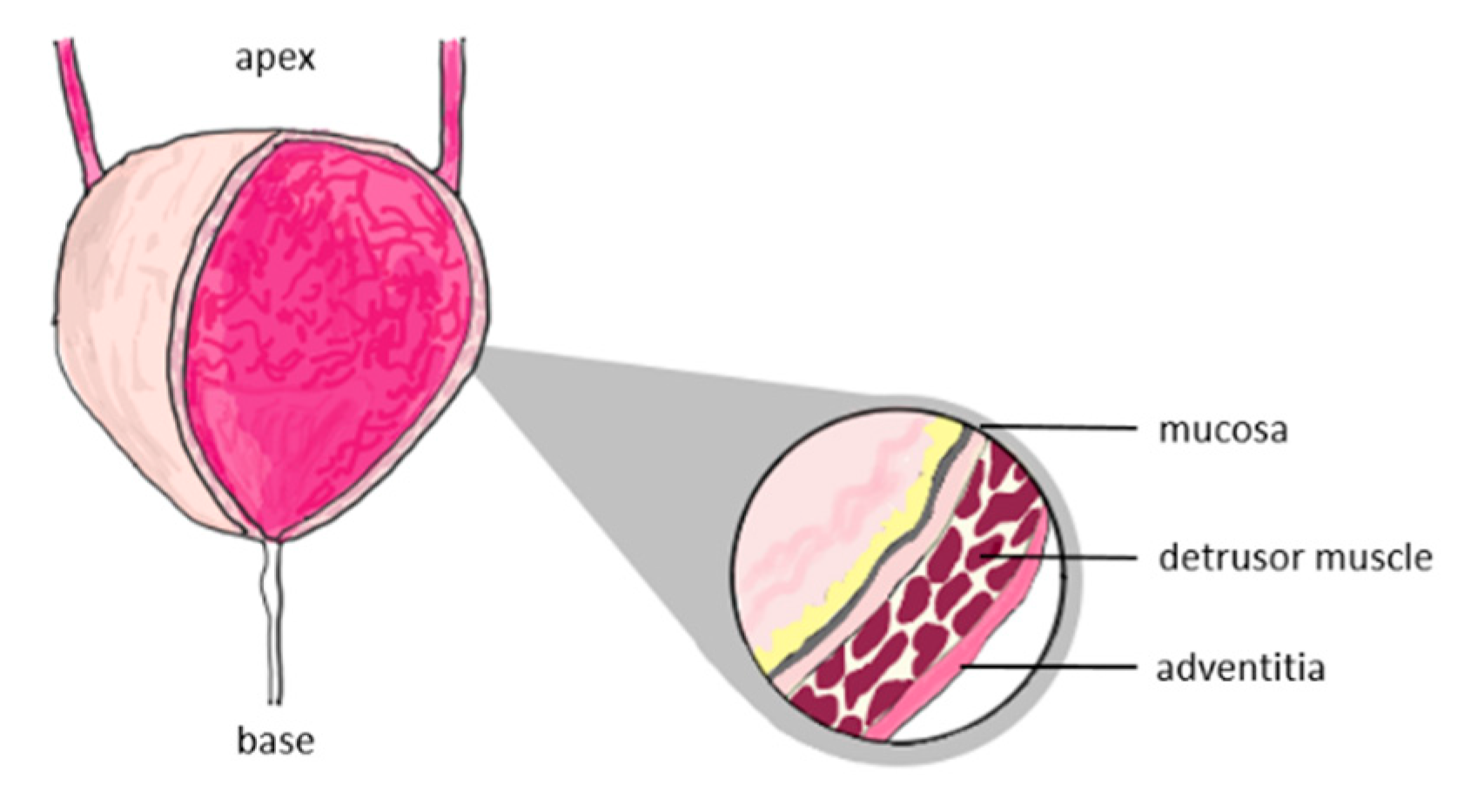
The structure of the bladder consists of three regions (Figure 1): mucosa, detrusor muscle and adventitia [22,23]. The mechanical properties of each region are different and cannot be determined. For this reason, we will consider the bladder wall as a homogeneous spherical shell, the mechanical properties of which represent the properties of each region.
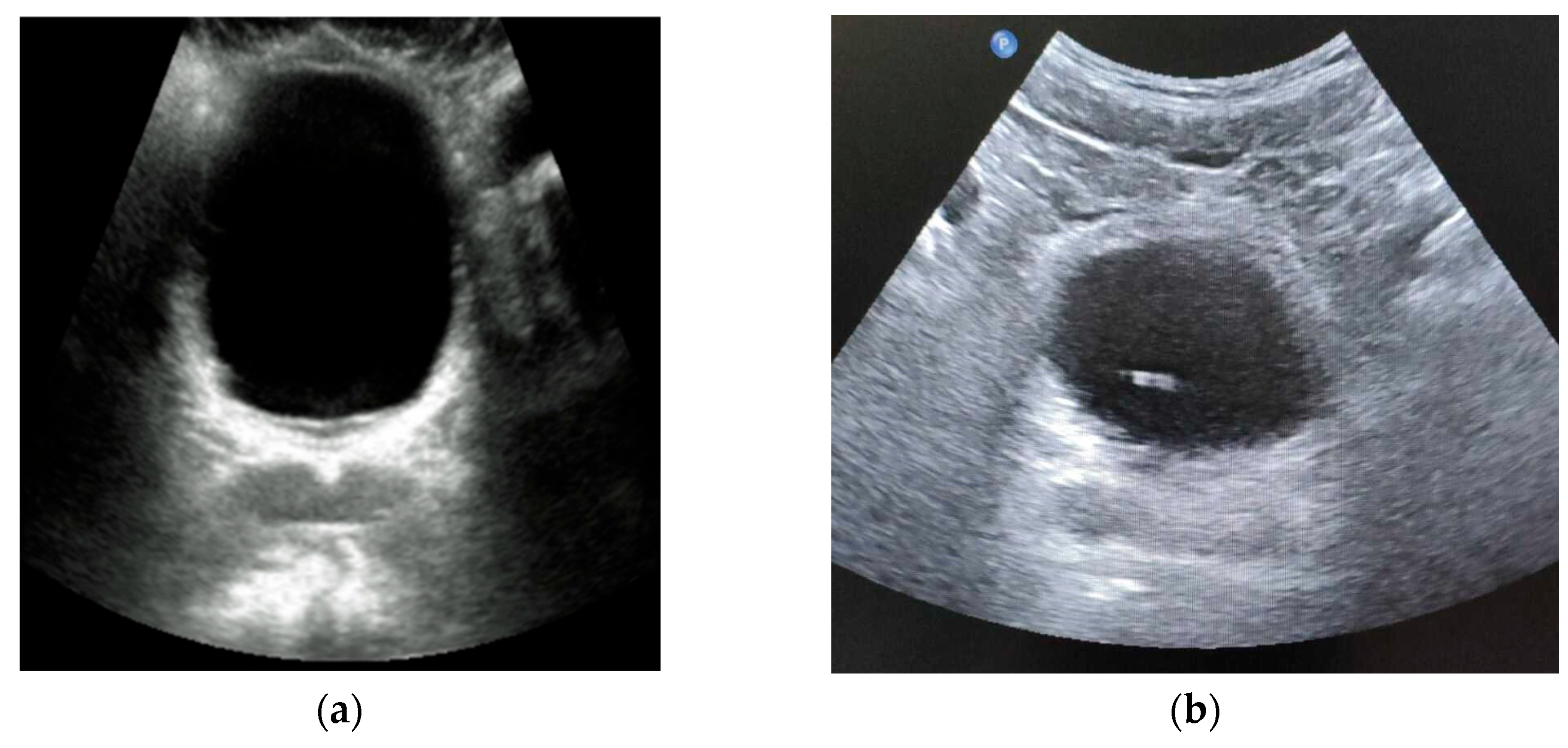
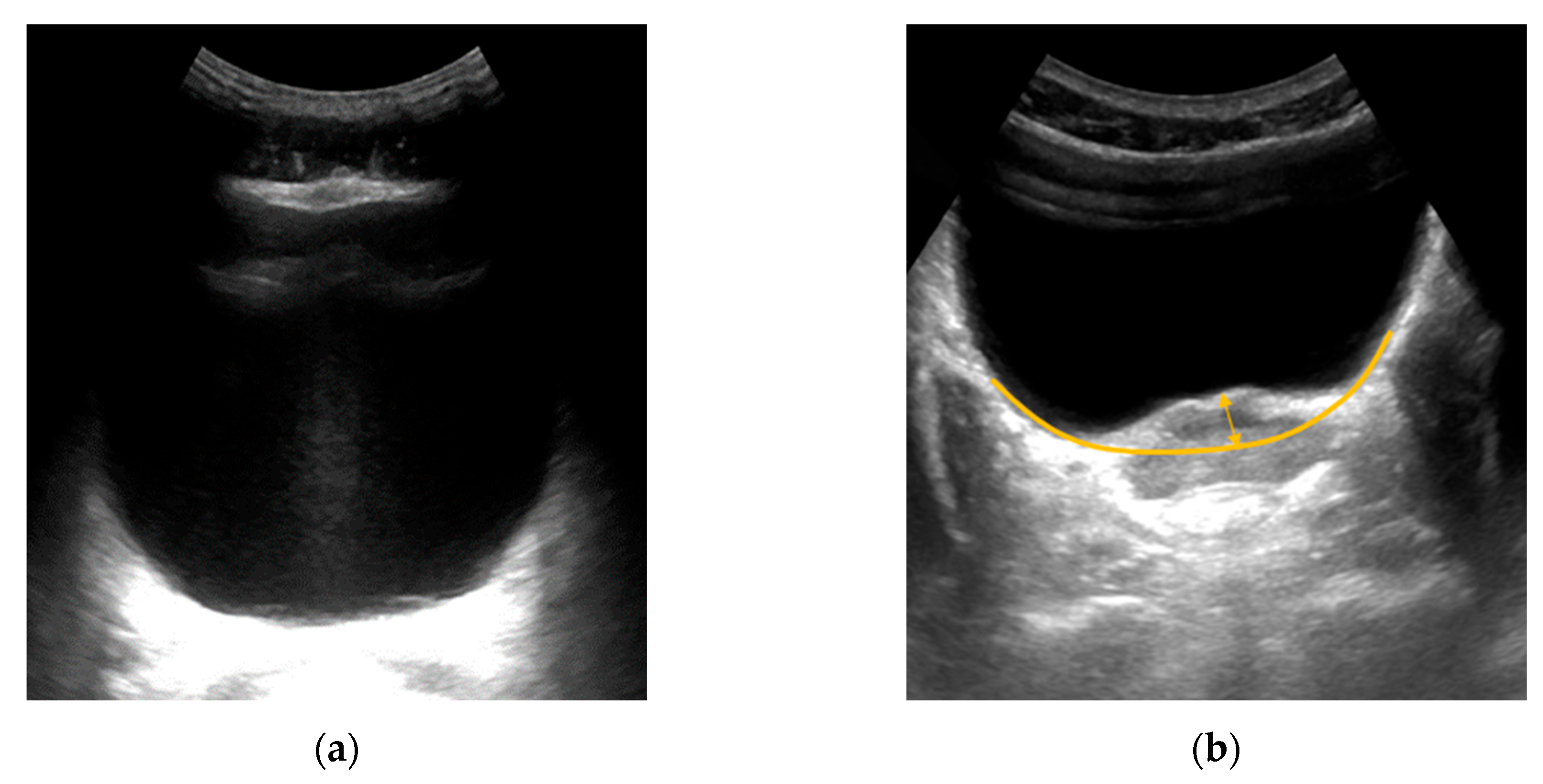
The bladder can expand 15 times compared to the unfilled state [24]. The volume of a full human bladder ranges from 330 to 440 ml [25]. In some cases, the bladder can enlarge to more than 600 ml. Existing research shows that considering a person’s bladder as a sphere right if its volume is at least 100 ml [26]. Also, ultrasound of a full bladder shows that its form remains spherical or elliptical (Figure 2). Therefore, to simplify the modeling of the stress-strain state of a filled bladder, we accept the assumption that its form is a sphere.

2.2. Biomechanical Properties

There is not enough data in the literature about the mechanical characteristics of the human bladder. For this reason, experiments were conducted on uniaxial tensile testing using a testing machine (Figure 3). To conduct this standardized test, samples are cut from the material. Next, the samples are placed between the grippers and the material is stretched until it breaks. Samples measuring was cut in a certain way from the human bladder.
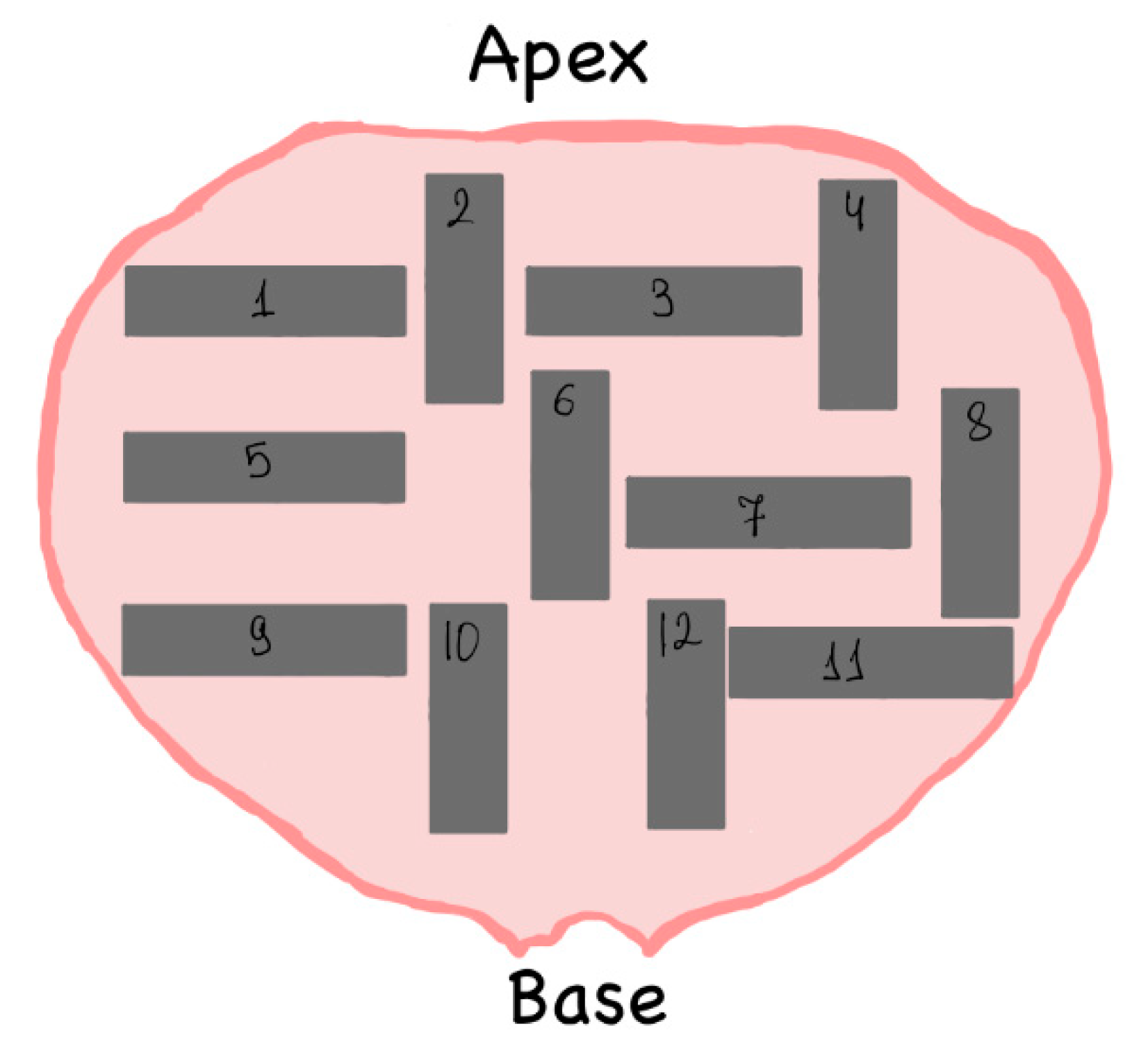
A sample section pattern is shown in Figure 4. This pattern is since the material of the bladder walls is an anisotropic material. The samples 2,4,6,8,10,12 were cut in the di-rection from the base to the apex and the samples 1,3,5,7,9,11 - in the perpendicular direction. Sample dimensions - 40 mm x 20 mm. The thickness of the samples was about 2.5 mm.
The samples were taken from five human bladders. They were not subjected to rotting or freezing processes. Next, the samples were treated with a mixture with formaldehyde. Then, the samples were wrapped in foil and placed on an ice substrate. Within 12 hours, the samples were transported for experiments to determine the mechanical properties of the material. Figure 5 shows the process of preparing human bladder samples and the image of the ready samples.
A uniaxial tensile test was performed to determine the mechanical characteristics of the human bladder wall. The distance between the grips was calibrated to 20 mm. Pre-conditioning was performed by repeatedly loading and unloading (cyclic) the specimens at strain rate of 50%/min. In each test, load and displacement data were obtained and converted into stress (σ) and strain (ε) using cross section area (true stress).
Preconditioning of biological soft tissue is considered as an essential step towards establishing a repeatable set of experiments [27,28]. A preconditioning procedure was carried out with a deformation amplitude of 10%. This amplitude was chosen to establish tissue resistance to subsequent loading. The hysteresis curve showed repeatability starting from the 7th series. To keep the loading history constant throughout the study, all samples were preconditioned at a fixed number of series.
The rupture of the samples was observed in the center. Samples cut from the base to the apex and perpendicular directions demonstrate different behavior. In the case of samples cut from the base to the apex there is greater rigidity compared to the other case.
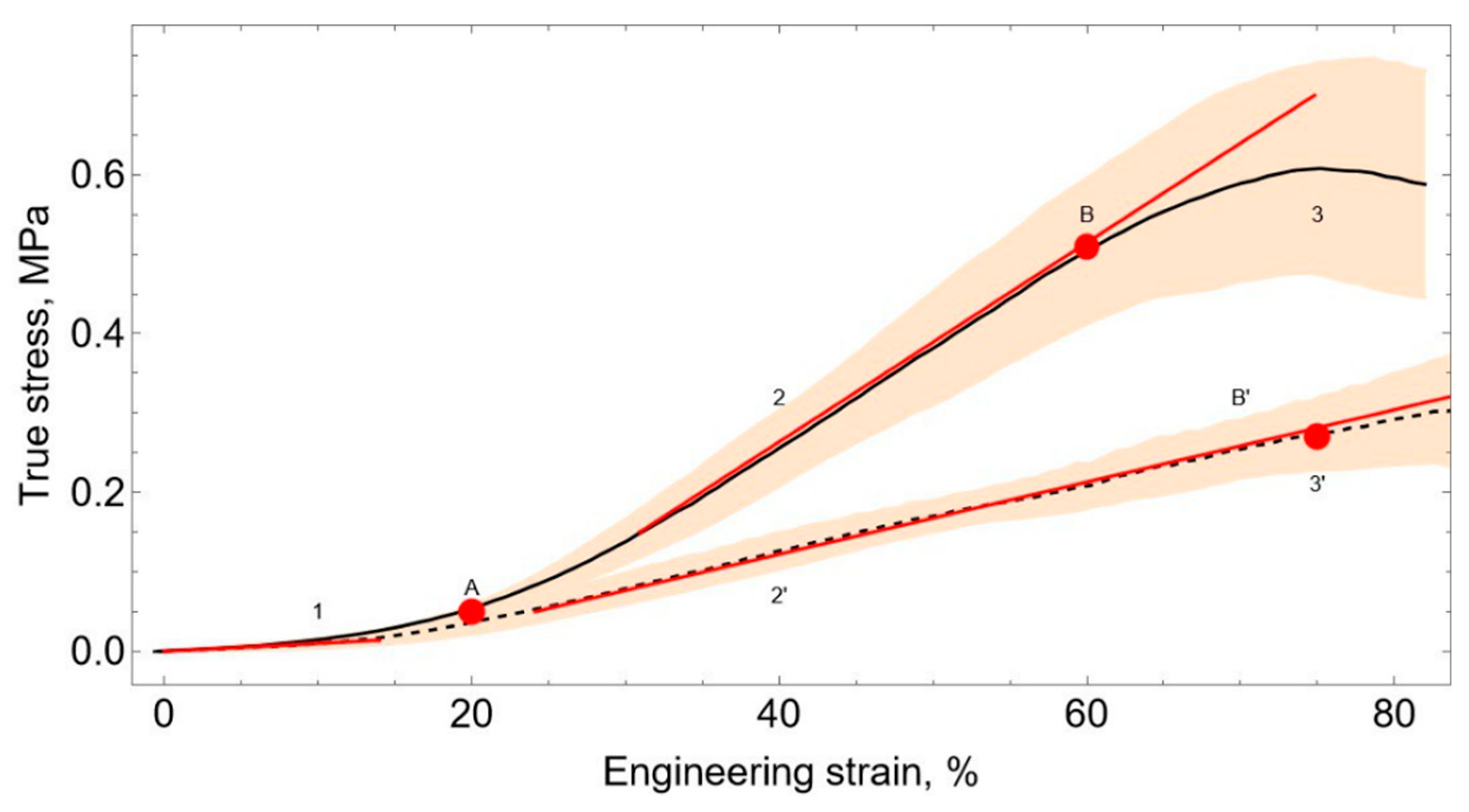
The mechanical properties of soft biological tissues are determined by three main components. In this regard, soft tissue is characterized by nonlinear elastic behavior [29]. Nonlinear behavior can be observed on the averaged graphs of stress-strain curves of bladder tissue obtained because of experiments (Figure 6). The arc-length corridor method was used to average the experimental curves.
Three characteristic regions can be seen in the stress-strain curves. The first area (Figure 6, zone 1) is a plateau, where there is a linear interrelation between stresses and de-formations. In this area, the deformation curves for the two orientations have no statistically significant differences. The Toe Modulus is 0.11±0.02 MPa. Next, a nonlinear transition is observed in the region of 20% deformations.
The transition is followed by a linear area (Figure 6, Zone 2). In this area, tissue hardening is observed due to the stretching of collagen fibers [30]. Heel modulus in the di-rection from the base to the apex of the human bladder is 0.42±0.03 MPa. In the perpendicular direction, the heel modulus is 1.24±0.17 MPa. The average value of the heel modulus is 0.83 MPa.
In the last area (Figure 6, zone 3), due to damage to the sample, the resistance decreases. This conduces to a breaking of the sample. The samples cut in the direction from the base to the apex show a high degree of hardening in Zone 2. Also, these samples have a greater tension drop in Zone 3.
In the future, we will look at areas 1-2 and will not consider area 3. This is because in the last section of the curve, the decrease in resistance with an increase in deformation is caused by tissue damage. Tissue damage does not occur during normal operation of the bladder inside the body. Therefore, the transition point from section 2 to section 3 will be described by the limit state [31,32,33].
The data obtained during the experiments correlate with the nature of the curves obtained in the article [34]. The study presented the results of uniaxial tensile of pig bladder samples in the axial and transverse directions. It has been shown that samples stretched in the transverse direction have a lower maximum stress than samples stretched in the axial direction. At the same time, when stretched in the axial direction, the maximum stress corresponds to a smaller deformation than in the transverse di-rection.
The ultimate tensile strain is 75±3% for the direction from the base to the apex and 60±6% in the perpendicular direction. These values turned out to be like the results from [35], where the ultimate tensile strain was 69 ± 17%.

2.3 Finite Elements Model

Finite element modeling was performed in a powerful engineering simulation software Ansys Workbench. A numerical and finite element model of the bladder and surrounding areas was developed.
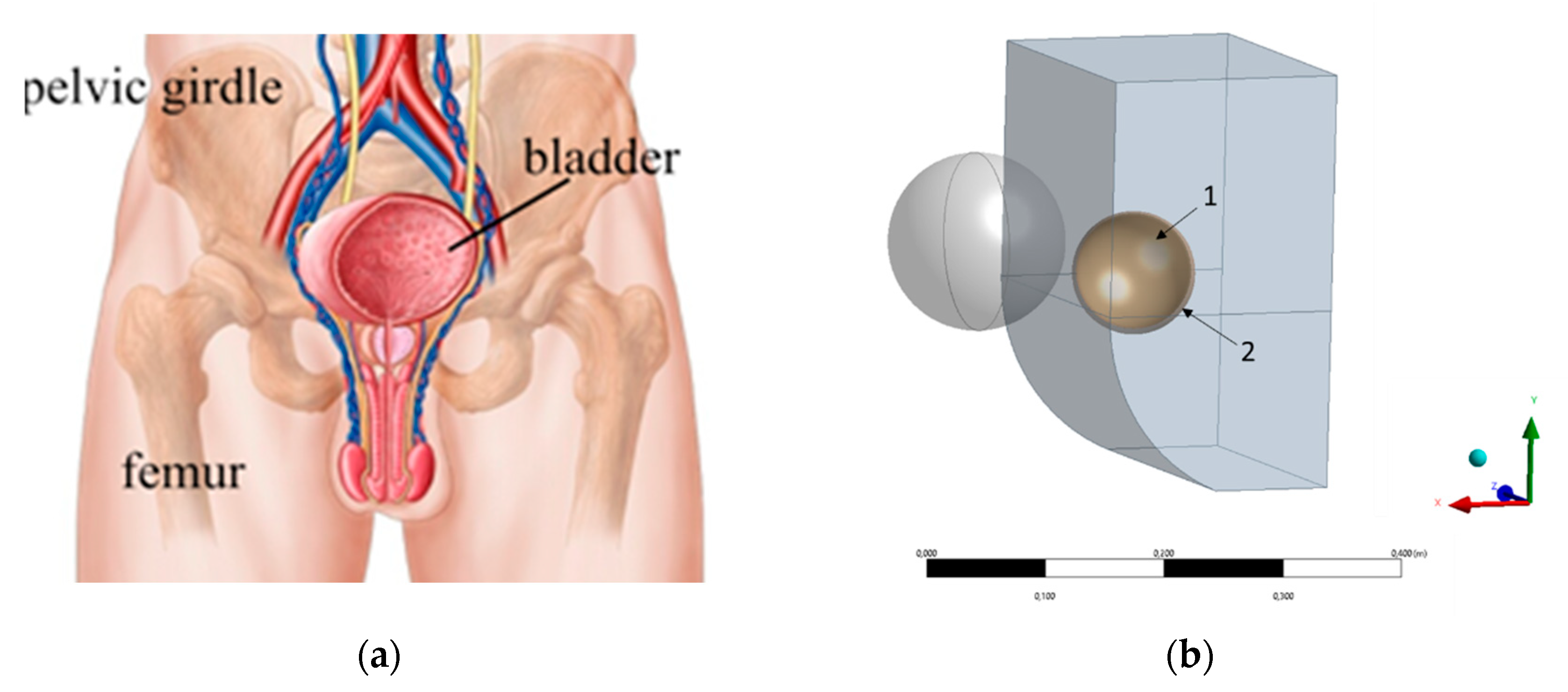
The bladder is in the pelvis (Figure 7). In the unfilled state, the bladder is completely protected by the pelvic girdle. However, when the bladder is filled, it can extend beyond the pelvic girdle.
It is known from the work [36], in which the urodynamic study of the human bladder by ultrasonic vibrometry was carried out, that the increase in the stiffness of the bladder wall begins when the volume reaches 300 ml. As can be seen from Figure 6, the onset of bio tissue stiffening corresponds to 20% strain. According to this, we will consider the volume of 300 ml as the initial undeformed state of the bladder. The stresses accumulated in zone 1 will be neglected because they are small compared to the stresses that occur during further deformation (Figure 6). The stress-strain state of the bladder wall will be described by the curve from zone 2 (2’).
As a first attempt to solve the problem, we will assume that the material of the bladder wall is a linear-elastic isotropic material. The average value of the Heel Modulus (E = 0.83 MPa) was taken as the value of the elastic modulus. Let us take the simplification that when the volume increases, the bladder will keep a spherical shape and has a homogeneous stress state. Since the filled bladder is of interest, the value of 400 ml is taken as the initial volume. However, in this case, the bladder rupture will occur at a lower stress. To perform the strength analysis, it will be necessary to consider the stresses that occurred in the bladder wall when the bladder was filled to 400 ml.
The fiber surrounding the bladder was defined as a spherical shell of variable thickness. The thickness of the fiber at the top of the bladder was 2 mm, and at the base 5 mm [37]. The fiber material was given by an incompressible linear elastic material with an elastic modulus of 3.5 kPa [38].
The surrounding organs were defined by a homogeneous incompressible linear elastic material with an elastic modulus of 5 kPa. This value was obtained by averaging the values of the elastic modulus of the abdominal cavity organs taken from the literature [38]. The surrounding organs were included in the model to obtain a believable distribution of pressure on the bladder. It was assumed that the fiber and surrounding organs do not have a prestressed state
The geometry of the surrounding organs (Figure 7) was built based on the distance (25 cm) between the distantia spinarum and the direct size of the conjugata externa (20 cm) taken from the literature [39,40].
With the help of boundary conditions in the form of fixed support, the influence of pelvic and spinal bones was considered. The case of thin subcutaneous fat was considered, so the distance from the bladder wall to the outer border of the body was set to 20 mm.
The impact of blunt abdominal trauma was modeled by pressing a rigid sphere with a radius of 75 mm in the pelvic region. The pressure was considered as crossing the sphere by 15 mm along the X-axis. A frictionless contact area was defined between the sphere and the front surface of the body model. A bonded contact was established between the bladder and the fiber (the geometry of the surrounding organs, fiber, and bladder was set so that all these components at the border had common nodes).
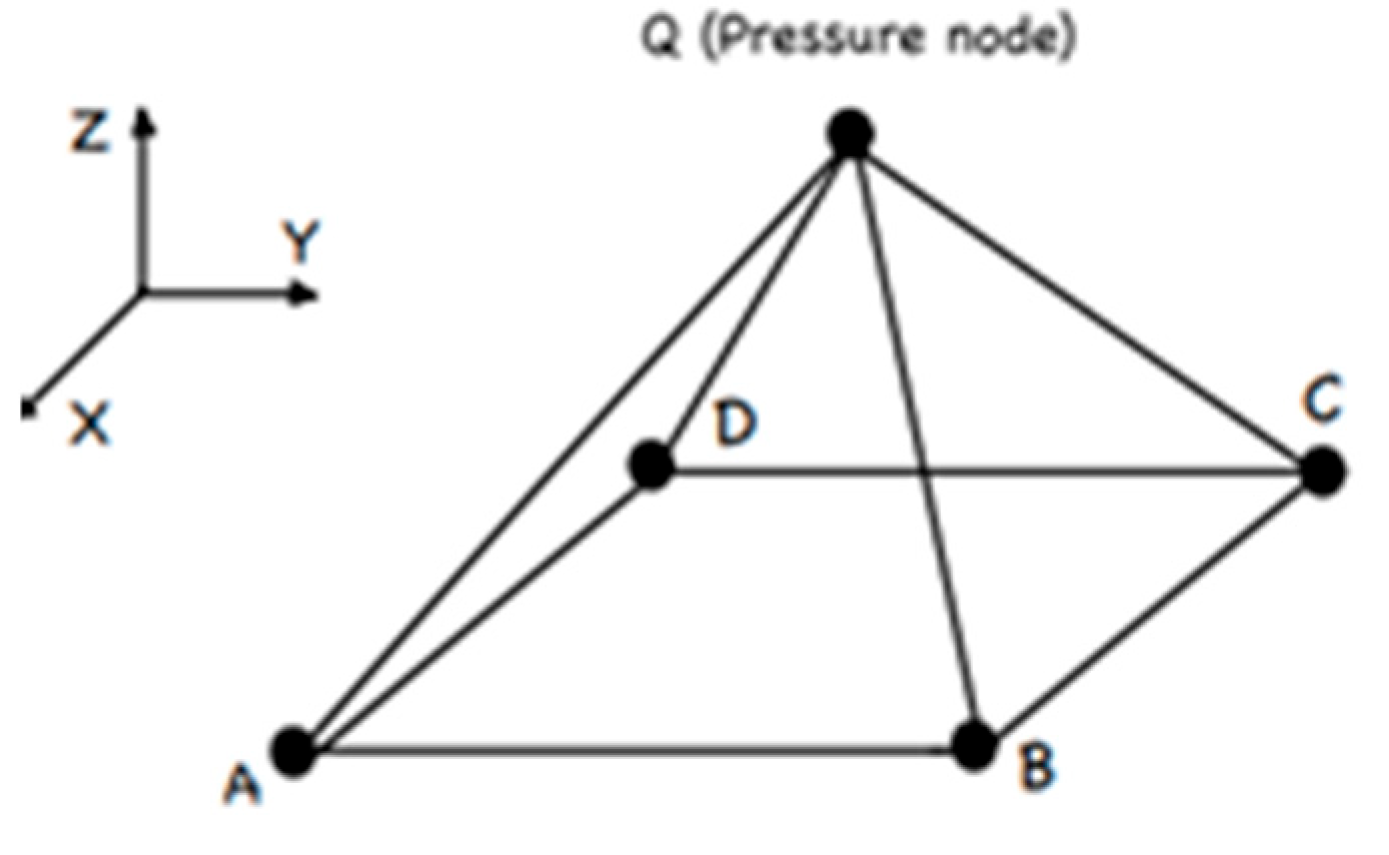
In this study, we will solve the problem of static deformation. In this regard, we assume that the volume of fluid inside the bladder is constant and there is no displacement of fluid inside the bladder. This assumption made it possible to use the hydrostatic three-dimensional fluid element HSFLD242 [41] (Figure 8) for modeling.
The HSFLD242 element is designed to study the effect of volume and pressure of a fluid in hydrostatic problems related to the interaction of a fluid and a solid. The HSFLD242 element is defined by a set of nodes that are common to the nodes of the inner surface of a solid. The main nodes have three degrees of freedom. Also, there is a pressure node, which is in the volume of the fluid.

3. Results

For numerical simulation, according to the experiments described in paragraph 2.2, the following mechanical parameters of the bladder were taken: Young’s Modulus 0.83 MPa, Poisson’s Ratio 0.5. The characteristics of the fiber around the bladder are Young’s Modulus 3.5 kPa, Poisson’s Ratio 0.5. The effective characteristics of the surrounding organs are Young’s Modulus 5 kPa, Poisson’s Ratio 0.5.
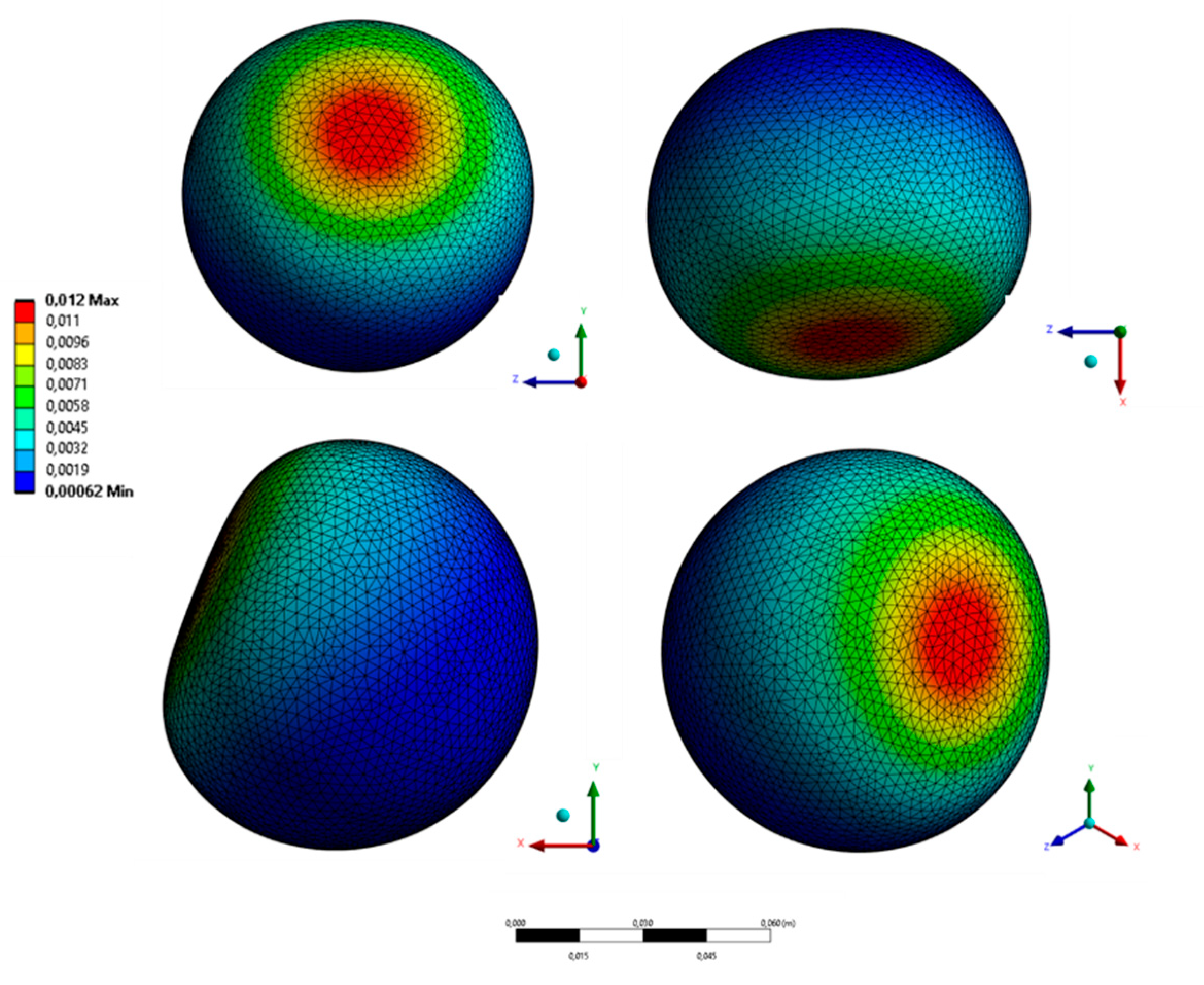
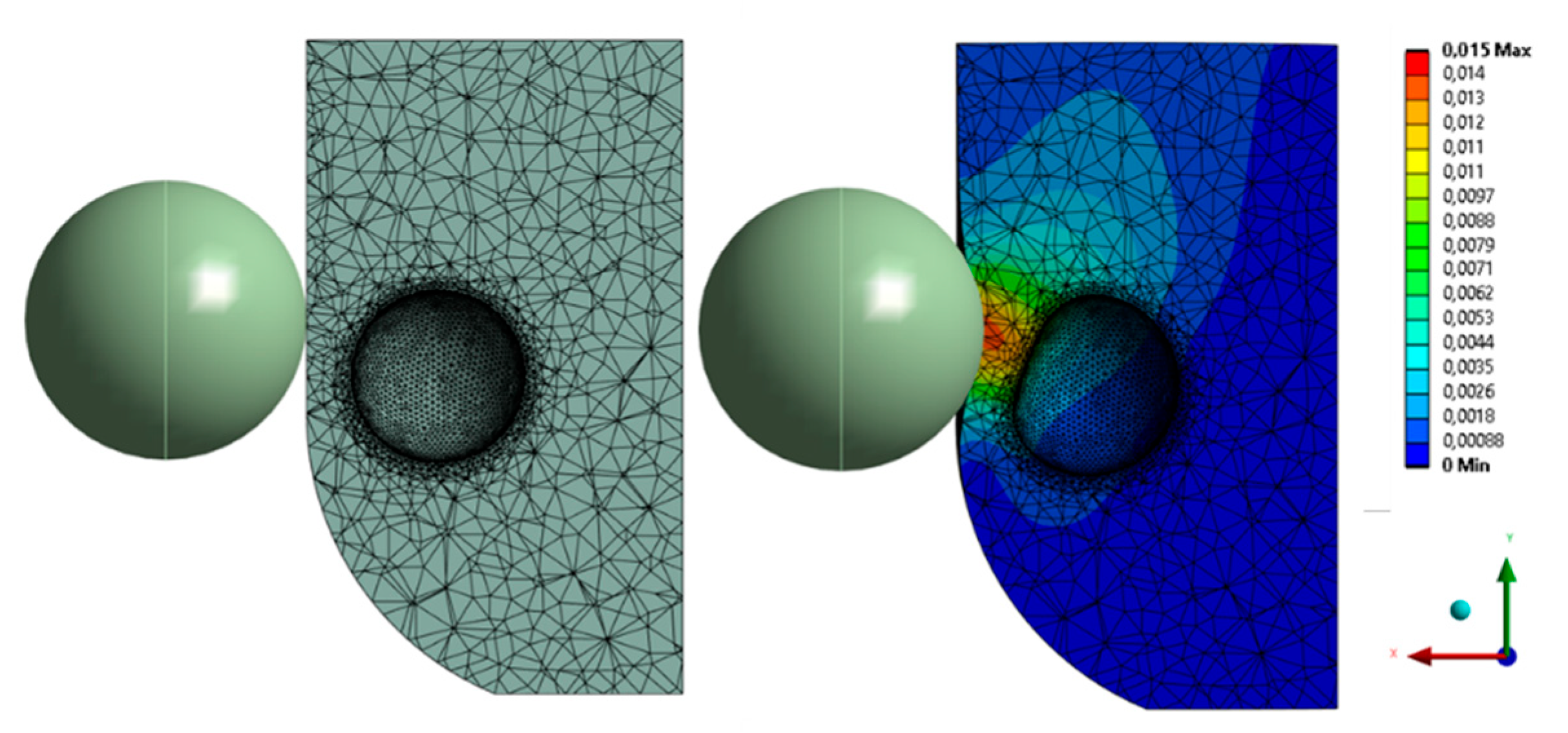
As a load, pressing on the abdominal area of a blunt object in the form of a rigid sphere was simulated (Young’s Modulus 100 GPa, Poisson’s Ratio 0.3) at 15 mm deep into the fiber. The place of application of the load was slightly higher than the bladder since most of the bladder is normally protected by the pelvic girdle. The general pattern of deformation in the cross section of the model is shown in Figure 10. Figure 11 shows the deformation of the bladder in different projections. The maximum displacement in the bladder was 12 mm.
Preprints 112151 g010
Figure 9. Different projections of deformed bladder (total deformation).
Figure 9. Different projections of deformed bladder (total deformation).
Preprints 112151 g010

4. Validation

Ultrasound of a bladder filled to 400 ml were performed to validate the constructed FEM model. Two volunteers with a small amount of adipose tissue in the pelvic girdle area drank water. Then, when filling the bladder, an ultrasound was performed in two ways: without pressing the ultrasound sensor on the area with the bladder and by pressing on the volunteer’s abdomen in the projection of the Lieto triangle. It should be noted that the ultrasound was conducted immediately after the volunteer assumed a horizontal position. It is important to emphasize this, since when in a horizontal position, the organs are additionally deformed.
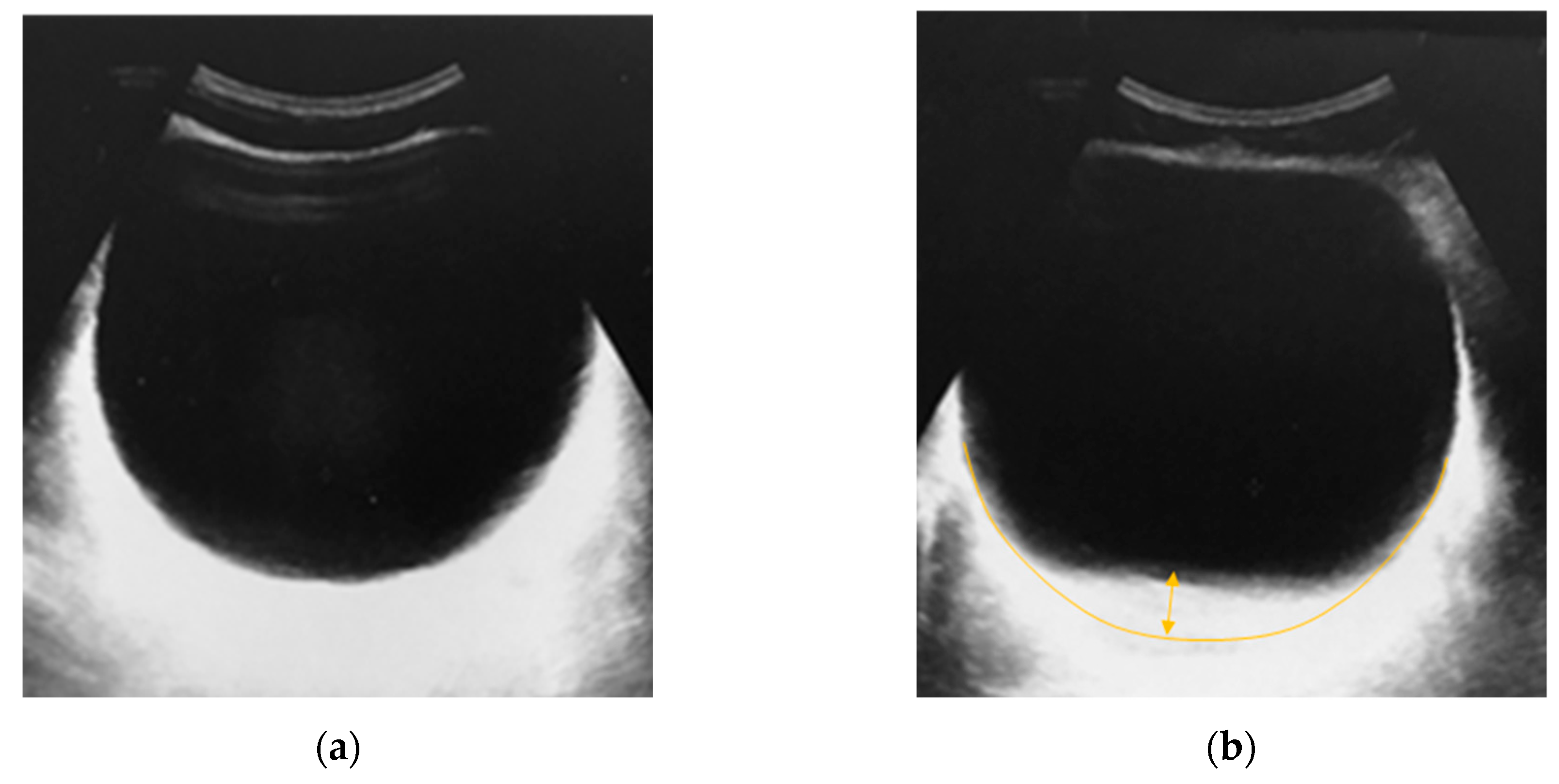
Figure 13a shows an undeformed bladder. Figure 13b shows the bladder when pressing on the patient’s abdomen by 1.5 cm. The deflection of the bladder was approximately 42px, which is 11.07 mm.
Figure 14 shows the results of a similar experiment on a second volunteer and on another ultrasound device. The deflection of the bladder was also about 11 mm.
The shape of the deformed bladder obtained during the experiments and the values of maximum deflections correspond to the digital FEM model described in this paper.

5. Discussion

During the experiments, the values of the anisotropic mechanical characteristics of the human bladder were obtained. The FEM model of the bladder was constructed considering the influence of fiber and abdominal organs.
It has been shown that isotropic mechanical characteristics of biological tissue can be used for the non-deformed state of a bladder filled up to 300 ml. This was shown by modeling the force effect on the bladder. Also, this is correct when the volume of the bladder increases.
The FEM model of the bladder was validated because of experiments by volunteers. In the future, it is planned to use the constructed model to study rupture deformations of the bladder under the influence of static and dynamic loads.

Supplementary Materials

Not applicable.

Author Contributions

Conceptualization, M.B and V.M; methodology, M.B and Ya.I..; software, T.T.; validation, T.T., Ya.I., K.V. and M.P.; formal analysis, M.B. and Ya.I.; investigation, T.T., Ya.I. and M.P.; resources, M.B.; data curation, V.M.; writing—original draft preparation, T.T., Ya.I. and M.P.; writing—review and editing, M.B.,Ya.I. and V.M.; visualization, T.T., Ya.I. and K.V.; supervision, M.B.; project administration, M.B. and Ya.I.; funding acquisition, M.B. All authors have read and agreed to the published version of the manuscript.

Funding

Not applicable.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable/.

Data Availability Statement

Not applicable.

Acknowledgments

In this section, you can acknowledge any support given which is not covered by the author’s contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Voitenko, A.N.; Neymark, A.I.; Bondarenko, A.V.; Razdorskaya, M.V. Hyperactive bladder syndrome as a consequence of pelvic ring injury. Polytrauma 2013, 2, 2–51. [Google Scholar]
  2. Munarriz, R.M.; Yan, Q.R.; Znehra, A.; Udelson, D.; Goldstein, I. Blunt trauma: the pathophysiology of hemodynamic injury leading to erectile dysfunction. Urol 1995, 153(6), 1831–1840. [Google Scholar] [CrossRef] [PubMed]
  3. Aghajanyan, V.V.; Pronskikh, A.A.; Ustyantseva, I.M.; Agalaryan, A.H.; Kravtsov, S.A.; Krylov, Yu.M. Polytrauma: Novosibirsk: Nauka, 2003. 492.
  4. Sokolov, V.A. Prevention and treatment of complications of polytrauma in the post-intensive care period. Bulletin of Traumatology and Orthopedics named after N.N. Priorov 2002, 1, 78–84. [Google Scholar]
  5. Smith, W.R.; Ziran, B.H.; Morgan, S.J. Fractures of the pelvis and acetabulum. I: York, 2007. [Google Scholar]
  6. Baker, S.P.; O’Neill, B.; Haddon, W.Jr.; Long, W.B. The Injury Severity Score: a method for describing patients with multiple injuries and evaluating emergency care. J. Trauma 1974, 14, 187–196. [Google Scholar] [CrossRef] [PubMed]
  7. Kraljević, L. Trauma and multiple trauma as one of the major problems of contemporary medicine and society. Lijec Vjesn 1977, 99(8), 507–10. [Google Scholar] [PubMed]
  8. Shen, W.; Niu, Y.; Mattrey, R.F., et. al. Development and Validation of Subject-Specific Finite Element Models for Blunt Trauma Study. 2008. [Google Scholar]
  9. Ackerman, Michael. The Visible Human Project. Studies in health technology and informatics 2022, 288, 134–140. [Google Scholar]
  10. Shao, Y.; Zou, D.; Li, Z.; Wan, L.; Qin, Z.; et al. Blunt Liver Injury with Intact Ribs under Impacts on the Abdomen: A Biomechanical Investigation. PLoS ONE 2013, 8(1), e52366. [Google Scholar] [CrossRef]
  11. Hu, Wenhu, Shao, Yu, Li, Zhengdong, et al. Mechanism of blunt spleen injury: a finite element analysis. J South Med Univ 2021, 41(3), 430-438.
  12. Kenji, Shigeta; Yuichi, Kitagawa; Tsuyoshi, Yasuki; et al. Development of next gen-eration human fe model capable of organ injury prediction. Toyota Motor Corporation 2016, 09-0111.
  13. Cirovic, S.; Bhola, R.M.; Hose, D.R.; Howard, I.C.; Lawford, P.V.; Marr, J.E.; Parsons, M.A. Computer modelling study of the mechanism of optic nerve injury in blunt trauma. Br J Ophthalmol 2006, 90(6), 778-83.
  14. Jaskowak, D.; Nunez, R.; Ramachandran, R. Mathematical modeling of the lower urinary tract: A review. Neurourology and Urodynamics 2022, volume 41, issue 6.
  15. Krywonos, J.; Fenwick, J.; Elkut, F.; Jenkinson, I.; Liu, Y. H.; Brunt, J. N.; Ren, X. J. MRI image-based FE modelling of the pelvis system and bladder filling. Computer Methods in Biomechanics and Biomedical Engineering 2010, 13(6), 669–676.
  16. Xiangfei, Chai; Marcel, van Herk; Jeroen, B. van de Kamer; Maarten, C. C. Finite element-based bladder modeling for image-guided radiotherapy of bladder cancer. Medical Physics 2011, 38 (1), 142-150.
  17. Alexander, R.S. Mechanical properties of urinary bladder. American journal of physiology 1971, 220, no. 5.
  18. Coolsaet, B.L.; van Duyl, W.A.; van Mastrigt, R.; van der Zwart, A. Visco-elastic properties of the bladder wall. Urol Int. 1975, 30(1), 16–26. [Google Scholar] [CrossRef] [PubMed]
  19. Jokandan, M.S.; Ajalloueian, F.; Edinger, M.; et al. Bladder wall biomechanics: A comprehensive study on fresh porcine urinary bladder. Journal of the Mechanical Behavior of Biomedical Materials 2018, 79, 92–103. [Google Scholar] [CrossRef]
  20. Korossis, S.; Bolland, F.; et al. Regional biomechanical and histological characterisation of the passive porcine urinary bladder: Implications for augmentation and tissue engineering strategies. Biomaterials 2009, 266–275. [Google Scholar] [CrossRef]
  21. Pedro, A. L.; Martins, S.; et. al. Uniaxial mechanical behavior of the human female bladder. Int Urogynecol J 2011, 22, 991–995. [Google Scholar]
  22. Robin, Trostorf; Enrique, M. O.; Amelie, Pötzke; Tobias, Siebert; Markus, Böl. A pilot study on active and passive ex vivo characterisation of the urinary bladder and its impact on three-dimensional modelling. Journal of the Mechanical Behavior of Biomedical Materials 2022, 133, 105347.
  23. Palugan, L.; Cerea, M.; Cirilli, M.; Moutaharrik, S.; Maroni, A.; Zema, L.; Melocchi, A.; Uboldi, M.; Filippin, I.; Foppol, A.i; Gazzaniga, A. Intravesical drug delivery approaches for improved therapy of urinary bladder diseases. International Journal of Pharmaceutics: X 2021, 3, 100100.
  24. Korossis, S.; Bolland, F.; Eileen Ingham; John Fisher; John Kearney; Jennifer Southgate. Review: Tissue Engineering of the Urinary Bladder: Considering Structure-Function Relationships and the Role of Mechanotransduction. Tissue Engineering 2006, 12(4), 635-44.
  25. Blanker, M.H.; Groeneveld, F.P.; Bohnen, A.M.; Bernsen, M.D.; Prins, A.; Thomas, S.; Ruud Bosch, J.L. Voided volumes: normal values and relation to lower urinary tract symptoms in elderly men, a community-based study. Urology 2001, Volume 57(6), 1093-1098.
  26. Jaskowak, D.; Nunez, R.; Ramachandran, R.; Alhajjar, E.; Yin, J.; Guidoboni, G.; Danziger, Z.C. Mathematical modeling of the lower urinary tract: A review. Neurourol Urodyn 2022, 41(6), 1305–1315. [Google Scholar] [CrossRef]
  27. Topaz, M.; Carmel, N.N.; Silberman, A.; et al. The TopClosure® 3S System, for skin stretching and a secure wound closure. Eur J Plast Surg 2012, 35, 533–543. [Google Scholar] [CrossRef] [PubMed]
  28. Liu, Z.; Yeung, K. The preconditioning and stress relaxation of skin tissue. Journal of Biomedical & Pharmaceutical Engineering 2008, Volume 2, 22-28.
  29. Silver, F.H. Biological Materials: Structure, Mechanical Properties, and Modeling of Soft Tissues. New York: New York University Press 1987, 304.
  30. Murakumo, M.; Ushiki, T.; Abe, K.; Matsumura, K.; Shinno, Y.; Koyanagi, T. Murakumo, M.; Ushiki, T.; Abe, K.; Matsumura, K.; Shinno, Y.; Koyanagi, T. Three-Dimensional Arrangement of Collagen and Elastin Fibers in the Human Urinary Bladder: A Scanning Electron Microscopic Study. The Journal of Urology 1995, Volume 154(1), 251-256.
  31. Chen, K.; Rowley, A.P.; Weiland, J.D. Elastic properties of porcine ocular posterior soft tissues. Journal of Biomedical Materials Research Part A 2010, Volume 93A(2), 634–645. [Google Scholar] [CrossRef]
  32. Wells, S.M.; Langille, B.L.; Lee, J.M.; Adamson, S.L. Determinants of mechanical properties in the developing ovine thoracic aorta. Am J Physiol. 1999, 277(4), H1385–91. [Google Scholar] [CrossRef] [PubMed]
  33. Ferrara, M; Lugano, G; Sandinha, M.T.; Kearns, V.R.; Geraghty, B. Biomechanical properties of retina and choroid: a comprehensive review of techniques and translational relevance. Eye (Lond) 2021, 35(7), 1818-1832.
  34. Korossis, S.; Bolland, F.; Southgate, J. Regional biomechanical and histological characterisation of the passive porcine urinary bladder: Implications for augmentation and tissue engineering strategies. Biomaterials 2009, 30(2), 266–275. [Google Scholar] [CrossRef] [PubMed]
  35. Hanczar, M.; Moazen, M.; Day, R. The Significance of Biomechanics and Scaffold Structure for Bladder Tissue Engineering. Int J Mol Sci. 2021, 22(23), 12657. [Google Scholar] [CrossRef] [PubMed]
  36. Zhang, X.; Husmann, D.A.; Mynderse, L.A.; Alizad, A.; Fatemi, M. Non-invasive assessment of urinary bladder compliance using ultrasound: first validation study based on clinical urodynamic study. Annals of Translational Medicine 2021, 9(7), 547–555. [Google Scholar] [CrossRef] [PubMed]
  37. Karelina, N.R.; Uvarova, E.S.; Khisamutdinova, A.R.; Zimina, M.A.; Artyukh, L.Y. Cellular spaces of the female pelvis. Russian Biomedical Research 2022, No.2, 91–101. [Google Scholar]
  38. Guimarães, C.F. , Gasperini, L., Marques, A.P. et al. The stiffness of living tissues and its implications for tissue engineering. Nat Rev Mater 2020, 5, 351–370. [Google Scholar] [CrossRef]
  39. Vraneš, H.S. , Radoš, S.N. Secular changes of pelvis in Croatian perinatal women. Homo 2014, 65(6), 509–515. [Google Scholar] [CrossRef] [PubMed]
  40. Däubler, K. Die Grundzüge der Tropenhygiene. Salzwasser Verlag GmbH 2013, 412. [Google Scholar]
  41. Kohnke, P. Ansys Mechanical APDL Theory Reference. ANSYS, Inc., SAS IP, Inc., USA 2013.
Preprints 112151 g001
Figure 1. Structure of the bladder
Figure 1. Structure of the bladder
Preprints 112151 g001
Preprints 112151 g002
Figure 2. Ultrasound of a full bladder: (a) 510 ml; (b) 420 ml (photographs get by the authors)
Figure 2. Ultrasound of a full bladder: (a) 510 ml; (b) 420 ml (photographs get by the authors)
Preprints 112151 g002
Preprints 112151 g003
Figure 3. Uniaxial testing machine for determining the mechanical characteristics of a material.
Figure 3. Uniaxial testing machine for determining the mechanical characteristics of a material.
Preprints 112151 g003
Preprints 112151 g004
Figure 4. Pattern of cutting samples from the human bladder.
Figure 4. Pattern of cutting samples from the human bladder.
Preprints 112151 g004
Preprints 112151 g005
Figure 5. Samples preparation process: (a) measurement and excision of bladder samples; (b) prepared samples (photographs got by the authors).
Figure 5. Samples preparation process: (a) measurement and excision of bladder samples; (b) prepared samples (photographs got by the authors).
Preprints 112151 g005
Preprints 112151 g006
Figure 6. Stress-strain curves of the bladder tissue. The rigid line shows the averaged deformation curve in the direction from the base to the apex and a speckled line in a perpendicular direction. The area of the RMS deviation of the true tension is marked orange. Point A is the transition point between zone 1 and 2(2’): the place of fiber stretching and hardening of biological tissue. Points B (B’) – The point of the beginning of the destruction of the biological tissue and the tension drop.
Figure 6. Stress-strain curves of the bladder tissue. The rigid line shows the averaged deformation curve in the direction from the base to the apex and a speckled line in a perpendicular direction. The area of the RMS deviation of the true tension is marked orange. Point A is the transition point between zone 1 and 2(2’): the place of fiber stretching and hardening of biological tissue. Points B (B’) – The point of the beginning of the destruction of the biological tissue and the tension drop.
Preprints 112151 g006
Preprints 112151 g007
Figure 7. The location of the bladder inside the pelvic girdle (a) and the digital model of the bladder (b): 1 - filled bladder, 2 - fiber.
Figure 7. The location of the bladder inside the pelvic girdle (a) and the digital model of the bladder (b): 1 - filled bladder, 2 - fiber.
Preprints 112151 g007
Preprints 112151 g008
Figure 8. HSFLD242 [41] geometry.
Figure 8. HSFLD242 [41] geometry.
Preprints 112151 g008
Preprints 112151 g009
Figure 8. Total deformation of the model.
Figure 8. Total deformation of the model.
Preprints 112151 g009
Preprints 112151 g011
Figure 13. Ultrasound of the bladder filled to 400 ml: (a) before the application of the load; (b) after the application of the load
Figure 13. Ultrasound of the bladder filled to 400 ml: (a) before the application of the load; (b) after the application of the load
Preprints 112151 g011
Preprints 112151 g012
Figure 14. Ultrasound of the bladder filled to 400 ml of the second volunteer: (a) before the application of the load; (b) after the application of the load
Figure 14. Ultrasound of the bladder filled to 400 ml of the second volunteer: (a) before the application of the load; (b) after the application of the load
Preprints 112151 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated