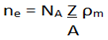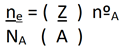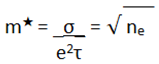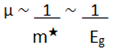Submitted:
13 July 2024
Posted:
15 July 2024
You are already at the latest version
Abstract
In this work, we will study at a basic level, a series of possible new three-dimensional monoclinic allotropes of silicon, with sp3 hybridization, of the bct type; where hexahedrons and octahedrons are combined, with other cluster shapes, with basic silicon geometries such as: triangles ( Si3 ), squares ( Si4 ), pentagons ( Si5 ) and hexagons ( Si6 ); similar to two-dimensional, sp2 hybridized graphene allotropes. Calculating its electron density, bandgap energy and electronic mobility.
Keywords:
alótropos
; materiales
; semiconductores
Introduction
Silicon, a basic semiconductor, with a cubic diamond or α - Si structure, with an indirect bandgap, which is the basis of solid-state electronics, today; because it is abundant, with good physical-chemical properties and is economical; However, it is not the best aemiconductor. This has led scientists to look for other allotropic forms of silicon, with high electronic mobility and a direct electronic bandgap, for applications in optelectronics; to replace silicon, with a diamond structure [1], in electronic applications.
As of 2010, a new form of carbon is described, tetragonal in shape, centered in the body (bct-C4) [3] with three-dimensional monoclinic structure and hybridization of chemical bonds, sp3; which is stable at normal pressure. They are made up of flat squares, composed of 4 atoms, which connect with four others, located in the upper corners; and another four, located this time, in the 4 lower corners, of an imaginary tetrahedron, since there is no direct connection, through covalent bond, between the C4 squares.
There is also a variant of the latter, bct-C8, in which, unlike the previous one, the atoms form octagonal rings in this phase. These phases are semiconductors, with an indirect bandgap of 1.66 eV.
In this work, we will study basic aspects of electronic density, effective mass, energy gap and electronic mobility, which characterize the silicon bct allotropes, similar to the different graphene allotropes; where different plane figures are combined, forming a two-dimensional mosaic of sp2 hybridization, in this case.
2. Calculation Model
The electrons that move freely through the solid, from the electrons of density, were established by the free electron gas model of Drude and Sommerfeld [4,5].
NA, is Avogadro's number or constant, Z indicates the electronic valence number, A is the atomic mass of the chemical element (in g/mol), ρm, is the mass density (mass, divided by volume) and ne, They are the conduction electrons, or number of free electrons. This is the basic equation to calculate its concentration.
For a unit cell, we can simplify the equation to the form:
In this equation, we replace the mass density, ρm, with nºA, which is the number of atoms that make up the unit cell [6].
The effective or dynamic mass of the electron is defined by the formula:
where, m*, is the effective mass of the electrons, σ, is the electronic conductivity, e, is the charge of an electron, and τ, is the Relaxation Time; which is the average time between consecutive collisions of an electron. It is an average value, since not all collisions occur at regular intervals.
There is a relationship between this effective or dynamic mass of free electrons in motion, and the forbidden energy gap or band gap [7].
And between these and electronic mobility [7], which measures the efficiency of semiconductors.
From these basic equations, we can calculate many materials.
3. Structure
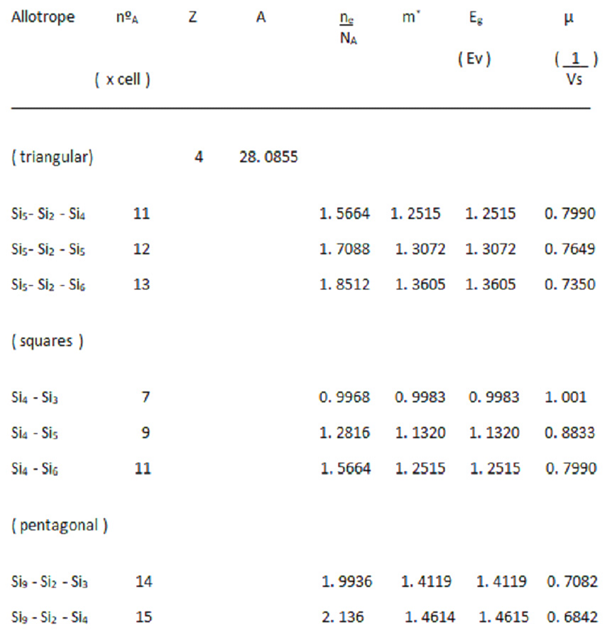
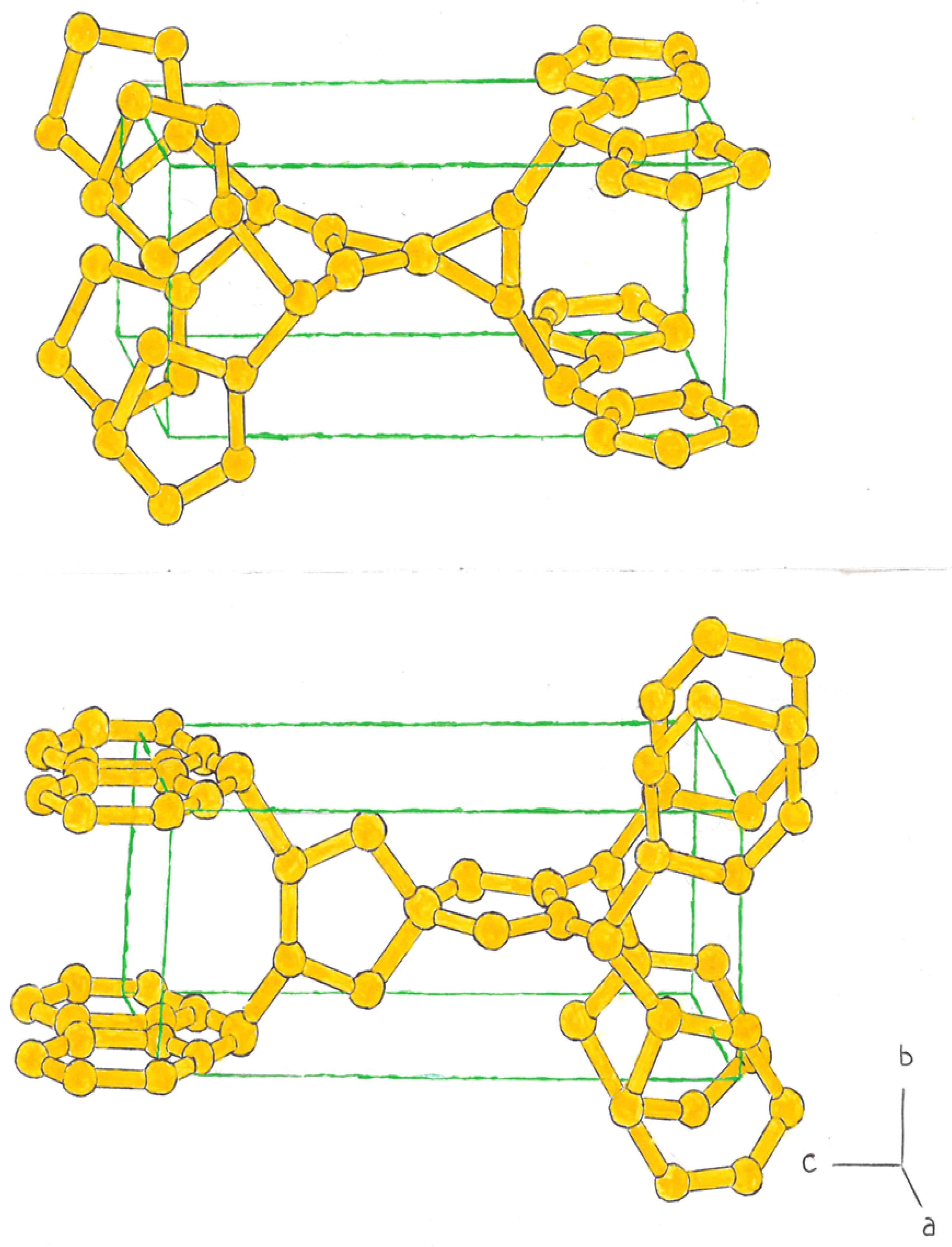
In this case, we have bcts, formed by central rings of 4 silicon atoms, combined with other rings, formed by 3, 5, or 6 atoms. (Figure 1, top).
In the second case, we have bcts, in which the central ring is formed by rings of 6 atoms, combined with rings that can be composed of 3, 4 and 5 atoms, at the ends of the imaginary tetrahedron (Figure 1, in the bottom.)
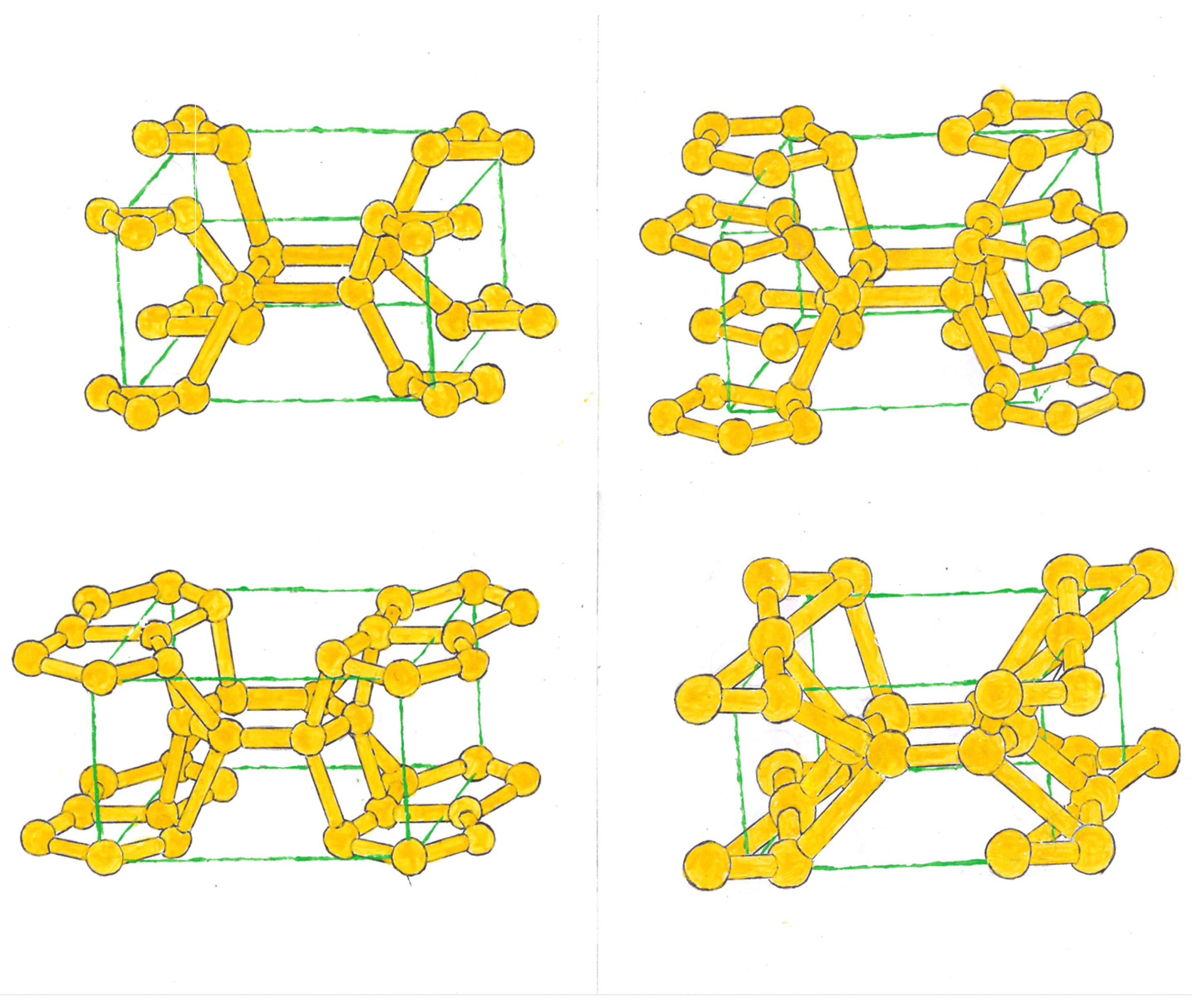
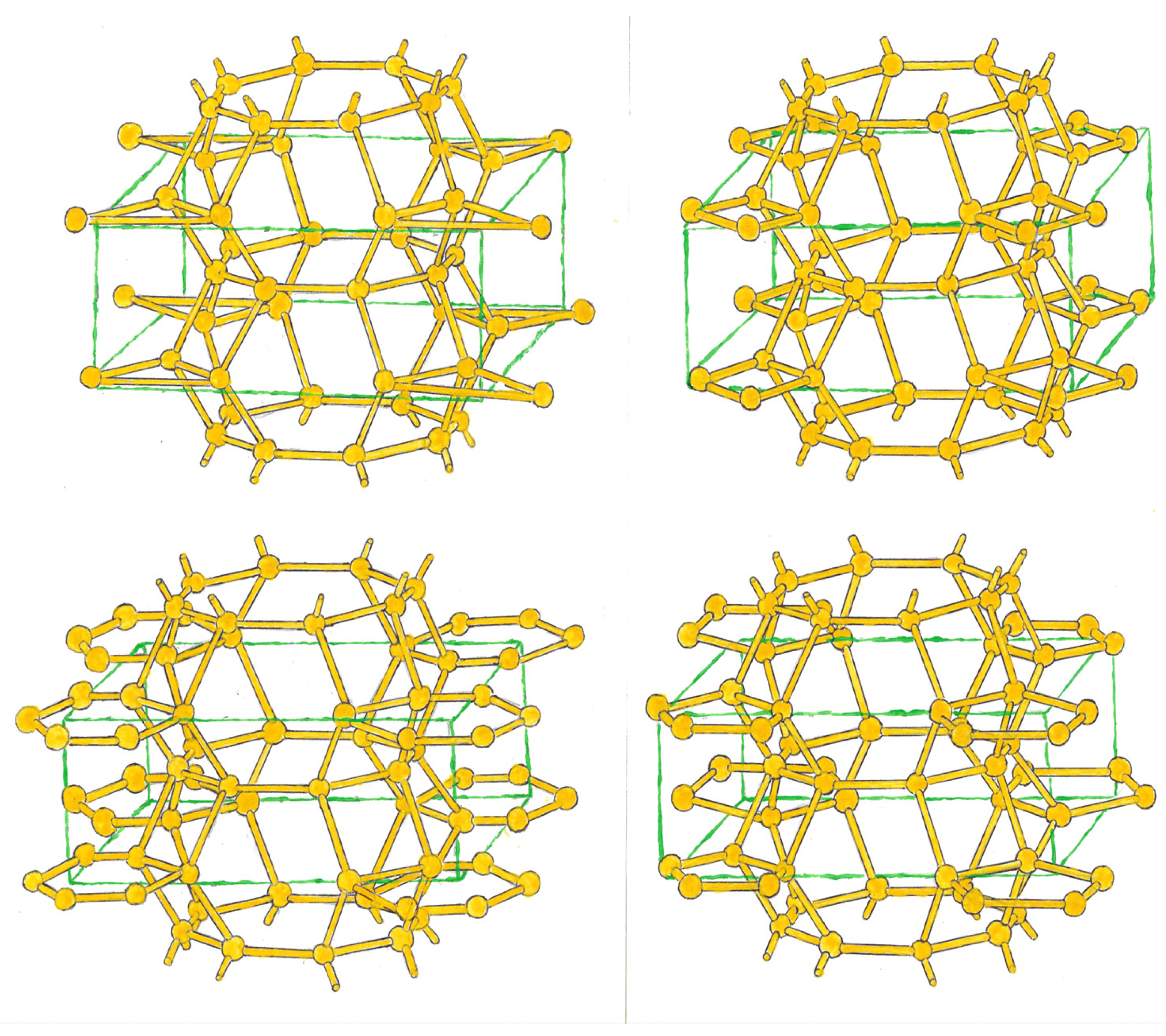
We can also form bcts, where two converging triangles link with 4 atoms, centered on the faces of an imaginary tetragon. These atoms, in turn, link with 4 rings that can be composed of 4, 5 and 6 silicon. (Figure 2, top.)
In the second group, two convergent pentagonal rings, as in the previous one, link with 4 atoms that center the faces of an imaginary tetrahedron. These atoms, in turn, can link with rings formed by 3, 4, 6, 7 and 8 atoms, which will be located at the ends of the tetrahedron. (Figure 2, at the bottom.)
Finally, a third group of bcts, formed by Si8 octahedra, can bond with rings of 3, 4, 5, 6 and 7 atoms, in an imaginary tetrahedron (Figure 3).
4. Results of Electrical Characteristics
In this work, basic calculations will be carried out for the results tables, in density of free electrons, their effective mass, as well as their mobility; that will be presented below.
Table 1.
Results of calculation of the basic electronic parameters of mixed bcts.
 |
 |
 |
Conclusions
The mixed, tetragonal, body-centered allotropes (bct), which have an energy gap closer to that of the diamond form of silicon (calc.: 1.0673, exp.: 1.1 eV), are: Si4 - Si 5, square (1, 1320 eV), and Si6 - hexagonal Si3 (1, 1320 eV). The others have an energy gap, somewhat below that reached by the atoms that form a diamond-type crystal, in the case of Si4 - Si3; with an Eg of 0.9983 eV; the triangular Si6 - Si3, the hexagonal Si6 - Si5 and the octagonal Si8 - Si3 (1, 2515 eV), are a little away from the energy gap of diamond. Others such as the hexagonal Si6 - Si4 (1, 1933 eV); Si5 - Si5 -Si2, triangular (1, 3072 eV), Si8 - Si6, octagonal (1, 4119 eV), or Si9 - Si5 - Si2, pentagonal (1, 5094 eV), are already further from the gap energy Eg, of the diamond. Other allotropes such as the hexagonal or lonsdaleite form of silicon, Si-4H, have an energy gap (Eg) of 1.2 eV.
References
- Where Does the Density Localize in the Solid State? Divergent Behavior for Hybrids and DFT+U. Qing Zhaoand Heather J. Kulik. Journal of Chemical Theory and Computation ( JCTC ).
- A Review on Metastable Silicon Allotropes. Linlin Fan,Deren Yang and Dongsheng Li, MDPI, 15 July 2021.
- Carbon-allotropes-metal-complex-chemistry-properties-and-applications-1st-ed, Chapter 6. Predicted Carbon Forms. 6.4 bct-Carbon 4 page 402.
- Kittel, Introduction to Solid State Physics, 7th Ed. Chapter 6 Free Electron Fermi Gas.
- vol-1-tipler-mosca-solucionario. Chapter 38.Solids and the Theory of Conduction. Page 2786.
- Combined theoretical and experimental characterizations of semiconductors for photoelectrocatalytic applications. Tangui Le Bahers and Kazuhiro Takanabe. ( Pág. 34 ).
- Analysis of Electron Mobility in Some " Problematic Materials " from Magnetoresistance E ect at High Magnetic Fields. V.V. Shchennikov, A.E. Kar'kin, , S.V. Ovsyannikov and N.V. Morozova.
- Predicted Carbon Forms. Carbon Allotropes: Metal-Complex Chemistry, Properties and Applications pp 375–411. Boris Ildusovich Kharisov & Oxana Vasilievna Kharissova. Springer, 2019.
- Body-centered tetragonal C4: a viable sp3 carbon allotrope. K. Umemoto, R. Wentzcovitch, Published in Physical Review Letters 26 March 2010. Materials Science, Physics.
- First-principles investigation in the Raman and infrared spectra of sp3 carbon allotropes. Ying Bai, Xiaoyan Zhao, Tongwei Li, Zhenlong Lv, Shijie Lv, Han Han, Yanfeng Yin, Hui Wang. El Sevier, Carbon, Volume 78, November 2014, Pages 70-78.
- A triatomic carbon and derived pentacarbides with superstrong mechanical properties. Bingcheng Luo, Longwen Wu, Zili Zhang, Guowu Li, Enke Tian. iScience, Volume 25, Issue 8, 19 August 2022.
- Graphene allotropes under extreme uniaxial strain: an ab initio theoretical study. Zacharias G. Fthenakis and Nektarios N. Lathiotakis. Physica Chemistry Chemical Physics, Royal Society of Chemistry ( RSC ) publishing, 25 /2015.
- A computational study on the mechanical properties of Pentahexoctite single-layer: Combining DFT and classical molecular dynamics simulations. W.H.S. Brandão, A.L. Aguiar, L.A. Ribeiro Júnior, D.S. Galvão, J.M. De Sousa. El Sevier,.
- Origin of anisotropic negative Poisson's ratio in graphene. Zhenzhen Qin, G. Qin, Ming Hu. Published in Nanoscale 7 June 2018. Materials Science, Physics. RSC Publishing. https://www.researchgate.net/publication/325123787_Origin_of_anisotropic_negative_Poisson's_ratio_in_graphene.
- New insights into the structure-nonlinear mechanical property relations for graphene allotropes. Hao Sun, Sankha Mukherjee, Matthew Daly, Ajay Krishnan, Manohar Harsha Karigerasi d, Chandra Veer Singh. El Sevier, 10 September 2016.
- Semiconducting allotrope of graphene. Jawad Nisar, Xue Jiang, Biswarup Pathak1, Jijun Zhao, Tae Won Kang and Rajeev Ahuja, Nanotechnology, Volume 23, Number 38. Published 4 September 2012 • © 2012 IOP Publishing Ltd.
Figure 1.
Mixed Silicon Bcts. Bct Si4: Si4 - Si3, ( Si7 ) and Si4 - Si5, ( Si9), at the top; and bct Si6: Si6 - Si5, ( Si11 ) and Si6 - Si3, ( Si9 ), at the bottom.
Figure 1.
Mixed Silicon Bcts. Bct Si4: Si4 - Si3, ( Si7 ) and Si4 - Si5, ( Si9), at the top; and bct Si6: Si6 - Si5, ( Si11 ) and Si6 - Si3, ( Si9 ), at the bottom.
Figure 2.
Mixed Bcts. Bct Si5: Si5 - Si2 - Si5 ( Si12 ), ( pentagons ), at the top; and bct Si8 - Si2 - Si6, ( Si16 ), at the bottom.
Figure 2.
Mixed Bcts. Bct Si5: Si5 - Si2 - Si5 ( Si12 ), ( pentagons ), at the top; and bct Si8 - Si2 - Si6, ( Si16 ), at the bottom.
Figure 3.
Mixed Bcts, Si8: Si8 - Si3, ( Si11 ); Si8 - Si4, ( Si12 ); Si8 - Si5, ( Si13 ) and Si8 - Si6, ( Si14 ).
Figure 3.
Mixed Bcts, Si8: Si8 - Si3, ( Si11 ); Si8 - Si4, ( Si12 ); Si8 - Si5, ( Si13 ) and Si8 - Si6, ( Si14 ).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
