Quarks and Leptons Formation from the Spontaneous Fractionation of a Pair of Elementary Particles with Proton Charge Units

Preprint

Article

Quarks and Leptons Formation from the Spontaneous Fractionation of a Pair of Elementary Particles with Proton Charge Units

Altmetrics

Downloads

Views

Comments

Massimo Auci^*

This version is not peer-reviewed

Submitted:

13 July 2024

Posted:

16 July 2024

You are already at the latest version

Alerts

Abstract

It is shown that if there exists in nature a pair of heavy elementary particles each with a charge equal to that of the proton and with mass energy , then their direct interaction gives rise to a spontaneous fractionation of the two charges into three pairs of elementary particles according to two equiprobable channels, one hadronic and one leptonic. The leptons and quarks produced are in agreement with the first generation of the Standard Model of matter. Fractionation suggests the relative abundances of the elementary particles, introducing some questions about the possibility of the real existence of a currently unknown particle and its role in the formation of an apparent matter-antimatter asymmetry in the universe.

Keywords:

Subject: Physical Sciences - Particle and Field Physics

1. Introduction

In the Standard Model (SM) the origin of the fractionary charges of quarks and nature of neutrinos are currently a thick mystery. In this work is proposed a simple model developed in the Bridge Theory (BT) context [1-2] able to propose a justification to the existence in nature of the quarks, electrons and neutrinos starting from an unknown particle that could be produced in the universe. The BT derives from a phenomenology described in the reference [3] and [4] according to which a pair of particles, independently by their value of charge

\pm q

, interacting produce a Dipole Electromagnetic Source (DEMS) which localizes in the source zone an energy

h^{*} c / λ

and a momentum

h^{*} / λ

in agreement with that one of a pseudo-photon of wavelength equal to the minimum interaction distance achieved by the particles. The action associated with such a direct interaction is

h^{*} = 2 π σ q^{2} / c

, with

σ

equal to the reciprocal value of the value of the Sommerfeld constant for the first time calculated theoretically in Ref. [5] and recently in the context of the hydrogen atomic model in Ref. [6]. Following the phenomenological approach of the BT, the present model proposes the possibility that a pair of charged particles with opportune characteristics can be spontaneously fractioned producing the elementary particles characterizing the SM.

In this article we will show that the pair of particle with units of electric charge

(Q = e^{†}, \bar{Q} = - e^{†})

equal to that of the proton, if attributed to a pair of heavy elementary leptons that interacting originate a DEMS as described in BT, provided that they have sufficient interaction energy to give rise to the up and down quarks to form a pair proton-antiproton, i.e.

E \geq 2 m_{p} c^{2}

, it undergoes a spontaneous fractionation along two equiprobable channels giving rise to two distinct groups of three pairs of elementary particles.

The first group consists of three pairs of fractional charges in the quark-antiquark form

Q \bar{Q} \to u \bar{u} + 2 d \bar{d}

while the second group consists in three pairs of leptons, one pair electron-positron and two pairs of neutrinos in the form

Q \bar{Q} \to e \bar{e} + 2 ν \bar{ν}

. In this model the neutrinos must got an extremely weak but not zero electric charge because they must be able to interact electromagnetically also if weakly with the other matter, thus the electron and positron consequently have a lower charge value than that of the original unit from which they are derived

e < e^{†}

. Below we will show how both fractional charge groups describe the particles in accordance with the first generation of elementary particles of the Standard Model.

2. Structure Function of Two Interacting Charge Fragment

In this model the BT (See Ref. [1] and [2]) is partially used to propose an explanation to the origins of quarks and leptons in the universe. Starting from the BT principle that all the DEMS produced by the direct electromagnetic interaction of a pair of particles with elementary charge

\pm e

are directly associated with a Dirac unit of Planck action

ℏ = σ \frac{e^{2}}{c}

(1)

with

c

speed of light,

e

electron charge unit and

σ

reciprocal value of the Sommerfeld constant

α

theoretically calculated (Cf. Ref. [1]) by using the structure function of the transversal component of the Poynting vector of the electromagnetic field of the DEMS

\begin{matrix} Θ_{t} (ρ, θ) = 16 \sqrt{\frac{1}{{(4 + ρ^{2} + 4 ρ \cos θ)}^{2}} + \frac{1}{{(4 + ρ^{2} - 4 ρ \cos θ)}^{2}} + \frac{2 (4 - ρ^{2})}{\sqrt{{[{(4 + ρ^{2})}^{2} - 16 ρ^{2} \cos^{2} θ]}^{3}}}} \\ \cdot | \frac{(2 + ρ \cos θ)}{\sqrt{{(4 + ρ^{2} + 4 ρ \cos θ)}^{3}}} + \frac{(2 - ρ \cos θ)}{\sqrt{{(4 + ρ^{2} - 4 ρ \cos θ)}^{3}}} | . \end{matrix}

(2)

In Gauss units the theoretical value of action (1) for an interaction between a pair of heavy elementary unknown X-particles with proton-antiproton electric charge

\pm e^{†}

is given by

ℏ = (\frac{4 π}{3} \int_{0}^{π} Θ_{t} (ρ, θ) d θ + \frac{1}{4 π ρ^{2}}) \frac{e^{† 2}}{c}

(3)

The value of the constant (3) depends from the structure function (2) varying with the ratio

ρ = R / λ

between the dipole moment length per unit of charge

R

and the wavelength

λ

of the DEMS.

For a free electromagnetic interaction between a pair of charged particles, i.e., without external constrains acting on the DEMS, the ratio acquires a precise estimated value

ρ^{*} = 1.275556618599942

giving a value of the structure constant

σ^{*} = 137.035989

(See Ref. [1]) independently by the value of the charge of the pair of the interacting particles.

Each external constraint acting on the pair during their direct interaction produces a variation of the value of the ratio

ρ

and consequently of the structure constant (Cf. Ref. [6]).

Considering a pair

Q \bar{Q}

, in this work one assumes that when the charges interact produce a DEMS corresponding to a growing electromagnetic spherical bubble delimited by the emitted spherical wave of wavelength

λ

in which the spontaneous fragmentation of the pair occurs dividing the primitive electromagnetic bubble into three cells, each of which acts as a sub-DEMS produced by the interaction of a pair of fractional charges

C_{i} = + χ_{i} e^{†}

and

{\bar{C}}_{i} = - χ_{i} e^{†}

, where

\pm χ_{i}

with

i = 1, 2, 3

are the fractional dimensionless charges such a that

0 < | χ_{i} | < 1

, with product of the pair of unitary charges generators

Q \bar{Q}

given by

| Q \bar{Q} | = \sum_{i} | C_{i} {\bar{C}}_{i} | = e^{†} ​^{2} \sum_{i} | χ_{i} {\bar{χ}}_{i} |

(4)

Using the Eq. (1) for the unit of charge

| e^{†} |

, the absolute value of action of each pair of charge fractions at the vary of the ratio

ρ

yields

| h_{{\bar{C}}_{i} C_{i}} (ρ) | = 2 π | σ_{{\bar{χ}}_{i} χ_{i}} | \frac{e^{†} ​^{2}}{c}

(5)

with

σ_{{\bar{χ}}_{i} χ_{i}} = (\frac{4 π}{3} \int_{0}^{π} Θ_{t} (ρ, θ) d θ + \frac{1}{4 π ρ^{2}}) χ_{i}^{2} = σ χ_{i}^{2}

(6)

structure constant of the single cell.

For any possible interaction

C_{i} C_{j}

also with different value of charge, the structure constant (6) acquires the general form

σ_{χ_{i} χ_{j}} = (\frac{4 π}{3} \int_{0}^{π} Θ_{t} (χ_{i}, χ_{j}, ρ, θ) d θ + \frac{χ_{i} χ_{j}}{4 π ρ^{2}})

(7)

with transversal component of the structure function of the Poynting vector

\begin{matrix} Θ_{t} (χ_{i}, χ_{j}, ρ, θ) = 16 \sqrt{\frac{χ_{i}^{2}}{{(4 + ρ^{2} + 4 ρ \cos θ)}^{2}} + \frac{χ_{j}^{2}}{{(4 + ρ^{2} - 4 ρ \cos θ)}^{2}} + \frac{2 χ_{i} χ_{j} (4 - ρ^{2})}{\sqrt{{[{(4 + ρ^{2})}^{2} - 16 ρ^{2} \cos^{2} θ]}^{3}}}} \\ \cdot | \frac{χ_{i} (2 + ρ \cos θ)}{\sqrt{{(4 + ρ^{2} + 4 ρ \cos θ)}^{3}}} + \frac{χ_{j} (2 - ρ \cos θ)}{\sqrt{{(4 + ρ^{2} - 4 ρ \cos θ)}^{3}}} | \end{matrix}

(8)

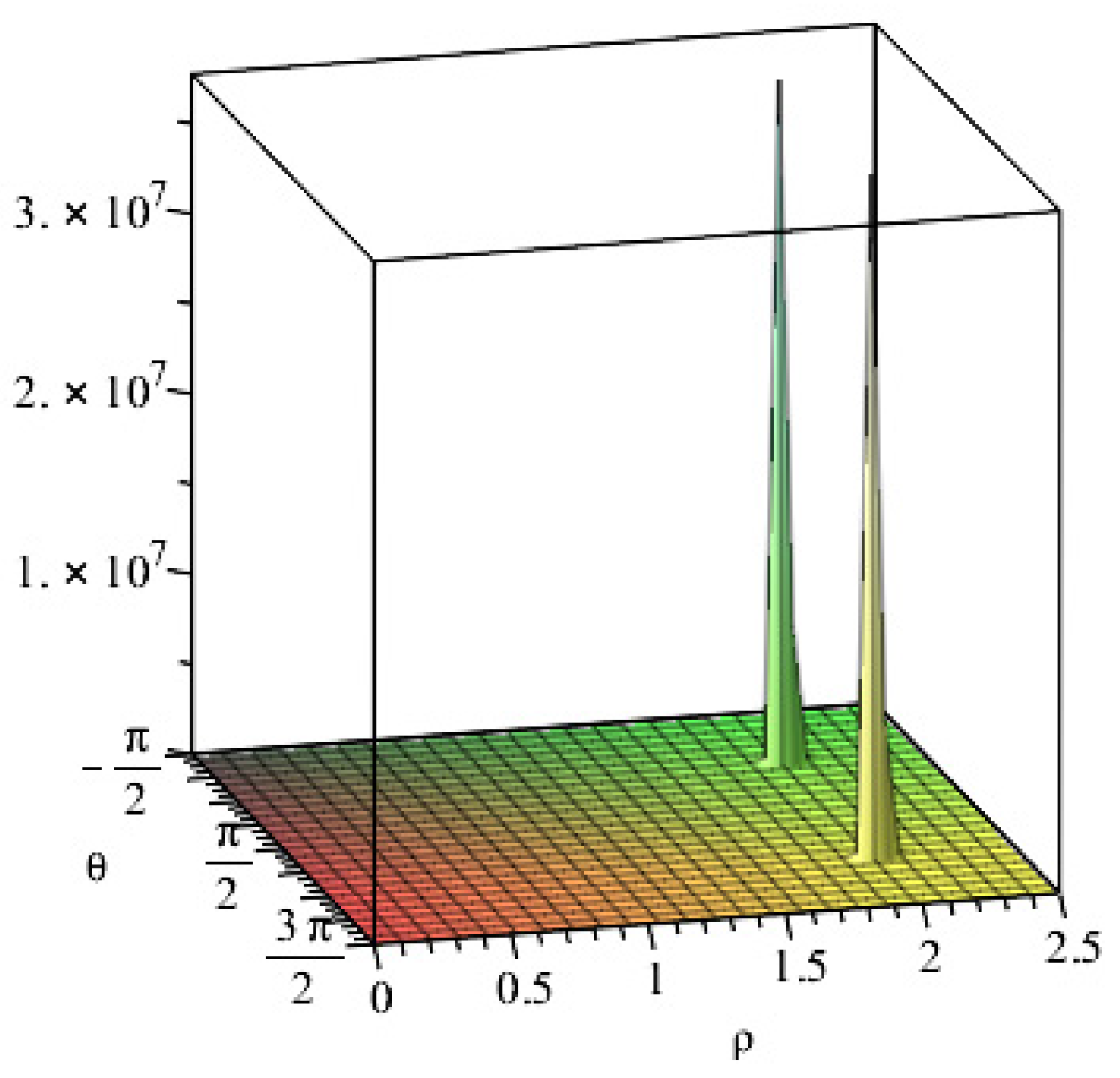
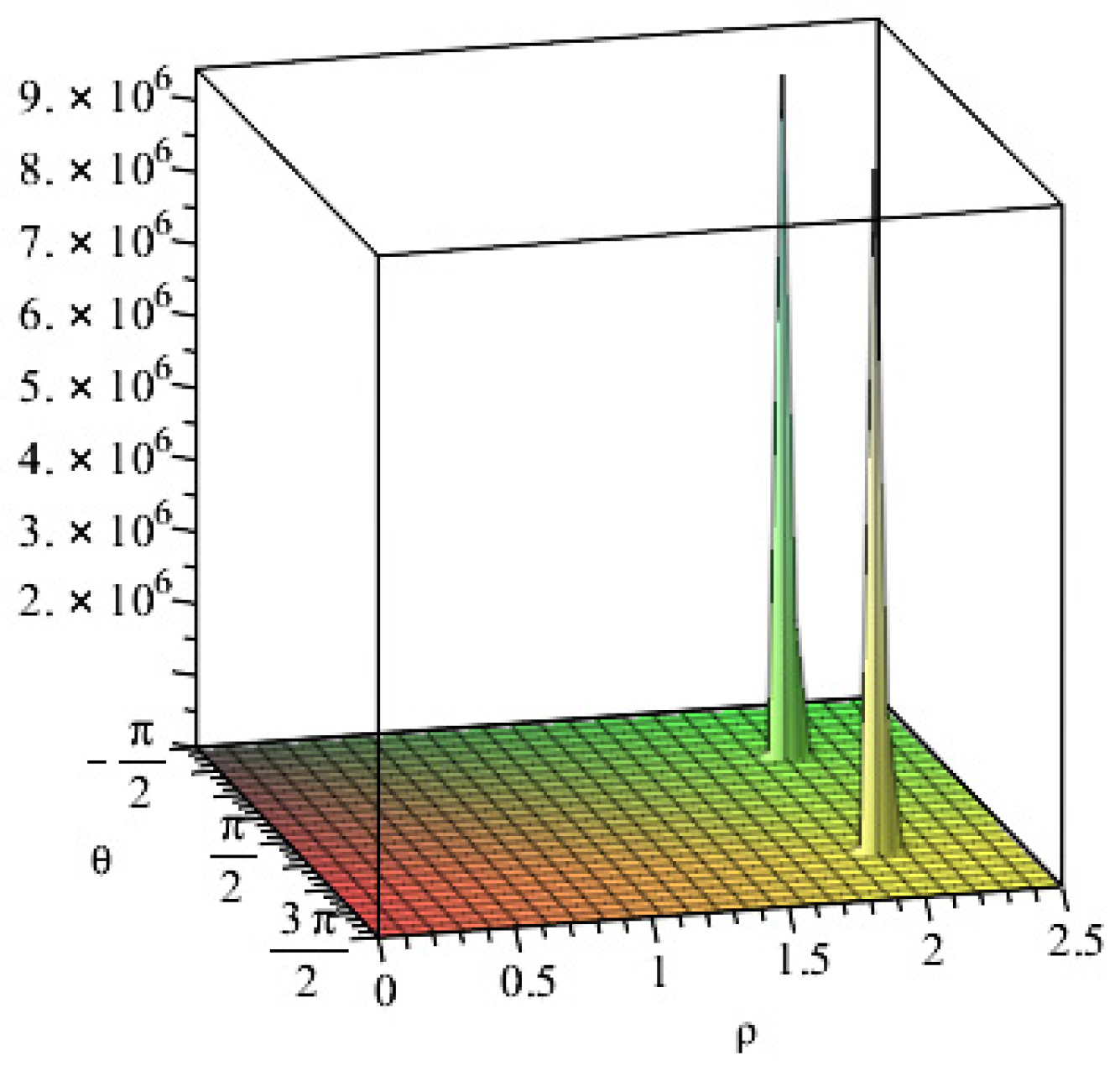
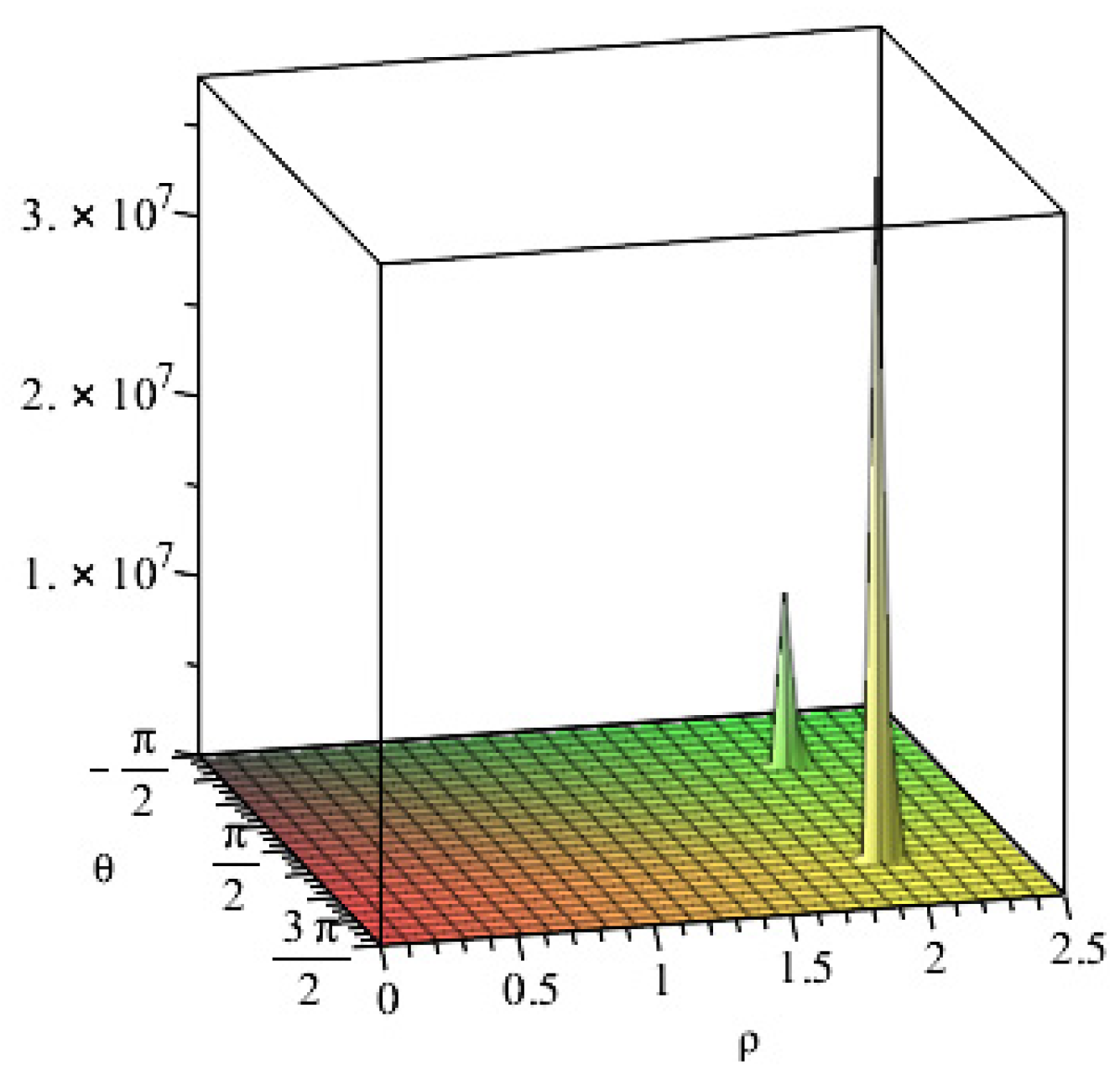
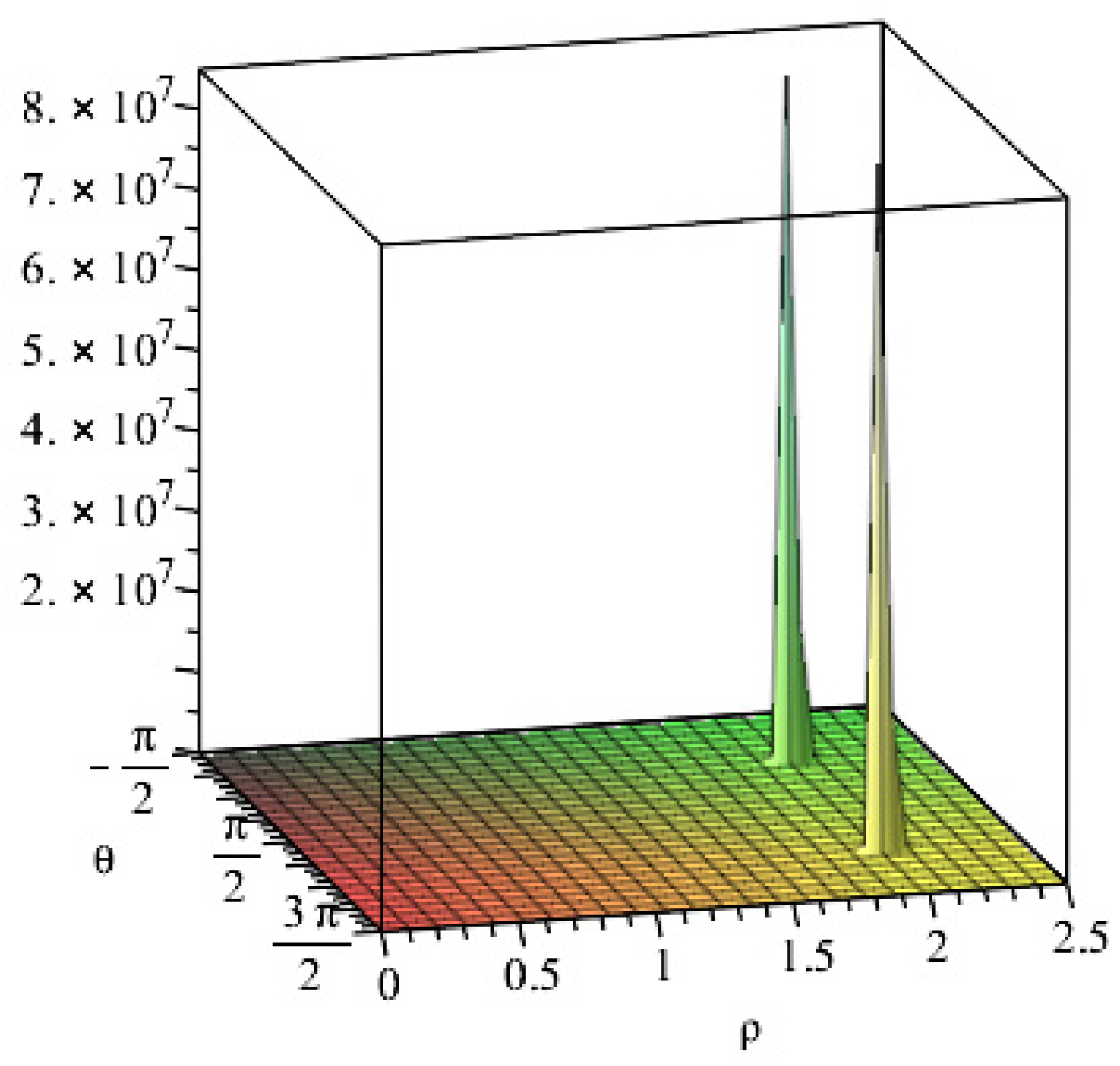
The application of Eq. (8) allows to estimate the structure constants for each pair of integer or fractional charges existing in nature. In the (Fig. 1a-b-c-d) are shown the structure functions (8) for some particular cases.

3. The Laws of Conservation of the DEMS and Fragmentation of Unitary Electric Charges

By considering:

A - the principle of conservation of the total action (3) of the original DEMS obtained by a pair of particles of charge

Q \bar{Q}

;

B - the conservation of the charge of a single interacting particle;

C - introducing the empirical observation that in nature protons are formed by two quarks with a same value of charge;

the DEMS produced by the original pair of generators

Q \bar{Q}

must satisfying the three conditions:

-: Using equations (4-6) the total action of the three cells must be equal to the total action of the primary bubble

$\sum_{i}^{n} χ_{i} ^{2} = 1$

(9)
-: The total fractional charge must be equal to that original:

$\sum_{i}^{n} χ_{i} = \pm 1$

(10)
-: Two of the three charge fragments must have equal value, as it is observed in the proton structure: $χ_{2} = χ_{3}$ .

To maintain the validity of the three previous conditions summarized by the system:

{\begin{matrix} χ_{1}^{2} + χ_{2}^{2} + χ_{3}^{2} = 1 \\ χ_{1} + χ_{2} + χ_{3} = \pm 1 \\ χ_{2} - χ_{3} = 0 \end{matrix}

(11)

the charges are divided into three elementary cells by providing two sets of solutions for each of the two signs of the charge generator:

(\begin{matrix} \mp \frac{1}{3}, & \pm \frac{2}{3}, & \pm \frac{2}{3} \end{matrix})

(12)

and

(\begin{matrix} \mp 1, & 0, & 0, \end{matrix})

(13)

In order to analyze the meaning of the solutions achieved one define as hadronic the solutions in which we have three fractional values of the generator in agreement with the existence of two flavors of quarks

H = (\mp \frac{1}{3}, \pm \frac{2}{3}, \pm \frac{2}{3})

(14)

and leptonic the solutions (13) assuming that the three particles in addition to the charge value have a charge tendency, i.e. that the unit of charge is not exactly equal to one and that the charges zero are not exactly zero. The superscriptions

(\pm)

at right of the values with its multiplicity expresses the sign of the charge tendency defined by arbitrary choice with the opposite sign to the electric charge, this does not define the value of the charge tendency but represents how each charge value exceeds or is lower than that assigned by the solution justifying also in the leptonic solution the fractioning principle

L = (\mp 1^{(\pm \pm)}, 0^{(\mp)}, 0^{(\mp)})

(15)

Considering that the tendency changes in signs if the sign of the unitary generator changes, charge tendency allows to all the cells has got a part of the total energy of the primordial DEMS allowing them to evolve energetically. It is important to highlight that in this model all neutral interactions to conserve the total charge must have null tendency, in general the sum of the charges tendency of the particles involved in the reaction channel must have before and after the reaction the same tendency. For the solution (15) the proton must have a value of charge a bit greater than the unit charge of the electron for coherence

e^{†} > e

by reopening a discussion on the neutrality of atoms and molecules [4].

4. Use of the Solutions L and H to Build the First Generation of the Elementary Particles

To analyze the composition in particles derived from the generators

\pm e^{†}

, using solutions (14) and (15) the charge values can be organized into two

2 \times 3

matrices. In column, particle-antiparticle pairs are arranged so that all solutions with the same charge mark appear on the same row. Each matrix is pure, that is, it contains all six elements associated with all the leptons or all the quarks respectively. To simplify the understanding of the formalism with which are denoted the particles, the symbols

e, \bar{e}

to denote electron and antielectron (positron),

ν, \bar{ν}

for electronic neutrino and antineutrino and the symbols

u, d

of the quarks up and down and

\bar{u}, \bar{d}

for the corresponding antiparticles.

Considering the pure leptonic solution

L = (\begin{matrix} L \\ \bar{L} \end{matrix})

, as (15) requires, the pairs of neutrinos cannot have a null fraction charge, i.e., their cells cannot have null energy:

L = (\begin{array}{l} \begin{matrix} + 1^{(- -)} & 0^{(+)} & 0^{(+)} \end{matrix} \\ \begin{matrix} - 1^{(+ +)} & 0^{(-)} & 0^{(-)} \end{matrix} \end{array}) \Leftrightarrow (\begin{array}{l} \begin{matrix} \bar{e} & ν & ν \end{matrix} \\ \begin{matrix} e & \bar{ν} & \bar{ν} \end{matrix} \end{array})

(16)

Eq. (16) put in evidence that in terms of solutions

L

and

\bar{L}

, the negative electron

e

usually considered as a particle would be defined more properly as an antiparticle because it appears in the row

\bar{L}

obtained using the anti-generator

\bar{Q} = - e^{†}

. On the other hand, a switched definition exchanging neutrinos with antineutrinos would be in contrast with all the definitions of physics we know, therefore we maintain the same definitions, but we will see later in the conclusions how this consideration could change our view of the universe.

Analogously for the pure hadronic solution

H = (\begin{matrix} H \\ \bar{H} \end{matrix})

in which appear three pairs of quarks

H = (\begin{array}{l} \begin{matrix} - \frac{1}{3} & + \frac{2}{3} & + \frac{2}{3} \end{matrix} \\ \begin{matrix} + \frac{1}{3} & - \frac{2}{3} & - \frac{2}{3} \end{matrix} \end{array}) \Leftrightarrow (\begin{array}{l} \begin{matrix} d & u & u \end{matrix} \\ \begin{matrix} \bar{d} & \bar{u} & \bar{u} \end{matrix} \end{array})

(17)

In this case, the tendency of the fractional charge value of hadrons was not reported because hadrons unlike neutrinos have enough charge to interact with each other and the determination of their charge tendency could only be derived from the study of their behavior during interaction in groups of particles. In this work, it is sufficient to hypothesize that there is a fractionation mechanism that leads the hadron charges not to have exactly the same value, therefore to have more or less marked positive or negative trends.

This mechanism could define the color charge of quarks allowing direct interaction between quarks of the same type, an example would be

({\frac{2}{3}}^{(-)}, {\frac{2}{3}}^{(- -)}, - {\frac{1}{3}}^{(+ + +)})

which for example can be considered equivalent to u-RED, u-GREEN and d-BLUE, in such a way that the resulting proton

u u d

formed by the three quarks taken together can form a unitary charge particle with zero tendency in agreement with QCD and with a charge only a bit greater than the electron one.

Particularly interesting is a mixed matrices

M = (\begin{matrix} H \\ \bar{L} \end{matrix})

and its symmetric

\bar{M}

obtained with a mixing of compatible solutions H and L:

M = (\begin{array}{l} \begin{matrix} - \frac{1}{3} & + \frac{2}{3} & + \frac{2}{3} \end{matrix} \\ \begin{matrix} - 1^{(+ +)} & 0^{(-)} & 0^{(-)} \end{matrix} \end{array}) \Leftrightarrow (\begin{array}{l} \begin{matrix} d & u & u \end{matrix} \\ \begin{matrix} e & \bar{ν} & \bar{ν} \end{matrix} \end{array})

(18)

\bar{M} = (\begin{matrix} \begin{matrix} + \frac{1}{3} & - \frac{2}{3} & - \frac{2}{3} \end{matrix} \\ \begin{matrix} + 1^{(- -)} & 0^{(+)} & 0^{(+)} \end{matrix} \end{matrix}) \Leftrightarrow (\begin{array}{l} \begin{matrix} \bar{d} & \bar{u} & \bar{u} \end{matrix} \\ \begin{matrix} \bar{e} & ν & ν \end{matrix} \end{array})

(19)

In this case one could have the coexistence in a same bubble of a proton or antiproton and of three leptons violating the principle of creation in pairs of the particles associated to the sub-DEMS. That can be possible if an electromagnetic bubble is formed by using two different fractional solutions, one hadronic and one leptonic, in this case the mixed bubble does not violate the invariance of the total charge, of the spin of the bubble and does not violate also the sum of the baryon and lepton numbers

B + L = 0

(20)

but violate the energy and action conservation, in fact, Eq. (11) and solutions (12) and (13) show that the process of fractionation of a heavy charged pair is invariant in energy and action only if fractionation occurs in symmetrical pairs. On the other hand, the asymmetric fractionation characterizing the mixed solutions (18) and (19) suggests that with the different charged particles collected in the X-matrix

Χ = (\begin{matrix} {\begin{matrix} - 1^{(+ +)} & 0^{(-)} & 0 \end{matrix}}^{(-)} \\ \begin{matrix} + 1^{(- -)} & 0^{(+)} & 0^{(+)} \end{matrix} \\ \begin{matrix} - \frac{1}{3} & + \frac{2}{3} & + \frac{2}{3} \end{matrix} \\ \begin{matrix} + \frac{1}{3} & - \frac{2}{3} & - \frac{2}{3} \end{matrix} \end{matrix}) \Leftrightarrow (\begin{matrix} \begin{matrix} e & \bar{ν} & \bar{ν} \end{matrix} \\ \begin{matrix} \bar{e} & ν & ν \end{matrix} \\ \begin{matrix} d & u & u \end{matrix} \\ \begin{matrix} \bar{d} & \bar{u} & \bar{u} \end{matrix} \end{matrix})

(21)

a direct electromagnetic interaction that forms a DEMS is invariant in energy and action only considering pairs of charges formed by clusters obtained by aggregating different elementary particles arranged in the X-matrix (21), each corresponding to a non-elementary particle.

Extending these considerations, charge clusters can be produced using the elementary particles in the matrix (21) in such a way that the initial charge values can be reproduced forming new non-elementary particles as for example

p \equiv u u d

\bar{p} \equiv \bar{u} \bar{u} \bar{d}

π^{+} \equiv u \bar{d}

π^{-} \equiv \bar{u} d

, but there is also the possibility of produce heavy clusters with fractional charges as

{\bar{d}}^{†} = d \bar{d} \bar{d}

{\bar{d}}^{*} = u \bar{u} \bar{d}

and

d^{†} = d \bar{d} d

d^{*} = u \bar{u} d

{\bar{u}}^{†} = d \bar{d} \bar{u}

{\bar{u}}^{*} = u \bar{u} \bar{u}

and

u^{†} = d \bar{d} u

u^{*} = u \bar{u} u

. These clusters and other possible could be connected to quarks belonging to the second and third generation using more elementary particles. In this sense, generations subsequent to the third would also be possible differing from previous generations only in energy content. This mode is the only one that can be used to keep the charge and action unchanged during the formation of a DEMS between pairs of charged clusters, so it is possible to think that the particles can be aggregated by means of charge clusters that necessarily have different energy and more mass because they are formed by a different number of active sub-DEMS.

Equation (21) puts in evidence a perfect symmetry in particles-antiparticles primary production with an abundance of two neutrinos for each hydrogen atom and two antineutrinos for each antihydrogen atom. Considering that at the current stage is not yet possible to know where and when antihydrogen disappear, starting from Eq. (21) could be interesting in the future to try to draw possible all possible scenario able to describe the current situation.

In Figure 1 are shown the structure functions associated with the direct interaction between fractional and integer charged particles.

Figure 1a. structure function (8c) for the direct interaction of pairs

u u, u \bar{u}, \bar{u} \bar{u}

Figure 1a. structure function (8c) for the direct interaction of pairs

u u, u \bar{u}, \bar{u} \bar{u}

Figure 1b. structure function (8c) for the direct interaction of pairs

d d, d \bar{d}, \bar{d} \bar{d}

Figure 1b. structure function (8c) for the direct interaction of pairs

d d, d \bar{d}, \bar{d} \bar{d}

Figure 1c. structure function (8c) for the direct interaction between two different particles

u d, \bar{u} d, u \bar{d}, \bar{u} \bar{d}

Figure 1c. structure function (8c) for the direct interaction between two different particles

u d, \bar{u} d, u \bar{d}, \bar{u} \bar{d}

Figure 1d. structure function (8c) for the direct interaction of pairs

e e, e \bar{e}, \bar{e} \bar{e}

Figure 1d. structure function (8c) for the direct interaction of pairs

e e, e \bar{e}, \bar{e} \bar{e}

4. Conclusions

In this article, starting from the principle of conservation of action and electric charge, is proposed a model of fractionation of the fundamental unit of charge which is assumed to be that of the proton.

The calculus is able to predict the existence of the first generation of elementary particles of the Standard Model in charge terms, but at the current stage not their mass. Since in BT an elementary particle can have interaction with other particles only electromagnetically, that occurs only if it has electric charge and consequently mass, therefore, all particles must have charge and mass. The neutrinos charge must be of course very weak and currently this value is unevaluated [7].

As a result of the model application, the positron has a unit of charge only slightly lower than that of the proton, the difference of which is instrumentally difficult to assess [8].

The introduction of the charge tendency to attribute a weak charge to the neutrino suggests a useful mechanism that explains the existence of the color charge of quarks, giving in this case the possibility for two apparently identical particles to interact by binding to each other.

Finally, it may be interesting to consider that following the logic of the model, matter and antimatter would have as a distinctive characteristic the sign of the charge generator, when the sign is positive the fractionation produces particles, when the sign is negative the fractionation produces antiparticles. So the electron would be the antiparticle of the positron, this for a hydrogen-filled universe means that there are as many protons as electrons, so since the proton is made up of three quarks

u u d

defined all as particles and one electron defined as antiparticle, defining a number of symmetry matter-antimatter

M = \pm 1

, a hydrogen atom would be formed by a particle (proton) with

M = 1

and an antiparticle (electron) with

M = - 1

, unless the negligible presence of neutrinos and antineutrinos in pairs, this would solve the problem of matter-antimatter asymmetry in the universe in conceptual terms in fact, for hydrogen

M = 0

Funding Statement

This study is not supported by grant.

Data Availability Statements

The presented article is not associated with any experimental data nor with theoretical data calculated using models. All necessary data is present in the text or associated references.

Conflict of Interest declaration

The author declare that they have NO affiliations with or involvement in any organization or entity with any financial interest in the subject matter or materials discussed in this manuscript.

Ethical Conduct

In these studies, no procedures involved human participants.

References

M. Auci, G. Dematteis. “An approach to unifying classical and quantum Electrodynamics”. Int. Journal of Modern Phys. B13, 1525 (1999). [CrossRef]
M. Auci. “Superluminality and Entanglement in an Electromagnetic Quantum-Relativistic Theory”. Journal of Modern Physics, 9, 2206-2222 (2018). [CrossRef]
M. Auci. “A conjecture on the physical meaning of the transversal component of the pointing vector”. Phys. Lett. A 135, 86 (1989). [CrossRef]
M. Auci. “A conjecture on the physical meaning of the transversal component of the Poynting vector. II. Bounds of a source zone and formal equivalence between the local energy and the photon.” Phys. Lett. A 148, 399 (1990). [CrossRef]
M. Auci. “A conjecture on the physical meaning of the transversal component of the Poynting vector. III. Conjecture, proof and physical nature of the fine structure constant”. Phys. Lett. A 150, 143 (1990). [CrossRef]
M. Auci. “Estimation of an absolute theoretical value of the Sommerfeld’s fine structure constant in the electron–proton capture process”. Eur. Phys. J. D 75, 253 (2021). [CrossRef]
S. Batkin and M. K. Sundaresan. “A new method to improve the limit on the electric charge of the neutrino”. J. Phys. G: Nucl. Part. Phys. 20 1749 (1994). [CrossRef]
Jens C. Zorn, George E. Chamberlain, and Vernon W. Hughes. “Experimental Limits for the Electron-Proton Charge Difference and for the Charge of the Neutron”. Phys. Rev. 129, 2566 (1963). [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Quarks and Leptons Formation from the Spontaneous Fractionation of a Pair of Elementary Particles with Proton Charge Units

Abstract

1. Introduction

2. Structure Function of Two Interacting Charge Fragment

3. The Laws of Conservation of the DEMS and Fragmentation of Unitary Electric Charges

4. Use of the Solutions L and H to Build the First Generation of the Elementary Particles

4. Conclusions

Funding Statement

Data Availability Statements

Conflict of Interest declaration

Ethical Conduct

References

MDPI Initiatives

Important Links

Subscribe