Implications of the Spin-Induced Accretion Disk Truncation on the X-ray Binary Broadband Emission

Preprint

Article

Implications of the Spin-Induced Accretion Disk Truncation on the X-ray Binary Broadband Emission

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Theodora Papavasileiou^*

,Ioannis Sinatkas,

Theocharis Kosmas

Theodora Papavasileiou^*

,Ioannis Sinatkas,

Theocharis Kosmas

This version is not peer-reviewed

Submitted:

15 July 2024

Posted:

16 July 2024

You are already at the latest version

Alerts

Abstract

Black hole X-ray binary systems consist of a black hole accreting mass from its binary companion, forming an accretion disk. As a result, twin relativistic plasma ejections (jets) are launched towards opposite and perpendicular directions. Moreover, multiple broadband emission observations from X-ray binary systems range from radio to high-energy gamma-rays. The emission mechanisms exhibit thermal origins from the disk, stellar companion, and non-thermal jet-related components (i.e., synchrotron emission, inverse comptonization of less energetic photons, etc.). In many attempts at fitting the emitted spectra, a static black hole is often assumed regarding the accretion disk modeling, ignoring the Kerr metric properties that significantly impact the geometry around the usually rotating black hole. In this work, we study the possible implications of the spin inclusion in predictions of the X-ray binary spectrum. We mainly focus on the most significant aspect inserted by the Kerr geometry, the innermost stable circular orbit radius dictating the disk’s inner boundary. The outcome suggests a higher-peaked and hardened X-ray spectrum from the accretion disk and a substantial increase in the inverse compton component of disk-originated photons. Jet-photon absorption is also heavily affected at higher energy regimes dominated by hadron-induced emission mechanisms. Nevertheless, a complete investigation requires the full examination of the spin contribution and the resulting relativistic effects beyond the disk truncation.

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

1. Introduction

Active Galactic Nuclei (AGNs) are the center of nearly every galaxy and are our universe’s most powerful particle accelerators. They consist of a supermassive black hole surrounded by an accretion disk of nearby gas and matter attracted by gravitational forces. Black hole X-ray binary systems (BHXRBs) are scaled-down systems of AGNs that host stellar instead of supermassive black holes. The mass supplier, in this case, is the secondary stellar component of the initial binary system instead of the galaxy host of the AGN.

The particle acceleration occurs inside the relativistic jets launched perpendicularly to the accretion disk’s plane. They often form observable radio lobes when interacting with the interstellar medium [1]. Depending on the nature of the accelerated particles, the jet emission mechanisms vary from synchrotron radiation and inverse comptonization (leptonic jet models) to proton-proton or proton-photon interactions, leading to a pion/muon distribution production (hadronic jet models). The latter mechanisms lead to higher-energy gamma-ray emission in addition to neutrino production [2,3,4]. Such energetically rich spectra can be detected by Earth-bound or space detectors that are continuously upgraded to reach even higher sensitivities [5,6].

In the current work, we present a lepto-hadronic jet emission model that integrates a variety of non-thermal emission mechanisms. Those include synchrotron emission from both leptons and hadrons accelerated by the system’s magnetic field, inverse compton scattering of thermal emission (mainly from the accretion disk and the companion star) due to interaction with the energetic jet electron distribution, and proton-proton interactions inside the co-moving jet frame. Photon annihilation due to pair (electron-positron) production occurs frequently in the vicinity of the black hole, leading to a substantial decrease in the produced spectra as seen by distant observers [7].

In many attempts at fitting the emitted spectra, a static black hole is often assumed regarding the accretion disk modeling, ignoring the Kerr metric properties that significantly impact the geometry around the black hole. The fact that most of the observed black holes, especially those involved in XRBs, exhibit extreme spin parameters poses the question of how long we can neglect the spin contribution in the XRB emission modeling [8]. Hence, we examine the possible implications of involving the black hole spin in our calculations through the disk truncation effect induced by the shifting radius of the innermost stable circular orbit (i.e., ISCO). The latter is often assumed to be the inner boundary of the accretion disk in the standard Shakura-Suniaev model.

We will first introduce the jet emission model and the accretion disk spectral aspects. Then, we will present our results for a common XRB similar to Cygnus X-1 while demonstrating the impact of one aspect of the Kerr metric input from general relativity. That aspect is the radius of the innermost stable circular orbit. Finally, we summarize and conclude while setting our next research targets.

2. Photon-Lepton/Hadron Interactions Inside the Jet Frame

Shock waves inside the jet co-moving frame cause additional acceleration to a particle fraction, leading to power-law energy distributions. The present work assumes equivalence between the leptonic and hadronic jet’s content. Hence, the emission mechanisms involved are synchrotron radiation, inverse comptonization, and proton-proton collisions between the power-law distribution and the rest of the cold proton density inside the jet.

The synchrotron spectrum component by a single particle accelerated by a magnetic field

B (z)

, where z the distance of the acceleration region from the black hole, is given by

q_{s y n} = \frac{\sqrt{3} e^{3} B (z)}{h m c^{2}} \frac{ϵ}{ϵ_{c r}} \int_{ϵ / ϵ_{c r}}^{\infty} K_{5 / 3} (ζ) d ζ .

(1)

The energy of the emitted photon is

ϵ

and the critical energy

ϵ_{c r}

is defined as

ϵ_{c r} = \frac{3 h e B (z) sin a_{p}}{4 π m c} γ^{2},

(2)

where

γ = ϵ_{e, p} / m c^{2}

and

a_{p}

denotes the pitch angle. The total spectrum emitted by a distribution of particles is calculated through multiplication with the distribution and integration over the particle energy and the solid angle corresponding to the pitch angle.

Respectively, the IC (inverse compton) component is obtained by employing the spectrum emitted by a single particle given by

q_{I C} = \frac{3 σ_{T} m^{2} c^{5}}{4 γ} \frac{d n}{ϵ d ϵ} [2 f l n f + (1 + 2 f) (1 - f) + F] .

(3)

The Thomson cross-section is denoted as

σ_{T}

. In addition, it holds

γ ≫ 1

and

f = ϵ ϵ_{e} / 4 ϵ_{0} γ^{2} (ϵ_{e} - ϵ)

. Also,

F = (k^{2} (1 - f)) / (2 (1 + k))

where

k = ϵ / (ϵ_{e} - ϵ)

. The total spectrum is obtained by integration over the energy

ϵ_{e}

of the electron distribution and the initial photon energy

ϵ_{0}

. The energy-dependent photon density scattered off the lepton distribution is given by

d n / d ϵ

Regarding the hadron-induced mechanisms, we assume predominantly the contribution of the proton-proton interactions, resulting in neutral and charged pion production. Our interest lies mainly in the emission of gamma-rays, so we take into account only the neutral pions that decay into gamma-ray photons with the following emissivity

q_{γ} = c n (z) \int_{ϵ / ϵ_{p, m a x}}^{1} \frac{d (ϵ / ϵ_{p})}{ϵ / ϵ_{p}} N_{p} (ϵ_{p}, z) F_{γ} (ϵ / ϵ_{p}, ϵ_{p}) σ_{p p}^{(i n e l)} (ϵ_{p}) .

(4)

In the above equation,

n (z)

stands for the cold proton density inside the jet and

F_{γ}

denotes the gamma-ray spectrum emitted per p-p collision [9].

2.1. Black-Body Spectrum of the Accretion Disk

The photon density emitted by the accretion disk in the standard Shakura-Suniaev model is approximated by a sum of black-body spectra. Given the torque-free inner boundary condition, which is a usual assumption, a single disk surface area emits a black-body spectrum with an effective temperature given by [10]

T (\bar{r}) = {(\frac{3 G M_{b h} \dot{M}}{8 π σ_{S B} r_{g}^{3}})}^{1 / 4} {[\frac{\bar{r} - 2 / 3}{\bar{r} {(\bar{r} - 2)}^{3}} (1 - \frac{3^{3 / 2} (\bar{r} - 2)}{2^{1 / 2} {\bar{r}}^{3 / 2}})]}^{1 / 4} .

(5)

Here,

\bar{r} = r / r_{g}

is the radius in units of

r_{g} = G M_{b h} / c^{2}

. The disk temperature profile of Eq. (5) is derived by assuming a Paczyński–Wiita pseudo-Newtonian potential around a Schwarzschild black hole. A more realistic approach requires the incorporation of the black hole spin input in the calculations since most of the compact objects in BHXRBs are rotating black holes with significant spin parameter values.

The inner disk edge is located at the radius of the innermost stable circular orbit (i.e.,

r_{I S C O}

), which for a static black hole is

6 r_{g}

. Nonetheless, the incorporation of the Kerr metric in general relativity dictates the following ISCO radius depending on the dimensionless spin parameter

α_{*}

r_{I S C O} = \frac{G M_{b h}}{c^{2}} (3 + λ_{2} \pm \sqrt{(3 - λ_{1}) (3 + λ_{1} + 2 λ_{2})}) .

(6)

In the above equation, it holds

\begin{matrix} λ_{1} & = 1 + {(1 - α_{*}^{2})}^{1 / 3} [{(1 + α_{*})}^{1 / 3} + {(1 - α_{*})}^{1 / 3}], \end{matrix}

(7)

\begin{matrix} λ_{2} & = {(λ_{1}^{2} + 3 α_{*}^{2})}^{1 / 2} . \end{matrix}

(8)

In this work, we only incorporate this aspect of the general relativity (i.e., the location of the

r_{I S C O}

), aiming to demonstrate its contribution. We neglect the necessary modifications of the gravitational potential, which will be studied thoroughly in future works.

3. Results

We apply the aforementioned jet emission model to an X-ray binary system similar to Cygnus X-1, which is characterized by the parameters of Table 1. The black hole accretes with a sub-Eddington rate that justifies the Shakura-Suniaev disk description.

The left panel of Figure 1 demonstrates the spin’s impact on the total disk luminosity. Co-rotating accretion disks around rapidly rotating black holes exhibit an amplified peak shifted to higher energies, while the opposite happens in the counter-rotation case. The respective IC emission component of the spectrum (right panel of Figure 1) also experiences a substantial increase that makes it comparable to the synchrotron counterpart (accelerated leptons cause both) in some cases.

The substantial increase in the photon annihilation rate for energies above 100 GeV due to the disk truncation at lower

r_{I S C O}

is displayed in Figure 2. The emission mechanisms contributing to this energy regime are primarily hadronic, such as the p-p collisions and synchrotron emission of accelerated protons.

The reason for such a steep drop in the luminosity is that the additional disk surface in close proximity to the black hole (i.e.,

\bar{r} < 6

) provides an additional source of higher-frequency photons capable of annihilating the jet-emitted ones. This portion of the disk surface assumes significantly higher temperatures than the rest, reaching

T \approx 10^{6} - 10^{7}

K depending on the black hole mass and the mass accretion rate.

4. Conclusions

Black hole X-ray binary systems (BHXRBs) are smaller versions of AGNs that host stellar instead of supermassive black holes. An accretion disk is formed when the compact object accretes mass out of its binary companion, and two relativistic jets are launched perpendicularly as a result. One of those is inclined towards the Earth, leading to a multi-wavelength emission detection caused by the highly accelerated particle interactions inside the jet frame.

Adopting a static compact object is a usual simplification in modeling the accretion disk and jet emission. However, that does not account for the additional rotational energy transferred to the accretion disk through the Kerr modification of a static curved spacetime. In the present work, we examine the implications of the spin-induced accretion disk truncation on the X-ray binary broadband emission. For that reason, we employ a jet lepto-hadronic emission model and a standard disk description.

Our findings show a substantial increase in the accretion disk luminosity and the hardening of its respective X-ray spectrum. That also affects the emitted inverse compton component due to the disk’s scattered photons off jet-accelerated leptons. The very high energy (i.e., VHE) gamma-ray spectrum counterpart experiences a substantially amplified quenching caused by photon annihilation (leading to pair production) with the disk-emitted photons. Our analysis is limited to the shift of the innermost stable circular orbit radius, neglecting the required modifications to the pseudo-Newtonian potential of Paczyński–Wiita. Our future goal is to derive a more complex spin-dependent temperature profile and integrate the angular dependence predicted by general relativity without further modifications of the standard disk model.

Author Contributions

Conceptualization, T.P.; methodology, T.P.; software, T.P.; validation, T.P. and T.S.; formal analysis, T.P. and I.S.; investigation, T.P.; resources, T.S.; data curation, I.S.; writing—original draft preparation, T.P.; writing—review and editing, T.P., I.S. and T.S.; visualization, T.P.; supervision, T.S.; project administration, T.S..; funding acquisition, T.S. All authors have read and agreed to the published version of the manuscript.

Funding

This work is financially supported by: “The Association for Advancement of Research on Open Problems in Nuclear Physics and Particle Physics (OPRA Association)”, Tel Aviv, Israel.

Data Availability Statement

The datasets generated during and/or analyzed in the present study are available upon request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

Saikia, P.; Russell, D.M.; Bramich, D.M.; Miller-Jones, J.C.A.; Baglio, M.C.; Degenaar, N. Lorentz Factors of Compact Jets in Black Hole X-Ray Binaries. Astrophys. J. 2019, 887, 21. [Google Scholar] [CrossRef]
Punsly, B. Models of the compact jet in GRS 1915+105. Monthly Notices of the Royal Astronomical Society 2011, 418, 2736–2743. [Google Scholar] [CrossRef]
Papavasileiou, T.; Kosmas, O.; Sinatkas, I. Simulations of Neutrino and Gamma-Ray Production from Relativistic Black-Hole Microquasar Jets. Galaxies 2021, 9. [Google Scholar] [CrossRef]
Papavasileiou, T.; Kosmas, O.; Sinatkas, I. Studying the Spectral Energy Distributions Emanating from Regular Galactic XRBs. Universe 2023, 9. [Google Scholar] [CrossRef]
Aartsen, M.G.; et al. Neutrino astronomy with the next generation IceCube Neutrino Observatory. 2019, arXiv:astro-ph.HE/1911.02561. [Google Scholar]
Cherenkov Telescope Array Consortium.; et al. Science with the Cherenkov Telescope Array 2019. [CrossRef]
Papavasileiou, T.V.; Kosmas, O.T.; Sinatkas, I. Prediction of gamma-ray emission from Cygnus X-1, SS 433, and GRS 1915+105 after absorption. Astron. Astrophys. 2023, in press. [Google Scholar] [CrossRef]
Qin, Y.; Shu, X.; Yi, S.; Wang, Y.Z. Hypercritical Accretion for Black Hole High Spin in Cygnus X-1. Research in Astronomy and Astrophysics 2022, 22, 035023. [Google Scholar] [CrossRef]
Kelner, S.R.; Aharonian, F.A.; Bugayov, V.V. Energy spectra of gamma rays, electrons, and neutrinos produced at proton-proton interactions in the very high energy regime. Phys. Rev. D 2006, 74, 034018. [Google Scholar] [CrossRef]
Gierliński, M.; Zdziarski, A.A.; Poutanen, J.; Coppi, P.S.; Ebisawa, K.; Johnson, W.N. Radiation mechanisms and geometry of Cygnus X-1 in the soft state. Mon. Not. R. Astron. Soc. 1999, 309, 496–512. [Google Scholar] [CrossRef]

Figure 1. The total luminosity emitted by the accretion disk (left panel) and the respective inverse compton (IC) component of the spectral distribution for different values of the black hole spin (right panel).

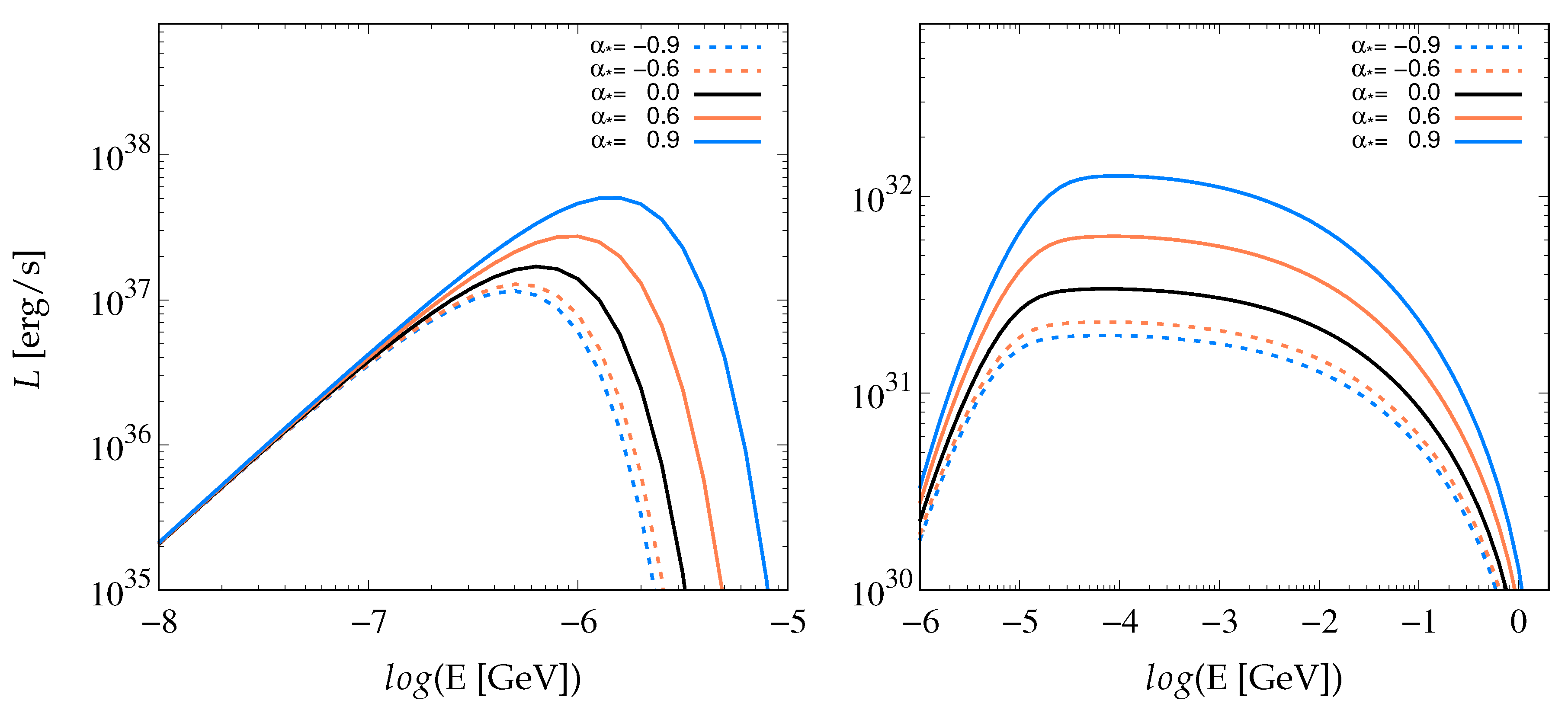
Figure 2. The spectral energy distribution after photon-photon interactions with the emission from the accretion disk for different black hole spins.

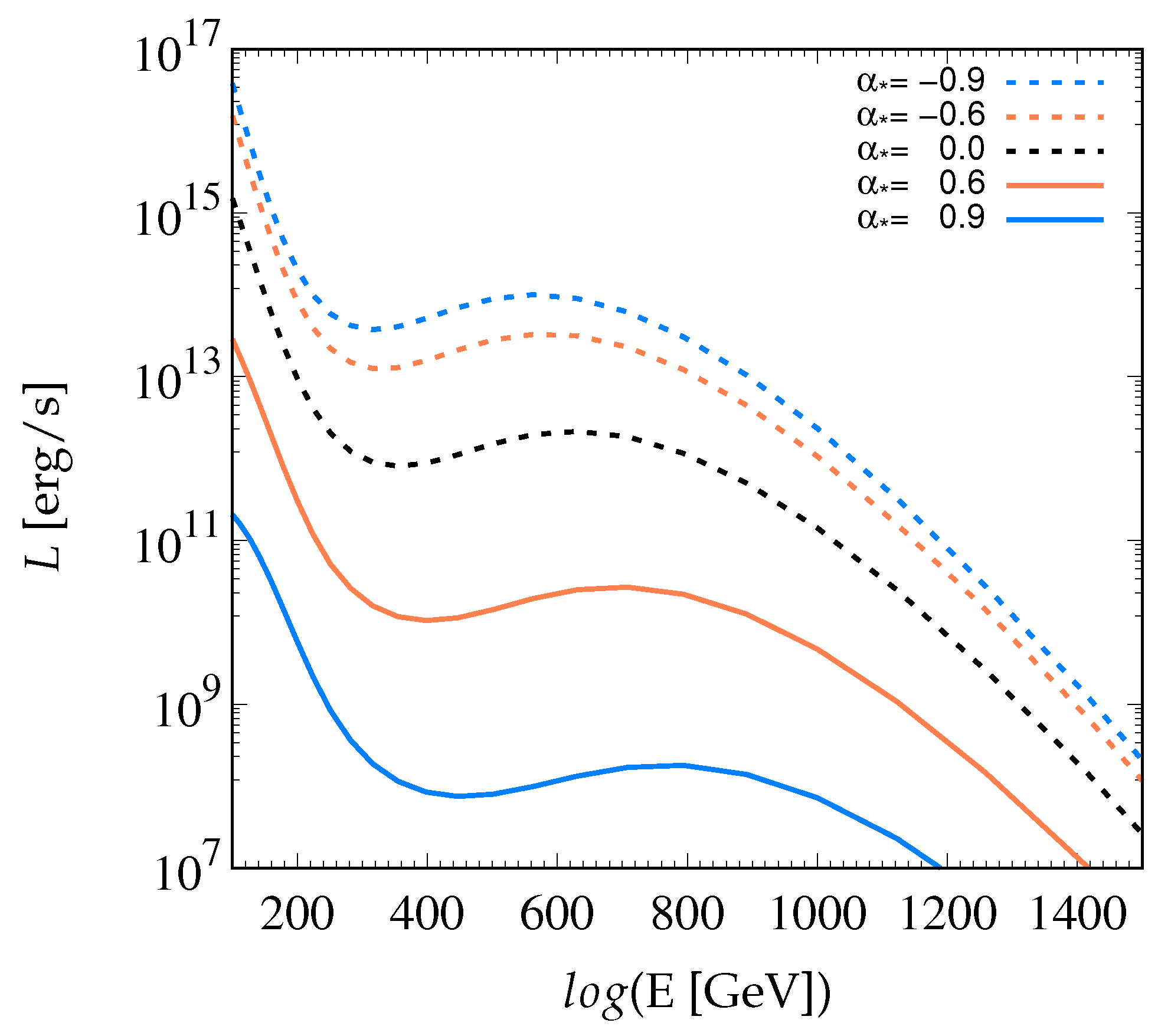
Table 1. The primary parameters used to describe the X-ray binary system on which the emission model is applied.

XRB Parameter	Symbol	Value	Units
Black hole mass	$M_{b h}$	20	$M_{⊙}$
Secondary stellar mass	$M_{*}$	15	$M_{⊙}$
Distance to Earth	d	2	kpc
XRB inclination	i	30	∘
Jet Lorentz factor	$Γ_{b}$	$2.29$	-
Mass accretion rate	$\dot{m}$	0.07	${\dot{M}}_{E d d}$
Dimensionless spin parameter	$α_{*}$	$\pm 0, 0.6, 0.9$	-
Jet’s emitting region height	z	$10^{8}$	cm

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Implications of the Spin-Induced Accretion Disk Truncation on the X-ray Binary Broadband Emission

Abstract

1. Introduction

2. Photon-Lepton/Hadron Interactions Inside the Jet Frame

2.1. Black-Body Spectrum of the Accretion Disk

3. Results

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe