Classification stands as a cornerstone in machine learning, tasked with assigning new data points to predefined classes. Commonly employed concept models such as decision trees (DTs), support vector machines (SVMs), and k-nearest neighbors (k-NNs) have long served this purpose [1]. Despite their prevalence, many existing classifiers encounter challenges, including overfitting, high computational costs, and a lack of interpretability—the infamous "black box" effect. Furthermore, these models often struggle to robustly handle noisy or missing feature values. Additionally, many existing classifiers rely on complex learning mechanisms by combining or transforming the data features, which can exacerbate issues such as overfitting, high computational costs, and a lack of interpretability—the so-called "black box" effect. Moreover, these models often grapple with effectively handling noisy or missing feature values. In response to these challenges, this paper devoted to classifiers based on feature interval learning (FIL), offering a distinct approach to traditional classification methods. FIL algorithms segment the feature space into distinct intervals for each feature, with each interval linked to a specific class. Feature intervals represent features as intervals rather than individual values, providing robustness to noise and variability in the input data, particularly for continuous data types [2]. A set of feature intervals embodies a concept on each feature dimension separately. Subsequently, each feature contributes to the classification process by distributing votes among classes, with the predicted class being the one receiving the highest vote [3]. This method’s reliance on clear feature ranges offers interpretability, rendering decision rules easy to understand [2]. Furthermore, FIL can be effective with smaller datasets compared to data-hungry deep learning models [4]. In response to these challenges, we introduce an approach to supervised classification that harnesses the synergies of feature interval learning and outranking measures, called Closest Resemblance (CR). Outranking, entrenched in preference learning [5,6], transcends simple distance measures by autonomously learning feature intervals from data, thereby capturing nuanced patterns and enhancing adaptation to specific datasets. Moreover, outranking adeptly navigates noise and uncertainties in real-world data through pairwise comparisons on each feature. The proposed CR method amalgamates FIL’s interpretability and efficiency with outranking’s data-driven pattern recognition and robustness to noise. This integrated approach aims to surmount the limitations of existing methods, particularly in scenarios with imbalanced data and irrelevant features. Empirical evaluations conducted on diverse datasets from the UCI repository compare the proposed classifier CR against established classifiers such as k-Nearest Neighbors (k-NN), Support Vector Machines (SVM), Random Forests (RF), Multi-Layer Perceptron Neural Networks (MLP), Naive Bayes (NB), and Nearest Centroid (NC). The results underscore the efficacy of FIL with outranking, showcasing comparable or superior performance while delivering more interpretable models. This enhanced interpretability fosters trust and understanding in the decision-making process, bridging the gap between predictive power and internal workings.

In the domain of supervised classification, various methodologies have been proposed to tackle the challenges posed by batch data and to enhance the interpretability and adaptability of classifiers. Among these, feature interval learning (FIL) techniques have emerged as prominent approaches. FIL approaches offer a distinct paradigm for classification, wherein the feature space is partitioned into intervals for each feature. Each interval is associated with a specific class, enabling a more nuanced representation of feature patterns and enhancing robustness to noise and variability in the data [2]. FIL methods encompass a range of techniques, including hypercuboid or hyperrectangle learning and prototype-based classification, which learn decision boundaries or representative prototypes to distinguish between classes. The concept of hypercuboid has been exploited for many years [7]

Hyper-cuboid approaches represent one category of FIL methods, where the feature space is partitioned into hyper-cuboid regions based on the distribution of training data [7]. These regions serve as decision boundaries, facilitating efficient classification of new instances. Hyper-cuboid approaches are particularly effective in handling high-dimensional data and are known for their computational efficiency and simplicity. Prototype-based FIL methods, on the other hand, generate prototypes for each class based on the distribution of feature intervals in the training data [3,8,9]. These prototypes encapsulate the characteristic features of each class and are used to classify new instances by measuring their resemblance to the prototypes. Prototype-based FIL methods offer interpretability and transparency in decision-making, as the classification process is based on clear feature ranges. In [2] describes a family of FIL algorithms. Some of FIL algorithms are voting feature intervals [3], k-nearest neighbor on feature projections [10] and Naive Bayes classifier (NBC) [1]. The common idea of the FIL algorithms, learn the concept description in the form of a set of disjoint intervals separately for each feature. At the testing phase the FIL algorithms predict the class of new data point as the label of with the highest total weighted votes of the individual features. 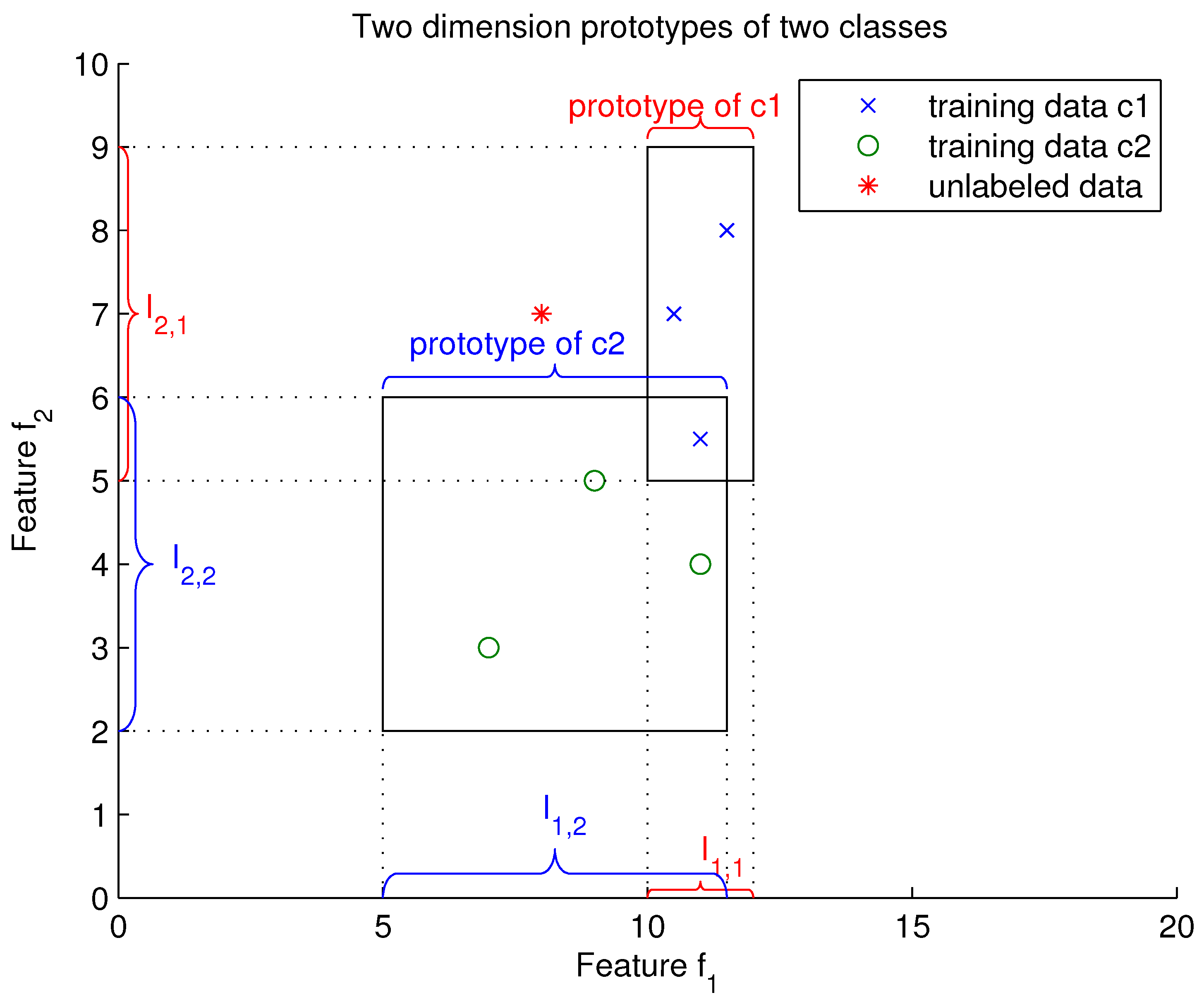For example in Figure 1, the horizontal axis is feature $f_1$ and the vertical axis is the feature $f_2$. The two rectangles represent the two prototypes of classes $C^1$ and $C^2$. The prototype of class $C^1$ is represented by the interval $I_{1,1}$ and $I_{2,1}$ (intervals determined using the training sets of class $C^1$ ’the blue x sign’. And the prototype of class $C^2$ is represented by the intervals $I_{1,2}$ and $I_{2,2}$ (intervals calculated using the training sets of class $C^2$ ‘the green o sign’. The objective is to assign the unlabeled data (the red star * in Figure 1) to the closest rectangular.

Overall, while hypercuboid or hyperrectangle learning algorithms offer computational efficiency and simplicity, FIL methods provide greater flexibility, robustness, and interpretability in classifying new data points, especially in scenarios with complex data distributions and high-dimensional feature spaces. However, predicting class labels based on the highest total weighted votes of individual features is a straightforward approach in FIL algorithms, it may have limitations in handling feature importance, noise, feature relationships, imbalanced datasets, and the trade-off between interpretability and accuracy. Addressing these inconveniences requires careful consideration of feature selection, noise reduction techniques, feature engineering, and robust mechanisms for handling imbalanced data. Beyond traditional majority voting approaches, another advancements in FIL is the integration of outranking measures into the classification process. Outranking measures, rooted in preference learning principles, extend the classification paradigm by capturing subtle preferences and trade-offs among alternative solutions [8,11]. By conducting pairwise comparisons on each feature, outranking measures facilitate more nuanced decision-making and enhance adaptability to specific datasets [5]. Several FIL classifiers based on outranking measures were developed since decades, among them we have PROAFTN [9], PROCFTN [12] and K Closest Resemblance (K-CR) or PROCTN [13]. These classifiers offer several advantages in the context of classification tasks. By evaluating the data points based on their pairwise performance on each feature, outranking techniques can capture subtle differences in feature importance and contribution to class membership. Instead of blindly aggregating votes from all features, outranking considers the relative performance of alternatives on each feature, effectively filtering out noise and focusing on discriminative features that contribute most to the classification decision. This robustness to noise enhances the reliability and accuracy of classification outcomes. Outranking techniques can capture complex relationships between features by conducting pairwise comparisons on each feature individually. Unlike majority voting, which treats features independently, outranking takes into account the interactions and dependencies between features, allowing for more accurate and nuanced classification decisions. Outranking techniques provide clear and interpretable decision rules by quantifying the resemblance relationship between data points. Instead of relying on a simple count of votes, outranking assigns a degree of resemblance between alternatives based on their pairwise comparisons, making the classification process more transparent and understandable. This enhanced interpretability fosters trust and understanding in the classification model’s decision-making process. Outranking techniques can effectively handle imbalanced datasets by considering the relative performance of alternatives on each feature [14]. Instead of biasing the classification decision towards the majority class, outranking evaluates alternatives based on their overall resemblance relationship, ensuring that all classes are appropriately considered in the classification process. This helps mitigate the impact of class imbalance and ensures more balanced and accurate predictions. Outranking techniques offer flexibility and adaptability to different types of data and classification tasks. By capturing subtle differences in feature importance and performance, outranking can accommodate various data distributions and class structures, making it suitable for a wide range of classification scenarios. The FIL classifiers based on outranking measures have been applied to the resolution on many real world practical problems such as medical diagnosis [11,15,16,17], image processing and classification [14,18], engineering design [19], recommendation system [20] and cybersecurity [21]. Even though, these classifiers have several advantages, they are suffering from the computation complexity in their learning phase specifically when the number of features is very large. The PROAFTN and the K-CR build a set of prototypes in each class and then the inductive is based on the recursive approach, which is very complex. In this paper, we will introduce the FIL approach based on outranking measures for classification problems called Closest Resemblance CR. The CR algorithm is simple, effective, efficient and robust to irrelevant features. In the remaining paper, we will present the CR classifier, where each class is represented by one prototype and the classification rule is expressed as: "the data point is assigned to the class if the data point is resembled or roughly equivalent to the prototype of this class". Therefore, our proposed CR classifier is a prototype-based classification method that incorporates the FIL techniques to build the prototype of each class during the learning phase. The intervals in CR are inspired from the reference intervals used in the era of evidence-based medicine [22]. Unlike confidence intervals, which quantify uncertainty around a parameter estimate, prediction intervals capture the range within which a data point is likely to fall — they estimate the uncertainty associated with individual predictions.

The CR is a supervised learning algorithm and it allows to calculate the resemblance measures by determining the preference relations. The rule of CR method in assigning a data points to a class is: “the data point s is assigned to a class if and only if s resemble or is (roughly) equivalent to the prototype of this class”. Therefore, in order to assign point s to an appropriate class, CR will calculate the resemblance relation in order to measure the closeness of the sample s to the prototype of the class. To calculate the resemblance relation between the data point to assign and the prototype of the classes, CR is based on the preference relational system [5,6]. It employs a partial comparison between the sample and the prototypes of the classes, for each feature. Then, it applies a global aggregation using the concordance principle on the partial resemblance measure [5,8]. The CR classification method is considered as a weighted voting classifier in which each feature or attribute "votes" for the class membership of an unknown sample according to which class’ prototype is the closest [8,9,13]. The partial comparison used by CR to calculate the resemblance between the sample and prototypes avoids resorting to conventional metric and non-metric distances that aggregate the score of all features in the same value unit. Hence, it helps to overcome some difficulties encountered when data is expressed in different units and to find the correct pre-processing and normalization data techniques. The algorithm CR proceeds into two phases:

The experiments were conducted on a PC with an Intel(R) processor running at 2.2 GHz and equipped with 2 processors and 32 GB of RAM. All classifiers and experiments in this research were implemented in Python, utilizing open-source libraries such as Scikit-learn [24] and Pandas [25]. The source code is available on GitHub at [GitHub link].

The real-world datasets used for benchmarking and performance evaluations are sourced from the UCI Machine Learning Repository, well-established in machine learning research [26]. Details regarding the datasets’ descriptions and their dimensionalities are summarized in Table 2.

Our developed algorithms, termed CR, include CR1, which employs mean and standard deviation, and CR2, utilizing percentile-based approaches during the learning phase (Section 3.1). These classifiers are benchmarked against well-known algorithms: k Nearest Neighbors (k-NN) with k=3, Random Forest (RF) with 300 trees, Support Vector Machine (SVM), Multi-Layer Perceptron (MLP) neural network, Naive Bayesian (NB), and Nearest Centroid (NC).

To evaluate classification models, various metrics such as accuracy, precision, recall, and AUC (Area Under the Curve) are commonly used. Unlike accuracy, which solely measures correct predictions without considering the model’s ability to rank positive instances higher than negatives, AUC provides a more comprehensive assessment. AUC evaluates the model’s performance across different thresholds, making it particularly effective for imbalanced datasets or scenarios where prioritizing true positives is crucial [27].

To ensure robust evaluation, we employed 5-fold cross-validation. This technique divides the dataset into five folds, using four for training and one for validation in each iteration. By averaging performance metrics such as AUC across these folds, we obtain a more reliable estimate of each classifier’s generalization ability and mitigate the risk of overfitting to specific training data.

This work represents a significant advancement in classification methodologies, aiming to enhance both the practicality and interpretability of machine learning models in complex real-world scenarios. By integrating Feature Interval Learning (FIL) and outranking measures, we propose a novel approach in the form of Nested Generalized Exemplars classifiers. These classifiers leverage outranking techniques and utilize feature projections of training samples to encapsulate induced classification knowledge. New sample classification is achieved through weighted majority voting of attribute predictions.

Our empirical evaluation on various datasets from the UCI repository compares our approach with established classifiers such as k Nearest Neighbors, Support Vector Machine, Random Forest, Neural Network, Naive Bayesian, and Nearest Centroid classifiers. The results demonstrate that our FIL-based classifiers with outranking approaches exhibit robustness to imbalanced data and irrelevant features, achieving comparable or superior performance across most experiments. Furthermore, these classifiers yield more interpretable models while maintaining high predictive accuracy levels.

.

The following abbreviations are used in this manuscript:

FIL	Feature Interval Learning
CR	Closest Resemblance classifier
CR1	CR uses reference interval based on mean and standard deviation
CR2	CR uses reference intervals based on percentile
DT	Decision Trees
SVM	Support Vector Machine
RF	Random Forest
NB	Naive Bayesian
NC	Nearest Centroid