Inequalities involving Higher Degree Polynomial Functions in $\pi(x)$

Preprint

Article

Inequalities involving Higher Degree Polynomial Functions in $\pi(x)$

Altmetrics

Downloads

330

Views

165

Comments

Subham De^*

This version is not peer-reviewed

Submitted:

19 August 2024

Posted:

20 August 2024

You are already at the latest version

Alerts

Abstract

The primary purpose of this article is to study the asymptotic and numerical estimates in detail for higher degree polynomials in $\pi(x)$ having a general expression of the form, \begin{align*} P(\pi(x)) - \frac{e x}{\log x} Q(\pi(x/e)) + R(x) \end{align*} $P$, $Q$ and $R$ are arbitrarily chosen polynomials and $\pi(x)$ denotes the \textit{Prime Counting Function}. The proofs require specific order estimates involving $\pi(x)$ and the \textit{Second Chebyshev Function} $\psi(x)$, as well as the famous \textit{Prime Number Theorem} in addition to certain meromorphic properties of the \textit{Riemann Zeta Function} $\zeta(s)$ and results regarding its non-trivial zeros. A few generalizations of these concepts have also been discussed in detail towards the later stages of the paper, along with citing some important applications.

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

MSC: Primary 11A41; 11A25; 11N05; 11N37; 11N56; Secondary 11M06; 11M26

1. Introduction and Motivation

The motivation for investigating the distribution of prime numbers over the real line

R

first reflected in the writings of famous mathematician Ramanujan, as evident from his letters [[12],pp. xxiii-xxx , 349-353] to one of the most prominent mathematicians of 20^th century, G. H. Hardy during the months of Jan/Feb of 1913, which are testaments to several strong assertions about prime numbers, especaially the Prime Counting Function,

π (x)

[6].

In the following years, Hardy himself analyzed some of thoose results [13,14], and even wholeheartedly acknowledged them in many of his publications, one such notable result is the Prime Number Theorem [9].

Ramanujan provided several inequalities regarding the behaviour and the asymptotic nature of

π (x)

. One of such relation can be found in the notebooks written by Ramanujan himself has the following claim.

Theorem 1.1. (Ramanujan’s Inequality [1]) For x sufficiently large, we shall have,

\begin{matrix} {(π (x))}^{2} < \frac{e x}{log x} π (\frac{x}{e}) \end{matrix}

(1)

Worth mentioning that, Ramanujan indeed provided a simple, yet unique solution in support of his claim.

One immediate question which may pop up inside the head of any Number Theorist is that, what is meant by the term "large"? Apparently, over many years and even recently, a huge amount of effort has been put up by eminent researchers from all over the world in order to study Ramanujan’s Inequality, and focusing on understanding the behaviour of

π (x)

and any other Arithmetic Function associated to it. For example, it can be found in the work of Wheeler, Keiper, and Galway, Hassani [[11], Theorem 1.2]. Later on thanks to Dudek and Platt [[2], Theorem 1.2], Mossinghoff and Trudgian [16] and Axler [15], it has been well established that, a large proportion of posiive reals x falls under the category for which the inequality in fact is true.

In recent years, some attempts have indeed been made in order to derive other versions analogous to the Ramanujan’s Conjecture. Hassani [8] came up with a generalization of (1) increasing the power upto

2^{n}

. Furthermore, he also studied (1) extensively for different cases [11], and eventually claimed that, the inequality (1) does in fact reverses if one can replace e by some

α

satifying,

0 < α < e

, although it retains the same sign for every

α \geq e

. In addition to providing several numerical justifications in support of his proposition, he also came up with a few inequalities using asymptotic relations involving

π (x)

(cf. Theorem 2, 5 [7]), one of which stated that, for large enough x,

\begin{matrix} {(\frac{\sqrt{e} x}{log x})}^{2} π (x / e) < {(π (x))}^{3} < \frac{e^{2} x}{log x} {(π (x / e))}^{2} \end{matrix}

This article serves as a humble tribute to arguably the most famous mathematician that there ever was, Srinivasa Ramanujan, and his stellar work on

π (x)

, where we shall investigate certain higher degree polynomial functions in

π (x)

for their asymptotic behaviour as compared to significantly higher values of x, along with numerical estimates in support of justifying each and every result thus obtained in this process. We shall primarily discuss two major results in this area, namely:

Cubic Polynomial Inequality
Higher-Degree Polynomial Inequality

In addition to above, we shall further look into the prospect of exploring the similar characteristics of functions when it involves weighted sums and logarithmic weighted sums of

π (x)

over small intervals. The two important results in this segment which we’ve proposed in this paper are:

Inequality involving Weighted Sums of $π (x)$
Logarithmic Weighted Sum Inequality

Moreover, the later sections have been devoted towards attempting to generalize some of the proposed inequalities, as well as discussing about working with functions involving arbitrarily chosen polynomials in

π (x)

in a more generalized framework.

Before getting into the intricate details of this article, let us provide a brief overview of some important concepts involving

π (x)

and the Second Chebyshev Function

ψ (x)

[5], which will be required extensively for establishing each and every result in later sections.

2. Important Derivations Regarding $π (x)$

We recall the definition of the Prime Counting Function [10,13] ,

π (x)

to be the number of primes less than or equal to

x \in R_{> 0}

. In addition to above, we further define the Second Chebyshev Function

ψ (x)

as follows.

Definition 2.1.

For every

x \geq 0

ψ (x) : = \sum_{n \leq x} Λ (n),

Where,

Λ (n)

is the "Mangoldt Function" having the definition,

\begin{matrix} Λ (n) : = \{\begin{matrix} log p, & i f n = p^{m}, p^{m} \leq x, m \in N \\ 0, & o t h e r w i s e . \end{matrix} \end{matrix}

(2)

Applying the meromorphic properties of the Riemann Zeta Function

ζ (s)

[3] and that, it’s non-trivial zeros lies inside the critical strip,

0 < ℜ (s) < 1

, it can further be commented that [4],

\begin{matrix} ψ (x) = x + O (x {log}^{2} x) \end{matrix}

(3)

A priori an application of the Prime Number Theorem [[10], Theorem 2.2.1, pp. 4] allows us to utilize (3) and obtain an estimate for

π (x)

in terms of

ψ (x)

Theorem 2.2.

\begin{matrix} π (x) = \frac{ψ (x)}{log x} + O (\frac{x}{{log}^{2} x}) \end{matrix}

(4)

Readers can refer to [[4], Theorem (3.3)] in for a detailed solution of this result. We shall be thoroughly applying (4) in the next two sections in order to study some specific polynomials involving

π (x)

and their weighted sums and more significantly observe their asymptotic behaviour corresponding to increasing values of x.

3. Inequalities Involving Polynomials in $π (x)$

3.1. Cubic Polynomial Inequality

The statement is as follows.

Theorem 3.1.

Let us consider the cubic polynomial of

π (x)

\begin{matrix} H (x) : = {(π (x))}^{3} - \frac{3 e x}{log x} {(π (x / e))}^{2} + \frac{3 e^{2} x}{{(log x)}^{2}} π (x / e^{2}) \end{matrix}

(5)

Given that

π (x)

is approximated by

\frac{x}{log x}

with a known error term, we can hypothesize that,

\begin{matrix} H (x) \approx O (\frac{x^{3}}{{(log x)}^{4}}) \end{matrix}

(6)

Furthermore,

H (x) < 0

for sufficiently large values of x.

Proof.

A priori from the order estimate between

π (x)

and

ψ (x)

as defined in (4) (cf. [4]), we compute the indivudual terms of

H (x)

as follows,

\begin{matrix} π (x / e) = \frac{ψ (x / e)}{log (x / e)} + O (\frac{x / e}{{(log (x / e))}^{2}}) = \frac{ψ (x / e)}{log x - 1} + O (\frac{x / e}{{(log x - 1)}^{2}}) \end{matrix}

(7)

and,

\begin{matrix} π (x / e^{2}) = \frac{ψ (x / e^{2})}{log (x / e^{2})} + O (\frac{x / e^{2}}{{(log (x / e^{2}))}^{2}}) = \frac{ψ (x / e^{2})}{log x - 2} + O (\frac{x / e^{2}}{{(log x - 2)}^{2}}) \end{matrix}

(8)

Furthermore,

\begin{matrix} {(π (x))}^{3} = {(\frac{ψ (x)}{log x} + O (\frac{x}{{(log x)}^{2}}))}^{3} = \frac{{(ψ (x))}^{3}}{{(log x)}^{3}} + 3 \cdot \frac{{(ψ (x))}^{2}}{{(log x)}^{3}} O (\frac{x}{{(log x)}^{2}}) \end{matrix}

\begin{matrix} + 3 \cdot \frac{ψ (x)}{{(log x)}^{3}} {(O (\frac{x}{{(log x)}^{2}}))}^{2} + {(O (\frac{x}{{(log x)}^{2}}))}^{3} \end{matrix}

(9)

Further simplification yields,

\begin{matrix} {(π (x))}^{3} = \frac{{(ψ (x))}^{3}}{{(log x)}^{3}} + O (\frac{x^{3}}{{(log x)}^{4}}) \end{matrix}

(10)

Finally,

\begin{matrix} \frac{3 e x}{log x} {(π (x / e))}^{2} = \frac{3 e x}{log x} {(\frac{ψ (x / e)}{log x - 1} + O (\frac{x / e}{{(log x - 1)}^{2}}))}^{2} \end{matrix}

\begin{matrix} = \frac{3 e x}{log x} (\frac{{(ψ (x / e))}^{2}}{{(log x - 1)}^{2}} + 2 \cdot \frac{ψ (x / e)}{{(log x - 1)}^{2}} O (\frac{x / e}{{(log x - 1)}^{2}}) + {(O (\frac{x / e}{{(log x - 1)}^{2}}))}^{2}) \end{matrix}

\begin{matrix} = \frac{3 e x {(ψ (x / e))}^{2}}{(log x) {(log x - 1)}^{2}} + O (\frac{x^{3}}{{(log x)}^{4}}) \end{matrix}

(11)

And,

\begin{matrix} \frac{3 e^{2} x}{{(log x)}^{2}} π (x / e^{2}) = \frac{3 e^{2} x}{{(log x)}^{2}} (\frac{ψ (x / e^{2})}{log x - 2} + O (\frac{x / e^{2}}{{(log x - 2)}^{2}})) \end{matrix}

\begin{matrix} = \frac{3 e^{2} x ψ (x / e^{2})}{{(log x)}^{2} (log x - 2)} + O (\frac{x^{3}}{{(log x)}^{4}}) \end{matrix}

(12)

Combining all the terms (7), (10), (11) and (12), we obtain,

\begin{matrix} H (x) = (\frac{{(ψ (x))}^{3}}{{(log x)}^{3}} + O (\frac{x^{3}}{{(log x)}^{4}})) - (\frac{3 e x {(ψ (x / e))}^{2}}{(log x) {(log x - 1)}^{2}} + O (\frac{x^{3}}{{(log x)}^{4}})) \end{matrix}

\begin{matrix} + (\frac{3 e^{2} x ψ (x / e^{2})}{{(log x)}^{2} (log x - 2)} + O (\frac{x^{3}}{{(log x)}^{4}})) \end{matrix}

Considering the dominant terms and the contributions of each term separately as compared to the error term, we get,

\begin{matrix} H (x) = \frac{{(ψ (x))}^{3}}{{(log x)}^{3}} - \frac{3 e x {(ψ (x / e))}^{2}}{(log x) {(log x - 1)}^{2}} + \frac{3 e^{2} x ψ (x / e^{2})}{{(log x)}^{2} (log x - 2)} + O (\frac{x^{3}}{{(log x)}^{4}}) \end{matrix}

(13)

Given the statement of the Prime Number Theorem [9,10],

ψ (x) \sim x

as x approaches ∞, thus we consider the dominant terms for sufficiently large x. Hence, substituting (3) in (13),

\begin{matrix} H (x) = \frac{x^{3}}{{(log x)}^{3}} - \frac{3 x^{3}}{e {(log x - 1)}^{3}} + \frac{3 x^{2}}{{(log x - 2)}^{3}} + O (\frac{x^{3}}{{(log x)}^{4}}) \end{matrix}

\begin{matrix} = - \frac{3 x^{3}}{e {(log x - 1)}^{3}} + O (\frac{x^{3}}{{(log x)}^{4}}) \end{matrix}

(14)

Since,

\frac{3 x^{3}}{e {(log x - 1)}^{3}} > 0

for sufficiently large x ( observe that higher-order terms diminish as x grows ), the dominant term is thus negative.

In coclusion, for sufficiently large values of x, one shall have (6) to satisfy and,

H (x) < 0

. □

Remark 3.2.

In other words, theCubic polynomial Inequalitycan be reformulated as,

\begin{matrix} {(π (x))}^{3} + \frac{3 e^{2} x}{{(log x)}^{2}} π (x / e^{2}) < \frac{3 e x}{log x} {(π (x / e))}^{2} \end{matrix}

(15)

for sufficiently large values of x.

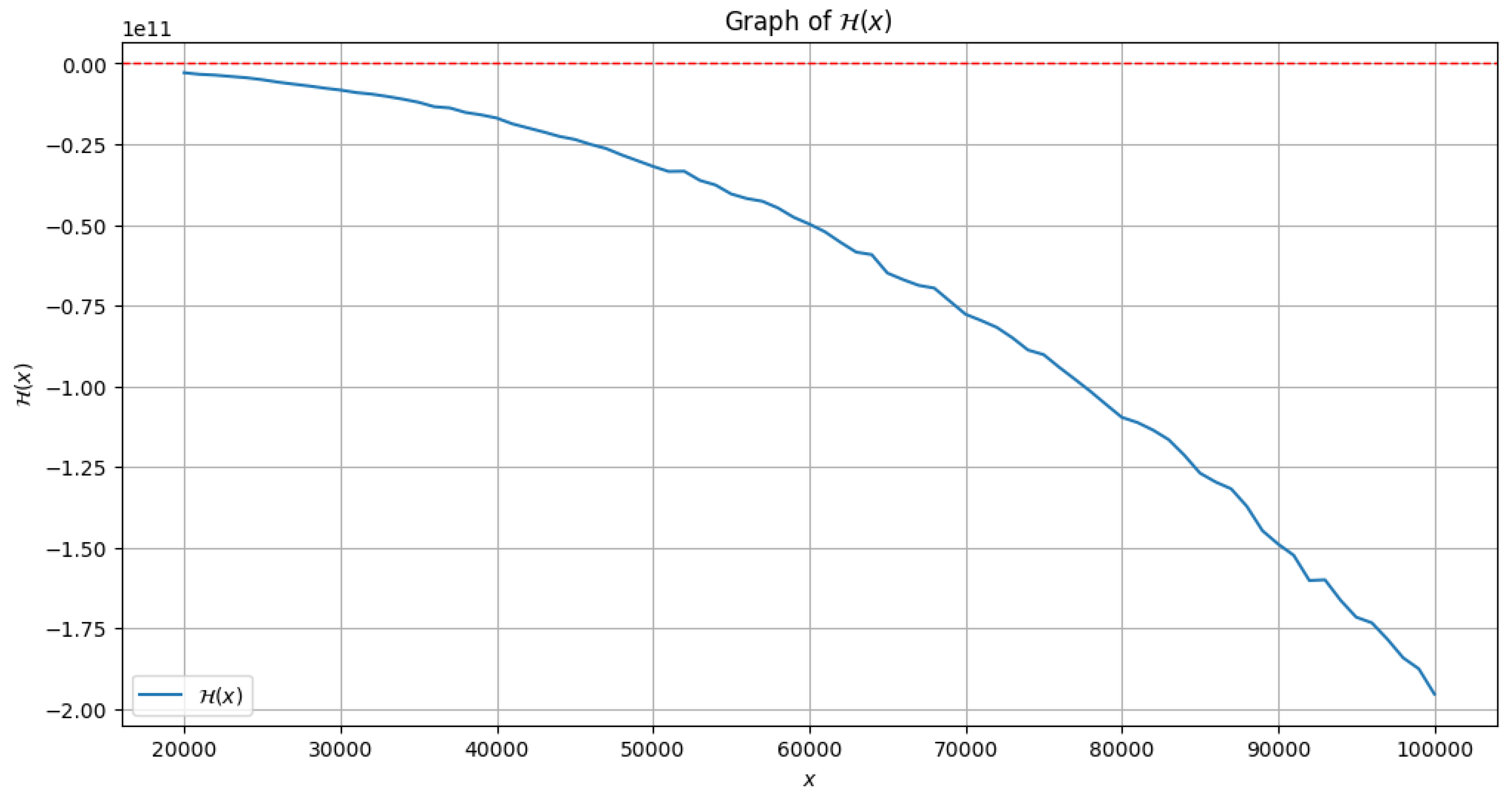
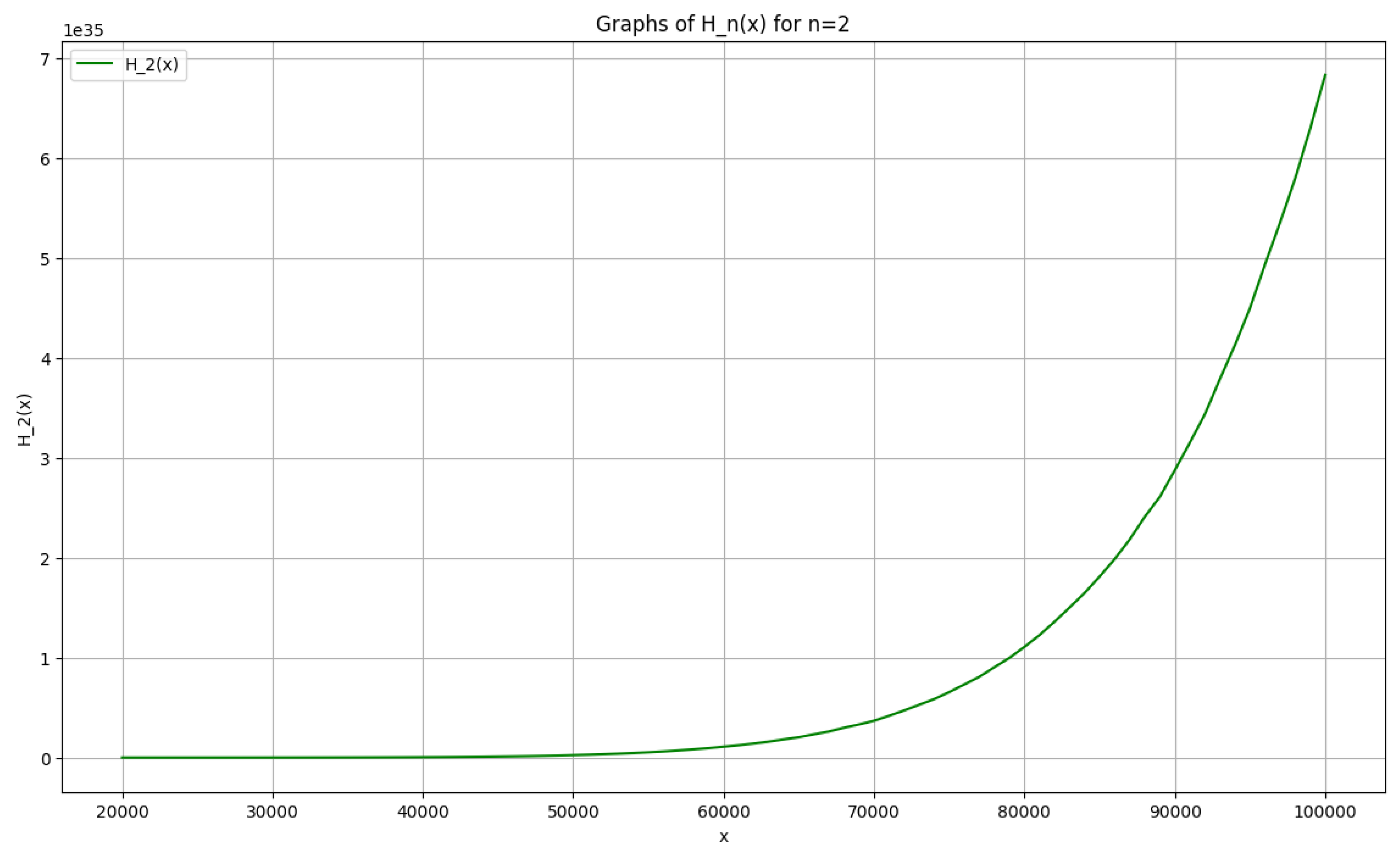
3.2. Numerical Estimates for $H (x)$

Important to note that, one can utilize PYTHON programming language1 in order to observe the plot of

H (x)

as compared to x. The following Figure 1 shows the graph for

2 \times 10^{4} \leq x \leq 10^{5}

. Furthermore, rigorous computation using MATHEMATICA1 yields the following values of

H (x)

as mentioned in Table 1 in the range,

10^{4} \leq x \leq 10^{18}

. The data clearly suggests that, the function

H (x)

is indeed decreasing in this interval, hence, our claim (15) can also be justified numerically.

3.3. Application: Equivalence with Ramanujan’s Inequality

The one question which might pop up at this point is to justify the sugnificance of studying inequalities like (15) involving cubic polynomials in

π (x)

. One such application which we shall observe in this section is the equivalence of the statements of the Cubic Polynomial Inequality (cf. Theorem (3.1)) and the Ramanujan’s Inequality (cf. Theorem (1.1)).

Assume that,

\begin{matrix} G (x) : = {(π (x))}^{2} - \frac{e x}{log x} π (\frac{x}{e}) \end{matrix}

(16)

Hence, the statement goes as follows.

Theorem 3.3.

The Cubic Polynomial Inequality is equivalentto proving the Ramanujan’s Inequality [1][2]. In other words, if

H (x) < 0

for large x, then,

G (x) < 0

for sufficiently large x and vice versa.

Proof.

A priori from (4) of Theorem (2.2), we attain the derivations (7) and (8).

First, we approximate

H (x)

\begin{matrix} H (x) = {(\frac{ψ (x)}{log x})}^{3} - \frac{3 e x}{log x} {(\frac{ψ (x / e)}{log x - 1})}^{2} + \frac{3 e^{2} x}{{(log x)}^{2}} (\frac{ψ (x / e^{2})}{log x - 2}) \end{matrix}

Ignoring higher-order error terms. Estimating

G (x)

in similar manner, we obtain,

\begin{matrix} G (x) = \frac{{(ψ (x))}^{2}}{{(log x)}^{2}} - \frac{e x}{log x} \frac{ψ (x / e)}{log x - 1} \end{matrix}

First we assume , if possible that,

H (x) < 0

for sufficiently large values of x. Given that

\frac{ψ (x)}{log x}

is the dominant term, for large x, thus the second term in the expression of

H (x)

will dominate the first and third terms due to the

e x

factor in the numerator. Hence, to maintain the inequality, we must have,

\begin{matrix} \frac{{(ψ (x))}^{3}}{{(log x)}^{3}} \approx \frac{3 e x}{log x} \frac{{(ψ (x / e))}^{2}}{{(log x - 1)}^{2}} \end{matrix}

Implying,

\begin{matrix} {(ψ (x))}^{3} \approx 3 e x {(ψ (x / e))}^{2} (log x) {(log x - 1)}^{2} \end{matrix}

(17)

Dividing both sides by

{(ψ (x))}^{2}

\begin{matrix} ψ (x) \approx 3 e x (log x) {(log x - 1)}^{2} \end{matrix}

N.B. Since

ψ (x)

is much larger than

ψ (x / e)

for large x, this approximation holds.

As for

G (x)

, again, given the dominance of

ψ (x)

\begin{matrix} \frac{{(ψ (x))}^{2}}{{(log x)}^{2}} \approx \frac{e x}{log x} \frac{ψ (x / e)}{log x - 1} \end{matrix}

(18)

Observe that, the leading term in

G (x)

is negative, implying

G (x) < 0

Conversely, consider that,

G (x) < 0

. This implies,

\begin{matrix} {(\frac{ψ (x)}{log x})}^{2} < \frac{e x}{log x} (\frac{ψ (x / e)}{log x - 1}) \end{matrix}

(19)

Dividing both sides by

(\frac{ψ (x / e)}{log x - 1})

, we get,

\begin{matrix} \frac{ψ (x)}{log x} < \frac{e x (ψ (x / e))}{(log x - 1)} \end{matrix}

Evaluate

H (x)

\begin{matrix} H (x) : = {(\frac{ψ (x)}{log x})}^{3} - \frac{3 e x}{log x} (\frac{{(ψ (x / e))}^{2}}{{(log x - 1)}^{2}}) + \frac{3 e^{2} x}{{(log x)}^{2}} (\frac{ψ (x / e^{2})}{log x - 2}) \end{matrix}

Given the dominance of

ψ (x)

, we can assert that,

\begin{matrix} {(\frac{ψ (x)}{log x})}^{3} < \frac{3 e x}{log x} (\frac{{(ψ (x / e))}^{2}}{{(log x - 1)}^{2}}) \end{matrix}

(20)

Which simplifies to,

\begin{matrix} {(\frac{ψ (x)}{log x})}^{3} \approx \frac{3 e x {(ψ (x / e))}^{2}}{{(log x - 1)}^{2}} \end{matrix}

(21)

Dividing both sides by

(\frac{ψ (x)}{log x})

\begin{matrix} {(\frac{ψ (x)}{log x})}^{2} \approx 3 e x (ψ (x / e)) (log x) (log x - 1) \end{matrix}

(22)

The dominant term in (22) indicates that the inequality

H (x) < 0

holds true for large enough x. This completes the proof.

□

3.4. Higher-Degree Polynomial Inequality

Theorem 3.4.

For higher powers, let’s consider,

\begin{matrix} K (x) : = {(π (x))}^{4} - \frac{4 e x}{log x} {(π (x / e))}^{3} + \frac{6 e^{2} x}{{(log x)}^{2}} {(π (x / e^{2}))}^{2} - \frac{4 e^{3} x}{{(log x)}^{3}} π (x / e^{3}) \end{matrix}

(23)

Then, the following holds true,

\begin{matrix} K (x) \approx O (\frac{x^{4}}{{(log x)}^{5}}) \end{matrix}

(24)

and for sufficiently large x we have,

K (x) > 0

Proof.

A priori using the relation (4) (cf. [4]) from Theorem (2.2), along with (7) and (8),

\begin{matrix} π (x / e^{3}) = \frac{ψ (x / e^{3})}{log x - 3} + O (\frac{x / e^{3}}{{(log x - 3)}^{2}}) \end{matrix}

(25)

Now, we compute,

\begin{matrix} {(π (x))}^{4} = {(\frac{ψ (x)}{log x} + O (\frac{x}{{(log x)}^{2}}))}^{4} = \frac{{(ψ (x))}^{4}}{{(log x)}^{4}} + O (\frac{x^{4}}{{(log x)}^{5}}) \end{matrix}

(26)

Moreover,

\begin{matrix} \frac{4 e x}{log x} {(π (x / e))}^{3} = \frac{4 e x}{log x} {(\frac{ψ (x / e)}{log x - 1} + O (\frac{x / e}{{(log x - 1)}^{2}}))}^{3} \end{matrix}

\begin{matrix} = \frac{4 e x {(ψ (x / e))}^{3}}{(log x) {(log x - 1)}^{3}} + O (\frac{x^{4}}{{(log x)}^{5}}) \end{matrix}

(27)

Subsequently, we approximate the rest of the terms of

K (x)

as follows.

\begin{matrix} \frac{6 e^{2} x}{{(log x)}^{2}} {(π (x / e^{2}))}^{2} = \frac{6 e^{2} x}{{(log x)}^{2}} {(\frac{ψ (x / e^{2})}{log x - 2} + O (\frac{x / e^{2}}{{(log x - 2)}^{2}}))}^{2} \end{matrix}

\begin{matrix} = \frac{6 e^{2} x {(ψ (x / e^{2}))}^{2}}{{(log x)}^{2} {(log x - 2)}^{2}} + O (\frac{x^{4}}{{(log x)}^{5}}) \end{matrix}

(28)

And,

\begin{matrix} \frac{4 e^{3} x}{{(log x)}^{3}} π (x / e^{3}) = \frac{4 e^{3} x}{{(log x)}^{3}} (\frac{ψ (x / e^{3})}{log x - 3} + O (\frac{x / e^{3}}{{(log x - 3)}^{2}})) \end{matrix}

\begin{matrix} = \frac{4 e^{3} x ψ (x / e^{3})}{{(log x)}^{3} (log x - 3)} + O (\frac{x^{4}}{{(log x)}^{5}}) \end{matrix}

(29)

Combining (25), (26), (27), (28) and (29), and sorting out the dominant terms and their contributions towards the error term,

\begin{matrix} K (x) = \frac{{(ψ (x))}^{4}}{{(log x)}^{4}} - \frac{4 e x {(ψ (x / e))}^{3}}{(log x) {(log x - 1)}^{3}} + \frac{6 e^{2} x {(ψ (x / e^{2}))}^{2}}{{(log x)}^{2} {(log x - 2)}^{2}} \end{matrix}

\begin{matrix} - \frac{4 e^{3} x ψ (x / e^{3})}{{(log x)}^{3} (log x - 3)} + O (\frac{x^{4}}{{(log x)}^{5}}) \end{matrix}

(30)

A simple application of (3) yields,

\begin{matrix} K (x) = \frac{x^{4}}{{(log x)}^{4}} (1 - \frac{4 e}{log x} + \frac{6 e^{2}}{{(log x)}^{2}} - \frac{4 e^{3}}{{(log x)}^{3}}) + O (\frac{x^{4}}{{(log x)}^{5}}) \end{matrix}

(31)

Since

(1 - \frac{4 e}{log x} + \frac{6 e^{2}}{{(log x)}^{2}} - \frac{4 e^{3}}{{(log x)}^{3}})

is positive for sufficiently large x (higher-order terms diminish as x grows), hence the dominant term is positive. Accordingly, the error term in the approximation is,

\begin{matrix} O (\frac{x^{4}}{{(log x)}^{5}}) \end{matrix}

In conclusion, we assert that, (24) indeed holds true, and

K (x) > 0

for sufficiently large enough x. □

Remark 3.5.

We can also rephrase the result obtained from Theorem (3.4) in the form,

\begin{matrix} \frac{4 e x}{log x} {(π (x / e))}^{3} + \frac{4 e^{3} x}{{(log x)}^{3}} π (x / e^{3}) < {(π (x))}^{4} + \frac{6 e^{2} x}{{(log x)}^{2}} {(π (x / e^{2}))}^{2} \end{matrix}

(32)

for sufficiently large values of x.

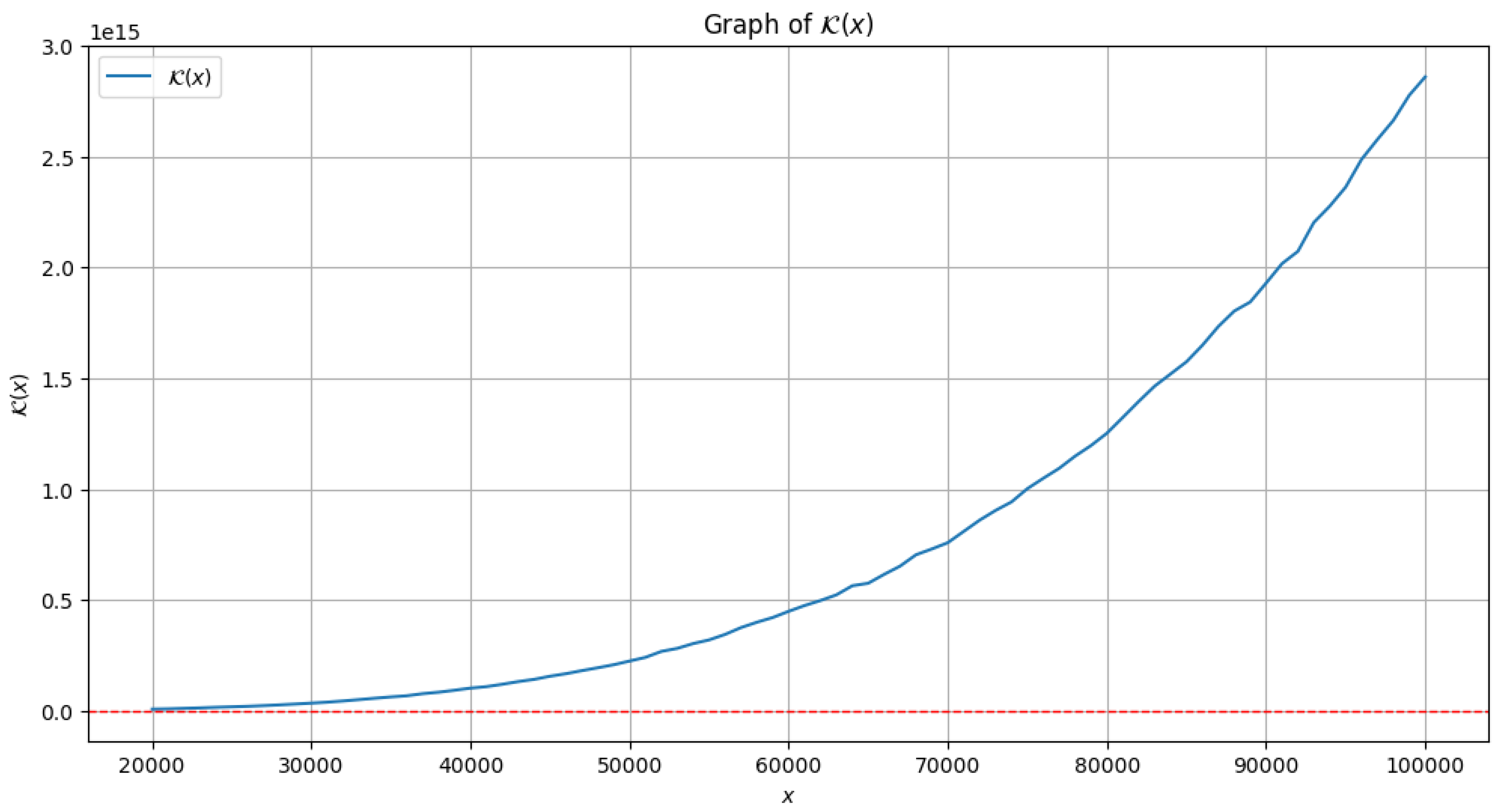
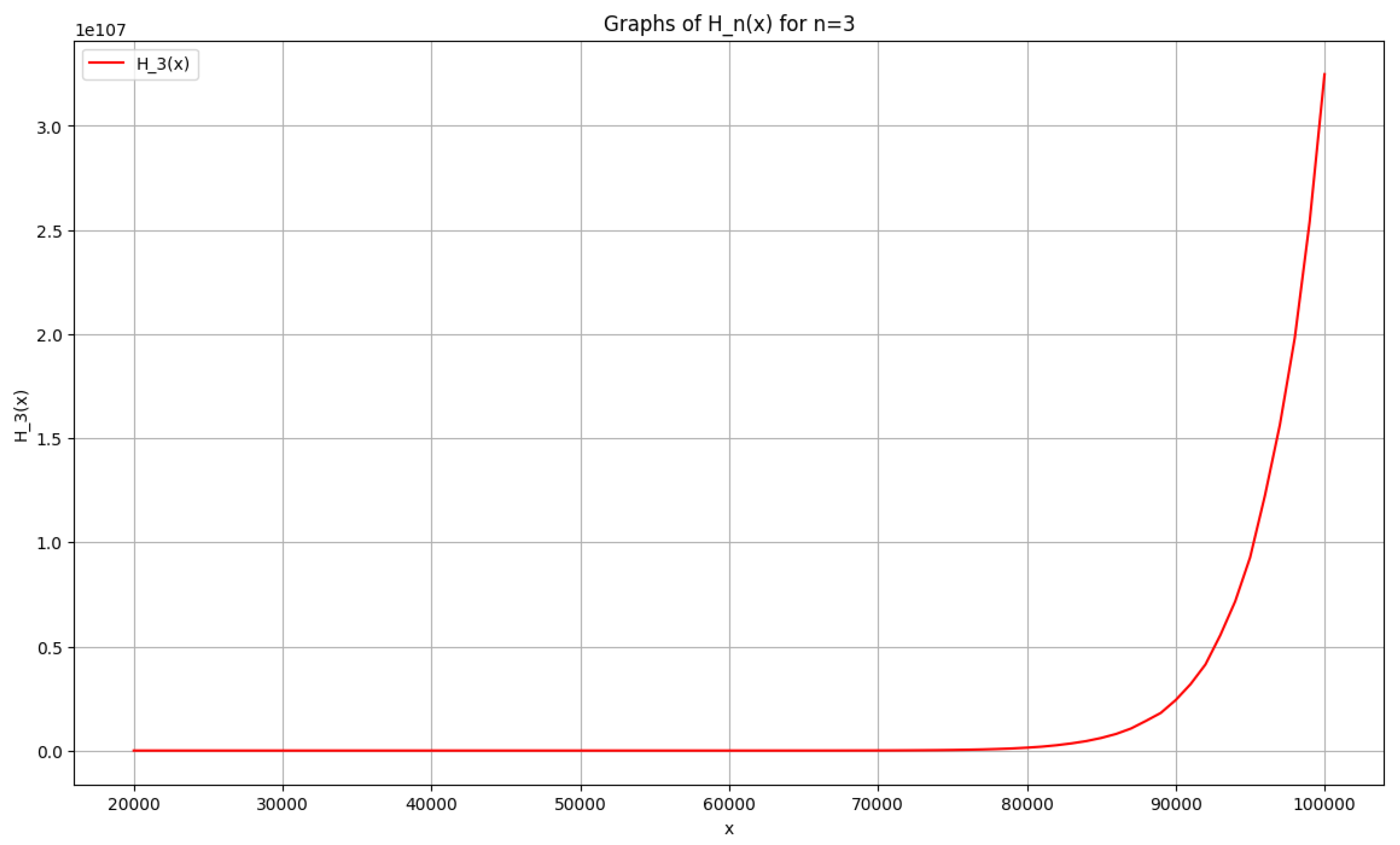
3.5. Numerical Estimates for $K (x)$

Important to observe that, one can apply PYTHON programming language1 in order to observe the plot of

K (x)

as compared to x. The following Figure 2 shows the plot for

2 \times 10^{4} \leq x \leq 10^{5}

. Moreover, the following values of

H (x)

can in fact be calculated using MATHEMATICA1, as evident from Table 2 in the range,

10^{4} \leq x \leq 10^{17}

. Using the data one can clearly infer that,

K (x)

is indeed increasing in this interval, hence, our claim (32) can be established numerically.

4. Quadratic Form Involving Sums of Prime Counting Function

4.1. Inequality Involving Weighted Sums of $π (x)$

Theorem 4.1.

Consider a quadratic form involving the sum of the prime counting function over smaller intervals,

\begin{matrix} L (x) = {(\sum_{k = 1}^{n} π (x / k))}^{2} - \frac{e x}{log x} (\sum_{k = 1}^{n} π (x / (e k))), n > 1 \end{matrix}

(33)

For some fixed n, then we have the following approximation,

\begin{matrix} L (x) \approx O (\frac{x^{2}}{{(log x)}^{2}}) \end{matrix}

(34)

With

L (x) > 0

for sufficiently large values of x.

Proof.

For the proof, we evaluate terms inside the summand of

L (x)

, a priori using the result (4) (cf. [4]) in Theorem (2.2).

\begin{matrix} π (x / k) = \frac{ψ (x / k)}{log x - log k} + O (\frac{x / k}{{(log x - log k)}^{2}}) \end{matrix}

(35)

\begin{matrix} π (x / (e k)) = \frac{ψ (x / (e k))}{log x - log (e k)} + O (\frac{x / (e k)}{{(log x - log (e k))}^{2}}) \end{matrix}

(36)

Hence,

\begin{matrix} \sum_{k = 1}^{n} π (x / k) = \sum_{k = 1}^{n} (\frac{ψ (x / k)}{log x - log k} + O (\frac{x / k}{{(log x - log k)}^{2}})) \end{matrix}

\begin{matrix} = \sum_{k = 1}^{n} \frac{ψ (x / k)}{log x - log k} + O (\sum_{k = 1}^{n} \frac{x / k}{{(log x - log k)}^{2}}) \end{matrix}

(37)

Similarly,

\begin{matrix} \sum_{k = 1}^{n} π (x / (e k)) = \sum_{k = 1}^{n} (\frac{ψ (x / (e k))}{log x - log (e k)} + O (\frac{x / (e k)}{{(log x - log (e k))}^{2}})) \end{matrix}

\begin{matrix} = \sum_{k = 1}^{n} \frac{ψ (x / (e k))}{log x - log (e k)} + O (\sum_{k = 1}^{n} \frac{x / (e k)}{{(log x - log (e k))}^{2}}) \end{matrix}

(38)

Squaring (37) gives,

\begin{matrix} {(\sum_{k = 1}^{n} π (x / k))}^{2} = {(\sum_{k = 1}^{n} \frac{ψ (x / k)}{log x - log k} + O (\sum_{k = 1}^{n} \frac{x / k}{{(log x - log k)}^{2}}))}^{2} \end{matrix}

\begin{matrix} \approx {(\sum_{k = 1}^{n} \frac{ψ (x / k)}{log x - log k})}^{2} \end{matrix}

Ignoring the higher-order terms for the time being. Further computation yields,

\begin{matrix} {(\sum_{k = 1}^{n} \frac{ψ (x / k)}{log x - log k})}^{2} = \sum_{k = 1}^{n} \sum_{j = 1}^{n} \frac{ψ (x / k) ψ (x / j)}{(log x - log k) (log x - log j)} \end{matrix}

(39)

Combining (38) and (39),

\begin{matrix} L (x) \approx {(\sum_{k = 1}^{n} \frac{ψ (x / k)}{log x - log k})}^{2} - \frac{e x}{log x} \sum_{k = 1}^{n} \frac{ψ (x / (e k))}{log x - log (e k)} \end{matrix}

(40)

An important observation is that, the leading term of

ψ (x)

is x, so for large x,

\begin{matrix} ψ (x / k) = \frac{x}{k} + O (\sqrt{\frac{x}{k}} {log}^{2} x) a n d, ψ (x / (e k)) = \frac{x}{e k} + O (\sqrt{\frac{x}{e k}} {log}^{2} x) \end{matrix}

Therefore, using the leading term approximation, we can deduce,

\begin{matrix} L (x) \approx {(\sum_{k = 1}^{n} \frac{x / k}{log x - log k})}^{2} - \frac{e x}{log x} \sum_{k = 1}^{n} \frac{x / (e k)}{log x - log (e k)} \end{matrix}

Where,

\begin{matrix} {(\sum_{k = 1}^{n} \frac{x / k}{log x - log k})}^{2} \approx {(\frac{x}{log x} \sum_{k = 1}^{n} \frac{1}{k})}^{2} \approx {(\frac{x}{log x} H_{n})}^{2} \end{matrix}

H_{n}

denoting the n-th Harmonic Number,

H_{n} \approx log n + γ

γ

being the Euler Constant.

As for the second term in the expression of

L (x)

\begin{matrix} \frac{e x}{log x} \sum_{k = 1}^{n} \frac{x / (e k)}{log x - log (e k)} \approx \frac{e x}{log x} \cdot \frac{x}{e log x} \sum_{k = 1}^{n} \frac{1}{k} \approx {(\frac{x}{log x})}^{2} H_{n} \end{matrix}

Therefore,

\begin{matrix} L (x) \approx {(\frac{x H_{n}}{log x})}^{2} - \frac{x^{2} H_{n}}{{(log x)}^{2}} \approx \frac{x^{2} {(log n)}^{2}}{{(log x)}^{2}} - \frac{x^{2} log n}{{(log x)}^{2}} \approx \frac{x^{2} log n (log n - 1)}{{(log x)}^{2}} \end{matrix}

On the other hand, analyzing the error terms from previously derived estimates, it can be deduced that,

\begin{matrix} L (x) = O (\frac{x^{2}}{{(log x)}^{2}}) \end{matrix}

(41)

Hence, (34) follows. Moreover, since the leading term

\frac{x^{2} log n (log n - 1)}{{(log x)}^{2}}

is positive for

n > 1

, thus it implies that

L (x)

is positive for large x, and the proof is complete. □

Remark 4.2.

We can rephrase Theorem (4.1) by claiming that, for every

n > 1

\begin{matrix} {(\sum_{k = 1}^{n} π (x / k))}^{2} > \frac{e x}{log x} (\sum_{k = 1}^{n} π (x / (e k))) \end{matrix}

(42)

for sufficiently large x.

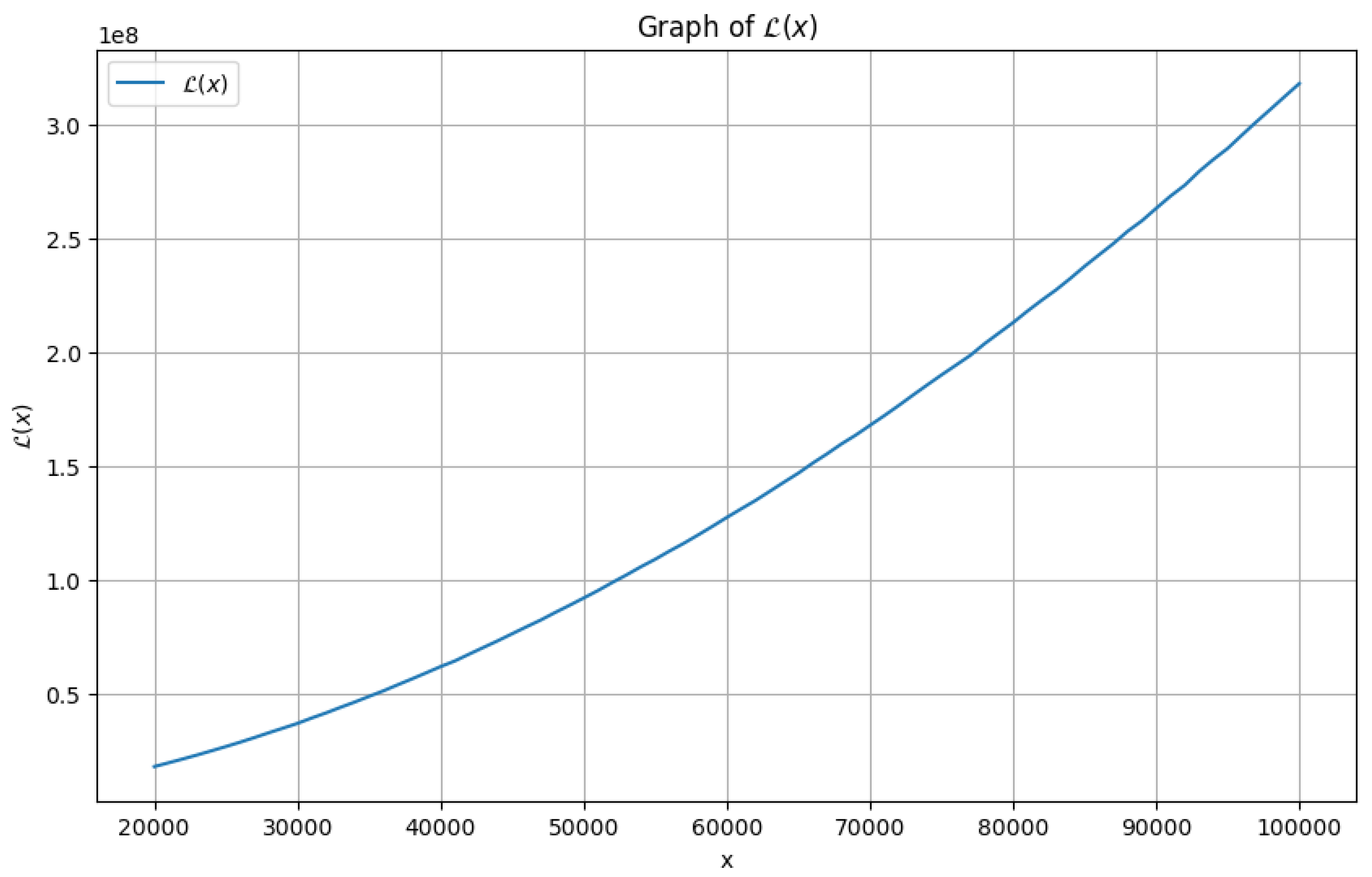
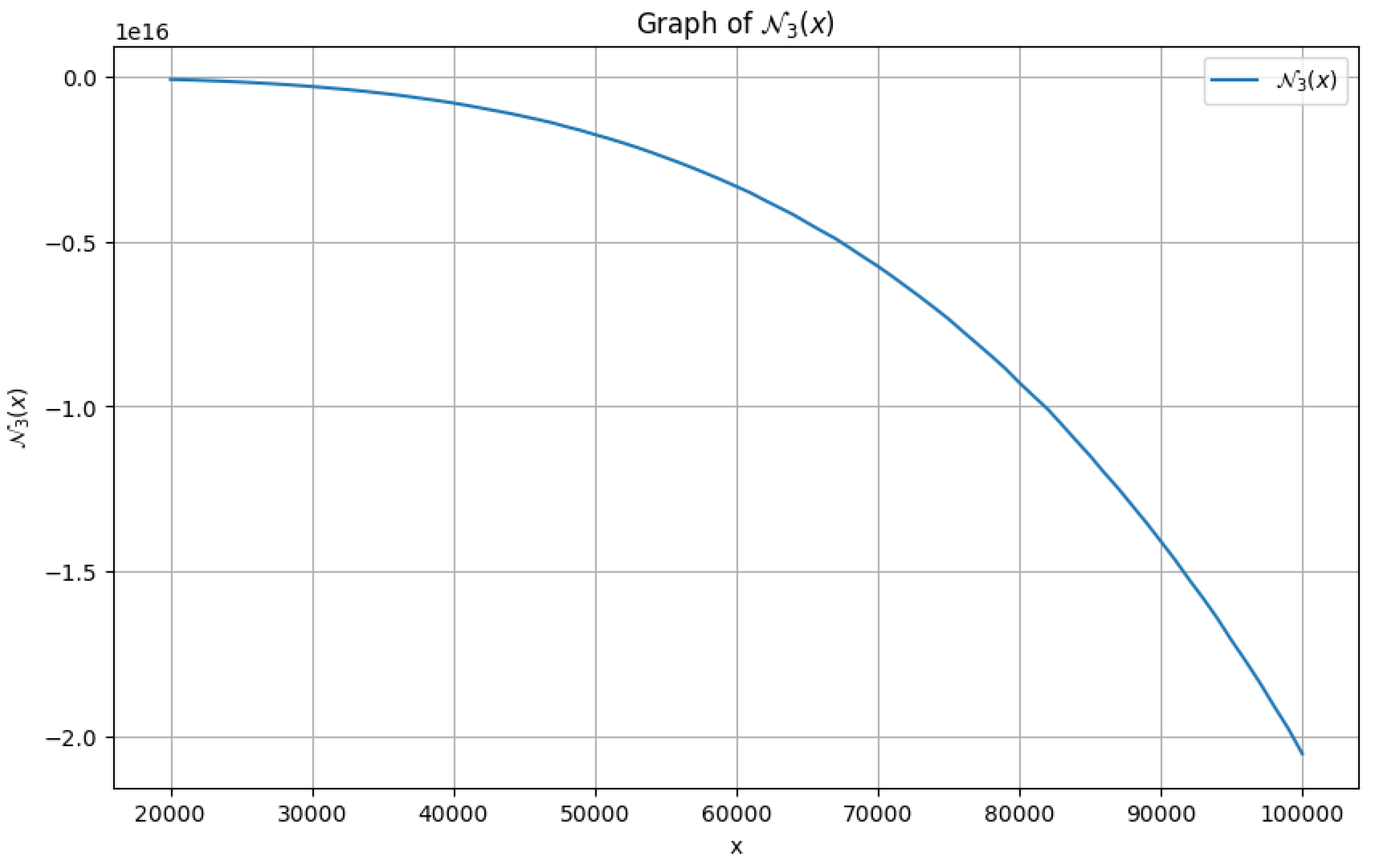
4.2. Numerical Estimates for $L (x)$

For a specific scenario when

n = 5

, plotting

L (x)

as compared to x using PYTHON programming language1 gives us the following graph as in Figure 3 for

2 \times 10^{4} \leq x \leq 10^{5}

. Moreover, applying MATHEMATICA1, it can be asserted using the data shown in Table 3 in the range,

10^{4} \leq x \leq 10^{16}

that,

L (x)

is indeed increasing. As a result, the statement (42) can be properly accepted.

4.3. Logarithmic Weighted Sum Inequality

It is very much possible to improve (34) even further, where one can also consider the case which involves logarithmic weights.

Theorem 4.3.

The following can in fact be conjectured for the logarithmic weights,

\begin{matrix} F (x) : = {(\sum_{k = 1}^{n} \frac{π (x / k)}{log (x / k)})}^{2} - \frac{e x}{log x} (\sum_{k = 1}^{n} \frac{π (x / (e k))}{log (x / (e k))}), n > 1 \end{matrix}

(43)

Then,

\begin{matrix} F (x) \approx O (\frac{x^{2}}{{(log x)}^{3}}) \end{matrix}

(44)

And,

F (x) < 0

for large values of x.

Proof.

A priori for large x, utilizing (3) (cf. [4]),

\begin{matrix} ψ (x / k) = \frac{x}{k} + O (\sqrt{\frac{x}{k}} {log}^{2} (\frac{x}{k})) a n d, ψ (x / (e k)) = \frac{x}{e k} + O (\sqrt{\frac{x}{e k}} {log}^{2} (\frac{x}{e k})) \end{matrix}

Rigorously computation each and every term of

F (x)

yields,

\begin{matrix} \sum_{k = 1}^{n} \frac{π (x / k)}{log (x / k)} = \sum_{k = 1}^{n} (\frac{ψ (x / k)}{{(log (x / k))}^{2}} + O (\frac{x / k}{{(log (x / k))}^{3}})), \end{matrix}

(45)

and similarly,

\begin{matrix} \sum_{k = 1}^{n} \frac{π (x / (e k))}{log (x / (e k))} = \sum_{k = 1}^{n} (\frac{ψ (x / (e k))}{{(log (x / (e k)))}^{2}} + O (\frac{x / (e k)}{{(log (x / (e k)))}^{3}})) . \end{matrix}

(46)

Subsequently squaring the left-hand side of (45),

\begin{matrix} {(\sum_{k = 1}^{n} \frac{π (x / k)}{log (x / k)})}^{2} = {(\sum_{k = 1}^{n} (\frac{ψ (x / k)}{{(log (x / k))}^{2}}) + \sum_{k = 1}^{n} O (\frac{x / k}{{(log (x / k))}^{3}}))}^{2} \end{matrix}

Using the Cauchy-Schwarz Inequality, and considering the main term and error terms separately,

\begin{matrix} {(\sum_{k = 1}^{n} \frac{x}{k {(log (x / k))}^{2}})}^{2} = \frac{x^{2}}{{(log x)}^{4}} {(\sum_{k = 1}^{n} \frac{1}{k})}^{2} = \frac{x^{2}}{{(log x)}^{4}} {(H_{n})}^{2} \end{matrix}

(47)

Where,

H_{n}

denotes the Harmonic Number. Using the harmonic series approximation,

\begin{matrix} H_{n} = \sum_{k = 1}^{n} \frac{1}{k} \approx log n + γ . \end{matrix}

(48)

Hence, from (47),

\begin{matrix} {(\sum_{k = 1}^{n} \frac{π (x / k)}{log (x / k)})}^{2} = \frac{x^{2} {log}^{2} n}{{(log x)}^{4}} . \end{matrix}

(49)

As for the error term,

\begin{matrix} O (\sum_{k = 1}^{n} \frac{x / k}{{(log (x / k))}^{3}}) = O (\sum_{k = 1}^{n} \frac{x / k}{{(log (x / k))}^{3}}) = O (\frac{x log n}{{(log x)}^{3}}) \end{matrix}

Thus, combining all our deductions,

\begin{matrix} {(\sum_{k = 1}^{n} \frac{π (x / k)}{log (x / k)})}^{2} = \frac{x^{2} {log}^{2} n}{{(log x)}^{4}} + O (\frac{x^{2} {log}^{2} n}{{(log x)}^{6}}) \end{matrix}

Furthermore, for the second term in (43), we have the following calculations,

\begin{matrix} \frac{e x}{log x} \sum_{k = 1}^{n} \frac{π (x / (e k))}{log (x / (e k))} = \frac{e x}{log x} \sum_{k = 1}^{n} (\frac{ψ (x / (e k))}{{(log (x / (e k)))}^{2}} + O (\frac{x / (e k)}{{(log (x / (e k)))}^{3}})) . \end{matrix}

(50)

Approximating the main term,

\begin{matrix} \frac{e x}{log x} \sum_{k = 1}^{n} \frac{x / (e k)}{{(log (x / (e k)))}^{2}} = \frac{e x^{2}}{log x} \sum_{k = 1}^{n} \frac{1}{e k {(log (x / (e k)))}^{2}} \end{matrix}

Using the harmonic series approximation,

\begin{matrix} \sum_{k = 1}^{n} \frac{1}{e k} \approx \frac{log n}{e} \end{matrix}

As a consequence,

\begin{matrix} \frac{e x^{2}}{log x} \frac{log n}{e {(log x)}^{2}} = \frac{x^{2} log n}{{(log x)}^{3}} . \end{matrix}

Combining all,

\begin{matrix} F (x) = {(\sum_{k = 1}^{n} \frac{π (x / k)}{log (x / k)})}^{2} - \frac{e x}{log x} (\sum_{k = 1}^{n} \frac{π (x / (e k))}{log (x / (e k))}) \end{matrix}

\begin{matrix} = \frac{x^{2} {log}^{2} n}{{(log x)}^{4}} + O (\frac{x^{2} {log}^{2} n}{{(log x)}^{6}}) - \frac{x^{2} log n}{{(log x)}^{3}} = - \frac{x^{2} log n}{{(log x)}^{3}} + O (\frac{x^{2} log n}{{(log x)}^{4}}) \end{matrix}

Considering the dominant term. As a result, we conclude,

\begin{matrix} F (x) \approx O (\frac{x^{2} log n}{{(log x)}^{4}}) = O (\frac{x^{2}}{{(log x)}^{3}}) \end{matrix}

for large x, and moreover, the dominant term,

\frac{x^{2} log n}{{(log x)}^{3}}

being always positive for

n > 1

, we can thus assert that,

F (x) < 0

for sufficiently large values of x. □

Remark 4.4.

We can reaffirm Theorem (4.3) in the following manner. For any

n > 1

\begin{matrix} {(\sum_{k = 1}^{n} \frac{π (x / k)}{log (x / k)})}^{2} < \frac{e x}{log x} (\sum_{k = 1}^{n} \frac{π (x / (e k))}{log (x / (e k))}) \end{matrix}

(51)

for sufficiently large values of x.

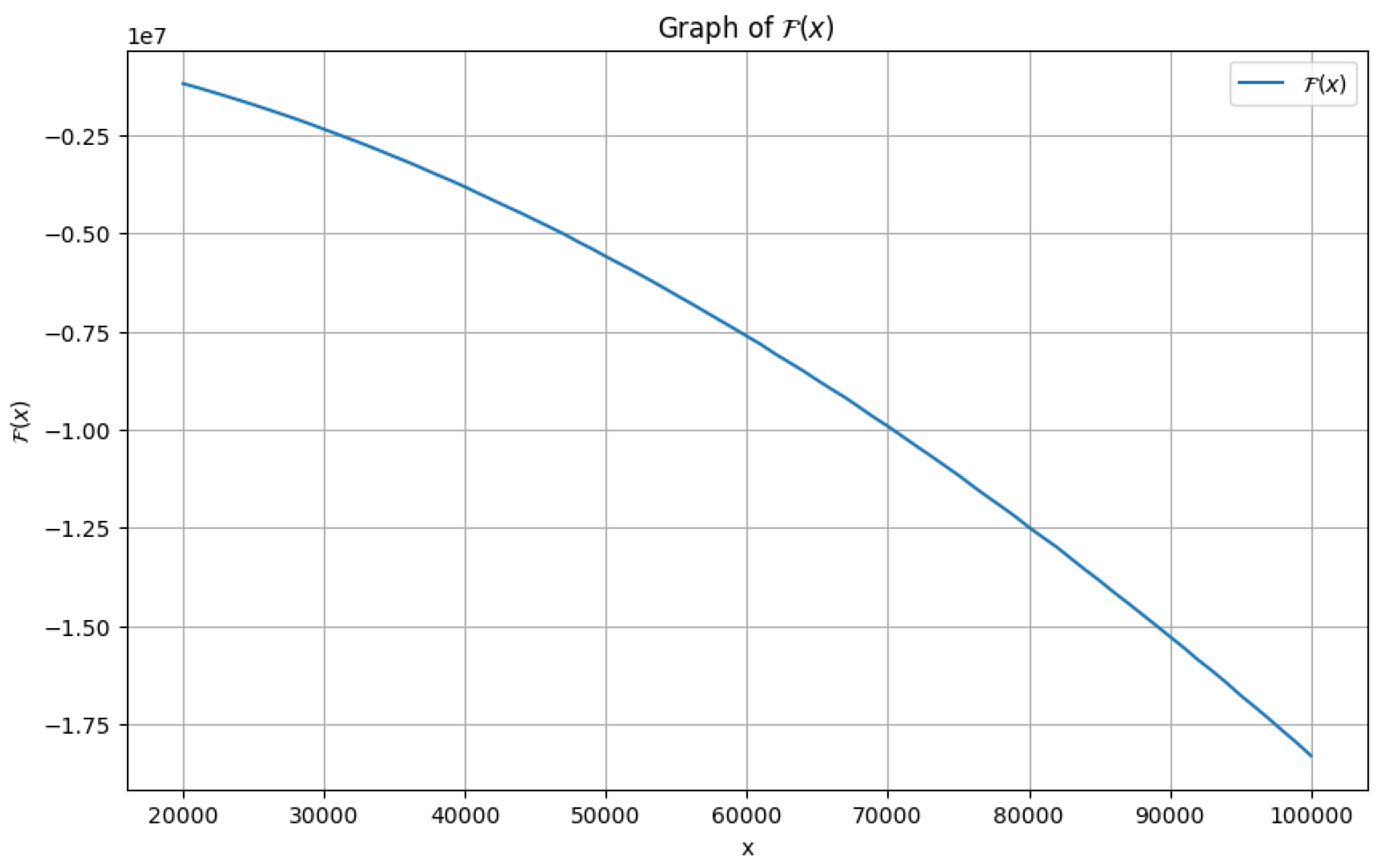
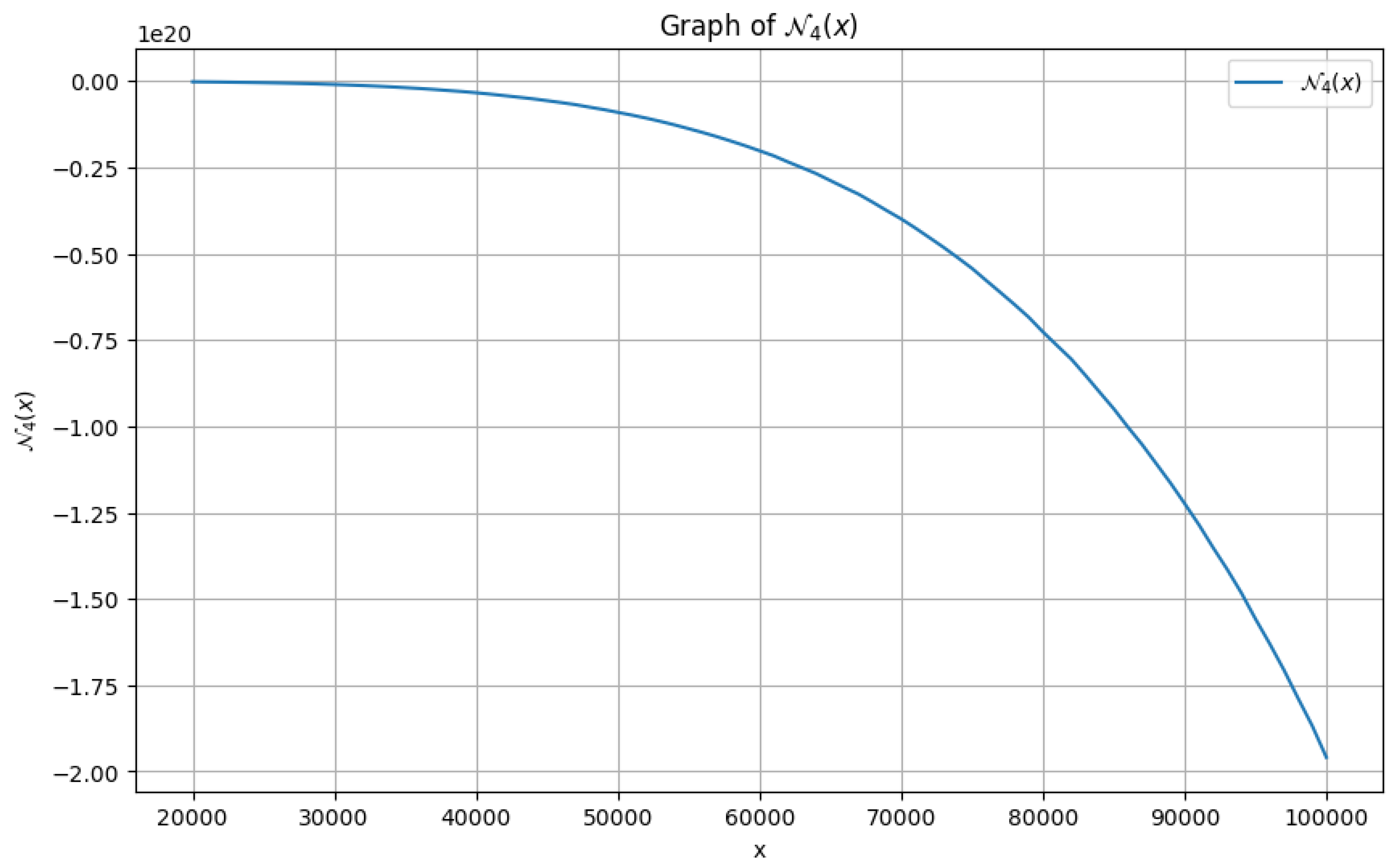
4.4. Numerical Estimates for $F (x)$

Similarly as in other cases, PYTHON programming language1 can in fact be applied in order to observe the plot of

F (x)

as compared to x. The following Figure 4 shows the graph for

2 \times 10^{4} \leq x \leq 10^{5}

and considering

n = 5

In addition to above, with the help of MATHEMATICA1, it can be observed in Table 4 that,

F (x)

is in fact decreasing in the range,

10^{4} \leq x \leq 10^{14}

. As a result, the statement (51) can also be numerically verified for large values of x.

5. A More General Framework

Given the asymptotic nature of the prime counting function

π (x)

, the general form of such polynomial functions can be formulated as follows.

\begin{matrix} N (x) : = P (π (x)) - \frac{e x}{log x} Q (π (x / e)) + R (x) \end{matrix}

(52)

where P and Q are polynomials and R is a term that compensates for higher-order error terms. Subsequently, one can claim that, the error term in (52) might behave similarly as in the previous cases. In mathematical terms, it might very well be possible that,

\begin{matrix} N (x) \approx O (\frac{x^{d}}{{(log x)}^{d + 1}}) \end{matrix}

(53)

for some degree d depending on the degrees of P and Q.

In order to justify our claim (53) corresponding to (52), let’s delve into a specific example by explicitly choosing polynomials P, Q, and

R (x)

and studying the function

N (x)

for different cases explicitely.

5.1. A Typical Example I : Generalized Cubic Polynomial Inequality

We assume,

\begin{matrix} P (π (x)) : = {(π (x))}^{3^{n}}, Q (π (x / e)) : = 3 {(π (x / e))}^{3^{n} - 1} \end{matrix}

and,

\begin{matrix} R (x) : = \frac{3 e^{2} x}{{(log x)}^{2}} {(π (x / e^{2}))}^{3^{n} - 2} \end{matrix}

for every

n > 1

. Then, in contrast to what we’ve discussed in Theorem (3.1), we can observe a significant change in the behaviour of the so-called Generalized Cubic Polynomial defined as,

\begin{matrix} H_{n} (x) : = {(π (x))}^{3^{n}} - \frac{3 e x}{log x} {(π (x / e))}^{3^{n} - 1} + \frac{3 e^{2} x}{{(log x)}^{2}} {(π (x / e^{2}))}^{3^{n} - 2} \end{matrix}

(54)

Furthermore, one has the following estimate for

H_{n} (x)

as x increases.

Theorem 5.1.

A priori

H_{n} (x)

defined as in (54) for every

n > 1

, we can derive that,

\begin{matrix} H_{n} (x) \approx O (\frac{x^{3^{n}}}{{(log x)}^{3^{n} + 1}}) \end{matrix}

(55)

Furthermore,

H_{n} (x) > 0

for sufficiently large values of x.

Proof.

Utilizing (4) in Theorem (2.2) as we’ve done in other cases, along with the derivations done in (7) and (8), we rigorously compute the following terms of

H_{n} (x)

indivudually for large values of n and x,

\begin{matrix} {(π (x))}^{3^{n}} = {(\frac{x}{log x})}^{3^{n}} + 3^{n} {(\frac{x}{log x})}^{3^{n} - 1} O (\frac{x}{{log}^{2} x}) + \dots \end{matrix}

\begin{matrix} = {(\frac{x}{log x})}^{3^{n}} + O (\frac{x^{3^{n}}}{{(log x)}^{3^{n} + 1}}) \end{matrix}

(56)

\begin{matrix} {(π (x / e))}^{3^{n} - 1} = {(\frac{x / e}{log x - 1})}^{3^{n} - 1} + (3^{n} - 1) {(\frac{x / e}{log x - 1})}^{3^{n} - 2} O (\frac{x}{{log}^{2} x}) + \dots \end{matrix}

\begin{matrix} = {(\frac{x}{e (log x - 1)})}^{3^{n} - 1} + O (\frac{x^{3^{n} - 1}}{{(log x)}^{3^{n}}}) \end{matrix}

(57)

and,

\begin{matrix} {(π (x / e^{2}))}^{3^{n} - 2} = {(\frac{x / e^{2}}{log x - 2})}^{3^{n} - 2} + (3^{n} - 2) {(\frac{x / e^{2}}{log x - 2})}^{3^{n} - 3} O (\frac{x}{{log}^{2} x}) + \dots \end{matrix}

\begin{matrix} = {(\frac{x}{e^{2} (log x - 2)})}^{3^{n} - 2} + O (\frac{x^{3^{n} - 2}}{{(log x)}^{3^{n}}}) \end{matrix}

(58)

Substituting (56), (57) and (58) back into

H_{n} (x)

yields,

\begin{matrix} H_{n} (x) = {(\frac{x}{log x})}^{3^{n}} + \frac{3 e^{2} x}{{(log x)}^{2}} {(\frac{x}{e^{2} (log x - 2)})}^{3^{n} - 2} - \frac{3 e x}{log x} {(\frac{x}{e (log x - 1)})}^{3^{n} - 1} \end{matrix}

\begin{matrix} + O (\frac{x^{3^{n}}}{{(log x)}^{3^{n} + 1}}) \end{matrix}

\begin{matrix} = \frac{x^{3^{n}}}{{(log x)}^{3^{n}}} (1 - \frac{3 e}{e^{3^{n} - 1} {(log x - 1)}^{3^{n} - 1}} + \frac{3 e^{2}}{e^{2 (3^{n} - 2)} {(log x - 2)}^{3^{n} - 2}} \frac{1}{x}) \end{matrix}

\begin{matrix} + O (\frac{x^{3^{n}}}{{(log x)}^{3^{n} + 1}}) \end{matrix}

(59)

Important to note that, for sufficiently large x, the dominant term on the R. H. S. of (59) will be

\frac{x^{3^{n}}}{{(log x)}^{3^{n}}}

. The other terms will have exponentially decaying factors due to the presence of

e^{- (3^{n} - 1)}

and

e^{- 2 (3^{n} - 2)}

, making them small relative to the leading term. Therefore, the dominant term is positive, and the higher-order error terms do not affect the sign significantly.

In other words, the terms

\frac{3 e}{e^{3^{n} - 1} {(log x - 1)}^{3^{n} - 1}}

and

\frac{3 e^{2}}{e^{2 (3^{n} - 2)} {(log x - 2)}^{3^{n} - 2}} \frac{1}{x}

on (59) are small for large x, the dominant term

\frac{x^{3^{n}}}{{(log x)}^{3^{n}}}

ensures that

H_{n} (x) > 0

. Moreover, we have,

\begin{matrix} H_{n} (x) \approx O (\frac{x^{3^{n}}}{{(log x)}^{3^{n} + 1}}) \end{matrix}

And thus the proof is complete.

□

5.2. Numerical Estimates for $H_{n} (x)$

Applying PYTHON programming language1, we can in fact observe the plot of

H_{n} (x)

(

n = 1, 2, 3

) as compared to x for some special cases respectively. (N.B. Ardent researchers are highly encouraged to study the same using any different values of n) Subsequently, Figure 1, Figure 5 and Figure 6 represents the respective graphs for

2 \times 10^{4} \leq x \leq 10^{5}

Furthermore, using MATHEMATICA1 it can be inferred from Table 1 and Table 5 that, unlike

H_{1} (x)

(in this case,

H_{1} (x)

is simply denoted by

H (x)

as defined in (5)) which is strictly monotone decreasing,

H_{2} (x)

and

H_{3} (x)

are strictly monotone increasing while x assumes values in the range,

10^{4} \leq x \leq 10^{18}

. As a result, it can surely be concluded that,

H_{n} (x) > 0

for sufficiently large x and for

n > 1

, having an exception for

n = 1

Again, choosing P, Q and R accordingly, we can indeed conjecture a certain generalization of the Weighted Sum Inequality (cf. Theorem (4.1)).

5.3. A Typical Example II : Generalized Weighted Sum Inequality

For some fixed

n > 1

, consider the polynomials,

\begin{matrix} P (π (x)) = Q (π (x)) = {(\sum_{k = 1}^{n} π (x / k))}^{r} \end{matrix}

To maintain symmetry and include higher-order error terms, we choose

R (x) = {(\sum_{k = 1}^{n} π (x / (e^{2} k)))}^{r}

. It can be observed that, degrees of each of the polynomials P, Q and R are the same

= r

(

> 1

). We study the polynomial,

\begin{matrix} N_{r} (x) : = {(\sum_{k = 1}^{n} π (x / k))}^{r} - \frac{e x}{log x} {(\sum_{k = 1}^{n} π (x / (e k)))}^{r} + {(\sum_{k = 1}^{n} π (x / (e^{2} k)))}^{r} \end{matrix}

(60)

under two circumstances separately.

5.3.1. deg(P), deg(Q) and deg(R) Are Odd

We assume,

r = 2 m + 1

, for any positive integer m. A priori from the approximations derived in (3) and (4) (cf. [4]), we substitute

(x / k)

(x / e k)

and

x / (e^{2} k)

in them to compute each and every term in the polynomial separately.

\begin{matrix} \sum_{k = 1}^{n} π (x / k) = \sum_{k = 1}^{n} (\frac{x}{k log (x / k)} + O (\frac{x / k}{{log}^{2} (x / k)})) = \sum_{k = 1}^{n} (\frac{x}{k log x} + O (\frac{x}{k {log}^{2} x})) \end{matrix}

\begin{matrix} = \frac{x}{log x} \sum_{k = 1}^{n} \frac{1}{k} + O (\frac{x}{{log}^{2} x} \sum_{k = 1}^{n} \frac{1}{k}) = \frac{x}{log x} (log n + γ) + O (\frac{x}{{log}^{2} x} (log n + γ)) \end{matrix}

(61)

Using the harmonic series approximation (48).

Thus,

\begin{matrix} {(\sum_{k = 1}^{n} π (x / k))}^{2 m + 1} = {(\frac{x}{log x} (log n + γ))}^{2 m + 1} + O (\frac{x^{2 m + 1}}{{(log x)}^{2 m + 2}} {(log n + γ)}^{2 m + 1}) \end{matrix}

(62)

For the second term in

N_{2 m + 1} (x)

\begin{matrix} \frac{e x}{log x} {(\sum_{k = 1}^{n} π (x / (e k)))}^{2 m + 1} = \frac{e x}{log x} {(\frac{x}{e log x} (log n + γ))}^{2 m + 1} + O (\frac{x^{2 m + 1}}{{(log x)}^{2 m + 2}}) \end{matrix}

\begin{matrix} = \frac{x^{2 m + 2}}{e^{2 m} {(log x)}^{2 m + 2}} {(log n + γ)}^{2 m + 1} + O (\frac{x^{2 m + 1}}{{(log x)}^{2 m + 2}}) \end{matrix}

(63)

Finally, for

R (x)

\begin{matrix} {(\sum_{k = 1}^{n} π (x / (e^{2} k)))}^{2 m + 1} = \frac{x^{2 m + 1}}{e^{4 m + 2} {(log x)}^{2 m + 1}} {(log n + γ)}^{2 m + 1} + O (\frac{x^{2 m + 1}}{{(log x)}^{2 m + 2}}) \end{matrix}

(64)

Combining (62), (63) and (64),

\begin{matrix} N_{2 m + 1} (x) = \frac{x^{2 m + 1}}{{(log x)}^{2 m + 1}} {(log n + γ)}^{2 m + 1} - \frac{x^{2 m + 2}}{e^{2 m} {(log x)}^{2 m + 2}} {(log n + γ)}^{2 m + 1} \end{matrix}

\begin{matrix} + \frac{x^{2 m + 1}}{e^{4 m + 2} {(log x)}^{2 m + 1}} {(log n + γ)}^{2 m + 1} + O (\frac{x^{2 m + 1}}{{(log x)}^{2 m + 2}}) \end{matrix}

\begin{matrix} = - \frac{x^{2 m + 2}}{e^{2 m} {(log x)}^{2 m + 2}} {(log n + γ)}^{2 m + 1} + O (\frac{x^{2 m + 1}}{{(log x)}^{2 m + 2}}) \end{matrix}

(65)

Subsequently, the dominant error term in

N_{2 m + 1} (x)

can be found as,

\begin{matrix} O (\frac{x^{2 m + 1}}{{(log x)}^{2 m + 2}}) \end{matrix}

5.3.2. deg(P), deg(Q) and deg(R) Are Even

In this case, we assume,

r = 2 m

, for any positive integer m. Similarly, as in the first case, we utilize the approximations deduced in (3) and (4) (cf. [4]), we substitute

(x / k)

(x / e k)

and

x / (e^{2} k)

in them to approximate each and every term in the polynomial individually. From (61),

\begin{matrix} {(\sum_{k = 1}^{n} π (x / k))}^{2 m} = \frac{x^{2 m}}{{(log x)}^{2 m}} {(log n + γ)}^{2 m} + O (\frac{x^{2 m}}{{(log x)}^{2 m + 1}}) \end{matrix}

(66)

Moreover, for the second term in

N_{2 m} (x)

\begin{matrix} \frac{e x}{log x} {(\sum_{k = 1}^{n} π (x / (e k)))}^{2 m} = \frac{e x}{log x} {(\frac{x}{e log x} (log n + γ))}^{2 m} + O (\frac{x^{2 m}}{{(log x)}^{2 m + 1}}) \end{matrix}

\begin{matrix} = \frac{x^{2 m + 1}}{e^{2 m - 1} {(log x)}^{2 m + 1}} {(log n + γ)}^{2 m} + O (\frac{x^{2 m}}{{(log x)}^{2 m + 1}}) \end{matrix}

(67)

Finally, for

R (x)

\begin{matrix} {(\sum_{k = 1}^{n} π (x / (e^{2} k)))}^{2 m} = \frac{x^{2 m}}{e^{4 m} {(log x)}^{2 m}} {(log n + γ)}^{2 m} + O (\frac{x^{2 m}}{{(log x)}^{2 m + 1}}) \end{matrix}

(68)

Combining (66), (67) and (68),

\begin{matrix} N_{2 m} (x) = \frac{x^{2 m}}{{(log x)}^{2 m}} {(log n + γ)}^{2 m} - \frac{x^{2 m + 1}}{e^{2 m - 1} {(log x)}^{2 m + 1}} {(log n + γ)}^{2 m} \end{matrix}

\begin{matrix} + \frac{x^{2 m}}{e^{4 m} {(log x)}^{2 m}} {(log n + γ)}^{2 m} + O (\frac{x^{2 m}}{{(log x)}^{2 m + 1}}) \end{matrix}

\begin{matrix} = - \frac{x^{2 m + 1}}{e^{2 m - 1} {(log x)}^{2 m + 1}} {(log n + γ)}^{2 m} + O (\frac{x^{2 m}}{{(log x)}^{2 m + 1}}) \end{matrix}

(69)

Important to assess that, the dominant error term in

N_{2 m} (x)

is,

\begin{matrix} O (\frac{x^{2 m}}{{(log x)}^{2 m + 1}}) \end{matrix}

In conclusion, in both the cases, we can properly justify in this example that, (53) is definitely satisfied. Moreover, as for the sign of

N_{r} (x)

, it can be duly noted that, the main term excluding the error term is indeed negative for sufficiently large values of x. Thus, in this scenario, one can safely conclude the following.

Theorem 5.2.

Given the weighted sum of Prime Counting Function over small intervals,

\begin{matrix} N_{r} (x) : = {(\sum_{k = 1}^{n} π (x / k))}^{r} - \frac{e x}{log x} {(\sum_{k = 1}^{n} π (x / (e k)))}^{r} + {(\sum_{k = 1}^{n} π (x / (e^{2} k)))}^{r}, n > 1 \end{matrix}

(70)

where,

r > 1

, the following holds true for sufficiently large values of x.

\begin{matrix} N_{r} (x) \approx O (\frac{x^{r}}{{(log x)}^{r + 1}}), a n d, N_{r} (x) < 0 . \end{matrix}

(71)

5.4. Numerical Estimates for $N_{r} (x)$

A priori with the help of PYTHON programming language1 we can indeed study the plot of

N_{3} (x)

(

m = 1, r = 3

) and

N_{4} (x)

(

m = 2, r = 4

) as compared to x for the odd and even cases respectively. (N.B. These two are some special cases for chosen values of m, one can study the same if interested using any different values of m) Subsequently, Figure 7 and Figure 8 represents the respective graphs for

2 \times 10^{4} \leq x \leq 10^{5}

and considering

n = 5

Furthermore, utilizing MATHEMATICA1, it can be inferred from Table 6 that,

N_{3} (x)

and

N_{4} (x)

are strictly monotone decreasing while x assumes values in the range,

10^{4} \leq x \leq 10^{15}

. As a result, it can surely be concluded that,

N_{r} (x) < 0

for sufficiently large x, and for this particular example, i.e. for this particular choice of P, Q and R.

6. Furture Scope for Research

It can definitely be said that, the results discussed in this article serves as a mere small version of what can be considered as a plethora of possibilities that future researchers can come up with.

It is very much possible to eventually derive a similar estimate for polynomials of degree

\geq 5

π (x)

, adopting similar techniques as devised in proposing the Cubic Polynomial Inequality and the Higher Degree Polynomial Inequality. It may very well help us to establish certain conjectures and even extend the study of primes even further.

Regarding the estimates which we’ve derived for functions involving weighted sums of

π (x)

over small intervals, it might be interesting to study them even further by varying indivudual weights of such funtions, and study their respective sign changes over increasing values of x.

On the other hand, it is very much possible to produce absolutely new results from the general polynomial (52), by choosing P, Q and R appropriately. As evident from the two examples which serves as generalizations of two of the inequalities which we’ve already discussed, it’s fascinating to observe that, the sign changes of the polynomials are completely unpredictable. For example, we’ve deduced that, for higher values of x, the generalized cubic polynomial

H_{n} (x)

as defined in (54) yields negative values for

n = 1

(in this case, we denote

H_{1} (x)

H (x)

, as defined in (5)), whereas, it’s sign reverses drastically for the case,

n > 1

(cf. Theorem (5.1)). Important to mention that, different conclusions may very well be possible for different types of examples. Although each and every such result involves some robust calculations and numerical computations, but it eventually opens up a whole new area for future researchers to explore, which might end up in enlightening us to some significant discoveries in the relevant field of Number Theory.

Data Availability Statement

I as the sole author of this article confirm that the data supporting the findings of this study are available within the article [and/or] its supplementary materials.

Acknowledgments

I’ll always be grateful to Prof. Adrian W. Dudek ( Adjunct Associate Professor, Department of Mathematics and Physics, University of Queensland, Australia ) for inspiring me to work on this problem and pursue research in this topic. His leading publications in this area helped me immensely in detailed understanding of the essential concepts.

Conflicts of Interest

I as the author of this article declare no conflicts of interest.

References

Ramanujan Aiyangar, Srinivasa, Berndt, Bruce C, Ramanujan’s Notebooks: Part IV, New York: Springer-Verlag, 1994. [CrossRef]
Dudek, Adrian W., Platt, David J., On Solving a Curious Inequality of Ramanujan, Experimental Mathematics, 2015, 24:3, 289-294. [CrossRef]
Titchmarsh, E. C., The Theory of the Riemann Zeta-function, Oxford University Press, 1951. Second edition revised by D. R. Heath-Brown, published by Oxford University Press, 1986. [CrossRef]
De, Subham, "On proving an Inequality of Ramanujan using Explicit Order Estimates for the Mertens Function", arXiv preprint arXiv:2407.12052 (2024). [CrossRef]
Schoenfeld, L., Sharper bounds for the Chebyshev Functions θ(x) and ψ(x). II, Mathematics of Computation, vol. 30, no. 134, pp. 337-360. [CrossRef]
ngham, A. E., The distribution of prime numbers, Cambridge University Press, 1932. Reprinted by Stechert-Hafner, 1964, and (with a foreword by R. C. Vaughan) by Cambridge University Press, 1990. [CrossRef]
Hassani, Mehdi, Remarks on Ramanujan’s Inequality Concerning the Prime Counting Function, Communications in Mathematics, Volume 29 (2021), Issue 3, Pages 473–482. [CrossRef]
Hassani, Mehdi, Generalizations of an inequality of Ramanujan concerning prime counting function, Appl. Math. E-Notes 13 (2013) 148-154.
Jameson, G.J.O., The Prime Number Theorem, Cambridge ; New York : Cambridge University Press, London Mathematical Society student texts, Vol. 53, 2003. [CrossRef]
De, Subham, On the proof of the Prime Number Theorem using Order Estimates for the Chebyshev Theta Function, International Journal of Science and Research (IJSR), Vol. 12 Issue 11, Nov. 2023, pp. 1677-1691. [CrossRef]
Hassani, Mehdi, “On an Inequality of Ramanujan Concerning the Prime Counting Function”, Ramanujan Journal 28 (2012), 435–442. [CrossRef]
Ramanujan, S, “Collected Papers”, Chelsea, New York, 1962.
Hardy, G. H., A formula of Ramanujan in the theory of primes, 1. London Math. Soc. 12 (1937), 94-98. [CrossRef]
Hardy, G. H., Collected Papers, vol. II, Clarendon Press, Oxford, 1967.
Axler, Christian, On Ramanujan’s prime counting inequality, arXiv preprint arXiv:2207.02486 (2022). arXiv:2207.02486 (2022).
Mossinghoff, M. J., Trudgian, T. S., Nonnegative Trigonometric Polynomials and a Zero-Free Region for the Riemann Zeta-Function, arXiv: 1410.3926, 2014.

1	Codes are available at: https://github.com/subhamde1/Paper-12.git

Figure 1. Graph of

H (x)

Figure 1. Graph of

H (x)

Figure 2. Graph of

K (x)

Figure 2. Graph of

K (x)

Figure 3. Graph of

L (x)

Figure 3. Graph of

L (x)

Figure 4. Graph of

F (x)

Figure 4. Graph of

F (x)

Figure 5. Graph of

H_{n} (x)

for

n = 2

Figure 5. Graph of

H_{n} (x)

for

n = 2

Figure 6. Graph of

H_{n} (x)

for

n = 3

Figure 6. Graph of

H_{n} (x)

for

n = 3

Figure 7. Graph of

N_{3} (x)

Figure 7. Graph of

N_{3} (x)

Figure 8. Graph of

N_{4} (x)

Figure 8. Graph of

N_{4} (x)

Table 1. Values of

H (x)

for

10^{4} \leq x \leq 10^{18}

Table 1. Values of

H (x)

for

10^{4} \leq x \leq 10^{18}

x	$H (x)$
$10^{4}$	$- 4.822952515086 \times 10^{8}$
$10^{5}$	$- 1.9535582364473376 \times 10^{11}$
$10^{6}$	$- 9.742665854621681 \times 10^{13}$
$10^{7}$	$- 5.373324095991878 \times 10^{16}$
$10^{8}$	$- 3.2776888213143585 \times 10^{19}$
$10^{9}$	$- 2.142500053569382 \times 10^{22}$
$10^{10}$	$- 1.4738226482632569 \times 10^{25}$
$10^{11}$	$- 1.0555737602257731 \times 10^{28}$
$10^{12}$	$- 7.810947114144009 \times 10^{30}$
$10^{13}$	$- 5.937547995444999 \times 10^{33}$
$10^{14}$	$- 4.6163278697477706 \times 10^{36}$
$10^{15}$	$- 3.65847701300371 \times 10^{39}$
$10^{16}$	$- 2.947501336471066 \times 10^{42}$
$10^{17}$	$- 2.4089115035201524 \times 10^{45}$
$10^{18}$	$- 1.9935903086211532 \times 10^{48}$

Table 2. Values of

K (x)

for

10^{4} \leq x \leq 10^{17}

Table 2. Values of

K (x)

for

10^{4} \leq x \leq 10^{17}

x	$K (x)$
$10^{4}$	$6.785501979995337 \times 10^{11}$
$10^{5}$	$2.858713229490609 \times 10^{15}$
$10^{6}$	$1.3657430631495643 \times 10^{19}$
$10^{7}$	$7.37684110441765 \times 10^{22}$
$10^{8}$	$4.2993020901898284 \times 10^{26}$
$10^{9}$	$2.6664968326322003 \times 10^{30}$
$10^{10}$	$1.7394264262779463 \times 10^{34}$
$10^{11}$	$1.1821189632007215 \times 10^{38}$
$10^{12}$	$8.310509439561298 \times 10^{41}$
$10^{13}$	$6.010924984361412 \times 10^{45}$
$10^{14}$	$4.454174125769207 \times 10^{49}$
$10^{15}$	$3.3701437003780375 \times 10^{53}$
$10^{16}$	$2.59663004179433 \times 10^{57}$
$10^{17}$	$2.0327843159078997 \times 10^{61}$

Table 3. Values of

L (x)

for

10^{4} \leq x \leq 10^{16}

Table 3. Values of

L (x)

for

10^{4} \leq x \leq 10^{16}

x	$L (x)$
$10^{4}$	$5.442878634267854 \times 10^{6}$
$10^{5}$	$3.182941989056241 \times 10^{8}$
$10^{6}$	$2.0720876553125698 \times 10^{10}$
$10^{7}$	$1.453173495473891 \times 10^{12}$
$10^{8}$	$1.0748621057424523 \times 10^{14}$
$10^{9}$	$8.271311872938837 \times 10^{15}$
$10^{10}$	$6.562072688654034 \times 10^{17}$
$10^{11}$	$5.3333332449648206 \times 10^{19}$
$10^{12}$	$4.4203146604764075 \times 10^{21}$
$10^{13}$	$3.723359062321086 \times 10^{23}$
$10^{14}$	$3.1792547132494815 \times 10^{25}$
$10^{15}$	$2.7463355733587377 \times 10^{27}$
$10^{16}$	$2.3962303815115464 \times 10^{29}$

Table 4. Values of

F (x)

for

10^{4} \leq x \leq 10^{14}

Table 4. Values of

F (x)

for

10^{4} \leq x \leq 10^{14}

x	$F (x)$
$10^{4}$	$- 377, 275.13516957406$
$10^{5}$	$- 1.830179494511997 \times 10^{7}$
$10^{6}$	$- 1.0203946684413686 \times 10^{9}$
$10^{7}$	$- 6.256701329540303 \times 10^{10}$
$10^{8}$	$- 4.1109224248432134 \times 10^{12}$
$10^{9}$	$- 2.8451189547136775 \times 10^{14}$
$10^{10}$	$- 2.0504855777527976 \times 10^{16}$
$10^{11}$	$- 1.5264989872331325 \times 10^{18}$
$10^{12}$	$- 1.1670093161419563 \times 10^{20}$
$10^{13}$	$- 9.121682100604639 \times 10^{21}$
$10^{14}$	$- 7.264828101112622 \times 10^{23}$

Table 5. Values of

H_{2} (x)

H_{3} (x)

for

10^{4} \leq x \leq 10^{18}

Table 5. Values of

H_{2} (x)

H_{3} (x)

for

10^{4} \leq x \leq 10^{18}

x	$H_{2} (x)$	$H_{3} (x)$
$10^{4}$	$6.353725021975254 \times 10^{27}$	$2.617585266401968 \times 10^{83}$
$10^{5}$	$6.835585478626048 \times 10^{35}$	$3.2474882786926336 \times 10^{107}$
$10^{6}$	$1.1261441103738037 \times 10^{44}$	$1.4493790443082677 \times 10^{132}$
$10^{7}$	$2.517601761588046 \times 10^{52}$	$1.6171807959592812 \times 10^{157}$
$10^{8}$	$6.965999334038062 \times 10^{60}$	$3.42269895601566 \times 10^{182}$
$10^{9}$	$2.2631415625131205 \times 10^{69}$	$1.1729707311062672 \times 10^{208}$
$10^{10}$	$8.334950926673871 \times 10^{77}$	$5.856806953089547 \times 10^{233}$
$10^{11}$	$3.393363660513159 \times 10^{86}$	$3.950820693357716 \times 10^{259}$
$10^{12}$	$1.4995319398929942 \times 10^{95}$	$3.408309291619576 \times 10^{285}$
$10^{13}$	$7.0941717053768875 \times 10^{103}$	$3.608074552069926 \times 10^{311}$
$10^{14}$	$3.555379086542425 \times 10^{112}$	$4.540919459707699 \times 10^{337}$
$10^{15}$	$1.8720454577090458 \times 10^{121}$	$6.627717169602305 \times 10^{363}$
$10^{16}$	$1.028783938302183 \times 10^{130}$	$1.0998319401738324 \times 10^{390}$
$10^{17}$	$5.869229663529639 \times 10^{138}$	$2.041946308723196 \times 10^{416}$
$10^{18}$	$3.460762114044545 \times 10^{147}$	$4.185719359179408 \times 10^{442}$

Table 6. Values of

N_{3} (x), N_{4} (x)

for

10^{4} \leq x \leq 10^{15}

Table 6. Values of

N_{3} (x), N_{4} (x)

for

10^{4} \leq x \leq 10^{15}

x	$N_{3} (x)$	$N_{4} (x)$
$10^{4}$	$- 6.204817261289663 \times 10^{12}$	$- 7.911694463952808 \times 10^{15}$
$10^{5}$	$- 2.0538877597403304 \times 10^{16}$	$- 1.9593096354084415 \times 10^{20}$
$10^{6}$	$- 8.54030555139954 \times 10^{19}$	$- 6.465704751724349 \times 10^{24}$
$10^{7}$	$- 4.1469160311751975 \times 10^{23}$	$- 2.597975844704281 \times 10^{29}$
$10^{8}$	$- 2.2502470326411468 \times 10^{27}$	$- 1.2022000181431568 \times 10^{34}$
$10^{9}$	$- 1.3249101964920937 \times 10^{31}$	$- 6.170254706864245 \times 10^{38}$
$10^{10}$	$- 8.304086276172884 \times 10^{34}$	$- 3.427910948552053 \times 10^{43}$
$10^{11}$	$- 5.4674077933205056 \times 10^{38}$	$- 2.026811001937711 \times 10^{48}$
$10^{12}$	$- 3.746002497341975 \times 10^{42}$	$- 1.260254434482889 \times 10^{53}$
$10^{13}$	$- 2.6523089311884873 \times 10^{46}$	$- 8.168086531604906 \times 10^{57}$
$10^{14}$	$- 1.930438588096488 \times 10^{50}$	$- 5.481394602239431 \times 10^{62}$
$10^{15}$	$- 1.4384149341267808 \times 10^{54}$	$- 3.7889284123142535 \times 10^{67}$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Inequalities involving Higher Degree Polynomial Functions in $\pi(x)$

Abstract

1. Introduction and Motivation

2. Important Derivations Regarding π ( x )

3. Inequalities Involving Polynomials in π ( x )

3.1. Cubic Polynomial Inequality

3.2. Numerical Estimates for H ( x )

3.3. Application: Equivalence with Ramanujan’s Inequality

3.4. Higher-Degree Polynomial Inequality

3.5. Numerical Estimates for K ( x )

4. Quadratic Form Involving Sums of Prime Counting Function

4.1. Inequality Involving Weighted Sums of π ( x )

4.2. Numerical Estimates for L ( x )

4.3. Logarithmic Weighted Sum Inequality

4.4. Numerical Estimates for F ( x )

5. A More General Framework

5.1. A Typical Example I : Generalized Cubic Polynomial Inequality

5.2. Numerical Estimates for H n ( x )

5.3. A Typical Example II : Generalized Weighted Sum Inequality

5.3.1. deg(P), deg(Q) and deg(R) Are Odd

5.3.2. deg(P), deg(Q) and deg(R) Are Even

5.4. Numerical Estimates for N r ( x )

6. Furture Scope for Research

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

2. Important Derivations Regarding $π (x)$

3. Inequalities Involving Polynomials in $π (x)$

3.2. Numerical Estimates for $H (x)$

3.5. Numerical Estimates for $K (x)$

4.1. Inequality Involving Weighted Sums of $π (x)$

4.2. Numerical Estimates for $L (x)$

4.4. Numerical Estimates for $F (x)$

5.2. Numerical Estimates for $H_{n} (x)$

5.4. Numerical Estimates for $N_{r} (x)$