Prerpints.org logo
Preprint
Article

Free Energy Evaluation of Homogeneous Bubble Nucleation based on Stochastic Thermodynamics

Altmetrics

Downloads

169

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 July 2024

Posted:

16 July 2024

You are already at the latest version

Alerts
Abstract
Nucleation is a fundamental and general process at the initial stage of first order phase transition. Although various models based on the classical nucleation theory (CNT) have been proposed to explain the energetics and kinetics of nucleation, detailed understanding on nanoscales are still required. Here we focus on homogeneous bubble nucleation, in which evaluation of the size dependence of bubble free energy is the key issue. We propose application of a formula in stochastic thermodynamics, the Jarzynski’s equality, for data analysis of molecular dynamics (MD) simulation to evaluate the free energy of bubble nucleation. As a test case, we performed a series of MD simulations with Lennard-Jones (LJ) fluid system. By applying an external spherical force field to equilibrated LJ liquid, we evaluated the free energy change during bubble growth as the Jarzynski’s ensemble average of required works. A fairly smooth free energy curve was obtained as a function of bubble radius in metastable liquid of mildly negative pressure conditions.
Keywords: 
Subject: Physical Sciences  -   Thermodynamics

1. Introduction

In this research we focus on the energetics of homogeneous bubble nucleation in stretched metastable liquid. Inception of bubble nucleation is a fundamental process in the first order liquid-vapor phase transition in general, and has been investigated long in various fields, such as cavitation [1,2], nucleate boiling [3,4], and metastability limit of liquids [5,6,7,8], but the understanding of microscopic details are still required.
The mechanism of nucleation has been studied based mainly on the so-called classical nucleation theory (CNT) [5,6,9,10,11]. In a simplest form of CNT, the free energy change Δ F of the system during the growth of a spherical bubble is given by the following equation,
Δ F ( r ) = − 4 3 π r 3 Δ f V + 4 π r 2 γ
where r is the bubble radius, Δ f V the difference in free energy density between liquid and vapor phases, and γ the surface tension. Although the physics for Eq. (1) is clear as a base of energetics of homogeneous bubble nucleation, discrepancy in the nucleation rate between CNT models and experiments is often extremely large [12], and various improvements in theoretical models have been proposed [6,11,13,14,15].
In this study, we revisit the free energy change in CNT of homogeneous bubble nucleation by utilizing molecular dynamics (MD) simulations combined with stochastic thermodynamics. Several MD simulations on homogeneous bubble nucleation were reported [16,17,18,19,20]. Due to the spatial and temporal scale limits of the simulation method, however, the conditions used in these MD simulations are highly non-equilibrium, closer to the spinodal lines, under which spontaneous bubble generation occurs within the simulation time. Furthermore, kinetics (or the nucleation rate) was the main target in these simulations while energetics is still hard to investigate because the system is in highly non-equilibrium state during this kind of simulations.
Here we want to investigate the free energy during the bubble nucleation. For that purpose, we adopt a basic formula of stochastic thermodynamics, with which we are able to evaluate the free energy from a special type of ensemble average of works to create and expand a bubble.

2. Stochastic Thermodynamics: Theoretical Background

Among several variations of free energy evaluation scheme proposed in the field of stochastic thermodynamics [21], we here adopt the simplest form, the Jarzynski equality. Assuming any path L in the configurational space from a starting point to a goal, this equality describes a relationship between the free energy F ( s ) on a point s ∈ L ( s = 0 is the starting point) and the work W ( s ) required along the path. If we can assume that the process along the path is always quasistatic, the conventional thermodynamics tells us
F ( s ) − F ( 0 ) = W ( s )
but in general
F ( s ) − F ( 0 ) ≤ W ( s )
which is a representation of the second law of thermodynamics. The difference is of course dissipated, as heat Q in most cases,
F ( s ) − F ( 0 ) = W ( s ) − Q ( s )
In microscale processes where fluctuations are not negligible, W also contains fluctuations, and Eq. (3) should be expressed as
F ( s ) − F ( 0 ) ≤ W ( s )
where 〈 〉 represents the ensemble average.
In 1997 [22], Jarzynski showed that the following equality holds for “any” processes
exp − F ( s ) − F ( 0 ) k B T = exp W ( s ) k B T
where T is the temperature of thermal reservoir, and k B is the Boltzmann constant. The point in Eq. (6) is that we can evaluate the state quantity F ( s ) without the conventional assumption of quasistatic process. This gives a great merit for us to evaluate free energy with MD simulations because a typical time scale of MD simulations is so short that, in many cases, we cannot assume thermal equilibrium however slow the system change is.
In this work, we targeted simple liquid and conducted a series of MD simulations to observe a “bubble” generation by applying an external force. Then, by adopting Eq. (6), the free energy change during the bubble growth was evaluated. Since Eq. (6) was proposed, several extensions and generalizations have been proposed [21,23,24], such as the Crooks fluctuation theorem [25], which relates the probability distributions of the forward process and the backward one. These extended methods may provide a better tool to investigate the bubble nucleation, which is left for future study.

3. System and Method

We carried out a series of MD simulations to investigate the free energy for a tiny bubble in model liquid. All MD simulations were executed with LAMMPS [26,27]. OVITO [28] was utilized to visualize the atomic configurations.

3.1. Simulation System and Procedure

We adopted a simple monatomic liquid, in which the Lennard-Jones (LJ) 12-6 potential was assumed as the particle-particle interaction,
ϕ ( r ) = 4 ε σ r 12 − σ r 6 ,
where r is the particle-particle distance. ε and σ are the parameters for energy and length, respectively. The interaction is truncated at r = r c = 3.5 σ . In the following descriptions, all quantities are expressed with the conventional reduced units, such as ε :energy, σ :length, and m:particle mass. Just for reference, typical values for argon [29] are ε ≃ 1.66 × 10 − 21 J, σ ≃ 0.34 × 10 − 9 m, and the time unit τ ≡ σ m / ε ≃ 2.15 × 10 − 12 s. All MD simulations were executed with time step 0.002 τ .
With conventional NPT ensemble conditions, where the temperature is controlled with the Nosé-Hoover thermostat [30] and the pressure with the Martyna barostat [31], we performed a series of MD simulations for cavitation under “external force” and evaluated the free energy change based on the Jarzynski formula, eq. (6). Each simulation consists of three steps:
  • Liquid in equilibrium at given temperature T 0 and pressure p 0 is prepared using a standard procedure of MD simulation.
  • A spherical force field ϕ B at the center of the system box is applied for all LJ particles, and the system is equilibrated again at ( T 0 , p 0 ) . We assume an LJ-type field as
    ϕ B r o , t = 0 = 4 ε σ r o 12 − σ r o 6 ,
    where r o is the distance of each particle from the box center. The field is also truncated at r o = r c = 3.5 σ .
  • For the main simulation, the radius of the force field is increased and the resulting “bubble” growth is monitored.
    ϕ B r o , t = 4 σ r o − R ( t ) 12 − σ r o − R ( t ) 6 ,
    where R ( t ) is a time-dependent variable corresponding to the bubble radius, where the bubble is the region of excluding LJ particles. In this paper we adopted ϕ B with a size linearly increasing with time,
    R ( t ) = v 0 t
    where v 0 is a positive constant.
During the MD calculation, atomic data (position r → i , velocity v → i , and the exerted external force f → i ≡ − ∂ ϕ B / ∂ r → i ) for each LJ particle i are stored every k steps for later analysis.
To apply the Jarzynski equality to our system for the free energy evaluation, a large number of samplings are required; for that purpose, we took ensemble average over 100 different atomic configurations at equilibrium as the initial conditions.
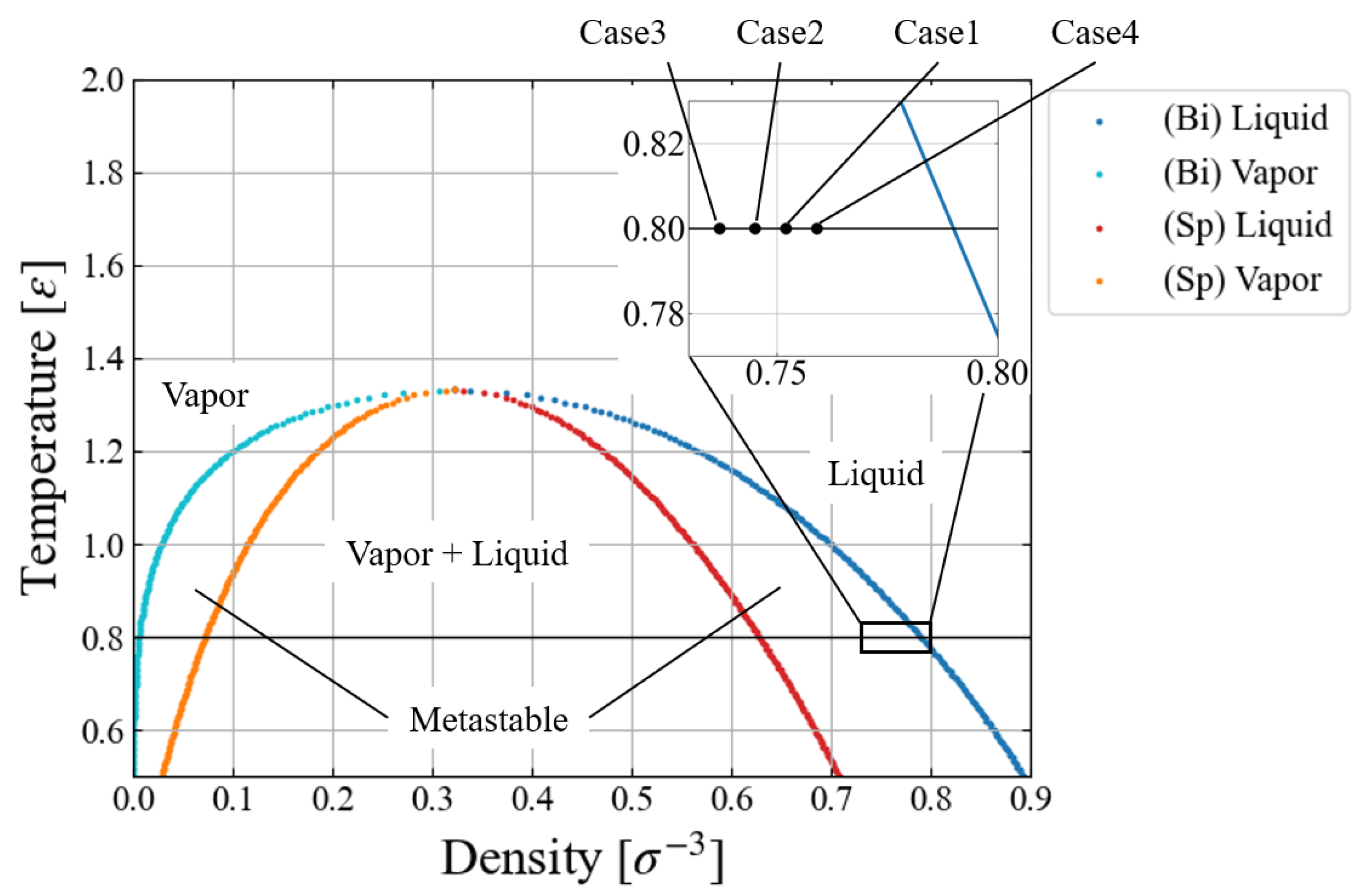
The simulation conditions are summarized in Table 1. We chose a relatively low temperature ( T = 0.8 ) since we have to assume vacuum in the “bubble” for this free energy evaluation with applying an external force field. Four different environmental pressure conditions, − 0.30 ≤ p 0 ≤ − 0.15 , are investigated to see how p 0 affects the nucleation behavior. In view of the standard phase diagram and the equation of states for LJ fluid [32,33,34], these pressure conditions are extremely mild, i.e., much closer to the binodal line than to the spinodal one, as shown in Figure 1. This is the region difficult for conventional MD simulations to access [16,17,18,35] due to the large activation energy. Since a large size of critical nucleus was expected for the largest pressure condition (Case 4), we prepared a larger system with 108 , 000 particles to mitigate the artifact of the finite system size. The growth speed v 0 = 0.01 corresponds to 1.6 m/s in argon units, being still very fast; the speed dependence of results is shortly discussed later. For the larger system, Case 4, we adopted an even larger speed v 0 = 0.02 to save the computation time.

3.2. Free Energy Evaluation

On completing the MD simulations for each Case, we adopted the Jarzynski equality, Eq. (6), to evaluate the free energy change during the “bubble” growth with the following steps:
Step. 1:
The work during a short period from time t and t + Δ t is evaluated as
w ( t ) = ∑ i = 1 f → i ( t ) · v → i ( t ) Δ t
In this simulation we chose Δ t = 5 MD steps = 0.01 [ τ ].
Step. 2:
The accumulated work, which is the sum of the instantaneous work up to time t = n Δ t , is determined.
W ( t ) = ∑ n ′ = 0 n w ( n ′ Δ t )
Step. 3:
We perform simulations multiple times, with calculating W ( t ) for each case. The free energy change Δ F ( t ) from the initial state is evaluated by taking the ensemble average as the Jarzynski equality, Eq. (6), as a function of t.
Step. 4:
Since the bubble “radius” is directly related to time t with Eq. (10), we finally obtain the free energy as a function of bubble radius.

4. Results

4.1. Thermodynamic Properties

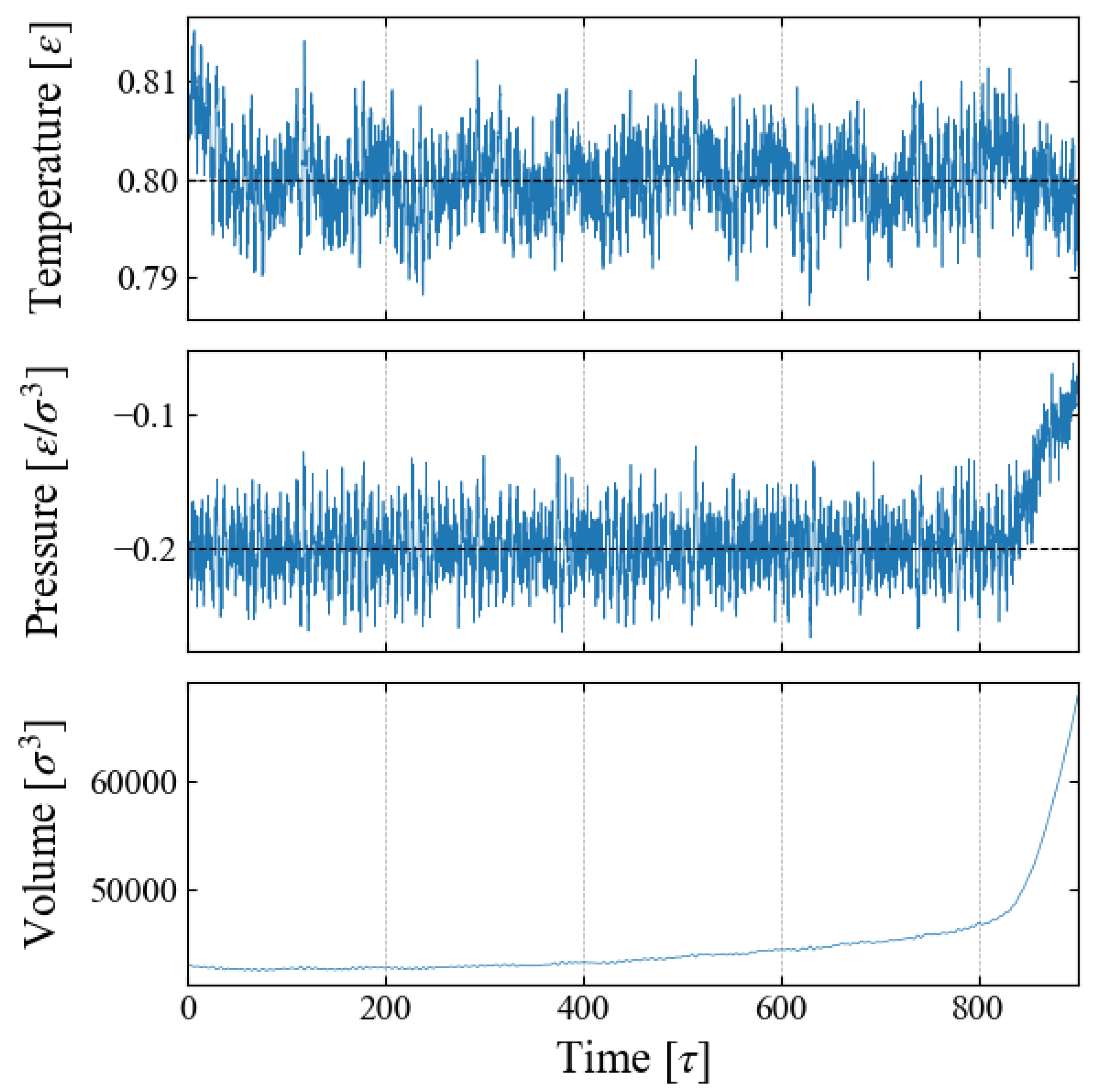
We carried out NPT ensemble MD simulations for the main sampling, during which the system volume V changes due to the time-varying external field ϕ B ( t ) . An example is shown in Figure 2 for Case 1, indicating that the barostat to control the system pressure fails after time t ∼ 800 [ τ ]. This is caused by a spontaneous bubble growth, as discussed below.

4.2. Bubble Growth

Figure 3 indicates a series of snapshots (cross-sectional views) for Case 1. The “bubble” generated by the external field ϕ B gradually grows up to t ≃ 700 ; it seems to become unstable at t ∼ 800 , where its shape is distorted and the growth is accelerated, and finally the thin liquid film between the neighboring bubbles due to the periodic boundary conditions is broken.
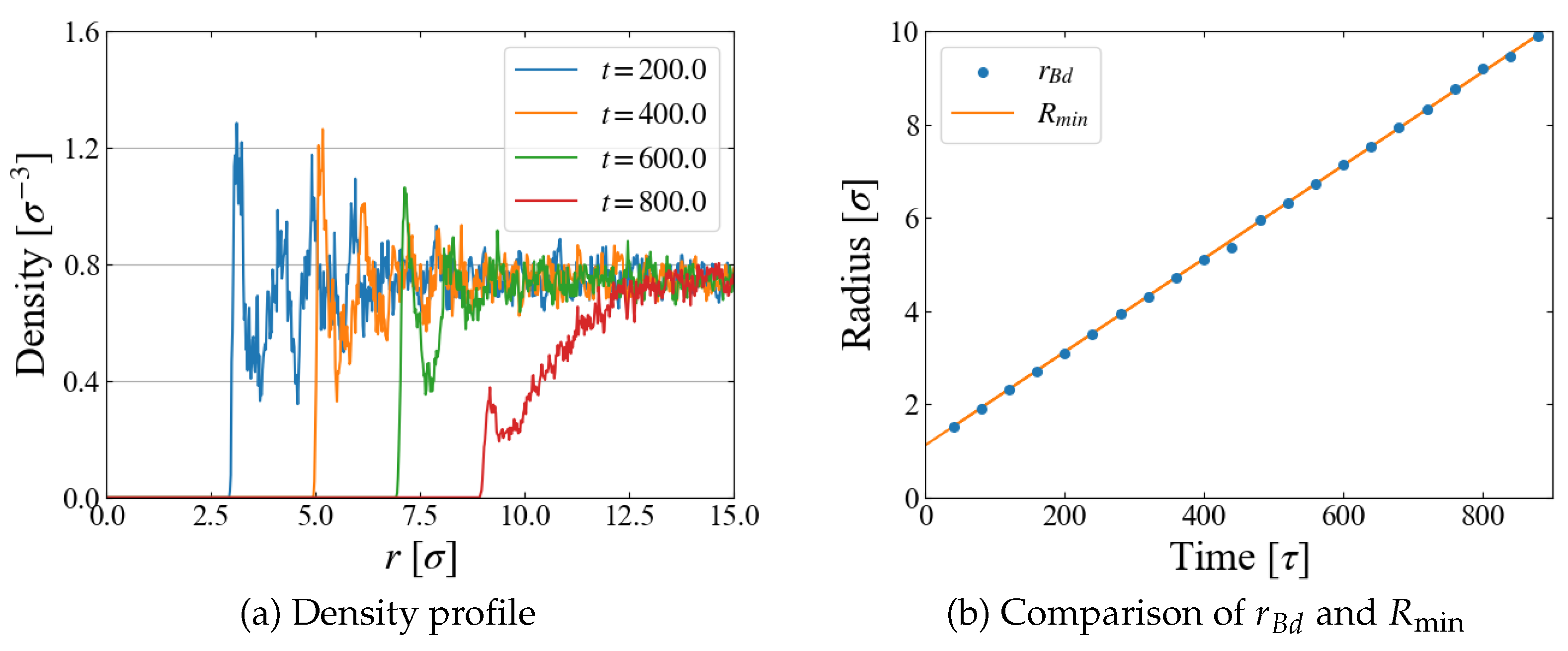
A quantity relevant to the nucleation analysis is the bubble radius at time t, and we evaluate it in two ways here. One is based on the density profile of LJ particles. An example for Case 1 ( p 0 = − 0.2 ) is shown in Figure 4 (a), where the number density is plotted as a function of the distance r from the box center, i.e., the center of the external field ϕ B . The first peak indicates the particles situated on the “bubble surface”, from which we define the bubble radius r B d . As the size R of ϕ B increases with time, Eq. (10), the position of the first peak shifts to larger r accordingly. We expect that r B d is close to the position of ϕ B minimum, R min ( t ) ≡ R ( t ) + 2 1 / 6 σ ; comparison is made in Figure 4 (b), which shows they are almost identical. In the density profile, it is still possible to see the first peak after the bubble becomes unstable at t ≥ 800 [ τ ], but the peak is very small and the density in its vicinity is much less than the bulk liquid one, which suggests that the first peak at this stage is brought by weak “adsorption” on, or entrapment by, the external field.
The change of the total volume of the system during the simulation V ( t ) , an example of which is shown in Figure 2, provides another way to define the bubble radius. We assume that the density of “bulk” liquid is constant, which is apparent in Figure 4 (a). Then the change of V ( t ) is brought only by the bubble growth, and we define and evaluate the bubble radius r B v with spherical bubble assumption.
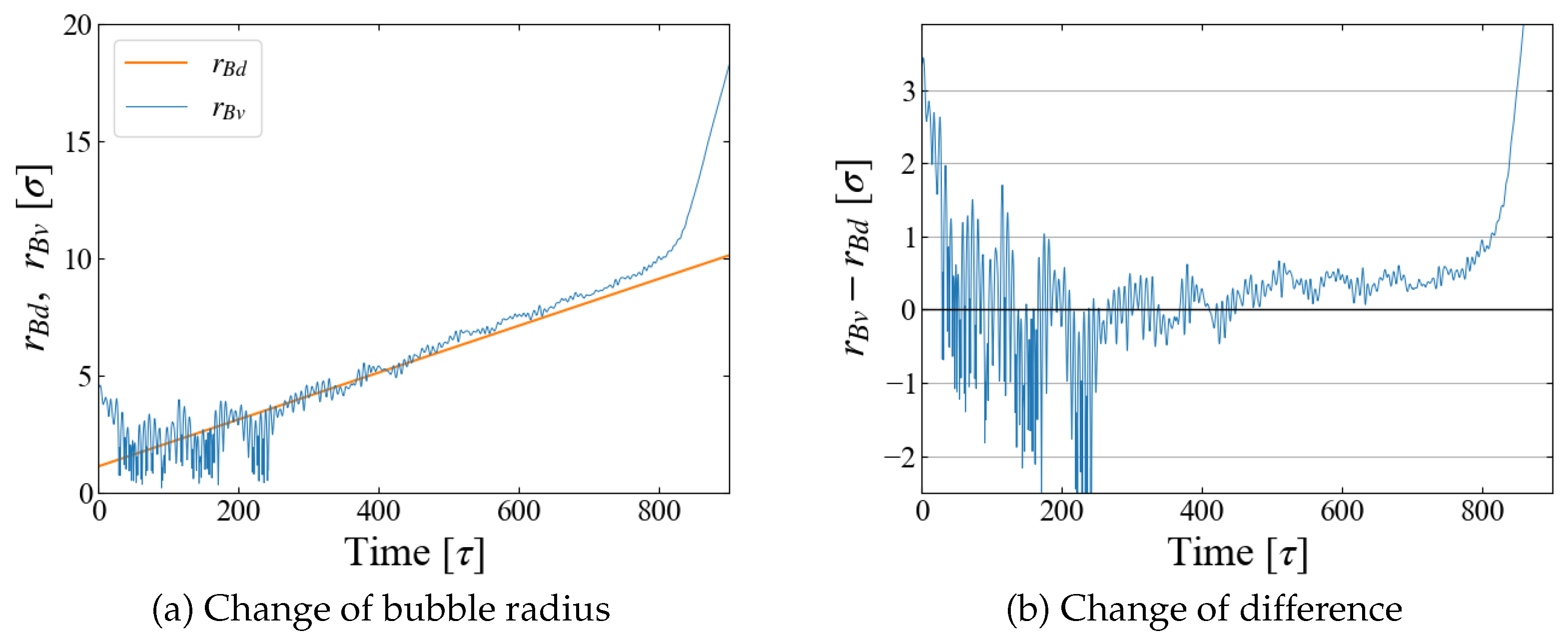
The obtained r B v is compared with r B d in Figure 5. The fluctuations in box size bring the large fluctuations in r B v especially at the initial stage of t ≤ 300 [ τ ], but the agreement of r B d and r B v is reasonable for t ≤ 700 [ τ ], as seen in Figure 5 (b). Based on these data, we adopt a rather arbitrarily determined criterion in the following data analyses that the spontaneous bubble growth starts when the difference r B v − r B d exceeds 1 σ ; in this time region, the application of the Jarzynski’s scheme fails because the “work” may not be properly evaluated with Eq. (11).

4.3. Work and Free Energy

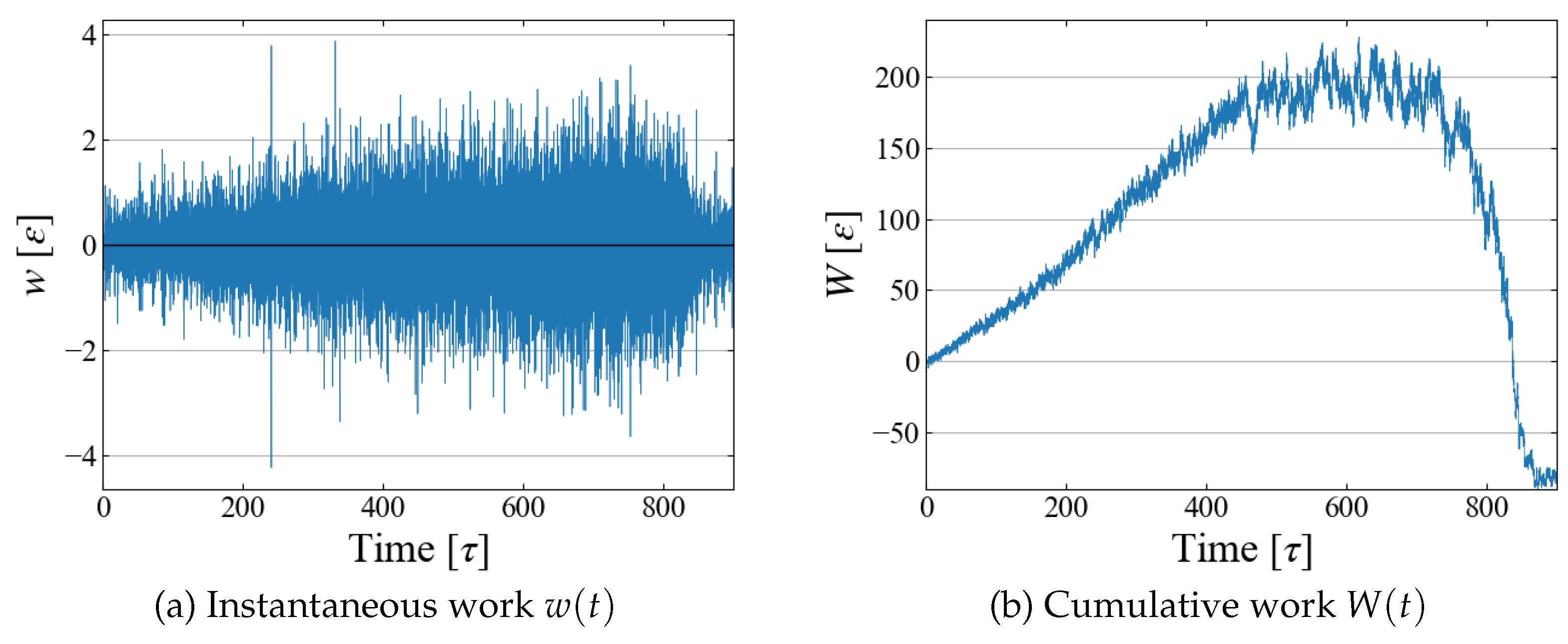
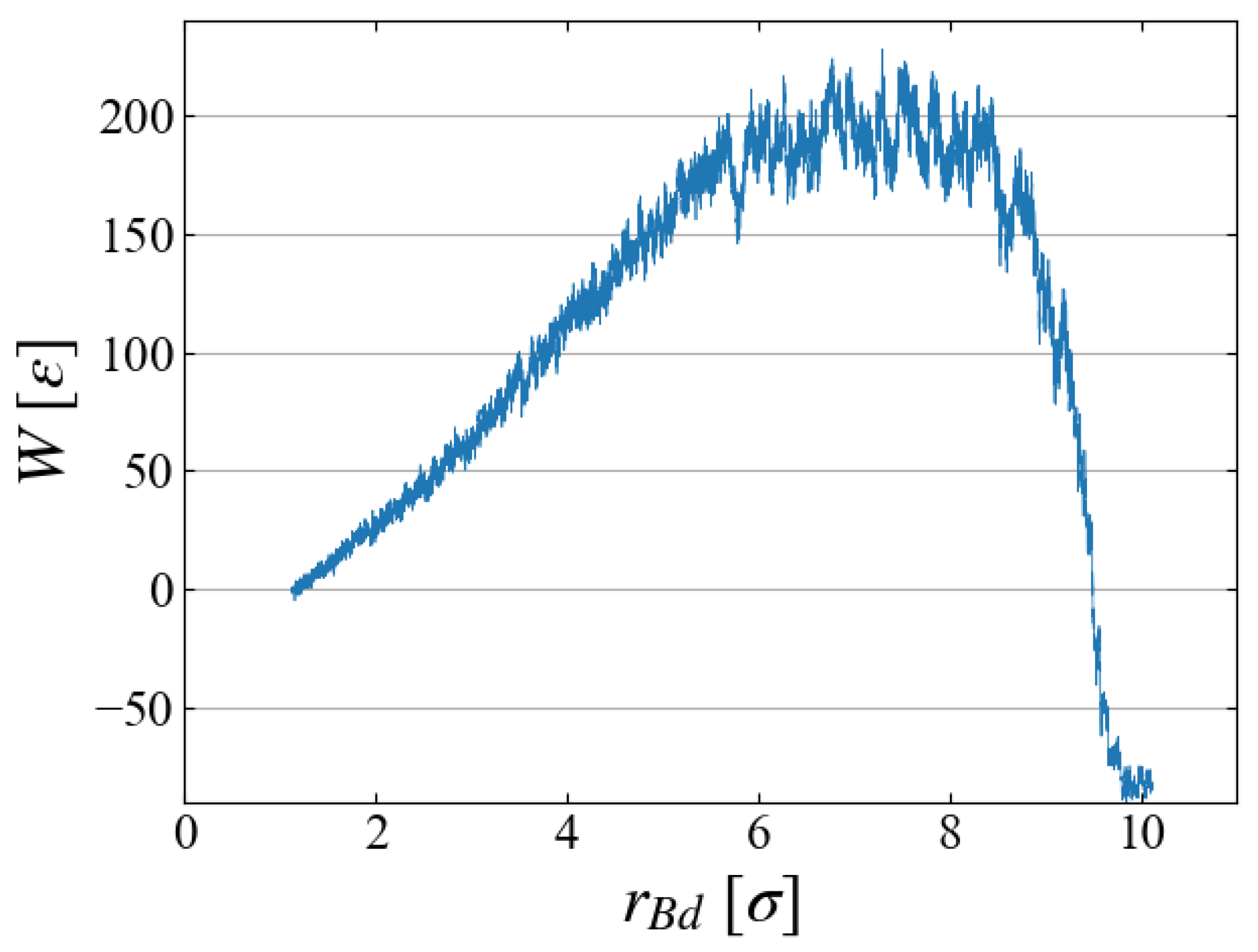
Example data of stepwise work w ( t ) and cumulative one W ( t ) are shown in Figure 6; although fluctuations are large in w ( t ) , their running sum W ( t ) seems to have a reasonable shape as expected in typical nucleation processes. By utilizing the relation between r B d and t as in Figure 4 (b), the cumulative work W is plotted as a function of bubble radius r B d in Figure 7, which illustrates the work required to generate a bubble of size r B d . As expected in CNT, W ( r B d ) increases up to some “critical size”; bubbles larger than this size spontaneously grows, leading to negative W.
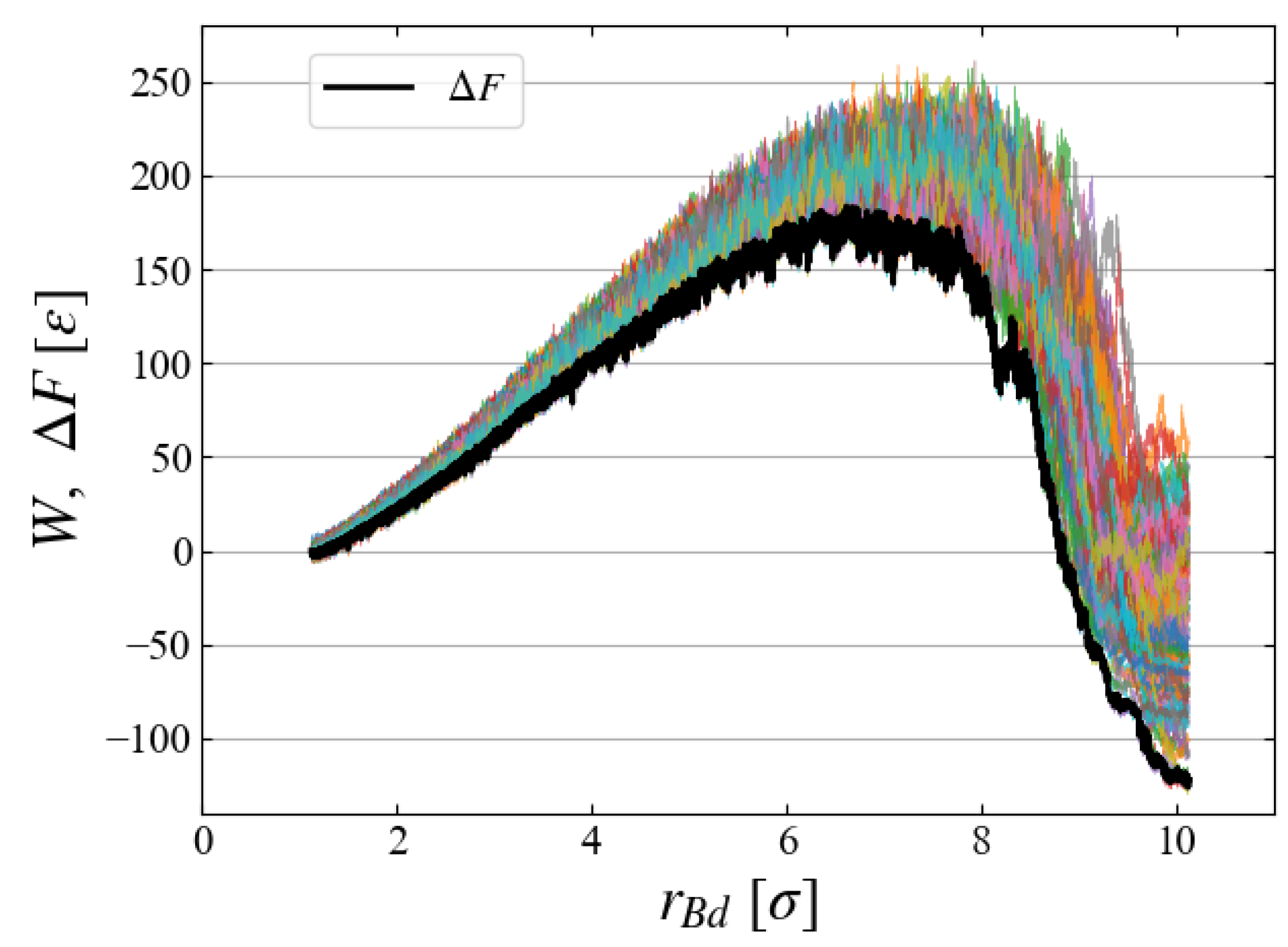
To evaluate the free energy change, we carried out 100 MD simulations starting from different initial configurations, each of which gives a different W ( r B d ) curve. All curves are superimposed in Figure 8, indicating large fluctuations of ∼ 50 [ ϵ ]. Ensemble average based on Eq. (6) gives a relatively smooth curve of free energy difference
Δ F ( r B d ) ≡ F ( r B d ( t ) ) − F ( r B d ( t = 0 ) )
Note that the applied external field ϕ B , Eqs. (9) and (10), has a finite size even at t = 0 , thus Δ F ( r B d ) does not start from the origin but from r B d ≃ 2 1 / 6 [ σ ]. Figure 8 clearly indicates the existence of a critical nucleus at ≃ 6.5 [ σ ] with activation energy 190 ± 10 [ ϵ ]. It is apparent that the Jarzynski equality gives the Δ F curve very close to the data of minimum W.
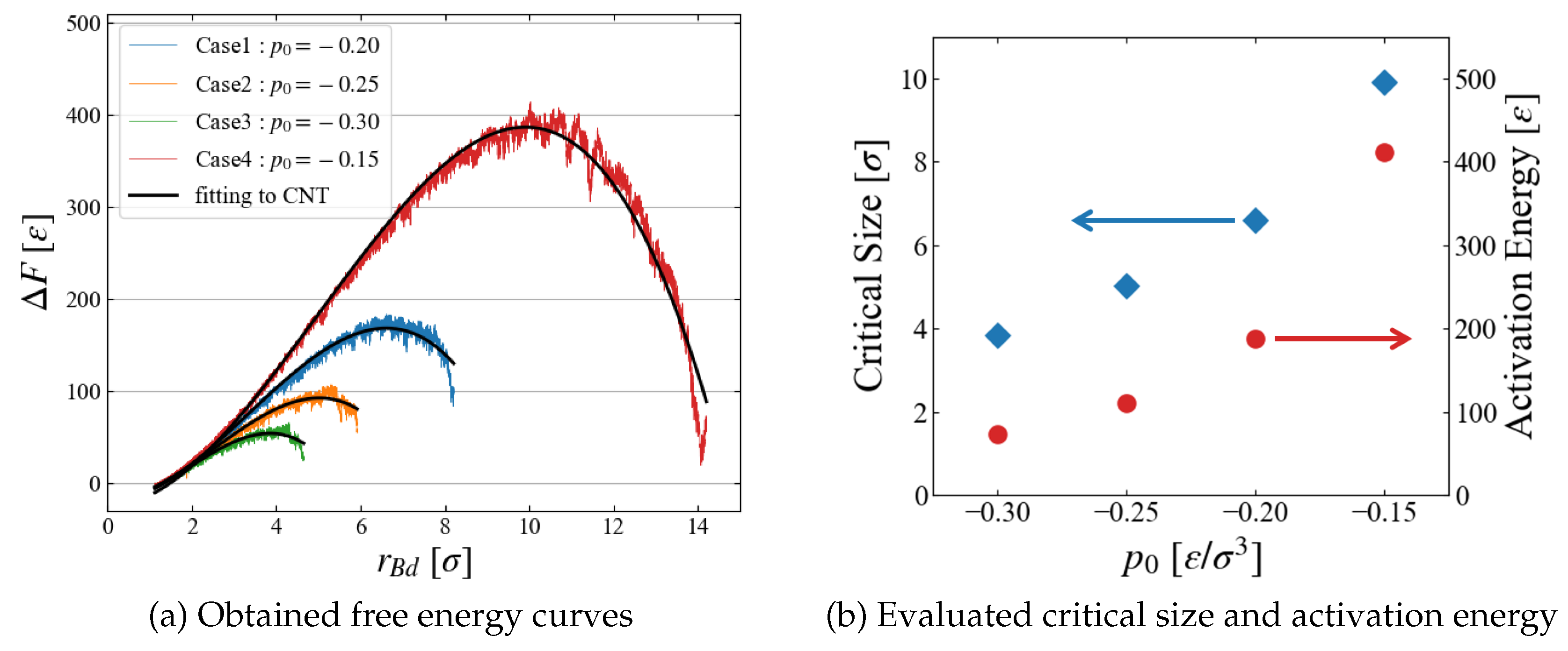
The results of Δ F ( r B d ) are summarized for all four cases of different pressure conditions in Figure 9 (a). We successfully obtained a smooth curve for each condition; as expected, the critical bubble size and the energy barrier reduces as p 0 becomes more negative. The critical size and the activation energy are roughly estimated from the data in Figure 9 (b); the dependence on the surrounding pressure p 0 seems reasonable.
The evaluated activation energy is very large because we investigated systems under mild p 0 conditions. For example, the obtained energy is about 400 [ ϵ ] at p 0 = − 0.15 , leading to an extremely small Boltzmann factor exp − 400 / 0.8 ∼ 10 − 216 , which is not accessible with conventional molecular simulation techniques.

5. Discussion

5.1. Comparison with CNT

Here we only make comparison with the simplest form of CNT. The obtained Δ F ( r B d ) data are fitted to a simple equation by the least squares method,
Δ F ( r ) = a r 3 + b r 2 + c
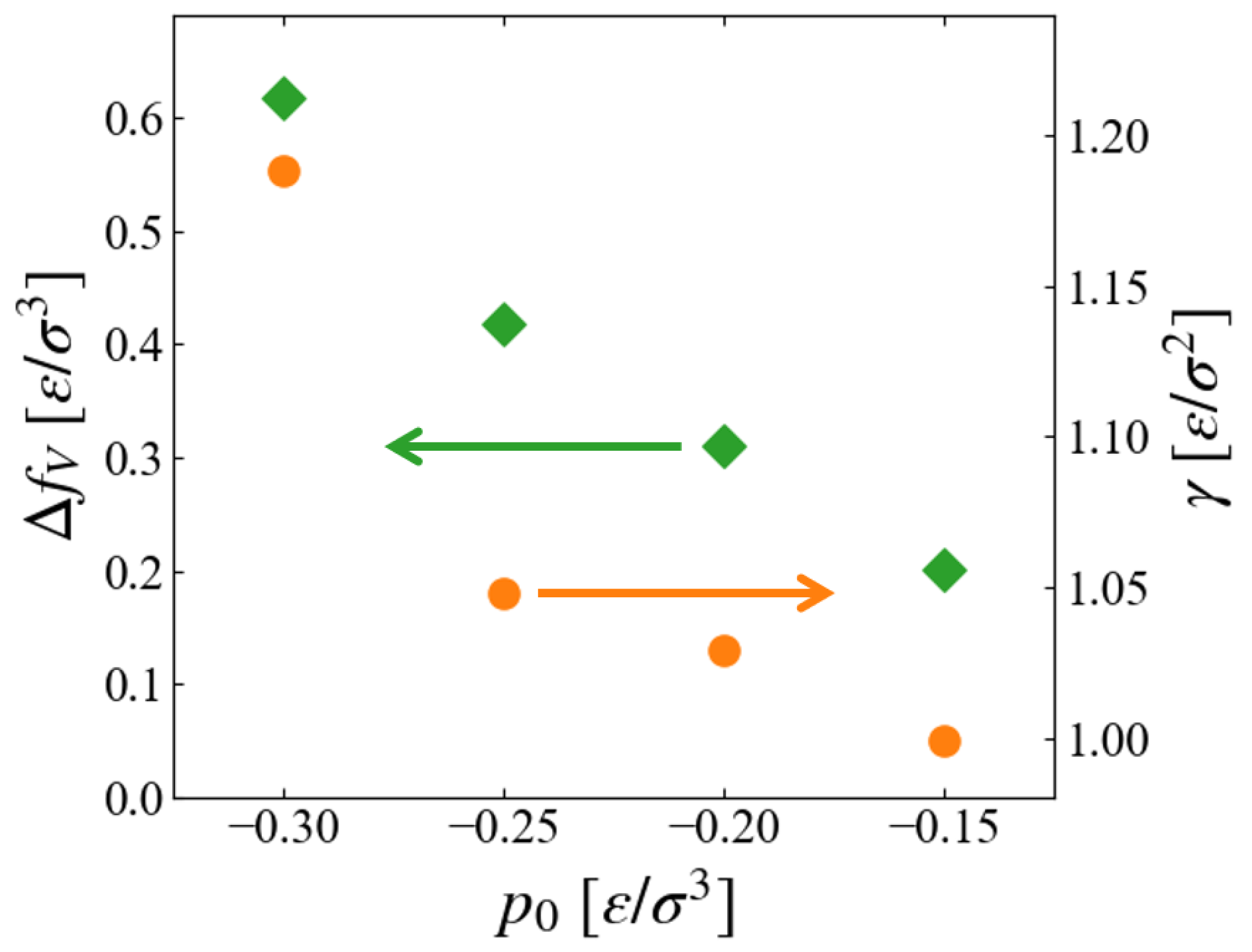
where a, b, and c are the fitting parameters. In a simplest CNT as shown in Eq. (1), a and b are related to the free energy density difference between the bulk liquid and bulk vapor, Δ f V ≡ f liq − f vap , and the surface tension γ , respectively. As Figure 9 (a) indicates, the obtained free energy curves are well approximated by Eq. (14). Plotted in Figure 10 are the p 0 dependence of extracted values,
Δ f V = a 4 π / 3
and
γ = b 4 π
Since the inside of the generated “bubble” is vacuum in this scheme, Δ f V should correspond to the free energy density of expanded liquid, and the results seem reasonable that f V of liquid increases for larger metastability, or negatively larger p 0 .
The pressure dependence of surface tension is worthy to be noted. As far as we have noticed, no data for surface tension (interfacial tension between liquid and vapor) in non-equilibrium states are reported, although a number of studies exist for its curvature dependence for nano-bubbles [36,37,38,39]. For equilibrium LJ fluid at T = 0.8 . γ ≃ 0.8 − 0.9 [ ϵ / σ 2 ] is often referred [33]. Figure 10 suggests that γ , or the surface excess free energy, is an increasing function of the “degree of non-equilibrium,” which seems reasonable; the evaluation of its accuracy is left for future investigation.

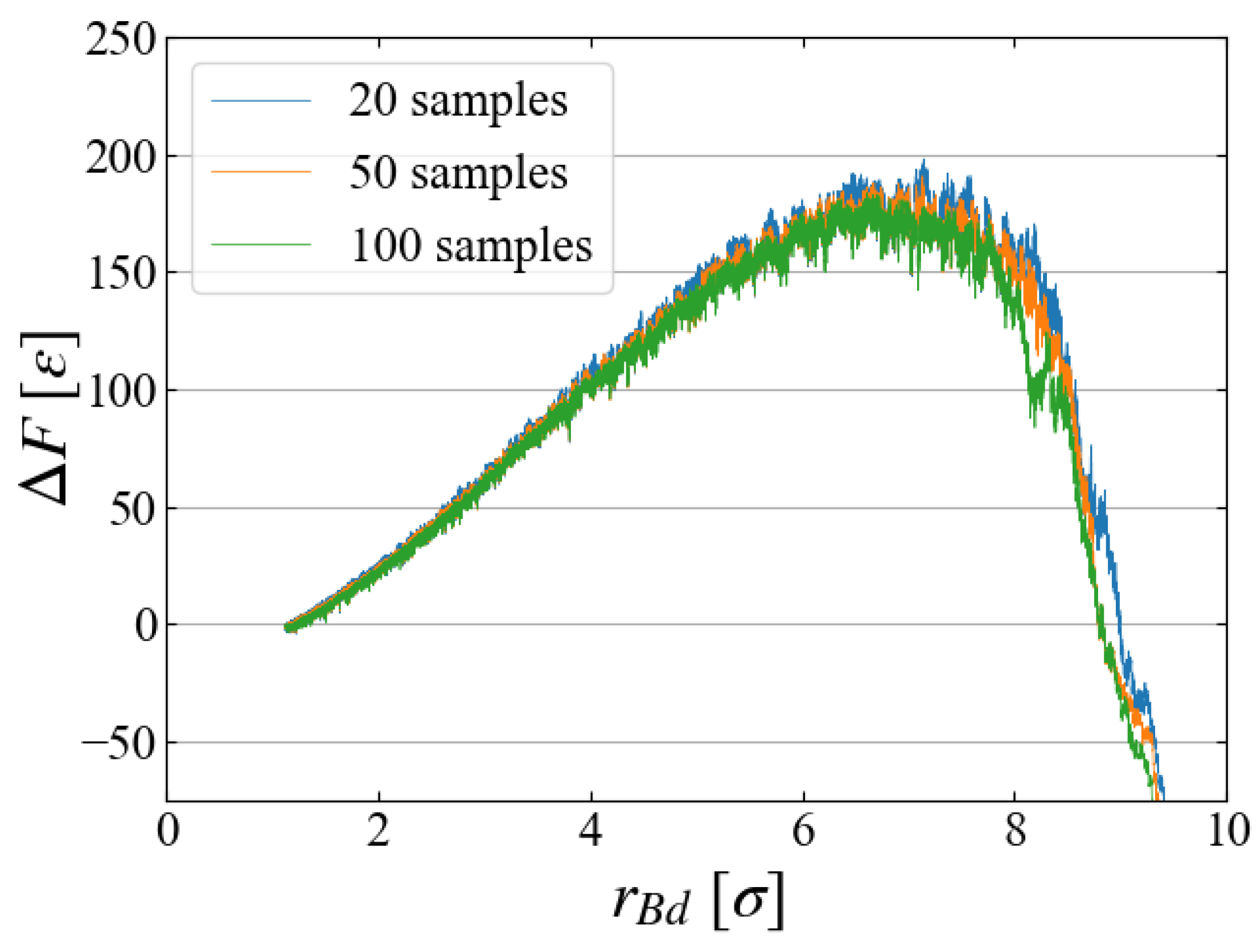
5.2. Sampling

As the main part of free energy evaluation, we used 100 samples for each Case. To see if 100 samples are sufficient or not, we compared the evaluated Δ F in Figure 11 for Case 1, where the results using the first 20, the first 50, and all 100 samples are plotted. The difference in the averaged values seems negligibly small, and we may conclude that 100 samples are sufficient. However, closer look at the distribution of work may give a different view.
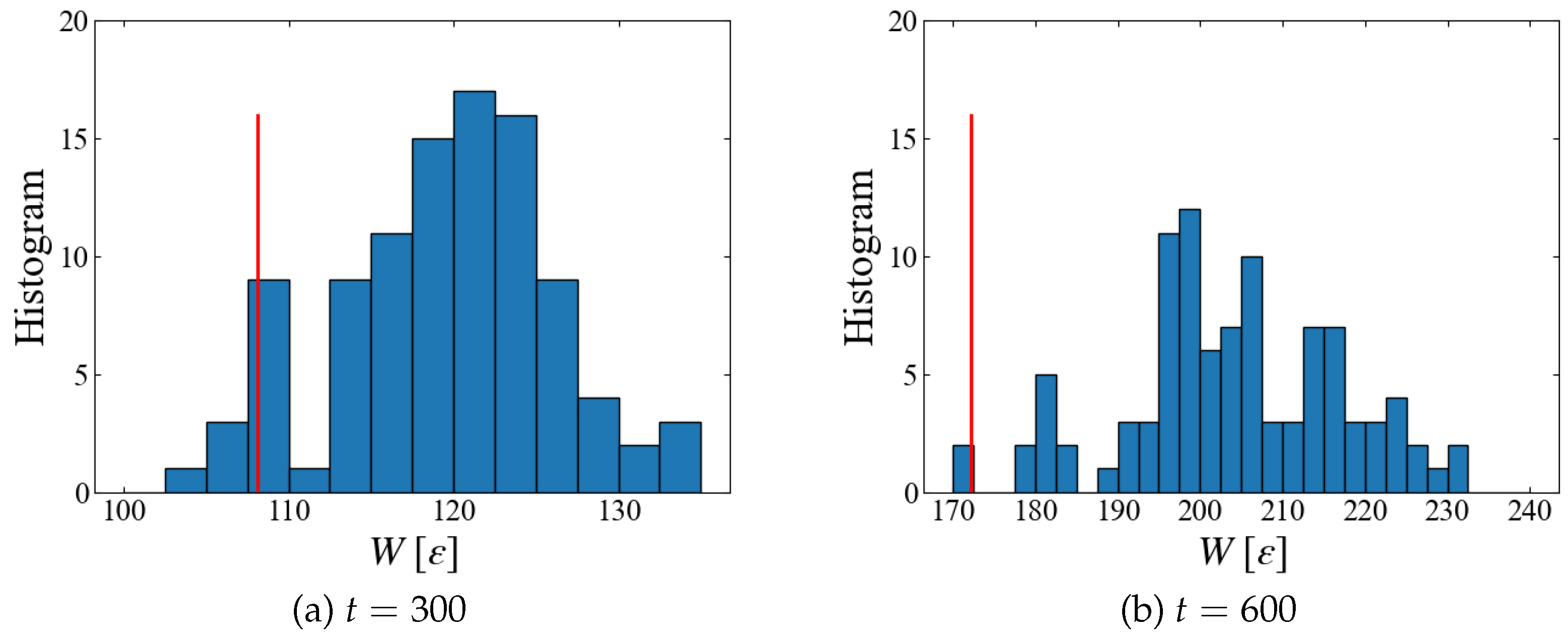
Plotted in Figure 12 are a histogram of instantaneous work w ( t ) at different time. Since data with smaller w has larger weight in Jarzynski’s average, Eq. (6), we need sufficient number of samples in the region of smaller w. However we have only four samples at t = 300 and two at t = 600 which are smaller than the obtained Δ F , suggesting that 100 samples may not be sufficient. Thus, further increase in the number of samples may significantly lower the free energy.

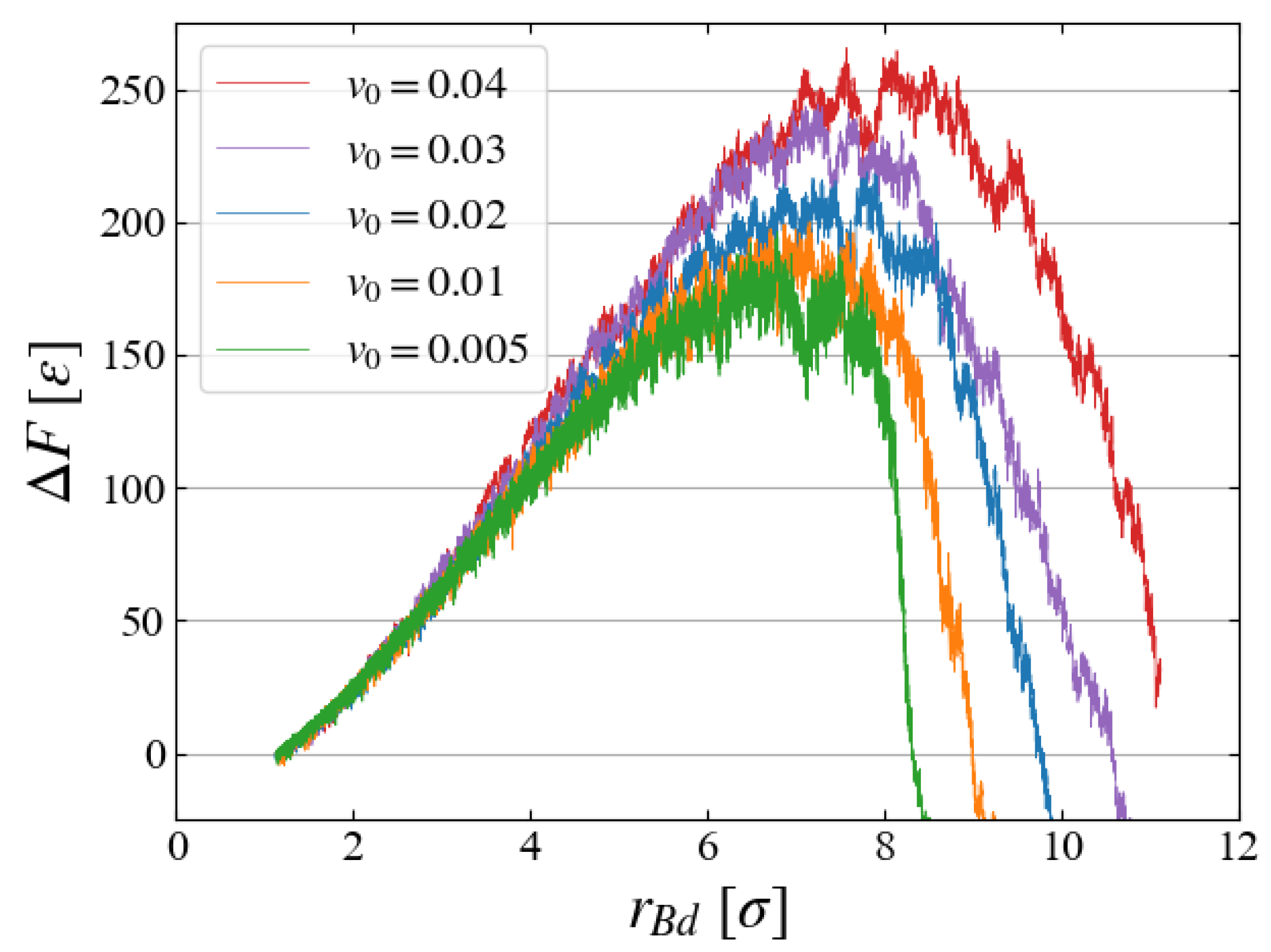
5.3. Growth Speed

Finally, we briefly discuss how the bubble growth speed v 0 affects the evaluation of Δ F . In preliminary investigations, five cases with different v 0 ( 0.005 ≤ v 0 ≤ 0.04 ) are compared, as in Figure 13, where Δ F is evaluated with Eq. (6) with ten samples for each case. The free energy increases for larger expanding speeds probably because the liquid structure is not sufficiently relaxed for faster bubble expansion, but the results for v 0 = 0.01 and 0.005 look similar, and thus we have chosen v 0 = 0.01 for the main simulations.

6. Conclusions

Using a standard molecular dynamics (MD) simulation technique, we investigated the free energy change during homogeneous bubble nucleation based on a stochastic thermodynamics formulation, namely, the Jarzynski’s equality, for a simple Lennard-Jones fluid system with an expanding external force field. It is shown that, when compared with the direct application of conventional MD simulations for various types of nucleation processes, we can evaluate the free energy under much milder (i.e., closer to the binodal lines) conditions. Yet assumption of thermal equilibrium is not required for free energy evaluation, in contrast to the often-adopted molecular simulations for thermal properties.
It should be noted, however, sufficient number of samplings is essential, and may require much computational resources. Also exist technical restrictions for this method, that the inside of the bubble should be vacuum due to the external force field, and the bubble shape should be spherical. Therefore application of this method is currently limited only to bubble nucleation at low temperature conditions.

Author Contributions

Conceptualization, I.S. and M.M.; software development, I.S.; investigation, I.S. and M.M.; data curation, I.S. and M.M.; writing—original draft preparation, I.S.; writing—review and editing; M.M.; supervision, M.M.; funding acquisition, M.M.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

Data are available from the authors upon request.

Acknowledgments

A part of this research was supported by JSPS KAKENHI (Grant Number 21L03897 and 24K07358).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Brennen, C.E. Cavitation and Bubble Dyamics; Oxford University Press, 1995. [Google Scholar]
  2. Duana, C.; Karnik, R.; Lu, M.C.; Majumdar, A. Evaporation-induced cavitation in nanofluidic channels. PNAS 2012, 109, 3688–3693. [Google Scholar] [CrossRef]
  3. Thome, J.R. Enhanced Boiling Heat Transfer, 1 ed.; CRC Press, 1990. [Google Scholar]
  4. Karayiannis, T.; Mahmoud, M. Flow boiling in microchannels: Fundamentals and applications. Applied Thermal Engineering 2017, 115, 1372–1397. [Google Scholar] [CrossRef]
  5. Skripov, V.P. Metastable Liquids; Wiley, 1974. [Google Scholar]
  6. Debenedetti, P.G. Metastable Liquids: Concepts and Principles, 1 ed.; Princeton University Press, 1997. [Google Scholar]
  7. Wheeler, T.D.; Stroock, A.D. Stability Limit of Liquid Water in Metastable Equilibrium with Subsaturated Vapors. Langmuir 2009, 25, 7602–7622. [Google Scholar] [CrossRef] [PubMed]
  8. Caupin, F.; Stroock, A.D. The Stability Limit and Other Open Questions on Water. Advances in Chemical Physics 2013, 152, 51–80. [Google Scholar]
  9. Hirth, J.P.; Pound, G.M.; Pierre, G.R.S. Bubble Nucleation. Metallurgical Transactions 1970, 1, 939–945. [Google Scholar] [CrossRef]
  10. Oxtoby, D.W. Homogeneous nucleation: theory and experiment. Journal of Physics: Condensed Matter 1992, 4, 7627–7650. [Google Scholar] [CrossRef]
  11. Baidakov, V.G. Attainable superheating of liquefied gases and their solutions. Low Temperature Physics 2013, 39, 643–664. [Google Scholar] [CrossRef]
  12. Zeng, X.C.; Oxtoby, D.W. Gas-liquid nucleation in Lennard-Jones fluids. Journal of Chemical Physics 1991, 94, 4472–4478. [Google Scholar] [CrossRef]
  13. Delale, C.F.; Hruby, J.; Marsik, F. Homogeneous bubble nucleation in liquids: The classical theory revisited. Journal of Chemical Physics 2003, 118, 792–806. [Google Scholar] [CrossRef]
  14. Lutsko, J.F. Density functional theory of inhomogeneous liquids. III. Liquid-vapor nucleation. Journal of Chemical Physics 2008, 129, 244501. [Google Scholar] [CrossRef]
  15. Němec, T. Scaled nucleation theory for bubble nucleation of lower alkanes. European Physical Journal E 2014, 37, 111. [Google Scholar] [CrossRef] [PubMed]
  16. Kinjo, T.; Matsumoto, M. Cavitation Processes and Negative Pressure. Fluid Phase Equilibria 1998, 144, 343–350. [Google Scholar] [CrossRef]
  17. Park, S.; Weng, J.G.; Tien, C.L. Cavitation and Bubble Nucleation using Molecular Dynamics Simulation. Microscale Thermophysical Engineering 2000, 4, 161–175. [Google Scholar] [CrossRef]
  18. Tsuda, S.; Takagi, S.; Matsumoto, Y. A study on the growth of cavitation bubble nuclei using large-scale molecular dynamics simulations. Fluid Dynamics Research 2008, 40, 606–615. [Google Scholar] [CrossRef]
  19. Baidakov, V.; Protsenko, K. Molecular dynamics simulation of cavitation in a Lennard-Jones liquid at negative pressures. Chemical Physics Letters 2020, 760, 138030. [Google Scholar] [CrossRef]
  20. Xie, H.; Xu, Y.; Zhong, C. A study of cavitation nucleation in pure water using molecular dynamics simulation. Chinese Physics B 2022, 31, 114701. [Google Scholar] [CrossRef]
  21. Peliti, L.; Pigolotti, S. Stochastic Thermodynamics: An Introduction; Princeton University Press, 2021. [Google Scholar]
  22. Jarzynski, C. Nonequilibrium equality for free energy differences. Physical Review Letters 1997, 78, 2690. [Google Scholar] [CrossRef]
  23. Jarzynski, C. Equalities and Inequalities: Irreversibility and the Second Law of Thermodynamics at the Nanoscale. Annual Review on Condensed Matter Physics 2011, 2, 329–351. [Google Scholar] [CrossRef]
  24. Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Reports on Progress in Physics 2012, 75, 126001. [Google Scholar] [CrossRef]
  25. Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Physical Review E 1999, 60, 2721–2726. [Google Scholar] [CrossRef]
  26. https://www.lammps.org (Last access on 1 May 2024).
  27. Thompsona, A.; Aktulgab, H.M.; Berger, R.; S.Bolintineanu, D.; Brown, W.; Crozier, P.S.; Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; Shan, R.; Stevens, M.J.; Tranchida, J.; Trott, C.; Plimpton, S.J. LAMMPS – a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Computer Physics Communications 2022, 271, 108171. [Google Scholar] [CrossRef]
  28. https://www.ovito.org/ (Last access on 1 May 2024).
  29. Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, second ed.; Oxford University Press, 2017. [Google Scholar]
  30. Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Molecular Physics 1984, 52, 255–268. [Google Scholar] [CrossRef]
  31. Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant pressure molecular dynamics algorithms. Journal of Chemical Physics 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
  32. Punnathanam, S.; Corti, D.S. Work of cavity formation inside a fluid using free-energy perturbation theory. Physical Review E 2004, 69, 036105. [Google Scholar] [CrossRef]
  33. Stephan, S.; Thol, M.; Vrabec, J.; Hasse, H. Thermophysical Properties of the Lennard-Jones Fluid: Database and Data Assessment. Journal of Chemical Information and Modeling 2019, 59, 4248–4265. [Google Scholar] [CrossRef]
  34. Stephan, S.; Staubach, J.; Hasse, H. Review and comparison of equations of state for the Lennard-Jones fluid. Fluid Phase Equilibria 2020, 523, 112772. [Google Scholar] [CrossRef]
  35. Zou, Y.; Huai, X.; Lin, L. A Molecular Dynamics Simulation of Bubble Nucleation in Homogeneous Liquid under Heating with Constant Mean Negative Presure. Applied Thermal Engineering 2010, 30, 859–863. [Google Scholar] [CrossRef]
  36. Matsumoto, M. Surface Tension and Stability of a Nanobubble in Water: Molecular Simulation. Journal of Fluid Science and Technology 2008, 3, 922–929. [Google Scholar] [CrossRef]
  37. Block, B.J.; Das, S.K.; Oettel, M.; Virnau, P.; Binder, K. Curvature dependence of surface free energy of liquid drops and bubbles: A simulation study. Journal of Chemical Physics 2010, 133, 154702. [Google Scholar] [CrossRef]
  38. Hewage, S.A.; Meegoda, J.N. Molecular dynamics simulation of bulk nanobubbles. Colloids and Surfaces A: Physicochemical and Engineering Aspects 2020, 650, 129565. [Google Scholar] [CrossRef]
  39. Bosserta, M.; Trimaille, I.; Cagnon, L.; Chabau, B.; Gueneau, C.; Spathis, P.; Wolf, P.E.; Rolley, E. Surface tension of cavitation bubbles. PNAS 2023, 120, e2300499120. [Google Scholar] [CrossRef] [PubMed]
Preprints 112243 g001
Figure 1. Simulation conditions plotted in a liquid-vapor phase diagram of LJ fluid based on an empirical equation of states[34]. Blue and cyan symbols: binodal lines, red and orange: spinodal (stability limit) lines.
Figure 1. Simulation conditions plotted in a liquid-vapor phase diagram of LJ fluid based on an empirical equation of states[34]. Blue and cyan symbols: binodal lines, red and orange: spinodal (stability limit) lines.
Preprints 112243 g001
Preprints 112243 g002
Figure 2. Property change during a simulation; example for Case 1 ( p 0 = − 0.20 ).
Figure 2. Property change during a simulation; example for Case 1 ( p 0 = − 0.20 ).
Preprints 112243 g002
Preprints 112243 g003
Figure 3. Examples of cross-sectional view for Case 1 ( p 0 = − 0.20 ).
Figure 3. Examples of cross-sectional view for Case 1 ( p 0 = − 0.20 ).
Preprints 112243 g003
Preprints 112243 g004
Figure 4. (Left) Density profile, the first peak of which defines the bubble radius r B d , (Right) change of r B d compared with the position of external field minimum R min . Example data for Case 1.
Figure 4. (Left) Density profile, the first peak of which defines the bubble radius r B d , (Right) change of r B d compared with the position of external field minimum R min . Example data for Case 1.
Preprints 112243 g004
Preprints 112243 g005
Figure 5. Comparison of bubble radius r B d and r B v ; example data for Case 1.
Figure 5. Comparison of bubble radius r B d and r B v ; example data for Case 1.
Preprints 112243 g005
Preprints 112243 g006
Figure 6. Obtained work as a function of time; example data for Case 1.
Figure 6. Obtained work as a function of time; example data for Case 1.
Preprints 112243 g006
Preprints 112243 g007
Figure 7. Cumulative work as a function of bubble radius; example for Case 1.
Figure 7. Cumulative work as a function of bubble radius; example for Case 1.
Preprints 112243 g007
Preprints 112243 g008
Figure 8. (Color curves) 100 samples of cumulative W, (Black) evaluated free energy difference Δ F ; example for Case 1.
Figure 8. (Color curves) 100 samples of cumulative W, (Black) evaluated free energy difference Δ F ; example for Case 1.
Preprints 112243 g008
Preprints 112243 g009
Figure 9. (Left) Obtained free energy Δ F and fitting to a simple CNT as discussed in §5.1. (Right) critical bubble size and activation energy.
Figure 9. (Left) Obtained free energy Δ F and fitting to a simple CNT as discussed in §5.1. (Right) critical bubble size and activation energy.
Preprints 112243 g009
Preprints 112243 g010
Figure 10. Parametes of CNT depending on the environment pressure p 0 .
Figure 10. Parametes of CNT depending on the environment pressure p 0 .
Preprints 112243 g010
Preprints 112243 g011
Figure 11. Comparison of Δ F with different number of samples for Case 1.
Figure 11. Comparison of Δ F with different number of samples for Case 1.
Preprints 112243 g011
Preprints 112243 g012
Figure 12. Distribution of accumulated work W ( t ) ; red line indicates the free energy estimated with Eq. (6); examples for Case 1.
Figure 12. Distribution of accumulated work W ( t ) ; red line indicates the free energy estimated with Eq. (6); examples for Case 1.
Preprints 112243 g012
Preprints 112243 g013
Figure 13. v 0 dependence for systems with p 0 = − 0.2 ; average is taken over ten samples as this preliminary evaluation.
Figure 13. v 0 dependence for systems with p 0 = − 0.2 ; average is taken over ten samples as this preliminary evaluation.
Preprints 112243 g013
Table 1. Conditions for the main simulation.
Table 1. Conditions for the main simulation.
Number of particles Temperature Pressure Equilibrium Density Growth speed Number of samplings
N [–] T 0 [ ε ] p 0 [ ε / σ 3 ] ρ [ σ − 3 ] v 0 [ σ / τ ] [–]
Case 1 32,000 0.80 − 0.20 0.752 0.01 100
Case 2 32,000 0.80 − 0.25 0.745 0.01 100
Case 3 32,000 0.80 − 0.30 0.737 0.01 100
Case 4 108,000 0.80 − 0.15 0.759 0.02 100
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated