Preprint
Article
Edges vs. Centers: Variability of Sarcomere Lengths Depends on What You Choose as “Sarcomere Ends”
Altmetrics
Downloads
101
Views
34
Comments
0
This version is not peer-reviewed
Submitted:
16 July 2024
Posted:
16 July 2024
You are already at the latest version
Alerts
Abstract
In our recent experimental study we found that variability in sarcomere lengths (SLs) is lower if we get them from A-band centers (visualized by Second Harmonic Generation microscopy, SHG) vs. Z-disks (ANEPPS-staining of t-tubules). In the present study we demonstrate, using a simulation approach, that the extent of variability and “randomness” in SL are directly affected by what “sarcomeric structure” is used to calculate the SL. We simulated randomly dispersed positions of Z-disks and calculated the center points between two Z-disks as A-band centers. We found that variance in SL, if calculated from A-band centers (A-SL), was twice lower vs. variance in Z-disk-based SL (Z-SL), regardless the predefined dispersion of Z-disks. Furthermore, A-SLs were “non-randomly” interrelated – each next A-SL tended to be longer if the preceding one was longer – in contrast to Z-SLs which were truly random. Next, we demonstrated the presence and prevalence of this “non-random” effect for A-SL vs. Z-SL in our previously acquired experimental records. The rationale for this artifact is the “mathematical dependence” of sarcomere center on its edges, and it must always be taken into account in the interpretation of smaller variability of the distance between sarcomeric A-band centers vs. the distance between Z-disks.
Keywords:
Subject: Biology and Life Sciences - Biophysics
1. Introduction
The mechanical activity of a sarcomere, the elementary contractile structure in muscle cells, is regulated by its actual length. The increase in sarcomere length (SL) within physiological range results in an increase in its active and passive forces (the Frank-Starling Mechanism). The in-series alignment of sarcomeres in a myofibril dictates that the mechanical force of each individual sarcomere is “transmitted” to neighboring sarcomeres thus constantly regulating their lengths and activation state of myofilaments [1]. This sarcomeric interplay determines collective dynamic mechanical behavior of sarcomere population and bears important physiological role in modulating integral contractile response of muscle cells [2].
Despite the prominent regularity of sarcomeres in myofibrils, as well as their highly organized structure, their lengths are not equal, with the dispersion up to 20% of the average SL according to published data [3,4,5,6]. Sarcomeres also differ in their stiffness, mostly due to the length-dependent features of giant protein titin [7], which contributes not only to the SL itself (as structural protein) but also to the SL variability as well as the variability in I-band and A-band width [8]. Furthermore, SL variability is shown to be dependent both on activation state of cell (in cardiomyocytes, [4,9,10] and in skeletal myocytes, [11,12,13]) and on the extent of cell stretch [14,15]. Very recently, it was reported that the variability in SL is even not randomly occurring but rather is “regulated” by sarcomeric features and probably by local populations of shorter/longer sarcomeres [10]. This is why the role of inter-sarcomeric heterogeneity remains in the focus of numerous studies carried out on striated muscles.
Careful determination of subtle differences in individual SL is critical for revealing whether and how SL variability can modulate cellular contractile response. The ability for high-precise measurements in live cardiomyocytes is often limited either by physical and/or methodological reasons: for example, in electron microscopy or due to phototoxicity in fluorophore-based optical measurements. For intact living cells, the use of fluorescent (two-photon) microscopy is likely the most wide used and advantageous method. However, without preliminary treatment for specific labeling of sarcomeric structures by (non)viral transfection/transduction methods, this method is often limited to staining of t-tubules. While fluorescent visualization of t-tubules is the very important tool for understanding cell physiology, unfortunately, it does not provide highly accurate spatial reconstruction of sarcomeric Z-disks. Indeed, t-tubules are heterogeneous in their width, morphology, and often not localized strongly at the centerline of Z-disks—please see good examples in Figure 1C in [16], Figure 1(bottom right panel) in [17], Figure 1A in [18]. Their typical cross-sectional diameter in mammalian ventricular cardiomyocytes is between 150 and 400 µm, depending on species [19]—this is wider than the Z-line width (~100 nm in cardiac fibers, [20]) and about ~10% of average sarcomere length that can substantially “mask” the actual position of Z-disk.
The alternative method is Second Harmonic Generation (SHG) microscopy that provides visualization of sarcomeric A-bands instead of Z-disks. This optical method is based on nonlinear optical effects (in contrast to the absorption of light in fluorescence imaging), it is less damaging, allows for deep sectioning (up to 1 mm) because of low-energy excitation light, and can be easily applied for live cells [21]. Importantly that it does not require pretreatment of cells with fluorescent dye [22]. The molecular origin of SHG images taken from muscle cell is myosin filaments, not other sarcomeric components like actin or titin [23,24]. The protein-specific nature of the SHG signal allows for sensitive identification of specific intrasarcomeric structure [25]. SHG microscopy is successfully used for evaluation of sarcomeric ultrastructure and myofiber morphology in skeletal and heart muscles, in situ and in vivo [23,26,27].
In our recent paper, we implemented simultaneous measurement of SL in live isolated rat ventricular cardiomyocytes using fluorescent staining by di-4-ANEPPS to visualize t-tubules (Z-disks) and SHG to visualize A-bands [28]. Consequently, “sarcomere length” was obtained either as the distance between two neighboring Z-disks or as the distance between the peaks of two neighboring A-bands (Figure 1). Our main finding was that the variability in SL is roughly twice lower for the latter method. We concluded that SHG microscopy is better method to quantify SL variability due to its higher specificity and precision.
However, now we hypothesize that this is might be a direct outcome of the inherent dependence of A-band center position on the Z-disk positions. If the positions of the two Z-disks are randomly dispersed at some extent, the position of A-band center (i.e., the center of sarcomere) is affected by this dispersion with some factor, and therefore some mathematical artifacts are introduced and should not be ignored. Therefore, the purpose of our present study is to understand: 1) how the dispersion in the central point between two neighboring Z-disks (we refer to it as an A-band center) relates to the dispersion of the Z-disk positions themselves, and 2) whether the calculated extent of SL variability depends on what is interpreted as sarcomere—the distance between Z-disks (Z-SL) or the distance between A-band centers (A-SL).
2. Materials and Methods
This study is based on our theoretical assumptions and provides computational results which were then compared to our previously measured experimental data. We kindly ask the reader to refer to our published paper [28] for methodological details and results related to the optical measurements in live rat cardiomyocytes.
To answer the two aforementioned questions (please see last paragraph in Introduction), we simulated an in-series sequence of Z-disks with their positions dispersed in a predefined extent, i.e., ±5, ±10, ±20, and ±40% of the mean SL, which is 2 µm throughout all simulations. The total number of “sarcomeres” in each individual sequence was set to 500 just to provide smoother distribution plots. The type of dispersion was Gaussian, with 2σ deviation level. In all simulations, we used exactly the same preset values like mean SL or type of dispersion, except the extent of dispersion in Z-disk position and/or A-band center position—we further refer to them as Z-disk and A-band center, respectively. For each preset Z-disk dispersion, we tested different dispersions in A-band center, all up to the given Z-disk dispersion but not exceeding this value. To simulate variation between different “myofibrils”, we used 10 consecutive independent runs to simulate 10 different 500-sarcomere long “myofibrils”. Each run was ended up by the calculation of certain statistical measures (e.g., actual mean and median SL, variance, standard deviation, coefficient of variation, median absolute deviation, etc.). Finally, the statistical measures were averaged by these 10 individual runs for further analysis.
For every pair of neighboring Z-disks, the exact central point was determined and then this central position was affected by an additional dispersion (Gaussian as well) with step-wise increase in the extent, from 0 to the predefined dispersion of Z-disk positions. For example, in the simulation of Z-disk dispersion by ±40% of mean SL (in this example it was 2.0±0.8 µm), A-band centers were dispersed by 0 to ±40% of mean SL with the step of 4% (Figure 2). Note that if the additional dispersion of A-band centers is set to 0%, their actual dispersion is still non-zero because of the dispersion in Z-disk—each A-band center is always first calculated as the distance between the neighboring Z-disks, so the distance between two A-band centers is always a subject of Z-disk-related dispersion (Figure 2A, top and bottom panels). Note also that without additional dispersion in A-band centers, the distribution of Z-SL is remarkably wider compared to the calculation of A-SL (Figure 2B). However, if we simulate additional dispersion for A-band centers in an increasing manner, the width of A-SL distribution becomes gradually higher. For example, for simulation of ±40% dispersion in both Z-disk and A-band center positions, the A-SL distribution is much wider than the Z-SL distribution (Figure 2C).
3. Results
Our simulations show that independent of the extent of Z-disk dispersion, if the dispersion in A-band centers is preset to 0% (meaning that the only factor affecting their dispersion is preset Z-disk dispersion), the calculated dispersion of the A-SL is always lower than that of Z-SL. Figure 3A shows the actual variances of Z-SL and A-SL calculated for Z-disk dispersion at the level of ±20% of mean SL while no additional dispersion in A-band center is applied. The example consists of 10 independent simulation runs, where each of them gave sustainably higher variance in Z-SL compared to A-SL. Similar differences were found for any Z-disk dispersion tested, from ±5% to ±40% of mean SL, where the additional dispersion in A-band center was always set to 0%. Furthermore, the ratio of the variances in Z-SL and A-SL, calculated for any dispersion in Z-disk, was quantitatively nearly the same, approximately ≈2 (Figure 3B). Therefore, we can conclude that regardless the actual level of dispersion of Z-disk (assuming it is normally distributed), the calculated variances of A-SL is approximately two-fold smaller than that of Z-SL, if no additional dispersion is applied to A-band centers.
This nearly constant value of the ratio of variances in Z-SL and A-SL, if no additional dispersion of A-band center is introduced, may indicate that this is due to mathematical reasons. If so, it becomes critical which part of sarcomere is used for direct evaluation of SL variability in a natural experiment.
We would like to note that the following theoretical background is quite basic but it is important to describe it in details here for clarity. Lets consider a stochastic process with random variables Zi, where Z indicates sarcomere length. We assume that Zi are independent of each other and all have the same variance Var(Zi) = σ2. The process describes a chain of sarcomeres, with the length Zi of i-th sarcomere in the chain. As a surrogate metric for the sarcomere length, we want to use distances Ai between centers of neighboring sarcomeres with indices i and i + 1. The sequence of Ai is another stochastic process. Our goal is to find the variance Var(Ai) of random variables Ai in this process. The distance Ai between centers of sarcomeres i and i + 1 is an average of lengths of sarcomeres:
Ai = (Zi+1 + Zi) / 2
Next, we will use two basic formulas from Probability Theory for a variance of a sum of two independent random variables X1 and X2:
and for multiplication of a random variable X with scalar a:
Var(X1 + X2) = Var(X1) + Var(X2),
Var(a + X) = a2 × Var(X)
These two formulas are trivial to derive from the definition of variance:
where E(X) is an expectation (mean value) of a variable X. For instance:
Var(X) = E[(E(X) – X)2],
Var(a × X) = E[(E(a × X) – a × X)2] = E[(a × E(X) – a × X)2]
= E[a2 × (E(X) –X)2] = a2 × E[(E(X) – X)2] = a2 × Var(X)
Using the above formulas, the variance of Ai is:
Var(Ai) = Var((Zi + Zi+1) / 2) = (Var(Zi) + Var(Zi+1)) / 4
(σ2 + σ2) / 4 = σ2 / 2
The mathematical formulas above show that the variance in “sarcomere length”, if derived from the distances between A-band centers, must be twice lower compared to the conventional sarcomere lengths obtained as the distances between Z-disks. This finding supports that the two-fold lower experimentally observed variability in A-SL, as compared to the Z-SL variability, is due to the mathematical rather than a technical reason (e.g., low resolution of an optical system) or methodological artifact (staining of sarcomeric structures not belonging purely to a sarcomere center or sarcomere edges).
However, in any real experiment, the A-band centers are also subjects of the additional variability, which is independent of the naturally existing Z-disk variability but may originate from e.g., relatively low resolution of a microscopy system. We therefore tested what is the value of additional dispersion of A-band center which corresponds to the equal variances in Z-SL and A-SL, i.e., the ratio of the variances is = 1. To find that value, we simulated various situations with the additional dispersion, ranged between 0% and the dispersion value preset for Z-disk, e.g., between 0% and ±40% of mean SL for ±40% of Z-disk dispersion. The number of steps for total change in the additional dispersion value was always set to 10 (plus 1 step for zero dispersion), so for the above-mentioned example, the step was ±4% of mean SL.
Figure 3C summarizes the results of these simulations run for four different preset values of Z-disk dispersions (between ±5 to ±40% of mean SL). The data here are the calculated ratio of variances in Z-SL and A-SL (Z/A ratio). Each data set consists of 11 points (mean ± SD) where each point is averaged by 10 individual simulations (to simulate variability between myofibrils). Note that the value of A-band center dispersion, which corresponded to the Z/A ratio = 1, was always twice lower compared to the extent of dispersion in Z-disk. For example, in the simulation of Z-disk dispersion at the level of ±5% of mean SL, the Z/A ratio was equal to 1 when the A-band dispersion was set to ±2.5% of mean SL (see vertical dotted lines in Figure 3C).
Finally, we evaluated in our simulations if the preset dispersion in Z-disks, which results in randomly assigned Z-SL, does or does not produce any non-random effect on calculated A-SL. Figure 4A demonstrates autocorrelation curves for the in-series sequence of Z-SL and A-SL (for first 10 lags) produced in an individual simulation run, where Z-disk dispersion was preset at the level of ±20% of mean SL but no additional dispersion was applied for A-band center. It is clearly seen that there is a non-random effect of each given A-SL on the next neighboring A-SL, because the autocorrelation function at the first lag (ACFLAG=1) was substantially non-zero. Therefore, each consecutive A-SL was dependent on the previous one. In contrast, autocorrelation curve for Z-SL was near to zero line indicating that in our simulation the Z-SL were indeed randomly preset. If we apply an additional dispersion of A-band center, increasing it in gradual manner and imitating the variability of sarcomere center, the ACFLAG=1 begins to decrease until the additional dispersion reaches the level of Z-disk dispersion divided by 2 (Figure 4B, red line). At this level of dispersion of A-band center, we can conclude that each A-SL is now purely independent of any neighboring A-SL, i.e., they are truly randomly distributed. Moreover, if we further gradually increase the dispersion in A-band center, the ACFLAG=1 becomes negative and continues to be quantitatively increasing. The negative values of the ACFLAG=1 indicate that the A-SL now inversely related, i.e., the greater the previous A-SL, the shorter the next one. Overall, these results show that the calculation of A-SL from randomly preset Z-SL in general does not produce the randomly distributed sequence of “sarcomeres”, as opposite to the randomly preset Z-SL.
To compare the simulation data with real optical records, we calculated the ACFLAG=1 for our previously acquired experimental measurements which were used in the above-mentioned publication. In that study, we measured the intensity profiles for sarcomeric striation based on either Z-disks or A-band centers using 5 individual regions of interest (ROI) overlaid to an image of isolated cardiomyocyte, with ~35-40 sarcomeres per region. In total, we studies 26 individual cells × 5 ROIs = 130 individual ROIs = 260 individual values for ACFLAG=1 (130 for Z-disks and 130 for A-band centers). The numerical value of each ACFLAG=1 was compared to the corresponding confidence intervals (upper and lower limits for positive and negative ACFLAG=1, respectively) calculated using the actual SL values, and we counted individual ROIs where the ACFLAG=1 value for A-SL and/or Z-SL was significantly beyond the upper/lower limits, i.e., where there is a “non-random” effect between the neighboring sarcomere lengths. The positive ACFLAG=1 above the upper limit indicated “positive” correlation between two neighboring sarcomere lengths: the next one sarcomere is tended to be longer if the preceding sarcomere is longer. (Of course, it does not turn to the gradual increase in the SL along a “myofibril” because the primary factor for A-SL is a randomly assigned next Z-disk position.) As similar, the negative ACFLAG=1 below the lower limit indicated “negative” correlation: each next sarcomere tends to be longer/shorter if the preceded sarcomere was shorter/longer.
The results of the analysis of ACFLAG=1 for experimentally measured Z-SL and A-SL were as follows. We found the significantly “non-random” effect for A-SL in 34 out of 130 ROIs, which was ~26% of the individual records. The average value of ACFLAG=1 was 0.51±0.13 and, more important, all the ACFLAG=1 were positive. Note that according to our simulation results the positive ACFLAG=1 for A-SL always corresponds with lower variability in the A-SL vs. Z-SL (see Figure 4B). In contrast, for Z-SL we found just 8 out of 130 records (~6%) with significantly “non-random” effect, and half of them were with negative ACFLAG=1, so the average value was 0.02±0.49. In fact, we did not observe any sustainability in ACFLAG=1 for Z-SL but we found a remarkable “regularity” in ACFLAG=1 for A-SL—a “non-randomness” occurred more often and always with “positive” dependence between neighboring A-SL values.
4. Discussion
The main outcome of our theoretical simulation study is that the extent of variability of sarcomere lengths in multisarcomere constructs like a myofibril is strongly affected by what the sarcomere part is used to calculate the lengths – either Z-disks (Z) or A-band centers (A). In contrast to the truly randomly assigned positions of Z-disks, A-band centers are always the subject of calculation of the middle point between the Z-disks, and therefore their variability is “linked” to the variability of Z-disk positions. This is “natural” variability but in various simulations we can introduce an additional variability, not linked with Z-disk-based variability. Our simulation results for zero dispersion of A-band center shows that the Z/A ratio of variances is equal to 2, as shown in Figure 3B. However, if one needs to calculate the ratio for other variability measures like standard deviation or median absolute deviation, the ratio is equal to √2 (as all the measures are related to the square root of variance). This mathematical factor must be taken into account during comparison between various variability measures or between different experimental data sets.
We would like to refer again to our recent paper [28] where we mentioned much lower variability in the SL obtained from A-bands vs. Z-disks.
First, if we compare the experimentally gathered SL distribution plots from that paper (see Figure 2F there) and the SL distribution plots obtained without additional A-band center dispersion in the present paper (see Figure 2B), we can note their very high similarity. In contrast, the experimental data are opposite to those shown in Figure 2C here, i.e., where high additional variation in A-band center is applied in the simulation. It might be important because it indicates that the center of natural sarcomere (center of A-band) is much less subjected to any individual variation and “regulated” mostly by the Z-disks. Therefore, the A-band related calculation of sarcomere lengths is much devoid of that extent of SL variability which can be naturally present in the cell.
Second, we welcome a reader to refer to Figure 2B-E in the same paper, where several variability measures for SL were compared between ANEPPS and SHG measurements: absolute values of inter-quartile range and median absolute deviation, as well as their relative measures. All these measures were roughly twice as low in SHG vs. ANEPPS; however, these plots presented measures related to the square root of variance, not to the variance directly. Therefore, our experimental findings must correspond to the ratio of variances ≈4, which is twofold higher compared to our simulation result. In fact, we found rather higher ratios of variances and standard deviations (square root of variance) for our experimental data sets. The median values (first and third quartile) for 26 individual cells were as follows: the ratio of standard deviations = 2.14 (1.79, 2.96), the ratio of variances = 4.56 (3.20, 8.78).
The reason why we observed such higher ratio in the experiment may be that ANEPPS is not purely specific to Z-disk proteins but stains t-tubules—this may constitute increased variability in Z-disk position (e.g., due to the different morphology of individual t-tubules) and, in turn, increased ratio of Z/A variances as well as the ratios for other variability measures. Another possible reason is that the full width of an individual Z-disk intensity profile in our optical measurements was typically narrower than that of A-band. In other words, on average an individual Z-disk profile had sharper peak compared to an individual A-band intensity profile (e.g., compare widths of the green and red bands in Figure 1). In our optical system, the X/Y-resolution of the images (scan pixel size) was ~0.15 µm, and this resolution provided ~13 pixels per 2 µm long sarcomere. Also, such resolution is not fully optimal to retrieve double-peaked A-band profile and this is why we typically observed single-peaked intensity profile, in contrast to commonly reported double-peaked profile, e.g., see Figure 3B in [24]. Therefore, the relatively sharper the intensity profile for Z-disks, the greater their chance to be randomly peaked at every of the two neighboring pixels of the optical sensor, as compared to a more shallowed peak of an individual A-band profile. This may directly contribute to the greater experimentally observed variance in Z-disk position but not in A-band center.
The results shown in our present paper does not imply anything against the reliability and effectiveness of SHG microscopy when used to study very subtle subsarcomeric structures. SHG is indeed a great tool for high-precision subsarcomeric measuring (two-photon microscopy is another one), with important advantage that it can be easily used in live and unstained myocytes [29]. According to recently coined conception of “SL nanometry” [30,31], the use of SHG seems to be more preferential instrumental method for revealing minor changes in sarcomere geometry (~50-100 nm), compared to the traditional fluorescent microscopy based on staining of t-tubules.
The principal physiological effect of SL heterogeneity on muscle cell contractility is based on dynamic mechanical intercommunication of short and long (strong and weak) sarcomeres during cellular contraction-relaxation [2]. The SL variability becomes substantially higher even if a single sarcomere is disrupted in the initially untreated intact myofibril [15] and this significantly decreases active force developed by the myofibril [32,33]. The extent of SL variability is sensitive to activation state and preload [6,7]. The SL variability may even demonstrate non-random spatial occurrence (at least in skeletal muscle) indicating that there are some intracellular mechanisms specific to the regulation of local SL dispersion [10]. Altogether supports that SL variability is an important contributor to the regulation of contractility in muscle cells made up of thousands of sarcomeres. Therefore, accurate quantification of SL heterogeneity in multisarcomeric constructs warrants that experimental findings are interpreted properly and remain physiologically relevant.
5. Conclusions
The conclusion of this simulation study is that the variance in sarcomere centers, if they are directly calculated from the neighboring randomly dispersed Z-disks, is always twice lower compared to the variance in Z-disks. This is due to the mathematical interrelation between the two characteristics. Consequently, if one calculates sarcomere length using A-band centers (A-SL), the obtained variability in the A-SL is always lower than that which come from using Z-disk (Z-SL). Moreover, there is remarkable “non-randomness” of the A-SL values. This finding is in the good agreement with our experimentally observed variabilities in “sarcomere” lengths, where we found much smaller A-SL variability (measured by Second Harmonic Generation microscopy) vs. Z-SL variability (measured by ANEPPS staining of t-tubules). Importantly, this smaller variability in the A-SL must not be interpreted as diminished natural SL variability but rather it should be figured out as the mathematical artifact closely linked with the natural physical “regulation” of sarcomeric center by its Z-disks. This is confirmed, at least in part, by our finding that A-SL values in isolated live cardiomyocytes display higher frequency and sustainability of “non-randomness” compared to the Z-SL values.
Author Contributions
Conceptualization, O.L., O.C., and P.dT.; methodology, O.L., O.C., and P.dT.; simulation and software, O.L.; formal analysis, O.L., O.C., and P.dT.; writing—O.L., O.C., and P.dT.; writing—review and editing, O.L., O.C., and P.dT. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data generated and analyzed in this study are available from the corresponding author upon reasonable request.
Acknowledgments
We would like to thank Dr. Viatcheslav Gurev (IBM Research) for his help with mathematical aspects of the computational results.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- de Tombe, P.P.; ter Keurs, H.E.D.J. Cardiac muscle mechanics: Sarcomere length matters. J. Mol. Cell. Cardiol. 2016, 91, 148–150. [CrossRef]
- Helmes, M.; Palmer, B.M. Sarcomere length in the beating heart: Synchronicity is optional. J. Gen. Physiol. 2022, 154, e202113022. [CrossRef]
- Johnston, K.; Jinha, A.; Herzog, W. The role of sarcomere length non-uniformities in residual force enhancement of skeletal muscle myofibrils. R. Soc. Open Sci. 2016, 3, 150657. [CrossRef]
- Kobirumaki-Shimozawa, F.; Oyama, K.; Shimozawa, T.; Mizuno, A.; Ohki, T.; Terui, T.; Minamisawa, S.; Ishiwata, S.; Fukuda, N. Nano-imaging of the beating mouse heart in vivo: Importance of sarcomere dynamics, as opposed to sarcomere length per se, in the regulation of cardiac function. J. Gen. Physiol. 2016, 147, 53–62. [CrossRef]
- Moo, E.K.; Fortuna, R.; Sibole, S.C.; Abusara, Z.; Herzog, W. In vivo sarcomere lengths and sarcomere elongations are not uniform across an intact muscle. Front. Physiol. 2016, 7, 187. [CrossRef]
- de Souza Leite, F.; Rassier, D.E. Sarcomere length nonuniformity and force regulation in myofibrils and sarcomeres. Biophys. J. 2020, 119, 1–6. [CrossRef]
- Herzog, W. What can we learn from single sarcomere and myofibril preparations? Front. Physiol. 2022, 13, 837611. [CrossRef]
- Li, J.; Sundnes, J.; Hou, Y.; Laasmaa, M.; Ruud, M.; Unger, A.; Kolstad, TR.; Frisk, M.; Norseng, P.A.; Yang, L.; Setterberg, I.E.; et al. Stretch harmonizes sarcomere strain across the cardiomyocyte. Circ. Res. 2023, 133, 255–270. [CrossRef]
- Lookin, O.; Khokhlova, A.; Myachina, T.; Butova, X.; Cazorla, O.; de Tombe, P. Contractile state dependent sarcomere length variability in isolated guinea-pig cardiomyocytes. Front. Physiol. 2022, 13, 857471. [CrossRef]
- Li, M.; Leonard, T.R.; Han, S.W.; Moo, E.K.; Herzog, W. Gaining new understanding of sarcomere length nonuniformities in skeletal muscles. Front. Physiol. 2024, 14, 1242177. [CrossRef]
- Moo, E.K.; Leonard, T.R.; Herzog, W. In vivo sarcomere lengths become more non-uniform upon activation in intact whole muscle. Front. Physiol. 2017, 8, 1015. [CrossRef]
- Johnston, K.; Moo, E.K.; Jinha, A.; Herzog, W. On sarcomere length stability during isometric contractions before and after active stretching. J. Exp. Biol. 2019, 222, jeb209924. [CrossRef]
- Moo, E.K.; Herzog, W. Sarcomere lengths become more uniform over time in intact muscle-tendon unit during isometric contractions. Front. Physiol. 2020, 11, 448. [CrossRef]
- Rassier, D.E.; Pavlov, I. Force produced by isolated sarcomeres and half-sarcomeres after an imposed stretch. Am. J. Physiol. Cell Physiol. 2012, 302, C240–C248, 2012. [CrossRef]
- Haeger, R.M.; Rassier, D.E. Force enhancement after stretch of isolated myofibrils is increased by sarcomere length non-uniformities. Sci. Rep. 2020, 10, 21590. [CrossRef]
- Scriven, D.R.L.; Asghari, P.; Moore, E.D.W. Microarchitecture of the dyad. Cardiovasc. Res. 2013, 98, 169–176. [CrossRef]
- Novotová, M.; Zahradníková, A.Jr.; Nichtová, Z.; Kováč, R.; Kráľová, E.; Stankovičová, T.; Zahradníková, A.; Zahradník, I. Structural variability of dyads relates to calcium release in rat ventricular myocytes. Sci. Rep. 2020, 10, 8076. [CrossRef]
- Rog-Zielinska, E.A.; Scardigli, M.; Peyronnet, R.; Zgierski-Johnston, C.M.; Greiner, J.; Madl, J.; O’Toole, E.T.; Morphew, M.; Hoenger, A.; Sacconi, L.; et al. Beat-by-beat cardiomyocyte t-tubule deformation drives tubular content exchange. Circ. Res. 2021, 128, 203–215. [CrossRef]
- Kong, C.H.T.; Rog-Zielinska, E.A.; Orchard, C.H.; Kohl, P.; Cannell, M.B. Sub-microscopic analysis of t-tubule geometry in living cardiac ventricular myocytes using a shape-based analysis method. J. Mol. Cell Cardiol. 2017, 108, 1–7. [CrossRef]
- Pradeep K Luther 1. The vertebrate muscle Z-disc: Sarcomere anchor for structure and signalling. J. Muscle Res. Cell Motil. 2009, 30, 171–185. [CrossRef]
- Campagnola, P.J.; Wei, M.D.; Lewis, A.; Loew, L.M. High-resolution nonlinear optical imaging of live cells by second harmonic generation. Biophys. J. 1999, 77, 3341–3349. [CrossRef]
- Recher, G.; Rouède, D.; Richard, P.; Simon, A.; Bellanger, J.-J.; Tiaho, F. Three distinct sarcomeric patterns of skeletal muscle revealed by SHG and TPEF microscopy. Opt. Express 2009, 17, 19763–19777. [CrossRef]
- Both, M.; Vogel, M.; Friedrich, O.; von Wegner, F.; Künsting, T.; Fink, R.H.A.; Uttenweiler, D. Second harmonic imaging of intrinsic signals in muscle fibers in situ. J. Biomed. Opt. 2004, 9, 882–892. [CrossRef]
- Plotnikov, S.V.; Millard, A.C.; Campagnola, P.J.; Mohler, W.A. Characterization of the myosin-based source for second-harmonic generation from muscle sarcomeres. Biophys. J. 2006, 90, 693–703. [CrossRef]
- Rouède, D.; Coumailleau, P.; Schaub, E.; Bellanger, J.-J.; Blanchard-Desce, M.; Tiaho, F. Myofibrillar misalignment correlated to triad disappearance of mdx mouse gastrocnemius muscle probed by SHG microscopy. Biomed. Opt. Express 2014, 5, 858–875. [CrossRef]
- Buttgereit, A. Second harmonic generation microscopy of muscle cell morphology and dynamics. Methods Mol. Biol. 2017, 1601, 229–241. [CrossRef]
- Varga, B.; Meli, A.C.; Radoslavova, S.; Panel, M.; Lacampagne, A.; Gergely, C.; Cazorla, O.; Cloitre, T. Internal structure and remodeling in dystrophin-deficient cardiomyocytes using second harmonic generation. Nanomedicine 2020, 30, 102295. [CrossRef]
- Lookin, O.; de Tombe, P.; Boulali, N.; Gergely, C.; Cloitre, T.; Cazorla, O. Cardiomyocyte sarcomere length variability: Membrane fluorescence versus second harmonic generation myosin imaging. J. Gen. Physiol. 2023, 155, e202213289. [CrossRef]
- Boulesteix, T.; Beaurepaire, E.; Sauviat, M.-P.; Schanne-Klein, M.-C. Second-harmonic microscopy of unstained living cardiac myocytes: Measurements of sarcomere length with 20-nm accuracy. Opt. Lett. 2004, 29, 2031–2033. [CrossRef]
- Shintani, S.A.; Oyama, K.; Kobirumaki-Shimozawa, F.; Ohki, T.; Ishiwata, S.; Fukuda, N. Sarcomere length nanometry in rat neonatal cardiomyocytes expressed with a-actinin-AcGFP in Z discs. J. Gen. Physiol. 2014, 143, 513–524. [CrossRef]
- Schmidt, J.; Jinha, A.; Herzog, W. Sarcomere length measurement reliability in single myofibrils. J. Biomech. 2021, 126, 110628. [CrossRef]
- Mendoza, A.C.; Rassier, D.E. Extraction of thick filaments in individual sarcomeres affects force production by single myofibrils. Biophys. J. 2020, 118, 1921–1929. [CrossRef]
- Haeger, R.; de Souza Leite, F.; Rassier, D.E. Sarcomere length nonuniformities dictate force production along the descending limb of the force–length relation. Proc. R. Soc. B 2020, 287, 20202133. [CrossRef]
Figure 1.
The image shows sarcomeric striation measured in two separate channels simultaneously. Green channel corresponds to Z-disks (visualized by staining of t-tubules by ANEPPS dye), where a sarcomere is defined as the distance between two Z-disks (conventional way). Red channel corresponds to A-bands (visualized by Second Harmonic Generation microscopy, SHG, without using of a fluorescent dye), and “sarcomere” here is defined as the distance between two neighboring A-bands (labeled here as “sarcomere”).
Figure 1.
The image shows sarcomeric striation measured in two separate channels simultaneously. Green channel corresponds to Z-disks (visualized by staining of t-tubules by ANEPPS dye), where a sarcomere is defined as the distance between two Z-disks (conventional way). Red channel corresponds to A-bands (visualized by Second Harmonic Generation microscopy, SHG, without using of a fluorescent dye), and “sarcomere” here is defined as the distance between two neighboring A-bands (labeled here as “sarcomere”).

Figure 2.
The example of a single simulation of dispersion in Z-disk with or without simultaneous dispersion of A-band center. (A) The initial trail of the simulated Z-disks and A-band centers, ~30 individual positions in each panel (out of 500 in a single simulation). Z-disks are shown in green, A-band centers are shown in red. The image on the top corresponds to the dispersion of Z-disk at the level of ±40% of mean SL without additional dispersion in the A-band centers. The image on the bottom corresponds to ±40% dispersion of Z-disk with ±40% additional dispersion of the A-band center. (B and C) The distributions of Z-SL and A-SL for the above described simulations (combined for 10 runs each of 500 “sarcomeres” in-series).
Figure 2.
The example of a single simulation of dispersion in Z-disk with or without simultaneous dispersion of A-band center. (A) The initial trail of the simulated Z-disks and A-band centers, ~30 individual positions in each panel (out of 500 in a single simulation). Z-disks are shown in green, A-band centers are shown in red. The image on the top corresponds to the dispersion of Z-disk at the level of ±40% of mean SL without additional dispersion in the A-band centers. The image on the bottom corresponds to ±40% dispersion of Z-disk with ±40% additional dispersion of the A-band center. (B and C) The distributions of Z-SL and A-SL for the above described simulations (combined for 10 runs each of 500 “sarcomeres” in-series).
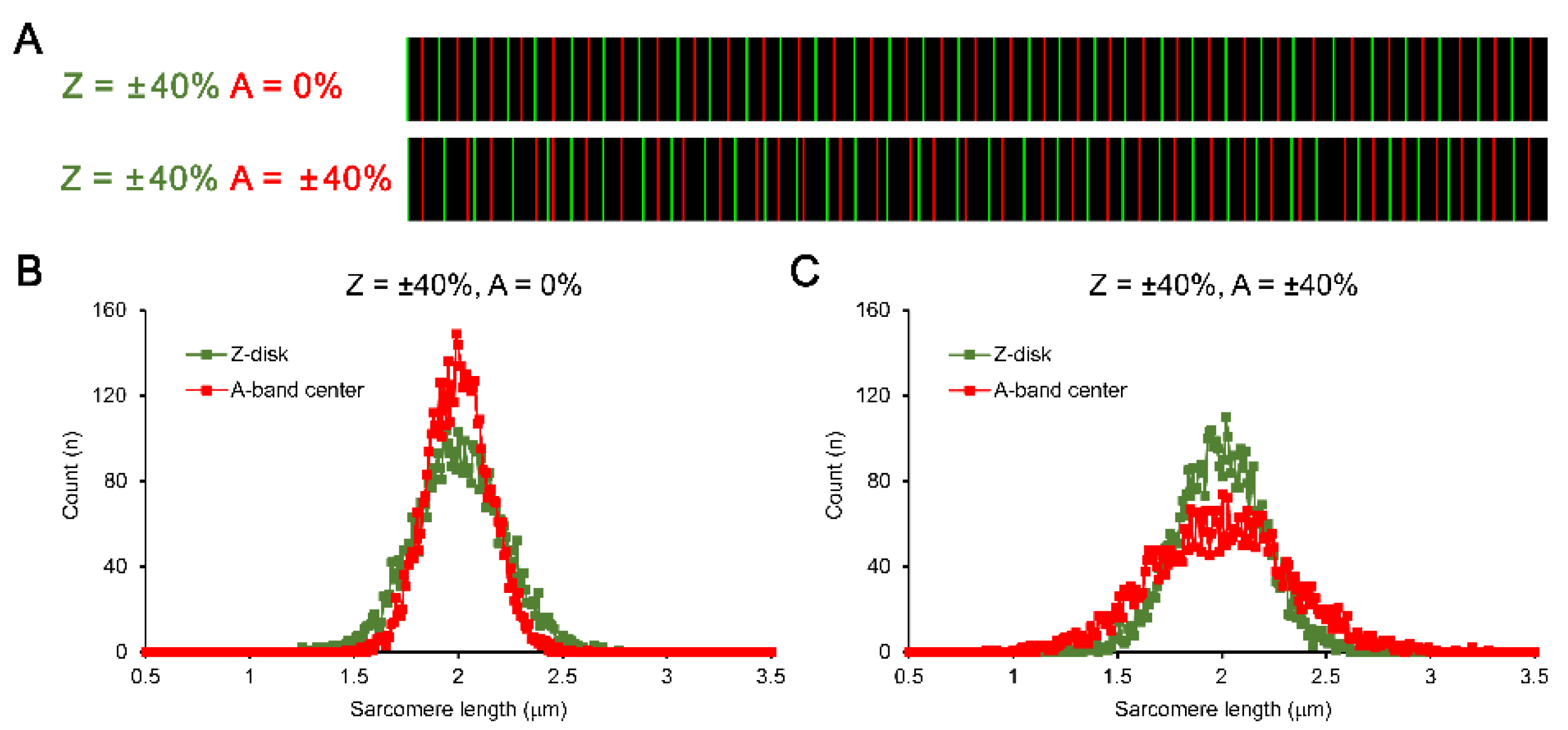
Figure 3.
The relationship between variances of sarcomere length (SL), calculated as the distance between A-band centers (A-SL) or between Z-disks (Z-SL), and obtained under different dispersion of Z-disks and with/without additional dispersion in A-band center. (A) SL variances for simulation of ±20% dispersion in Z-disk (mean SL = 2 µm) with no additional dispersion in A-band center; 10 independent simulation runs, each with 500 “sarcomeres”, are shown. (B) The ratio of calculated variances of Z-SL and A-SL (Z/A ratio) obtained for different dispersions of Z-disk, from ±5% to ±40%. Each individual point represents Z/A ratio obtained for 10 independent simulation runs, mean ± SD. This ratio is invariant to the dispersion in Z-disk and numerically it is ≈ 2 (dotted horizontal line). (C) The relationship between Z/A ratio and additional dispersion of A-band center (if any). Shown are different simulations for various dispersions of Z-disk (±5, ±10, ±20, and ±40% of mean SL), each for 10 individual simulation runs at the given Z-disk and A-band dispersions, mean ± SD. The horizontal dashed line follows the Z/A ratio = 1, i.e., equal variances in Z-disk and A-band center. Vertical dotted lines intersect X-axis at the value of additional A-band dispersion which corresponds to the Z/A ratio = 1. Note that these values are exactly the Z-disk dispersion divided by 2, e.g., for Z = ±10%, the additional dispersion of A-band center must be ±5% to obtain the Z/A ratio = 1.
Figure 3.
The relationship between variances of sarcomere length (SL), calculated as the distance between A-band centers (A-SL) or between Z-disks (Z-SL), and obtained under different dispersion of Z-disks and with/without additional dispersion in A-band center. (A) SL variances for simulation of ±20% dispersion in Z-disk (mean SL = 2 µm) with no additional dispersion in A-band center; 10 independent simulation runs, each with 500 “sarcomeres”, are shown. (B) The ratio of calculated variances of Z-SL and A-SL (Z/A ratio) obtained for different dispersions of Z-disk, from ±5% to ±40%. Each individual point represents Z/A ratio obtained for 10 independent simulation runs, mean ± SD. This ratio is invariant to the dispersion in Z-disk and numerically it is ≈ 2 (dotted horizontal line). (C) The relationship between Z/A ratio and additional dispersion of A-band center (if any). Shown are different simulations for various dispersions of Z-disk (±5, ±10, ±20, and ±40% of mean SL), each for 10 individual simulation runs at the given Z-disk and A-band dispersions, mean ± SD. The horizontal dashed line follows the Z/A ratio = 1, i.e., equal variances in Z-disk and A-band center. Vertical dotted lines intersect X-axis at the value of additional A-band dispersion which corresponds to the Z/A ratio = 1. Note that these values are exactly the Z-disk dispersion divided by 2, e.g., for Z = ±10%, the additional dispersion of A-band center must be ±5% to obtain the Z/A ratio = 1.
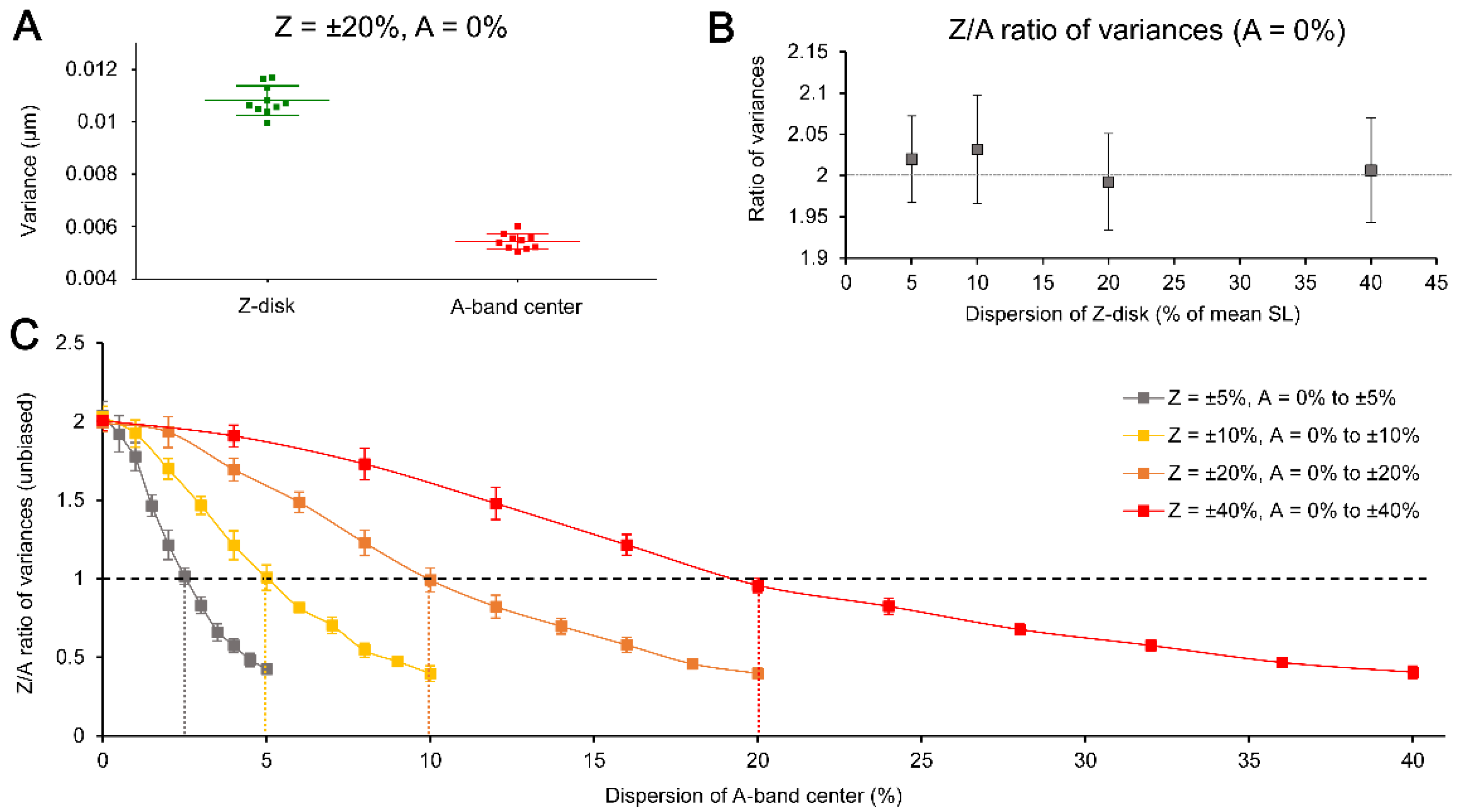
Figure 4.
The autocorrelation analysis for sarcomere length (SL), calculated as the distance between A-band centers (A-SL) or the distance between Z-disks (Z-SL), in our simulation runs. (A) The autocorrelation function at the first lag for Z-SL and A-SL for an individual simulation run, where the dispersion of Z-disk was preset at ±20% of mean SL while no additional dispersion of A-band center was used. Dotted line shows the confidence interval (CI) limit for autocorrelation function calculated for A-SL data. Note the substantial “non-randomness” of A-SL but not Z-SL at the first lag. (B) The analysis of autocorrelation coefficient at the first lag (ACFLAG=1) for Z-SL and A-SL at the same fixed dispersion of Z-disk (±20%) but with various additional dispersion in A-band center, as indicated in the panel caption. The ACFLAG=1 decreases gradually and becomes quantitatively minimal, where the additional dispersion in A-band center reaches the dispersion of Z-disk divided by 2 (±10% in this example). Further increase in A-band center dispersion results in the inversion of the ACF LAG=1, indicating that the neighboring A-SL are negatively correlated.
Figure 4.
The autocorrelation analysis for sarcomere length (SL), calculated as the distance between A-band centers (A-SL) or the distance between Z-disks (Z-SL), in our simulation runs. (A) The autocorrelation function at the first lag for Z-SL and A-SL for an individual simulation run, where the dispersion of Z-disk was preset at ±20% of mean SL while no additional dispersion of A-band center was used. Dotted line shows the confidence interval (CI) limit for autocorrelation function calculated for A-SL data. Note the substantial “non-randomness” of A-SL but not Z-SL at the first lag. (B) The analysis of autocorrelation coefficient at the first lag (ACFLAG=1) for Z-SL and A-SL at the same fixed dispersion of Z-disk (±20%) but with various additional dispersion in A-band center, as indicated in the panel caption. The ACFLAG=1 decreases gradually and becomes quantitatively minimal, where the additional dispersion in A-band center reaches the dispersion of Z-disk divided by 2 (±10% in this example). Further increase in A-band center dispersion results in the inversion of the ACF LAG=1, indicating that the neighboring A-SL are negatively correlated.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





