Prerpints.org logo
Preprint
Article

Research, Analysis and Improvement of Unmanned Aerial Vehicle Path Planning Algorithms in Urban Ultra-Low Altitude Airspace

Altmetrics

Downloads

78

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

16 July 2024

Posted:

16 July 2024

You are already at the latest version

Alerts
Abstract
Urban ultra-low altitude airspace (ULAA) presents unique challenges for unmanned aerial vehicle (UAV) path planning due to high building density and regulatory constraints. This study analyzes and improves classical path planning algorithms for UAVs in ULAA. Experiments were conducted using A*, RRT, RRT*, and artificial potential field (APF) methods in a simulated environment based on building data from Chengdu City, China. Results show that traditional algorithms struggle in dense obstacle environments, particularly APF due to local minima issues. Enhancements were proposed: a density-aware heuristic for A*, random perturbation for APF, and a hybrid optimization strategy for RRT*. These modifications improved computation time, path length, and obstacle avoidance. The study provides insights into the limitations of classical algorithms and suggests enhancements for more effective UAV path planning in urban environments.
Keywords: 
Subject: Engineering  -   Transportation Science and Technology

1. Introduction

The planning of flight paths for UAVs is of great importance to the management of air traffic by UAVs [1]. The development of safe and efficient path planning algorithms can assist UAV operators in reducing operational risks, improving operational efficiency, and increasing revenue [2]. Furthermore, these algorithms can facilitate the supervision of UAVs by relevant regulatory units, while simultaneously ensuring the safety and privacy of individuals within the operational environment [3,4]. In 2024, the Interim Regulations on the Administration of Unmanned Aircraft Flights were implemented in China, which proposed that "airspace outside the scope of controlled airspace shall be the airspace suitable for micro, light, and small UAVs [5]. Furthermore, the regulations stipulated that the airspace with a true height of less than 120 meters (excluding air exclusion zones, ultra-low The altitude flight airspace for military aviation, air restriction zones and surrounding airspace, and other areas requiring classification as controlled airspace shall be designated as controlled airspace. The flyable airspace for micro, light, and small UAVs is the key premise of this paper’s research and therefore falls under the category of controlled airspace [6,7,8,9]. In this paper, the aforementioned area is defined as urban ULAA. In normal circumstances, the maximum altitude of urban ULAA for micro, light, and small UAVs is 120 meters, which results in the presence of numerous high-rise buildings in this airspace. This not only increases the complexity of urban ULAA but also makes it more challenging for UAV flight path planning.
The majority of traditional UAV path planning algorithms can be classified into four main categories: geometric algorithms, artificial potential field methods, grid-based search algorithms, and sampling-based algorithms [10]. Geometric algorithms include visible graphs and cell decomposition methods, among others, but they are primarily suited to low-dimensional path planning problems [11,12]. APF assumes the existence of a virtual force, including the repulsive force of obstacles and the attractive force of the target area, and the system moves according to the direction of this combined force. However, APF is prone to the local minimum problem [13]. Grid-based search methods assume that each state corresponds to a grid point. The A* algorithm is a well-known example of this approach. However, the computation time and memory requirements grow exponentially with increasing dimensionality [14]. In high-dimensional state spaces, sampling-based algorithms offer superior performance and probabilistic completeness. This means that, if a feasible path exists, the probability that the algorithm will fail to find it tends to zero as the number of samples increases [15]. However, this class of algorithms also provides only weak global guarantees. Therefore, in terms of the characteristics of the algorithms themselves, sampling-based algorithms are more suitable for path planning in urban ultra-low altitude airspace.

2. Related Research

A preliminary examination of the existing literature indicates that the path planning problem in urban ultra-low altitude airspace can be effectively addressed through the use of sampling-based algorithms. The most widely used and influential sampling-based path planning algorithms are Probabilistic Roadmap (PRM) and Rapid Exploration Random Tree (RRT). The PRM algorithm is suitable for problems with environmental prior knowledge, which are difficult to deploy in terminals for UAVs flying in the complex environment of the urban ultra-low altitude airspace [16,17,18]. Conversely, RRT algorithms are favored by researchers for higher efficiency in practical applications [19]. Moreover, due to the differing problems to be solved, researchers have sought to enhance the RRT algorithm. The most fundamental improvement is the RRT* algorithm, which is a motion planning algorithm based on incremental sampling and guarantees asymptotic optimality, i.e., it can converge to the optimal solution almost deterministically [20,21]. Subsequently, some scholars enhanced the RRT* algorithm based on the RRT* algorithm and proposed the Potential function-based RRT* (P-RRT*). P-RRT* is distinguished by its integration of the APF into the RRT* and reduction in the number of invocations of the Collision Free procedure through modification of the RRT* [22].
In order to adapt RRT* to dynamic environments, scholars proposed Extended RRT* (ERRT*) and Dynamic RRT* (DRRT*) [23,24]. Based on these proposals, Quick-RRT*(Q-RRT*), PQ-RRT*, EB-RRT algorithms and Neural RRT* algorithms were developed. Q-RRT* expands the possible parent vertex collections by considering the vertex collections in the hyper-sphere as well as their ancestors up to a user-defined parameter Depth. This expansion of the set of possible parent vertices improves the quality of the initial solution and the convergence rate. The number of potential parent vertices is increased, thereby enhancing the quality of the initial solution and the convergence rate [25]. The PQ-RRT* algorithm, based on the P-RRT* and Q-RRT* algorithms, employs the attractiveness of the target region as a sampling strategy, extends the search scope of the Choose Parent process, and improves the reconnection PQ-RRT* process, which further improves the convergence speed [26]. The elastic bands-based Expeditious Exploration Random Tree (EB-RRT) algorithm constructs a hierarchical framework comprising two planners. The global planner generates feasible heuristic trajectories in dynamic environments using time-based RRT algorithms [27]. The dynamic replanner updates the heuristic trajectories in dynamic environments through internal contraction forces and obstacles’ repulsive forces, thereby updating the nodes on the time-based heuristic trajectory. The optimal path planning algorithm based on convolutional neural network Neural RRT* generates the training dataset, which includes map information and optimal paths, using the A* algorithm. The convolutional neural network is then trained to predict the probability distribution of the optimal paths on the map. This process guides the sampling process [28,29]. The NRRT* achieves a better performance in comparison with existing optimal path planning algorithms.

3. Research and Analysis

In order to ascertain the applicability of previous viewpoints on path planning algorithms to the path planning of UAVs in urban ultra-low altitude airspace, we designed experiments to that end. In the experiment, the complete building information of selected areas in Chengdu City, China was extracted from the OpenStreetMap website to serve as the obstacle environment for UAV path planning. Takeoff and landing points were established at locations with varying building densities, and distances between takeoff and landing points were adjusted to encompass short, medium, and long distances. Subsequent experiments were conducted using four algorithms: A*, RRT, RRT*, and the artificial potential field method. These experiments were performed for the same takeoff and landing points at each distance in order to assess the performance of each algorithm.

3.1. Research and Analysis of Builidings in ULAA

As previously stated, the urban ultra-low altitude airspace is characterized by a high density of buildings, which presents a significant challenge for the planning of UAV flight paths. In the environment model presented in this paper, we have intercepted the building planar model at different altitude layers, and the results indicate that the density of buildings decreases with the increase in altitude, from 0 meters to 120 meters, within each altitude layer. However, despite this decrease, the buildings remain densely populated. Please see Table 1 and Figure 1 for detailed statistics.

3.2. Research and Analysis on the Use of Classical Path Planning Algorithms in ULAA

In the experiment, take-off and landing points were established in areas with varying degrees of building density, with distances between them adjusted to simulate a range of scenarios. The experimental results demonstrated that the classical path planning algorithms cannot be directly adapted to the model of urban ULAA. Furthermore, the results of the experiment corroborated the conclusions previously drawn in the literature and provided more detailed insights.
As illustrated in Figure 2a, take-off and landing points were established in areas of greater urban density, with the distance between them being of medium length. The results of the path planning demonstrate that the artificial potential field method is unable to reach the target due to the "local minima" problem. As illustrated in the figure, the algorithm is unable to identify a viable path when the repulsive field around the obstacle traps the path. Although the RRT* algorithm generates a relatively smooth path that avoids the majority of major obstacles, the path exhibits some detours in proximity to the target point. This may be attributed to the additional distance traveled to circumvent the obstacles. This may indicate that the RRT* algorithm requires more iterations to identify a superior path in regions with a high density of obstacles. In comparison to the RRT* algorithm, the RRT algorithm generates more direct paths. However, these paths also exhibit some meandering, particularly in the middle portion, which is more tortuous. This may be attributed to the randomness of the algorithm in finding feasible paths. Furthermore, the paths are situated in closer proximity to obstacles, which may increase the risk of collisions. The paths generated by the A* algorithm are the most direct, demonstrating the algorithm’s capacity to identify the shortest paths within the mesh. However, the proximity to obstacles is particularly pronounced in certain areas, which may not be optimal in practical applications, particularly in instances where the boundaries of obstacles are uncertain or in a dynamic environment.
In Figure 2b, the building density around the takeoff and landing points is sparse, yet the distances are consistent with those depicted in Fig. a, which is also a medium distance. It is evident from this figure that all four algorithms are capable of accurately generating the paths between the take-off and landing points. Notably, the RRT and RRT* algorithms do not include the additional walking distance introduced in Fig. a to circumvent obstacles. The paths generated by the artificial potential field algorithm are consistently successful in reaching the landing point, whereas the paths generated by the A* algorithm are locally optimal in this instance, resulting in excessively lengthy generated paths. The length of the generated path is excessive.
As illustrated in Figure 3, the takeoff and landing points were positioned in regions with higher and lower densities of buildings, respectively, in a manner analogous to the experiment depicted in Figure 2. However, the distance between these points differed from that observed in the aforementioned experiment, which exhibited a longer distance. It can be observed that as the distance between the takeoff and landing points increases, the RRT, RRT*, and A* algorithms are still capable of generating a path between the takeoff and landing points. However, the artificial potential field method, which was previously planned to the region with dense buildings, is consistent with the experimental results in Figure 2 and falls into a local minimum.
Subsequently, the data from all experiments were tabulated and evaluated according to several metrics presented in Table 2, which assess the suitability of the four algorithms for operation in urban ULAA. The A* algorithm is presumed to exhibit the optimal performance based on the statistical results. However, as illustrated in the preceding plotting of Figure 2 and Figure 3, the A* algorithm tends to select routes that are excessively proximate to buildings in densely developed areas with the objective of generating paths of minimal length. This approach may potentially This approach may prove dangerous, as it is susceptible to falling into a local optimum when the distances between certain take-off and landing points are too great. This ultimately results in suboptimal overall paths. While the RRT and RRT* algorithms are similar, RRT* exhibits slight superiority over R. RT, both of which traverse considerable distances to circumvent potential collisions with buildings. APF, on the other hand, can only generate a complete path between the takeoff and landing points in the absence of excessive density of obstacles. However, this process is considerably more time-consuming than that of the other algorithms. Indicators specific to each type of example are shown in Figure 4.

4. Improvement of Classical Path Planning Algorithms in ULAA

In response to the issues identified in the preceding simulation experiments, this paper proposes targeted enhancements to the four algorithms. In order to address the issue of paths planned by the A* algorithm being situated in close proximity to buildings, this paper employs the standard A* search framework and modifies the heuristic function h to take into account the basic Euclidean distance from the node to the target and the environmental density. This approach can enhance the practical viability of path planning by circumventing complex or hazardous regions while maintaining the efficacy of the algorithm. The pseudo-code is illustrated in Table 3.
To address the APF algorithm’s susceptibility to local minima, a random perturbation (noise) is introduced into the calculation of the total force. This enables the path planning algorithm to "jump out" and continue searching for the globally optimal path in the vicinity of the potential local minima. This approach increases the randomness and exploratory nature of the algorithm, which helps to find better paths in complex environments and improve obstacle avoidance. The pseudo-code is shown in Table 4.
In order to address the issues of slow convergence of the RRT* algorithm and the tendency to take longer detours in order to avoid buildings, this paper proposes a hybrid optimization strategy comprising dynamic search radius, path smoothing, reconnection, and goal bias. Dynamic search radius: As the number of nodes in the tree increases, the search radius is decreased in a manner that is proportional to the number of nodes. This enables the algorithm to explore the space in greater depth during the initial stages, while directing its attention to local optimization in subsequent stages. Path smoothing entails the optimization of the initial path by eliminating superfluous nodes and creating shortcuts. This can result in a notable reduction in the length and complexity of the paths. Reconnection: Following the addition of new nodes to the tree, efforts are made to reconnect nearby nodes with the objective of reducing their path cost. This facilitates the identification of superior paths. A goal bias is introduced when randomly sampling nodes, whereby a probability is added to bias the search towards the goal node, thus accelerating the exploration of the target region. The probability of biasing towards the goal node is defined by a goal bias parameter, which determines whether a return to the goal node is made or not, based on this parameter when generating random nodes. The incorporation of a dynamic search radius and goal bias enables the algorithm to approach the target region in a more expeditious manner, thereby reducing the overall number of iterations. The application of path smoothing and reconnection techniques has been demonstrated to markedly enhance the quality of the paths generated, resulting in more streamlined and condensed routes while circumventing superfluous lengthy detours. The aforementioned optimization strategies enable the algorithm to adapt more effectively to scenarios involving increased obstacles or complex distributions, thereby improving the efficiency of pathfinding and enhancing the algorithm’s resilience. The pseudo-code is presented in Table 5.

5. Result

The RRT*, A*, and APF algorithms demonstrated notable improvements across all evaluation metrics. The most significant changes included substantial reductions in computation time, particularly for the APF algorithm, as well as enhancements in path length and safety for the RRT* and A* algorithms. These outcomes illustrate the efficacy of the implemented optimizations in enhancing the efficiency and reliability of these path planning algorithms in real-world applications, as illustrated in Table 6.
As illustrated in Figure 5, the paths generated by the enhanced A* algorithm are no longer situated in close proximity to buildings in regions with high building density. In contrast, the paths generated by the improved APF algorithm can already reach the take-off and landing points. In any case, the points are situated at an acceptable distance from the buildings and along paths of an appropriate length. Furthermore, the improved RRT* algorithm demonstrates a reduction in the number of nodes, a decrease in path length, and the avoidance of lengthy detours to circumvent obstacles when compared to the RRT algorithm.

6. Discussion

The experimental results highlighted several challenges faced by traditional path planning algorithms in ULAA. The A* algorithm, while computationally efficient, often planned paths too close to buildings, posing collision risks. The APF method was particularly ineffective in dense environments due to its propensity to fall into local minima. The RRT and RRT* algorithms, though more adaptable, required extensive computational resources and produced less optimal paths.
The proposed enhancements addressed these issues effectively. The density-aware heuristic for the A* algorithm resulted in safer paths by avoiding areas with high building density. Introducing random perturbation in the APF method helped it escape local minima, improving its performance in dense obstacle environments. The hybrid optimization strategy for RRT*, which included dynamic search radius adjustment, path smoothing, reconnection, and goal bias, significantly reduced computation time and path length while enhancing obstacle avoidance.
These improvements are consistent with findings from previous studies, such as the work on enhanced RRT* algorithms which emphasized the need for adaptive strategies in complex environments. The proposed enhancements align with modern approaches in robotics and AI, focusing on increasing adaptability and efficiency.
Future research should explore the application of these enhanced algorithms in dynamic environments, where obstacles can move or change. Integrating machine learning techniques to predict and adapt to environmental changes in real-time could further enhance UAV path planning in ULAA. Collaboration with urban planners and regulatory bodies is essential to ensure these advancements meet safety and privacy regulations.

Author Contributions

Conceptualization, methodology, Weijun Pan.; software, Jianwei Gao.; validation, Weijun Pan and Jianwei Gao.; formal analysis, Weijun Pan.; investigation, Jianwei Gao.; resources, Weijun Pan.; data curation, Jianwei Gao.; writing—original draft preparation, Jianwei Gao.; writing—review and editing, Weijun Pan and Jianwei Gao.; visualization, Jianwei Gao.; supervision, Weijun Pan.; project administration, Weijun Pan.; funding acquisition, Weijun Pan. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Research and Validation of Safety Risk Monitoring and Aided Decision Making Technology for Complex Operation Systems in Civil Aviation, grant number U2333207” and “The APC was funded by Research and Validation of Safety Risk Monitoring and Aided Decision Making Technology for Complex Operation Systems in Civil Aviation, grant number U2333207”.

Data Availability Statement

Information on building data used in the research for this paper was taken from the open street map website, URL: https://www.openstreetmap.org/.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Aggarwal S, Kumar N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges[J]. Computer communications, 2020, 149: 270-299. [CrossRef]
  2. Shakhatreh H, Sawalmeh A H, Al-Fuqaha A, et al. Unmanned aerial vehicles (UAVs): A survey on civil applications and key research challenges[J]. Ieee Access, 2019, 7: 48572-48634. [CrossRef]
  3. Park S, Kim H T, Lee S, et al. Survey on anti-drone systems: Components, designs, and challenges[J]. IEEE access, 2021, 9: 42635-42659. [CrossRef]
  4. Khan M A, Menouar H, Eldeeb A, et al. On the detection of unauthorized drones—Techniques and future perspectives: A review[J]. IEEE Sensors Journal, 2022, 22(12): 11439-11455. [CrossRef]
  5. Interim Regulations on the Administration of Unmanned Aircraft Flights. Available online: https://www.gov.cn/zhengce/content/202306/content_6888799.htm.
  6. Xu C, Liao X, Tan J, et al. Recent research progress of unmanned aerial vehicle regulation policies and technologies in urban low altitude[J]. Ieee Access, 2020, 8: 74175-74194. [CrossRef]
  7. Weibel R E, Hansman R J. Safety considerations for operation of unmanned aerial vehicles in the national airspace system[R]. 2006.
  8. Coppola M, McGuire K N, De Wagter C, et al. A survey on swarming with micro air vehicles: Fundamental challenges and constraints[J]. Frontiers in Robotics and AI, 2020, 7: 18. [CrossRef]
  9. Mohsan S A H, Othman N Q H, Li Y, et al. Unmanned aerial vehicles (UAVs): Practical aspects, applications, open challenges, security issues, and future trends[J]. Intelligent Service Robotics, 2023, 16(1): 109-137. [CrossRef]
  10. Liu L, Wang X, Yang X, et al. Path planning techniques for mobile robots: Review and prospect[J]. Expert Systems with Applications, 2023, 227: 120254. [CrossRef]
  11. Bhattacharya, S. Topological and geometric techniques in graph search-based robot planning[M]. University of Pennsylvania, 2012.
  12. Kallmann M, Kapadia M. Geometric and discrete path planning for interactive virtual worlds[M]//ACM SIGGRAPH 2016 Courses. 2016: 1-29. [CrossRef]
  13. Montiel O, Sepúlveda R, Orozco-Rosas U. Optimal path planning generation for mobile robots using parallel evolutionary artificial potential field[J]. Journal of Intelligent & Robotic Systems, 2015, 79: 237-257. [CrossRef]
  14. Persson S M, Sharf I. Sampling-based A* algorithm for robot path-planning[J]. The International Journal of Robotics Research, 2014, 33(13): 1683-1708. [CrossRef]
  15. Jaillet L, Cortés J, Siméon T. Sampling-based path planning on configuration-space costmaps[J]. IEEE Transactions on Robotics, 2010, 26(4): 635-646. [CrossRef]
  16. Bohlin R, Kavraki L E. Path planning using lazy PRM[C]//Proceedings 2000 ICRA. Millennium conference. IEEE international conference on robotics and automation. Symposia proceedings (Cat. No. 00CH37065). IEEE, 2000, 1: 521-528. [CrossRef]
  17. Jaillet L, Siméon T. A PRM-based motion planner for dynamically changing environments[C]//2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No. 04CH37566). IEEE, 2004, 2: 1606-1611. [CrossRef]
  18. Amato N M, Bayazit O B, Dale L K, et al. OBPRM: An obstacle-based PRM for 3D workspaces[C]//Proc. Int. Workshop on Algorithmic Foundations of Robotics (WAFR). 1998: 155-168.
  19. Kuffner J J, LaValle S M. RRT-connect: An efficient approach to single-query path planning[C]//Proceedings 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No. 00CH37065). IEEE, 2000, 2: 995-1001. [CrossRef]
  20. Karaman S, Walter M R, Perez A, et al. Anytime motion planning using the RRT*[C]//2011 IEEE international conference on robotics and automation. IEEE, 2011: 1478-1483. [CrossRef]
  21. Noreen I, Khan A, Habib Z. Optimal path planning using RRT* based approaches: a survey and future directions[J]. International Journal of Advanced Computer Science and Applications, 2016, 7(11). [CrossRef]
  22. Tahir Z, Qureshi A H, Ayaz Y, et al. Potentially guided bidirectionalized RRT* for fast optimal path planning in cluttered environments[J]. Robotics and Autonomous Systems, 2018, 108: 13-27. [CrossRef]
  23. Ji H, Xie H, Wang C, et al. E-RRT*: Path Planning for Hyper-Redundant Manipulators[J]. IEEE Robotics and Automation Letters, 2023. [CrossRef]
  24. Shome R, Solovey K, Dobson A, et al. drrt*: Scalable and informed asymptotically-optimal multi-robot motion planning[J]. Autonomous Robots, 2020, 44(3): 443-467. [CrossRef]
  25. Jeong I B, Lee S J, Kim J H. Quick-RRT*: Triangular inequality-based implementation of RRT* with improved initial solution and convergence rate[J]. Expert Systems with Applications, 2019, 123: 82-90. [CrossRef]
  26. Li Y, Wei W, Gao Y, et al. PQ-RRT*: An improved path planning algorithm for mobile robots[J]. Expert systems with applications, 2020, 152: 113425. [CrossRef]
  27. Wang J, Meng M Q H, Khatib O. EB-RRT: Optimal motion planning for mobile robots[J]. IEEE Transactions on Automation Science and Engineering, 2020, 17(4): 2063-2073. [CrossRef]
  28. Li Y, Cui R, Li Z, et al. Neural network approximation based near-optimal motion planning with kinodynamic constraints using RRT[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 8718-8729. [CrossRef]
  29. Wang J, Chi W, Li C, et al. Neural RRT*: Learning-based optimal path planning[J]. IEEE Transactions on Automation Science and Engineering, 2020, 17(4): 1748-1758. [CrossRef]
Preprints 112314 g001
Figure 1. Floor plan models of buildings at different height levels.
Figure 1. Floor plan models of buildings at different height levels.
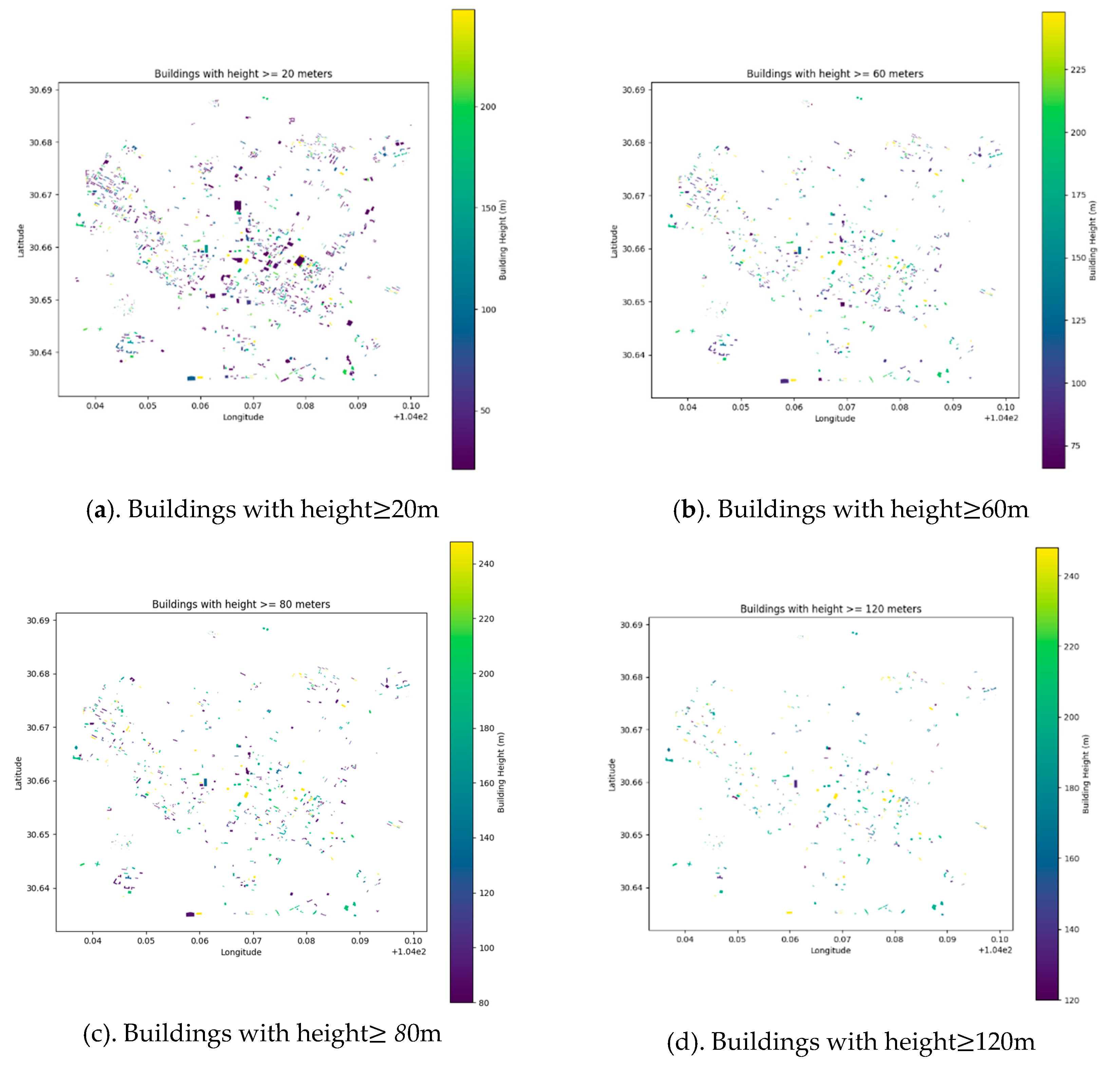
Preprints 112314 g001
Preprints 112314 g002
Figure 2. The effect of different densities of obstacles around the takeoff and landing points on the path planning algorithm for medium path lengths.
Figure 2. The effect of different densities of obstacles around the takeoff and landing points on the path planning algorithm for medium path lengths.
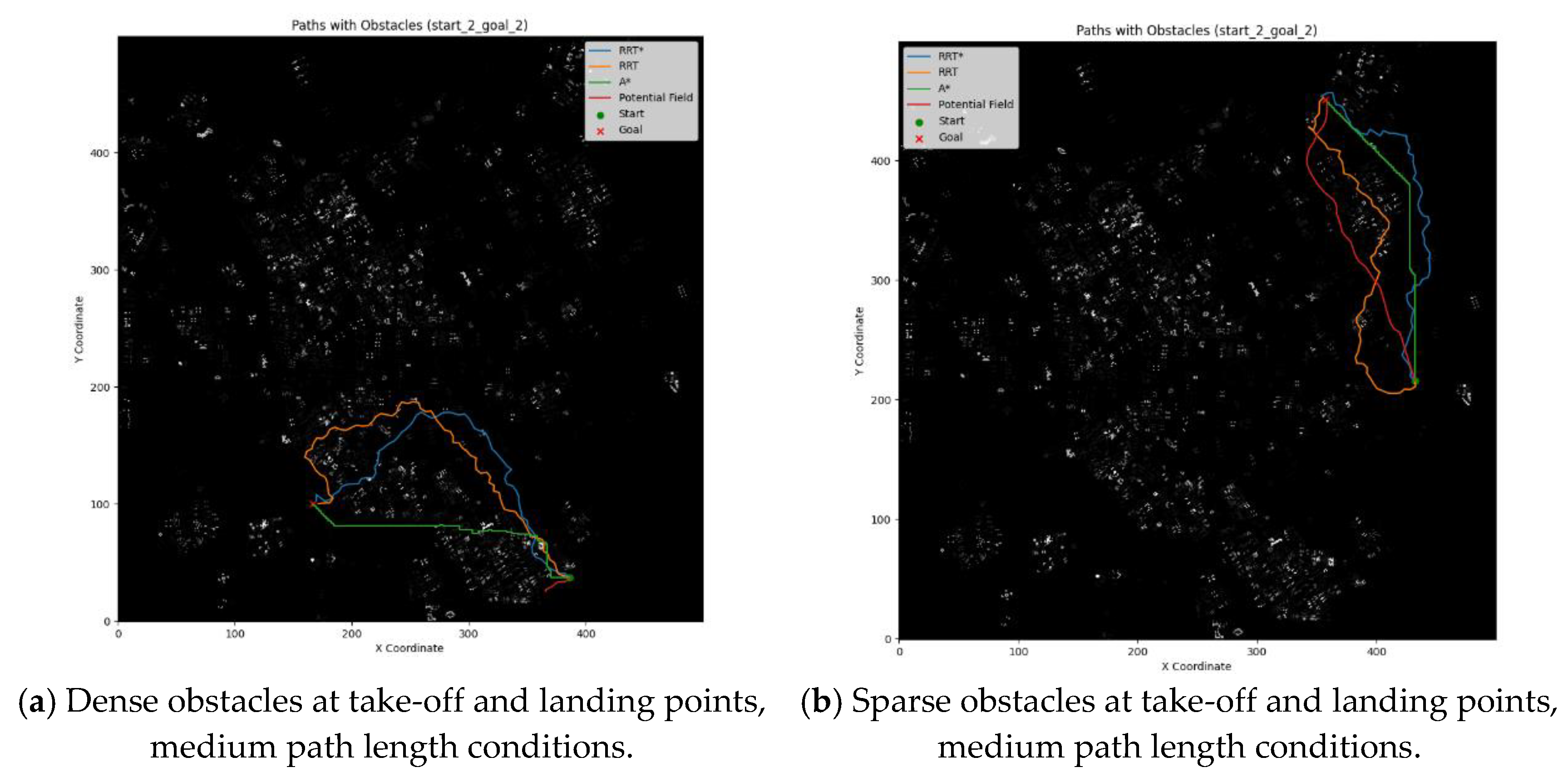
Preprints 112314 g002
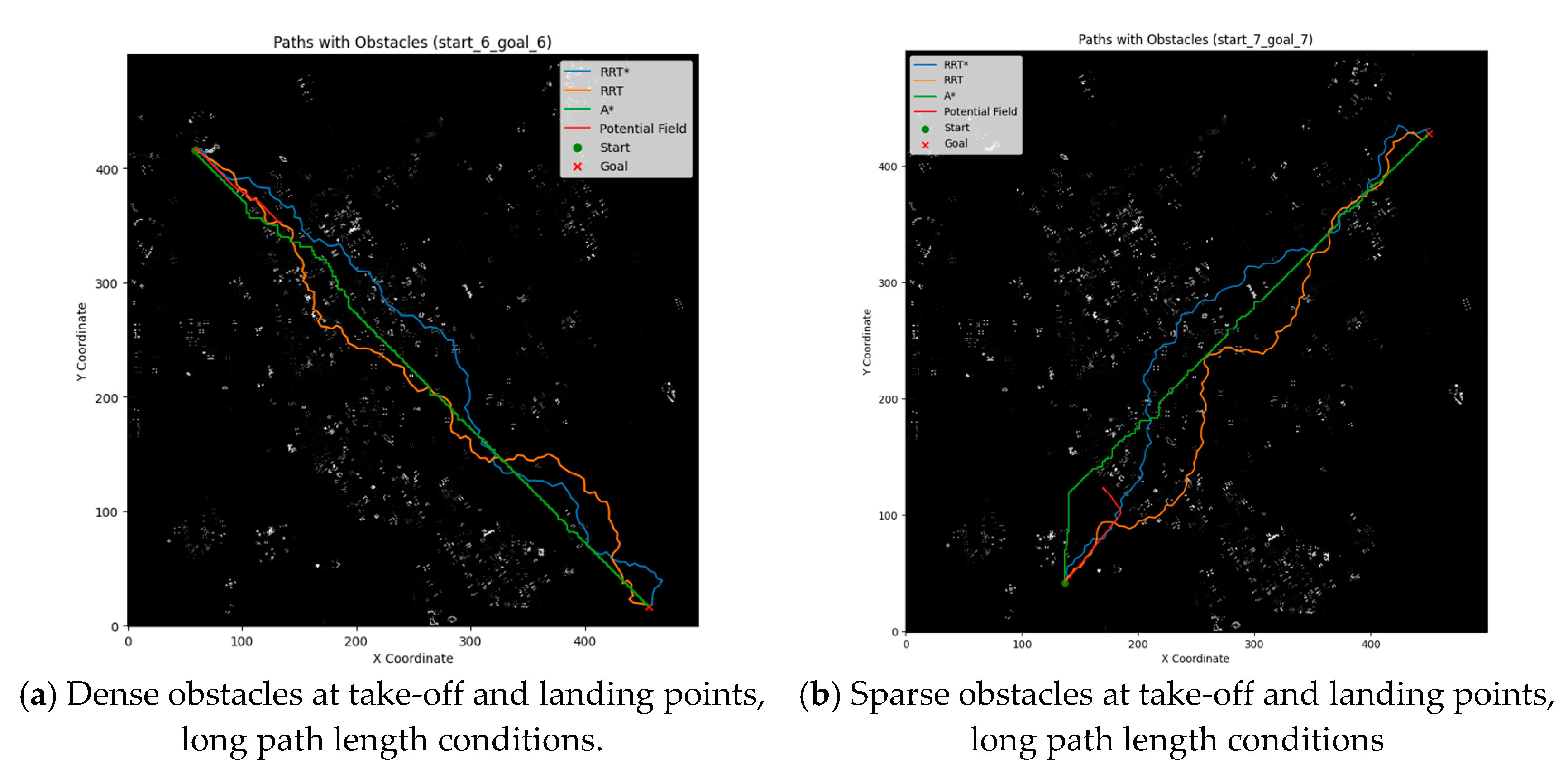
Preprints 112314 g003
Figure 3. The effect of different densities of obstacles around the takeoff and landing points on the path planning algorithm for long path lengths.
Figure 3. The effect of different densities of obstacles around the takeoff and landing points on the path planning algorithm for long path lengths.
Preprints 112314 g003
Preprints 112314 g004
Figure 4. Evaluation metrics for each algorithm in different examples.
Figure 4. Evaluation metrics for each algorithm in different examples.
Preprints 112314 g004
Preprints 112314 g005
Figure 5. Evaluation metrics for each algorithm in different examples.
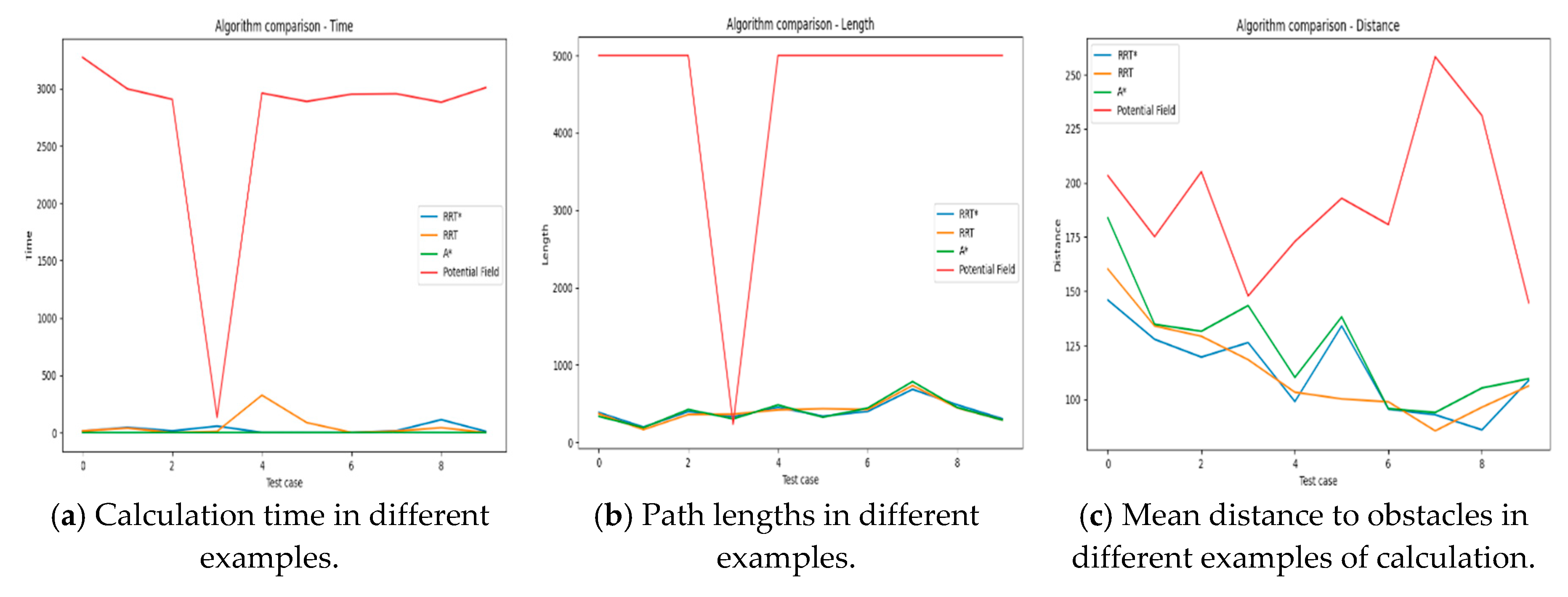
Figure 5. Evaluation metrics for each algorithm in different examples.
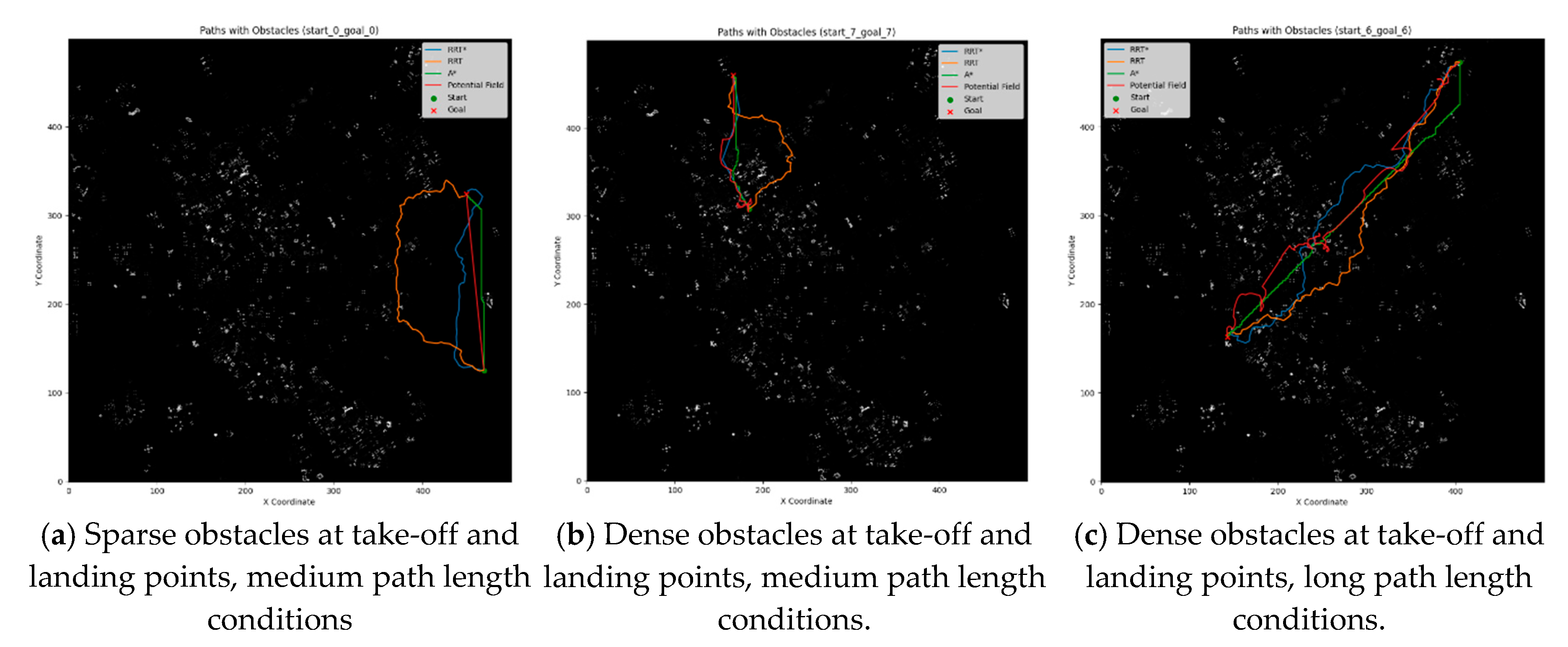
Preprints 112314 g005
Table 1. Information on buildings in ULAA.
Table 1. Information on buildings in ULAA.
Building Height 1 Number of Buildings Building Density 3
>0m 3323 8.86%
≥20m 1323 3.46%
≥40m 696 2 1.68%
≥60m 696 1.68%
≥80m 627 1.52%
≥100m 391 2 0.94%
≥120m 391 0.94%
1 This data is derived from the Open Street Map or calculated based on information on the number of floors in a building, which is assumed in the text to be 3 meters high on a single floor. 2 There are no buildings in the statistics with heights in the middle of 40-60 meters and between 100-120 meters, so there are two rows with the same data. 3 Building Density is calculated as the ratio of the sum of the projected area of the building’s architectural form to the area of the study area.
Table 2. Statistics of performance evaluation metrics for each algorithm.
Table 2. Statistics of performance evaluation metrics for each algorithm.
Algorithm Average Time (s) Average Path Length Average Distance to Obstacles
RRT* 56.78 373.16 142.64
RRT 57.14 393.00 136.67
A* 0.54 347.00 159.33
APF 2933.33 —— 191.79
Table 3. Enhanced A* with Density-Aware Heuristic.
Table 3. Enhanced A* with Density-Aware Heuristic.
Preprints 112314 i001
Table 4. Enhanced Potential Field with Random Perturbation.
Table 4. Enhanced Potential Field with Random Perturbation.
Preprints 112314 i002
Table 5. Improved RRT Star Algorithm with hybrid optimization method.
Table 5. Improved RRT Star Algorithm with hybrid optimization method.
Preprints 112314 i003
Table 6. Enhanced Potential Field with Random Perturbation.
Table 6. Enhanced Potential Field with Random Perturbation.
Algorithm Average Time (s) Average Path Length Average Distance to Obstacles
RRT* 56.78, (9.45) 1⬇83.40% 2 373.16, (252.97) ⬇32.20% 142.64, (164.37) ⬆15.23%
A* 0.54, (0.27) ⬇50.00% 347.00, (259.62) ⬇25.18% 159.33, (167.01) ⬆4.82%
APF 2933.33, (1.06) ⬇99.97% (349.57) —— 191.79, (165.97) ⬇13.46%
1 Data in parentheses are optimized test data, data before commas are from Table 2. 2 Percentages indicate the proportion of the changed data to the original data (Table II).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated