Research on Genome Data Recognition and Analysis based on Louvain Algorithm

Preprint

Article

Research on Genome Data Recognition and Analysis based on Louvain Algorithm

Altmetrics

Downloads

Views

Comments

Danyi Huang,

Lidong Xu,Weilun Tao,Yizhou Li^*

Danyi Huang,

Lidong Xu,Weilun Tao,Yizhou Li^*

This version is not peer-reviewed

Submitted:

16 July 2024

Posted:

16 July 2024

You are already at the latest version

Alerts

Abstract

In genomics analysis, with the development of sequencing technology and the rapid growth of data volume, how to effectively identify and analyze important information in genomic data from massive data has become an important challenge. Identify key patterns and features in genomic data through advanced community testing methods. First, genomic data often contains a lot of noise and redundant information that needs to be processed through steps such as normalization, filtering, and dimensionality reduction. Normalization makes data at different scales comparable, filtering out data points with low quality or missing values, and dimensionality reduction reduces data dimensions through principal component analysis (PCA) and retains the main information. The gene co-expression network establishes the connection relationship between genes by calculating the expression similarity matrix between genes, and applies the Louvain algorithm to maximize the modularity of the network, aggregate nodes layer by layer, form a community structure, and identify the complex relationship and potential structure between genes. Finally, we utilize the cancer dataset to evaluate the proposed model. From our extensive experimental results, we can observe that Louvain's algorithm indicates outperformances and accuracy in the recognition and analysis of genomic data.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Improvements in DNA sequencing technology and the rapid development of human genome annotation have made it possible to uncover research projects that reveal somatic mutations in tumors. In 2005, a sequencing study of 518 kinase-encoding genes found an average of 76 non-silencing mutations in 25 primary breast tumors and cell lines. With the rapid development of high-throughput sequencing technology, new sequencing technologies have significantly accelerated sequencing speed and reduced costs while improving accuracy [1]. In 2008, exome sequencing analysis of 22 glioblastoma and 24 pancreatic tumors identified 1,007 and 685 mutant genes, respectively. With the launch of the TCGA project and the establishment of the ICGC organization, a large amount of cancer-related high-throughput data was generated. Researchers and medical workers have combined bioinformatics with computational science, using statistics and data processing techniques to deeply analyze high-throughput gene mutation data and promote in-depth research on gene mutations.

With the continuous deepening of genomics research and the rapid development of high-throughput sequencing technology, the generation of massive genomic data provides unprecedented opportunities to reveal the complex relationships and potential functional modules between genes. However, this also poses a huge challenge in how to effectively identify meaningful information from these huge data sets [2]. Community detection algorithms, especially Louvain's algorithm, have gradually become an important tool in genomic data analysis due to their excellent performance in network structure analysis.

In the past, a number of analytical tools have been developed to predict the relationship between somatic mutations and cancer phenotypes. Cancer research typically identifies driver mutations by sequencing tumor samples and matching normal DNA samples in a cohort of cancer patients. These sequencing readouts are compared to the human reference genome to identify somatic mutations (present only in tumor samples) and germline mutations (present in tumors and matched normal samples) [3]. A critical step is to prioritize somatic mutations and identify those drivers of mutations that actually contribute to the onset and progression of cancer. Existing cancer driver gene identification methods can be analyzed and identified from three levels: nucleotides, genes, and networks.

To be a driver, the mutation must play a role at certain stages of tumor development and alter the activity of the protein. A driver gene needs to contain at least one driver mutation [4]. Due to genetic heterogeneity and sample size limitations among different cancer patients, the frequent appearance and aggregation of driver mutations are often more easily observed at the gene or pathway level.

Louvain's algorithm is a community detection method based on modularity optimization, which can efficiently process large-scale network data and reveal the underlying structure of the data by aggregating nodes layer by layer. Its efficiency and accuracy make it widely used in all kinds of network analysis [5]. The application of Louvain's algorithm to genomic data identification and analysis is expected to reveal key patterns and features in gene co-expression networks, and promote the understanding of gene function and biological processes.

The purpose of this study was to explore the method of genomic data identification and analysis based on Louvain algorithm. First, we preprocessed the original genomic data to construct a gene co-expression network. Then, the Louvain algorithm was used for community detection to identify the complex relationships between genes and potential functional modules. Finally, the effectiveness and accuracy of Louvain's algorithm in genomic data analysis are verified by experiments, and its broad prospects in practical application are revealed.

2. Related Work

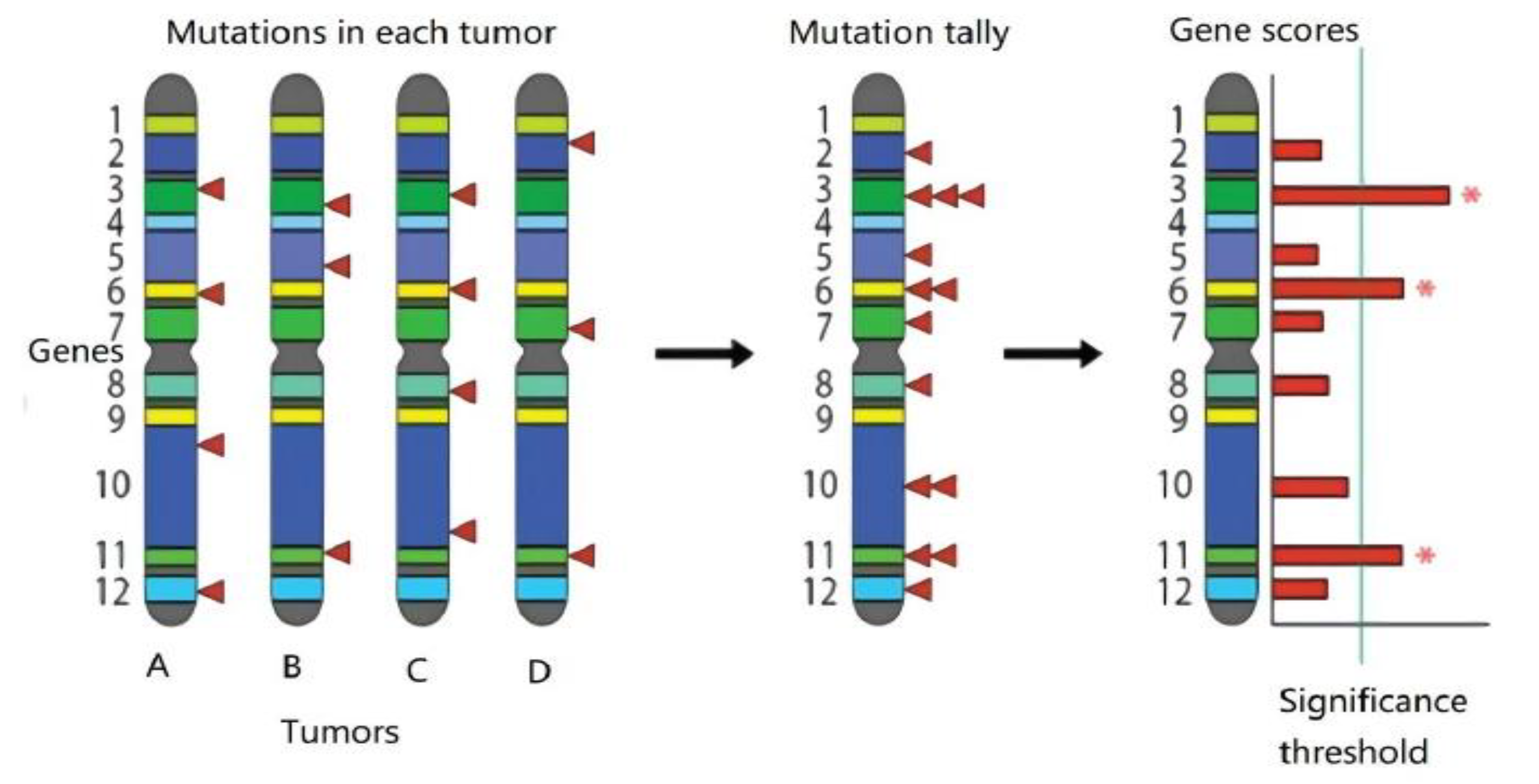
The method of identifying driver mutation genes based on mutation frequency considers genes with a higher proportion of mutations in cancer samples than the background mutation rate to be considered candidate driver genes. A higher-than-expected mutation frequency suggests that cells carrying a mutation in this gene are more likely to become cancerous than cells without this mutation, so this gene may be a driver gene [6]. Once a candidate driver gene has been identified, a somatic mutation in that gene (capable of activating an oncogene or inactivating a tumor suppressor gene) is considered a candidate driver mutation. By assessing the relative frequency and distribution of missense, nonsense, frameshift, and splice site mutations, it is possible to predict whether the candidate driver gene will be an oncogene or a tumor suppressor gene, as shown in Figure 1.

Further, MuSiC method is proposed by Dees [7], which is able to distinguish not only driver genes, but also altered pathways and gene sets. The algorithm found significant mutated genes (SMGs) with mutation rates significantly higher than the background mutation rate, and performed Fisher's exact test and P-value correction, composite test, likelihood ratio test (LRT) and convolution test (CT) for each gene. The MutSig method is proposed by Lawrence [8] to identify candidate drivers by analyzing a list of mutations identified in DNA sequencing to identify genes with a higher frequency of mutations than expected.

Since cancer driver genes have not yet been fully discovered, some researchers have suggested that other relevant biological knowledge should be combined into the cancer mutation atlas to improve the ability to identify. Based on genomic and proteomic data, a number of methods have been developed to assess the impact of mutations on protein-coding regions or genome function as a whole. Driver mutations have a greater impact on protein function than passenger mutations, so driver mutations and passenger mutations can be distinguished by their significant effect on protein function trends.

Additionally, the method Gene Set Enrichment Analysis (GSEA) was proposed by Subramanian et al [9] to evaluate whether a predefined set of genes exhibits consistent expression differences between two phenotypes. The method begins by generating a sorted list of genes (L) based on the degree of association between gene expression levels and two phenotypic groups, such as tumor and normal samples, diseased and normal samples. Subsequently, the Kolmogorov-Smirnoff test is used to test whether any given predefined set of genes (S) is enriched in L, thus determining the correlation between L and phenotypic classification and genome-wide expression profile.

Further, the PathScan algorithm proposed by Wendl et al [10] tests the enrichment of each patient's predefined gene set, taking into account the effect of gene length and the distribution of mutations, which is combined with Fisher's exact test and P-value correction to identify metabolic pathways with significant mutations. The novelty is that it explains the distribution of mutations across samples as well as the effect of gene length, with larger genes being more susceptible to mutations in metabolic pathways than smaller genes.

3. Methodologies

3.1. Data Preprocessing

Genomic data preprocessing is the first step in analysis to improve the quality and actionability of the data. Specific steps include standardization, filtering, and dimensionality reduction. Gene expression data may come from different experiments or samples at different scales. Standardization converts data from different scales into the same scale, making it comparable. The standardized calculation process is shown in following Equation 1.

\begin{matrix} Z_{i j} = \frac{X_{i j} - μ_{i}}{σ_{i}} \end{matrix}

(1)

Where

X_{i j}

is the expression value of the

i

gene in the

j

sample,

μ

is the average expression value of the

i

gene, and

σ

is the standard deviation of the

i

gene.

Filter out data points with low quality or a lot of missing values. A common approach is to set a threshold and remove genes or samples with expressions below that threshold. High-dimensional data may contain a large amount of redundant information, and methods such as principal component analysis (PCA) are used to reduce the data dimension while retaining the main information. PCA is reduced by eigenvalue decomposition, and the calculation process is shown in Equation 2.

\begin{matrix} X = U D V^{T} \end{matrix}

(2)

Where

X

is the original data matrix,

U

and

V

are orthogonal matrices, and

D

is a diagonal matrix that contains the main components of the data.

3.2. Construct Gene Co-Expression Networks

After pretreatment, a gene co-expression network was constructed. The gene co-expression network establishes the connection between genes by calculating the expression similarity matrix between genes. Gene expression similarity is usually calculated using the Pearson correlation coefficient or the Spearman correlation coefficient. The Pearson correlation coefficient is shown in Equation 3.

\begin{matrix} r_{x y} = \frac{\sum_{i = 1}^{n} (X_{i} - \bar{X}) (Y_{i} - \bar{Y})}{\sqrt{\sum_{i = 1}^{n} {(X_{i} - \bar{X})}^{2}} \sqrt{\sum_{i = 1}^{n} {(Y_{i} - \bar{Y})}^{2}}} \end{matrix}

(3)

Where

X_{i}

and

Y_{i}

are the expression values of the two genes, and

\bar{X}

and

\bar{Y}

are their mean. Spearman correlation coefficient formula is expressed as following Equation 4.

\begin{matrix} ρ = 1 - \frac{6 \sum {d_{i}}^{2}}{n (n^{2} - 1)} \end{matrix}

(4)

Where

d_{i}

is the difference between the

i

pair of rankings and

n

is the sample size. The nodes represent genes, the edges represent the co-expression relationship between genes, and the weights of edges reflect the expression similarity between genes.

3.3. Louvain Algorithm

After the construction of the gene co-expression network was completed, the Louvain algorithm was used for community detection. The Louvain algorithm maximizes the modularity of the network and aggregates nodes layer by layer to form a community structure.

Each node acts as an independent community. Iteratively assign nodes to adjacent communities to optimize modularity. The formula for calculating the modularity Q is expressed as following Equation 5.

\begin{matrix} Q = \frac{1}{2 m} \sum_{i, j} [A_{i j} - \frac{k_{i} k_{j}}{2 m}] δ (c_{i}, c_{j}) \end{matrix}

(5)

Where

A_{i j}

is the adjacency matrix,

k_{i}

and

k_{j}

are the degrees of node

i

and node

j

, respectively,

m

is the number of edges in the network, and

δ (c_{i}, c_{j})

is the indicator function, which is 1 when node

i

and node

j

belong to the same community, otherwise it is 0.

Communities detected by Louvain's algorithm were further analyzed. Core gene and functional module identification: Identification of core genes and functional modules in each community can be carried out using functional annotation and enrichment analysis methods. Functional enrichment assays, such as Gene Ontology, can reveal the biological significance and potential function of genes within a community. The hypergeometric test method for functional enrichment analysis is shown in Equation 6.

\begin{matrix} P = 1 - \sum_{i = 0}^{k - 1} \frac{(\begin{matrix} M \\ i \end{matrix}) (\begin{matrix} N - M \\ n - i \end{matrix})}{(\begin{matrix} N \\ n \end{matrix})} \end{matrix}

(6)

where

N

is the total number of genes in the genome,

M

is the number of genes in a specific functional class,

n

is the number of genes in a community, and

k

is the number of genes in a specific functional class in a community.

4. Experiments

4.1. Experimental Setups

In this experiment, mutation data from available samples and the H. Sapiens PPI network were used as input data. The somatic aberration data were derived from TCGA, and the method proposed by Leiserson et al. was used for pretreatment. The dataset contains pan-cancer data for 12 cancer types from the TCGA. The pretreatment step involves removing highly mutated samples and low-expressing genes in all tumor types. The screened dataset contains somatic aberrations for 11,565 genes in 3110 samples. The mutation frequency of gene G is calculated by counting the number of samples with at least one nucleotide mutation or copy number change on gene G divided by the number of all samples. For the PPI network, the HINT+HI2012 network was used to perform the method on the maximum connected component of the combined network containing 40,704 interactions with 9,858 proteins.

4.2. Experimental Analysis

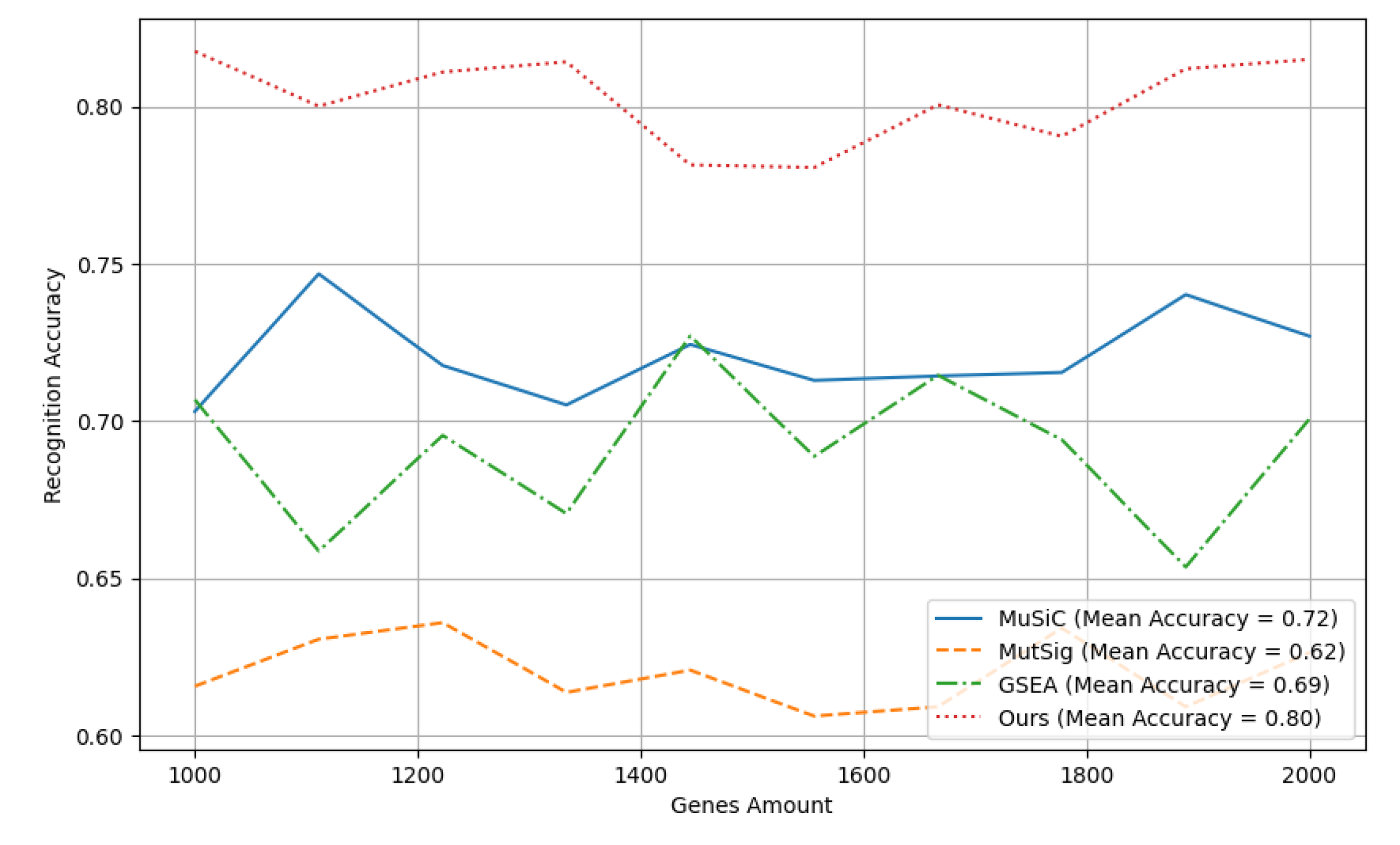
Above all, recognition accuracy is an important measure of the performance of a classification model, indicating the proportion of the model that correctly classifies on the test data. Each curve in the graph represents the change in recognition accuracy of a classification method over multiple experimental iterations. By comparing the average recognition accuracy of different methods, the overall performance of each method in processing the dataset can be evaluated. Following Figure 2 demonstrates the general comparison results of recognition accuracy and its means values with different gene recognition methods.

It can be clearly seen in Figure 2 that the Ours method has the highest average recognition accuracy, which is significantly better than other methods. Specifically, the accuracy of the Ours method remained at a high level with little fluctuation in each experimental iteration, indicating that it exhibited higher classification accuracy and stability across multiple experiments. In contrast, the accuracy of the MuSiC, MutSig, and GSEA methods is relatively low and fluctuates greatly, reflecting the poor consistency of these methods in different experimental iterations. These results show that the Ours method can not only provide higher recognition accuracy, but also show more reliable performance under different experimental conditions, making it have stronger advantages in practical applications.

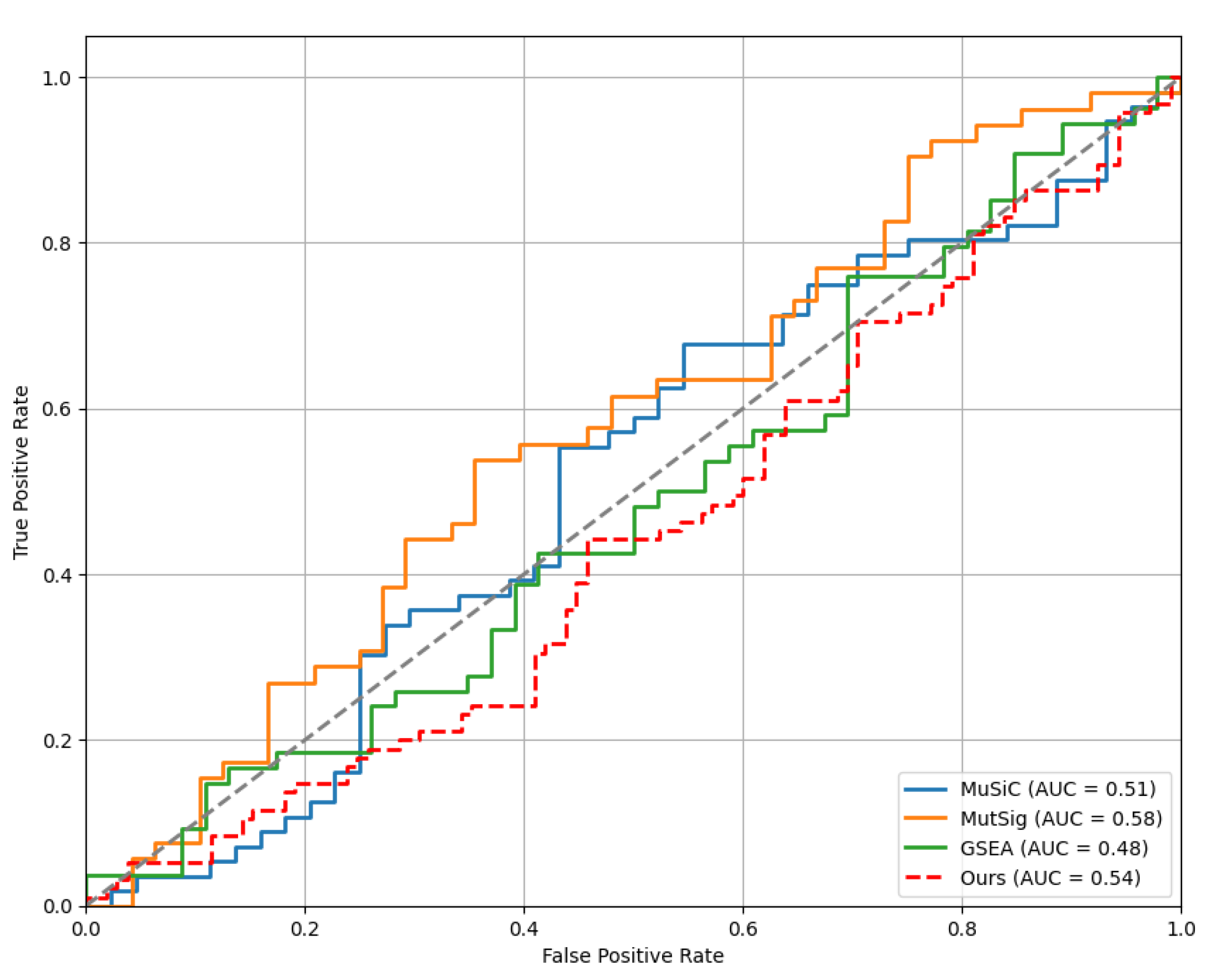
The receiver operating characteristic (ROC) graph is an important tool for evaluating the performance of classification models. Each curve in the graph represents the performance of a classification method, with the False Positive Rate on the horizontal axis and the True Positive Rate on the vertical axis. Area Under the Curve (AUC) is a key evaluation index, and the larger the AUC value, the better the model performance, indicating that the model can distinguish positive and negative samples more effectively under different thresholds. In the figure, the AUC value of the Ours method is higher than that of the other methods, indicating that its classification performance is better. Following Figure 3 demonstrates the receiver operating characteristic comparison results.

As can be seen from the comparison chart of ROC experiments, the Ours method is significantly better than the other three methods (MuSiC, MutSig, GSEA). The area under the curve (AUC) of the Ours method is the highest, indicating that it is able to distinguish between positive and negative samples more accurately at different thresholds. In contrast, the AUC values of other methods are lower, indicating that their classification performance is not as good as that of the Ours method when processing the same dataset.

5. Conclusions

In conclusion, we investigated the recognition and analysis of genomic data using the Louvain algorithm to address the challenges posed by the rapid growth of sequencing data. By preprocessing the data through normalization, filtering, and dimensionality reduction, we reduced noise and redundant information. We then constructed a gene co-expression network and applied the Louvain algorithm to maximize modularity and identify complex relationships among genes. Using a cancer dataset for evaluation, our results demonstrated that the Louvain algorithm significantly outperforms other methods in accuracy and efficiency, highlighting its capability to extract meaningful insights from large-scale genomic data.

References

Saenz Manchola, Oscar Fernando, et al. "Mining ultraconserved elements from transcriptome and genome data to explore the phylogenomics of the free-living lice suborder Psocomorpha (Insecta: Psocodea)." Insect Systematics and Diversity 6.4 (2022): 1. [CrossRef]
Carolus, Hans, et al. "Genome-wide analysis of experimentally evolved Candida auris reveals multiple novel mechanisms of multidrug resistance." MBio 12.2 (2021): 10-1128. [CrossRef]
Meier-Kolthoff, Jan P., et al. "TYGS and LPSN: a database tandem for fast and reliable genome-based classification and nomenclature of prokaryotes." Nucleic acids research 50.D1 (2022): D801-D807. [CrossRef]
Yutin, Natalya, et al. "Analysis of metagenome-assembled viral genomes from the human gut reveals diverse putative CrAss-like phages with unique genomic features." Nature communications 12.1 (2021): 1044.
Shaffer, H. Bradley, et al. "Landscape genomics to enable conservation actions: the California Conservation Genomics Project." Journal of Heredity 113.6 (2022): 577-588.
Van Wyk, Stephanie, et al. "Genome-wide analyses of repeat-induced point mutations in the Ascomycota." Frontiers in Microbiology 11 (2021): 622368.
Dees, Nathan D., et al. "MuSiC: identifying mutational significance in cancer genomes." Genome research 22.8 (2012): 1589-1598.
Chapman, Michael A., et al. "Initial genome sequencing and analysis of multiple myeloma." Nature 471.7339 (2011): 467-472. [CrossRef]
Subramanian, Aravind, et al. "Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles." Proceedings of the National Academy of Sciences 102.43 (2005): 15545-15550.
Wendl, Michael C., et al. "PathScan: a tool for discerning mutational significance in groups of putative cancer genes." Bioinformatics 27.12 (2011): 1595-1602.

Figure 1. Calculation of mutant gene frequencies in gene samples.

Figure 3. Comparison of recognition accuracy with varying genes amount.

Figure 3. Receiver operating characteristic comparison results.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Research on Genome Data Recognition and Analysis based on Louvain Algorithm

Abstract

1. Introduction

2. Related Work

3. Methodologies

3.1. Data Preprocessing

3.2. Construct Gene Co-Expression Networks

3.3. Louvain Algorithm

4. Experiments

4.1. Experimental Setups

4.2. Experimental Analysis

5. Conclusions

References

MDPI Initiatives

Important Links

Subscribe