Prerpints.org logo
Preprint
Article

Hyperspectral Imaging for Phenotyping Plant Drought Stress Using Univariate and Multivariate Modelling Techniques

Altmetrics

Downloads

145

Views

85

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

16 July 2024

Posted:

17 July 2024

You are already at the latest version

Alerts
Abstract
Due to the adverse effect of prolonged drought stress on plants, accurate detection is essential for water use efficiency and maintaining productivity. Hyperspectral imaging is frequently used for non-invasive plant phenotyping, allowing for the long-term monitoring of crop health due to its sensitivity to subtle changes in leaf constituents. The broad spectrum of hyperspectral data enables the development of multiple vegetation indices (Vis) derived from the different spectral regions to estimate plant biophysical and biochemical traits. However, the known VIs often do not generalize well and perform poorly for multiple plant stresses. This study proposes new VIs combined with machine learning models to identify drought stress in wheat species under different nitrogen (N) levels. A wheat experiment was set up in the glasshouse with four treatments: well-watered high-N (WWHN), well-watered low-N (WWLN), drought-stress high N and drought-stress low-N. In addition to ensuring that plants were watered according to the experiment design, photosynthetic rate (Pn) and stomatal conductance (gs) were taken regularly, serving as the ground truth data for this study. Sensitive spectral features were selected using a custom-designed ensemble modelling technique. New drought VIs are proposed using different combinations of the selected features. Three classification models (support vector machines, random forest and deep neural network) were developed and trained using four sets of data: known VIs, proposed VIs, combined VIs (from the known and proposed VIs) and PCA-transformed features (over the whole spectral data). From the results, the proposed VIs outperformed the known VIs, yielding > 0.94 accuracies for all three models, and the performance improved when they were trained with the combined VIs. The combined VIs were used to train three regression models to predict the stomatal conductances and photosynthetic rates of plants. The random forest regression model performed best, suggesting that it could be used as a stand-alone tool to forecast gs and Pn and track drought stress in wheat.
Keywords: 
Subject: Biology and Life Sciences  -   Agricultural Science and Agronomy

1. Introduction

Despite advancements in agronomic management and breeding procedures, crop productivity remains susceptible to abiotic stresses such as drought. During drought stress, plants close their stomata to conserve water, decreasing the absorption of carbon dioxide required for photosynthesis (Pirasteh-Anosheh et al., 2016). Furthermore, drought stress can affect nutrient absorption and cause nutrient imbalances, impacting plant metabolic processes. Hence, developing tools to detect plant drought stress is essential for prompt intervention and management to minimize crop losses.
Conventionally, agronomists and breeders evaluate drought stress by visual grading, for example of the stay-green morphological features of plants (Duan et al., 2018). However, this method is subjective and prone to errors since stresses like iron and nitrogen deficiency could exhibit similar colour changes. Multiple approaches, including gas exchange measurements- stomatal conductance (gs) and photosynthetic rate (Pn) (Xu and Baldocchi 2003), soil moisture monitoring (Leone, 2022), leaf temperature measurement (Grant et al., 2016) and water potential assessment (Zhang et al., 2022) have been deployed to detect drought stress in plants. While these methods provide detailed and precise information, they are low throughput and may have limited applicability to field conditions. Furthermore, some of these methods are invasive, limited to real-time monitoring, and subject to the spatial variability of field crops.
With advancements in computer vision, remote sensing data derived from different sensors, such as thermal, visible and hyperspectral imaging (HSI), can effectively detect and monitor the temporal and spatial impact of drought conditions (Mertens et al., 2021; Proctor et al., 2021). Recently, there has been a surge of interest in HSI applications for abiotic stress assessment, especially nutrient and drought stress analysis. Drought stress leads to subtle modifications in the chemical, physiological and structural components of plants, which can be detected within the short-wave infrared region (1300-1500 nm) of the spectrum (Peñuelas & Filella, 1998). With prolonged drought stress, there are changes in leaf pigments, which can also be measured through the spectral variations in the visible region (Satterwhite & Henley, 1990). The complex dynamics of drought stress initiation and progression suggest that a single spectral band or VIs is unlikely to be sufficient to detect and monitor drought stress over time.
One standard method for analyzing HSI data in plant phenotyping is to extract vegetation indices (VIs), which are mathematical combinations of spectral reflectance characteristics of vegetation at different wavelengths (Asaari et al., 2019). VIs have the benefit of reducing the effect of scale factors, including lighting conditions and slope effects (Jay et al., 2017). VIs such as the Renormalized Difference Vegetation Index (RDVI), normalized Photochemical Reflectance Index (PRInorm), Photochemical Reflectance Index (PRI570), Normalized Difference Vegetation Index (NDVI), Water Index (WI) and Normalized Water Index (NWI) have been used to detect drought stress and monitor its progression. Ihuoma and Madramootoo (2017) presented a review of different VIs for monitoring plant drought stress for irrigation management.
To develop VIs for stress monitoring, spectral averaging, which calculates the average spectrum over the pixel domain, is performed after pre-processing. After spectral averaging, the resulting data is still huge and multicollinear. These high dimensional features can cause algorithmic instability, which can affect the accuracy of data analysis (Sun et al., 2010). Moreover, from the hundreds of wavelengths scanned, only a small subset may be associated with the desired trait; the remainder is usually redundant or irrelevant, which may increase the computational processing and overfitting. The high-dimensional data may also be susceptible to noise and non-uniformity, which may affect the interpretation and accuracy of the analysis. This may be mitigated by employing dimensionality reduction techniques, either feature extraction or selection. In feature extraction, the data is transformed from a high to a low-dimensional space. In contrast, a subset of relevant features from the original hyperspectral datasets is selected for feature selection, discarding redundant or irrelevant ones. Linear Discriminant Analysis (LDA) and principal component analysis (PCA) are examples of feature extraction methods. Filter ( e.g. ReliefF and correlation-based feature selection (Chutia et al., 2017)), wrapper (Sequential feature selection, recursive feature elimination (Rady et al., 2017; Nagasubramanian et al., 2018)) and embedding techniques (e.g. Random Forest and LASSO (Yang et al., 2013) are examples of feature selection methods. Remeseiro and Bolon-Canedo., (2019) documented detailed operation of different feature selection methods for HSI analysis. Determining a standard method to select spectral features in HSI analysis is challenging despite the availability of several feature selection methods (Damodaran et al., 2017). Each feature selection strategy has its benefits and setbacks. Ensemble learning methods that combine the predictions of multiple selection methods to improve the overall accuracy and robustness are often employed to minimize the effect of using a single feature selection model.
Machine learning (ML) models have been widely used for hyperspectral data analysis because they handle complex data patterns and relationships. ML methods such as support vector machines (SVM) and random forest (RF), among others, have been used to evaluate the predictive power of multiple spectral indices for plant drought (Mertens et al., 2021) and nutrient stress (Pandey et al., 2017) analysis. Pairing whole spectra, extracted or selected features with different ML methods can improve the accuracy of plant drought stress classification. VIs are usually developed for specific stresses and may fail in plants with multiple stresses. Since N is a critical component of proteins, understanding the dynamics of plant spectral characteristics in response to drought stress under different N content is essential. From previous studies, adequate N content promotes growth and yield of plants. However, excess N levels may increase plant water demand, potentially worsening drought stress. Currently, there is little knowledge on the non-invasive assessment of excess in inadequate N levels on plants with variable water content.
This study aims to understand plant canopy spectral interactions under different N and water levels. First, we assessed the effectiveness of using various known VIs to assess plant drought stress under different N regimes. An ensemble machine learning method was developed to select sensitive features from which new VIs corresponding to drought stress under low and high N content were proposed. Finally, a deep neural network was proposed and trained with the known and proposed VIs to predict the stomatal conductance and photosynthetic rate of plants. Since gas exchange measurements are effective in assessing drought stress, the proposed and known Vis were used as input to train conventional ML models to predict Pn and gs in wheat.

2. Materials and Methods

Figure 1 shows a workflow of the methods used in this experiment. The general steps include HSI acquisition, data pre-processing, selection of known VIs, sensitive waveband selection, development of proposed VIs, development of ML models identification of drought stress, and prediction of Pn and gs.

2.1. Experiment Setup

A drought experiment was set up in a glasshouse facility (https://www.cranfield.ac.uk/facilities/plant-growth-facility, accessed on 10 November 2022) at Cranfield University. This facility has a state-of-the-art phenotyping platform (Lemnatec Scanalyzer system) for high throughput data acquisition. In this experiment, a wheat cultivar, Cadenza, was planted in 8 cm by 6 cm pots filled with low-N peat soil (Levington Advance M3, CTS, Garden Supplies, UK). Plants were grown under natural light (with an average light intensity of 450-600 µmol/m2/s PAR) with a 20 ° C to 23 ° C day temperature range while the optimum night temperature was between 18 ° C to 20 ° C. Plants (48) consisting of four treatments and 12 replicates were arranged in a randomized complete block pattern. The treatments comprised plants with two N and water content levels: WWHN, WWLN, DSHN and DSLN (WW= well-watered, DS= Drought stress, HN= high N and LN= low N). The plants were fertilized with two N levels, high N and low N, made of 42.5 mM and 4.25 mM concentrations, respectively, at 30, 37 and 44 DAS (days after sowing). They were prepared from a modified Letcombe nutrient solution (Masters-Clark et al., 2020). For the drought stress treatment, all the plants were first watered with equal amounts of deionized water until the tillering stage (44 DAS), when the drought stress was imposed (0 DADS - day after drought stress). All the well-watered treatments (WWHN and WWLN) were kept at 80% field capacity (FC) (% FC is the proportion of soil moisture content at field capacity), while the watering was stopped for the drought stress treatments (DSHN and DSLN). To ensure the WW plants were at 80% FC or above, a portable soil moisture meter was used to measure the volumetric soil water content daily. In addition, the pots were weighed daily to determine the rate of water decrease in the DS-based treatments. The soil surface was covered with white pebbles to minimize water loss through evaporation.

2.2. Physiological Measurements of Drought Stress

Drought stress can significantly affect the gas exchange rate of plants, reflecting plant physiological responses to low water content. Gas exchange measurements such as stomatal conductance (gs), transpiration rate and photosynthetic rate (Pn) can often be used to track changes in the physiological properties of plants before noticeable symptoms such as yellowing or wilting become apparent (Thameur et al., 2012). This study used the gs (mmol H2O m−2 s−1) and Pn (µmol CO2 m−2 s−1) as ground truth measurements to track changes in plant physiological traits resulting from drought stress and N deficiencies. Stomatal conductance measures the rate at which CO2 or water vapor enters and exits through plant stomata pores. It is a critical physiological indicator for screening drought tolerance genotypes of plants (Keshtiban et al., 2015).Additionally, the photosynthetic rate represents the capacity of plants to convert carbon dioxide into organic compounds (Nguyen et al., 2003).
A LI-6400XT portable photosynthesis system (LI-COR Biosciences Inc., Lincoln, NE, USA) was used to measure the gas exchange measurements of the plants a day before the water stress was induced and continued every three days until the end of the experiment. Stomatal conductance measurements were made between midday and 1700 h on the fully expanded leaf of the main stem that had been marked and tagged. The CO2 concentration in the leaf chamber was fixed at 400 μmol CO2 mol-1. To achieve the maximum photosynthetic capacity, the leaf flow rate, temperature, relative humidity and photosynthetically active radiation were set at 200 µmol s−1, 20 °C, 50–65% and 1800 µmol m-2s-1, respectively. The stomatal conductance values were recorded once the measurement was stabilized. The leaf area was corrected during data processing when the leaf was smaller than the cuvette of the chamber.

2.3. Hyperspectral Data Acquisition

The Lemnatec Scanalyzer housing a hyperspectral camera (hyperspec® inspectorTM Headwall Photonic) in the glasshouse was used to acquire spectral images 3 m above the ground. The camera is a push broom type that covers the visible-and-near-infrared (VNIR) regions with wavelengths between 390 nm and 1015 nm. The sensor uses an FWHM (full width at half maximum) image slit of 2.5 nm to gather data at 0.7 nm (in the VNIR area). As a result, a hypercube with a dynamic range of 16 bits containing 1015 spectral bands was produced. Data were collected between 1000 h and 1200 h on each imaging day. Imaging began on the day the drought was induced and continued every other day until the end of the experiment. This produced a total of 252 sets of hyperspectral imaging data.

2.4. Hyperspectral Image Pre-Processing

Obtaining useful information from hyperspectral images requires pre-processing to normalize spectral data from ambient illumination and reduce noise and other artefacts and to improve the data quality for further processing. The pre-processing steps include radiometric calibration, spectral down-sampling, and noise removal. Radiometric calibration standardizes and adjusts the radiometric data recorded by converting the raw sensor measurements to meaningful physical units such as radiance or reflectance. This is important in reducing the variable illumination and the dark current effect on the spectra. In this study, a white panel (Zenith Lite™ Ultralight Targets 95%R, Sphereoptics®) was imaged as the white reference data ( R e f w h i t e ) while the camera lens was covered with an opaque cap to collect the dark reference data ( R e f d a r k ) (Zhu et al., 2013). The reflectance image was obtained by using Equation 1.
r e f l e c t a n c e i m a g e = Raw image - Ref dark Ref white - Ref dark
Hyperspectral imaging captures high-resolution images across a wide range of narrow and continuous spectral bands. The massive amount of information presents computational challenges that require down-sampling of the data for effective processing. Down-sampling involves reducing the number of spectral bands or channels in the data, subsequently reducing the spectral resolution. According to Sadeghi-Tehran et al. (2021), down-sampling helps reduce the computational complexities and noise generated during hyperspectral data acquisition. This study used a band averaging technique of 2 nm spectral width to down-sample the data. The process involves grouping two adjacent spectral bands and finding the average values to generate a new set of bands. As a result, the down-sampled data had fewer wavebands overall but still had a representative spectral character.
Spectral smoothing and denoising methods were applied to the raw spectra to reduce noise levels and improve signal-to-noise ratio, revealing underlying spectral patterns. Spectral smoothing and denoising include using filters on the spectral bands to remove spikes and smooth spectral curves. This process also isolates sensitive features that could be masked by noise at various wavelengths. Here, a Savitzky-Golay filter (a commonly used low-pass filter) to smooth and denoise the spectral bands was used to fit a polynomial to the data inside a moving window as a form of polynomial smoothing. The filter chooses an odd-sized window of spectral points for each data point in the spectrum and then fits the least square using the high-order polynomial. During this process, the relevant data points are eventually swapped out for the matching values of the fitted polynomial. A window of size 13 and a second-degree polynomial were used as the parameters. It should be noted that a small window size generates significant artefacts, while a large window size can be more effective in reducing large-scale noise, smoothing out noise of variable frequencies. However, large window sizes tend to blur fine spectral details which could distort the originality of the spectral signature (Rinnan et al. 2009).

2.5. Segmenting the Hyperspectral Data

After pre-processing, the HSI data were segmented using a selected spectral ratio and Otsu thresholding. A method that exploits the difference in the shape of the infrared red regions of the spectrum in the plant and background was developed for the spectral ratio. In this case, a normalized difference ratio between 910 and 950 nm wavelengths was extracted to create the spectral ratio. The combination of spectral ratio and the Otsu thresholding resulted in a binary image where the vegetation pixels were labelled as one and the non-vegetation pixels as zeros.

2.6. Extracting Known Vegetation Indices

Vegetation indices (VIs) of plants derived from reflectance values in specific bands are indicative of responses to different stresses. Combining VIs or customizing them based on unique vegetation characteristics and environmental conditions is a common practice to monitor plant stress (Koh et al., 2022). This study extracted twenty-five known VIs sensitive to nitrogen variations and drought stress (Table 1). The top ten VIs that correlated well with the gas exchange measurements were evaluated to understand their sensitivities to subtle changes in the nitrogen and water content of plants. The selected VIs were used subsequently to identify drought stress.

2.7. Wavelength Selection and New Drought Stress Indices

2.7.1. Wavelength Selection Using Ensemble Learning

Hyperspectral images have a high spectral resolution comprising hundreds of narrow bands. However, a significant portion of the spectral bands may be strongly correlated (multicollinear). To reduce this multicollinearity, sensitive features related to the phenotypic traits of interest are extracted using machine learning and statistical methods. This study implemented an ensemble learning method to select the most sensitive features (Figure 2). Three feature selection models, correlation feature selection (CFS), ReliefF (RFF) and chi-square (CS), were developed on 70% of training datasets and tested on 30% of test datasets. Each model was trained using a k-fold cross-validation technique where the training dataset was divided into K (5) subsets to train and validate the model multiple times. After training, the model was tested on the 30% test dataset. The features selected were ranked in order of importance, and the top ten features from each model were selected. Because each model had its drawbacks, the feature subset that was ultimately selected might not be the best in the feature space. The features selected were combined to obtain 30 features. A further selection was made on the combined feature subset from all the models using a Boruta SHAP algorithm, which was ranked using a recursive feature selection method.
The selected wavelengths were used to develop new indices: drought-N ratio index (RDI), normalized difference drought-N index (NDDI) and drought difference index (DDI) using equations 2- 4.
RDI =   RD λ 1 RD λ 2
N D D I = RD λ 1 -   RD λ 2 RD λ 1 +   RD λ 2
D D I = R D λ 1 − R D λ 2
Where R D λ 1 and R D λ 1 are any two selected wavelengths
Using a custom-developed algorithm, the three proposed indices were calculated for every possible pair combination of the selected wavelengths. The relationship between the generated indices and the gas exchange measurements were ascertained using correlation analysis. A matrix plot displaying a distinct pattern with multiple hotspots with somewhat varied R2 values was produced by plotting all the squares of correlation coefficient r values, which reflect the coefficient of determination. The optimal wavelength combinations with the highest R2 values were chosen as the proposed indices.

2.8. Machine Learning Models for Drought Stress Identification

Three machine learning algorithms, support vector machines (SVM), random forest (RF) and deep neural networks (DNN), were trained using the selected known VIs, proposed VIs and combined Vis (combination of known and proposed Vis) to identify drought stress in wheat.
RF is a popular and adaptable machine-learning technique for regression and classification tasks (Rodriguez-Galiano et al., 2012). It is an ensemble supervised learning algorithm that enhances the overall accuracy and robustness by combining the predictions of several decision trees (Belgiu & Drăgu, 2016). The fundamental idea in RF modelling is to use bootstrap aggregation to create homogenous subgroups (about two-thirds of training samples) from training sets and then develop a decision tree in each subset (number of trees: tree). The output of the RF model is achieved by averaging all the decision trees. RF model was chosen for this study because it can effectively reduce overfitting due to repeated sampling. Moreover, it is less sensitive to outliers and noise and has a low bias utilizing the concept of bagging (Breiman, 2020).
SVM is a supervised learning for classification or regression tasks. They effectively work well for linear and non-linear data separation and perform well in high-dimensional spaces. The basic principle behind SVM is to find the optimal hyperplane that maximally separates different classes of data points in an n-dimensional feature space. The hyperplane that separates the various classes is set by finding the largest margin between data points of different classes while minimizing the classification errors and is estimated using a loss function. The main hyperparameters of the SVM algorithm that need tuning are the kernel parameter (y), the regularization parameter (c) and the gamma parameter (ϓ). SVM was selected for this work because it is effective for high-dimensional space modelling and is robust to overfitting.
A deep neural network (DNN) is a fully connected feedforward architecture based on a multi-layer artificial neural network. The DNN model is trained on the back-propagation supervision learning technique (Rumelhart et al., 1986). A DNN model typically has an input layer and an output layer interspersed with one or multiple hidden layers (dense layers) with an arbitrary number of hidden neurons. DNN can tackle a variety of complex classification problems due to the existence of various hidden layers. The DNN model was selected for this study because it is simple and regarded as a more potent and effective algorithm in neural networks. It has been used effectively for phenotyping other plant phenotypic traits (Mandal et al., 2023).

2.9. Multivariate Analysis for Stomatal Conductance and Photosynthetic Rate Predictions

Based on prior research, gas exchange measures can evaluate and track the dynamics of drought stress since minute changes in these physiological traits indicate responses of plants to water availability. However, the tools for measuring gas exchange are costly, low throughput and sometimes destructive. Hence, regression models were developed to predict the plant gs and Pn using the plant VIs, which could be used as a proxy tool to monitor drought stress. Four models, a polynomial regression (PR), random forest regression (RFR), support vector regression (SVR) and partial least square regression (PLSR), were trained to evaluate their abilities to predict gs and Pn. The RFR, SVR and PR were each trained with the VIs as the independent factors, while the gs or Pn was the dependent variable. The PLSR model was computed considering the whole spectral reflectance as the independent variable and gs or Pn as the dependent variable. Here, the PLSR model was trained by concurrently finding the principal components that account for the highest variance and low multicollinearity in the dependent and independent variables (Helmholz et al., 2014). This results in fewer uncorrelated components (variables) from the large spectrum with little loss of information.

2.10. Model Training and Testing

All the models were trained with 70% of the dataset and tested on the remaining 30%. In ML training, optimization of parameters by cross-validation (CV) search over various parameter settings is required to improve the accuracy of predictions and classification and minimize errors. Popular optimization techniques include gridsearchCV (Buitinck et al., 2013), randomized search (Bergstra & Bengio, 2012) and Bayesian optimization (Brochu et al., 2010). Since random search is computationally less expensive and consumes less time for processing, the randomsearchCV tool in the scikit learn package (Python 3) was used to fine-tune the parameters of the ML models. Table 2 includes the list of parameters tuned and the range of values considered. Following the model parameter tuning and training, the best-performing set of parameters was used for model fitting and classification or regression.
The root mean square error (RMSE), coefficient of determination (R2), and mean absolute error (MAE), as shown mathematically from equations 5 to 7, were used to evaluate the regression models for predicting the Pn and gs. To objectively assess the performance of the classification models, we used three widely used classification metrics: average accuracy (AA), F-score, and Cohen's kappa score, as shown in equations 5.8 to 5.10.
R 2 = ∑ i = 1 n ( x i - x ̄ ) ( y i - ȳ ) ∑ i = 1 n ( x i - x ̄ ) 2 X ∑ i = 1 n y i - ȳ 2
M A E = 1 n ∑ i = 1 n | x i - y i |
R M S E = ∑ i = 1 n ( x i - y i ) 2 n
Where n is the number of data, xi is the observed values, yi is the predicted values and the bar denotes the mean of the variable. Statistical calculations were performed using the statistical package in RStudio.
A A = T P + T N T P + T N + F P + F N
F − S c o r e = 2 x P   X   R P + R
Where P= T P TP + FP and R = TP T P + F N
K = P o − P c 1 − P c
Where TP: true positive, TN: true negative, FP: false positive, FN: false negative, Po is the probability of observed agreements and Pc is the expected agreement.

3. Results

3.1. Reference Data of Gas Exchange Measurements

Figure 3 is a box and whisker plot of the Pn measurements of the plants from the 0-15 DADS. The WWHN treatment produced the highest Pn throughout the drought stages, while the DS treatments (DSHN, DSLN) steadily declined with time. It was observed that the DS treatments were not significantly different at the beginning of the drought (0 DADS), despite the variations in their N levels. However, the DSHN treatment was statistically different from the WWLN treatment. Plants with varying N levels exhibited statistical differences three days after drought stress initiation. That is, the WWLN and WWHN were statistically different (p < 0.049), while the DSLN plants showed differences with the WWHN (p < 0.045). The WWLN and DSLN, however, showed no differences at this stage. The stress in the DS treatments became more noticeable on the 6 DADS, where the means of both treatments (DSHN and DSLN) were statistically different from the WWHN treatment (p < 0.026 and p < 0.015 for DSHN and DSLN, respectively). In contrast, the WWLN did not differ much from the DSLN (p < 0.97) treatment, however, it was statistically different from the WWHN (0.036). At the end of the experiment, there were clear distinctions between the drought-stressed (DSHN and DSLN) and well-watered (WWHN and WWLN) treatments.
The gs measurement of the plants revealed a pattern comparable to the Pn measurement, as shown in Figure 4. Throughout the drought stages, the WWHN treatment had the highest gs with the maximum at 6 DADS (0.37 mol H2Os-1). Despite having varying N levels, the DS treatments showed no significant differences at 0 DADS. At 0 DADS, the means of the DS treatments (DSHN and DSLN) were statistically different from the WWLN treatment. After three days, the WWHN treatment had the highest gs (0.341 mol H2Os-1), while the DSLN obtained the lowest gs (< 0.252 mol H2Os-1). There were observable differences in the ranges and mean values of the WWHN treatments and the other treatments with p-values = 0.025, 0.011 and 0.012 for the WWLN, DSLN and DSHN treatments, respectively. However, the DS treatments were not significantly different from the WWLN. On the 6 DADS, the WW treatments (WWHN and WWLN) were observed to have higher mean gs than the DS treatments. While the DS treatments were statistically different from the WWHN treatment, the DSLN and WWLN treatments were statistically not different. On the 12 DADS, there were 80.3% and 60.2% decreases in gs for the DSHN and DSLN, respectively (indicating a fast decline of gs for the DS- treatments). On the final day (15 DADS), a significant difference was observed in drought-stressed and well-watered plants, with the WWHN having the highest and the DSHN having the lowest gs measurements.

3.2. Spectral Reflectance Analysis

Mean spectral curves for the different treatments at 0, 6 and 15 DADS are shown in Figure 5. The spectral curves for all the treatments showed peaks at 570 nm and troughs at 680 nm. The spectral reflectance of all the treatments exhibited comparable patterns at 0 DADS, with relatively low reflectance in the visible region. The well-watered plants showed a relatively high reflectance in the visible spectrum, with WWLN having the highest. Although there were differences between the HN and LN treatments in the visible spectrum, they were not significantly different. The treatments were not visibly different along the red-edge region (700-750 nm). There was a characteristic peak in the NIR region with visible differences between the two nitrogen levels where the low N treatment had higher reflectance comparably. Moreover, in the NIR and infrared regions, a physical observation shows a distinction between the treatments. However, these differences were significant for WW and DS treatments. At 6 DADS, a high reflectance was observed for the DSHN, WWHN with DSLN recording the lowest reflectance. The differences between the WW-based treatments and the DS-based treatments were visible in the green region between 500 nm and 600 nm. The shape of the red edge regions changed, attributing to the different N levels and drought stress progression. All the treatments exhibited high reflectance in the NIR region (700-1000 nm), with the DSHN and WWHN having the highest on 6 DADS. On the last day of the experiment (15 DADS), there was an observable difference among the four treatments in the visible spectrum (500-650 nm), red-edge regions (600-700 nm) and infrared regions (700-1000 nm). The treatments with low N and drought stress were highly reflected in these regions.

3.3. Correlation Between the Known VIs And Gas Exchange Measurements (Pn and gs)

Figure 6 displays heat maps of the Pearson correlation coefficient (r) between the known VIs and the two gas exchange variables (Pn and gs). The correlation analysis was performed for each treatment and the combined treatments (ALL). Figure 6a shows good relationships between the VIs and gs in the WWHN treatment. PSSRa had the highest correlation coefficient (0.88), while TCARI obtained the lowest (-0.04). Similarly, most VIs had strong correlations in the WWLN treatment, with DVI, SAVI and MSAVI obtaining the highest correlation coefficient (0.94) and TCARI with the lowest (-0.29). However, a contrasting trend was observed in the DS-based treatment. With the DSHN, while the MTCI with r =0.92 had the best correlation with the gs, a third of the extracted VIs had a poor relationship with the gs (r < 0.4). The DSLN treatment reported the lowest correlation with the gs measurements. SAVI (0.79) and RSVI (-0.79) were observed to have the highest correlation, while NDVI (0.20) had the lowest correlation with the gs. When the treatments were combined, most of the known VIs showed a positive correlation with the gs except NDWII, RVSI, TCARI and RD indices. The RVSI and SAVI had the highest correlation coefficient (-0.79 and 0.79 respectively) and the NDVI800 with the lowest (0.18).
From Figure 6b, a positive correlation was observed between the known VIs and the Pn measurements in the WWHN treatment, except for a few indices (NDWII, RVSI, TCARI and RD) which were negatively correlated. Most indices had a high correlation coefficient, with RENDVI (0.87). The results obtained for the WWLN treatment show that compared to the WWHN, there was a relatively low correlation between the indices and the Pn measurements. MTCI had the best correlation (0.74) while the NDWII (-0.03) had the lowest. In the DSHN treatment, the VSR index obtained the highest correlation coefficient (0.84) and the NDII (0.19) had the lowest. Unlike the gs, the indices in the DSLN treatment had relatively good correlations with the Pn. The highest correlation was observed in the OSAVI index (0.88), while the lowest was recorded in the CI_green index (0.10). With the combined treatments, the MSAVI, SAVI and DVI reported the highest correlation with the Pn (0.78) while the RD had the lowest correlation (-0.07).

3.4. Waveband Selection and Proposed Indices

3.4.1. Spectral Band Pair Correlation

Spectral band pair correlation is the correlation analysis between two specific spectral wavelengths. It aids in understanding the interactions of different spectral bands, providing insights into the characteristics of the observed traits. In HSI data, a significant portion of the spectrum suffers from multicollinearity, which refers to the presence of strong correlations or dependencies between spectral wavelengths in a hyperspectral dataset. Figure 7 is a colour map showing the correlation between all pairs of wavebands of the data in this study. It is observed that the band pair correlation within the NIR region (700– 1015 nm) follows a general pattern: adjacent bands had a strong tendency to correlate with one another. Most of the wavelengths had a correlation coefficient between 0.8 to 1.0. However, among the highly correlated spectral bands in this region, a few bands had low correlations with their adjacent bands. Some of these bands are within 735 nm to 768 nm. Spectral bands within the visible range (394–650 nm) had a low correlation between adjacent wavebands. However, bands between 511 nm and 576 nm were highly correlated to each other and to bands between 702 nm and 746 nm, showing the redundancy of some of these spectral features.

3.4.2. Output of the Ensemble Model Waveband Selection

Feature selection is critical in hyperspectral imaging analysis to enhance model performance by reducing overfitting, interpretability and computational complexity (Koh et al., 2022). The high correlation between the different spectral wavebands shows the significance of feature selection in eliminating redundant information while keeping the relevant data. Each model in this study selected the sensitive spectral features based on the order of importance. Table 3 reports the top ten spectral wavelengths selected by the ensemble model. The Chi-square method selected most of the top features within the green spectrum from 555-570 nm and the rest within the red regions (670-675 nm). The top ten features using the ReliefF method were within the red (674-690 nm), red-edge (722 nm) and infrared (949-957 nm) regions. The CFS selection method identified the top ten features within the green regions (542-547 nm), the red region (669-671 nm) and the infrared regions (939-957 nm). Generally, all three selection methods identified wavelengths 674 nm as one of the most informative features. Also, the ReliefF and CFS identified 669, 949, 940 and 957 nm as the most sensitive features.
The output of the individual models was integrated with the Boruta SHAP model to improve the selection process and reduce the dimensions of the selected features. The output of the Boruta model was ranked in order of importance using the RF-RFE model. The ReliefF model ranked wavelengths in the green region as the top two (553 nm and 557 nm), followed by the red wavelengths (669 nm and 674 nm). Wavelength in the near-infrared region followed as the fifth most important feature. The 542 nm wavelength was selected as the tenth most important feature.

3.4.1. Proposed Drought Stress Indices

The selected wavelengths were combined in different forms using the RDI, NDDI and DDI equations to get the proposed drought stress indices. To analyze the relationship between the drought stress and the proposed indices, the indices with high R2 values were selected. From supplementary information (Table E-1), the NDDI and RDI produced the best indices that correlated highly with the gas exchange measurements (Pn and gs). Figure 8 is a correlation heatmap showing the relationship between the top ten proposed indices and the gas exchange measurements (Pn and gs). Based on the R2 values, the NDDI with wavelengths ( λ 940 and λ 957 ) had the best correlation for Pn (r= 0.78), whereas RDI with wavelengths ( λ 669 and λ 636 ) ,   ( λ 636 and λ 542 )   and NDDI with wavelengths ( λ 940 and λ 557 ) produced the best correlation (r=0.67) with the gs.

3.5. Machine Learning-Based Drought Detection

This section evaluated the performance of the three traditional classification models (RF, SVM and the DNN model in identifying plants with drought stress with different nitrogen levels. Four different training features were used: the known VIs, proposed VIs, combined VIs (proposed and known VIs) and the PCA transformed features. The performances of the models were evaluated based on the type of training features used.

3.5.1. Drought Stress Identification Using Machine Learning Models

Figure 9 presents the confusion matrices of the three models on the test dataset. This depicts the performance of the models in classifying the treatments: WWHN, WWLN, DSHN and DHLN, which corresponds to the different nitrogen and drought stress levels. The confusion matrices are displayed as heatmaps, with the classification accuracy increasing with the depth of colour. The number of predictions made by the model for each class is shown by the cells in the heatmap. The x-axis shows the actual class, while the y-axis displays the predicted class. From Figure 9a, all the models displayed a ceiling effect performance when trained with the known VIs, with the DNN model slightly outperforming the others. The DNN model resulted in an appreciable number of true positives in each class, where the WWHN (0.97) and WWLN (0.94) had the highest number of true positives. All the models had high accuracies in identifying the high N-based treatments (DSHN and WWHN), with the RF model achieving a perfect accuracy score for the DSHN treatment identification. However, the SVM model had a relatively low accuracy (0.83) for WWHN treatment. In contrast, there was an increase in misclassification for low N-based treatments, especially the DSLN treatments. Additionally, it was noted that the models had difficulty differentiating between the DSLN and WWLN, hence the misclassification of some DSLNs as WWLN. From Table 4, the high F1-score of the DNN (0.935) and RF (0.920) models indicate the excellent performance of the models are in precisely identifying the true class (treatment). Moreover, all the models had above 0.80 Cohen Kappa scores, indicating a good agreement between the predicted and actual class labels.
Figure 9b and Table 4 show a performance improvement when the SVM (4.17%) and DNN (1.067%) models were trained with the proposed VIs. The performance of the RF model was slightly reduced (0.765%). The DNN model had the best performance with 0.948, 0.949 and 0.933 for the accuracy, F-score and Kappa score, respectively. It perfectly classified the WWHN treatment while having low misclassification for the other treatments. The highest misclassification was for WWLN, where 7% was misclassified as WWHN and the remaining as DSLN. While the SVM model had good performance with a perfect accuracy score for DSHN treatment, the high misclassification (11%) of the WWLN as DSLN class affected the overall performance of the model. On the other hand, although the RF accurately identified the WWHN treatment (0.941 accuracy score), it mostly identified DSLN as WWHN and WWLN as DSLN. A high F1-score (0.911) and relatively low Kappa score (0.881) for the RF model shows that the model has resulted in false positives in contrast to false negatives for classifying the treatments.
Figure 9c shows the confusion matrices of the three models trained with the combined indices (known and proposed VIs). All the models demonstrated good performance, as shown by the high percentage of correctly predicted (true) instances presented in the diagonal elements of the matrices. The models' high accuracy and F-score demonstrate their ability to precisely identify positive cases in every class. The RF model had the best performance with 0.983, 0.984 and 0.965 accuracy, F1-score and kappa score, respectively, followed by the SVM and DNN models. However, a one-way ANOVA test on the F1-scores scores shows no significant variation in the performance of the models (Supplementary information Table E-2). The WWHN treatment was correctly classified by all the models, with the DNN achieving a minimum accuracy score (0.962). Interestingly, the DNN and SVM models perfectly identified WWLN treatments, while the RF and SVM also had 100% accuracy in classifying the WWHN treatments. It was also observed that all the models showed relatively high misclassification for the drought-based treatments comparatively. Although the DNN model had a < 2% misclassification for the DSHN plants, it misclassified about 3% of the DSLN treatment. In contrast, the SVM model achieved a 100% accuracy score for the DSHN treatment, however, 6% of the DSLN was misclassified as WWHN (3%) and WWLN (3%).
From the confusion matrices in Figure 9d, the three models had above 87% accuracy when trained with the PCA-transformed features. The RF model outperformed the others, producing above 0.90 accuracy scores in all four classes. However, this model had difficulty identifying DSHN, as 6% of this treatment was classified as WWLN. Similarly, 3% of WWLN was misclassified as WWHN, while 6% of DSLN was misclassified as WWHN. The SVM model with 0.941, 0.940 and 0.921 accuracy, F-score and kappa score, respectively, followed the RF model as the most performing model. This recorded the best performance in DSLN classification with a misclassification error of 4%. Again, the SVM model had difficulty differentiating between WWHN and WWLN, with an 8% classification error. Comparably, the DNN model had poor performance with 0.901, 0.900 and 0.868 AA, F-score and kappa scores, respectively. The DNN model misclassified DSLN as DSHN with 7% misclassification, while 13% of DSHN treatment was misclassified as DSLN (6%), WWHN (6%) and WWN (1%).

3.5.2. Multivariate Model Analysis for Stomatal Conductance and Photosynthetic Rate Predictions

Figure 10 and Figure 11 are scatter plots illustrating the relationship between the actual and predicted gs and Pn. Table 5 also summarizes R2, RMSE and MAE, depicting the performance of the regression models. It was observed in Figure 5.10 that most of the models achieved high prediction accuracy, with the Random Forest regression (RFR) outperforming the others with R2= 0.87, RMSE = 0.035 and MAE = 0.015. The high R2 and low RMSE suggest that the RFR model is robust and insensitive to noise. In contrast, the PR model with an average R2 of 0.53 and RMSE of 0.52 was the least accurate in predicting the gs values. During the PLSR modelling using the whole spectra, optimal latent features were selected to train the model to avoid the curse of dimensionality. In this case, fewer latent variables with maximum R2 and minimum RMSE were selected. For the gs-based PLSR models, 20 latent variables were selected. The PLSR model exhibited a high prediction score with a mean R2 of 0.842 ± 0.02 for the test scores. Although the RFR and SVR were trained with a limited number of features (10 sensitive spectral features), their performances were as good as the PLSR model.
Figure 11 shows that all the models achieved considerably high performance in predicting the Pn values except the PR model, which had R2 = 0.74. The RFR model exhibited the highest score with R2 = 0.940 ± 0.05, RMSE= 0.015 and MAE= 0.004. Also, the PR model underperformed when trained with the combined VIs, achieving 0.740 ± 0.01 (R2), 0.144 ± 0.281 (RMSE) and 0.127 ± 0.04 (MAE). Similarly, to the PLSR model for predicting gs, 25 sensitive latent variables were selected for training the Pn-based PLSR model, which performed well with R2 = 0.910±0.04, RMSE= 0.015 and MAE= 0.004.

4. Discussion

This study utilized the spectral information from hyperspectral imaging combined with different machine-learning models to identify drought stress in wheat species supplied with varying N levels. Gas exchange measurements were first monitored to analyze plant canopy response to drought stress. From the results, the gs detected drought stress on the 3 DADS since the control group (WWHN) and the DS treatments significantly differed on this day. Drought stress was detectable on the 6 DADS using the Pn measurements, indicating the viability of gas exchange measurements to be used to track drought dynamics in plants. This supports the findings of Flexas et al., (2009) who analyzed the dynamics of plant water stress and recovery using the photosynthetic parameters; as gs and mesophyll conductance CO2 (gm), where the gs declined to 0.1 and less than 0.05 mol CO2 m−2 s−1 in moderately and severely water-stressed plants, respectively.
Analysis of the spectral curves of the hyperspectral data reveals differences in treatments at the visible and near-infrared regions. Generally, the reflectance was low in the visible spectrum due to high chlorophyll absorption. It was relatively high in the near-infrared region due to internal scattering and little absorption (Knipling, 1970). With increased drought stress and variation in N concentration, the reflectance was higher in the DSLN treatment than in the healthy plants (WWHN). This could be attributed to the decreased leaf pigments, which affected the leaf chlorophyll content and causing high reflectance in the visible spectrum (Debnath et al., 2021; Li et al., 2014).
Twenty-five known VIs were extracted with some VIs (RVSI, SAVI, NDVI705, NDVI750 and EVI) revealing high correlations with the two gas exchange measurements. From previous studies (Gao, 1996; Haboudane et al., 2002), some of these VIs are associated with plant N, which shows that these indices may not be effective for drought stress analysis. Hence, further analysis proposing drought spectral indices was performed. Due to the high dimensionality of HSI, spectral averaging and sensitivity analysis were performed to select the wavebands responsive to drought stress and nitrogen deficiency. Over 600 features were discarded during the feature selection process, revealing that a small subset of spectral features could capture a significant amount of the most valuable information. In contrast, most of the remaining features are typically redundant or contribute to noise (Moghimi et al., 2019). The selection of sensitive spectral features in the red-edge and green spectral regions shows the responsiveness of the wavelengths in these regions to both N variations and drought stress. Additionally, the selection and ranking the 553 nm wavelength by the ensemble model as the most sensitive shows that it could decipher a physical meaning hidden in the high-dimensional spectral data of drought-stressed plants irrespective of the nitrogen level present.
The evaluation of the proposed VIs using a spectral combination of the sensitive features selected revealed that the NDDI and RDI-based indices had strong relationships with drought stress, with NDDI30 and NDI20 having the strongest R2 values of 0.78 and 0.69, respectively. The proposed indices were primarily derived from wavelengths in the blue (500, 550 and 580 nm) and near-infrared (710, 760, 770 and 783 nm) regions, which are reported as wavebands commonly used to measure drought stress and plant N status (Thenkabail et al., 1995). This finding is confirmed by the work of Colovic et al., (2022) who identified the double difference index (DDI) produced from the near-infrared regions (749, 720 and 701nm) as the best-performing index in explaining the variation in plant water levels. This shows the relatively important function of the near-infrared spectrum in drought stress analysis and that a single band might not be practical to evaluate plant health (drought stress) due to ’lant fluctuating nitrogen status and the dynamic nature of the drought stress.
Three models (SVM, RF and DNN) were developed to identify stressed plants using the known VIs, the proposed VIs and the combined VIs and PCA transformed dataset. Generally, all three classifiers had outstanding performances. This shows that traditional machine learning models such as SVM and RF perform well in detecting drought stress in wheat species with the right feature selection. Although the models performed well when trained with the known or proposed VIs, their performance significantly improved when the two sets of VIs were combined. This could be because the combined VIs features cover the spectral areas strongly linked to both nitrogen and drought stress. For instance, indices such as OSAVI, RVSI and NDDI30 are derived from the green and near-infrared regions, which strongly correlate to nitrogen concentration and drought stress. The PCA method reduced the dimensionality of the hyperspectral dataset 622 wavebands to 2 feature sets representing the principal components. While PCA produces new feature components which maximize data variance, ignoring the lower-order PC components may have resulted in information loss, which affected the performance of the models (Cheriyadat, 2003).
Finally, while previous studies show that gas exchange measurements can monitor drought stress dynamics in plants, the process is costly and has low throughput. This study demonstrates the capability of training regression models using the combined VIs to accurately predict gs and Pn, as shown in subsection 5.4.5; however, it is essential to note some limitations. The combined VIs were formulated from different spectral data, resulting in non-linear and complex data. Due to the non-linear and non-addictive nature of the data, the PR model was unable to learn the non-linear trend in the data

5. Conclusions

In the field, crops can suffer multiple stresses, such as drought and nutrient deficiencies, affecting their yield and overall production cost. While these stresses have separate effects on plants, they also interact and have some common responses. Hence, identifying key traits to monitor drought-stressed plants at variable N status is crucial to improving crop yield. This study utilized spectral information from HSI combined with machine learning to identify drought stress and predict gas exchange measurements (gs and Pn) in wheat species. The experimental results demonstrated the capability of our proposed ensemble model in selecting spectral features that are highly responsive to drought dynamics in plants. A combination of the selected features resulted in proposed VIs, which achieved high accuracy in identifying the drought-stressed plants compared to using known VIs when used to train traditional machine learning models. However, the performance of the models improved significantly when they were trained with a combination of proposed and known VIs, where DNN, RF and SVM improved by 2.5%, 1.2% and 1.8% compared to the models trained with the known VIs. In addition to identifying drought stress by classification, the combined VIs were also used to train three regression models to predict gs and Pn measurements. The RF regression model outperformed the others in accurately predicting gs and Pn with error margins of 0.8 and 0.4, respectively. Although excellent results were obtained, more research is required to validate the conclusions on a larger spatial scale, exploring the potential application of the models for other plant species.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Table -E1: Table -E2.

Author Contributions

Conceptualization, F.G.O. and D.C.; methodology, F.G.O..; software, F.G.O.; validation, M.J.H., F.M. and D.S.; formal analysis, F.G.O.; investigation, N.V. and L.G.; resources, M.C. and A.B.R.; data curation, F.G.O. and D.C.; writing—original draft preparation, F.G.O.; writing—review and editing, M.J.H., N.V., F.M.., D.S. and L.G.; visualization and supervision, M.J.H. and F.M.; project administration, M.M.; funding acquisition, M.J.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the OCP S.A. under the University of Mohammed VI Polytechnic, Rothamsted Research and Cranfield University project (FPO4). Rothamsted Research receives grant-aided support from the Biotechnology and Biological Sciences Research Council (BBSRC) through the Delivering Sustainable Wheat program (BB/X011003/1).

Data Availability Statement

The data used in this study are available from the corresponding author on request. Conflicts.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Asaari, M. S. M., Mertens, S., Dhondt, S., Inzé, D., Wuyts, N., & Scheunders, P. Analysis of hyperspectral images for detection of drought stress and recovery in maize plants in a high-throughput phenotyping platform. Computers and Electronics in Agriculture, 162(May), 749–758 (2019). [Google Scholar] [CrossRef]
  2. Belgiu, M., & Drăgu, L. (2016). Random forest in remote sensing: A review of applications and future directions. ISPRS Journal of Photogrammetry and Remote Sensing, 114, 24–31. [CrossRef]
  3. Bergstra, J., & Bengio, Y. (2012). Random search for hyper-parameter optimization. Journal of Machine Learning Research, 13, 281–305.
  4. Blackburn, G. A. (1998). Spectral indices for estimating photosynthetic pigment concentrations: A test using senescent tree leaves. International Journal of Remote Sensing, 19(4), 657–675. [CrossRef]
  5. Breiman, L. (2020). RFRSF: Employee Turnover Prediction Based on Random Forests and Survival Analysis. Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 12343 LNCS, 503–515. [CrossRef]
  6. Brochu, E., Cora, V. M., & de Freitas, N. (2010). A Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning. arXiv:1012.2599.
  7. Buitinck, L., Louppe, G., Blondel, M., Pedregosa, F., Mueller, A., Grisel, O., Niculae, V., Prettenhofer, P., Gramfort, A., Grobler, J., Layton, R., Vanderplas, J., Joly, A., Holt, B., & Varoquaux, G. (2013). API design for machine learning software: experiences from the scikit-learn project. 1–15. arXiv:1309.0238.
  8. Buschmann, C., & Nagel, E. (1993). In vivo spectroscopy and internal optics of leaves as basis for remote sensing of vegetation. International Journal of Remote Sensing, 14(4), 711–722. [CrossRef]
  9. Cheriyadat, A. (2003). Limitations of principal component analysis for dimensionality-reduction for classification of hyperspectral data. December http://en.scientificcommons.org/49172179.
  10. Chutia, D., Bhattacharyya, D. K., Sarma, J., & Raju, P. N. L. (2017). An effective ensemble classification framework using random forests and a correlation based feature selection technique. Transactions in GIS, 21(6), 1165–1178. [CrossRef]
  11. Colovic, M., Yu, K., Todorovic, M., Cantore, V., Hamze, M., Albrizio, R., & Stellacci, A. M. (2022). Hyperspectral Vegetation Indices to Assess Water and Nitrogen Status of Sweet Maize Crop. Agronomy, 12(9), 1–17. [CrossRef]
  12. Damodaran, B. B., Courty, N., & Lefevre, S. (2017). Sparse Hilbert Schmidt Independence Criterion and Surrogate-Kernel-Based Feature Selection for Hyperspectral Image Classification. IEEE Transactions on Geoscience and Remote Sensing, 55(4), 2385–2398. [CrossRef]
  13. Datt, B. (1999). A new reflectance index for remote sensing of chlorophyll content in higher plants: Tests using Eucalyptus leaves. Journal of Plant Physiology, 154(1), 30–36. [CrossRef]
  14. Debnath, S., Paul, M., Motiur Rahaman, D. M., Debnath, T., Zheng, L., Baby, T., Schmidtke, L. M., & Rogiers, S. Y. (2021). Identifying individual nutrient deficiencies of grapevine leaves using hyperspectral imaging. Remote Sensing, 13(16), 1–21. [CrossRef]
  15. Duan, L., Han, J., Guo, Z., Tu, H., Yang, P., Zhang, D., Fan, Y., Chen, G., Xiong, L., Dai, M., Williams, K., Corke, F., Doonan, J. H., & Yang, W. (2018). Chapter 3. Novel digital features discriminate between drought resistant and drought sensitive rice under controlled and field conditions. Frontiers in Plant Science, 9(April). [CrossRef]
  16. Flexas, J., Barón, M., Bota, J., Ducruet, J. M., Gallé, A., Galmés, J., Jiménez, M., Pou, A., Ribas-Carbó, M., Sajnani, C., Tomàs, M., & Medrano, H. (2009). Photosynthesis limitations during water stress acclimation and recovery in the drought-adapted Vitis hybrid Richter-110 (V. berlandieri×V. rupestris). Journal of Experimental Botany, 60(8), 2361–2377. [CrossRef]
  17. Gamon, J.A, P. and C. B. F. (1992). A Narrow-Waveband Spectral Index That Tracks Diurnal Changes in Photosynthetic Efficiency. REMOTE SENS. ENVIRON, 6(1), 22–42.
  18. Gao, B. (1996). NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sensing of Environment, 58(3), 257–266. [CrossRef]
  19. Gitelson, A. A., Gritz †, Y., & Merzlyak, M. N. (2003). Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. Journal of Plant Physiology, 160(3), 271–282. [CrossRef]
  20. Grant, O. M., Ochagavía, H., Baluja, J., Diago, M. P., & Tardáguila, J. (2016). Thermal imaging to detect spatial and temporal variation in the water status of grapevine (Vitis vinifera L.). The Journal of Horticultural Science and Biotechnology, 91(1), 43–54. [CrossRef]
  21. Haboudane, D., Miller, J. R., Pattey, E., Zarco-Tejada, P. J., & Strachan, I. B. (2004). Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sensing of Environment, 90(3), 337–352. [CrossRef]
  22. Haboudane, D., Miller, J. R., Tremblay, N., Zarco-Tejada, P. J., & Dextraze, L. (2002). Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sensing of Environment, 81(2–3), 416–426. [CrossRef]
  23. Helmholz, P., Rottensteiner, F., & Heipke, C. (2014). Semi-automatic verification of cropland and grassland using very high resolution mono-temporal satellite images. ISPRS Journal of Photogrammetry and Remote Sensing, 97, 204–218. [CrossRef]
  24. Hossain, M. A., Wani, S. H., Bhattacharjee, S., Burritl, D. J., & Tran, L. S. P. (2016). Drought stress tolerance in plants, vol 1: Physiology and biochemistry. In Drought Stress Tolerance in Plants, Vol 1: Physiology and Biochemistry (Vol. 1, Issue March). [CrossRef]
  25. Ihuoma, S. O., & Madramootoo, C. A. (2017). Recent advances in crop water stress detection. Computers and Electronics in Agriculture, 141, 267–275. [CrossRef]
  26. Jay, S., Gorretta, N., Morel, J., Maupas, F., Bendoula, R., Rabatel, G., Dutartre, D., Comar, A., & Baret, F. (2017). Estimating leaf chlorophyll content in sugar beet canopies using millimeter- to centimeter-scale reflectance imagery. Remote Sensing of Environment, 198, 173–186. [CrossRef]
  27. Keshtiban, R. K., Carvani, V., & Imandar, M. (2015). Effects of salinity stress and drought due to different concentrations of sodium chloride and polyethylene glycol 6000 on germination and seedling growth characteristics of pinto bean (Phaseolus vulgaris L.). Advances in Environmental Biology, 237+. https://link.gale.com/apps/doc/A417473553/AONE?u=anon~b1456800&sid=googleScholar&xid=d9e51878.
  28. Knipling, E. B. (1970). Physical and physiological basis for the reflectance of visible and near-infrared radiation from vegetation. Remote Sensing of Environment, 1(3), 155–159. [CrossRef]
  29. Koh, J. C. O., Banerjee, B. P., Spangenberg, G., & Kant, S. (2022). Automated hyperspectral vegetation index derivation using a hyperparameter optimisation framework for high-throughput plant phenotyping. New Phytologist, 233(6), 2659–2670. [CrossRef]
  30. Leone, M. (2022). Advances in fiber optic sensors for soil moisture monitoring: A review. Results in Optics, 7(December 2021), 100213. [CrossRef]
  31. Li, F., Mistele, B., Hu, Y., Chen, X., & Schmidhalter, U. (2014). Reflectance estimation of canopy nitrogen content in winter wheat using optimised hyperspectral spectral indices and partial least squares regression. European Journal of Agronomy, 52, 198–209. [CrossRef]
  32. Mandal, N., Adak, S., Das, D. K., Sahoo, R. N., Mukherjee, J., Kumar, A., Chinnusamy, V., Das, B., Mukhopadhyay, A., Rajashekara, H., & Gakhar, S. (2023). Spectral characterization and severity assessment of rice blast disease using univariate and multivariate models. Frontiers in Plant Science, 14(February), 1–21. [CrossRef]
  33. McFeeters, S. K. (1996). NDWI BY McFEETERS. Remote Sensing of Environment, 25(3), 687–711.
  34. Mertens, S., Verbraeken, L., Sprenger, H., Demuynck, K., Maleux, K., Cannoot, B., De Block, J., Maere, S., Nelissen, H., Bonaventure, G., Crafts-Brandner, S. J., Vogel, J. T., Bruce, W., Inzé, D., & Wuyts, N. (2021). Proximal Hyperspectral Imaging Detects Diurnal and Drought-Induced Changes in Maize Physiology. Frontiers in Plant Science, 12(February), 1–18. [CrossRef]
  35. Moghimi, A., Yang, C., & Marchetto, P. M. (2019). Thesis- Integrating Hyperspectral Imaging and Artificial Intelligence to Develop Automated Frameworks for High-throughput Phenotyping in Wheat. February.
  36. Nagasubramanian, K., Jones, S., Singh, A. K., Singh, A., Ganapathysubramanian, B., & Sarkar, S. (2018). Explaining hyperspectral imaging based plant disease identification: 3D CNN and saliency maps. Nips 2017, 3–10. arXiv:1804.08831.
  37. Nguyen, N. T., Mohapatra, P. K., Fujita, K., Nakabayashi, K., & Thompson, J. (2003). Effect of nitrogen deficiency on biomass production, photosynthesis, carbon partitioning, and nitrogen nutrition status of Melaleuca and Eucalyptus species. Soil Science and Plant Nutrition, 49(1), 99–10. [CrossRef]
  38. Pandey, P., Ge, Y., Stoerger, V., & Schnable, J. C. (2017). High throughput in vivo analysis of plant leaf chemical properties using hyperspectral imaging. Frontiers in Plant Science, 8(August), 1–12. [CrossRef]
  39. Penuelas, J., Baret, F., & Filella, I. (1995). Semi-empirical indices to assess carotenoids/chlorophyll a ratio from leaf spectral reflectance. Photosynthetica, 31(2), 221–230.
  40. Peñuelas, J., & Filella, L. (1998). Technical focus: Visible and near-infrared reflectance techniques for diagnosing plant physiological status. Trends in Plant Science, 3(4), 151–156. [CrossRef]
  41. Perry, C. R., & Lautenschlager, L. F. (1984). Functional equivalence of spectral vegetation indices. Remote Sensing of Environment, 14(1–3), 169–182. [CrossRef]
  42. Pirasteh-Anosheh, H., Saed-Moucheshi, A., Pakniyat, H., & Pessarakli, M. (2016). Stomatal responses to drought stress. Water Stress and Crop Plants: A Sustainable Approach, 1–2, 24–40. [CrossRef]
  43. Podani, J., & Czárán, T. (1997). Individual-centered analysis of mapped point patterns representing multi-species assemblages. Journal of Vegetation Science, 8(2), 259–270. [CrossRef]
  44. Proctor, C., Dao, P. D., & He, Y. (2021). Close-range, heavy-duty hyperspectral imaging for tracking drought impacts using the PROCOSINE model. Journal of Quantitative Spectroscopy and Radiative Transfer, 263, 107528. [CrossRef]
  45. Qi, J., Chehbouni, A., Huete, A. R., Kerr, Y. H., & Sorooshian, S. (1994). A modified soil adjusted vegetation index. Remote Sensing of Environment, 48(2), 119–126. [CrossRef]
  46. Rady, A., Ekramirad, N., Adedeji, A. A., Li, M., & Alimardani, R. (2017). Hyperspectral imaging for detection of codling moth infestation in GoldRush apples. Postharvest Biology and Technology, 129, 37–44. [CrossRef]
  47. Remeseiro, B., & Bolon-Canedo, V. (2019). A review of feature selection methods in medical applications. Computers in Biology and Medicine, 112(February), 103375. [CrossRef]
  48. Rinnan, Å., Berg, F. van den, & Engelsen, S. B. (2009). Review of the most common pre-processing techniques for near-infrared spectra. TrAC - Trends in Analytical Chemistry, 28(10), 1201–1222. [CrossRef]
  49. Rodriguez-Galiano, V. F., Ghimire, B., Rogan, J., Chica-Olmo, M., & Rigol-Sanchez, J. P. (2012). An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS Journal of Photogrammetry and Remote Sensing, 67(1), 93–104. [CrossRef]
  50. Rondeaux, G., Steven, M., & Baret, F. (1996). Optimization of soil-adjusted vegetation indices. Remote Sensing of Environment, 55(2), 95–107. [CrossRef]
  51. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323(6088), 533–536. [CrossRef]
  52. Sadeghi-Tehran, P., Virlet, N., & Hawkesford, M. J. (2021). A neural network method for classification of sunlit and shaded components of wheat canopies in the field using high-resolution hyperspectral imagery. Remote Sensing, 13(5), 1–17. [CrossRef]
  53. Satterwhite, M., & Henley, J. (1990). Hyperspectral signatures (400 to 2500 nm) of vegetation, minerals, soils, rocks, and cultural features: Laboratory and field measurements. 478. http://oai.dtic.mil/oai/oai?verb=getRecord&metadataPrefix=html&identifier=ADA239496.
  54. Sims, D. A., & Gamon, J. A. (2002). Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sensing of Environment, 81(2), 337–354. [CrossRef]
  55. Sun, Y., Todorovic, S., & Goodison, S. (2010). Local-learning-based feature selection for high-dimensional data analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence, 32(9), 1610–1626. [CrossRef]
  56. Thameur, A., Lachiheb, B., & Ferchichi, A. (2012). Drought effect on growth, gas exchange and yield, in two strains of local barley Ardhaoui, under water deficit conditions in southern Tunisia. Journal of Environmental Management, 113, 495–500. [CrossRef]
  57. Thenkabail, P. S., Smith, R. B., & De Pauw, E. (1995). Wiegand and Richardson, † International Center for Agricultural Research in the Dry Areas 1990), natural vegetation (Friedl et al., 1994), and in (ICARDA). Environ, 71(99), 158–182.
  58. Tucker, C. J. (1979). Red and photographic infrared linear combinations for monitoring vegetation. Remote Sensing of Environment, 8(2), 127–150. [CrossRef]
  59. White, D. C., Williams, M., & Barr, S. L. (2008). Detecting sub-surface soil disturbance using hyperspectral first derivative band ratios of associated vegetation stress. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences - ISPRS Archives, 37(Figure 1).
  60. Xu, H. R., Ying, Y. B., Fu, X. P., & Zhu, S. P. (2007). Near-infrared Spectroscopy in detecting Leaf Miner Damage on Tomato Leaf. Biosystems Engineering, 96(4), 447–454. [CrossRef]
  61. Xu, L., & Baldocchi, D. D. (2003). Seasonal trends in photosynthetic parameters and stomatal conductance of blue oak (Quercus douglasii) under prolonged summer drought and high temperature. Tree Physiology, 23(13), 865–877. [CrossRef]
  62. Yang, P., Liu, W., Zhou, B. B., Chawla, S., & Zomaya, A. Y. (2013). Ensemble-based wrapper methods for feature selection and class imbalance learning. Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 7818 LNAI(PART 1), 544–555. [CrossRef]
  63. Zhang, Y., Zha, Y., Jin, X., Wang, Y., & Qiao, H. (2022). Changes in Vertical Phenotypic Traits of Rice (Oryza sativa L.) Response to Water Stress. Frontiers in Plant Science, 13(July), 1–19. [CrossRef]
  64. Zhu, F., Zhang, D., He, Y., Liu, F., & Sun, D. W. (2013). Application of Visible and Near Infrared Hyperspectral Imaging to Differentiate Between Fresh and Frozen-Thawed Fish Fillets. Food and Bioprocess Technology, 6(10), 2931–2937. [CrossRef]
Preprints 112380 g001
Figure 1. The schematic diagram of the methodology for analyzing spectral images for drought stress identification (A) is the preprocessing step (involving data calibration, denoising, desampling and segmentation, (B) drought stress-related physiological measurements (gs and Pn), (C) the extraction of known VIs (D) ensemble learning model for selecting sensitive spectral wavelengths (E) the development of classification and regression models for identification of drought stress and prediction of gas exchange traits (Pn and gs).
Figure 1. The schematic diagram of the methodology for analyzing spectral images for drought stress identification (A) is the preprocessing step (involving data calibration, denoising, desampling and segmentation, (B) drought stress-related physiological measurements (gs and Pn), (C) the extraction of known VIs (D) ensemble learning model for selecting sensitive spectral wavelengths (E) the development of classification and regression models for identification of drought stress and prediction of gas exchange traits (Pn and gs).
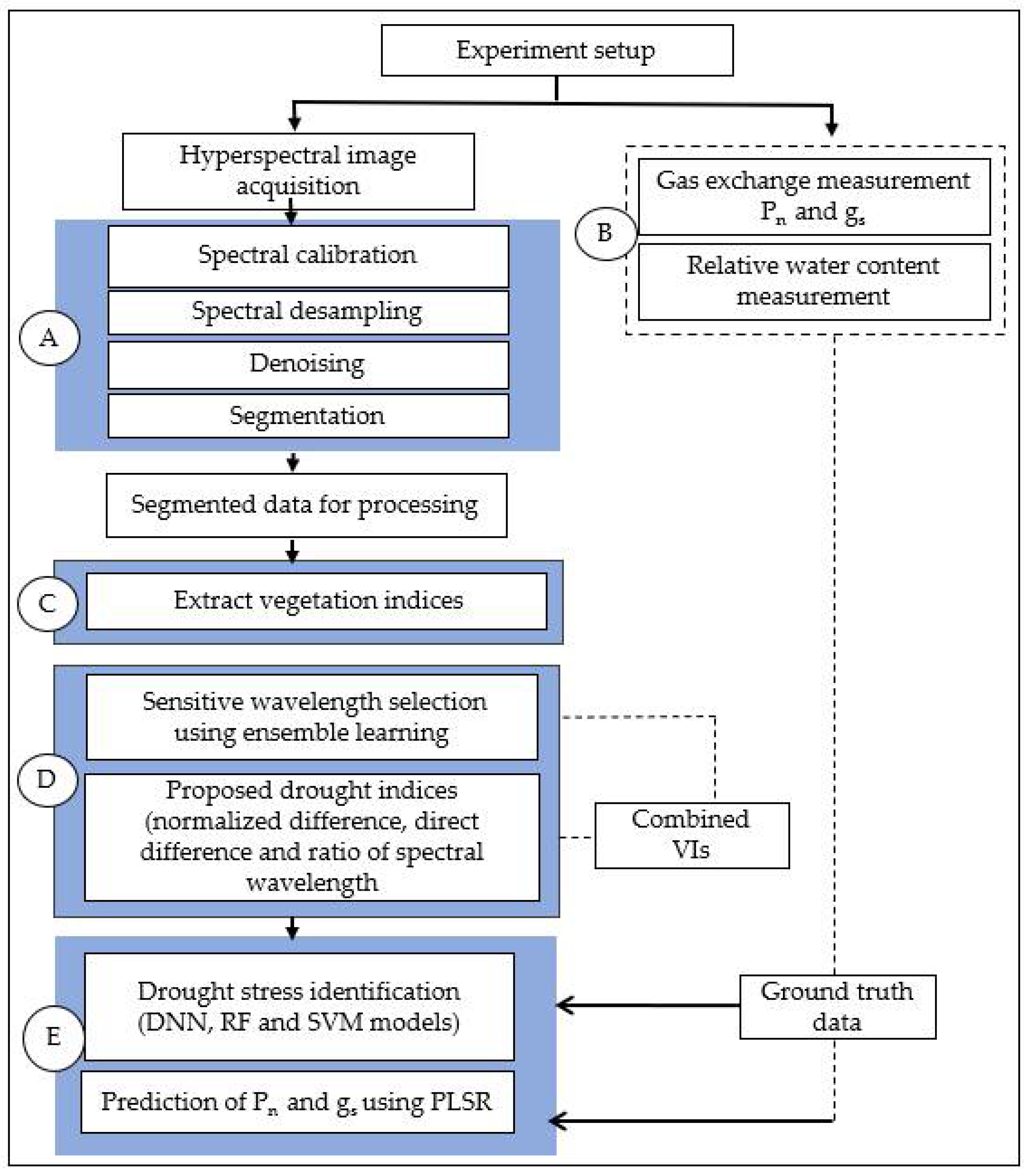
Preprints 112380 g001
Preprints 112380 g002
Figure 2. Workflow of the ensemble feature selection pipeline.
Figure 2. Workflow of the ensemble feature selection pipeline.
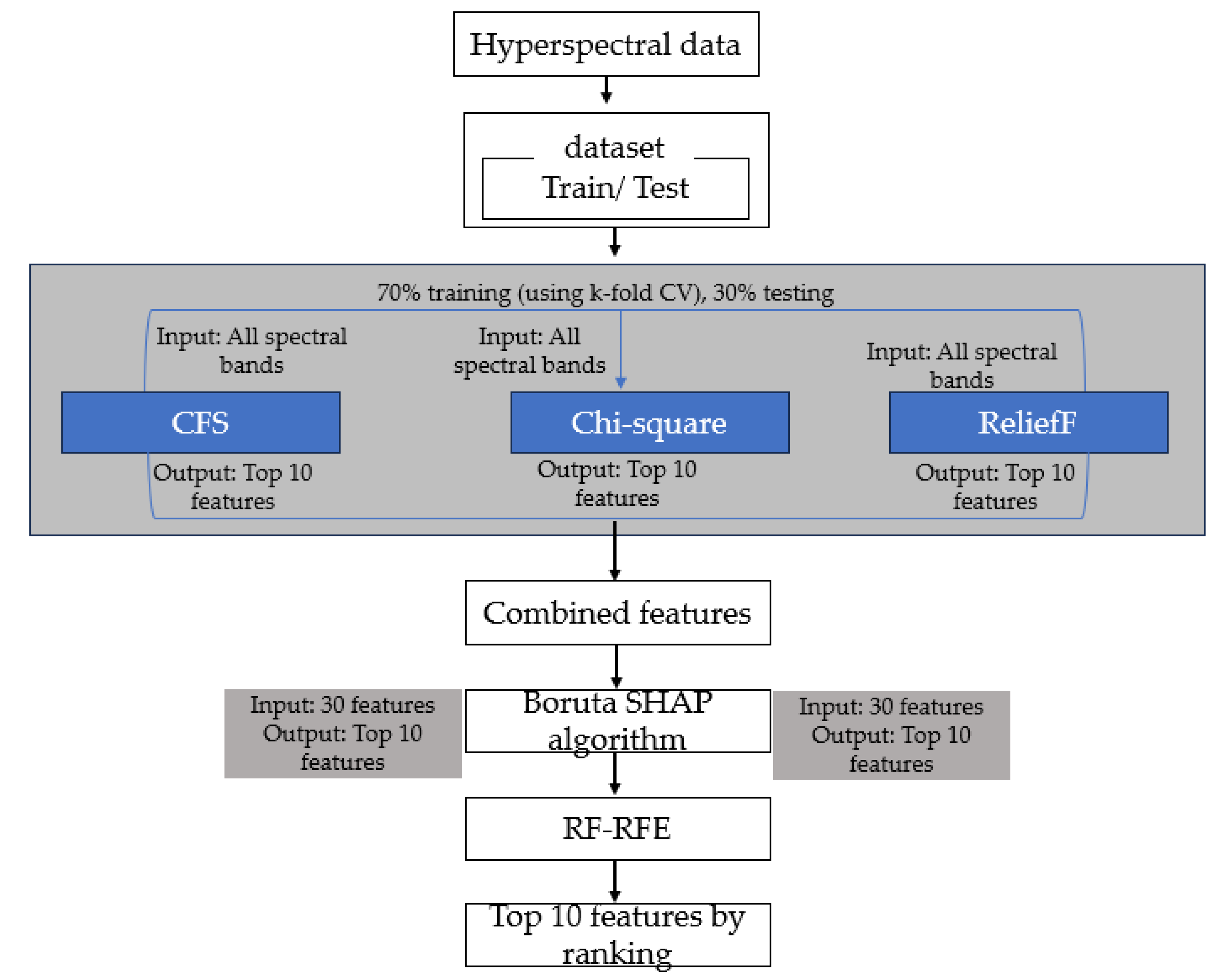
Preprints 112380 g002
Preprints 112380 g003
Figure 3. Photosynthetic rates from 0-15 DADS. The results presented are mean and standard deviations from the original data; the dissimilar lower-case group (a, b, c) represents a significant difference with p <0.05.
Figure 3. Photosynthetic rates from 0-15 DADS. The results presented are mean and standard deviations from the original data; the dissimilar lower-case group (a, b, c) represents a significant difference with p <0.05.
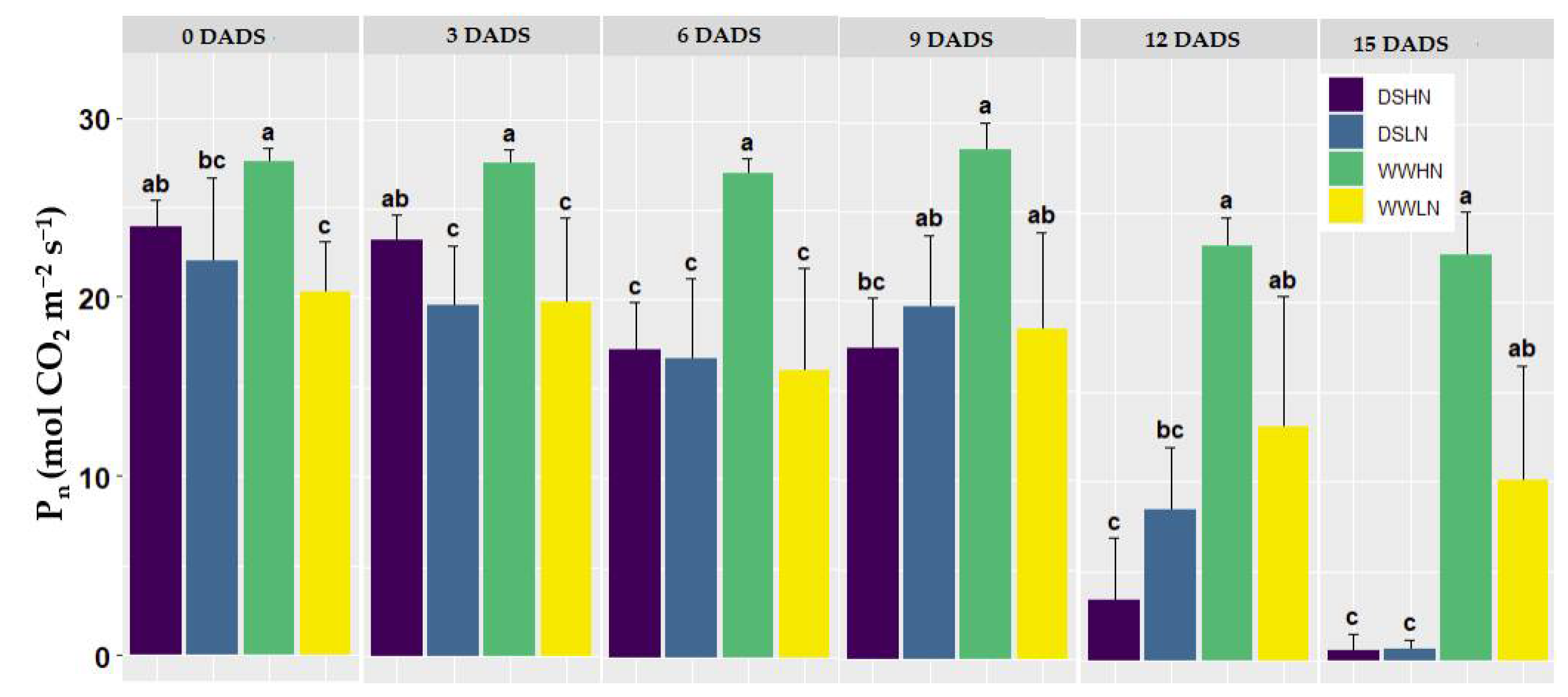
Preprints 112380 g003
Preprints 112380 g004
Figure 4. Stomatal conductance from 0-15 DADS. The results presented are mean and standard deviations from the original data; the dissimilar lower-case group (a, b, c) represents a significant difference with p < 0.05.
Figure 4. Stomatal conductance from 0-15 DADS. The results presented are mean and standard deviations from the original data; the dissimilar lower-case group (a, b, c) represents a significant difference with p < 0.05.
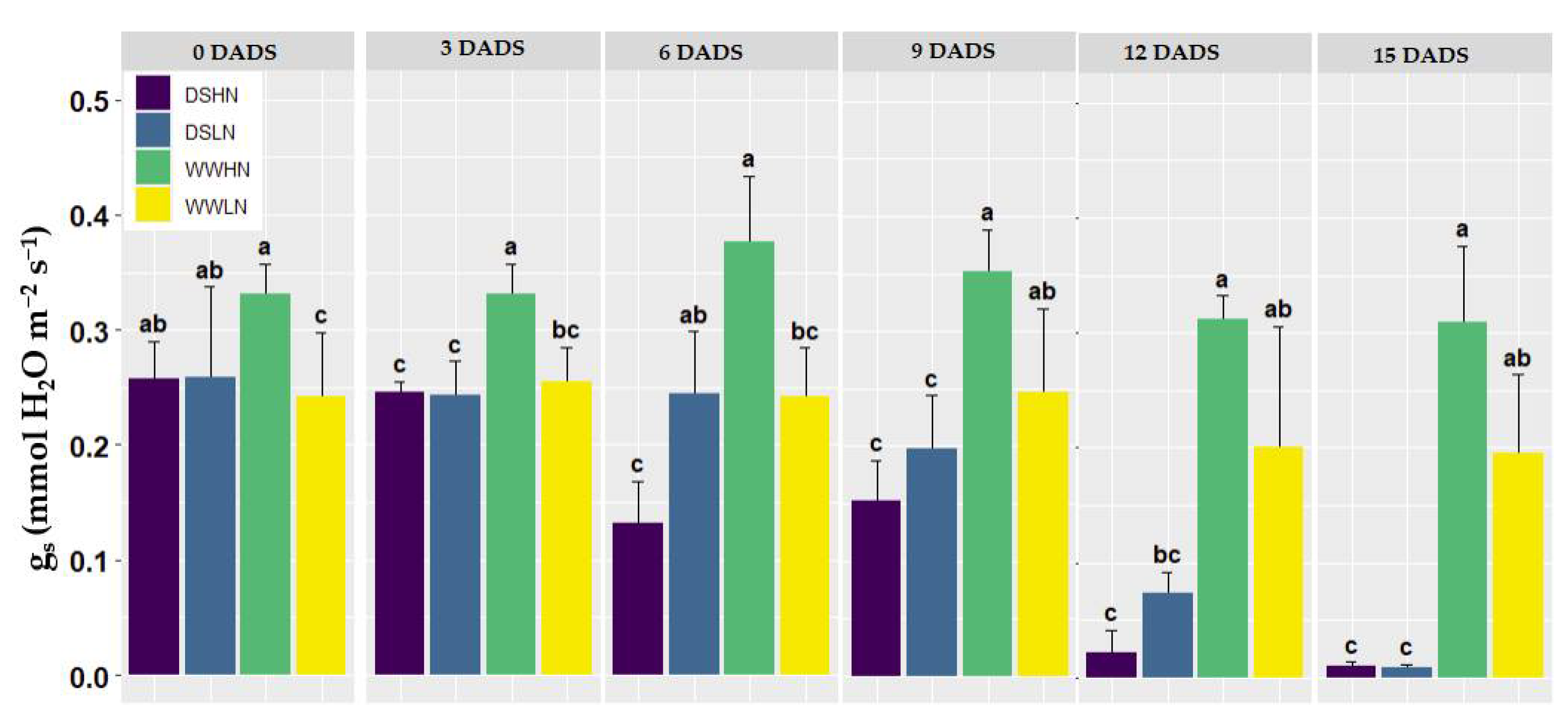
Preprints 112380 g004
Preprints 112380 g005aPreprints 112380 g005b
Figure 5. Spectral reflectance of the averaged DSHN, DSLN, WWHN and WWLN treatments for 0 DADS (a), 6 DADS (b) and 15 DADS (c). Spectral values are shown as mean ± standard deviation.
Figure 5. Spectral reflectance of the averaged DSHN, DSLN, WWHN and WWLN treatments for 0 DADS (a), 6 DADS (b) and 15 DADS (c). Spectral values are shown as mean ± standard deviation.
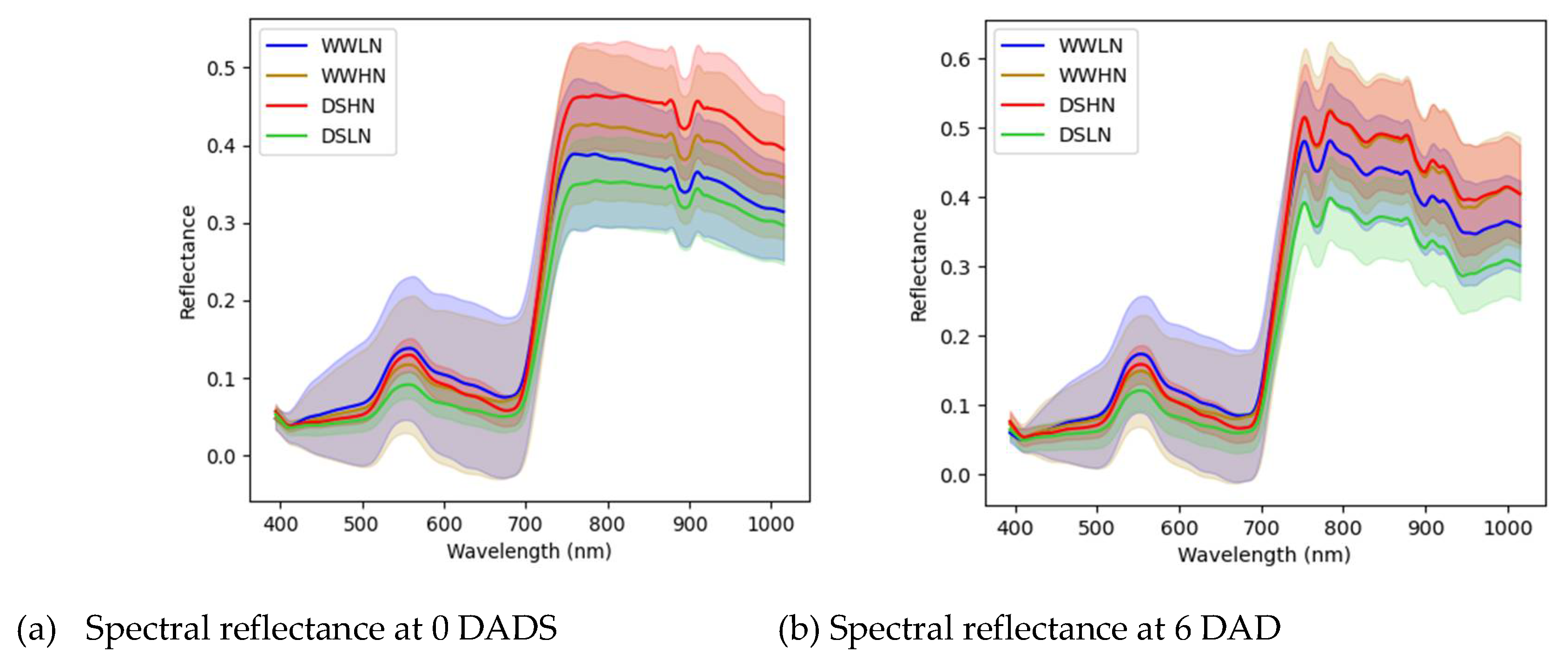
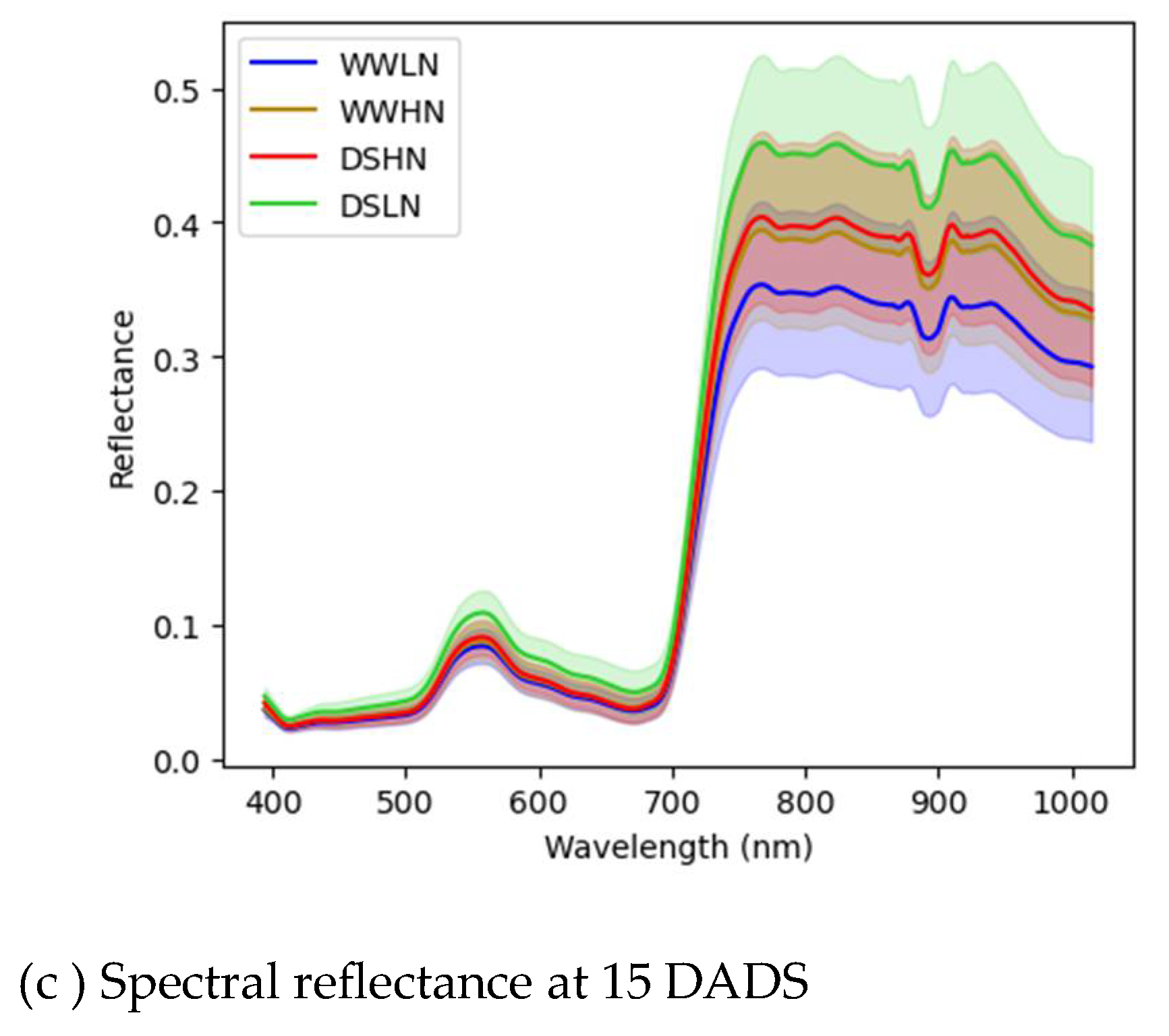
Preprints 112380 g005aPreprints 112380 g005b
Preprints 112380 g006
Figure 6. Pearson correlations between the extracted features and the gas exchange measurements (Pn and gs). VIs with a correlation of more than 0.5 were selected for further analysis. See Table 1 for abbreviations of VIs.
Figure 6. Pearson correlations between the extracted features and the gas exchange measurements (Pn and gs). VIs with a correlation of more than 0.5 were selected for further analysis. See Table 1 for abbreviations of VIs.
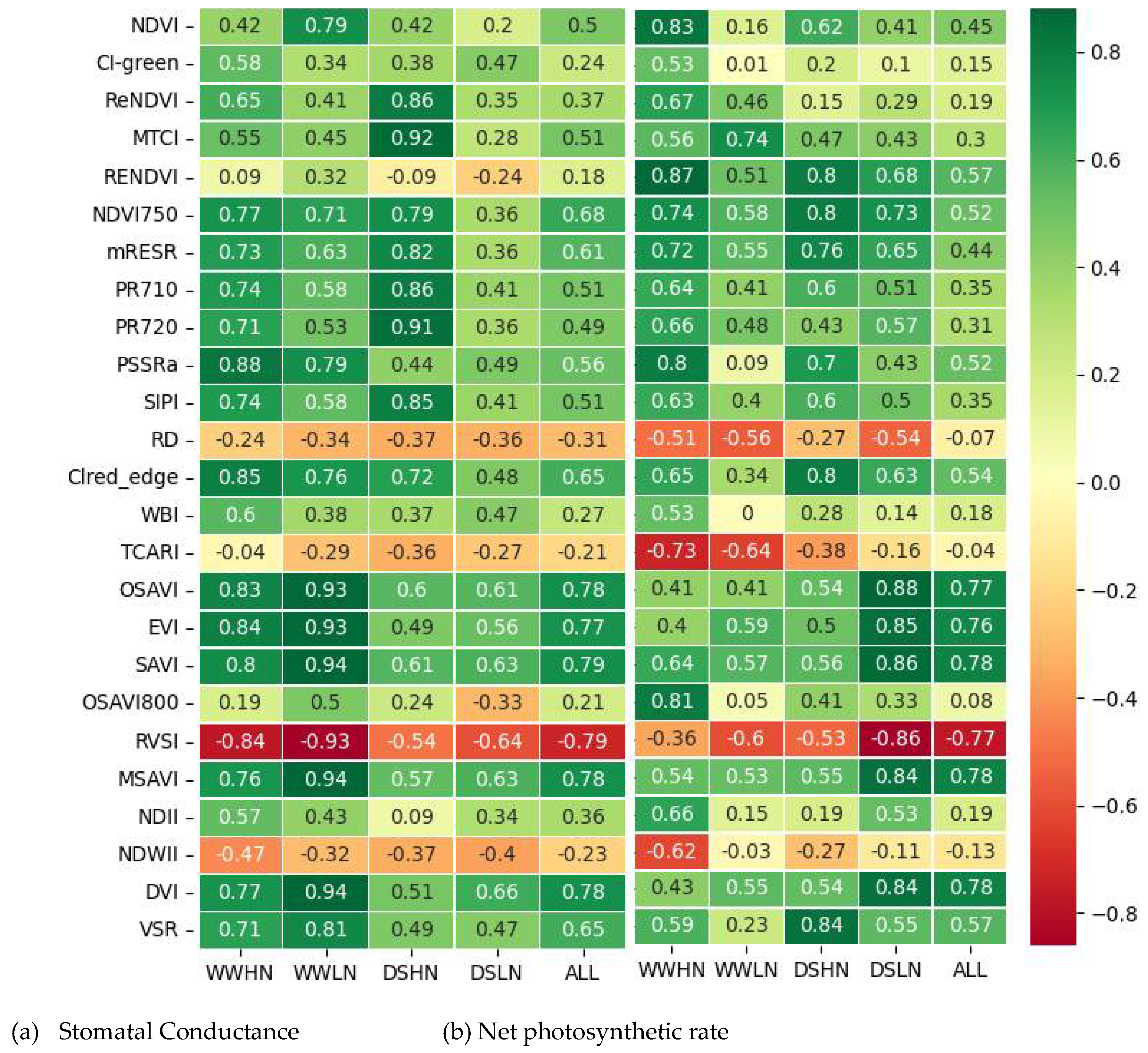
Preprints 112380 g006
Preprints 112380 g007
Figure 7. A colourmap image of the correlation between all pairs of spectral features from 394 to 1015 nm.
Figure 7. A colourmap image of the correlation between all pairs of spectral features from 394 to 1015 nm.
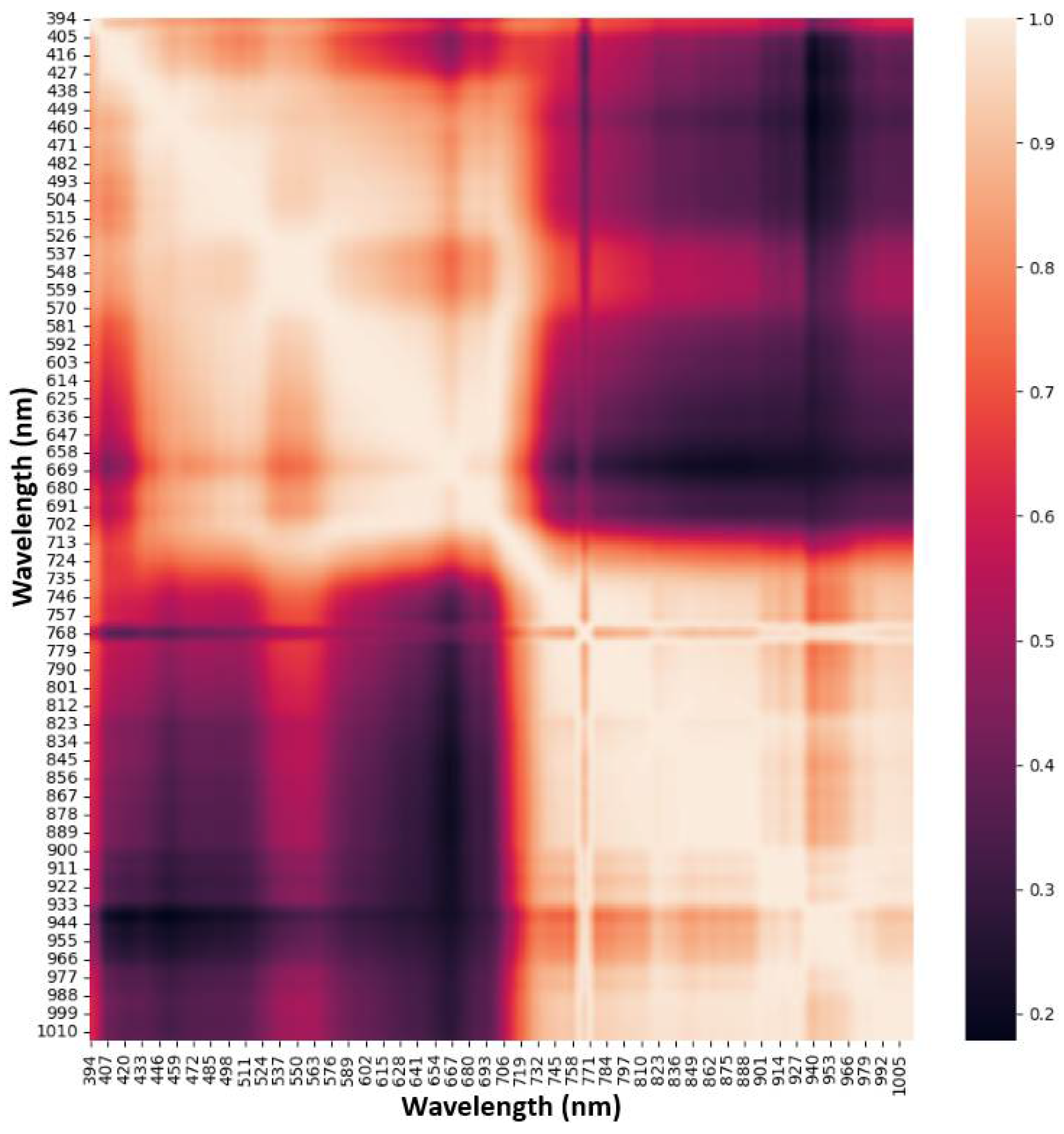
Preprints 112380 g007
Preprints 112380 g008
Figure 8. Correlations between the proposed indices and the Pn and gs measurements.
Figure 8. Correlations between the proposed indices and the Pn and gs measurements.
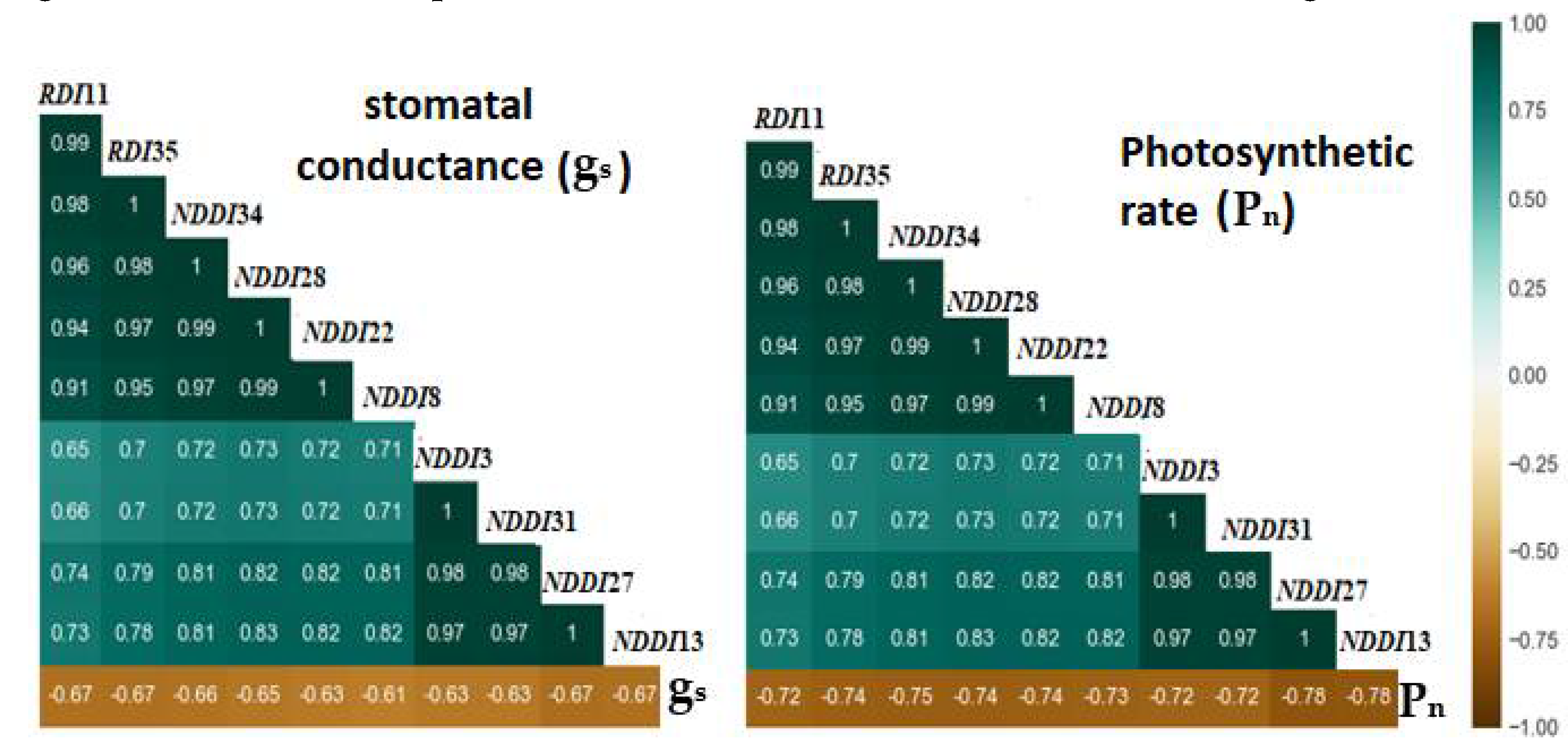
Preprints 112380 g008
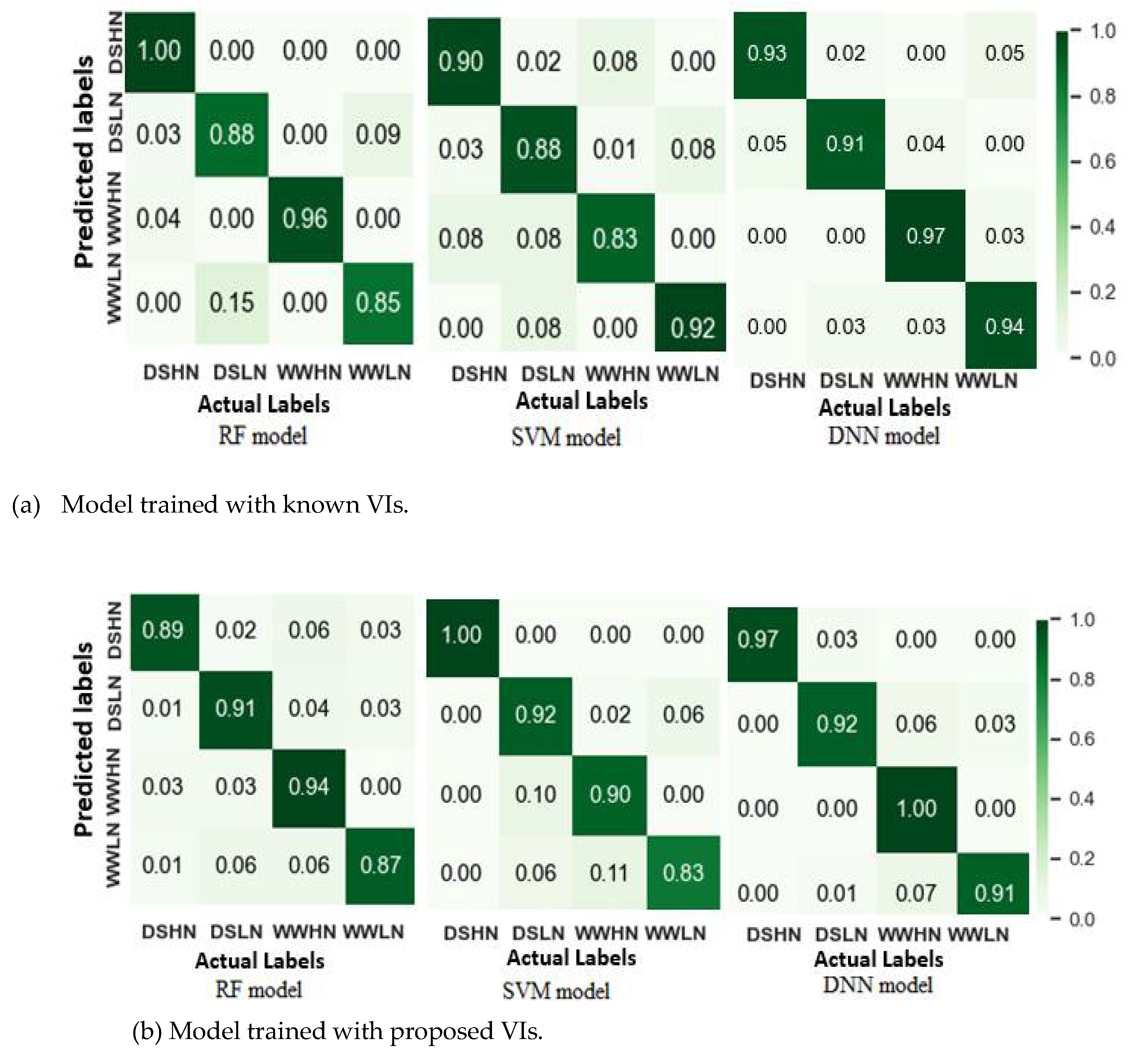
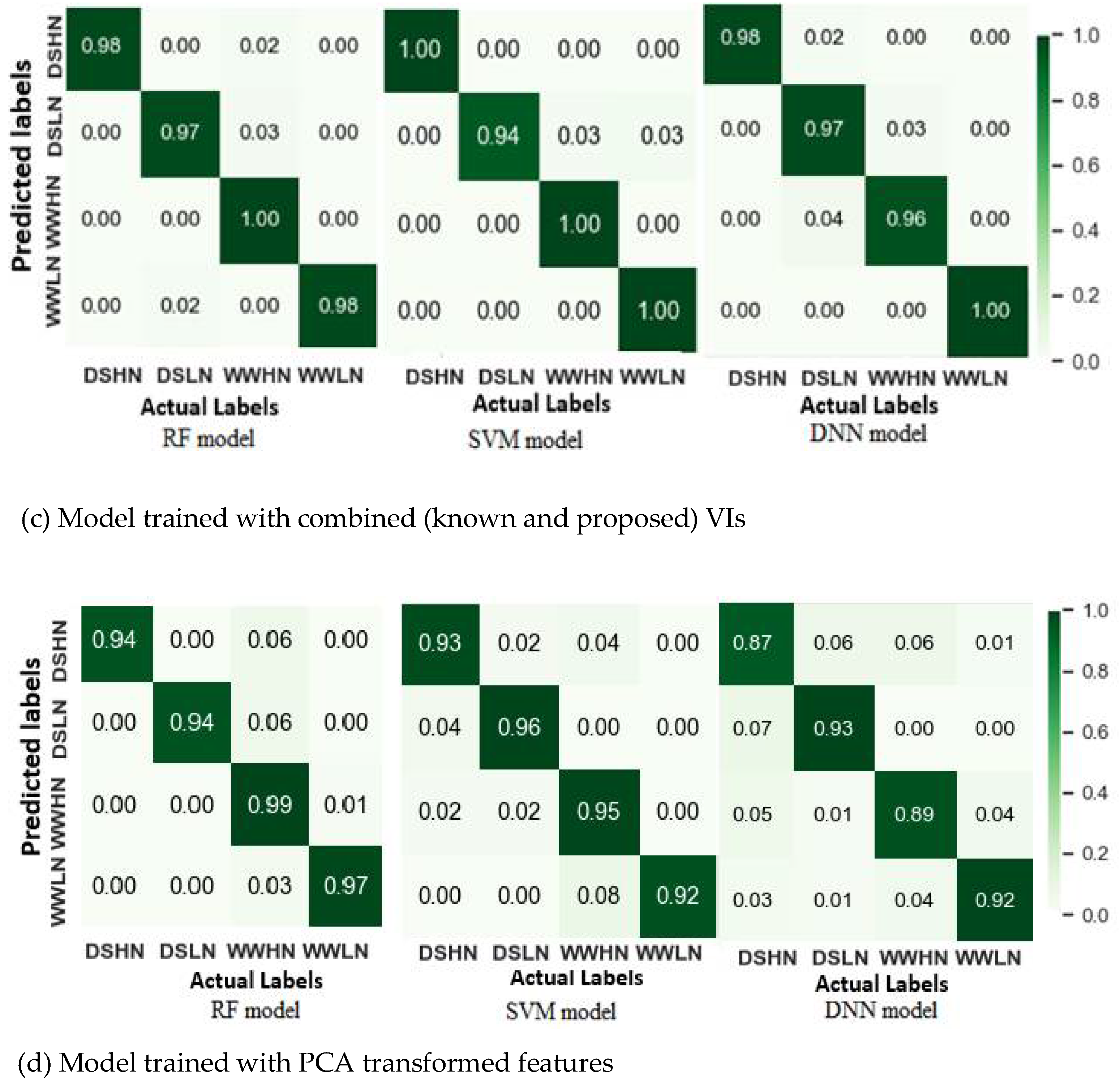
Preprints 112380 g009aPreprints 112380 g009b
Figure 9. Confusion matrices depicting the performance of the SVM, RF and DNN classifiers trained with (a) known VIs, (b) proposed VIs, (c) combined VIs and (d) PCA transformed features.
Figure 9. Confusion matrices depicting the performance of the SVM, RF and DNN classifiers trained with (a) known VIs, (b) proposed VIs, (c) combined VIs and (d) PCA transformed features.
Preprints 112380 g009aPreprints 112380 g009b
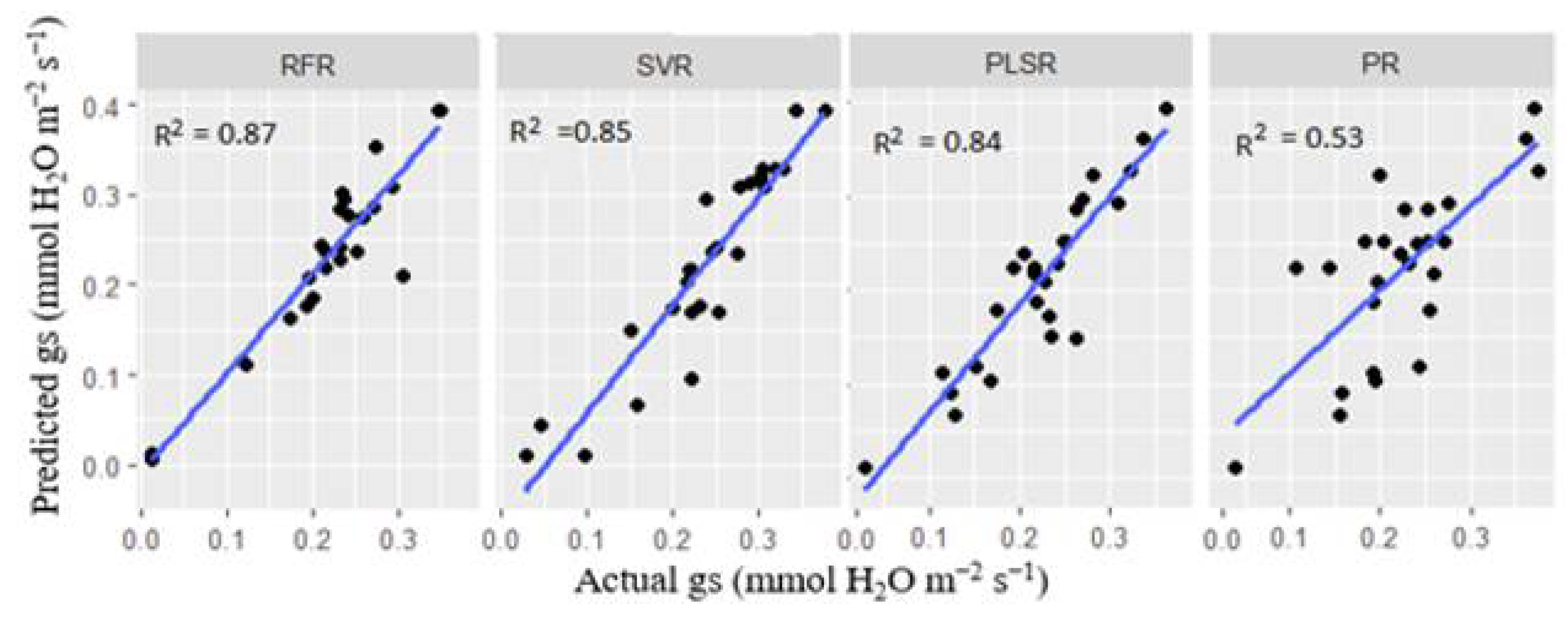
Preprints 112380 g010
Figure 10. Prediction of plant gs using four models (Random Forest regression (RF), Support vector regression (SVR), Partial least square regression (PLSR) and Polynomial regression (PR)). All the models were trained with the combined VIs except the PLSR, which were trained with the whole spectra.
Figure 10. Prediction of plant gs using four models (Random Forest regression (RF), Support vector regression (SVR), Partial least square regression (PLSR) and Polynomial regression (PR)). All the models were trained with the combined VIs except the PLSR, which were trained with the whole spectra.
Preprints 112380 g010
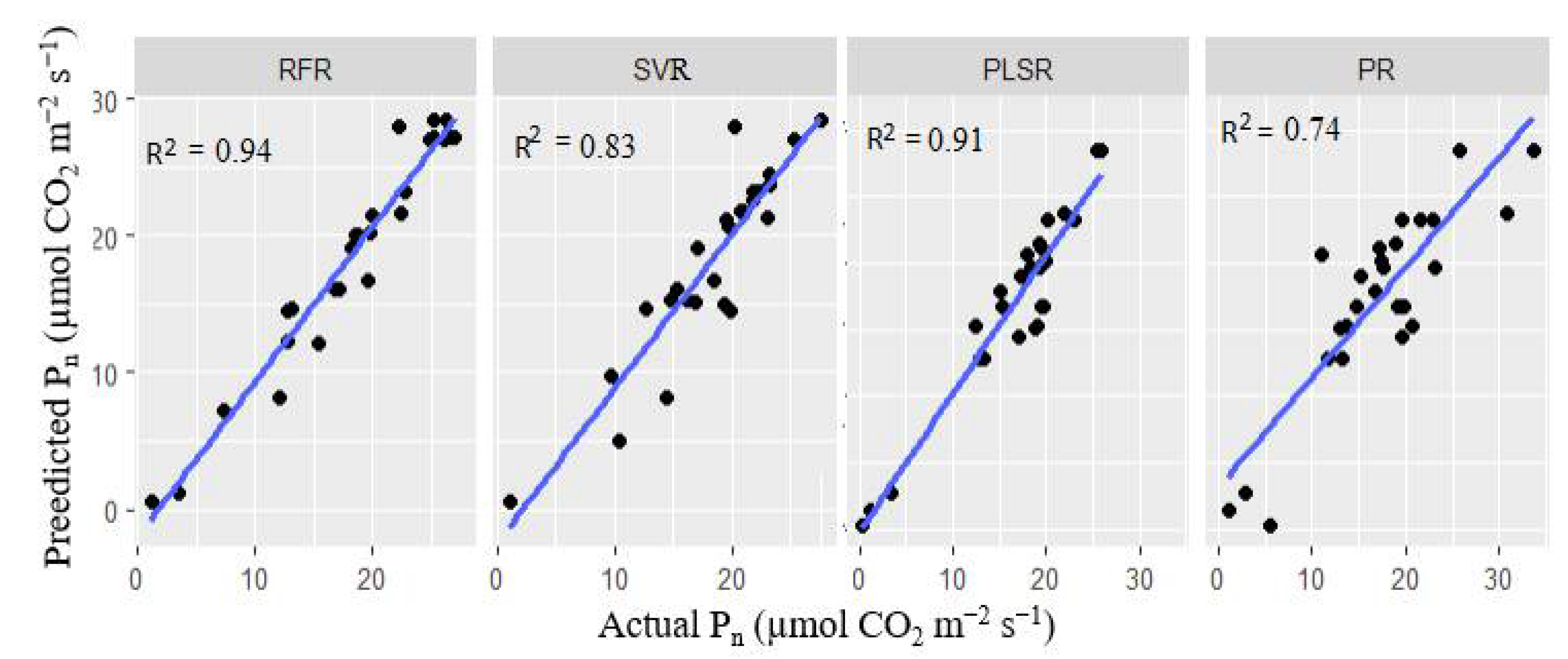
Preprints 112380 g011
Figure 11. Prediction of plant Pn using four models (Random Forest regression (RF), Support vector regression (SVR), Partial least square regression (PLSR) and Polynomial regression (PR)). All the models were trained with the combined VIs except the PLSR, which was trained with the whole spectra.
Figure 11. Prediction of plant Pn using four models (Random Forest regression (RF), Support vector regression (SVR), Partial least square regression (PLSR) and Polynomial regression (PR)). All the models were trained with the combined VIs except the PLSR, which was trained with the whole spectra.
Preprints 112380 g011
Table 1. List of selected VIs to monitor plant drought stress.
Table 1. List of selected VIs to monitor plant drought stress.
Vegetation Indices Formula Reference
Normalized Difference Vegetation Index (NDVI) (R800 − R680)/ (R800 + R680) Tucker, 1979
Chlorophyll Index Green (Cl-green) NIR / Green -1 Gitelson et al., 2003
Renormalized Difference Vegetation Index (ReNDVI) R800 - R670 / (R800 + R670) ½ Sims and Gamon, 2002
MERIS Terrestrial Chlorophyll Index (MTCI) (R753-R708) / (R708 - R681) Haboudane et al., 2004
Red edge NDVI (RENDVI) (R705 – R740) / (R705 + R740) Tucker, 1979
Normalized Difference Vegetation Index (NDVI750) (R750 − R680) / (R750 + R680) Tucker, 1979
Modified Red Edge Simple Ratio Index (mRESR) (R750 - R445) / ( R750 + R445) Sims and Gamon, 2002
Photochemical Reflectance Index (PRI710) (R531 – R710) / (R531 + R710) Gamon et al, 1992
Photochemical Reflectance Index (PRI720) (R531 − R720) / (R531 + R720) Gamon et al, 1992
Structure insensitive pigment index (SIPI) (R800−R455) / (R800+R705) (Penuelas et al., 1995)
Pigment Specific Simple Ratio (PSSRa) R800 / R680 Blackburn, 1998
Reflectance Difference (RD) R800 - R680 Blackburn, 1998
Chlorophyll index red edge (CIred edge) (R750 - R700) / (R700) Podani and Czárán, 1997
Water band index (WBI) (R950 / R900 Xu et al., 2007
Transformed chlorophyll absorption in reflectance index (TCARI) 3X [(R705 - 665) - 0.2X (R705 - R560) X (R705 / R665)]) Haboudane et al., 2004
Optimized soil-adjusted vegetation index (OSAVI) ((1 + 0.16) * (R865 - R665) / (R865 - R665 + 0.16)) Rondeaux et al., 1996
Enhanced Vegetation Index (EVI) 2.5 × [(R800 − R680)/ (R800 + 6 × R680 − 7.5 × R450 + 1)] Buschmann and Nagel, 1993
Soil adjusted vegetation index (SAVI) ((1 + 0.5) X (R801 - R670) / (R801 + R670 + 0.5) Huete, 1988
Optimized Soil Adjusted Vegetation Index (OSAVI800) (1 + 0.16) (R800 + R670)/(R800 + R670 + 0.61) Rondeaux et al., 1996
Red-edge vegetation index (RSVI) (NIR/Red)-1 Huete, 1988
Improved SAVI with self-adjustment factor L (MSAVI) 0.5 × {2 × R800 + 1 −(2 × R800 + 1)2 − 8 × (R800 − R670)} Qi et al., 1994
Normalized Difference Infrared Index (NDII) (R780 − R710)/(R780 − R680) Datt, 1999
Normalized Difference Water Index (NDWI) (R560 − R830)/(R560 +R830) McFeeters, 1996
Difference Vegetation Index (DVI) R800 − R670 Perry and Lautenschlager, 1984
Vegetation Stress Ratio (VRS) R725 / R702 White et al., 2008
Table 2. Model parameters for tuning and training using random search CV.
Table 2. Model parameters for tuning and training using random search CV.
Model Parameters Range
DNN Hidden layers 1,2,3,4,5
Number of neurons 50, 100, 150, 200, 300
Activation function identity, logistics, tanh, ReLU
Weight optimization lbfgs, sgd, adam
Regularization penalty (α) 0.00001, 0.0001, 0.001, 0.01
Learning rate constant, adaptive, in scaling
Batch size 200, 300, 400, 500, 600, 700
Momentum for gradient descent update 0.9
Exponential decay rate (β) 0.9
SVM Kernel type rbf, poly, linear
Degree of the polynomial kernel 1, 2, 3
Regularization parameter (C) 0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000
Kernel coefficient (gamma) 0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000,
RF Number of trees 10, 30, 50, 70, 90, 110, 130, 150, 170, 190
Maximum depth of the tree 10, 20, 30, 40, 50, 60, 70, 80, 90, 100
Number of features for the best split sqrt (1 8 1), log2 (1 8 1), 181
Minimum samples for splitting 2, 5, 10
Bootstrap samples for building tree True, False
Table 3. The top 10 wavelengths selected by the different machine learning models.
Table 3. The top 10 wavelengths selected by the different machine learning models.
Selected Wavelengths (nm)
Rank Chi-Square ReliefF CFS RFE
1 555 680 669 553
2 554 689 674 557
3 556 949 939 669
4 553 722 936 674
5 557 683 957 722
6 552 674 949 940
7 636 940 671 957
8 673 670 547 636
9 674 669 546 683
10 672 957 542 542
Table 4. Performance metrics for RF, SVM and DNN models for identification of drought stress plants (metrics include Average Accuracy (AA), F1-score, Kappa score).
Table 4. Performance metrics for RF, SVM and DNN models for identification of drought stress plants (metrics include Average Accuracy (AA), F1-score, Kappa score).
Metrics
Features Model AA F-score Kappa
Known VIs RF 0.921 0.925 0.893
SVM 0.887 0.881 0.882
DNN 0.938 0.935 0.914
Proposed VIs RF 0.914 0.911 0.881
SVM 0.924 0.930 0.919
DNN 0.948 0.949 0.933
Combined VIs RF 0.983 0.984 0.965
SVM 0.981 0.982 0.975
DNN 0.977 0.979 0.969
PCA Features RF 0.961 0.962 0.960
SVM 0.941 0.940 0.921
DNN 0.901 0.900 0.868
Table 5. Performance of regression models for gs and Pn.
Table 5. Performance of regression models for gs and Pn.
Stomatal conductance (gs)
Metrics RFR SVR PR PLSR
R2 0.871 0.845 0.534 0.842
RMSE 0.035 0.038 0.221 0.031
MAE 0.015 0.011 0.142 0.017
Photosynthetic rate (Pn)
Metrics RFR SVR PR PLSR
R2 0.940 0.830 0.740 0.910
RMSE 0.015 0.063 0.144 0.018
MAE 0.004 0.013 0.127 0.007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated