Prerpints.org logo
Preprint
Article

A Study of Differential Topology on the Magnetically Induced Isotropically Averaged Lorentz Force Density of Few Simple MoleculesSupporting Information

Altmetrics

Downloads

82

Views

23

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.pdf (772.57KB )

Submitted:

16 July 2024

Posted:

17 July 2024

You are already at the latest version

Alerts
Abstract
Quantum chemical topology addresses the study of the chemical structure by applying the tools of differential topology to scalar and vector fields obtained by quantum mechanics. Here the magnetically induced isotropically averaged Lorentz force density has been computed and topologically analysed for 11 small molecules. Critical points (attractors, repellers and saddles) have been determined and trajectories connecting the attractors have been computed. It is shown that kinds and numbers of the critical points are rather transferable in similar molecules. CC bonds of different order are endowed with critical points of different kind close to their centre. The long range behaviour of the force allows understanding the value of the sum of topological indices of the isolated critical points.
Keywords: 
Subject: Chemistry and Materials Science  -   Theoretical Chemistry

1. Introduction

Quantum Chemical Topology (QCT), the field of research intending to study, via differential topology, scalar and vector fields which are useful to characterise molecules [1,2], has its origin in the work of Bader, who first showed that basic features of a chemical structure, i . e . atoms, bonds, faces and cages, can be associated to the occurrence of critical points (CPs) of the gradient of the electron density, i.e. the points where ∇ ρ = 0 [3,4]. While the location of maxima of the density turned out unexpected (non-nuclear maxima) only in few special though interesting cases [5,6,7], the possibility to identify the most relevant atomic interactions, the "chemical bonds", via a topological analysis, i.e. by assessing whether the maxima of the electron density of two atoms are connected by a trajectory passing through the so-called Bond Critical Point (BCP), has animated an amazingly long list of contributions in literature, as in the case, to cite just one of the many discussed systems, of the H-H bonding [8,9,10,11,12,13,14,15,16], which well testifies how much the chemical community is reluctant to any shift of paradigm on bonding. In the spirit of the original Atoms In Molecules (AIM) theory [3] the topological analysis of ∇ ρ is sufficient to extract a molecular graph, capturing the main elements of the molecule: the atoms and the bond paths linking a subset of atom pairs. Although the choice of density gradient as the field to unravel the chemical structure finds its physical justification in its homeomorphism with the virial field, i.e. the electronic potential energy density of an electron [17], and in the identification of density-driven bond paths as privileged exchange channels [18,19], different fields have also been used to that end [20]. We have recently studied the magnetically induced isotropically averaged Lorentz force density F [21], which offers a promising avenue to reveal the chemical electronic structure starting from the magnetic response.
In the present paper we are giving a thorough discussion of the topology of F in few simple molecules built from atoms of the first and second period, aiming at showing some of its features in the realm of QCT. The attractors of F occur in correspondence of both atoms and bonds, and thus their connection, as captured by trajectories passing through the saddles equivalent to the BCPs, can be expected to be more complicated than that of ∇ ρ , but likely similar to that obtained from the Laplacian of the density. The latter has been used to introduce L − graph [22], and, by analogy, we will here introduce F − graphs. The analysis will be enriched with a discussion on the count of critical points, whose topological indices should be bound by relations of the kind of the Poincaré-Hopf theorem.
The paper is organised as follows: after some basic information on the Lorentz force field (Section 2.1), an introduction to the needed items of differential topology (Section 2.2), and some computational details (Section 3), we will first present in Section 4 a systematic report of the topological features of F computed in prototypes of acyclic molecules (lithium hydride, methane, ethane, ethylene, acetylene, propyne and 3-borapropyne), aromatic, antiaromatic and non-aromatic molecules (benzene, planarized cyclooctateraene and borazine, respectively) and a cage molecule (cubane), and we will then discuss and resume the main finding in Section 5.

2. Theory

2.1. The Magnetically Induced Isotropically Averaged Lorentz Force Density

At second order in the external magnetic field B , the energy acquired by a freely tumbling isolated closed shell molecule is [23,24]
W = − 1 2 ξ i s o B 2
where the isotropically averaged magnetizability is obtained as one third of the trace of the magnetizability tensor, ξ i s o = 1 3 ( ξ x x + ξ y y + ξ z z ) , or more briefly, using here and in the following the Einstein convention of summing over repeated indices, ξ i s o = 1 3 ξ α α .
Magnetizability can be computed from the magnetizability density [25,26],
ξ iso = ∫ Ξ iso d 3 r ,
where [21]
Ξ iso = ϵ α β γ 6 ( r β − r 0 β ) J γ α ,
with ϵ α β γ the Levi-Civita symbol, r β a Cartesian displacement from an origin with Cartesian coordinates r 0 β , and J is the 3 × 3 current density tensor, which allows the computation of the magnetically induced first order current density via J B = J B . The magnetizability density depends on the arbitrary origin of the coordinates r 0 , so that it is not considered a useful tool for QCT. However, by manipulation of the magnetically induced energy [21],
W = − B 2 2 ∫ Ξ i s o d 3 r = − B 2 12 ∫ ϵ α β γ ( r β − r 0 β ) J γ α d 3 r
= − ∫ F β ( r β − r 0 β ) d 3 r ,
it can be realised that the isotropically averaged Lorentz force density
F β = B 2 12 ϵ β γ α J γ α ,
is an origin-independent vector (and not tensor) field amenable to QCT studies, like ∇ ρ . A positive or negative value of the Divergence of the Isotropically Averaged Lorentz force density (DIAL) indicates whether the local contribution to the magnetizability is positive or negative. The usefulness for the study of magnetic aromaticity of π -DIAL (the contributions of π electrons to DIAL) has been recently discussed [27].
Apart from a factor, DIAL, the divergence of 5, has been independently introduced in quantum chemistry by Barquera-Lozada, who called it tp J ( r ) [28].

2.2. Topological Analysis of the Critical Points

The critical points of a 3-dimensional vector field v can be classified according to their rank r and signature s as ( r , s ) [3], where r is the number of non-null eigenvalues of the Jacobian matrix at the critical point, and s = p − n is the difference between the number p of positive and the number n of negative real components of the eigenvalues of the Jacobian. The sign of the determinant of the Jacobian matrix at the critical point x * is known as its index: ind x * ( v ) = sign det J [ v ( x * ] = ( − 1 ) n [29]. In appropriate cases the sum of the indices of the critical points of a vector field must follow the Poincaré-Hopf theorem, which has been considered a check of consistency of the topological analysis [30].
Before discussing this constraint for our field F , we find it useful to introduce the Euler characteristic χ ( K ) of a CW-complex K, which is a collection of cells[31]. In our case it will be sufficient to consider 4 kinds of cells: 0-cells (isolated points in space), 1-cells (deformable lines connecting two 0-cells), 2-cells (the deformable 2-dimensional space contained within a closed loop of 1-cells) and 3-cells (the deformable 3-dimensional space contained between 2 or more 2-cells). The Euler characteristic of the CW-complex χ ( K ) can be obtained as the difference between even-dimensional cells and odd-dimensional cells:
χ ( K ) = ∑ k ( − 1 ) k c k = c 0 − c 1 + c 2 − c 3 ,
where c k is the number of k-cells. If the CW-complex is compact, it can be contracted to a single point and χ ( K ) = 1 . Contraction can be equally performed on a subset of cells of the CW-complex, while leaving the Euler characteristic unchanged. A sketch of contraction of 2 CW-complex, each of them compact, is given in Figure 1.
Eq. 6, which, for a single compact CW-complex, can be read as V − E + F − C = 1 , where V, E, F and C denote the number of vertices, edges, faces and cages, is consistent with the classical Euler equation V − E + F = 2 , proposed long ago for a convex polyhedron.
Coming back to the critical points of a 3-dimensional vector field, we will be interested only in full-rank CPs (those with r = 3 , and thus no null eigenvalue of the Jacobian) and Table 1 resumes their indices.
The four possible full-rank CPs, when ordered for decreasing number of negative eigenvalues, are ( 3 , − 3 ) , ( 3 , − 1 ) , ( 3 , 1 ) and ( 3 , 3 ) , and will occur in number n 3 , n 2 , n 1 , n 0 , respectively. In that order, the indices have alternating sign, so that, if the one-to-one correspondence given in column 5 of Table 1 occurs between the critical points of a given kind and the cells of a compact CW-complex ( n k = c k for each k), Eq.6 can be rewritten as
∑ k = 0 3 ind k ( v ) n k = 1 ,
which matches the 3-dimensional Poincaré-Hopf theorem,
∑ k = 0 3 ind k ( v ) n k = χ ( M ) ,
where χ ( M ) = 1 is the Euler characteristic of the compact 3-dimensional manifold where the vector field is computed. The Euler characteristic χ ( M ) is an invariant in differential topology, so that it only depends on the manifold M and not on the vector field. To understand how this statement can be compatible with a non-zero value of χ ( M ) , it is important to recall that, if the manifold M has a boundary ∂ M , the theorem holds provided that the vector field is everywhere outward oriented on the boundary [32]. For a vector field v that is everywhere inward-oriented on the boundary, the outward orientation can be recovered simply changing sign to the field, v ′ = − v , which implies a change of sign of the signature, of all indices, and therefore, for the one-to-one correspondence given in the last column of Table 1 ( n 3 − k = c k for each k),
∑ j = 0 3 ind j ( v ) n j = ∑ j = 0 3 ind 3 − j ( v ) n 3 − j = − ∑ k = 0 3 ind k ( v ′ ) c k = − 1 ,
which, considering that the Euler characteristic of a spherical surface is χ ( ∂ M ) = 2 , can be recognised as a special case of the equation for an inward-oriented field [33]
∑ k = 0 3 ind k ( v ) n k = χ ( M ) − χ ( ∂ M ) .
For a 3-manifold, χ ( M ) = 1 . However, if one intends considering the real coordinate space including points at infinity, one must consider the real projective space R P 3 , which can be thougth as a closed 3-dimensional ball with antipodal points identified, and has χ ( M ) = 0 . To get a zero in Eq. 8, it is necessary to sum also the asymptotic CPs: the n 3 a asymptotic attractors (with index ind 3 = − 1 , which are maxima if the vector field is a gradient) and the n 0 a asymptotic repellers (with index ind 0 = 1 , which are minima if the vector field is a gradient). Consistency with the alternative description of a 3-manifold with a boundary ∂ M , shows that if the field is everywhere inward/outward oriented on the boundary there is a single asymptotic repeller/attractor. In the general case, when the orientation of the vector field is changing over a boundary enclosing all isolated CPs, the sum of indices of the isolated CPs, Σ ind k n k can differ from χ ( M ) . It has been proposed, in a study of the molecular electrostatic potential (MEP), to deduce the number of asymptotic CPs by plotting the MEP on a spherical surface large enough to contain all isolated critical points, and counting the numbers of closed island-like regions of negative and positive values [30]. In our case, the vector field generally has ( 3 , − 3 ) CPs on the outer part of the molecule (an inward-directed field) and thus will have Σ ind k n k = − 1 . This should not hold when ( 3 , + 3 ) CPs occur on the outer part of the molecule.
Eq. 8, the celebrated Poincaré-Hopf theorem assumes that CPs are isolated, although generalization are possible [33]. In acetylene, we will find loops of degenerate ( 2 , s ) CPs. It has been proposed that similar cases should be dealt considering a symmetry-breaking and then considering the resulting isolated CPs [30]. Indeed, one feature of the indices is their stability, which means that small perturbation do not change the sum of the indices of close critical points. A loop of ( 2 , s ) CPs can always be thought as a loop of alternating ( 2 , s − 1 ) and ( 2 , s + 1 ) CPs having a null sum of indices.

3. Computational Methods

Optimised geometries and magnetically perturbed wavefunctions have been obtained using Gaussian 16 [34] and the BHandHLYP functional, recently assessed to perform well in calculation of magnetic properties [35], combined with the pcSseg-4 basis set [36]. Essential parameters of the optimised geometries are given in Table S1.
Critical points have been determined by the Newton-Raphson algorithm as implemented in SYSMOIC [37], starting from nuclei and then from points sampled out from a parallelepiped containing the molecule, with a step of 0.1 au, reduced to 0.05 au, for molecules with triple bonds, and checking that further reduction did did not increase thje number of CPs.
The CPs found are sometimes in disagreement with a previous calculation carried out with the smaller 6-31G(d) basis set [21]. We have checked that number and kind of critical points is stable upon basis set enlargement, by performing a calculation at the aug-pcSseg4 level for benzene, as well as adding additional basis functions on points that were missing in lower level calculations (Table S2). Calculation with additional basis set functions on the ( 3 , + 3 ) CPs above faces in benzene, borazine, cyclooctatetraene and cubane gave the same unaltered set of CPs. Considering the small size of the molecule studied, all calculations (both geometry optimisation and magnetic perturbation) have been carried out at the BHandHLYP/pcSseg-4 level.
The critical points are displayed according to the following convention: ( 3 , − 3 ) CPs are small red spheres, (3,+3) CPs are small blue spheres, ( 3 , ± 1 ) CPs (with distinguished eigenvalues) are displayed as three crossing segments going along the eigenvectors of the Jacobian, blue for positive eigenvalues, red for negative eigenvalues. In case of degenerate eigenvalues a circle is shown in the plane of the eigenvectors corresponding to the degenerate eigenvalues, with the same colour code convention: a blue circle for positive degenerate eigenvalues, a red circle for negative degenerate eigenvalues. Once the CPs have been found, we have computed trajectories moving out of the ( 3 , − 1 ) CPs along the single positive eigenvalue, to define what we call the F -graph. F -graphs are fairly rich 3-dimensional objects; they can be best appreciated moving them interactively, which is possible operating on the 3d files generated for all of them, using the the v3d code, freely distributed on the SYSMOIC website.

4. Results

We are going now to report the location and number of the CPs found for the molecules chosen. A summary of the results is given in Table 2. Lists of location and eigenvalues of the Jacobian at the CPs are given in the Supporting Information (Table S3).

4.1. Lithium Hydride

As a first example we show the F field for LiH. In this simple molecule the field has two attractors separated by a ( 3 , − 1 ) CP. The field is everywhere inward-oriented (on a boundary containing all isolated CPs) and the sum of indices is consistently equal to − 1 .

4.2. Methane

Figure 3 shows the 29 critical points of F for methane (their list is given in the Supporting Information). There are 5 ( 3 , − 3 ) attractors, 1 on the C atom and 4 on the C–H σ bonds. If connected by trajectories passing through the ( 3 , − 1 ) CPs, they form a tetrahedral shaped complete graph K 5 : every attractor is bound to any other one, and indeed the number of ( 3 , − 1 ) CPs is n 2 = 5 2 = 10 . The number of topologically triangular faces is also n 1 = 5 3 = 10 and a ( 3 , + 1 ) face critical point can be associated to each of them. Eventually, the n 0 = 4 ( 3 , + 3 ) CPs can be associated to tetrahedral cages formed by three H atoms and the central C atom. The sum of indices is − 1 as expected for an inward-oriented vector field, with a single repeller at infinity.
The complete graph K 5 is one of the two basic g t -nonplanar graphs, those that cannot be drawn on a sheet of paper without crossing of edges. g t -nonplanar graphs are unusual topologies in organic chemistry [38,39], when one considers standard bonding schemes, often compatible with the molecular graphs obtained from ∇ ρ . However, we see that even the simplest organic molecule, namely methane, shows a g t -nonplanar graph, when studied with the F field.

4.3. Ethane

Figure 3 shows the 57 critical points of F and the trajectories defining the F − graph for staggered ethane. All topological features are preserved in eclipsed ethane (see Supporting Information, Figure S1). The number of CPs is just one less than the sum of the CPs of two methane molecules: indeed one of the ( 3 , − 3 ) CPs is shared between the two methyl moieties. The methyl unit has thus a conservative pattern of CPs, much as reported for the Laplacian of the density [22]. The sum of indices equals -1, as expected for an inward-oriented vector field.

4.4. Ethylene

The F field for ethylene has 31 isolated CPs. 8 CPs are attractors of F : 2 on the C atoms, 4 on the C–H σ bonds and a pair above and below the molecular plane in correspondence with the double bond. As a consequence, in the middle of the C–C bond, rather than finding an attractor, we find a ( 3 , − 1 ) CP. In addition to these CPs, on each methylene moiety we find 5 ( 3 , − 1 ) , 4 ( 3 , + 1 ) and 2 ( 3 , + 3 ) CPs. The ( 3 , − 1 ) CPs are half of those found in the methyl moiety in ethane: The CH attractors are linked to the π -bond attractors from above and below (4 paths for each methylene); the ( 3 , − 1 ) CP close to the C attractor, in the HCH region, has paths going on either of the close CH attractors, separated by a single path that goes directly in the ( 3 , + 1 ) CP. The (3,+3) CPs appear between two topological triangles formed by the two π − bond attractors and either the CH-bond attractor or a ( 3 , + 1 ) CP located close to the C atom. The sum of indices is − 1 as expected for an inward-oriented vector field.

4.5. Acetylene

The F field of acetylene is not formed by isolated CPs only, but three circles of critical points appear: a circle of ( 2 , − 2 ) CPs in the middle of the molecule and two circles of (2,0) CPs close to the location of C atoms. Along the molecular axis 9 CPs are found: 4 ( 3 , − 3 ) CPs located on C atoms and on C–H bonds, a ( 3 , + 1 ) CP in the middle of the C–C bond, two (3,+3) CPs between the middle of the C–C bond and the C atoms, and two ( 3 , − 1 ) CPs between the C atoms and the attractors on C–H bonds. The latter ( 3 , − 1 ) CPs are only 0.097 au far apart from the ( 3 , − 3 ) CPs located on C atoms. Disregarding the continuous circles of CPs, the sum of indices is − 1 as in all previous molecules. It is to be noted that, as far as the change of the vector field is considered only along the molecular axis, the sequence of the 3 CPs ( 3 , + 3 ) − ( 3 , + 1 ) − ( 3 , + 3 ) is equivalent to a sequence ( 3 , − 1 ) − ( 3 , − 3 ) − ( 3 , − 1 ) which could have been expected for a σ bond.

4.6. Propyne

The F of propyne has 55 CPs. The insertion of the methyl has perturbed each of the three circles of rank-2 CPs of acetylene, producing two sets of three alternating CPs. In the case of the central circle of ( 2 , − 2 ) CPs, 3 ( 3 , − 3 ) points are generated alternating with ( 3 , − 1 ) CPs. In the case of the C-centred circles of ( 2 , 0 ) CPs, 3 ( 3 , − 1 ) CPs are formed alternating with 3 ( 3 , + 1 ) CPs. The sum of indices along each circle is zero. Excluding these 3 × 6 = 18 CPs, we have 37 CPs, just one less than the sum of the isolated CPs of acetylene and methyl: 9+29=38. Indeed, location and kind of CPs are very similar to those of the smaller molecules, and the ( 3 , − 3 ) on the C-Me bond is shared by the two moieties.

4.7. 3-Borapropyne

The F field of 3-borapropyne has 43 isolated CPs. 7 out of the 9 ( 3 , − 3 ) CPs occur close to atoms or to the centres of σ bonds. Two further attractors occur in the plane bisecting the HBH angle, in place of the circle of ( 2 , − 2 ) CPs found in acetylene. The ( 3 , + 3 ) repellers occur 3 around the B atom, 2 around the central C atom, and 1 close to the peripheral C atoms. Of the 15 ( 3 , − 1 ) CPs, 12 are out-of-plane (the 4 connecting the attractors on BH bonds and the B atom have 2 complex eigenvalues with negative real component) and the remaining 3 occur on the symmetry axis. No trajectory passing through a ( 3 , − 1 ) CP links directly the BH attractors. Of the 13 ( 3 , + 1 ) CPs, 7 can be associated to loops of alternating ( 3 , − 3 ) and ( 3 , − 1 ) CPs, 3 alternate with repellers close to the B atom, 2 alternate with repellers close to the central C atom, and 1 acts as a repeller of trajectories (not shown) originating from the ( 3 , + 3 ) CP close to the B atom along the bisector of the HBH angle.

4.8. Benzene

The F field of benzene has 99 CPs. The 18 ( 3 , − 3 ) CPs are located on C atoms, CH and CC bonds. Of the 14 ( 3 , + 3 ) CPs, 12 are close to the C atoms, located towards the inside and the outside of the ring, and 2 are above and below the ring. The 36 ( 3 , − 1 ) CPs come from 6 sextets around the C atom. Each sextet, in turn, is composed by two triplets of CPs placed symmetrically above and below the ring. The 3 symmetry-unique ( 3 , − 1 ) CPs all occur in the plane of symmetry containing two opposing CH bonds, one very close to the C atom, one at some distance from the centre of the CH bond and one inside the ring, at an height of 0.952 bohr, close to the height traditionally chosen to display maps of the π current density [37,40]. Notably, along the CH bond, we do not find a ( 3 , − 1 ) CP, but the two attractors are separated by a ( 3 , + 3 ) CP. The 4 symmetry-unique CPs out of the 31 ( 3 , + 1 ) CPs occur one in the middle of the ring, one in the CH bond direction inside the ring, and two flanking the CH bond on either side. The sum of indices is +1. This can be understood in terms of presence of a repeller and two attractors at infinity, according to Leboeuf et al. Indeed the map of the flux of F out of a spherical surface shows two zones of positive values, compatible with the presence of two asymptotic attractors (see Supporting Information, Figure S2).

4.9. Cyclooctatetraene

The F field of planarised cyclooctatetraene has 123 CPs, with 28 ( 3 , − 3 ) CPs, occurring on atoms on CH and long CC bonds, and in pairs above and below the middle of short CC bonds. The trajectories following the eigenvector corresponding to the positive eigenvalue of the 44 ( 3 , − 1 ) CPs connect the C atom attractor with the CC long bond attractor, the two π -bond attractors, the CH-bond attractor with the adjacent CC bond and π -bond attractors. The trajectories passing through the CH-bond attractor form topological triangles or squares each associated with a ( 3 , + 1 ) CP. Of the remaining 17 ( 3 , + 1 ) CPs, 16 occur in pairs close to the C atom, alternating with an equal number of ( 3 , + 3 ) CPs (much alike the case of benzene, although with less symmetry), and 1 in the ring centre separating two ( 3 , + 3 ) CPs located above and below the ring. The sum of indices is +1. This can be understood in terms of presence of a repeller and two attractors at infinity, according to Leboeuf et al. Indeed the map of the flux of F shows two zones of positive values, compatible with the presence of two asymptotic attractors (see Supporting Information, Figure S2).

4.10. Borazine

The F field of borazine has 129 isolated CPs. The 24 attractors are located on N and B atoms, on BH and NH bonds (closer to the more electronegative atom), and in pairs, above and below the BN bonds, shifted towards the more electronegative N atom. Around B and N atoms there are 2 and 3 ( 3 , + 3 ) repellers, respectively, and other 2 repellers occur above and below the ring as in benzene and cyclooctatetraene. The 48 ( 3 , − 1 ) CPs are 1 for each of the 6 close pairs of π CN bonds attractors, 8 around each N atom and 6 around each B atom. Both atoms have 2 ( 3 , − 1 ) CPs above and below them, shifted towards the inside of the ring in case of B atoms; through any of these CPs a trajectory passes linking two up or down pairs of π attractors. The pair of π -linking trajectories are slightly on the outside of the ring for N atoms, and in the inside for B atoms. The inside location of the B trajectories is reminiscent of those of benzene. A second difference between B and N atoms is that, for the B atoms, 4 CPs occur on the sides of the BH bond and hold 4 trajectories linking the BH attractor to the π attractors, while for the N atoms 2 CPs occur in the vertical plane containing the NH bond; from these CPs trajectories are also found towards the π maxima, but they do so after being scattered away by the ( 3 , − 1 ) CP located above the N atom. The latter ( 3 , − 1 ) CP works as a scatterer towards the π attractors also for the trajectories starting from the C and N nuclear attractors. The 40 ( 3 , + 1 ) CPs occur 1 at the ring centre, 2 and 3 alternating with repellers close to N and B atoms, respectively, and then 3 and 5 around the trajectories of the F field clustering around B and N atoms and forming topologically square pyramids, one squeezed (for N atoms).

4.11. Cubane

The F field of cubane has 137 CPs. The 28 ( 3 , − 3 ) attractors correspond to the 8 C nuclei and the 20 σ bonds. Notably the ( 3 , − 3 ) CPs of C–C bonds are shifted towards the outer part of the cube, much as happens for the bond paths obtained from ∇ ρ [41]. 23 ( 3 , + 3 ) CPs are found: 6 above the faces, 1 in the middle of the cube and, 2 for each C atom, along the diagonal of the cube, one towards the exterior and one towards the interior. The 48 ( 3 , − 1 ) CPs are 8 symmetry-equivalent sextets located around C atoms. The distortion of the valence angles from the tetrahedral values is associated with reduction of the number of CPs, if one compares them with the 10 ( 3 , − 1 ) CPs of methane. The 5 attractors close to a C atom, if considered as graph vertices, do not form any more a complete graph using ( 3 , − 1 ) CPs as edges: the central attractor on the C atom is connected via ( 3 , − 1 ) CPs to only the three attractors on the C-C bonds but it is connected to the ( 3 , − 1 ) CH-attractor via a ( 3 , + 3 ) CP. The CH-attractor is connected to the CC-attractors, but there are no ( 3 , + 1 ) CPs on the topological triangle formed by two CC-attractors and the CH-attractor. Each of the 4 = 4 3 topological triangles formed of by the C atom and the 3 CC-attractors is associated with a ( 3 , + 1 ) CP. 6 More ( 3 , + 1 ) CPs occur on the faces of the cube; they can be thought as the result of the disappearance of the ( 3 , + 1 ) CPs on the topological triangles CH-CC-CC upon joining the 8 CH units forming the molecule. The sum of indices is +5, which can be understood, in terms of the algorithm proposed by Leboeuf in terms of 6 positive zones inside an overall negative zone on the sphere (Figure 9).

5. Discussion

The molecules studied in this paper give some insight on the capability of the isotropically averaged Lorentz force density F to contribute in the study of the molecular electronic structure.
As a first point, we note that the attractors of F tend to be greater in number than the attractors of ∇ ρ , where their number corresponds to the number of nuclei (apart from the seldom observed non-nuclear maxima). In the case of F , the attractors correspond to both nuclei and bonds. In effect, attractors are found very close to H nuclei, only for the ionic Li–H bond, while for B–H, C–H and N–H bonds the attractors are somewhere along the bonds, closer to the more electronegative atom. In all cases where the electronic structure can be described by core 1 s electrons pairs and σ bonds, the total number of attractors n 3 equals the number of electron pairs (see Table 1). This holds true also for ethylene and cyclooctatetraene, but not for benzene and borazine, showing less (18 vs 21) and more (24 vs 21) CPs than the stoichiometric electron pairs. The case of the triple bond also deserves attention. In acetylene the number of attractors n 3 is 3 less than the number of stoichiometric electron pairs, which hints at the missing triple bond. Then, in propyne, n 3 matches the number of stoichiometric electron pairs, but in 3-borapropyne n 3 is 1 less than the number of stoichiometric electron pairs. To summarise, although a one-to-one correspondence between electron pairs and attractors holds for saturated molecules, it fails in most cases where bonding can be expected to develop far off of the lines joining the nuclei.
We find most interesting that C–C bonds of different order are not characterised by the same ( 3 , − 3 ) CP as for ∇ ρ : only for σ bonds, we find a single ( 3 , − 3 ) attractor, while for the double bond of ethylene we find a ( 3 , − 1 ) saddle flanked by two close attractors, for the triple bond of acetylene we find a ( 3 , + 1 ) saddle surrounded by a circle of ( 2 , − 2 ) CPs. Notably, in propyne, the circle of ( 2 , − 2 ) CPs splits in 3 attractors and 3 saddles, while the ( 3 , + 1 ) CP is preserved. The appearance of three ( 3 , − 3 ) CPs is a feature of the symmetry of the molecule, as exemplified by the a d h o c studied C 2 v BH2−CCH molecule, where only two ( 3 , − 3 ) CPs are found. However, the ( 3 , + 1 ) CPs in the middle of the bond remains, indicating that it is a characteristic feature of the triple bond. The correspondence between bond orders and number and kind of attractors seems preserved to some extent. In cyclooctatetraene, long and short bonds are associated with 1 and 2 attractors, respectively. For the partial bond orders of benzene we found a single attractor. We note that the possibility to reveal different orders of chemical bonds has been very early noted in QCT, in studies of the electron localisation function [42] and the Laplacian of the density [22]. To our knowledge, this is the first time that this possibility is highlighted in terms of the magnetic response.
As a second point, when one considers the critical points close to an atom, a certain degree of transferability can be observed, as previously observed for the Laplacian [22]. Indeed, location and kinds of CPs in ethane and the methyl group of propyne are almost coincident with those of methane. Some transferability is also observed among the critical point found close to the CH2 group of ethylene and the CH groups of benzene and cyclooctatetraene. Differences are observed instead in the trajectories connecting the attractors on the ring bonds: in benzene these trajectories are shifted towards the inside of the ring, while in cyclooctatetraene they are shifted towards the outside. Notably, in borazine these trajectories are shifted alternatively inside and outside. This hybrid behaviour is well compatible with the main characterisation of borazine as a non-aromatic molecule [43], although the different dimensions of the domains of N-centred and B-centred trajectories could well be compatible with some weak aromaticity, which, using ring current strength was proposed several years ago [44] and recently rediscovered, and enriched with considerations based on excited state currents [45].
As a last point, we notice that for the 4 molecules studied, endowed with a ring structure, the F field turns out not everywhere inward-oriented like ∇ ρ , but lines of positive (outward) flux of the force have been found above and below all rings. In this case, the straightforward expectation of a sum of topological indices equal to -1 is not valid. An adaptation of the algorithm proposed by Leboeuf [30] of counting islands of positive and negative flux of the vector over a sphere surrounding the molecule allows in these 4 cases to justify the sum of indices. We find it noteworthy that closed-shell diamagnetic molecules can have at large distance narrow spherical angles where the local magnetic response is paramagnetic.
We are confident that further studies on the F field will be useful in the study of molecular electronic structure from the QCT perspective.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Author Contributions

writing—original draft preparation, and funding acquisition, G.M.; all authors have equally contributed to data curation, software development and investigation, and have read and agreed to the published version of the manuscript.

Funding

This research was funded by MUR, grant number FARB 2022 and FARB 2023.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Acknowledgments

Discussion with Prof. S. Blatt and enlightening correspondence with Prof. A. Hatcher is gratefully acknowledged.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
BCP Bond Critical Point
CP Critical Point
DIAL Divergence of the Isotropically Averaged Lorentz force density
QCT Quantum Chemical Topology

References

  1. Popelier, P.L.A. The QTAIM Perspective of Chemical Bonding. In The Chemical Bond; Wiley-VCH Verlag GmbH & Co. KGaA, 2014; pp. 271–308. [CrossRef]
  2. Popelier, P.L.A. On Quantum Chemical Topology. In Applications of Topological Methods in Molecular Chemistry; Springer International Publishing, 2016; pp. 23–52. [CrossRef]
  3. Bader, R.F.W. Atoms in Molecules: A Quantum Theory (International Series of Monographs on Chemistry); Clarendon Press, 1994.
  4. Matta, C.F.; Boyd, R.J. (Eds.) The quantum theory of atoms in molecules: from solid state to DNA and drug design; WILEY-VCH: Weinheim, 2007. [Google Scholar]
  5. Cao, W.; Gatti, C.; MacDougall, P.; Bader, R. On the Presence of Non-Nuclear Attractors in the Charge Distributions of Li and Na Clusters. Chem Phys Lett 1987, 141, 380–385. [Google Scholar] [CrossRef]
  6. Madsen, G.K.H.; Gatti, C.; Iversen, B.B.; Damjanovic, L.; Stucky, G.D.; Srdanov, V.I. F center in sodium electrosodalite as a physical manifestation of a non-nuclear attractor in the electron density. Phys. Rev. B 1999, 59, 12359–12369. [Google Scholar] [CrossRef]
  7. Pendás, A.M.; Blanco, M.A.; Costales, A.; Sánchez, P.M.; Luaña, V. Non-nuclear Maxima of the Electron Density. Phys. Rev. Lett. 1999, 83, 1930–1933. [Google Scholar] [CrossRef]
  8. Matta, C.F.; Hernández-Trujillo, J.; Tang, T.H.; Bader, R.F. Hydrogen-Hydrogen Bonding: A Stabilizing Interaction in Molecules and Crystals. Chem. Eur. J. 2003, 9, 1940–1951. [Google Scholar] [CrossRef] [PubMed]
  9. Poater, J.; Solà, M.; Bickelhaupt, F.M. Hydrogen-Hydrogen Bonding in Planar Biphenyl, Predicted by Atoms-In-Molecules Theory, Does Not Exist. Chem. Eur. J. 2006, 12, 2889–2895. [Google Scholar] [CrossRef]
  10. Grimme, S.; Mück-Lichtenfeld, C.; Erker, G.; Kehr, G.; Wang, H.; Beckers, H.; Willner, H. When Do Interacting Atoms Form a Chemical Bond? Spectroscopic Measurements and Theoretical Analyses of Dideuteriophenanthrene. Angew. Chem. Int. Ed. 2009, 48, 2592–2595. [Google Scholar] [CrossRef]
  11. Bader, R.F.W. Bond Paths Are Not Chemical Bonds. J. Phys. Chem. A 2009, 113, 10391–10396. [Google Scholar] [CrossRef]
  12. Cukrowski, I.; de Lange, J.H.; Adeyinka, A.S.; Mangondo, P. Evaluating common QTAIM and NCI interpretations of the electron density concentration through IQA interaction energies and 1D cross-sections of the electron and deformation density distributions. Comput Theor Chem 2014, 0000. [Google Scholar] [CrossRef]
  13. Della Porta, P.; Zanasi, R.; Monaco, G. Hydrogen-Hydrogen Bonding: The Current Density Perspective. J Comput Chem, 36, 707–716. [CrossRef]
  14. Popelier, P.L.A.; Maxwell, P.I.; Thacker, J.C.R.; Alkorta, I. A relative energy gradient (REG) study of the planar and perpendicular torsional energy barriers in biphenyl. Theor Chem Acc 2019, 138, 12. [Google Scholar] [CrossRef]
  15. Laplaza, R.; Boto, R.A.; Contreras-García, J.; Montero-Campillo, M.M. Steric Clash in Real Space: Biphenyl Revisited. Phys. Chem. Chem. Phys. 2020, 22, 21251–21256. [Google Scholar] [CrossRef]
  16. Landeros-Rivera, B.; Hernández-Trujillo, J. Control of Molecular Conformation and Crystal Packing of Biphenyl Derivatives. ChemPlusChem 2022, 87. [Google Scholar] [CrossRef] [PubMed]
  17. Keith, T.A.; Bader, R.F.W.; Aray, Y. Structural homeomorphism between the electron density and the virial field. Int. J. Quantum Chem. 1996, 57, 183–198. [Google Scholar] [CrossRef]
  18. Bader, R.F.W. A Bond Path: A Universal Indicator of Bonded Interactions. J. Phys. Chem. A 1998, 102, 7314–7323. [Google Scholar] [CrossRef]
  19. Pendás, A.; Francisco, E.; Blanco, M.; Gatti, C. Bond Paths as Privileged Exchange Channels. Chem. Eur. J. 2007, 13, 9362–9371. [Google Scholar] [CrossRef] [PubMed]
  20. Martín Pendás, A.; Francisco, E.; Gallo Bueno, A.; Guevara Vela, J.M.; Costales, A. Emergent Scalar and Vector Fields in Quantum Chemical Topology. In Applications of Topological Methods in Molecular Chemistry; Chauvin, R., Lepetit, C., Silvi, B., Alikhani, E., Eds.; Springer International Publishing: Cham, 2016. [Google Scholar] [CrossRef]
  21. Monaco, G.; Zanasi, R. The Molecular Electronic Structure Revealed by the Magnetically Induced Lorentz Force Density. J. Chem. Phys., 153, 104–114. [CrossRef]
  22. Popelier, P.L.A.; Burke, J.; Malcolm, N.O.J. Functional Groups Expressed as Graphs Extracted from the Laplacian of the Electron Density. Int J Quantum Chem 2003, 92, 326–336. [Google Scholar] [CrossRef]
  23. Lazzeretti, P. Handbook of Molecular Physics and Quantum Chemistry, Wilson, S., Ed. John Wiley & Sons, Ltd.: Chichester, 2003. [Google Scholar]
  24. Sauer, S.P.A. Molecular electromagnetism: a computational chemistry approach; Oxford graduate texts, Oxford University Press: Oxford ; New York, 2011. OCLC: ocn753655526.
  25. Jameson, C.J.; Buckingham, A.D. Molecular Electronic Property Density Functions: The Nuclear Magnetic Shielding Density. J. Chem. Phys. 1980, 73, 5684. [Google Scholar] [CrossRef]
  26. Monaco, G.; Zanasi, R. Magnetically Induced Current Density Spatial Domains. J. Phys. Chem. A 2019, 123, 1558–1569. [Google Scholar] [CrossRef] [PubMed]
  27. Monaco, G.; Summa, F.F.; Zanasi, R.; Lazzeretti, P. Electronic Current Density Induced by UniformMagnetic Fields in Clarenes. Chemistry – A European Journal 2024, e202401167. [Google Scholar] [CrossRef]
  28. Barquera-Lozada, J.E. Vorticity: Simplifying the Analysis of the Current Density. J Comput Chem 2019, 40, 2602–2610. [Google Scholar] [CrossRef]
  29. Tricoche, X.; Garth, C. Topological Methods for Visualizing Vortical Flows. In Mathematical Foundations of Scientific Visualization, Computer Graphics, and Massive Data Exploration; Möller, T., Hamann, B., Russell, R.D., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2009; pp. 89–107. [Google Scholar] [CrossRef]
  30. Leboeuf, M.; Köster, A.M.; Jug, K.; Salahub, D.R. Topological analysis of the molecular electrostatic potential. J. Chem. Phys. 1999, 111, 4893–4905. [Google Scholar] [CrossRef]
  31. Hatcher, A. Algebraic topology, 14th printing 2015 ed.; Cambridge University Press: Cambridge, 2015. [Google Scholar]
  32. Milnor, J.W.; Weaver, D.W. Topology from the Differentiable Viewpoint, rev. ed ed.; Princeton Landmarks in Mathematics and Physics, Princeton university press: Princeton (N. J.), 1997. [Google Scholar]
  33. Brasselet, J.P.; Seade, J.; Suwa, T. Vector fields on singular varieties; Number 1987 in Lecture notes in mathematics, Springer: Heidelberg London, 2009. [Google Scholar]
  34. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01, 2016. Gaussian Inc. Wallingford CT.
  35. Summa, F.F.; Monaco, G.; Lazzeretti, P.; Zanasi, R. Assessment of the Performance of DFT Functionals in the Fulfillment of Off-Diagonal Hypervirial Relationships. Phys Chem Chem Phys, p. 10.1039/D1CP01298C. [CrossRef]
  36. Jensen, F. Segmented Contracted Basis Sets Optimized for Nuclear Magnetic Shielding. J. Chem. Theory Comput. 2015, 11, 132–138. [Google Scholar] [CrossRef] [PubMed]
  37. Monaco, G.; Summa, F.F.; Zanasi, R. Program Package for the Calculation of Origin-Independent Electron Current Density and Derived Magnetic Properties in Molecular Systems. J. Chem. Inf. Model., 61, 270–283. [CrossRef]
  38. Kuck, D.; Schuster, A. Centrohexaindan, The First Hydrocarbon with Topologically Non-Planar Molecular Structure. Angew. Chem. Int. Ed. Engl. 1988, 27, 1192–1194. [Google Scholar] [CrossRef]
  39. Rücker, C.; Meringer, M. How Many Organic Compounds Are Graph–Theoretically Nonplanar? MATCH Communications in Mathematical and in Computer Chemistry 2002, 45, 153–172. [Google Scholar]
  40. Zanasi, R.; Fowler, P. Ring Currents and Magnetisability in C60. Chem Phys Lett 1995, 238, 270–280. [Google Scholar] [CrossRef]
  41. Matta, C.F.; Boyd, R.J. An Introduction to the Quantum Theory of Atoms in Molecules. In The Quantum Theory of Atoms in Molecules, 1 ed.; Matta, C.F.; Boyd, R.J., Eds.; Wiley, 2007; pp. 1–34. [CrossRef]
  42. Silvi, B.; Savin, A. Classification of Chemical Bonds Based on Topological Analysis of Electron Localization Functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
  43. Soncini, A.; Fowler, P.W.; Jenneskens, L.W. Angular Momentum and Spectral Decomposition of Ring Currents: Aromaticity and the Annulene Model. In Intermolecular Forces and Clusters I; Wales, D.J., Ed.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2005. [Google Scholar] [CrossRef]
  44. Monaco, G.; Zanasi, R.; Pelloni, S.; Lazzeretti, P. Relative Weights of σ and π Ring Currents in a Few Simple Monocycles. J Chem Theory Comput, 6, 3343–3351. [CrossRef]
  45. Báez-Grez, R.; Pino-Rios, R. The Hidden Aromaticity in Borazine. RSC Adv. 2022, 12, 7906–7910. [Google Scholar] [CrossRef]
Preprints 112355 g001
Figure 1. The Euler characteristic of two disconnected CW-complexes is invariant upon contraction of CW-the complexes.
Figure 1. The Euler characteristic of two disconnected CW-complexes is invariant upon contraction of CW-the complexes.
Preprints 112355 g001
Preprints 112355 g002
Figure 2. The field F plotted on a plane containing the LiH bond. The critical points are displayed according to the convention given in the Computational Methods section.
Figure 2. The field F plotted on a plane containing the LiH bond. The critical points are displayed according to the convention given in the Computational Methods section.
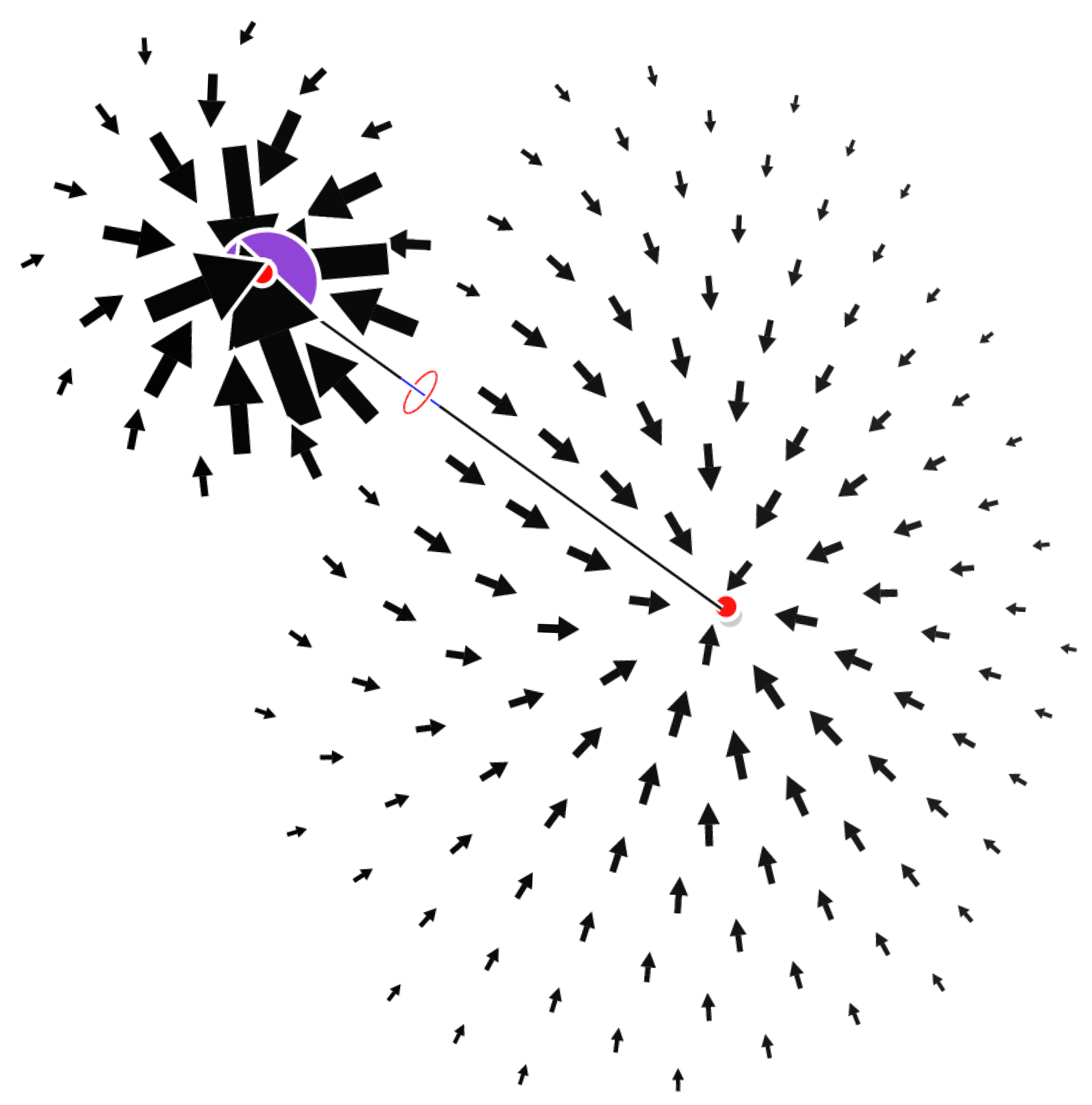
Preprints 112355 g002
Preprints 112355 g003
Figure 3. Critical points of F and trajectories defining the F − graph for methane (left) and staggered ethane (right). Please see the Computational Methods section for graphical conventions.
Figure 3. Critical points of F and trajectories defining the F − graph for methane (left) and staggered ethane (right). Please see the Computational Methods section for graphical conventions.
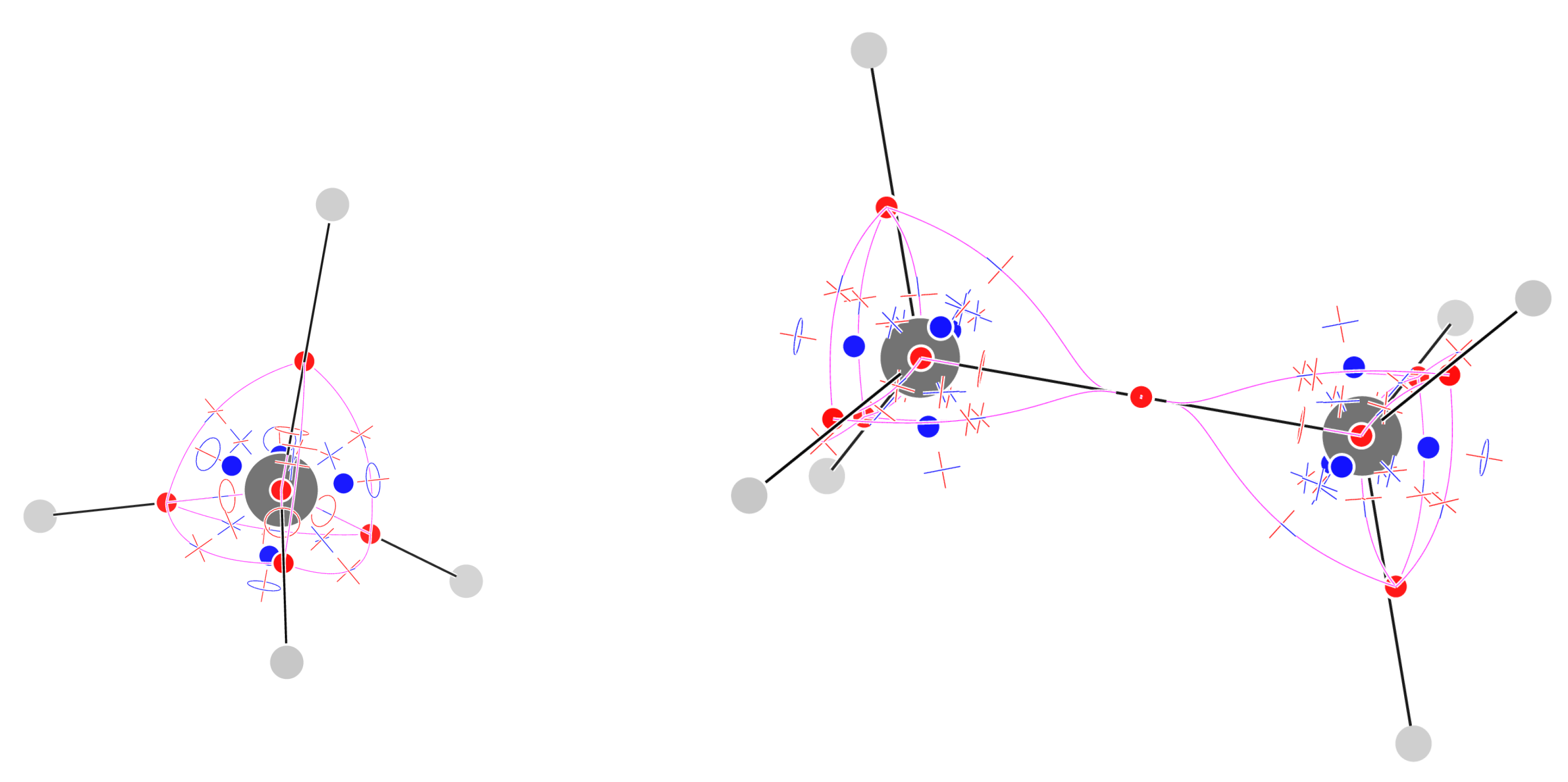
Preprints 112355 g003
Preprints 112355 g004
Figure 4. Critical points of F and trajectories defining the F − graph for ethylene.
Figure 4. Critical points of F and trajectories defining the F − graph for ethylene.
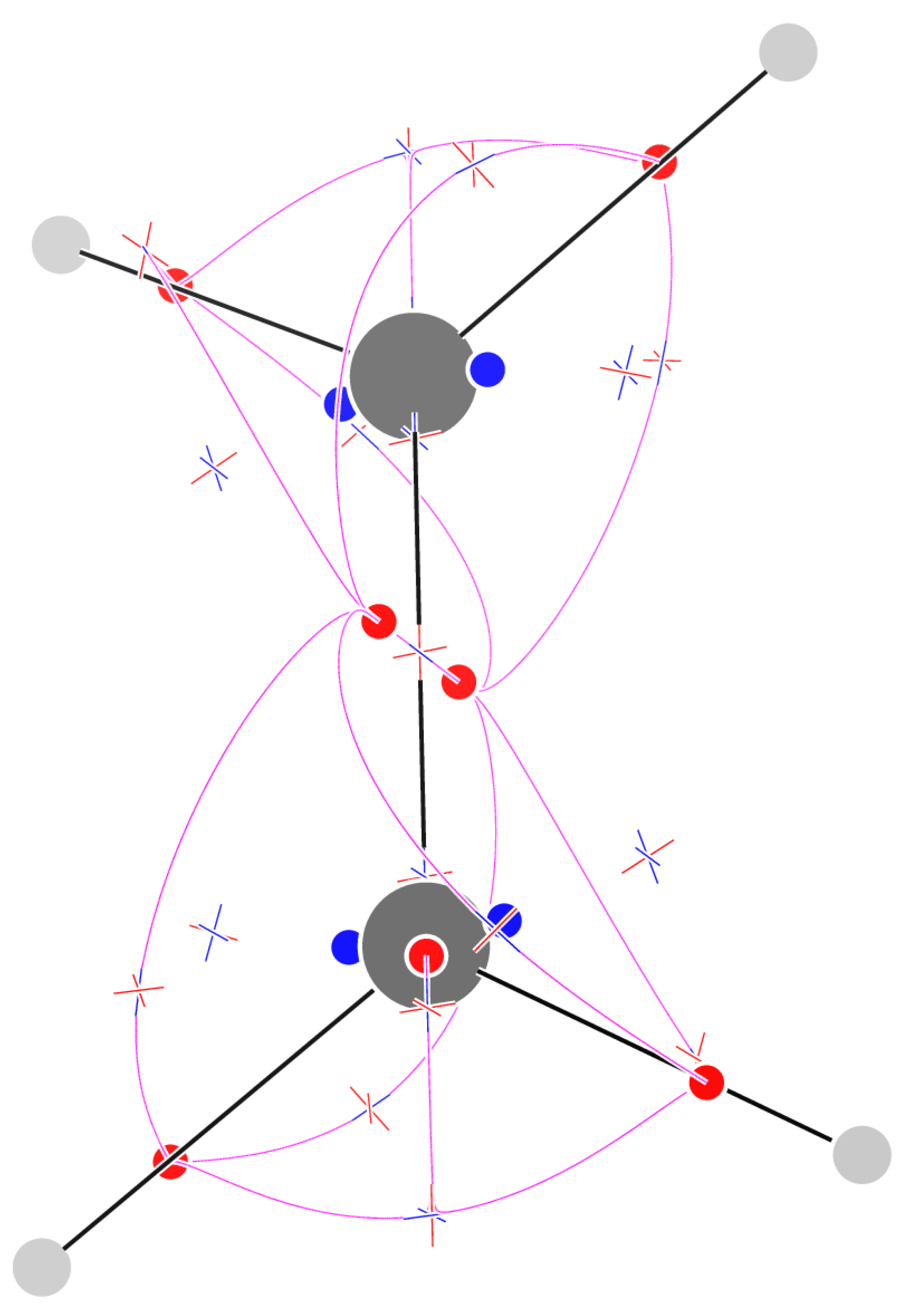
Preprints 112355 g004
Preprints 112355 g005
Figure 5. Critical points of F for acetylene. On the right only the 9 critical points along the molecular axis are shown, and the grey spheres centred on C and H nuclei have been scaled down.
Figure 5. Critical points of F for acetylene. On the right only the 9 critical points along the molecular axis are shown, and the grey spheres centred on C and H nuclei have been scaled down.
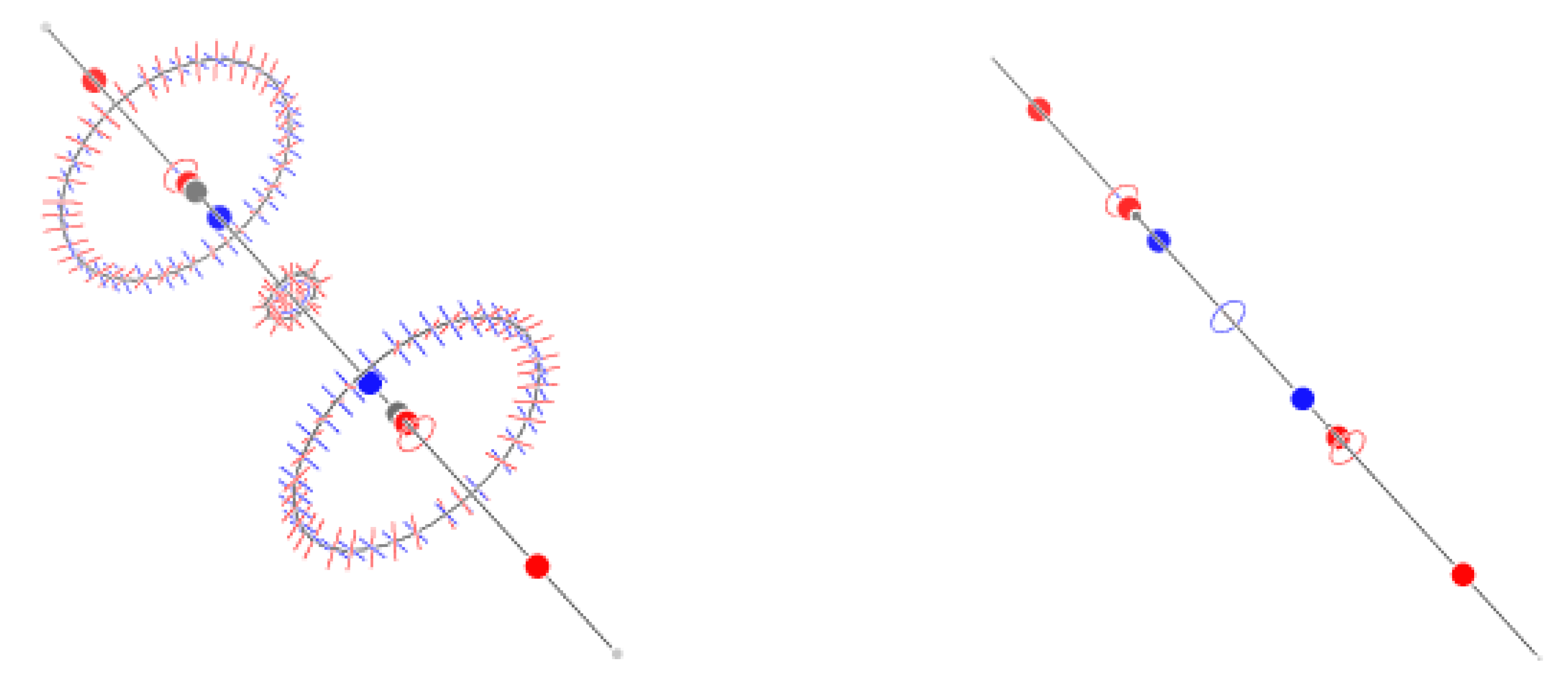
Preprints 112355 g005
Preprints 112355 g006
Figure 6. Critical points of F and trajectories defining the F − graph for propyne (left) and 3-borapropyne (right).
Figure 6. Critical points of F and trajectories defining the F − graph for propyne (left) and 3-borapropyne (right).
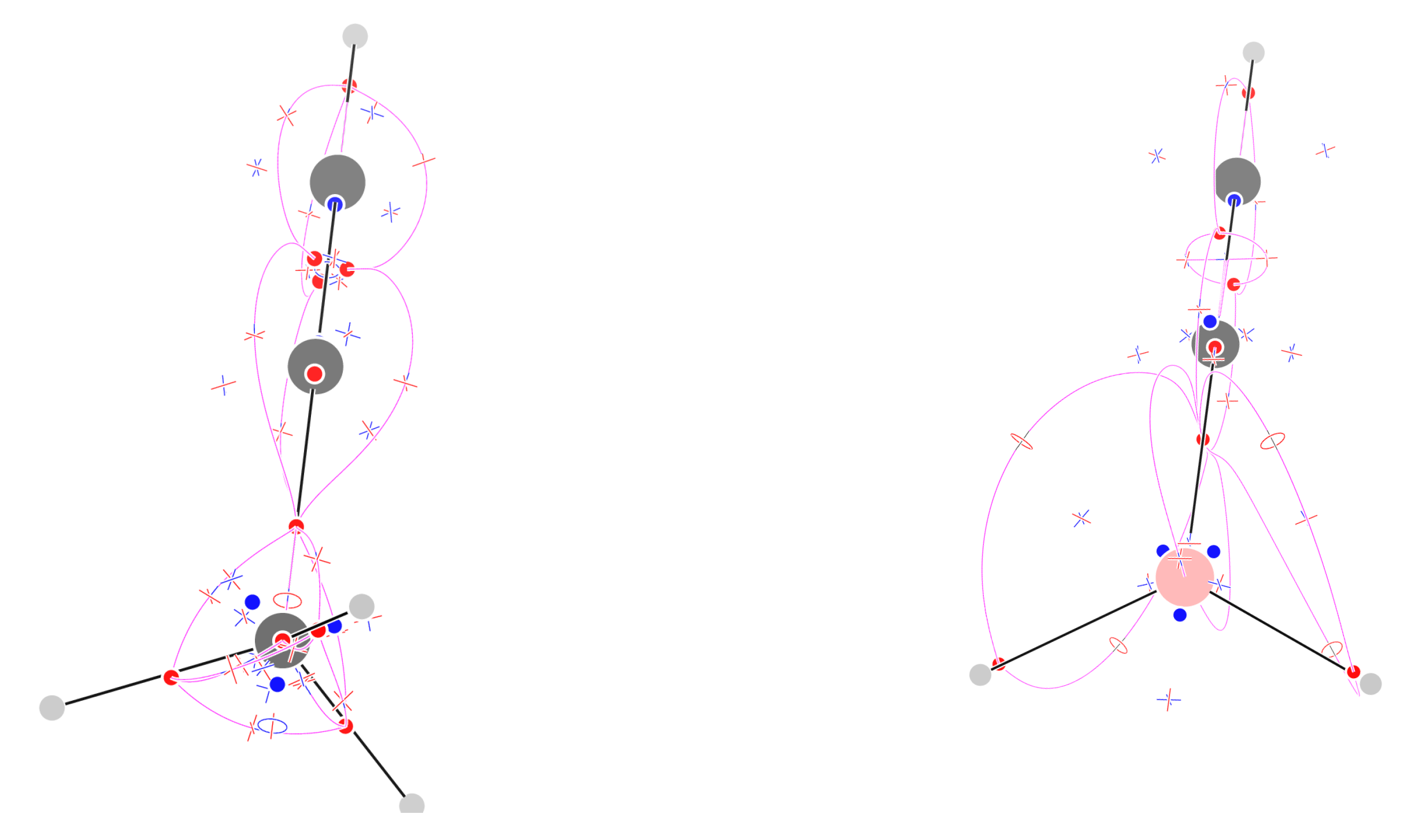
Preprints 112355 g006
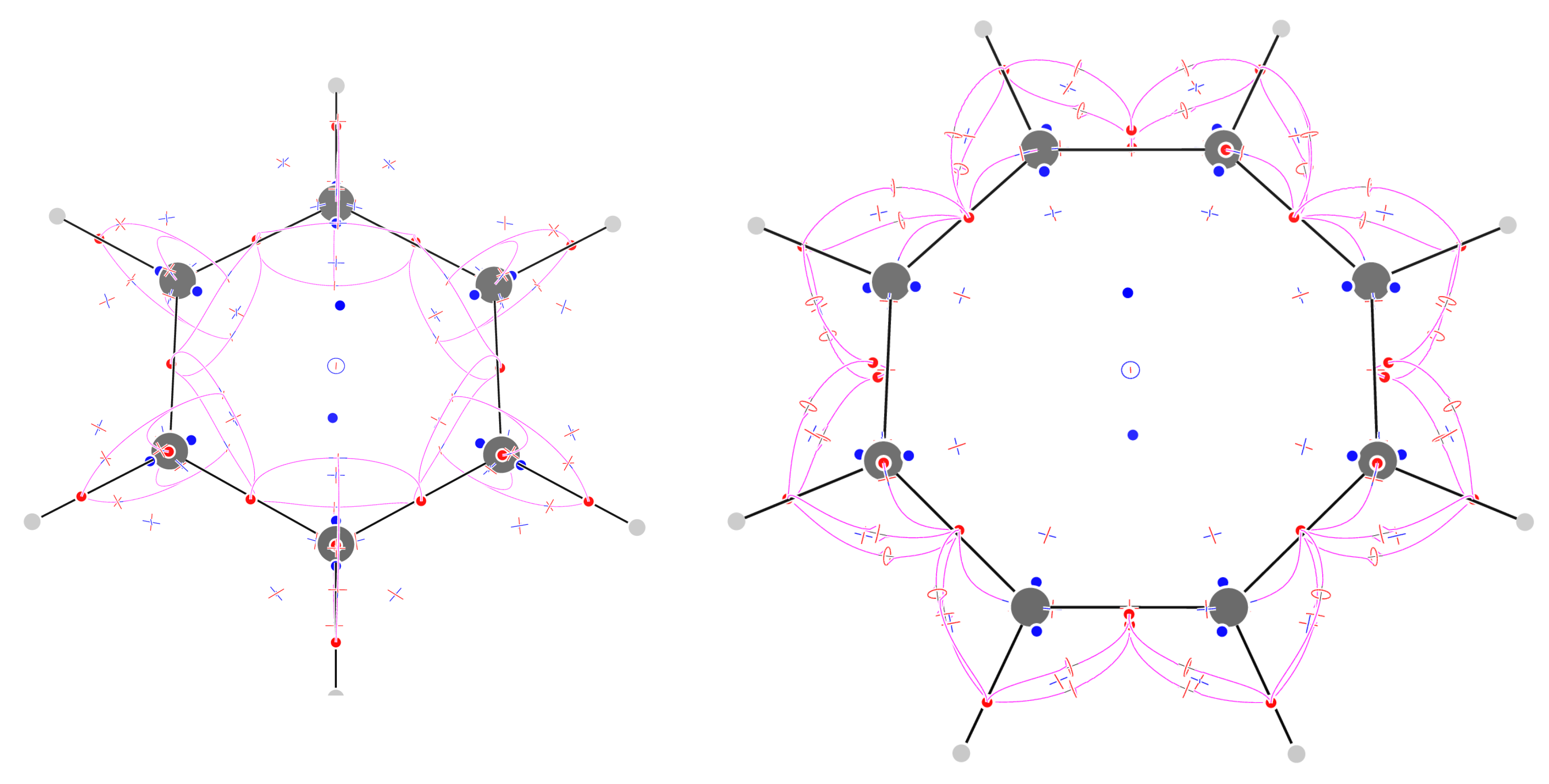
Preprints 112355 g007
Figure 7. Critical points of F and trajectories defining the F − graph for benzene (left) and cyclooctatetraene (right).
Figure 7. Critical points of F and trajectories defining the F − graph for benzene (left) and cyclooctatetraene (right).
Preprints 112355 g007
Preprints 112355 g008
Figure 8. Critical points of F trajectories defining the F -graph for borazine
Figure 8. Critical points of F trajectories defining the F -graph for borazine
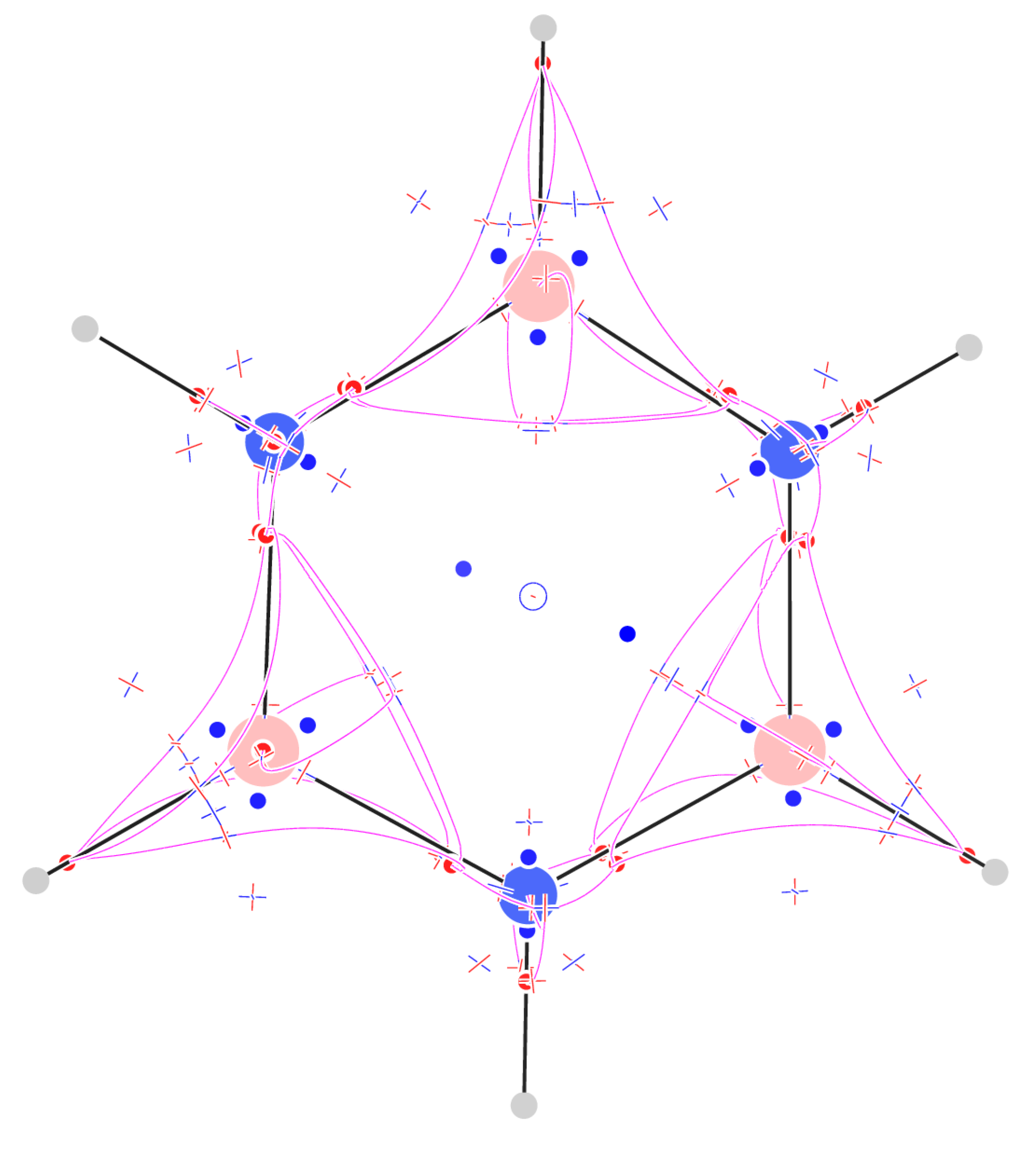
Preprints 112355 g008
Preprints 112355 g009
Figure 9. Critical points of F trajectories defining the F -graph for cubane (left); a sphere at a radius of 5 au with value of positive and negative flux of F represented as red and blue dots, respectively.
Figure 9. Critical points of F trajectories defining the F -graph for cubane (left); a sphere at a radius of 5 au with value of positive and negative flux of F represented as red and blue dots, respectively.
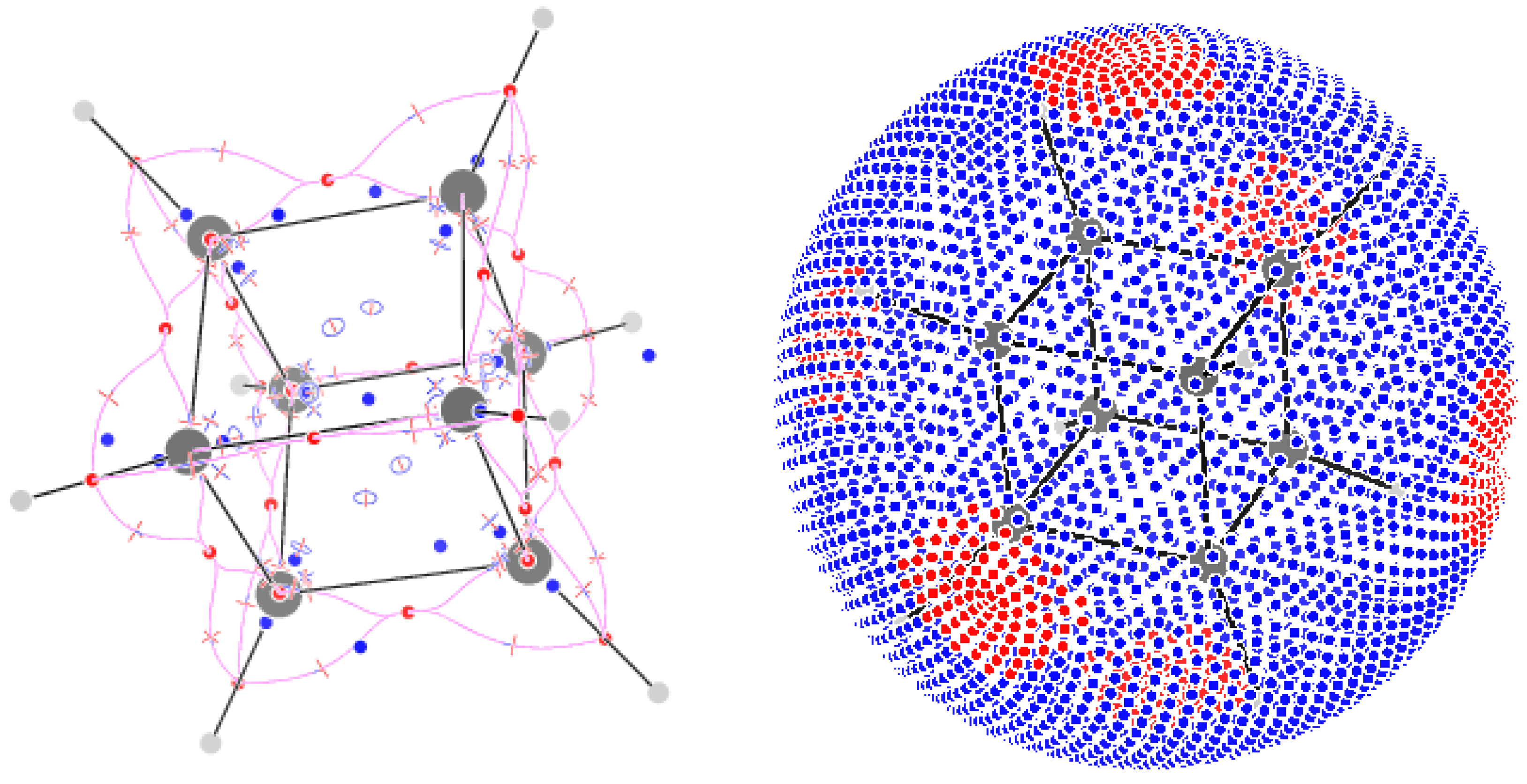
Preprints 112355 g009
Table 1. Critical points considered in this paper, and two possible one-to-one correspondences with cells of a CW-complex. r, sn and ind are rank, signature, number of negative eigenvalues, and the topological index.
Table 1. Critical points considered in this paper, and two possible one-to-one correspondences with cells of a CW-complex. r, sn and ind are rank, signature, number of negative eigenvalues, and the topological index.
r s n ind k − cell k − cell
3 -3 3 -1 3-cell 0-cell
3 -1 2 1 2-cell 1-cell
3 1 1 -1 1-cell 2-cell
3 3 0 1 0-cell 3-cell
Σ j ind j n j 1 -1
Table 2. Number of isolated critical points with different index and signed sum of indices.
Table 2. Number of isolated critical points with different index and signed sum of indices.
Molecule Formula - n 3 + n 2 - n 1 + n 0 = Σ k ind k n k
Lithium hydride LiH - 2 + 1 - 0 + 0 = − 1
Methane CH4 - 5 + 10 - 10 + 4 = − 1
Ethane C2H6 - 9 + 20 - 20 + 8 = − 1
Ethene C2H4 - 8 + 11 - 8 + 4 = − 1
Acetylene C2H2 - 4 + 2 - 1 + 2 = − 1
Propyne C3H4 - 11 + 21 - 17 + 6 = − 1
3-Borapropyne BC2H3 - 9 + 15 - 13 + 6 = − 1
Benzene C6H6 - 18 + 36 - 31 + 14 = + 1
Cyclooctateraene C8H8 - 28 + 44 - 33 + 18 = + 1
Borazine B3N3H6 - 24 + 48 - 40 + 17 = + 1
Cubane C8H8 - 28 + 48 - 38 + 23 = + 5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated