Camouflage Breaking with Stereo-vision Assisted Imaging

1. Introduction

Camouflage is a natural concealment capability of animals to hunt and to avoid being hunted [1,2]. The making and breaking of camouflage become important for achieving advantages for various confrontation circumstances [3,4]. Camouflage is usually achieved by combination of structures, colors and illuminations to hide the identity of the object from its background [5,6]. There has been consistent interest in the subject of camouflage, as the topic is not only scientifically interesting but technologically important. Among various technique for camouflage breaking, 3D convexity, machine learning and artificial intelligence have been widely studied [7,8]. It has been suggested that breaking camouflage is one of the major functions of stereopsis [9,10]. Recent development with 3D photographic and stereopsis technology [11,12] paves the way for stereo image reconstruction. However, the capability of stereo computer vision is yet not in any way comparable with human vision. It is then necessary to re-examine the effect of stereopsis on camouflage breaking and to analyze its impact on its real-world applications.

In this work, we show with vision’s energy model [13,14,15] that 3D structures hidden deep in the background can be retrieved with binocular vision via stereoacuity. This theoretical analysis is applied to the extreme case where the object is completely submerged with background noises. The results show that the submerged 3D structures can be recovered if the recorded images are rightly perceived with human vision’s stereopsis. A field experiment is carried out with natural images taken by a drone camera. These image data are processed with computer, displayed in an autostereoscopy [16,17] and perceived with vision. The removal of the background noises for both the random noise and the natural images clearly demonstrates the general applicability of the novel technique for camouflage breaking.

2. Theoretical Analysis

The theoretical analysis presented in this work is based on the vision’s energy model proposed by Ohzawa et al. [13,14,15]. The image information is provided by the spatial array of binocular energy neurons that are identical with each other except for their receptive field locations. We use $L\left(x\right)$ and $R\left(x\right)$ to respectively represent the complex monocular linear responses of the left and right eye, at receptive position $x$. The spatial array of energy responses, $E\left(x\right)$, is expressed as:

$$\begin{array}{l}E(x)=|L(x)+R(x){|}^2\\ =|Re[L(x)]+Re[R(x)]{|}^2+|Im[L(x)]+Im[R(x)]{|}^2\end{array}$$

(1)

While Re means the real part, Im means the imaginary part. The left and right eye responses are denoted as $L(x)={\mathsf{\rho }}_l^2{e}^{{i\mathsf{\varphi }}_l(x)}$, $R(x)={\mathsf{\rho }}_r^2{e}^{{i\mathsf{\varphi }}_r\left(x\right)}$, where ${\mathsf{\rho }}_l^2$ and ${\mathsf{\rho }}_r^2$ are the monocular energy containing amplitude information, ${\mathsf{\varphi }}_l\left(x\right)$ and ${\mathsf{\varphi }}_r\left(x\right)$ are the phase angle of the monocular response. With the amplitude and phase information, the above equation can be simplified as:

$$E(x)={\rho }_l^2(x)+{\rho }_r^2(x)+2{\rho }_l{\rho }_r\cos (\Delta \varphi )$$

(2)

$\mathsf{\Delta }\mathsf{\varphi }={\mathsf{\varphi }}_l\left(x)-{\mathsf{\varphi }}_r\right(x)$ refers to interocular phase difference.

Notice that the equation shows that the images processed with stereo-vision contains a crossed term between the left and right eyes. This binocular interaction gives rise to the additional information that is not available with single eye vision or with their addition and it can be recovered only with simultaneous binocular vision.

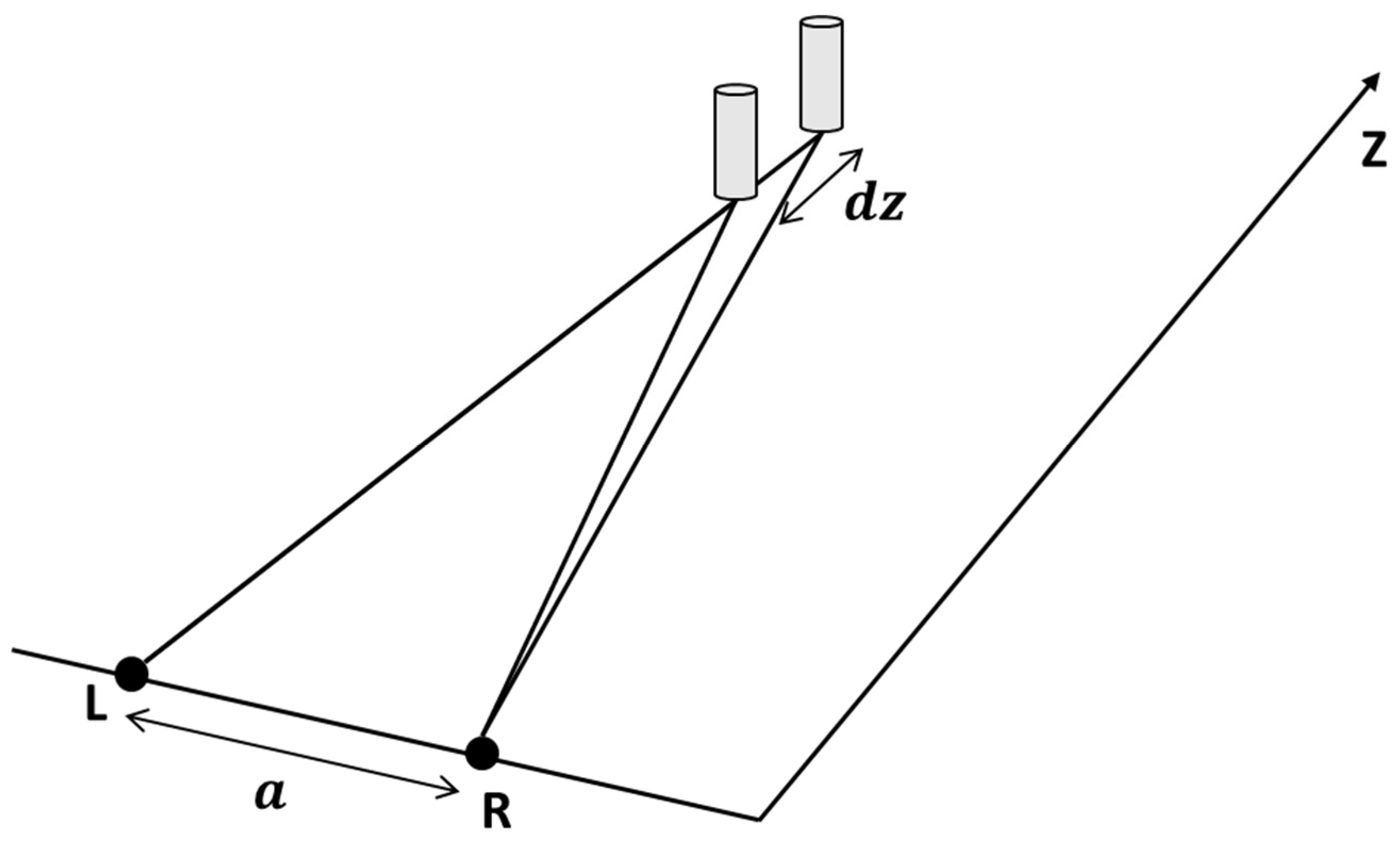
To analyze the stereo-vision with the energy model, it is important to note how the lateral and longitudinal spatial resolutions are related to the stereo-vision. Stereoacuity is defined as human’s vision ability to resolve the smallest depth difference measured with angular difference, described as $\text{∆}T$ [18,19]:

$$\Delta T={\displaystyle \frac{dZ\times a}{Z^2}}$$

(3)

The parameters for stereoacuity are shown in Figure 1, where $a$ is the interocular separation of the observer, $Z$ represents the distance of the fixed peg from the eye and $dZ$ means the position difference.

For object taken with a camera and displayed on a stereopsis, images can be magnified with optics and stereopsis screen size. Considering total magnification factor and baseline difference, the stereoacuity can be approximated with Equation (4): [18,19]

$$\Delta T={\displaystyle \frac{dZ\times M\times N\times a}{Z^2}}$$

(4)

where $M$ is magnification (ratio of display FOV and camera FOV), $N$ is the effective interocular separation (ratio of baseline and interocular separation).

An interesting but rarely discussed topic is how the stereoacuity is affecting the lateral resolution of the image. In general, the depth resolved measurement should enhance the lateral resolution in a similar way as with a confocal configuration while the rejection of the out of focus component is expected to increase the lateral resolution [20,21,22].

3. Results and Discussion

As the first step, we examine an extreme case where the object is a randomly sampled blocks of the letter “SYSU” of which each block in the left-hand and right-hand image consists of a random disparity. The object is completely swamped with random dot noises as shown in the Figure 2a,b. The Figure 2a,b show no useful information except for a noise background. On the other hand, when these left and right images are perceived with a stereopsis, meaningful signal clearly appears, as shown in the Figure 2c. The appearance of Figure 2c can be readily observed by delivering the left and right images into the left and right eyes, with which a pattern of “SYSU” is imaged and located at the center of the picture. The estimation of pixel disparity between Figure 2a,b is necessary for the calculation of Figure 2c. Equation (2) could be regarded as the summation of two components, the constant item originated from monocular energy and the binocular crossed item which takes the disparity as variable.

Notice that the appearance of the pattern with stereopsis is a conventional technique for the screening of stereoacuity [23] and it is an implication of how binocular viewing can be applied to perceive the signal that is not possible with a single eye. With this result, one can see that the object can be concealed within a 2D imaging, either by the left or right eye, but it becomes visible with binocular viewing.

For the test of the camouflage breaking in natural scene, a field experiment is carried out to show the retrieval of object with stereoacuity assisted image sensing. The difficulty of 3D remote sensing with stereopsis arises from the required large baseline distance, which is studied in this work with a drone equipped with a single camera. For the purpose of executing stereoacuity functioning, an experimental architecture similar as Figure 1 is carried out and left- and right-images are selected from a video taken by the flying camera. The key parameters to be considered are the relative positions of the object with its background, and the baseline of the two-positions to provide the stereo-viewing so that the object can be resolved with stereoacuity measurement. Assuming, for example, an object located 100 meters away from the camera, and an object is 1 meter away from its background. It can be estimated that the baseline of the dual cameras must be approximately 57 cm apart. With the recorded navigating speed of the drone, it is straight forward to choose left and right images from the video format to meet the requirement of the baseline length.

To meet the sensing requirement, a drone (DJI Mavic2 pro: 28 mm equivalent lens on the 1-inch CMOS sensor) equipped with a camera is employed to take the video for the scene and the two images from selected positions are employed as input for the left- and right-eye images. The flying altitude of the drone is 90 m. The dual images are transmitted to an autostereoscopy for 3D viewing at a viewing distance of 90 cm. The autostereoscopy is a directional backlight illuminated liquid crystal display with the feature size of 24 inch and single eye resolution at 1080 P (Type Midstereo 2468) [16,17]. With this autostereoscopy, the 3D scene is clearly visible. For the convenience of 3D perception, we convert the left and right images by coding it with blue and red, so that the image can be perceived with a 3D anaglyph.

The use of an autostereoscopy makes it possible to study the difference between 2D and 3D perception. For 2D mode, the left and right eyes are perceiving planar image. With 3D perception, the left and right images are delivered to the left and right eyes respectively. It becomes evident that 3D perception provides detailed object structures due to the perception of layered structures of the scene assisted with stereoacuity. With 2D mode, the information in different depths is intermixed, giving rise to the opportunity for camouflaging. With 3D, the concealed can be retrieved with binocular vision.

In order to further view the effect of stereopsis on the resolved 3D object (compared with Figure 3a), image is synthesized using disparity discriminated image pixels as input information. Detailed structures can be observed with stereo-vision concentrating on a unique disparity layer. By enhancing the image structure in one particular layer while removing structures from other layers, the lateral structures of the scene is substantially enhanced.

Figure 4a shows the energy distribution, in which binocular vision focus on the ground layer, while Figure 4b illustrates the situation when two eyes are concentrating on the top tree layer, within which the tree branches and leaves are clearly visible. The pixel disparity between two visual angles, which is related to the interocular phase difference in Equation (2), is indispensable for the calculation of the energy distribution. The summation of the monocular energy from two eyes could be regarded as a constant offset.

Figure 4c is obtained by dot multiplication of the energy pattern at a particular height of the tree with input of Figure 3a. Similarly, Figure 4d is resulted from multiplying the energy pattern at the height of the ground with a Figure 3a. Prominent difference is clearly visible in the comparison of these two cases mentioned above, showing substantially enhanced camouflage breaking capability. With binocular energy model, Figure 4c,d show corresponding sectioning of the 3D scene for the different disparities, corresponding to pattern at different altitude. The sectioning images are in accord with the direct perception shown in Figure 3c. With the synergistic effect of both eyes, the focusing layer could be differentiated in depth and clearer in lateral resolution by rejecting structure information from different sections of the object. Compared with the corresponding region of the original image given in Figure 3a, neither ground or tree characteristics can be identified with the original image, which proves a promising way for camouflage breaking for stereo-vision and stereo-vision based optical imaging.

To better illustrate the advantages of layered discrimination with the energy model, we select a region in Figure 3a marked by a green square, which is amplified in Figure 5. It becomes clear that the image structures unclear from a bright background can be sectioned. The 2D image sections focusing to the ground and to the tree branches are clearly visible.

4. Conclusion

In conclusion, based on the energy model of binocular vision, we analyze stereoacuity for image sensing, which is applied to camouflage breaking to the case where the object is completely obscured by the background noises. We employed the stereoacuity resolved sensing to a field experiment, and we restore the object which is concealed in 2D settings, hence demonstrating the enhanced capability for camouflage breaking even for complex background. It is shown that the present technique is versatile and powerful on the basis of a well understanding of stereopsis and binocular interaction. We anticipate that the proposed and demonstrated technique has immediate applications for scientific research and technological applications.