Time Dependent Retarded Electromagnetic Motors

Preprint

Article

Time Dependent Retarded Electromagnetic Motors

Altmetrics

Downloads

Views

Comments

Asher Yahalom^*

This version is not peer-reviewed

Submitted:

18 July 2024

Posted:

18 July 2024

You are already at the latest version

Alerts

Abstract

We have shown that Newton’s third law does not strictly hold in a system with remote elements, due the finite speed of signal propagation and thus force imbalance occurs at the system’s center of mass. As the said system is affected by a total force for a finite duration, mechanical energy and momentums are gained by the system. In early works we assumed that the bodies were macroscopically charge neutral. Later we removed this restriction, thus analyzing the consequences on a possible electric charged relativistic motor. On the first published paper on this subject we studied this phenomena in general but gave only an example of a system reaching a stationary state, in this paper we shall analyze a charged retarded electromagnetic motor in a more general time dependent setting giving specific examples in which the system never reaches a stationary state yet produces steady linear momentum non the less.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

The emergence of Special Relativity in the early 20th century was a revolutionary event in the world of physics, fundamentally altering our understanding of space and time. Albert Einstein, a relatively unknown Swiss patent examiner at the time, published this ground breaking theory in 1905 [1,2].

Special Relativity originated from Einstein’s quest to resolve inconsistencies between the principles of electromagnetism and classical mechanics. The key insight came with the recognition that the speed of light is constant for all observers, regardless of their relative motion. This revelation challenged the classical notion of absolute space and time and led to the development of a new framework. Moreover, it was postulated that no particle of matter, field or signal can move faster than the velocity of light in vacuum denoted by the letter c.

Einstein’s theory introduced several revolutionary concepts. The most famous is the equation

E = m c^{2}

, revealing the equivalence of the rest energy E and rest mass m. Special Relativity also introduced time dilation and length contraction, demonstrating that time passes differently for observers in relative motion, and objects shrink along their direction of motion at high speeds.

Special Relativity was initially met with skepticism, but its validity was confirmed through experimental evidence, such as the Michelson-Morley experiment [3]. It laid the foundation for subsequent developments in theoretical physics, including General Relativity, which describes the gravitational force, and later integrated by Dirac and others into quantum mechanics, the other pillars of modern physics.

In summary, the emergence of Special Relativity marked a pivotal moment in scientific history, reshaping our understanding of the universe and laying the groundwork for many scientific advancements to come.

One of the important consequence or special relativity which in fact can be deduced based on Maxwell electromagnetism [4,5,6] alone even for slow (nonrelativistic matter) is the phenomena of retardation, that is the fact that any change will not affect a distant observer before a time is passed which is equal to the distance between source and observer over c. This fact is expressed mathematically through retarded scalar and vector potentials:

Φ ({\vec{x}}_{2}) = \frac{1}{4 π ϵ_{0}} \int d^{3} x_{1} \frac{ρ_{1} ({\vec{x}}_{1}, t_{r e t})}{R}, \vec{R} \equiv {\vec{x}}_{12}, t_{r e t} \equiv t - \frac{R}{c} .

(1)

\vec{A} ({\vec{x}}_{2}) = \frac{μ_{0}}{4 π} \int d^{3} x_{1} \frac{{\vec{J}}_{1} ({\vec{x}}_{1}, t_{r e t})}{R} .

(2)

The notation and symbols in the above expressions are standard [7,8,9,10] and in particular can be found also in [11].

Retarded electromagnetic potentials are a fundamental concept in the realm of classical electrodynamics, and they play a pivotal role in understanding the behavior of electromagnetic fields in a time-dependent manner. These potentials are intimately connected to the theory of electromagnetism and provide a means to describe the propagation of electromagnetic waves and the interaction of charged particles with their own electromagnetic fields.

The term "retarded" in this context refers to the notion that the electromagnetic potentials at a given point and time are influenced only by the charge and current distributions in the past, taking into account the finite speed of light. In essence, when a charged particle moves, it generates electromagnetic waves that travel outward at the speed of light. The potentials at a particular location are the result of these waves arriving from all past events.

The concept of retarded potentials helps address the issue of causality in electrodynamics, ensuring that the effects of electromagnetic interactions do not propagate faster than the speed of light. It also provides a mathematical framework for solving Maxwell’s equations in various situations, making it a valuable tool for describing the behavior of electromagnetic fields generated by moving charges.

In summary, retarded electromagnetic potentials are a crucial aspect of classical electrodynamics, serving as a bridge between the behavior of charged particles and the resulting electromagnetic fields, while also preserving the causality and finite speed of light inherent in the theory of electromagnetism. In particular they are used for the analysis of superconductivity [12] and surface magnon-polaritons [13]. And to calculate single-photon superradiance in nanophotonics: a multiple-scattering perspective [14]. A (second) quantized version of the retarded vector potential is the basis for quantum electrodynamics, which was recently used [15] for analysis of dispersive dielectric objects.

Newton’s physical theory of motion is encapsulated in three laws that, combined, are the essence of classical mechanics. The content of those laws depicts the connection between the body, forces acting on the body, and movement of the body responding to said forces. The three laws of motion were described by Isaac Newton in his most important book: Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy), first published in 1687 [16,17]. In the current work, we are interested mainly in the first and third laws (while using the second law but not criticizing its content). We shall first discuss the third law stating that: If one body exerts a force on a second body, the second body simultaneously applies a force of the same magnitude but opposite in direction on the first body. In other words, when one object exerts a force on a second object, the second object exerts an equal force in the opposite direction on the first object. This law highlights the inherent symmetry in interactions, illustrating that forces are always mutual and result in pairs. Whether you push a wall, jump from the ground, or row a boat, Newton’s Third Law underscores the reciprocal nature of forces and is a cornerstone in our understanding of how objects move and interact in the physical world.

However, our earlier discussion of retarded potentials shows that this law cannot be exactly correct. Because if we have two distant objects affecting the motion of each other by their fields (that is not contact forces but say electric forces between two charged bodies), then a change in one body’s state say its motion will affect immediately the force it feels due to the field of the second body but the second body will not know simultaneously of this motion because not enough times has passed and the field effect is retarded. This leads to the notion of retarded electromagnetic motor (some times called relativistic motor but has nothing to do with exotic matter or other inventions of the imagination), which takes advantage of the imbalance of forces in the center of mass. If we take

{\vec{F}}_{12}

to be the force operating by body 1 on body 2 and

{\vec{F}}_{21}

the force operating by body 2 on body 1, and if body 1 has a

m_{1}

mass and velocity

v_{1}

and body two has a

m_{2}

mass and velocity

v_{2}

, than by Newton’s second law we have:

m_{1} \frac{d {\vec{v}}_{1}}{d t} = {\vec{F}}_{21}, m_{2} \frac{d {\vec{v}}_{2}}{d t} = {\vec{F}}_{12}

(3)

Adding up the above equations we obtain the following equation for the system total force

{\vec{F}}_{T}

\frac{d (m_{1} {\vec{v}}_{1} + m_{2} {\vec{v}}_{2})}{d t} = {\vec{F}}_{21} + {\vec{F}}_{12} \equiv {\vec{F}}_{T} .

(4)

Defining the center of mass location and velocity for a system of particles located at

{\vec{x}}_{1}

and

{\vec{x}}_{2}

in terms of the total mass:

M = m_{1} + m_{2}

as follows:

{\vec{x}}_{c m} \equiv \frac{m_{1} {\vec{x}}_{1} + m_{2} {\vec{x}}_{2}}{M}, {\vec{v}}_{c m} \equiv \frac{d {\vec{x}}_{c m}}{d t} = \frac{m_{1} {\vec{v}}_{1} + m_{2} {\vec{v}}_{2}}{M},

(5)

we may write Equation (4) in the form:

M \frac{d {\vec{v}}_{c m}}{d t} = \frac{d {\vec{p}}_{T}}{d t} = {\vec{F}}_{T}, {\vec{p}}_{T} \equiv {\vec{p}}_{1} + {\vec{p}}_{2} = m_{1} {\vec{v}}_{1} + m_{2} {\vec{v}}_{2},

(6)

in the above

{\vec{p}}_{T}

is the system’s total linear momentum and

{\vec{p}}_{1}, {\vec{p}}_{2}

are the linear momentums of particles 1 and 2 respectfully. Now if Newton’s third law is assumed it follows that

{\vec{F}}_{21} = - {\vec{F}}_{12}

and hence

{\vec{F}}_{T} = 0

. This entails that:

\frac{d {\vec{v}}_{c m}}{d t} = \frac{d {\vec{p}}_{T}}{d t} = 0,

(7)

thus if the center of mass is at rest at any time it will remain at rest for all time, and the total linear momentum is conserved. However, if retardation is assumed then

{\vec{F}}_{T} \neq 0

although for many (and most) practical systems it can be assumed to be negligible. This means that the total linear momentum is not conserved (which seems to contradict Noether theorem applied with the symmetry of translations) it also suggests that

{\vec{v}}_{c m}

must not remain null but may acquire a finite value.

The prevalent vehicles of today rely on reacting material parts; each material component obtains momentum that is equal and opposite to the momentum gained by the other. A well known example for this momentum balance is a rocket ejecting gas to propel itself in the forward direction. However, the retardation phenomena suggest a different engine which is not a combination of two material parts but of field and matter. If we ignore the field, it may seem to us that the material component gains momentum thus the total momentum grows violating the law of momentum conservation. However, it has been shown that the opposite amount of momentum is carried by the field [18], thus the total momentum of the physical system composed of both field and matter is conserved indeed. This is can be traced to Noether’s theorem which implies that a system that possesses vector translational symmetry will conserve vector linear momentum. As previously stated, the total physical system which is a combination of matter and field will not change under translations, while every specific component of the system (be it either matter or field) will indeed change with respect to the other. Feynman [19] has indicated that two orthogonally moving point charges are apparently contradicting Newton’s third law as the forces that the charges induce do not cancel (last part of 26-2), this is explained in (27-6) in which it is shown that the momentum gained by the two charge system is subtracted from the field momentum.

Newton’s First Law of Motion, often referred to as the law of inertia, is a fundamental concept in physics. It states that an object at rest tends to stay at rest, and an object in motion tends to stay in motion unless acted upon by an external force. In essence, it underscores the idea that objects will maintain their state of motion, be it stationary or moving in a straight line, unless compelled to change by an external force. This law lays the foundation for understanding how objects behave and is crucial for comprehending motion, equilibrium, and the natural tendency of objects to resist changes in their state of rest or motion. However, again retardation implies that this law is not accurate and the body center of mass may acquire a finite velocity

{\vec{v}}_{c m} \neq 0

even if there is no external force and the body’s center of mass was initially at rest. This leads naturally to the technological question, that is, can one take advantage of retardation in order to propel bodies to move.

A comprehensive review and introduction to the subject of retarded electromagnetic motors in general and microscopic retarded electromagnetic engines in particular with many references is given in [11,20,21] and will not be rewritten here, the reader interested in additional background and history of the subject is welcome to read the original text. However, for the readers’ convenience we provide a short introduction to the current work which is given below.

The work on retarded electromagnetic motors is dependent on the retarded magnetic and electric field formulae introduced by Jefimenko [6,22]. Those mathematical expressions were used to evaluate the total force operating on the center of mass of a system of two time dependent loop currents [23]. This was later generalized to evaluate the total force in a system composed of a current loop and a permanent magnet [25]. If a force is generated for a non vanishing length of time, momentum and kinetic energy will gained by the material part of the system. It may superficially look like that the laws of momentum and energy conservation are not respected, but this is so only if one ignores the interchange of linear momentum and energy with the field.It was shown [18] that the linear momentum gained by the material part of the system is lost by the field component of the same system, that is it was demonstrated that the linear momentum obtained by the material parts of the retarded electromagnetic motor is deducted in equal amount of momentum (but in opposite direction) by the electromagnetic field. The exchange of energy between the kinetic material part of the relativistic engine and the electromagnetic field energy was discusses in [26,28,29]. It was demonstrated that the electromagnetic energy used is six times the kinetic energy provided to the engine. It was also deduced that energy is radiated from the motor if the coils are not aligned.

Our preliminary analysis assumed bodies that were devoid of electric charge (neutral). In a later paper [11] charged bodies were analyzed. The charged motor allows to obtain a non vanishing linear momentum also in cases in which the current is not continuously enlarged, this is not the case in electrically neutral engines. Notice, however, that dielectric breakdown dictates a maximal value for charge density. Current density is also practically limited even for superconducting wires. It was demonstrated that for any practical motor size the linear momentum that can be obtained in a relativistic charged motor is quite limited.

The limitations of a macroscopic relativistic motor imply that one should use the extremely high charge and current densities that are available in the microscopic realm, for example in ionic crystals. This idea was studied in an earlier paper [20] in which we made good use of the high charge densities and high current densities in the atomic scale.

We shall not derive the basic equations of the retarded electromagnetic engine here, the interested reader can be find a detailed derivation in [11,20]. The definition of symbols and notations are the same as in the earlier works and will not be redefined.

In the previous paper we only considered a relativistic engine at a stationary state while ignoring the possibility of engines which do not reach a stationary state as well as the transient stage of engines that do. The same criticism holds for the second part of the same paper dealing with a relativistic engine on the atomic scale [20]. Here we make a more general analysis leading to a different kind of charged relativistic engine of a type that does not reach a stationary state.

We shall quote the two main results of [11] but omit the definition of symbols and derivation which can be found in the original publication. The total force (correct to the second order in

\frac{R}{c}

) in the center of mass of the retarded electromagnetic engine composed of two subsystems 1 and 2 is:

{\vec{F}}_{T}^{[2]} = \frac{μ_{0}}{4 π} \partial_{t} \int \int d^{3} x_{1} d^{3} x_{2} [\frac{1}{2} (ρ_{2} \partial_{t} ρ_{1} - ρ_{1} \partial_{t} ρ_{2}) \hat{R} - (ρ_{1} {\vec{J}}_{2} + ρ_{2} {\vec{J}}_{1}) R^{- 1}]

(8)

And the momentum gained by the system which is assumed at rest, that is

\vec{P} (- \infty) = 0

\vec{P} (t) = \frac{μ_{0}}{4 π} \int \int d^{3} x_{1} d^{3} x_{2} [\frac{1}{2} (ρ_{2} \partial_{t} ρ_{1} - ρ_{1} \partial_{t} ρ_{2}) \hat{R} - (ρ_{1} {\vec{J}}_{2} + ρ_{2} {\vec{J}}_{1}) R^{- 1}]

(9)

2. Engine Optimization

We investigate what are the conditions for a retarded electromagnetic engine in terms of composition and structure to generate a maximal amount of momentum. To this end we write the charge density and current density in the form:

ρ (\vec{x}, t) = \bar{ρ} \sum_{n} ρ^{n} (\vec{x}) f^{n} (t)

(10)

in which

\bar{ρ}

is a constant which has the units of charge density,

ρ^{n} (\vec{x})

are spatial functions and

f^{n} (t)

temporal functions, both functions are dimensionless. Similarly:

\vec{J} (\vec{x}, t) = \bar{J} \sum_{n} {\vec{J}}^{n} (\vec{x}) g^{n} (t)

(11)

in which

\bar{J}

is a constant which has the units of current density,

{\vec{J}}^{n} (\vec{x})

are spatial vector functions and

g^{n} (t)

temporal functions, both functions are dimensionless. We shall write the dimensional constants in terms of a generic charge Q, typical length scale h, and typical time scale

τ

, that is:

\bar{ρ} \equiv \frac{Q}{h^{3}}, \bar{J} \equiv \bar{ρ} \frac{h}{τ} = \frac{Q}{h^{2} τ} .

(12)

Next we shall attribute an expansion of the type given in Equation (10) and Equation (11) to each of the subsystems introduced previously this is done by adding a subscript with the relevant subsystem number:

ρ_{1} (\vec{x}, t) = {\bar{ρ}}_{1} \sum_{n} ρ_{1}^{n} (\vec{x}) f^{n} (t), ρ_{2} (\vec{x}, t) = {\bar{ρ}}_{2} \sum_{n} ρ_{2}^{n} (\vec{x}) f^{n} (t) .

(13)

{\vec{J}}_{1} (\vec{x}, t) = {\bar{J}}_{1} \sum_{n} {\vec{J}}_{1}^{n} (\vec{x}) g^{n} (t), {\vec{J}}_{2} (\vec{x}, t) = {\bar{J}}_{2} \sum_{n} {\vec{J}}_{2}^{n} (\vec{x}) g^{n} (t) .

(14)

Next we define the following dimensionless vector constants:

{\vec{Γ}}^{m n} \equiv {\vec{Γ}}_{21}^{m n} \equiv \frac{1}{2 h^{6}} \int d^{3} x_{1} d^{3} x_{2} ρ_{1}^{n} ρ_{2}^{m} \frac{{\vec{x}}_{1} - {\vec{x}}_{2}}{| {\vec{x}}_{1} - {\vec{x}}_{2} |} = - {\vec{Γ}}_{12}^{n m}

(15)

which depend on the spatial structure of the two charged systems. Similarly we define:

{\vec{Λ}}_{21}^{m n} \equiv \frac{1}{h^{5}} \int d^{3} x_{1} d^{3} x_{2} \frac{ρ_{2}^{m} {\vec{J}}_{1}^{n}}{| {\vec{x}}_{1} - {\vec{x}}_{2} |}, {\vec{Λ}}_{12}^{m n} \equiv \frac{1}{h^{5}} \int d^{3} x_{1} d^{3} x_{2} \frac{ρ_{1}^{m} {\vec{J}}_{2}^{n}}{| {\vec{x}}_{1} - {\vec{x}}_{2} |},

(16)

we notice that generically:

{\vec{Λ}}_{21}^{m n} \neq {\vec{Λ}}_{12}^{m n} .

(17)

Using the typical time scales of each of the systems

τ_{1}

and

τ_{2}

we define:

{\vec{Λ}}^{m n} \equiv \frac{1}{τ_{1} + τ_{2}} (τ_{2} {\vec{Λ}}_{21}^{m n} + τ_{1} {\vec{Λ}}_{12}^{m n}), \bar{τ} = \frac{τ_{1} τ_{2}}{τ_{1} + τ_{2}} .

(18)

Plugging Equation (13) and Equation (14) into Equation (9) (Equation (83) of [11]) and using the definitions above we arrive at the expression:

\vec{P} (t) = \frac{μ_{0}}{4 π} Q_{1} Q_{2} \sum_{m n} [{\vec{Γ}}^{m n} (f^{m} \partial_{t} f^{n} - f^{n} \partial_{t} f^{m}) - \frac{1}{\bar{τ}} {\vec{Λ}}^{m n} f^{m} g^{n}] .

(19)

We remind the reader that

ρ

and

\vec{J}

are not independent as they are connected through the continuity Equation (16) of [11]:

\vec{\nabla} \cdot \vec{J} + \partial_{t} ρ = 0 \Rightarrow \sum_{n} [\bar{ρ} ρ^{n} (\vec{x}) \partial_{t} f^{n} (t) + \bar{J} \vec{\nabla} \cdot {\vec{J}}^{n} g^{n} (t)] = 0 .

(20)

Taking into account Equation (12) it follows that:

\sum_{n} [ρ^{n} (\vec{x}) τ \partial_{t} f^{n} (t) + h \vec{\nabla} \cdot {\vec{J}}^{n} (\vec{x}) g^{n} (t)] = 0 .

(21)

As we can always choose:

g^{n} (t) = τ \partial_{t} f^{n} (t),

(22)

the following equation must be satisfied:

\sum_{n} [(ρ^{n} (\vec{x}) + h \vec{\nabla} \cdot {\vec{J}}^{n} (\vec{x})) g^{n} (t)] = 0 .

(23)

One possible solution is by choosing:

ρ^{n} (\vec{x}) = - h \vec{\nabla} \cdot {\vec{J}}^{n} (\vec{x}),

(24)

for all n. In this case we can choose

{\vec{J}}^{n}

but

ρ^{n}

are dictated.

3. General Considerations

Looking at the momentum Equation (19) it is obvious that the higher the charge the higher the momentum, also a short time scale

\bar{τ}

and a high time derivative will also increase momentum. Counter intuitively a proximity of charge and currents is also a contributing factor, through the lambda terms given in Equation (16) this can be explained due to the fact that interaction is stronger in close proximity despite the fact that retardation is smaller. In fact interaction increases in proportion to the inverse of the distance square as distances are shortened and the systems become closer, however, retardation only decreases linearly for closer distances. We remind the reader that in a previous paper [11] we have shown that the amount of charge in a given volume is limited due to the phenomenon of dielectric breakdown, hence to achieve high momentum one needs high charge and thus a large engine as expected.

4. Example

Let us consider a set of two functions:

f^{1} (t) = sin ϕ_{1} (t), f^{2} (t) = sin ϕ_{2} (t)

(25)

in which

ϕ_{1} (t)

and

ϕ_{2} (t)

are arbitrary time dependent phases. We use Equation (22) to choose corresponding g functions:

g^{1} (t) = τ {\dot{ϕ}}_{1} (t) cos ϕ_{1} (t), g^{2} (t) = τ {\dot{ϕ}}_{2} (t) cos ϕ_{2} (t) .

(26)

We shall assume two sub systems each described by only one component in the sum:

{\vec{J}}_{1} (\vec{x}, t) = {\bar{J}}_{1} {\vec{J}}_{1}^{1} (\vec{x}) g^{1} (t), {\vec{J}}_{2} (\vec{x}, t) = {\bar{J}}_{2} {\vec{J}}_{2}^{2} (\vec{x}) g^{2} (t) .

(27)

Taking into account Equation (24) it follows that:

ρ_{1} (\vec{x}, t) = {\bar{ρ}}_{1} ρ_{1}^{1} (\vec{x}) f^{1} (t), ρ_{2} (\vec{x}, t) = {\bar{ρ}}_{2} ρ_{2}^{2} (\vec{x}) f^{2} (t) .

(28)

Only the following terms in Equation (15) and Equation (16) are non zero:

{\vec{Γ}}^{21} = \frac{1}{2 h^{6}} \int d^{3} x_{1} d^{3} x_{2} ρ_{1}^{1} ρ_{2}^{2} \frac{{\vec{x}}_{1} - {\vec{x}}_{2}}{| {\vec{x}}_{1} - {\vec{x}}_{2} |},

(29)

{\vec{Λ}}_{21}^{21} \equiv \frac{1}{h^{5}} \int d^{3} x_{1} d^{3} x_{2} \frac{ρ_{2}^{2} {\vec{J}}_{1}^{1}}{| {\vec{x}}_{1} - {\vec{x}}_{2} |}, {\vec{Λ}}_{12}^{12} \equiv \frac{1}{h^{5}} \int d^{3} x_{1} d^{3} x_{2} \frac{ρ_{1}^{1} {\vec{J}}_{2}^{2}}{| {\vec{x}}_{1} - {\vec{x}}_{2} |} .

(30)

Assuming

τ_{1} = τ_{2}

it follows from Equation (18) that

\bar{τ} = \frac{τ_{1}}{2}

, we shall take

τ = \bar{τ}

. Also it follows from Equation (18) that:

{\vec{Λ}}^{12} = \frac{1}{2} {\vec{Λ}}_{12}^{12}, {\vec{Λ}}^{21} = \frac{1}{2} {\vec{Λ}}_{21}^{21} .

(31)

Inserting the above results in Equation (19) will yield:

\vec{P} (t) = \frac{μ_{0}}{4 π} Q_{1} Q_{2} [{\vec{Γ}}^{21} (f^{2} \partial_{t} f^{1} - f^{1} \partial_{t} f^{2}) - \frac{1}{\bar{τ}} {\vec{Λ}}^{21} f^{2} g^{1} - \frac{1}{\bar{τ}} {\vec{Λ}}^{12} f^{1} g^{2}] .

(32)

Let us make the following assumptions. First: we assume that the phases differ by a constant value

Δ ϕ

. This means that the derivatives of the phases are the same. Taking into account Equation (25) and Equation (26) we thus obtain:

\vec{P} (t) = \frac{μ_{0}}{4 π} Q_{1} Q_{2} \dot{ϕ} [{\vec{Γ}}^{21} sin Δ ϕ - {\vec{Λ}}^{21} sin ϕ_{2} cos ϕ_{1} - {\vec{Λ}}^{12} sin ϕ_{1} cos ϕ_{2}] .

(33)

The

Γ

and

Λ

constants are determined by the distribution of charges and currents. Let us consider two thin wires of current as depicted in Figure 1.

In this case we obtain:

\begin{matrix} {\vec{J}}_{1}^{1} & = & h^{2} δ (z_{1}) δ (y_{1} - y_{01}) [u (x_{1} + x_{01}) - u (x_{1} - x_{01})] \hat{x}, \\ {\vec{J}}_{2}^{2} & = & h^{2} δ (z_{2}) δ (y_{2} - y_{02}) [u (x_{2} + x_{02}) - u (x_{2} - x_{02})] \hat{x} . \end{matrix}

(34)

in which

δ

is Dirac’s delta function and u is a step function,

\hat{x}

is a unit vector in the x direction. It follows from Equation (24) that we also have:

\begin{matrix} ρ_{1}^{1} & = & h^{3} δ (z_{1}) δ (y_{1} - y_{01}) [δ (x_{1} - x_{01}) - δ (x_{1} + x_{01})], \\ ρ_{2}^{2} & = & h^{3} δ (z_{2}) δ (y_{2} - y_{02}) [δ (x_{2} - x_{02}) - δ (x_{2} + x_{02})] . \end{matrix}

(35)

we shall take the characteristic length of the system to be the distance between the two wires (see Figure 1):

h = y_{02} - y_{01} .

(36)

Now, we can plug Equation (35) into Equation (29) and obtain:

{\vec{Γ}}^{21} = h \hat{y} \{\frac{1}{\sqrt{{(x_{01} + x_{02})}^{2} + h^{2}}} - \frac{1}{\sqrt{{(x_{01} - x_{02})}^{2} + h^{2}}}\},

(37)

For the simple case: of

x_{01} = x_{02}

, it follows that for a wire of length

L = 2 x_{01} = x_{01} + x_{02}

, it takes the form:

{\vec{Γ}}^{21} = \hat{y} \{\frac{1}{(\sqrt{{(\frac{L}{h})}^{2} + 1}} . - 1\},

(38)

Thus if the wires is very long with respect to the distance between wires,

L ≫ h

it follows that:

{\vec{Γ}}^{21} = - \hat{y} .

(39)

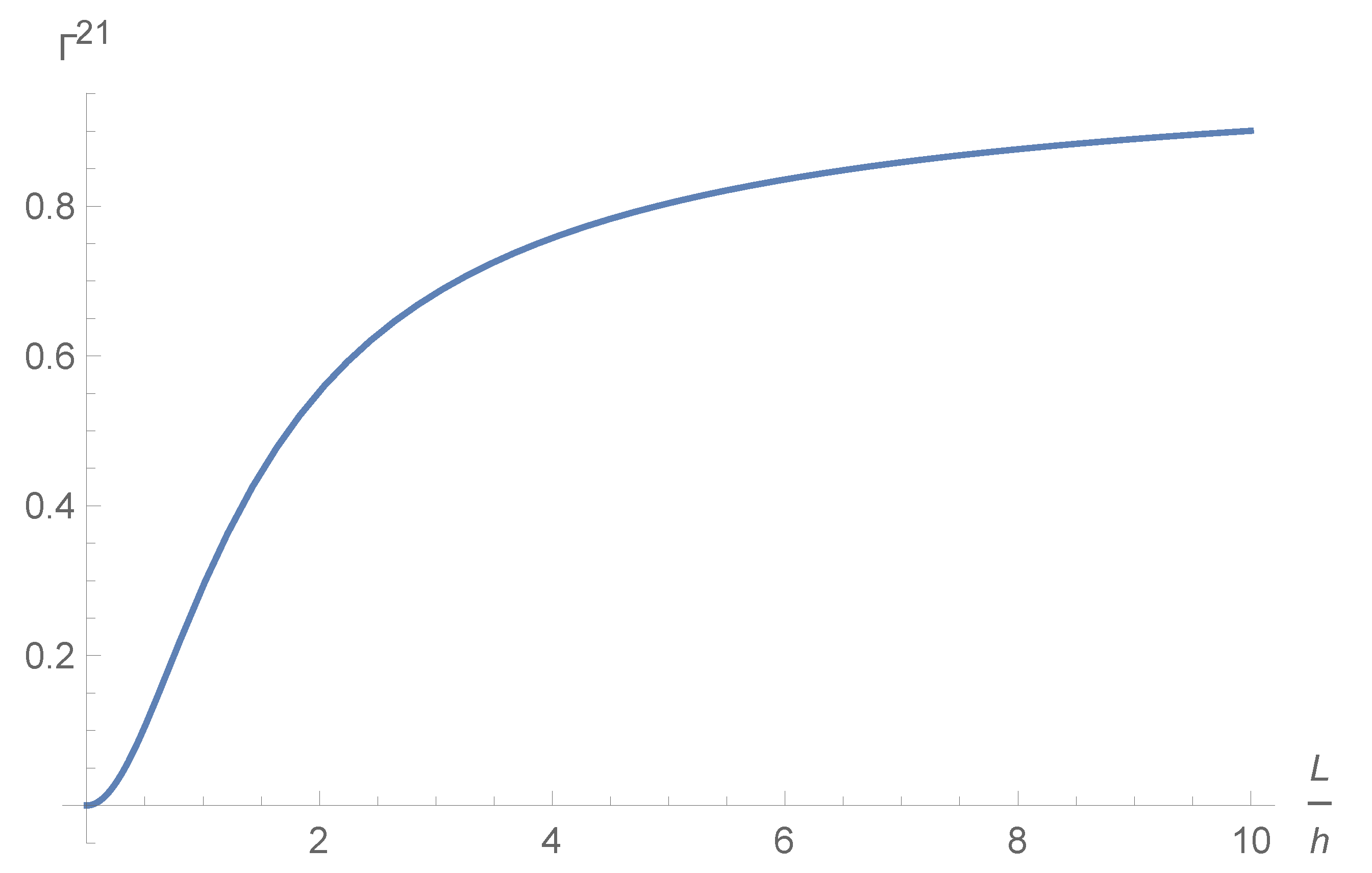
For a vanishing short wire

{\vec{Γ}}^{21} = 0

, while for a short wire

L ≪ h

, we have:

{\vec{Γ}}^{21} = - \frac{1}{2} {(\frac{L}{h})}^{2} \hat{y} .

(40)

The absolute value of

| Γ^{21} |

is depicted in Figure 2:

Let us now insert Equation (34) and Equation (35) into Equation (30) and Equation (31) its follows that:

Λ_{12}^{12} = Λ_{21}^{21} = 0 \Rightarrow {\vec{Λ}}^{12} = {\vec{Λ}}^{21} = 0 .

(41)

Thus according to Equation (33):

\vec{P} (t) = \frac{μ_{0}}{4 π} Q_{1} Q_{2} \dot{ϕ} {\vec{Γ}}^{21} sin Δ ϕ .

(42)

Assuming

Δ ϕ = \frac{π}{2}

and a long enough wire:

\vec{P} (t) = - \frac{μ_{0}}{4 π} Q_{1} Q_{2} \dot{ϕ} \hat{y} .

(43)

Hence, such a system will gain momentum in the y direction (perpendicular to the wire direction) depending on the phase temporal derivative. The total current flowing through the wire (say wire 1) is:

I_{1} (t) = \int {\vec{J}}_{1} \cdot \hat{x} d y d z = Q_{1} \dot{ϕ} cos ϕ_{1}, - x_{01} < x < + x_{01}

(44)

If we take

ϕ_{1} = ω t

I_{1} (t) = Q_{1} ω cos (ω t)

(45)

which is the current that is needed to charge and discharge the ends of the wire. The amplitude of the said current is:

I_{a 1} = Q_{1} ω .

(46)

From Equation (25), Equation (28) and Equation (35) it follows that the total charge in the wire is null because the charge accumulated in one end is equal and opposite to the other end with a maximal value of

Q_{1}

. The same goes of course in the case of wire 2. Thus we may write the momentum equation as:

\vec{P} (t) = - \frac{μ_{0}}{4 π ω} I_{a 1} I_{a 2} \hat{y} .

(47)

5. Discussion

In our earlier works it was demonstrated that the third law of Newton is contradiction to the retardation phenomena and the combined force (the force operating on the center of mass) on a two charged body systems is not null. Linear momentum is, however, constant provided that the field linear momentum is taken into consideration, this is also true for energy.

The main result is provided by Equation (47), which describe the total force for a unique configuration. Although more general configurations are allowed (see Equation (19)).

The result demonstrates that the higher the current amplitude and counterintuitive the lower the frequency, the higher the momentum obtained. This is somewhat misleading because if the frequency is too low one may risk an aerial discharge (see discussion in [11]). However, neglecting this problem we obtain for two wires carrying a 10 kiloampere current, with 1 Hz frequency a momentum of 1.6 kg meter/second.

We remark that an "antigravity" effect may be obtain by changing the phase quadratically in time, this will cause a second derivative of phase that may cause a temporal first derivative of momentum, i.e. a force.

Obviously to perform an experiment of the suggested retarded electromagnetic motor is much preferable in order to validate the calculations and formulae given above this is also remains as a task for future research.

6. Conclusions

For this last paragraph of the current work we make a short comparative study between the retarded electromagnetic motor and the photon engine. The principle of operation of a photon engine is the following. The photon engine eject photon (say a laser beam or a radio-frequency cavity [30]) in the backward direction and thus propel its material part forward. Of course the photons of a visual band laser and a radio-frequency cavity are quite different with respect to the energy and momenta of a single photon. To obtain a p momentum with a photon engine propulsion one needs to invest an energy of at least

E_{p} = p c

while for the same momentum a retarded electromagnetic engine will require an energy of about

E \sim \frac{1}{2} p v

. The ratio of the required energies is

\frac{E_{p}}{E} = \frac{2 c}{v}

which is enormous number for any non relativistic speed.

Today’s standard electric cars (Tesla for example) can reach high speed and momentum, but notice that unlike the relativistic motor they need a road to push against in order to balance their momentum, otherwise no motion is possible in a non retarded motor.

References

Einstein, Albert (1905d) "Zur Elektrodynamik bewegter Körper" [On the Electrodynamics of Moving Bodies]. Annalen der Physik. Leipzig, Germany: Verlag von Johann Ambrosius Barth (published 26 September 1905). 17 (all series: 322) (10): 891–921.
Einstein, Albert (1905e) "Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?" [Does the Inertia of a Body Depend Upon Its Energy Content?]. Annalen der Physik. Vierte Folge (in German). Leipzig, Germany: Verlag von Johann Ambrosius Barth (published 21 November 1905). 18 (all series: 323) (13): 639–641.
Michelson, Albert A.; Morley, Edward W. (1887). "On the Relative Motion of the Earth and the Luminiferous Ether". American Journal of Science. 34 (203): 333–345.
J.C. Maxwell, "A dynamical theory of the electromagnetic field" Philosophical Transactions of the Royal Society of London 155: 459-512 (1865).
O. Heaviside, "On the Electromagnetic Effects due to the Motion of Electrification through a Dielectric" Philosophical Magazine, (1889).
J. D. Jackson, Classical Electrodynamics, Third Edition. Wiley: New York, (1999).
Rohrlich, F (1993). "Potentials" (https://archive.org/details/mcgrawhillencycl1993park/page/1 072/). In Parker, S.P. (ed.). McGraw Hill Encyclopaedia of Physics (2nd ed.). New York.p. 1072.
Garg, A., Classical Electromagnetism in a Nutshell, 2012, p. 129.
Electromagnetism(2ndEdition),I.S.Grant,W.R.Phillips,ManchesterPhysics,JohnWiley & Sons,2008.
Introduction to Electrodynamics (3rd Edition), D.J. Griffiths, Pearson Education, Dorling Kindersley, 2007.
Rajput, Shailendra, and Asher Yahalom. 2021. "Newton’s Third Law in the Framework of Special Relativity for Charged Bodies" Symmetry 13, no. 7: 1250. [CrossRef]
Pascal Derendorf, Anatoly F. Volkov, Ilya M. Eremin "Nonlinear Response of Diffusive Superconductors to ac-electromagnetic Fields" arXiv:2308.00838 [cond-mat.supr-con].
L Q Dantas et al 2023 J. Phys.: Condens. Matter 35 375801.
Mads Anders Jørgensen, 2023, Single-photon superradiance in nanophotonics: a multiple-scattering perspective, Department of Electrical and Photonics Engineering DTU, PhD thesis.
Carlo Forestiere and Giovanni Miano "Integral formulation of the macroscopic quantum electrodynamics in dispersive dielectric objects" Phys. Rev. A 107, 063705 – Published 14 June 2023.
I. Newton, Philosophiae Naturalis Principia Mathematica (1687).
H. Goldstein , C. P. Poole Jr. & J. L. Safko, Classical Mechanics, Pearson; 3 edition (2001).
Miron Tuval and Asher Yahalom "Momentum Conservation in a Relativistic Engine" Eur. Phys. J. Plus (2016) 131: 374. [CrossRef]
R. P. Feynman, R. B. R. P. Feynman, R. B. Leighton & M. L. Sands, Feynman Lectures on Physics, Basic Books; revised 50th anniversary edition (2011).
Yahalom, Asher. 2022. "Newton’s Third Law in the Framework of Special Relativity for Charged Bodies Part 2: Preliminary Analysis of a Nano Relativistic Motor" Symmetry 14, no. 1: 94.
Yahalom, Asher. 2023. "Implementing a Relativistic Motor over Atomic Scales" Symmetry 15, no. 8: 1613. [CrossRef]
Jefimenko, O. D. , Electricity and Magnetism, Appleton-Century Crofts, New York (1966); 2nd edition, Electret Scientific, Star City, WV (1989).
Miron Tuval & Asher Yahalom "Newton’s Third Law in the Framework of Special Relativity" Eur. Phys. J. Plus (11 Nov 2014) 129: 240 DOI: 10.1140/epjp/i2014-14240-x. (arXiv:1302.2537 [physics.gen-ph]). [CrossRef]
Miron Tuval and Asher Yahalom "A Permanent Magnet Relativistic Engine" Proceedings of the Ninth International Conference on Materials Technologies and Modeling (MMT-2016) Ariel University, Ariel, Israel, July 25-29, 2016.
Asher Yahalom "Retardation in Special Relativity and the Design of a Relativistic Motor". Acta Physica Polonica A, Vol. 131 (2017) No. 5, 1285-1288. [CrossRef]
Yahalom "Preliminary Energy Considerations in a Relativistic Engine" Proceedings of the Israeli-Russian Bi-National Workshop, page 203-213, 28-31 August 2017, Ariel, Israel.
S. Rajput and A. Yahalom, "Preliminary Magnetic Energy Considerations in a Relativistic Engine: Mutual Inductance vs. Kinetic Terms" 2018 IEEE International Conference on the Science of Electrical Engineering in Israel (ICSEE), Eilat, Israel, 2018, pp. 1-5. [CrossRef]
S. Rajput and A. Yahalom, "Material Engineering and Design of a Relativistic Engine: How to Avoid Radiation Losses". Advanced Engineering Forum ISSN: 2234-991X, Vol. 36, pp 126-131. Submitted: 2019-06-16, Accepted: 2020-05-18, Online: 2020-06-17. ©2020 Trans Tech Publications Ltd, Switzerland.
Shailendra Rajput, Asher Yahalom & Hong Qin "Lorentz Symmetry Group, Retardation and Energy Transformations in a Relativistic Engine" Symmetry 2021, 13, 420. [CrossRef]
Harold White, Paul March, James Lawrence, Jerry Vera, Andre Sylvester, David Brady and Paul Bailey, Measurement of Impulsive Thrust from a Closed Radio-Frequency Cavity in Vacuum, Journal of Propulsion and Power, Vol. 33, No. 4, July-August 2017.

Figure 1. Two current strips.

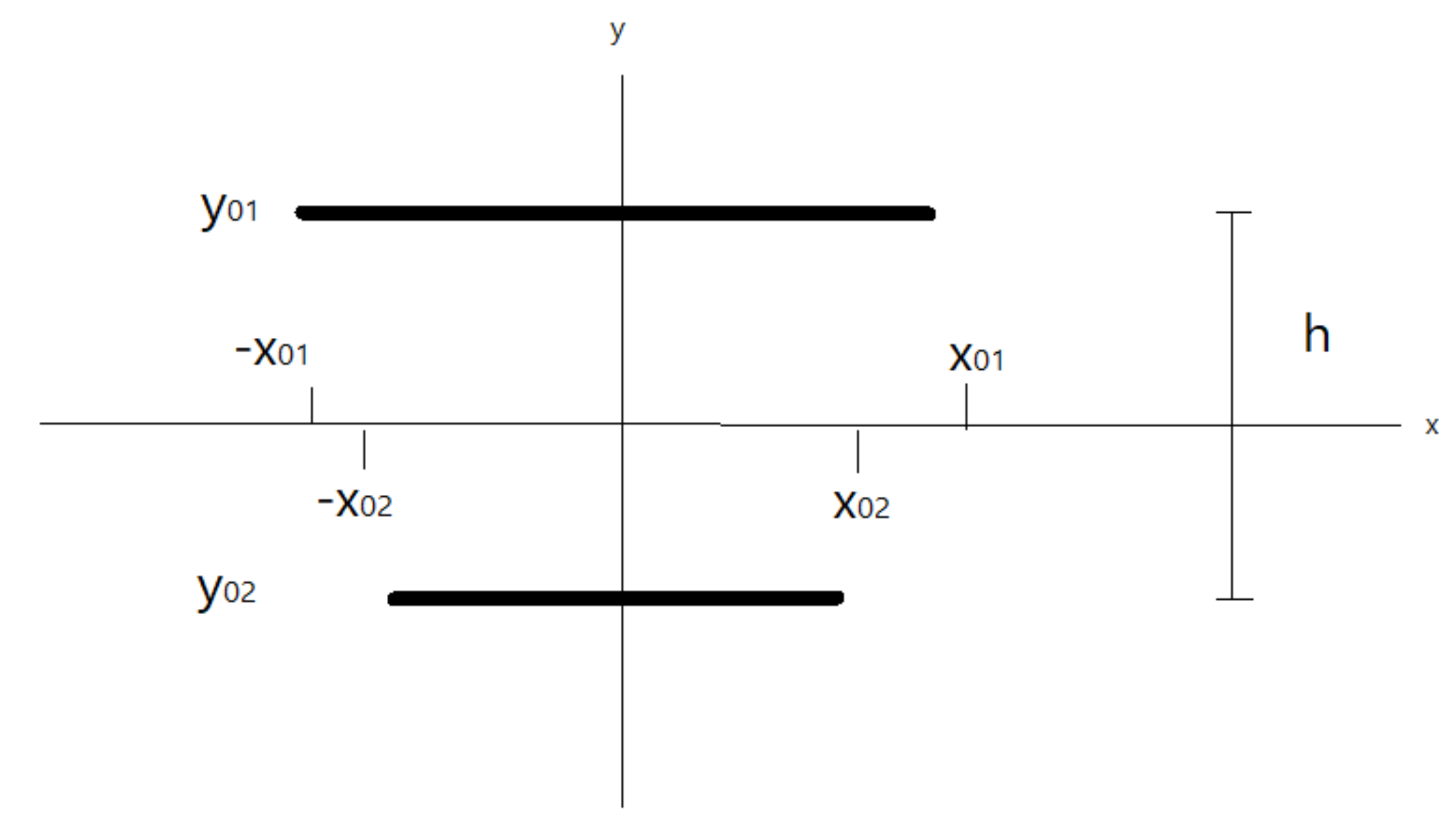
Figure 2.

| Γ^{21} |

, the functions approached asymptotically to a unit value.

Figure 2.

| Γ^{21} |

, the functions approached asymptotically to a unit value.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Time Dependent Retarded Electromagnetic Motors

Abstract

1. Introduction

2. Engine Optimization

3. General Considerations

4. Example

5. Discussion

6. Conclusions

References

MDPI Initiatives

Important Links

Subscribe