Prerpints.org logo
Preprint
Article

Mechanics of Topological High-Entropy Structures Made Out of ‘Einstein’ Puzzle Pieces

Altmetrics

Downloads

183

Views

121

Comments

0

This version is not peer-reviewed

Submitted:

18 July 2024

Posted:

19 July 2024

You are already at the latest version

Alerts
Abstract
People have always hoped to be able to fill an entire plane with ``single unit cells'' without periodicity. This wish was realized after the mathematician discovered a 13-sided ``single unit cell'' named `einstein'. These non-periodic tessellations generally exhibit anisotropic properties, making them superior in terms of mechanical performance compared to periodic structures. From the perspective of information entropy, the reason behind the improved mechanical properties of these structures is the higher entropy associated with non-periodic configurations. To quantify the disorder of non-periodic structures, we propose an entropy expression for the `einstein' metamaterial. To demonstrate the mechanical properties of these high-entropy structures, we fabricate specimens using 3D printing and conducte mechanical experiments. For comparative analysis, we also use ABAQUS to perform finite element analysis of the problem. The research results reveal that the mechanical properties of high-entropy structures created by the non-periodic stacking of cells are significantly improved compared to those of low-entropy structures created by periodic stacking. The conclusions drawn from the study of individual issues are generalizable and may be of assistance in future material and structural design.
Keywords: 
Subject: Physical Sciences  -   Applied Physics

1. Introduction

A few years ago, the first author of this paper attended an international academic conference in Rome, Italy. During a visit to the Colosseum, he noticed on the roadside near the ancient amphitheater a wall constructed from blocks of various shapes, stacked upon each other as shown in Figure 1. He marveled at the high level of mechanical expertise in Italian architecture and took a special photograph to remember the sight. At that time, it struck him that this wall, made from blocks of different shapes, possessed anisotropic properties within its surface, which obviously endowed it with excellent shear resistance. However, he also noticed that the blocks came in shapes with three, four, five, or even six sides, making it difficult to cover the entire wall using only one type of block. Since then, the quest for a “single tiling block” has been a persistent challenge for the first author.
In April 2023, the first author of this paper came across a news report [1] announcing the discovery of an elusive `einstein’ tile with 13 sides as shown in Figure 2. Upon seeing this news report, he promptly downloaded and studied the paper introducing the `einstein’ [2]. Then, on June 20, 2023, the first author sent an email to co-authors of the paper [2], and on June 21, 2023, received a reply from one of them, Craig S. Kaplan [3], who provided the coordinates of the `einstein’. Since then, we have begun to utilize the discovered `einstein’ for the design simulation and experimentation of mechanical metamaterials.
Although the name `einstein’ conjures up the iconic physicist, it comes from the German ein Stein, meaning `one stone’, referring to the single tile. The `einstein’ sits in a weird purgatory between order and disorder. Though the tiles fit neatly together and can cover an infinite plane, they are aperiodic, meaning they cant form a pattern that repeats [1].
Nonrepeating patterns can have real-world connections. Materials scientist Dan Shechtman won the 2011 Nobel Prize in chemistry for his discovery of quasicrystals [4], materials with atoms arranged in an orderly structure that never repeats, often described as analogs to Penroses tilings [5].
Metamaterials are materials or devices with artificial structures that can control and utilize physical mechanisms in novel ways, achieving properties or functions that are not possible with natural materials. Metamaterials (or a type of mechanism with functionality) possess unprecedented characteristics, which have promoted the development of advanced devices and equipment. Mechano-metamaterials, with unique mechanical properties, can provide some novel functional characteristics, such as high energy absorption efficiency, ultra-toughness, complex bistable states, tunable stiffness, negative thermal expansion, and tension-compression behavior, etc. For examples, Bertoldi et al. [6] discuses the main fundamental mechanisms underlying mechanical metamaterials. Ashby [7] studies the bending-dominated and stretching-dominated density scaling of mechanical properties in cellular solids. Lakes [8] provides an introduction to auxetic materials (foam structures) showing negative Poissons ratio. Hanifpour et al. [9] provides a systematic study of the role of disorder in auxetic metamaterials.
The standard design strategy for mechanical metamaterials, based on the periodic replication of unit cells, appears in contrast to many functionally efficient but structurally disordered biological materials observed in nature and mega engineering structures as shown in Figure 3, this is incorporating disorder into their design can provide improved functionalities over ordered structures. This suggests that including randomness in meta material design could provide advantages that are yet to be explored [10].
Due to the benefits of disorder, non-periodicity, or randomness in improving material performance, there has been increasing interest. Tüzes et al. [11] study the fracture problem and state that disorder is beneficial for influencing local disorder on strain localization and ductility in strain softening materials. Bonfanti et al. [12] demonstrate how to generate disordered metamaterials using Monte Carlo simulations combined with deep learning. Liu et al. [13] show how to design irregular architected metamaterials with a random growth algorithm. Li and Sun [14,15] study the optimization of a lattice structure inspired by glass sponge, and low-speed impact response of sandwich panels with bio-inspired diagonal-enhanced square honeycomb core. Wu and Sun [16] study on functional mechanical performance of array structures inspired by cuttlebone. Guo and Sun [17,18] study assembly and disassembly mechanics of elastic snap-fit cells, the detachable connection mechanics of thin-walled cylindrical/segmented torus snap fit docking. Wei and Sun [19,20] study pull-out mechanical properties of the Jigsaw connection of diabolical ironclad Beetles Elytra and cylindrical mechanical metamaterials with biomimetic honeycomb units of the diabolical ironclad beetle. Clarke et al. [21] investigate an isotropic zero Poisson’s ratio metamaterial based on the aperiodic `hat’ monotile. Moat [22] study a class of aperiodic honeycombs with tuneable mechanical properties. Wang et al. [23] study the unprecedented strength enhancement observed in interpenetrating phase composites of aperiodic lattice metamaterials. Naji and Abu Al-Rub [24] study the effective elastic properties of novel aperiodic monotile-based lattice metamaterials. Jung et al. [25] study aperiodicity is all you need: aperiodic monotiles for high-performance composites.

2. Entropy of Topological Disorder Materials

From a thermodynamic perspective, disorder can be quantified by borrowing the concept of thermodynamic entropy. Clearly, for periodic structures, the entropy is relatively low, whereas for disordered structures, the entropy should be relatively high. Therefore, to obtain supramaterials with superior mechanical properties, one design philosophy is to incorporate high entropy, therefore Sun [26,27] proposed a conceit of high-entropy structural mechanics by in two seminars. However, complete disorder would present challenges for manufacturing and controlling mechanical properties. An ideal situation is that any structure can be constructed by stacking montile; `einstein’ is currently the best choice for these montile [1,2]. The question arises as to how to define the entropy of structures composed of `einstein’ units. The difficulty here is how to characterize the change in entropy that occurs when the topology is altered while maintaining the material’s properties unchanged. This is different from the definition of entropy in high-entropy materials, which is calculated based on the ratio of components from different materials.

2.1. Entropy Definition of Topological Disorder Materials

Defining entropy for disordered materials is complex because it requires understanding the disorder and randomness within the system. For topological disordered cells, the entropy might also involve the topology and geometry of the disorder. This could mean considering the spatial distribution of the cells, their relative orientations, and any patterns or correlations that may emerge.
The structure composed of cells named `einstein’ exhibits a uniformity in size, shape, and topology among its cells. The only difference lies in each cell’s unique orientation. This diversity in directionality signifies disorder and forms the basis for our definition of entropy.
By coloring the `einstein’ cells with the same orientation within the structural diagram with the same color, each color represents a specific orientation. Therefore, the entropy of this structure can be defined as the sum of the product of each color’s proportion and its corresponding entropy value and can be characterised by Shannon entropy [28]. Claud Shannons paper ’A mathematical theory of communication’ [28] published in July and October of 1948 is the Magna Carta of the information age. Shannon’s discovery of the fundamental laws of data compression and transmission marks the birth of information theory.
Assuming there are a total of N `einstein’ cells, with N a cells facing upwards and N b cells facing downwards, that is, N = N a + N b . If the proportion of each orientation among the cells facing upwards is p i ( i = 1 , 2 , . . . , n ) , then the entropy of this structure can be defined as follows:
H a = − ∑ i = 1 K a p i N a log 2 p i N a ,
where K a is the number of same-orientation in type-a. (Here it is assumed that 0 log 2 0 = 0 ).
If the proportion of each orientation among the cells facing downwards is q i ( i = 1 , 2 , . . . , m ) , then the entropy of this structure is:
H b = − ∑ i = 1 K b q i N b log 2 q i N b ,
where K b is the number of same-orientation in type-a.
By considering the weightage of the upwards-facing cells as N a N a + N b and the downwards-facing cells as N b N a + N b , the total entropy can be obtained as:
H = N a N a + N b H a + N b N a + N b H b .

2.2. Entropy of the `Einstein’ Tile Honeycomb Metamaterial

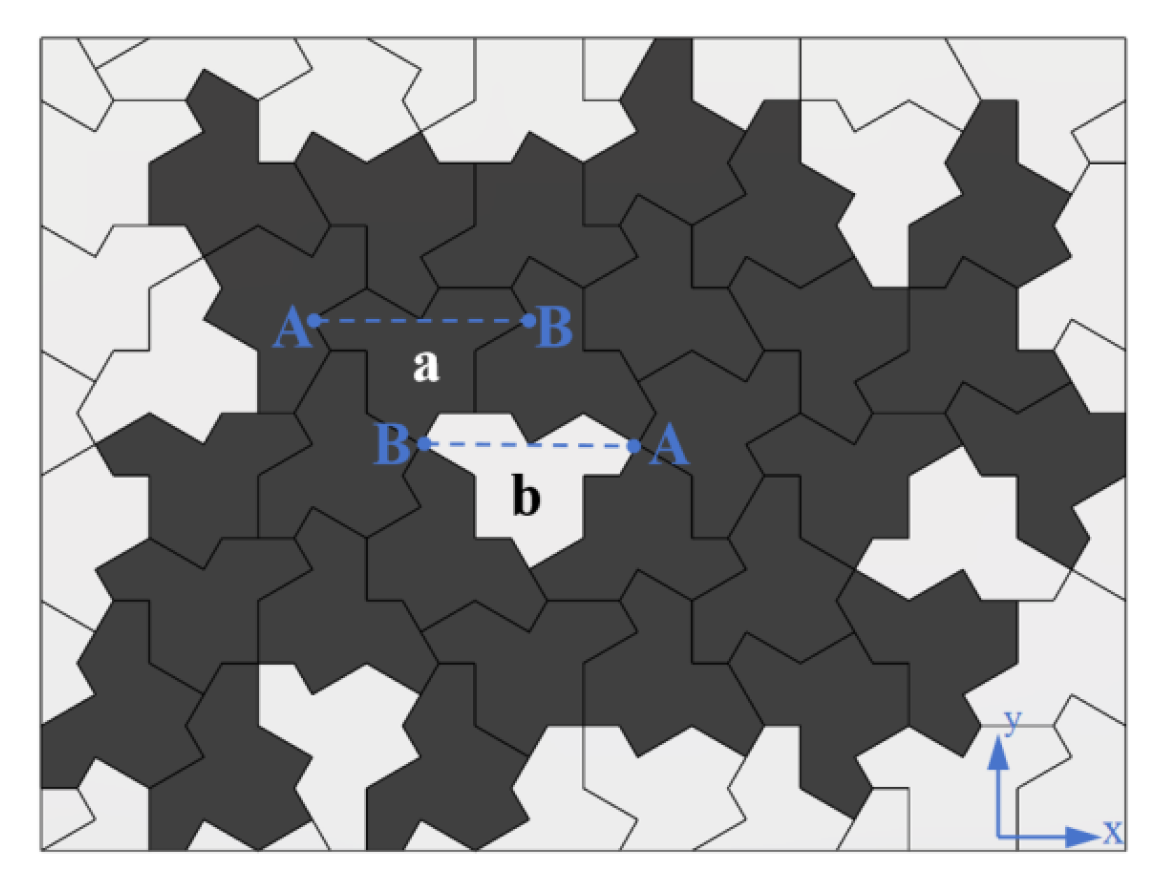
We consider the two-dimensional plane of the `einstein’ tile honeycomb metamaterial designed as described above, as illustrated in Figure 4. Since the `einstein’ tile is obtained by rotation and mirroring of a non-periodic arrangement, we divide the `einstein’ tile into two types, labeled as type-a and type-b (where type-a and type-b are mirror images of each other). The line connecting the two outermost points of the `einstein’ tile cell is AB/BA, and the rotation angle of the `einstein’ tile with respect to the x-axis (clockwise rotation is positive, counterclockwise rotation is negative) is defined as the relative rotation angle θ of the `einstein’ tile. Only the rotation of the complete `einstein’ tile cell is considered within the entire plane system. Table 1 lists the relative rotation angles and quantities of the two types of `einstein’ tiles. In the same scenario, the relative rotation angle of each square cell in the two-dimensional plane of the square honeycomb metamaterial is 0.
Applying the entropy definition in Eq.1 to the Type-a (black color in Figure 4), we have its entropy as follows
H a = − ( 5 29 log 2 5 29 + 8 29 log 2 8 29 + 6 29 log 2 6 29 + 5 29 log 2 5 29 + 2 29 log 2 2 29 + 3 29 log 2 3 29 ) ≈ 2.461982945 .
Applying the entropy definition in Eq.2 to the Type-a (white color in Figure 4), we have its entropy as follows
H b = − ( 1 5 log 2 1 5 + 1 5 log 2 1 5 + 2 5 log 2 2 5 + 1 5 log 2 1 5 ) ≈ 1.921928095 .
By considering the weightage of the upwards-facing cells as N a N a + N b and the downwards-facing cells as N b N a + N b , the total entropy can be obtained as:
H e i n s t e i n = 29 34 H a + 5 34 H b = 2.38 .
For any periodic structure as shown in Figure 5, since the cells do not rotate, all cells have the same directionality, that is, p i = N a ( i = 1 , 2 , 3 , . . . N a ) , which implies p i N a = 1 . Therefore, the entropy of the periodic structure is zero, that is,
H p e r i o d i c = − ∑ i = 1 K a p i N a log 2 p i N a = − ∑ i = 1 K a ( 1 ) log 2 ( 1 ) = 0 .
The quantitative study from here reveals that the entropy of non-periodic structures is much higher than that of periodic structures. Since high entropy corresponds to anisotropy in materials, generally, anisotropic materials have better mechanical properties than isotropic materials. Therefore, structures with high entropy have superior mechanical properties compared to those with low entropy. This allows for the prediction of a material’s mechanical properties in advance, without the need for specific experiments and numerical simulations, by calculating the structural information entropy.

3. Numerical Simulation Compared with Experiment

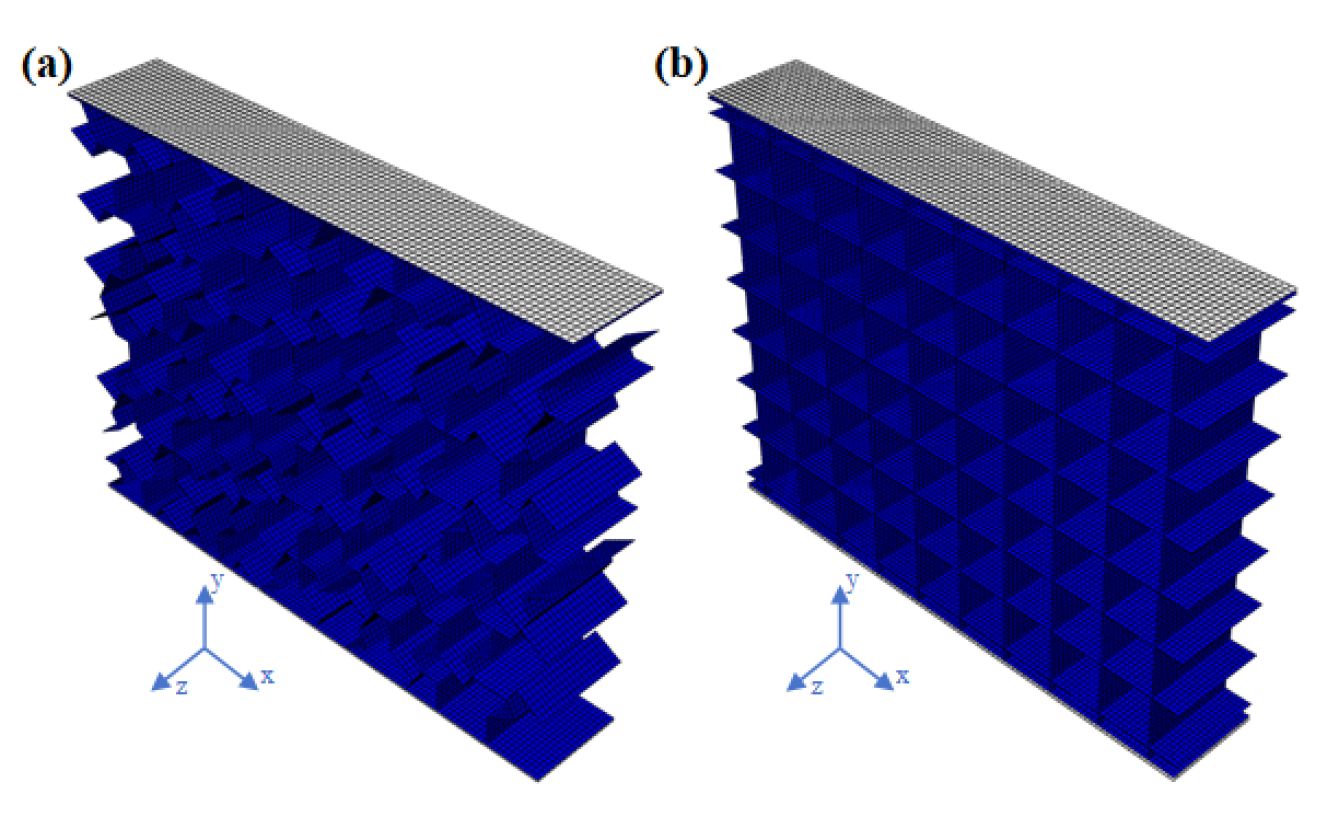
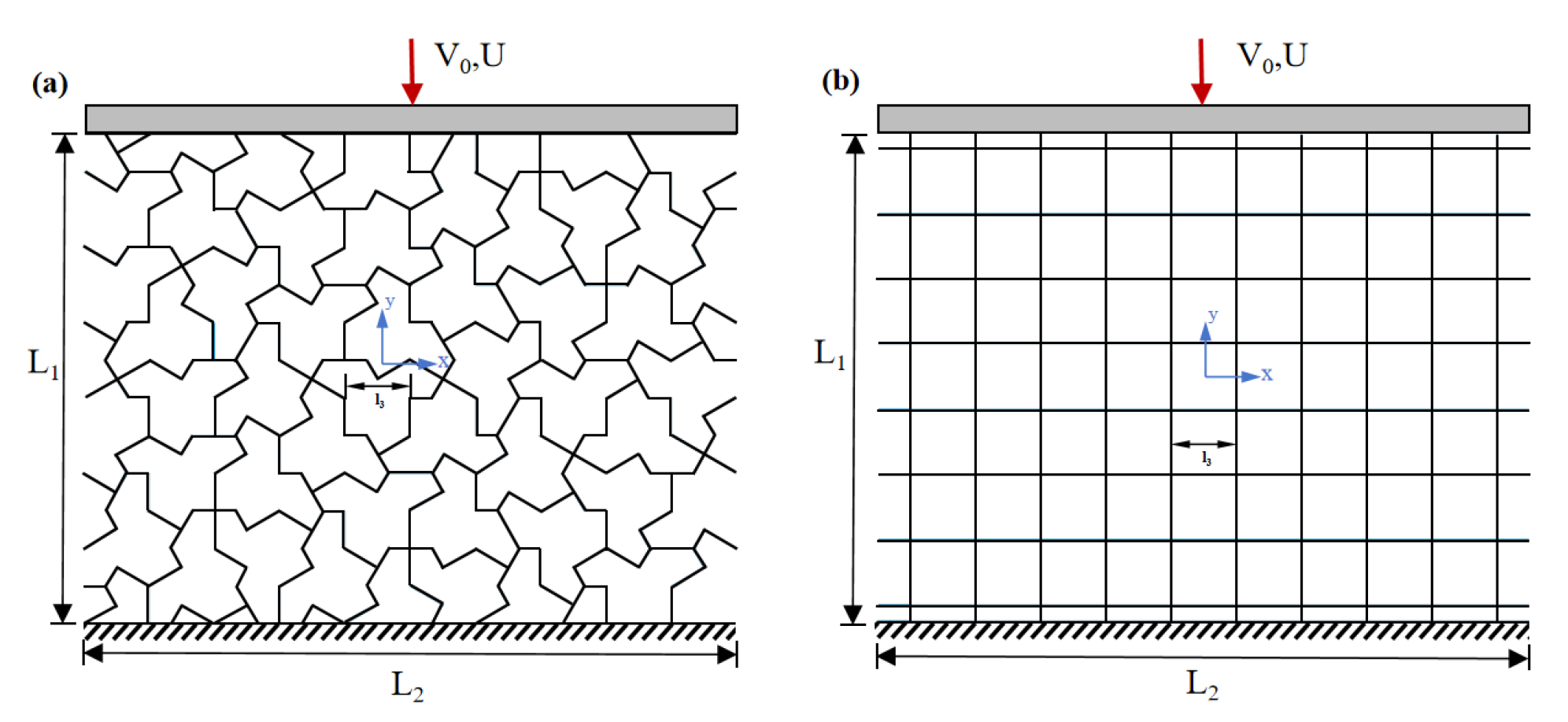
The compression and deformation mechanism of two types of honeycomb metamaterials were studied by ABAQUS/EXPLICIT 2023 simulation software. Based on the designed geometries, three-dimensional finite element models of the honeycomb metamaterials with different cells were established. The finite element models were meshed using shell elements (S4R). To simulate the compression experimental conditions in the numerical simulation, rigid plates were placed on the top and bottom surfaces of the structure. As shown in Figure 6, the longitudinal direction within the finite element structures plane is the y direction, and the transverse direction within the plane is the x direction. The rigid plate on the top surface was moved downward along the y direction at a constant velocity of V 0 = 4 m m / m i n (the overall displacement of the structure is U), while the rigid plate on the bottom surface was fully fixed. In the finite element simulation, a friction coefficient μ = 0.3 was used, with a general contact implementation, normal contact set as hard contact, and penetration was not allowed.

3.1. Compression Deformation Characteristics and Mechanical Properties

The experimental and simulated deformation processes of the `einstein’ tile honeycomb and square honeycomb metamaterials are shown in Figure 7. We were able to clearly observe the deformation patterns of the two honeycomb metamaterials during compression and evaluate their mechanical properties.
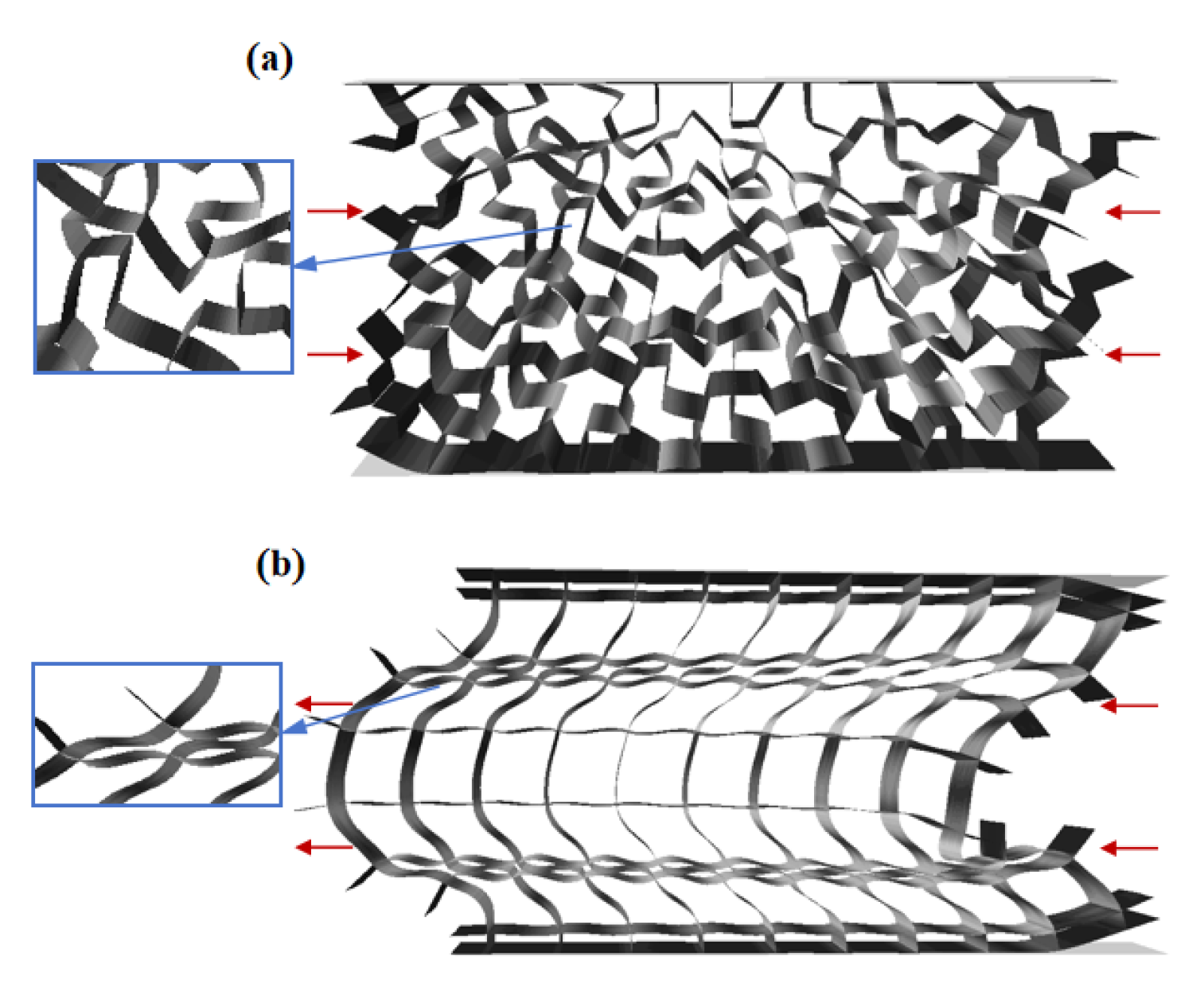
Figure 7(a) shows the experimental and simulated deformation processes and comparisons of the `einstein’ tile honeycomb metamaterial. It can be clearly observed that due to the non-periodic arrangement of the `einstein’ tiles, there is a trend of mutual interference and resistance to deformation during the compression process, and the honeycomb metamaterial generally has a stable deformation pattern. The entire structure undergoes axial compression-contraction, and the `einstein’ tile honeycomb metamaterial exhibits excellent mechanical properties. As the amount of compression increases, the structure begins to collapse, and ultimately the structure is densely solidified, but there is no buckling deformation in the overall structure. The deformation of this finite element model is consistent with the experimental results. Figure 7(b) presents the experimental and simulated deformation processes and comparisons of the square honeycomb metamaterial. It can be clearly observed that due to the asymmetric deformation of the square honeycomb metamaterial, the nodes at the structures edges fail prematurely, leading to a tendency of the overall structure to tilt primarily to one side and overall buckling deformation. The deformation of this finite element model is also consistent with the experimental results. In summary, compared to the traditional periodically arranged square honeycomb metamaterials, the non-periodically arranged `einstein’ tile honeycomb metamaterials have a more stable compression deformation process, as shown in Figure 8.
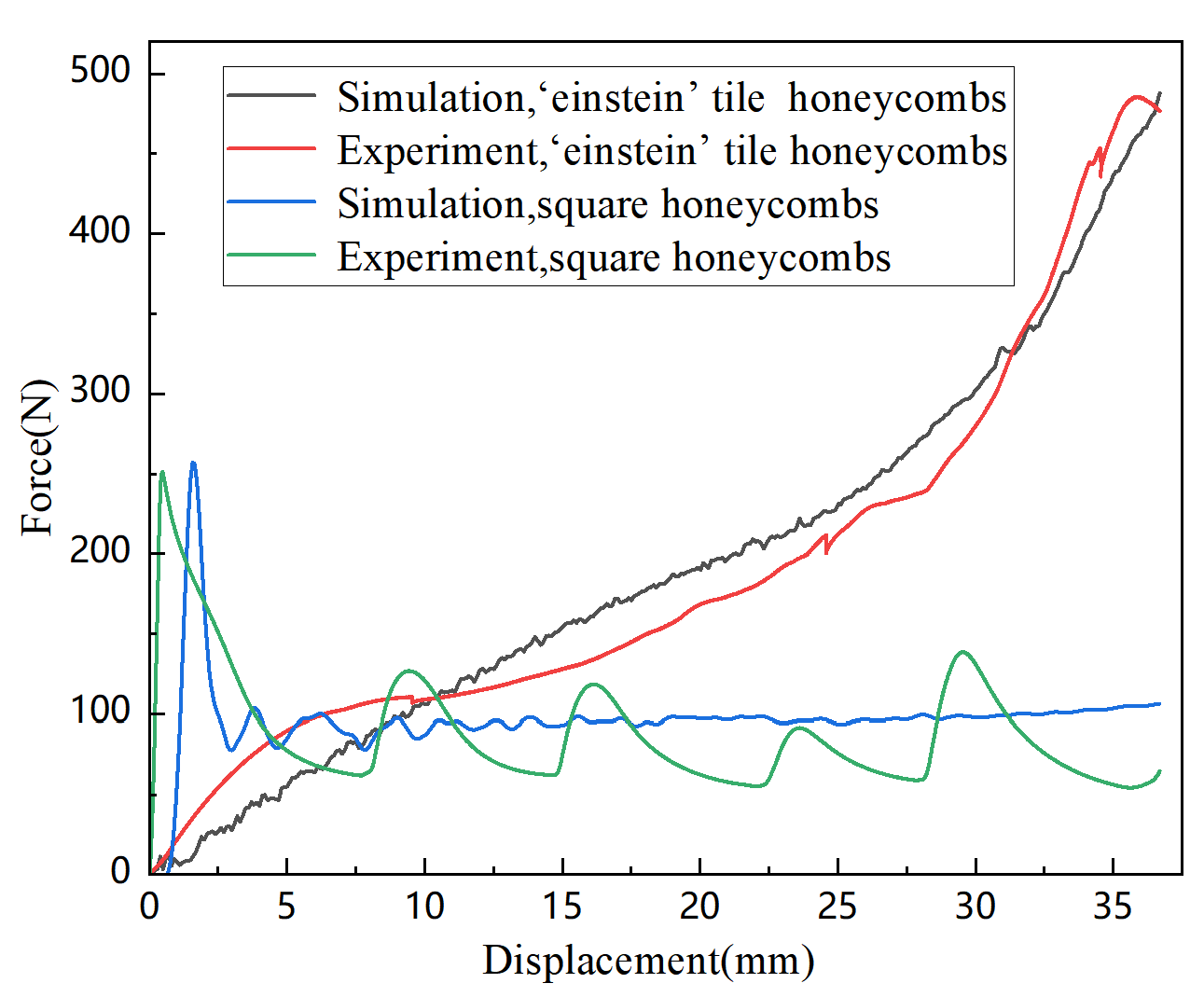
To evaluate the compressive mechanical properties of the `einstein’ tile honeycomb and square honeycomb metamaterials at room temperature, we have plotted the force-displacement curves of the two honeycomb metamaterials at room temperature, including both experimental and simulated results, as shown in Figure 9.
Finite element simulations successfully predicted the force-displacement relationships during in-plane compression of the two honeycomb metamaterials. Figure 9 confirms the good agreement between the simulated curves and the experimental force-displacement curves of compression. We only compare the force-displacement curves for the overall vertical displacement U < 38 m m , as after U > 38 m m the force increases sharply due to the compaction of the honeycomb structure. It can be observed from Figure 8 that the stiffness and strength of the `einstein’ tile honeycomb metamaterial are significantly higher than those of the square honeycomb metamaterial, and the force-displacement curve of the `einstein’ tile honeycomb metamaterial rises steadily without any obvious peaks or valleys (the sharp points on the red curve represent local fractures, which are related to the material properties selected for the experiment), indicating excellent overall stability of the structure. In summary, compared to the traditional periodic square honeycomb metamaterial with periodic arrangement, the `einstein’ tile honeycomb metamaterial with non-periodic arrangement exhibits superior mechanical properties.

3.2. Absorption Performance Analysis

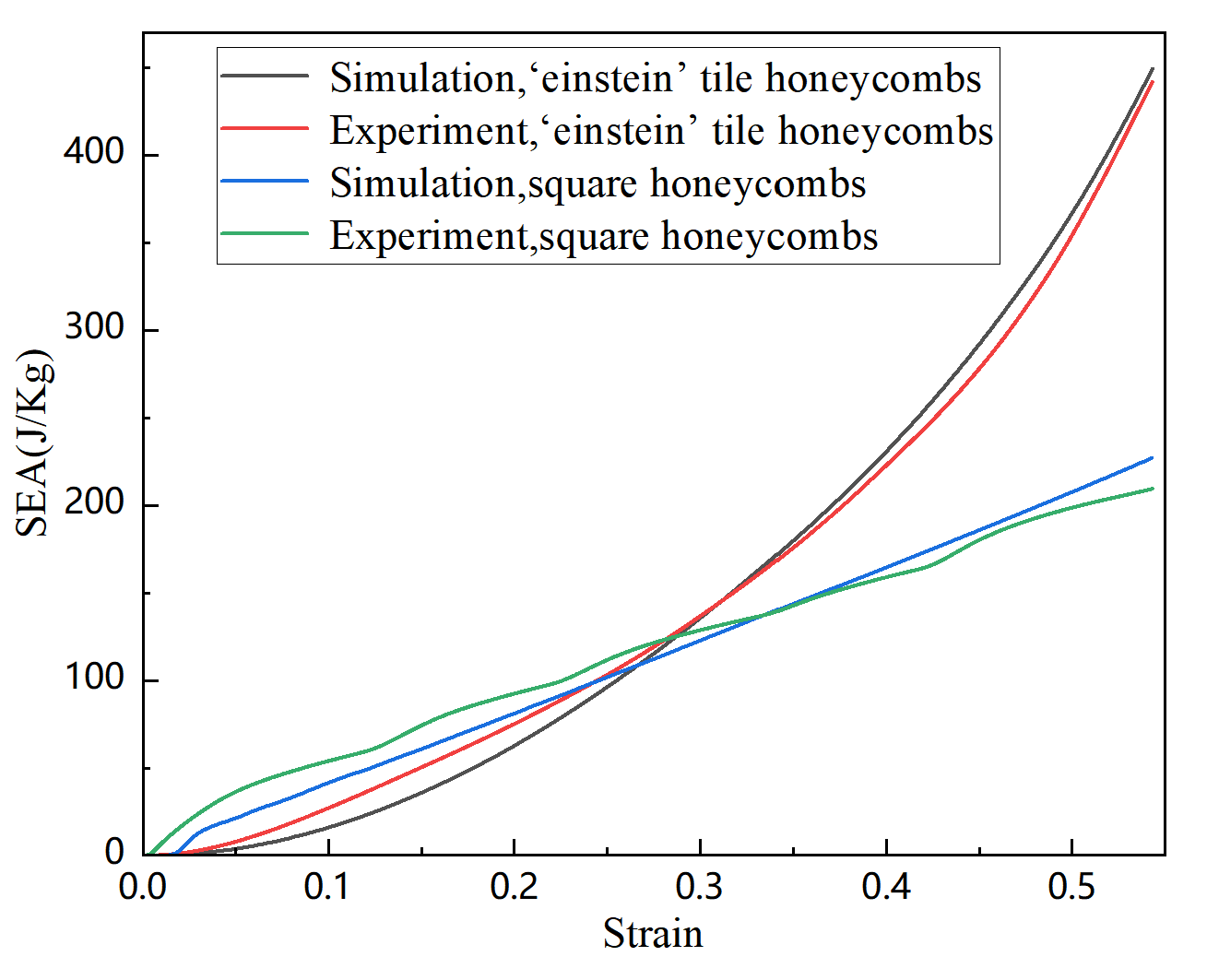
Specific energy absorption (SEA) is a common index to assess the energy absorption of a structure. The value of SEA is proportional to the energy absorption capacity of the structure.SEA generally indicates the energy absorbed per cell element mass and can be written as:
S E A = E A ε M
where E A ε is the energy absorbed when the axial deformation is ε . M is the weight of the energy-absorbing structure. We weighed three specimens of the two 3D-printed honeycomb metamaterials before the experiment, as shown in Figure 10. Based on Eq.8, the relationship between the energy absorption per unit mass and the nominal strain of the `einstein’ tile honeycomb and square honeycomb metamaterials, including both experimental and simulated results, is shown in Figure 11. It can be seen that under quasistatic compression, the `einstein’ tile honeycomb metamaterial absorbs significantly more energy. In conclusion, compared to the traditional periodic square honeycomb metamaterial with periodic arrangement, the non-periodic `einstein’ tile honeycomb metamaterial has a superior energy absorption capacity.

4. Conclusions and Perspectives

Through the study of structural mechanics derived from the Einstein cell puzzle, the following conclusion can be drawn. The non-periodic structures generated by introducing disorder exhibit superior mechanical properties compared to periodic structures, and the underlying reason for this is that non-periodic structures generally have high information entropy. By utilizing the information entropy of structures, it is possible to qualitatively predict the mechanical properties of materials without the need for experimental or computational simulations. Therefore, this research aids in the structural design of materials. It is particularly noted that, to the best of the author’s knowledge, this paper is the first to propose a definition of topological entropy from an information-theoretic perspective. Such theoretical research should be considered a theoretical contribution to the design of metamaterials.

5. Experimental Section

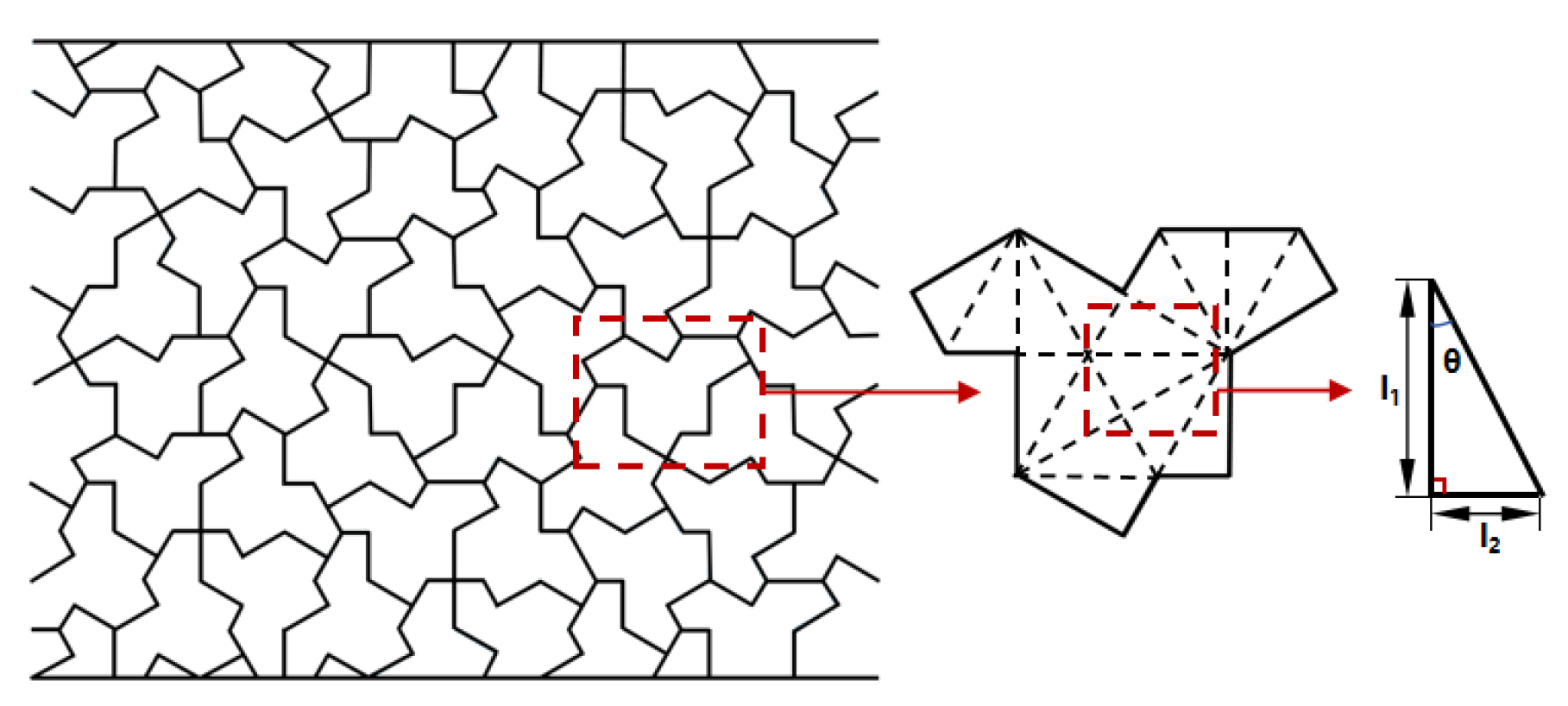
Structural design The `einstein’ tile is applied as a honeycomb unit in the design of metamaterials, named the `einstein’ tile honeycomb. As shown in Figure 12, the two-dimensional microstructure of the `einstein’ tile honeycomb is a 13-sided polygon, consisting of 16 right-angled triangle units. The sides of the 13-sided unit are constructed from the sides of the right-angled triangles, with the parameters defined as follows [3]: tan θ = l 2 l 1 = 1 3 . The established `einstein’ tile honeycomb is formed by rotating the 13-sided units along the x,y directions and mirroring the non-periodic arrangement.
To better understand the mechanical properties and energy absorption of the `einstein’ tile honeycomb (Figure 13(a)), a honeycomb structure with regular square cells was also established for comparison. The square honeycomb metamaterial is composed of square cells arranged periodically along the x,y directions, as shown in Figure 13(b).
A series of geometric parameters were established, where the side lengths of the right-angle triangle cells are l 1 = 3 3 m m , l 2 = 3 m m and the side length of the square cells is l 3 = 9 m m . The other parameters of the two honeycomb structures are the same, including the cell wall thickness t = 0.6 m m and the out-of-plane thickness h = 16 m m .
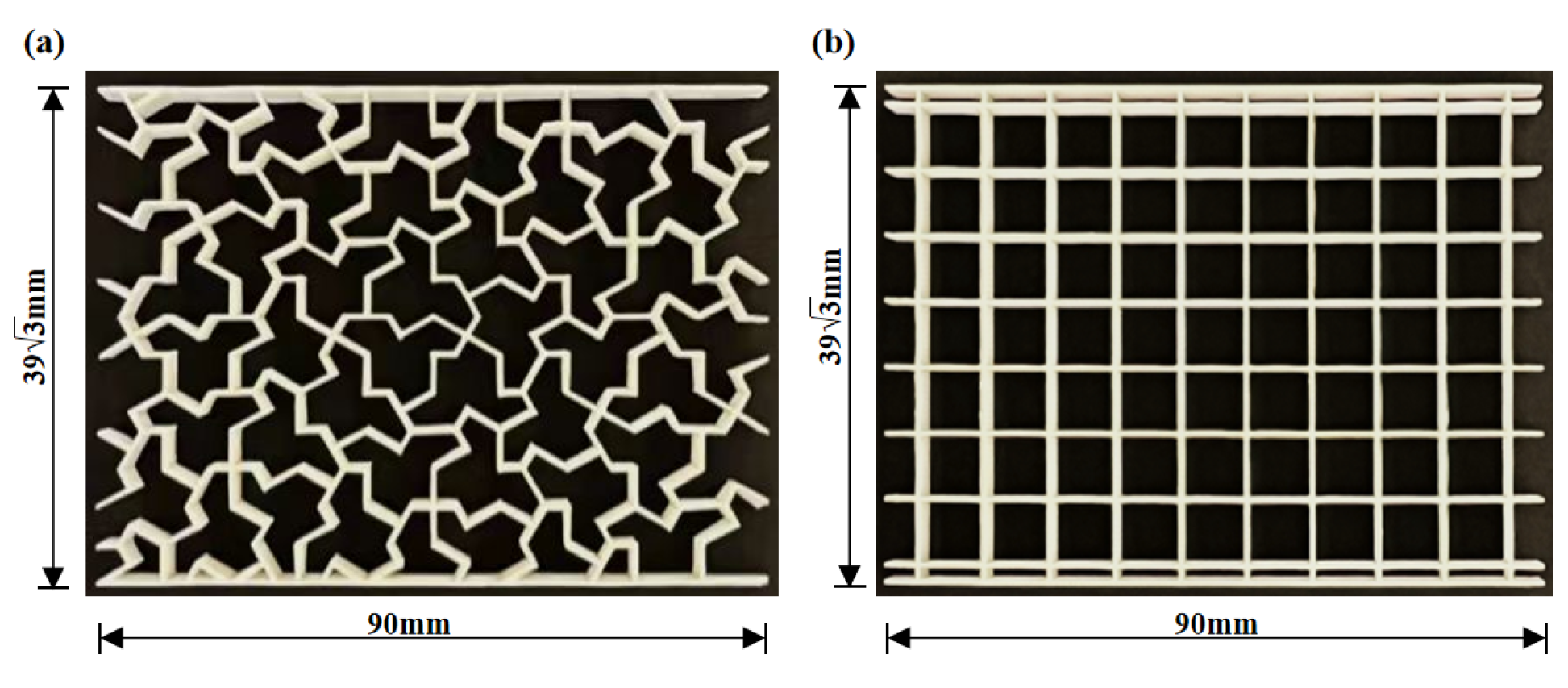
Sample manufacturing The experimental specimens were fabricated using the Chinese-Swedish iSLA880 photocurable laser 3D printer, with white photoresin as the printing material, to print two configurations of honeycomb metamaterials. To ensure accurate and efficient printing, the process was carried out at room temperature with a printing layer thickness 0.1 m m . Figure 14 shows the specimens of the two honeycomb metamaterials, both with dimensions of 90 m m × 90 3 m m × 16 m m .
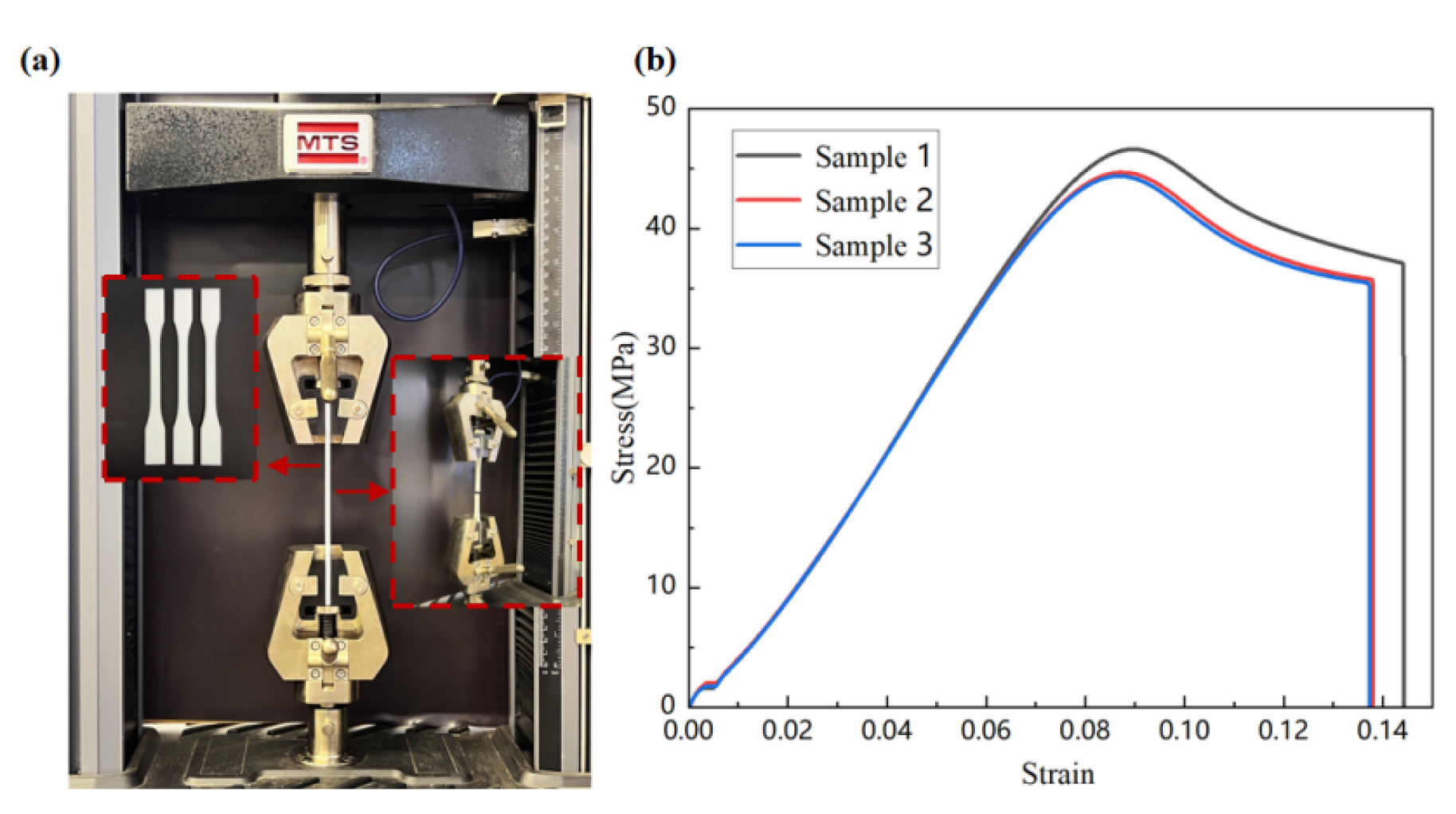
Mechanical testing First, the material properties of the honeycomb structure were tested, and then these obtained material properties were applied to finite element simulations to model the compression deformation process of the two types of honeycomb structures. Specimens were prepared using a Sweden-China iSLA880 photocurable laser 3D printer in the shape of a dumbbell, with white photocurable resin as the printing material. Quasi-static isothermal tensile experiments were conducted at room temperature using a universal testing machine (MTS) to determine the stress-strain curve, thereby obtaining the tensile performance parameters of the material. The experimental equipment for determining the tensile specimens are shown in Figure 15 and the stress-strain curve are shown in Figure 16.
The unit design of the metamaterial structure determines the mechanical properties and energy absorption capacity of the metamaterial. To evaluate the mechanical properties and energy absorption capabilities of the two honeycomb metamaterials, we conducted quasistatic compression tests at room temperature using an MTS universal testing machine. The loading rate was set at 4 m m / m i n , and the loading process continued until the specimens reached their compaction stage. To ensure the accuracy of the experiments, the same type of specimen was tested under the same conditions three times. The deformation process of the specimens during compression was recorded using a camera.

Data Availability Statement

The data supporting the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare that there are no competing financial interests.

References

  1. E. Conover, Mathematicians have finally discovered an elusive ’einstein’ tile, Science News, April 24, 2023.
  2. Smith, D. , Myers, J. S., Kaplan, C. S. Goodman-Strauss, C. An aperiodic monotile, arXiv preprint. arXiv:2303.10798 (2023).
  3. C. S. Kaplan, Private commumication, 21 June, 2023.
  4. D. Shechtman, et al. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 53, 1951 (1984).
  5. I. Georgescu, 50 years of Penrose tilings, Nat Rev Phys 6, 408 (2024).
  6. K. Bertoldi, V. K. Bertoldi, V. Vitelli, J. Christensen & M. van Hecke, Flexible mechanical metamaterials. Nat. Rev. Mater. 2, 17066 (2017).
  7. M. Ashby, The properties of foams and lattices. Phil. Trans. R. Soc. A 364, 15-30 (2006).
  8. R. Lakes, Foam structures with a negative Poissons ratio. Science 235, 1038C1040 (1987).
  9. M. Hanifpour, C.F. M. Hanifpour, C.F. Petersen, M.J. Alava & S. Zapperi, Mechanics of disordered auxetic metamaterials. Eur. Phys. J. B 91, 271 (2018).
  10. M. Zaiser and S. Zapperi, Disordered mechanical metamaterials, Nat Rev Phys 5, 679-688 (2023).
  11. D. Tüzes, P.D. D. Tüzes, P.D. Ispnovity & M. Zaiser, Disorder is good for you: the influence of local disorder on strain localization and ductility of strain softening materials, Materials Today, Volume 73, March/April 2024.
  12. S. Bonfanti, R. S. Bonfanti, R. Guerra, F. Font-Clos, D. Rayneau-Kirkhope & S. Zapperi, Automatic design of mechanical metamaterial actuators. Nat. Commun. 11, 4162 (2020).
  13. K. Liu, R. K. Liu, R. Sun, & C. Daraio, Growth rules for irregular architected materials with programmable properties. Science 377, 975-981 (2022).
  14. Q.W. Li, B.H. Q.W. Li, B.H. Sun, Optimization of a lattice structure inspired by glass sponge. Bioinspiration & Biomimetics, 18(1): 016005 (2022).
  15. Q.W. Li, B.H. Q.W. Li, B.H. Sun, Numerical analysis of low-speed impact response of sandwich panels with bio-inspired diagonal-enhanced square honeycomb core. International Journal of Impact Engineering, 173, 104430 (2023).
  16. F. Wu and B.H. Sun, Study on functional mechanical performance of array structures inspired by cuttlebone. Journal of the Mechanical Behavior of Biomedical Materials, 136, 105459 (2022).
  17. X.L. Guo and B.H. Sun, Detachable connection mechanics of thin-walled cylindrical snap fit docking. Extreme Mechanics Letters, 67, 102122 (2024).
  18. X.L. Guo and B.H. Sun, Mechanics of a thin-walled segmented torus snap fit. Thin-Walled Structures, 198, 111676 (2024).
  19. J. Wei and B.H. Sun, Bioinspiration: Pull-Out Mechanical Properties of the Jigsaw Connection of Diabolical Ironclad Beetles Elytra, Acta Mech. Solida Sin. 36, 86C94 (2023).
  20. J. Wei and B.H. Sun, Study on the mechanical properties of cylindrical mechanical metamaterials with biomimetic honeycomb units of the diabolical ironclad beetle, Extreme Mechanics Letters, 67 102127 (2024).
  21. D.J. Clarke, F. D.J. Clarke, F. Carter, I. Jowers, R.J. Moat, An isotropic zero Poisson’s ratio metamaterial based on the aperiodic `hat’ monotile, Applied Materials Today, 35 101959 (2023).
  22. R.J. Moat et al., A class of aperiodic honeycombs with tuneable mechanical properties, Aplied Materials Today, 37 102127 (2024).
  23. X.X. Wang, et al. Unprecedented Strength Enhancement Observed in Interpenetrating Phase Composites of Aperiodic Lattice Metamaterials, Adv. Funct. Mater, 2406890 2024.
  24. M.M. Naji and R.K. Abu Al-Rub, study the effective elastic properties of novel aperiodic monotile-based lattice metamaterials, Materials & Design, 244 113102(2024).
  25. J. Jung, A.L. J. Jung, A.L. Chen, G.X. Gu, Aperiodicity is all you need: Aperiodic monotiles for high-performance composites. Materials Today. 73, 1-8 (2024).
  26. B.H. Sun, High-entropy structural mechanics, Lect. 25, a series seminar of Inst. of Mechanics and Technology, Xi’an Uni. of Architecture and Technology, 26 Oct. 2023. https://imt.xauat.edu.cn/info/1008/3763.htm.
  27. B.H. Sun, Thermodynamics and high-entropy structural mechanics, Lect. 27, a series seminar of Inst. of Mechanics and Technology, Xi’an Uni. of Architecture and Technology, 15 Nov. 2023. https://imt.xauat.edu.cn /info/1008/3801.htm.
  28. C.E. Shannon, A mathematical theory of communication, Bell Syst. Tech. J., vol. 27, 379-423, 623-656, July-Oct. 1948.
Preprints 112582 g001
Figure 1. On the way to the Colosseum, photos took by Bohua Sun.
Figure 1. On the way to the Colosseum, photos took by Bohua Sun.
Preprints 112582 g001
Preprints 112582 g002
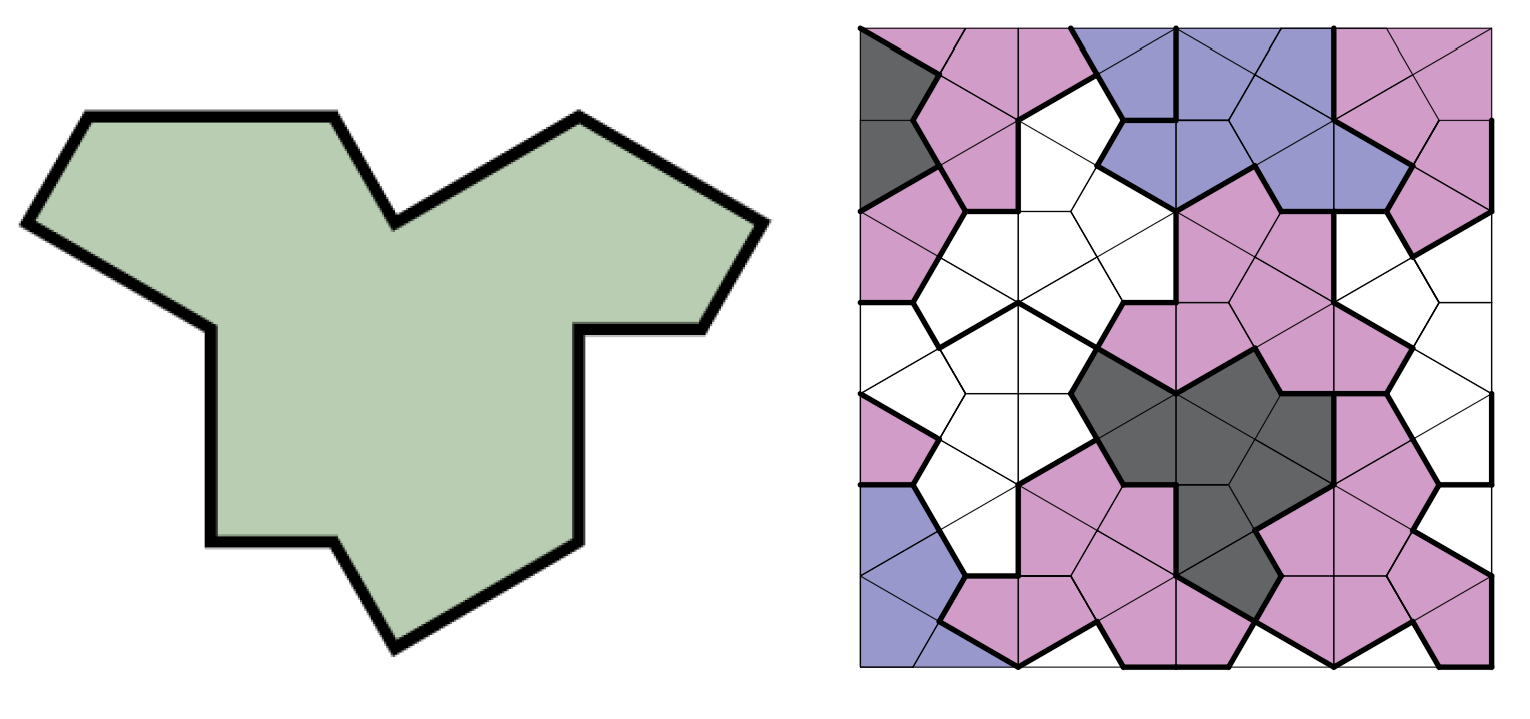
Figure 2. Left: Monotile: A 13-sided tile called `einstein’. Right: The ’einstein’ forms a pattern that covers an infinite plane yet it cannot repeat [1,2].
Figure 2. Left: Monotile: A 13-sided tile called `einstein’. Right: The ’einstein’ forms a pattern that covers an infinite plane yet it cannot repeat [1,2].
Preprints 112582 g002
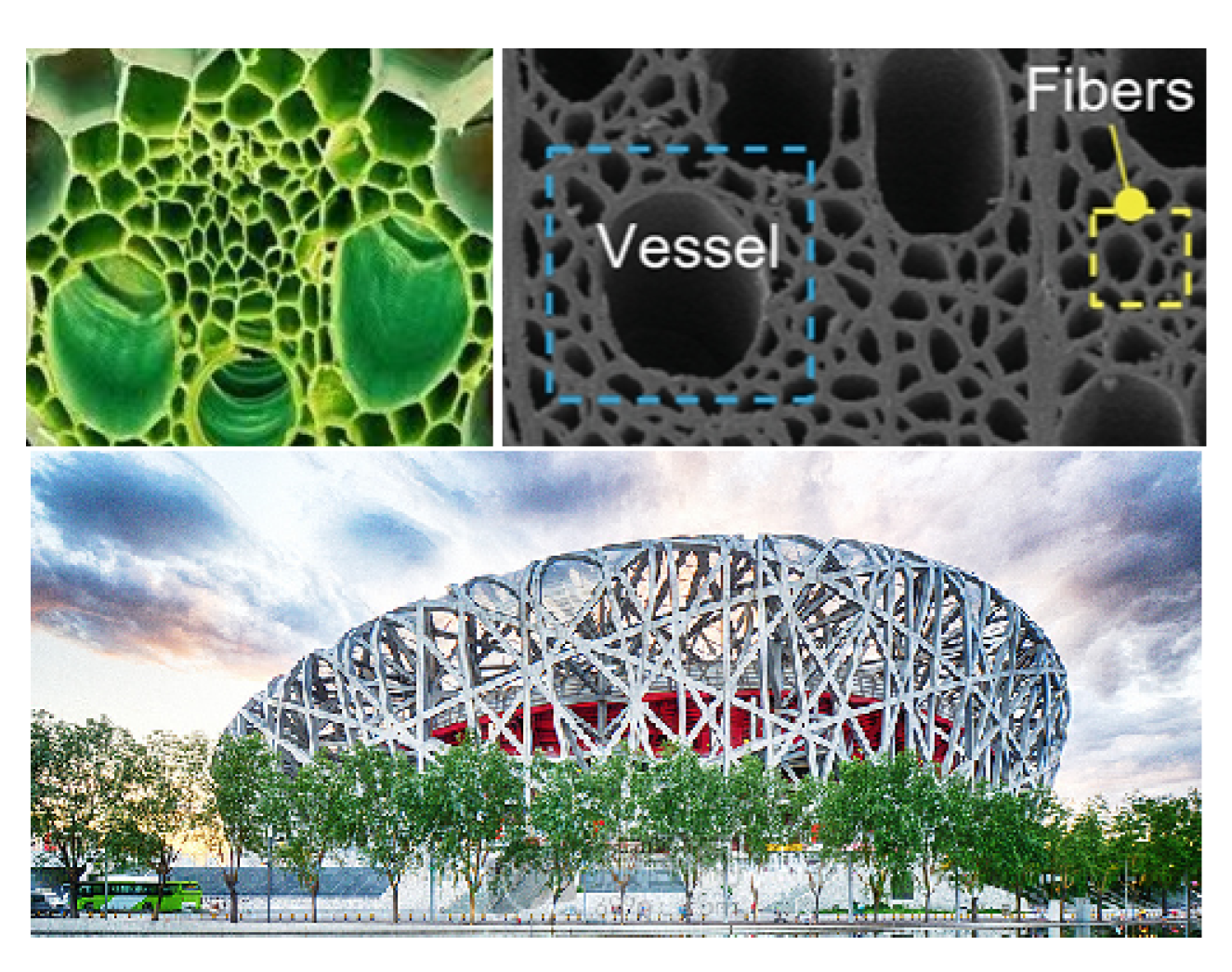
Preprints 112582 g003
Figure 3. Top left: Bamboo cellulose. Top right: Natural wood cellulose. Bottom: The Bird’s Nest in Beijing
Figure 3. Top left: Bamboo cellulose. Top right: Natural wood cellulose. Bottom: The Bird’s Nest in Beijing
Preprints 112582 g003
Preprints 112582 g004
Figure 4. The `einstein’ tile honeycomb metamaterial two-dimensional plane definition
Figure 4. The `einstein’ tile honeycomb metamaterial two-dimensional plane definition
Preprints 112582 g004
Preprints 112582 g005
Figure 5. A periodic structure: Honeycomb. The periodic structure is generated by a unit cell through translation without rotation, hence it is generally isotropic.
Figure 5. A periodic structure: Honeycomb. The periodic structure is generated by a unit cell through translation without rotation, hence it is generally isotropic.
Preprints 112582 g005
Preprints 112582 g006
Figure 6. The finite element model
Figure 6. The finite element model
Preprints 112582 g006
Preprints 112582 g007
Figure 7. Comparison of experimental and simulated deformation of two honeycomb metamaterials under room temperature compression
Figure 7. Comparison of experimental and simulated deformation of two honeycomb metamaterials under room temperature compression
Preprints 112582 g007
Preprints 112582 g008
Figure 8. Macroscopic and microscopic deformation patterns of two honeycomb metamaterials
Figure 8. Macroscopic and microscopic deformation patterns of two honeycomb metamaterials
Preprints 112582 g008
Preprints 112582 g009
Figure 9. Comparison of force-displacement curves between finite element simulations and experiments
Figure 9. Comparison of force-displacement curves between finite element simulations and experiments
Preprints 112582 g009
Preprints 112582 g010
Figure 10. Weight of the two honeycomb metamaterial specimen samples (example)
Figure 10. Weight of the two honeycomb metamaterial specimen samples (example)
Preprints 112582 g010
Preprints 112582 g011
Figure 11. Energy absorption versus nominal strain relationship of two honeycomb metamaterials at room temperature
Figure 11. Energy absorption versus nominal strain relationship of two honeycomb metamaterials at room temperature
Preprints 112582 g011
Preprints 112582 g012
Figure 12. The `einstein’ tile honeycomb and one of its cells
Figure 12. The `einstein’ tile honeycomb and one of its cells
Preprints 112582 g012
Preprints 112582 g013
Figure 13. The geometric configurations and boundary conditions of two types of honeycomb metamaterials
Figure 13. The geometric configurations and boundary conditions of two types of honeycomb metamaterials
Preprints 112582 g013
Preprints 112582 g014
Figure 14. Two types of 3D-printed honeycomb metamaterial specimens:(a)The `einstein’ tile honeycomb,(b)The square honeycomb,both thicknesses are t = 0.6 m m
Figure 14. Two types of 3D-printed honeycomb metamaterial specimens:(a)The `einstein’ tile honeycomb,(b)The square honeycomb,both thicknesses are t = 0.6 m m
Preprints 112582 g014
Preprints 112582 g015
Figure 15. Experimental set up
Figure 15. Experimental set up
Preprints 112582 g015
Preprints 112582 g016
Figure 16. (a) Tensile specimen and testing equipment, (b) Stress-strain curve of the tensile specimen
Figure 16. (a) Tensile specimen and testing equipment, (b) Stress-strain curve of the tensile specimen
Preprints 112582 g016
Table 1. Orientation and number of `einstein’ tile
Table 1. Orientation and number of `einstein’ tile
Type 0 ∘ 60 ∘ − 60 ∘ 120 ∘ − 120 ∘ 180 ∘ Total No. K
type-a 5 8 6 5 2 3 N a = 29 K a = 6
type-b 1 1 0 2 0 1 N b = 5 K b = 4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated