Prerpints.org logo
Preprint
Article

Optimal Management of Renewable Energy Sources for Industrial Applications: A South African Inland Downstream Oil Refinery Case Study

Altmetrics

Downloads

86

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Energy and Environmental Situation Awareness

Submitted:

17 July 2024

Posted:

18 July 2024

You are already at the latest version

Alerts
Abstract
Motivated by South Africa's need in the transition to a net-zero economy; this study 10 investigates the integration of renewable energy sources (RES) into oil refineries, considering 11 therein unique challenges and opportunities. The research focuses on optimizing RES allocation 12 using Particle Swarm Optimization (PSO), a data-driven approach that adapts to real-time 13 operational conditions. Traditional energy management systems often struggle with the inherent 14variability of RES, leading to suboptimal energy distribution and increased emissions. Therefore, 15 this study proposes a PSO-based renewable energy allocation strategy specifically designed for oil 16 refineries. It considers factors like the levelized cost of energy, geographical location, and available 17 technology. The methodology involves formulating the optimization problem, developing a PSO 18 model, and implementing it in a simulated oil refinery environment. The results demonstrate 19 significant convergence of the PSO algorithm, leading to an optimal configuration for integrating 20 RES and achieving cost reductions and sustainability goals. The optimization result of 4,457,527.00 21 Rand achieved by iterations is much better than the result of 4,829,638.88 Rand acquired using 22Linear Programming as the baseline model. The mean cost, indicating consistent performance, has 23 remained at its original value of 4,457,527.00 Rand, highlighting the convergence. Key findings 24 include the average distance measure decreasing from 4.2 to 3.4, indicating particle convergence; 25 swarm diameter decreasing from 4.7 to 3.8, showing swarm concentration on promising solutions; 26 average velocity decreasing from 7.8 to 4.25, demonstrating refined particle movement; and the 27 optimum cost function achieved at 4,457,527 Rand with zero standard deviation, highlighting 28 stability and optimal solution identification. This research offers a valuable solution for oil 29 refineries seeking to integrate RES effectively, contributing to South Africa's transition to a 30sustainable energy future.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

By the year 2050, South Africa intends to have achieved net-zero carbon emissions [1,2]. This ambitious objective necessitates substantial investment and effort from the private and public sectors. A significant focal point pertains to the utility industry, which presently accounts for approximately 60% of the entirety of the nation's greenhouse gas emissions [3]. The majority of South Africa's electricity is produced by coal-fired power facilities, a significant contributor to carbon emissions. South Africa must invest in renewable energy sources, including wind, solar, and hydroelectric power, to transition to a net-zero economy. Given the proper investment and policy backing, these plentiful resources have the potential to constitute a substantial component of the nation's energy portfolio. Additionally, South Africa must prioritise the petrochemicals and chemicals industries, which are major contributors to the nation's greenhouse gas emissions [4]. These sectors are highly dependent on fossil fuels and must adopt more sustainable, environmentally friendly alternatives to help South Africa reach its net-zero emissions targets. Various factors must be considered to achieve the most effective integration of renewable energy technologies into oil refinery operations. These factors include the levelized cost of energy, geographical location, available technology, plant processes, equipment lifetime, and equipment optimisation options. Insights regarding the optimal assimilation of renewable energy sources into oil refinery operations were obtained from the subsequent search results.
Conventional energy management and distribution approaches often fail to meet the precision needed to maximise the use of renewable resources. The inherent variability of renewable energy sources, such as solar and wind, required the implementation of timely decision-making processes to effectively capture and use the available energy resources. To guarantee the long-term sustainability and dependability of renewable energy sources in the industrial sector, it is essential to use innovative and data-driven methodologies. The following strategies may be used to enhance the integration of renewable energy via the utilisation of data-driven methodologies: Data-Driven Energy Solutions, Data-Driven Artificial Intelligence Techniques, Data-Driven Strategic Energy Management, and Data-Driven Next-Generation Smart Grid [5,6]. The PSO can optimise the allocation of renewable energy resources by using real-time data and adapting to dynamic operating circumstances [7,8]. The electricity produced by hybrid renewable energy systems (HRES) has been optimised in numerous researches using PSO techniques. An instance of PSO was used in research to enhance the energy management system of an autonomous hybrid renewable energy system (HRES) [9]. Subsequent research presented an enhanced PSO method to optimise the arrangement of components in a freestanding solar system [10]. PSO has been used in the development of an optimum sizing algorithm for a hybrid renewable energy system. This method incorporates a smart grid load management application, which is based on the available data [7].
Particle Swarm Optimisation (PSO) has considerable potential as a viable approach for effectively optimising the allocation of renewable energy resources, considering real-time data and the dynamic nature of operating circumstances. The tool is very effective in optimising the energy management process and can accommodate variations in parameters, changes in constraints, and characteristics particular to different locations. The primary objective is to develop and execute a PSO-based renewable energy allocation strategy that is specifically designed to meet the distinct needs of oil refineries. This strategy must take into consideration various factors, including the intricacies of energy storage, dynamic limitations, equipment deterioration, levelized cost of energy, and geographic factors. By implementing this approach, it should be possible to significantly decrease electricity usage, attain financial benefits, and improve dependability. As a result, there will be less dependence on national electricity networks that are primarily powered by coal, and the strategy will be in line with sustainability and environmental goals.

2. Materials and Methods

2.1. Theoretical Background of PSO

The PSO algorithm was first proposed in 1995 by Kennedy and Eberhart [11] In a swarm, each particle is composed of three A-dimensional vectors, where A represents the dimensionality of the search space. The three vectors under consideration are the present location X i of the particle, its velocity V i , and its prior best position P i . Furthermore, it is worth noting that every individual particle inside the swarm knows the present global best solution, denoted as g . The velocity of each particle is repeatedly adjusted to ensure that all particles converge towards the locations of g and P i . In the end, the whole swarm will converge towards an optimal solution of the fitness function under consideration. The algorithm depicted in Table 1 illustrates this procedure.

2.2. Rationale for the Use of Particle Swarm Optimisation

The PSO is a computational technique that draws inspiration from the coordinated movement of bird flocks. The algorithm mentioned is a distributed behaviour algorithm designed for performing multidimensional searches [12,13]. The PSO algorithm is classified as a metaheuristic method because it does not rely on specific assumptions about the solutions. The algorithm operates by manipulating particles within the search space using efficient algorithms that leverage the particles' position and velocity. The decision to use PSO as the primary optimisation technique in this research is based on its effectiveness in efficiently exploring complex solution spaces. The adaptability and capacity to identify global optima make it a viable contender for addressing the complexities of managing renewable energy in an industrial setting.

2.3. Model Background

As reported in the works [14,15,16,17] the adoption of renewable energy sources, including solar photovoltaic, wind turbines, biomass, and others, is growing in industrial applications. This trend is driven by the desire to achieve sustainability goals and decrease reliance on traditional fossil fuels. However, the optimisation problem of fully utilising renewable sources, while also considering cost efficiency and energy reliability, is complex and has multiple facets. The formulation of the optimisation model is a crucial stage in researching the best management of renewable energy sources. The objective is to develop an optimisation model that will aid in determining the optimal mix and capacity of renewable energy sources and energy efficiency measures. The optimization model is represented as follows in Equation (2.3).
M i n ∑ t = 1 T P g r i d , t × G E C i + ∑ i N P R E , i , t × R E T C
Where:
T − is the total amount of time intervals;
N − is the number of renewable energy technologies that have been considered
P g r i d , t − is the electricity purchased from the grid in time t
P R E , i , t − is the energy generated by renewable energy technology i in time t
G E C i − is the cost of grid power in time t
R E T C − is the cost of renewable energy technology i
The model described above is subject to the constraints described in the following subsections.

2.3.1. Energy Balance Constraint

It is essential to satisfy the overall energy requirements of the refinery by using a mix of power derived from the grid and sustainable energy sources as follows in Equation (2.4).
∑ i N P R E , i , t + P g r i d , t + ∑ j = 1 M P s t o r a g e , j , t = E D t ,     ∀ t
Where,
E D − Energy Demand

2.3.2. Capacity Constraint

To effectively assess the potential of renewable energy technologies, it is imperative to establish a comprehensive understanding of their respective maximum capacities while considering the inherent limitations imposed by equipment constraints as follows in Equations (2.5) and (2.5a).
P R E , i , t ≤ M C i , ∀ i , ∀ t
P s t o r a g e , j , t ≤ M S C j , ∀ i , ∀ t
Where,
M C − Maximum Capacity
M S C − Maximum Storage Capacity

2.3.3. Energy Efficiency Constraints

To effectively promote energy efficiency, it is imperative to establish a framework wherein the aggregate energy output derived from renewable sources surpasses or equals a predetermined proportion of the overall energy consumption as follows in Equation (2.6).
1 T ∑ t = 1 T ∑ i = 1 N P R E , i , t + ∑ j = 1 M P s t o r a g e , j , t ≥ E E T × 1 T ∑ t = 1 T E D t
Where,
E E T − Energy Efficiency Threshold

2.3.4. Renewable Energy Generation Limit

It is important to maintain a balance between renewable energy output and the available resources within each period.
P R E , i , t ≤ R R i ∀ i , ∀ t
Where,
R R − Renewable Resource

2.3.5. Energy Storage Constraints

It is important to ensure that energy storage technologies conform to their charging and discharging limitations following their specific attributes, such as capacity and charge/discharge rates as follows in Equations (2.8) and (2.8a).
P s t o r a g e , j , t ≤ M C R i , ∀ j , ∀ t
− P s t o r a g e , j , t ≤ M D R j , ∀ j , ∀ t
Where,
M C R − Max Charge Rate
M D R − Max Discharge Rate

2.3.6. State of Charge (SOC) Constraints

Incorporate constraints on the state of charge (SOC) of energy storage devices to accommodate their dynamic characteristics as follows in Equation (2.9).
S O C s t o r a g e , j , t = S O C , j , t − 1 + η c h a r g e , j ⋅ P s t o r a g e , j , t − P s t o r a g e , j , t P η c h a r g e , j   ,     ∀ j ,   ∀ t
It is important to provide the initial SOC values for the storage technologies as follows in Equation (2.10).
S O C s t o r a g e , j , 0 = I n i t i a l S O C j ,     ∀ j
The key decision variables for the optimization model are tabulated in Table 2.

2.4. Model Development

This study employed the PSO to optimise the management of renewable energy sources in an oil refinery. PSO is a stochastic optimisation approach that is based on populations. It was created by Kennedy and Eberhart and draws inspiration from social behaviours observed in bird flocking, fish schooling, and swarm theory [18]. This approach is based on a straightforward principle, where a collective of swarm particles actively explores a predetermined solution space to find the most effective solution.

2.4.1. Particle Swamp Optimization

This optimisation approach was derived from the collective movement patterns shown by bird flocks in computational space. This method initialises the particle's movement throughout the space to seek the optimal solution based on the objective function. The ultimate optimum solution is reached by considering a larger number of particles. During each cycle, the optimal current position will update its position by incorporating the current velocity, current best position, and current global position as described in Figure 1.
The optimisation model, as described in Equation (2.3), incorporates factors such as energy balance, capacity, energy efficiency, constraints on renewable energy output, and energy storage. The cost function is represented by the encoding shown in Figure 1. The energy data used to implement the PSO algorithms is sourced from the grid energy demand and solar power framework. The energy data inputs are included in the cost functions, which embody the model formulation in this research. One method for reducing the overall cost of the system is through the implementation of the PSO which comprises of the following fundamental components [18]:
Particle X: is a bird in search of a certain location, represented by a vector. At iteration time, the i t h particle X i may be characterised as X i = x 1 i ,   x 2 i , x n i , ,   represents the i t h particle's location relative to the vector.
Population P: The number of particles to run for iteration count, denoted as P = x 1 i ,   x 2 i , … x n i , T Swarm: a group of particles that move in random directions within each population and get together as they move forward.
Particle velocity V: refers to the vector representation of the velocity of moving particles. During the process of iteration, the velocity of the i t h particle can be represented as, V = V 1 i ,   V 2 i , … V n i .
Individual best: The particle advances in the search area when the present optimal position based on fitness value is contrasted with the optimal position based on fitness value in the subsequent iteration. The individual best is derived from the maximum fitness value as the iteration progresses.
pbest(t): The pbest is determined through iteration by modifying the value of the fitness function; the position best is then identified and denoted as P   P b e s t t = P b e s t 1 ,   … , P b e s t 2 , … , P b e s t n .
Global best, denoted as gbest(t): The individual best position is determined from the count of the best positions during the iteration.
Therefore, denoted as g b e s t t = G b e s t 1 , … , G b e s t 2 , … , G b e s t n .
Stopping criteria: This criterion dictates that the search process shall cease either upon achieving the expected or ideal value or upon reaching the maximum iteration count.
The particle update is as follows in Equation (2.11).
X i , t + 1 = X i , t + v i , t + 1
The constants C 1 and C 2 are positive values and reflect the value of each particle in the swarm. The variables r 1 and r 2 are uniformly distributed random numbers in the range of 0 to 1. Each stage involves evaluating the fitness function of individual particles. The inertial factor governs the magnitude of the step size. A higher inertia weight promotes extensive exploration of the global search space while also assisting in local search. Updates to velocity and position are as follows in Equation (2.12) to Equation (2.14).
X i = r a n d ∙ * X i m a x − X i m i n + X i m i n
v i k = r a n d ∙ * v i m a x − v i m i n + v i m i n
The formula for inertia weight is as follows in Equation (2.14).
w = w m a x − w m a x − w m i n * i t e r i t e r m a x
Where,
w m a x / w m i n − the inertia maximum and minimum weight.
Equation (2.11) to Equation (2.14) play a crucial role in preventing our optimisation algorithms from running indefinitely. In essence, they facilitate the convergence of our algorithm, allowing us to obtain the desired results. The PSO technique starts by randomly distributing particles inside the problem area. Every individual particle is utilised to calculate the goal function. During each cycle, the velocities of particles are computed using a specific method. Once the velocities have been determined, the location of the particle is estimated. The particle's location will change if the requirement is met. The subsequent instructions outline the process of determining the solution:
  • Assign random values to the positions.
  • The velocity must be initialised with randomly generated values.
  • The objective function of each particle will be calculated.
  • Pbest denotes the initial population as the local best position.
  • Save the optimal values for the global best position (Gbest) that you select from Pbest.
  • Start the iteration counter and PSO loop.
  • Determine the inertia weight of the particle, its velocity, and its position.
  • Evaluate the cost function defined in Equation (2.3).
  • Update Pbest and Gbest.
  • Iterate over the numbers 7, 8, and 9 in each iteration until the stop condition is met.
  • Print Gbest Values.

2.4.2. Methodology for Implementing the Linear Programming as a Baseline Model

The flowchart as described in Figure 2 provides a concise representation of the sequential actions required to execute the LP model in Python to reduce overall energy expenses. The process begins with the establishment of inputs, which include variables such as time of use, energy requirements, and grid and solar energy costs. The choice variable is defined for grid electricity, solar electricity, battery charge, and disc. The objective function is formulated to reduce overall energy expenses. The constraints to meet energy demand, considering the limitations of solar capacity, manufacturing capabilities, and battery efficiency are defined. The methodology utilises the PuLP library to establish and solve the LP problem. Subsequently, the optimal choice variables with the minimal cost are generated as the outcome.
The all-encompassing expression of the optimization problem combines the objective function, decision variables, and constraints that underpin the administration of renewable energy sources within an industrial context. The establishment of the problem formulation serves as the fundamental basis upon which the PSO-based optimization model is built, thereby establishing the framework for subsequent investigation and analysis in subsequent sections. The implementation of the refinery basic model is presented using the LP methodology in Python, specifically within the Anaconda framework.

3. Results

This section focuses on implementing the methodology established in Section 2, which supports the management of renewable energy sources in an industrial setting. It also investigates the potential energy efficiency measures and their effects on electricity consumption, and cost savings by using particle swamp optimisation. The goal is to reduce reliance on the coal-dominated national electricity network.

3.1. Data Gathering

Data gathering is crucial for industrial facilities aiming to attain optimal efficiency, as it enables further analysis via the use of key performance indicators (KPIs). The data modelling approach involved integrating on-site observations with computational models. This section classifies the data as profiles of refinery energy consumption, refinery geographic location, and refinery landscape. A South African inland downstream oil refinery has implemented the methodology. The refinery features a decanter and centrifuge plant, which cleans and dries products for further processing or mixing (3 million). The local municipal grid meets the 500-kW peak electrical consumption as shown in Figure 3, with a diesel generator serving as backup during outages.
The parameters for the refinery under study are tabulated in Table 3.
Figure 4 is utilised to characterise the time-of-use features of the refinery, further details on the Refinery’s high and low demand seasons properties are detailed in the Appendix section. This data is utilised to establish the time intervals during which the suggested solar PV system would exhibit optimal efficiency.

3.2. Refinery Energy Consumption Profile

The energy consumption profile includes the utilization of power from the grid, the energy demand of the refinery. Figure 5 depicts the refinery’s annual electricity consumption for each Time of Use (TOU).

3.3. Refinery Geographic Location Profile

A geographical study highlights the potential of different renewable energy sources and energy optimization measures for the inland oil refinery under consideration. This investigation tailors its results to the unique needs of the refinery. The Global Horizontal Irradiation Map in Figure 6 indicates that the refinery's geographic area can achieve an average of 5.4 hours of daily solar PV electricity production, typically between 10 a.m. and 3 p.m.
This assessment is guided by the following criteria:
  • PV solar potential: Global Horizontal Irradiation (GHI) and Photovoltaic Power Potential (PVOUT) maps shown in Figure 6, depict the feasibility of directly harvesting solar energy in South Africa.
  • Possibility of CSP: The Direct Normal Irradiation (DNI) map shown in Figure 6 illuminates the potential efficacy of Concentrator Solar Photovoltaic (CSP) technology in South Africa.
  • Wind energy evaluation: The Wind Atlas for South Africa (WASA) map shown in Figure 6 informs the refinery's appraisal of wind as a renewable energy source.
The criteria outcomes and supports for solar PV taken into account include solar insolation, grid power pricing, land availability, and government incentives. High degrees of insolation are essential for optimizing solar power output. When the price of buying electricity from the grid is expensive, solar power becomes a more financially appealing option. Adequate land space is required to establish a solar panel array with a capacity that can fulfill the electrical demands of the refinery. Monetary incentives like as subsidies or tax exemptions may greatly enhance the feasibility of solar systems.

3.4. Refinery Landscape

The Refinery's layout drawings illuminate available land and roof space, paving the way for the potential implementation of various renewable energy solutions. The collected data fuels the study's objectives by:
Building a rock-solid foundation for seamless integration and optimization of renewable energy down the line
Opening up a world of possibilities for exploring and evaluating a diverse range of renewable energy solutions and energy optimization strategies. These, meticulously tailored to the specific needs of the inland oil refinery, guide the path towards identifying the most optimal approaches
Shining a light on the direct impact of identified renewable energy solutions on critical factors like electricity consumption rates, operational reliability, and overall cost-effectiveness.
Subject to the land limitations within the Refinery, the office building and testing laboratory roof were considered for the solar PV solution as shown in Figure 7.
In this framework, PV solar technology with and without a battery energy storage system (BESS) was considered subject to the potential renewable PV solar energy available in the area and the number of hours of load-shedding experienced in 2022 of 3773 hours as shown in Figure 8.

3.5. Model Implementation for Optimal Management of Renewable Energy Sources for an Oil Refinery

The flowchart shown in Figure 1 is utilized to implement the PSO model for the optimal management of renewable energy sources in an oil refinery. A validation test is employed to ascertain the effectiveness of the proposed method. The essential data utilized in this analysis were Time of Use, Energy Demand, Solar Levelized Cost of Electricity (LCOE) without battery, Solar LCOE with battery, Solar resource, Maximum solar capacity, Average daily solar production, battery capacity, charging efficiency, and discharging efficiency.

3.6. Baseline for Validating the Optimal Management of Renewable Energy Source Problem

To provide a baseline for assessing the feasibility of optimum management of renewable energy sources, the initial cost of electricity for the Refinery was considered before the hybrid Solar plus Battery Energy Storage System adoption. Subject to Figure 5 above which depicts the Refinery’s Time of Use annual consumption and the Levelized Cost of Electricity for the Refinery of R5,98 as shown under Table 3 above, the summary of the costs can be presented as follows in Table 4.
Based on the Refinery's PV Solar peak hours indicated in the Global Horizontal Irradiation map (Figure 6), and considering the Refinery's high and low demand seasons (Figure 4 and the Appendix), the PV solar system is most effective during the standard tariff Time of Use (TOU). During the low-demand season, the PV Solar system can meet the peak tariff TOU for 1 hour each day, while the rest of the time falls under the standard tariff TOU. As a result, the system will reduce the standard tariff cost of 743,680.15 kWh per annum, as shown in Figure 5 (Refinery's TOU kWh per annum). To calculate the Annual Solar Production (ASP) for the Refinery, which amounts to 281,601.60 kWh, Equation (3.1) was used.
A S P = P s , P V × G H I a n n u a l × P R s
Where,
P s , P V , t − Energy generated from solar PV
P R s − Solar System Performance Ratio
G H I a n n u a l − Global Horizontal Irradiation in the refinery’s geographic location
Furthermore, as indicated in Table 4, the levelized cost of electricity for the solar and battery energy storage systems is R2,83. This means that the refinery's electricity cost after the solar and battery energy storage system applications are as follows in Table 5.
For the statistical calculation expressed in Table 4 and Table 5 above the following assumptions were considered:
Average grid power tariff as expressed in the Appendix which considers the average annual cost of grid power over the low and high demand seasons.
Share of power contribution to the Refinery is split between the grid and diesel generator at 85/15%, thus the LCOE for grid/genset encompasses both the average cost of grid power and the diesel genset power.
Solar PV System Performance Ratio = 85%,
Annual Solar Panel Degradation = 0,5%,
Solar Utilization = 100%
Cost of Operations and Maintenance = R250/kWp
Future annual grid price increase (AGP) averaged at 10%
Future annual diesel price increase (ADP) at 3%
The LP approach is employed to simulate the problem. The LP algorithms aim to pinpoint the ideal solution for a specific problem. An objective function formulates the problem and aims to maximise or minimise its value within a specified set of limits and constraints. In this particular case study, the target function is to minimise costs, enhance energy dependability, and, where appropriate, mitigate environmental impacts. Figure 9 displays the flow chart that demonstrates the iterative LP approach for effectively managing the renewable energy source problem. The implementation of this method is done in Python 3.11.5 utilising JupyterLab within the Anaconda framework. The LP solution is evaluated, resulting in an evaluation function value of R4 829 638.88. As shown in Figure 10(a), the projected total cost is also R4 829 638.88, with an absolute deviation of 0.0 and a percentage variance of 0.0% as shown in Figure 10(b).
An absolute deviation as described in Figure 10(a,b) of 0.0 in the context of linear programming problem implementation signifies that the observed values are precisely equivalent to the expected values, thereby signifying a perfect fit or absence of deviation from the mean. In contrast, a percentage variance of 0% signifies the absence of dispersion or variability in the data, signifying that all data points are identical or remain constant. By employing mean absolute deviation (MAD) in linear programming to analyse the optimal strategy for managing renewable energy sources, the obtained values indicate that maintaining the expected returns without any fluctuations or deviations is the most effective approach. Such a refinery is either risk-free or optimally optimised as a result.

3.7. Results and Analyses

Ultimately, the parameters indicated in Table 6 are employed to fine-tune the PSO model.
The observed trend in the average distance measure during the iterative process is significant for the research. The average distance, which began at 4.2 and decreased to 3.4 over the iteration, indicates particle convergence in the solution space. This decrease as shown in Figure 11 indicates that the swarm is efficiently exploring and exploiting the solution space, focusing on promising locations. In terms of our project's aims, this pattern is consistent with our goal of identifying optimal configurations for combining energy efficiency measures and renewable sources in an oil refinery, suggesting that the PSO algorithm refines its search successfully.
The evolution of Swarm Diameter during the iterative process is important in this section. For example, the iterative trajectory from an initial diameter of 4.7 to a lowered size of 3.8 shows that the swarm's particles are gradually converging (See Figure 12). This convergence is consistent with our project's goal of reducing the solution space to discover the best configurations for energy-saving measures and renewable energy integration in an industrial context. The decreasing Swarm Diameter demonstrates the PSO algorithm's effectiveness in concentrating the search and exploitation of prospective solutions, which contributes to the attainment of our project objectives.
The progressive decrease in average velocity from 7.8 to 4.25 as shown in Figure 13 indicates that the particles in the swarm are converging more carefully. This planned convergence is consistent with our project's goal of refining and optimising solutions. The decreasing velocity indicates that the particles are fine-tuning their locations with greater accuracy, highlighting the PSO algorithm's ability to iteratively explore the solution space. This fine-tuned control over particle mobility helps the programme find ideal designs for energy efficiency and renewable energy integration.
The remarkable outcomes of this research highlight the PSO algorithm's efficiency as summarised in Figure 14. The best cost attained, R4,457,527 per annum over iterations, is a remarkable optimisation result. The average cost, which implies steady performance, has stayed at its initial amount of R4,457,527, emphasising the convergence. The zero standard deviation highlights the algorithm's stability, indicating a strong convergence to the optimal solution. This extraordinary stability is critical for the effective integration of energy-saving measures and renewable sources in an industrial environment, and it aligns well with the project's goals.
The objection function value of R4,457,527.00 over iterations, is a remarkable optimisation result as compared to the R4,829,638.88 obtained using Linear Programming. The average cost, which implies steady performance, has stayed at its initial amount of R4,457,527.00, emphasising the convergence.

4. Discussion

Based on the Refinery’s geographic location and landscapes, the introduction of a RES such as a hybrid Solar PV plus Battery Energy Storage System has potential to reduce the Refinery’s energy consumption by 281,601.60 kWh per annum. This reduction has a direct impact on the Refinery’s electricity costs. A statistical calculation was considered in this research which revealed the initial electricity cost for the refinery to be R11,660,623.56 prior to the application of the RES and R10,773,578.52 post the RES implementation, resulting in approximately 8% reduction on the Refinery’s electricity costs per annum. This outcome provided a projection on the expected percentage cost reduction when modeling the function objective via the PSO model. To thoroughly assess the PSO’s ability to improve the function objective of cost, LP was used to model the baseline scenario for the refinery’s initial cost of electricity, which was R4,829,638.88 Rands. However, this value differs from the annual cost of electricity of R11,660,623.56 Rands achieved using the statistical calculation due to the variation in the LCOE input data. The statistical calculation considers the average annual grid cost for the low and high seasonal tariffs and encompasses the average annual cost of diesel for the genset backup power supply, whereas the LP model makes use of the monthly grid power tariffs. The PSO model was used to simulate the post RES application which resulted in the cost of R4,457,527.00, achieving an approximate cost reduction for the Refinery of 8%, subject to the LP’s baseline cost of R4,829,638.88, showcasing its ability to minimise the objective function of cost.

5. Conclusions

The results and discussions demonstrate the PSO model's usefulness in optimizing the management of renewable energy sources in oil refineries. The changes seen in average distance, swarm diameter, and velocity measurements show that particles are effectively focusing and fine-tuning. This fits with the project's goals of finding the best configurations for integrating renewable energy and saving energy. The PSO algorithm's efficiency, which demonstrates the excellent results of the research, suggests the best cost of R4,457,527.00 Rand over repetitions with a constant average cost and zero standard deviation. This stability is critical for effectively integrating energy-saving measures and renewable sources in an industrial context, and it is consistent with the project's sustainability and environmental aims. In conclusion, the findings of this research provide important insights into the challenges of renewable energy integration in industrial settings. The suggested PSO-based strategy offers a strong approach to addressing difficulties and paving the path for a more sustainable and efficient energy future in oil refineries.

Author Contributions

All authors, conceptualized, carried out the computations, investigated, wrote, and prepared the article. The published version of the article has been reviewed and approved by all authors.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgements

The authors would like to thank local manufacturers and utilities for their contribution in the database.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix: Refinery High and Low-Demand Season Properties

Preprints 112489 i001

References

  1. Anika, S.G. Nnabuife, A. Bello, E.R. Okoroafor, B. Kuang, R. Villa, Prospects of low and zero-carbon renewable fuels in 1.5-degree net zero emission actualization by 2050: A critical review, Carbon Capture Science & Technology, 5, 2022, 100072.
  2. L. Chapungu, G. Nhamo, D. Chikodzi, M.A. Maoela, BRICS and the Race to Net-Zero Emissions by 2050: Is COVID-19 a Barrier or an Opportunity?, Journal of Open Innovation: Technology, Market, and Complexity, 8, 2022, 172.
  3. V.D. Dragomir, The disclosure of industrial greenhouse gas emissions: a critical assessment of corporate sustainability reports, Journal of Cleaner Production, 29, 2012, 222-237.
  4. S. Ma, T. Lei, J. Meng, X. Liang, D. Guan, Global oil refining's contribution to greenhouse gas emissions from 2000 to 2021, The Innovation, 4, 2023.
  5. K. Ning, Data driven artificial intelligence techniques in renewable energy system, Massachusetts Institute of Technology, 2021.
  6. Pasichnyi, F. Levihn, H. Shahrokni, J. Wallin, O. Kordas, Data-driven strategic planning of building energy retrofitting: The case of Stockholm, Journal of cleaner production, 233, 2019, 546-560.
  7. M. Amer, A. Namaane, N. M'sirdi, Optimization of hybrid renewable energy systems (HRES) using PSO for cost reduction, Energy Procedia, 42 (2013, 318-327. [CrossRef]
  8. F. Menzri, T. Boutabba, I. Benlaloui, D. Khamari, Optimization of Energy management using a particle swarm optimization for hybrid renewable energy sources, 2022 2nd International Conference on Advanced Electrical Engineering (ICAEE), IEEE, 2022, pp. 1-5.
  9. H. Liu, B. Wu, A. Maleki, F. Pourfayaz, An improved particle swarm optimization for optimal configuration of standalone photovoltaic scheme components, Energy Science & Engineering, 10, 2022, 772-789.
  10. M.A. Mohamed, A.M. Eltamaly, A.I. Alolah, PSO-based smart grid application for sizing and optimization of hybrid renewable energy systems, PloS one, 11.2016. e0159702. [CrossRef]
  11. J. Kennedy, R. Eberhart, Particle swarm optimization, Proceedings of ICNN'95-international conference on neural networks, IEEE, 1995, pp. 1942-1948.
  12. M. Clerc, Particle swarm optimization, John Wiley & Sons, 2010.
  13. J. Kennedy, R. Eberhart, Particle swarm optimization, Proceedings of ICNN'95-international conference on neural networks, IEEE, 1995, pp. 1942-1948.
  14. Ellabban, H. Abu-Rub, F. Blaabjerg, Renewable energy resources: Current status, future prospects and their enabling technology, Renewable and sustainable energy reviews, 39, 2014, 748-764. [CrossRef]
  15. M. Farghali, A.I. Osman, Z. Chen, A. Abdelhaleem, I. Ihara, I.M. Mohamed, P.-S. Yap, D.W. Rooney, Social, environmental, and economic consequences of integrating renewable energies in the electricity sector: a review, Environmental Chemistry Letters, 21, 2023, 1381-1418.
  16. Qazi, F. Hussain, N.A. Rahim, G. Hardaker, D. Alghazzawi, K. Shaban, K. Haruna, Towards sustainable energy: a systematic review of renewable energy sources, technologies, and public opinions, IEEE access, 7, 2019, 63837-63851.
  17. M.S. Salvarli, H. Salvarli, For sustainable development: Future trends in renewable energy and enabling technologies, Renewable energy-resources, challenges and applications, IntechOpen, 2020.
  18. J. Kennedy, R.C. Eberhart, A discrete binary version of the particle swarm algorithm, 1997 IEEE International conference on systems, man, and cybernetics. Computational cybernetics and simulation, IEEE, 1997, pp. 4104-4108.
  19. J.L. ERERO, Impact of loadshedding in South Africa: A CGE analysis, Journal of Economics and Political Economy, 10, 2023, 78-94.
Preprints 112489 g001
Figure 1. Implementation of PSO algorithm.
Figure 1. Implementation of PSO algorithm.
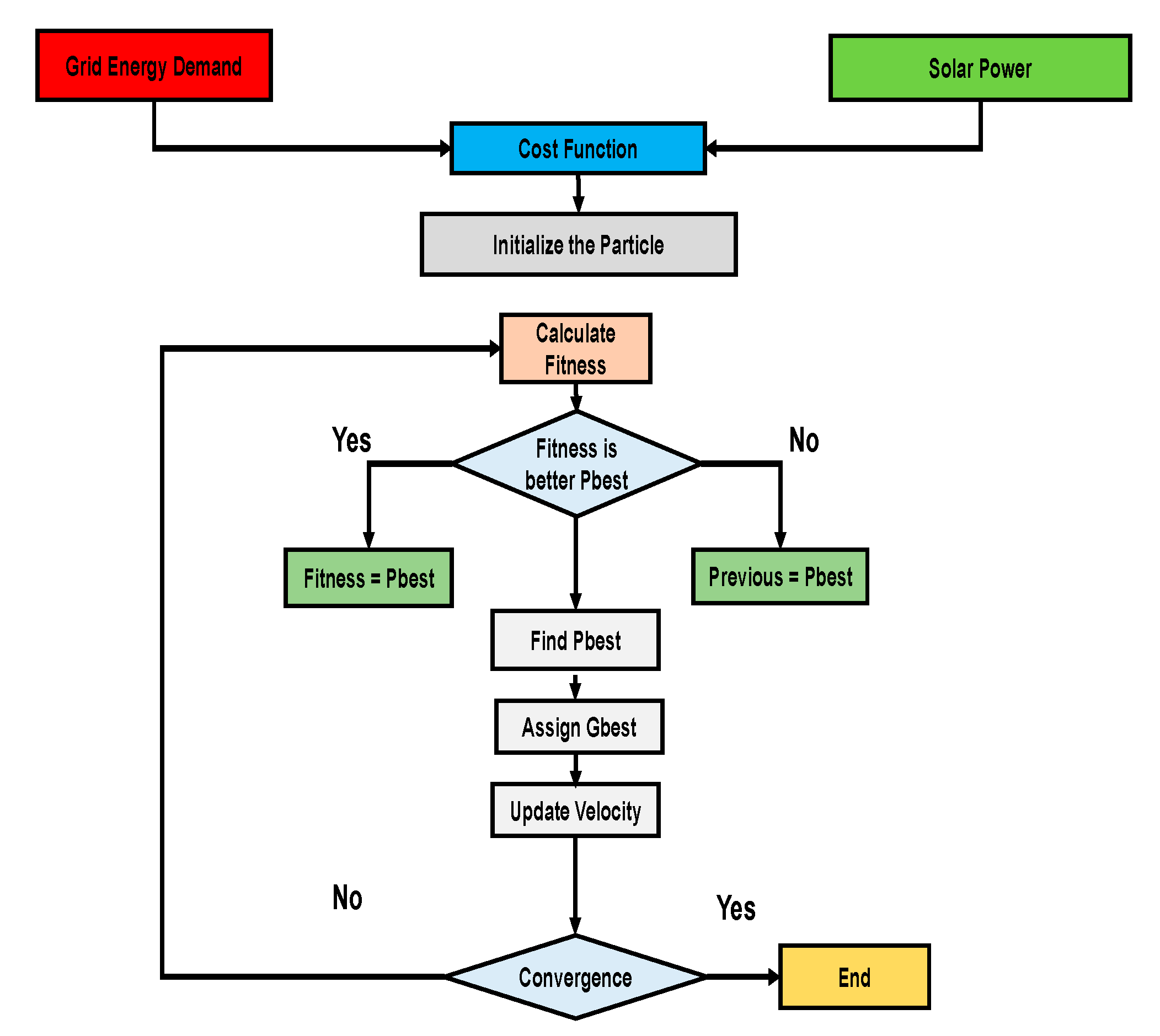
Preprints 112489 g001
Preprints 112489 g002
Figure 2. Flowchart for Implementing an LP Model in Python to Minimise Total Energy Cost.
Figure 2. Flowchart for Implementing an LP Model in Python to Minimise Total Energy Cost.
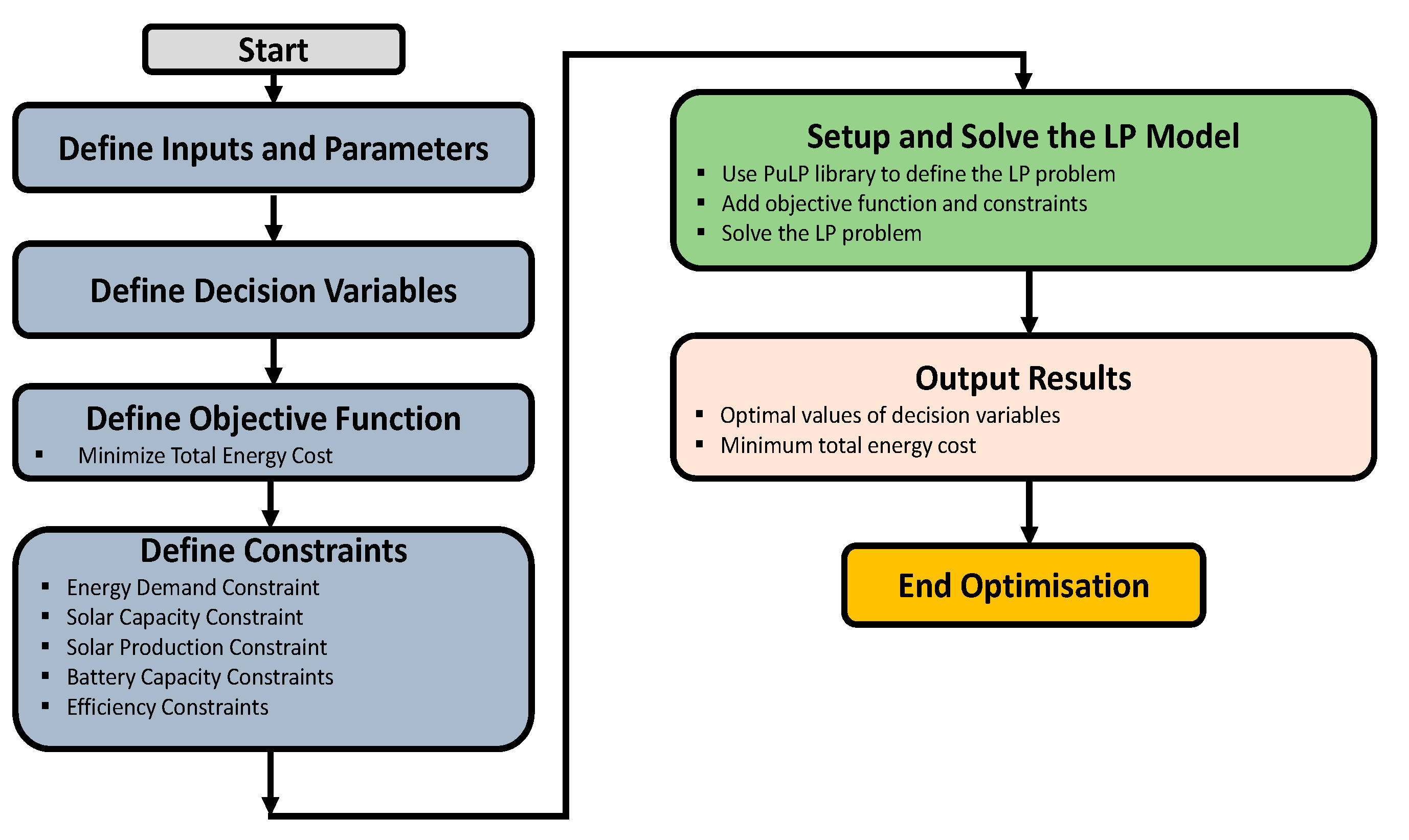
Preprints 112489 g002
Preprints 112489 g003
Figure 3. Oil Refinery 12 Months Electricity Consumption Profile.
Figure 3. Oil Refinery 12 Months Electricity Consumption Profile.
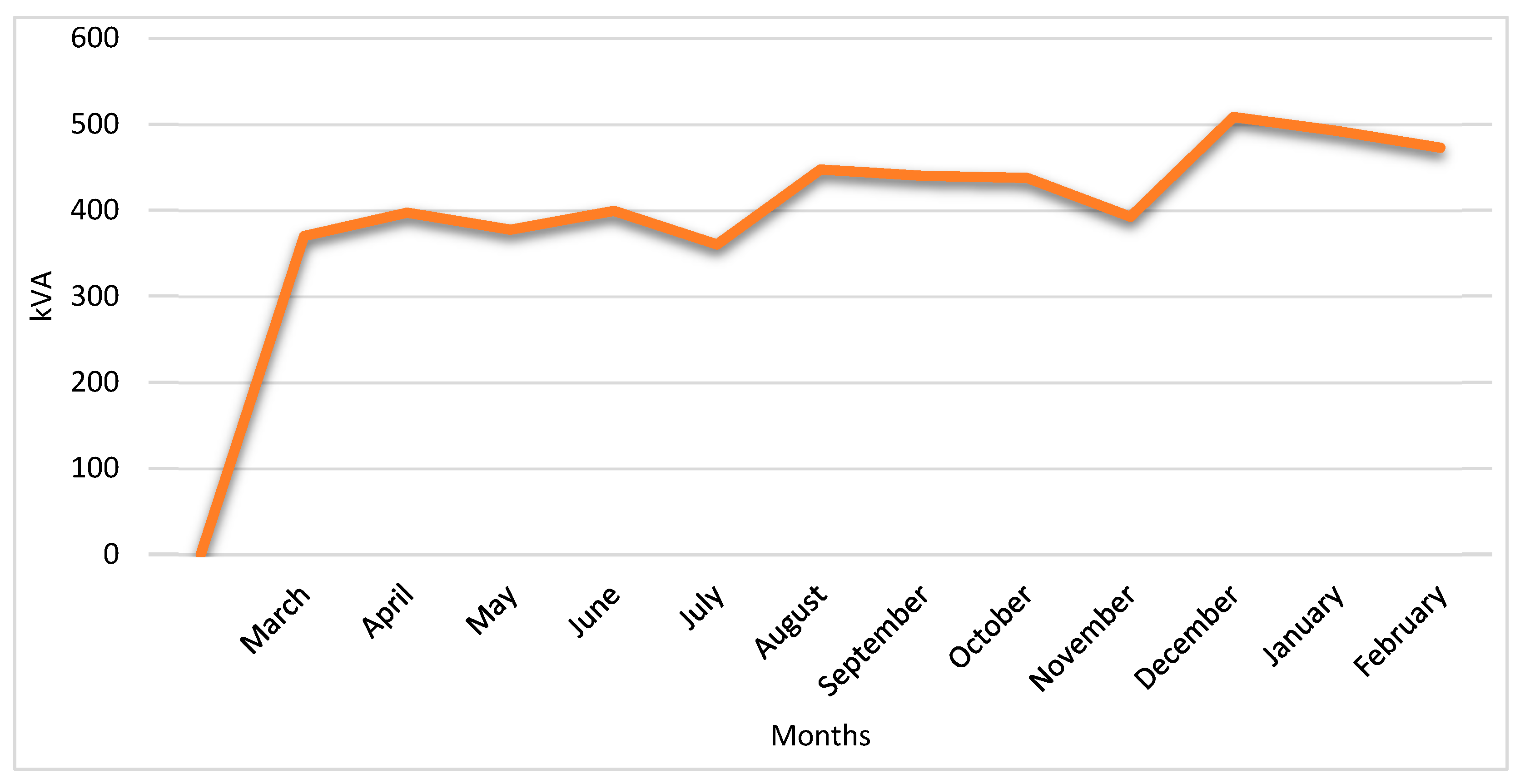
Preprints 112489 g003
Preprints 112489 g004
Figure 4. Low and High Demand Seasons in South Africa.
Figure 4. Low and High Demand Seasons in South Africa.
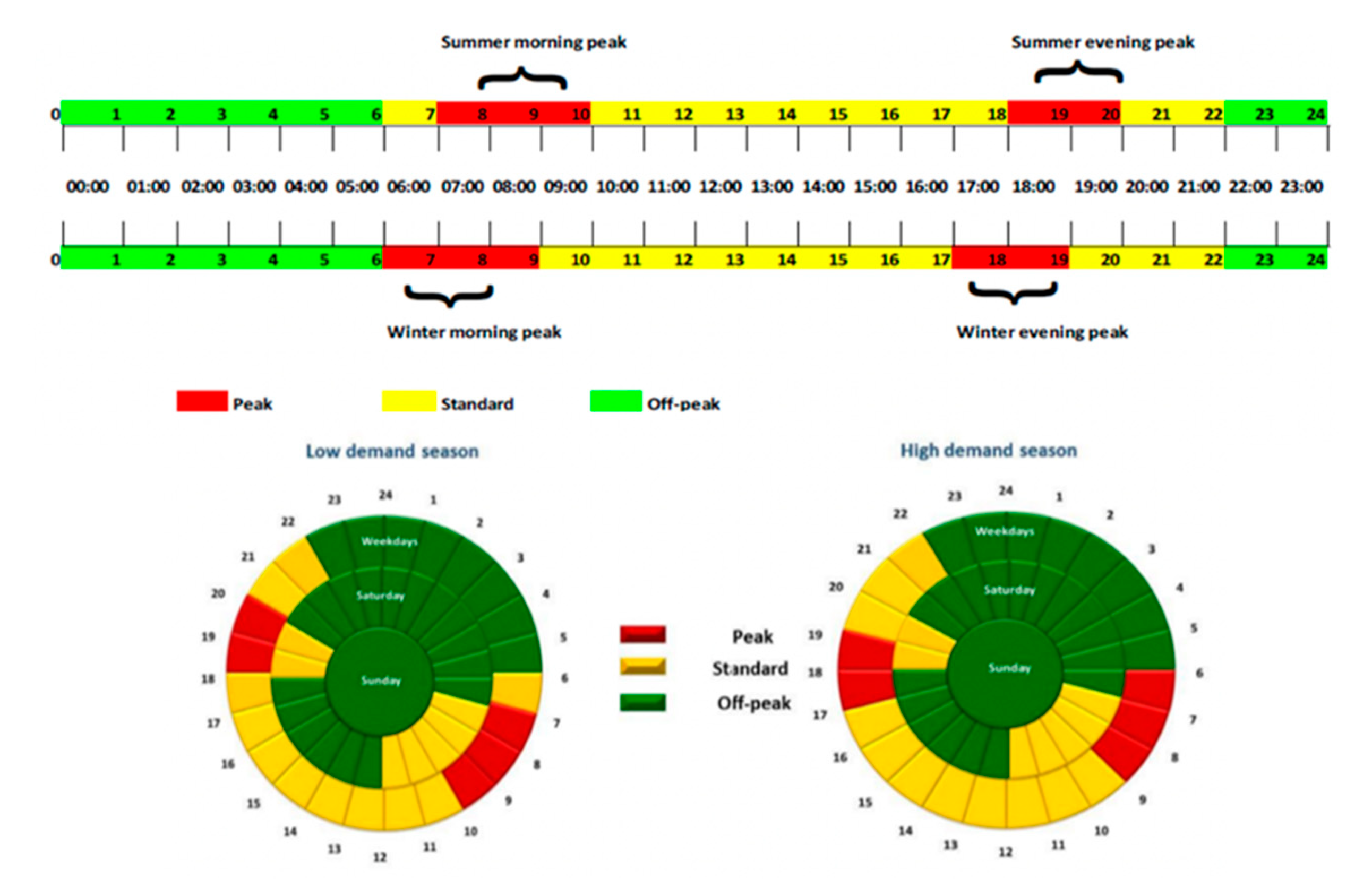
Preprints 112489 g004
Preprints 112489 g005
Figure 5. Refinery’s Annual kWh for each TOU category.
Figure 5. Refinery’s Annual kWh for each TOU category.
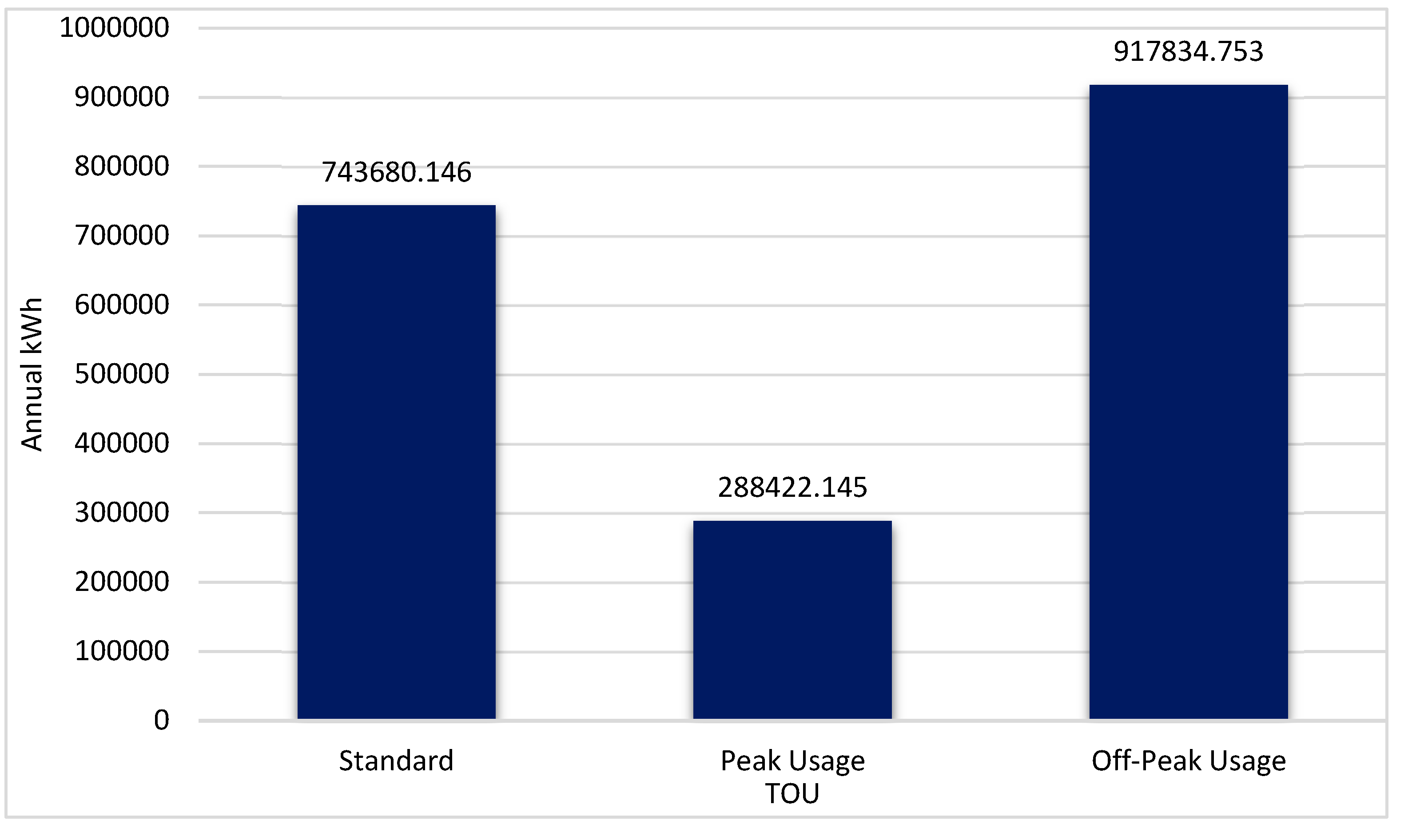
Preprints 112489 g005
Preprints 112489 g006
Figure 6. Solar Resource & Wind Atlas for South Africa Maps.
Figure 6. Solar Resource & Wind Atlas for South Africa Maps.
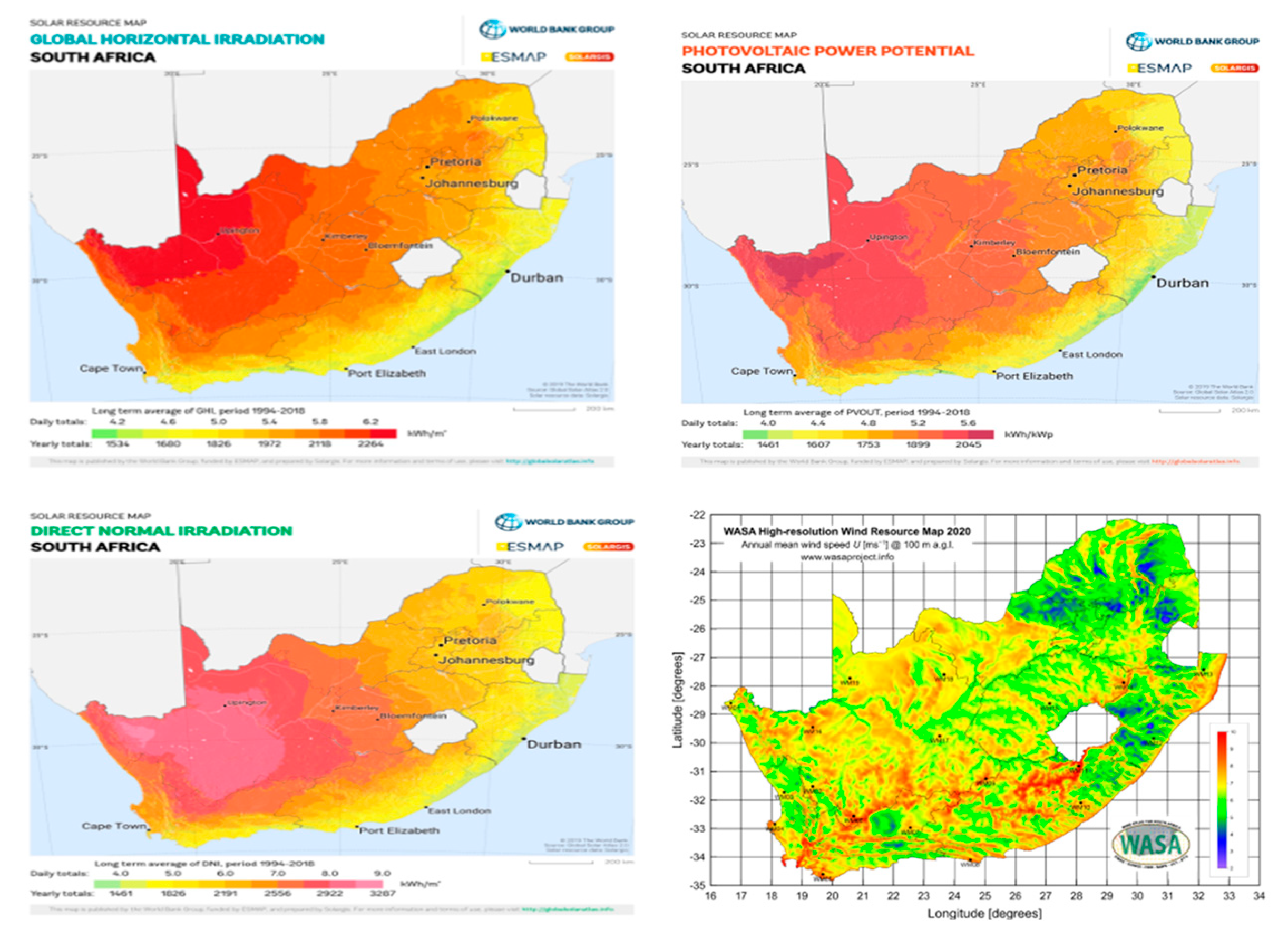
Preprints 112489 g006
Preprints 112489 g007
Figure 7. Refinery’s Site Layout.
Figure 7. Refinery’s Site Layout.
Preprints 112489 g007
Preprints 112489 g008
Figure 8. South African Load Shedding Analysis: 2007 to 2022 [19].
Figure 8. South African Load Shedding Analysis: 2007 to 2022 [19].
Preprints 112489 g008
Preprints 112489 g009
Figure 9. Flowchart of iterative Linear Program algorithm Optimal Management of Renewable Energy Source Problem.
Figure 9. Flowchart of iterative Linear Program algorithm Optimal Management of Renewable Energy Source Problem.
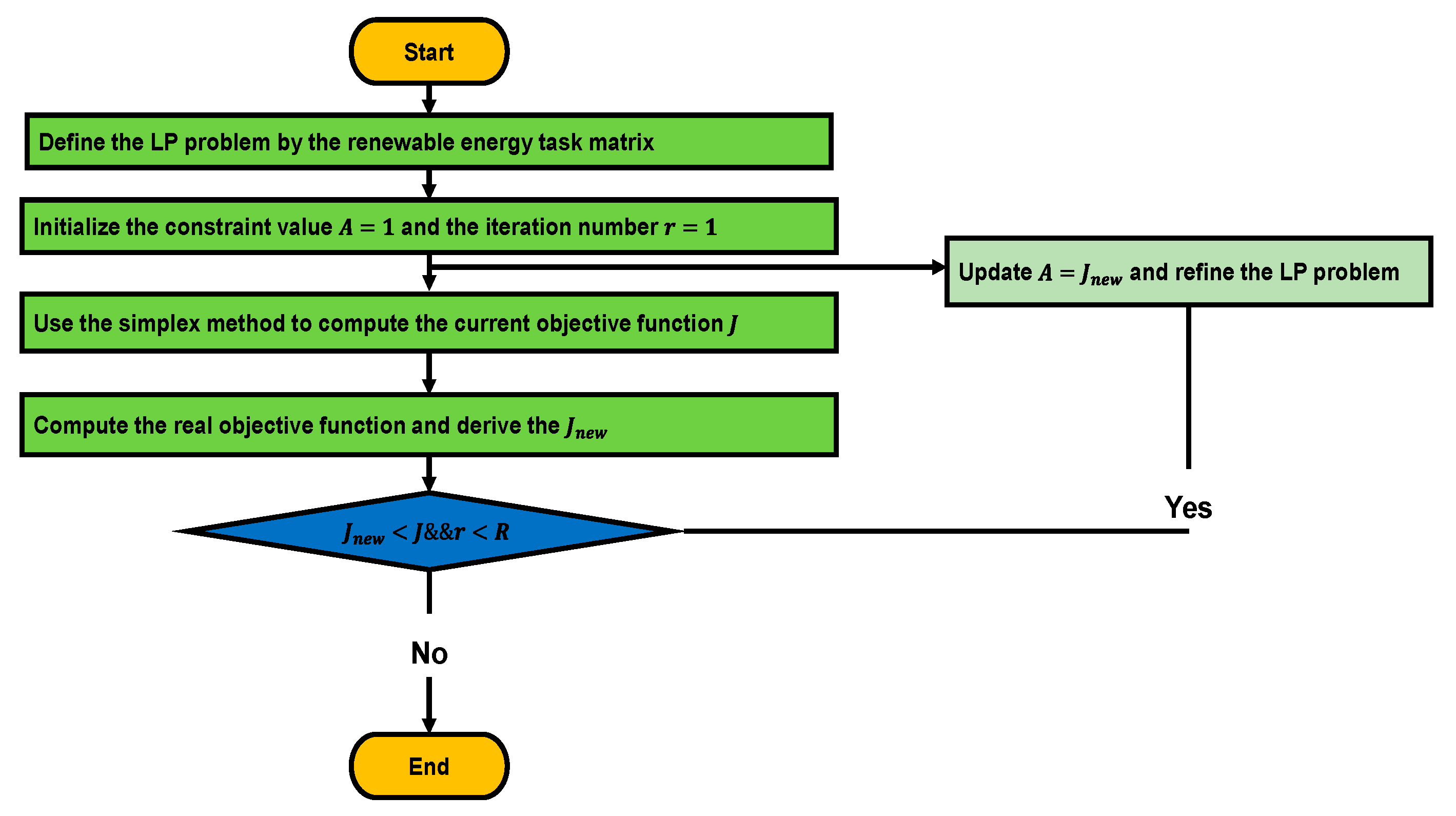
Preprints 112489 g009
Preprints 112489 g010
Figure 10. (a) Optimal solution to the Management of Renewable Energy Source Problem using LP. (b) Absolute deviation analysis for the LP problem.
Figure 10. (a) Optimal solution to the Management of Renewable Energy Source Problem using LP. (b) Absolute deviation analysis for the LP problem.
Preprints 112489 g010
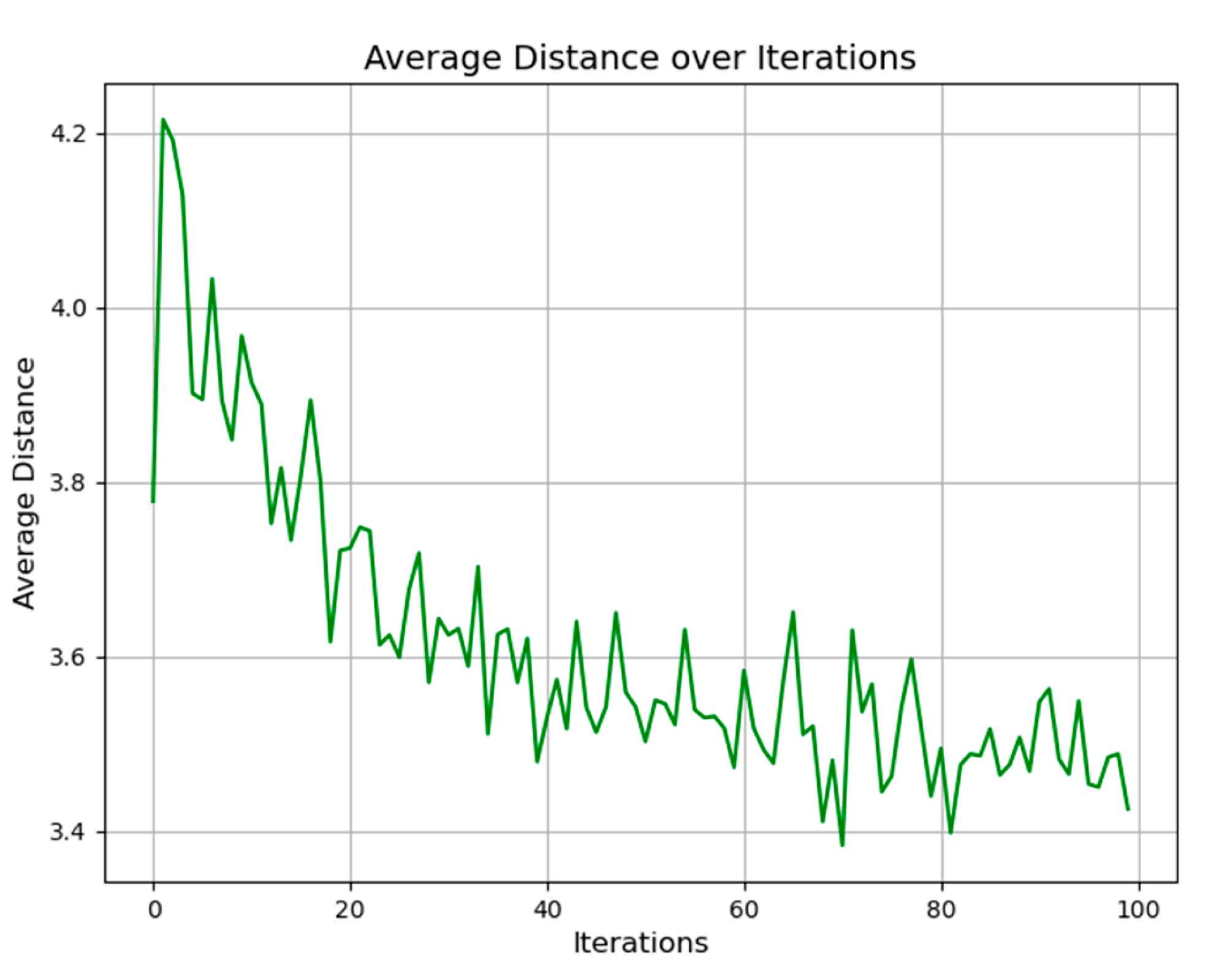
Preprints 112489 g011
Figure 11. Average Distance over Iterations.
Figure 11. Average Distance over Iterations.
Preprints 112489 g011
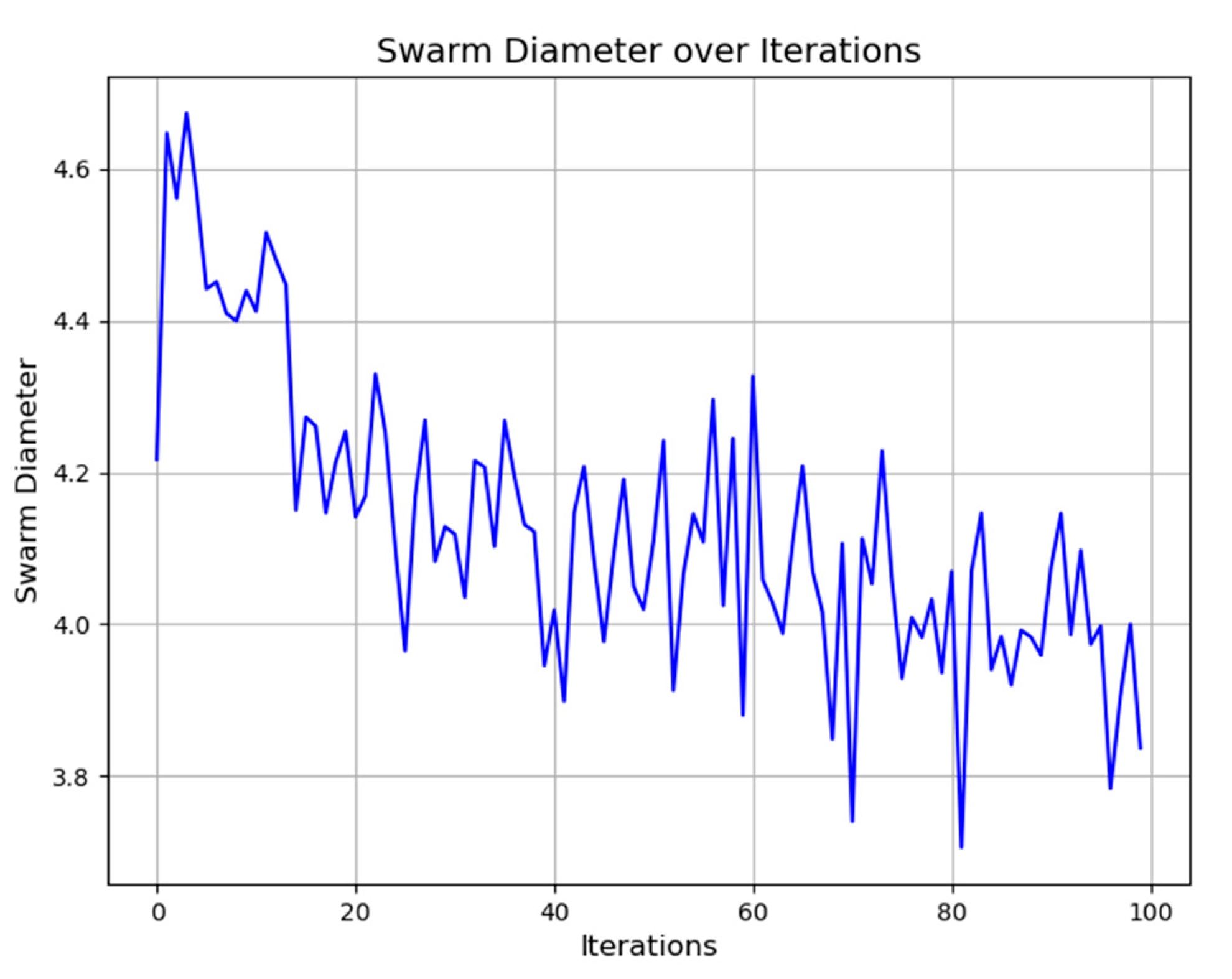
Preprints 112489 g012
Figure 12. Average Diameter over Iterations.
Figure 12. Average Diameter over Iterations.
Preprints 112489 g012
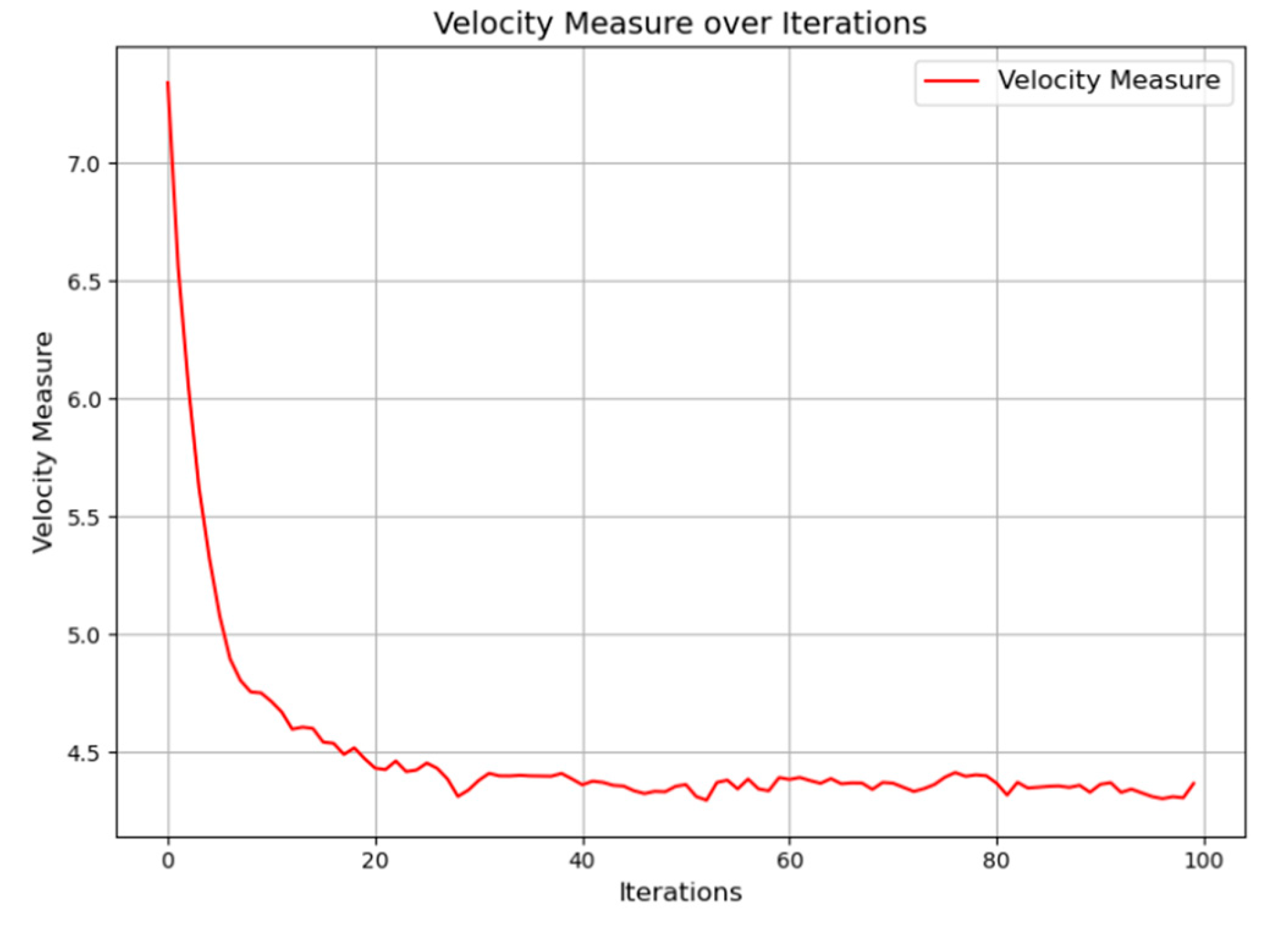
Preprints 112489 g013
Figure 13. Velocity Measure over Iterations.
Figure 13. Velocity Measure over Iterations.
Preprints 112489 g013
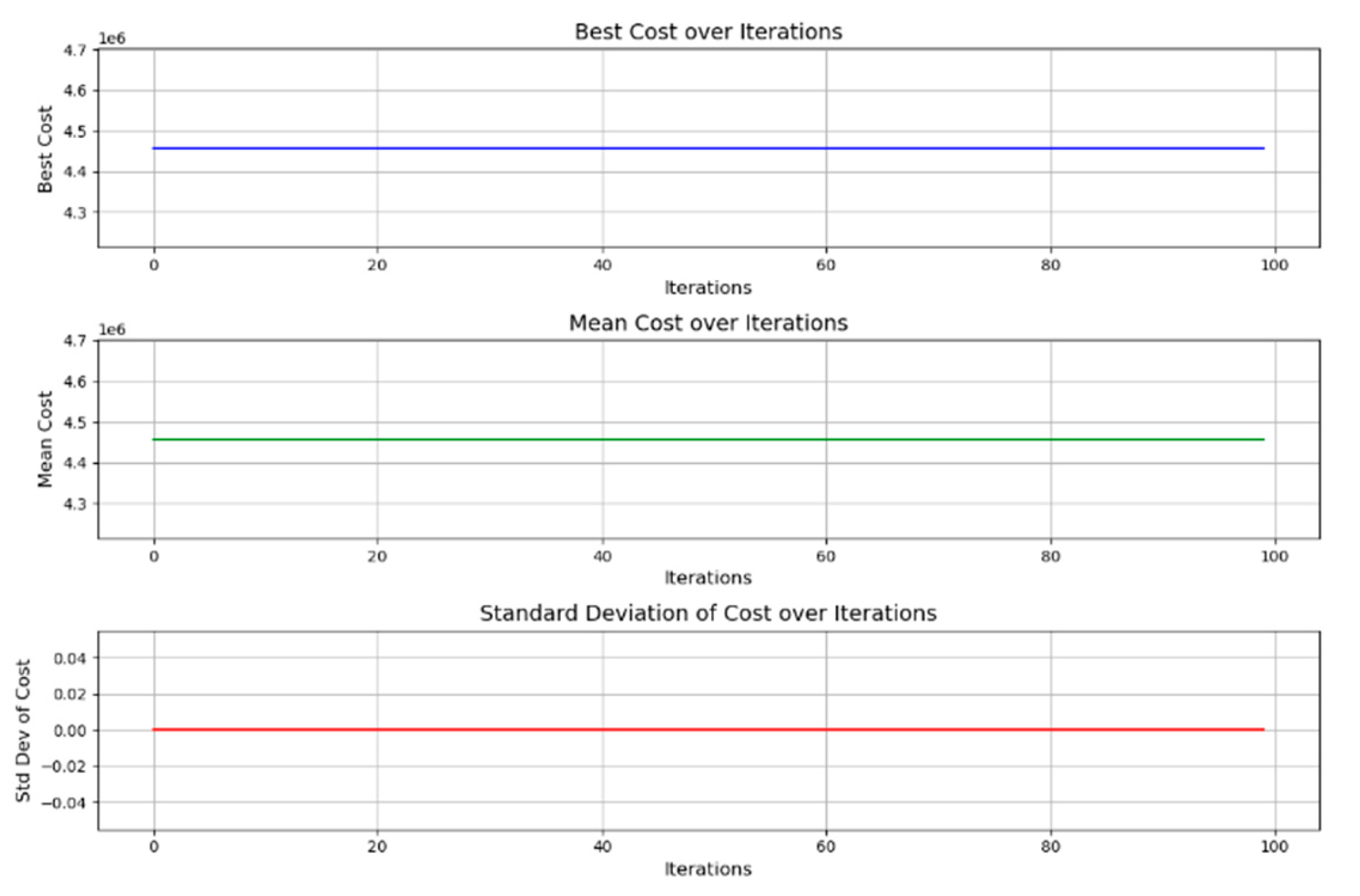
Preprints 112489 g014
Figure 14. Best Cost, Mean Cost and Standard Deviation over Iterations.
Figure 14. Best Cost, Mean Cost and Standard Deviation over Iterations.
Preprints 112489 g014
Table 1. Particle Swarm Optimization Algorithm.
Table 1. Particle Swarm Optimization Algorithm.
Step Description
1 Initialisation: The process begins by creating a swarm of particles, each assigned random positions and velocities within the given solution space. The particles should be assigned fitness values according to the objective function. The personal best position of each particle and the global best position discovered by any particle in the swarm are recorded.
2 Iterative Update: To ensure the termination criterion is met, the following steps are repeated for each particle in the swarm until either a maximum number of iterations is reached, or sufficient convergence is achieved.
3 Velocity Update: The new velocity for the particle can be determined by applying the given formula.
V i t + 1 = w ∙ V i t + c 1 ∙ r 1 ∙ P i − X i t + c 2 ∙ r 2 ∙ P g l o b a l − X i t (2.1)
Where:
V i t + 1 − is the updated velocity of particle i in the next iteration
w − is the inertia weight
c 1 and c 2 − are the cognitive and social learning rates
r 1 and r 2 − are random values between 0 and 1
P i is the personal best solution of particle i
P g l o b a l − is the global best solution found by any particle
4 Position Update: The particle's position is updated by incorporating the new velocity.
X i t + 1 = X i t + V i t + 1 (2.2)
5 Fitness Evaluation: Assess the level of suitability of the new position by utilising the objective function. When the fitness of the particle improves, it is necessary to update its personal best solution. If the solution is deemed the most optimal within the entire swarm, proceed to update the global best solution.
6 Termination Check: Examine the termination criteria. If the conditions are satisfied, the algorithm is terminated; otherwise, go to Step 3 for the next iteration.
7 Conclusion: The algorithm reaches its conclusion when the termination criteria are satisfied. At this point, the global best solution is determined, which represents the optimised solution to the given problem.
Table 2. Decision Variables.
Table 2. Decision Variables.
Variable Meaning
P R E , i , t The optimisation of energy produced by renewable energy technologies in a certain time, denoted as t , is the focus of this study.
P g r i d , t The purchase of electricity from the power grid at a certain time interval t .
P s t o r a g e , j , t The energy that is either stored or released by storage technology j within a certain time t .
S O S s t o r a g e , j , t The present level of energy storage technology j state of charge (SOC) throughout the period t .
Table 3. Refinery Input Parameters.
Table 3. Refinery Input Parameters.
Refinery Input Parameters. Specification
Roof Area available for renewable energy installations 1198m2
Global horizontal irradiation 1972 kWh/m2
Municipality Ekurhuleni
Diesel Consumption
Diesel Tariff R13/litre
Area of each PV Module 2,564m2
Power on each PV module 540W
Annual Average Grid Power tariff R2,168
Levelized Cost of Electricity (LCOE) Grid+Genset R5,98
Levelized Cost of Electricity (LCOE) PV Solar+BESS R2,83
Table 4. Refinery’s Cost of Electricity before Solar System + BESS application.
Table 4. Refinery’s Cost of Electricity before Solar System + BESS application.
Electricity component Cost (R)
Std TOU kWh/annum 743 680,15
Peak TOU kWh/annum 288 422,15
Offpeak TOU kWh/annum 917 834,75
Total TOU kWh/annum 1 949 937,05
LCOE (grid/genset) R5,98
Std TOU Cost/annum R4 447 207,30
Peak TOU Cost/annum R1 724 764,46
Offpeak TOU Cost/annum R5 488 651,81
Total Cost/annum R11 660 623,56
Table 5. Refinery’s Cost of Electricity after Solar System + BESS application.
Table 5. Refinery’s Cost of Electricity after Solar System + BESS application.
Post Solar System + BESS Electricity Profile Cost (R)
Solar Std TOU kWh/annum R281 601,60
Grid Std TOU kWh/annum R462 078,55
Peak TOU kWh/annum R288 422,15
Offpeak TOU kWh/annum R917 834,75
Total TOU kWh/annum 1 949 937,05
LCOE (grid/genset) R5,98
LCOE (solar system + BESS) R2,83
Solar Std TOU Cost/annum R796 932,53
Grid Std TOU Cost/annum R2763229,729
Peak TOU Cost/annum R1 724 764,46
Offpeak TOU Cost/annum R5 488 651,81
Total Cost/annum R10 773 578,52
Table 6. Parameter of the PSO algorithm.
Table 6. Parameter of the PSO algorithm.
c 1 c 2 ω m a x ω m i n n − p a r t i c l e s n − i t e r a t i o n f t o l _ i t e r c e n t r e b h _ s t r a t e g y
0.5 0.3 0.9 0.4 10 100 1 1.0 periodic
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated