Prerpints.org logo
Preprint
Article

Toward Automated Controlled Vibration Characteristics Structural Design through Topology Optimization and Computer Vision for Space Mission

Altmetrics

Downloads

98

Views

41

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

18 July 2024

Posted:

19 July 2024

You are already at the latest version

Alerts
Abstract
This study explores the integration of computer vision with topology optimization for additive manufacturing, with a focus on maximizing eigenfrequency in a design domain. Utilizing cus-tom-developed photogrammetry software, high-resolution images are processed to generate de-tailed 3D models, subsequently converted to STL files with precision. Adaptive meshing in COMSOL Multiphysics, controlled through a MATLAB API, ensures optimal mesh resolution. Prioritizing resource conservation in extraterrestrial environments, the original volume is reduced by 50% while preserving structural integrity. The design domain undergoes rigorous topology optimization in MATLAB, supported by COMSOL's advanced FEM simulation. The optimized design exhibits a 57% performance improvement and a 50% weight reduction, maintaining desired vibration characteristics, validating the efficacy of the modifications. Moreover, the case with an eccentric mass shows a significant 64% increase in eigenfrequency.
Keywords: 
Subject: Engineering  -   Architecture, Building and Construction

1. Introduction

The pursuit of space exploration and the extraction of extraterrestrial resources are fundamentally intertwined with the trajectory of human advancement and scientific inquiry. Earth's finite resources, juxtaposed with the burgeoning global population and escalating demands for energy and materials, underscore the imperative to expand our endeavors beyond terrestrial confines. The potential discovery and utilization of extraterrestrial resources present transformative opportunities for addressing critical challenges facing humanity, from energy sustainability to the colonization of distant celestial bodies [1,2,3].
Advancements in space exploration technologies have significantly enhanced our comprehension of the cosmos and broadened the spectrum of accessible space resources. For instance, the prospecting of asteroids, which are abundant in precious metals and rare earth elements, represents a promising avenue for resource extraction. These celestial bodies contain vast quantities of materials essential for high-tech industries and renewable energy technologies, such as platinum, cobalt, and lithium, which are crucial for manufacturing batteries, electronics, and catalytic converters. The utilization of these resources could alleviate the strain on Earth's limited reserves, thereby supporting technological progress and economic growth [4,5,6,7].
In space missions, the preparation and construction of new installations necessitate a high degree of adaptability to dynamic and unforeseen situations. The constraints of space environments, coupled with the inherent limitations of pre-mission planning on Earth, underscore the critical importance of real-time design adjustments and improvisation. Unlike terrestrial operations, where modifications can be implemented with relative ease, the isolated and hostile conditions of space amplify the consequences of errors, making the stakes significantly higher. Real-time adaptability is essential for several reasons. First, the unpredictable nature of space missions often results in unforeseen challenges that cannot be fully anticipated during the planning phase. This includes technical malfunctions, unexpected environmental conditions, and emergent logistical needs. To effectively address these issues, space missions must incorporate flexible design principles and robust contingency planning. This approach ensures that astronauts and mission control can promptly respond to and mitigate adverse conditions, thereby safeguarding the mission’s objectives and crew safety. Moreover, the logistical complexity and resource constraints of space missions necessitate the capability for on-the-spot problem-solving. The vast distance and communication delays between Earth and space installations limit the feasibility of relying solely on ground-based support. Therefore, mission designs must incorporate autonomous systems and decision-making frameworks that enable the crew to execute critical adjustments independently. This includes the ability to modify infrastructure, repair essential systems, and adapt operational procedures in response to real-time data and situational changes. The fatal risks associated with space missions further emphasize the necessity for such adaptability. The inability to correct errors or address emergent issues can lead to catastrophic outcomes, including mission failure and loss of life. Consequently, space mission protocols must prioritize flexibility and resilience, integrating advanced technologies and adaptive strategies to ensure mission success and the safety of all personnel involved. This paradigm shift from rigid pre-mission planning to dynamic, real-time management is pivotal for the advancement of sustainable and successful space exploration endeavors. Structural design within the realm of space exploration, coupled with autonomous construction capabilities, is imperative due to the formidable challenges posed by vast distances and communication delays inherent in extraterrestrial endeavors [8,9,10,11,12]. The exigencies of space missions, characterized by substantial time lags in transmitting instructions and uploading designs from Earth due to considerable distances, underscore the critical necessity for autonomous structural design and construction processes [13,14,15,16,17,18,19,20,21,22]. Moreover, in space missions, significant signal transmission delays occur due to Earth's varying distance from celestial bodies like Mars, which can reach up to 401 million kilometers. This results in communication latencies ranging from 3 to 22 minutes, depending on their relative orbital positions [23,24,25,26,27,28].
Reliance on Earth-based instructions and designs becomes impractical for timely decision-making and execution in space missions due to significant communication delays. Autonomous structural design and construction methodologies enable spacecraft and habitats to adapt to dynamic environmental conditions and unforeseen challenges without constant Earth-based intervention. Integrating artificial intelligence and advanced robotics into these processes allows for the autonomous formulation and execution of optimized structural designs. This capability mitigates the impact of communication delays, enhancing mission efficiency and resilience. By leveraging AI-driven systems and robotic technologies, space missions can achieve greater flexibility, enabling real-time adjustments and responses to emergent situations, thereby ensuring the safety and success of long-duration extraterrestrial endeavors. This autonomous approach is crucial for maintaining operational integrity and addressing the complexities of space environments, where rapid adaptation is essential for survival and mission accomplishment [8,9,10,11,12].
Structural design is an intellectual endeavor rooted in the discernment and expertise of the designer, varying with their experience and overarching vision. The advent of topology optimization, pioneered by Michell [29] through the solving structural optimization design utilizing Maxwell’s lemma [30], has significantly advanced computer-aided design, enabling the creation of designs based on rigorous non-parametric optimization principles. While the complete automation of evaluation and design processes remains an aspirational goal, it is a crucial imperative for advancing future transportation technologies, particularly in the realm of deep space missions. This integration of sophisticated computational methods into the design process not only enhances precision and efficiency but also paves the way for innovations that are essential for overcoming the unique challenges of extraterrestrial exploration and transportation [31,32,33].
Topology optimization encompasses two main categories: non-parametric optimization and generalized shape optimization. It involves dividing a domain into discrete parts with defined spatial relationships, such as finite differences, boxes, elements, and volumes. Initially addressing layout challenges, topology optimization concentrates on configuring designated regions (design domains) within a specified space, each having fixed traction and support points [34,35,36,37]. Numerous efforts have been invested in advancing topology optimization methodologies. A significant contribution to this field has been the utilization of numerical discretization of structures, as proposed by Dorn et al. [38], to enhance the efficiency and precision of topology optimization techniques. This approach involves the detailed numerical representation of structural elements, allowing for more accurate and refined optimization outcomes. Bartel [39] leveraging sequential unconstrained minimization and constrained steepest descent techniques to minimize structure weight. Charrett and Rozvany [40] adopted the Prager–shield implementation to identify optimal design criteria for rigid-perfectly plastic systems under multiple loading conditions. Rozvany and Prager [41] investigated the optimal design of grillage-like continua, emphasizing spatial distribution within confined grillage units. Rossow and Taylor [42] utilized the finite element method to determine the optimal thickness of variable thickness sheets, addressing potential energy considerations for elastic sheet in-plane stress assumptions and pioneering shape optimization by introducing holes into plate structures. Cheng and Olhoff [43] implemented the finite element method to optimize the thickness of annual plates with a stiffened approach, incorporating homogenization as an averaging method in topology optimization. The discretized continuous optimality criterion (DCOC) further advanced topology optimization, leading to the conceptualization of fictitious materials by Bendsoe and the subsequent development of the Solid Isotropic Material with Penalization (SIMP) method [44,45,46]. SIMP method has been instrumental in optimizing structures with minimal stress concentrations, leveraging image processing techniques to construct design cases and transform them into the topology optimization process.
Moreover, several other effective methods for topology optimization exist, including the Evolutionary Structural Optimization (ESO) method [47,48] and the Metaheuristic Structure Binary-Distribution (MSB) method [49,50]. Additionally, shape optimization methods that focus on the boundaries of the structure are currently showing promising results, such as the level-set method [51] and the H1 gradient method [52].
This study delves into the integration of camera technology aboard spacecraft, aiming to optimize eigenfrequency for structures automatically modeled through computer vision and optimized via topology optimization with minimal human intervention. The research focuses on advancing the design and construction of habitable structures using state-of-the-art 3D printing methods [53,54,55,56]. Topology optimization is a sophisticated computational technique utilized to maximize eigenfrequency, a critical parameter in structural dynamics. This method employs mathematical algorithms to iteratively adjust material distribution within a predefined design domain, aiming to achieve the highest possible natural frequency while adhering to specified constraints such as volume or stress limits. By systematically removing material from non-critical regions and reinforcing critical areas, topology optimization enhances structural stiffness, thereby elevating eigenfrequencies. This approach has been extensively studied and applied across various engineering disciplines, including aerospace, mechanical, and civil engineering, where enhancing structural performance under dynamic loading conditions is essential[57]. Several researchers investigated topology optimization for design structures with a desirable vibration characteristic. Zuo et al. and Liu et al. performed topology optimization in 2D and 3D models to maximize the natural frequencies [58,59]. Liang et al. established both multi-material and multi-scale models for concurrent vibroacoustic topology optimization [60], and Zhang et al. used shape interpolation to generate multiple microstructure samples for concurrent optimization of the macrostructure and multiple microstructures and their distributions to maximize natural frequencies [61]. Dynamic problems often involve eigenfrequency problems because when a structure has undesirable natural frequencies relative to its surrounding environment, resonance phenomena can lead to structural destruction and noise. Therefore, it is important to design the natural frequencies of vibration modes so that they do not match the excitation frequency in order to avoid resonance phenomena.
By utilizing camera vision, the computational system identifies design domain parameters and applies topology optimization techniques for efficient design execution. The research is motivated by several factors. Firstly, the weight constraints of space missions necessitate minimizing additional measurement devices like laser scanners to reduce costs. Secondly, considering energy efficiency, computationally intensive methods such as machine learning, while effective for emulating expert systems, impose significant computational loads compared to more resource-efficient optimization approaches like the Method of Moving Asymptotes or optimality criteria [62]. Thirdly, the logistical challenges of vast distances in space emphasize the importance of locally executable design processes for swift communication between Earth and extraterrestrial habitats. Lastly, topology optimization is well-suited for 3D printing applications, supporting its viability for space construction projects. The paper is structured as follows: Section 2.1 discusses computer vision, Section 2.2 covers topology optimization, Section 3 presents numerical investigations, and Section 5 provides conclusions.

2. Materials and Methods

2.1. Computer Vision 3D Simulation Using Computer Vision

In this study, we propose the integration of Photogrammetry into the realm of design engineering to facilitate 3D modeling of the design domain using camera alone [63,64,65,66,67,68,69]. Photogrammetry, a technique widely utilized in modern engineering for 3D modeling of objects, leverages principles of optics, geometry, and computer vision to reconstruct physical objects from photographic images. This method enables engineers to create accurate digital representations of real-world objects, which are crucial for various applications such as industrial design, architecture, archaeology, and forensics. The process of photogrammetry begins with capturing multiple photographs of an object from different angles using calibrated cameras. These images, along with known camera parameters such as focal length and sensor size, serve as inputs for computational algorithms. Through feature extraction and matching techniques, corresponding points across images are identified, forming a point cloud representation of the object's surface as presented in Eq. 1. Subsequently, these points are used to generate a dense mesh, which accurately describes the object's geometry in three-dimensional space (as illustrated in Figure 1).
Where P represents the perceived size of an object in an image, f is the focal length of the camera lens, B denotes the actual size of the object, and D signifies the distance between the camera and the object.
P = f . B . D − 1
The transformation in photogrammetry is depicted in Eq. 2
X = T − 1 . x ¯
Where X represents the coordinates of a point in the object's 3D space, T denotes the transformation matrix derived from camera calibration and orientation, and x ¯ corresponds to the homogeneous coordinates of the point in the image. This equation encapsulates the process of triangulation, enabling the computation of accurate 3D coordinates from 2D image data. The accuracy and resolution of photogrammetric models depend on several factors, including the quality of input images, camera parameters, and the computational algorithms used for point cloud generation and mesh reconstruction. Advanced photogrammetric software packages facilitate automated processing and refinement of models, offering tools for texture mapping, surface reconstruction, and error minimization techniques.

2.2. Topology and Shape Optimization

Topology optimization originated as a discipline rooted in deterministic functional analysis, initially employing tangible physical models. As mathematical understanding and techniques advanced, various methodologies were developed to tackle previously underdetermined problems. The introduction of virtual work significantly broadened the range of viable solutions for practical applications. Structural optimization is broadly classified into parametric and non-parametric approaches. Parametric optimization utilizes heuristic and metaheuristic methods to manipulate parameters within a defined domain, guided by well-approximated mathematical models that adhere to constraints and optimality criteria. For example, sizing optimization directly links variables such as cross-section, material size, and hole placement to minimize stress.
However, determining the optimal material distribution within a structural space presents challenges, as it cannot be straightforwardly represented by known quantities like masses, loads, or reactions. The difficulty lies in establishing a direct correlation between topology design and known constraints while formulating a universally applicable parametric objective. This challenge has spurred the development of non-parametric optimization methods, exemplified by topology optimization encompassing layout and shape optimization.
Topology optimization, known for its conceptual clarity rooted in mathematical rigor, opens new avenues in design. It focuses on mathematically optimizing a predefined state space or higher-order set of criteria, driven solely by the imperative to fulfill the optimization process. The resultant designs theoretically offer the best possible solutions within defined constraints, representing an optimal solution bounded by prescribed parameters [70,71,72].
This paper addresses the optimal topology of the structure, aiming to maximize the natural frequency of a specified mode while imposing a mass constraint to limit material usage. The optimization objective is to enhance the natural frequency of the selected mode, with the volume fraction of each node serving as the design variable. The topology optimization problem can be formulated as shown in Eq. (3):
max             ω i s . t . :           ( K − ω 2 M ) U = F                     ∫ Ω d ρ d ρ ≤ v ,   ρ ∈ ( 0 , 1 ] , ∀ ρ ∈ Ω d
Where ω i represents the eigen frequency of the designated mode, ρ is the design variable of topology optimization. K is the global stiffness matrix, and M is the global mass matrix. Moreover, v is the volume reduction condition, withing the design domain Ω d .
In the context of the present study, topology optimization is employed to maximize the first eigen frequency, i.e., ω   1 .

3. Results

This section introduces a numerical study to explore the innovative integration of computer vision with topology optimization for additive manufacturing. We employ custom-developed photogrammetry software to process imagery captured by cameras within the design domain. This software captures dynamic, high-resolution photographs that facilitate the creation of detailed 3D models through comprehensive object scanning protocols. The imagery, rich in detail, serves as the foundation for the subsequent 3D modeling process.
We utilized in this paper a square-based pillar measuring 192 mm in height and with a square base side length of 96 mm, illustrated in Figure 2. The model underwent scanning, employing photogrammetry to construct a comprehensive 3D spatial matrix. This involved a 360-degree scan using cameras to capture detailed spatial configurations.
Upon completing the 3D modeling phase, the resulting model is converted into a STL file format, a standard in both additive manufacturing and computational modeling. This conversion is performed with high precision using an automated approach to ensure that the intricate details captured during the initial scanning phase are preserved.
Following the conversion to STL, the file undergoes remeshing using an adaptive meshing algorithm within the COMSOL Multiphysics environment. This process is controlled by a custom-built MATLAB application programming interface, which integrates MATLAB's computational capabilities with COMSOL's simulation tools. This synergy enables the refinement of the mesh structure to meet the demands of subsequent computational simulations.
The adaptive meshing strategy employed ensures optimal mesh resolution by dynamically adjusting to local geometric complexities. This approach enhances the accuracy and fidelity of the computational analyses that follow, providing a robust framework for investigating the proposed design methodologies in additive manufacturing.
The preliminary phase of our investigation entailed a thorough examination of the parameters essential for the design and fabrication of a concrete pillar using advanced 3D printing techniques. This pillar is intended to serve as a structural component for supporting vertical structures, necessitating strict considerations for stability and material efficiency. Given the imperative of resource conservation, especially in extraterrestrial environments like the Moon or Mars where time and materials are scarce, our study prioritizes optimizing printing time while minimizing material usage.
To achieve this objective, we adopt a strategy of volumetric reduction, aiming to decrease the original volume of the solid block configuration by 50% (i.e., 0.5 volume fraction). This reduction is a central tenet of our optimization approach, utilizing constrained optimization techniques to reduce volume while maintaining the pillar's structural integrity and functionality.
The initial step involves digitally inserting the pillar into the design environment through a comprehensive scanning process. This process employs a camera array positioned for 360-degree rotation around the object, capturing images at one-degree increments, as illustrated in Figure 3. This panoramic scanning protocol ensures the acquisition of complete spatial data, essential for subsequent modeling and optimization efforts. The design domain, captured through this detailed scanning process, is imported into the MATLAB topology optimization environment. Here, we rigorously explore structural optimization strategies. MATLAB's robust computational platform and advanced optimization algorithms enable a systematic investigation of material-efficient design configurations. This integrated framework facilitates the development of optimized, resource-efficient structural components for advanced additive manufacturing, addressing the challenges of extraterrestrial construction with precision and efficiency. The computational capabilities of MATLAB are significantly enhanced through integration with COMSOL Multiphysics, utilized as both a mesher and a FEM solver. This synergy improves the fidelity and computational efficiency of the optimization process. COMSOL's advanced meshing capabilities generate high-quality finite element meshes that accurately represent the intricate details of the imported design domain. Its powerful FEM solver then facilitates precise simulations of structural behavior under various loading conditions.
In Figure 4, the computer modeling for topology optimization is presented, with a pillar is simulated for two cases, first case is with central mass (as shown in Figure 4a) and the second case is with mass on the far side of the pillar as shown in Figure 4b). Topology optimization endeavors to minimize the volume of the design while concurrently improving the structure dynamic stability addressing the reduction of natural frequency. The Young modulus of elasticity, and mass are standardized to unity, with a Poisson ratio set at 0.3 to maintain consistency across analyses. The results are depicted in Figure 5. Topology optimization gave a result of is an elongated hollow pillar. In the three-dimensional perspective (a), the pillar exhibits distinct vertical and horizontal striations, oriented along the z-axis. The cross-sectional profile (b) provides a detailed view of the internal structure. From the frontal view (c), the pillar reveals a symmetrical narrowing towards the bottom, maintaining alignment with the z-axis. The rear view (d) highlights a concentric circular design centered on the z-axis. The top view (e) emphasizes the striated texture and the tapering shape towards each end. Finally, the side view (f) within a bounding box illustrates the uniform width of the pillar and its tapered ends, providing a comprehensive understanding of the structure’s geometry.
Our investigation reveals a significant reduction in the volume of the design domain, a central goal in our comprehensive optimization framework. Notably, this volume reduction demonstrates a clear spatial pattern, with the most pronounced decreases occurring towards the central region of the design domain and gradually tapering towards the periphery near the structural constraints. This deliberate spatial distribution of volume reduction is strategically designed to enhance the stability of the resulting structure while also optimizing the utilization of materials. This approach, rooted in optimization principles, parallels strategies seen in civil engineering where minimizing weight often involves incorporating hollow structures within solid frameworks.
Figure 5 illustrates the convergence pattern of our optimization algorithm across multiple iterations. The x-axis tracks the iteration count, while the y-axis represents the value of a normalized objective function. Initially, the objective function value starts near 1, indicating suboptimal conditions at the outset. As iterations progress, there is a sharp decline in the objective function value, signaling rapid convergence towards an optimal solution. By around the 50th iteration, the curve begins to plateau, approaching a value close to zero, indicating diminishing returns from subsequent iterations. This plateau suggests that the algorithm has effectively maximized the objective function and is nearing its optimal value. The steep initial descent followed by the leveling off underscores the efficiency and stability of the algorithm in achieving optimization. Such behavior is highly desirable in optimization techniques, showcasing both computational efficiency and robustness in achieving convergence. The results also demonstrated a significant enhancement in performance, with a 57% improvement observed in shifting eigen frequency to become higher compared to the non-optimized structure. Additionally, we achieved a substantial reduction in weight by 50%, resulting in a lighter structure. This weight reduction was achieved without compromising the desired vibration characteristics. We can conclude that, the optimized design not only maintains the structural integrity but also enhances the dynamic performance, showcasing the effectiveness of the applied modifications.
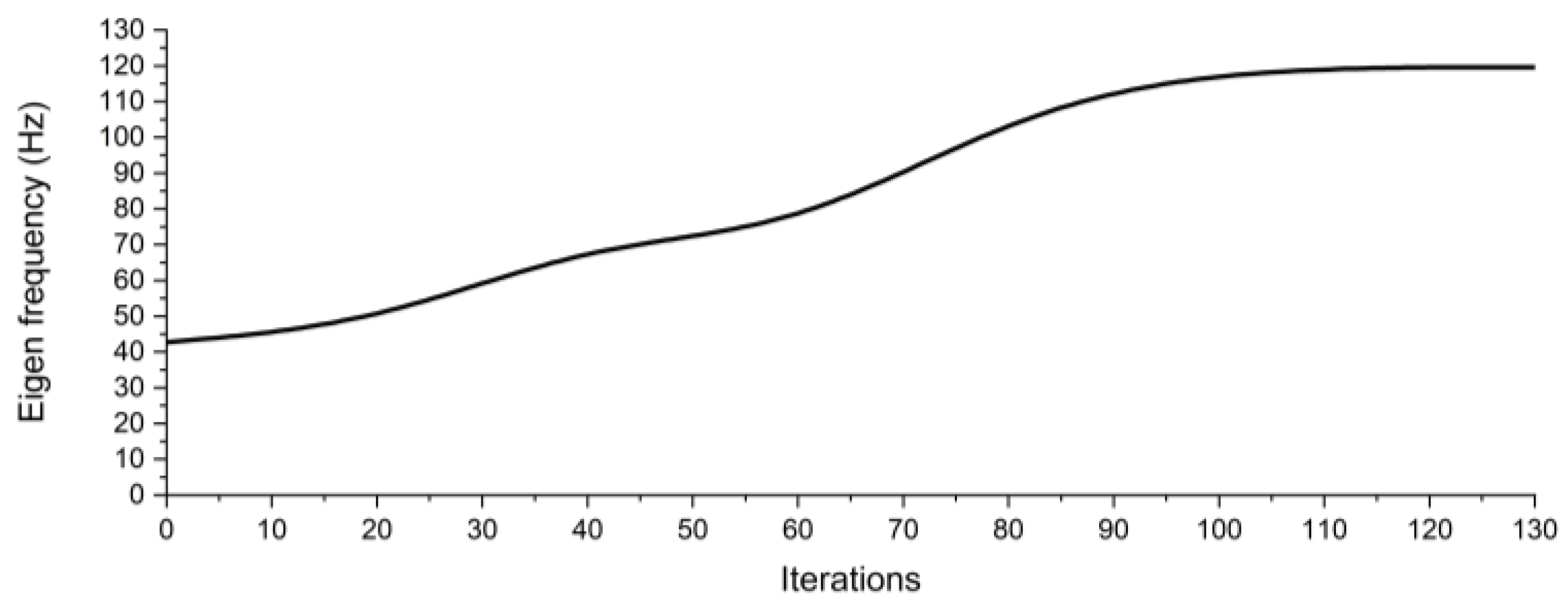
By incorporating an eccentric mass, engineers can purposefully adjust the natural frequency of structures, thereby enhancing stability and performance. The result structure shown in Figure 6. (b) features a pillar-like design with a square base, poised for modifications aimed at altering its dynamic behavior. The diagrams Figures (a), (c), (d), (e) and (f) provide different perspectives of the original structure, showcasing side, front, and top views, respectively. These views collectively illustrate the structural geometry and form the basis for subsequent modifications. Figure 7 depicts the convergence pattern of our optimization algorithm throughout numerous iterations. The findings further illustrated a notable performance enhancement, manifesting as a 64% increase in eigenfrequency compared to the non-optimized structure. Concurrently, there was a substantial 50% reduction in weight, contributing to a lighter structure without compromising desired vibration characteristics. These results affirm that the optimized design effectively preserves structural integrity while significantly enhancing dynamic performance. This underscores the efficacy of the applied modifications in achieving superior structural efficiency and resilience.

5. Conclusions

In conclusion, this numerical study demonstrates the innovative integration of computer vision with topology optimization for additive manufacturing, specifically targeting the minimization of eigenfrequency in a design domain. Using custom-developed photogrammetry software, dynamic, high-resolution images were captured, forming the basis for precise 3D models. These models were converted into STL files through an automated, high-precision process, and subsequently meshed with an adaptive algorithm within the COMSOL Multiphysics environment, controlled via a custom MATLAB API. The study investigated two cases of a pillar with a central mass on top and an eccentric mass, where the center of gravity is positioned on the left side of the top surface.
The results from the first case highlight the significant advancements realized through topology optimization. Specifically, there was a 57% increase in performance, demonstrated by a substantial elevation in eigenfrequency, coupled with a 50% reduction in structural weight. Importantly, these enhancements were achieved while preserving the desired vibration characteristics, thereby affirming the effectiveness of the applied modifications. These findings provide a robust foundation for future innovations in extraterrestrial construction and resource-efficient structural design. Similarly, the second case exhibited comparable improvements, with a notable increase in eigenfrequency, further validating the high-performance outcomes of the optimization process. This dual success underscores the potential for implementing such optimization strategies in demanding environments where material efficiency and structural integrity are paramount. Moreover, the eccentric mass case results showed a significant 64% increase in eigenfrequency and a 50% weight reduction without compromising vibration characteristics, demonstrating that the optimized design maintains structural integrity while enhancing dynamic performance, highlighting the efficacy of the applied modifications.

Author Contributions

Conceptualization, M.A.; methodology, M.A., M.S.; numerical simulations, M.A. M.S., M.N.; writing—original draft preparation, M.A., M.S., and M.N.; All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

Data may be available from the correspondent author upon reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Dallas, J.A.; Raval, S.; Gaitan, J.P.A.; Saydam, S.; Dempster, A.G. Mining beyond Earth for Sustainable Development: Will Humanity Benefit from Resource Extraction in Outer Space? Acta Astronaut. 2020, 167, 181–188. [Google Scholar] [CrossRef]
  2. Xu, F. The Approach to Sustainable Space Mining: Issues, Challenges, and Solutions. In Proceedings of the IOP Conference Series: Materials Science and Engineering; 2020; Vol. 738, p. 12014.
  3. Steffen, O. Explore to Exploit: A Data-Centred Approach to Space Mining Regulation. Space Policy 2022, 59, 101459. [Google Scholar] [CrossRef]
  4. Baumgart, A.; Vlachopoulou, E.I.; Vera, J.D.R.; Di Pippo, S. Space for the Sustainable Development Goals: Mapping the Contributions of Space-Based Projects and Technologies to the Achievement of the 2030 Agenda for Sustainable Development. Sustain. Earth 2021, 4, 6. [Google Scholar] [CrossRef]
  5. Maiwald, V.; Schubert, D.; Quantius, D.; Zabel, P. From Space Back to Earth: Supporting Sustainable Development with Spaceflight Technologies. Sustain. Earth 2021, 4, 1–16. [Google Scholar]
  6. Iliopoulos, N.; Esteban, M. Sustainable Space Exploration and Its Relevance to the Privatization of Space Ventures. Acta Astronaut. 2020, 167, 85–92. [Google Scholar] [CrossRef]
  7. Santomartino, R.; Averesch, N.J.H.; Bhuiyan, M.; Cockell, C.S.; Colangelo, J.; Gumulya, Y.; Lehner, B.; Lopez-Ayala, I.; McMahon, S.; Mohanty, A.; et al. Toward Sustainable Space Exploration: A Roadmap for Harnessing the Power of Microorganisms. Nat. Commun. 2023, 14, 1391. [Google Scholar] [CrossRef] [PubMed]
  8. Ma, Y.; Yao, X.; Su, Y. Shape Optimization and Material Gradient Design of the Sharp Hot Structure. Acta Astronaut. 2014, 103, 106–112. [Google Scholar] [CrossRef]
  9. Stevenson, T.H.; Lightsey, E.G. Design and Optimization of a Multifunctional 3D-Printed Structure for an Inspector Cubesat. Acta Astronaut. 2020, 170, 331–341. [Google Scholar] [CrossRef]
  10. Kalapodis, N.; Kampas, G.; Ktenidou, O.J. A Review towards the Design of Extraterrestrial Structures: From Regolith to Human Outposts. Acta Astronaut. 2020, 175, 540–569. [Google Scholar] [CrossRef]
  11. Feng, S.; Wang, C.; Duan, B.; Ban, Y. Design of Tipping Structure for 110 m High-Precision Radio Telescope. Acta Astronaut. 2017, 141, 50–56. [Google Scholar] [CrossRef]
  12. Xu, W. xuan; Zhang, J.; Guo, H. wei; Liu, R. qiang; Kou, Z. ming Design of a Deployable Aerodynamic Decelerator Based on a Tensegrity Structure. Acta Astronaut. 2024, 215, 315–324. [Google Scholar] [CrossRef]
  13. Pernigoni, L.; Grande, A.M. Advantages and Challenges of Novel Materials for Future Space Applications. Front. Sp. Technol. 2023, 4, 1253419. [Google Scholar] [CrossRef]
  14. Williams, M.K.; Gibson, T.L.; Jolley, S.T.; Caraccio-Meier, A.J. Self-Healing Technologies for Wiring and Surfaces in Aerospace and Deep Space Exploration Applications. In Proceedings of the Smart Coatings Conference; 2017.
  15. Ramos, M.; Bender, S.; Smith, N. Passive Self-Healing Composite Dielectric Elastomer Sensors for Structural Health Monitoring of Inflatable Space Structures. 2022. [Google Scholar]
  16. Chamkouri, H.; Ahmadlouydarab, M.; Chamkouri, M.; Hosseini saeidavi, F. Epoxy Resin Matrix Integrating Epoxy-Polydimethylsiloxane Based Self-Healing Microcapsules: Healing Efficiency, Mechanical and Thermal Stability. Polym. Eng. Sci. 2022, 62, 2302–2311. [Google Scholar] [CrossRef]
  17. Pernigoni, L.; Lafont, U.; Grande, A.M. Self-Healing Materials for Space Applications: Overview of Present Development and Major Limitations. CEAS Sp. J. 2021, 13, 341–352. [Google Scholar] [CrossRef]
  18. Levchenko, I.; Bazaka, K.; Belmonte, T.; Keidar, M.; Xu, S. Advanced Materials for Next-Generation Spacecraft. Adv. Mater. 2018, 30, 1802201. [Google Scholar] [CrossRef] [PubMed]
  19. Almutairi, M.D.; Aria, A.I.; Thakur, V.K.; Khan, M.A. Self-Healing Mechanisms for 3D-Printed Polymeric Structures: From Lab to Reality. Polymers (Basel). 2020, 12, 1534. [Google Scholar] [CrossRef] [PubMed]
  20. McLemore, C.A.; Kennedy, J.P.; Rose, F.A.; Evans, B.W. Exploration Challenges: Transferring Ground Repair Techniques to Space Flight Application. In Proceedings of the AIP Conference Proceedings; 2007; Vol. 880, pp. 719–727.
  21. Wright, M.; Manuel, M.; Wallace, T.; Newman, A.; Brinson, K. Self-Repairing Fatigue Damage in Metallic Structures for Aerospace Vehicles Using Shape Memory Alloy Self-Healing (SMASH) Technology; 2015.
  22. Taminger, K.; Hafley, R.A.; Dicus, D.L. Solid Freeform Fabrication: An Enabling Technology for Future Space Missions. In Proceedings of the 2002 International Conference on Metal Powder Deposition for Rapid Manufacturing; 2002.
  23. Shayler, D.J.; Salmon, A.; Shayler, M.D. Voyage to Mars. Marswalk One First Steps a New Planet 2005, 43–73. [Google Scholar]
  24. Chick, G. Length of Time Such Civilizations Release Detectable Signals into Space, L, 1961 to the Present. Drake Equ. Estim. Preval. Extraterr. Life through Ages 2015, 8, 270. [Google Scholar]
  25. Liu, M.; Chen, L.; Jian, N.; Guo, P.; Kong, J.; Wang, M.; Han, Q.; Ping, J.; Wu, M. Preliminary Estimations of Mars Atmospheric and Ionospheric Profiles from Tianwen-1 Radio Occultation One-Way, Two-Way, and Three-Way Observations. Remote Sens. 2023, 15, 5506. [Google Scholar] [CrossRef]
  26. Beckman, M. Orbit Determination Issues for Libration Point Orbits. In Libration Point Orbits and Applications; World Scientific, 2003; pp. 1–17.
  27. Albee, A.L.; Arvidson, R.E.; Palluconi, F.; Thorpe, T. Overview of the Mars Global Surveyor Mission. J. Geophys. Res. Planets 2001, 106, 23291–23316. [Google Scholar] [CrossRef]
  28. Towfic, Z.J.; Volk, C.P.; Border, J.S.; Voss, T.J.; Shihabi, M.M. Improved Signals for Differential One-Way Range. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 70–79. [Google Scholar] [CrossRef]
  29. Michell, A.G.M. LVIII. The Limits of Economy of Material in Frame-Structures. London, Edinburgh, Dublin Philos. Mag. J. Sci. 1904, 8, 589–597. [Google Scholar] [CrossRef]
  30. Maxwell, J.C. I. —on Reciprocal Figures, Frames, and Diagrams of Forces. Earth Environ. Sci. Trans. R. Soc. Edinburgh 1870, 26, 1–40. [Google Scholar] [CrossRef]
  31. Barta, J. On the Minimum Weight of Certain Redundant Structures. Acta Tech. Acad. Sci. Hungaricae 1957, 18, 67–76. [Google Scholar]
  32. Sved, G. The Minimum Weight of Certain Redundant Structures. Aust. J. Appl. Sci. 1954, 5, 1–9. [Google Scholar]
  33. Hemp, W.S. Notes on the Problem of the Optimum Design of Structures. Aust. J. Appl. Sci. 1958, 5, 1–9. [Google Scholar]
  34. Al Ali, M.; Shimoda, M. Exploring the Influence of Initial Design Domain Dependencies in Concurrent Multiscale Topology Optimization for Heat Conductivity Maximization. Comput. Phys. Commun. 2024, 295, 108968. [Google Scholar] [CrossRef]
  35. Al Ali, M.; Shimoda, M.; Benaissa, B.; Kobayashi, M.; Takeuchi, T.; Al-Shawk, A.; Ranjbar, S. On Metaheuristic Aided Structural Topology Optimization Method for Heat Sink Design with Low Electromagnetic Interference. 2023. [Google Scholar] [CrossRef]
  36. Fujioka, M.; Shimoda, M.; Al Ali, M. Concurrent Shape Optimization of a Multiscale Structure for Controlling Macrostructural Stiffness. Struct. Multidiscip. Optim. 2022, 65, 211. [Google Scholar] [CrossRef]
  37. Al Ali, M.; Shimoda, M. Toward Multiphysics Multiscale Concurrent Topology Optimization for Lightweight Structures with High Heat Conductivity and High Stiffness Using MATLAB. Struct. Multidiscip. Optim. 2022, 65, 1–26. [Google Scholar] [CrossRef]
  38. Dorn, W S, Gomory, R. E., and Greenberg, H.G. Automatic Design of Optimal Structures. J. Mec. 1964, 3, 25–52.
  39. Bartel, D.L. Optimum Design of Spatial Structures; 1969.
  40. Charrett, D.E.; Rozvany, G.I.N. Extensions of the Prager-Shield Theory of Optimal Plastic Design. Int. J. Non. Linear. Mech. 1972, 7, 51–64. [Google Scholar] [CrossRef]
  41. Rozvany, G.I.N.; Prager, W. Optimal Design of Partially Discretized Grillages. J. Mech. Phys. Solids 1976, 24, 125–136. [Google Scholar] [CrossRef]
  42. Rossow, M.P.; Taylor, J.E. A Finite Element Method for the Optimal Design of Variable Thickness Sheets. Aiaa J. 1973, 11, 1566–1569. [Google Scholar] [CrossRef]
  43. Cheng, K.T.; Olhoff, N. An Investigation Concerning Optimal Design of Solid Elastic Plates. Int. J. Solids Struct. 1981, 17, 305–323. [Google Scholar] [CrossRef]
  44. Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer Science & Business Media, 2003.
  45. Bendsoe, M.P.; Guedes, J.M.; Haber, R.B.; Pedersen, P.; Taylor, J.E. An Analytical Model to Predict Optimal Material Properties in the Context of Optimal Structural Design. 1994. [Google Scholar]
  46. Bendsøe, M.P. Optimal Shape Design as a Material Distribution Problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
  47. Zhou, M.; Rozvany, G.I.N. On the Validity of ESO Type Methods in Topology Optimization. Struct. Multidiscip. Optim. 2001, 21, 80–83. [Google Scholar] [CrossRef]
  48. Huang, X.; Xie, Y.-M. A Further Review of ESO Type Methods for Topology Optimization. Struct. Multidiscip. Optim. 2010, 41, 671–683. [Google Scholar] [CrossRef]
  49. Al Ali, M.; Shimoda, M.; Benaissa, B.; Kobayashi, M. Non-Parametric Optimization for Lightweight and High Heat Conductive Structures under Convection Using Metaheuristic Structure Binary-Distribution Method. Appl. Therm. Eng. 2023, 233, 121124. [Google Scholar] [CrossRef]
  50. Al Ali, M.; Shimoda, M.; Benaissa, B.; Kobayashi, M.; Takeuchi, T.; Al-Shawk, A.; Ranjbar, S. Metaheuristic Aided Structural Topology Optimization Method for Heat Sink Design with Low Electromagnetic Interference. Sci. Rep. 2024, 14, 3431. [Google Scholar] [CrossRef] [PubMed]
  51. Wang, M.Y.; Wang, X.; Guo, D. A Level Set Method for Structural Topology Optimization. Comput. Methods Appl. Mech. Eng. 2003, 192, 227–246. [Google Scholar] [CrossRef]
  52. Fujioka, M.; Shimoda, M.; Ali, M. Al Concurrent Shape Optimization for Multiscale Structure with Desired Static Deformation. Proc. Comput. Mech. Conf. 2021, 2021.34, 3. (in Japanese). [Google Scholar] [CrossRef]
  53. Madhavan, B.B.; Wang, C.; Tanahashi, H.; Hirayu, H.; Niwa, Y.; Yamamoto, K.; Tachibana, K.; Sasagawa, T. A Computer Vision Based Approach for 3D Building Modelling of Airborne Laser Scanner DSM Data. Comput. Environ. Urban Syst. 2006, 30, 54–77. [Google Scholar] [CrossRef]
  54. Brutto, M. Lo; Meli, P. Computer Vision Tools for 3D Modelling in Archaeology. Int. J. Herit. Digit. Era 2012, 1, 1–6. [Google Scholar] [CrossRef]
  55. Aicardi, I.; Chiabrando, F.; Lingua, A.M.; Noardo, F. Recent Trends in Cultural Heritage 3D Survey: The Photogrammetric Computer Vision Approach. J. Cult. Herit. 2018, 32, 257–266. [Google Scholar] [CrossRef]
  56. Xu, S.; Wang, J.; Shou, W.; Ngo, T.; Sadick, A.-M.; Wang, X. Computer Vision Techniques in Construction: A Critical Review. Arch. Comput. Methods Eng. 2021, 28, 3383–3397. [Google Scholar] [CrossRef]
  57. Costa, G.; Montemurro, M. Eigen-Frequencies and Harmonic Responses in Topology Optimisation: A CAD-Compatible Algorithm. Eng. Struct. 2020, 214, 110602. [Google Scholar] [CrossRef]
  58. Zuo, Z.H.; Huang, X.; Rong, J.H.; Xie, Y.M. Multi-Scale Design of Composite Materials and Structures for Maximum Natural Frequencies. Mater. Des. 2013, 51, 1023–1034. [Google Scholar] [CrossRef]
  59. Liu, Q.; Chan, R.; Huang, X. Concurrent Topology Optimization of Macrostructures and Material Microstructures for Natural Frequency. Mater. Des. 2016, 106, 380–390. [Google Scholar] [CrossRef]
  60. Liang, X.; Du, J. Concurrent Multi-Scale and Multi-Material Topological Optimization of Vibro-Acoustic Structures. Comput. Methods Appl. Mech. Eng. 2019, 349, 117–148. [Google Scholar] [CrossRef]
  61. Zhang, Y.; Gao, L.; Xiao, M. Maximizing Natural Frequencies of Inhomogeneous Cellular Structures by Kriging-Assisted Multiscale Topology Optimization. Comput. Struct. 2020, 230, 106197. [Google Scholar] [CrossRef]
  62. Svanberg, K. The Method of Moving Asymptotes—a New Method for Structural Optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
  63. Colomina, I.; Molina, P. Unmanned Aerial Systems for Photogrammetry and Remote Sensing: A Review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
  64. Baqersad, J.; Poozesh, P.; Niezrecki, C.; Avitabile, P. Photogrammetry and Optical Methods in Structural Dynamics--A Review. Mech. Syst. Signal Process. 2017, 86, 17–34. [Google Scholar] [CrossRef]
  65. Baltsavias, E.P. A Comparison between Photogrammetry and Laser Scanning. ISPRS J. Photogramm. Remote Sens. 1999, 54, 83–94. [Google Scholar] [CrossRef]
  66. Fraser, C.S.; Brown, D.C. Industrial Photogrammetry: New Developments and Recent Applications. Photogramm. Rec. 1986, 12, 197–217. [Google Scholar] [CrossRef]
  67. Hanke, K.; Grussenmeyer, P. Architectural Photogrammetry: Basic Theory, Procedures, Tools. In Proceedings of the ISPRS Commission; 2002; Vol. 5, pp. 1–2.
  68. Valença, J.; Júlio, E.; Araújo, H.J. Applications of Photogrammetry to Structural Assessment. Exp. Tech. 2012, 36, 71–81. [Google Scholar] [CrossRef]
  69. Sapirstein, P. Accurate Measurement with Photogrammetry at Large Sites. J. Archaeol. Sci. 2016, 66, 137–145. [Google Scholar] [CrossRef]
  70. Al Ali, M.; Shimoda, M. On Multiphysics Concurrent Multiscale Topology Optimization for Designing Porous Heat-Activated Compliant Mechanism under Convection for Additive Manufacture. Eng. Struct. 2023, 294, 116756. [Google Scholar] [CrossRef]
  71. Al Ali, M.; Shimoda, M. Investigation of Concurrent Multiscale Topology Optimization for Designing Lightweight Macrostructure with High Thermal Conductivity. Int. J. Therm. Sci. 2022, 179, 107653. [Google Scholar] [CrossRef]
  72. Al Ali, M.; Shimoda, M. Hygrally Activated Displacement Inverter Using a Multiphysics Multiscale Topology Optimization with Considering Evaporation. Struct. Multidiscip. Optim. 2023, 66, 1–16. [Google Scholar] [CrossRef]
Preprints 112554 g001
Figure 1. Simulation 3D objects using photogrammetric.
Figure 1. Simulation 3D objects using photogrammetric.
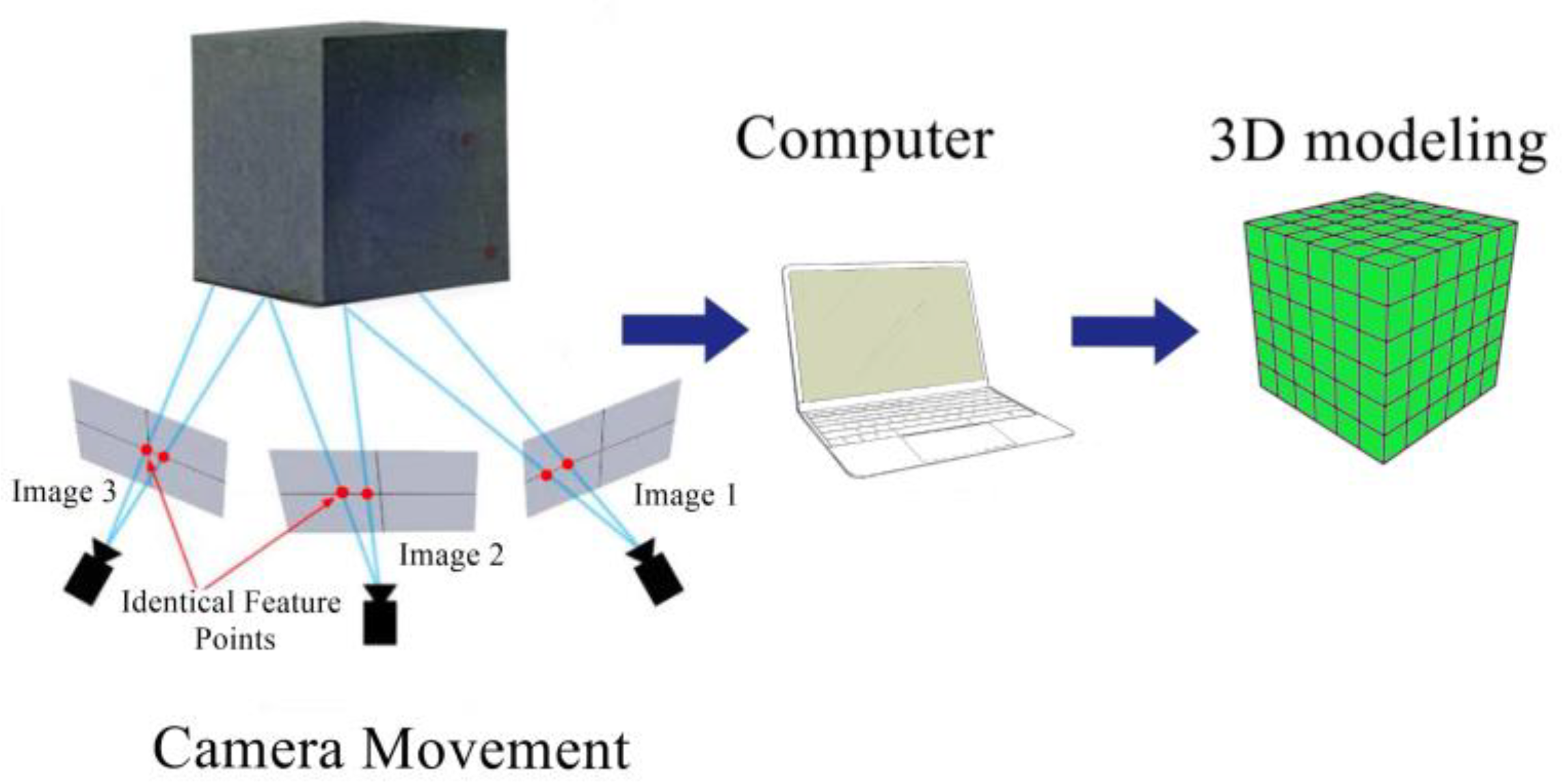
Preprints 112554 g001
Preprints 112554 g002
Figure 2. The design domain for a pillar.
Figure 2. The design domain for a pillar.
Preprints 112554 g002
Preprints 112554 g003
Figure 3. The computer vision-based design domain includes the following configurations: (a) a pillar with a central mass, and (b) a pillar with an eccentric mass, where the center of gravity is positioned on the left side of the top surface.
Figure 3. The computer vision-based design domain includes the following configurations: (a) a pillar with a central mass, and (b) a pillar with an eccentric mass, where the center of gravity is positioned on the left side of the top surface.
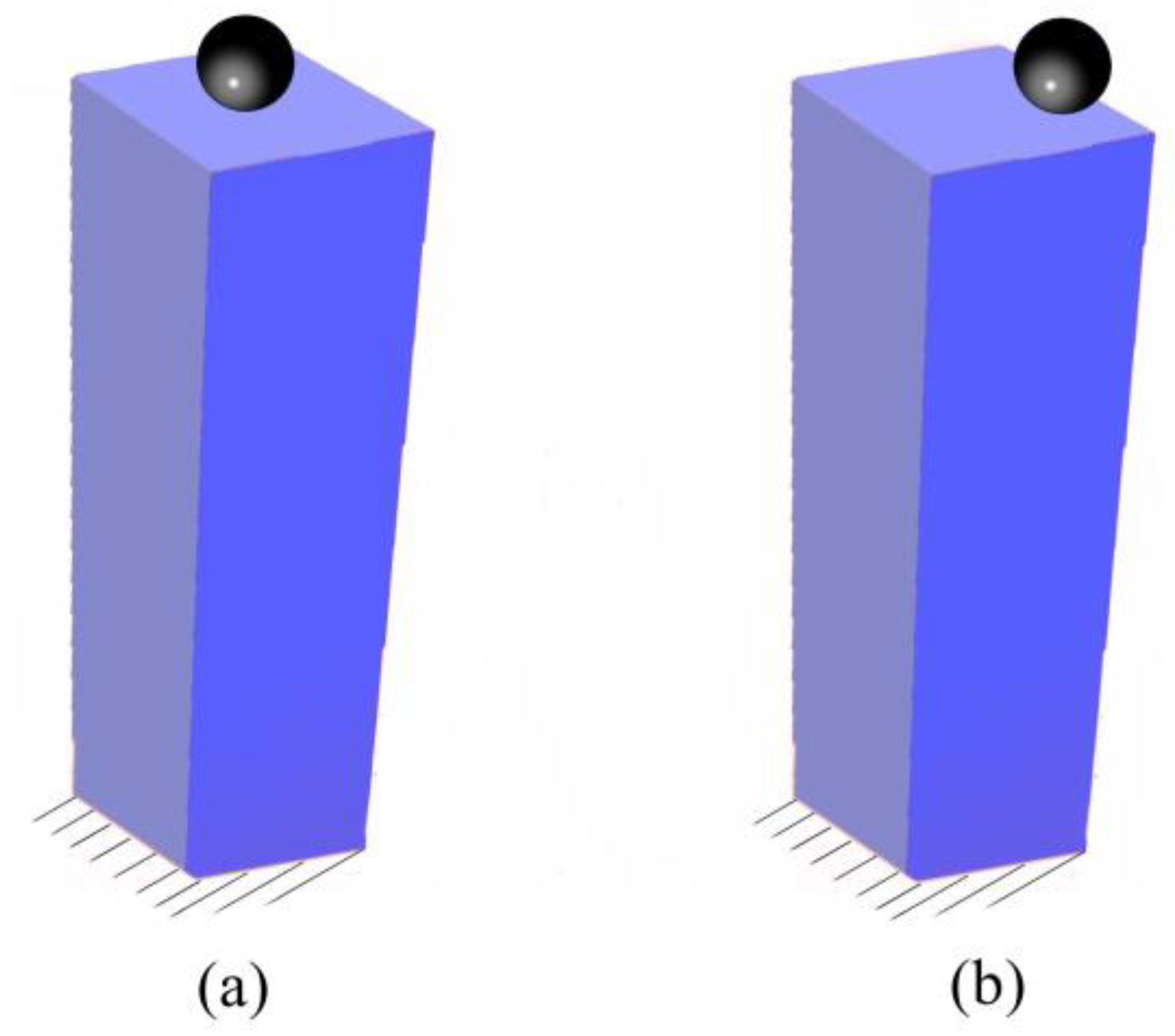
Preprints 112554 g003
Preprints 112554 g004
Figure 4. Topology optimization designs of central mass shown from multiple perspectives: (a) isometric projection of the design, (b) middle section view, (c) front view, (d) rear view, (e) top view, and (f) side view.
Figure 4. Topology optimization designs of central mass shown from multiple perspectives: (a) isometric projection of the design, (b) middle section view, (c) front view, (d) rear view, (e) top view, and (f) side view.
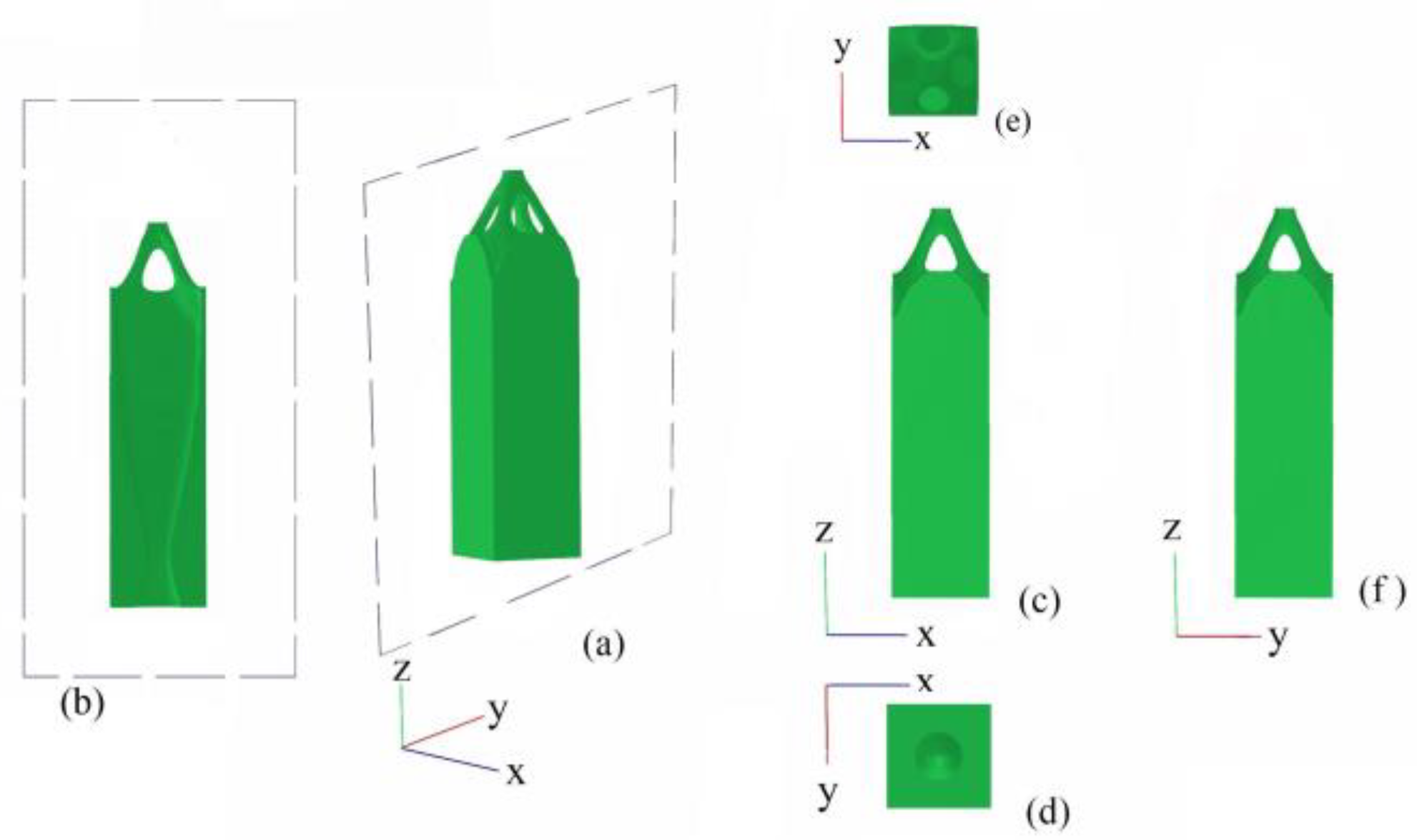
Preprints 112554 g004
Preprints 112554 g005
Figure 5. Eigen frequency history of the pillar design domain with central mass.
Figure 5. Eigen frequency history of the pillar design domain with central mass.
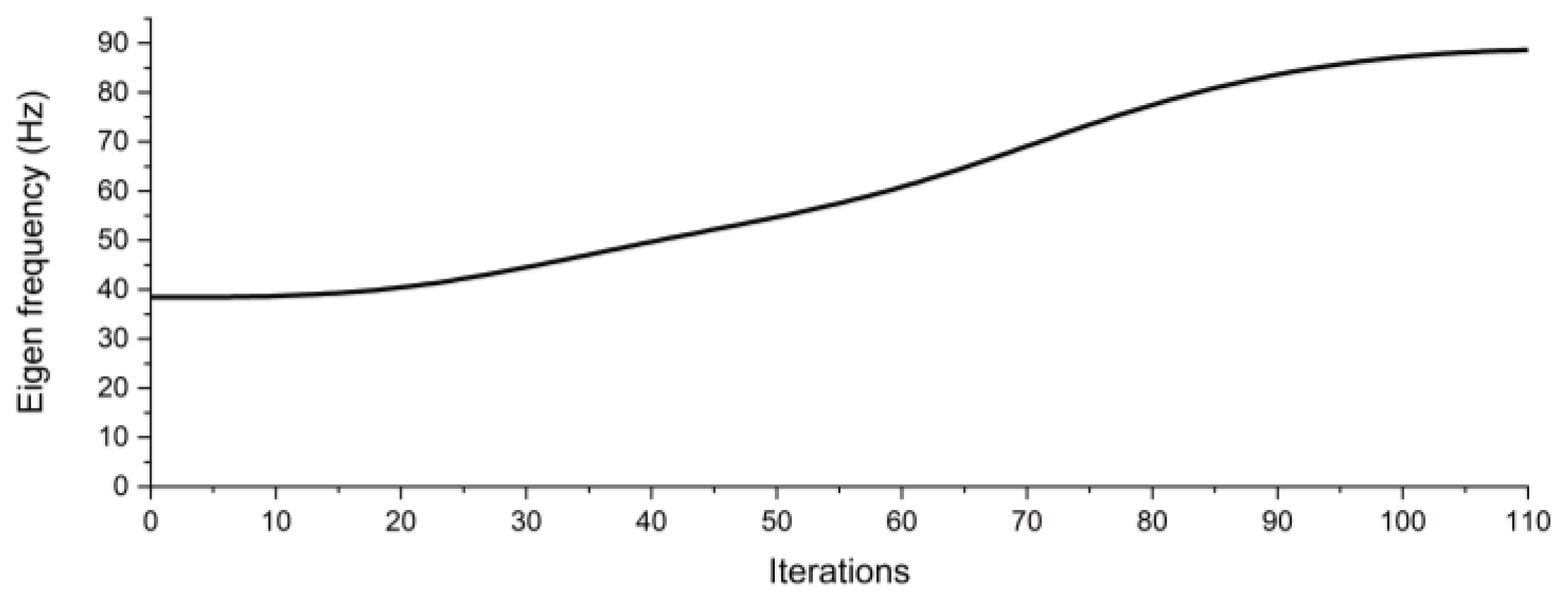
Preprints 112554 g005
Preprints 112554 g006
Figure 6. Topology optimization designs of eccentric mass shown from multiple perspectives: (a) isometric projection of the design, (b) middle section view, (c) front view, (d) rear view, (e) top view, and (f) side view.
Figure 6. Topology optimization designs of eccentric mass shown from multiple perspectives: (a) isometric projection of the design, (b) middle section view, (c) front view, (d) rear view, (e) top view, and (f) side view.
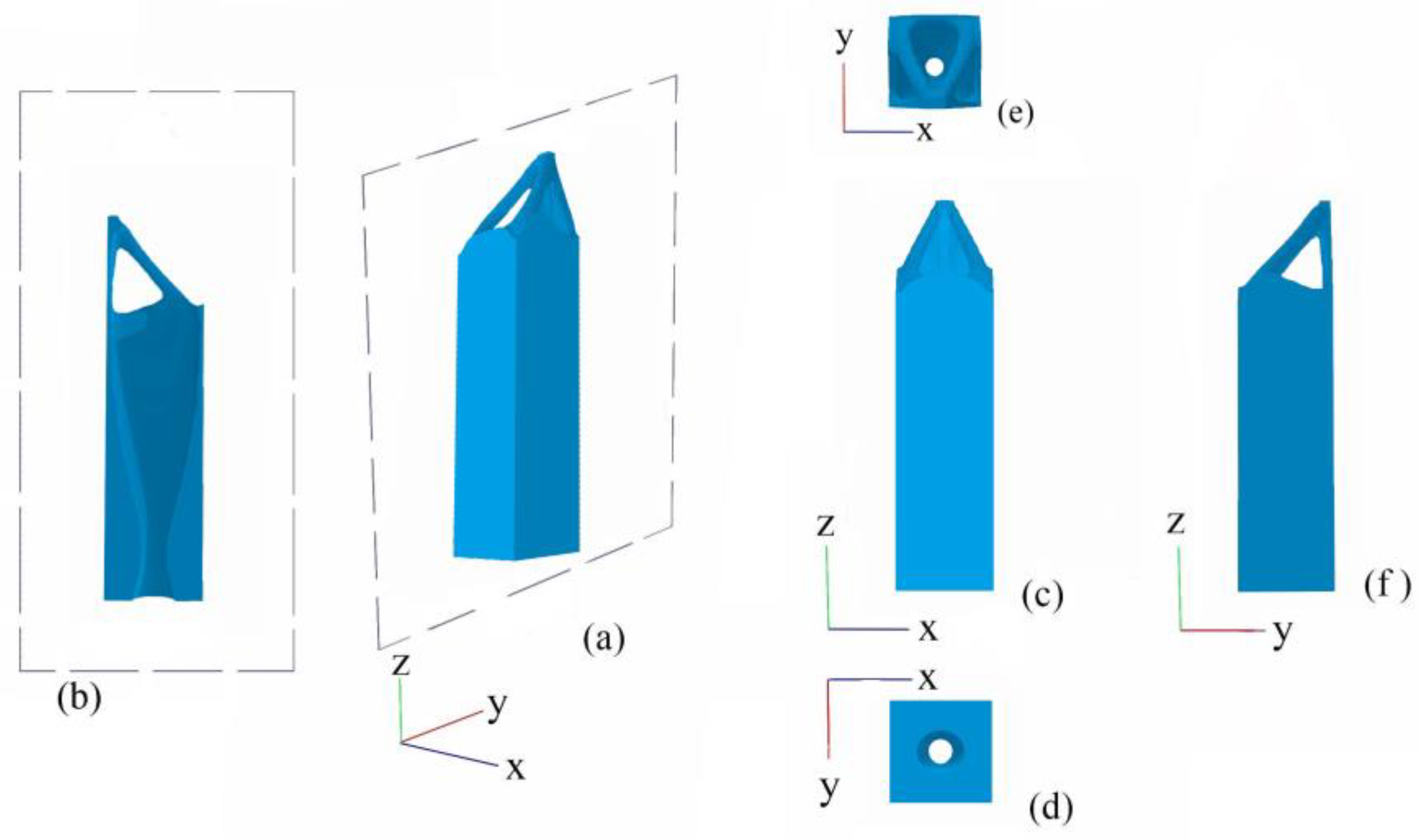
Preprints 112554 g006
Preprints 112554 g007
Figure 7. Eigen frequency history of the pillar design domain with eccentric mass.
Figure 7. Eigen frequency history of the pillar design domain with eccentric mass.
Preprints 112554 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated