Prerpints.org logo
Preprint
Article

Limits of Special Relativity

Altmetrics

Downloads

162

Views

106

Comments

0

This version is not peer-reviewed

Submitted:

06 September 2024

Posted:

09 September 2024

You are already at the latest version

Alerts
Abstract
HIGHLIGHTS This paper is presenting an experiment based on Ehrenfest's paradox where an effect of special relativity was expected but not observed. The validity of special relativity in our macro world will be questioned and an alternative will be offered. Indeed, special relativity has been successful in describing the behaviour of particles (Rossi & Hall, 1941), but since particles obey quantum rules, there is no observation of special relativity in our everyday world. On the contrary, there are at least two paradoxes based on special relativity: the twin paradox (Langevin, 1911) and Ehrenfest's paradox (1909). ABSTRACT After presenting the history of special relativity, the non-simultaneity of special relativity is questioned in our macro world. In addition, some issues between light clocks and the application of Lorentz transformation are presented. All this indicates that special relativity appears to be correct only for particles and would be invalid in our macro world. A new hypothesis is presented based on an adaptation of special relativity; this new hypothesis solves the anomalies and could be a solution to the twin paradox. This new hypothesis has a prediction in disagreement with special relativity. To test that prediction, a new experiment has been carried out and the preliminary results support the new hypothesis. Previously, a lack of special relativistic effects has been observed in the universe (Davis et al., 2004); that second observation is also explained with the new hypothesis.
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics
N.B.: This paper has been written for non-specialists, but requires a basic knowledge of physics.

History of Special Relativity

Einstein is always presented as the father of relativity. There are two theories, the special and the general relativity. The history of special relativity started long before Einstein. There are some equations, known as Maxwell’s equations (1873) which describe electromagnetism. These equations show that the speed of light is constant, which was a problem with our everyday conception of speed. Special relativity solves this problem.
The first stepping stone on the way to special relativity is the Lorentz transformation which was presented in 1892 (Lorentz, 1892). Einstein notably said that he couldn’t have found special relativity without the groundwork of Lorentz. With the Lorentz transformation, the time-flow is changing: a clock travelling near the speed of light seems to run slower than a clock at rest. This is called time dilation. The ratio between the two time-flows is the Lorentz factor and there is a formula to calculate it. Also there is Lorentz contraction (by Lorentz factor): a metre rod travelling near the speed of light and aligned with the direction of the motion appears smaller to an observer at rest. A metre rod perpendicular to the motion keeps its normal length. Lorentz transformation was without justification; Einstein added two postulates from which Lorentz’s equations can be logically derived.
So, in 1892, Lorentz presented his work. Then Poincaré (1900) was working on the synchronisation of clocks with the idea that time-flow is changing and concluded that, if time-flow changes, then there is a loss of simultaneity. In 1905, Einstein wrote his first papers on special relativity (Einstein,1905) justifying the Lorentz transformation.
In 1909, Ehrenfest wrote a paradox: if special relativity is applied to a rotating disk, the circumference is contracted by the Lorentz factor while the radius stays the same; so C ≠ 2 π r. This paradox must have had a big impact on Einstein, as it provoked the idea of ‘space being non-flat’, which is a key to general relativity. In 1916, Einstein wrote his book Relativity (Einstein,1916) which will be quoted many times in this work.
Meanwhile, Langevin (1911) presented the twin paradox.
Special relativity was widely criticised until 1941 when observations of the change of muons life-time were proof that special relativity is correct (Rossi & Hall, 1941).
I will argue that special relativity works only for particles (or in the “quantum world”), so I will add some context. Heavyside (1889) predicted that the magnetic field of an electron travelling through aether should lose its spherical property; a characteristic that is present in Lorentz transformation. There was the Fizeau experiment (1851) which is about light travelling through liquid, the speed of the liquid was changing the speed of light. There was also the Morley-Michelson experiment (1887), the observation that the speed of light is constant, i.e., doesn’t change with the hypothetical aether. Lorentz was probably trying to find a model that fitted all those observations. De Sitter’s double star results (1913) was the first observation of the constancy of the speed of light, and confirmed special relativity.
So special relativity solved the constancy of the speed of light and all observations or reasoning are about light or electrons (therefore a particle) then about muons (another particle). This paper is not questioning the validity of special relativity in those cases, but questions when and where special relativity should be used.

The Principle of Special Relativity

The principle of special relativity is often called ‘principle of relativity’ as in section 5 of Einstein’s Relativity, but has nothing to do with general relativity. To avoid confusion, I re-instated ‘special’ in the name.
Here is a quote from Einstein’s Relativity (Appendix V of (Einstein,1916)):”Classical mechanics … teaches the equivalence of all inertial systems ... i.e., the invariance of natural laws with respect to the transition from one inertial system to another.” An inertial system is simply a system at rest or travelling in a straight line at constant speed; this definition is important.
To explain special relativity, Alice and Bob are commonly used and are often in a spaceship. Each represents an inertial system and they are inertial observers so both have the right to consider they are immobile. For example, Alice passes Bob nearly at the speed of light; Alice observes that Bob’s clock runs slower than hers. And Bob observes that Alice’s clock is slower than his. The meaning of relativity in ‘principle of relativity’ is that Alice is travelling relative to Bob and Bob is travelling relative to Alice. The invariance idea is such that what Alice observes about Bob, Bob observes the same about Alice: the other clock running slower is an example. As soon as there is an acceleration (or a rotation), the system is no longer an “inertial system”, the principle of special relativity no longer applies.

Simultaneity and Special Relativity

The loss of simultaneity is obtained from Lorentz equations: this section is not questioning the validity of that deduction but its validity in our macro world.
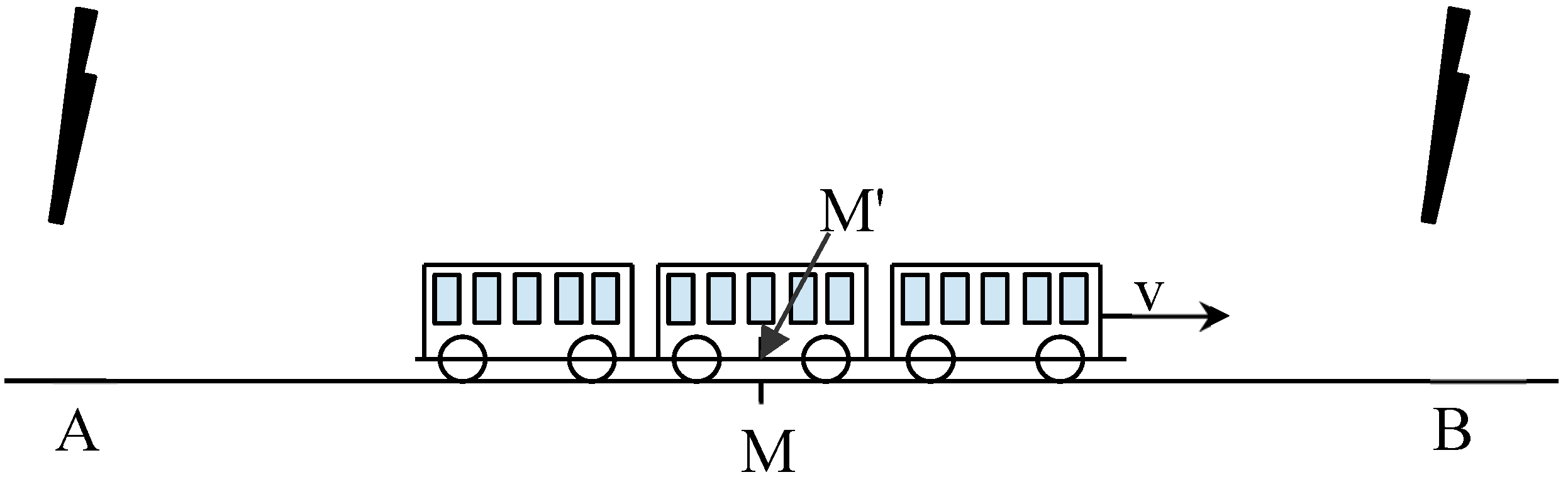
We have seen that the loss of simultaneity was Poincaré’s idea and it was probably accepted before Einstein’s first paper on relativity. In Relativity, Einstein presents the constancy of the speed of light in section 6. In other words the speed of light is constant for an inertial observer whatever her/his speed. This was difficult to present in 1916, but it is now generally accepted. Then, in section 8, he presents how to determine the simultaneity of two events. An observer has to be at equal distance to the events, and if the lights of the events reach her/him at the same time, it is simultaneous. Then, section 9 is about the loss of simultaneity, there is a railway train and the embankment; Einstein presents a figure similar to Figure 1.
M and M’ are two inertial systems moving relative to each other. In that Section 9, concerning the observer M’ on the train and simultaneous flashes at A and B, you will read: “Now in reality (considered with reference to the railway embankment) he is hastening towards the beam of light coming from B, whilst he is riding on ahead of the beam of light coming from A. Hence the observer will see the beam of light emitted from B earlier than he will see that emitted from A. Observers who take the railway train as their reference-body must therefore come to the conclusion that the lightning flash B took place earlier than the lightning flash A.” There is a change of reference, which has been highlighted by me; the brackets are in the original text. As Figure 1 represents the position of the train when the bolts occur, observer M and observer M’ are at equal distance from the two bolts when light is leaving points A and B. Because A-M’ equals B-M’ at the time light leaves A and B (as required in section 8), because the speed of light is relative to the train for the observer M’ (as stated in section 6), the light from A and B will reach observer M’ at the same instant. Observer M’ will reach the conclusion of simultaneity.
Because observer M’ is not at the same place as observer M when light reaches observer M, observer M concludes that observer M’ cannot conclude on a simultaneity. The conclusion of observer M is logical but disagrees with the reasoning above which shows that the reasoning of observer M is an illusion as if (s)he should not judge for M’. This idea (not to judge for others) will come back again and again.
If you think there is no argument, what about this little puzzle? With the principle of special relativity and Figure 1, M’ has the right to believe (s)he is immobile and M is moving. So if you still believe that there is non-simultaneity, as only one party should observe simultaneity, who is it? Who is immobile? What about if the scalar value of v is identical to the rotation of the earth but in the opposite direction so M’ is immobile seen from space. Secondly, if you think the example is wrong, and M’ should observe something different to M; isn’t it in contradiction with the principle of special relativity?
Poincaré would say that, because simultaneity is back, then time-flow cannot change. This is a very important point because it would contradict special relativity. With special relativity, time-flow changes, and that change has been observed. Muons (a particle) can be observed at the surface of the Earth and they are made at the top of the atmosphere. The time to travel through the atmosphere is longer than the lifetime of a muon; because time-flow is dilated (due to special relativity), muons have the time to reach the surface of the Earth. That observation validates special relativity, Lorentz transformation and the change of time-flow (Rossi & Hall, 1941).
If I emphasise the work of Poincaré, it is because it will support this work; so we should keep it in mind: maybe sometimes time-flow doesn’t change. One subject of this paper is what is meant by “sometimes”. Please note that the observation of the reality of time-flow change is about a particle: the muon. The train and embankment scenario is about our macro-world.
Photon clock-1
The light clock is a thought experiment well known to physicists. Two mirrors face each other and a photon is trapped, bouncing endlessly between the mirrors. By counting the bounces, one gets a clock. I prefer to call this clock: photon clock. That thought experiment is always used to show time dilation and length contraction of special relativity; we will check the accuracy of it and go one step further.
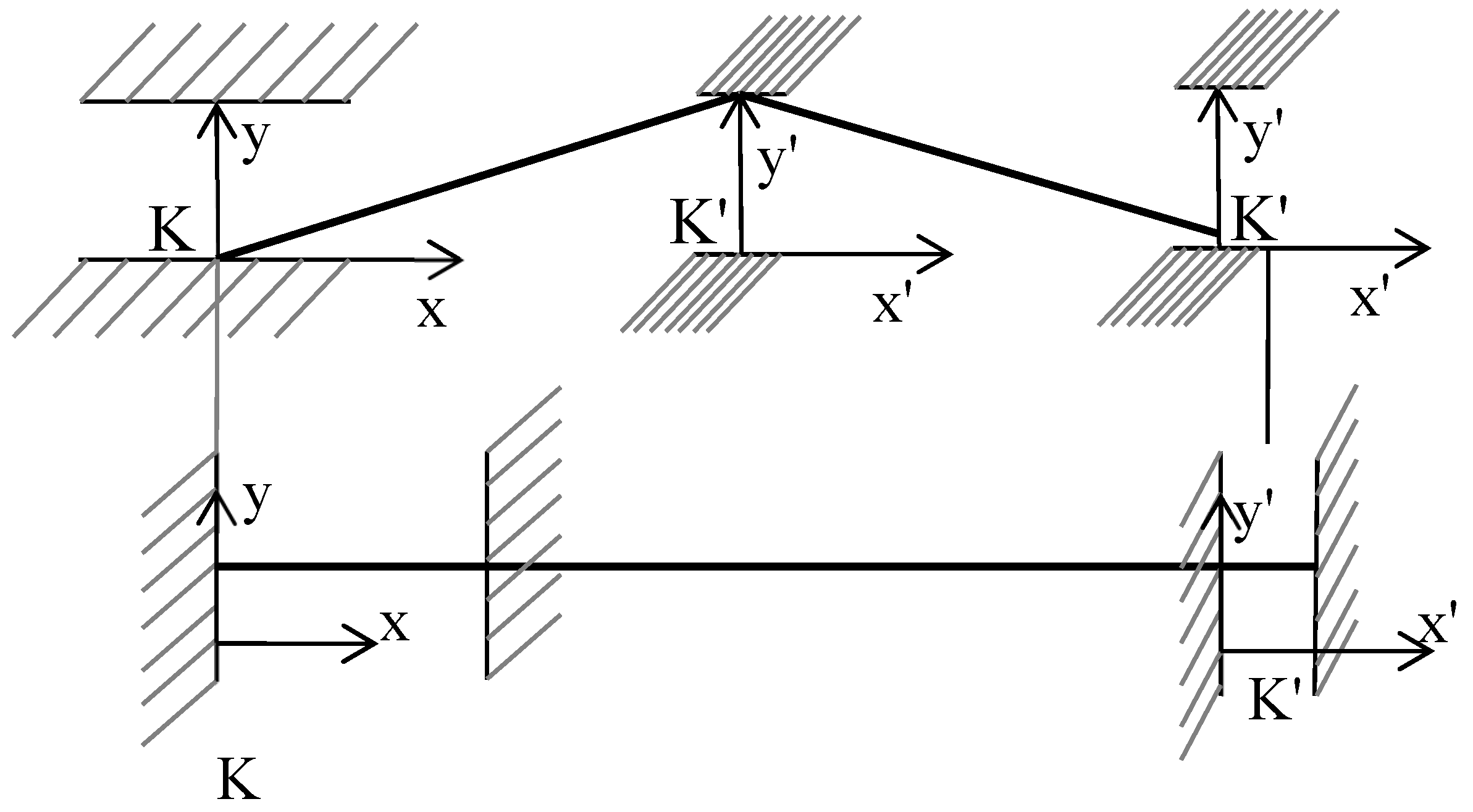
We will use Alice and Bob, each one in a spaceship and each one represent an inertial system (constant speed, no gravity, no acceleration). Alice is travelling at 0.99c (Lorentz factor =7) compared to Bob. Alice has two photon clocks, the second one will be used later. For this clock-1, the photon is moving parallel to the direction of motion (bottom clock of Figure 2). Seen by Bob, there is length contraction between the two mirrors and the photon has to catch up with a mirror which is running away, before bouncing back towards the other mirror. The Lorentz factor changes time-flow, but there is more in Lorentz transformation. The direction of the speed and the direction of the photon are involved and, with the transformation, time-flow dilation changes with those directions: a long time-flow dilation to give time for the photon to catch up the mirror (a long tick) then a short time-flow dilation for the return (a short tock) (for physicists: during the tock, time flows faster than the proper time; is that allowed?). For Alice there is no problem, time flows normally, tick and tock are equal.
So, time would flow at two different rhythms for the same place as seen by Bob. As far as I know, nobody questioned those different rhythms. The only explanation I can offer is that the two different time-flows are an illusion, the same illusion as the non-simultaneity seen above as it is a very similar situation. It would mean that only Alice can check her clock, not Bob, and Lorentz transformation explains the illusion observed by Bob. Again, Bob shouldn’t judge for Alice or it seems something is wrong.
Photon clock-2
For clock-2 the photon travels perpendicular to the motion: for Bob who is observing Alice’s clocks, there is no observable length contraction between the mirrors of this clock-2 with the current theory. That no-length contraction assures that clock-1 and clock-2 beat at the same rhythm (see Figure 2). The time-flow is reduced by the Lorentz factor, so by a factor 7. The thick line of clock-2 from one mirror to the other is 7 times longer than the distance between the two mirrors (the figure is for illustration purpose only). As the speed of light is constant, it means the clock beats 7 times slower than at rest. Notice also that clock-1, the “tick” is much longer than the “tock” as we have explained above.
With Figure 2, we can visualise that the ticks are not synchronised but the tocks of both clocks are synchronised.

Event Distances

Using those two clocks, one can calculate a distance ds between two events (called ‘event distance’ from now on, to differentiate with ‘mirror distance’). The term ‘between two events’ means that time will be taken into account. I am not sure who found how to calculate ds (the event distance) but certainly Poincaré presented a formula before Einstein. In appendix 5 of Relativity, Einstein said clearly that “ds2 is invariant with respect to Lorentz transformation”. Bob is immobile and observes Alice’s clocks; and Alice is moving at 0.99c. The first event is the photon leaving one mirror, the second event is the photon hitting the opposite mirror. We should get the same event distance for Alice and Bob. For Bob we should apply the Lorentz transformation to the calculation of the event distance.
As the events are dictated by a photon, ds is zero; this is the consequence of the chosen formula. There is no problem with clock-1, ds is the same for Alice and Bob (ds=0). But for clock-2, the mirror distance between the two mirrors has to be contracted by the Lorentz factor. (The calculation is presented in the Appendix A). This is a problem because if the mirror distance is contracted, then the clocks are no longer synchronised. If the mirror distance is not contracted then the event distances are not the same. There is something wrong, an absurdity.
Back to the simultaneity section. If observer M concludes that A and B are simultaneous, Lorentz equations tell us that observer M’ cannot conclude on simultaneity although we saw that he did. So, the simultaneity deduced by logic is not in agreement with Lorentz equations; there is something wrong again.

Possible Solution

The contraction required for the event distance has an interesting consequence. If the mirror distance is contracted by the Lorentz factor then the time-flow is identical to the clock at rest. In other words there is no time-flow dilation, the time-flow is not changing. It would have been just an anomaly, except that Poincaré predicted that if simultaneity is back, there shouldn’t be any change in time-flow. So let’s imagine that the contraction for the event distance is correct for clock-2, how can we recover the synchronicity with clock-1? Clock-1 has to be contracted a second time by the Lorentz factor. Both clocks are now clicking at the same rhythm as a clock at rest. N.B.: the illusion of a tick longer than a tock is still observed by Bob, but we have shown that Bob is not at the right place to observe the correct tick and tock.
To recap: if we use special relativity, there is a problem with the distance event and I don’t see how this problem can be solved. The possible solution consists of using the Lorentz factor as calculated for special relativity, then applying the corresponding contraction to the length in the direction of the motion and adding a contraction by the Lorentz factor on all three dimensions.
That last sentence is in fact an important point of this paper. I would call this new hypothesis, combined relativity: special relativity is combined with general relativity as we will see. There are many observations that confirm the validity of special relativity and cannot be explained with combined relativity. So, it is not the end of special relativity as we will see later. But in this case, combined relativity seems to work and special relativity doesn’t.
From Relativity, it is clear that Einstein got the idea that space is non-flat from Ehrenfest’s paradox. Deformed space is a cornerstone for general relativity. With special relativity alone, there is no deformation of space and Ehrenfest’s paradox uses special relativity alone. By adding the contraction of combined relativity in the three dimensions, space is deformed. Space is deformed in the same manner as a mass deforms, as Einstein expected around the disk of Ehrenfest’s paradox: « Because of the Lorentz contraction in a reference frame that rotates relative to an inertial frame, the laws that govern rigid bodies do not correspond to the rules of Euclidean geometry.». So the additional contraction, calculated with Lorentz factor, deforms space and is due to speed.
In 1952, Einstein added an appendix to his book Relativity. In that appendix, you can read “… without the question of the existence of masses which produce this [gravitational] field being raised”. Why does he insist on the fact that a mass is not necessary to create a field? Einstein was studying a rotating disk to reach his general relativity and he used his equivalence principle. A force is the result of ‘space deformed’, if the reason for ‘space deformed’ is a mass, the force is gravity; if the reason for ‘space deformed’ is a speed (as seen above), the force will be called speed-force. Speed-force is equivalent (following the equivalence principle) to gravity; as acceleration is equivalent to mass. Einstein didn’t need a mass to deform space but a change of speed, and this could explain the quote above.

Extension on the Twin Paradox

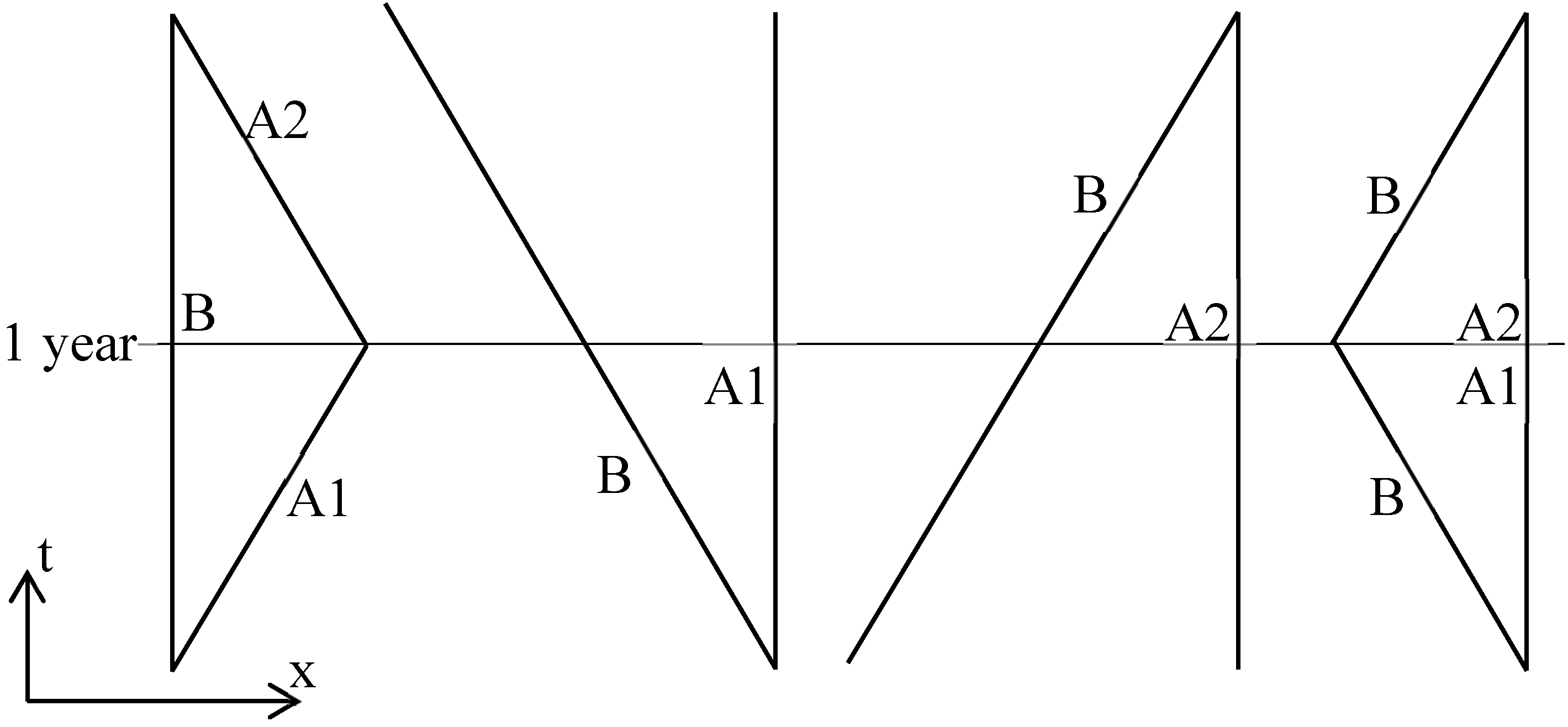
The twin paradox is based on special relativity alone. We will use Alice1, Alice2 and Bob, who are each in a space-ship, each is an inertial system (constant speed, no gravity, no acceleration). Alice1 passes by Bob at 0.99c (Lorentz factor =7), they both set their clock at zero. Alice’s clock will be our time reference and after one year, Alice1 should do her U-turn. To avoid the problem of acceleration/U-turn (Simonetti,1997), Alice1 crosses Alice2 who is travelling at 0.99c towards Bob and Alice2 synchronises her clock on Alice1’s (and they share information). After one more year, when Alice2 crosses Bob, they compare their clocks.
Bob is watching Alice’s clock (our reference) and notices the time-flow dilation of a factor 7 as with special relativity. When they meet, Alice has aged by 2 years and Bob by 14 years. That is the paradox.
By applying the principle of special relativity, Alice has the right to consider that she is stationary and Bob is moving at 0.99c. So Alice sees that Bob’s time-flow is dilated. At the end of the 1 year of Alice1 (our reference), Bob’s clock is at 1/7 year. When Bob comes back (Alice2 thinks she is stationary), Alice(s) have measured that Bob’s clock has moved by only 2/7 year.
This result is not a difference of age between two persons as with the twin paradox but two different ages for Bob. It is an absurdity, it shows there is something wrong in the sense that special relativity is invalid under those conditions. Those conditions are mainly about a person or a clock in our macro-world.
This absurdity must have been noticed before and the reasoning is that we cannot consider both Alice1 and Alice2 as immobile (Bondi,1964) (I couldn’t find the origin of this reasoning and Bondi’s book is presenting spacetime diagram in a very clear manner, the best I know). But that reasoning seems to exist only to avoid the absurdity. In this case, we are not considering Alice1 and Alice2 immobile at the same time but at two consecutive times; the principle of special relativity should apply in the sense that Bob, Alice 1 and Alice 2 are inertial observers.
Space-time diagrams may help (Figure 3), we are taking the bottom part of the diagram where Alice1 is immobile then the top part of the diagram where Alice2 is immobile and put those two parts together in the diagram on the right. When Alice1 meets Alice2, they exchange information but the exchange doesn’t invalidate either space-time diagram. Both full diagrams are correct and the fact we choose to use one part then the other part is not forbidden as far as I know.
The distance separating Alice and Bob at the U-turn also changes depending on the observer. For Bob watching Alice, the first year of Alice is 7 years for Bob. If Alice has travelled only 0.99 ly in 7 years, then for Bob, Alice is not travelling at 0.99c. So, for Bob, Alice is doing her U-turn at 6.93 ly and Alice at 0.99 ly. Alice is at two places at once, an absurdity in our world; but is it an absurdity if Alice is a particle?
Again, this anomaly has been noticed before. This time Bondi (1964) simply states that the correct distance is 6.93ly and the time to use is Bob’s. Alice’s time could be used resulting in a speed exceeding the speed of light which is accepted and called proper speed in his book. Proper speed is just a mathematical tool and is not a real speed; and using Alice’s time (or distance) seems forbidden. Alice is an inertial system as Bob, why Alice is treated differently is not explained. If considering that Alice’s distance is not allowed, then Ehrenfest’s paradox which uses the contraction of the circumference (equivalent to Alice’s distance) disappeared. Either the rule about Alice’s observation (which I have never seen stated or justified) is wrong or Ehrenfest’s paradox is solved.
If we apply combined relativity, clocks are synchronised, the paradox is solved. Solving a paradox is sometimes a clue of an important breakthrough.

Observing Combined Relativity-Ehrenfest’s Paradox

With special relativity, a measuring rod oriented in the direction of the motion and moving fast will seem contracted by the Lorentz factor. By extension, the circumference of a hypothetical disk rotating fast should be contracted by the Lorentz factor.
It is clear that Ehrenfest’s paradox is expressed using special relativity only, which obeys the principle of special relativity. Surely, following the principle of special relativity, an observer immobile looking at a rotating disk or an observer rotating looking at a fixed disk should get the same result.
So I decided to mount a digital camera on a power drill, added a layer of Mylar to reflect 99% of the sun’s light and watched the sun through my home-made rotating camera. No contraction has been observed (N.B. This is a preliminary result, a more professional instrument has to be developed). If special relativity was at work, the illusion of a reduction of the diameter of the sun was expected.
The disk I have observed is the sun (radius: 696,300km). The camera is rotating at about 5 cycles per second. Because of the principle of special relativity, it is equivalent to a disk the size of the sun with a circumference rotating at 21.9 106 km/s (speed of light is nearly 0.3 106 km/s). The contraction should have been obvious: nearly a factor 100. Even with a home-made equipment, the contraction should have been observed. The video can be found following this link: https://youtu.be/8I8pmmNm3rI
In fact, there is a problem with the above case. Imagine a powerful red laser at the circumference of the sun flashing every second in our direction. The expected contraction is due to special relativity, with this contraction there is time dilation. An immobile observer will observe the flash every second, and the rotating camera would see the flash at a different frequency because of time dilation. That doesn’t seem right. Combined relativity solves that problem.
Combined relativity can explain the lack of contraction. The principle of special relativity doesn’t work with general relativity. If one observer is in space and one on earth, one would feel gravity and not the other one; so they cannot have the same experience: an object falls on earth and floats in space. Therefore, combined relativity which uses general relativity doesn’t follow the principle of special relativity: if a disk is rotating, the person on the disk will feel that speed-force (and the centrifugal force), the person in space won’t feel it. If combined relativity is correct, the principle of special relativity doesn’t apply, rotating a camera is not the same as rotating the disk, no effect is expected.
Until now, all experiments showing that special relativity is correct have been carried out with particles. The rotating camera is probably the first experiment that is testing special relativity in our macro world, so this test is very important and has to be repeated. Also, my explanation has to be scrutinised. Many scientists tried to incorporate the centrifugal force, and therefore will disagree with the principle of special relativity for Ehrenfest’s paradox. But as the paradox is currently written, the principle of special relativity can be applied. Either the paradox has to be rewritten, or the observation shows that special relativity is not at work for the paradox (Grøn, private communication).

Observing Combined Relativity-Redshift

Inside a star, a photon is emitted or a photon is absorbed. Emission and absorption are due to clocks at atomic or molecular level; those clocks are like a photon clock.
The redshift uses those special emissions and absorptions (therefore uses the clocks), it is measured to calculate the speed at which a galaxy is moving away from us; the redshift being simply a Doppler effect and considers that those clocks out there and on Earth are synchronised. But at 8 billion ly, galaxies are receding at 0.4c, corresponding to a Lorentz factor of 1.1. In theory, time dilation of special relativity should be taken into account.
So, beyond 8 billion ly, redshift with combined relativity will give one speed while redshift with special relativity will give a different speed because of the corresponding time dilation. By using other observations like density and distances, astronomers should be able to tell us which theory is correct as there is a law linking density, distance and speed.
Some years ago, astronomers didn’t know about combined relativity but you can read: “Finally, in Section 4 we provide explicit observational tests demonstrating that attempts to apply special relativistic concepts to the Universe are in conflict with observations.” (Davis et al., 2004). In other words, observations of redshift correspond to combined relativity.

Limits of Special Relativity

We know that special relativity has been observed as correct with elementary particles. This work presents two observations where combined relativity seems to work and special relativity cannot work. Those two observations are not about particles but about our macro-world. In addition the return of simultaneity and the light-clocks are thought experiments in our macro-world. I would conclude that special relativity works in the quantum-world and combined relativity works in our macro-world.
We observe the quantum world from our macro world. But the observation is correct as long as we don’t try to deduce what another frame of reference should observe (again, the idea of not judging for others). One problem surfaces when observer M tries to deduce what observer M’ should observe; or when Bob tries to deduce what Alice should observe. The move from M to M’ or from Bob to Alice is a move in our macro world and that seems to be problematic for special relativity. Also absurdities are deduced using the logic of our macro-world. But what seems absurd in our world is accepted in the quantum world like Alice being at two places at once.
Therefore, this work suggests that special relativity is part of quantum mechanics and is valid only with a particle: no particle, no special relativity on its own. Special relativity solved the problem of the constancy of light. Light is made of photons, a photon is a particle therefore special relativity solved a problem of particles; it has to be considered as part of quantum mechanics.
Conversely, combined relativity would be a theory for our macro-world.

Quantum Mechanics-Causality

We would have two worlds, our macro-world where time-flow is constant and simultaneity is not a problem and the quantum world where time-flow can change and there should be non-simultaneity. A world with non-simultaneity is a world without causality, and here is why.
In Figure 1, observer M sees that light from B reaches M’ before light from A. If the train goes the other way, light from A would reach M’ before light from B. This is the non-simultaneity described by Einstein. It is a mistake in our world but it is a good example for non-simultaneity and it has been used many times. In the quantum-world there is time-flow change and with time-flow change, Poincaré told us there is non-simultaneity. A before B, or B before A are both possible in the quantum-world so there is no temporal order because of the non-simultaneity. Let’s add causality: E is an effect of C (C is the cause); in our macro world, it means C always happens before E. But if there is no temporal order, E can happen before C. So, if there is still causality in quantum mechanics, E can happen before C but happens because C happens. It would mean that information of C happening is able to come from the future to make E happen before C. It would also mean that information doesn’t respect the direction of time. I would not reject that possibility as I always justified that way (without any ground) the “spooky action at a distance” (EPR paper, 1935); but the space-time diagrams section below is not allowing information to come from the future (yet?).
There was a problem of causality and the loss of temporal order (Mamone-Capria,2012). Now we are showing that causality is present when there is temporal order and causality disappears when temporal order disappears.

Quantum Mechanics–Gravity

Quantum mechanics had a problem, for example an electron should have a volume so could well be a sphere but when scientists want to use a sphere instead of a point in quantum mechanics, it is a disaster in the sense that impossibilities arise (Greene, 1999). So quantum mechanics consider an elementary particle as a point with a mass. When two points meet up, as they are points, there is no distance between the two points, you take the law of gravity of Newton and you find that the gravitational force is infinite. General relativity cannot be included in quantum mechanics because of this infinity but special relativity has been included. Is this another indication that special relativity is part of quantum mechanics?
Quantum mechanics is a difficult subject and has to deal with the duality wave/particle. I will hypothesise that there are two parts for quantum mechanics: one described by the equations of quantum field theory, and another about the mechanics of particles. And this last part should be a 1D theory. This suggestion is on very thin ground: only 1D is considered for the Lorentz transformation.
If you are careful with the Lorentz transformation, you will notice that it has been developed with only one dimension in mind. In the appendix, the calculation of the event distance of the photon clock has been made and shows that other dimensions shouldn’t even exist. In “the Meaning of Relativity” (1922), to deduce the Lorentz transformation, Einstein himself wrote twice: “we disregard the number of dimensions”. So, if Lorentz transformation is 1D, special relativity could indeed be a 1D theory. And special relativity is about the mechanics of particles.
Quantum mechanics includes special relativity which seems to be 1D, it also includes electromagnetism which seems 3D. The magnetic field is represented with lines which form loops. An electric circuit forms a loop. Loops are 1D. It seems that, by adding one physical dimension to our usual 3D, Kaluza (1921) had been able to put electromagnetism and general relativity into one package. Further studies have shown it wasn’t fully satisfactory; but if only one additional dimension was enough to unify both theories in 1921, is electromagnetism 1D? In Einstein’s “The Meaning of Relativity” electromagnetism is linked to special relativity; if special relativity is indeed 1D then electromagnetism should be 1D as well; again, 1D when it is about mechanics and 3D when it is about describing the field.
If particle mechanics is 1D theory, there is no way that it can include a 3D theory like general relativity. If particle mechanics is only 1D, that would explain why elementary particles don’t obey the law of gravity (it is an open question). It would explain why passing from a point to a sphere for elementary particles is problematic. The hypothetical sphere expected for the shape of the electron in 1D is suddenly a string. If string theory is successful is it because considering a string instead of a point is closer to reality? It would also mean that the only vibration is a longitudinal wave. I don’t think a string in 1D has ever been considered in string theories, probably with good reasons.
One good reason for 3D is a need for the wave function. With the double-slit experiment, a particle is aware of the other slit, this awareness is not 1D. But a particle is passing through one slit or the other (Greenberger, 1988). There is the duality wave/particle. This paper is suggesting that the particle part could follow a 1D theory while the wave part is clearly 3D. I hope that other scientists will take the 1D idea further before discarding it. But I would agree that the idea is on thin ground.

Space-Time Diagrams

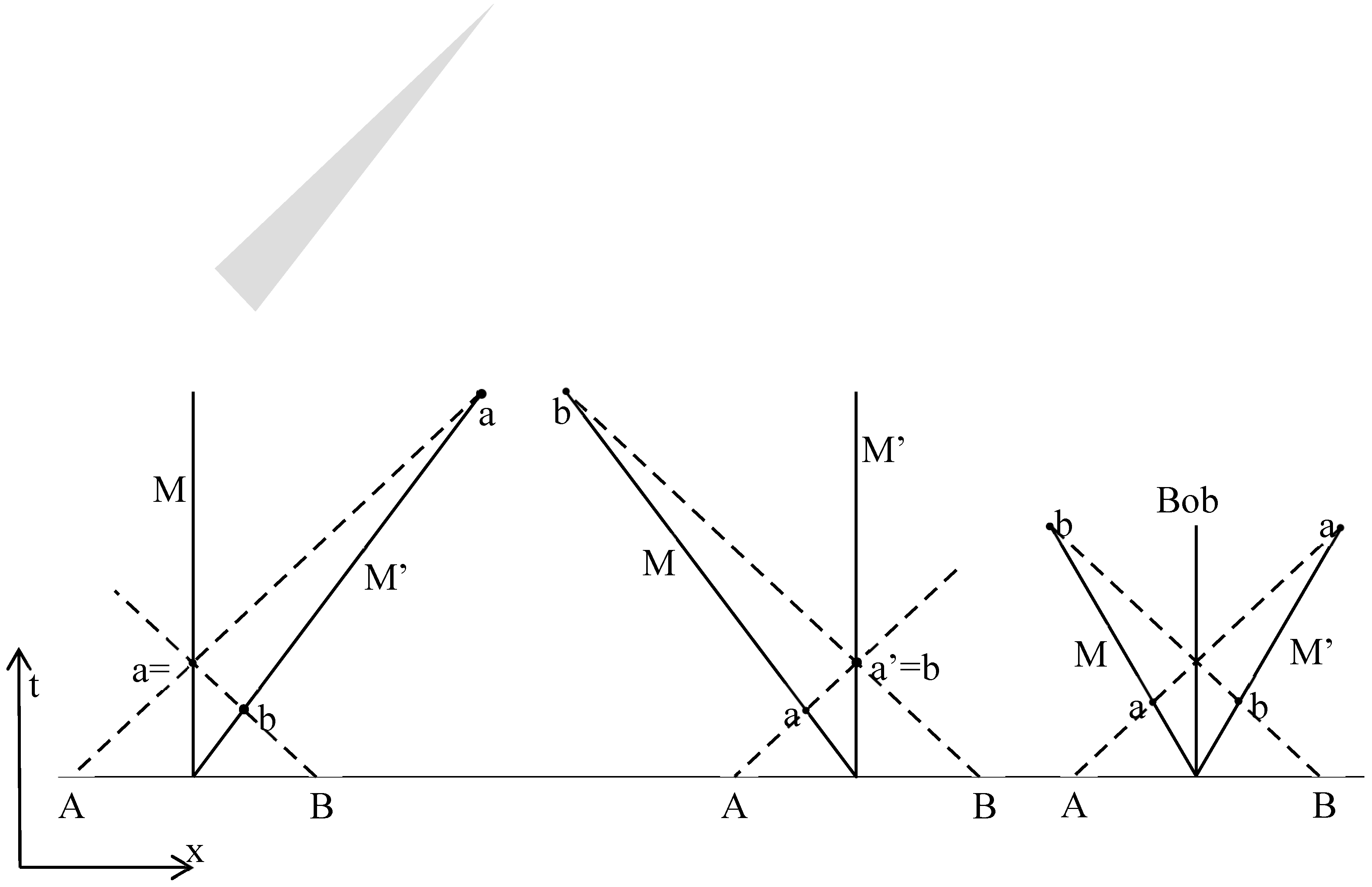
Let’s push the thought experiment of Figure 1 further. Bob will be our reference. And he observes M and M’. This time M travels towards point A at 0.99c and M’ travels towards point B at 0.99c. Bob, M and M’ form three different inertial systems presented in Figure 4. On that figure, photon A reaching M is denoted by dot a, and by dot a’ for M’; similarly for photon B with dots b and b’. Dots a, a’, b and b’ represent each one position and the corresponding time but for this argument we will solely consider time. Bob sees that the photon from A is catching up with M’ and time-flow is dilated by a factor 13.8 as with clock-1, while the photon from B is rushing towards M’ (the same observer) and this time, time-flow is contracted by a factor 0.2. Photons A and B reach M’ at the same time, so a’=b’ and the dots are at the same spot in the middle diagram. But a’=b’ even if the dots are not on the same spot in the left and right diagrams of Figure 4. And the reasoning is similar for M (a=b). If that is correct, Figure 4 shows clearly that time cannot be judged by others as for example a’ and b’ of the left diagram are not at the same spot even if they should represent the same time.
N.B.: Arbitrary factors of 13.4 and 0.6 were used for Figure 2. The calculation is 13.8 and 0.2 but this is impossible to represent on a figure. Figure 4 is purely for illustration, no numbers should be deduced from it.
In other words, space-time diagrams are not using our common space and time as there is a triangle/rectangle (grey in the left diagram) where time doesn’t flow for M’. M’ shouldn’t be represented with M on the left diagram, and M shouldn’t be represented with M’ on the middle diagram (not to judge for others); or grey areas (both meanings) will appear.
When Bob is watching photon A with observer M, the time-flow for photon A is contracted by a factor 0.2 and a factor 13.8 with observer M’. So photon A has two time-flows, one for M and one for M’. For Bob, M and M’ are at the receiving end of two different time-flows, one with a factor of 0.2 and the other one with a factor of 13,8. Bob sees clearly that photon A passes first by M then by M’ but somehow, photon A reaches M and M’ at the same time. Not only a=b and a’=b’ but also a=b=a’=b’. Those space-time diagrams are using our logic for a problem where our logic doesn’t seem to work. So should we use quantum mechanics logic (if such a thing exists)?
This reasoning, if correct, could shed light on the problem of measurement in quantum mechanics (Bell,1990). The EPR paradox (EPR, 1935) is well known (“the spooky action at a distance”). If a photon can move from M to M’ in no time seen by Bob, information could move from one entangled particle to its partner in no time. The measurement of time by Bob seems impossible as if particles can use another time (another dimension of time? Or another physical dimension?). The measurement problem could be why Alice is at two places at once for her U-turn. If the observer is sharing Alice’s reference then Alice will be at 0.99ly; if the observer is sharing Bob’s reference then Alice will be at 6.93ly (and don’t judge for others). The time interval difference (twin paradox) described as an absurdity may not be an absurdity in quantum mechanics but a problem of measurement/observer (and don’t judge for others).
It seems that what we call space-time diagrams are not space and time as we know it. The corresponding time of a, b, a’ and b’ are equal even when they are not at the same spot on the diagrams; so the time of the diagrams which is supposed to be our time is not the time of others. In that case, we should also question space: Alice is at different two spots but there is only one Alice. To obtain a=b=a’=b’, would observer M agree with M’ about the positions of points A and B? Is the uncertainty of Heisenberg linked with all this? This is a bit confusing and it is not my field so I stop here.
As it stands, this reasoning doesn’t show that temporal order has disappeared (contrary to what I used in the causality section). This reasoning also leaves one problem: simultaneity is obtained with changing time-flow. Is the non-simultaneity an illusion: M trying to deduce what M’ observes? Non-simultaneity can be deduced from Lorentz equations and space-time diagrams. The meaning of the space-time diagram is now questioned and we saw that the Lorentz transformation explained the illusion for the clocks. The non-simultaneity with time-flow change could indeed be an illusion. So simultaneity is back even with a changing time-flow. Can temporal order be lost if simultaneity is back?
In our macro-world, time-flow seems constant, so simultaneity is observed when photons A and B reach the middle. So, with combined relativity, if the observers are in the middle when photons reach the middle, the observers will conclude on simultaneity whatever is their speed. With special relativity, the observers have to be in the middle when photons A and B leave their starting point. Interesting to see that the starting point is what counts for special relativity and the end point is what counts for combined relativity. If correct, this observation could be important for describing the difference between our world where the result seems to be what counts, and the quantum world where the start seems to define the way time will behave.
The simultaneity with combined relativity is not rigorous; if the constancy of the speed of light is explained with special relativity, its meaning with combined relativity is not clear.

The Constancy of the Speed of Light

With the limit of the validity of special relativity there may be a change to the meaning of the constancy of the speed of light. Figure 1, with special relativity, photons A and B will reach M at the same time; and they will also reach M’ at the same time. But how does it work with combined relativity?
With some double-slit experiment (Greenberger, 1988), there is an experiment where interference is observed and at the same time one can determine which slit the photon is coming from, so the photon is not in two places at once. But the photon is aware of its surroundings as it interferes only if the other slit is open. So what happened with Figure 1? Because it is aware of its surroundings, my suggestion is that the photon would go to the speed of light with the embankment as reference while surrounded by the embankment, and to the speed of light with the train as reference while surrounded by the train. Einstein avoided this question by considering a “very long train” stretching from before A to beyond B. So with Einstein, the photons are either in the train or are outside with the embankment. Why did he avoid this question?
Instead of a train, imagine a “very long” spaceship going at 0.99c. A photon goes through the spaceship. The photon goes at the speed of light compared to the spaceship. Observed from outside the spaceship, the metre in the direction of the motion inside the spaceship is contracted twice with our new hypothesis (factor 7x7=49). The metre seems to be 0.02m long. The photon seems to travel at 0.02c compared to the spaceship. The speed of the spaceship being 0.99c, the photon seems to travel at 1.01c. That is not accepted with special relativity and the current constancy of the speed of light.
If the photon goes in the opposite direction to the spaceship, the photon would move backwards, following the motion of the spaceship. Therefore the need of a new definition of the constancy of the speed of light: it is constant but only in the correct frame of reference therefore the backwards motion or the speed of 1.01c.
Intuition tells us that this is wrong because of current special relativity; but if special relativity is wrong in those cases, the meaning of the constancy of the speed of light may have to change.

Fizeau Experiment

The Fizeau experiment could be confusing. Light goes through a tube filled with a liquid. The liquid flows one way or the other, the speed of light is measured. Section 13 of Einstein’s relativity, you can read that: “The tube plays the part of the railway embankment … the liquid plays the part of the carriage... the light plays the part of the man walking along the carriage...”. So this seems to be two references (M and M’) and one particle. This should be out of the limit of validity of special relativity but the result agrees with special relativity; therefore the result would question all this work. In fact, the result agrees with the Lorentz transformation, and we saw that the Lorentz transformation explains an illusion when it is outside the validity of special relativity. I would conclude that the Fizeau experiment does not contradict this work.
This exposes a difficulty: Lorentz transformation predicts the effect of special relativity on elementary particles but also predicts the illusion of special relativity seen in our macro world. In the Fizeau experiment, I decided that we observe an illusion but this needs to be confirmed. There is more because the Fizeau experiment is similar to the idea of a very long spaceship; could it be a path to check the new constancy of the speed of light? But the index of refraction is in the way so I cannot get a clear picture in my mind at the moment.

Discussion

This work is based on the principle of special relativity; but is that principle correct? It should be because special relativity is based on two postulates, one of them being the principle of special relativity. Accepting that Einstein is right with the non-simultaneity of special relativity, then observer M does not observe the same thing as observer M’ so the principle of special relativity is not correct with special relativity which should have been noticed as an absurdity. One consequence would have been that the rotating camera is not equivalent to observing a rotating disk. So the absence of contraction couldn’t lead to the conclusion that special relativity doesn’t work, etc. BUT, the return of simultaneity presented in this work validates the principle of special relativity with special relativity itself; this is critical for this work and many others.
The non-simultaneity was a reason for limiting “locally” the laws of conservation (charge, energy, etc.); that limit may not be justified any longer.
The speed-force has the potential to explain dark matter and dark energy. A book is needed to thoroughly investigate these questions (Danis,2024a). Here is a very short account. The direction of the speed-force is dictated by the change of speed. For a galaxy, as the rotating speed is the highest near the edge of the bulge, the speed-force is from the outer edge towards the centre until normal gravity takes over near the centre where the direction of change of speed is inverted. With a force, there is a potential, the corresponding potential energy is changed into a kinetic energy, justifying the observed rotating speed around the centre of the galaxy without the need for dark matter. For the universe, as the speed is greater away from us compared to near us, the speed-force is away from us. This speed-force could also explain gravitational lensing, nucleosynthesis and the speed of formation of galaxies. But something is missing for galaxy clusters and the centre of galaxies. That something is Mach’s principle but that is another subject (Danis, 2024b).
If time-flow can change for elementary particles and not for our macro-world, it could mean that we don’t share the same time with elementary particles; or if we do, particles are not subject to the same rules like the arrow of time. A positron being an electron moving backwards in time could make sense. A second dimension of time is another idea. A new space-time diagram has to be developed.
The principle of equivalence states that gravity and change of speed are equivalent; but this may need a rethink as time-flow changes with gravity and doesn’t change with a change of speed in our macro-world. If time is no longer deformed but space is still deformed, what is the fourth dimension? One possibility is energy as proposed in (Danis, 2024a).
With all those particularities (time-flow sometimes changing, sometimes not changing), is time still a fundamental physical quantity?
If special relativity is confirmed to be uniquely part of quantum mechanics, as combined relativity uses special relativity it would be a hypothesis that mixes a part of quantum mechanics with general relativity. This could be important for scientists looking for the “unified field theory”.
With the 1D idea, at what point do we pass from 1D to 3D? Is a proton 3D? Is an atom 3D?
I am sure there will be many more points to address like superposition, wave function and its collapse, Copenhagen interpretation. What about if special relativity is the key to understanding quantum mechanics as I tried to show in the space-time diagrams section?

Conclusion

This work seems to tick all the boxes of Feynman’s lecture “seeking new laws” [Feynman, 1960]: simple with some disagreements with current theory and agreement with new observations. This paper is a call to the scientific community, first to raise awareness, second to complete the study, and then to validate (or refute) the ideas. It is a work in progress and please let me know if you cite this paper in your work.
This work has many sections. Some sections could be wrong (the “junk” ideas in Feynman’s lecture) but the observations are there and need an explanation. If you think I am wrong somewhere, please feel free to contact me with a specific reason why I should be wrong (error in logic/mathematics or in the use of Einstein’s postulates). The exchange will improve the clarity of this paper either with me retracting a part of it or adding clarity to a section. For example, the space-time diagrams section has been added following one reviewer’s comments. I would prefer a public exchange in a forum as it would include many people. https://physicsoverflow.org was suggested with the first version of this paper but I am still waiting for approval after more than a month and https://physics.stackexchange.com doesn’t accept papers.

Acknowledgements

With Prof. Ø.Grøn I have had some interesting exchanges. He has studied Ehrenfest’s paradox in depth and told me the rotating camera experiment is new and would test special relativity in our macro-world. Thank you Prof. Grøn, you gave me confidence to publish it. Prof Gilmore has directed me to (Davis et al.,2004). It is an important reference because one observation (the rotating camera) can simply be an anomaly. Davis’ paper is very solid; without it there would be doubts. Thank you Prof. Gilmore.

Appendix A

The Event Distance
ds2 = (x1-x2)2 + (y1-y2)2 + (z1-z2)2 – c2 (t1-t2)2
It is a theoretical exercise; here the distance between the mirrors is not 1m but c: the distance covered by the light (in vacuo) in one second. By using c instead of 1m (1m and a time interval of 1/c second), because of the huge dimension, I hope people will realise that time-flow changes for clock-1 depending on the direction of the photon doesn’t make sense.
As special relativity is invariant, we can swap the moving reference with the immobile reference. So, Alice’s reference is K and considered as non-moving for the calculation even if she is moving on Figure 2. We will work from K to K’ so K’ is travelling at v = -0.99c viewed from K.
Lorentz factor is:
γ = 1/√(1-v2/c2)
and v = -0.99 c.
For K and clock-1, the events gives:
x1 = 0 y1 = 0 z1 = 0 and t1 = 0
x2 = c y2 = 0 z2 = 0 and t2 = 1 (one second)
ds2 = (c)2 + 0 + 0 -c2 = 0
The same two events for K’ give:
x’1 = 0 y’1 = 0 z’1 = 0 and t’1 = 0
x’2 = ? y’2 = 0 z’2 = 0 and t’2 = ?
Lorentz transformation gives:
t’2 = γ (t2 – (v.c/c2) = γ (1 + 0.99) = 1.99 γ
x’2 = γ (c + 0.99 c) = 1.99 γ.c
ds’2 = (1.99 γ.c)2 + 0 + 0 – (1.99 γ)2 c2 = 0
Now clock-2.
For K, the events give:
x1 = 0 y1 = 0 z1 = 0 and t1 = 0
x2 = 0 y2 = c z2 = 0 and t2 = 1 (one second)
ds2 = 0 + (c)2 + 0 - c2 = 0
For K’:
x’1 = 0 y’1 = 0 z’1 = 0 and t’1 = 0
x’2 = ? y’2 = ? z’2 = 0 and t’2 = ?
First problem, Lorentz transformation uses x and with this clock, x (x1 - x2) would give 0 so the correct time dilation for clock-2 should be:
t’2 = γ (t2 – (v.0/c2) = γ (1-0) = γ
Strangely, the time has different values depending on the orientation of the clock; the time dilation for clock-1 is.
t’2 = γ (t2 – (v.c/c2) = γ (1 + 0.99) = 1.99 γ
Then Lorentz transformation gives:
x’2 = γ (0 + 0.99c) = 0.99 γ.c
y’2 = c
There are two t’2 so two possible ds’2:
ds’2 = (0.99 γ.c)2 + c2 + 0 – (1.99 γ)2 c2 ≠ 0
ds’2 = (0.99 γ.c)2 + c2 + 0 – (γ)2 c2 ≠ 0
Clearly the fact that y’2 does not include γ is problematic.
If there is a length contraction along y we get:
y’2 = γ (c – 0.c) = γ.c
ds’2 = (0.99 γ.c)2 + (γ.c)2 + 0 – (1.99 γ)2 c2 = 0
ds’2 = (0.99 γ.c)2 + (γ.c)2 + 0 – (γ)2 c2 ≠ 0
There is no choice: to get the correct distance, first a length contraction has to be applied along the y axis and second, for the time dilation, instead of x it should be √(x2 + y2 + z2). This is a very easy correction to avoid the problem of two different time dilations. Clearly, it shows that the Lorentz transformation has been developed with only one dimension in mind. This is confirmed in (Einstein, 1922).

References

  1. Bell, John (1990) Phys. World 3 (8) 33 “Against measurements”.
  2. Danis, Francois (2024a), “Eintein revisited”. Draft of the book is available on justified request until the book is on sale.
  3. Danis, Francois (2024b), “Mach’s principle against dark matter”. [CrossRef]
  4. Davis, Tamara and Lineweaver, Charles (2004),“Expanding Confusion: common misconceptions of cosmological horizons and the superluminal expansion of the universe”. Publications of the Astronomical Society of Australia. 2004;21(1):97-109. doi:10.1071/AS03040. https://arxiv.org/abs/astro-ph/0310808.
  5. de Sitter, Willem (1913), “A proof of the constancy of the velocity of light” , Proceedings of the Royal Netherlands Academy of Arts and Sciences, 15 (2): 1297–1298, Bibcode:1913KNAB...15.1297D.
  6. Ehrenfest, P. (1909). “Gleichförmige Rotation starrer Körper und Relativitiitstheorie”, Phys. Zeits., 10, 918.
  7. Einstein, A. (1905). “Zur Elektrodynamik bewegter Körper”, Annalen der Physik 17: 891.
  8. Einstein, A. (1911). “Zum Ehrenfestschen Paradoxon“, Physik. Zeitschrift, 12, 509.
  9. Einstein, A. (1916). “Relativity: The Special and the General Theories.” The folio society, London, 2004.
  10. Einstein, A. (1922). “The Meaning of Relativity”, RoutledgeClassics, 2003.
  11. EPR, (1935). Einstein, A; B Podolsky; N Rosen (1935-05-15). “Can Quantum-Mechanical Description of Physical Reality be Considered Complete?”. Physical Review. 47 (10): 777–780. [CrossRef]
  12. Feynman, R. (1960). “The Character of Physicsl Law”, Penguin Books 1992.
  13. Fizeau, H. (1851). “Sur les hypothèses relatives à l’éther lumineux”. Comptes Rendus. 33: 349–355. “The Hypotheses Relating to the Luminous Aether, and an Experiment which Appears to Demonstrate that the Motion of Bodies Alters the Velocity with which Light Propagates itself in their Interior”. Philosophical Magazine. 2: 568–573.
  14. Greenberger, D.M. and Yasin, A. (1988) “Simultaneous wave and particle knowledge in a neutron interferometer”, Physics Letters A 128, 391–4.
  15. Greene, Brian (1999) “The Elegant Universe”, chapter 6, subsection “A sleight of hand?
  16. Heaviside, Oliver (1888/89), “Electromagnetic waves, the propagation of potential, and the electromagnetic effects of a moving charge”, The Electrician.
  17. Kaluza, Th (1921) “On the Unification Problem in Physics. [CrossRef]
  18. Langevin, P. (1911). “The evolution of space and time”, Scientia, X: 31–54 (translated by J. B. Sykes, 1973 from the original French: “L’évolution de l’espace et du temps”).
  19. Lorentz, H. (1892). “La théorie électromagnétique de Maxwell et son application aux corps mouvants” Archives néerlandaises (1892).
  20. Mamone-Capria, M. (2012). “Simultaneity as an invariant equivalence relation”, Foundations of Physics, 42 (11): 1365–1383.
  21. Maxwell, J. C. (1873). “A Treatise on Electricity And Magnetism” – Posner Memorial Collection – Carnegie Mellon University.
  22. Michelson, Albert A.; Morley, Edward W. (1887). “On the Relative Motion of the Earth and the Luminiferous Ether”. American Journal of Science. 34 (203): 333–345. Bibcode:1887AmJS...34..333M. doi:10.2475/ajs.s3-34.203.333. S2CID 124333204.
  23. Poincaré, H. (1900). “La théorie de Lorentz et le principe de réaction”, Archives Néerlandaises des Sciences Exactes et Naturelles, 5: 252–278.
  24. Rossi, B. , Hall, D. B. (1941). “Variation of the Rate of Decay of Mesotrons with Momentum”. Physical Review. 59 (3): 223–228.
  25. Simonetti, J. (1997). “Frequently Asked Questions About Special Relativity - The Twin Paradox”. Virginia Tech Physics. https://www1.phys.vt.edu/~jhs/faq/twins.html.
  26. Varićak, V. (1911). “Zum Ehrenfestschen Paradoxon“, Physik.Zeitschrift, 12, 169.
Preprints 117563 g001
Figure 1. : Simultaneity: an adaptation of Einstein’s figure. This is representing the position when two bolts of lightning strike. M and M’ are above each other at mid-distance between A and B. The train is moving towards B at v speed.
Figure 1. : Simultaneity: an adaptation of Einstein’s figure. This is representing the position when two bolts of lightning strike. M and M’ are above each other at mid-distance between A and B. The train is moving towards B at v speed.
Preprints 117563 g001
Preprints 117563 g002
Figure 2. photon clocks seen by Bob, the clocks move from left to right. Lower figure is clock-1, upper figure clock-2. The photons are represented by the thick line and also travel from left to right. The figure represents the instant when the photon of clock-1 hits the second mirror on the right. Notice the photon of clock-2 has not yet hit the bottom mirror on the right. Clock-1, the first mirror will have time to move to the level of the dash line before the photon comes back to it. By that time, the photon of clock-2 will have hit the bottom mirror. This is how the synchronisation of the clocks is observed.
Figure 2. photon clocks seen by Bob, the clocks move from left to right. Lower figure is clock-1, upper figure clock-2. The photons are represented by the thick line and also travel from left to right. The figure represents the instant when the photon of clock-1 hits the second mirror on the right. Notice the photon of clock-2 has not yet hit the bottom mirror on the right. Clock-1, the first mirror will have time to move to the level of the dash line before the photon comes back to it. By that time, the photon of clock-2 will have hit the bottom mirror. This is how the synchronisation of the clocks is observed.
Preprints 117563 g002
Preprints 117563 g003
Figure 3. Space-time diagrams. A1 is for Alice1, A2 for Alice2 and B for Bob. First diagram, Bob is immobile as in the twin paradox. Second, A1 is immobile and sees B moving away. Third, A2 is immobile and sees B approaching. Forth, combination of A1 and A2 immobile. The horizontal line represent 1 year of Alice, our time reference. As the time reference is Alice, with the first diagram, Bob has aged by 14 years, with the last diagram, Bob has aged by 2/7 year.
Figure 3. Space-time diagrams. A1 is for Alice1, A2 for Alice2 and B for Bob. First diagram, Bob is immobile as in the twin paradox. Second, A1 is immobile and sees B moving away. Third, A2 is immobile and sees B approaching. Forth, combination of A1 and A2 immobile. The horizontal line represent 1 year of Alice, our time reference. As the time reference is Alice, with the first diagram, Bob has aged by 14 years, with the last diagram, Bob has aged by 2/7 year.
Preprints 117563 g003
Preprints 117563 g004
Figure 4. space-time diagrams for Figure 1 but with Bob “immobile” in the middle (right diagram), M moving towards A and M’ moving towards B. Left diagram considers M immobile, middle diagram considers M’ immobile. a represents when photon A is passing by M, b when B is passing by M, a’ when A is passing by M’ and b’ when B is passing by M’. The dash lines represent the photons.
Figure 4. space-time diagrams for Figure 1 but with Bob “immobile” in the middle (right diagram), M moving towards A and M’ moving towards B. Left diagram considers M immobile, middle diagram considers M’ immobile. a represents when photon A is passing by M, b when B is passing by M, a’ when A is passing by M’ and b’ when B is passing by M’. The dash lines represent the photons.
Preprints 117563 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated