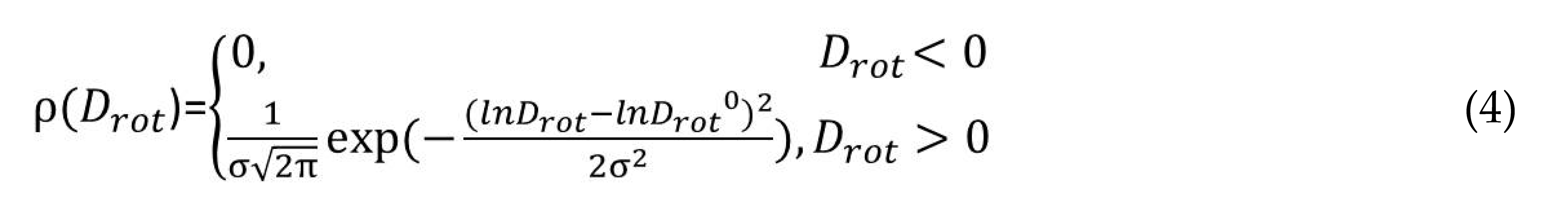Prerpints.org logo
Preprint
Article

Rotational Mobility of TEMPO Spin Probe in Polypropylene: EPR Spectra Simulation and Calculation via Approximated Formulas

Altmetrics

Downloads

84

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.pdf (543.25KB )

Submitted:

19 July 2024

Posted:

22 July 2024

You are already at the latest version

Alerts
Abstract
The rotational correlation times of a small compact spin probe (2,2,6,6-tetramethylpiperidin-1-yl)oxyl in isotactic polypropylene were obtained over a wide temperature range by EPR spectra simulation taking into account anisotropic rotation as well as distribution of probe molecules by rotational mobility. The averaged values of rotational correlation times were compared with the corresponding values calculated using well-known approximated formulas based on the intensities and widths of the spectral lines. It was shown that the calculated values can be used as effective parameters to characterize rotational mobility of the spin probe in the polymer matrix in a wide range of rotational correlation times.
Keywords: 
Subject: Chemistry and Materials Science  -   Polymers and Plastics

1. Introduction

The spin probe technique has been widely used for a long time to characterize the segmental mobility of polymers [1]. It is currently a routine method for polymer studies, and the novel approaches based on pulsed and high-field EPR as well as spatial EPR imaging are constantly being proposed [2,3,4]. The spin probe technique is based on the introduction of stable paramagnetic molecules with strongly anisotropic spin-Hamiltonian parameters, more often, nitroxide radicals, into the polymer matrix. The molecular mobility of probes inside the polymer, which can be determined by analyzing the shape of their EPR spectra, reflects the mobility of macromolecules. Of course, the information obtained in this way depends on the size and shape of the probe. Radicals with different geometry can exhibit various mobility in the same polymer under the same conditions. On the one hand, this makes the results obtained unambiguous; on the other hand, it is possible to characterize various dynamic processes in the polymer matrix using several probes of different structures (see, for example, [5]).
A common parameter used to characterize the molecular mobility of spin probes is the rotational correlation time (τc) which is related to the rotational diffusion coefficient as follows: τc=1/(6·Drot). There are two methods to extract information about the rotational mobility of radicals from their EPR spectra. The first and the most common approach is to measure spectral features, such as intensities and widths of the spectral lines and to derive correlation. A general theory of EPR linewidth for paramagnetic species has been developed in the 1960s by Kivelson [6]. According to the theory, the peak-to-peak Lorentzian linewidth of an individual hyperfine line of the nitroxide is given by:
∆ H m = A + B m N + C m N 2
where mN is the magnetic quantum number equal to -1, 0, and 1 for 14N nucleus. The A, B, C coefficients depend on the rotational correlation times. Substituting the three values of mN into Eq. (1), and replacing Δ H 1 Δ H 0 by I 0 I 1 for the measurement convenience (it is valid for other mN values, I1, I0, I-1 are intensities of the corresponding lines), one can derive several expressions for the rotational correlation time [7,8]:
τ c ( 1 ) = κ 1 ∙ ∆ H 0 ∙ I 1 I − 1 − I 1 I 1
τ c ( 2 ) = κ 2 ∙ ∆ H 0 ∙ I 0 I 1 + I 0 I − 1 − 2
τ c ( 3 ) = κ 3 ∙ ∆ H 1 ∙ I 1 I − 1 − 1
τ c ( 4 ) = κ 4 ∙ ∆ H 0 ∙ I 0 I 1 − 1
where the coefficients κ1, κ2, κ3, κ4 are determined from the principal values of g- and A-tensors of the nitroxide (see Appendix A). The expressions (2)-(5) have been derived for isotropic rotation of nitroxide in the fast motion regime (5‧10-11 < τc < 10-9). Another assumption of exp. (2)-(5) is that the individual line shape is Lorentzian. However, it was shown in [Santiago 2008] that these formulas are applicable in the case when the inhomogeneous Gaussian broadening contributes to the spectrum due to unresolved proton hyperfine structure.
Another approach to the rotational correlation times determination is the simulation of EPR spectra. The most widely used software are EasySpin [9] and the program package developed by Freed et al. [10]. They are based on the stochastic Liouville equation. The EPR spectra simulation have been broadly applied for various spin-probed or spin-labelled systems due to high reliability of this approach. It should be noted that in the case of polymer matrices there is a distribution of probe molecules by rotational mobility. Indeed, any polymer is a heterogeneous medium at the molecular level; it includes regions of tightly coiled and loosely arranged macromolecular fragments. The probes being localized in these regions would differ in their rotational mobility. When a polymer includes several regions that differ significantly in the packing density, more mobile and less mobile radicals contribute to the EPR spectrum as a set of characteristic lines (see, for example, [3]). Such a spectrum can be simulated as the sum of several signals related to the probes with different mobility. However, if the polymer is heterogeneous at the nanometer level, spin probes would be distributed in regions with gradually changing mobility, and the EPR line shape would differ significantly from the line shape for a homogeneous sample. This is the most complicated case, when it is necessary to simulate the spectra considering the continuous distribution of the probes by their rotational correlation times. This approach was implemented in [11,12,13] for simulation of CW EPR spectra and in [14,15] for describing 2D ELDOR spectra with the use of lognormal radical distribution by rotational correlation times. In [11,13] it was shown that the width of distribution decreases with increasing temperature that means more uniform radical mobility at higher temperatures.
Unfortunately, the simulation of EPR spectra using distribution of radicals by rotational mobility is a complicated procedure. For this reason, spectra simulation is rarely used to analyze the spin probes mobility in polymers. Most researchers determine rotational correlation times from EPR spectra using the approximated formulas (2)-(5). It should be noted that the formulas were proposed for analysis of isotropic rotation and, generally speaking, were not intended for studying heterogeneous systems. However, since it is desirable to have a simple way for assessment of polymer mobility without complicated spectral simulation, the applicability of the formulas for calculation of “effective” τc* values should be considered. In paper we showed several examples of satisfactory agreement between the rotational correlation time values obtained by spectra simulation and calculated by the formulas for TEMPO in polymer matrices.
It seems appropriate to establish the range of applicability of the approximated approach by comparing τc* values ​​obtained using different formulas among themselves and with those obtained by spectra simulation. That was the goal of this work. We chose a small compact nitroxide radical TEMPO as a spin probe and isotactic polypropylene (PP) as a matrix because of absence of functional groups in this polymer that could interact specifically with the probe molecules. The EPR spectra of the probe inside the polymer were recorded in a wide temperature range and simulated taking into account the lognormal distribution of the probe molecules by rotational mobility. The rotational correlation times obtained as a result of EPR spectra simulation were compared with the values calculated by formulas (2-5). It was shown that different formulas return different results in the case of strongly anisotropic rotation of radicals. The best approximation in a wide range 2‧10-11<τc < 5‧10-9 is given by eq. (5).

2. Materials and Methods

2.1. Materials

Isotactic polypropylene was kindly provided to us by Prof. P.M. Nedorezova (N.N. Semenov Federal Research Center for Chemical Physics, Russia). The polymer characteristics (stereoregularity, melting point, and degree of crystallinity) are given in [16].
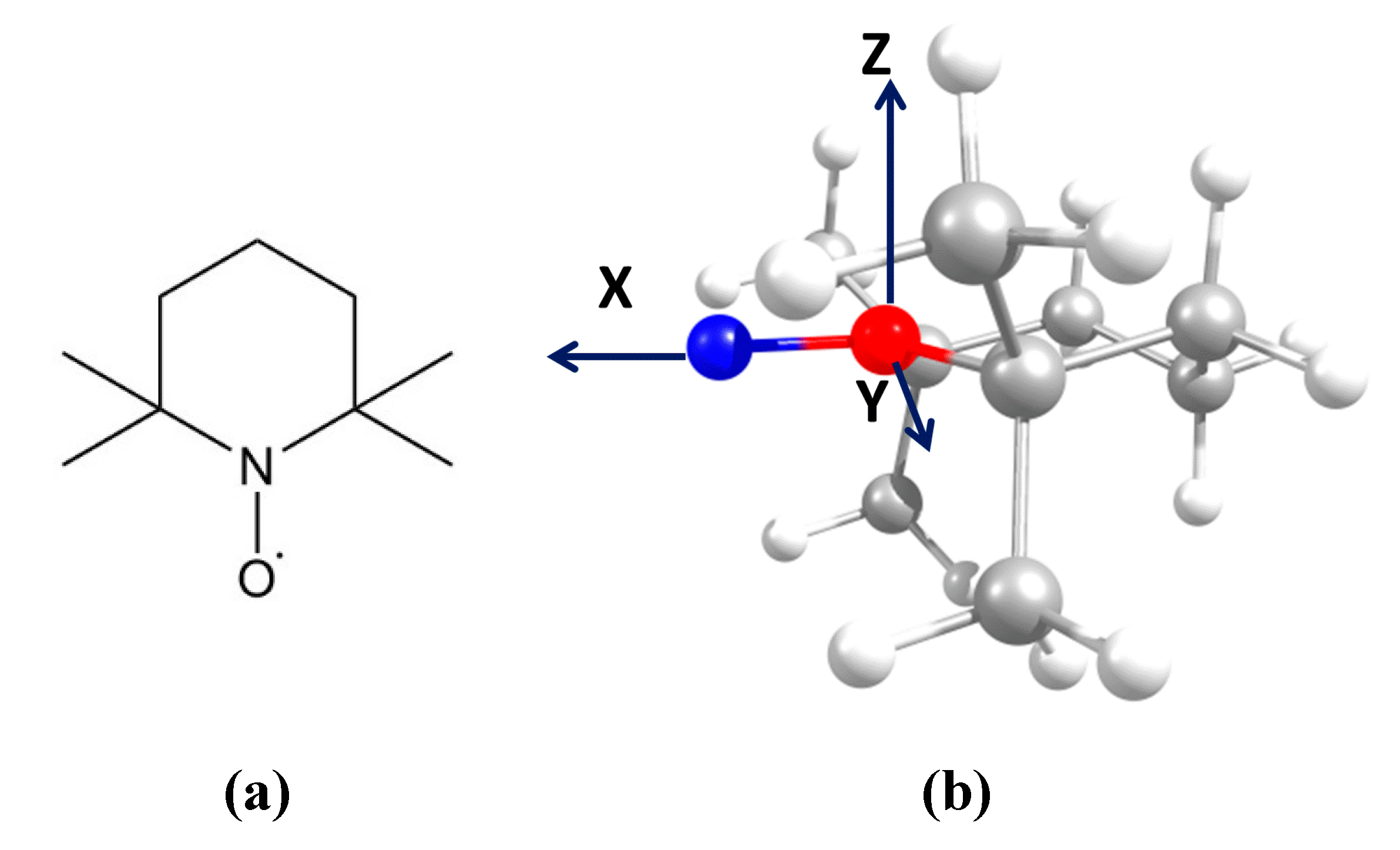
The stable nitroxide radical (2,2,6,6-tetramethylpiperidin-1-yl)oxyl (TEMPO) was purchased from Sigma-Aldrich (Figure 1a). The optimized radical geometry (Figure 1b) was calculated using the ORCA software package [17]. The B3LYP – 6-31g(d,p) model was used for the calculation.

2.2. Sample Preparation

TEMPO was introduced into powdered PP through diffusion from the gas phase. The number of spins as well as their distribution in PP were monitored by EPR spectroscopy. The spectra at 295 K were recorded periodically for 1-3 weeks until the spectrum shape and the line width remain constant. The sample contained 2·1014 spins per 1 mg of PP. It should be noted that the probes were localized only in the amorphous phase of PP.

2.3. EPR Spectroscopy

EPR spectra were recorded with BrukerEMXplus spectrometer equipped with a high- sensitive resonator ER 4119 HS and the temperature control unit (temperature setting accuracy ±1 K). The EPR measurements were performed at microwave power values of 0.5-1mW and magnetic field modulation amplitude of 0.05-0.10 mT.

2.4. EPR Spectra Simulation

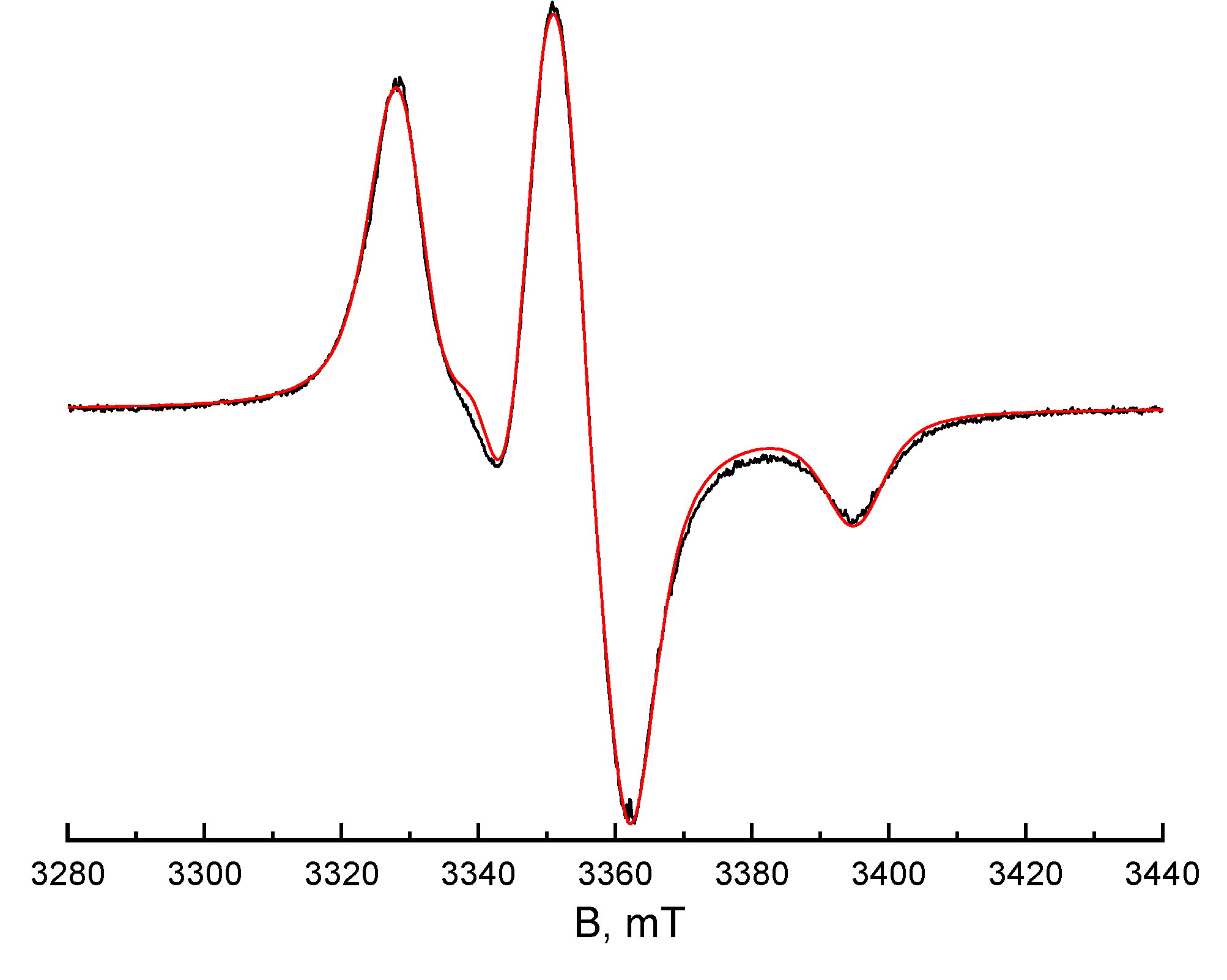
The spin-Hamiltonian parameters of TEMPO in PP were found by simulation of the EPR spectrum recorded at a temperature of 100K in the absence of paramagnetic molecules mobility (in rigid limit). The ODF3 program available at https://www.chem.msu.ru/rus/lab/chemkin/ODF3/ and described in detail in [18] was used for simulation. The simulation result is shown in Figure 2. The magnetic resonance parameters of the spin probe in the polymer were found to be gxx=2.0096, gyy=2.0061, gzz=2.0022, Axx=0.67 mT, Ayy=0.73 mT, Azz=3.34 mT.
The EPR spectra recorded in the temperature range 165-435 K were simulated taking into consideration the distribution of radicals by their rotational mobility [13]:
Preprints 112711 i001
Here ρ is the probability density function, Drot is the rotational diffusion coefficient, Drot0 and σ are the center and dispersion of the distribution, respectively. The software developed by Prof. A. Kh. Vorobiev and Dr. D.A. Chernova (Moscow State University, Russia) was used. The principal axes of the g- and hyperfine interaction tensors of unpaired electron with 14N nuclei were supposed to coincide. The shape of the individual resonance line was expressed by Voigt function. The contributions of Gauss and Lorentz functions were described by tensors of the second rank, the principal axes of the tensors coincided with the magnetic axes of the radical.
Generally speaking, the simulation of EPR spectra is an inverse ill-posed mathematical problem. The main difficulty in solving such a problem lies in the correlation between the varied parameters. Simulating the spectra of mobile radicals, one should take into account that τc significantly correlates with the contribution of Lorentz function to the spectral line width [19]. According to our experience, in the case of distribution of the radicals by rotational mobility, a correlation between the width of the distribution and rotational correlation times may take place. To avoid the correlations, we simulated the spectra by varying the least number of parameters that yields an adequate simulation result, namely, the description of positions, widths and intensities of the spectral lines. A perfect fitting of the spectra was not considered necessary. The optimal parameters should be physically meaningful, as well as independent on the initial approximation.

3. Results

Figure 3 shows the examples of simulation of EPR spectra recorded at different temperatures. More spectra are given in the Supplementary Materials (Figure S1). It is seen that the simulation quality is quite good. In the high-temperature range the spectra can be simulated quite perfectly. With temperature decrease the simulation quality slightly worsens, but the positions, intensities, and shapes of the spectral lines are reproduced satisfactorily. It should be noted that we did not strive for a perfect simulation, although that was possible through increasing the number of variable parameters, but such increasing could lead to uniqueness decrease.
In Table 1 one can see the parameters obtained as a result of EPR spectra simulation. Parameters that were not being varied during the simulation are marked with asterisks. More detailed information, including the contribution of Gauss and Lorentz functions to the Voigt function describing the shape of an individual spectral line is given in Table S1 (Supplementary Materials). It should be noted that we simulated EPR spectra over a wide temperature range using almost the same distribution of TEMPO molecules by rotational mobility. It can be assumed that the mobility distribution of the probes reflects their distribution by localization in the polymer matrix. Another important result is that the rotational mobility of TEMPO around the molecular X-axis (bound N-O) (see Figure 1b) was found to be strongly hindered. Within the temperature range of 395-435 K the rotational correlation time τx exhibited an increase with decreasing of temperature. At temperatures below 395 K this value turned out to be outside the range of X-band EPR spectra sensitivity, so, we fixed it as 1.7·10−7 s. The phenomenon of hindered rotational mobility around X-axis for piperidine-type nitroxide radical TEMPOL in polymer matrices was previously observed in [20,21]. The authors explained this observation by a weak complexation between the probe molecule and polymer fragments. However, in our work, the polymer does not contain any fragments other than fully saturated -CH3 groups, thus, the polymer contains only sp3-hybridized carbon atoms that are incapable of any specific interaction. We suppose that the strongly hindered rotational mobility of TEMPO around X-axis can be explained by its molecular geometry. Indeed, in a confined space, four CH3-substituents would inhibit the rotation of the molecule around X-axis in the higher extent comparing to the rotation around Y-axis. The results of spectra simulation confirm this assumption – the fastest rotation of TEMPO in PP occurs around the Y-axis.
It should also be noted that in the temperature range of 245-345 K the quasi-librations of the spin probes [13] were taken into consideration, that improved the quality of spectra simulation. At temperatures above 345 K, the librations cannot be observed due to the intense rotational motion of the radicals. At temperatures below 243 K, the libration amplitudes become small and do not manifest themselves in the EPR spectra. The separation of rotational and librational mobility is an ill-posed problem, since these motions both lead to averaging of the anisotropic spin-Hamiltonian parameters of the radicals. For this reason, we use the isotropic librational motion. As it was previously estimated [13], anisotropy of rotation and anisotropy of librations cannot be extracted simultaneously from EPR spectra.

4. Discussion

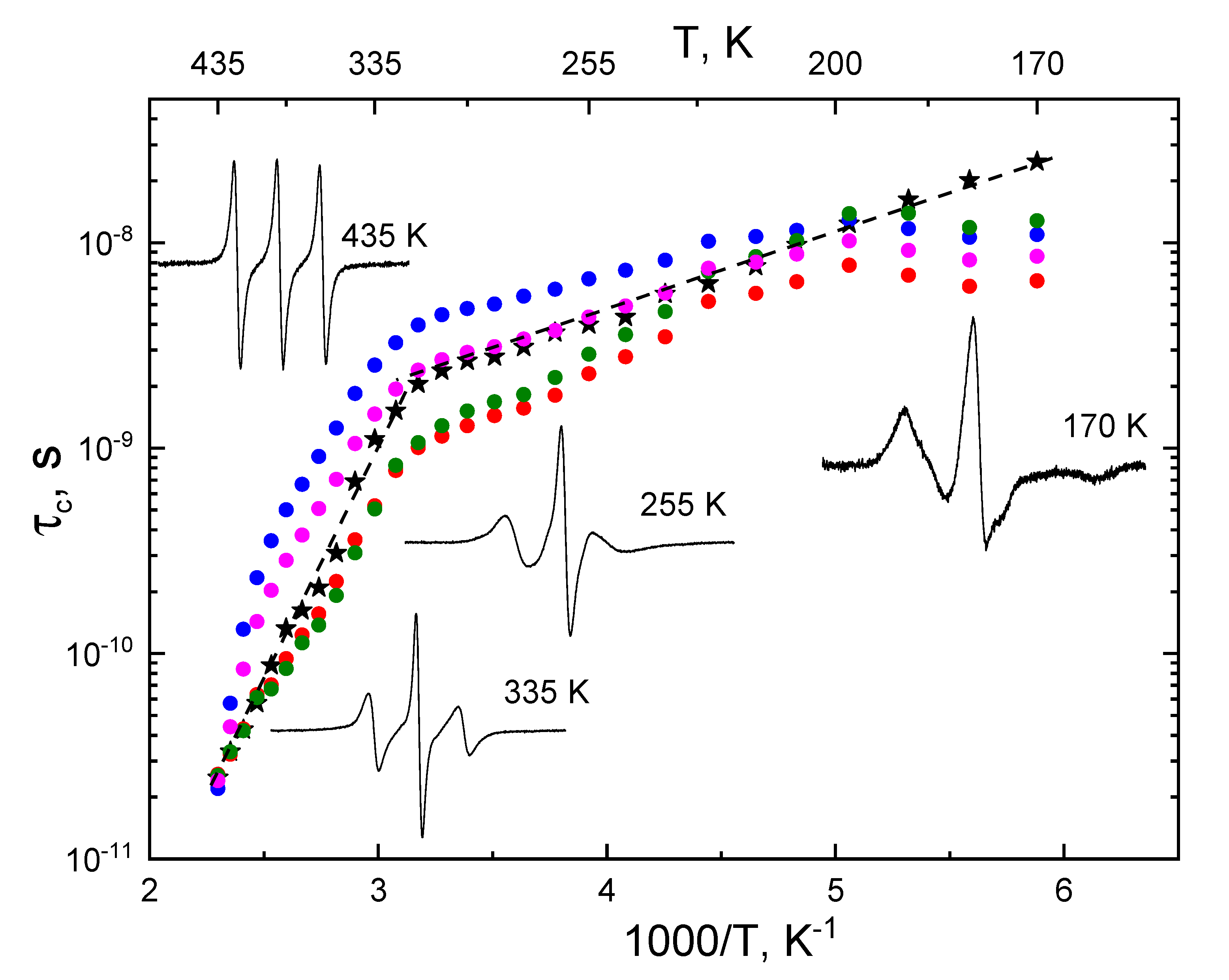
Simulation of the EPR spectra revealed highly anisotropic rotational mobility of TEMPO spin probes in PP. To compare the rotational correlation times obtained by simulation of the spectra and those calculated by approximated formulas, we calculated the average rotational correlation time of the radicals at each temperature as <τc> = (τx + τy + τz)/3. Figure 4 shows the temperature dependences of this value as well as the parameters τc*(1), τc*(2), τc*(3), and τc*(4), calculated by formulas (2), (3), (4) and (5), respectively. The spectra, representative for different temperature intervals are shown on the insets. One can see that the shapes of all temperature dependences are similar. In all cases, the crossover between two modes of the polymer motion can be seen in the temperature range 305-315 K. These temperatures are higher than Tg for isotactic PP (~ 263 K). Similar patterns were observed previously in [22] for cis-1,4-poly(isoprene) using the spin probe method with TEMPO radical. The effective activation energies for TEMPO rotational diffusion (Erota), obtained from the <τc> temperature dependence, were found to be 43.5 kJ/Mol and 7.3 kJ/Mol for high and low temperature regions, respectively. The second value is close to Erota for TEMPO in various polymers [23]. It should be noted, that <τc> changes monotonically with temperature, while τc(1), τc(2), τc(3), and τc(4) demonstrate non-monotonic behavior below T=200 K (<τc> >1‧10-8 s). We can conclude that the approximated formulas are inapplicable at such a slow rotational mobility of the radical.
Figure 5 shows differences between the <τc> values determined via spectral simulation and τc*(1), τc*(2), τc*(3), and τc*(4). One can see that formula (2) and (4) return values the closest to <τc> at τc < 7‧10-10 s, while formula (5) gives the best approximation to the simulation result at longer τc, up to 5‧10-9 s. One can see the shapes of EPR spectra within the range of 7‧10-10 < τc < 5‧10-9 are far from the fast-motional spectra, nevertheless, formula (5) allows obtaining of reasonable results. Formula (3) was shown to give the results which significantly decline from <τc> almost in all mobility range, therefore, this formula is not suitable for analysis of EPR spectra of the radicals with strongly anisotropic rotation in the polymer matrix. It should be reminded that all the approximated formulas were proposed for analysis of EPR spectra of isotropically rotating radicals.
The results obtained showed that, in the majority of cases, when the researcher is not interested in fine details of polymer organization, but is looking for a way to determine the change in the mobility of macromolecules under an impact on the system, the reliable data can be obtained using the spin probe method without simulation of EPR spectra, which is complicated, time-consuming, and requires special qualification of the researcher. It should be underlined that in the present work we investigated the behavior of the spin probe which did not contain any functional groups except for the paramagnetic N-O fragment. The studied polymer also did not contain groups capable to complexation with the probe molecules. In cases of polymers and/or probes bearing functional groups, the possibility of using the approximated formulas should be tested additionally.

5. Conclusions

The applicability of different approximated formulas for characterization of the mobility of spin probe in polymer matrix was analyzed on the example of TEMPO spin probe and isotactic polypropylene. The calculated values of rotational correlation time were compared with those obtained by simulation of EPR spectra taking into account the rotational anisotropy and lognormal distribution of radicals by rotational mobility. It was shown that in the case of strongly anisotropic rotation of probe molecules in polymer matrix, different formulas give different results. In general, the approximated method can be used for analysis of EPR spectra up to rotational correlation times τc < 5‧10-9 s.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1: EPR spectra of TEMPO in PP (black lines) and the results of their simulation (red lines); Table S1: Rotational characteristics of TEMPO in PP.

Author Contributions

Conceptualization and methodology, N.Ch.; formal analysis, N.Ch.; investigation, T.Ya.; resources, A.K.; writing—original draft preparation, N.Ch.; writing—review and editing, T.Ya. and A.K. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded within the framework of the Program of Fundamental Research of the Russian Federation (Reg. № 122040500068-0). The authors acknowledge M.V. Lomonosov Moscow State University Program of Development for EMXplus-10/12 PX X-band EPR Bruker spectrometer.

Acknowledgments

The authors acknowledge Prof. A.L. Iordansky for fruitful discussion.

Conflicts of Interest

The authors declare no conflicts of interest. .

Appendix A

In the case of nitroxide probes in the fast motion regime, as described in the main text, the equations derived by Kivelson [Kivelson, D. J. Chem. Phys. 1960, 33, 1094] can be combined to obtain the rotational correlation time (see Eqs. (2)-(5)).
The rotation correlation times
κ 1 = κ 3 = π 3 b 4 Δ γ B 0 15 − 1 g 0 μ B h
κ 2 = π 3 b b 8 − 1 g 0 μ B h
κ 4 = π 3 b b 8 − 4 Δ γ B 0 15 − 1 g 0 μ B h
where h is the Planck constant, μB is the Bohr magneton, and g0 is the isotropic g-factor:
g 0 = g x x + g y y + g z z 3
b = 4 π 3 A z z − A x x + A y y 2
Δ γ = 2 π μ B h g z z − g x x + g y y 2
The magnetic parameters of the spin probe in the polymer were found to be gxx=2.0096, gyy=2.0061, gzz=2.0022, Axx=18.8 mHz, Ayy=20.5 mHz, Azz=93.78 mHz and central field B0=0.3356 T. Thus, κ1= κ3 = 5.54·10-10 G/s, κ2=6.34·10-10 G/s, κ4=5.17·10-10 G/s.

References

  1. Rånby, B.; Rabek, J.F. “ESR Spectroscopy in Polymer Research” Berlin Heidelberg New York,Springer-Verlag; Springer-Verlag Berlin Heidelberg: New York, 1977; Vol. 1, ISBN 9783642666025. [Google Scholar]
  2. Naveed, K.-R.; Wang, L.; Yu, H.; Ullah, R.S.; Haroon, M.; Fahad, S.; Li, J.; Elshaarani, T.; Khan, R.U.; Nazir, A. Recent Progress in the Electron Paramagnetic Resonance Study of Polymers. Polym. Chem. 2018, 9, 3306–3335. [Google Scholar] [CrossRef]
  3. Veksli, Z. ESR Spectroscopy for the Study of Polymer Heterogeneity. Prog. Polym. Sci. 2000, 25, 949–986. [Google Scholar] [CrossRef]
  4. Schlick, S. Advanced ESR Methods in Polymer Research; SCHLICK, S., Ed.; John Wiley & Sons, Inc. Publication:: Hoboken, NJ, USA, 2006; ISBN 0471731897. [Google Scholar]
  5. Švajdlenková, H.; Račko, D.; Bartoš, J. Spin Probe Reorientation and Its Connections with Free Volume and Relaxation Dynamics: Diglycidyl-Ether of Bis-Phenol A. J. Non. Cryst. Solids 2008, 354, 1855–1861. [Google Scholar] [CrossRef]
  6. Kivelson, D. Theory of ESR Linewidths of Free Radicals. J. Chem. Phys. 1960, 33, 1094–1106. [Google Scholar] [CrossRef]
  7. Schreier, S.; Polnaszek, C.F.; Smith, I.C.P. Spin Labels in Membranes Problems in Practice. Biochim. Biophys. Acta - Rev. Biomembr. 1978, 515, 395–436. [Google Scholar] [CrossRef] [PubMed]
  8. Santangelo, M.G.; Levantino, M.; Cupane, A.; Jeschke, G. Solvation of a Probe Molecule by Fluid Supercooled Water in a Hydrogel at 200 K. J. Phys. Chem. B 2008, 112, 15546–15553. [Google Scholar] [CrossRef] [PubMed]
  9. Stoll, S.; Schweiger, A. EasySpin, a Comprehensive Software Package for Spectral Simulation and Analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef] [PubMed]
  10. Budil, D.E.; Lee, S.; Saxena, S.; Freed, J.H. Nonlinear-Least-Squares Analysis of Slow-Motion EPR Spectra in One and Two Dimensions Using a Modified Levenberg–Marquardt Algorithm. J. Magn. Reson. Ser. A 1996, 120, 155–189. [Google Scholar] [CrossRef]
  11. Faetti, M.; Giordano, M.; Leporini, D.; Pardi, L. Scaling Analysis and Distribution of the Rotational Correlation Times of a Tracer in Rubbery and Glassy Poly(Vinyl Acetate): An Electron Spin Resonance Investigation. Macromolecules 1999, 32, 1876–1882. [Google Scholar] [CrossRef]
  12. Bercu, V.; Martinelli, M.; Massa, C.A.; Pardi, L.A.; Leporini, D. Signatures of the Fast Dynamics in Glassy Polystyrene: First Evidence by High-Field Electron Paramagnetic Resonance of Molecular Guests. J. Chem. Phys. 2005, 123. [Google Scholar] [CrossRef] [PubMed]
  13. Chernova, D.A.; Vorobiev, A.K. Molecular Mobility of Nitroxide Spin Probes in Glassy Polymers: Models of the Complex Motion of Spin Probes. J. Appl. Polym. Sci. 2011, 121, 102–110. [Google Scholar] [CrossRef]
  14. Dubinskii, A.A.; Maresch, G.G.; Spiess, H.-W. Two-Dimensional Electron Paramagnetic Resonance Spectroscopy of Nitroxides: Elucidation of Restricted Molecular Motions in Glassy Solids. J. Chem. Phys. 1994, 100, 2437–2448. [Google Scholar] [CrossRef]
  15. Saalmueller, J.W.; Long, H.W.; Volkmer, T.; Wiesner, U.; Maresch, G.G.; Spiess, H.W. Characterization of the Motion of Spin Probes and Spin Labels in Amorphous Polymers with Two-Dimensional Field-Step ELDOR. J. Polym. Sci. Part B Polym. Phys. 1996, 34, 1093–1104. [Google Scholar] [CrossRef]
  16. Yankova, T.S.; Chumakova, N.A.; Nedorezova, P.M.; Palaznik, O.M.; Kokorin, A.I. Behavior of Spin Probe TEMPO in Composites Based on Polypropylene with Different Content of Single-Wall Carbon Nanotubes. Polym. Sci. Ser. A 2024. [Google Scholar] [CrossRef]
  17. Neese, F. The ORCA Program System. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
  18. Vorobiev, A.K.; Chumakova, N.A. Simulation of Rigid-Limit and Slow-Motion EPR Spectra for Extraction of Quantitative Dynamic and Orientational Information. 2012. In Nitroxides–Theory, Experiment and Applications; InTech: Rijeka, Croatia, 2012; pp. 57–112. [Google Scholar]
  19. Vorobiev, A.K.; Bogdanov, A. V.; Yankova, T.S.; Chumakova, N.A. Spin Probe Determination of Molecular Orientation Distribution and Rotational Mobility in Liquid Crystals: Model-Free Approach. J. Phys. Chem. B 2019, 123, 5875–5891. [Google Scholar] [CrossRef] [PubMed]
  20. Chernova, D.A.; Vorobiev, A.K. Molecular Mobility of Nitroxide Spin Probes in Glassy Polymers. Quasi-libration Model. J. Polym. Sci. Part B Polym. Phys. 2009, 47, 107–120. [Google Scholar] [CrossRef]
  21. Kh. Vorobiev, A.; Gurman, V.S.; Klimenko, T.A. Rotational Mobility of Guest Molecules Studied by Method of Oriented Spin Probe. Phys. Chem. Chem. Phys. 2000, 2, 379–385. [Google Scholar] [CrossRef]
  22. Švajdlenková, H.; Šauša, O.; Adichtchev, S. V.; Surovtsev, N. V.; Novikov, V.N.; Bartoš, J. On the Mutual Relationships between Molecular Probe Mobility and Free Volume and Polymer Dynamics in Organic Glass Formers: Cis-1,4-Poly(Isoprene). Polymers (Basel). 2021, 13, 294. [Google Scholar] [CrossRef] [PubMed]
  23. Vasserman, A.M.; Barashkova, I.I.; Yasina, L.L.; Pupov, V.S. Rotary and Progressive Diffusion of the Nitroxyl Radical in Amorphous Polymers. Polym. Sci. U.S.S.R. 1977, 19, 2389–2398. [Google Scholar] [CrossRef]
Preprints 112711 g001
Figure 1. Structure (a) and optimized geometry (b) of TEMPO spin probe.
Figure 1. Structure (a) and optimized geometry (b) of TEMPO spin probe.
Preprints 112711 g001
Preprints 112711 g001
Figure 2. EPR spectrum of TEMPO in PP recorded at 100K (black line) and the result of its simulation (red circles).
Figure 2. EPR spectrum of TEMPO in PP recorded at 100K (black line) and the result of its simulation (red circles).
Preprints 112711 g001
Preprints 112711 g002
Figure 3. EPR spectra of TEMPO in PP (black lines) and the results of their simulation (red lines).
Figure 3. EPR spectra of TEMPO in PP (black lines) and the results of their simulation (red lines).
Preprints 112711 g002
Preprints 112711 g003
Figure 4. Temperature dependences of averaged rotational correlation time <τc> = (τx + τy + τz)/3 obtained by EPR spectra simulation (black asterisks) and rotational correlation times τc(1) (red squares), τc(2) (blue circles), τc(3) (open green squares), and τc(4) (open magenta circles) calculated by formulas (2), (3), (4) and (5), correspondently.
Figure 4. Temperature dependences of averaged rotational correlation time <τc> = (τx + τy + τz)/3 obtained by EPR spectra simulation (black asterisks) and rotational correlation times τc(1) (red squares), τc(2) (blue circles), τc(3) (open green squares), and τc(4) (open magenta circles) calculated by formulas (2), (3), (4) and (5), correspondently.
Preprints 112711 g003
Preprints 112711 g004
Figure 5. Differences between values of <τc> calculated via spectral simulation and τc*(1) (red squares), τc*(2) (blue circles), τc*(3) (open green squares), and τc*(4) (open magenta circles) via <τc>.
Figure 5. Differences between values of <τc> calculated via spectral simulation and τc*(1) (red squares), τc*(2) (blue circles), τc*(3) (open green squares), and τc*(4) (open magenta circles) via <τc>.
Preprints 112711 g004
Table 1. Rotational characteristics of TEMPO in PP.
Table 1. Rotational characteristics of TEMPO in PP.
T,K τx
(s)		 τy
(s)		 τz
(s)		 <τc>
(s)		 <σ> Libr
 τc*(1)
(s)		 τc*(2)
(s)		 τc*(3)
(s)		 τc*(4)
(s)
435 2.5·10-11 2.5·10-11 0.70# − 2.58·10-11 2.20·10-11 2.55·10-11 2.41·10-11
425 3.3·10-11 3.3·10-11 0.70# − 3.24·10-11 5.72·10-11 3.32·10-11 4.40·10-11
415 4.25·10-9 1.53·10-11 2.09·10-10 4.26·10-11 0.70# − 4.29·10-11 1.31·10-10 4.21·10-11 8.41·10-11
405 7.15·10-8 2.02·10-11 3.58·10-10 5.74·10-11 0.70# − 6.31·10-11 2.34·10-10 6.10·10-11 1.43·10-10
395 1.67·10-7 3.09·10-11 5.31·10-10 8.76·10-11 0.70# − 7.05·10-11 3.54·10-10 6.72·10-11 2.03·10-10
385 1.7·10-7 # 4.68·10-11 7.72·10-10 1.32·10-10 0.70# − 9.43·10-11 5.00·10-10 8.45·10-11 2.84·10-10
375 1.7·10-7 # 5.65·10-11 1.24·10-9 1.62·10-10 0.70# − 1.23·10-10 6.66·10-10 1.13·10-10 3.77·10-10
365 1.7·10-7 # 7.31·10-11 1.59·10-9 2.10·10-10 0.70# − 1.56·10-10 9.10·10-10 1.37·10-10 5.08·10-10
355 1.7·10-7 # 1.08·10-10 2.03·10-9 3.08·10-10 0.70# − 2.24·10-10 1.25·10-9 1.92·10-10 7.05·10-10
345 1.7·10-7 # 2.43·10-10 4.31·10-9 6.88·10-10 0.70# 27° 3.58·10-10 1.84·10-9 3.09·10-10 1.05·10-9
335 1.7·10-7 # 3.92·10-10 6.41·10-9 1.11·10-9 0.70# 28° 5.23·10-10 2.53·10-10 5.05·10-10 1.46·10-10
325 1.7·10-7 # 5.46·10-10 7.47·10-9 1.52·10-9 0.70# 25° 7.76·10-10 3.26·10-10 8.25·10-10 1.94·10-10
315 1.7·10-7 # 5.44·10-10 9.06·10-9 2.05·10-9 0.70# 25° 1.01·10-9 3.97·10-9 1.06·10-9 2.39·10-9
305 1.7·10-7 # 8.68·10-10 9.86·10-9 2.38·10-9 0.70# 21° 1.14·10-9 4.45·10-9 1.28·10-9 2.69·10-9
295 1.7·10-7 # 9.80·10-10 9.98·10-9 2.66·10-9 0.70# 19° 1.29·10-9 4.78·10-9 1.52·10-9 2.92·10-9
285 1.7·10-7 # 1.03·10-9 1.03·10-8 2.79·10-9 0.70# 20° 1.44·10-9 5.02·10-9 1.68·10-9 3.11·10-9
275 1.7·10-7 # 1.16·10-9 1.05·10-8 3.11·10-9 0.70# 17° 1.56·10-9 5.47·10-9 1.82·10-9 3.39·10-9
265 1.7·10-7 # 1.39·10-9 1.05·10-8 3.65·10-9 0.70# 15° 1.81·10-9 5.92·10-9 2.21·10-9 3.73·10-9
255 1.7·10-7 # 1.54·10-9 1.02·10-8 3.99·10-9 0.70# 10° 2.30·10-9 6.66·10-9 2.86·10-9 4.34·10-9
245 1.7·10-7 # 1.69·10-9 1.09·10-8 4.35·10-9 0.70# <1° 2.78·10-9 7.34·10-9 3.56·10-9 4.91·10-9
235 1.7·10-7 # 2.44·10-9 8.55·10-9 5.63·10-9 0.89 − 3.48·10-9 8.22·10-9 4.61·10-9 5.70·10-9
225 1.7·10-7 # 2.91·10-9 8.05·10-9 6.33·10-9 0.86 − 5.17·10-9 1.01·10-8 7.24·10-9 7.50·10-9
215 1.7·10-7 # 3.59·10-9 9.47·10-9 7.69·10-9 0.88 − 5.66·10-9 1.07·10-8 8.54·10-8 8.02·10-9
207 1.7·10-7 # 4.79·10-9 1.08·10-8 9.75·10-9 0.91 − 6.45·10-9 1.14·10-8 1.02·10-8 8.80·10-9
198 1.7·10-7 # 6.24·10-9 1.30·10-8 1.23·10-8 0.94 − 7.76·10-9 1.29·10-8 1.38·10-8 1.02·10-8
188 1.7·10-7 # 8.77·10-9 1.53·10-8 1.62·10-8 0.93 − 6.94·10-9 1.16·10-8 1.39·10-8 9.17·10-9
179 1.7·10-7 # 1.20·10-8 1.67·10-8 2.01·10-8 0.92 − 6.13·10-9 1.06·10-8 1.19·10-8 8.23·10-9
170 1.7·10-7 # 1.71·10-8 1.77·10-8 2.48·10-8 0.90 − 6.52·10-9 1.09·10-8 1.28·10-8 8.59·10-9
τxx, τyy, and τzz are rotational τx, τy, and τz are rotational correlation times corresponding to molecular axes of TEMPO X, Y, and Z (see Figure S2); <τc> is averaged rotational correlation time <τc> = (τx + τy + τz)/3; τc*(1), τc*(2), τc*(3), and τc*(4) are rotational correlation times calculated by empirical formulas (2), (3), (4), and (5); <σ> is width of the lognormal distribution of the rotational diffusion coefficient; Libr is the amplitude of quasilibrations [20].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated