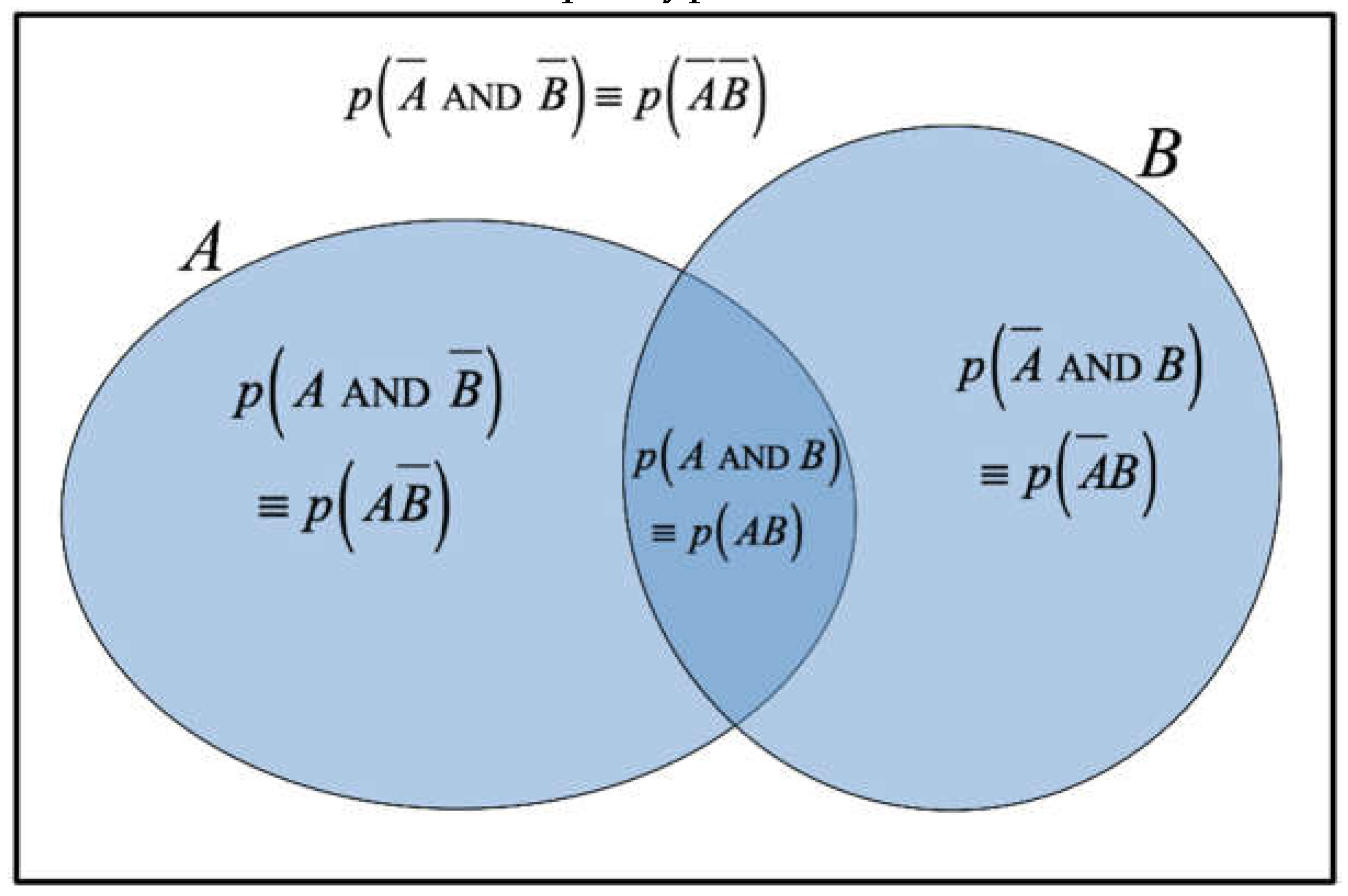
1.1. Probability in Science
Probability has always been extraordinarily difficult to tie down. Edwin Jaynes made fundamental contributions to the subject, and in his magisterial monograph (published posthumously: “
Probability Theory: The Logic of Science”[
1]) spends two chapters on its principles and elementary applications, commenting on its ‘weird’ and ‘complicated’ history. Indeed, Jaynes’ motivation was aimed at helping the interested reader who already has “
a previous acquaintance with probability and statistics” to essentially “
unlearn” much of what they may have previously learned!
The ubiquity (and longevity) of fallacies in the use of statistics indicates its difficulty (on the misuse of the “p-value” see for example Goodman 2008[
2] and Halsey 2019[
3]; on the persistence of fallacies see Smaldino & McElreath 2016[
4]). A significant part of the problem may be related to the fact that the “probability” of an event is apparently not a property solely of “external reality”: since there must be
someone assessing the probability, it must be a function of not only
what information already exists about the event but also
who knows. The fact that our estimates of the probability of some event invariably involve our prior knowledge, combined with the fact that all knowledge ultimately involves the properties of recursive statements (by Gödel’s Theorem[
5]; this point has recently been elaborated by Jeynes
et al. [
6]) mean that some part of this difficulty must be due to the neglecting, in current (simplified) treatments, of recursive dependencies (such as the “Chicken and Egg” problem, on which see §2.3 below).
In 1946 R.T.Cox observed, acutely, that the concept of
probability mixes two separate concepts (“
the idea of frequency in an ensemble and the idea of reasonable expectation”[
7]) which are now represented by two schools usually called the “frequentists” and the “Bayesians”. We point out that Enßlin
et al. [
8] comment that, “
The different views on probabilities of frequentists and Bayesians are addressed by … Allen Caldwell[
9]
[who] builds a bridge between these antagonistic camps by explaining frequentists’ constructions in a Bayesian language”, and we will assume that Caldwell is right and therefore that we can ignore the philosophical distinction between the frequentists and the Bayesians.
Building on Cox’s fundamental work we will here derive a rigorous treatment of recursive probability which is of general applicability. In particular, we will treat probability as a
physical quantity grounded in hyperbolic Minkowski spacetime, and obeying all the appropriate physical laws. The close relation of probability to the new Quantitative Geometrical Thermodynamics[
10] (
QGT: this constructs the quantity
info-entropy by treating
information and
entropy as Hodge duals) is due to the fact that the (hyperbolic)
entropic velocity q′≡d
q/d
x in QGT is dimensionless and has properties akin to a probability (0≤
q′≤1); noting that
q′ is isomorphic to the more familiar kinematic velocity
ẋ ≡ d
x/d
t (0≤
ẋ ≤
c, where
c is the speed of light) in hyperbolic (Minkowski) spacetime (see ref.[
10]), and which also obeys the well-known velocity addition theorem of Special Relativity.
The treatment of probability as a
physical quantity (and obeying
physical laws) is as fundamental a concept as the well-known statement by Rolf Landauer that “
Information is Physical”[
11].
We are used to treating both
probability and
information anthropomorphically (that is, depending on what you or I might be expected to know): here we will establish an impersonal sense for
probability, in the same way that Landauer insisted on the (impersonal)
Shannon entropy sense of his
Information. Note that each of information and entropy both use and require probabilistic quantities in their fundamental definitions; and also note that the consequences of treating
information as being a quantity as physical as is
energy (for example) has led to important insights, and not only into basic engineering problems of the global internet (for an example of which see Parker
et al. 2015[
12]). We expect similar advances to follow from recognising
probability as also being an equally physical quantity.
The relationship between probability and the quantification of information using the Shannon entropy is well understood mathematically, but its interpretation as a physical theory has been convoluted. Although the Shannon entropy was quickly recognised as important, Edwin Jaynes’ formulation of Maximum Entropy (
MaxEnt) theory, where the Shannon metric plays a key role, was initially controversial and took some decades to achieve acceptance (see Jaynes’ 1978 summary[
13]). However, MaxEnt as a powerful scientific and engineering tool has helped considerably to underpin the physicality of
information, and therefore also acts as a support to the underlying assertion of this paper (paraphrasing Landauer) that “
Probability is Physical”. We will also explore the implications of this assertion.
Since the concept of MaxEnt will be centrally important in this work, it is worth adding Jaynes’ authoritative definition (1982)[
14]: “
The MaxEnt principle, stated most briefly, is: when we make inferences based on incomplete information, we should draw them from that probability distribution that has the maximum entropy permitted by the information we do have”.
1.2. Probability is Physical
Torsten Enßlin’s treatment[
15] of information as a field is interesting in this context: he considers that a “physical field has an infinite number of degrees of freedom since it has a field value at each location of a continuous space” where he is specifically considering imaging problems of astrophysical datasets. Enßlin et al. [ref.8] treat information informally as an anthropomorphic concept: to the question, “What is information?” they answer “Anything that changes our minds and states of thinking!” But here we will treat information (and probability) as physical quantities, not as anthropomorphic concepts; and especially noting that infinite quantities are inimical to physical phenomena. In particular, in our QGT treatment, information is formally defined as a physical quantity (albeit in terms making full use of the properties of analytical continuation, which is itself closely related to fundamental physical precepts such as causality[
16] and square-integrability ensuring finite physical quantities[
17]), so that the number of degrees of freedom are finite and may be very small, as is observed for the geometrical entropy of isotopes of the helium nucleus[
18]. Such results for information were already pointed out by Parker & Walker (2004)[
19] who investigated the residues of a meromorphic function (that is, a function analytic nearly everywhere) due to the presence of isolated singularities in the complex plane (singularities which are entirely analogous to particles in their behaviour); and show that the information (entropy) of such a function is simply given by the sum of the residues.
This is immediately applicable to the Schrödinger equation: it is interesting that we will conclude (Eq.7) that the appropriate
Sum Rule for recursive probabilities has a
hyperbolic form, and we will draw out the relation of this to the (hyperbolic)
entropic velocities in the QGT formalism[
20], in which the
entropic Uncertainty Principle and
entropic isomorphs of the Schrödinger equation may be derived from the
entropic Liouville Theorem; all based on the Boltzmann constant as the relevant quantum of entropy. Of course, QGT is constructed in a hyperbolic (complex) Minkowski 4-space (see §18.4 in Roger Penrose’s “
Road to Reality”[
21]; as another pertinent example, Maxwell’s electro-magnetic field is a hyperbolic version of the Cauchy-Riemann Equations: see Courant & Hilbert[
22] vol.II ch.III §2 Eq.8
passim).
The ramifications of this are very wide. Parker & Jeynes [ref.10] have already shown the relevance of QGT to the stability and structure of spiral galaxies (using the properties of black holes), and also that
entropy production (d
S/d
t) is conserved even in relativistic Maximum Entropy systems[
23]. These issues up to now have been treated as problems in quantum gravity, and Matt Visser[
24] very helpfully reviews conservative entropic forces (in Euclidean space and non-relativistically, although he comments that representing general relativity entropically should be possible). Note also that Visser suggests that the negative entropies that appear in his treatment can be regarded as
information, citing Brillouin’s idea of “negentropy” which Parker & Jeynes [ref.10] have shown to be a subtle misapprehension of information and entropy (which are actually Hodge duals).
We believe that much progress may be made by using the coherent formalism of QGT (defined in hyperbolic space) which has been shown to apply to both quantum mechanical and gravitational systems (that is, at all scales from sub-atomic to cosmic: see [refs.18,10]), and since quantum mechanics is built on probabilities, the demonstration here that the general recursive sum rule for probabilities is hyperbolic is a significant conceptual regularisation. This conclusion is reinforced by Knuth’s demonstration[
25] that: “
The sum and product rules, which are familiar from, but not unique to, probability theory, arise from the fact that logical statements form a distributive (Boolean) lattice, which exhibits the requisite symmetries”. Moreover, Jaeger[
26] reviews a variety of treatments, some of which involve theories of generalized probability, aimed at deriving quantum mechanics from information theory.
The basic isomorphism for the hyperbolic sum rule for probabilities (that we will prove, see Eq.7) is the (purely mathematical) double-angle identity for the hyperbolic tangent function:
Another interesting and very simple isomorphism is the well-known relativistic sum rule for velocities {
u,
v}, given by Jackson[
27] in his well-known textbook (in the context of a discussion of aberration and the Fizeau experiment; §11.4, Eq.11.28):
where
c is the speed of light. Jackson comments that if
u =
c then also
w =
c, which is an “
explicit statement of Einstein’s second postulate” (
c is a constant).
This latter (Eq.1b) is clearly physical (since
c is involved) where the former (Eq.1a) is a mathematical identity. Note also that in optics the basic formula for the two-layer Fabry-Perot cavity (etalon) is well-known[
28]:
where the overall scattering (reflectivity) coefficient
r3 is due to a pair of sequential Fresnel reflections (
r1,
r2) separated by a distance Δ
z for a light ray of propagation constant
k; and where we note that light is the physical phenomenon
par excellence exhibiting the physics of Special Relativity within the context of hyperbolic (Minkowski) spacetime. Corzine
et al.[
29] demonstrate that this formula is closely related to the hyperbolic addition rule (Eq.1a) specifically by using a hyperbolic tangent substitution which dramatically simplifies the use of the formula in real (multilayer) cases – see
Appendix F for additional and related discussion.
This approach has recently been supported in an interesting way by Skilling & Knuth[
30], who conclude: “
it must be acknowledged, quantum theory works. So does probability. And the two are entirely mutually consistent.” Their argument shows logical reasons why
probability should be regarded as
physical.
Skilling & Knuth claim not to be interested (for these purposes) in the distinction between ontology and epistemology. They say (ibid. §3.5):
The ontology–epistemology divide is, for quantitation at least, a distinction without a difference. A bit of information carries no flag to inform us whether it was assigned by a conscious agent or by a mechanical switch. Our job in science is to make sense of our observations, not to indulge in empty disputation between isomorphic views. Our goal here is derivation of a calculus fit for general purpose. Ontology and epistemology share the same symmetries, the same rules, and the same assignments. So they share a common calculus.
which is suggestive of Karen Barad’s (2007[
31]) insistence that the distinction between ontology and epistemology is not a real one, and therefore speaking strictly we should refer to “
onto-epistemology” (
ibid. p.43). Skilling & Knuth also say (
ibid. §1):
But, if our object can perturb a partner object, then by symmetry the partner object can also perturb our object. We could assign either role to either.
Our calculus, whatever it is, must be capable of representing such interactions … This insight that interactions are basic is the source of “quantum-ness.”
Again, this recalls Barad’s thesis that “the primary ontological unit is the phenomenon” (ibid. p.333). However, when Skilling & Knuth (ibid. §4) say, “We start with an identifiable object”, this is directly contradicted by Barad, who asserts that “objects” do not have “an inherent ontological separability” (ibid. p.340); that is, strictly speaking, identifiable objects do not actually exist per se (since everything is entangled with everything else). But Skilling & Knuth are not aiming at philosophical precision, only at a demonstrable computability; for these purposes such fine distinctions do not matter. They are right to avoid metaphysical considerations in scientific work: although when wider social implications are important it may be necessary to consider the metaphysics (see for example [ref.6]).
However, it turns out that the inescapable human dimension appears to be especially pronounced in
probability, in the sense that the very
idea of a probability entails one’s personal state of knowledge or ignorance (and Michael Polanyi insisted long ago that all knowledge is necessarily personal[
32]). Howson & Urbach[
33] have carefully explained why, although Bayesian (and Maximum Entropy) methods are fully (and helpfully) rational: “
there seems to be no way of ‘objectively’ defining prior probabilities … this is really no weakness [since] it allows expert opinion due weight, and is a candid admission of the personal element which is there in all scientific work”. Assessing probabilities necessarily entails assessing uncertainties, and this must always involve some value judgments: although we may do our best to speak rationally about such judgments, it cannot be excluded that different people will (rationally) come to different conclusions.
Note that although scientists have a duty to argue rationally, non-scientists also normally behave rationally. Rationality is a property of humans, and only a rather small subset of humans are scientists.
1.3. Maximum Entropy
It is necessary to make a few initial simple remarks about Maximum Entropy (
MaxEnt) methods, to clarify the discussion. Jaynes said in 1957[
34]: “
The guiding principle is that the probability distribution over microscopic states which has maximum entropy subject to whatever is known, provides the most unbiased representation of our knowledge of the state of the system. The maximum-entropy distribution is the broadest one compatible with the given information; it assigns positive weight to every possibility that is not ruled out by the initial data.” In our derivation here of the Hyperbolic Sum Rule we emphasise that the proper application of MaxEnt methods precludes the surreptitious introduction of tacit assumptions (“knowledge”). That is,
all the “priors” (prior knowledge that conditions the data) must be stated explicitly (and our ignorance implies that some priors must sometimes be estimated, which may involve personal value judgments).
A fully Bayesian analysis requires that all prior knowledge is explicitly stated, including the “knowledge” that there is no knowledge available, in which case an “unbiassed” estimate is required. This is usually stated in terms of the “Principle of Indifference” (
PI), but unfortunately there are a set of (“Bertrand”) paradoxes which appear to invalidate the PI. But Parker & Jeynes[
35] have resolved these paradoxes using QGT methods by supplying the missing prior information (in the form of the scale invariance condition).
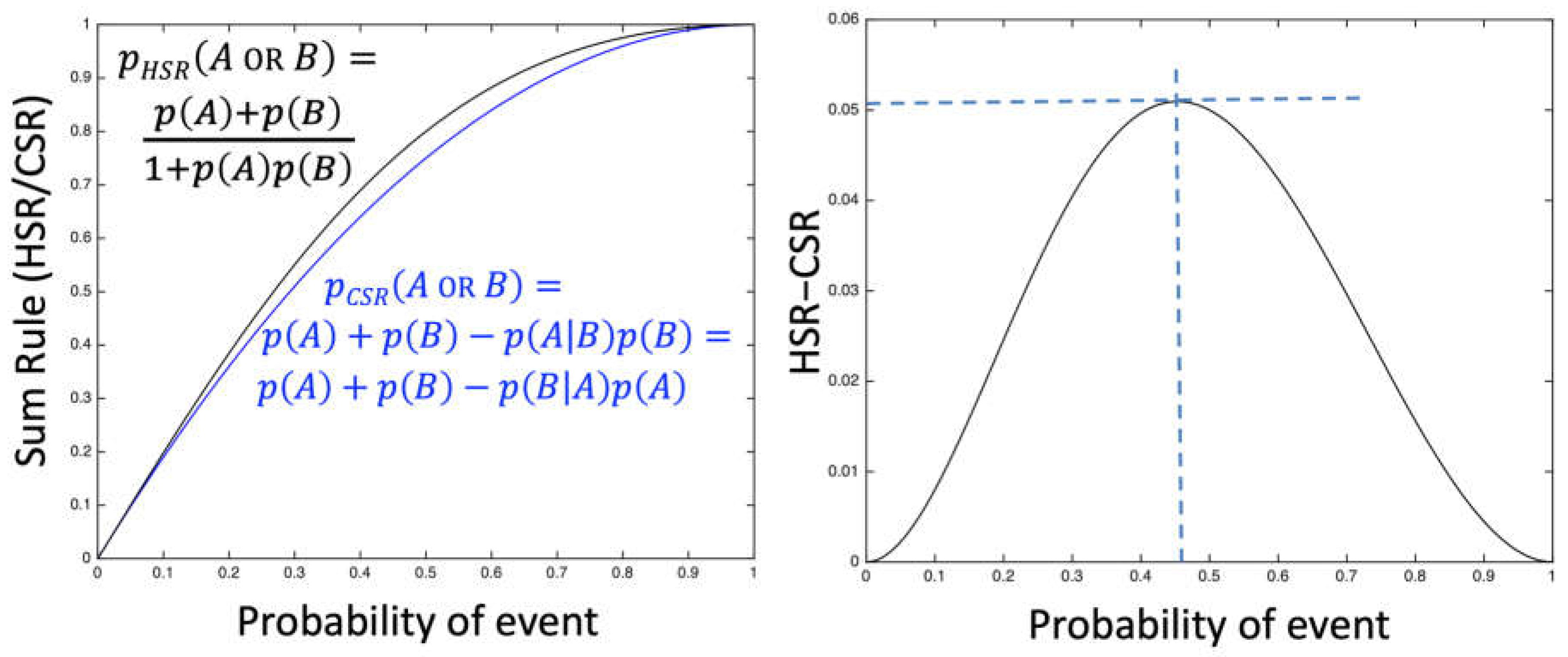
It is essential to handle the “priors” correctly: our Eq.6 below (which is for the recursive case) asserts a hyperbolic relation for the compound “p(A or B | C)” where in general A may depend both on prior conditions C, and also on B (that is, involving the probabilities of A|BC and B|AC). But if {A,B} are recursively dependent, then p(A|BC) simplifies to p(A|C) (because, for recursive {A,B}, p(A|B)= p(A) since B is ultimately dependent on A; and similarly, p(B|A)= p(B) since A is ultimately dependent on B) giving the general relation describing the “Hyperbolic Sum Rule”, HSR (Eq.7).
In the
Appendices we explore the Maximum Entropy (MaxEnt) properties of the HSR, including a proof that it really is MaxEnt. We first show how to impose the MaxEnt criterion (
Appendix A) using the Partition Function description, and then show (
Appendix B) how other simple sum rules may be “MaxEnt” but are otherwise inadmissible. We prove explicitly that the HSR is MaxEnt (
Appendix C) and also generalise it for multiple recursive hypotheses (
Appendix D). We show that the Conventional Sum Rule (
CSR) is also MaxEnt (
Appendix E) within its own domain of applicability, and we also generalise the CSR for multiple hypotheses. Both are MaxEnt, that is, neither the HSR nor the CSR ‘smuggle’ in inadvertent or implicit assumptions within their specified contexts; yet, the HSR encompasses a wider domain of physical application that includes recursion between phenomena, whereas the CSR
a priori excludes recursion (although there may still be various mutual dependencies). The HSR must also be used where the properties of the recursion are unknown; that is to say, a set of phenomena are known to be correlated, but the mechanism (or ordering) of causation is not known.
Finally in
Appendix F, we show the immediate relevance of this treatment to digital signal processing; in particular the handling of “infinite impulse response” and “finite impulse response” filters.
It is important here to point out that the fact that an entity is Maximum Entropy does not mean that the entity has no structure (even though MaxEnt necessarily implies “maximum ignorance”). The reality is more nuanced. For example, we have shown that, at a certain scale, the alpha particle is a (MaxEnt) unitary entity (than which exists no simpler) [ref.18]. But of course, at a different scale we may see the alpha’s constituent four nucleons (protons and neutrons).
Also, being MaxEnt does not preclude change: for example, free neutrons decay (with a half-life calculated
ab initio from QGT by Parker & Jeynes 2023[
36]). The most extreme known entity that is MaxEnt is the black hole, and black holes necessarily grow (proved by Parker & Jeynes in 2021 [ref.23] and confirmed in 2023[
37]). Nor does the fact that some entities are unconditionally stable mean that the Second Law doesn’t apply to them. On the contrary! The matter radius of the alpha is correctly calculated
ab initio from QGT [ref.18].
The physical principle of Maximum Entropy embodies the (physical) Second Law of Thermodynamics. Both the CSR and the HSR are MaxEnt, and therefore each also embodies important aspects of the Second Law. Moreover, the probabilities calculated by either Rule (each with its own particular domain of applicability) refer to the probability either of the events themselves or of our reasonable expectations; these are both physical things since both we and they are physical. Either way, our conclusion is underlined that Probability is Physical.