Prerpints.org logo
Preprint
Article

A Regularized Tree Forest for Classification in the Presence of Extreme Class Imbalance

Altmetrics

Downloads

75

Views

32

Comments

0

supplementary.pdf (522.57KB )

This version is not peer-reviewed

Submitted:

19 July 2024

Posted:

22 July 2024

You are already at the latest version

Alerts
Abstract
Machine-learning methods used for classification are challenged by the class imbalance problem, where a certain class is underrepresented. Over/under-sampling the majority/minority class observations or model selection for ensemble methods alone might not be effective if the class imbalance ratio is very high. To address this concern, a novel method is presented for generating synthetic data for minority class observations in conjunction with an optimal tree ensemble classifier (OTEC). This novel synthetic method first generates minority class instances to balance the training data. Then it applies OTEC, where models are selected based on their performance using out-of-bag observations and training subsamples. A total of 20 benchmark problems on binary classification with moderate to extreme class imbalance are used to assess the efficacy of the proposed method against other well-known methods, including optimal tree ensemble, smote random forest, under-sampling random forest, oversampling random forest, k-nearest-neighbor, support vector machine, tree, and artificial neural network, using classification error rate, sensitivity, specificity, precision, recall and F1-score as performance metrics to assess the efficacy of the proposed method. The analyses presented in this study revealed that the proposed method based on data balancing and model selection yielded better results than other methods.
Keywords: 
Subject: Computer Science and Mathematics  -   Probability and Statistics

MSC:  68U01; 62P10; 62P20

1. Introduction

One of the most challenging issues when using a machine-learning method for binary classification is the uneven distribution of classes in the given training data. This problem is referred to as the class imbalance problem [1,2,3,4]. Several studies have been conducted on the issue of class imbalance [5,6,7,8]. Class imbalance problems can be addressed at four levels associated with various learning phases. To this end, ensemble learning, feature selection at the feature level, internal classifier modification at the classifier level, and resampling methods that change the class distributions can be used to tackle the issue. Among the resampling methods, random under-and oversampling is a non-heuristic method [9]. Under-and oversampling techniques are likely to improve learner generalization when datasets are significantly skewed [10,11,12]. Random under-sampling aims to balance the class distributions by randomly removing samples from the majority class. However, under-sampling can result in information loss and poor model performance.
By contrast, random oversampling attempts to equalize class distributions by randomly replicating minority class instances. Two problems arise from random oversampling. It first increases the likelihood of over-fitting because it perfectly replicates the minority class samples [13], and the second generation of a minority class can significantly increase the data size, resulting in a prolonged training time and high computational requirements. The synthetic minority oversampling technique (SMOTE) [14] provides more minority instances, which helps the machine-learning model learn more efficiently and assists in tackling the issue of class imbalance. However, certain disadvantages of SMOTE include its noise sensitivity and dependence on its nearest neighbor. An advanced sampling technique, boosting, was applied to mitigate this issue. Boosting focuses on the incorrectly classified instances. Boosting significantly affects the distribution of the training data. Other methods for finding training data close to the optimal value include heuristic, budget-sensitive, and progressive sampling methods [15,16]. OSPC, an oversampling technique based on preliminary classification, performs better in minority/majority class classification than SMOTE and under-sampling methods.
The goal of each of the aforementioned methods for changing class distributions is to address the issue of between-class imbalance. A cluster-based oversampling method was proposed [17] to simultaneously improve the accuracy of minority classes and address the issues of both within- and between-class imbalances. Both oversampling and under-sampling can be addressed using approaches, such as SMOTE, paired with the Tomek link and ENN [18] when there are only a few samples of the minority class or when the datasets are significantly skewed. Most machine-learning methods rarely yield satisfactory results in real-world applications with class imbalance problems. The key causes of the poor performance of the classifier on imbalanced datasets are accuracy, class distribution, and error costs. Numerous approaches have been proposed to solve these problems and to improve the efficiency of binary classification models [19].
Several other dedicated research endeavors have been conducted to address the class imbalance problem. The authors in [20] have provided a thorough comparison of several existing remedies for mitigating this problem. While most typical learning algorithms can achieve high global accuracy by correctly classifying majority class observations, improving the minority class accuracy remains a significant challenge [21]. To this end, the authors in [22] proposed the idea of a k-fold division of the majority class to generate a pool of classifiers that divides an imbalanced problem into numerous balanced ones, while guaranteeing that all available samples are used in the training process. In the context of ensemble learning, the model performance is significantly associated with the performance of the base classifier, weight computation method, and selection strategy when dealing with class-imbalanced datasets. This notion has led to the development of several ensemble learning methods. For example, the algorithm given in [23], which employs under-sampling of the majority class for classifying imbalanced datasets, has been proposed. Similar methods can be found in the literature that address the issue of class imbalances in binary classification problems. These techniques primarily exploit the idea of under-sampling the majority class observations or oversampling the majority class observations. Both these ideas have certain limitations, and the consequent machine-learning method may still fail to achieve the desired classification performance.
A binary classification model must perform well for both classes to achieve the desired classification performance. In certain situations, when there are insufficient instances in one or both classes, machine-learning algorithms [24] may find it challenging to identify patterns in the data and correctly classify minority class samples because of this imbalance. To address this issue, researchers developed learning algorithms to process and extract information from data with significantly skewed distributions. Specifically, instead of ignoring minority classes in the data, an imbalanced learning technique allows the prediction algorithm to predict the outcome variables with a more realistic level of accuracy. The model was trained to distinguish between instances belonging to two separate classes. Nevertheless, several factors can significantly affect the performance of a binary classification model, including class noise, class imbalance, and insufficient data.
Several tree-based methods have been modified to address class imbalance problems. However, little attention has been paid to simultaneously balancing data and selecting optimal base models for the final tree ensemble. In constructing an efficient ensemble, accuracy, and diversity are the main features that significantly regulate the overall performance of the final model. In the case of random forest, Breiman provided an upper bound for the overall prediction error as a function of the accuracy and diversity of the base tree models: i.e.
ε = ρ ^ ϵ t
where ε is the total prediction error of the forest, ϵ t is the estimate of any t tree in the forest, and ρ ^ is the weighted correlation between the residuals from two independent classification trees expressed as the mean correlation over the entire random forest. Therefore, developing a tree ensemble [25,26,27] that ensures the accuracy and diversity of the base model is believed to yield promising results. In the presence of class-imbalanced problems, allowing the ensemble to learn from balanced data leads to further improvements. Therefore, this study proposes an ensemble method that uses the above concepts to learn effectively from datasets with class-imbalanced problems.
To build an efficient tree ensemble, this study first balanced the given training data by generating new synthetic observations for the minority class. Consequently, datasets with extreme class imbalances were considered in this study. These data sets were obtained from several publicly available sources. Once the dataset was balanced, classification trees were grown on bootstrap/subsamples from the data. The training prediction accuracy of each tree was estimated, and the top-performing trees were selected for the final ensemble. Based on the above notion, this study attempted to increase the accuracy of individual tree models in forests, in addition to randomizing their construction. The accuracy was increased by balancing the given training data with the model selection based on individual prediction performance.
The remainder of this article is organized as follows. The proposed methods are given in Section 2, and the experiments and results are described in Section 3. Section 4 presents the simulations, which include both of the simulated scenarios for the proposed method. The final section concludes by summarizing the main findings and providing suggestions for future work.

2. Materials and Methods

2.1. Balancing the Training Data

Let Υ= (X, Y) be the given data; X is an n × p matrix, that is, X = [ x i × j ] n × p where i = 1,2 , 3 , . . . , n , and j = 1,2 , 3 , . . . p , and Y are two-class vectors, that is, Y ϵ (0,1) of length n. y i are the values of the binary response variable with a value 1for one class and a value 0 for the other class; that is,
y i = 1 ,   i f   n = n 1 0 ,   i f   n = n 0 ,   i = 1,2 , 3 , . . . , n .
Out of the total n sample points, there were n 1 majority and n 0 minority class observations, with a severely skewed class distribution, i.e., i.e., n 1 ≫ n 0 . The following procedures were considered to balance the training data before building the tree ensembles. The given dataset Υ was balanced by selecting K b = n 1 − n 0 bootstrap samples each of size, i.e. n 0 , equal to the number of observations in the minority class, from the minority class observations. Let the sample be X v , where v = 1, 2, …, K b . Each bootstrap sample had n 0 observations of p features. Each bootstrap sample was used to generate an additional row in the data by estimating the mean u ¯ of each column if it was numeric and mode u ~ if it was categorical. Let there be p 1 continuous features and p 2 categorical features in the bootstrap samples; calculating the means and modes of the features gives a vector of p = p 1 + p 2 observations, that is,
X n e w r = ( u ¯ 1 ,   u ¯ 2 , . . . , u ¯ p 1 , u ~ 1 , u ~ 2 , … ,   u ~ p 2 ,
where r = 1, 2, …,p, and the elements in X n e w r are arranged according to the original order of the features in the bootstrap sample. The generated rows are arranged in the matrix, and the last column comprises the class labels of the minority class, that is,
Υ ´ = ( X ^ , Y = 0 ) n o × p ,
where, X ^ denotes a newly generated vector. The given training data was combined with the generated data Υ ´ to obtain balanced data, that is,
Υ ~ =   Υ   ∪ Υ ´ .
For each class, there were equal numbers of data points in Υ ~ . To grow optimal trees, the data Υ ~ was used instead of the original data Υ . Two methods are used to grow and select optimal trees ensemble using balanced data Υ ~ . The first method uses the corresponding out-of-bag (oob) observations to assess each tree individually. Trees were ranked based on how well they performed individually based on oob observations. The second method involved random subsets of training data for tree growth. In this study, balanced data, i.e., Υ ~ was used in conjunction with an ensemble method, i.e., optimal tree ensemble classifier using out-of-bag, i.e., OTEC (oob) and optimal tree ensemble classifier using sub-sample, i.e., OTEC (sub), on balanced data.

2.2. Out-of-Bag based Assessment with Balanced Data

The first proposed method, i.e., OTEC (oob) used out-of bag (oob) observations for trees grown on the balanced training data Υ ~ . Studies [28,29] have observed that samples during bootstrapping omit approximately 1/3 of the overall training data [30]. These observations play no role in model construction and can be used as independent validation data for model assessment. From the balanced data Υ ~ , we took T bootstrap samples, i.e., B τ , Υ ~ = 1,2,3, …,T , and let B ¯ τ be the corresponding value of oob observations from each sample. G( B τ ) represents the classification tree that was grown on B τ . It was further assumed that e r r o r ~ τ represented the oob error, which is the error of G( B τ ) on B ¯ τ , i.e.,
e r r o r ~ τ = 1 | B ¯ τ | ∑ x i ϵ B ¯ τ ϕ y ≠ y ~ ,
where, y is the true class label in the bootstrap sample, i.e., B ¯ τ , y ~ is the corresponding predicted value via classification tree G( B τ ), and | B ¯ τ | is the size of the oob sample. ϕ is an indicator function, expressed as:
ϕ ( y ≠ y ~ ) = 1 ,               i f   y ≠ y ~   2 ,   O t h e r w i s e .
G( B τ ), After growing the desired number of classification trees, they were arranged in ascending order of their error rates on the oob samples. Let the top-ranked, second-top-ranked, etc. trees be
G r 1 , G r 2 , … , G r Q
A number of trees from the above-ranked trees were selected for the final ensemble. The ensemble was then used to predict the new/test data. The number of trees grown and the number of trees selected were two potential hyper-parameters for this method.

2.3. Sub-Sample based Assessment with Balanced Data

The second proposed method, i.e., OTEC(sub) used sub-sample based method where trees were grown on sub-samples from the balanced data ( Υ ~ ). Unlike the oob observations, the remaining observations from each sample acted as test data for evaluating the predictive performance of each corresponding tree. Given that B τ , τ = 1,2,3, …, T be the random sample of size m < n. Additionally, let B ¯ τ represent the corresponding remaining subset of observations of size n - m. G( B τ ), where, τ =1,2, …,T, is the classification tree built on B τ . It is also assumed that the error of G( B τ ) on B ¯ τ is represented by e r r o r ~ s u b τ . On τ , τ = 1,2, …,T, for the T classification trees. was used to estimate e r r o r s u b ~ τ on each tree.
Let the top, second highest, and so on ranked trees be, that is,
G r 1 , G r 2 , … , G r Q
The remaining procedure was the same as that for OTEC(sub). This method might be useful in small-sample situations in which one wants to retain large amounts of training data to build trees. This method can also be tuned by selecting the optimal values for the initial number of trees grown and the number of trees selected for the final ensemble. The pseudo-code of the proposed ensemble is provided in Algorithm 1.
Preprints 112703 i001
This study considered extremely imbalanced classification datasets to assess the performance of the proposed method for benchmark problems. The efficacy of the proposed method, i.e., OTEC(oob) and OTEC(sub) in comparison with the state-of-the-art methods, i.e., optimal tree ensemble (OTE), random forest in conjunction with using synthetic minority over-sampling technique (RF(smote)), random forest combined with over-sampling method (RF(over)), under-sampling method coupled with random forest (RF(under)), support vector machine, k-nearest neighbor (k-NN), artificial neural network (ANN), and classification tree (Tree) was assessed using 20 benchmark datasets. The evaluation metrics considered were the classification error rate, sensitivity, specificity, precision, recall, and F1 score, which is a measure that combines precision and recall into a single value, providing a balanced assessment of a model’s performance. R programming software was used to perform the experiments.
Table 1 provides a concise summary of the datasets considered. The data name is displayed in the second column and the numbers of instances/observations (n) and features (p) are shown in the third and fourth columns, respectively. The fifth column provides the classwise distribution, the sixth column provides the imbalance ratio ( n 1 / n 0 ), and the final column contains the data source. Additional information on the remaining datasets is provided in Table S1. This section describes the experimental design of this study.
The proposed methods, OTEC(oob) and OTEC(sub), were applied to extremely imbalanced datasets, with 95% of the observations belonging to the majority class and 5% to the minority class. This indicates that the observations were made at a 19:1 ratio. This was performed by randomly discarding minority class observations in which the original data did not have an uneven ratio of 19:1. A total of 1,000 realizations were made from the resulting data, which were split into 90% training and 10% testing parts. Model fitting was performed on the training part of the data, and evaluation was performed on the testing part. To generate T = 1,000 classification trees, bootstrap samples from 90% of the training data were obtained using the OTEC(oob) and OTEC(sub) methods described in Algorithm 1. The testing part was used for external validation.
The final ensemble contained all of the top Q trees that were chosen. The final result was the average of all 1,000 runs. The training and testing parts were the same for all methods under consideration. The findings presented in Table 2 and Table 3, along with the box plots displayed in Figure 1, Figure 2, Figure 3 and Figure 4, show the results of the proposed method, that is, OTEC(oob) and OTEC(sub), in terms of the classification error rate and precision compared with the other methods. The results for the rest of the methods, that is, OTEC(oob) and OTEC(sub), in terms of sensitivity, specificity, recall, and F1 score, are given in Tables S2–S5 of Supplementary Materials. The plots are shown in Figures S1–S14 in Supplementary Materials. Table 2 shows the results of the proposed method’s classification error rate for the datasets with those of the other state-of-the-art methods. The OTEC(oob) results are shown in bold numbers, and the OTEC(sub) results are italicized. It is evident from the tables that the proposed methods, that is, OTEC(oob) and OTEC(sub), outperform all other procedures in terms of the classification error rate, having the lowest error rate compared to the other methods. The proposed methods, that is, OTEC(oob) and OTEC(sub), showed minimal classification error rates ranging from 0 to 0.0005. OTEC(sub) did not perform well in breast cancer, drug classification, glass classification, or KDD. By contrast, RF (smote) yielded a low error rate on the glass classification dataset. The RF(under), k-NN, SVM, and ANN did not perform well on any of the datasets. In terms of the classification error rate, OTEC(oob) performed better on 19 out of 20 datasets than the other methods. For 17 of the 20 datasets, OTEC(sub) performed better in terms of classification error rate. However, the other methods failed to yield satisfactory results.
Table 3 presents a detailed comparison of the proposed method with other state-of-the-art methods on the datasets. OTEC(oob) yielded better results for the majority of datasets in terms of precision. The results given in Table 4 show that OTEC(oob), in terms of precision, yields promising results ranging from 93.36% to 100% for several datasets. This demonstrated the effectiveness of the proposed method. In contrast, OTEC(sub) provided better results in terms of precision for 14 datasets, except for the breast, liver disorder, and ionosphere. Moreover, RF (smote) and RF (over) demonstrate high precision in kc2 and glass classification. The box plots revealed the best findings of the proposed method, that is, OTEC(oob) and OTEC(sub), in terms of the classification error rate and precision with other methods given in Figure 1, Figure 2, Figure 3 and Figure 4. A box plot of the remaining datasets in terms of the classification error rate and precision is shown in Figures S1 and S2 of Supplementary Materials.
The parameter W, which represents the percentage of the best trees selected for the final ensemble, is crucial for the OTEC(oob) and OTEC(sub) methods. The diverse values of W indicate the different behaviors of the method. This study assessed the impact of W = (10%, 30%, 50%, 70%, 90%) of the total number of trees on the classification method. As shown in Figure 5, subsets of the total number of trees ranging from 10% to 90% were used to calculate the classification error rate. For each dataset, Figure 5 shows that an increase in the number of trees used by the ensemble decreased the OTEC(oob) classification error rate. Similar to OTEC(oob), Figure 6 shows that the classification error rate of OTEC(sub) decreased with an increase in the number of trees in the ensemble. In Figure 5 and Figure 6, the x-axis represents the percentage of the best trees selected, while the y-axis represents classification error rate results.

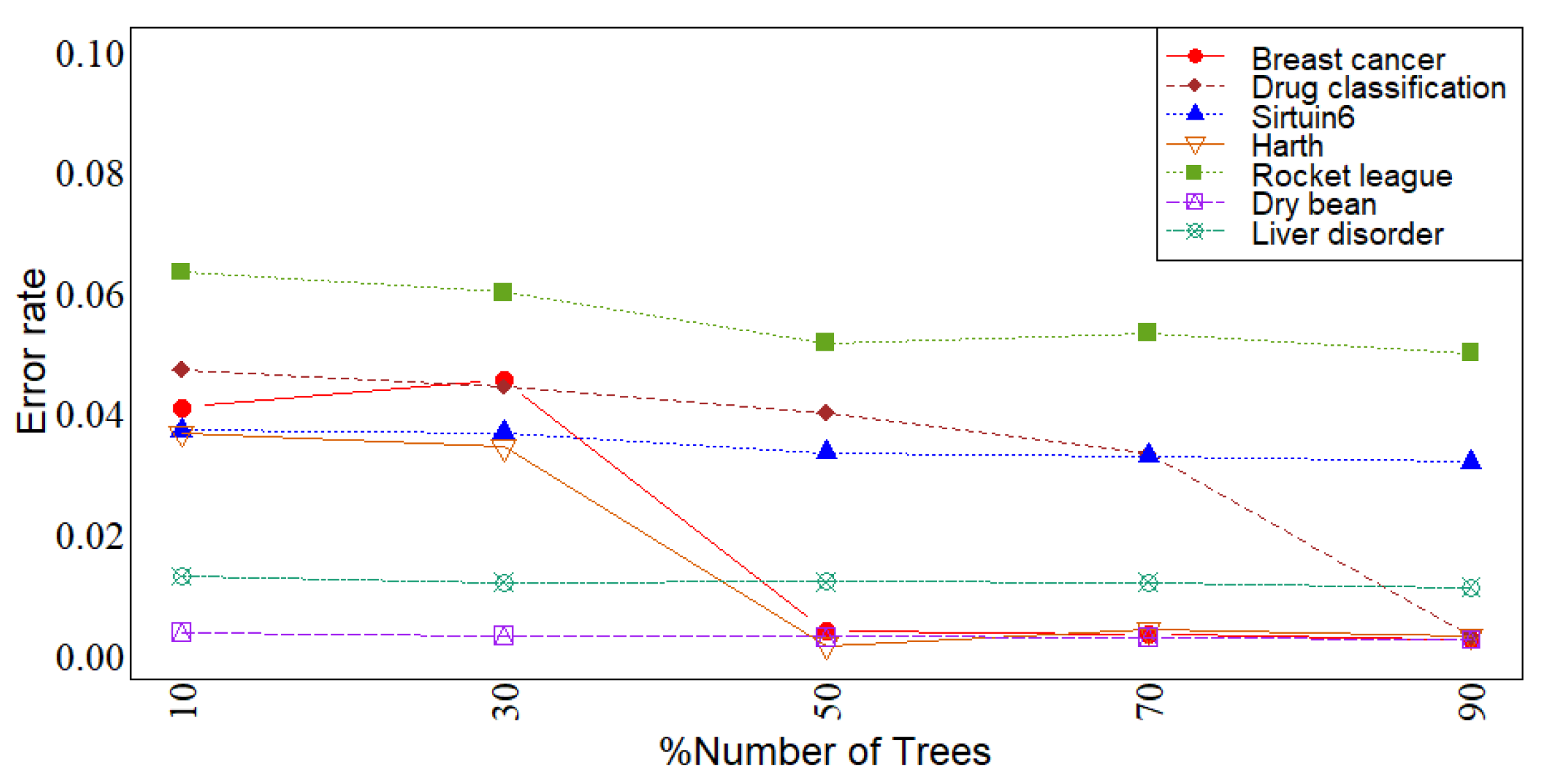
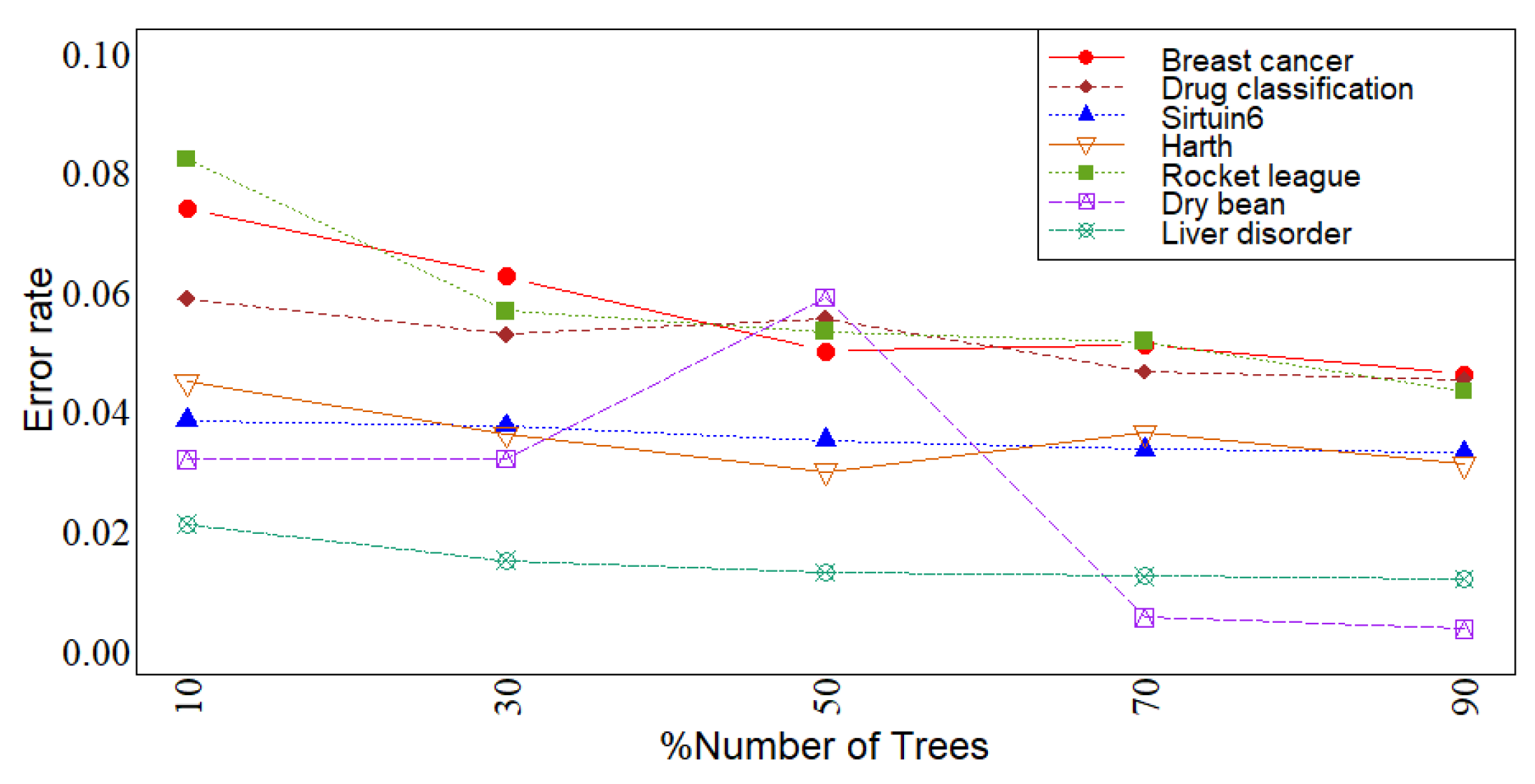
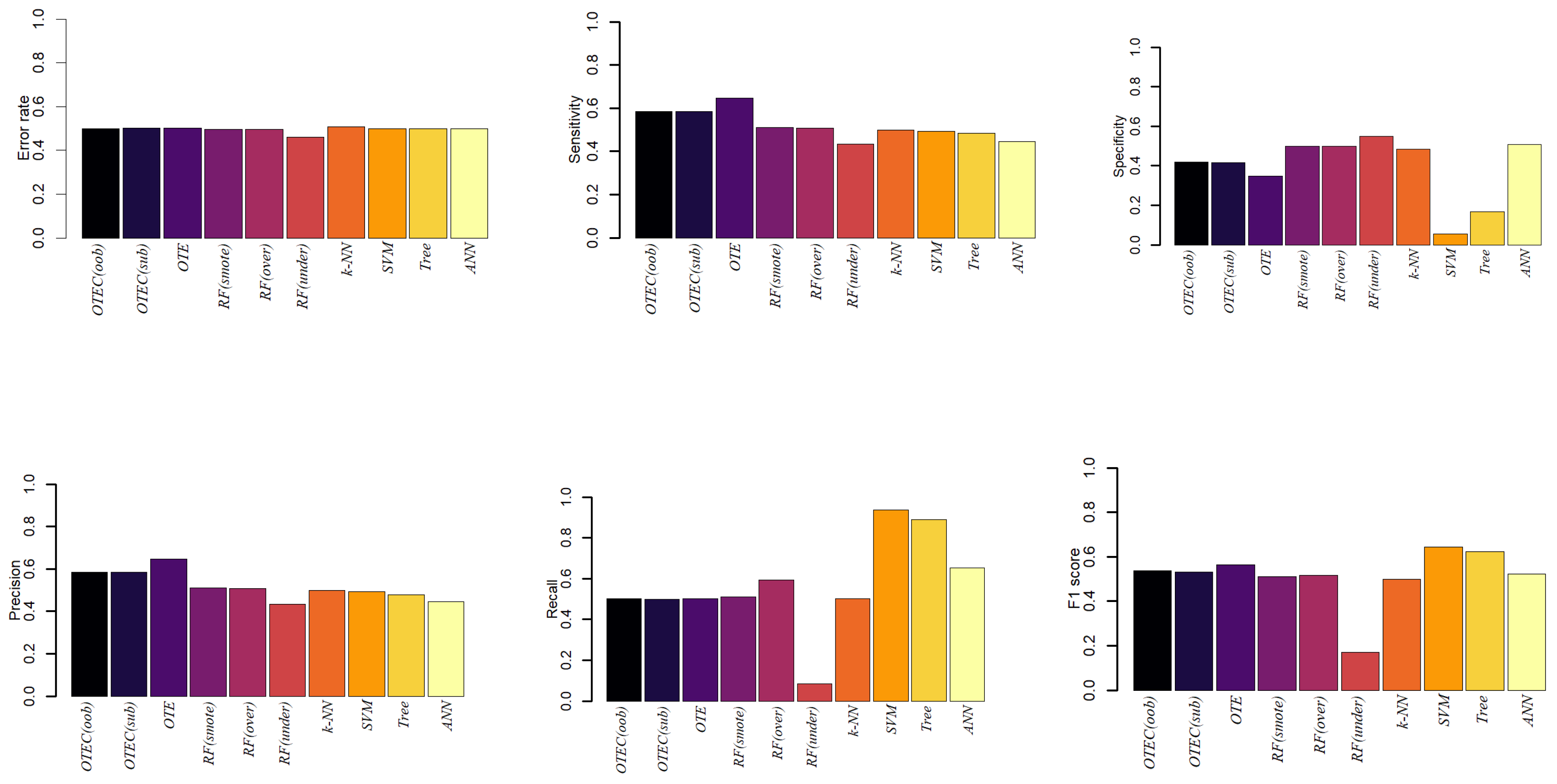
3. Simulation

In this section, we present two simulation scenarios for the proposed method. The first scenario is intended to show the circumstances in which the proposed method is useful, whereas the second scenario shows a data-generating setting where the proposed method might not be suitable. In total, 10,000 instances across 19 variables were synthetically generated. Each of these variables generates observations as a multivariate normal distribution with different means and variances, whereas the other generates observations with a multinomial distribution with four categories. To generate observations from a binary response, the first imbalance ratio specifies the imbalance in the observations. The binary response, Y = B p , is generated using a logit-type function given the variables P y | X :
p ( y i m b | X ) = e x p ( y i m b ) 1 + e x p ( 1 − y i m b ) .
The imbalance ratio of the number of instances in the majority class compared to the minority class observations n 0 was 5.67, of which 8500 belonged to the majority class and 1500 to the minority class. The values of y used in Equation 2 are as follows:
y = X β +
This setup was used to generate 10,000 observations. All the methods presented in this study were applied using the same experimental setup as that used for the benchmark datasets. The second model was constructed similarly. The class-wise distribution was 50/50, where a class ratio of 1.02 indicated that the data were balanced. The difference between the two models was that the former contained an imbalanced class distribution, whereas the latter did not. A total of 100 realizations were performed. The proposed methods, OTEC(oob) and OTEC(sub), outperformed the other rivals in the first scenario. In the second scenario, OTEC(oob) and OTEC(sub) did not perform well because there was no class imbalance problem. Bar plots of the proposed method on the simulated datasets are shown in Figure 7 and Figure 8. The results demonstrate that the proposed methods are appropriate in the presence of a severe class imbalance problem in the data.

4. Conclusions

The uneven distribution of observations into two classes, where one of the classes significantly outperforms the other, adversely affects the performance prediction of machine-learning methods. Therefore, balancing the data by synthetically generating additional observations for minority classes, a class that is usually of high interest, along with model selection for a decision-tree ensemble, has resulted in improved prediction performance. The proposed ensemble algorithm, along with synthetic data generation for data balancing, effectively solved the key challenge of extremely imbalanced classification problems.
The two methods proposed in this study address the imbalanced data problem, as shown by the analysis of several benchmark and simulated datasets. The proposed methods outperformed conventional machine-learning tools, such as optimal tree ensemble, random forest with SMOTE, random forest with under-sampling, random forest with oversampling, k-NN, SVM, classification tree, and artificial neural networks, in terms of error rate, sensitivity, specificity, precision, recall, and F1-score. With the help of the proposed method, the performance of machine-learning models on extremely imbalanced binary classification problems can be significantly improved, producing more dependable and robust classification results in practical applications.
For future work in the direction of this paper, one may consider the use of SMOTE and ADASYN (Adaptive Synthetic Minority Oversampling Technique) for data augmentation methods customized to the dataset. Using these methods, the performance of the model can be improved by adding artificial data points for the minority class. Using the active learning strategy, the model may be trained to automatically search for new data points, particularly from the minority class. This will allow the underrepresented class most informative data to be the model’s key focus. Feature engineering methods that can generate new features that are more informative for the underrepresented class in conjunction with the proposed method might improve the performance further. Feature selection could also be used to determine which features are most relevant for classification in an unbalanced context. Other methods, such as cost-sensitive learning, could be combined with the regularized tree forest. Cost-sensitive learning enables the model to concentrate its performance on underrepresented data by providing greater weight to minority class misclassifications.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Table S1, Figures S1–S14.

Author Contributions

Conceptualization, S.S.; methodology, S.S. and S.G.; software, S.G.; validation, S.S. and S.G.; formal analysis, S.G. and S.S.; investigation, S.S. and S.G.; resources, S.S.; data curation, S.S., and S.G.; writing—original draft preparation, S.S., and S.G.; writing—review and editing, S.G. and S.S.; visualization, S.S. and S.G.; supervision, S.S.; project administration, S.S.; funding acquisition, S.S. Both authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the START-UP Research, grant number 12B025, College of Business and Economics at the United Arab Emirates University.

Data Availability Statement

The data supporting the findings of this study are available upon request. Interested researchers may contact the corresponding author to obtain access to the data for further analysis and validation.

Acknowledgments

The authors gratefully acknowledge funding support from the United Arab Emirates University, which made this research possible.

Conflicts of Interest

The authors declare no conflicts of interest. The authors have no relevant financial or non-financial interests to disclose.

References

  1. Weiss, G. M. (2004). Mining with rarity: a unifying framework. ACM Sigkdd Explorations Newsletter, 6(1), 7-19. [CrossRef]
  2. Parmar, J.; Chouhan, S.S.; Raychoudhury, V.; Rathore, S.S. Open-world Machine Learning: Applications, Challenges, and Opportunities. ACM Comput. Surv. 2023, 55, 1–37. [CrossRef]
  3. Wang, L.; Han, M.; Li, X.; Zhang, N.; Cheng, H. Review of Classification Methods on Unbalanced Data Sets. IEEE Access 2021, 9, 64606–64628. [CrossRef]
  4. de Giorgio, A.; Cola, G.; Wang, L. Systematic review of class imbalance problems in manufacturing. J. Manuf. Syst. 2023, 71, 620–644. [CrossRef]
  5. Kotsiantis, S., Kanellopoulos, D., & Pintelas, P. Handling imbalanced datasets: A review, gests international transactions on computer science and engineering 30 (2006) 25–36. Synthetic Oversampling of Instances Using Clustering.
  6. Visa, S., & Ralescu, A. (2005, April). Issues in mining imbalanced data sets-a review paper. In Proceedings of the sixteen midwest artificial intelligence and cognitive science conference (Vol. 2005, pp. 67-73). sn.
  7. Monard, M. C., & Batista, G. E. A. P. A. (2002). Learning with skewed class distributions. Advances in Logic, Artificial Intelligence and Robotics, 85, 173-180.
  8. Prince, M.; Prathap, P.M.J. An Imbalanced Dataset and Class Overlapping Classification Model for Big Data. Comput. Syst. Sci. Eng. 2023, 44, 1009–1024. [CrossRef]
  9. Kotsiantis, S. B., & Pintelas, P. E. (2003). Mixture of expert agents for handling imbalanced data sets. Annals of Mathematics, Computing & Teleinformatics, 1(1), 46-55.
  10. Improving identication of di cult small classes by balancing class distribution. In Articial Intelligence in Medicine: 8th Conference on Articial Intelligence in Medicine in Europe, AIME 2001 Cascais, Portugal, July 14, 2001, Proceedings 8, pages 6366. Springer, 2001.
  11. Han, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. In Proceedings of the International Conference on Intelligent Computing, Hefei, China, 23–26 August 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 878–887. [CrossRef]
  12. Han, H., Wang, L., Wen, M., & Wang, W. Y. (2006). Oversampling Algorithm Based on Preliminary Classification in Imbalanced Data Sets Learning. Journal of computer allocations (in Chinese), 26(8), 1894-1897.
  13. Kubat, M., & Matwin, S. (1997, July). Addressing the curse of imbalanced training sets: one-sided selection. In Icml (Vol. 97, No. 1, p. 179).
  14. Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [CrossRef]
  15. Weiss, G. M. (2003). The effect of small disjuncts and class distribution on decision tree learning. Rutgers The State University of New Jersey, School of Graduate Studies.
  16. Weiss, G.M.; Provost, F. Learning When Training Data are Costly: The Effect of Class Distribution on Tree Induction. J. Artif. Intell. Res. 2003, 19, 315–354. [CrossRef]
  17. Jo, T.; Japkowicz, N. Class imbalances versus small disjuncts. ACM SIGKDD Explor. Newsl. 2004, 6, 40–49. [CrossRef]
  18. Batista, G.E.A.P.A.; Prati, R.C.; Monard, M.C. A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD Explor. Newsl. 2004, 6, 20–29. [CrossRef]
  19. Leevy, J.L.; Hancock, J.; Khoshgoftaar, T.M. Comparative analysis of binary and one-class classification techniques for credit card fraud data. J. Big Data 2023, 10, 1–13. [CrossRef]
  20. Wongvorachan, T.; He, S.; Bulut, O. A Comparison of Undersampling, Oversampling, and SMOTE Methods for Dealing with Imbalanced Classification in Educational Data Mining. Information 2023, 14, 54. [CrossRef]
  21. Chaabane, I.; Guermazi, R.; Hammami, M. Enhancing techniques for learning decision trees from imbalanced data. Adv. Data Anal. Classif. 2019, 14, 677–745. [CrossRef]
  22. Ksieniewicz, P. (2018, November). Undersampled majority class ensemble for highly imbalanced binary classification. In Second International Workshop on Learning with Imbalanced Domains: Theory and Applications (pp. 82-94). PMLR.
  23. Du, H.; Zhang, Y.; Zhang, L.; Chen, Y.-C. Selective ensemble learning algorithm for imbalanced dataset. Comput. Sci. Inf. Syst. 2023, 20, 831–856. [CrossRef]
  24. Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [CrossRef]
  25. Sebbanü, M., NockO, R., Chauchat, J., & Rakotomalala, R. (2000). Impact of learning set quality and size on decision tree performances. IJCSS, 1(1), 85.
  26. Khan, Z., Gul, A., Mahmoud, O., Miftahuddin, M., Perperoglou, A., Adler, W., & Lausen, B. (2016). An ensemble of optimal trees for class membership probability estimation. In Analysis of Large and Complex Data (pp. 395-409). Springer International Publishing. [CrossRef]
  27. Khan, Z.; Gul, A.; Perperoglou, A.; Miftahuddin, M.; Mahmoud, O.; Adler, W.; Lausen, B. Ensemble of optimal trees, random forest and random projection ensemble classification. Adv. Data Anal. Classif. 2019, 14, 97–116. [CrossRef]
  28. Efron, B., & Tibshirani, R. (1997). Improvements on cross-validation: the 632+ bootstrap method. Journal of the American Statistical Association, 92(438), 548-560. [CrossRef]
  29. Adler, W.; Lausen, B. Bootstrap estimated true and false positive rates and ROC curve. Comput. Stat. Data Anal. 2009, 53, 718–729. [CrossRef]
  30. Johnson, R.W. An Introduction to the Bootstrap. Teach. Stat. 2001, 23, 49–54. [CrossRef]
Preprints 112703 g001
Figure 1. Box-plots of OTEC(oob), OTEC(sub) with other state-of-the-art method in term of classification error rate on various datasets.
Figure 1. Box-plots of OTEC(oob), OTEC(sub) with other state-of-the-art method in term of classification error rate on various datasets.
Preprints 112703 g001
Preprints 112703 g002
Figure 2. Box-plots of OTEC(oob), OTEC(sub) with other state-of-the-art method in term of classification error rate on various datasets.
Figure 2. Box-plots of OTEC(oob), OTEC(sub) with other state-of-the-art method in term of classification error rate on various datasets.
Preprints 112703 g002
Preprints 112703 g003
Figure 3. Box-plots of OTEC(oob), OTEC(sub) with other state-o-the-art method in term of precision on various datasets.
Figure 3. Box-plots of OTEC(oob), OTEC(sub) with other state-o-the-art method in term of precision on various datasets.
Preprints 112703 g003
Preprints 112703 g004
Figure 4. Box-plots of OTEC(oob), OTEC(sub) with other state-o-the-art method in term of precision on various datasets.
Figure 4. Box-plots of OTEC(oob), OTEC(sub) with other state-o-the-art method in term of precision on various datasets.
Preprints 112703 g004
Preprints 112703 g005
Figure 5. Multi-line plot shows the percentage of the best trees in the ensemble with the classification error rate of the proposed method, OTEC (oob).
Figure 5. Multi-line plot shows the percentage of the best trees in the ensemble with the classification error rate of the proposed method, OTEC (oob).
Preprints 112703 g005
Preprints 112703 g006
Figure 6. Multi-line plot shows the percentage of the best trees in the ensemble with the classification error rate of the proposed method, OTEC (sub).
Figure 6. Multi-line plot shows the percentage of the best trees in the ensemble with the classification error rate of the proposed method, OTEC (sub).
Preprints 112703 g006
Preprints 112703 g007
Figure 7. Bar plots of the proposed method, i.e., OTEC(oob), OTEC(sub) comparing with other state-of-the-art methods in terms of classification error rate, sensitivity, specificity, precision, recall, and F1 score on the imbalanced simulated dataset.
Figure 7. Bar plots of the proposed method, i.e., OTEC(oob), OTEC(sub) comparing with other state-of-the-art methods in terms of classification error rate, sensitivity, specificity, precision, recall, and F1 score on the imbalanced simulated dataset.
Preprints 112703 g007
Preprints 112703 g008
Figure 8. Bar plots of the proposed method, i.e., OTEC(oob), OTEC(sub) comparing with other methods in terms of classification error rate, sensitivity, specificity, precision, recall, and F1 score on the balanced simulated dataset.
Figure 8. Bar plots of the proposed method, i.e., OTEC(oob), OTEC(sub) comparing with other methods in terms of classification error rate, sensitivity, specificity, precision, recall, and F1 score on the balanced simulated dataset.
Preprints 112703 g008
Table 1. Summary of datasets with class-imbalanced problem.
Table 1. Summary of datasets with class-imbalanced problem.
No Dataset Instances Features Class-Based
Distribution		 Imbalance Ratio
n 1/n 0 		Source
1 Breast Cancer 569 31 357/212 (1.6839:1) https://www.kaggle.com/datasets/utkarshx27/breast-cancer-wisconsin-diagnostic-dataset
2 Credit Card 284807 30 284807/492 (578.876:1) https://www.kaggle.com/datasets/mlg-ulb/creditcardfraud
3 Drug Classification 200 6 145/54 (2.685:1) https://openml.org/search?type=data&status=active&id=43382
4 Kc2 520 21 414/106 (3.905:1) https://openml.org/search?type=data&status=active&sort=runs&id=1063
5 Eeg eye 5856 14 5708/148 (38.567:1) https://openml.org/search?type=data&status=active&sort=runs&id=1471
6 Glass Classification 213 9 144/69 (2.086:1) https://openml.org/search?type=data&status=active&id=43750
7 Pc4 1339 37 1279/60 (21.316:1) https://openml.org/search?type=data&status=active&sort=runs&id=1049
Table 2. The proposed methods, i.e., OTEC(oob), OTEC(sub), and other state-of-the-art methods, in terms of classification error rate.
Table 2. The proposed methods, i.e., OTEC(oob), OTEC(sub), and other state-of-the-art methods, in terms of classification error rate.
Dataset OTEC(oob) OTEC(sub) OTE RF(smote) RF(over) RF(under) k-NN SVM ANN Tree
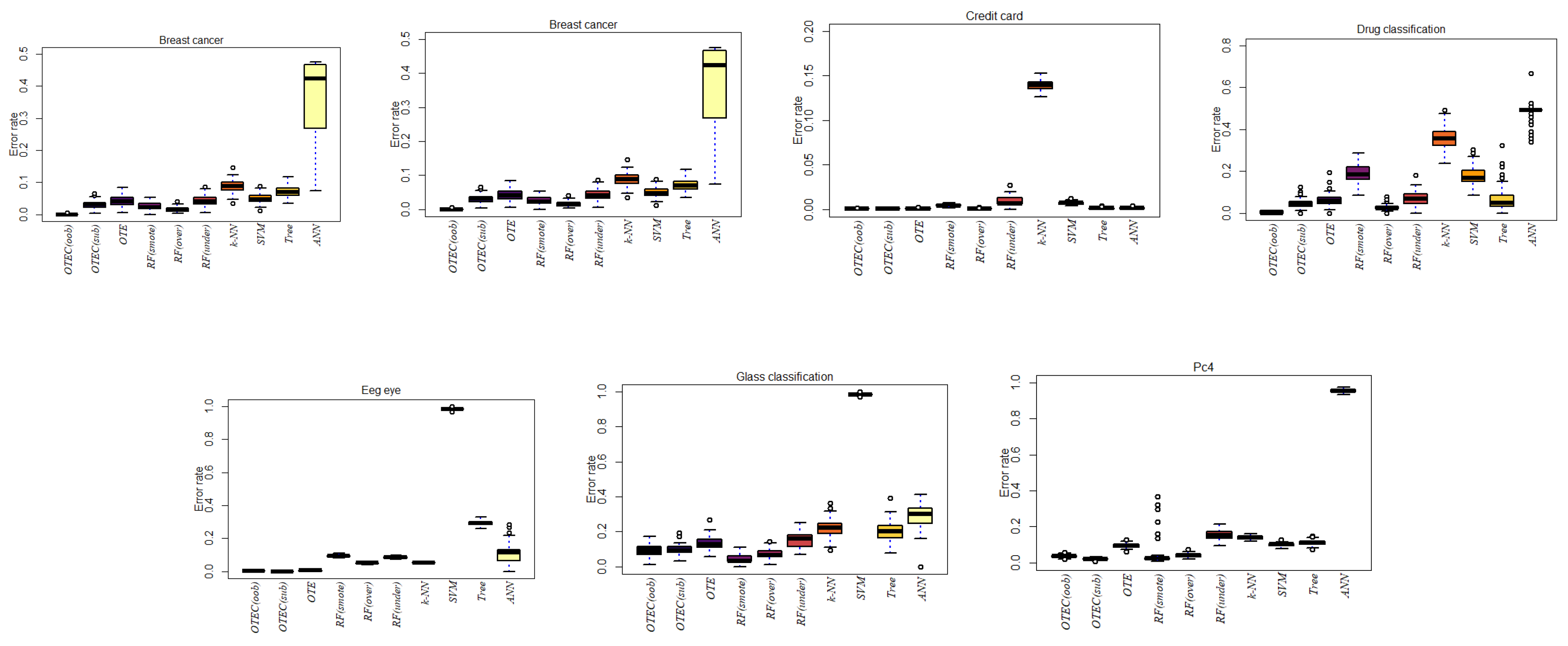
Breast Cancer 0.0015 0.0311 0.0427 0.0264 0.0166 0.0422 0.0851 0.0486 0.3625 0.0723
Credit Card 0.0005 0.0005 0.0010 0.0046 0.0006 0.0083 0.1395 0.0071 0.0016 0.0014
Drug Classification 0.0038 0.0461 0.0624 0.1875 0.0296 0.0650 0.3542 0.1771 0.4998 0.0697
Kc2 0.0093 0.0099 0.1743 0.0213 0.0213 0.2060 0.1579 0.9943 0.1925 0.1735
Eeg eye 0.0035 0 0.0063 0.0942 0.0521 0.0872 0.0553 0.9827 0.1094 0.2947
Glass Classification 0.0914 0.0974 0.1330 0.0405 0.0710 0.1518 0.2194 0.9839 0.2879 0.1993
Pc4 0.0384 0.0213 0.0945 0.0411 0.0421 0.1519 0.1392 0.1006 0.9555 0.1120
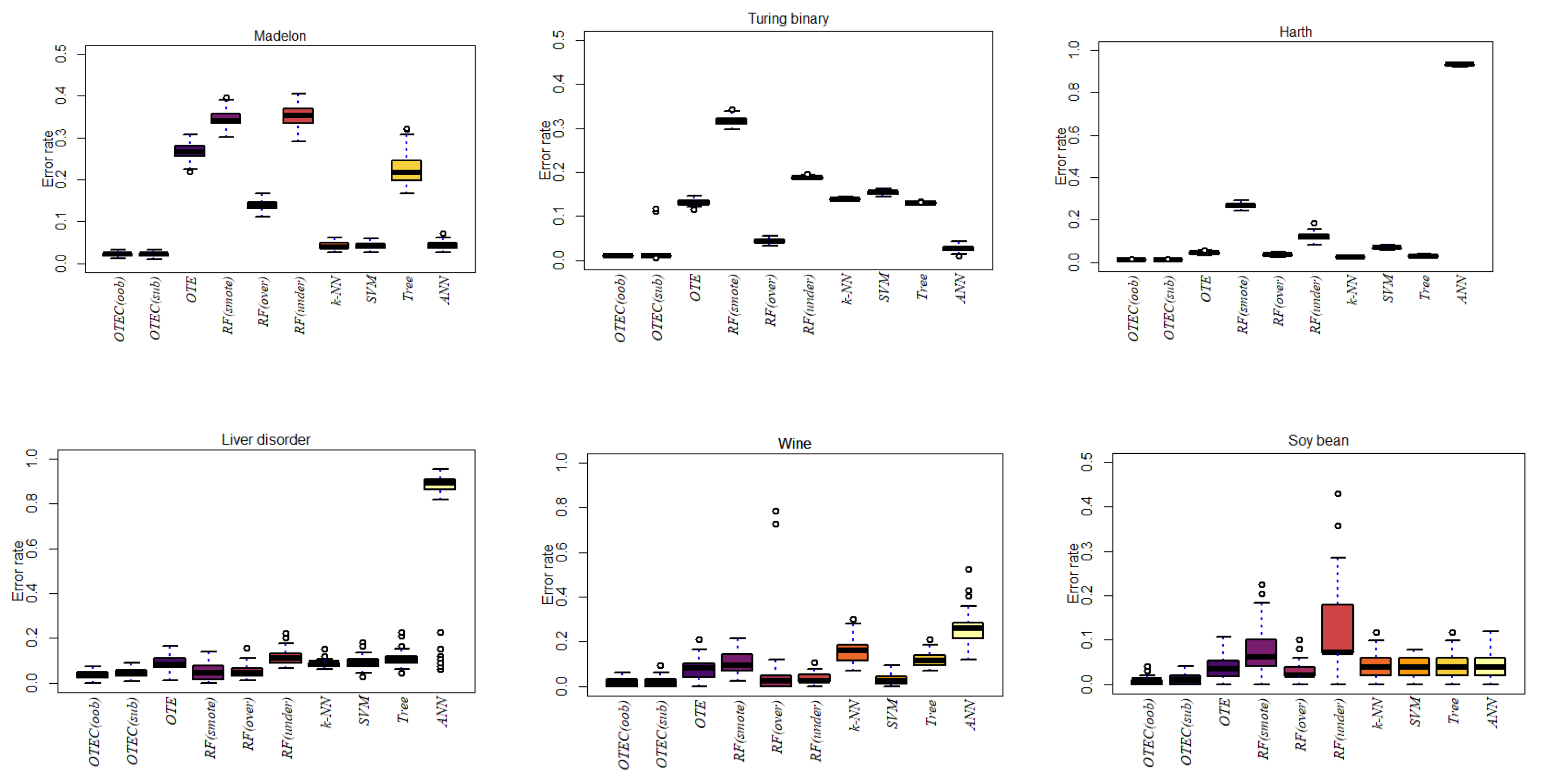
Madelon 0.0222 0.0218 0.2675 0.3459 0.1397 0.3525 0.0416 0.0420 0.0435 0.2260
Turing binary 0.0102 0.0214 0.1321 0.3173 0.0437 0.1882 0.1392 0.1541 0.0271 0.1303
KDD 0.0099 0.0101 0.0355 0.1394 0.0098 0.1191 0.0198 0.0226 0.9804 0.0185
Liver disorder 0.0400 0.0453 0.0864 0.0469 0.0512 0.1153 0.0862 0.0915 0.7661 0.1126
Wine 0.0227 0.0173 0.0796 0.1029 0.0680 0.0324 0.1605 0.0305 0.2574 0.1235
Soy bean 0.0093 0.0100 0.0364 0.0706 0.0308 0.1229 0.0416 0.0420 0.0428 0.0402
Ionosphere 0.0429 0.0172 0.1168 0.2830 0.0985 0.1531 0.1107 0.0898 0.8913 0.1093
Room Occupancy 0 0 0.0002 0.0034 0.0003 0.0020 0.0001 0.00001 0.0211 0.0002
Harth 0.0121 0.0119 0.0438 0.2698 0.0379 0.1214 0.0253 0.0682 0.9318 0.0303
Rocket League 0.0334 0.0331 0.1032 0.4525 0.0914 0.1158 0.0622 0.0616 0.0614 0.0613
Sirtuin6 0.0516 0.0516 0.2433 0.2680 0.1200 0.3275 0.0700 0.0965 0.6519 0.0847
Toxicity 0.0339 0.0352 0.1241 0.3828 0.1392 0.2750 0.0645 0.0570 0.0694 0.0692
Dry bean 0.0030 0.0035 0.0102 0.0500 0.0075 0.0134 0.0301 0.0103 0.0295 0.0091
Table 3. The proposed methods, i.e., OTEC(oob), OTEC(sub), and other state-of-the-art methods, in terms of precision.
Table 3. The proposed methods, i.e., OTEC(oob), OTEC(sub), and other state-of-the-art methods, in terms of precision.
Dataset OTEC(oob) OTEC(sub) OTE RF(smote) RF(over) RF(under) k-NN SVM ANN Tree
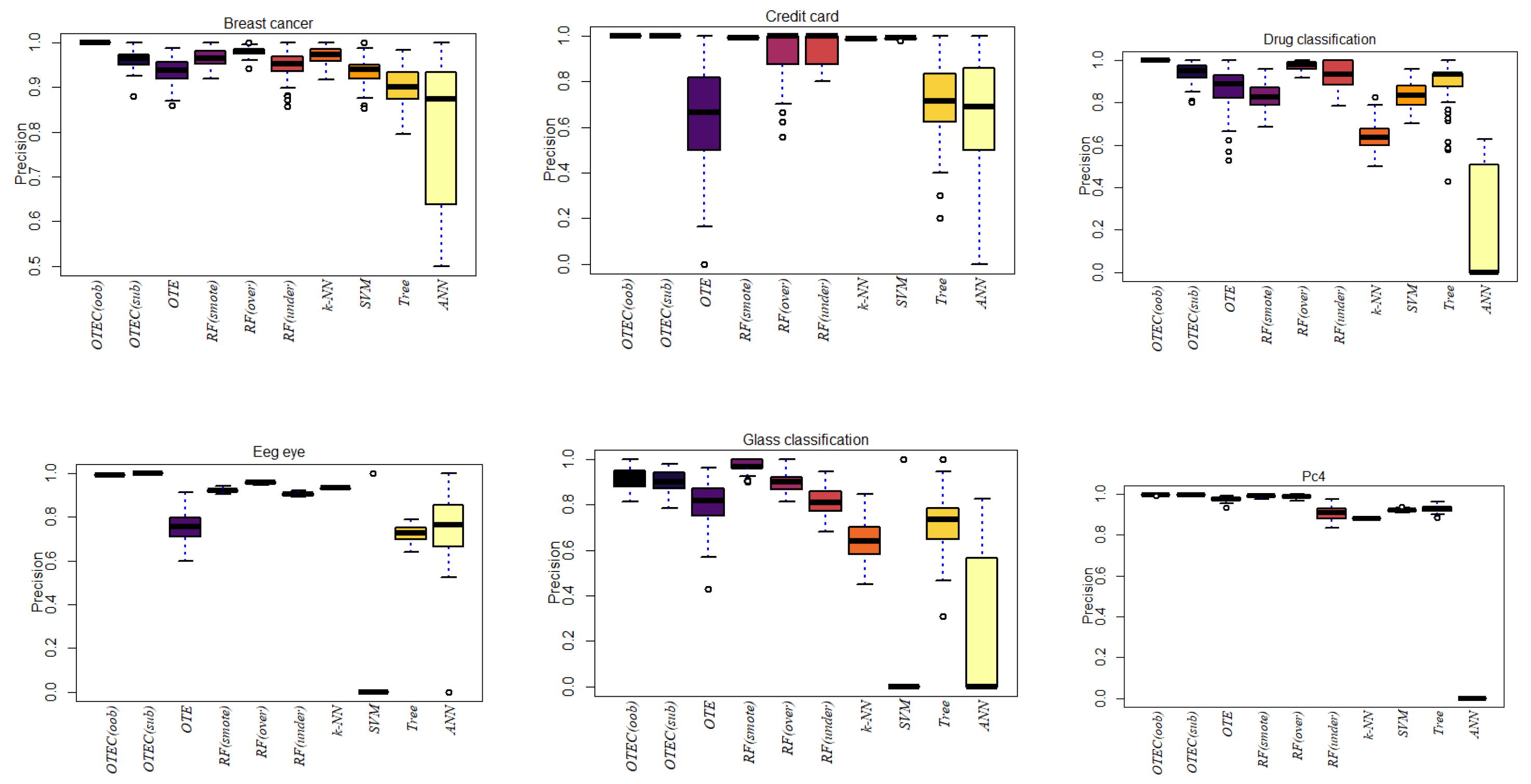
Breast Cancer 1.0000 0.9629 0.9364 0.9670 0.9795 0.9517 0.9696 0.9353 0.7200 0.9029
Credit Card 0.9993 0.9992 0.6503 0.9923 0.9241 0.9505 0.9860 0.9889 0.6123 0.7284
Drug Classification 1.0000 0.9378 0.8655 0.8277 0.9714 0.9361 0.6401 0.8328 0.2006 0.9031
Kc2 0.9267 0.8698 0.4658 0.9572 0.9996 0.6335 0.4017 0.1900 0.1407 0.5908
Eeg eye 0.9929 1 0.7578 0.9216 0.9576 0.9049 0.9327 0.0700 0.6646 0.7257
Glass Classification 0.9153 0.9022 0.8050 0.9739 0.8984 0.8166 0.6440 0.1300 0.2665 0.7204
Pc4 0.9981 0.9971 0.9755 0.9904 0.9885 0.9059 0.8811 0.9207 0 0.9287
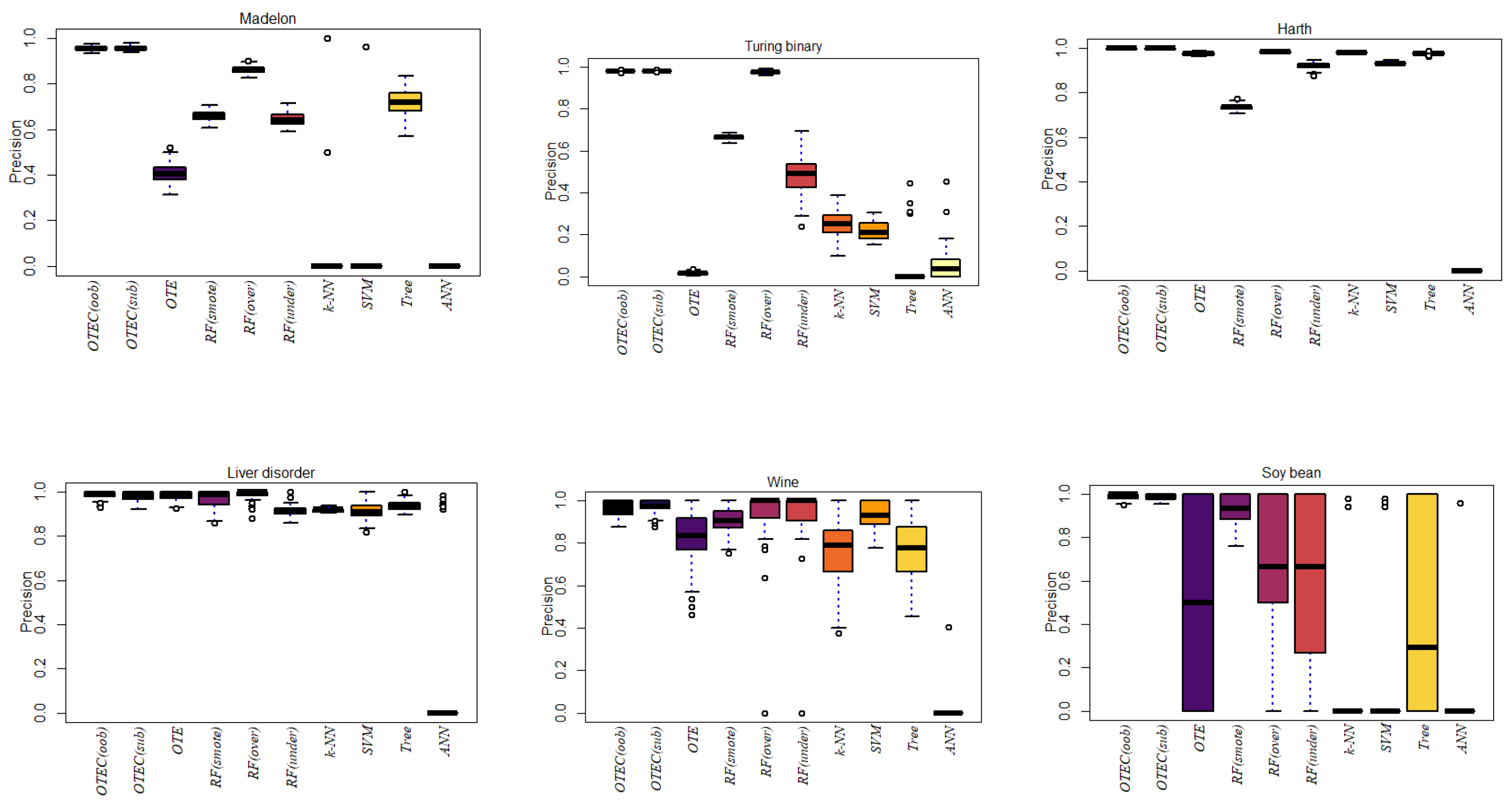
Madelon 0.9554 0.9563 0.4063 0.6586 0.8614 0.6449 0.1750 0.0192 0 0.7171
Turing binary 0.9796 0.9799 0.0162 0.6648 0.9757 0.4800 0.2519 0.2176 0.0541 0.0140
KDD 1 1 0.9987 0.8649 0.9896 0.2506 0.9802 0.9794 0 0.9830
Liver disorder 0.9860 0.9830 0.9835 0.9713 0.9835 0.9134 0.9206 0.9135 0.1604 0.9365
Wine 0.9584 0.9720 0.8302 0.9111 0.9187 0.9218 0.7678 0.9296 0.0041 0.7702
Soy bean 0.9888 0.9864 0.4845 0.9309 0.6332 0.5975 0.0286 0.0288 0.0096 0.3968
Ionosphere 0.9733 0.6763 0.9292 0.7239 0.9589 0.9209 0.8954 0.9137 0 0.9397
Room Occupancy 1 1 0.9971 0.9962 0.9971 0.9936 0.9943 1 0 0.9948
Harth 0.9980 0.9976 0.9750 0.7336 0.9828 0.9190 0.9800 0.9317 0 0.9749
Rocket League 0.9336 0.9362 0.0759 0.5431 0.3916 0.0890 0.1240 0 0 0
Sirtuin6 0.9554 0.9589 0.6373 0.7638 0.9509 0.7683 0.9200 0.9235 0 0.9182
Toxicity 0.9323 0.9314 0.0386 0.5924 0.4527 0.1049 0.0100 0 0 0
Dry bean 0.9961 0.9952 0.8161 0.9503 0.9639 0.9702 0.0353 0.9283 0 0.8880
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated