Preprint
Article
A Spatial-Seasonal Study for Dynamics of Pollutant Concentration in Water on the Danube River in the Adjacent Danube Delta Area and the Evaluation of the Attenuation and Transfer Coefficients. Part 1 – Case Study – Monitored Heavy Metals
Altmetrics
Downloads
131
Views
74
Comments
0
A peer-reviewed article of this preprint also exists.
Submitted:
20 July 2024
Posted:
22 July 2024
You are already at the latest version
Alerts
Abstract
Monitoring and protecting flowing watercourses is a complex and challenging task that requires the collaboration and coordination of various stakeholders such as governments, industries, farmers, consumers and environmental groups. The study of the dynamics of the concentration of polluting factors and especially the concentrations of heavy metals and highlighting a seasonal variation is a necessary element from this point of view. In this article, we present the results of our analyzes carried out in two measurement campaigns executed in 10 monitoring points along the Danube River, between Braila city and Isaccea city in the pre-deltaic area, during the summer season and autumn season 2022. The importance of this area is given by the fact that the Dan-ube Delta is part of the UNESCO heritage and the monitoring of polluting factors is a necessity in the desire to protect this area. The data measured during the July and August 2022 campaign co-vers a wide range of chemical species: Phosphate, CCO, CBO5, NH4+, N-NO2, N-NO3-, N-Total, P-PO4 3-, SO42-, Cl-, phenols, as well as metals with a harmful effect: Aluminum, Arsenic, Cad-mium, Chromium, Iron. The study includes an evaluation based on the statistical approach of the results to highlight the significant correlations and differences identified between the two data sets. Next, to highlight the obtained results, a numerical model was considered using HEC-RAS and ESRI ArcGis applications in a two-dimensional unsteady flow model in order to get the non-homogenous concentrations’distributions in the studied area. These two-dimensional models have been less studied in the specialized literature. In this way, interesting results could be ob-tained and prediction methods regarding the dynamics of metal concentrations could be struc-tured. The data obtained was used for the terrain model from the USGS service and the flows of the Danube and its two tributaries were simulated using the data provided by the national ser-vices. In this work, we present the results obtained for the dynamics of the concentrations of the metals Aluminum, Arsenic, Cadmium, Chromium and Iron and the evaluation of the specific ab-sorption coefficients for the explanation and correlation with the results of the measurements. The study is part of a more complex project in which the spatio-temporal distribution of the polluting factors in the water was evaluated and the habitats in the study area were inventoried - especially those of community interest. the aspects related to the influence of the distribution of polluting factors on the state of health will be the subject of another article.
Keywords:
Subject: Environmental and Earth Sciences - Environmental Science
1. Introduction
The problem of pollution of running water courses is a serious and widespread problem [1], affecting the health and welfare of people [2], animals and plants [3]. Flowing watercourses such as streams, rivers, lakes and estuaries are vital sources of drinking water, irrigation, recreation and biodiversity [4]. However, they are also vulnerable to contamination from various sources [5], such as industrial waste [2], agricultural runoff [6], sewage, oil spills, and radioactive materials [5]. These pollutants can alter the physical, chemical and biological properties of water, making it unsuitable for its intended uses and damaging natural ecosystems [4]. Some of the negative effects of water pollution include: reduced oxygen levels [7], which can cause fish kills and affect aquatic life; increased nutrient levels that can lead to eutrophication and algal blooms [6], resulting in decreased water quality and increased toxicity [8]; increased sedimentation, which can reduce water clarity and clog the gills of fish and other organisms [9]; increased acidity [10], which can corrode metal pipes and damage aquatic life [11]; increasing temperatures, which can affect the metabolism and reproduction of aquatic organisms and increase the risk of invasive species and disease; increased presence of pathogens such as bacteria, viruses and parasites that can cause waterborne diseases and infections in humans and animals; the increased presence of toxic substances such as heavy metals, pesticides and pharmaceuticals, which can accumulate in the food chain and pose health risks to humans and wildlife [11,12].
Some examples of water pollutants are: pathogens, such as bacteria, viruses and parasites, which can cause waterborne diseases and infections in humans and animals [13]. For example, mercury can accumulate in the food chain and pose health risks to humans and wildlife [5]; organic materials such as pesticides, pharmaceuticals [6], and petroleum products can degrade water quality and increase water toxicity [1,14]. For example, methyl tert-butyl ether (MTBE) is a volatile organic chemical that was previously used as an air-cleaning gas additive and can cause leukemia, lymphoma, and tumors in humans and animals; macroscopic pollutants such as plastic waste, wood, metal and shipwrecks [6,13], which can reduce water clarity and clog waterways. For example, plastic waste can form large patches in the oceans and harm marine life.
There are many examples of successful river restoration projects around the world [15,16] that have improved the ecological, social and economic benefits of rivers [17]: - the Herring River Restoration Project in Cape Cod, Massachusetts, which aims to restore the natural tidal flow and the salinity of the Herring River estuary, which was altered by a levee built in 1909; - the Reedy River Master Plan in Greenville, South Carolina is a comprehensive vision for the revitalization of the urban river corridor, which has been degraded by industrial pollution and urban development, etc.
For these reasons, the study of stream water monitoring is a vital and challenging field that requires the use of various methods and technologies to collect, analyze and interpret water quality and quantity data [18,19]. Some of the most innovative study methods in this field are: - IoT-based water monitoring systems [20,21] - these systems use sensors, wireless networks, cloud computing and data analysis to measure and transmit water parameters in real-time, such as temperature, pH, turbidity, dissolved oxygen and conductivity [22]. These systems can provide accurate, timely and cost-effective information on water quality and quantity, as well as enable remote control and management of water resources.
Studying the Danube in the Danube Delta area is important for several reasons [2,23]. The Danube Delta is one of the continent's most valuable habitats for delta-specific wildlife and biodiversity [6,24,25]. It is the second largest delta in Europe and the best preserved of the European deltas [18]. It is also a UNESCO World Heritage Site and a Ramsar site, meaning it is a wetland of international importance [1]. The Danube Delta is home to over 300 species of birds and 45 species of freshwater fish in all of its lakes and marshes [6]. They also provide important ecosystem services such as drinking water, food, flood protection, nutrient recycling and recreation [5,6].
The Danube Delta is a unique and valuable ecosystem, but it faces many challenges that threaten its sustainability [8,24]. Some of the challenges are:
- Nutrient overload: the Danube River carries large amounts of nutrients from agricultural runoff [11], sewage and industrial waste [2], which cause eutrophication and algal blooms in the Delta [8]. This reduces water quality, oxygen levels and the biodiversity of aquatic habitats [26].
- Biodiversity loss: the Delta is home to many rare and endangered species of plants and animals [8], but these are threatened by habitat loss [5], fragmentation, degradation, invasive species, overfishing [13], hunting and climate change. Some of the species at risk include the sturgeon [27], pelican, pygmy cormorant and red-breasted goose [28].
- Land use transformations: the Delta has been altered by human activities such as drainage, irrigation, rehabilitation, deforestation and urbanization [5], which have reduced natural wetlands [8] and floodplains and increased the risk of erosion [29], salinization and desertification. These changes have also affected the livelihoods and culture of local communities that depend on the Delta's resources [19].
- Organic pollution and microplastics: the Danube River and its Delta are polluted with various organic contaminants [24,28], such as pesticides [6], pharmaceuticals, hormones and personal care products, which can have negative effects on the health of organisms and the ecosystem [27]. In addition, the river and Delta are also contaminated with microplastics [28], which are small plastic particles that can accumulate in the environment and food chain and pose a threat to wildlife and human health [6].
These are some of the challenges facing the Danube Delta, but there are also many opportunities and initiatives to address them and promote the conservation and restoration of this precious natural heritage. The distribution and dispersion of heavy metals in the Danube Course is a complex and important environmental issue [2], as the Danube River is the second-longest river in Europe and flows through 10 countries, affecting millions of people and ecosystems. Heavy metals can originate from various sources, such as natural weathering, industrial activities, agricultural runoff, urban wastewater, and mining operations. Some of the heavy metals, such as cadmium (Cd), and arsenic (As), etc. [24], are toxic and can accumulate in the aquatic organisms and sediments, posing health risks to humans and wildlife [8]. In this respect, the aim tTo assess the seasonal variation in the concentrations of heavy metals (such as cadmium, chromium, arsenic, etc.) in the aquatic ecosystems of the Danube River Braila-Galati area, and to evaluate the potential use of local aquatic plants or fish species as bioindicators of environmental pollution. The aim of the study is to investigate the distributions and dispersions of heavy metals on the Danube Course.
2. Materials and Methods
2.1. Data Collection
In order to determine the polluted areas in the Lower Danube region in Romania, we carried out a monitoring study of the physico-chemical parameters of the aquatic ecosystems in the study area (the Lower Danube and the adjacent Siret and Prut rivers) in order to assess and establish the degree of their pollution, according to the Water Framework Directive (https://environment.ec.europa.eu/topics/water/water-framework-directive_en). As it is known, the ‘water framework directive’ is a law that aims to protect and improve the quality and quantity of water resources in the European Union [30]. It applies to rivers, lakes, groundwater, coastal and transitional waters. It requires member states to achieve good status for all water bodies by 2015, and to prevent deterioration. It also promotes an integrated approach to water management, based on river basin districts and cooperation among countries
Water samples were analyzed from 10 sampling stations (P1-P10) – see Table 1, whose distribution includes the warm spots of the Danube, Siret, Prut (Figure 1). There are very important industrial objectives: the Galati steel plant (P3), the mineral port of the steel plant (P3), the Damen shipyard (P5), the international port at the confluence of the Prut river with the Danube river (P8), the Ukrainian port of Reni (P9), etc.;
Below, we present the main data analysis methods and procedures.
A total of 17 physicochemical parameters were determined: pH, conductivity, CCO, CBO5, NH4+, N-NO2-, N-NO3-, N-Total, P-PO43-, SO42-, Cl-, phenols, Al, As, Be, Cd, Cr. Some of the parameters were analyzed in situ, namely pH, conductivity, and dissolved oxygen, using a portable multiparameter equipped with a multisensory electrode and the turbidity using Turb 430 T – Turbidimeter (www.rexdan.ugal.ro).
The remaining parameters were analyzed in the laboratory in accordance with the standards in force, as follows : metals were analyzed using the Inductively coupled plasma mass spectrometry (ICP-MS) technique; nutrients, chlorides, sulfates, CCO and phenols were analyzed spectrophotometrically using Spectroquant® test kits; biochemical oxygen demand (CBO5) was determined using VELP respirometric BOD Sensor Sistem and FOC 200E Cooled Incubator (www.rexdan.ugal.ro ).
2.2. Methodology
2.2.a. Water and Sediment Sampling Methodology
Water samples were taken from 10 sampling stations placed on the Danube, Siret and Prut rivers using the sampling in monitoring points illustrated in Figure 1. Water samples were collected in polyethylene containers (PE) and were transported to the CREDENTIAL laboratory that is part of the European Center of Excellence for the Environment (ECEE) of “Dunarea de Jos” University of Galati [14]. The water sample collection methods were carried out as in most campaigns described in the literature: the samples were collected mainly in the minor basin, and the samples were taken from a minimum depth of 1.5 m. The samples were collected for each point every 48 hours. For this reason, the data showed a tight clustering. No storm or rain samples were collected - being a dry year. The instrument used was - ORION VERSA STAR 90 ThermoFisher Scientific - more details presented at the address - https://www.rexdan.ugal.ro/index.php/en/rexdan-ri/rexdan-research-center - see The REXDAN Research Center (includes 9 laboratories) and respectively The REXDAN Research Vessel (includes 9 laboratories). Collected samples were preserved at a temperature of 4 ◦C and analyzed within 24 hours. Surface sediment samples were collected using a Van Veen Grab Sampler (KC Denmark A/S, Silkeborg, Denmark) from the first 10 cm of the sediment surface and stored in polyethylene recipients. The sediment samples were preserved at 4 ◦C [24].
Metals from the IARC list (Aluminium, Arsenic, Beryllium, Cadmium, Chromium) were analyzed using ICP-MS Nexion 2000C (PerkinElmer, Massachusetts, United States) [24] (https://www.rexdan.ugal.ro/index.php/en/rexdan-ri/rexdan-research-center/ the-chromatography - laboratory ), in the Spectrometry Laboratory of the REXDAN Research Infrastructure, “Dunarea de Jos” University of Galati ( https://rexdan.ugal.ro/index.php/en/ ). The quantification limit for each metal was 0.001 µg/L. Regarding the detection limits for the 5 analysed metals were the following: Al ( 0.01 ng/L), As (0.3 ng/L), Be (0.5 ng/L) , Cd (0.06 ng/L), Cr (0.05 ng/L). For the analysis of water samples, the blank was water acidified 5% with nitric acid 65% (Suprapur, Darmstadt, Germany).[5]. The International Agency for Research on Cancer (IARC) selects metals for analysis based on several criteria. Primarily, they consider the evidence of human exposure and the potential or known carcinogenicity of the substances. Metals like Aluminium, Arsenic, Beryllium, Cadmium, and Chromium have been included in their analyses because of their significant presence in the environment and their potential health impacts. The calibration curve for each element was made in the concentration range of 0-15 μg/L. Also, calibration curves are linear with a correlation coefficient (R2) greater than 0.999 for the five trace metals analyzed [13].
The operating conditions were as follows: nebulizer gas (argon) flow rate: 1.1 L/min, auxiliary gas (argon) flow 1.2 L/min, plasma (Argon) gas flow: 15 L/min, Pulse Stge Voltage 800 V, ICP RF power: 1600 W, CeO/Ce ≤0.022 and Ce++/Ce+≤ 0.012, Dual Detector Mode: Pulse, Aqc. Dead Time (ns):35, Current Dead Time (ns): 35, Torch Z position (mm): 0.00. Method parameters were the following: Sweeps/Reading 20, Readings/Replicate=1, Replicates = 3 [24]. Three water samples were taken from each station and a mixed sample was taken and analysed. The water samples were taken in two seasons: summer and autumn.
2.2.b. Methodology for Statistical Analysis
The statistical analysis methods used were: the Pearson correlation method, the univariate parametric and non-parametric ANOVA analysis method, the Principal Components Analysis (PCA) and Factor Analysis (FA) analysis methods [2]. The used software is TIBCO Statistica V13 and MATLAB.
2.2.c. Methodology for Numerical Analysis
The terrain map was constructed using OpenTopography data service (Figure 2.). The spatial resolution using the USGS database (https://earthexplorer.usgs.gov/) was enough to build an appropriate hydrological model [19].
A series of 23 cross-sections were considered for unsteady flow regime simulation and diffusion modeling [19,29]. The cross-sections used in the simulation are shown in Appendix- Section A.
The used hydrodynamic model was constructed, calibrated and validated with the 1D HEC-RAS (version 6.4.1) software under an unsteady flow regime [29] (Figure 3), with hydrologic at the two upstream and downstream gauging stations [31]. The used procedure was the one used in the literature in our previous studies with the same team [29]. The step of applying the model was 12 hours, in non-stationary mode, with graphic presentation every 7 days and the flow data of the Danube that were measured by the authorities were used [19,29,32].
In order to optimize the results (using for example R2 criterion) a series of successive simulations were performed in order to refine the results. The numerical interpolation algorithm for the sources identified in the study area was described by the following steps:
Step 1 - a definition of the parameters that describe the distribution of pollution sources - the initial distribution - is made
Step 2: a monitoring point is considered - starting with the first upstream point and continuing successively downstream
Step 3: enter the parameters related to the local sources and perform the numerical simulation - HEC - RAS two-dimensional
step 4: the downstream concentrations are evaluated and the comparison is made with the measured ones, determining the quantities to be applied for correction
step 5 - change the concentrations from the upstream points to adjust the difference and repeat step 3
if the difference between the concentrations in the considered point has reached a minimum, move to the next downstream point and repeat step 3.
3. Results
3.1. Data Analysis
In the following, the statistical and numerical approaches’ results will be provided.
Table 2.
Results of the parameters from the IARC list analyzed from the water samples taken in July 2022.
Table 2.
Results of the parameters from the IARC list analyzed from the water samples taken in July 2022.
| Station | Aluminium (µg/L) | Arsenic (µg/L) | Beryllium (µg/L) |
Cadmium (µg/L) | Chromium (µg/L) | Phosphate - P-PO4 (mg/L) |
|---|---|---|---|---|---|---|
| P1 | 14.468 | 0.002 | <LOD (< 0.5 ng/L) | 0.008 | 1.027 | 0.080 |
| P2 | 19.670 | 0.001 | <LOD (< 0.5 ng/L) | 0.004 | 0.764 | 0.040 |
| P3 | 46.890 | 0.002 | <LOD (< 0.5 ng/L) | 0.021 | 1.280 | 0.070 |
| P4 | 15.704 | 0.002 | <LOD (< 0.5 ng/L) | 0.016 | 1.605 | 0.140 |
| P5 | 38.868 | 0.002 | <LOD (< 0.5 ng/L) | 0.016 | 1.239 | 0.090 |
| P6 | 17.214 | 0.001 | <LOD (< 0.5 ng/L) | 0.008 | 1.123 | 0.070 |
| P7 | 24.168 | 0.001 | <LOD (< 0.5 ng/L) | 0.038 | 1.291 | 0.050 |
| P8 | 8.665 | 0.001 | <LOD (< 0.5 ng/L) | 0.004 | 0.771 | 0.070 |
| P9 | 28.889 | 0.001 | <LOD (< 0.5 ng/L) | 0.020 | 2.318 | 0.080 |
| P10 | 32.650 | 0.002 | <LOD (< 0.5 ng/L) | 0.019 | 1.694 | 0.080 |
3.1. Statistical Approach
3.1.1. Descriptive Statistics
In this section, the elementary statistical results are presented. In tis respect, Table 3 and Table 4 show the elements of the preliminary description of chemical species.
Table 3 shows the values describing the preliminary statistics of the values measured in the monitoring campaigns
Table 3 shows the descriptive statistics for the chemical species that were measured in the two monitoring campaigns. Mean values and standard deviations and erros are determined. There are also a number of significant differences. These significant differences are presented in Table 4.
Table 4 shows the t-test values – bold values correspond to significant differences
The table above shows the results of the Fisher - t test that evaluates the different sets of measurements from the two measurement campaigns. The normal distribution was tested as in all our previous papers [2,25]. It is observed that for Phosphate, CBO5, N-NO2, N-NO3, P-PO4 3-, SO4 2-, Cl-, phenols the differences are significant. This fact is probably due to the mechanisms and processes that influence these factors and that have different effects in the two studied seasons. For the studied set of metallic species, the descriptive statistics of the measurements from the two measurement campaigns are presented in Table 5.
Table 5 shows the values describing the preliminary statistics of the values measured in the monitoring campaigns.
Necessarily, a comparison between the two data sets could be presented to highlight the differences and the seasonal variability.
Thus, for aluminium, arsenic, cadmium, chromium, and phosphate, the results of the Fisher type T-tests were calculated to highlight differences and to identify significant differences (Table 6).
Table 6 shows the t-test values – bold values correspond to significant differences.
It is observed that in the case of arsenic (p<0.001) and chromium (p<0.001) there are significant differences between the two data sets. In the case of cadmium and aluminum, the differences are insignificant, with approximately constant values recorded during the two seasons. Cadmium (Cd) could suggests Natural Sources because Cadmium occurs naturally in the Earth’s crust and can be released through geological processes. In the same time Cd could suggests Agricultural Runoff or Anthropogenic Sources. Considering the boxplot representation (Figure 4.c) the last source case could be more credible. The same discussion could be done for Aluminum.
Table 7 shows the values of the correlation coefficients between the elements that make up the entire database:
Table 7 shows the values of the coefficients – bold values correspind to significant differences
Table 7 shows the values of the correlation coefficients for the values measured during the summer season. It is observed that the number of significant correlations is relatively few - except the link between the concentration of Cr and CCO - the link is easy to understand from the literature: as it is known [2] the link between the concentration of chromium (Cr) and CCO-Cr, in the context of water quality, is primarily concerned with the potential contamination of water by chromium compounds and their impact on human health and the environment [33]. As it is known, chromium can exist in several oxidation states, but the most common and stable forms are Cr(III) and Cr(VI). Cr(VI) is particularly harmful due to its high solubility and mobility, which makes it more bioavailable and toxic [15]. Water quality assessments often measure the concentration of total chromium and specifically Cr(VI) to ensure they are below the permissible limits set by regulatory bodies [17]. In summary, the link between Cr concentration and CCO-Cr in water quality is a measure of the potential toxicity and pollution levels in water, which is critical for ensuring safe drinking water and maintaining ecological balance [1]. There are also links between the concentration of chlorine ions and the concentrations of total Nitrogen - Ntotal and the SO4 group. These aspects have been identified in the literature and have been explained [2,34]. The fact that during the summer season, the influences between the parameters are less and is largely due to the high flow of the Danube river (Figure 9) which ensures a significant dilution of the concentrations of the studied chemical species.
Table 8 shows the values of the correlation coefficients for the values measured during the autumn campaign. In this case, the number of significant correlations is significantly higher than in the previous case [2]. this situation of this kind was encountered in previous studies and was scientifically explained [2,14]. Thus, in the case of the autumn season, due to the low flow of the Danube, the influences between the different chemical elements become easier to identify. The above table shows the values of the correlation coefficients for the measurements made in the autumn season. It is observed that the number of significant correlations is significantly higher mainly due to the low recorded flow of the Danube. In these conditions of low flow in the autumn season, the influences between the measured quantities are easier to highlight.
Thus, the links between the concentration of aluminum and cadmium ions can be highlighted (r=-0.6543, p=0.04). We can also emphasize the correlation between the concentration of Fe and As ions (r=0.6954, p=0.025), a fact that could be determined by the existence of a common source. Also, there is a correlation between cadmium and phosphate concentrations (r=0.7652, p=0.010) and the link between Cd and N-NO2 (r=0.7522, p=0.027). The fact that there is obviously a seasonal variability for the concentration of N-NO2 was also highlighted in the literature [34]. The existence of a link between the two polluting factors is an original aspect that has not been highlighted until now. There is also an extremely interesting correlation factor between the concentration of Cr and that of N-NO3 (r=0.6923, p=0.027) respectively that between the concentration of Cr and the concentration of Ntotal (r=0.8094, p=0.005). These connections between the concentration of chromium ions and the other two chemical species represent a specific aspect. Our previous study [25] sheded light on the complex interactions between chromium ions, nitrate nitrogen (N-NO3), and total nitrogen (Ntotal) in the Danube River, emphasizing the need for vigilant monitoring and sustainable water management practices [10,24].
Last but not least, the links between CBO5 and NH4 (r=0.6358, p=0.048), CBO5 and Ntotal (r=0.6813, p=0.030) and between NH4 and SO4 (r=0.6907, p=0.027) should be listed, which links were also noticed in the literature[2]. Further on, we present in the form of a Boxplot the identification of the seasonal dynamics of the parameters that are included in the IARC database that studies heavy metals [24].
Figure 4 shows the Boxplot representations for heavy metal concentrations measured in the 10 monitoring points. Thus, figure 4.a shows the concentration of aluminum ions measured in the 10 monitoring points. The existence of insignificant differences can be observed (see Table 4). It is observed that during the summer season, the concentrations are significantly higher (mainly due to the increased reactivity of aluminum ions and the obvious higher contribution recorded near the monitoring point P3. Necessarily, this aspect was reported in the specialized literature and probably is due to the activity of the steel industry in the area [2,25] By analyzing the spatial distribution of aluminum concentrations than higher levels of aluminum downstream of industrial or urban areas as compared to upstream can indicate human influence.Figure 4.b shows the concentration of arsenic. The differences recorded in the two monitoring seasons are significant (Table 4) and the values measured in the warm season are systematically lower than those measured in the cold season. Arsenic is a ubiquitous toxic metal belonging to the metalloid group of the periodic system of the main group II, which occurs naturally in the lithosphere, hydrosphere and atmosphere, as well as generally in the biosphere [18]. The higher value in the cold season could be due by local industries seasonal cycles of production and reduced water flow values.
Both organic and inorganic forms of arsenic exist in nature (mostly in the form of complexes); various environmental transport routes have been identified and fairly high concentrations (mainly in water sources) have been reported in several regions around the world. Mainly, the increased concentration during the cold season could be explained by the reduced reactivity in the case of lower temperatures. In Figure 4.c, they are represented in the form of a box plot for cadmium and in Figure 4.d are represented in the form of a boxplot for the measured values of chromium. In the case of cadmium, the differences measured in the two seasons do not differ significantly (Table 4). The high contribution in the case of monitoring point P3 is also clearly observed, and an exponential decrease in the concentration of chromium along the water course is also observed. Regarding the chromium distribution, the differences recorded in the two seasons are obviously significant (Table 4) and significantly high values are also observed near monitoring points P4 and P7 respectively. However it has to be emphasized the comprehensiveness and adequacy of existing data from previous studies and monitoring efforts that have consistently shown metal concentrations within acceptable limits [5,14].
Figure 5 shows the Box plot representations for phosphate, CCO, CBO5 and NH4 concentrations measured in the 10 monitoring points. Thus, figure 5.a shows the concentration of the phosphate group measured in the 10 monitoring points. The existence of insignificant differences between the two sets of data is observed. The distribution is of a bimodal type, with a more intense contribution near point P3 with an exponential decreasing tendency - characteristic of the diffusion phenomenon. It is observed that during the summer season, the concentrations are significantly higher (mainly due to the increased reactivity of the phosphate group and the obvious higher contribution recorded near the monitoring point P3. Necessarily, this aspect was reported in the literature of specialty and is mainly due to human activity [2,25].
Figure 5.b shows the concentration of the CCO group. The differences recorded in the two monitoring seasons are insignificant and the values measured in the warm season are systematically higher than those measured in the cold season. Mainly, the concentration of CCO - the mass concentration of oxygen equivalent to the amount of potassium bichromate consumed for the oxidation in an acid environment of the dissolved and suspended organic matter present in the wastewater, is lower during the cold season [1,2]. This fact could be probably explained by the reduced chemical activity at lower temperatures. In figure 5.c, they are represented in the form of a boxplot for CBO5 and in figure 5.d, they are represented in the form of a boxplot for the measured values of NH4. In the case of CBO5 - an index that represents a measure of the organic impurity of wastewater and the amount of oxygen (mg/mass) that is required for the oxidative degradation by microorganisms of the organic substances contained in the water volume humidity, the measured differences in the two seasons are not significantly different. Also, the high contribution in the case of the monitoring points P6 and P7 is clearly observed, and an exponential decrease in concentration along the water course is also observed. Regarding the distribution of NH4, the differences recorded in the two seasons are obviously insignificant and significantly high values are also observed near the monitoring points P6 and P7 respectively. These aspects obviously represent original aspects, because such measurements with such a resolution could not be carried out until now.
Figure 6 shows the Boxplot representations for the concentrations of Ntotal, N-NO2, N-NO3 and P-PO4 measured in the 10 monitoring points. Thus, figure 6.a shows the concentration of the N-NO2 group measured in the 10 monitoring points. There are significant differences between the two data sets. The distribution is of a bimodal type, with a more intense contribution near point P3 with an exponential decreasing tendency - characteristic of the diffusion phenomenon. It is observed that during the summer season, the concentrations are significantly higher (mainly due to the increased reactivity of the N-NO2 group and the obvious higher contribution recorded during the hot season). Necessarily, this aspect was reported in the literature of specialty and is mainly due to anthropogenic activity. Figure 6.b shows the concentration of the N-NO3 group. The differences recorded in the two monitoring seasons are insignificant and the values measured in the warm season are systematically higher than those measured in the cold season. In figure 6.c, they are represented in the form of a boxplot for Ntotal and in figure 5.d, they are represented in the form of a boxplot for the measured values kf P-PO4 And the differences are insignificant
Figure 7 shows the Boxplot representations for SO4, Cl, phenols and Fe concentrations measured in the 10 monitoring points. Thus, figure 7.a shows the concentration of the SO4 group measured in the 10 monitoring points. There are significant differences between the two data sets. The distribution is of a bimodal type, with a more intense contribution near point P7 with an exponential decreasing tendency - characteristic of the diffusion phenomenon. It is observed that during the summer season, the concentrations are significantly lower (mainly due to the increased reactivity of the SO4 group and the obviously higher contribution recorded during the hot season). Necessarily, this aspect has been reported in the specialized literature and is mainly due to anthropogenic activity. Figure 7.b shows the gde Cl concentration. The differences recorded in the two monitoring seasons are significant and the values measured in the warm season are systematically lower than those measured in the cold season. In figure 7.c, they are represented in the form of a boxplot for phenols and in figure 7.d the measured values for Fe are represented in the form of a boxplot And the differences are insignificant.
3.3. PCA Method Analysis
The Principal Factors method is a classic method, often found in specialized literature and is a versatile statistical method for reducing a cases-by-variables data table to its essential features, called principal components [2,25]. Thus, several variables or studied parameters can be grouped in order to categorize them into factors/groups of influence on the variability of the data set. This method was also used in our previous studies [2,25] carried out over a period of 10 years. in that article, the classification of the factors and the identification of related sources were presented. Interestingly, unlike previous studies that revealed a low number of main influence groups, in the case of this investigation, the number of factors that were identified as main factors (i.e. with determined eigenvalues greater than unity) was 6 (see Table 9). The theorem known as the Kaiser criterion in (PCA) which stated that the stable solution correspond to eigenvalues grater that 1 should be considered. Thus, for the summer season campaign, 6 main factors are identified that can explain 91.82% of the variability of the entire data set. In the case of the autumn measurement session, the main significant factors identified are also 6, thus covering more than 91% of the variability of the collected data set. This aspect is extremely interesting because in the studies carried out between 1990 and 2000 in the study area, the number of significant factors was a maximum of 4 [2].
Next, we will present the results of the PCA analysis applied to the database containing the concentration of heavy metals (Figure 8). Thus, in the case of these two measurement campaigns, it is observed that the data sets are grouped differently. If in the summer campaign, the data set contains a number of 2 main factors (Table 9), the same can be said for the autumn campaign (Table 9). This derives from the fact that the eigenvalues that are identified and that have the higher value as a unit determine the consideration of the first 2 factors (Figure 8.a). The main factor 1 corresponds to the groups formed by Aluminum and Cadmium and Chromium between which there is a fairly strong correlation, a fact that leads us to the idea of a common source. Figure 8.b shows the fact that there is a fairly strong connection between the measured aluminum concentration and the minimum surface obtained based on the Cd and Cr concentration values. In the case of the autumn measurement campaign, the configuration of the PCA diagram changes, with Aluminum being negatively correlated in relation to the concentrations of the two metals Cd and Cr. This fact is also observable from the surface plot diagram in Figure 8.d.
Figure 8.a shows the elements that form the first main factor in the set of data measured in the summer campaign. This factor which is responsible for explaining 34.47% of the variance of the data set (Figure 8.a) includes the elements: Aluminum, Cadmium, phosphate, pH, N-NO2, N-NO3, the SO4 group, chlorine and conductivity. This factor which could be attributed more to the influence of anthropic activity brings together elements that are related to industrial activities in the area.
Factor 2 which is responsible for explaining 17.17% of the variation of the data set includes elements such as Chromium, CBO5, NH4, N-NO3, N-total would represent a factor related to pollution due to biological factors in the study area. Factor 3, which explains approximately 14.58% of the variance of the data set from the July campaign, includes elements such as Arsenic and Iron (see Appendix - section B). Factor 3 (Figure 8.c) which explains approximately 14.58% of the variation of the data group includes elements such as Aluminum and pH - a factor that includes components with high chemical influence. Factors 4 (Figure 8.e) which explain approximately 11.44%, respectively factors 5 and 6 which explain 7.78% and 6.41% include CCO - factor 5 and phenols (factor 6).
In the case of the autumn campaign, the situation has changed quite significantly (Figure 8.b). Thus, the factor that is responsible for explaining 31.17% (Table 9) of the variance of the October data set (Figure 8.b) includes the elements: Cadmium, phosphate, pH, N-NO2, the SO4 group, chlorine and conductivity. Note the elimination of the aluminum element from this factor. This factor could also be attributed to the influence of human activity in the area. The main factor 2 that explains 24.70% of the data set variant (see Appendix - section C) includes Chromium, CBO5, NH4, N-NO3, N-total would represent a factor related to pollution due to biological factors in the study area. It is observed the elimination of the N-NO2 group within this factor is found in the group of factor 3. Factor 3, which explains approximately 14.58%. Factor 3 (Figure 8.d) which explains approximately 11.63% of the variation of the data group includes elements such as Arsenic and Fe - a factor that includes components with similar chemical reactivity. This aspect represents a difference from the previous case. Factor 4 (Figure 8.d) which explains approximately 10.16% of the variation of the data group includes elements such as Aluminum and pH - a factor that includes components with high chemical influence. Factors 5 and 6 which explain 7.30% and 6.41% include CCO - factor 5 and phenols respectively (factor 6).
3.4. Cluster Method Analysis
In the following, the results of the cluster analysis are presented to identify, depending on the geometric distance between the elements, the way of grouping and ranking between the sizes determined in the two campaigns. This topological analysis method was chosen in order to highlight more easily the difference between the two data sets [35]. The main reason to use cluster analysis in statistical analysis is to group similar data points together based on their characteristics - topological distance. This unsupervised machine learning technique helps to identify patterns and structure in data, making it easier to understand and analyze [36]. By organizing data into clusters, we can uncover hidden insights and make predictions about future data points. In this sense, the Euclidean distance calculation method and the Weighted pair centroid method were chosen - a method often found in specialized literature. [37]. Figure 9.a,b show the analysis results of these classifications based on distances. It is observed the existence of some changes regarding the closest group - respectively the group in which Cadmium was replaced with Arsenic in the group located at the smallest distance. There was also a permutation in the group formed by the radical SO4, CBO5 and respectively Cl.
In this sense, we can state that the structure of the topological cluster model for the Danube is given in Figure 9 [35,37]. In this way, the fact that there is an absolutely striking similarity in the two sets of data was observed. Identified clusters have a similar component with two small exceptions. the method allows the classification of groups that seem to be closely related using the tolopogical criterion. For example - the first cluster is formed by cadmium, arsenic and N-NO2. A cluster with cadmium, arsenic, and nitrite (N-NO2) could indicate a common source or similar behavior of these substances in the water environment. Here are some possible explanations for such a cluster: a) industrial pollution: these substances are often byproducts of industrial processes as in the studied area- in the study area there are a number of important industrial objectives.; b) Agricultural Runoff: Cadmium and arsenic can be present in pesticides and fertilizers used in agriculture, and nitrites are a common component of nitrogen-based fertilizers. Runoff from agricultural fields can carry these substances into water bodies; c) Natural Occurrence: While often associated with human activity, these substances can also occur naturally. Arsenic, for instance, can be released into groundwater through the erosion of natural deposits. Further researches need to be developed.
3.4. PCA Method Analysis for Metals Samples
In what follows, we will consider the PCA method applied only to the metal species identified and studied in the two measurement campaigns in the Danube River water. Table 10 shows the coordinates of the variables according to the main factors in the July database. It is observed that factor 1 (Figure 9.a) which describes the variant of over 41.84% of the total set, includes Al and Cadmium. Factor 2 which describes the variation of over 24.67% of the total set includes Chrome and Iron. The last factor, which is responsible for 20.37% of the total variation, includes Arsenic (Figure 9.c).
*Marked values are those with significant eigenvalues.
In the case of the October database, things are a little different. Within this data set, there are only two significant main values. It can be observed that factor 1, which describes the variation of more than 45.53% of the total set, includes Al, Cr and Iron (Figure 9.b). Factor 2 describes the variation of over 34.48% of the total set including Arsenic and Cadmium (Figure 9.d).
Figure 10.a shows that factor 1, which describes the variation of more than 50% of the total set, includes Al, Cr and Cadmium.
In the same time, Figure 10.b shows that factor 1, which describes the variant of over 50% of the total set, includes Al, Cr and Cadmium.
3.4. Numerical Analysis
For a numerical simulation and an evaluation of the distribution of the concentrations of the studied metals in the investigation area, we considered the possibility of using dedicated software programs, often used in the literature [1,6,23]. HEC-RAS is a program that allows, in the new version, to solve diffusion-type equations in the 2D case, such as the equations below[18]:
where is the height of the surface (in m), is the elevation of the cell in the Cartesian coordinate system,, - is the water depth (in m), and are the specific flows along the axes and respectively ; and and are the specific speeds along the axes nd respectively ; - is the gravitational acceleration (in ), is the Manning roughness coefficient (in ), - is the density (in ), iar - represents the components of the flow tensor and is the Corriolis parameter (in ). These equations can be solved within Hec-Ras using finite element calculation [32,38,39]). The term represents the attenuation term - correlated with the transfer phenomenon. In the context of the HEC-RAS bidimensional model, an additive terms can be significant in order to obtain a correlation for concentration variability by two reasons: a) model complexity: an additive term can account for additional physical processes or factors that affect concentration variability but are not captured by the primary terms of the model; b) accuracy and precision: additive term can improve the accuracy and precision of the model by fine-tuning the representation of the transport and diffusion of substances in water which is the main aim; c) calibration and validation: These terms can be crucial for the calibration and validation of the model, ensuring that the simulated data matches observed data as closely as possible.
The modeler in HEC-RAS allowed the development of geometric data either by primary drawing in the river system scheme using the Geometric Data Window (Figure 3) or by developing a scheme in HEC-RAS Mapper (HEC-RAS Mapper). Thus the river system diagram is a diagram of how the water flow system is connected together. In the present case, 2D models were considered because the existence of weirs in the river bed make the evaluated concentrations differ and there are differences between areas related to the two banks. The calibration of the hydraulic model was first performed upstream of the study area, more precisely in the Braila sector for Danube river, and later downstream, at the mouth of the Ceatal branch in the Reni - Tulcea area. The calibration of the model in the HEC-RAS software was made by alternate values of the Manning roughness coefficients, between 0.025 and 0.03, and by applying the rating curve data from the Tulcea hydrometric station [13,19]. In this respect, by considering the disadvantage of the static method is that the simulations cannot be calibrated with field data, was used the dynamic methodology has the advantage of introducing a much more complex input data set, including calibration data, which gives a higher confidence in the results obtained.
In general, the time of concentration (TC) is a parameter in runoff estimation, used for the study and design of different types of hydrographic systems (Pierfranco Costabile, Masih Zolghadr). Any error in the TC calculation leads to an inaccurate flux estimate, which can lead to over- or under-dimensioning of the results. Therefore, choosing the correct time estimation method is of great importance.
Figure 11.
representation the graph showing the monthly evolution of the Danube flow in the monitored area - for the non-stationary study.
Figure 11.
representation the graph showing the monthly evolution of the Danube flow in the monitored area - for the non-stationary study.
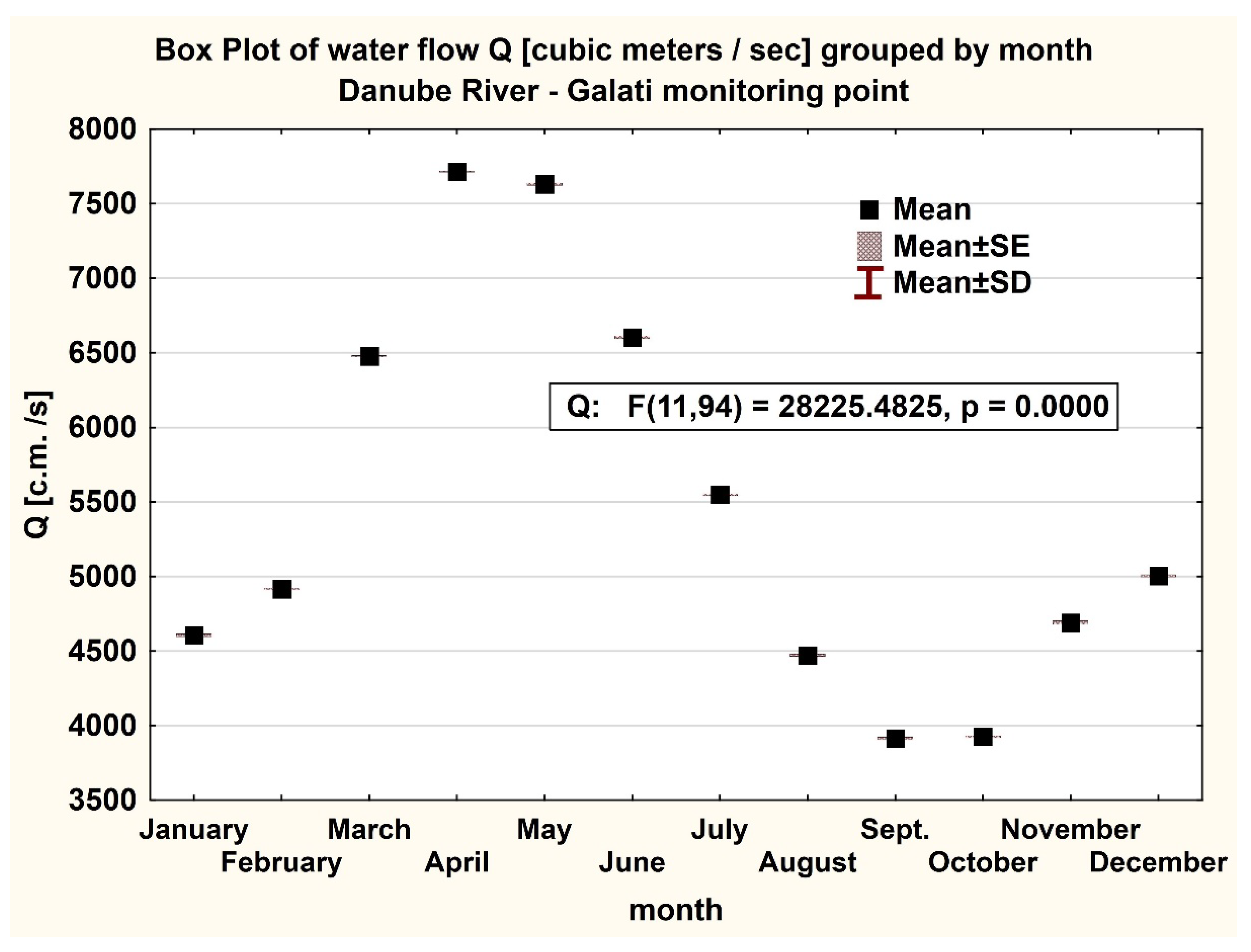
In the present case, we considered unsteady modeling using the data on the monthly flow of the Danube throughout the year 2022, with a sampling rate of 1 hour, an average rate of 1 week and a graphic evaluation with a rate of 1 month. In this way, we considered the model data to be the closest to reality. Also, I entered the monthly flow data for the Siret and Prut rivers according to https://www.hidro.ro/prognoze/.
Considering the ratio between the flows of the tributaries and that of the Danube, the contribution related to the transport attributed to the tributaries is significant only in the areas close to the confluence points, manifesting a dilution along the main flow.
For each chemical species, a number of simulations were carried out, the scenarios being selected based on the comparison between the measured values and those evaluated within the 2D used models.
Figure 12 shows the results of the 2D diffusion models for the two measurement campaigns - from July (Figure 12.a) and from October (Figure 12.b) respectively for iron. Thus, in Figure 12.a, because the flow of the Danube is higher, the flood zones that are recorded near the right bank are also considered [1,32,39]. The measured values and those obtained after the evaluation are in agreement. Thus, during the summer, the values obtained are systematically higher - an observation made in other previous studies [2,34]. The most interesting aspect is given by the possibility of predicting the downstream values, although the distances between the monitoring points cover a distance of 57.8 km. The quality of fit between the measured and evaluated values is in good agreement (R² = 0.8715).
Figure 13 shows the results of the 2D diffusion models for the two measurement campaigns - from July (Figure 13.a) and from October (Figure 13.b) respectively for chromium. Thus, in Figure 13.a, the evaluated and measured values have a constant trend with minimal variations, a maximum being recorded next to the monitoring points P4 and P9 respectively (Figure 13.b). this aspect may be related to the industrial activities near the two points. Similarly, during the autumn campaign, the tendency to keep a constant value is respected with a tendency to reduce values downstream. The measured values and those obtained after the evaluation are in accordance with the measured values (R² > 0.80). This is relatively easy to understand, considering the fact that there are values that tend to maintain a constant trend along the studied 57.8 km.
Figure 14 shows the results of the 2D diffusion models for the two measurement campaigns - from July (Figure 14.a) and from October (Figure 14.b) respectively for Cadmium. In figure 14.a, the evaluated and measured values have a constant trend with minimal variations, a maximum being recorded near the monitoring point P7 (Figure 14.a). This aspect may be related to the industrial activities near this point. Similarly, during the autumn campaign, the tendency to maintain a constant value is respected. The measured values and those obtained after the evaluation are in accordance with the measured values (R² > 0.67).
This is relatively easy to understand, considering the fact that there are values that tend to maintain a constant trend along the studied 57.8 km.
Figure 15 shows the results of the 2D diffusion models for the two measurement campaigns - from July (Figure 15.a) and from October (Figure 15.b) respectively for arsenic. Thus, in Figure 15.a, the evaluated and measured values have a constant tendency, however, being maximum near the monitoring points P5 and P9, respectively (Figure 15.a). Similarly, during the autumn campaign, the tendency to keep a constant value is respected with a tendency to reduce values downstream. The measured and evaluated values are in agreement, the values from the autumn campaign being significantly higher than those during the summer. This was also observed by other authors [1,32].
4. Discussion
The aims of this paper were the distributions and dispersions structures of heavy metals in the Danube Course - in this complex and important environmental issue [26,40].
In the present study, the influences of river-tributary connectivity on metal migration were analyzed and their contributions were neglijables. The average concentrations of Cr, Al, Cd, Fe and As were considered statistically and dynamically approaches.
In our previous studies, we analyzed the seasonal variation of water quality parameters in the area of Municipality of Galati city [2,14,25]. Thus, through statistical approaches [2], significant seasonal differences were highlighted using Factor Analysis, Principal Component Analysis and ANOVA methods. Following the studies carried out, the existence of a self-purification capacity was found.
In this respect, In current campaign, each measured parameter presents a seasonal variation (table 3 and Table 4). Comparing with previous studies, we can highlight some aspects. As example, for N-NO3 the values are much lower than those recorded in our previous campaign carried out between 1990-1998 [2]. The trend is still respected i.e. the values in summer are lower than those in autumn. The smaller amounts of NO3- are attributed to the rivers’ intense photosynthesis that occurs in summer. The large amounts of NO3- are attributed to the water discharges of municipal waste [2,18].
Generaly, the measured parameters’ variations in the current campain are similarly the variations found by in the previous our study during 1990-1998 [24,27].
PCA Method Analysis
In the related section, the PCA results obtained by this specific statistical method based on the correlations. In this respect, were identified a number of six important factors that directly influences the state parameters of the Danube River [15,16,41]. These main key identified factors [2,42,43], shows different seasonal weights , based on a clear seasonal variability [2,16,25]: - in the summer we highlighted the anthropogenic footprint on water quality ecosystem [41,44]. In the autumn season, reducing or even missing the natural biological activity leads to decrease of pollution caused by natural sources of the region [38,45].
The most important factor group includes the elements: Aluminum, Cadmium, phosphate, pH, N-NO2, N-NO3, the SO4 group, chlorine and conductivity (Figure 8.a and Figure 8.b). This factor which could be at-tributed more to the influence of anthropic activity brings together elements that are related to industrial activities in the area [41,46,47]. The second factor includes elements such as Chromium, CBO5, NH4, N-NO3, N-total would represent a factor related to pollution due to biological factors in the study area [13,33,46].
From the point of view of the PCA method, the summer campaign allows the identification of some elements that form the six main factors [6,41,48]. Thus, the main factor F1 - the factor: N-Total, P-PO4 3-, N-NO2, SO42-, Cl-, Arsenic, respectively the main factor F2: Cadmium, N-NO2, N-NO3-, Fe, Chromium, Aluminium (Figure 8.a and Figure 8.b). These factors can be attributed to a combination of natural geological processes [41,42,43] and human activities [49] which contributes to the simultaneous presence of these chemical substances in the Danube River area [5,18,34,48]. For the autumn campaign, the PCA method presents a set of 6 main factors. Thus, for the main factors F1 which includes: Aluminium, Chromium, CCO, CBO5, NH4+, N-NO3-, N-Total respectively factor F2 which includes: Cadmium, N-NO2, phenols, P-PO4 3. The seasonal variation can be explained by: Agricultural Runoff and Wastewater Discharges (for N-Total); Wastewater Discharges, Biological Processes and Urban Runoff (for P-PO4 3-); Biological Processes and Wastewater Discharges (for N-NO2); Natural Sources and industrial Processes (for SO₄); Industrial Discharges (for Cl-) respectively Natural Sources and Agricultural Runoff (for As).
In this way, they can be identified and explained through these groupings and through the variation of the water flow, the seasonal variation.
What is interesting is that the cluster type method presents a relatively simpler way of grouping sources with a relatively point-like character (Figure 9.a and Figure 9.b): thus the easiest cluster to identify - Cadmium, N-NO2 and As presents practically a Similarity Metrics: because there were calculated similarity metrics between Cd, N-NO₂, and As concentrations which lead to consider there are common sources [50] (e.g., industrial discharges) for these substances with influence form biological process [51]. This fact is easy to highlight considering the position of the points where the maximum values are recorded. What is important is that Iron is adherent, correlated with a greater distance to this cluster(Figure 9.a and Figure 9.b) [52]. The possible source is near the monitoring point P5 (Figure 3.c) and the adherence from the topological point of view to this kernel can be explained mainly by the decreasing trend for the downstream areas (Figure 9.a and Figure 9.b). Mainly, the downward trend has the same configuration, which explains this cluster membership [53].
Another important aspect is that presented by the cluster formed by phosphates and phenols [54]. It can be seen that there is an accession to the previous group in the case of autumn, but the configuration remains similar [2]. The distributions from the summer campaign have a bimodal configuration and a decreasing trend for the downstream points, with local maxima near points P3 and P9. In the case of phenols, the higher values in the case of the cooler season determine the fact that phenols adhere differently.
The group formed by N-NH4 and N-NO3 (Figure 9.a and Figure 9.b) during the summer campaign is easy to understand through the trimodal configuration shown (Figure 5.d and Figure 6.c). as is known, if NH₄ and NO₃ tend to co-occur or exhibit similar patterns, they may form a cluster, which is the case.
The last group consisting of Chromium, N-total and N-NH4 (Figure 9.a and Figure 9.b) can be easily understood through the prism of environmental context by considering the sources of these substances and their transport mechanisms respectively seasonal variations and spatial distribution also play a role.
Numerical Approach
In the new conditions, the studies carried out in different areas on the course of the Danube illustrate the existence of certain spatial distributions, especially for the concentrations of As, Cr, Fe, etc. in the surface water of the lower basin of the Danube [19,26,29].
in this sense, a numerical approach to highlight the dynamics, using numerical methods of hydraulic modeling proved to be necessary. We chose a 2-dimensional approach [55], because previous evaluations were one-dimensional and cannot explain specific aspects [32].
In the articles from the literature, sets of in situ measurements were taken and one-dimensional modeling [56] was carried out, not highlighting point sources or areas where the concentrations present obvious differences along the course [31,55]. In the case of the present study, we took water samples from the main tributaries of the Danube in the study area [33]. Considering the ratio between the flows of the tributaries and those of the Danube, the influences proved to be without obvious significance.
However, it was necessary to create a non-stationary 2D model because certain values of the measured concentrations can only be explained by certain plume effects inside the water flow [22,38].
The sampling points were carefully selected, being the hypothesis of the existence of point sources that increase the concentration of metals on the Danube course in the studied area.
The sampling points were carefully selected, being the hypothesis of the existence of point sources that increase the concentration of metals on the Danube course in the studied area.
A trend of increasing pollution with aluminum ions can be observed along the course of the Danube, especially in the downstream area of the studied area [23]. This aspect can only be explained by the influence of human activity in the area of the last three study points. Also, a similar trend is observed regarding the concentration of chromium. the existence of some ports / shipyards could be the cause of such consequences [57].
For example, the cadmium concentration has a maximum recorded around point P7 and an attenuation of the concentration is observed in the downstream area, an aspect that could be deepened through sediment analyzes for the evaluation of a mitigation process.
The PCA and Pearson correlation analysis showed that for As and Cr originate mainly from the natural environment with antropic additional contribution; Cd, Al and Fe were affected by industry and agriculture throughout the studied route.
These aspects are obviously original and underline the main characteristic of the river and specify its self-purification capacity
Metals being difficult to diffuse, there is a need to be monitored during precipitation events and the relationship between soil properties and the degree of use will be investigated in future experiments.
An important aspect that emerged from the study is the fact that, despite the fact that there is an uneven distribution of the concentrations of heavy metals studied in the river bed, in the areas where there are no point sources, the concentrations are relatively low and the habitats of community interest are not under pressure important.
- -
- A further study on heavy metals on the Danube Course should include the following elements:
- -
- A complex analysis of the bioavailability of heavy metals in sediments using high-performance analytical methods such as inductively coupled plasma mass spectrometry (ICP-MS) or atomic absorption spectroscopy (AAS) from our laboratory.
- -
- An assessment of factors influencing the sorption and mobility of heavy metals in soils and their mechanisms of accumulation.
- -
- A comparison of different technologies for the remediation of soils polluted with heavy metals, such as in-situ or ex-situ physico-chemical processes, or bioremediation using microorganisms or plants.
Author Contributions
Conceptualization, C.T. and G.M.; methodology, C.T. and G.M.; software, M.A. and G.M.; validation, M.A. and G.M. and M.C.; formal analysis, V.C. and G.M.; investigation, V.C. and M.C.; resources, X.X.; data curation, V.C. and M.C..; writing—original draft preparation, C.S. and C.C.; writing—review and editing, M.A. and G. M.; visualization, C.S. and C.C.; supervision, V.C. and M.C.; project administration, C.T. and G.M.; funding acquisition, C.T.. All authors have read and agreed to the published version of the manuscript. All the authors have equal contributions.
Funding
This study was supported by project „Advanced nanotechnology based approaches to waste water purification form organic pollutants and their monitoring in water bodies”, 2SOFT/1.2/139”.
Acknowledgments
This study was supported by project „Advanced nanotechnology based approaches to waste water purification form organic pollutants and their monitoring in water bodies”, 2SOFT/1.2/139”.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Supplementary data – www.physugal.ro/Art_W_appendix.pdf.
References
- Popescu, F.; Trumić, M.; Cioabla, A.E.; Vujić, B.; Stoica, V.; Trumić, M.; Opris, C.; Bogdanović, G.; Trif-Tordai, G. Analysis of Surface Water Quality and Sediments Content on Danube Basin in Djerdap-Iron Gate Protected Areas. Water 2022, 14, 2991. [Google Scholar] [CrossRef]
- Popa, P.; Murariu, G.; Timofti, M.; Georgescu, L.P. MULTIVARIATE STATISTICAL ANALYSES OF DANUBE RIVER WATER QUALITY AT GALATI, ROMANIA. Environ. Eng. Manag. J. 2018, 17, 1249–1266. [Google Scholar] [CrossRef]
- Fang, T.; Lu, W.; Cui, K.; Li, J.; Yang, K.; Zhao, X.; Liang, Y.; Li, H. Distribution, Bioaccumulation and Trophic Transfer of Trace Metals in the Food Web of Chaohu Lake, Anhui, China. Chemosphere 2019, 218, 1122–1130. [Google Scholar] [CrossRef] [PubMed]
- Hakanson, L. An Ecological Risk Index for Aquatic Pollution Control.a Sedimentological Approach. Water Research 1980, 14, 975–1001. [Google Scholar] [CrossRef]
- Simionov, I.-A.; Călmuc, M.; Iticescu, C.; Călmuc, V.; Georgescu, P.-L.; Faggio, C.; Petrea, Ş.-M. Human Health Risk Assessment of Potentially Toxic Elements and Microplastics Accumulation in Products from the Danube River Basin Fish Market. Environmental Toxicology and Pharmacology 2023, 104, 104307. [Google Scholar] [CrossRef] [PubMed]
- Teodorof, L.; Ene, A.; Burada, A.; Despina, C.; Seceleanu-Odor, D.; Trifanov, C.; Ibram, O.; Bratfanof, E.; Tudor, M.-I.; Tudor, M.; et al. Integrated Assessment of Surface Water Quality in Danube River Chilia Branch. Applied Sciences 2021, 11, 9172. [Google Scholar] [CrossRef]
- Fishes-08-00387.Pdf.
- Matache, M.L.; Marin, C.; Rozylowicz, L.; Tudorache, A. Plants Accumulating Heavy Metals in the Danube River Wetlands. J Environ Health Sci Engineer 2013, 11, 39. [Google Scholar] [CrossRef] [PubMed]
- Georgescu, P.-L.; Moldovanu, S.; Iticescu, C.; Calmuc, M.; Calmuc, V.; Topa, C.; Moraru, L. Assessing and Forecasting Water Quality in the Danube River by Using Neural Network Approaches. Science of The Total Environment 2023, 879, 162998. [Google Scholar] [CrossRef] [PubMed]
- Bąk, Ł.; Szeląg, B.; Sałata, A.; Studziński, J. Modeling of Heavy Metal (Ni, Mn, Co, Zn, Cu, Pb, and Fe) and PAH Content in Stormwater Sediments Based on Weather and Physico-Geographical Characteristics of the Catchment-Data-Mining Approach. Water 2019, 11, 626. [Google Scholar] [CrossRef]
- Iticescu, C.; Georgescu, P.-L.; Arseni, M.; Rosu, A.; Timofti, M.; Carp, G.; Cioca, L.-I. Optimal Solutions for the Use of Sewage Sludge on Agricultural Lands. Water 2021, 13, 585. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, Z.; Cao, H.; Xu, M.; Xu, L. Concentrations, Speciation, and Ecological Risk of Heavy Metals in the Sediment of the Songhua River in an Urban Area with Petrochemical Industries. Chemosphere 2019, 219, 538–545. [Google Scholar] [CrossRef] [PubMed]
- Simionov, I.-A.; Cristea, D.S.; Petrea, Ștefan-M. ; Mogodan, A.; Jijie, R.; Ciornea, E.; Nicoară, M.; Turek Rahoveanu, M.M.; Cristea, V. Predictive Innovative Methods for Aquatic Heavy Metals Pollution Based on Bioindicators in Support of Blue Economy in the Danube River Basin. Sustainability 2021, 13, 8936. [Google Scholar] [CrossRef]
- Calmuc, M.; Calmuc, V.; Arseni, M.; Topa, C.; Timofti, M.; Georgescu, L.P.; Iticescu, C. A Comparative Approach to a Series of Physico-Chemical Quality Indices Used in Assessing Water Quality in the Lower Danube. Water 2020, 12, 3239. [Google Scholar] [CrossRef]
- Dong, D.; Zhao, X.; Hua, X.; Liu, J.; Gao, M. Investigation of the Potential Mobility of Pb, Cd and Cr(VI) from Moderately Contaminated Farmland Soil to Groundwater in Northeast, China. Journal of Hazardous Materials 2009, 162, 1261–1268. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Xu, Z.; Hu, X.; Zhang, N.; Chen, T.; Ding, Z. Sorption of Pb(II) and Cu(II) on the Colloid of Black Soil, Red Soil and Fine Powder Kaolinite: Effects of pH, Ionic Strength and Organic Matter. Environmental Pollutants and Bioavailability 2019, 31, 85–93. [Google Scholar] [CrossRef]
- Resz, M.-A.; Roman, C.; Senila, M.; Török, A.I.; Kovacs, E. A Comprehensive Approach to the Chemistry, Pollution Impact and Risk Assessment of Drinking Water Sources in a Former Industrialized Area of Romania. Water 2023, 15, 1180. [Google Scholar] [CrossRef]
- Takić, L.; Mladenović-Ranisavljević, I.; Vasović, D.; Đorđević, L. The Assessment of the Danube River Water Pollution in Serbia. Water Air Soil Pollut 2017, 228, 380. [Google Scholar] [CrossRef]
- Banescu, A.; Arseni, M.; Georgescu, L.P.; Rusu, E.; Iticescu, C. Evaluation of Different Simulation Methods for Analyzing Flood Scenarios in the Danube Delta. Applied Sciences 2020, 10, 8327. [Google Scholar] [CrossRef]
- Zhang, W.; Long, J.; Zhang, X.; Shen, W.; Wei, Z. Pollution and Ecological Risk Evaluation of Heavy Metals in the Soil and Sediment around the HTM Tailings Pond, Northeastern China. IJERPH 2020, 17, 7072. [Google Scholar] [CrossRef]
- Da Silva Júnior, R.O.; Almeida, H.P.; Da Silva, M.S.; França, A.C.; Balleroni, E.; Dos Santos, N.; Vilela, P.H.; De Melo, A.M.Q.; Guimarães, J.T.F. Methodological Approach for an Online Water Quality Monitoring System in an Iron Ore Tailing Dam. Water 2023, 15, 3663. [Google Scholar] [CrossRef]
- Pham Van, C.; Chua, V. Numerical Simulation of Hydrodynamic Characteristics and Bedload Transport in Cross Sections of Two Gravel-Bed Rivers Based on One-Dimensional Lateral Distribution Method. International Journal of Sediment Research 2020, 35, 203–216. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, W.; Zeng, Y.; Liang, D.; Deng, Y.; Zhang, X.; Li, Y. How Does Three Gorges Dam Regulate Heavy Metal Footprints in the Largest Freshwater Lake of China. Environmental Pollution 2022, 292, 118313. [Google Scholar] [CrossRef] [PubMed]
- Calmuc, V.A.; Calmuc, M.; Arseni, M.; Topa, C.M.; Timofti, M.; Burada, A.; Iticescu, C.; Georgescu, L.P. Assessment of Heavy Metal Pollution Levels in Sediments and of Ecological Risk by Quality Indices, Applying a Case Study: The Lower Danube River, Romania. Water 2021, 13, 1801. [Google Scholar] [CrossRef]
- Iticescu, C.; Georgescu, L.P.; Murariu, G.; Topa, C.; Timofti, M.; Pintilie, V.; Arseni, M. Lower Danube Water Quality Quantified through WQI and Multivariate Analysis. Water 2019, 11, 1305. [Google Scholar] [CrossRef]
- Saeed, O.; Székács, A.; Jordán, G.; Mörtl, M.; Abukhadra, M.R.; Eid, M.H. Investigating the Impacts of Heavy Metal(Loid)s on Ecology and Human Health in the Lower Basin of Hungary’s Danube River: A Python and Monte Carlo Simulation-Based Study. Environ Geochem Health 2023, 45, 9757–9784. [Google Scholar] [CrossRef] [PubMed]
- Cordeli, A.N. Bioaccumulation of Metals in Some Fish Species from the Romanian Danube River: A Review. 2023.
- Simionov, I.-A.; Călmuc, M.; Iticescu, C.; Călmuc, V.; Georgescu, P.-L.; Faggio, C.; Petrea, Ş.-M. Human Health Risk Assessment of Potentially Toxic Elements and Microplastics Accumulation in Products from the Danube River Basin Fish Market. Environmental Toxicology and Pharmacology 2023, 104, 104307. [Google Scholar] [CrossRef]
- "; Dunarea de Jos"; University of Galati, Romania; Arseni, M. ; Roșu, A.; “Dunarea de Jos” University of Galati, Romania; Murariu, G.; “Dunarea de Jos” University of Galati, Romania; Georgescu, L.P.; “Dunarea de Jos” University of Galati, Romania; et al. The Role of River Channel Roughness for Water Level Modeling during the 2005 Year Flood on Siret River Using HEC-RAS Model. Ann_UGAL_Math_Phys_Mec 2019, 42, 68–76. [Google Scholar] [CrossRef]
- Water Directive.
- Barrero-Moreno, M.C.; Diaz-Vargas, C.A.; Restrepo-Parra, E. Computational Simulation of Filters Used in the Removal of Heavy Metals Using Rice Husks. Agriculture 2021, 11, 146. [Google Scholar] [CrossRef]
- Zolghadr, M.; Rafiee, M.R.; Esmaeilmanesh, F.; Fathi, A.; Tripathi, R.P.; Rathnayake, U.; Gunakala, S.R.; Azamathulla, H.M. Computation of Time of Concentration Based on Two-Dimensional Hydraulic Simulation. Water 2022, 14, 3155. [Google Scholar] [CrossRef]
- Maxim, C.; Filote, C.; Cojocaru, D.C. COMPARATIVE STUDY OF PHYSICAL INDICATORS AND THOSE OF THEIR REGIME OF OXYGEN, ON WATER QUALITY OF THE GREAT ùOMUZU RIVER, IN THE YEAR 2009. 2011.
- Iticescu, C.; Georgescu, L.P.; Murariu, G.; Topa, C.; Timofti, M.; Pintilie, V.; Arseni, M. Lower Danube Water Quality Quantified through WQI and Multivariate Analysis. Water 2019, 11, 1305. [Google Scholar] [CrossRef]
- Crişan, V.-E.; Dincă, L.; Bragă, C.; Murariu, G.; Tupu, E.; Mocanu, G.D.; Drasovean, R. The Configuration of Romanian Carpathians Landscape Controls the Volume Diversity of Picea Abies (L.) Stands. Land 2023, 12, 406. [Google Scholar] [CrossRef]
- Crişan, V.-E.; Dincă, L.; Bragă, C.; Murariu, G.; Tupu, E.; Mocanu, G.D.; Drasovean, R. The Configuration of Romanian Carpathians Landscape Controls the Volume Diversity of Picea Abies (L.) Stands. Land 2023, 12, 406. [Google Scholar] [CrossRef]
- Murariu, G.; Dinca, L.; Tudose, N.; Crisan, V.; Georgescu, L.; Munteanu, D.; Dragu, M.D.; Rosu, B.; Mocanu, G.D. Structural Characteristics of the Main Resinous Stands from Southern Carpathians, Romania. Forests 2021, 12, 1029. [Google Scholar] [CrossRef]
- Jin, Y.; Zhou, Q.; Wang, X.; Zhang, H.; Yang, G.; Lei, T.; Mei, S.; Yang, H.; Liu, L.; Yang, H.; et al. Heavy Metals in the Mainstream Water of the Yangtze River Downstream: Distribution, Sources and Health Risk Assessment. IJERPH 2022, 19, 6204. [Google Scholar] [CrossRef] [PubMed]
- Costabile, P.; Costanzo, C.; Ferraro, D.; Macchione, F.; Petaccia, G. Performances of the New HEC-RAS Version 5 for 2-D Hydrodynamic-Based Rainfall-Runoff Simulations at Basin Scale: Comparison with a State-of-the Art Model. Water 2020, 12, 2326. [Google Scholar] [CrossRef]
- Luo, K.; Liu, H.; Yu, E.; Tu, Y.; Gu, X.; Xu, M. Distribution and Release Mechanism of Heavy Metals in Sediments of Yelang Lake by DGT. Stoch Environ Res Risk Assess 2020, 34, 793–805. [Google Scholar] [CrossRef]
- Ha, M.; Schleiger, R. Environmental Science.
- Githaiga, K.B.; Njuguna, S.M.; Gituru, R.W.; Yan, X. Water Quality Assessment, Multivariate Analysis and Human Health Risks of Heavy Metals in Eight Major Lakes in Kenya. Journal of Environmental Management 2021, 297, 113410. [Google Scholar] [CrossRef]
- Feng, W.; Wang, T.; Zhu, Y.; Sun, F.; Giesy, J.P.; Wu, F. Chemical Composition, Sources, and Ecological Effect of Organic Phosphorus in Water Ecosystems: A Review. Carbon Res. 2023, 2, 12. [Google Scholar] [CrossRef]
- Xu, M.; Wang, R.; Yang, X.; Yang, H. Spatial Distribution and Ecological Risk Assessment of Heavy Metal Pollution in Surface Sediments from Shallow Lakes in East China. Journal of Geochemical Exploration 2020, 213, 106490. [Google Scholar] [CrossRef]
- Bąk, Ł.; Szeląg, B.; Sałata, A.; Studziński, J. Modeling of Heavy Metal (Ni, Mn, Co, Zn, Cu, Pb, and Fe) and PAH Content in Stormwater Sediments Based on Weather and Physico-Geographical Characteristics of the Catchment-Data-Mining Approach. Water 2019, 11, 626. [Google Scholar] [CrossRef]
- Pavel, A.; Durisch-Kaiser, E.; Balan, S.; Radan, S.; Sobek, S.; Wehrli, B. Sources and Emission of Greenhouse Gases in Danube Delta Lakes. Environ Sci Pollut Res 2009, 16, 86–91. [Google Scholar] [CrossRef] [PubMed]
- Feng, W.; Wang, T.; Zhu, Y.; Sun, F.; Giesy, J.P.; Wu, F. Chemical Composition, Sources, and Ecological Effect of Organic Phosphorus in Water Ecosystems: A Review. Carbon Res. 2023, 2, 12. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Barbeş, L.; Dani, A. Statistical Analysis of the Quality Indicators of the Danube River Water (in Romania). In Frontiers in Water-Energy-Nexus—Nature-Based Solutions, Advanced Technologies and Best Practices for Environmental Sustainability; Naddeo, V., Balakrishnan, M., Choo, K.-H., Eds.; Advances in Science, Technology & Innovation; Springer International Publishing: Cham, 2020; pp. 277–279. ISBN 978-3-030-13067-1. [Google Scholar]
- Hakanson, L. An Ecological Risk Index for Aquatic Pollution Control.a Sedimentological Approach. Water Research 1980, 14, 975–1001. [Google Scholar] [CrossRef]
- Ultsch, A.; Lötsch, J. Euclidean Distance-Optimized Data Transformation for Cluster Analysis in Biomedical Data (EDOtrans). BMC Bioinformatics 2022, 23, 233. [Google Scholar] [CrossRef] [PubMed]
- Hemming, K.; Eldridge, S.; Forbes, G.; Weijer, C.; Taljaard, M. How to Design Efficient Cluster Randomised Trials. BMJ 2017, j3064. [Google Scholar] [CrossRef] [PubMed]
- Staples, L.; Ring, J.; Fontana, S.; Stradwick, C.; DeMaio, J.; Ray, H.; Zhang, Y.; Zhang, X. Reproducible Clustering with Non-Euclidean Distances: A Simulation and Case Study. Int J Data Sci Anal 2023. [Google Scholar] [CrossRef]
- Feio, M.J.; Hughes, R.M.; Callisto, M.; Nichols, S.J.; Odume, O.N.; Quintella, B.R.; Kuemmerlen, M.; Aguiar, F.C.; Almeida, S.F.P.; Alonso-EguíaLis, P.; et al. The Biological Assessment and Rehabilitation of the World’s Rivers: An Overview. Water 2021, 13, 371. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Xu, Z.; Hu, X.; Zhang, N.; Chen, T.; Ding, Z. Sorption of Pb(II) and Cu(II) on the Colloid of Black Soil, Red Soil and Fine Powder Kaolinite: Effects of pH, Ionic Strength and Organic Matter. Environmental Pollutants and Bioavailability 2019, 31, 85–93. [Google Scholar] [CrossRef]
- Brunner, G. HEC-RAS Verification and Validation Tests.
- Calmuc, M.; Calmuc, V.; Arseni, M.; Topa, C.; Timofti, M.; Georgescu, L.P.; Iticescu, C. A Comparative Approach to a Series of Physico-Chemical Quality Indices Used in Assessing Water Quality in the Lower Danube. Water 2020, 12, 3239. [Google Scholar] [CrossRef]
- Antohi, V.M.; Ionescu, R.V.; Zlati, M.L.; Iticescu, C.; Georgescu, P.L.; Calmuc, M. Regional Regression Correlation Model of Microplastic Water Pollution Control Using Circular Economy Tools. IJERPH 2023, 20, 4014. [Google Scholar] [CrossRef]
Figure 1.
The the map of monitoring points configuration and a broader regional map.
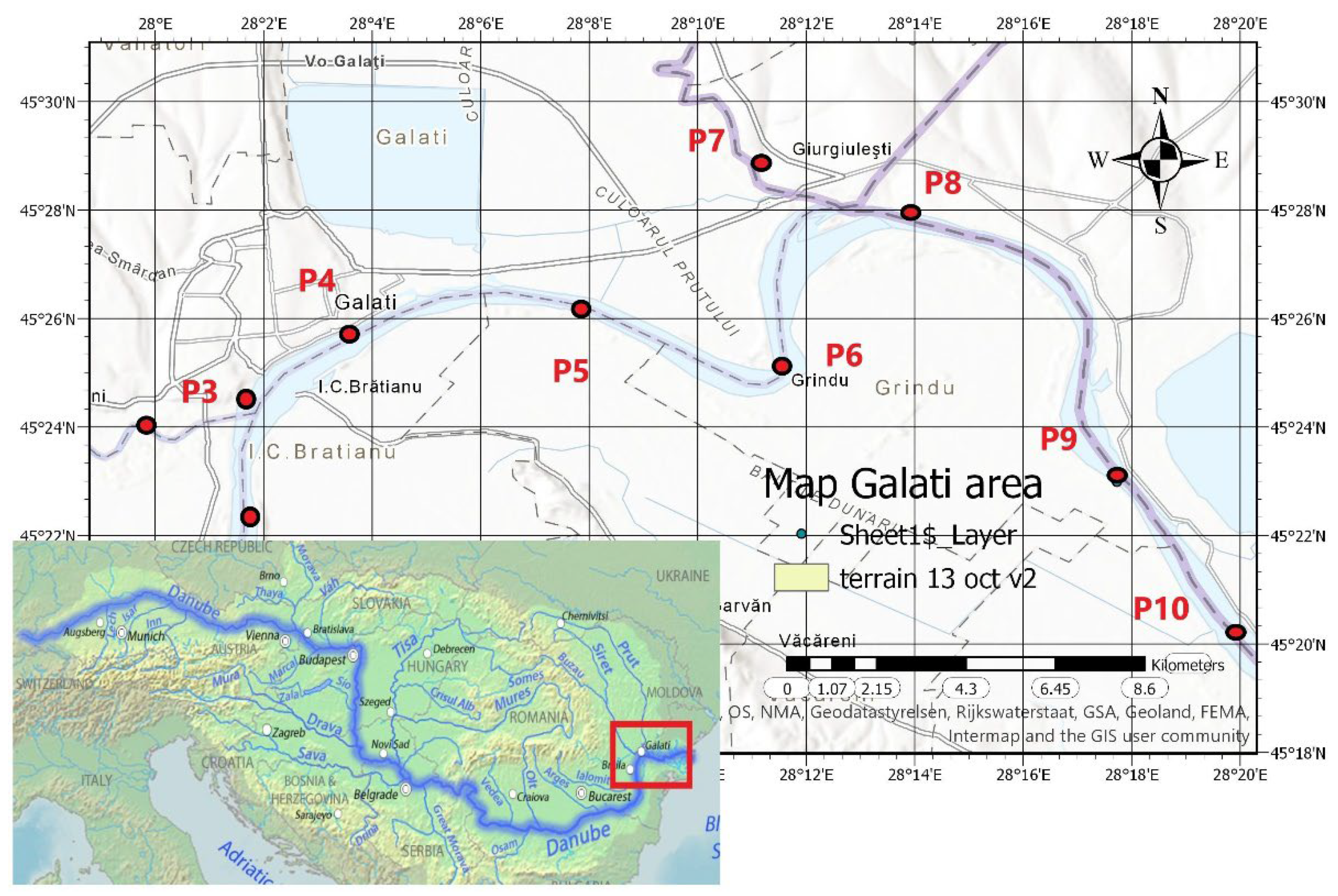
Figure 2.
USGS database terrain map for hydrodynamic model.
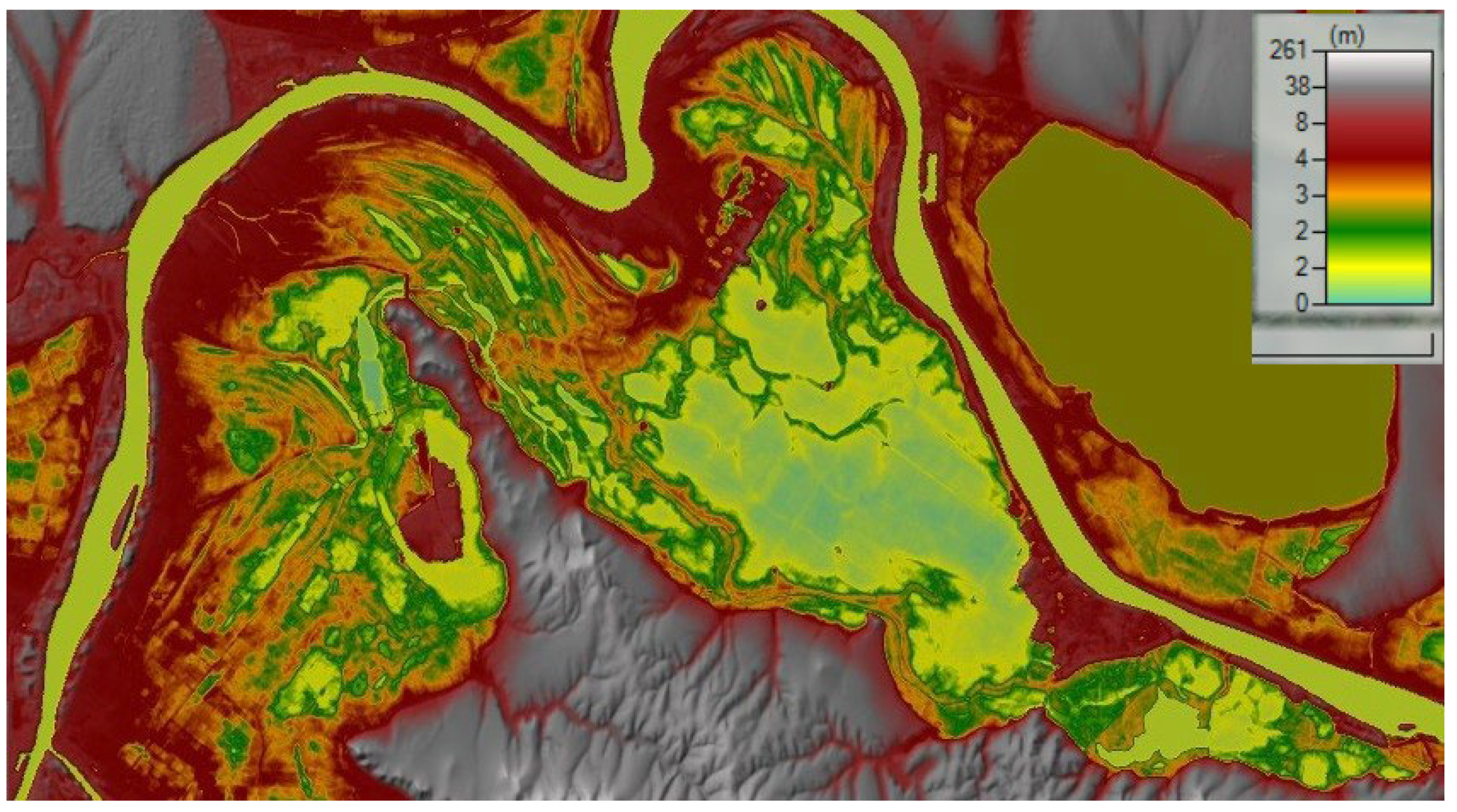
Figure 3.
The HEC-RAS hydrological terrain map with transversal cross sections for numerical model.
Figure 4.
boxplot representation for heavy metals and phenols in the two measurement campaigns in the Danube River study area: (a) boxplot representation for aluminium concentration seasonally measured in the 10 monitoring points; (b) boxplot representation for arsenic concentration seasonally measured in the 10 monitoring points; (c) boxplot representation for the cadmium concentration seasonally measured in the 10 monitoring points; (d) boxplot representation for the chromium concentration seasonally measured in the 10 monitoring points;.
Figure 4.
boxplot representation for heavy metals and phenols in the two measurement campaigns in the Danube River study area: (a) boxplot representation for aluminium concentration seasonally measured in the 10 monitoring points; (b) boxplot representation for arsenic concentration seasonally measured in the 10 monitoring points; (c) boxplot representation for the cadmium concentration seasonally measured in the 10 monitoring points; (d) boxplot representation for the chromium concentration seasonally measured in the 10 monitoring points;.
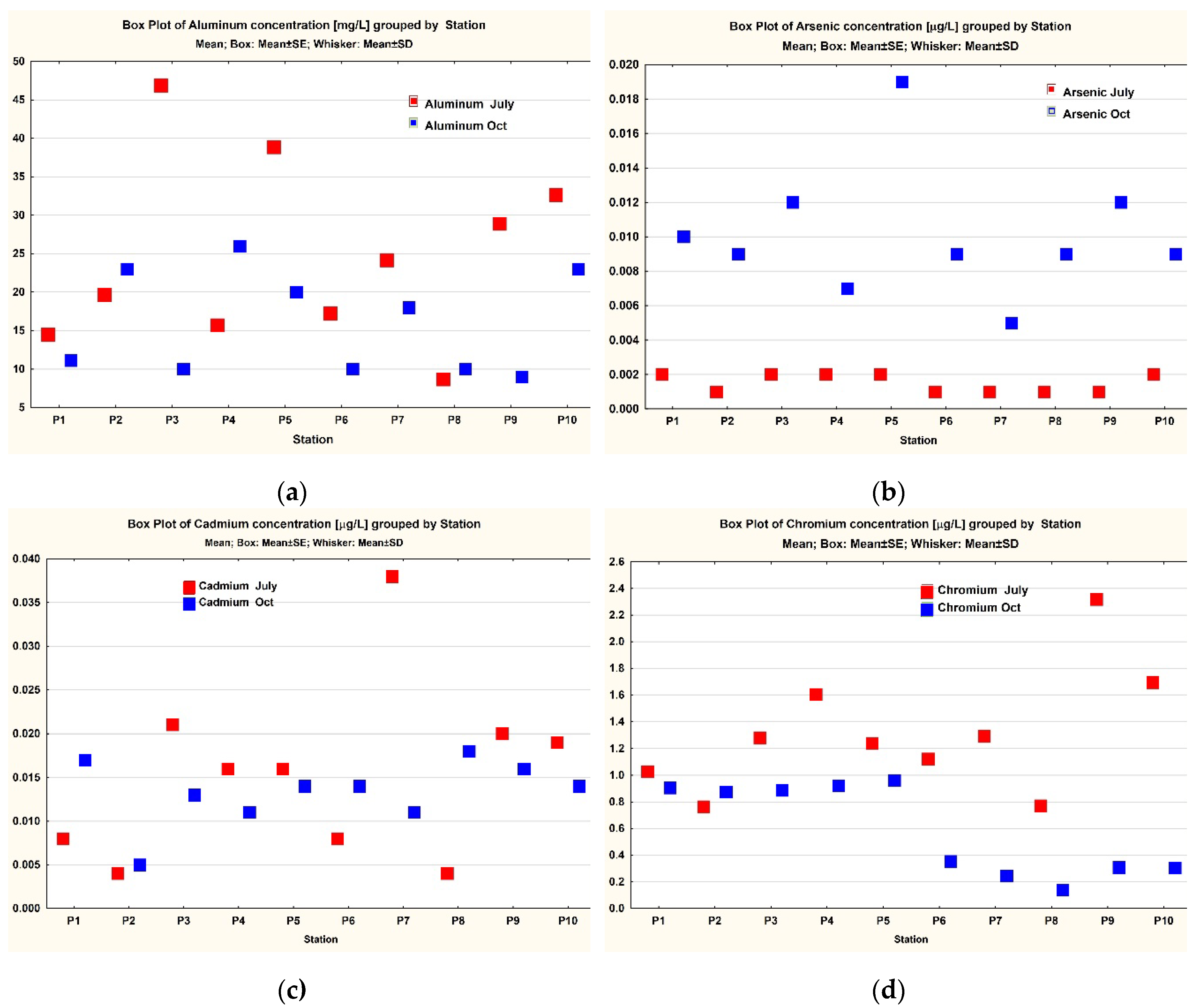
Figure 5.
boxplot representation for the two measurement campaigns in the Danube River study area: (a) boxplot representation for phosphonate concentration seasonally measured in the 10 monitoring points; (b) boxplot representation for CCO concentration seasonally measured in the 10 monitoring points; (c) boxplot representation for CBO5 concentration seasonally measured in the 10 monitoring points; (d) boxplot representation for NH4 concentration seasonally measured in the 10 monitoring points;.
Figure 5.
boxplot representation for the two measurement campaigns in the Danube River study area: (a) boxplot representation for phosphonate concentration seasonally measured in the 10 monitoring points; (b) boxplot representation for CCO concentration seasonally measured in the 10 monitoring points; (c) boxplot representation for CBO5 concentration seasonally measured in the 10 monitoring points; (d) boxplot representation for NH4 concentration seasonally measured in the 10 monitoring points;.
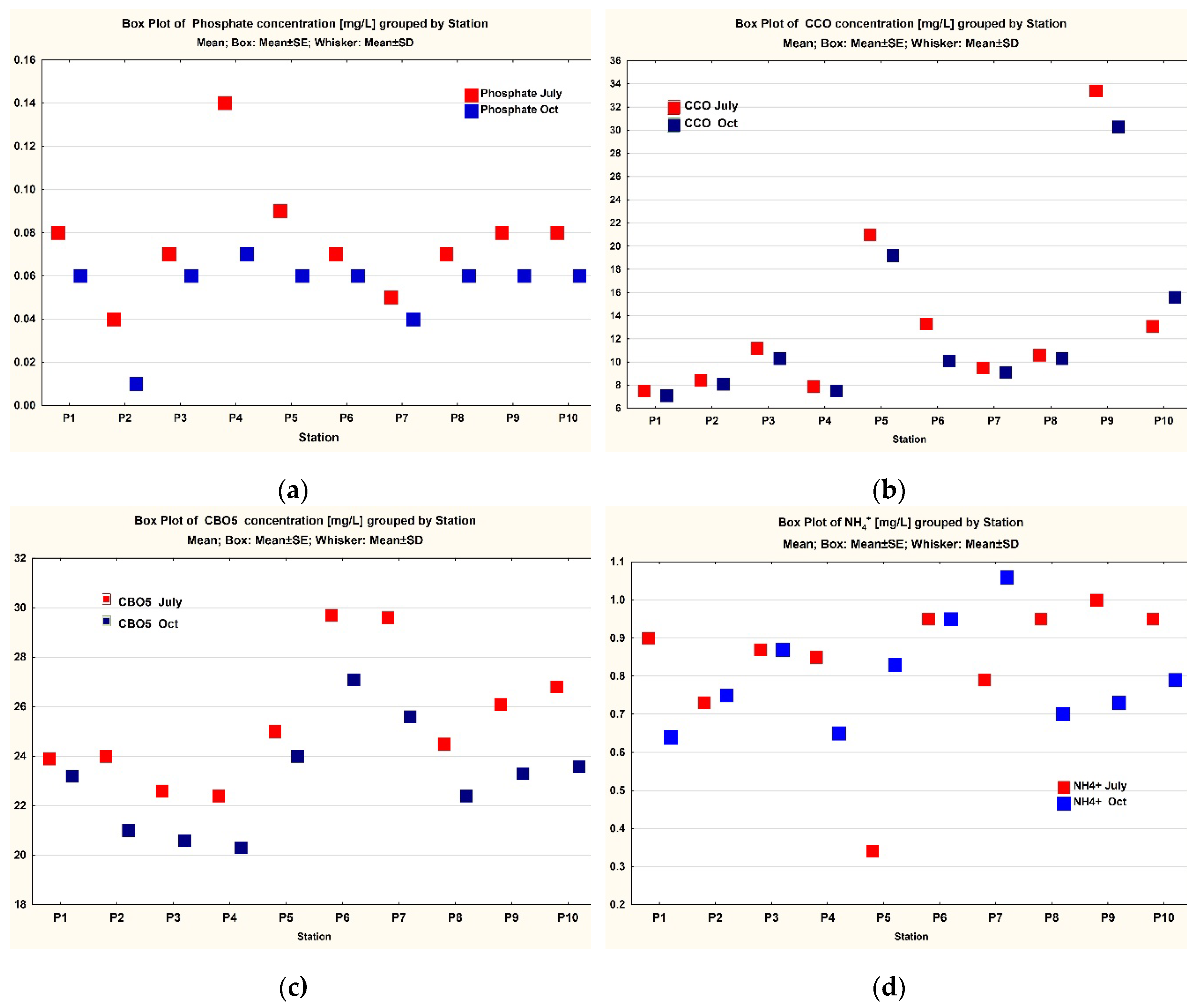
Figure 6.
boxplot representation the two measurement campaigns in the Danube River study area: (a) boxplot representation for the N-NO2 concentration seasonally measured in the 10 monitoring points; (b) boxplot representation for the N-NO2 concentration seasonally measured in the 10 monitoring points; (c) boxplot representation for the N-total concentration seasonally measured in the 10 monitoring points; (d) boxplot representation for the P-PO4 concentration seasonally measured in the 10 monitoring points;.
Figure 6.
boxplot representation the two measurement campaigns in the Danube River study area: (a) boxplot representation for the N-NO2 concentration seasonally measured in the 10 monitoring points; (b) boxplot representation for the N-NO2 concentration seasonally measured in the 10 monitoring points; (c) boxplot representation for the N-total concentration seasonally measured in the 10 monitoring points; (d) boxplot representation for the P-PO4 concentration seasonally measured in the 10 monitoring points;.
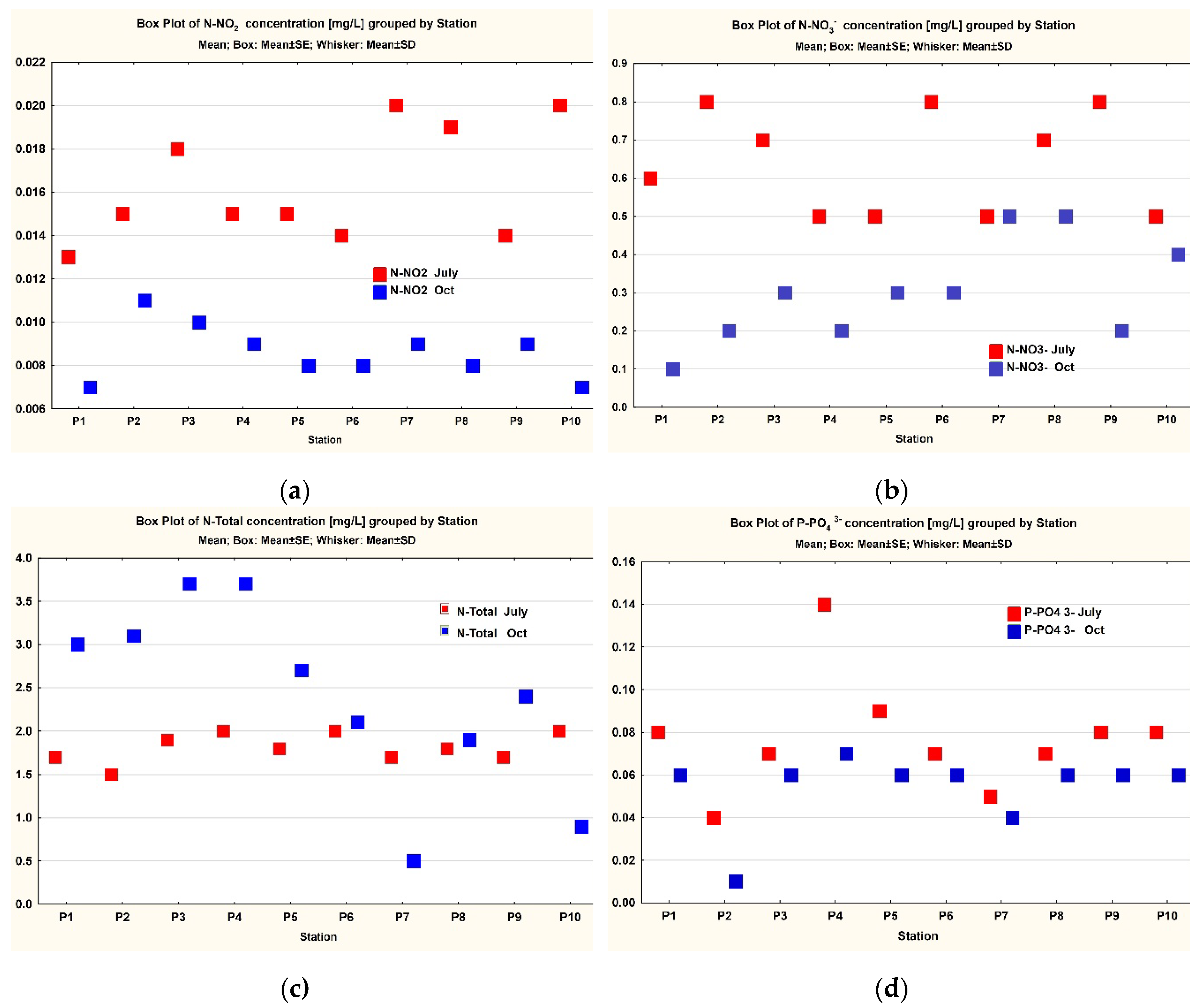
Figure 7.
boxplot representation the two measurement campaigns in the Danube River study area: (a) boxplot representaiton for SO4 concentration seasonally measured in the 10 monitoring points; (b) boxplot representation for Cl concentration seasonally measured in the 10 monitoring points; (c) boxplot representation for phenols concentration seasonally measured in the 10 monitoring points; (d) boxplot representation for Fe concentration seasonally measured in the 10 monitoring points.
Figure 7.
boxplot representation the two measurement campaigns in the Danube River study area: (a) boxplot representaiton for SO4 concentration seasonally measured in the 10 monitoring points; (b) boxplot representation for Cl concentration seasonally measured in the 10 monitoring points; (c) boxplot representation for phenols concentration seasonally measured in the 10 monitoring points; (d) boxplot representation for Fe concentration seasonally measured in the 10 monitoring points.
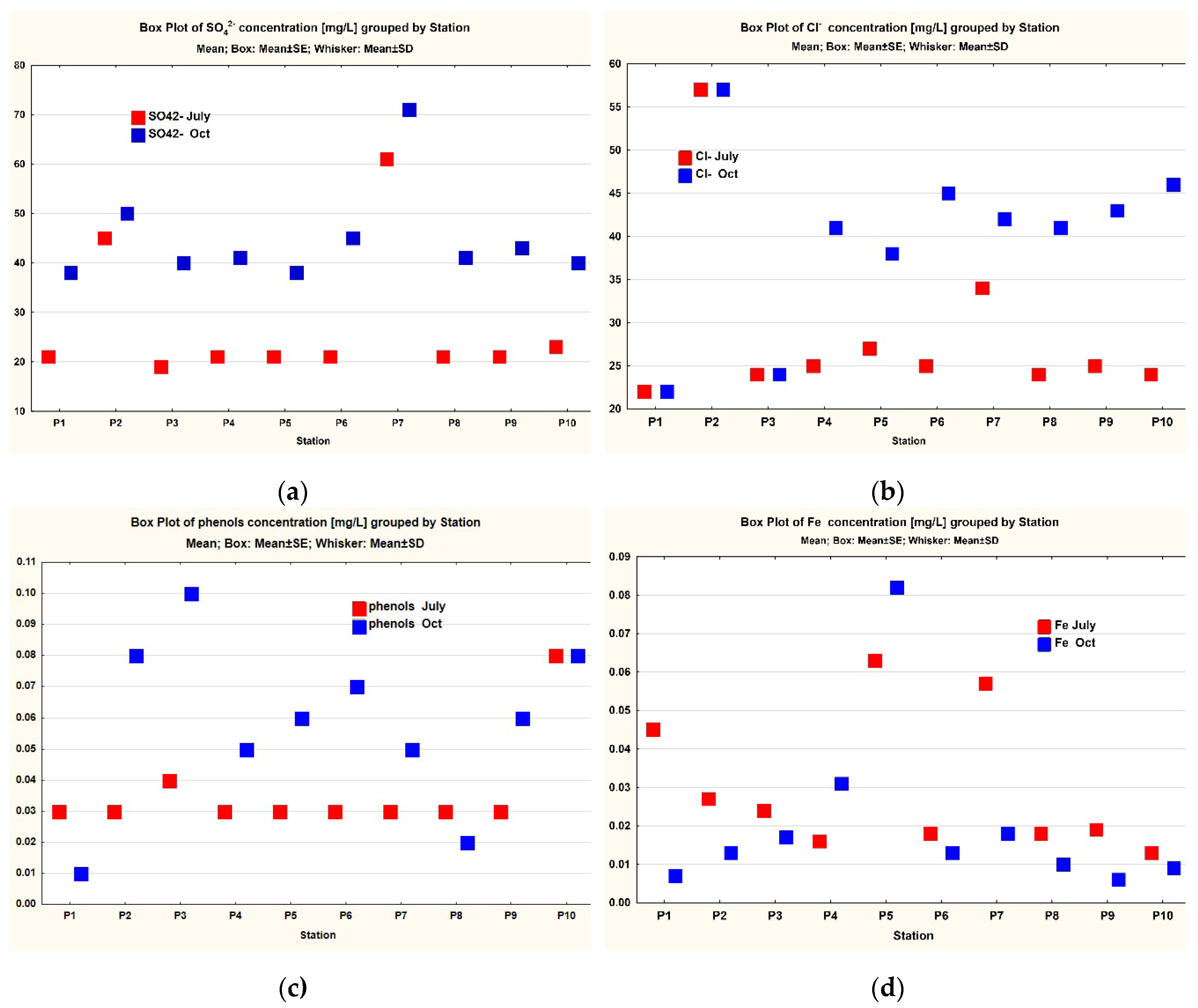
Figure 8.
PCA representation of the two measurement campaigns in the Danube River study area: (a) PCA representation with main factors 1 and 2 for the July campaign; (b) 3D surface representation for aluminium as a function of the other two metals in factor 1; (c) PCA representation with main factors 1 and 2 for the October campaign; (d) 3D surface plot for aluminium as a function of the other two metals in factor 1;.
Figure 8.
PCA representation of the two measurement campaigns in the Danube River study area: (a) PCA representation with main factors 1 and 2 for the July campaign; (b) 3D surface representation for aluminium as a function of the other two metals in factor 1; (c) PCA representation with main factors 1 and 2 for the October campaign; (d) 3D surface plot for aluminium as a function of the other two metals in factor 1;.
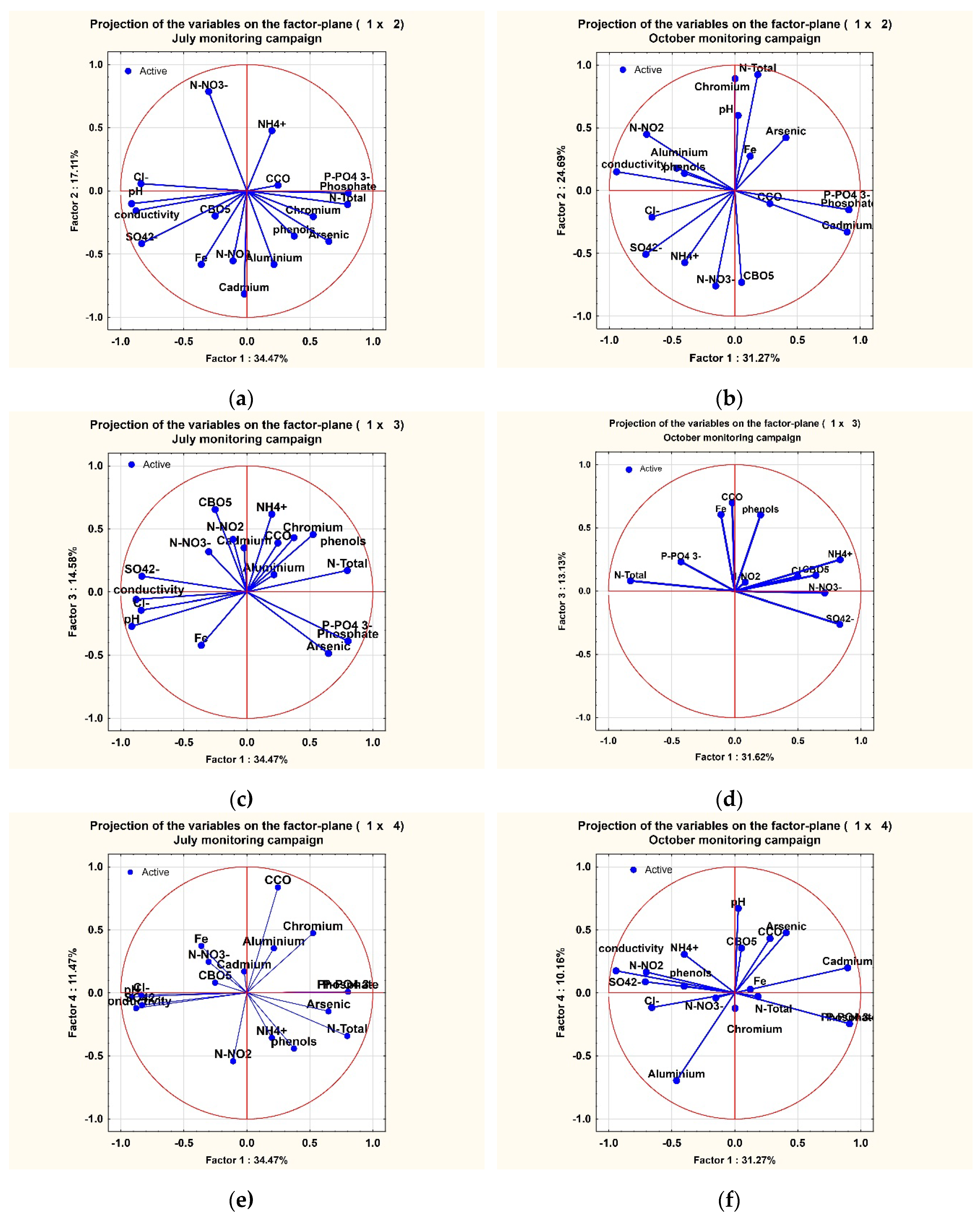
Figure 9.
a) Tree Diagram for monitored Variables - Weighted pair-group centroid (median) - Euclidean distances- July monitoring campaign; b) Tree Diagram for monitored Variables - Weighted pair-group centroid (median) - Euclidean distances- October monitoring campaign.
Figure 9.
a) Tree Diagram for monitored Variables - Weighted pair-group centroid (median) - Euclidean distances- July monitoring campaign; b) Tree Diagram for monitored Variables - Weighted pair-group centroid (median) - Euclidean distances- October monitoring campaign.
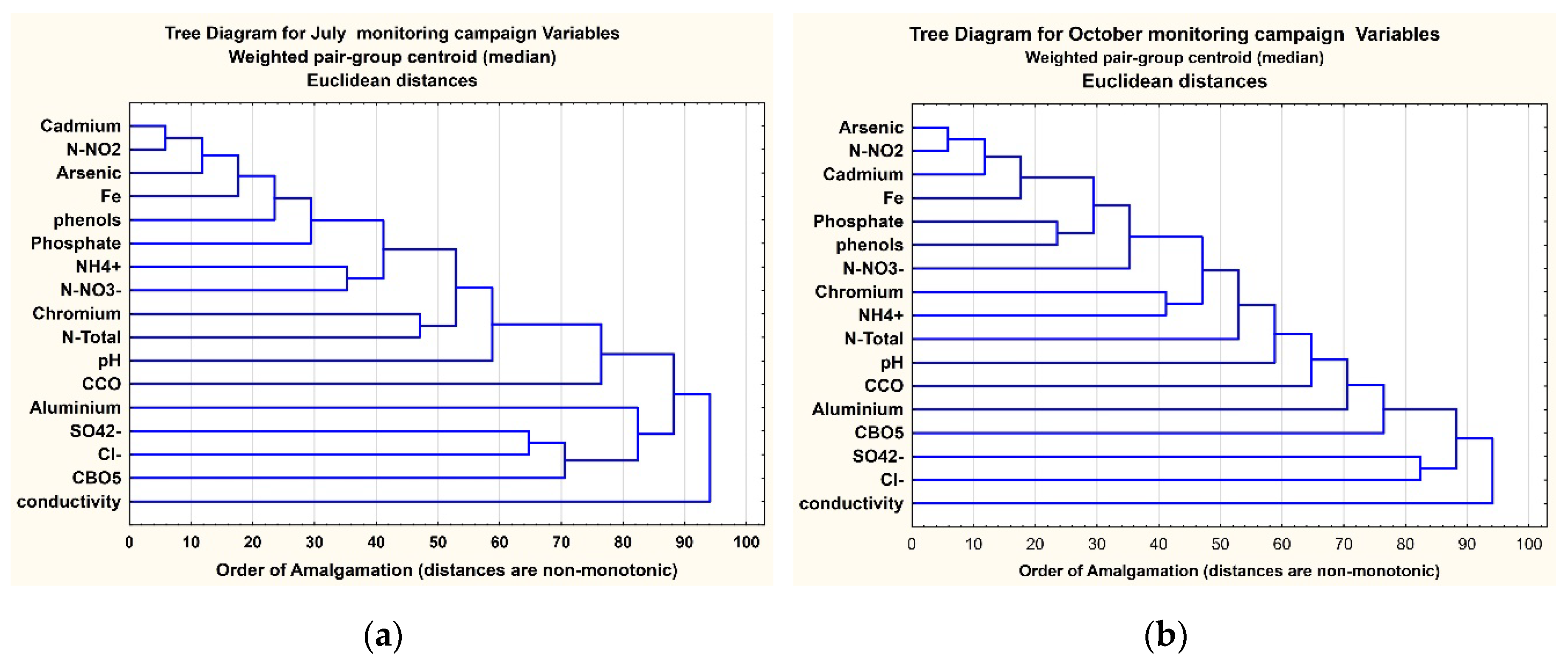
Figure 10.
PCA representation of the two measurement campaigns in the Danube River study area: (a) PCA representation with main factors 1 and 2 for the July campaign; (b) PCA representation with main factors 1 and 3 for the July campaign; (c) PCA representation with main factors 1 and 2 for the October campaign; (d) PCA representation with main factors 1 and 3 for the October campaign.
Figure 10.
PCA representation of the two measurement campaigns in the Danube River study area: (a) PCA representation with main factors 1 and 2 for the July campaign; (b) PCA representation with main factors 1 and 3 for the July campaign; (c) PCA representation with main factors 1 and 2 for the October campaign; (d) PCA representation with main factors 1 and 3 for the October campaign.
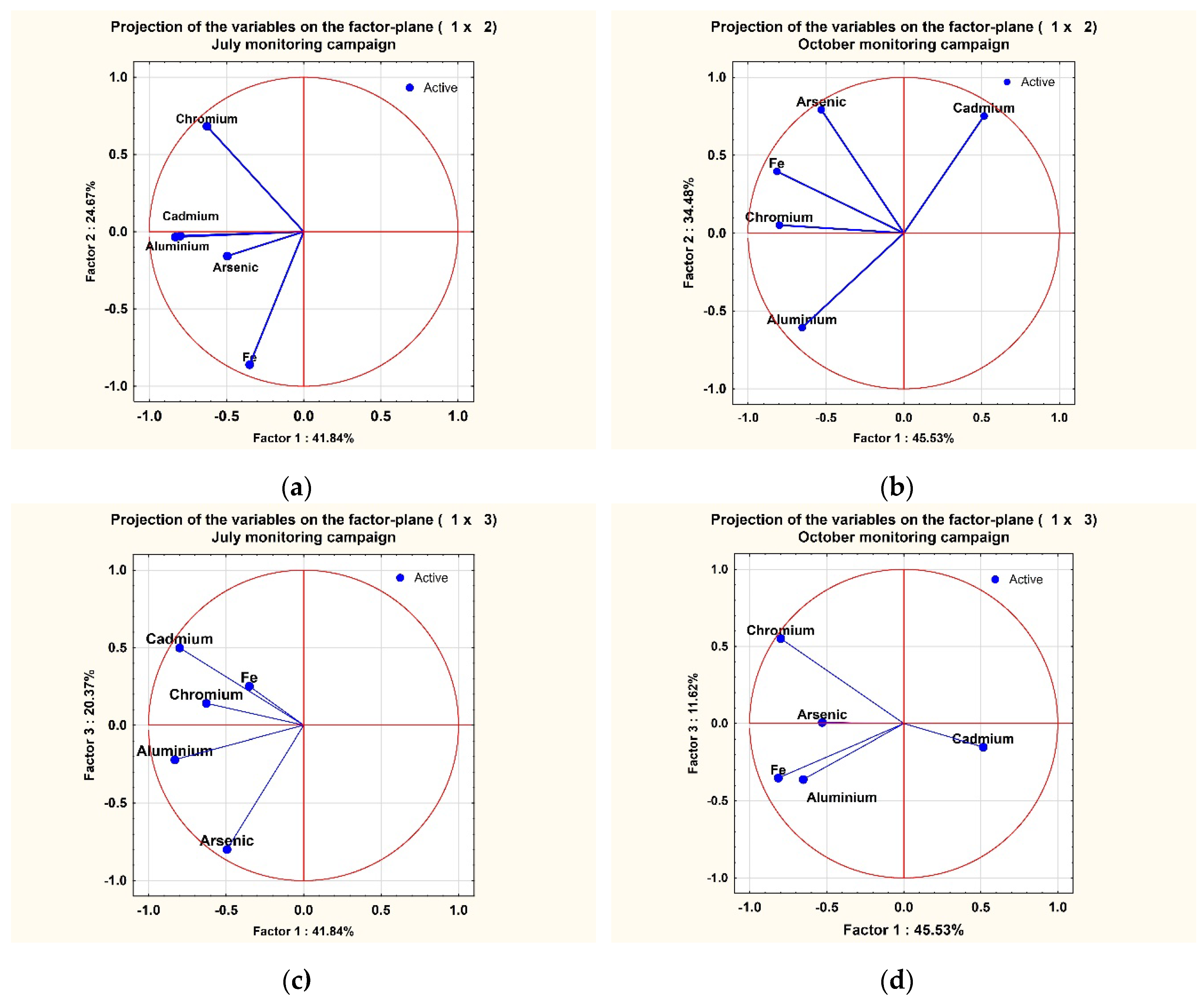
Figure 12.
representation in the form of distribution maps: (a) representation of distribution maps for Fe concentration – July campaign; (b) representation of distribution maps for Fe concentration – October campaign;
Figure 12.
representation in the form of distribution maps: (a) representation of distribution maps for Fe concentration – July campaign; (b) representation of distribution maps for Fe concentration – October campaign;
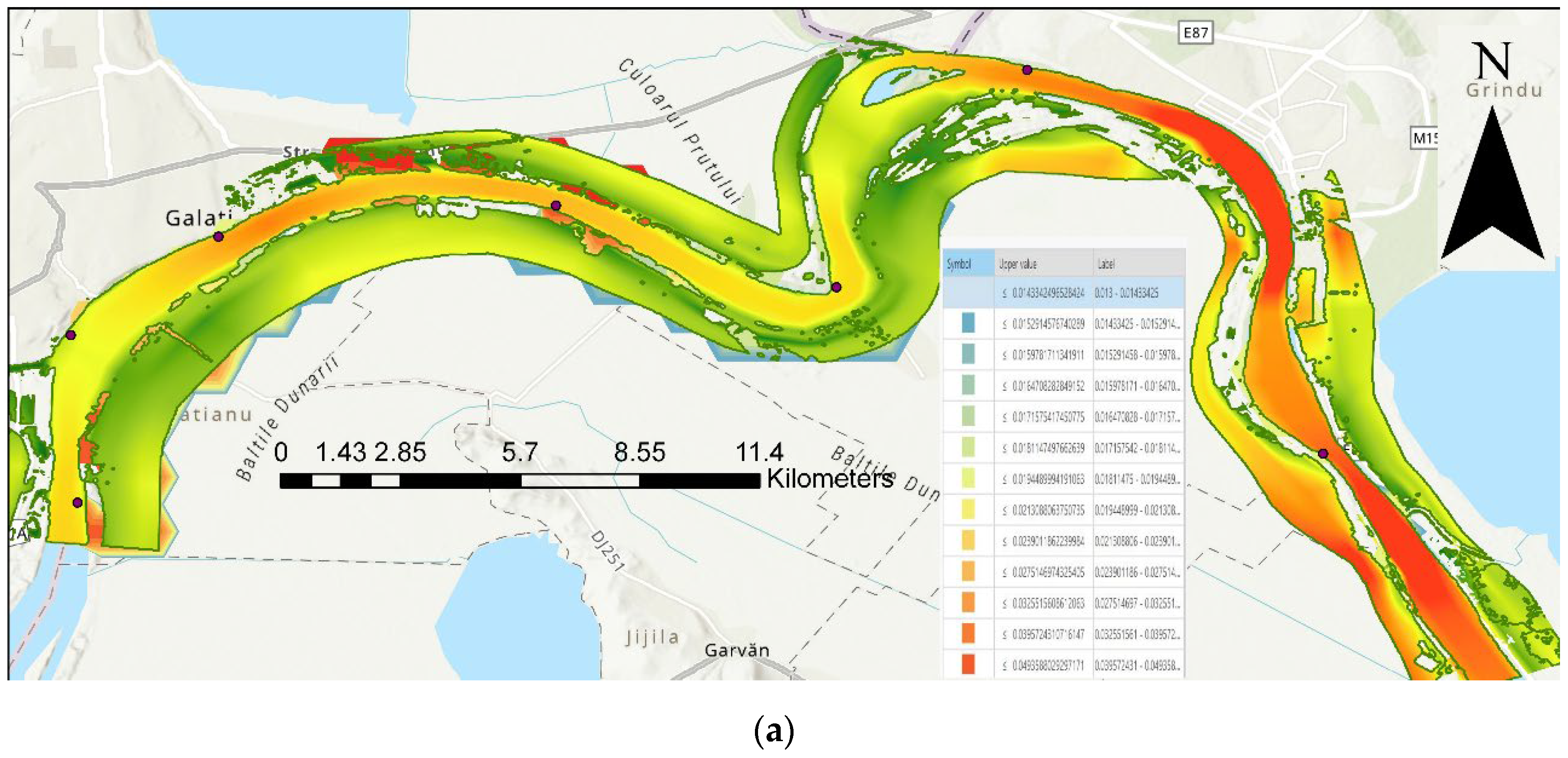
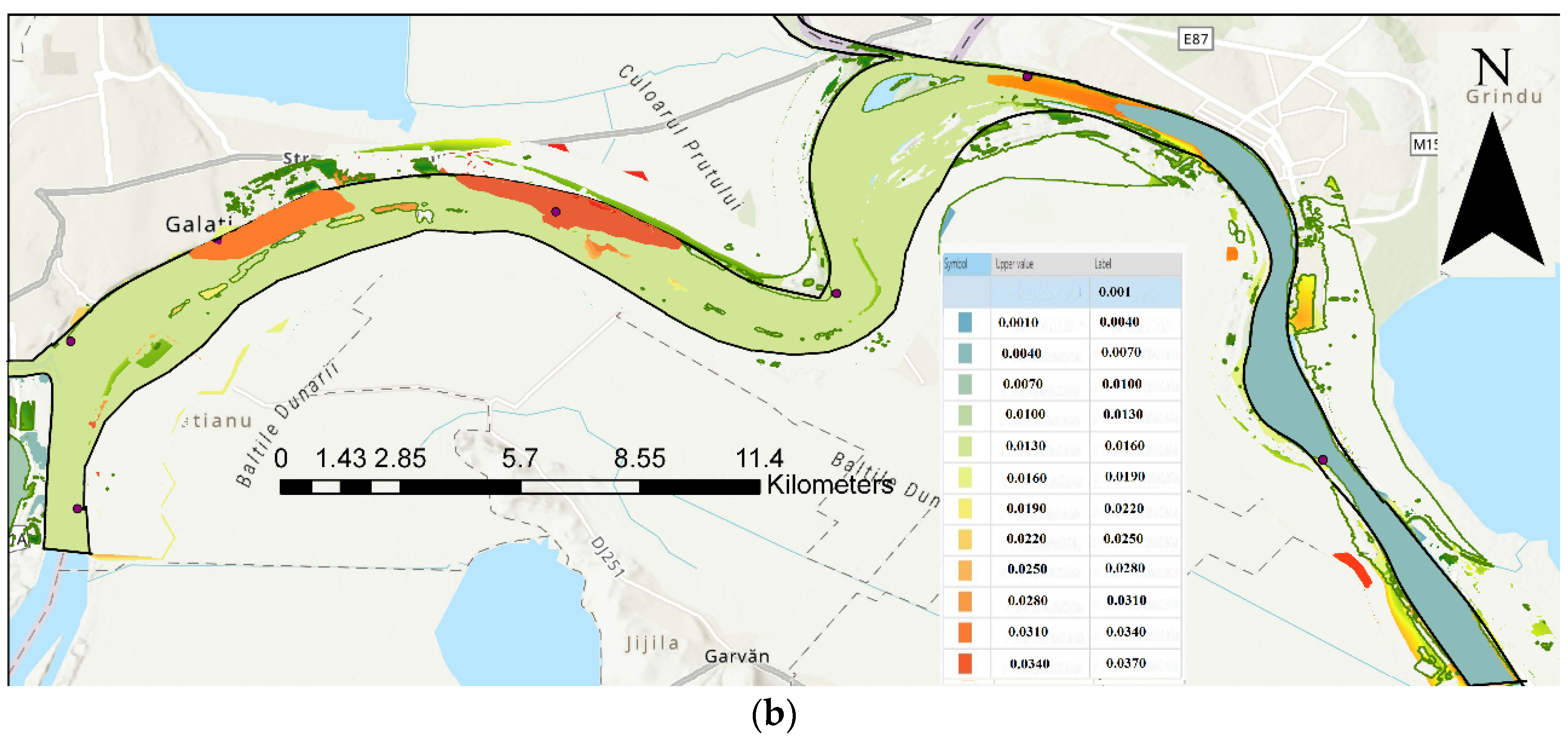
Figure 13.
representation in the form of distribution maps: (a) representation of distribution maps for Cr concentration – July campaign; (b) representation of distribution maps for Cr concentration – October campaign;
Figure 13.
representation in the form of distribution maps: (a) representation of distribution maps for Cr concentration – July campaign; (b) representation of distribution maps for Cr concentration – October campaign;
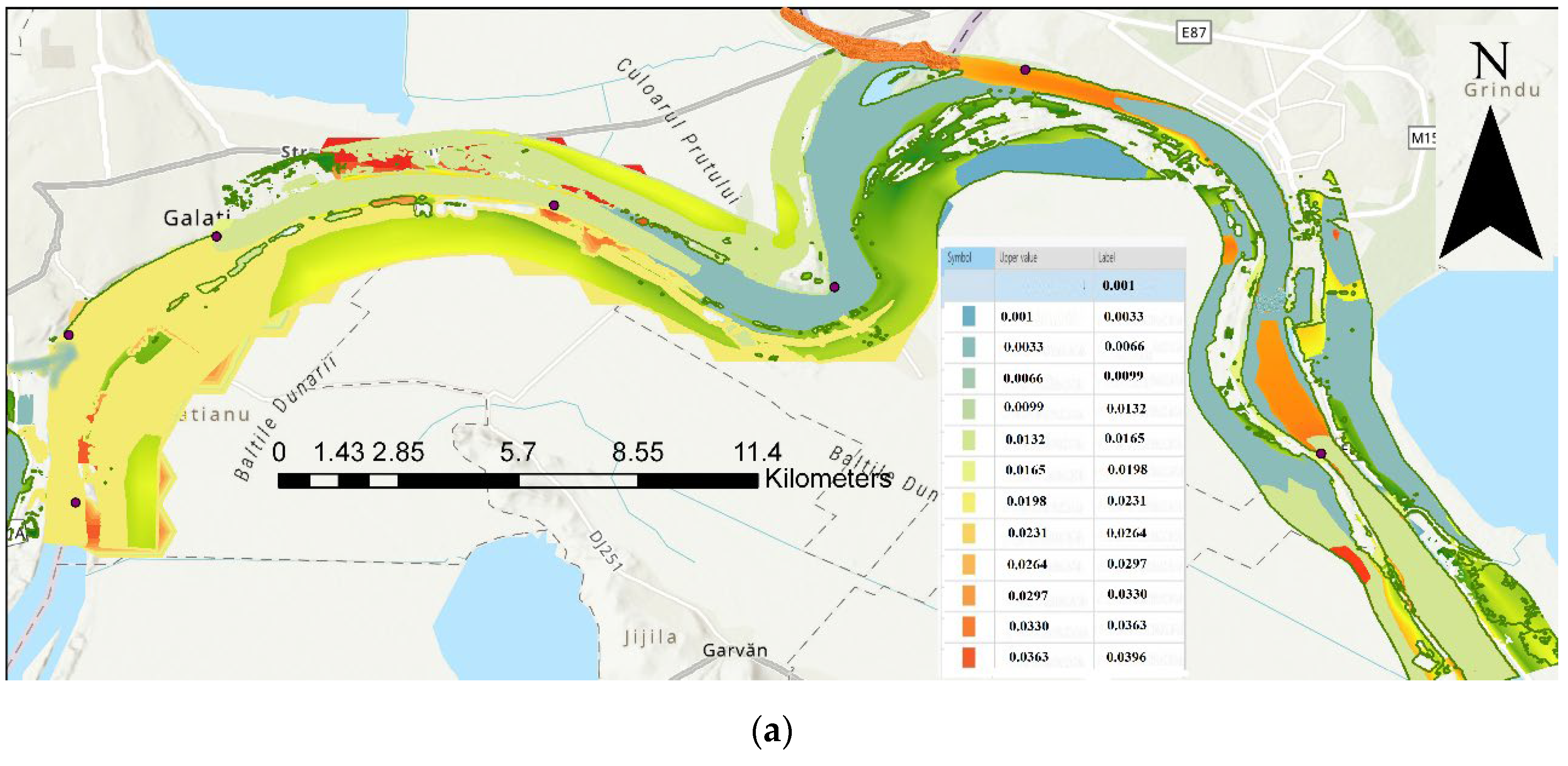
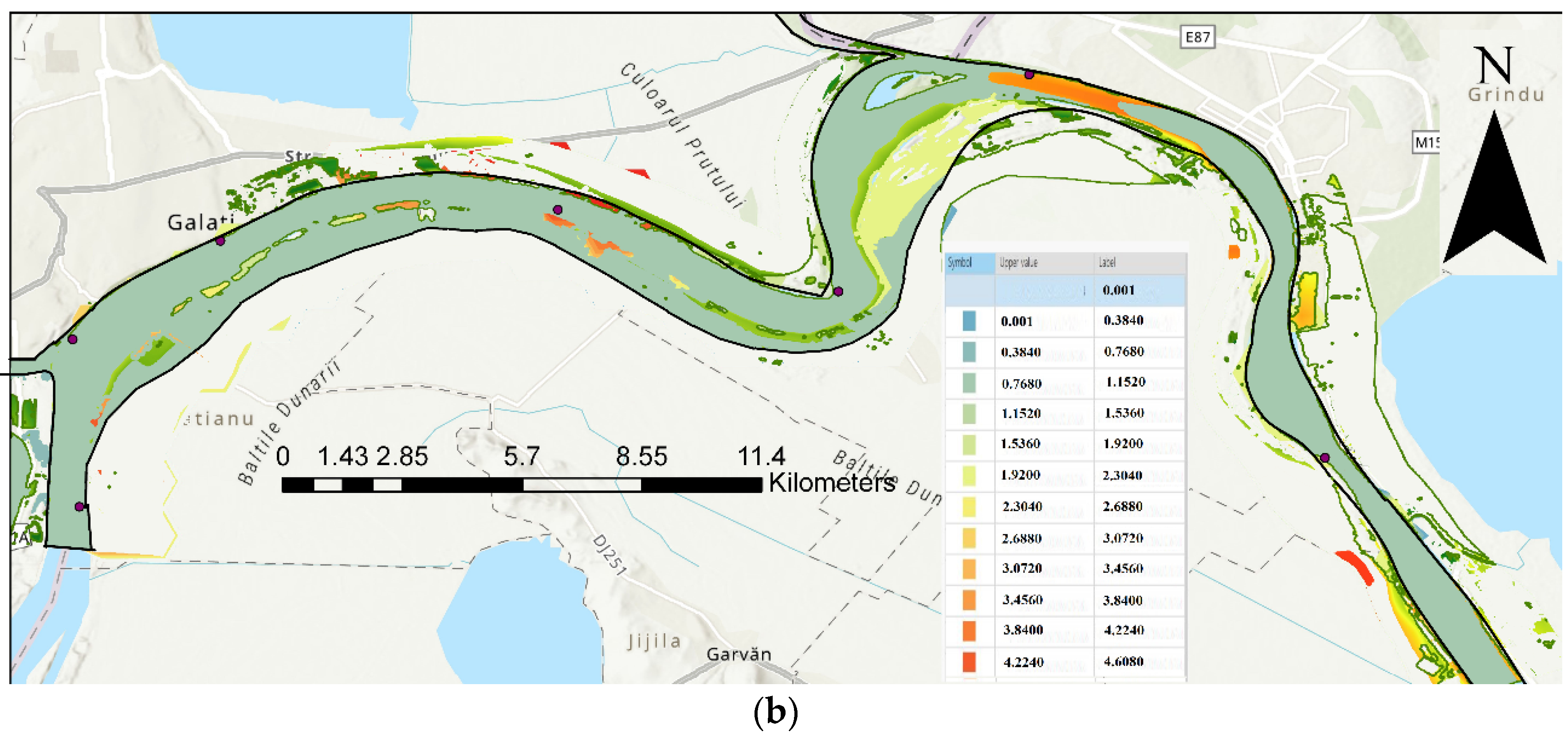
Figure 14.
representation in the form of distribution maps: (a) representation of distribution maps for Cd concentration – July campaign; (b) representation of distribution maps for Cd concentration – October campaign;.
Figure 14.
representation in the form of distribution maps: (a) representation of distribution maps for Cd concentration – July campaign; (b) representation of distribution maps for Cd concentration – October campaign;.
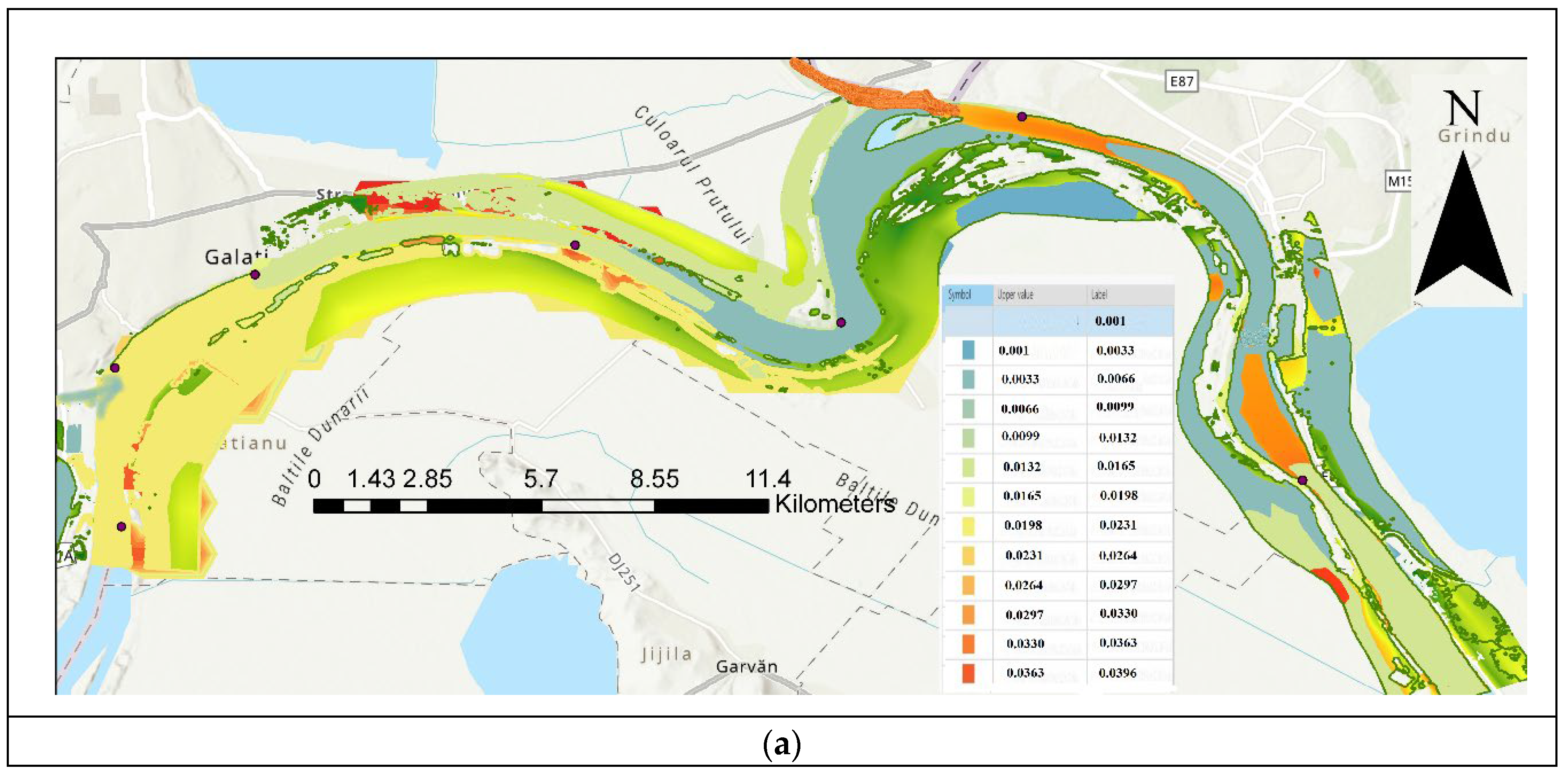

Figure 15.
representation in the form of distribution maps: (a) representation of distribution maps for As concentration – July campaign; (b) representation of distribution maps for As concentration – October campaign;.
Figure 15.
representation in the form of distribution maps: (a) representation of distribution maps for As concentration – July campaign; (b) representation of distribution maps for As concentration – October campaign;.
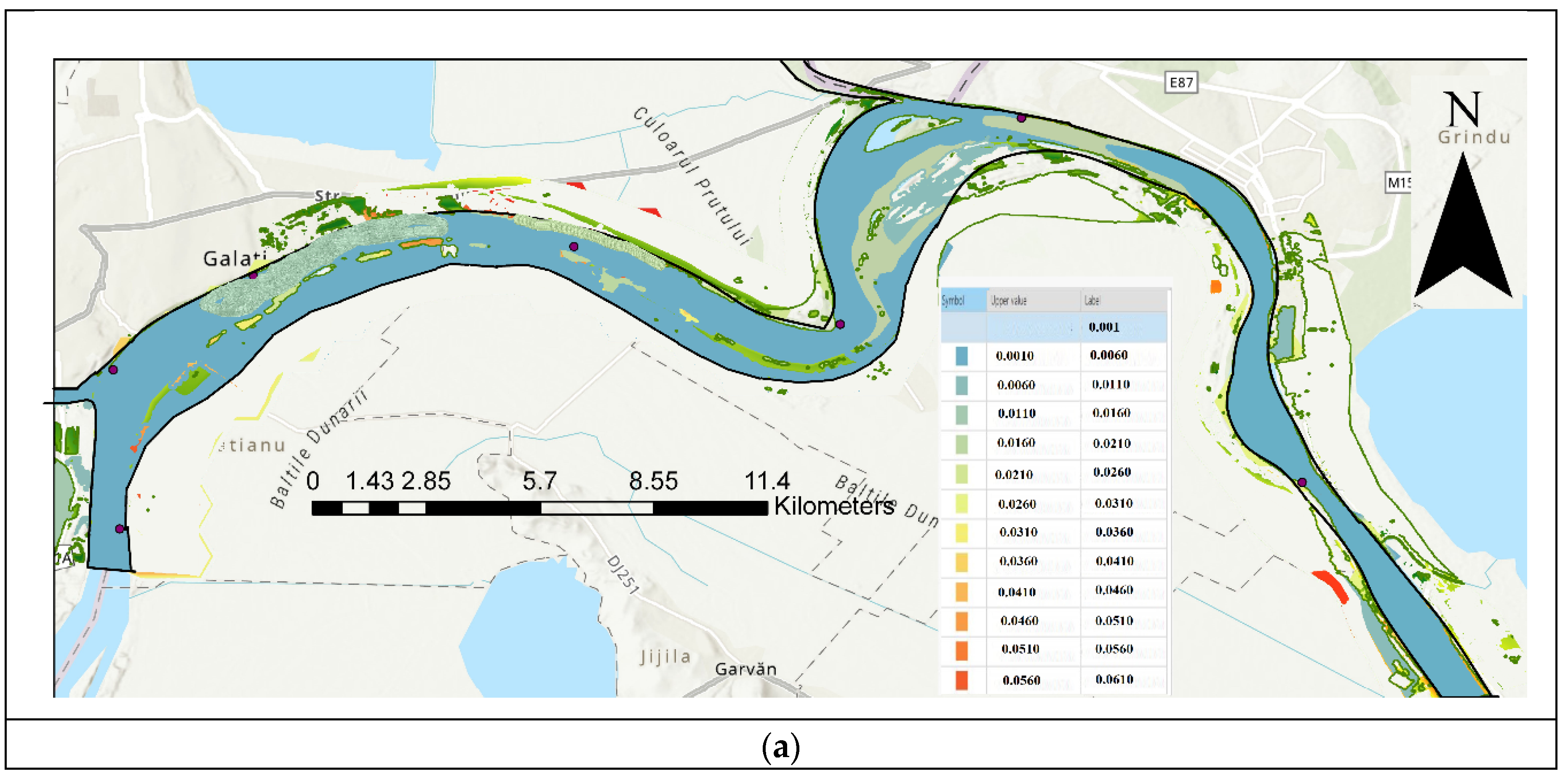
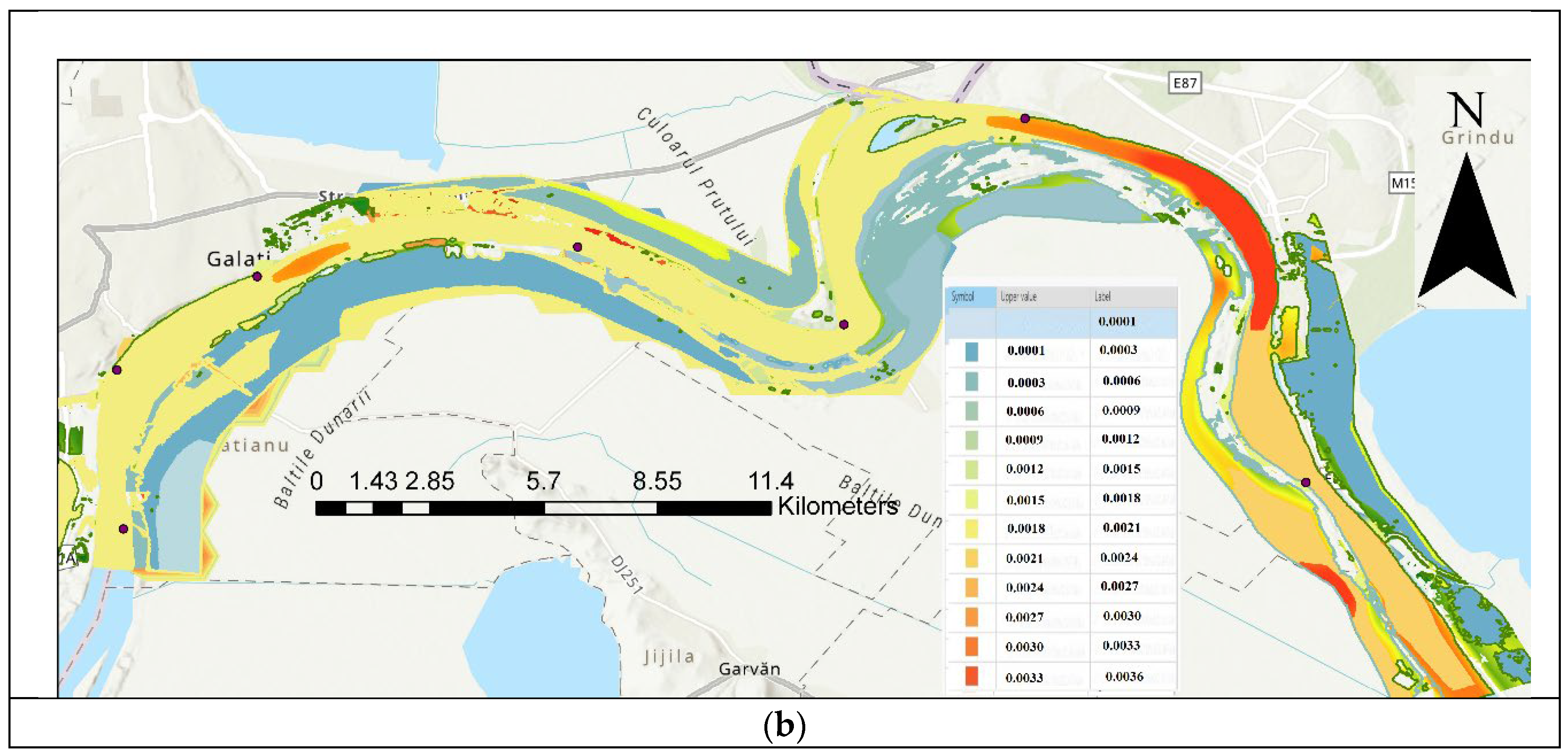
Figure 16.
representation in the form of distribution maps: (a) representation of distribution maps for Al concentration – July campaign; (b) representation of distribution maps for Al concentration – October campaign;.
Figure 16.
representation in the form of distribution maps: (a) representation of distribution maps for Al concentration – July campaign; (b) representation of distribution maps for Al concentration – October campaign;.
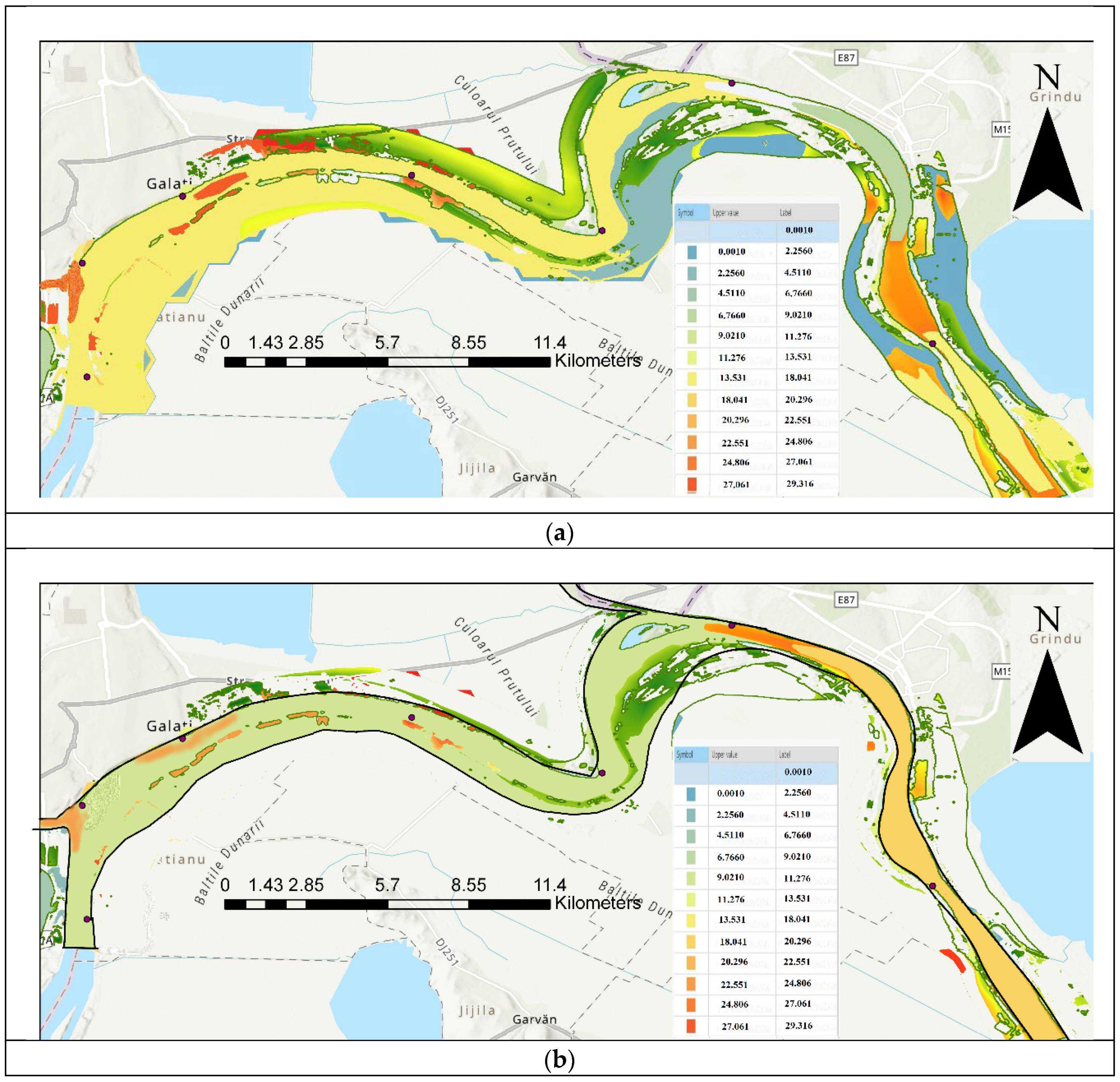
Table 1.
Monitoring stations.
| Code/name | Station | GPS Coordinates [d.d.] |
|---|---|---|
| P1 | City water Danube Pump Station –on the Danube course | 45.37261173; 28.02879381 |
| P2 | Siret River monitoring point - on the Siret River upstream course | 45.40016436; 27.9973168 |
| P3 | Siret River confluence with Danube River monitoring point | 45.40848419; 28.027358 |
| P4 | Libertatea restaurant monitoring point –on the Danube course | 45.42957954; 28.05900221 |
| P5 | Damen Ship Yard Downstream monitoring point –on the Danube course | 45.43628888; 28.13124235 |
| P6 | Cotul Pisicii recreation area monitoring point –on the Danube course | 45.41873878; 28.19135779 |
| P7 | Prut River– Giurgiulesti monitoring point – on the Prut River upstream course | 45.48016; 28.185536 |
| P8 | Prut River confluence with Danube River monitoring point | 45.46528806; 28.23220795 |
| P9 | Ucrainean ship yard Reni monitoring point–on the Danube course | 45.38315546; 28.29554717 |
| P10 | Ucrainean passing border Isaccea monitoring point–on the Danube course | 45.28405785; 28.45693996 |
Table 3.
Descriptive Statistics (July - October databases ) The units of measure are those indicated above – Table 2.
Table 3.
Descriptive Statistics (July - October databases ) The units of measure are those indicated above – Table 2.
| July database | October database | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variable | Valid N | Mean | Median | Min. | Max. | Std. Dev. |
Std. Error |
Mean |
Median |
Min. |
Max. |
Std. Dev. |
Std. Error |
| Phosphate | 10 | 0.077 | 0.075 | 0.04 | 0.14 | 0.02669 | 0.008439 | 0.054 | 0.06 | 0.01 | 0.07 | 0.01713 | 0.005416 |
| CCO | 10 | 13.59 | 10.9 | 7.5 | 33.4 | 7.99617 | 2.528612 | 12.76 | 10.2 | 7.1 | 30.3 | 7.23559 | 2.288095 |
| CBO5 | 10 | 25.46 | 24.75 | 22.4 | 29.7 | 2.5941 | 0.820325 | 23.11 | 23.25 | 20.3 | 27.1 | 2.1692 | 0.685962 |
| NH4+ | 10 | 0.833 | 0.885 | 0.34 | 1 | 0.19166 | 0.060609 | 0.797 | 0.77 | 0.64 | 1.06 | 0.13392 | 0.042349 |
| N-NO2 | 10 | 0.0163 | 0.015 | 0.013 | 0.02 | 0.00267 | 0.000844 | 0.0086 | 0.0085 | 0.007 | 0.011 | 0.00126 | 0.0004 |
| N-NO3- | 10 | 0.64 | 0.65 | 0.5 | 0.8 | 0.13499 | 0.042687 | 0.3 | 0.3 | 0.1 | 0.5 | 0.13333 | 0.042164 |
| N-Total | 10 | 1.81 | 1.8 | 1.5 | 2 | 0.16633 | 0.052599 | 2.4 | 2.55 | 0.5 | 3.7 | 1.08115 | 0.34189 |
| P-PO4 3- | 10 | 0.077 | 0.075 | 0.04 | 0.14 | 0.02669 | 0.008439 | 0.054 | 0.06 | 0.01 | 0.07 | 0.01713 | 0.005416 |
| SO42- | 10 | 27.4 | 21 | 19 | 61 | 14.04121 | 4.44022 | 44.7 | 41 | 38 | 71 | 9.91127 | 3.13422 |
| Cl- | 10 | 28.7 | 25 | 22 | 57 | 10.45679 | 3.306727 | 39.9 | 41.5 | 22 | 57 | 10.26807 | 3.24705 |
| phenols | 10 | 0.036 | 0.03 | 0.03 | 0.08 | 0.01578 | 0.004989 | 0.058 | 0.06 | 0.01 | 0.1 | 0.02741 | 0.008667 |
Table 4.
T-test for Independent Samples (July - October databases). Note: Variables were treated as independent samples - P 2-sided refers to the p-value for a two-tailed test.
Table 4.
T-test for Independent Samples (July - October databases). Note: Variables were treated as independent samples - P 2-sided refers to the p-value for a two-tailed test.
| Group 1 -July vs. Group 2 - Oct | Mean Group 1 |
Mean Group 2 |
t-value | df | p | t separ. var.est. | df | P 2-sided | Std. Dev. Group 1 | Std. Dev. Group 2 | F-ratio Variances |
p Variances |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Phosphate July - Phosphate Oct | 0.07700 | 0.05400 | 2.2936 | 18 | 0.034064 | 2.2936 | 15.33828 | 0.036325 | 0.02669 | 0.01713 | 2 | 0.202485 |
| CCO July vs. CCO Oct | 13.59000 | 12.76000 | 0.2434 | 18 | 0.810456 | 0.2434 | 17.82312 | 0.810483 | 7.99617 | 7.23559 | 1 | 0.770730 |
| CBO5 July vs. CBO5 Oct | 25.46000 | 23.11000 | 2.1976 | 18 | 0.041303 | 2.1976 | 17.45324 | 0.041738 | 2.59410 | 2.16920 | 1 | 0.602631 |
| NH4+ July vs. NH4+ Oct | 0.83300 | 0.79700 | 0.4869 | 18 | 0.632211 | 0.4869 | 16.09645 | 0.632899 | 0.19166 | 0.13392 | 2 | 0.300431 |
| N-NO2 July vs. N-NO2 Oct | 0.01630 | 0.00860 | 8.2447 | 18 | 0.000000 | 8.2447 | 12.84941 | 0.000002 | 0.00267 | 0.00126 | 4 | 0.036529 |
| N-NO3- July vs. N-NO3- Oct | 0.64000 | 0.30000 | 5.6667 | 18 | 0.000022 | 5.6667 | 17.99726 | 0.000022 | 0.13499 | 0.13333 | 1 | 0.971262 |
| N-Total July vs. N-Total Oct | 1.81000 | 2.40000 | -1.7056 | 18 | 0.105272 | -1.7056 | 9.42581 | 0.120742 | 0.16633 | 1.08115 | 42 | 0.000005 |
| P-PO4 3- July vs. P-PO4 3- Oct | 0.07700 | 0.05400 | 2.2936 | 18 | 0.034064 | 2.2936 | 15.33828 | 0.036325 | 0.02669 | 0.01713 | 2 | 0.202485 |
| SO42- July vs. SO42- Oct | 27.40000 | 44.70000 | -3.1831 | 18 | 0.005150 | -3.1831 | 16.18487 | 0.005713 | 14.04121 | 9.91127 | 2 | 0.314085 |
| Cl- July vs. Cl- Oct | 28.70000 | 39.90000 | -2.4167 | 18 | 0.026502 | -2.4167 | 17.99403 | 0.026505 | 10.45679 | 10.26807 | 1 | 0.957620 |
| phenols July vs. phenols Oct | 0.03600 | 0.05800 | -2.2000 | 18 | 0.041109 | -2.2000 | 14.37439 | 0.044629 | 0.01578 | 0.02741 | 3 | 0.115426 |
Table 5.
Descriptive Statistics for metals ( July - October database final) The units of measure are those in table 2.
Table 5.
Descriptive Statistics for metals ( July - October database final) The units of measure are those in table 2.
| July database | October database | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variable | Valid N | Mean | Median | Minim. | Maxim. | Std. Dev. |
Std. Error |
Mean | Median | Minim. | Maxim. | Std. Dev. |
Std. Error |
| Al | 10 | 24.71860 | 21.91900 | 8.665000 | 46.89000 | 12.01038 | 3.798014 | 16.01210 | 14.56050 | 9.000000 | 26.00000 | 6.656686 | 2.105029 |
| As | 10 | 0.00150 | 0.00150 | 0.001000 | 0.00200 | 0.00053 | 0.000167 | 0.01010 | 0.00900 | 0.005000 | 0.01900 | 0.003755 | 0.001187 |
| Cd | 10 | 0.01540 | 0.01600 | 0.004000 | 0.03800 | 0.01025 | 0.003243 | 0.01330 | 0.01400 | 0.005000 | 0.01800 | 0.003713 | 0.001174 |
| Cr | 10 | 1.31120 | 1.25950 | 0.764000 | 2.31800 | 0.46673 | 0.147593 | 0.58920 | 0.61350 | 0.137000 | 0.96200 | 0.343044 | 0.108480 |
| Fe | 10 | 0.030000 | 0.021500 | 0.013000 | 0.063000 | 0.018203 | 0.020600 | 0.013000 | 0.006000 | 0.082000 | 0.022751 | 0.007194 | 0.020600 |
Table 6.
T-test for Independent Samples (01 July - October IARC database). Note: Variables were treated as independent samples - The units of measure are those in table 2.
Table 6.
T-test for Independent Samples (01 July - October IARC database). Note: Variables were treated as independent samples - The units of measure are those in table 2.
| Group 1 vs. Group 2 |
Mean Group 1 |
MeanGroup 2 | t-value | df | p | t separ. var.est. |
df | p2-sided | Std. Dev.Group 1 | Std. Dev.Group 2 | F-ratioVariances | pVariances |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Al. Jul vs. Al. Oct |
24.71860 | 16.01210 | 2.005017 | 18 | 0.060237 | 2.005017 | 14.05258 | 0.064618 | 12.01038 | 6.656686 | 3.255346 | 0.093547 |
| As Jul vs. As Oct |
0.001500 | 0.010100 | -7.17220 | 18 | 0.000001 | -7.17220 | 9.354472 | 0.000043 | 0.000527 | 0.003755 | 50.76000 | 0.000002 |
| Cd. Jul vs. Cd Oct |
0.015400 | 0.013300 | 0.608902 | 18 | 0.550198 | 0.608902 | 11.32041 | 0.554612 | 0.010255 | 0.003713 | 7.626108 | 0.005756 |
| Cr Jul. vs. Cr oct |
1.311200 | 0.589200 | 3.941673 | 18 | 0.000956 | 3.941673 | 16.52723 | 0.001104 | 0.466729 | 0.343044 | 1.851099 | 0.372571 |
| Fe Jul vs. Fe Oct |
0.030000 | 0.020600 | 1.020213 | 18 | 0.321144 | 1.020213 | 17.17325 | 0.321785 | 10 | 10 | 0.018203 | 0.022751 |
| Phosphate Jul vs. Phosphate Oct |
0.07700 | 0.05400 | 2.2936 | 18 | 0.034064 | 2.2936 | 15.33828 | 0.036325 | 0.02669 | 0.01713 | 2 | 0.202485 |
Table 7.
Pearson correlation (2-tailed) between studied parameters - Correlations table for the IARC July database.
Table 7.
Pearson correlation (2-tailed) between studied parameters - Correlations table for the IARC July database.
| Variable | Al | As | Cd | Cr | Fe | CCO | CBO5 | NH4+ | N-NO2 | N-NO3- | N-Total | P-PO4 3- | SO42- | Cl- | phenols |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Al | 1 | 0.4386 | 0.4822 | 0.3696 | 0.2077 | 0.3736 | -0.0869 | -0.366 | 0.2185 | -0.1587 | 0.1489 | -0.0579 | -0.1131 | -0.1075 | 0.3626 |
| p= --- | p=.205 | p=.158 | p=.293 | p=.565 | p=.288 | p=.811 | p=.298 | p=.544 | p=.661 | p=.681 | p=.874 | p=.756 | p=.768 | p=.303 | |
| As | 0.4386 | 1 | 0.0617 | 0.1305 | 0.1274 | -0.1911 | -0.5364 | -0.2805 | -0.0395 | -0.6247 | 0.4436 | 0.5925 | -0.4805 | -0.4335 | 0.4009 |
| p=.205 | p= --- | p=.866 | p=.719 | p=.726 | p=.597 | p=.110 | p=.432 | p=.914 | p=.053 | p=.199 | p=.071 | p=.160 | p=.211 | p=.251 | |
| Cd | 0.4822 | 0.0617 | 1 | 0.4969 | 0.372 | 0.1694 | 0.3799 | -0.0781 | 0.4864 | -0.4944 | 0.0886 | -0.0195 | 0.4834 | -0.1407 | 0.1621 |
| p=.158 | p=.866 | p= --- | p=.144 | p=.290 | p=.640 | p=.279 | p=.830 | p=.154 | p=.146 | p=.808 | p=.957 | p=.157 | p=.698 | p=.655 | |
| Cr | 0.3696 | 0.1305 | 0.4969 | 1 | -0.2396 | 0.713 | 0.1156 | 0.255 | -0.0617 | -0.1081 | 0.2698 | 0.4192 | -0.2223 | -0.3824 | 0.2841 |
| p=.293 | p=.719 | p=.144 | p= --- | p=.505 | p=.021 | p=.750 | p=.477 | p=.866 | p=.766 | p=.451 | p=.228 | p=.537 | p=.276 | p=.426 | |
| Fe | 0.2077 | 0.1274 | 0.372 | -0.2396 | 1 | -0.0137 | 0.161 | -0.7392 | -0.0526 | -0.4477 | -0.4184 | -0.2059 | 0.4286 | 0.1185 | -0.3521 |
| p=.565 | p=.726 | p=.290 | p=.505 | p= --- | p=.970 | p=.657 | p=.015 | p=.885 | p=.195 | p=.229 | p=.568 | p=.216 | p=.744 | p=.318 | |
| CCO | 0.3736 | -0.1911 | 0.1694 | 0.713 | -0.0137 | 1 | 0.1856 | -0.0485 | -0.2571 | 0.2691 | -0.0784 | 0.0623 | -0.2814 | -0.2178 | -0.0426 |
| p=.288 | p=.597 | p=.640 | p=.021 | p=.970 | p= --- | p=.608 | p=.894 | p=.473 | p=.452 | p=.829 | p=.864 | p=.431 | p=.545 | p=.907 | |
| CBO5 | -0.0869 | -0.5364 | 0.3799 | 0.1156 | 0.161 | 0.1856 | 1 | 0.1306 | 0.2122 | 0.0336 | 0.086 | -0.4144 | 0.4239 | -0.0132 | 0.1043 |
| p=.811 | p=.110 | p=.279 | p=.750 | p=.657 | p=.608 | p= --- | p=.719 | p=.556 | p=.927 | p=.813 | p=.234 | p=.222 | p=.971 | p=.774 | |
| NH4+ | -0.366 | -0.2805 | -0.0781 | 0.255 | -0.7392 | -0.0485 | 0.1306 | 1 | 0.1153 | 0.3942 | 0.229 | -0.0263 | -0.1665 | -0.285 | 0.2286 |
| p=.298 | p=.432 | p=.830 | p=.477 | p=.015 | p=.894 | p=.719 | p= --- | p=.751 | p=.260 | p=.525 | p=.943 | p=.646 | p=.425 | p=.525 | |
| N-NO2 | 0.2185 | -0.0395 | 0.4864 | -0.0617 | -0.0526 | -0.2571 | 0.2122 | 0.1153 | 1 | -0.3763 | 0.1927 | -0.2668 | 0.3582 | -0.0362 | 0.5331 |
| p=.544 | p=.914 | p=.154 | p=.866 | p=.885 | p=.473 | p=.556 | p=.751 | p= --- | p=.284 | p=.594 | p=.456 | p=.309 | p=.921 | p=.113 | |
| N-NO3- | -0.1587 | -0.6247 | -0.4944 | -0.1081 | -0.4477 | 0.2691 | 0.0336 | 0.3942 | -0.3763 | 1 | -0.3167 | -0.4565 | -0.1266 | 0.2928 | -0.3339 |
| p=.661 | p=.053 | p=.146 | p=.766 | p=.195 | p=.452 | p=.927 | p=.260 | p=.284 | p= --- | p=.373 | p=.185 | p=.727 | p=.412 | p=.346 | |
| N-Total | 0.1489 | 0.4436 | 0.0886 | 0.2698 | -0.4184 | -0.0784 | 0.086 | 0.229 | 0.1927 | -0.3167 | 1 | 0.6082 | -0.5538 | -0.6944 | 0.4404 |
| p=.681 | p=.199 | p=.808 | p=.451 | p=.229 | p=.829 | p=.813 | p=.525 | p=.594 | p=.373 | p= --- | p=.062 | p=.097 | p=.026 | p=.203 | |
| P-PO4 3- | -0.0579 | 0.5925 | -0.0195 | 0.4192 | -0.2059 | 0.0623 | -0.4144 | -0.0263 | -0.2668 | -0.4565 | 0.6082 | 1 | -0.5776 | -0.557 | 0.0211 |
| p=.874 | p=.071 | p=.957 | p=.228 | p=.568 | p=.864 | p=.234 | p=.943 | p=.456 | p=.185 | p=.062 | p= --- | p=.080 | p=.094 | p=.954 | |
| SO42- | -0.1131 | -0.4805 | 0.4834 | -0.2223 | 0.4286 | -0.2814 | 0.4239 | -0.1665 | 0.3582 | -0.1266 | -0.5538 | -0.5776 | 1 | 0.6744 | -0.1525 |
| p=.756 | p=.160 | p=.157 | p=.537 | p=.216 | p=.431 | p=.222 | p=.646 | p=.309 | p=.727 | p=.097 | p=.080 | p= --- | p=.032 | p=.674 | |
| Cl- | -0.1075 | -0.4335 | -0.1407 | -0.3824 | 0.1185 | -0.2178 | -0.0132 | -0.285 | -0.0362 | 0.2928 | -0.6944 | -0.557 | 0.6744 | 1 | -0.1899 |
| p=.768 | p=.211 | p=.698 | p=.276 | p=.744 | p=.545 | p=.971 | p=.425 | p=.921 | p=.412 | p=.026 | p=.094 | p=.032 | p= --- | p=.599 | |
| phenols | 0.3626 | 0.4009 | 0.1621 | 0.2841 | -0.3521 | -0.0426 | 0.1043 | 0.2286 | 0.5331 | -0.3339 | 0.4404 | 0.0211 | -0.1525 | -0.1899 | 1 |
| p=.303 | p=.251 | p=.655 | p=.426 | p=.318 | p=.907 | p=.774 | p=.525 | p=.113 | p=.346 | p=.203 | p=.954 | p=.674 | p=.599 | p= --- |
Table 8.
Pearson correlation (2-tailed) between studied parameters - Correlations table for the IARC October database.
Table 8.
Pearson correlation (2-tailed) between studied parameters - Correlations table for the IARC October database.
| Variable | Al | As | Cd | Cr | Fe | CCO | CBO5 | NH4+ | N-NO2 | N-NO3- | N-Total | P-PO4 3- | SO42- | Cl- | phenols |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Al | 1 | -0.1423 | -0.6543 | 0.335 | 0.3737 | -0.2228 | -0.2869 | -0.0909 | 0.1558 | -0.0155 | -0.0174 | -0.2819 | 0.1452 | 0.4777 | 0.2096 |
| p= --- | p=.695 | p=.040 | p=.344 | p=.287 | p=.536 | p=.422 | p=.803 | p=.667 | p=.966 | p=.962 | p=.430 | p=.689 | p=.163 | p=.561 | |
| As | -0.1423 | 1 | 0.2526 | 0.4151 | 0.6964 | 0.5281 | -0.0315 | -0.1253 | -0.1076 | -0.2441 | 0.3421 | 0.2177 | -0.5693 | -0.2475 | 0.1641 |
| p=.695 | p= --- | p=.481 | p=.233 | p=.025 | p=.117 | p=.931 | p=.730 | p=.767 | p=.497 | p=.333 | p=.546 | p=.086 | p=.490 | p=.651 | |
| Cd | -0.6543 | 0.2526 | 1 | -0.3699 | -0.0839 | 0.3284 | 0.2796 | -0.2214 | -0.7522 | 0.1346 | -0.1661 | 0.7652 | -0.4501 | -0.5557 | -0.5284 |
| p=.040 | p=.481 | p= --- | p=.293 | p=.818 | p=.354 | p=.434 | p=.539 | p=.012 | p=.711 | p=.647 | p=.010 | p=.192 | p=.095 | p=.116 | |
| Cr | 0.335 | 0.4151 | -0.3699 | 1 | 0.4802 | -0.2653 | -0.5368 | -0.3392 | 0.2875 | -0.6923 | 0.8094 | -0.0756 | -0.3728 | -0.3436 | 0.1409 |
| p=.344 | p=.233 | p=.293 | p= --- | p=.160 | p=.459 | p=.110 | p=.338 | p=.421 | p=.027 | p=.005 | p=.836 | p=.289 | p=.331 | p=.698 | |
| Fe | 0.3737 | 0.6964 | -0.0839 | 0.4802 | 1 | 0.1544 | 0.026 | 0.1082 | -0.0448 | 0.0037 | 0.1974 | 0.1528 | -0.1647 | -0.0506 | 0.0752 |
| p=.287 | p=.025 | p=.818 | p=.160 | p= --- | p=.670 | p=.943 | p=.766 | p=.902 | p=.992 | p=.585 | p=.673 | p=.649 | p=.890 | p=.836 | |
| CCO | -0.2228 | 0.5281 | 0.3284 | -0.2653 | 0.1544 | 1 | 0.1611 | -0.0473 | -0.0906 | -0.0656 | -0.1426 | 0.2274 | -0.2014 | 0.1353 | 0.1732 |
| p=.536 | p=.117 | p=.354 | p=.459 | p=.670 | p= --- | p=.657 | p=.897 | p=.804 | p=.857 | p=.694 | p=.528 | p=.577 | p=.709 | p=.632 | |
| CBO5 | -0.2869 | -0.0315 | 0.2796 | -0.5368 | 0.026 | 0.1611 | 1 | 0.6358 | -0.4884 | 0.3304 | -0.6813 | 0.0825 | 0.3676 | 0.1288 | -0.123 |
| p=.422 | p=.931 | p=.434 | p=.110 | p=.943 | p=.657 | p= --- | p=.048 | p=.152 | p=.351 | p=.030 | p=.821 | p=.296 | p=.723 | p=.735 | |
| NH4+ | -0.0909 | -0.1253 | -0.2214 | -0.3392 | 0.1082 | -0.0473 | 0.6358 | 1 | 0.143 | 0.56 | -0.5372 | -0.2122 | 0.6907 | 0.129 | 0.422 |
| p=.803 | p=.730 | p=.539 | p=.338 | p=.766 | p=.897 | p=.048 | p= --- | p=.694 | p=.092 | p=.109 | p=.556 | p=.027 | p=.722 | p=.224 | |
| N-NO2 | 0.1558 | -0.1076 | -0.7522 | 0.2875 | -0.0448 | -0.0906 | -0.4884 | 0.143 | 1 | -0.1318 | 0.4062 | -0.636 | 0.3439 | 0.3217 | 0.5192 |
| p=.667 | p=.767 | p=.012 | p=.421 | p=.902 | p=.804 | p=.152 | p=.694 | p= --- | p=.717 | p=.244 | p=.048 | p=.331 | p=.365 | p=.124 | |
| N-NO3- | -0.0155 | -0.2441 | 0.1346 | -0.6923 | 0.0037 | -0.0656 | 0.3304 | 0.56 | -0.1318 | 1 | -0.7322 | 0 | 0.454 | 0.2191 | 0.0304 |
| p=.966 | p=.497 | p=.711 | p=.027 | p=.992 | p=.857 | p=.351 | p=.092 | p=.717 | p= --- | p=.016 | p=1.00 | p=.187 | p=.543 | p=.934 | |
| N-Total | -0.0174 | 0.3421 | -0.1661 | 0.8094 | 0.1974 | -0.1426 | -0.6813 | -0.5372 | 0.4062 | -0.7322 | 1 | 0.096 | -0.5641 | -0.3383 | 0.1087 |
| p=.962 | p=.333 | p=.647 | p=.005 | p=.585 | p=.694 | p=.030 | p=.109 | p=.244 | p=.016 | p= --- | p=.792 | p=.089 | p=.339 | p=.765 | |
| P-PO4 3- | -0.2819 | 0.2177 | 0.7652 | -0.0756 | 0.1528 | 0.2274 | 0.0825 | -0.2122 | -0.636 | 0 | 0.096 | 1 | -0.542 | -0.5598 | -0.2414 |
| p=.430 | p=.546 | p=.010 | p=.836 | p=.673 | p=.528 | p=.821 | p=.556 | p=.048 | p=1.00 | p=.792 | p= --- | p=.106 | p=.092 | p=.502 | |
| SO42- | 0.1452 | -0.5693 | -0.4501 | -0.3728 | -0.1647 | -0.2014 | 0.3676 | 0.6907 | 0.3439 | 0.454 | -0.5641 | -0.542 | 1 | 0.3414 | 0.0344 |
| p=.689 | p=.086 | p=.192 | p=.289 | p=.649 | p=.577 | p=.296 | p=.027 | p=.331 | p=.187 | p=.089 | p=.106 | p= --- | p=.334 | p=.925 | |
| Cl- | 0.4777 | -0.2475 | -0.5557 | -0.3436 | -0.0506 | 0.1353 | 0.1288 | 0.129 | 0.3217 | 0.2191 | -0.3383 | -0.5598 | 0.3414 | 1 | 0.2756 |
| p=.163 | p=.490 | p=.095 | p=.331 | p=.890 | p=.709 | p=.723 | p=.722 | p=.365 | p=.543 | p=.339 | p=.092 | p=.334 | p= --- | p=.441 | |
| phenols | 0.2096 | 0.1641 | -0.5284 | 0.1409 | 0.0752 | 0.1732 | -0.123 | 0.422 | 0.5192 | 0.0304 | 0.1087 | -0.2414 | 0.0344 | 0.2756 | 1 |
| p=.561 | p=.651 | p=.116 | p=.698 | p=.836 | p=.632 | p=.735 | p=.224 | p=.124 | p=.934 | p=.765 | p=.502 | p=.925 | p=.441 | p= --- |
Table 9.
Eigenvalues of correlation matrix, and related statistics (01 July - October database). Active variables only.
Table 9.
Eigenvalues of correlation matrix, and related statistics (01 July - October database). Active variables only.
| July monitoring campaign | October monitoring campaign | |||||||
|---|---|---|---|---|---|---|---|---|
| Value number | Eigenvalue | % Total variance |
Cumulative Eigenvalue |
Cumulative % |
Eigenvalue | % Total variance |
Cumulative Eigenvalue |
Cumulative % |
| 1 | 6.204681* | 34.47045 | 6.20468 | 34.4705 | 5.628626* | 31.27015 | 5.62863 | 31.2701 |
| 2 | 3.07987* | 17.11041 | 9.28455 | 51.5809 | 4.444705* | 24.69281 | 10.07333 | 55.963 |
| 3 | 2.625296* | 14.58498 | 11.90985 | 66.1658 | 2.093713* | 11.63174 | 12.16705 | 67.5947 |
| 4 | 2.063760* | 11.46534 | 13.97361 | 77.6312 | 1.828940* | 10.16078 | 13.99599 | 77.7555 |
| 5 | 1.401129* | 7.78405 | 15.37474 | 85.4152 | 1.312745* | 7.29303 | 15.30873 | 85.0485 |
| 6 | 1.153074* | 6.40597 | 16.52781 | 91.8212 | 1.198617* | 6.65898 | 16.50735 | 91.7075 |
| 7 | 0.603383 | 3.35213 | 17.1312 | 95.1733 | 0.687419 | 3.81899 | 17.19477 | 95.5265 |
| 8 | 0.460789 | 2.55994 | 17.59199 | 97.7333 | 0.469 | 2.60556 | 17.66377 | 98.132 |
| 9 | 0.408013 | 2.26674 | 18 | 100 | 0.336233 | 1.86796 | 18 | 100 |
*Marked values are those with significant eigenvalues.
Table 10.
Eigenvalues of correlation matrix, and related statistics for IARC database of metals.
| July monitoring campaign | October monitoring campaign | |||||||
|---|---|---|---|---|---|---|---|---|
| Value number | Eigenvalue | % Total variance |
Cumulative Eigenvalue |
Cumulative % |
Eigenvalue | % Total variance |
Cumulative Eigenvalue |
Cumulative % |
| 1 | 2.091981* | 41.83961 | 2.091981 | 41.8396 | 2.276505* | 45.53009 | 2.276505 | 45.5301 |
| 2 | 1.233531* | 24.67062 | 3.325512 | 66.5102 | 1.724148* | 34.48295 | 4.000652 | 80.013 |
| 3 | 1.018576* | 20.37151 | 4.344087 | 86.8817 | 0.581033 | 11.62066 | 4.581685 | 91.6337 |
| 4 | 0.423145 | 8.46291 | 4.767233 | 95.3447 | 0.282902 | 5.65804 | 4.864587 | 97.2917 |
| 5 | 0.232767 | 4.65535 | 5 | 100 | 0.135413 | 2.70825 | 5 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







