Prerpints.org logo
Preprint
Article

Improved Apriori Method for Safety Signal Detection using Post-Marketing Clinical Data

Altmetrics

Downloads

121

Views

56

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.zip (12.82MB )

This version is not peer-reviewed

Submitted:

20 July 2024

Posted:

22 July 2024

You are already at the latest version

Alerts
Abstract
Safety signal detection, an integral component of Pharmacovigilance (PhV), aims to identify new or known adverse events (AEs) resulting from the use of pharmacotherapeutic products. Post-marketing spontaneous reports from different sources are commonly utilized as a data source for detecting these signals but there are underlying challenges arising from data complexity. This paper investigates the implementation of the Apriori algorithm, a popular method in association rule mining, to identify frequently co-occurring drugs and AEs within safety data. We discuss previous applications of the Apriori algorithm for safety signal detection and conduct a detailed study of an improved method specifically tailored for this purpose. This enhanced approach refines the classical Apriori method to effectively reveal potential associations between drugs/vaccines and AEs from post-marketing safety monitoring datasets, especially when AEs are rare. Detailed comparative simulation studies across varied settings, coupled with the application of the method to vaccine safety data from the Vaccine Adverse Event Reporting System (VAERS), demonstrate the efficacy of the improved approach. In conclusion, the improved Apriori algorithm is shown to be a useful screening tool for detecting rarely occurring potential safety signals from the use of drugs/vaccines using post-marketing safety data.
Keywords: 
Subject: Computer Science and Mathematics  -   Probability and Statistics

1. Introduction

1.1. Safety Data Analysis

Drug safety, also known as Pharmacovigilance, is a field in the pharmaceutical science. Its primary objective is to collect, detect, assess, monitor, and prevent adverse events (AE, i.e., side effect) that are caused by medicines, vaccines, and other types of pharmaceutical productions [1]. The history of drug safety study in US can date back to the Elixir Sulfanilamide Disaster in 1937, in which one hundred and five patients died from the therapeutic use of sulfanilamide, and as a consequence, the U.S. Congress passed the 1938 Federal Food, Drug and Cosmetic Act, which required proof of safety before the release of a new drug [2]. The U.S. Kefauver-Harris Amendment, i.e., Drug Efficacy Amendment, was also passed by Congress in 1962 as a response to the Thalidomide Tragedy, in which over ten thousand children were born with defects due to their mothers using thalidomide to treat morning sickness during pregnancy [3]. Drug safety is a critical component spanning across the entire life cycle of the drug development from pre-clinical and early phase to post-market stage. It has obtained significant attentions from both governments and pharmaceutical companies globally, due to the potential for substantial losses arising from drug safety concerns. For example, the nonsteroidal anti-inflammatory drug Rofecoxib (Vioxx) was withdrawn from the market in 2004, due to increased cardiovascular risks, leading to significant financial losses for its manufacturer, Merck, largely from legal expenses [4,5].
However, the analysis of post-market drug safety data is often challenging, because of their intrinsic nature, specifically:
  • High dimensionality: The number of AEs can be large (hundreds or even thousands), especially during the post-approval marketing phase when the medicine becomes available for broad populations. However, only a few of these AEs are significant for new discoveries about the product’s clinical safety.
  • Sparsity: Most types of AEs are rare, especially in the stage of post-market surveillance, due to factors such as selective participant profiles in clinical trials, rare events in large populations, long-term effects and drug interactions, and so on.
  • Weak signal: Certain AEs may exhibit a low signal strength related to the drug or vaccine under investigation, which potentially impact the efficacy of the methodologies employed to detect the association.
  • Complex correlation: AEs may demonstrate complex correlation structure, either positive or negative, among themselves, which poses significant challenges in identifying drug or vaccine associated AE signals.
Considering the cruciality of early detection of drug/vaccine-associated AEs, it has been an ongoing endeavor to establish methods to enhance the analysis of post-market safety data. Some notable approaches that have been proposed include a Double False Discovery Rate (DFDR) approach by Mehrotra and Heyse (2012) [6], a two-stage hierarchical testing approach by Tan et al. (2020) [7], a hierarchical Bayesian mixture model for binary outcomes by Berry and Berry (2004) [8], a Poisson likelihood-based approach by Xia et al. (2011) [9], and a multivariate Bayesian logistic regression (MBLR) by DuMouchel (2012) [10].

1.2. Apriori Method

The inherent attributes of post-market safety data also render data mining tools great potential advantageous in this context. Among various data mining tools, Apriori method exhibits substantial utility in detecting drug/vaccine-AE associations.
Apriori method, proposed by Agrawal and Srikant (1994) [11], is a foundational algorithm in the field of data mining. It is known for the application in frequent itemset mining and association rule learning, especially in the field of marketing analysis. The Apriori algorithm employs an iterative approach, known as "bottom up" search, where frequent subsets are extended one item at a time, and groups of candidates are tested against the data. The algorithm terminates when no further successful extensions are found. Apriori approach is an efficient screening tool as it prunes the search space of associations in a dataset based on the “Apriori" property of frequency – if certain combinations of items in a dataset are infrequent, any larger combination built upon those will also be infrequent [12].
In a classical Apriori algorithm, two parameters are employed to measure the strength of the association rule. The first parameter is called "Support", which measures how often data items in a rule occur together in a transaction. "Confidence" is the second parameter that measures the reliability of the inference made by the rule.
Consider a transaction/reports dataset with n total transactions out of which n A transactions contain item A, n B transactions contain item B, and n A B transactions contain both items A and B. The Support of the association rule A → B is the joint proportion of A and B transactions [13], i.e.,
S u p p o r t ( A → B ) = P ( A ∩ B ) = p A B = n A B n .
For the Boolean depiction of a transactions dataset,
S u p p o r t ( A → B ) = P ( { A = 1 } ∩ { B = 1 } ) .
The Confidence of the rule is denoted by the conditional probability of B given A, i.e., the proportion of occurrences of B among the reports containing occurrences of A in the dataset.
C o n f i d e n c e ( A → B ) = S u p p o r t ( A → B ) S u p p o r t ( A ) = p B | A = n A B n A .
Itemsets/Association Rules from the dataset are extracted according to user-defined thresholds for Support and Confidence, namely minsup and minconf respectively. The algorithm first searches for rules whose support exceeds minsup as the candidate itemsets. Then, for each rule in the candidate itemsets, only those rules with Confidence larger than minconf are selected.
Kuo et al. (2009) [14] applied the Apriori method to detect Adverse Drug Reaction (ADR) from a dataset containing reports on 13 patients, 5 drugs, and 13 AEs. They also proposed that Apriori can be used to perform association analysis on characteristics of patients, drugs consumed, primary diagnosis, co-morbid conditions, and ADRs experienced, which can be leveraged further to study what combination of medications and patient characteristics could lead to Adverse Drug Reactions (ADRs).
Though the study in Kuo et al. (2009) show the ability of Apriori method in detecting drug/vaccine associated AEs with efficient searching, it has certain limitations. This study only focused on a small dataset, in contrast to the expansive nature of an actual post-market safety database, which often contains thousands of reports on many drugs and hundreds of AEs. Furthermore, the author employed the methodology merely as an illustrative example, lacking a comprehensive and systematic evaluation of the validity and efficiency of the Apriori approach, especially when applied to large-scale datasets. Hence, in this paper, we perform a comprehensive study on the performance of an improved Apriori-based approach that is capable of identifying potentially important drug/vaccine-AE associations, particularly when AE frequencies are rare, drug-AE signals are weak, and there are underlying correlations among AEs. Our study aims to address the challenges posed by these scenarios in detecting drug-AE associations within large scale datasets and to compare the performance of the improved Apriori approach with the classical one.
The rest of this article is organized as follows. In Section 2, we first introduce the improvement to the classical Apriori approach, then present the numerical studies designed to investigate the performance of the improved Apriori method. The corresponding results from numerical studies, including both simulations and real data analysis, are summarized in Section 3. This is followed by a discussion of our inferences and observations from our studies in Section 4. Finally, we present our concluding remarks in Section 5 of the article.

2. Method

2.1. Improved Apriori Method

Our comprehensive study of Apriori method with disproportionality measures is motivated by noticing that the use of Confidence in Apriori has been found to be unsuitable. According to Harpaz et al. (2010) [15], Confidence is not an appropriate parameter for the application of Apriori in surveillance data, as frequent AEs will have larger Confidence values, while infrequent AEs would have smaller Confidence even when they are strongly associated with a drug. There have been other studies aimed at leveraging the efficiency of Apriori in the context of extensive spontaneous reports databases, by use of modified Apriori-based approaches, involving use of disproportionality measures, such as Proportional Reporting Ratio (PRR) [16,17,18,19], Relative Reporting Ratio (RR) [15,20,21], and Reporting Odds Ratio (ROR) [21,22], as an alternative to Confidence. Furthermore, different levels of thresholds have been used for these parameters – [21,23,24] suggest there should be at least 3 reports for a suspected drug-AE combination, RR threshold of 2 was used in [15,20,21], and the PRR threshold was set to 2 in [18,25,26,27].
Disproportionality measures are used to detect safety signals from drugs in spontaneous reporting databases. For any drug-AE combination, the disproportionality measures quantify the extent of disproportionality between observed and expected number of reports of an AE to a drug, compared to the generality of the database. Particularly, PRR, RR, and ROR can be computed from a 2 × 2 contingency table, shown in Table 1. In Table 1, a represents the number of reports containing both the drug and AE of interest, b signifies reports containing the drug of interest and all other AEs, c denotes the number of reports including the AE of interest with all other drugs, and d is the number of reports containing all other AEs and drugs in the database.
Proportional Reporting Ratio (PRR), defined in Equation (3), is the ratio between the proportion of a suspected AE (eg. fever) among individuals who consume a particular drug (eg. Drug A) to the proportion of this AE among subjects that consume other medications (but not Drug A). A PRR exceeding 1 suggests an elevated prevalence of reports featuring the suspected AE (e.g. fever) in association with the specified drug (e.g. Drug A), relative to reports of this AE occurring with alternative medications [22,23].
PRR = a / ( a + b ) c / ( c + d ) = a ( c + d ) c ( a + b ) .
Relative Reporting Ratio (RR) represents the ratio between a rule’s observed frequency to a baseline expected frequency for all reports in the database [15], and can be used to assess the strength and significance of that rule. It is denoted as
RR = Pr ( AE ∩ Drug ) Pr ( AE ) . Pr ( Drug ) = N . a ( a + c ) ( a + b ) ,
where N = a + b + c + d is the total number of observed records. To illustrate with the association between the AE of fever and Drug A, for example, the RR quantifies the extent to which occurrences of Drug A and fever together are more frequent than would be expected under the assumption of independence between Drug A and fever. Consequently, a RR exceeding 1 indicates that the co-occurrence of Drug A and fever is more frequent than would be expected if they were independent of each other. This elevated RR thereby offers compelling evidence for a significant association between the AE and the drug.
Reporting Odds Ratio (ROR), defined in Equation (5), is the ratio between the reporting odds of a suspected AE among individuals exposed to a specific drug, and the reporting odds of this AE among subjects that are not exposed to the specific drug. It measures the likelihood of an AE being reported in the presence of a certain drug compared to the likelihood of that AE being reported in the absence of that drug.
ROR = ( a / b ) ( c / d ) = a d b c
According to Rothman et al [22], ROR is analogous to relative risk in a case-control study and can be used for signal detection even with rare AEs. Still considering the example of association between fever and Drug A, ROR offers a metric for assessing the likelihood of fever being reported in association with Drug A, as compared to its reporting with other drugs in the database. A larger ROR value provides a stronger indication of an association between Drug A and the occurrence of fever.
Therefore, in this paper, we call it the improved Apriori approach, when the disproportionality measures, PRR, RR, and ROR, are used to substitute Confidence as the second parameter in implementing Apriori for safety data.

2.2. Numerical Study

To examine and compare the performance of our proposed improved Apriori approach to the classical one, i.e., the Apriori using Confidence as the second parameter, we conduct extensive simulation studies under various parameter settings and simulation designs. Our simulation studies, along with an additional analysis for a real world vaccine safety data, aim to assess the best choice of secondary parameter for the implementation of Apriori approach in detecting drug-AE associations.

2.2.1. Simulation Studies

In the simulation studies, we conduct comparative studies to evaluate the performance of Apriori across different levels of AE frequencies, potential exhibition of correlations among AEs, and strength of signals for drug-AE associations.
Particularly, in the simulation studies, AEs are generated as binary random variables from Bernoulli distribution, with a value of 1 denoting a reported AE and 0 otherwise. In the simulations, the success probability for the Bernoulli distribution is set to be p = 0.1 , 0.3 , and 0.5 , reflecting different AE frequencies (rare, moderate, and common, respectively). Moreover, to account for potential correlations among AEs, we generate correlated binary AEs based on the approach described in Lunn and Davies [28]. Specifically, the levels of correlations between AEs are set to be ρ = 0 for linearly independent AEs, and ρ = ± 0.3 , ± 0 , 5 , and ± 0.7 for weak, moderate, and strong correlations, respectively. A binary indicator variable ( D ) is used to denote whether a particular drug or vaccine was taken ( D = 1 ), or not ( D = 0 ), and is generated according to a logistic regression model as described in Equation 6, where β varies under different simulation scenarios to mimic the strength of association between a drug and an AE.
l o g i t ( D ) = β 1 A E 1 + ⋯ + β k A E k
In addition, in the simulation studies, we consider three different scenarios.
In the first scenario, we consider the situation when there are 1 drug and 3 independent AEs, among which only the first AE is truly associated with drug 1. That is, the indicator variable for drug is generated as l o g i t ( D 1 ) = β A E 1 , where β is set to be 1, 10, 50, and 100. The purpose of this setting is to study the effect of signal strength and AE frequency on the ability of each of the four second parameters, Confidence, PRR, RR, and ROR, to correctly identify the associated drug-AE pairs.
The second setting comprises 3 drugs and 5 AEs with drug 1 associated with both AE 1 and AE 2. That is, l o g i t ( D 1 ) = β 1 A E 1 + β 2 A E 2 , where β 1 = β 2 = 1 , 10 , 50 , and 100 . The indicator variables ( D 2 and D 3 ) for drug 2 and drug 3 are generated from Bernoulli distribution with success probability as p = 0.1 , 0.3 , and 0.5 . In this setting, we consider AE 1 and AE 2 are correlated with a positive correlation ρ as described above. It is used to study performance of the method for each of the four second parameters in the presence of AE correlations.
Finally, in scenario 3, we setup 5 drugs and 10 AEs, where drug 1 is associated with AE 1 to AE 5, drug 2 is associated with AE 1 to AE 3, and drug 3 is associated with AE 1. That is, the indicator variables for drugs 1 to 3 are generated from models l o g i t ( D 1 ) = β A E 1 + β A E 2 + β A E 3 + β A E 4 + β A E 5 , l o g i t ( D 2 ) = β A E 1 + β A E 2 + β A E 3 , and l o g i t ( D 3 ) = β A E 1 , respectively. The other two drug variables are generated from Bernoulli ( p = 0.1 , 0.3 , and 0.5 ) . In setting 3, multiple AE correlation scenarios were considered. We first set AE 1 to AE 5 to be correlated at positive ρ values described above, referred to as positive correlation setting in the results section. For the scenario referred to as negative correlation setting in the results section, we let AE 1 to AE 3 to be positive correlated, AE 4 and AE 5 to be negatively correlated, both having absolute correlation values | ρ | as before. In both cases, the remaining AE 6 to AE 10 are set to be independent. This negative correlation scenario takes into account the direction of correlation, in addition to the magnitude of correlation.
In the Apriori searching process, we first search drug-AE pairs that pass the minimum support threshold, then search pairs from the previous step that pass the threshold of second parameter, and the selected "frequent 2-itemsets", i.e., drug-AE pairs, are the ones that we believe are associated with each other. Since, in this paper, the focus is to detect 2-item association rules that include one drug and one AE, we do not search all 2-item rules when applying Apriori method. As a result, in the simulation studies, we only search 3 out of 6, 15 out of 28, and 50 out of 105 2-items rules in three simulation scenarios, respectively, which results a pruning of 50 % , 46.43 % , and 52.38 % , respectively.
Moreover, when applying the Apriori method to the simulated data sets, the threshold values for the first parameter, support, are set to be 0.05 for rare AEs, 0.15 for moderately frequent AEs, and 0.30 for common AEs. We also compare the disproportionality measures, PRR, RR, and ROR, along with Confidence, for detecting frequent itemsets. The threshold values for these secondary parameters are 0.4 , 0.5 , 0.6 , and 0.7 (for Confidence), and 1, 1.2 , 1.5 , and 2 (for PRR, RR, and ROR).
Finally, for each of the above three simulation scenarios, we generate N = 500 reports for a simulated data set with 1000 replications.

2.2.2. VAERS Data

To further illustrate the implementation of the improved Apriori algorithm, we also apply it to a real spontaneous reports data, the Vaccine Adverse Event Reporting System (VAERS) [29]. The Vaccine Adverse Event Reporting System (VAERS), jointly overseen by the Centers for Disease Control and Prevention (CDC) and the U.S. Food and Drug Administration (FDA), is designed to identify potential safety issues related to vaccines licensed in the United States. VAERS operates by receiving and examining reports detailing adverse events that occur subsequent to a person receiving a vaccination.
We used the reports between years 2010 to 2019 in VAERS database as an example, which include 746 patient reports on 1094 AEs for a total of 47 vaccines. In addition to the information on vaccines administered and AEs reported, VAERS data also includes other variables, such as the sex and age of the patient and so on. In Table 2, we display a subset of data from the VAERS data set from January 2010 as an example.

3. Results

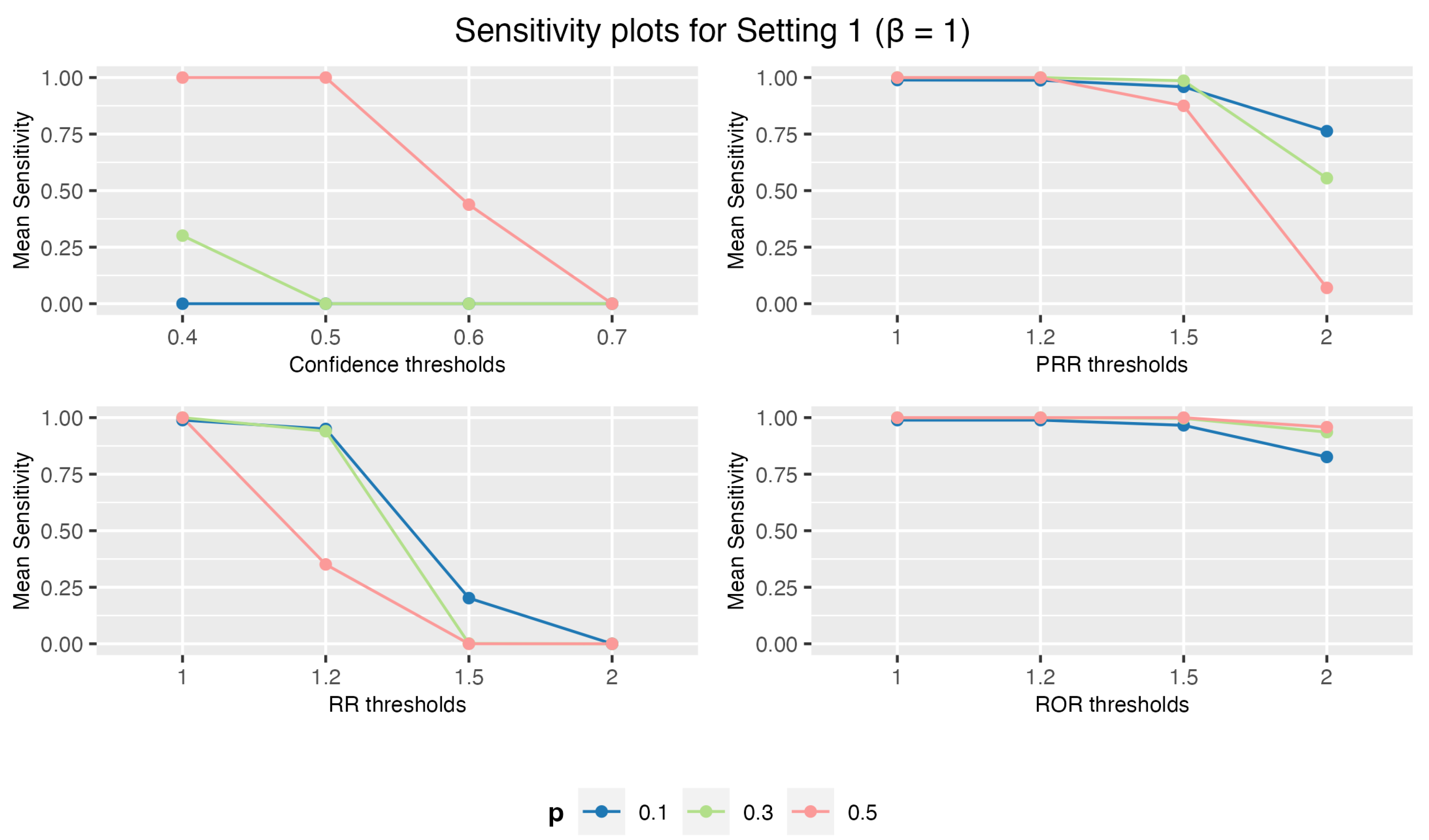
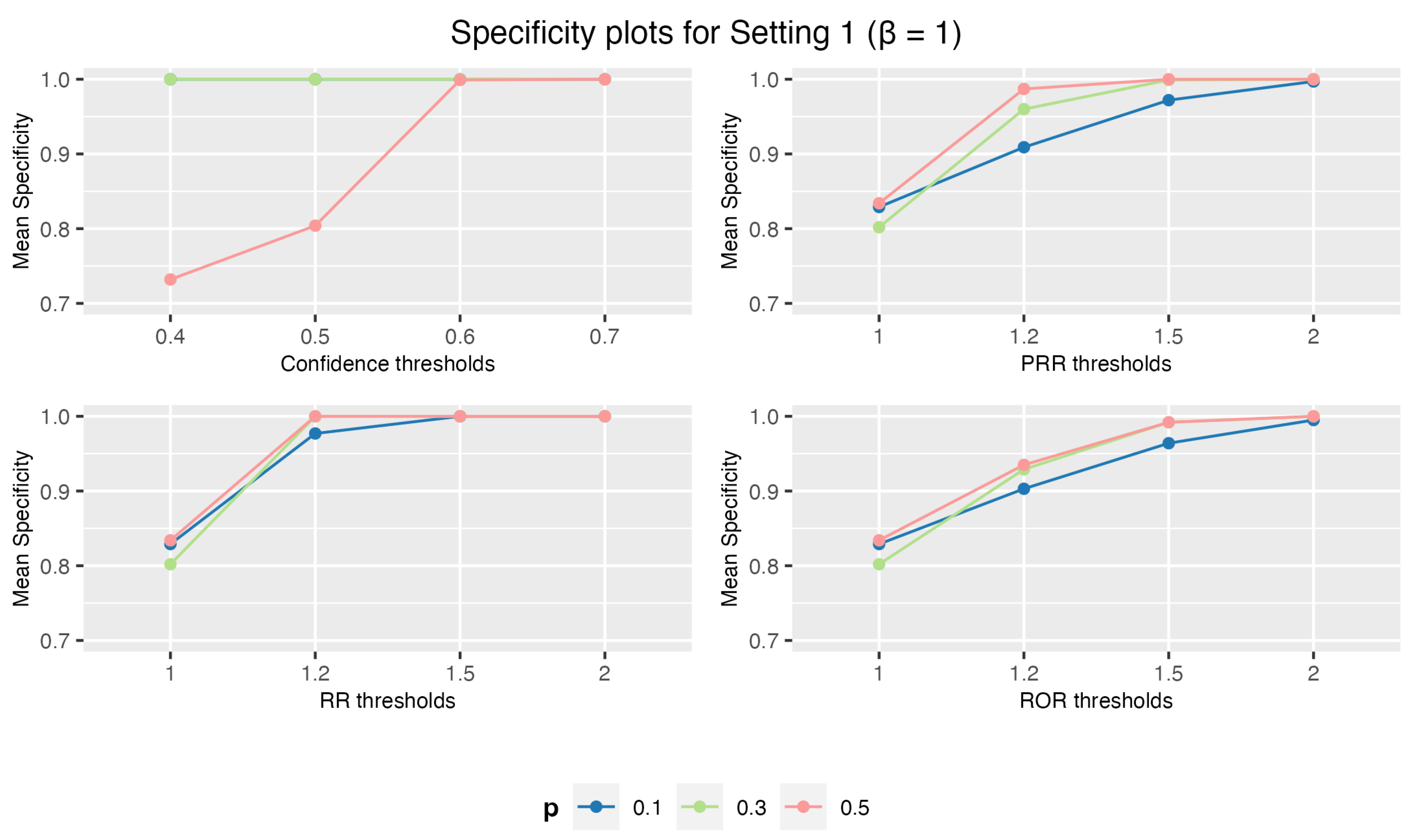
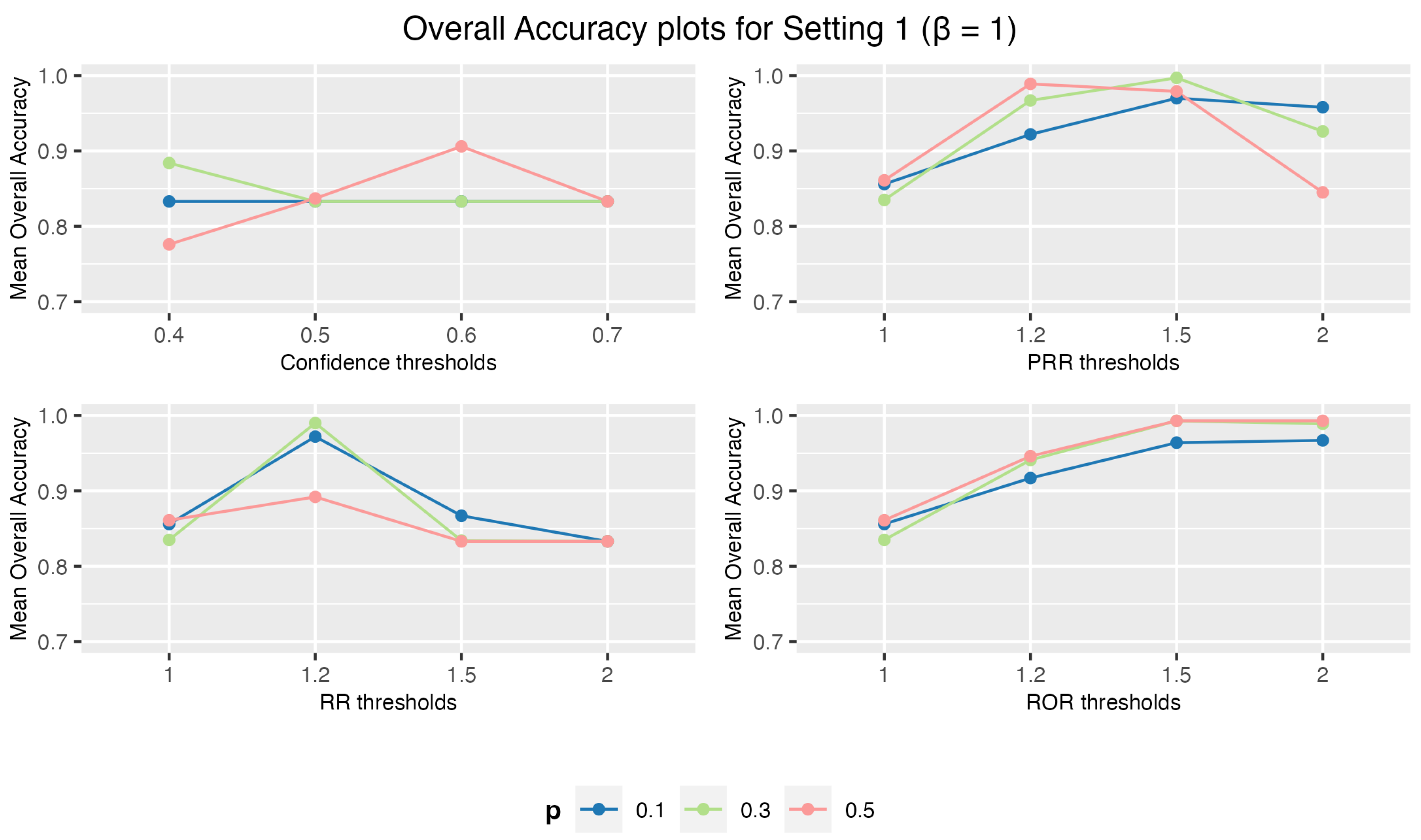
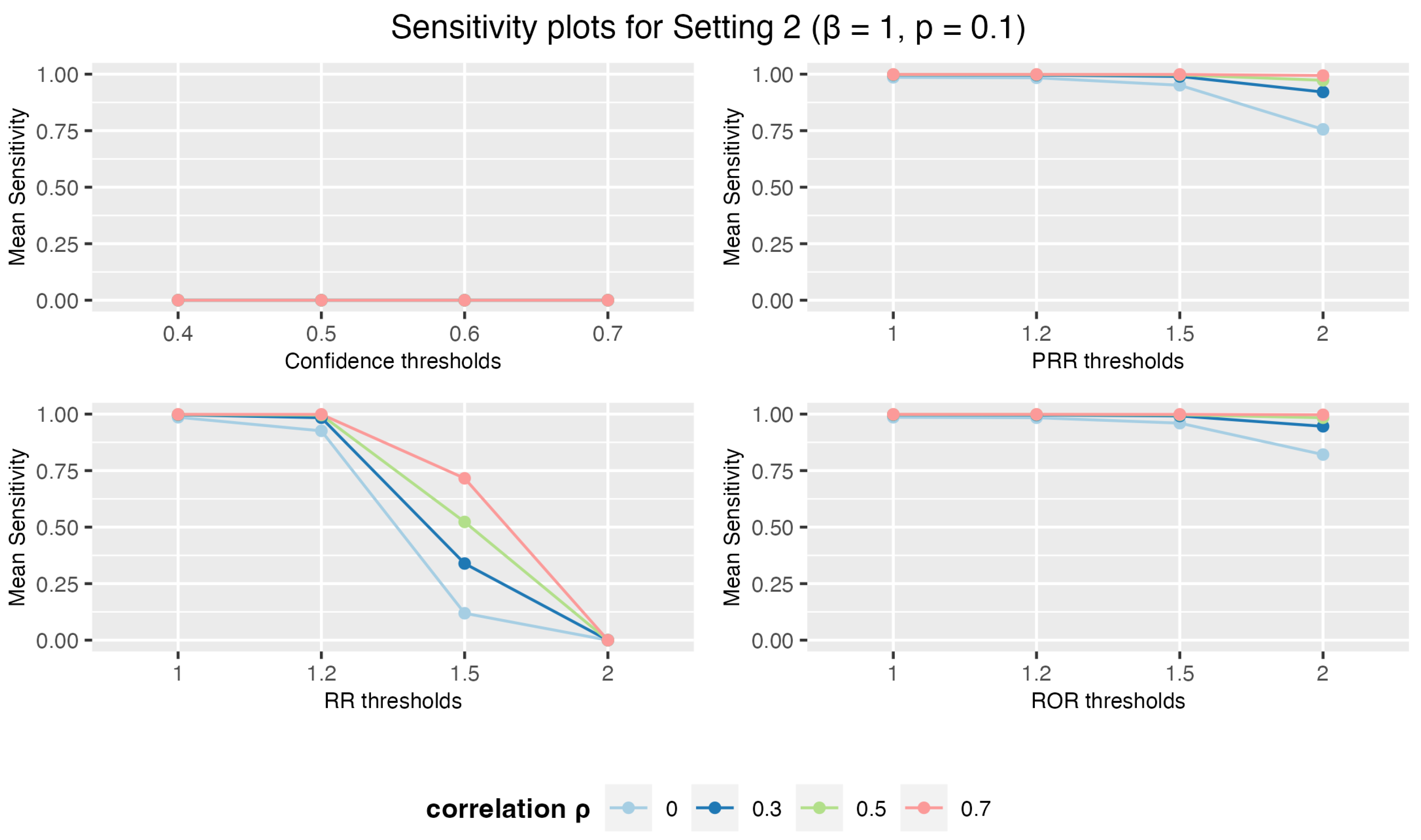
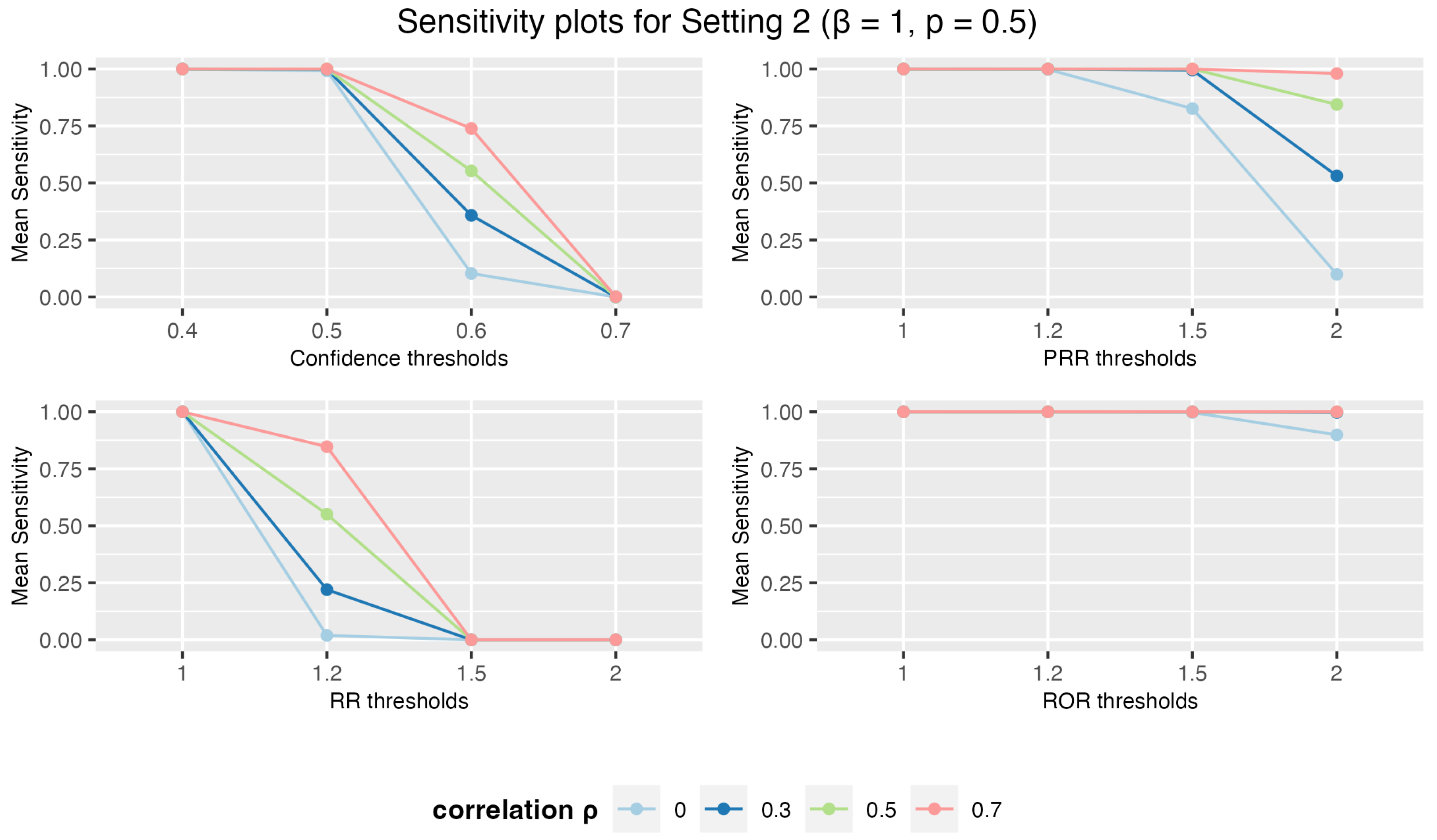
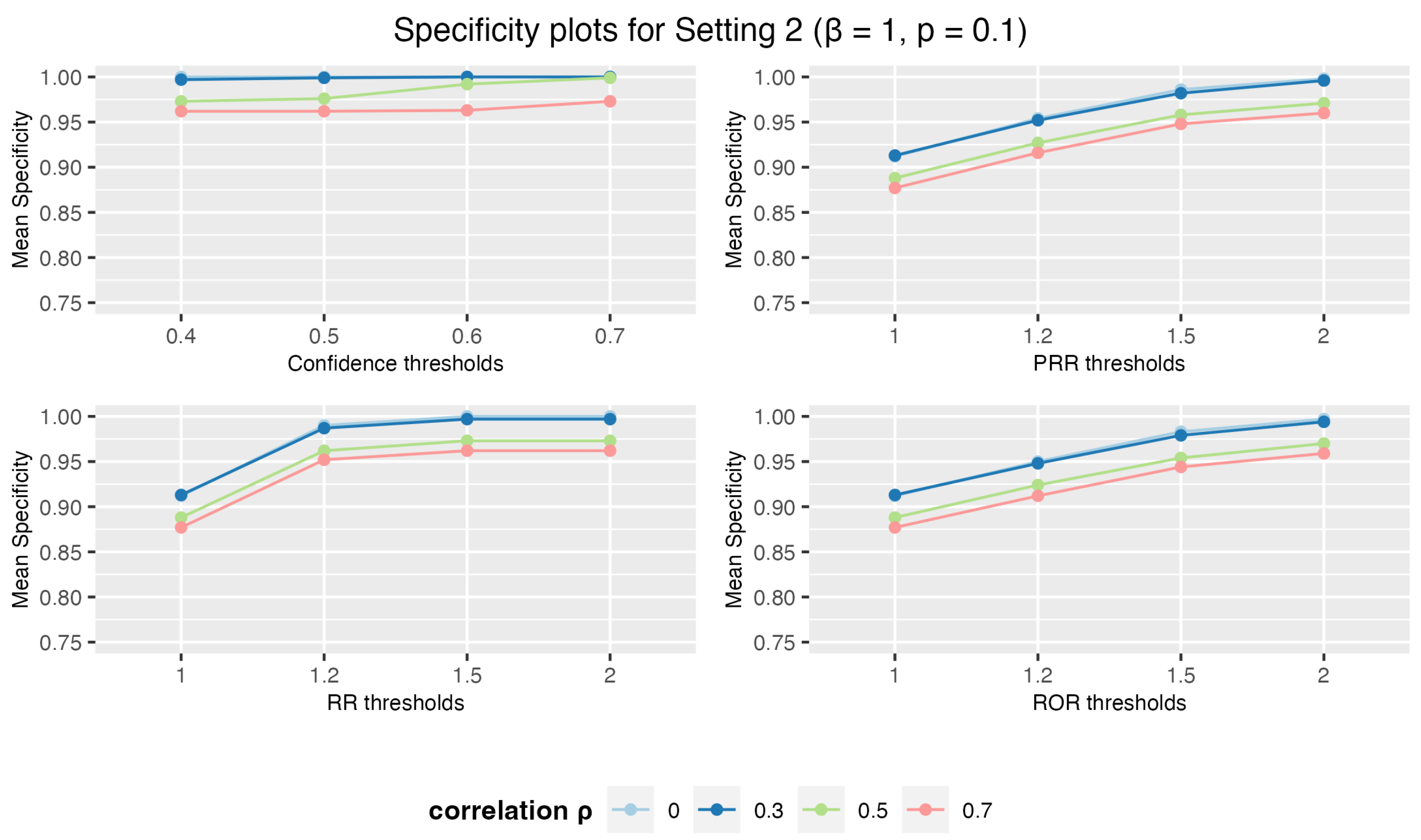
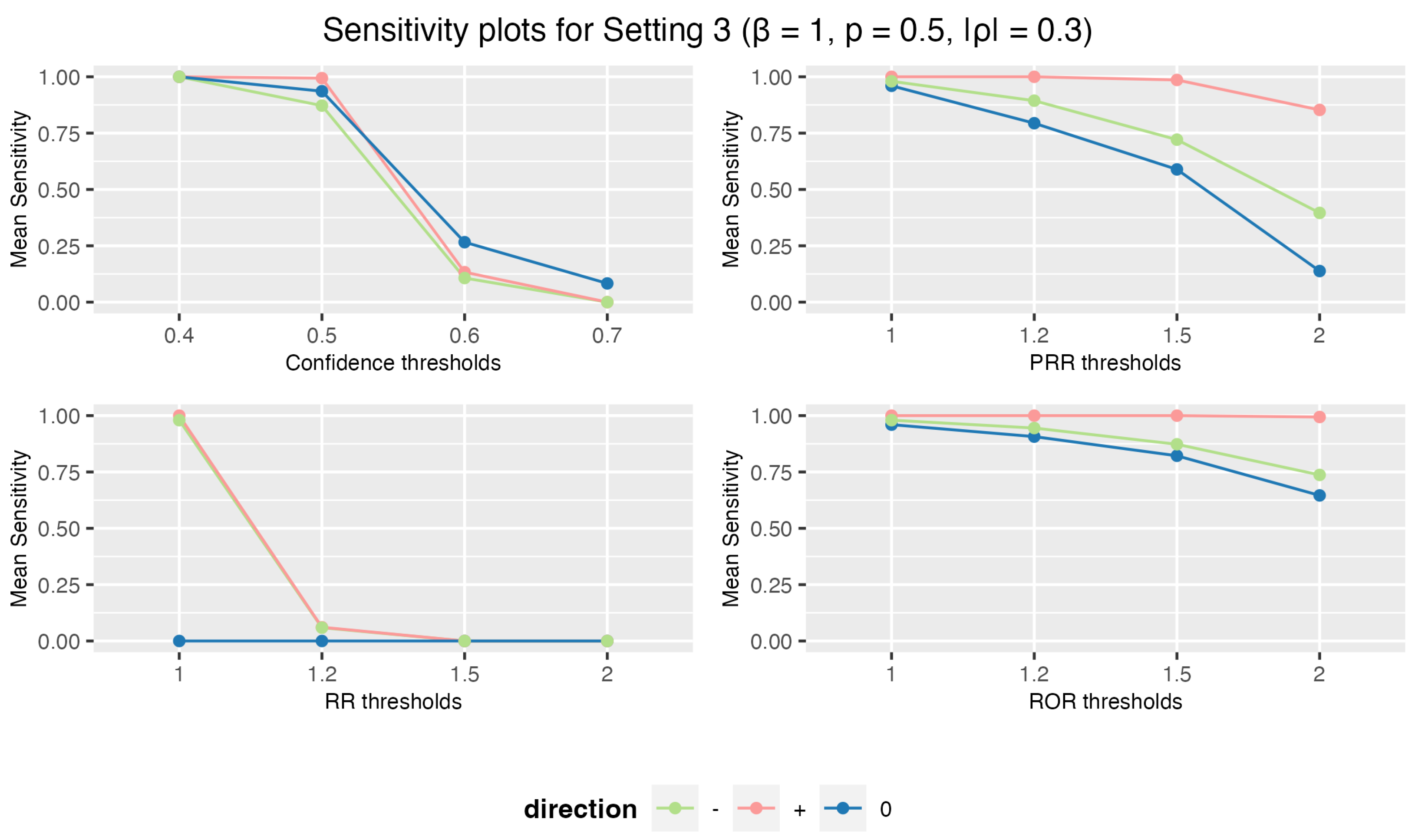
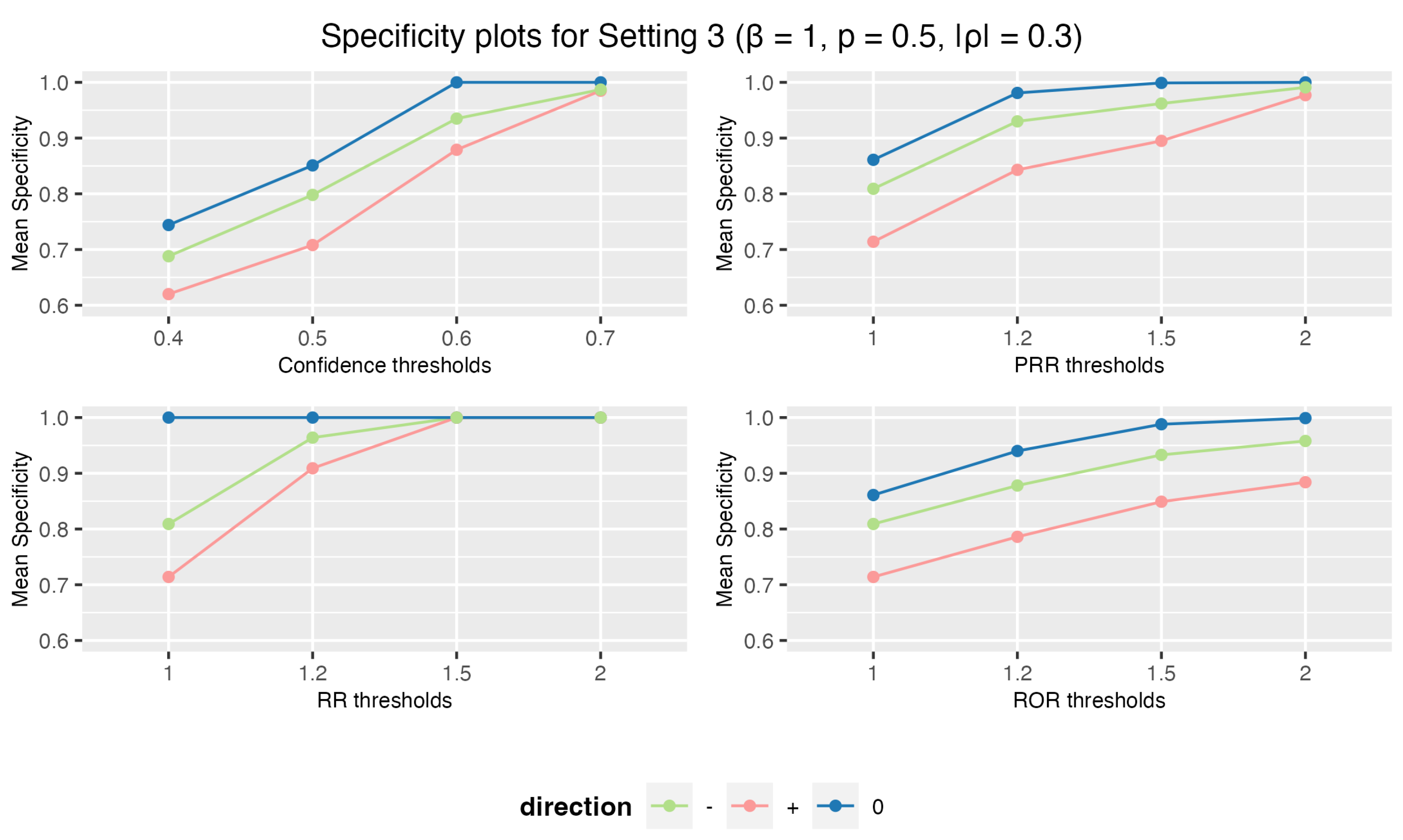
In this section, we report the results from our numerical study, separated by simulations and VAERS data analysis.

3.1. Simulation Study

To evaluate and compare the performances between the proposed improved Apriori and classical Apriori approaches, we use Sensitivity ( S n ), Specificity ( S p ), and Overall Accuracy (OA) [30,31] as the criteria. These measures can be calculated based the below 2 × 2 contingency table (Table 3), in which the columns represent the truly associated and non-associated pairs, while rows indicate the pairs selected and not selected by the method. In the table, TP signifies true positives, FP stands for false positives, FN represents false negatives, and TN denotes true negatives.
Sensitivity, also known as true positive rate, is defined as
S n = a a + c = T P T P + F N .
Specificity, that is true negative rate, is calculated as
S p = d b + d = T N F P + T N .
The overall accuracy is then defined as
OA = a + d a + b + c + d = T P + T N T P + F P + F N + T N .

3.1.1. Setting 1: 1 Drug and 3 AEs

In Setting 1, we consider the scenario of 1 drug and 3 AEs, where only one AE is associated with the drug. The purpose of this setting is to examine the impact of AE frequency, p, and the signal strength β .
Figure 1 shows the comparison of sensitivity among four choices of second parameter when β is fixed at 1. Overall speaking, ROR shows the most robust sensitivity results, while the sensitivity for the other three parameter choices all decrease sharply when threshold increased. In addition, when considering rare AEs, i.e., the AE frequency p = 0.1 , Confidence provides very low sensitivity, which is consistent to the finding in Harpaz et al. [15,20], while PRR and ROR perform much better under this situation. PRR shows the ability to have higher sensitivity when AE is rare and threshold is high. Though the sensitivity for ROR decreases when AE is rare and threshold is high, the decline is slow, so ROR can still provide high sensitivity for rare AE scenarios.
Regarding specificity, Figure 2 shows all four choices of second parameter have higher specificity when threshold increase, which is as expected because when threshold increases, fewer drug-AE pairs would be detected and hence the S n would decrease while S p increases. Besides, rare AEs tend to have lower specificity when compared with the scenarios of more frequent AEs.
The performance of overall accuracy is illustrated by Figure 3. It shows the combined performance of sensitivity and specificity, and both PRR and ROR demonstrate better overall accuracy compared with the Confidence and RR.
It is not surprising to see that when signal strength β increases, both sensitivity and specificity for all four choices increases. Since the simulations show similar trends at other β values, to save the space, the corresponding figures for the remaining β values are listed in the Supplementary Material.

3.1.2. Setting 2: 3 Drugs and 5 AEs

There are 3 drugs and 5 AEs in the second simulation setting, where Drug 1 is associated with AE 1 and AE 2. To explore the impact of correlations among AEs, in this setting, we also set AE 1 and AE 2 to be correlated with a correlation of ρ =0.3, 0.5, 0.7. With signal strength, β , fixed at 1, the results of simulations are shown below.
Figure 4 and Figure 5 show the sensitivity under Setting 2 when β = 1 , and AE frequency p = 0.1 and 0.5, respectively. Both figures illustrate that sensitivity would be improved when correlation between AEs increases. This is as per expectation, as stronger positive correlation leads to increased co-occurrences of the correlated AEs, and as a results, more drug-AE pairs are identified. Additionally, similar as in Setting 1, PRR and ROR perform better by showing stable high sensitivities. However, the sensitivities for both the Confidence and RR decrease quickly when threshold increase. Moreover, comparing Figure 4 and Figure 5, we can see that when AE frequency p, increases, the sensitivity for PRR decreases more than that for ROR at high threshold level, which demonstrates that ROR performs best in terms of sensitivity under this setting.
For specificity (Figure 6), similar as in setting 1, the high threshold values result in better specificity. Besides, when correlation increases, the specificity decreases. As the magnitude of correlation increases, the co-occurrences of positively correlated AEs increase, thereby increasing the chance of false positive findings, compared to zero correlated AEs.
Since as expected, the overall accuracy shows dual effects of sensitivity and specificity, similar as the one in setting 1, the corresponding figures can be found in the Supplementary Material. Similar trends are also observed for other combinations of β and p values, and the corresponding simulation results are listed in the Supplementary Material as well.

3.1.3. Setting 3: 5 Drugs and 10 AEs

Setting 3 includes 5 drugs and 10 AEs, where 5 AEs are associated with drugs. To evaluate the effect of the direction (positive or negative) of AE correlations, in addition to the magnitude of ρ , we also consider both positive and negative correlations among the associated drug-AE pairs.
Figure 7 shows the sensitivity results when β = 1, AE frequency, p = 0.5, and absolution correlation among AEs, | ρ | = 0.3, where we use notations -, +, and 0 to indicate negative ρ , positive ρ , and ρ = 0, respectively. Again, both PRR and ROR show better performance than Confidence and RR, and ROR is the most robust one, due to its slowly declined sensitivity when threshold value increases. In addition, we can also see from Figure 7 that for all three disproportionality measures, both positive and negative correlation increase sensitivity compared with when AEs are uncorrelated, but positive correlation increases sensitivity more than negative correlation. As we discussed before, when AEs are positively correlated, the co-occurrence counts of correlated AEs increase which results in more associated drug-AE pairs to be selected, but in the presence of negatively correlated AEs, the co-occurrence counts of correlated AEs decrease, hence less drug-AE pairs might be detected.
For the specificity in Figure 8, similar as the other two settings, all four choices of second parameter show increased specificity when threshold values increase. In addition, compared with uncorrelated AEs, both positive and negative correlations among AEs would result the decline of specificity. Since negative AE correlations will not have an incremental effect on AE co-occurrence counts compared to when AEs are positively correlated, the chance of false positives (1 - specificity) in the presence of negatively correlated AEs is lower.
The remaining combinations of AE frequencies/signal strengths/AE correlations for settings 1, 2, and 3 typically demonstrate trends similar to what has been already shown above. The corresponding plots have been provided as Supplementary Material.

3.2. VAERS Data

In a total of 746 reports between years 2010 to 2019, that are retrieved from VAERS database, there are 1094 AEs reported for 47 vaccines. The most frequently reported AE is Death with a prevalence rate [32] of 0.764 (570 reports). Some of the least frequently reported AEs are Eyelid Function Disorder, Blood Fibrinogen Increased, Biopsy Soft Tissue, with a prevalence rate of 0.0013 (1 report). This is inline with over-reporting of severe AEs compared to AEs that are more moderate in severity in surveillance monitoring datasets. In addition, the most frequently reported vaccine administered is Pneumococcal, 13-Valent Vaccine (PREVNAR13) with 280 cases reported (prevalence rate of 0.375), while the most infrequently reported vaccines include BCG, Meningococcal B, and Japanese Encephalitis Virus Vaccine, Inactivated, Adsorbed with only 1 reported case. Some of the AEs reported in the VAERS dataset have strong positive correlations such as (Ammonia Decreased, Alpha 1 Foetoprotein Normal) and (Lymphocyte Percentage Decreased, Blood Calcium Decreased), while some AEs have weak negative correlations such as (Encephalopathy, Death).
To implement the Apriori approach, for each unique report, we use binary code 1 and 0 to represent whether a particular vaccine was administered, and whether a specific AE was reported in this report. The threshold for the first parameter, support, is set to be minsup = 3, as the overall mean of all AE frequencies in the data was 3. The levels of threshold for the four second parameters, Confidence, PRR, RR, and ROR, are the same as the ones used in the simulation studies (Section 2.2.1).
In this analysis, there are 51 , 418 out of 650 , 370 total possible 2-item rules that contain one vaccine and one AE for further investigation, which results a pruning rate of 92.09 % .
In Table 4, we list the number of associated vaccine-AE pairs identified by using the Apriori approach under different four choices of the second parameter across varying thresholds. Notably, when using the Confidence as the second parameter, the classical Apriori approach detects much fewer number of vaccine-AE pairs than the other choices of second parameter, even at a low threshold of 0.4. This underscores a limitation highlighted by Harpaz et al. [15,20], revealing the propensity to overlook rare yet strongly associated AEs when employing Confidence in the Apriori algorithm.
Using PRR, RR, and ROR as the second parameter, the improved Apriori approach identifies the same 341 vaccine-AE pairs when threshold is 1. However, as the threshold value increases, the number of association pairs detected by RR declines the most steeply, followed by PRR and then ROR.
Table 5 displays 10 out of 232 vaccine-adverse event (AE) pairs that were identified to be frequent using ROR at a threshold of 2, which involve 7 unique vaccines and 9 unique AEs. The rows in the table denote the first 10 pairs from the list of all 232 selected pairs sorted in increasing order of their respective ROR values. The corresponding values of PRR, RR, and Confidence for each of these vaccine-AE pairs are also shown in the table.
From Table 5, we can see that some of the pairs, such as such as Haemophilus B Conjugate Vaccine (HIBV) →Pallor, have support as low as the minimum threshold of 3. In addition, for these pairs, PRR shows closed values to ROR, and RR values are also not far from ROR and PRR. This further illustrates the benefits of using disproportionality measures as the second parameter in the Apriori approach, especially when the association is rare or not frequent. On the contrary, 29 out of 33 selected pairs by using Confidence (with a threshold 0.4) as the second parameter contain Death as AE, the most frequently reported AE in this data set, which again confirms the limitation of using Confidence as the second parameter. Within these 33 pairs, 20 are also identified by using PRR or ROR at threshold value 1 (see Table S1 in the Supplementary Material for more detail). We also notice that the rules DTAPIPVHIB→Unresponsive to Stimuli, FLU3 (SEASONAL)→Nausea, DTAPHEPBIP→Respiratory Arrest, RV5→Resuscitation, HIBV→Pallor, and HIBV→ Apnoea have been studied before [33,34,35,36,37,38,39,40,41,42,43,44], which confirms the validity of our proposed improved Apriori approach.

4. Discussion

This paper involves detailed study of an improved Apriori approach, wherein disproportionality measures, PRR, RR, and ROR, are used to substitute Confidence as the second parameter in implementing Apriori for safety data. This method incorporates the advantages of disproportionality measures to detect rare safety signals that may be associated with a drug/vaccine. Our comprehensive studies have also taken into account challenges that are specific to safety data, such as rarely occurring AEs, underlying AE correlations, and varying levels of safety signal strength. We have also investigated the performance of each parameter choice at different thresholds to understand how it affects the accuracy of association identification.
Our numerical studies have shown that using Confidence in Apriori implementation for safety data results in infrequent AEs having smaller Confidence even when they are strongly associated with a drug. Relative Reporting Ratio (RR), which has also been suggested in some literature, has high sensitivity at a threshold of 1 but demonstrates decreased sensitivity at higher thresholds. In our simulation studies, PRR and ROR have been compared extensively in different settings, revealing that PRR tends to have a sharply declining sensitivity at higher thresholds compared to ROR when signal strength between an AE and a drug/vaccine is weak, even when AE frequencies are high. The stability in the performance of ROR in identifying drug/vaccine-AE pairs is particularly useful in identifying rare associations that are not observed during pre-clinical studies, but are reported during the post-market stage when there are more data due to the drug or vaccine being available for a larger population.
Furthermore, from the real data studies, it is observed that using Confidence as a parameter for screening vaccine-AE pairs leads to selection of pairs majorly containing Death as the AE. Though the usage of disproportionality measures leads to identification of only some of the rules that contain Death as the AE, in practice, we suggest that the severe adverse events, such as death should always be added manually for further investigation, regardless of screening analysis results.
Conclusions based on disproportionality measures implemented in post-marketing surveillance reports can only be made about the risk of AE reporting and not the risk of the AE itself. Additionally, disproportionality measures do not establish association or causation and results therefrom should be strictly considered exploratory for further investigation.
Future work in this area includes statistical hypothesis testing of the important pairs screened by the improved Apriori technique to determine whether a vaccine/drug is associated with the reporting of an AE. In addition, extending the current Apriori search from two-item, i.e., one-drug-one-AE association, to K-item for K>2, could assist further accounting for the interactions between drugs or AEs.

5. Conclusion

Our comprehensive study shows the benefit of using disproportionality measures as the second parameter in the Apriori method for screening of important associations between drugs/vaccines and AEs in post-marketing safety data, particularly when the goal is to identify AEs that are rarely co-occurring with a drug or a vaccine. However, due to its screening nature, the improved Apriori should be used in conjunction with conventional Apriori (using Confidence as second parameter) and/or manual investigation. It is also important to note that the generated rules do not imply genuine association or causality. Further studies and clinical assessment are needed to ascertain whether association/causality exists between a drug/vaccine and an AE.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Author Contributions

Methodology, J.S. and R.S.; study design, J.S. and R.S.; computation, R.S.; data analysis, R.S.; investigation, R.S.; resources, R.S.; data curation, R.S.; manuscript writing – original draft preparation, R.S.; manuscript writing – review and editing, J.S. and R.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are publicly available.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. World Health Organization (WHO). The Importance of Pharmacovigilance, 2022. By WHO Quality Assurance and Safety Team. ISBN 9241590157. Retrieved December 18, 2023.
  2. Wax, P.M. Elixirs, diluents, and the passage of the 1938 Federal Food, Drug and Cosmetic Act. Annals of internal medicine 1995, 122, 456–461. [Google Scholar] [CrossRef] [PubMed]
  3. Vargesson, N. Thalidomide-induced teratogenesis: History and mechanisms. Birth Defects Research Part C: Embryo Today: Reviews 2015, 105, 140–156. [Google Scholar] [CrossRef] [PubMed]
  4. Sibbald, B. Rofecoxib (Vioxx) voluntarily withdrawn from market. CMAJ : Canadian Medical Association Journal 2004, 171, 1027–1028. [Google Scholar] [CrossRef] [PubMed]
  5. Krumholz, H.M.; Ross, J.S.; Presler, A.H.; Egilman, D.S. What have we learnt from Vioxx? BMJ : British Medical Journal 2007, 334, 120–123. [Google Scholar] [CrossRef] [PubMed]
  6. Mehrotra, D.V.; Adewale, A.J. Flagging clinical adverse experiences: reducing false discoveries without materially compromising power for detecting true signals. Statistics in Medicine 2012, 31, 1918–1930. [Google Scholar] [CrossRef] [PubMed]
  7. Tan, X.; Chen, B.E.; Sun, J.; Patel, T.; Ibrahim, J.G. A hierarchical testing approach for detecting safety signals in clinical trials. Statistics in Medicine 2020, 39, 1541–1557. [Google Scholar] [CrossRef] [PubMed]
  8. Berry, S.M.; Berry, D.A. Accounting for multiplicities in assessing drug safety: a three-level hierarchical mixture model. Biometrics 2004, 60, 418–426. [Google Scholar] [CrossRef] [PubMed]
  9. Amy Xia, H.; Ma, H.; Carlin, B.P. Bayesian hierarchical modeling for detecting safety signals in clinical trials. Journal of Biopharmaceutical Statistics 2011, 21, 1006–1029. [Google Scholar] [CrossRef] [PubMed]
  10. DuMouchel, W. Multivariate Bayesian Logistic Regression for Analysis of Clinical Study Safety Issues. Statistical Science 2012, 319–339. [Google Scholar] [CrossRef]
  11. Agrawal, R.; Srikant, R.; others. Fast algorithms for mining association rules. Proc. 20th int. conf. very large data bases, VLDB. Santiago, Chile, 1994, Vol. 1215, pp. 487–499.
  12. Srikant, R.; Agrawal, R. Mining sequential patterns: Generalizations and performance improvements. Advances in Database Technology — EDBT ’96; Apers, P., Bouzeghoub, M., Gardarin, G., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 1996; pp. 1–17. [Google Scholar]
  13. Lallich, S.; Teytaud, O.; Prudhomme, E. Association Rule Interestingness: Measure and Statistical Validation. Springer Berlin Heidelberg, 2007, Vol. 43, pp. 251–275. [CrossRef]
  14. Kuo, M.H.; Kushniruk, A.W.; Borycki, E.M.; Greig, D. Application of the Apriori Algorithm for Adverse Drug Reaction Detection. In Detection and Prevention of Adverse Drug Events; IOS Press, 2009; pp. 95–101. [CrossRef]
  15. Harpaz, R.; Chase, H.S.; Friedman, C. Mining multi-item drug adverse effect associations in spontaneous reporting systems. BMC Bioinformatics 2010, 11, S7. [Google Scholar] [CrossRef]
  16. van Puijenbroek, E.P.; Bate, A.; Leufkens, H.G.M.; Lindquist, M.; Orre, R.; Egberts, A.C.G. A comparison of measures of disproportionality for signal detection in spontaneous reporting systems for adverse drug reactions. Pharmacoepidemiology and Drug Safety 2002, 11, 3–10. [Google Scholar] [CrossRef] [PubMed]
  17. Evans, S.J.W.; Waller, P.; Davis, S. Proportional reporting ratios: the uses of epidemiological methods for signal generation. Pharmacoepidemiol Drug Saf 1998, 7, S102. [Google Scholar]
  18. Szarfman, A.; Machado, S.G.; O’Neill, R.T. Use of screening algorithms and computer systems to efficiently signal higher-than-expected combinations of drugs and events in the US FDA’s spontaneous reports database. Drug safety 2002, 25, 381–392. [Google Scholar] [CrossRef] [PubMed]
  19. Meyboom, R.H.; Hekster, Y.A.; Egberts, A.C.; Gribnau, F.W.; Edwards, I.R. Causal or casual? The role of causality assessment in pharmacovigilance. Drug safety 1997, 17, 374–389. [Google Scholar] [CrossRef] [PubMed]
  20. Harpaz, R.; Haerian, K.; Chase, H.S.; Friedman, C. Statistical Mining of Potential Drug Interaction Adverse Effects in FDA’s Spontaneous Reporting System. AMIA Annual Symposium Proceedings 2010, 2010, 281–285. [Google Scholar] [PubMed]
  21. Wang, C.; Guo, X.J.; Xu, J.F.; Wu, C.; Sun, Y.L.; Ye, X.F.; Qian, W.; Ma, X.Q.; Du, W.M.; He, J. Exploration of the Association Rules Mining Technique for the Signal Detection of Adverse Drug Events in Spontaneous Reporting Systems. PLOS ONE, 7, e40561. [CrossRef]
  22. Rothman, K.J.; Lanes, S.; Sacks, S.T. The reporting odds ratio and its advantages over the proportional reporting ratio. Pharmacoepidemiology and Drug Safety, 13, 519–523. [CrossRef]
  23. Evans, S.J.W.; Waller, P.C.; Davis, S. Use of proportional reporting ratios (PRRs) for signal generation from spontaneous adverse drug reaction reports. Pharmacoepidemiology and Drug Safety 2001, 10, 483–486. [Google Scholar] [CrossRef] [PubMed]
  24. Avery, A.; Anderson, C.; Bond, C.; Fortnum, H.; Gifford, A.; Hannaford, P.; Hazell, L.; Krska, J.; Lee, A.; McLernon, D.; others. Evaluation of patient reporting of adverse drug reactions to the UK ‘Yellow Card Scheme’: literature review, descriptive and qualitative analyses, and questionnaire surveys. Health Technology Assessment 2011, 15, 1–234. [Google Scholar] [CrossRef] [PubMed]
  25. Sindhu, M.S.; Kannan, B. Detecting signals of drug-drug interactions using association rule mining methodology. IJCSIT) Int J Comput Sci Inf Technol 2013, 4, 590–594. [Google Scholar]
  26. Bate, A.; Lindquist, M.; Edwards, I.R.; Olsson, S.; Orre, R.; Lansner, A.; De Freitas, R.M. A Bayesian neural network method for adverse drug reaction signal generation. European journal of clinical pharmacology 1998, 54, 315–321. [Google Scholar] [CrossRef]
  27. Bate, A.; Evans, S.J.W. Quantitative signal detection using spontaneous ADR reporting. Pharmacoepidemiology and Drug Safety 2009, 18, 427–436. [Google Scholar] [CrossRef]
  28. Lunn, A.D.; Davies, S.J. A Note on Generating Correlated Binary Variables. Biometrika 85, 487–490. [CrossRef]
  29. Shimabukuro, T.T.; Nguyen, M.; Martin, D.; DeStefano, F. Safety monitoring in the vaccine adverse event reporting system (VAERS). Vaccine 2015, 33, 4398–4405. [Google Scholar] [CrossRef]
  30. Kohl, M. Performance Measures in Binary Classification. International Journal of Statistics in Medical Research 1, 79–81. [CrossRef]
  31. Alberg, A.J.; Park, J.W.; Hager, B.W.; Brock, M.V.; Diener-West, M. The Use of “Overall Accuracy” to Evaluate the Validity of Screening or Diagnostic Tests. Journal of General Internal Medicine 2004, 19, 460–465. [Google Scholar] [CrossRef] [PubMed]
  32. Marshall, S.W. Prevalence and Incidence. In Encyclopedia of Social Measurement; Kempf-Leonard, K., Ed.; Elsevier: New York, 2005; pp. 141–147. [Google Scholar] [CrossRef]
  33. Hansen, J.; Decker, M.D.; Lewis, E.; Fireman, B.; Pool, V.; Greenberg, D.P.; Johnson, D.R.; Black, S.; Klein, N.P. Hypotonic-hyporesponsive Episodes After Diphtheria, Tetanus and Acellular Pertussis Vaccination. The Pediatric Infectious Disease Journal 2021, 40, 1122–1126. [Google Scholar] [CrossRef] [PubMed]
  34. Baxter, R.; Patriarca, P.; Ensor, K.; Izikson, R.; Goldenthal, K.; Cox, M. Evaluation of the safety, reactogenicity and immunogenicity of FluBlok® trivalent recombinant baculovirus-expressed hemagglutinin influenza vaccine administered intramuscularly to healthy adults 50–64 years of age. Vaccine 2011, 29, 2272–2278. [Google Scholar] [CrossRef]
  35. Yang, L.P. Recombinant trivalent influenza vaccine (Flublok®): a review of its use in the prevention of seasonal influenza in adults. Drugs 2013, 73, 1357–1366. [Google Scholar] [CrossRef] [PubMed]
  36. Halperin, S.A.; Smith, B.; Clarke, K.; Treanor, J.; Mabrouk, T.; Germain, M. A Phase I, Randomized, Controlled Trial to Study the Reactogenicity and Immunogenicity of a Nasal, Inactivated Trivalent Influenza Virus Vaccine in Healthy Adults. Human Vaccines 2005, 1, 37–42. [Google Scholar] [CrossRef] [PubMed]
  37. Baldo, V.; Bonanni, P.; Castro, M.; Gabutti, G.; Franco, E.; Marchetti, F.; Prato, R.; Vitale, F. Combined hexavalent diphtheria-tetanus-acellular pertussis-hepatitis B-inactivated poliovirus-Haemophilus influenzae type b vaccine; Infanrix™ hexa: Twelve years of experience in Italy. Human vaccines & immunotherapeutics 2014, 10, 129–137. [Google Scholar]
  38. Zangwill, K.M.; Eriksen, E.; Lee, M.; Lee, J.; Marcy, S.M.; Friedland, L.R.; Weston, W.; Howe, B.; Ward, J.I. A population-based, postlicensure evaluation of the safety of a combination diphtheria, tetanus, acellular pertussis, hepatitis B, and inactivated poliovirus vaccine in a large managed care organization. Pediatrics 2008, 122, e1179–e1185. [Google Scholar] [CrossRef]
  39. Omeñaca, F.; Vázquez, L.; Garcia-Corbeira, P.; Mesaros, N.; Hanssens, L.; Dolhain, J.; Gómez, I.P.; Liese, J.; Knuf, M. Immunization of preterm infants with GSK’s hexavalent combined diphtheria-tetanus-acellular pertussis-hepatitis B-inactivated poliovirus-Haemophilus influenzae type b conjugate vaccine: A review of safety and immunogenicity. Vaccine 2018, 36, 986–996. [Google Scholar] [CrossRef] [PubMed]
  40. Loughlin, J.; Mast, T.C.; Doherty, M.C.; Wang, F.T.; Wong, J.; Seeger, J.D. Postmarketing evaluation of the short-term safety of the pentavalent rotavirus vaccine. The Pediatric infectious disease journal 2012, 31, 292–296. [Google Scholar] [CrossRef] [PubMed]
  41. McGrath, E.J.; Thomas, R.; Duggan, C.; Asmar, B.I. Pentavalent rotavirus vaccine in infants with surgical gastrointestinal disease. Journal of pediatric gastroenterology and nutrition 2014, 59, 44–48. [Google Scholar] [CrossRef] [PubMed]
  42. Black, S.; Greenberg, D.P. A combined diphtheria, tetanus, five-component acellular pertussis, poliovirus and Haemophilus influenzae type b vaccine. Expert Review of Vaccines 2005, 4, 793–805. [Google Scholar] [CrossRef] [PubMed]
  43. Silfverdal, S.A.; Coremans, V.; François, N.; Borys, D.; Cleerbout, J. Safety profile of the 10-valent pneumococcal non-typeable Haemophilus influenzae protein D conjugate vaccine (PHiD-CV). Expert review of vaccines 2017, 16, 109–121. [Google Scholar] [CrossRef]
  44. Botham, S.; Isaacs, D.; Henderson-Smart, D. Incidence of apnoea and bradycardia in preterm infants following DTPw and Hib immunization: A prospective study. Journal of Paediatrics and Child Health 33, 418–421. [CrossRef]
Preprints 112750 g001
Figure 1. Sensitivity plots for Setting 1: 1 drug and 3 AEs when β = 1 and AE frequency p = 0.1 , 0.3 , 0.5 .
Figure 1. Sensitivity plots for Setting 1: 1 drug and 3 AEs when β = 1 and AE frequency p = 0.1 , 0.3 , 0.5 .
Preprints 112750 g001
Preprints 112750 g002
Figure 2. Specificity plots for Setting 1: 1 drug and 3 AEs when β = 1 , and AE frequency p = 0.1 , 0.3 , 0.5 .
Figure 2. Specificity plots for Setting 1: 1 drug and 3 AEs when β = 1 , and AE frequency p = 0.1 , 0.3 , 0.5 .
Preprints 112750 g002
Preprints 112750 g003
Figure 3. Overall Accuracy plots for Setting 1: 1 drug and 3 AEs when β = 1 , and AE frequency p = 0.1 , 0.3 , 0.5 .
Figure 3. Overall Accuracy plots for Setting 1: 1 drug and 3 AEs when β = 1 , and AE frequency p = 0.1 , 0.3 , 0.5 .
Preprints 112750 g003
Preprints 112750 g004
Figure 4. Sensitivity plots for Setting 2: 3 drugs and 5 AEs when β = 1, p = 0.1.
Figure 4. Sensitivity plots for Setting 2: 3 drugs and 5 AEs when β = 1, p = 0.1.
Preprints 112750 g004
Preprints 112750 g005
Figure 5. Sensitivity plots for Setting 2: 3 drugs and 5 AEs when β = 1, p = 0.5.
Figure 5. Sensitivity plots for Setting 2: 3 drugs and 5 AEs when β = 1, p = 0.5.
Preprints 112750 g005
Preprints 112750 g006
Figure 6. Specificity plots for Setting 2: 3 drugs and 5 AEs when β = 1, p = 0.1.
Figure 6. Specificity plots for Setting 2: 3 drugs and 5 AEs when β = 1, p = 0.1.
Preprints 112750 g006
Preprints 112750 g007
Figure 7. Sensitivity plots for Setting 3: 5 drugs and 10 AEs when β = 1, p = 0.5, and | ρ | = 0.3.
Figure 7. Sensitivity plots for Setting 3: 5 drugs and 10 AEs when β = 1, p = 0.5, and | ρ | = 0.3.
Preprints 112750 g007
Preprints 112750 g008
Figure 8. Specificity plots for Setting 3: 5 drugs and 10 AEs when β = 1, p = 0.5, and | ρ | = 0.3.
Figure 8. Specificity plots for Setting 3: 5 drugs and 10 AEs when β = 1, p = 0.5, and | ρ | = 0.3.
Preprints 112750 g008
Table 1. Contingency table for Disproportionality Measures
Table 1. Contingency table for Disproportionality Measures
Suspected AE All other AEs Total
Suspected drug a b a + b
All other drugs c d c + d
Total a + c b + d a + b + c + d
Table 2. Subset of VAERS data from January 2010
Table 2. Subset of VAERS data from January 2010
VAERS ID VAERS ID Code Vaccine Type Vaccine Type Code Symptoms Symptoms Code
0376710-1 0376710-1 DIPHTHERIA AND TETANUS TOXOIDS AND ACELLULAR PERTUSSIS VACCINE + INACTIVATED POLIOVIRUS VACCINE + HAEMOPHILUS B CONJUGATE VACCINE DTAPIPVHIB DEATH 10011906
0376710-1 0376710-1 DIPHTHERIA AND TETANUS TOXOIDS AND ACELLULAR PERTUSSIS VACCINE + INACTIVATED POLIOVIRUS VACCINE + HAEMOPHILUS B CONJUGATE VACCINE DTAPIPVHIB UNRESPONSIVE TO STIMULI 10045555
0376710-1 0376710-1 INFLUENZA VIRUS VACCINE, TRIVALENT (INJECTED) FLU3(SEASONAL) DEATH 10011906
0376710-1 0376710-1 INFLUENZA VIRUS VACCINE, TRIVALENT (INJECTED) FLU3(SEASONAL) UNRESPONSIVE TO STIMULI 10045555
0376710-1 0376710-1 PNEUMOCOCCAL, 7-VALENT VACCINE (PREVNAR) PNC DEATH 10011906
0376710-1 0376710-1 PNEUMOCOCCAL, 7-VALENT VACCINE (PREVNAR) PNC UNRESPONSIVE TO STIMULI 10045555
0376969-1 0376969-1 INFLUENZA (H1N1) MONOVALENT (INJECTED) FLU(H1N1) COAGULOPATHY 10009802
0376969-1 0376969-1 INFLUENZA (H1N1) MONOVALENT (INJECTED) FLU(H1N1) DEATH 10011906
0376969-1 0376969-1 INFLUENZA (H1N1) MONOVALENT (INJECTED) FLU(H1N1) DRUG INTERACTION 10013710
Table 3. Contingency table for validity measurement of binary classification. TP: true positive; FP: false positive; FN: false negative; and TN: true negative.
Table 3. Contingency table for validity measurement of binary classification. TP: true positive; FP: false positive; FN: false negative; and TN: true negative.
Associated pairs Non-associated pairs Total
Selected a (TP) b (FP) a + b
Not selected c (FN) d (TN) c + d
Total a + c b + d a + b + c + d
Table 4. Counts of selected vaccine-AE association pairs from VAERS data.
Table 4. Counts of selected vaccine-AE association pairs from VAERS data.
Parameter Threshold Selected pairs
Confidence 0.4 33
0.5 30
0.6 28
0.7 26
PRR 1 341
1.2 308
1.5 272
2 214
RR 1 341
1.2 300
1.5 246
2 153
ROR 1 341
1.2 321
1.5 282
2 232
Table 5. Ten vaccine-AE pairs selected using Apriori with ROR at the threshold of 2, along with their corresponding values of ROR, PRR, RR, and Confidence.
Table 5. Ten vaccine-AE pairs selected using Apriori with ROR at the threshold of 2, along with their corresponding values of ROR, PRR, RR, and Confidence.
Vaccine Code Vaccine Name AE/Symptom Name Support ROR PRR RR Confidence
DTAPIPVHIB DIPHTHERIA AND TETANUS TOXOIDS AND ACELLULAR PERTUSSIS VACCINE + INACTIVATED POLIOVIRUS VACCINE + HAEMOPHILUS B CONJUGATE VACCINE UNRESPONSIVE TO STIMULI 25 2.059 1.867 1.609 0.181
FLU3(SEASONAL) INFLUENZA VIRUS VACCINE, TRIVALENT (INJECTED) NAUSEA 8 2.061 2.002 1.681 0.056
DTAPHEPBIP DIPHTHERIA AND TETANUS TOXOIDS AND ACELLULAR PERTUSSIS VACCINE + HEPATITIS B + INACTIVATED POLIOVIRUS VACCINE RESPIRATORY ARREST 15 2.063 1.939 1.668 0.116
RV5 ROTAVIRUS VACCINE, LIVE, ORAL, PENTAVALENT RESUSCITATION 35 2.074 1.853 1.551 0.206
HEPA HEPATITIS A INTENSIVE CARE 4 2.074 1.972 1.870 0.095
HIBV HAEMOPHILUS B CONJUGATE VACCINE PALLOR 3 2.077 2.055 1.703 0.020
HIBV HAEMOPHILUS B CONJUGATE VACCINE DEHYDRATION 3 2.077 2.055 1.703 0.020
HIBV HAEMOPHILUS B CONJUGATE VACCINE RHINORRHOEA 3 2.077 2.055 1.703 0.020
PPV PNEUMOCOCCAL VACCINE, POLYVALENT INTENSIVE CARE 3 2.082 1.977 1.900 0.097
HIBV HAEMOPHILUS B CONJUGATE VACCINE APNOEA 4 2.084 2.055 1.703 0.027
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated