Prerpints.org logo
Preprint
Article

Description of Ion Properties Using Molecular Orbital Energy Levels

Altmetrics

Downloads

75

Views

37

Comments

0

supplementary.pdf (9.27MB )

This version is not peer-reviewed

Submitted:

20 July 2024

Posted:

23 July 2024

You are already at the latest version

Alerts
Abstract
The study reveals correlations between the parameters of ions and their HOMO and LUMO orbital energy level values. In particular, it demonstrates a clear correlation for the ion adsorption parameters on model electrodes: the aluminum oxide (0001) surface, graphene and Au (111) surface. Correlations are also observed for the parameters of ion binding to water and dimethyl carbonate molecules, which are often used as solvents. In addition, the dipole moment, polarizability and solvation energy of ions are well correlated with the values of the molecular orbital energies, and for anions a dependence on the oxidation potential is observed. The obtained descriptors make it possible to select ions with desired values for a specific problem. As an illustrative example, in this work we consider the problem of displacement of water molecules from the inner electric double layer by ions, which is one of the factors increasing the potential window in electrolytes of aqueous batteries. This approach can be applied in the rapidly developing field of aqueous electrolytes for battery or supercapacitor design, catalysis control through surface composition variations, as well as in studies of heavy metal ion binding to sorption materials.
Keywords: 
Subject: Chemistry and Materials Science  -   Theoretical Chemistry

1. Introduction

The vast majority of activity parameters (descriptors) characterize the catalytic activity of heterogeneous catalysts. [1,2] Researchers have proposed a lot of electronic parameters that quite accurately describe the activity of various materials: centers of transition metal atomic bands, [3–5] orbital occupancy for transition metal oxides, [6] Fermi level, [7,8] effective coordination numbers [9] and associated electron density for metals, [10–12] density of states at the Fermi level for graphene, [13,14] etc. Such studies normally consider industrial reactions, for example, oxygen reduction, [14,15] hydrogen oxidation, [13,16] nitrogen fixation, [17,18] CO2 conversion, [19,20] etc.
The activity parameters for molecules, [21–25] which are mainly used in molecular catalysis, design of biologically active substances, etc., are somewhat different. First and foremost in this list of parameters are the values of ionization potential (IP) and electron affinity (EA) and the associated energies of the highest occupied molecular orbital (HOMO) IP=-εHOMO and the lowest unoccupied molecular orbital (LUMO) EA=-εLUMO. [23] There are also a number of derived parameters based on HOMO and LUMO: [21–23] orbital energy difference (εHOMO-LUMO), chemical potential (µ), hardness (η), softness (S), electronegativity (χ), and global electrophility index (ω). These molecular descriptors find applications in catalysis, [21,24] corrosion studies, [25] evaluation of biological activity of compounds, [24] etc. In addition, complex descriptors for neutral molecules [26] and ions [26,27] were proposed for characterizing some parameters of complexes (dissociation constants, reaction rate constants, etc.). These parameters describe specific properties of complexes of molecules or ions based on a whole range of parameters of the system under study (dipole moment, molecular volume, hydrogen bonding strength, etc.).
The vast majority of studies devoted to searching for activity descriptors usually consider a specific reaction proceeding on a variety of materials or active centers. [6,13–15,17–20] The main goal of such studies is to select materials on which the considered reaction has the highest rate. Despite the current trends, it is also appropriate to consider the reverse problem, where the study concerns the interaction of a variety of absorbents on the surface of one catalyst or molecule. Such studies can be extremely important for controlling the surface composition and surface activity of various applications in various industrial processes. In addition to catalysis, an example of an applied problem that can be solved is selection of the optimal electrolyte [28] for a particular electrode material in batteries or supercapacitors. Another practical application is binding of toxic impurities from solutions, especially binding of heavy metal ions. [29–31] Such descriptors will make it possible to evaluate the efficiency of a particular sorbent for a range of ions.
The existence of such descriptors is confirmed by the data of refs, [32–34] which show correlations of the adsorption energy of neutral molecules on the oxide surface with the HOMO and LUMO energy level and other parameters. Refs. [35,36] reveals correlations of the solvation energy with hardness. These facts suggest the possibility of a simplified description of the dependence of adsorption and some physicochemical and electrochemical parameters of molecules or ions on the energy level of the orbitals.
For better clarity and potential practical application, the present work analyzes the adsorption coupling of various ions on the surface of a dielectric (aluminum oxide (0001) surface), a semiconductor (graphene) and a metal (gold (111) surface). The intermolecular interaction is analyzed by studying the binding of water and dimethyl carbonate (solvents frequently used in chemical and electrochemical practice) to ions of molecules. Correlations between some physicochemical and electrochemical parameters of ions and their electronic structure are also analyzed. The systems under study are a number of surface inactive and active ions, which are used in electrochemical investigations of surface phenomena [37,38] and electron transfer, [37,39] organic electrochemistry [40–43] and potentially applicable in chemical current sources, [28,44–51] such as batteries, supercapacitors, etc.

2. Methods

Quantum-chemical calculations of ion adsorption on slabs were performed in the Quantum Espresso software package [52] within the generalized gradient approximation by the Perdew-Burke-Ernzerhof (PBE) functional [53] using standard PAW pseudopotentials. [54,55] Spin polarization was taken into account in the calculations and the maximum energy limit was 600 eV. The Monkhorst-Pack special point method [56] with an electron smearing of 0.1 eV and a k-grid density of 5x5x1 by the Methfessel-Paxton method [57] was selected for integration over the Brillouin zone. The energy convergence criterion of the self-consistent field method was set at 10- [5] eV. The van der Waals interactions were considered within the Grimme method (DFT-D3). [58]
The relaxation of atoms in the slabs was carried out by the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm, the convergence criterion for the energy optimization of the atom geometry was set at 10– [4] eV and the maximum force was 0.01 eV/Å.
A 72-atom graphene, a 60-atom Au(111), and a 60-atom α-Al2O3 (0001) slabs with cross-sectional dimensions of 6x6, 4x4, and 4x4 unit cells, respectively, were used as the model electrodes. The adsorption energy was calculated as the energy of the optimized slab with the ion on the surface minus the energy of the slab with the ion at a distance of 9−11 Å from the surface.
The cations in the study were the following systems contained in ionic liquids, [42,43] electrolytes for power sources, [48] including aqueous batteries that have been popular in the last decade, [28,47] as well as supporting electrolytes used in organic electrochemistry: [40,41] alkali metal cations (Li+, Na+, K+, Cs+, Rb+), tetraalkylammonium cations R4N+ (R = -Me, -Et, -Pr, -Bu), derivatives of the pyridinium cation RPy+ (R = -H, -Me, -Et), alkylmethylpyrrodilidone cation RMPyr+ (R = -Et, -Bu) and alkylmethylimidazolium cation RMI+ (R = -Et, -Bu, -Hexcyl (H), -Octyl (O), -Dodecyl (D), -Ph), cetyltrimethylammonium Me3NCet+ (CTA+) and cetylpyridinium CetPy+ (CP+) cations.
The anions were selected in a similar way: [47–49] OH-, ClO4-, NO3-, and dycyanamide (DCA-) grouped into a separate category for convenience; halides (F-, Cl-, Br-); RSO3- derivatives (R = -NH2, -Me, -Et, -Cet, -Ph) and HSO4- (R = -OH) added here; RCOO- carboxylates (R= -Me, -Et, -Pr, i-Pr and -Bu) and fluorine-containing anions (CF3COO-, tetrafluoroborate BF4-, hexaflurophosphate PF6-, trifluromethanesulfonate TfO- and bis(trifluromethylsulfonyl) imide TFSI-).
In addition to the above systems, we considered the products of water autoprotholysis: hydroxide (OH-) and hydroxonium (H3O+) ions.
The geometry optimization of ion complexes with water and dimethyl carbonate (DMC) molecules was carried out in the ORCA software package [59] with the B3LYP functional [60,61] and the 6-31++G(d,p) basis set. The free energy of ion-molecule binding was calculated as the difference between the free energy of the optimized aqueous complex and the original ions and water or DMC molecule in vacuum.
The dipole moment, polarizability, solvation energy and redox potential were calculated in the 6-311++G(3df,3pd) basis set. The solvation and redox potentials were determined within the PCM model [62–64] taking into account the dielectric parameters of the respective solvent; H2O or DMC was used as the environment. The dielectric and other physical parameters of DMC for the PCM model construction were taken from refs. [65–67] For simplicity, the solvation energy (Gsolv) was calculated as the difference between the free energy of the ion in the PCM model (GPCM) and that of the ion in vacuum (Gvac): Gsolv = GPCM – Gvac+G°→*, where G°→*=-kBT∙ln(24.4509) at T = 298 K is the term describing the process transition of the solute from gas 1 atm to solution 1 mole/L. The redox potential was calculated for the cations from the reduction reaction Ion+ + e- = Ion [0] and for the anions from the oxidation reaction Ion- – e- = Ion [0] as the difference between the energy of the initial ion (GPCM(Ion±)) and that of the reduced or oxidized ion (GPCM(Ion0)): [28,68] Epot = – [GPCM(Ion+) – GPCM(Ion [0] )]/F or [GPCM(Ion [0] ) – GPCM(Ion-)]/F, where F was the Faraday constant. The absolute value of the redox potential (Epot) was converted to a value relative to the standard hydrogen electrode (SHE): Epot (vs. SHE) =Epot - 4.44 V. [69] The values of the electronic levels of the ions were calculated by the B3LYP functional in the 6-311++G(3df,3pd) basis set in vacuum.
The distance between the center of mass of the ion and the surface (z0) or the center of mass of the solvent molecule (r0) was calculated using the Python library of the Atomic Simulation Environment (ASE). [70] A number of adsorbent and aqueous complex parameters, such as adsorption energies (Eads), binding energies (Gbind) and distances (z0 and r0), were statistically averaged taking into account different conformations of the ions and solvent molecules.

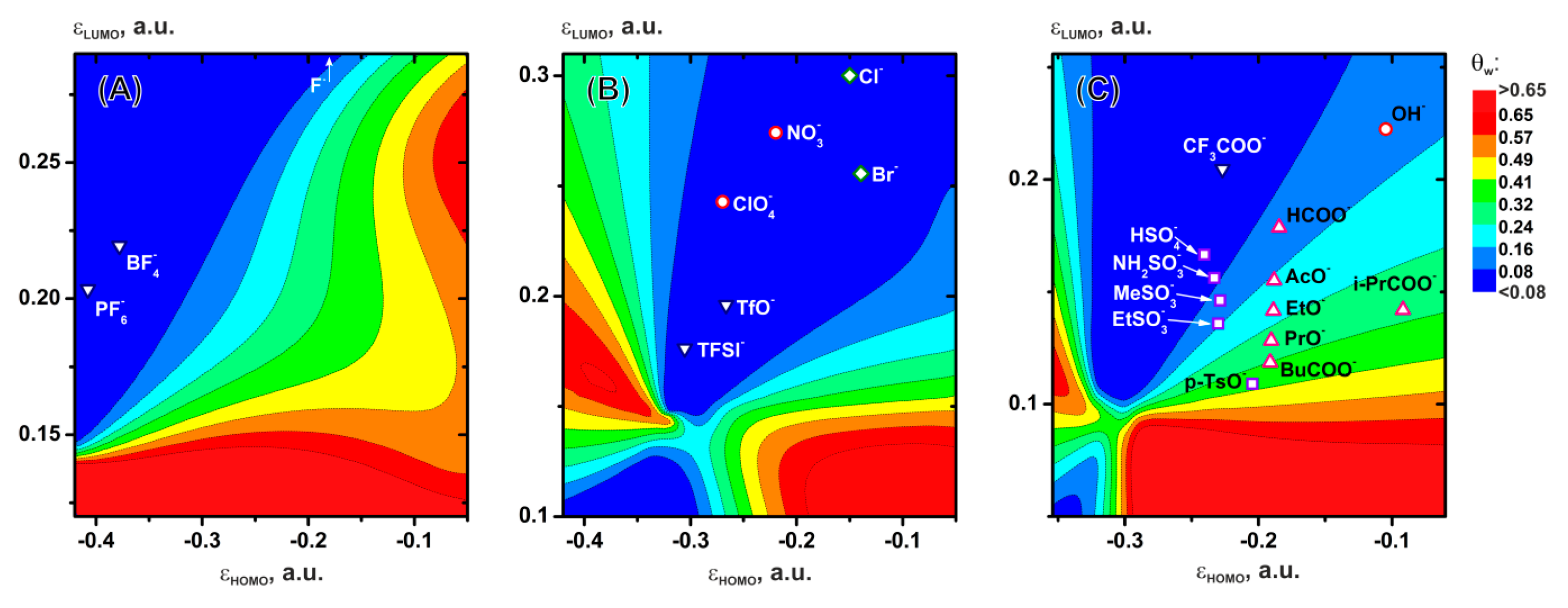
3. Results and Discussion

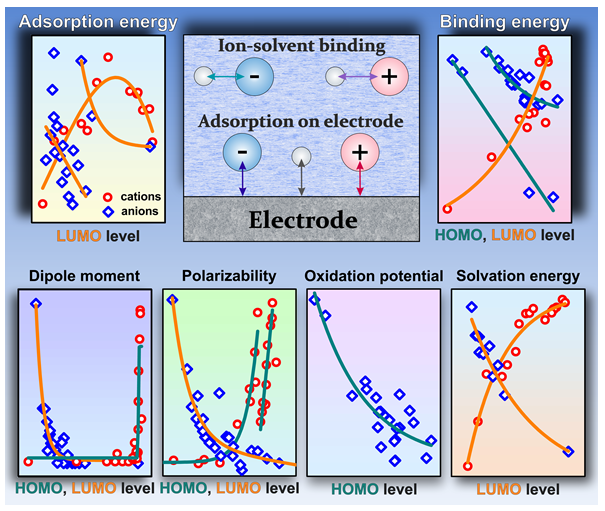
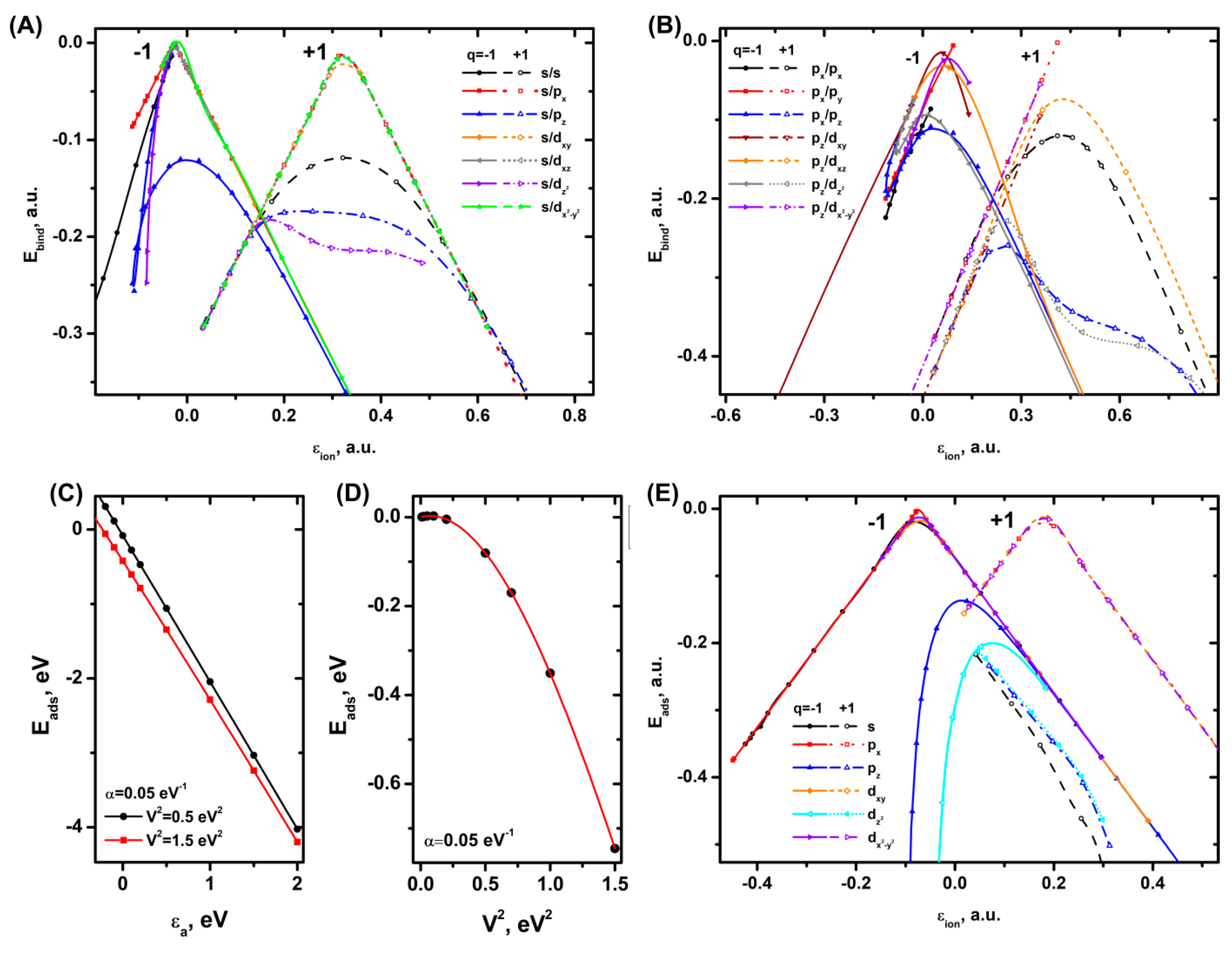
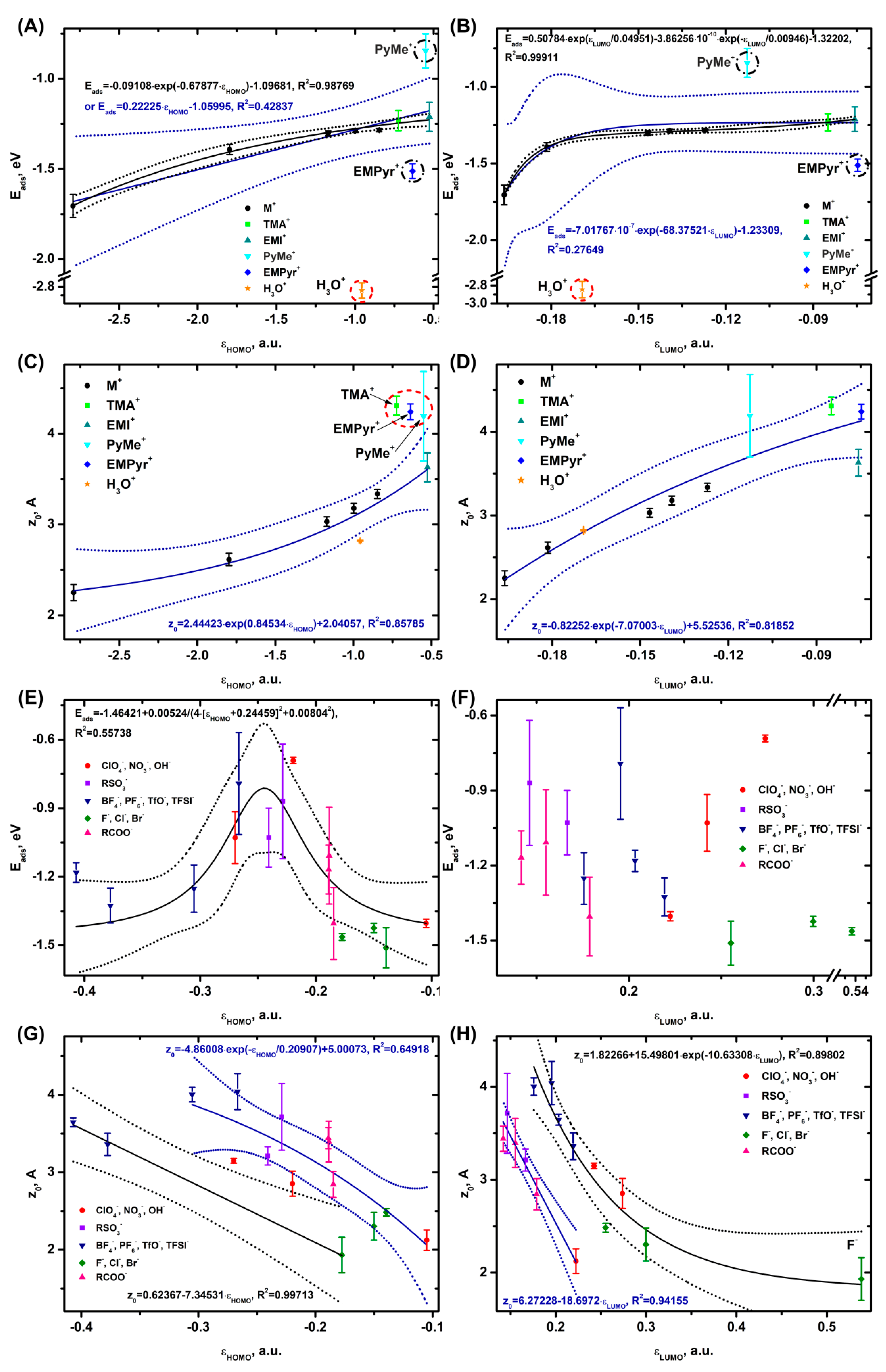
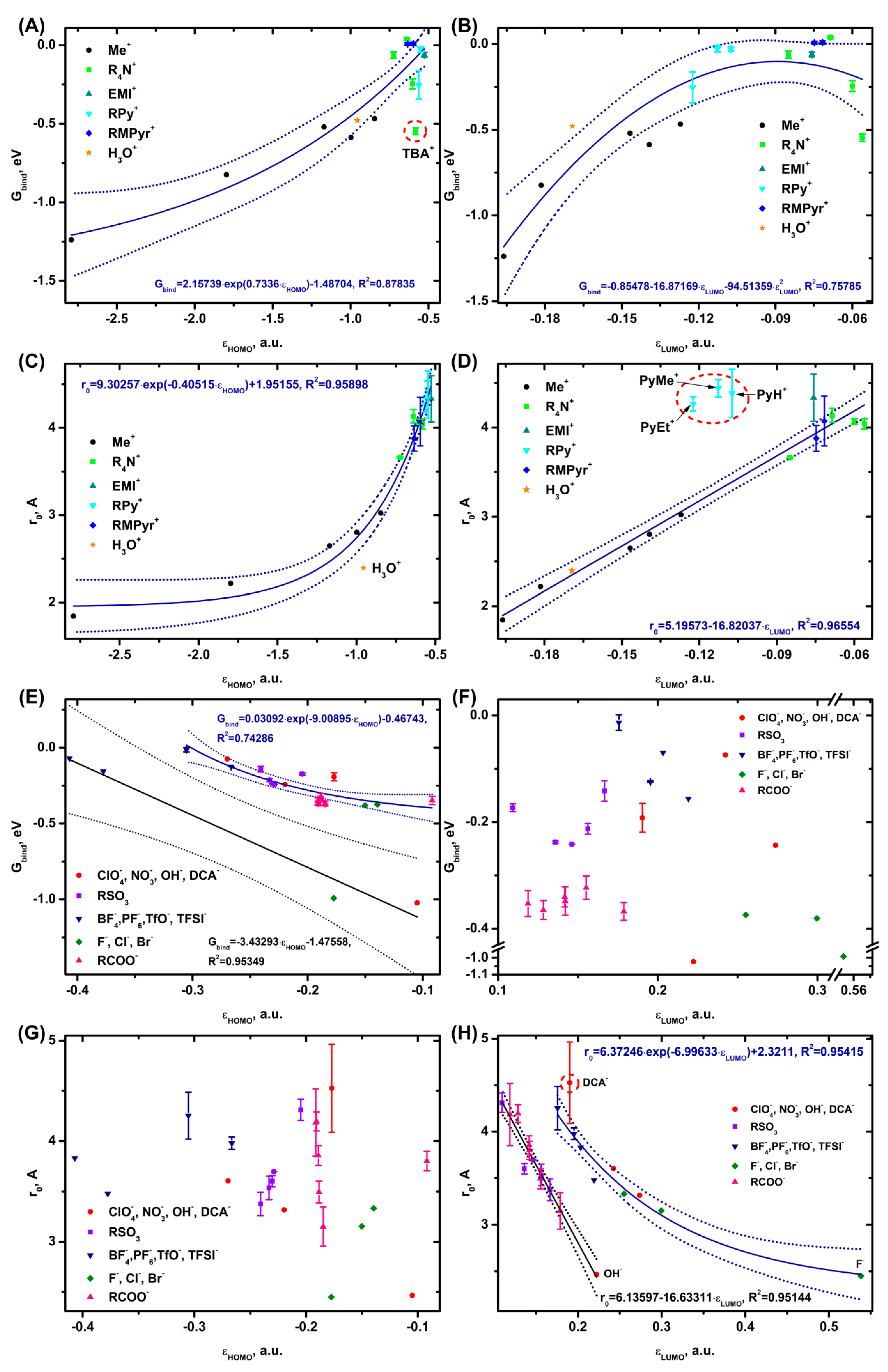
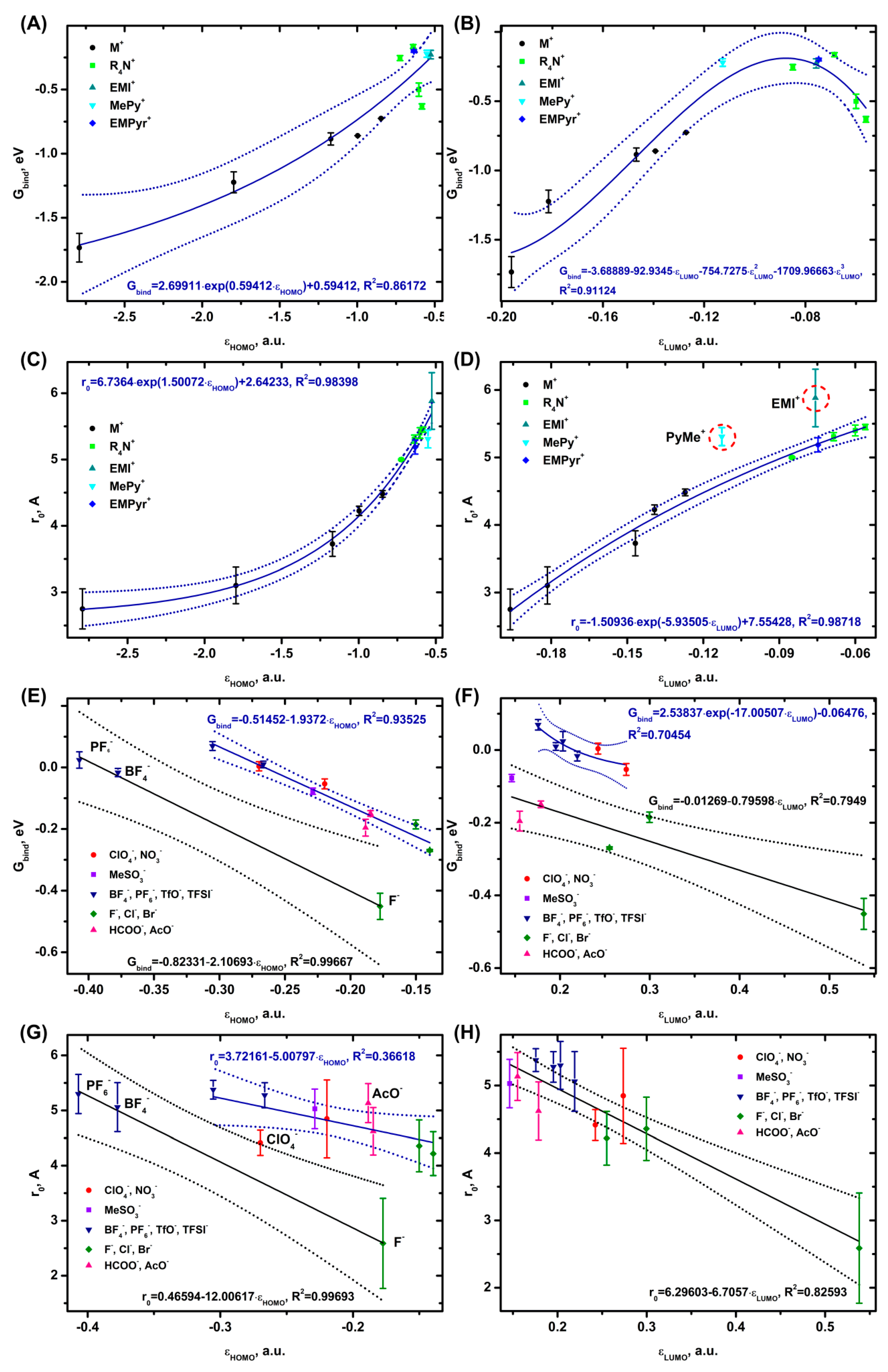
3.1. Relation of Electronic Levels of Ions to Adsorption and Binding Energy

Let us evaluate how the energy level of an ion's orbitals can affect binding into an adsorption complex with solvent molecules or an electrode surface.
To consider the simplest scenario of the interaction of an ion with a solvent molecule through a one-electron operator, let us represent their wave functions in terms of Gaussian orbitals for a solvent molecule (assuming that the solvent consists of sufficiently light atoms) ψsolv=Asolv∙rn∙exp(-αsolv∙r [2]), where n=0 for the s-orbital and n=1 for the p-orbital and ψion=Aion∙rn∙exp(-αion∙r [2]) for the s-, p- or d-orbital for the ion (n=2 for the d-orbital). Asolv and Aion are normalizing coefficients, αsolv=0.1 a.u.- [2] and αion are exponential coefficients, and all the wave functions are normalized ψ solv | ψ solv = ψ ion | ψ ion = 1 . The overlap of the wave functions is given by the expression S = ψ solv | ψ ion .
The eigenvalues of the orbitals of the solvent molecule and ion [71,72] will look as follows:
ε solv = ψ solv H ∧ ψ solv
and   ε ion = ψ ion H ∧ ψ ion
where
H ∧ = H kin + H en = − h 2 2 m e ∇ 2 + ∑ i e 0 2 q i ε 0 r − r i is the one-electron perturbation operator, which is the sum of the electron kinetic energy (Hkin) and electron-nuclear interaction (Hen); ∇ 2 is the Laplace operator; r − r i = x − x i 2 + y − y i 2 + z − z i 2 is the distance between the electron density (product of the wave functions) at an arbitrary point x, y, z and a point charge qi with xi, yi, and zi coordinates of the i-atom; h is the Planck constant; me and e0 are the mass and charge of the electron; ε0 is the vacuum dielectric constant; i is the serial number of an atom in the solvent molecule.
The matrix element (V) for the orbitals is expressed through operator H ∧ :
V = ψ solv H ∧ ψ ion
The binding energy between the ψsolv and ψion orbitals is described by the expression: [4]
E bind = 2 ε + − ε solv − ε ion
where ε + is the solution to the Schrödinger equation for the ground state,
ε + = ε solv + ε ion − 4 V 2 + 1 − S 2 ε solv − ε ion 2 2 1 − S 2
The energy level of the ψion orbital can be changed by varying the αion parameter in the range of 0.001 – 0.5 a.u.- [2].
Now let us consider the adsorption of ions on the electrode using the Newnes-Andersen (NA) model. [3,73] According to the NA model, Eads is determined by the sum of the contributions: [4,5,74,75]
E ads = E hyb + E ortho
The first term E hyb = ∫ − ∞ + ∞ ε f ( ε ) ρ a ( ε ) d ε − 2 ε a represents the hybridization energy due to the overlap between the adsorbent orbitals and the electronic states of the electrode, the second term E ortho = − 2 n a + f S V ak is the orthogonalization energy (Pauli repulsion),
where f(ε) is the Fermi function, εa is the energy level of the adsorbent valence orbital, na is the filling of the adsorbent valence orbital determined by the expression n a = ∫ − ∞ + ∞ f ( ε ) ρ a d ε , and f = ∫ − ∞ + ∞ f ( ε ) ρ el d ε / ∫ − ∞ + ∞ ρ el d ε is the degree of filling of the electrode electronic level.
For simplicity, we assume that V is proportional to S=-α∙|V|, where α is a coefficient, and thus arrive at E ortho = 2 n a + f α V a 2 .
The density of states on the adsorbent is given by the expression
ρ a ( ε ) = 1 π Δ 2 ( ε ) ε − ε a − Λ ( ε ) 2 + Δ 2 ( ε )
where Δ and Λ are the chemisorption functions described by the expressions [76] Δ ε = π ∑ k V k 2 δ ε - ε k , and Λ is the Hilbert transform of Δ: Λ ε = 1 π P ∫ Δ (   ε   ′   ) ε -   ε   ′ , where P denotes the principal part. For simplicity, instead of the sum of values for all the k-vectors, we represent Δ(ε) in the form Δ ε ≈ π ρ el ε V 2 . [5,72,77]
The adsorbent nature in the NA model, eq. (6−7), is given directly only by parameters εa and V [2,5] S is indirectly related to the matrix element. In case of the ions, as the data show (Supplementary Material of ref. [72]) for O2 and intermediates of oxygen reduction OH and OOH, the matrix element increases significantly due to the contribution of the electron-nuclear interaction. That is why we will evaluate the influence of, first of all, V [2] and then εa on Eads.
Another way to estimate adsorption is to represent the effective orbital of an electrode as an s-function distributed along the z-axis perpendicular to the electrode, as in the jellium model: [78,79]
ψel=Ael∙exp(-αel∙z[2]) (8)
Such approach has been used in numerous works [71,72,80,81,82,83,84] to estimate the matrix element of the overlap between the electrode and redox system orbitals. In the following calculations, αel was set at 0.01 a.u.- [2] and the normalization factor Ael in (8) was calculated at the electrode surface (z=0) and at some distance from it using the expression 1 = ∫ z = 0 z = + ∞ ψ el 2 .
In this method, the ψel function substitutes for ψsolv in expressions (1−3). After that, all further calculations are made using equations (4, 5), and the final expression for the adsorption energy can be rewritten as
E ads = 2 ε + − ε el − ε ion
where S = ψ solv | ψ ion , ε el = ψ el H ∧ ψ el , ε ion = ψ ion H ∧ ψ ion , V = ψ el H ∧ ψ ion and the ground state energy ε + = ε el + ε ion − 4 V 2 + 1 − S 2 ε el − ε ion 2 2 1 − S 2 .
The results of the calculations of binding of the orbitals of cations and anions with the solvent orbital using the model of eq. (1−5) give a set of graphs that fully or partially form two volcano-shaped dependencies (Figure 1 A,B). The graphs show that the orbital energies for the anions are mostly lower than those for the cations. It means that the centers of the volcano-shaped dependencies on the energy scale are shifted to the left for the anions and to the right for the cations.
In the regions of decreasing or increasing Ebind values, the graphs are quite close to linear or exponential dependencies. In case of s/s (schematic notation: solvent molecule orbital/ion orbital), s/pz and s / d z 2 cation orbital interactions, the maximum region becomes sloped, which is caused by a large overlap of the orbitals due to their shape (σ-bond formation), lowering the binding energy value. When the solvent s-orbitals are combined with the d xy and d xz orbitals of the ions, rather weak π-bonds are formed. In case of the solvent p-orbitals, similar trends are observed for px/pz and pz/ d z 2 and, to a lesser extent, for pz/dxz and px/px. The steeper slope of pz/dxz and px/px compared to s/px, etc. is explained by the larger extent of the p-orbital compared to the s-orbital, which results in a strong overlap and a decrease in the Ebind value. The specific shape of pz/ d z 2 is caused by the orientation of pz-orbital directly towards the point charge of the ion. As a result, the contribution of the Hne operator makes the bond stronger.
The most interesting trend is observed when the pz-orbital of the anion participates in the binding, which causes a split in the left side of the branch (Figure 1 A,B). A special case are the results for the combination of s/s, and s/ d z 2 orbitals at q=-1; px/px and px/py at q= -1 and px/px, px/py, and pz/dxy at q= +1, for which stable solutions are obtained only for one of the branches, the shape of which is close to a linear function, and in some cases (s/ d z 2 ) to an exponential one.
The dependence of Eads(εa) according to the NA model, eq. (6, 7), is almost linear and does not depend significantly on coefficient α (Figure 1C), while in case of Eads(V [2]) an exponential dependence is observed (Figure 1D). In the region of moderately high values V [2]> 0.5 eV [2], the dependence of Eads(V [2]) is almost linear. Notably, the approximation of specific results of DFT calculations of DOS adsorbents, for example, [74,75] shows that each bond type or band involved in the adsorption can have its own set of parameters εa and εc (band center). Therefore, for sufficiently high adsorption energies and, respectively, high V [2], the shape of the Eads(V [2]) or Eads(εa) dependencies may become more complicated due to the contribution of a larger number of electrode bands and adsorbent orbitals involved in the adsorption process.
The calculations for the ions carried out by eq. (9) for the p x , d xy , d x 2 - y 2 orbitals lead to two volcano-shaped dependencies (Figure 1E). Their side branches are close to linear dependencies and the interaction of the orbitals with the electrode is rather weak in this case. In case of the p z and d z 2 orbitals, a quickly decreasing exponential dependence is observed. For the cations involving these orbitals, the Eads dependence represents a function that decreases as the εion value becomes higher. In general, this result is very close to the data obtained by the first model by eq. (1−5).
Since the HOMO or LUMO orbitals of real ions represent a superposition of a number of MOs, the total contribution of such composite orbitals to the final adsorption energy or energy of binding can become more complicated. If we consider the interaction between the solvent molecules and the ions, the dependence of the binding energy on the ion energy level becomes volcano-shaped. When the p-orbitals of the ion are oriented along the z-axis (perpendicular to the MO of the solvent molecule), the left side of the volcano-shaped Ebind dependence splits into two branches. In addition to the splitting, a scenario of parallel dependencies caused by the simultaneous contribution of multiple MOs of the ion is also possible. Within the NA model, the adsorption dependencies can be linear or exponential. However, if we consider the adsorption on the electrode through the effective wave function by eq. (8, 9), we can expect the same trends as those obtained in the first model by eq. (1−5), i.e. formation of volcano-like dependencies or an exponential or linear decrease/increase in the adsorption energy.

3.2. Trends in Ion Adsorption on α-Al2O3 (0001), Graphene and Au (111)

Summarizing the data on the adsorption of ions (Figure S1.1−S1.12, Table S2.3 in Supplementary Information) and their binding into complexes (Figure S2.1−S2.4, Table S3.3), we can conclude that it is most convenient to evaluate the energy levels of the HOMO (εHOMO) and LUMO (εLUMO) orbitals (Table S4.1, S4.2). In some cases, second highest (HOMO-1) and second lowest (LUMO+1) molecular orbitals can also be used. In addition, there are descriptors that combine HOMO and LUMO with HOMO-1 and LUMO+1 orbitals, e.g. hyperhardness or hypersoftness. [21] In case of strong correlations, combining parameters into descriptors may well make practical sense in some problems. Working directly with εHOMO and εLUMO levels allows us to describe the adsorption and distance from the electrode to the ion, avoiding additional calculations of descriptors made up of number of parameters. Therefore, we will mainly focus on the analysis of trends in adsorption and binding depending on one orbital only.
In case of Al2O3, quantum chemical calculations show that the value of the cation adsorption energy decreases exponentially (Figure 2A) as the εHOMO value becomes lower and almost linearly when the εLUMO value goes down (Figure 2B). The strongest binding to the surface is observed for alkali metal cations and H3O+ and the weakest binding for EMI+. The distance from the electrode surface to the cation also follows the Eads trends, where z0 becomes lower as the εHOMO (Figure 2A) and εLUMO (Figure 2B) values decrease. Only H3O+ is slightly out of the general Eads(εHOMO) trend, which may be caused by the formation of strong adsorption bonds between the hydrogen of H3O+ and the oxygen of the Al2O3 surface.
In case of z0(εLUMO), only PyMe+ does not follow the linear trend. Since the z0 distance is determined at the ion center of mass, the elongated shape of the PyMe molecule and, consequently, the orbitals may cause overestimation of the z0 value.
No correlation is observed between the anion adsorption and εHOMO (Figure 2E), while in case of Eads(εLUMO), there is a volcano-like dependence with a maximum at εLUMO = 0.245 a.u. (Figure 2F). The strongest binding to the surface is observed for the RCOO-, OH-, and F- systems, while that for the PF6- anion is the weakest. OH- and F- are out of the Eads(εLUMO) trend, with the adsorption energies for the above ions getting as high as -4.0 and -4.3 eV, respectively; the adsorption energy in these cases is close to that of a strong chemical bond with the Al atoms.
The shape of z0(εHOMO) and z0(εLUMO) becomes more complicated (Figure 2G,H), with the dependencies splitting into two curves that are reasonably well approximated by linear and exponential functions. In case of z0(εHOMO), the linear dependence is formed by PF6-, BF4- and F-, while the exponential one is represented by the other anions (TFSI-, TfO-; HSO4-, MeSO3-; ClO4-, NO3-, OH-; HCOO-, AcO-, EtCOO- and Cl-, Br-). z0(εLUMO) also splits into two dependencies, with the first linear one consisting of OH-; HSO4-, MeSO3-; HCOO-, AcO-, and EtCOO- and the second exponential one represented by the TFSI-, TfO-, BF4-, PF6-; ClO4-, and NO3- anions and halides. In all the cases, z0 decreases smoothly as the HOMO and LUMO energy values increase.
As the analysis (Figure S1.13) shows, the distance from the ions to the electrode surface for a number of systems correlates with the adsorption energy. For the anions, there is no Eads(z0) correlation, while for the cations a linear dependence is observed (Figure S1.13 A, B).
It can be concluded that the adsorption of cations on aluminum oxide is the result of contributions of both the HOMO and the LUMO orbitals. The adsorption of the anions is determined by the LUMO, HOMO-1, and LUMO+1 levels (B, D in Figure S1.1, S1.2) and is independent of the HOMO one.
Let us continue our consideration of adsorption by studying a semiconductor as an example. As in the previous system, the alkali metal cations are strongly adsorbed on the graphene surface, the PyMe+ cation is weakly bound to the surface. The Eads value for the cations on graphene decreases linearly as the εHOMO value becomes lower (Figure 3A) and in case of Eads(εLUMO), the dependence (Figure 3B) is a volcano-shaped plot with an energy maximum in the region where εLUMO ~ -0.10 a.u. At the minimum distance from the electrode are the compact alkali metal cations, whereas the farthest from the surface are the voluminous TPA+ and TBA+ ions. As the εHOMO value becomes higher, the z0 distance from the electrode increases exponentially (Figure 3C), and at an increase in the εLUMO value, z0 grows linearly (Figure 3D).
The Eads(εHOMO) dependence for the anions is almost linear; in case of Eads(εLUMO) two branches are observed, the first linear one is represented by the ClO4-, NO3-, OH-; RSO3-; TFSI-, TfO-, BF4-, PF6-; and RCOO- anions and the second one consisting of halides is close to an exponential dependence. Only i-PrCOO- is out of the trend. The presence of an i-Pr- voluminous group probably leads to a rather strong repulsion due to the van der Waals interactions, making the adsorption energy value for this ion positive. The lowest adsorption energy values are observed for BF4-, PF6- and NO3-, the highest energies are registered for some of the halides (Cl-, Br-), EtSO3- and i-PrCOO-.
z0(εHOMO) for the anions splits into two linear dependencies, the first one represented by the BF4-, PF6-, F- and OH- ions, the second one – by the other ions; i-PrCOO- and p-TsO- are noticeably out of the trend. In case of p-TsO-, such spread of values may also be caused by the total volume and the associated asymmetry of the system due to the Ph- group, leading to an overestimation of the z0 distances relative to the trend. The i-PrCOO- distance from the electrode is also associated with the voluminous i-Pr group. The z0(εLUMO) plot, as the one for the ions on Al2O3 (Figure 2H), is formed by a linear dependence consisting of the OH-; HSO4-, MeSO3-, EtSO3-, NH2SO3-, p-TsO-; HCOO-, AcO-, EtCOO-, PrCOO-, and i-PrCOO- ions and an exponential dependence consisting of TFSI-, TfO-, BF4-, PF6-; ClO4-, NO3- and halides.
As in case of Al2O3, the Eads(z0) dependence on graphene is observed only for the cations (Figure S1.13 C, D) and has a volcano shape with a maximum at z0 ~ 4 Å and Eads ~ -0.5 eV. According to the above dependencies (Figure 3) and the data of (Figure S1.5 B, D), the adsorption of the cations is determined by the HOMO orbital (except HOMO-1), as well as LUMO and LUMO+1. In case of the anions (Figure 3, Figure S1.7 B, D), the HOMO, HOMO-1 and LUMO orbitals are involved in the adsorption.
The strongest binding to the gold surface is observed for hydroxonium, which is followed by alkali metal cations and EMPyr+. PyMe+, as in case of graphene, is weakly bound to the surface. For the Au (111) surface, the voluminous organic PyMe+ and EMPyr+ cations drop out of the exponential dependence of Eads(εHOMO) and Eads(εLUMO) (Figure 4A,B). In addition, a significant shift towards negative energies is observed for H3O+. In case of the alkali metal, TMA+ and EMI+ cations, the dependencies are almost exponential, the Eads value in both cases decreases with an increase in εHOMO and εLUMO.
z0 grows exponentially with an increase in εHOMO and εLUMO (Figure 4С,D). Quite far from the z0(εHOMO) dependence are only TMA+, EMPyr+ and PyMe+. The alkali metal cations, H3O+, and EMI+ fit quite well into the exponential dependence (Figure 4 С), and all the ions considered fit into the linear z0(εLUMO) dependence (Figure 4 D).
Among the anions, the strongest interaction with the surface is observed for halides, which are followed by OH- and HCOO-. The weakest interaction with the (111) Au surface is observed for the nitrate ion, followed by TfO- and MeSO3-. The anions form a characteristic volcano-shaped Eads(εHOMO) dependence (Figure 4E) with a maximum at εHOMO ~ -0.25 a.u., while no correlation is found for Eads(εLUMO) (Figure 4F). The z0(εHOMO) dependence is represented by a linear relationship consisting of BF4-, PF6- and OH- ions and an exponential relationship with the other systems (Figure 4G). Two dependencies are observed for z0(εLUMO) (Figure 4H), with the first linear one formed by OH-; HSO4-, MeSO3-, EtSO3-, NH2SO3-, p-TsO-; HCOO-, AcO-, EtCOO-, PrCOO-, and i-PrCOO- ions and the second exponential one made up by TFSI-, TfO-, BF4-, PF6-; ClO4-, NO3- and halides.
Some degradation of the correlations on the metal and deviation of a number of cations (on average, cations have stronger binding to Au (111) than anions) can be caused by the increased complexity of the adsorption process of bulk systems on the metal. In addition to a bigger population of electronic states in the metal and, consequently, a bigger number of electrode wave functions involved in the adsorption, there are also local perturbations of the electron density in the vicinity of the ions. In particular, we can talk about image charges, [79,85,86] which can make a significant contribution to the adsorption energy [87] when the adsorbent approaches the metal electrode at a sufficiently close distance. [85]
Unlike the previous model electrodes, on Au (111) the Eads(z0) dependence is observed for both the cations (an exponential one, Figure S1.13 E, except for PyMe+, EMPyr+ and H3O+) and the anions (a linear one, Figure S1.13 F).
To sum it up (Figure 4, Figure S1.9 B, D and Figure S1.11 B, D), the adsorption of the cations, except for some systems, and the anions on Au (111) is formed by both HOMO, HOMO-1 and LUMO, LUMO-1. Such conclusion is expectable considering the high density of electronic levels in the metal involved in the adsorption process.
The proposed descriptors characterize the adsorption parameters of cations on Al2O3 and graphene quite well (R [2]=0.64−0.86 for Eads and R [2]=0.87−0.96 for z0). On Au (111), the correlations for the cations look slightly worse because some organic cations fall out of the dependencies. The correlation coefficients of adsorption and distances for the cations increase as follows: Au (111) < graphene < Al2O3 (0001). In case of the anions, the correlations for Eads are somewhat worse R [2]=0.35−0.55, but still acceptable for qualitative and semi-quantitative evaluations. And the correlations for the z0 parameter are approximately at the same level R [2]=0.64−0.95 as those for the cations.
Most of the dependencies on the orbital energy are exponential, in some cases they are close to the linear type, as the theoretical estimates suggest (Figure 1). Linear dependencies are also reported for the adsorption of neutral molecules on metal oxides in refs. [32,33,34] Volcano-shaped dependencies are observed for the anions on Al2O3 (Figure 2F) and cations on graphene (Figure 3B), which is also in agreement with the theory. The splitting of the dependencies for Eads into two branches is observed only for the anions on graphene (Figure 3F). There is a split in all the z0 anion dependencies on εHOMO and εLUMO. One cause of the division of the anions into two groups may be the presence of several MOs with the same energy (Table S6.1). This effect will be discussed in more detail in the next paragraph.
Some limitations on the applicability of εHOMO and εLUMO as adsorption descriptors may arise in case of voluminous organic ions whose interaction with the electrode is poorly described by the MO energy level due to steric perturbations. Another limiting factor may be strong chemisorption involving the formation of a chemical bond with the surface, comparable in energy to the interatomic bond in a solid. In general, the descriptors provided in the manuscript are best suited for characterizing semiconductors and dielectrics.

3.3. Ion Binding in Complexes with Water and Dimethyl Carbonate

The free energy of cation binding into an aqueous complex is described well by an exponential function of εHOMO (Figure 5A), the TBA+ cation falls out of the trend, and a polynomial dependence is observed for Gbind(εLUMO) (Figure 5B). The distance from the center of mass of the cation and water is reasonably well described by the exponential r0(εHOMO) and linear r0(εLUMO) functions (Figure 5C,D). Only the pyridinium derivatives (RPy+) fall out of the r0(εLUMO) trend; the distance between the centers of mass for RPy+ according to quantum chemical calculations is almost 1 Å longer than the obtained trend. The cause of this discrepancy may be greater asymmetry of RPy+ compared to the other systems. The lowest binding energies and shortest distances are registered for the alkali metal cations, while the highest values are observed for the organic cations.
For the anions, the dependence of Gbind on εHOMO is divided into linear and exponential curves (Figure 5E), while there is no correlation between Gbind and εLUMO (Figure 5F). The lower linear Gbind(εHOMO) correlation (Figure 5E) is formed by BF4-, PF6-, F- and OH- ions, the upper one is made up by ClO4-, NO3-, DCA-; TFSI-, TfO-; Cl-, Br-; RSO3-; and RCOO- ions. The ion-water distances (Figure 5G, H) depend only on εLUMO, and no correlations are observed for εHOMO. The linear dependence of ro(εLUMO) is represented by OH-; HSO4-, MeSO3-, EtSO3-, NH2SO3-, p-TsO-; HCOO-, AcO-, EtCOO-, PrCOO-, and i-PrCOO- ions, the exponential one – by TFSI-, TfO-, BF4-, PF6-; ClO4-, NO3-; F-, Cl-, and Br- ions. Only DCA- deviates slightly from the exponential trend. The lowest values of binding energies and distances are observed for F- and OH-, while the highest values are observed for the organic cations. The highest values of binding energies are observed for fluorine-containing anions TFSI-, TfO-, BF4-, and PF6-, as well as DCA- and RSO3-. The longest r0 distances are found for BF4-, PF6- and DCA-.
For the cations, Gbind is exponentially related to r0 (Figure S2.9 A), while for the anions there is no such correlation (Figure S2.9 B).
It can be concluded that the HOMO, LUMO (Figure 5A,B) and HOMO-1, LUMO+1 orbitals (Figure S2.1. B, D) are actively involved in the cation binding to water. The anionic aqueous complex is only made up of HOMO and HOMO-1 orbitals (Figure 5E, Figure S2.3 C), but not the LUMO orbitals.
The dependence of the free energy of cation binding to DMC on εHOMO is approximated by an exponential function (Figure 6A) and on εLUMO by a polynomial function with a maximum at -0.09 a.u. (Figure 6B). The distances from the center of mass of the cation and DMC grow exponentially depending on εHOMO and inversely exponentially depending on εLUMO (Figure 6C,D). Only PyMe+ and EMI+ drop out of the r0(εLUMO) dependence, with the predicted r0 values tending to be almost 1 Å lower than the calculated r0 ones. The strongest binding to DMC is observed for the alkali metal cations, while the weakest interaction is registered for TEA+ and EMPyr+.
The plot of the anion binding energy vs εHOMO represents two linear dependencies (Figure 6E), the first one consisting of PF6-, BF4- and F-, the second one — of ClO4-, NO3-; MeSO3-; TfO-, TFSI-, halides and RCOO- ions. Gbind(εLUMO) is formed (Figure 6F) by a linear relationship composed of MeSO3- anions, halides and RCOO- and an exponential one consisting of ClO4-, NO3-; PF6-, BF4-, TfO-, and TFSI-. Like Gbind(εHOMO), r0(εHOMO) for the anions also represents two dependencies (Figure 6G), while r0(εLUMO) is a linear relationship (Figure 6H). The strongest interaction with the solvent is observed for F- and the weakest one — for the TFSI- and PF6- anions.
For the cations, the Gbind(r0) data are approximated by an exponential function (Figure S2.9 C) and for the anions — by a linear function (Figure S2.9 D).
The HOMO, LUMO (Figure 6A,B), HOMO-1, and LUMO+1 orbitals (Figure S2.6B,D) are actively involved in the binding of cations to DMC. However, the formation of the anionic complex with DMC involves only the HOMO, LUMO (Figure 6E,B), and HOMO-1 (Figure S2.7 B) orbitals.
In addition to describing the adsorption on the electrode, the energy level of the HOMO and LUMO is an excellent descriptor of the energy of binding into a complex (R [2]=0.70−0.95) and the distance between the solvent molecule and the ions (R [2]=0.36−0.98). In almost all the cases, the correlation coefficients are much better for the complexes than for the electrodes. Reducing the number of orbitals involved in the binding makes the complex formation easier and closer to theoretical models (paragraph 1).
The splitting of the dependencies is mainly due to the orbital type of the ion involved in the complex formation. For example, the dependence of the energy of solvent binding to anions on the εHOMO parameter (Figure 5E, Figure 6E) is split into two curves: one consisting of OH-, F-, BF4-, and PF6- and the second one comprised of the other ions. The MO analysis shows (Table S6.1) that the ions from the first dependence possess multiple HOMOs of the same energy. A similar division into two dependencies can be seen in z0(εHOMO), for example, for the complexes with DMC (Figure 6G) and for the adsorption of anions on Al2O3 (0001) (Figure 2G), graphene (Figure 3G), and Au (111) (Figure 4G). The z0(εLUMO) plots are also represented by two dependencies: a linear one consisting of OH-; RSO3-; and RCOO- and an exponential one composed of ClO4-, NO3-; BF4-, PF6-, TfO-, TFSI-, and halides. There is a similar trend for the adsorption on electrodes (Figures 2−4H) and for complexation with water (Figure 5H), while it is not observed for DMC (Figure 6H). Theoretical evaluations can shed light on the nature of such dependencies by establishing the distance between the ion and the electrode or solvent molecule at which the total energy of the system would be minimized. Taking into account the available data, we can assume that the division is caused by the specific composition of the LUMO orbital and does not depend on the number of LUMO orbitals with the same energy. Taking into account the data on DMC, it is quite natural to conclude that the molecular orbitals of the solvent molecule influence the complex formation.

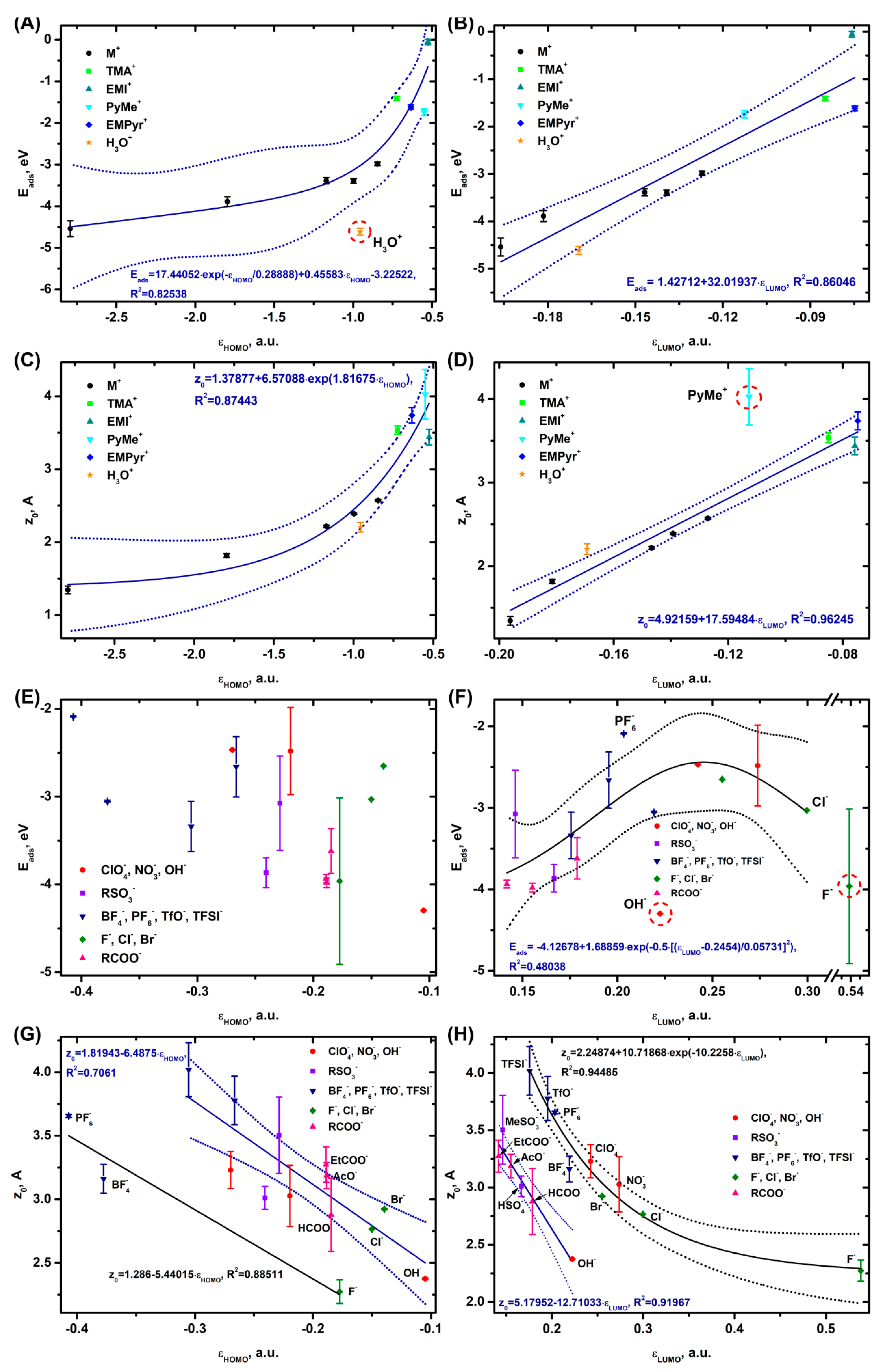
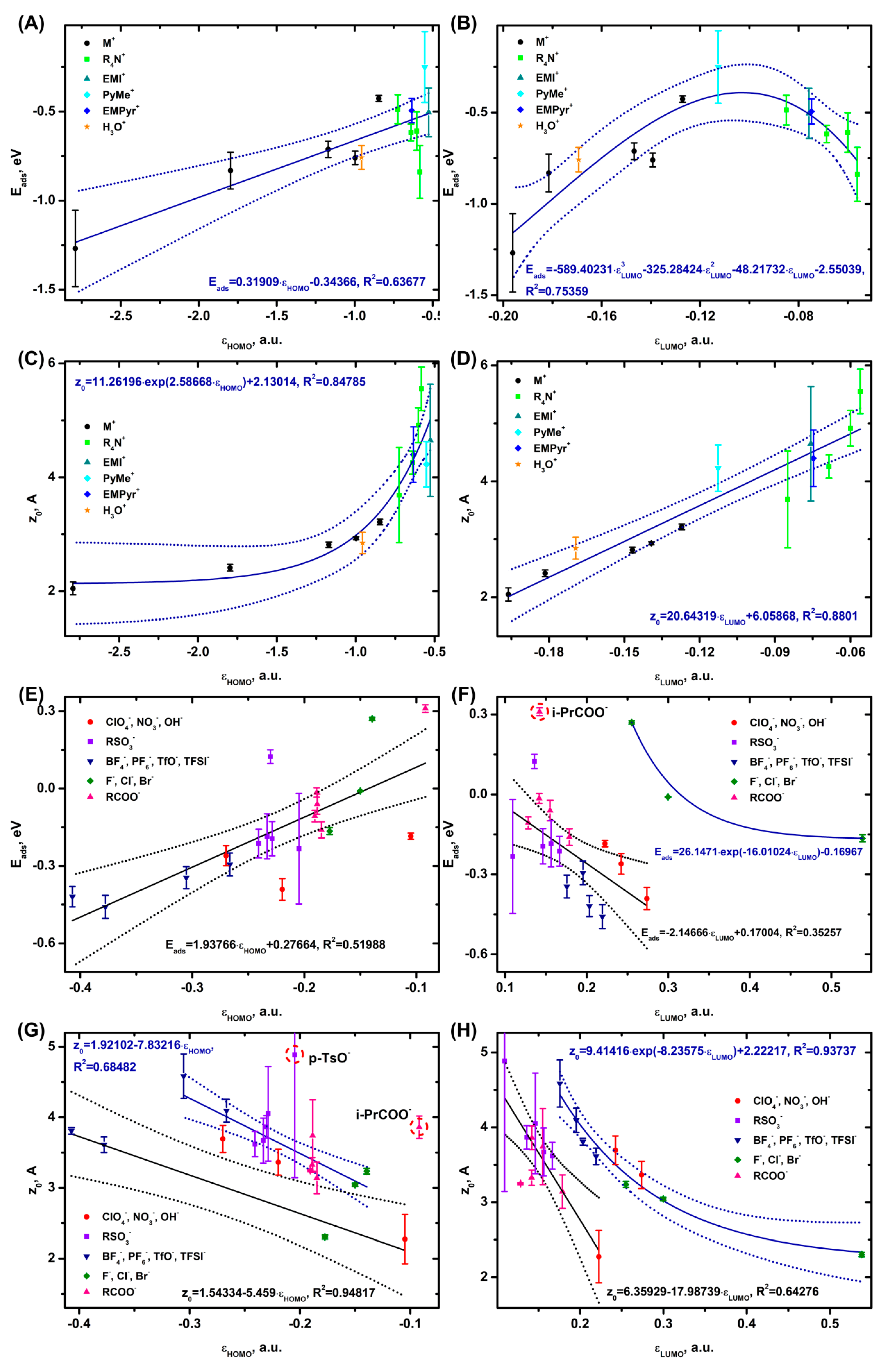
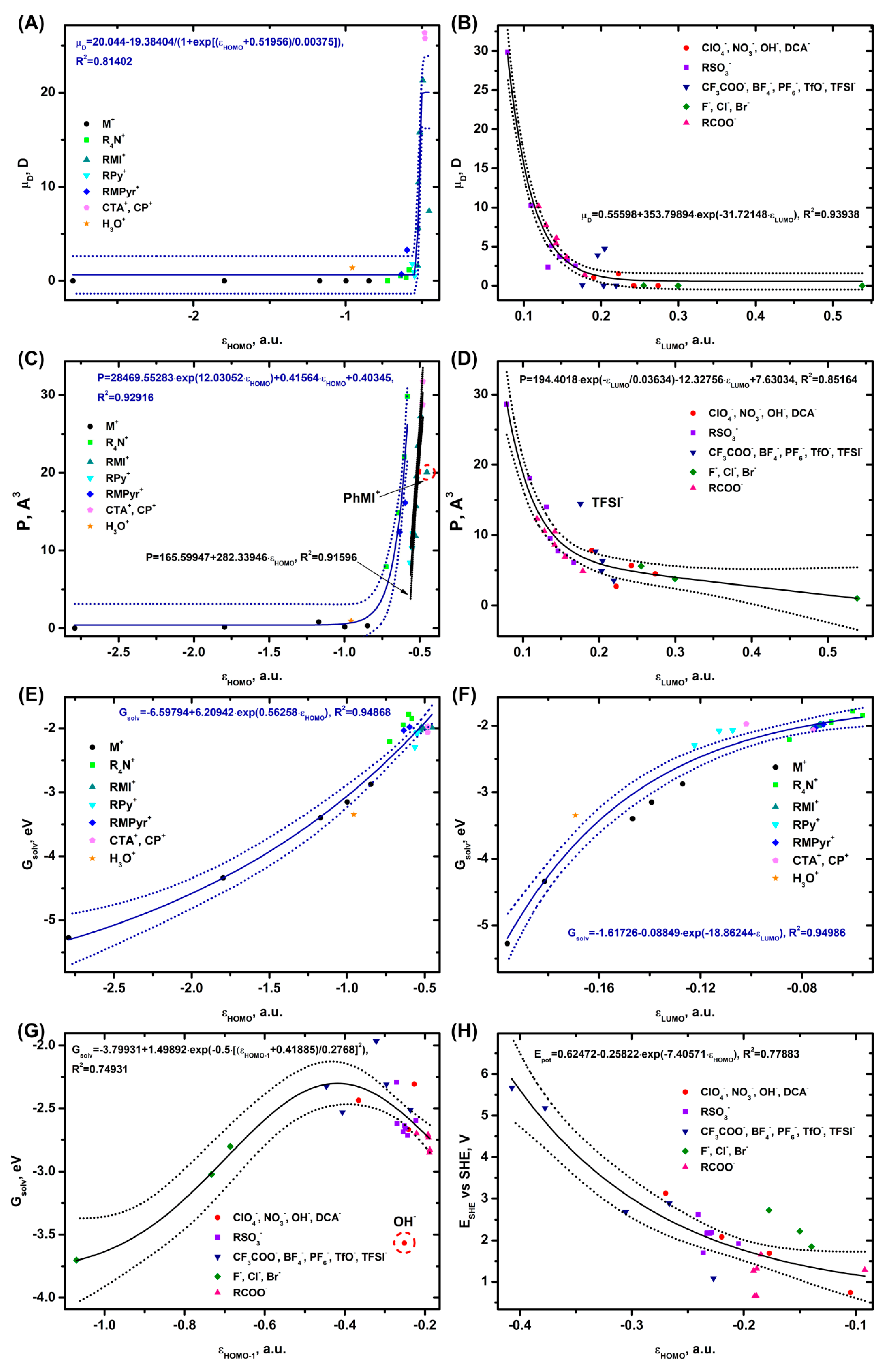
3.4. Correlations with Physicochemical and Electrochemical Parameters of Ions

Judging by the dependence for dipole moment [88] and the more complicated one for polarization [89] (since the perturbation of the system by the external field is calculated), the wave functions are explicitly included in all the expressions of these parameters. In several models, the wave functions are also included in some terms of the solvation energy expression. [63] Notably, in addition to a number of summands responsible for the environment polarization, [63,64] cavity formation and other contributions, [90] the solvation energy is determined by the first solvation shell, [91,92] which is formed by the solvent directly bound to the ion. As paragraph 3 shows, the energy of binding to water and the intermolecular distances are related to the HOMO and LUMO. The redox potential, in turn, contains the solvation energies of the reactants [93,94] in the original entry and, therefore, depends on the internal rearrangement of the bonds and the environment response to the charge. Such facts and some literature data [35] suggest a possible correlation of the mentioned parameters with the orbital energy level. In general, the mentioned physicochemical parameters, as in works, [26,27] are likely to depend on a whole range of descriptors, but for simplicity of the analysis we will focus on the correlations with MO levels only..
According to the calculations (Figure 7A), the dependence of the dipole moment for the cations on εHOMO is nearly sigmoidal, for compact one-atom ions (alkali metals) and symmetric ions (TMA+) in the range εHOMO = -3 – -0.7 a.u. the dipole moment is equal to zero. Starting from εHOMO > -0.62 a.u. a sharp increase in the dipole moment value is observed, with the maximum values corresponding to the voluminous and asymmetric CP+, CTA+ and DMI+ cations. The dependence of the dipole moment of anions on εLUMO (Figure 7B) decreases exponentially in the range εLUMO = 0.08 − 0.25 a.u., the maximum dipole moment is observed for voluminous DS-, followed by BuCOO-, p-TsO-. At εLUMO > 0.25 a.u. the dipole moment of the anions becomes close to zero (for halides and symmetric NO3-, ClO4-, etc.).
The polarization dependence on εHOMO for the cations (Figure 7C) is split into two curves: an exponential one represented by H3O+, alkali metal cations, RMPyr+, and R4N+, and a linear one represented by CTA+, CP+, RMI+ (except PhMI+, which is out of the trend), and RPy+. The dependence of P on εLUMO, as the one for the dipole moment, decreases exponentially (Figure 7D), with TFSI- falling out of the trend. The maximum polarization values are obtained for the voluminous and heavy DS- and p-TsO- cations, the lowest ones for the light F-, OH- and BF4- ions.
The value of the solvation energy for the cations decreases exponentially with an increase in the εHOMO or εLUMO values (Figure 7E,F). The lowest solvation values are observed for Li+, which is followed by the other alkali metals, with the maximum values obtained for the organic cations. The Gsolv(εHOMO-1) dependence for the anions has a characteristic volcano shape with a maximum at εHOMO-1 = -0.42 a.u. (Figure 7G). The left part of the dependence is formed by the halides, the right part – by the other ions. A significant deviation from the trend is observed for OH-, the energy value of which is significantly underestimated. TFSI-, the solvation energy of which is slightly overestimated, is out of the trend. The lowest values of Gsolv are observed for F-, OH- and the highest values for TFSI-.
A dependence of the oxidation potentials on εHOMO is only observed for the anions (Figure 7H). ESHE decreases exponentially as εHOMO goes up.
The present paragraph clearly shows that in addition to describing the adsorption of ions or their binding to the solvent, the HOMO and LUMO parameters are also well suited for characterizing a number of physicochemical and electrochemical parameters. The latter, first of all, include dipole moment and polarization, whose correlation coefficients of the approximations reach R [2]=0.8−0.94 and the cation solvation energy R [2]=0.95. Slightly worse are R [2]=0.74−0.78, but there are clear dependencies on the solvation energy and oxidation potential of anions.

3.5. Practical Evaluations

In this paragraph, we will show how orbital values can be applied to solving a practical problem. For this purpose, in continuation of the study of aqueous electrolytes, [28,44,45,46,47,50,51] let us consider the ability of cations and anions to displace water from the inner layer of the electric double layer (EDL). The point of this task is to displace the electroactive component of the electrolyte water as far away from the electrode surface as possible [28,44,45,46] and, as a result, to increase the electrochemical potential window and energy capacity of the batteries. Since such problem considers a potential electrolyte for a battery, we will use a Li+ ion as the cation. The parameters of the anions will be calculated using the approximations obtained previously (Table S2.3, S3.3, S5.3). We will use graphene as the electrode because it can serve as a simplified model system representing different carbon materials for supercapacitors [95,96] and batteries. [97,98] By varying the εHOMO and εLUMO parameters in the range characteristic of anions, we will find systems with the minimal water concentration in the inner layer of EDL.
Under equilibrium conditions, the reversible process of displacement of ions (i) by water molecules (w) in the inner layer from the surface into the bulk i b u l k + w s u r f ⇄ i s u r f + n i w b u l k is described by a multicomponent adsorption isotherm: [99,100,101]
ln θ i θ W n i + ln f i s u r f f w s u r f n i = ln β i f i b u l k с i b u l k f w b u l k с w b u l k n i − q i e 0 φ d k B T − q i e 0 l e f f − r i l k B T + b i − n i b w Δ φ + c i − n i c w Δ φ 2 ,
and parameters
b j = μ j / l e f f k B T ( j = i , w )
с j = ε 0 ε j A j / 2 l e f f k B T ,
where θi and θw are the degrees of surface coverage by ions and water molecules, Δ φ = σ 0 + σ i o n s l e f f ε e f f ε 0 is the potential drop in the inner layer of the EDL, σ0 is the surface charge density on the electrode, σ i o n s = ∑ i θ i q i e 0 π r i 2 is the surface charge density of adsorbed ions in the inner layer, φ d = 2 R T F arcsin h − ( σ 0 + σ i o n s ) 8 R T ε b ε 0 c 0 ⋅ 1000 is the potential drop in the diffuse layer according to the Gui-Chapman model, [102] εb is the dielectric permittivity of the solution in the bulk (since dilute aqueous solutions are considered, the value is approximated as 78 [103]), c0 is the concentration of the supporting electrolyte in mol/L, qi is the i ion charge, n i = r i 2 / r w 2 is the ratio of areas of the i ion and water molecule, ri and rw are the effective radius of the ion or water molecule. [28]
The parameters included in coefficients bj and cj (11,12) have the following physical meaning: μj is the dipole moment perpendicular to the electrode surface; ε j = 1 + P j / ε 0 A j l e f f is the dielectric constant of component j, calculated according to the model described in ref. [104] (Pj is the polarizability); A j = 2 π r j 2 is the area occupied by component j; ε = ∑ j = i , w ε j θ j and l e f f = ∑ j = i , w z j θ j are the effective values of the dielectric constant and thickness of the inner layer.
The f i s u r f / f w s u r f n i ratio of the activity coefficients of the electrolyte components in the inner layer according to the mean field approximation [99,100] is generally determined by the expression
ln θ m f W r m = θ w 1 − θ m − r m θ m 1 − θ w A m k + 1 + ∑ g ≠ m , k + 1 θ g 1 − θ m + r m θ m A g m − ∑ g ≠ m , k + 1 θ w θ g + r m θ g 1 − θ w A g k + 1 + ∑ g < h θ g θ h r m − 1 A g h
For a 1:1 electrolyte (A stands for cations, B designates anions) and a solvent, equation (13) looks as follows:
ln f A f W n A = θ B 1 + n A − 1 θ A A A B + θ W 1 − θ A − θ A 1 − θ W n A A A W − θ B n A − n A − 1 θ W A B W
ln f B f W n B = θ A 1 + n B − 1 θ B A A B + θ W 1 − θ B − θ B 1 − θ W n B A B W − θ A n B − n B − 1 θ W A A W
If k≠m, the Akm coefficients between components k and m are written as
A k m = z C N E k m − E k k + E m m / 2 / k B T
where zCN is the effective coordination number in the two-dimensional lattice, E is the energy of the interaction between the electrolyte components, when k=i and m=w: Eiw is the energy of binding of the ion and the water molecule (taken equal to the free binding energy of the components in the following estimations), Eww is the energy of binding of the water molecules into a dimer, Eii is the energy of binding of the ions with each other.
For simplicity, Eii is represented as a Coulomb interaction of charges qi separated from each other by the distance of their own effective ionic radii: E A A = 1 4 π ε 0 ε e f f q + 2 e 0 2 ( 2 r + ) for two cations, E B B = 1 4 π ε 0 ε e f f q − 2 e 0 2 ( 2 r − ) for two anions, and E A B = 1 4 π ε 0 ε e f f q + q − e 0 2 ( r + + r − ) for one cation and one anion.
βi is the parameter which determines the difference between the chemical potentials of the reaction components on the surface and in the bulk.
ln β i = μ i 0 , b u l k − μ i 0 , s u r f − n i μ w 0 , b u l k − μ w 0 , s u r f / k B T
To simplify the problem, let us write this parameter as a function of the adsorption energies of the components on the electrode
ln β i = ( − E i , a d s ) − n i ( − E w , a d s ) / k B T = n i E w , a d s − E i , a d s / k B T
As work [28] suggests, the effective radius of cations should be estimated taking into account the solvation water. Keeping that in mind, we used the following parameters as the initial data for the lithium cation with a correction for solvation water: Eads = -1.27 eV, Ebind,w = -0.33 eV, r L i + = 3.00 Å (including the solvation water (Table S7.1)), z0 = 3.45 Å, μ and P are equal to zero; the parameters for the water molecule are Eads = -0.11 eV, rw = 1.41 Å, z0 = 3.29 Å, μ = 2.19 D, P =7.21 Å [3], Eww = -0.13 eV. We described the dipole moment and polarizability of all the anions by the expressions µD=0.55598+353.79894∙exp(-31.72148∙εLUMO) and P=194.4018∙exp(-εLUMO/0.03634) 12.32756∙εLUMO+7.63034. The effective coordination number was taken to be zCN = 6.
In accordance with the specific features of the dependencies of adsorption of the anions and their interaction with water on εHOMO and εLUMO, we divided all the systems into three sets (Figure 8A–C).
The first set of systems (A) consists of F-, BF4- and PF6-; the adsorption of these ions is described by the expressions: Eads=1.93766∙εHOMO+0.27664 and z0=1.54334-5.459∙εHOMO, the aqueous complex parameters – by the expressions Gbind=-3.43293∙εHOMO-1.47558 and r0=6.13597-16.63311∙εLUMO. According to the obtained solutions (Figure 8A) to equations (10−18), the lowest water coverage degree (θw < 0.08) is observed for the BF4- and PF6- ions. The only practical limitation on using BF4- and PF6- as aqueous electrolytes is their slow hydrolysis, [105,106,107,108,109] which is why they have not been mentioned as salts for aqueous systems. Figure 8А does not show F-, which lies much higher at εLUMO= 0.54 a.u., but this system also extends to the region of low values θw < 0.08. In contrast to BF4- and PF6-, the fluoride appears in studies [97,110] as a component of an aqueous electrolyte with a wide potential window.
The second set of systems (B) is represented by ions whose adsorption is described in a way similar to the systems in (Figure 8A), except for the parameter z0=1.92102-7.83216∙εHOMO, and the aqueous complex parameters are expressed as Gbind=0.03092∙exp(-9.00895∙εHOMO)-0.46743 and r0=6.13597-16.63311∙εLUMO. All the systems (Figure 8B) lie in the region θw < 0.08. Almost all of the above systems are reported in the literature as aqueous electrolytes with a wide potential window: TFSI-, [44,45,46] TfO-, [111] ClO4-, [112,113] and NO3-. [114,115] The exceptions are Cl- and Br- halides, whose electroactivity is quite high, especially that of Br-, due to the relatively low oxidation potential, which limits their use in high voltage electrolytes. Only KCl is employed in supercapacitors but its use is limited too. [116,117,118]
The third set of systems (C) is represented by OH-, HSO4-, CF3COO-, RSO3-, and RCOO- anions whose adsorption is described by expressions similar to those in (Figure 8B), the parameters of interaction with water are described by the equations Gbind=0.03092∙exp(-9.00895∙εHOMO)-0.46743 and r0=6.37246∙exp(-6.99633∙εLUMO)+2.3211. The lowest water coverage θw < 0.08 (Figure 8C) is observed for the CF3COO- system as well as for HSO4- and NH2SO3-. CF3COO- is mentioned in refs. [119,120] In general, the application of such system is limited by their cost and toxicity. HSO4- in an aqueous medium is characterized by dissociation with a marked pH decrease, [121] which significantly narrows the potential window by shifting the cathodic region in the acidic medium. NH2SO3- is electrochemically unstable as the experiments and calculations show. [28] The MeSO3-, EtSO3-, and HCOO- systems lie in the moderate water coverage degree region 0.08 < θw < 0.16, AcO- lies at the boundary of the region θw ~ 0.16. OH- itself is quite electroactive and shifts the potential window; however, in concentrated alkalis the potential window slightly increases to ~1.6 V, [116,117,122,123] which is higher than in pure water (1.23 V [115]). Such systems are used in supercapacitors. [116,117,123] In practice, sulfonate is more often used in its acid form as an additive to electrolytes in electroplating and hydrometallurgy, [124] and as an anion in redox flow batteries. [125] EtSO3- has hardly ever been mentioned as an aqueous electrolyte in the literature, except for some references where it was mentioned as an electrolyte for zinc-ion batteries. [126] HCOO- as an electrolyte was mentioned in ref. [127]; in general, alkaline salts of carboxylic acids are often reported as potential electrolytes. [28,127,128,129,130]
The low values of the electrode water coverage in electrolytes are in most cases consistent with the electrochemical stability of the system, confirming that the coverage is one of the main parameters [28] determining the potential window. In addition to the known systems, electrolytes with anions represented by sulfonic acid derivatives are potentially interesting as objects of further investigation. Of course, a comprehensive analysis of the ion suitability for electrolytes requires, in addition to the water coverage, evaluation of the electrochemical stability of the anion itself and its potential intermediates during electrochemical decomposition, as it was done in case of NH2SO3-. [28]
The use of the εHOMO and εLUMO parameters makes it possible to quickly evaluate the water coverage of the electrode and select the optimal anions, as it has been shown by a particular example. Due to the dependencies of the other electrochemical parameters (solvation energy, redox potential, etc.) on MO energy levels, such analysis can be performed in a comprehensive way, taking into account all the necessary parameters of cations and anions at the same time.

4. Conclusions

In contrast to a lot of other works that study the effect of the electrode material or solvent type on the interactions of ions with the electrode surface and solvent molecules, the present work shows the dependence of these interactions on the ion nature. The calculations carried out using theoretical models of adsorption and complex formation for ions showed that the energy of adsorption on the electrode or the energy of binding into a complex with the solvent depends on the energy of the ion valence orbital. Most of the obtained dependencies are close to linear and exponential types, in some cases the solution leads to volcano-shaped dependencies.
A comparison of a number of ion parameters obtained by quantum chemical calculations revealed clear correlations with the HOMO and LUMO energies of the ion orbitals. The first parameter to be considered was the adsorption energies on model electrodes represented by aluminum oxide (0001), graphene and Au (111). The best correlations were observed for graphene and aluminum oxide; in case of gold, some deviations were found for the organic cations. Volcano-like correlations were revealed between the adsorption energy of anions on Al2O3 (0001) and graphene surfaces with εLUMO, and on Au (111) with εHOMO. Strong correlations were found for the energies of ion binding to solvent molecules represented by water and dimethyl carbonate. Volcano-like dependencies were also observed for the energy of binding of cations to H2O and DMC on εLUMO. In addition, a clear relationship was observed between the dipole moment, polarization and solvation energy of ions, on the one hand, and the HOMO and LUMO energy level. For the anions, the oxidation potential was found to be dependent on the HOMO energy level.
The described dependencies of the ion parameters on the energy levels of molecular orbitals were approximated by expressions that allow us to use the energy level of orbitals as a descriptor in applied problems. The use of such parameters makes the search for ions with desired properties a lot easier. First of all, such descriptors can be relevant in the field of catalysis, especially for catalyst surface composition control and in surface chemistry, for example, when searching for ions with the highest adsorption for a given material to solve the problem of heavy metal binding by different sorbents. An example of possible practical application of the descriptors was clearly demonstrated by aqueous electrolytes for batteries. Li+ was used as the cation, the anion parameters were estimated by the previously obtained expressions, the task was to select an anion the use of which would minimize the degree of water coverage of the electrode surface. Reduction in the water coverage increases the working window potential of the electrolyte. The obtained estimates for the anions widely applied in electrochemical practice agree with the experimental data, new electrolytes can be potentially found among alkaline salts of sulfonic acid derivatives.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Acknowledgments

Calculations were made using resources of the Joint Supercomputer Center of the Russian Academy of Sciences.

Conflicts of Interest

There are no conflicts to declare.

References

  1. Li, B.; Gao, W.; Jiang, Q. Electronic and Geometric Determinants of Adsorption: Fundamentals and Applications. Journal of Physics: Energy 2021, 3, 022001. [Google Scholar] [CrossRef]
  2. Zhao, Z.-J.; Liu, S.; Zha, S.; Cheng, D.; Studt, F.; Henkelman, G.; Gong, J. Theory-Guided Design of Catalytic Materials Using Scaling Relationships and Reactivity Descriptors. Nature Reviews Materials 2019, 4, 792–804. [Google Scholar] [CrossRef]
  3. Newns, D.M. Self-Consistent Model of Hydrogen Chemisorption. Physical Review 1969, 178, 1123–1135. [Google Scholar] [CrossRef]
  4. Hammer, B.; Nørskov, J.K. (1997). Theory of Adsorption and Surface Reactions. In: Lambert, R.M., Pacchioni, G. (eds) Chemisorption and Reactivity on Supported Clusters and Thin Films. NATO ASI Series, vol 331. Springer, Dordrecht. [CrossRef]
  5. Hammer, B. Special Sites at Noble and Late Transition Metal Catalysts. Top Catal, 2006, 37, 3–16. [Google Scholar] [CrossRef]
  6. Suntivich, J.; Gasteiger, H.A.; Yabuuchi, N.; Nakanishi, H.; Goodenough, J.B.; Shao-Horn, Y. Design Principles for Oxygen-Reduction Activity on Perovskite Oxide Catalysts for Fuel Cells and Metal–Air Batteries. Nature Chemistry 2011, 3, 546–550. [Google Scholar] [CrossRef] [PubMed]
  7. Jaksic, M.M.; Jaksic, J.M. Fermi Dynamics and Some Structural Bonding Aspects of Electrocatalysis for Hydrogen Evolution. Electrochimica Acta 1994, 39, 1695–1714. [Google Scholar] [CrossRef]
  8. JJakšić, M.; Krstajić, N.V.; Grgur, B.N.; Jakšić, M.M. Hydridic and Electrocatalytic Properties of Hypo-Hyper-d-Electronic Combinations of Transition Metal Intermetallic Phases*1. International Journal of Hydrogen Energy 1998, 23, 667–681. [Google Scholar] [CrossRef]
  9. Abild-Pedersen, F.; Greeley, J.; Studt, F.; Rossmeisl, J.; Munter, T.R.; Moses, P.G.; Skúlason, E.; Bligaard, T.; Nørskov, J.K. Scaling Properties of Adsorption Energies for Hydrogen-Containing Molecules on Transition-Metal Surfaces. Physical Review Letters 2007, 99. [Google Scholar] [CrossRef] [PubMed]
  10. Calle-Vallejo, F.; Inoglu, N.G.; Su, H.-Y.; Martínez, J.I.; Man, I.C.; Koper, M.T.M.; Kitchin, J.R.; Rossmeisl, J. Number of Outer Electrons as Descriptor for Adsorption Processes on Transition Metals and Their Oxides. Chemical Science 2013, 4, 1245. [Google Scholar] [CrossRef]
  11. Gao, W.; Chen, Y.; Li, B.; Liu, S.-P.; Liu, X.; Jiang, Q. Determining the Adsorption Energies of Small Molecules with the Intrinsic Properties of Adsorbates and Substrates. Nature Communications 2020, 11. [Google Scholar] [CrossRef]
  12. Doronin, S.V.; Dokhlikova, N.V.; Grishin, M.V. Descriptor of Catalytic Activity Nanoparticles Surface: Atomic and Molecular Hydrogen on Gold. Molecular Catalysis 2022, 529, 112534. [Google Scholar] [CrossRef]
  13. Jiao, Y.; Zheng, Y.; Davey, K.; Qiao, S.-Z. . Activity Origin and Catalyst Design Principles for Electrocatalytic Hydrogen Evolution on Heteroatom-Doped Graphene. Nature Energy 2016, 1. [Google Scholar] [CrossRef]
  14. Doronin, S.V.; Volykhov, A.A.; Inozemtseva, A.I.; Usachov, D.Y.; Yashina, L.V. Comparative Catalytic Activity of Graphene Imperfections in Oxygen Reduction Reaction. The Journal of Physical Chemistry C 2020, 124, 6038–6053. [Google Scholar] [CrossRef]
  15. Kulkarni, A.; Siahrostami, S.; Patel, A.; Nørskov, J.K. Understanding Catalytic Activity Trends in the Oxygen Reduction Reaction. Chemical Reviews 2018, 118, 2302–2312. [Google Scholar] [CrossRef] [PubMed]
  16. Jiang, B.; Tian, Y.; An, Y.; Liu, R.; Shaik, F. Electrocatalytic Activity Analysis of Vinegar Residue-Based Heteroatom-Doped Carbon Quantum Dots Integrated on Vertically Aligned Graphene Arrays for Hydrogen Evolution Reaction. International Journal of Hydrogen Energy 2023, 48, 38686–38698. [Google Scholar] [CrossRef]
  17. Cui, X.; Tang, C.; Zhang, Q. . A Review of Electrocatalytic Reduction of Dinitrogen to Ammonia under Ambient Conditions. Advanced Energy Materials 2018, 8. [Google Scholar] [CrossRef]
  18. Manjunatha, R.; Karajić, A.; Liu, M.; Zhai, Z.; Dong, L.; Yan, W.; Wilkinson, D.P.; Zhang, J. A Review of Composite/Hybrid Electrocatalysts and Photocatalysts for Nitrogen Reduction Reactions: Advanced Materials, Mechanisms, Challenges and Perspectives. Electrochemical Energy Reviews 2020, 3, 506–540. [Google Scholar] [CrossRef]
  19. Masoumi, Z.; Tayebi, M.; Tayebi, M.; Lari, S.A.M.; Sewwandi, N.; Seo, B.; Lim, C.-S.; Kim, H.-G.; Kyung, D. Electrocatalytic Reactions for Converting CO2 to Value-Added Products: Recent Progress and Emerging Trends. International Journal of Molecular Sciences 2023, 24, 9952. [Google Scholar] [CrossRef]
  20. Sajna, M.S.; Zavahir, S.; Popelka, A.; Kasak, P.; Al-Sharshani, A.; Onwusogh, U.; Wang, M.; Park, H.; Han, D.S. Electrochemical System Design for CO2 Conversion: A Comprehensive Review. Journal of Environmental Chemical Engineering 2023, 11, 110467. [Google Scholar] [CrossRef]
  21. Cardenas, C.; Rabi, N.; Ayers, P.W.; Morell, C.; Jaramillo, P.; Fuentealba, P. Chemical Reactivity Descriptors for Ambiphilic Reagents: Dual Descriptor, Local Hypersoftness, and Electrostatic Potential. The Journal of Physical Chemistry A 2009, 113, 8660–8667. [Google Scholar] [CrossRef]
  22. Pearson, R.G. The Electronic Chemical Potential and Chemical Hardness. Journal of Molecular Structure: THEOCHEM 1992, 255, 261–270. [Google Scholar] [CrossRef]
  23. Choudhary, V.K.; Bhatt, A.K.; Dash, D.; Sharma, N. DFT Calculations on Molecular Structures, HOMO–LUMO Study, Reactivity Descriptors and Spectral Analyses of Newly Synthesized Diorganotin(IV) 2-chloridophenylacetohydroxamate Complexes. Journal of Computational Chemistry 2019, 40, 2354–2363. [Google Scholar] [CrossRef]
  24. Karelson, M.; Lobanov, V.S.; Katritzky, A.R. Quantum-Chemical Descriptors in QSAR/QSPR Studies. Chemical Reviews 1996, 96, 1027–1044. [Google Scholar] [CrossRef] [PubMed]
  25. Kokalj, M. On the Alleged Importance of the Molecular Electron-Donating Ability and the HOMO–LUMO Gap in Corrosion Inhibition Studies. Corrosion Science 2021, 180, 109016. [Google Scholar] [CrossRef]
  26. Abraham, M.H.; Acree, W.E. The Transfer of Neutral Molecules, Ions and Ionic Species from Water to Wet Octanol. Physical Chemistry Chemical Physics 2010, 12, 13182. [Google Scholar] [CrossRef]
  27. Abraham, M.H.; Acree, W.E. Descriptors for Ions and Ion-Pairs for Use in Linear Free Energy Relationships. Journal of Chromatography A 2016, 1430, 2–14. [Google Scholar] [CrossRef]
  28. Doronin, S.V.; Nazarov, M.A. Superconcentrated Electrolytes for Aqueous Batteries Based on Alkali Metal Formates and Propionates. The Journal of Physical Chemistry C 2022, 126, 14611–14625. [Google Scholar] [CrossRef]
  29. Bailey, E.; Olin, T.J.; Bricka, R.M.; Adrian, D.D. A Review of Potentially Low-Cost Sorbents for Heavy Metals. Water Research 1999, 33, 2469–2479. [Google Scholar] [CrossRef]
  30. Burakov, E.; Galunin, V.; Burakova, V.; Kucherova, E.; Agarwal, S.; Tkachev, G.; Gupta, K. Adsorption of Heavy Metals on Conventional and Nanostructured Materials for Wastewater Treatment Purposes: A Review. Ecotoxicology and Environmental Safety 2018, 148, 702–712. [Google Scholar] [CrossRef] [PubMed]
  31. Chai, W.S.; Cheun, J.Y.; Kumar, P.S.; Mubashir, M.; Majeed, Z.; Banat, F.; Show, P.L. A Review on Conventional and Novel Materials towards Heavy Metal Adsorption in Wastewater Treatment Application. Journal of Cleaner Production 2021, 296, 126589. [Google Scholar] [CrossRef]
  32. Kamachi, T.; Tatsumi, T.; Toyao, T.; Hinuma, Y.; Maeno, Z.; Takakusagi, S.; Furukawa, S.; Takigawa, I.; Shimizu, K. Linear Correlations between Adsorption Energies and HOMO Levels for the Adsorption of Small Molecules on TiO2 Surfaces. The Journal of Physical Chemistry C 2019, 123, 20988–20997. [Google Scholar] [CrossRef]
  33. Liu, C.; Li, Y.; Takao, M.; Toyao, T.; Maeno, Z.; Kamachi, T.; Hinuma, Y.; Takigawa, I.; Shimizu, K. Frontier Molecular Orbital Based Analysis of Solid–Adsorbate Interactions over Group 13 Metal Oxide Surfaces. The Journal of Physical Chemistry C 2020, 124, 15355–15365. [Google Scholar] [CrossRef]
  34. Hamamoto, N.; Tatsumi, T.; Takao, M.; Toyao, T.; Hinuma, Y.; Shimizu, K.; Kamachi, T. Effect of Oxygen Vacancies on Adsorption of Small Molecules on Anatase and Rutile TiO2 Surfaces: A Frontier Orbital Approach. The Journal of Physical Chemistry C 2021, 125, 3827–3844. [Google Scholar] [CrossRef]
  35. Pérez, P.; Contreras, R.; Aizman, A. Relationship between Solvation Energy, Chemical Potential and Hardness Variations. Journal of Molecular Structure: THEOCHEM 1997, 390, 169–175. [Google Scholar] [CrossRef]
  36. Miranda-Quintana, R.A.; Smiatek, J. Theoretical Insights into Specific Ion Effects and Strong-Weak Acid-Base Rules for Ions in Solution: Deriving the Law of Matching Solvent Affinities from First Principles. ChemPhysChem 2020, 21, 2605–2617. [Google Scholar] [CrossRef] [PubMed]
  37. Doronin, S.V.; Manzhos, R.A.; Krivenko, A.G.; Manzhos, A.P. Electron Transfer Kinetics of the Ferrous/Ferric Redox System on the Platinum Deposits on Gold. Journal of Electroanalytical Chemistry 2017, 784, 140–144. [Google Scholar] [CrossRef]
  38. Doronin, S.V. Energy of the Surface Segregation of Ag Atoms in Ag–Au Alloys in an Aqueous Solution. Mendeleev Communications 2020, 30, 288–290. [Google Scholar] [CrossRef]
  39. Doronin, S.V.; Manzhos, R.A.; Krivenko, A.G. EDL Structure and Peculiarities of Ferricyanide Cyclic Voltammetry for Silver Deposits on Gold. Electrochemistry Communications 2015, 57, 35–38. [Google Scholar] [CrossRef]
  40. Fuchigami, T.; Atobe, M.; Inagi, S. Fundamentals and Applications of Organic Electrochemistry: Synthesis, Materials, Devices; John Wiley & Sons, 2014, p.
  41. Volke, J.; Liška, F. Electrochemistry in Organic Synthesis; Springer Science & Business Media, 2012, p.153.
  42. Galiński, M.; Lewandowski, A.; Stępniak, I. Ionic Liquids as Electrolytes. Electrochimica Acta 2006, 51, 5567–5580. [Google Scholar] [CrossRef]
  43. Zhang, S.; Sun, N.; He, X.; Lu, X.; Zhang, X. Physical Properties of Ionic Liquids: Database and Evaluation. Journal of Physical and Chemical Reference Data 2006, 35, 1475–1517. [Google Scholar] [CrossRef]
  44. Yang, C.; Chen, J.; Qing, T.; Fan, X.; Sun, W.; von Cresce, A.; Ding, M.S.; Borodin, O.; Vatamanu, J.; Schroeder, M.A.; Eidson, N.; Wang, C.; Xu, K. 4.0 V Aqueous Li-Ion Batteries. Joule 2017, 1, 122–132. [Google Scholar] [CrossRef]
  45. Vatamanu, J.; Borodin, O. Ramifications of Water-in-Salt Interfacial Structure at Charged Electrodes for Electrolyte Electrochemical Stability. The Journal of Physical Chemistry Letters 2017, 8, 4362–4367. [Google Scholar] [CrossRef] [PubMed]
  46. Zhang, R.; Han, M.; Ta, K.; Madsen, K.E.; Chen, X.; Zhang, X.; Espinosa-Marzal, R.M.; Gewirth, A.A. Potential-Dependent Layering in the Electrochemical Double Layer of Water-in-Salt Electrolytes. ACS Applied Energy Materials 2020, 3, 8086–8094. [Google Scholar] [CrossRef]
  47. Han, J.; Mariani, A.; Passerini, S.; Varzi, A. A Perspective on the Role of Anions in Highly Concentrated Aqueous Electrolytes. Energy & Environmental Science 2023, 16, 1480–1501. [Google Scholar] [CrossRef]
  48. Jow, T.R.; Xu, K.; Borodin, O.; Ue, M. Electrolytes for Lithium and Lithium-Ion Batteries; Springer, 2014, 476. [CrossRef]
  49. Jonsson, E.; Johansson, P. Electrochemical Oxidation Stability of Anions for Modern Battery Electrolytes: A CBS and DFT Study. Physical Chemistry Chemical Physics 2015, 17, 3697–3703. [Google Scholar] [CrossRef] [PubMed]
  50. Zhang, Y.; Lewis, N.H.C.; Mars, J.; Wan, G.; Weadock, N.J.; Takacs, C.J.; Lukatskaya, M.R.; Steinrück, H.-G.; Toney, M.F.; Tokmakoff, A.; Maginn, E.J. Water-in-Salt LiTFSI Aqueous Electrolytes. 1. Liquid Structure from Combined Molecular Dynamics Simulation and Experimental Studies. The Journal of Physical Chemistry B 2021, 125, 4501–4513. [Google Scholar] [CrossRef]
  51. Vazquez, D.G.; Pollard, T.P.; Mars, J.; Yoo, J.M.; Steinrück, H.-G.; Bone, S.E.; Safonova, O.V.; Toney, M.F.; Borodin, O.; Lukatskaya, M.R. Creating Water-in-Salt-like Environment Using Coordinating Anions in Non-Concentrated Aqueous Electrolytes for Efficient Zn Batteries. Energy & Environmental Science 2023, 16, 1982–1991. [CrossRef]
  52. P. Giannozzi et al., J. Phys. Condens. Matter 2009, 21, 395502. [CrossRef]
  53. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Physical Review Letters 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
  54. Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Physical Review B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  55. Blöchl, P.E. Projector Augmented-Wave Method. Physical Review B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
  56. Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Physical Review B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  57. Methfessel, M.; Paxton, A.T. High-Precision Sampling for Brillouin-Zone Integration in Metals. Physical Review B 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
  58. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurateab Initioparametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. The Journal of Chemical Physics 2010, 132. [Google Scholar] [CrossRef]
  59. Neese, F. The ORCA Program System. WIREs Computational Molecular Science 2011, 2, 73–78. [Google Scholar] [CrossRef]
  60. Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. The Journal of Chemical Physics 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
  61. Stephens, J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. The Journal of Physical Chemistry 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
  62. Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. The Journal of Physical Chemistry A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
  63. Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab Initio Study of Solvated Molecules: A New Implementation of the Polarizable Continuum Model. Chemical Physics Letters 1996, 255, 327–335. [Google Scholar] [CrossRef]
  64. Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chemical Reviews 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
  65. Tundo, P.; Selva, M. The Chemistry of Dimethyl Carbonate. Accounts of Chemical Research 2002, 35, 706–716. [Google Scholar] [CrossRef]
  66. Comelli, F.; Francesconi, R. Isothermal Vapor-Liquid Equilibria, Densities, Refractive Indices, Excess Molar Volumes, and Excess Molar Enthalpies of Dimethyl Carbonate + 1,2-Dichloroethane and + 1,1,1-Trichloroethane. Journal of Chemical & Engineering Data 1994, 39, 560–564. [Google Scholar] [CrossRef]
  67. Aminabhavi, T.M.; Banerjee, K. Density, Viscosity, Refractive Index, and Speed of Sound in Binary Mixtures of Dimethyl Carbonate with Methanol, Chloroform, Carbon Tetrachloride, Cyclohexane, and Dichloromethane in the Temperature Interval (298.15−308.15) K. Journal of Chemical & Engineering Data 1998, 43, 1096–1101. [Google Scholar]
  68. Cramer, C.J.; Truhlar, D.G. A Universal Approach to Solvation Modeling. Accounts of Chemical Research 2008, 41, 760–768. [Google Scholar] [CrossRef]
  69. Trasatti, S. The Absolute Electrode Potential: An Explanatory Note (Recommendations 1986). Pure and Applied Chemistry 1986, 58, 955–966. [Google Scholar] [CrossRef]
  70. A.H. Larsen et al, The Atomic Simulation Environment—a Python Library for Working with Atoms. Journal of Physics: Condensed Matter 2017, 29, 273002. [CrossRef]
  71. Gao, Y.Q.; Georgievskii, Y.; Marcus, R.A. On the Theory of Electron Transfer Reactions at Semiconductor Electrode/Liquid Interfaces. The Journal of Chemical Physics 2000, 112, 3358–3369. [Google Scholar] [CrossRef]
  72. Doronin, S.V.; Budkov, Y.A.; Itkis, D.M. Electrocatalytic Activity of Doped Graphene: Quantum-Mechanical Theory View. Carbon 2021, 175, 202–214. [Google Scholar] [CrossRef]
  73. Anderson, P.W. Localized Magnetic States in Metals. Physical Review 1961, 124, 41–53. [Google Scholar] [CrossRef]
  74. Rosen, A.S.; Vijay, S.; Persson, K.A. Free-Atom-like d States beyond the Dilute Limit of Single-Atom Alloys. Chemical Science 2023, 14, 1503–1511. [Google Scholar] [CrossRef]
  75. Vijay, S.; Kastlunger, G.; Chan, K.; Nørskov, J.K. Limits to Scaling Relations between Adsorption Energies? The Journal of Chemical Physics 2022, 156. [Google Scholar] [CrossRef]
  76. Schmickler, W.; Santos, E.; Bronshtein, M.; Nazmutdinov, R. Adiabatic Electron-Transfer Reactions on Semiconducting Electrodes. ChemPhysChem 2016, 18, 111–116. [Google Scholar] [CrossRef]
  77. Santos, E.; Nazmutdinov, R.; Schmickler, W. Electron Transfer at Different Electrode Materials: Metals, Semiconductors, and Graphene. Current Opinion in Electrochemistry 2020, 19, 106–112. [Google Scholar] [CrossRef]
  78. Schmickler, W.; Henderson, D. New Models for the Structure of the Electrochemical Interface. Progress in Surface Science 1986, 22, 323–419. [Google Scholar] [CrossRef]
  79. Guidelli, R.; Schmickler, W. Recent Developments in Models for the Interface between a Metal and an Aqueous Solution. Electrochimica Acta 2000, 45, (15–16). [Google Scholar] [CrossRef]
  80. Nazmutdinov, R.R.; Berezin, A.S.; Soldano, G.; Schmickler, W. Orbital Overlap Effects in Electron Transfer Reactions across a Metal Nanowire/Electrolyte Solution Interface. The Journal of Physical Chemistry C 2013, 117, 13021–13027. [Google Scholar] [CrossRef]
  81. Kornyshev, A.A.; Kuznetsov, A.M.; Ulstrup, J. Effect of Overpotential on the Electronic Tunnel Factor in Diabatic Electrochemical Processes. The Journal of Physical Chemistry 1994, 98, 3832–3837. [Google Scholar] [CrossRef]
  82. Gao, Y.Q.; Georgievskii, Y.; Marcus, R.A. On the Theory of Electron Transfer Reactions at Semiconductor Electrode/Liquid Interfaces. The Journal of Chemical Physics 2000, 112, 3358–3369. [Google Scholar] [CrossRef]
  83. Nazmutdinov, R.R.; Tsirlina, G.A.; Manyurov, I.R.; Bronshtein, M.D.; Titova, N.V.; Kuzminova, Z.V. Misleading Aspects of the Viscosity Effect on the Heterogeneous Electron Transfer Reactions. Chemical Physics 2006, 326, 123–137. [Google Scholar] [CrossRef]
  84. Gao, Y.Q.; Marcus, R.A. On the Theory of Electron Transfer Reactions at Semiconductor/Liquid Interfaces. II. A Free Electron Model. The Journal of Chemical Physics 2000, 113, 6351–6360. [Google Scholar] [CrossRef]
  85. Medvedev, G. Non-Local Effects in the Kinetics of Heterogeneous Charge Transfer Reactions. Journal of Electroanalytical Chemistry 2000, 481, 215–221. [Google Scholar] [CrossRef]
  86. Schmickler, W. The Surface Dipole Moment of Species Adsorbed from a Solution. Journal of Electroanalytical Chemistry and Interfacial Electrochemistry 1988, 249, (1–2). [Google Scholar] [CrossRef]
  87. Krylov, V.S.; Damaskin, B.B.; Kir, V.A. The Present State and Problems of the Theory of the Kinetics of Electrode Reactions Accompanied by the Adsorption of Inactive Substances and Reagents. Russian Chemical Reviews 1986, 55, 706–720. [Google Scholar] [CrossRef]
  88. Brown, W.B.; Chang, T.Y. Exact Formula for the Dipole Moment of a One-Electron Diatomic Molecule. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences 1985, 401, 373–392. [Google Scholar] [CrossRef]
  89. Mitroy, J.; Safronova, M.S.; Clark, C.W. Theory and Applications of Atomic and Ionic Polarizabilities. Journal of Physics B: Atomic, Molecular and Optical Physics 2010, 43, 202001. [Google Scholar] [CrossRef]
  90. Cramer, C.J.; Truhlar, D.G. A Universal Approach to Solvation Modeling. Accounts of Chemical Research 2008, 41, 760–768. [Google Scholar] [CrossRef]
  91. Bryantsev, V.S.; Diallo, M.S.; Goddard, W.A., III. Calculation of Solvation Free Energies of Charged Solutes Using Mixed Cluster/Continuum Models. The Journal of Physical Chemistry B 2008, 112, 9709–9719. [Google Scholar] [CrossRef]
  92. Kelly, C.P.; Cramer, C.J.; Truhlar, D.G. Aqueous Solvation Free Energies of Ions and Ion−Water Clusters Based on an Accurate Value for the Absolute Aqueous Solvation Free Energy of the Proton. The Journal of Physical Chemistry B 2006, 110, 16066–16081. [Google Scholar] [CrossRef] [PubMed]
  93. Parker, V.D. Energetics of Electrode Reactions. II. The Relationship between Redox Potentials, Ionization Potentials, Electron Affinities, and Solvation Energies of Aromatic Hydrocarbons. Journal of the American Chemical Society 1976, 98, 98–103. [Google Scholar] [CrossRef]
  94. Marenich, A.V.; Ho, J.; Coote, M.L.; Cramer, C.J.; Truhlar, D.G. Computational Electrochemistry: Prediction of Liquid-Phase Reduction Potentials. Phys. Chem. Chem. Phys. 2014, 16, 15068–15106. [Google Scholar] [CrossRef]
  95. Chen, T.; Dai, L. Carbon Nanomaterials for High-Performance Supercapacitors. Materials Today 2013, 16, (7–8). [Google Scholar] [CrossRef]
  96. Lemine, A.S.; Zagho, M.M.; Altahtamouni, T.M.; Bensalah, N. Graphene a Promising Electrode Material for Supercapacitors-A Review. International Journal of Energy Research 2018, 42, 4284–4300. [Google Scholar] [CrossRef]
  97. Iamprasertkun, P.; Ejigu, A.; Dryfe, R.A.W. Understanding the Electrochemistry of “Water-in-Salt” Electrolytes: Basal Plane Highly Ordered Pyrolytic Graphite as a Model System. Chemical Science 2020, 11, 6978–6989. [Google Scholar] [CrossRef]
  98. Kumar, R.; Sahoo, S.; Joanni, E.; Singh, R.K.; Tan, W.K.; Kar, K.K.; Matsuda, A. Recent Progress in the Synthesis of Graphene and Derived Materials for next Generation Electrodes of High Performance Lithium Ion Batteries. Progress in Energy and Combustion Science 2019, 75, 100786. [Google Scholar] [CrossRef]
  99. Nikitas, P. Theory of Electrochemically Modulated Liquid Chromatography. Journal of Electroanalytical Chemistry 2000, 484, 137–143. [Google Scholar] [CrossRef]
  100. Nikitas, P.; Pappa-Louisi, A. Adsorption Isotherms for Coadsorption Studies from Solution. Canadian Journal of Chemistry 1986, 64, 328–332. [Google Scholar] [CrossRef]
  101. Nikitas, P. A Unified Treatment of the Equilibrium Properties of Electrosorbed Layers Composed of Neutral and Ionic Species. Electrochimica Acta 1996, 41, 2159–2170. [Google Scholar] [CrossRef]
  102. Grahame, D.C. The Electrical Double Layer and the Theory of Electrocapillarity. Chemical Reviews 1947, 41, 441–501. [Google Scholar] [CrossRef] [PubMed]
  103. CRC Handbook of Chemistry and Physics, 95th Edition by William M. Haynes. CRC Press. 2014.
  104. Macdonald, J.R.; Barlow, C.A. Work Function Change on Monolayer Adsorption. The Journal of Chemical Physics 1963, 39, 412–422. [Google Scholar] [CrossRef]
  105. Di Muzio, S.; Palumbo, O.; Brutti, S.; Paolone, A. Thermodynamic Analysis of the Hydrolysis of Borate-Based Lithium Salts by Density Functional Theory. Journal of The Electrochemical Society 2022, 169, 070523. [Google Scholar] [CrossRef]
  106. Younesi, R.; Veith, G.M.; Johansson, P.; Edstrom, K.; Vegge, T. Lithium Salts for Advanced Lithium Batteries: Li–Metal, Li–O2, and Li–S. Energy & Environmental Science 2015, 8, 1905–1922. [Google Scholar] [CrossRef]
  107. Kawamura, T.; Sonoda, T.; Okada, S.; Yamaki, J. Improvement of the Stability of LiPF6 Electrolytes toward Water by the Addition of LiCl. Electrochemistry 2003, 71, 1139–1141. [Google Scholar] [CrossRef]
  108. Nagayama, K.; Kamioka, K.; Iwata, E.; Oka, H.; Tokunaga, Y.; Okada, T. The Reaction of Lithium-Manganese Oxides for the Cathode Materials of Rechargeable Lithium Batteries with Nonaqueous Electrolyte. Electrochemistry 2001, 69, 6–9. [Google Scholar] [CrossRef]
  109. Wang, J.; Yamada, Y.; Sodeyama, K.; Chiang, C.H.; Tateyama, Y.; Yamada, A. Superconcentrated Electrolytes for a High-Voltage Lithium-Ion Battery. Nature Communications 2016, 7, 12032. [Google Scholar] [CrossRef] [PubMed]
  110. Hou, R.; Wang, Y.; Sun, Y.; Lang, J.; Yang, S.; Yan, X. “Cation/Anion with Co-Solvation” Type High-Voltage Aqueous Electrolyte Enabled by Strong Hydrogen Bonding. Nano Energy 2022, 99, 107377. [Google Scholar] [CrossRef]
  111. Suo, L.; Borodin, O.; Sun, W.; Fan, X.; Yang, C.; Wang, F.; Gao, T.; Ma, Z.; Schroeder, M.; von Cresce, A.; Russell, S.M.; Armand, M.; Angell, A.; Xu, K.; Wang, C. Advanced High-Voltage Aqueous Lithium-Ion Battery Enabled by “Water-in-Bisalt” Electrolyte. Angewandte Chemie International Edition 2016, 55, 7136–7141. [Google Scholar] [CrossRef]
  112. Wu, S.L.; Su, B.Z.; Sun, M.Z.; Gu, S.; Lu, Z.G.; Zhang, K.L.; Yu, D.Y.W.; Huang, B.L.; Wang, P.F.; Lee, C.-S.; Zhang, W.J. Dilute Aqueous-Aprotic Hybrid Electrolyte Enabling a Wide Electrochemical Window through Solvation Structure Engineering. Advanced Materials 2021, 33. [Google Scholar] [CrossRef] [PubMed]
  113. Tomiyasu, H.; Shikata, H.; Takao, K.; Asanuma, N.; Taruta, S.; Park, Y.-Y. An Aqueous Electrolyte of the Widest Potential Window and Its Superior Capability for Capacitors. Scientific Reports 2017, 7. [Google Scholar] [CrossRef] [PubMed]
  114. Zheng, J.; Tan, G.; Shan, P.; Liu, T.; Hu, J.; Feng, Y.; Yang, L.; Zhang, M.; Chen, Z.; Lin, Y.; Lu, J.; Neuefeind, J.C.; Ren, Y.; Amine, K.; Wang, L.-W.; Xu, K.; Pan, F. Understanding Thermodynamic and Kinetic Contributions in Expanding the Stability Window of Aqueous Electrolytes. Chem 2018, 4, 2872–2882. [Google Scholar] [CrossRef]
  115. Li, W.; Dahn, J.R.; Wainwright, D.S. Rechargeable Lithium Batteries with Aqueous Electrolytes. Science 1994, 264, 1115–1118. [Google Scholar] [CrossRef]
  116. Sajjad, M.; Khan, M.I.; Cheng, F.; Lu, W. A Review on Selection Criteria of Aqueous Electrolytes Performance Evaluation for Advanced Asymmetric Supercapacitors. Journal of Energy Storage 2021, 40, 102729. [Google Scholar] [CrossRef]
  117. Tomiyasu, H.; Shikata, H.; Takao, K.; Asanuma, N.; Taruta, S.; Park, Y.-Y. An Aqueous Electrolyte of the Widest Potential Window and Its Superior Capability for Capacitors. Scientific Reports 2017, 7. [Google Scholar] [CrossRef] [PubMed]
  118. Redondo, E.; Goikolea, E.; Mysyk, R. The Decisive Role of Electrolyte Concentration in the Performance of Aqueous Chloride-Based Carbon/Carbon Supercapacitors with Extended Voltage Window. Electrochimica Acta 2016, 221, 177–183. [Google Scholar] [CrossRef]
  119. Li, C.; Zhang, S.; Wang, Y.; Liu, H.; Xing, T.; Lin, Y.; Rong, X.; Ren, H.; Wu, M.; Abbas, Q.; Li, Z. Dual Breaking of Ionic Association in Water-in-LiTFSI Electrolyte for Low Temperature Battery Applications. Journal of Power Sources 2022, 544, 231874. [Google Scholar] [CrossRef]
  120. Yang, B.; Tang, X.; She, W.; Zhang, D.; He, Y.; Wang, B.; Xia, X.; Li, Y.; Han, Z.; Wang, K. Exploring Potassium Trifluoroacetate as a Novel Electrolyte for Enhancing Energy Density of Biomass-Derived Carbon-Based Supercapacitors and Improving Electrolyte-Electrode Adaptability. Journal of Energy Storage 2023, 73, 108805. [Google Scholar] [CrossRef]
  121. Li, M.; Su, H.; Zheng, G.; Kuhn, U.; Kim, N.; Li, G.; Ma, N.; Pöschl, U.; Cheng, Y. Aerosol pH and Ion Activities of HSO4– and SO4 [2]– in Supersaturated Single Droplets. Environmental Science & Technology 2022, 56, 12863–12872. [Google Scholar] [CrossRef]
  122. A. Guha; Sahoo, M.; Alam, K.; Rao, D.K.; Sen, P.; Narayanan, T.N. Role of Water Structure in Alkaline Water Electrolysis. iScience 2022, 25, 104835. [Google Scholar] [CrossRef]
  123. He, Z.-H.; Gao, J.-F.; Kong, L.-B. Electrolyte Effect on Electrochemical Behaviors of Manganese Fluoride Material for Aqueous Asymmetric and Symmetric Supercapacitors. Rare Metals 2023, 43, 1048–1061. [Google Scholar] [CrossRef]
  124. Binnemans, K.; Jones, P.T. Methanesulfonic Acid (MSA) in Hydrometallurgy. Journal of Sustainable Metallurgy 2022, 9, 26–45. [Google Scholar] [CrossRef]
  125. Amini, K.; Pritzker, M.D. Improvement of Zinc-Cerium Redox Flow Batteries Using Mixed Methanesulfonate-Chloride Negative Electrolyte. Applied Energy 2019, 255, 113894. [Google Scholar] [CrossRef]
  126. Li, Z.; Robertson, A.W. Electrolyte Engineering Strategies for Regulation of the Zn Metal Anode in Aqueous Zn-ion Batteries. Battery Energy 2022, 2. [Google Scholar] [CrossRef]
  127. Liu, T.; Tang, L.; Luo, H.; Cheng, S.; Liu, M. A Promising Water-in-Salt Electrolyte for Aqueous Based Electrochemical Energy Storage Cells with a Wide Potential Window: Highly Concentrated HCOOK. Chemical Communications 2019, 55, 12817–12820. [Google Scholar] [CrossRef] [PubMed]
  128. Deng, W.; Wang, X.; Liu, C.; Li, C.; Chen, J.; Zhu, N.; Li, R.; Xue, M. Li/K Mixed Superconcentrated Aqueous Electrolyte Enables High-Performance Hybrid Aqueous Supercapacitors. Energy Storage Materials 2019, 20, 373–379. [Google Scholar] [CrossRef]
  129. Han, J.; Zhang, H.; Varzi, A.; Passerini, S. Fluorine-Free Water-in-Salt Electrolyte for Green and Low-Cost Aqueous Sodium-Ion Batteries. ChemSusChem 2018, 11, 3704–3707. [Google Scholar] [CrossRef]
  130. Lukatskaya, M.R.; Feldblyum, J.I.; Mackanic, D.G.; Lissel, F.; Michels, D.L.; Cui, Y.; Bao, Z. Concentrated Mixed Cation Acetate “Water-in-Salt” Solutions as Green and Low-Cost High Voltage Electrolytes for Aqueous Batteries. Energy & Environmental Science 2018, 11, 2876–2883. [Google Scholar] [CrossRef]
Preprints 112778 g001
Figure 1. Dependence of the binding energy of cations (q=+1) and anions (q=-1) according to models (1−5) on their valence orbital energy level εion. The solvent molecules are described by s- (A) and px- and pz-orbitals (B). Adsorption energy of the ions in the Newns-Andersen model according to equations (6, 7) as a function of the energy level εa of the adsorbent (C) and the square of the matrix element V [2] (D). Estimation of the adsorption energy of the ions by eq. (9) (E).
Figure 1. Dependence of the binding energy of cations (q=+1) and anions (q=-1) according to models (1−5) on their valence orbital energy level εion. The solvent molecules are described by s- (A) and px- and pz-orbitals (B). Adsorption energy of the ions in the Newns-Andersen model according to equations (6, 7) as a function of the energy level εa of the adsorbent (C) and the square of the matrix element V [2] (D). Estimation of the adsorption energy of the ions by eq. (9) (E).
Preprints 112778 g001
Preprints 112778 g002
Figure 2. Adsorption energy (A, B, E, F) and distance to the surface (C, D, G, H) for cations and anions on α-Al2O3 (0001) as a function of their HOMO and LUMO orbital energy levels.
Figure 2. Adsorption energy (A, B, E, F) and distance to the surface (C, D, G, H) for cations and anions on α-Al2O3 (0001) as a function of their HOMO and LUMO orbital energy levels.
Preprints 112778 g002
Preprints 112778 g003
Figure 3. Adsorption energy (A, B, E, F) and distance to the surface (C, D, G, H) for cations and anions on graphene as a function of their HOMO and LUMO orbital energy levels.
Figure 3. Adsorption energy (A, B, E, F) and distance to the surface (C, D, G, H) for cations and anions on graphene as a function of their HOMO and LUMO orbital energy levels.
Preprints 112778 g003
Preprints 112778 g004
Figure 4. Adsorption energy (A, B, E, F) and distance (C, D, G, H) to the Au (111) surface for cations and anions as a function of their HOMO and LUMO orbital energy levels. In Figures (A) and (B), the black colored approximations do not include PyMe+ and EMPyr+, while the royal-colored approximations include these ions.
Figure 4. Adsorption energy (A, B, E, F) and distance (C, D, G, H) to the Au (111) surface for cations and anions as a function of their HOMO and LUMO orbital energy levels. In Figures (A) and (B), the black colored approximations do not include PyMe+ and EMPyr+, while the royal-colored approximations include these ions.
Preprints 112778 g004
Preprints 112778 g005
Figure 5. Ion-water binding energies (A, B, E, F) and distances (C, D, G, H) between the centers of mass of the ions and water molecules as a function of the energy level of the HOMO and LUMO orbitals.
Figure 5. Ion-water binding energies (A, B, E, F) and distances (C, D, G, H) between the centers of mass of the ions and water molecules as a function of the energy level of the HOMO and LUMO orbitals.
Preprints 112778 g005
Preprints 112778 g006
Figure 6. Ion-DMC binding energies (A, B, E, F) and distances (C, D, G, H) between the centers of mass of the ions and dimethyl carbonate molecules as a function of the energy level of the HOMO and LUMO orbitals.
Figure 6. Ion-DMC binding energies (A, B, E, F) and distances (C, D, G, H) between the centers of mass of the ions and dimethyl carbonate molecules as a function of the energy level of the HOMO and LUMO orbitals.
Preprints 112778 g006
Preprints 112778 g007
Figure 7. Dependence of the dipole moment (A, B), polarizability (C, D), solvation energy (E−G) and oxidation potential (H) of ions on their HOMO, HOMO-1 and LUMO orbital levels.
Figure 7. Dependence of the dipole moment (A, B), polarizability (C, D), solvation energy (E−G) and oxidation potential (H) of ions on their HOMO, HOMO-1 and LUMO orbital levels.
Preprints 112778 g007
Preprints 112778 g008
Figure 8. Water coverage (θw) of the model electrode depending on the value of the anion εHOMO and εLUMO, Li+ is used as the cation, the concentration of the supporting electrolyte is 1 M. (A) − F-, BF4- and PF6-, (B) − TFSI-, TfO-, ClO4-, NO3- and Cl-, Br-, (C) − OH-, HSO4-, CF3COO-, RSO3-, and RCOO- anions.
Figure 8. Water coverage (θw) of the model electrode depending on the value of the anion εHOMO and εLUMO, Li+ is used as the cation, the concentration of the supporting electrolyte is 1 M. (A) − F-, BF4- and PF6-, (B) − TFSI-, TfO-, ClO4-, NO3- and Cl-, Br-, (C) − OH-, HSO4-, CF3COO-, RSO3-, and RCOO- anions.
Preprints 112778 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated