Control of the Properties of the Voronoi Tessellation Technique and Biomimetic Patterns: A Review

The cellular behavior of Voronoi tessellation has generated interest due to its applicability in various fields and its notable structural properties. Controlling factors such as the gradient of the cells, the position of seed points and the thickness of the arms allows for adjusting rigidity and flexibility according to specific needs. This article analyzes the state of the art of this technique, exploring its modification for applications in engineering and design, complemented with information on natural structural properties. This comprehensive analysis provides a complete overview of Voronoi tessellation and its potential in engineering and design, categorizing methodologies according to selected processing methods and highlighting techniques for altering structural behavior. Additionally, it emphasizes the integration of biomimetic approaches, connecting nature with technology to foster continuous innovation. Finally, the article addresses encountered limitations, offering future perspectives for the cellular technique and highlights the complexity of reproducibility due to reserved or generalized steps, despite the significant diversity in implemented techniques.

Keywords:

Subject: Engineering - Other

1. Introduction

Voronoi tessellation is a term that dates back to the early 20th century, named after the Russian algebraist and mathematician Georgy Fedoseevich Voronoi (1868-1908) [1]. Referencing a fundamental geometric construction [2], based on a given set of points [3]. Voronoi tessellation is widely used to approximate and model various cellular structures and stochastic patterns found in nature. It allows for the description of materials with cellular characteristics, such as trabecular bone, polycrystalline alloys or foams [4].

However, the central idea of the term has been applied since earlier times. One of its earliest implementations was probably represented in the book “Le Monde / Traité du monde et de la lumière” by the philosopher, mathematician, and scientist René Descartes (1596–1650). Published in 1644 (but written between 1629 and 1633), the author uses Voronoi diagrams to show the arrangement of matter in the solar system and its surroundings [5].

Since Voronoi diagrams initially referred to regions surrounding a finite set of points in a multidimensional space [1], one of their primary uses was in crystallography. Additionally, they have been involved in other areas related to spatial interpolation. For example, in meteorology by Alfred H. Thiessen in 1911, who used Voronoi regions to aid in calculating more accurate estimates of average regional precipitation. They have also been implemented to approximate mineral reserves in a deposit using information obtained from drilling [6].

It is also possible to visualize applications ranging from urban planning and network optimization to geospatial modeling and mesh generation in computational design. Additionally, in crime mapping through spatial analysis using cartography [7]. Voronoi tessellation can also be implemented in 3D models due to the vast technological innovation possibilities it offers, thanks to efficient spatial division into three-dimensional regions. For example, in engineering fields, Voronoi tessellation can be applied to the fabrication of structural proposals. This includes creating prostheses that simulate the internal cellular behavior of human bones for biomedical purposes by controlling the internal density of the models [8,9,10,11,12,13,14,15,16,17], or in structures for industrial applications, such as the manufacturing of internally porous tires [18].

This article aims to provide relevant information about the Voronoi tessellation technique, presenting the terminology conceptually and conducting an exhaustive analysis of methodologies proposed by various authors to control the properties of the Voronoi tessellation technique. It also highlights the importance of implementing biomimetic patterns to create models adaptable to the aforementioned cellular technique.

2. Biomimetics

The Greek philosopher Aristotle said, “to achieve defined purposes, art imitates nature.”

Over time, individuals from various fields have sought inspiration from the natural world, aiming not only for aesthetic outcomes but also exploring the environment for functional solutions to specific problems. This is because nature, through millions of years of evolution, has developed solutions that benefit human adaptation.

Biomimetics (from Greek bios, life, and mimesis, imitation) is a concept that has been scientifically studied for a long time, considered to have one of its earliest mentions in literature in 1950 by Otto Schmitt [19]. It draws inspiration from nature in terms of functional concepts of an organism or an ecosystem.

According to Janine Benyus, biomimicry is a science that, in addition to drawing inspiration, seeks to mimic natural processes to provide innovative design solutions [20]. On the other hand, Rajshekhar Rao, Associate Professor at Ramaiah Institute of Technology in Bangalore, India, believes that nature itself has already solved many existing problems. He compares animals, plants, and microbes to accomplished engineers who have found what works and endures on Earth. Therefore, he views biomimicry as the science that allows for the emulation of existing forms in the natural world, using ecological criteria to assess the sustainability of innovations [21].

When discussing biomimetic patterns, one can recognize structures already applied to contemporary life challenges. For instance, termite mounds, which studies show function very similarly to mammalian lungs by facilitating gas exchange in underground nests, can be adapted to buildings or homes to act as temperature regulators in extreme conditions [22]. Similarly, aircraft wings mimic aerodynamic shapes found in birds. Often, the aim is to simulate structural properties and behaviors to meet specific requirements, such as materials resembling spider silk.

From the emergence of design techniques to the present day, various authors have sought to emulate specific patterns found in nature. The development of bio-inspired techniques allows for adapting natural pattern characteristics and translating them into prototypes using computer-aided design software and additive manufacturing.

An example can be found in the pattern implemented by Zainab Alknery in her article “Effect of Cell Geometry on the Mechanical Properties of 3D Voronoi Tessellation” [9]. Here, she considers the mosaic technique applied to vary the gradient of the Voronoi diagram. She contemplates structural design based on rocks like diabase and basalt, known for their high mechanical strength due to their geometric structure. She also explores the microstructure of human bone to enhance permeability compared to regular pores, ensuring uniform distribution of stresses and rigidity.

Similarly, Mark Frenkel and Irina Legchenkova, in their article “Voronoi Diagrams Generated by the Archimedes Spiral: Fibonacci Numbers, Chirality and Aesthetic Appeal” [23], draw inspiration from phyllotaxis, a biomimetic technique involving the spiral arrangement of leaves, petals, or other plant parts. They generate Voronoi cells from seed points positioned in Archimedean spirals. Their study highlights the prevalence of hexagonal cells, resulting in both aesthetic appeal and optimal physical properties.

2.1. Biomimetic Patterns and Their Properties

Nature, in its quest to ensure survival, exhibits a remarkable ability to overcome its own disadvantages through the creation of innovative mechanisms. Organisms, in their process of adapting to the environment and overcoming inherent challenges, develop strategies and solutions to thrive.

Such situations are exemplified continuously. One example is how some insects utilize the natural transpiration process of plants to protect their eggs by regulating temperature during the hottest parts of the day, thus reducing the risk of sunburn [24]. Another example is found in cellular patterns in plants that allow oxygen passage to roots, as seen in reeds (such as common reed, Phragmites australis) and other wetland plants. Their energy processes are affected in highly moist soils where oxygen diffusion in water is 10,000 times slower than in air [25].

Considering construction properties, one can observe the work done by oysters. They gather to form reefs, aiming to create habitats for other aquatic species, filter and improve water quality, dampen waves, and protect coastlines from erosion. This work is made possible by the natural cement they produce, mainly composed of organic matter and abundant calcium carbonate. This results in structures that behave like skyscrapers, needing to be both rigid and flexible to sway slightly with the wind. The oysters’ adhesive allows them to withstand strong tidal forces while keeping their colonies intact [26].

Thus, nature not only demonstrates beauty in numerous cases but also provides functionality. For instance, the hundreds of thousands of microscopic scales covering butterfly wings reflect light and display intense, vibrant colors, serving not just an aesthetic purpose. The size, shape, and orientation of these scales alter the relative size of the four forces of flight (lift, weight, thrust, and drag), affecting how air flows over the butterfly’s wings and enabling movements like ascending, descending, forward, or backward [27].

Table 1. Biomimetic patterns with mechanical properties.

Biomimetic Pattern	Description	Properties
Silica skeleton of the marine sponge Venus’ flower basket (Euplectella aspergillum) [28].	▪ Marine animal anchored to the ocean floor near the Philippines. ▪ Tubular shape. ▪ Measures between 10 and 30 cm in height. ▪ Cylindrical skeleton made of layers of silica formed by colloidal spheres with diameters of about 50 to 200 nm, which are composed of even smaller spheres with diameters around 2.8 nanometers.	▪ Resistant to lateral forces and stable due to its composition and organization, despite the fragile nature of its main ingredient. ▪ Considerable hardness. ▪ Cemented structure thanks to embedded spicules.
Fluted underside of the Amazon water lily [29].	▪ Fluted support structure resembling a beam. ▪ It has a main vein running along the center of the leaf, with additional veins radiating from the center and gradually bifurcating along the leaf. ▪ Vein thickness gradient decreasing towards the leaf edge.	▪ Structural support to keep the leaf afloat and hold small loads (up to 70 pounds). ▪ Total weight of the structure reduced because the veins are filled with air.
Spongy bone plate located in the frontal skull of the golden carpenter bird [30,31,32].	▪ Cranial bone: A blend of compact, dense bone tightly surrounding a deeper bone structured in layered plate-like structures, creating a dense impact absorption system.	▪ Impact force is reduced by two to eight times upon reaching the center. ▪ Dispersion of frequencies in divergent directions away from the central point of impact, facilitated by the porous and stratified structure. ▪ Bone is flexible and fragile on its own, but encapsulated by compact bone that maintains such properties.
Structural layers of grapefruits [33].	▪ Compressible skin, 2-3 cm thick. ▪ Layers are not clearly defined. ▪ Skin layers: ▪ Exocarp: outermost layer densely populated with cells, gradually transforming into mesocarp. ▪ Mesocarp: forms the bulk of the peel. Layer responsible for protecting the fruit from impacts, composed of many interconnected air cells. ▪ Endocarp: located within the mesocarp, containing all seeds and fruit pulp segments.	▪ Absorption of impact energy through filament breakage and collapse of cells present in the mesocarp.
Honeycomb structure [34].		▪ Strength and space efficiency through the use of hexagonal cells. ▪ “A hexagon inscribed in a circular figure encloses the most space.” Marcus Terentius Varro, 36 BCE. ▪ “A hexagonal honeycomb is the way to pack the most area with the least perimeter.” Thomas Hales, 2019. ▪ High resistance to compression. ▪ Heat dissipating structure.
Hexagons formed by lava [35].	▪ Structures formed due to differential heat and crack generation. The inner parts cool faster than the outer parts, causing contraction and the formation of adjacent cracks at 90-degree angles. As they continue to cool and shrink, the cracks open, allowing more lava to flow, resulting in angles increasing to 120 degrees.	▪ Space saving. ▪ Distribution of pressure points. ▪ High compressive strength.
Peacock mantis shrimp [36,37,38].	▪ A colorful crustacean measuring 5 inches, found in coral reefs from Guam to East Africa. ▪ Hunting method: Capable of breaking hard shells with its club-shaped appendage. ▪ Its club can strike at speeds over 50 mph. ▪ Note: Difficult to keep in captivity due to their ability to easily break glass.	▪ Made of material designed to resist cracks. ▪ Resistance to lateral expansion during impact due to composite fibers of calcium carbonate and calcium phosphate that biomineralize into circular layers. ▪ Impact absorption and reduced likelihood of straight crack formation, thanks to sheets formed between the circular layers, composed of chitin and proteins that create a spiral structure in the cross-section.
Cuticle of the Desert Locust legs [39].	▪ Exoskeletons formed by cuticle (common biomaterial). ▪ No mineral reinforcement (such as found in bone).	▪ Extremely lightweight. ▪ Great strength and durability. ▪ Resistance to withstand many high and repetitive forces (e.g., jumps). ▪ Flexibility. ▪ Prevention of desiccation and damage.
Elephant trunk [40,41].	▪ Complex musculature thanks to intricate patterns of muscle fibers. ▪ They contain over 40,650 muscles. ▪ Muscular hydrostats: muscular organs without bones or joints. ▪ Muscle fibers arranged in three patterns: ▪ parallel to the length of the organ, ▪ perpendicular to its length, ▪ obliquely wrapped along its length.	▪ Mobility of the organ due to the constant volume of water inside. ▪ Loading capacity of up to 159 kg. ▪ Holding fragile objects without breaking them. ▪ Resistance to bending compression thanks to tension exerted by perpendicular fibers arranged radially along the cross-section. ▪ Specific actions according to each fiber pattern: ▪ Folding: longitudinal fibers on the outside contract and shorten on one side. ▪ Flexion: radial fibers form rings that extend along the trunk. ▪ Twisting: oblique fibers twist in different orientations allowing movements to the left and right.
Elk antlers [42,43,44,45].	▪ The antlers are composed of the same ingredients as human bone; however, they have fewer hard calcium crystals and higher amounts of flexible collagen. ▪ Composed of cylindrical structures called osteons. ▪ Between the osteons, there are thick regions covered with excess calcium. ▪ They possess hardening mechanisms.	▪ Highly resistant biomaterial. ▪ Great flexibility due to its composition. ▪ High toughness (fracture resistance). ▪ Less strength (bending resistance).
Golden scale snail (Crisomallon squamiferum) [46].	▪ Ecosystem: It is found in hydrothermal vents that emit hot water and minerals on the floor of the Indian Ocean. ▪ It has a hard shell composed of three layers with varying properties: ▪ Outer layer: thin organic layer reinforced by particles of greigite (iron sulfide) expelled by thermal vent grilles. ▪ Intermediate layer: thick and dense layer of organic material. ▪ Calcified inner layer: This is the innermost layer and acts like a brick wall.	▪ Outer layer: Upon impacts, it creates a large number of small fissures instead of a large one to prevent damage to the shell. ▪ Intermediate layer: It is flexible and easily deforms. It acts as a cushion, relieving grip pressure and dampening crushing blows from predators.

In the pursuit of proposing biomimetic patterns with mechanical properties adaptable to three-dimensional manufacturing processes, the following can be listed:

Figure 1. Venus’ Flower Basket (Euplectella aspergillum) De NOAA Photo Library - expn4384, Public domain, https://commons.wikimedia.org/w/index.php?curid=65929647.

Figure 2. Amazon water lily By Laitr Keiows - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=9653171.

Figure 3. Spongy bone in the skull of a woodpecker. Source: Wang et al. [CC-BY] via asknature.org. Image: https://journals.plos.org/plosone/artcile?id=10.1371/journal.pone.0026490#pone-0026490-g008/.

Figure 4. Pomelo peel by Ivar Leidus - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=98331782.

Figure 5. Beehive. Photograph taken by Merdal from Wikipedia in Turkish, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=121469.

Figure 6. Hexagonal basalt columns by Patrice78500 - Own work, Public domain https://commons.wikimedia.org/w/index.php?curid=5576765.

Figure 7. Peacock mantis shrimp (Odontodactylus scyllarus) by Jens Petersen - Own work, CC BY 2.5 https://commons.wikimedia.org/w/index.php?curid=1322905.

Figure 8. Desert locust by Compton Tucker, NASA GSFC - An Insect’s Alter Ego, Public domain https://commons.wikimedia.org/w/index.php?curid=526037.

Figure 9. Elephant trunk by Diego Delso, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=74484663.

Figure 10. Elk antlers by Donna Dewhurst - http://images.fws.gov, Public domain https://commons.wikimedia.org/w/index.php?curid=2072582.

Figure 11. Scaly-foot gastropod (Chrysomallon squamiferum) by Chong Chen, Katsuyuki Uematsu, Katrin Linse & Julia D. Sigwart - (2017). ‘By more ways than one: Rapid convergence at hydrothermal vents shown by 3D anatomical reconstruction of Gigantopelta.’ https://commons.wikimedia.org/wiki/File:Chrysomallon_squamiferum_9.png#/media/File:Chrysomallon_squamiferum_9.png.

As seen in Table 1, there are natural models whose mechanical properties provide unique characteristics aimed at solving specific issues. Most of these biomimetic patterns offer features related to force distribution and impact support, enabling proper structural handling. A notable case is represented by technology based on the peacock mantis shrimp’s behavior, namely helicoidal technology. This seeks to incorporate such design into composite materials, thereby creating products with reduced weight, increased toughness, and improved impact resistance, all while reducing costs [47]. Alternatively, innovations related to the muscular behavior of elephant trunks are applied in the development of robotic arms and grippers, focusing on the safe handling and lifting of objects or people without causing damage [48,49].

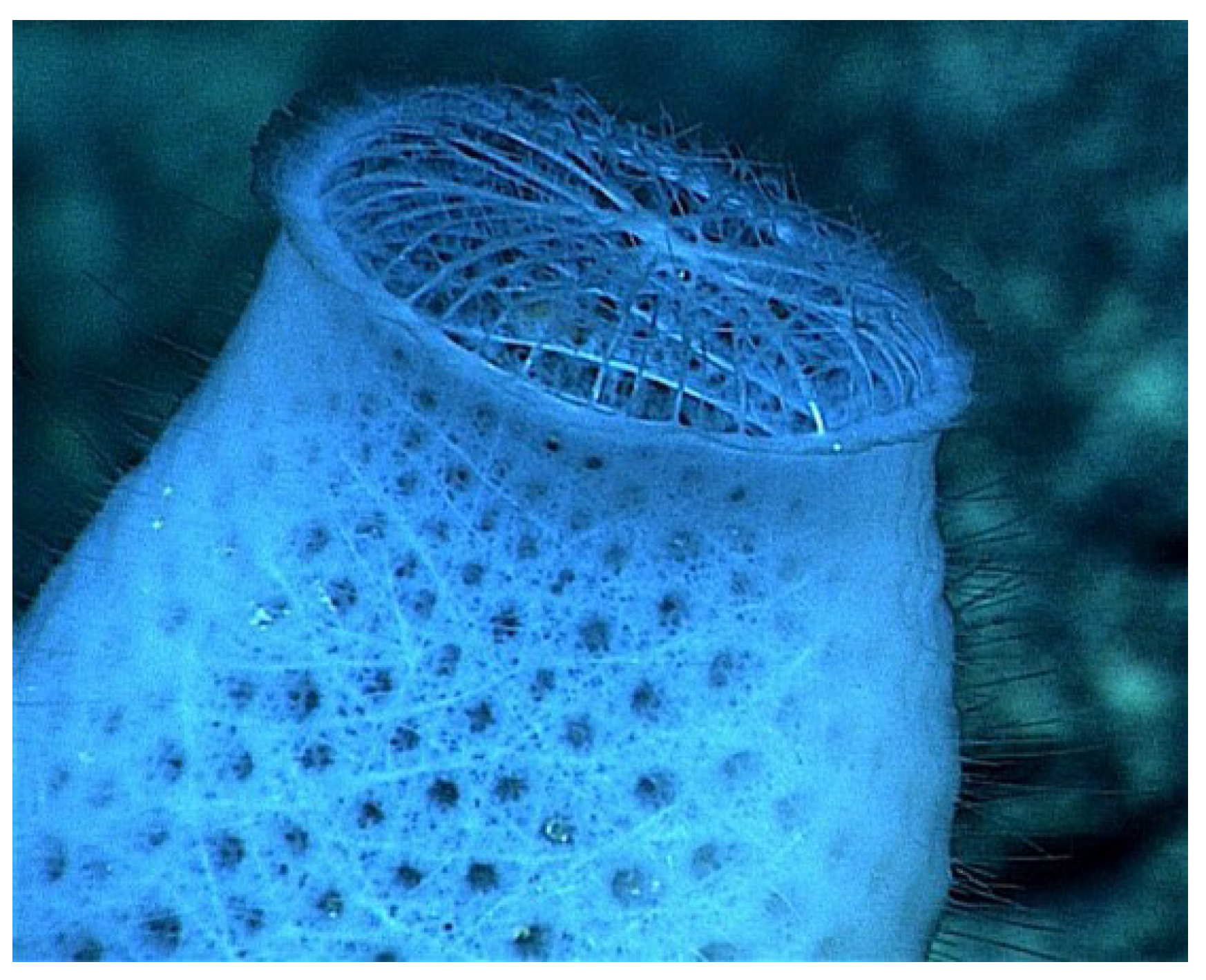
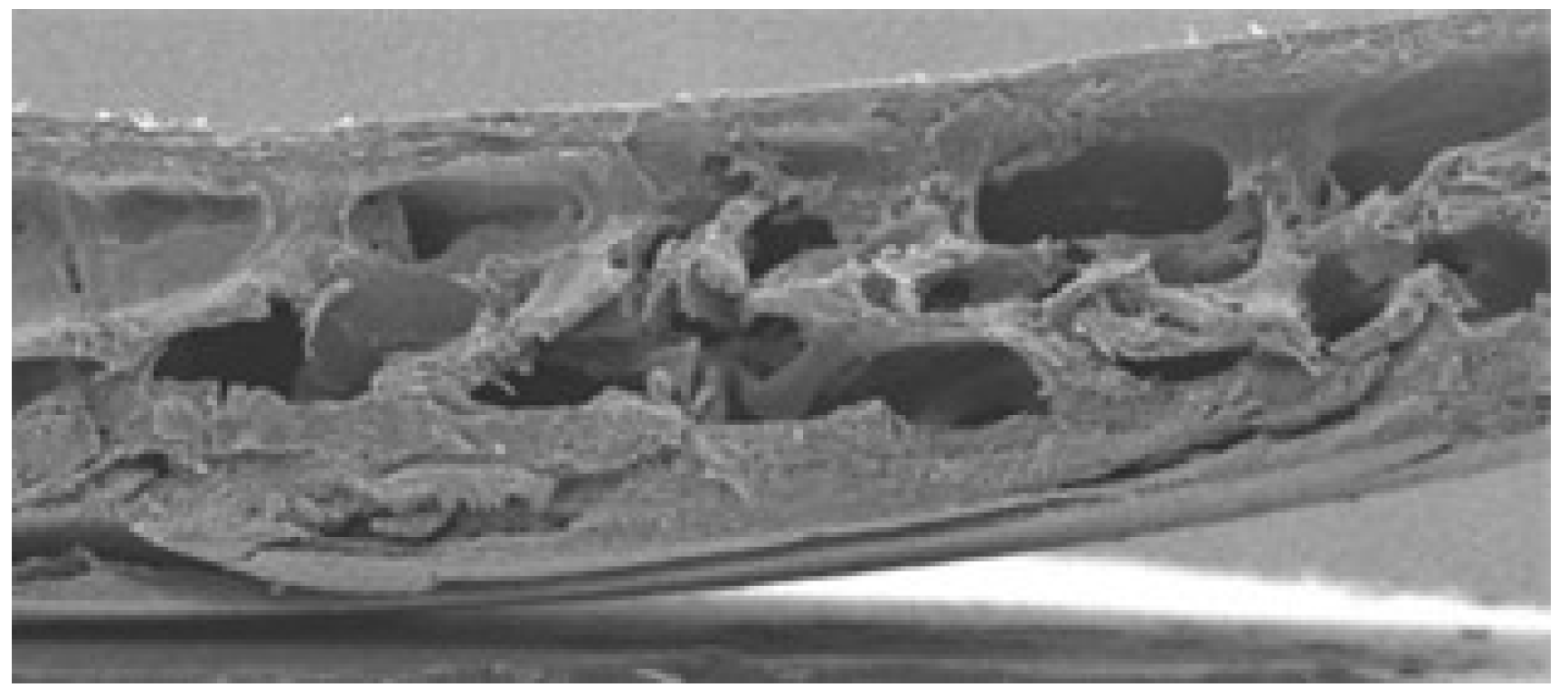
3. Techniques for Controlling Voronoi Cells

Over time, various authors have proposed modifications to the cellular properties of Voronoi tessellation techniques. These include controlling density and gradient, as well as arm thickness, seed point positions, and cell angles. All of these adjustments are achieved through diverse methods such as the development of flow-based programming algorithms, image processing techniques, or the generation of mathematical pseudocode.

Table 2. Processing methods developed from flow-based programming.

Article	Description
Effect of Cell Geometry on the Mechanical Properties of 3D Voronoi Tessellation [9].	Algorithm developed in Grasshopper based on flow-based programming. It implements the Voronoi tessellation technique and controls the extension of cells to achieve elongation, aiming to resemble basaltic columns in the model.
Design and Mechanical Properties Verification of Gradient Voronoi Scaffold for Bone Tissue Engineering [8].	Algorithm developed in Grasshopper based on flow-based programming. It aims to achieve a trabecular structure with a gradient distribution of pores similar to natural bone. To accomplish this, it randomly generates a certain number of seeds, extracts their X, Y, and Z coordinates. Subsequently, it establishes a control expression, eliminating points that do not conform to the applied distribution law, and modifies the remaining ones using a boolean operation.
Parametric Design and Mechanical Characterization of 3D-Printed PLA Composite Biomimetic Voronoi Lattices Inspired by the Stereom of Sea Urchins [50].	Model based on the structure and properties of the exoskeleton of the sea urchin Paracentrotus lividus, commonly found in the Mediterranean Sea and northeast Atlantic Ocean. Initially, a microscopic analysis was conducted to examine the mesoscopic structure of the echinoid test. Subsequently, this analysis served as the basis for the biomimetic design phase using Grasshopper and Rhinoceros.
Design and properties of biomimetic irregular scaffolds for bone tissue engineering [13].	Irregular biomimetic scaffold with applications in bone tissue engineering based on the Voronoi tessellation method, resembling key histomorphological indices of bone, modeled using Rhinoceros 6 computer-aided design (CAD) software and Grasshopper plugin. Initially, data was obtained from computed tomography (CT) scans of the bone, which required remodeling using a Philips iCT 256 CT scanner. Subsequently, the images were imported into Mimics Research for remodeling. The reconstructed model was exported to Rhinoceros 6 to extract the necessary basic surface for UV curve unfolding. Gradient cubes were then constructed using the length and width of the UV curve as x and y values, respectively, with variable heights. Within this space, a random number of seed points were generated for the application of Voronoi cells.
Design and statistical analysis of irregular porous scaffolds for orthopedic reconstruction based on Voronoi tessellation and fabricated via selective laser melting (SLM) [14].	A design method is proposed to construct irregular porous structures based on Voronoi tessellation. The irregular, controllable porous structure was designed using Rhinoceros 6 computer software, with the parametric design plugin Grasshopper. In the model design process, a set of points uniformly distributed in space was first generated. From these points, a series of cubes were developed, with their original points being the centroid of the bottom surface area of each cube. Subsequently, a random point was generated within each cube area to obtain the cells of the 3D Voronoi diagram. Finally, the skeleton of these cells was extracted to create the porous structure with a strut diameter.
Design and Compressive Behavior of Controllable Irregular Porous Scaffolds Based on Voronoi-Tessellation and for Additive Manufacturing [15].	A descending design method (probability sphere method) based on Voronoi tessellation was proposed to construct controllable porous scaffolds. The irregular, controllable porous structure was designed using Rhinoceros 6 computer software, with the parametric design plugin Grasshopper. Initially, a cubic region was generated whose volume encompassed the exterior volume of the porous structure. Secondly, an ordered cubic lattice containing n layers was generated within this region. Subsequently, spheres were centered at each point where a new point would randomly replace its predecessors. Finally, the skeleton of these cells was extracted to create the porous structure with a strut diameter.
Analysis of Mechanical Properties and Permeability of Trabecular-Like Porous Scaffold by Additive Manufacturing [17].	A porous model based on the complex microstructure of human bones is developed using Voronoi tessellation, applied to the design of spongy porous structures. Design parameters of the porous structure are determined, including porosity, aperture distribution, and mechanical property relationships. Grasshopper is used to control the irregularity of the structure. The basic idea involves generating a regular lattice with a specified spacing in space and establishing spherical regions with the regular lattice points as centers. A random seed point is then generated within each spherical region.
Mechanical and energy absorption properties of 3D-printed honeycomb structures with Voronoi tessellations [51].	In the study, a structure composed of hexagonal honeycomb blocks filled with Voronoi tessellations arranged in a repeated pattern and joined by magnetic coupling is proposed. To create the Voronoi cellular pattern, Rhinoceros 3D CAD software in conjunction with Grasshopper plugin was utilized to provide an effective 3D model. Subsequently, it was exported as an STL (Standard Tessellation Language) file for 3D printing. The structural design followed three phases: 1. A closed hexagonal periphery was created, and random points were generated on the generated spiral lines. 2. Points generated outside the hexagon were removed, and a rectangular boundary was created to generate the Voronoi cells. 3. A loop function was initiated to: 1) Generate Voronoi cells, 2) Use the Lloyd’s algorithm [52] to obtain relaxed Voronoi tessellations, 3) Modify the cell distribution to optimize the final design weight. To optimize the final design weight and enhance its strength, the distribution of Voronoi tessellations was adjusted. This adjustment pushed the Voronoi cells to increase in density near the edges and reduce in the center of the hexagon, thereby optimizing the final weight.

Table 3. Processing methods based on images.

Article	Description
Procedural Voronoi Foams for Additive Manufacturing [53].	A model oriented towards manufacturing using photopolymerization technology with resin 3D printers, implements an algorithm that works in conjunction with 2D images (pixels) representing the solid part of the faces of the Voronoi diagram with a certain thickness.
Generación de modelos tridimensionales de hueso esponjoso a partir de imágenes de su estructura trabecular [54].	The goal is to achieve a trabecular structure with a gradient pore distribution similar to natural bone through three-dimensional image acquisition modeling. Bone samples were taken, cleaned, and cut into specimens of various sizes. Subsequently, they were polished to remove protrusions and stained navy blue to highlight the structure and facilitate proper photography. Each photograph was then transformed into an STL file format to be imported into CAD software. Here, they were converted into solid models and corrected for any errors before constructing the three-dimensional model. This involved intersecting faces with their respective thicknesses using Boolean operations.
Three-dimensional Voronoi analysis of realistic grain packing: An XCT assisted set Voronoi tessellation framework [55].	Three-dimensional Voronoi analysis is used in the study of realistic grain packing, employing XCT (X-ray computed tomography) assisted by the Voronoi tessellation framework. The methodology followed to obtain the necessary data on the behavior of the sand is as follows: Initially, a batch of natural sand was prepared and placed in a container. The X-ray exploration process produces a back-projection image [56], from which corresponding 8-bit grayscale images can be obtained for subsequent segmentation through sequential processing. Following this, it is possible to construct a 3D distance map in which a binary image is mapped specifying the distance between pixels. Once the markers are defined, the flood-fill model is used to label the particles, assigning a unique identification number to each of them.
Voronoi analysis of bubbly flows via ultrafast X-ray tomographic Imaging [57].	As part of the methodology, ultra-fast X-ray tomographic images of 240 × 240 pixels were taken over a 1-second interval (1000 images) to obtain a three-dimensional phase fraction. Subsequently, centroids of the objects were extracted from the Eulerian field, which were then used as input to create a Voronoi diagram for further analysis. The aim was to analyze the clustering behavior of bubbles in a cylindrical column. It’s worth noting that image processing facilitated the analysis of cellular behavior using Voronoi diagrams, but no modification of the cellular pattern was performed.
Flexural properties of porcupine quill-inspired sandwich panels [58].	The article presents a study on the bending behavior of porcupine quills and bio-inspired Voronoi sandwich panels using X-ray micro-computed tomography, allowing for an analysis of their internal morphology. African porcupine quills (Hystrix cristata) were categorized into five groups based on their length. They were then examined and cleaned with ethanol to remove residues. To understand the structural behavior of the quills in different environments, measurements were taken after exposing them to dry and humid conditions (75% relative humidity) at a constant speed, aiming to identify how these conditions affect the mechanical performance of the keratin composing them. Following this, to investigate the internal morphology of the quills, they were cut into 5 mm lengths and scanned using the Bruker SKYSCAN 1275. Image stacks were reconstructed using SkyScan’s NRecon software for volumetric reconstruction, followed by CTan (CT-Analyser) software for analysis. After this investigation, the longitudinal cross-section was analyzed using MATLAB’s image processing tool. Scripts were developed to convert the grayscale image into a binary image. Voronoi tessellation was generated using computational geometry via the “divide and conquer” method. Finally, the 3D foam structure was translated into 2D to simplify the design. Similarly, the Voronoi diagram was generated by partitioning a region based on the number of seeds, designing Voronoi sandwich structures based on controlled random seed distribution. Despite having variable configurations, the sandwich panels are controlled by the number of seeds, relative density, and mass.
Mechanical and geometrical study of 3D printed Voronoi scaffold design for large bone defects [16].	The article proposes a model implementing the Voronoi tessellation technique, which was used to create a personalized biodegradable bone scaffold for each patient, aimed at surgically treating a critical-sized defect. To obtain the specific scaffold for each patient, the anatomical shape of the tumor resection was segmented from the computed tomography (CT) scan of a patient using Amira (version 6.2, Thermo Fisher Scientific Inc, Massachusetts, USA) and converted into a 3D model. Subsequently, tessellation was implemented using Voxelizer (ZMorph, Warsaw, Poland) to generate the CAD model. After the design phase, 5 PLA specimens were manufactured using Fused Filament Fabrication (FFF), and simultaneously, their morphology was analyzed. Once manufactured, the scaffolds were scanned using micro-computed tomography (µCT) and reconstructed in 3D to obtain the manufacturing geometry.

Table 4. Processing methods based on mathematical formulas and programming languages.

Article	Description
	Following and in accordance with the methodology described in Table 3 of the article “Three-dimensional Voronoi analysis of realistic grain packing: An XCT assisted set Voronoi tessellation framework” [55] the Poisson-disk Sampling algorithm is introduced. In this algorithm, given a reconstructed surface, a set of samples is computed that are randomly distributed on the surface, ensuring that the samples are at least a minimum distance apart. Subsequently, a parallel processing tool, PySVT, is proposed for Set Voronoi tessellation (SVT) in a hybrid programming environment using C++ and Python.
Polyhedral Voronoi diagrams for additive manufacturing [59].	The methodology followed to control the parameters of Voronoi cells involves using a mesh K that satisfies two manufacturing constraints: the angle constraint and the continuity constraint. The angle constraint ensures that each facet of the mesh is printable using Fused Filament Fabrication (FFF), while the continuity constraint ensures that the mesh is self-supporting and can be printed without support structures. The article does not provide details about the specific algorithm used to control the parameters of the Voronoi cells.
Generation of Numerical Models of Anisotropic Columnar Jointed Rock Mass Using Modified Centroidal Voronoi Diagrams [60].	The model is based on jointed columnar rock, a typical geological structure formed by ordered columns resulting from crack propagation in cooling lava flows. As a methodology, a Voronoi diagram was generated using 10 random seeds. The domain was divided into 10 patches, each containing a unique seed. Subsequently, Delaunay triangulation was implemented, and perpendicular bisectors were graphed to partition the domain into different Voronoi cells. Finally, for the implementation of the Voronoi tessellation technique, various software and packages can be used, such as MATLAB, Mathematica, and SciPy. They also employ an algorithm that generates closed Voronoi cells where the seed point coincides with its centroid. Examples of methods used for creating these cells include algorithms proposed by Lloyd and MacQueen [52,61].
Optimization of mechanical properties of bio-inspired Voronoi structures by genetic algorithm [62].	The article systematically analyzes the improvement of mechanical properties of Voronoi structures using genetic algorithms (GA). Initially, random Voronoi structures with different regularities were gradually optimized through iterative processes, increasing tensile strength and toughness. Finally, the mechanical performance of the structures before and after GA optimization was compared using additive manufacturing and tensile testing. In this experiment, six Voronoi structures with varying regularities were explored, each containing 128 pores. After generating the preliminary diagram, its dividing lines were thickened into walls, forming a 50% porous structure. As part of the methodology, an initial population of 100 points was established for each region. During selection, only 10 Voronoi structures with the highest fitness were chosen as parents for the next generation. These selected parents crossed their left and right parts to produce 90 offspring. Each offspring randomly changed the position of some points to induce mutation. The 10 parents and 90 offspring underwent finite element simulation to identify the top 10 structures with the highest fitness as parents for the subsequent generation. The process continued for 30 generations or until fitness values converged.
Mechanical properties of the hierarchical honeycombs with stochastic Voronoi sub-structures [63].	A periodically hierarchical honeycomb was designed with irregular substructure cells based on the Voronoi tessellation algorithm. A numerical investigation was conducted to determine the influence of structural hierarchy and irregularity on in-plane elastic properties. The effect of irregularity on the in-plane elastic properties of the periodic hierarchical honeycomb was assessed using ABAQUS/Standard software. Two-dimensional finite element models were generated for each representative unit cell using Timoshenko 2D beam elements, and various values were determined through proposed mathematical formulas.
M-Voronoi and other random open and closed-cell elasto-plastic cellular materials: Geometry generation and numerical study at small and large strains [64].	From a random sphere adsorption (RSA) algorithm with spherical voids embedded in a nonlinear, incompressible elastic matrix phase, a numerical design strategy is presented for a new class of three-dimensional Voronoi-like geometries, called M-Voronoi. These geometries consist of non-quadratic convex void shapes and non-uniform ligament thicknesses, spanning from high to low relative densities.
Extension of the Voronoi Diagram Algorithm to Orthotropic Space for Material Structural Design [65].	A model developed from a modified “flood fill” algorithm (a variant of the classic flood fill algorithm used in computer graphics to fill connected areas with a specific color), used to create and analyze structures based on Voronoi diagrams in an orthotropic space. It started with an initial geometry based on non-intersecting basic cells, defining subsequently the relationship between the components of the stiffness tensor and the parameters of ellipticity and porosity. Matlab R2019a software was implemented for developing and testing the smoothing algorithm.
Construction and deformation behavior of metal foam based on a 3D-Voronoi model with real pore structure [66].	The deformation behavior of metal foam based on a 3D Voronoi model with a real pore structure was investigated. Specifically, the aim was to understand how variations in cell wall thickness, defect size, and density gradient affect the load properties and deformation behavior of aluminum foam.

Table 5. Methods of processing developed using Generative Design and Topological Optimization software and CAD software.

Article	Description
	Following up on the article “M-Voronoi and other random open and closed-cell elasto-plastic cellular materials: Geometry generation and numerical study at small and large strains [64]”, as stated in Table 4, various additional software tools were mentioned for modeling, analysis, and mesh creation, namely nTopology 4.17.3, Creo Parametric 8.0, ABAQUS, and MeshLab.
Advancing 3D Dental Implant Finite Element Analysis: Incorporating Biomimetic Trabecular Bone with Varied Pore Sizes in Voronoi Lattices [67]	A three-dimensional model was designed based on the complex architecture of the human bone, particularly the trabecular or spongy bone of the jaw, crucial for dental implants. The software nTopology 4.17.3 and Creo Parametric 8.0 were used to create Voronoi lattices with pore sizes ranging from 1.0 mm to 2.5 mm. Finally, the finite element method was employed to examine displacements, stresses, and deformations in dental implants with different components subjected to bite loads.

Article

Description

Following up on the article “M-Voronoi and other random open and closed-cell elasto-plastic cellular materials: Geometry generation and numerical study at small and large strains [64]”, as stated in Table 4, various additional software tools were mentioned for modeling, analysis, and mesh creation, namely nTopology 4.17.3, Creo Parametric 8.0, ABAQUS, and MeshLab.

Advancing 3D Dental Implant Finite Element Analysis: Incorporating Biomimetic Trabecular Bone with Varied Pore Sizes in Voronoi Lattices [67]

A three-dimensional model was designed based on the complex architecture of the human bone, particularly the trabecular or spongy bone of the jaw, crucial for dental implants. The software nTopology 4.17.3 and Creo Parametric 8.0 were used to create Voronoi lattices with pore sizes ranging from 1.0 mm to 2.5 mm.
Finally, the finite element method was employed to examine displacements, stresses, and deformations in dental implants with different components subjected to bite loads.

4. Limitations

As can be observed in the tables presented in the previous section, each author follows different paths and techniques in pursuit of reaching an objective. However, the methods listed predominantly aim to control a single property of Voronoi tessellation, in most cases focusing on modifying density and porosity of the models, or presenting methodologies where cells are treated as a secondary element rather than the main focus of the article.

The implemented techniques require machinery, equipment, and essential tools for obtaining the models, making replication difficult due to limited information and generalized steps.

5. Perspectives

Considering the approach taken by the authors in each of the articles, it could be a good starting point to complement the techniques with biomimetic patterns that suit the requirements of each three-dimensional model. This includes focusing not only on individual cellular properties but also on globally modifying Voronoi cells. This approach ensures complete control over the structures and their application across various fields.

6. Conclusions

▪ There is a significant diversity in the techniques implemented by different authors aimed at controlling Voronoi cells. However, most of the approaches focus on modifying a single property of tessellation, especially density and porosity gradient, while leaving other properties underexplored.
▪ In many cases, the reviewed techniques emphasize Voronoi cells as secondary elements rather than the primary focus of the study. This limits comprehensive understanding of cellular properties and their potential applications across various fields.
▪ Most of the reviewed techniques require specific machinery and tools, which complicates their replicability. Limited information and generalized steps provided in the articles may hinder effective reproduction of the models.
▪ There is a promising opportunity to complement Voronoi cell control techniques with biomimetic patterns. This synergy could be tailored to meet the specific requirements of each three-dimensional model, expanding the scope of cellular modification and enabling more comprehensive control over structures.
▪ By focusing on the global modification of Voronoi cells, there is potential to effectively apply these techniques across different industries. This multidisciplinary approach could lead to more versatile and adaptable solutions for various engineering and design needs.

Author Contributions

A.K.A.A., E.N.A.M.; Conceptualization, A.K.A.A., E.N.A.M.; methodology, E.R.R., C.A.C.A.; validation, A.K.A.A., E.N.A.M.; formal analysis A.K.A.A., E.N.A.M., E.R.R.; investigation, A.K.A.A., E.N.A.M.; resources, A.K.A.A.; data curation, A.K.A.A., E.N.A.M.; writing—original draft preparation, A.K.A.A., E.R.R..; writing—review and editing, A.K.A.A., E.N.A.M.; visualization, E.N.A.M., C.A.C.A.; supervision and project administration. All authors have read and agreed to the published version of the manuscript.

Funding

This research did not receive funding for its realization.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Georgy Fedoseevich Voronoi,” ed.
N. Sukumar and J. J. T. i. t. S. Bolander, “Voronoi-based interpolants for fracture modelling,” vol. 485, 2009.
Drezner, T.; Drezner, Z. Voronoi diagrams with overlapping regions. OR Spectr. 2012, 35, 543–561. [Google Scholar] [CrossRef]
Xu, T.; Li, M. Topological and statistical properties of a constrained Voronoi tessellation. Philos. Mag. 2009, 89, 349–374. [Google Scholar] [CrossRef]
R. Descartes, Le monde ou traité de la lumière: Die Welt oder Abhandlung über das Licht. Walter de Gruyter GmbH & Co KG, 2022.
Senechal, M.; Okabe, A.; Boots, B.; Sugihara, K. Spatial Tessellations: Concepts and Applications of Voronoi Diagrams. Coll. Math. J. 1995, 26, 79. [Google Scholar] [CrossRef]
de Melo, S.N.; Frank, R.; Brantingham, P. Voronoi Diagrams and Spatial Analysis of Crime. Prof. Geogr. 2017, 69, 579–590. [Google Scholar] [CrossRef]
Zhao, H.; Han, Y.; Pan, C.; Yang, D.; Wang, H.; Wang, T.; Zeng, X.; Su, P. Design and Mechanical Properties Verification of Gradient Voronoi Scaffold for Bone Tissue Engineering. Micromachines 2021, 12, 664. [Google Scholar] [CrossRef] [PubMed]
Alknery, Z.; Sktani, Z.D.I.; Arab, A. Effect of Cell Geometry on the Mechanical Properties of 3D Voronoi Tessellation. J. Funct. Biomater. 2022, 13, 302. [Google Scholar] [CrossRef] [PubMed]
Du, Y.; Liang, H.; Xie, D.; Mao, N.; Zhao, J.; Tian, Z.; Wang, C.; Shen, L. Finite element analysis of mechanical behavior, permeability of irregular porous scaffolds and lattice-based porous scaffolds. Mater. Res. Express 2019, 6, 105407. [Google Scholar] [CrossRef]
Zhang, Q.; Li, B.; Wei, G.; Liu, G.; Liu, J. PARAMETRIC DESIGN, MECHANICAL PROPERTIES AND PERMEABILITY OF BIOMEDICAL POROUS SCAFFOLDS BASED ON TYPICAL STRUCTURE UNITS. J. Mech. Med. Biol. 2022, 22. [Google Scholar] [CrossRef]
S. G. González, M. D. Vlad, J. L. López, and E. F. Aguado, “Novel bio-inspired 3D porous scaffold intended for bone-tissue engineering: Design and in silico characterisation of histomorphometric, mechanical and mass-transport properties,” Materials & Design, vol. 225, p. 111467, 2023.
Chen, H.; Liu, Y.; Wang, C.; Zhang, A.; Chen, B.; Han, Q.; Wang, J. Design and properties of biomimetic irregular scaffolds for bone tissue engineering. Comput. Biol. Med. 2021, 130, 104241. [Google Scholar] [CrossRef] [PubMed]
Du, Y.; Liang, H.; Xie, D.; Mao, N.; Zhao, J.; Tian, Z.; Wang, C.; Shen, L. Design and statistical analysis of irregular porous scaffolds for orthopedic reconstruction based on voronoi tessellation and fabricated via selective laser melting (SLM). Mater. Chem. Phys. 2019, 239, 121968. [Google Scholar] [CrossRef]
Wang, G.; Shen, L.; Zhao, J.; Liang, H.; Xie, D.; Tian, Z.; Wang, C. Design and Compressive Behavior of Controllable Irregular Porous Scaffolds: Based on Voronoi-Tessellation and for Additive Manufacturing. ACS Biomater. Sci. Eng. 2018, 4, 719–727. [Google Scholar] [CrossRef] [PubMed]
Herath, B.; Suresh, S.; Downing, D.; Cometta, S.; Tino, R.; Castro, N.J.; Leary, M.; Schmutz, B.; Wille, M.-L.; Hutmacher, D.W. Mechanical and geometrical study of 3D printed Voronoi scaffold design for large bone defects. Mater. Des. 2021, 212, 110224. [Google Scholar] [CrossRef]
Chao, L.; Jiao, C.; Liang, H.; Xie, D.; Shen, L.; Liu, Z. Analysis of Mechanical Properties and Permeability of Trabecular-Like Porous Scaffold by Additive Manufacturing. Front. Bioeng. Biotechnol. 2021, 9, 779854. [Google Scholar] [CrossRef] [PubMed]
Armendáriz-Mireles, E.N.; Raudi-Butrón, F.D.; Olvera-Carreño, M.A.; Rocha-Rangel, E. Design of bio-inspired irregular porous structure applied to intelligent mobility products. Nexo Rev. Cient. 2023, 36, 110–121. [Google Scholar] [CrossRef]
Pawlyn, M. Biomimicry in Architecture; Taylor & Francis: London, United Kingdom, 2019. [Google Scholar]
J. M. Benyus, “Biomimicry: Innovation inspired by nature,” ed: Morrow New York, 1997.
R. J. I. J. o. A. R. i. C. Rao, Structural, Environmental, I. Engineering, and Developing, “Biomimicry in architecture,” vol. 1, no. 3, pp. 101-107, 2014.
J. S. Turner, “On the Mound of Macrotermes michaelseni as an Organ of Respiratory Gas Exchange,” Physiological and Biochemical Zoology, vol. 74, no. 6, pp. 798-822, 2001/11/01 2001.
M. Frenkel, I. Legchenkova, N. Shvalb, S. Shoval, and E. J. S. Bormashenko, “Voronoi Diagrams Generated by the Archimedes Spiral: Fibonacci Numbers, Chirality and Aesthetic Appeal,” vol. 15, no. 3, p. 746, 2023.
Potter, K.; Davidowitz, G.; Woods, H.A. Insect eggs protected from high temperatures by limited homeothermy of plant leaves. J. Exp. Biol. 2009, 212, 3448–3454. [Google Scholar] [CrossRef] [PubMed]
Colmer, T.D. Long-distance transport of gases in plants: a perspective on internal aeration and radial oxygen loss from roots. Plant, Cell Environ. 2003, 26, 17–36. [Google Scholar] [CrossRef]
Burkett, J.R.; Hight, L.M.; Kenny, P.; Wilker, J.J. Oysters Produce an Organic−Inorganic Adhesive for Intertidal Reef Construction. J. Am. Chem. Soc. 2010, 132, 12531–12533. [Google Scholar] [CrossRef] [PubMed]
Slegers, N.; Heilman, M.; Cranford, J.; Lang, A.; Yoder, J.; Habegger, M.L. Beneficial aerodynamic effect of wing scales on the climbing flight of butterflies. Bioinspiration Biomimetics 2017, 12, 016013. [Google Scholar] [CrossRef] [PubMed]
asknature,” Accessed on: Julio 02Available: https://asknature.
Ralevski, “AskNature,” Accessed on: Marzo 25Available: https://asknature.
Miller, “AskNature,” Accessed on: Septiembre 03Available: https://asknature.
Wang, L.; Cheung, J.T.-M.; Pu, F.; Li, D.; Zhang, M.; Fan, Y. Why Do Woodpeckers Resist Head Impact Injury: A Biomechanical Investigation. PLOS ONE 2011, 6, e26490. [Google Scholar] [CrossRef] [PubMed]
Yoon, S.-H.; Park, S. A mechanical analysis of woodpecker drumming and its application to shock-absorbing systems. Bioinspiration Biomimetics 2011, 6, 016003. [Google Scholar] [CrossRef] [PubMed]
E. Banwell, “AskNature,” Accessed on: Julio 23Available: https://asknature.
Carstens, “AskNature,” Accessed on: Noviembre 11Available: https://asknature.
Hofmann, M.; Anderssohn, R.; Bahr, H.-A.; Weiß, H.-J.; Nellesen, J. Why Hexagonal Basalt Columns? Phys. Rev. Lett. 2015, 115, 154301–154301. [Google Scholar] [CrossRef] [PubMed]
Grunenfelder, L.; Suksangpanya, N.; Salinas, C.; Milliron, G.; Yaraghi, N.; Herrera, S.; Evans-Lutterodt, K.; Nutt, S.; Zavattieri, P.; Kisailus, D. Bio-inspired impact-resistant composites. Acta Biomater. 2014, 10, 3997–4008. [Google Scholar] [CrossRef] [PubMed]
Raabe, D.; Sachs, C.; Romano, P. The crustacean exoskeleton as an example of a structurally and mechanically graded biological nanocomposite material. Acta Mater. 2005, 53, 4281–4292. [Google Scholar] [CrossRef]
Andersons, J.; König, M. Dependence of fracture toughness of composite laminates on interface ply orientations and delamination growth direction. Compos. Sci. Technol. 2004, 64, 2139–2152. [Google Scholar] [CrossRef]
Dirks, J.-H.; Taylor, D. Fracture toughness of locust cuticle. J. Exp. Biol. 2012, 215, 1502–1508. [Google Scholar] [CrossRef] [PubMed]
K. K. Smith and W. M. Kier, “Trunks, tongues, and tentacles: moving with skeletons of muscle,” American Scientist, vol. 77, no. 1, pp. 28-35, 1989.
Liang, Y.; McMeeking, R.; Evans, A. A finite element simulation scheme for biological muscular hydrostats. J. Theor. Biol. 2006, 242, 142–150. [Google Scholar] [CrossRef] [PubMed]
Chen, P.-Y.; Stokes, A.; McKittrick, J. Comparison of the structure and mechanical properties of bovine femur bone and antler of the North American elk (Cervus elaphus canadensis). Acta Biomater. 2009, 5, 693–706. [Google Scholar] [CrossRef] [PubMed]
S. Vogel, Comparative biomechanics: life’s physical world. Princeton University Press, 2013.
Kulin, R.M.; Chen, P.-Y.; Jiang, F.; McKittrick, J.; Vecchio, K.S. Dynamic fracture resilience of elk antler: Biomimetic inspiration for improved crashworthiness. JOM 2010, 62, 41–46. [Google Scholar] [CrossRef]
Landete-Castillejos, T.; Currey, J.; Estevez, J.; Gaspar-López, E.; Garcia, A.; Gallego, L. Influence of physiological effort of growth and chemical composition on antler bone mechanical properties. Bone 2007, 41, 794–803. [Google Scholar] [CrossRef] [PubMed]
Yao, H.; Dao, M.; Imholt, T.; Huang, J.; Wheeler, K.; Bonilla, A.; Suresh, S.; Ortiz, C. Protection mechanisms of the iron-plated armor of a deep-sea hydrothermal vent gastropod. Proc. Natl. Acad. Sci. 2010, 107, 987–992. [Google Scholar] [CrossRef] [PubMed]
asknature, “Strong, Durable Composite Technology Inspired by the Mantis Shrimp,” ed: Biomimicry institute, 2020.
asknature,” Available: https://asknature.
Hoang, T.T.; Phan, P.T.; Thai, M.T.; Lovell, N.H.; Do, T.N. Bio-Inspired Conformable and Helical Soft Fabric Gripper with Variable Stiffness and Touch Sensing. Adv. Mater. Technol. 2020, 5. [Google Scholar] [CrossRef]
Efstathiadis, A.; Symeonidou, I.; Tsongas, K.; Tzimtzimis, E.K.; Tzetzis, D. Parametric Design and Mechanical Characterization of 3D-Printed PLA Composite Biomimetic Voronoi Lattices Inspired by the Stereom of Sea Urchins. J. Compos. Sci. 2022, 7, 3. [Google Scholar] [CrossRef]
Ahmed, A.M.R.M.; Mahdi, E.; Oosterhuis, K.; Dean, A.; Cabibihan, J.-J. Mechanical and energy absorption properties of 3D-printed honeycomb structures with Voronoi tessellations. Front. Mech. Eng. 2023, 9, 1204893. [Google Scholar] [CrossRef]
Du, Q.; Faber, V.; Gunzburger, M. Centroidal Voronoi Tessellations: Applications and Algorithms. Siam Rev. 1999, 41, 637–676. [Google Scholar] [CrossRef]
Martínez, J.; Dumas, J.; Lefebvre, S. Procedural voronoi foams for additive manufacturing. ACM Trans. Graph. 2016, 35, 1–12. [Google Scholar] [CrossRef]
Loera, E., Ramírez, O. Ruíz, and A. Ortíz, “Generación de modelos tridimensionales de hueso esponjoso a partir de imágenes de su estructura trabecular,” in B Memorias del XXVI Congreso Internacional Anual de la SOMIM, 2020.
Zhang, C.; Zhao, S.; Zhao, J.; Zhou, X. Three-dimensional Voronoi analysis of realistic grain packing: An XCT assisted set Voronoi tessellation framework. Powder Technol. 2020, 379, 251–264. [Google Scholar] [CrossRef]
Kak, A.C.; Slaney, M.; Wang, G. Principles of Computerized Tomographic Imaging. Am. Assoc. Phys. Med. 2002, 29, 107–107. [Google Scholar] [CrossRef]
Lau, Y.M.; Müller, K.; Azizi, S.; Schubert, M. Voronoï analysis of bubbly flows via ultrafast X-ray tomographic imaging. Exp. Fluids 2016, 57, 1–12. [Google Scholar] [CrossRef]
Tee, Y.L.; Nguyen-Xuan, H.; Tran, P. Flexural properties of porcupine quill-inspired sandwich panels. Bioinspiration Biomimetics 2023, 18, 046003. [Google Scholar] [CrossRef] [PubMed]
Martínez, J.; Hornus, S.; Song, H.; Lefebvre, S. Polyhedral voronoi diagrams for additive manufacturing. ACM Trans. Graph. 2018, 37, 1–15. [Google Scholar] [CrossRef]
Meng, Q.; Yan, L.; Chen, Y.; Zhang, Q. Generation of Numerical Models of Anisotropic Columnar Jointed Rock Mass Using Modified Centroidal Voronoi Diagrams. Symmetry 2018, 10, 618. [Google Scholar] [CrossRef]
Du, Q.; Wong, T.-W. Numerical studies of MacQueen's k-means algorithm for computing the centroidal voronoi tessellations. Comput. Math. Appl. 2002, 44, 511–523. [Google Scholar] [CrossRef]
Tung, C.-C.; Lai, Y.-Y.; Chen, Y.-Z.; Lin, C.-C.; Chen, P.-Y. Optimization of mechanical properties of bio-inspired Voronoi structures by genetic algorithm. J. Mater. Res. Technol. 2023, 26, 3813–3829. [Google Scholar] [CrossRef]
Du, Y.; Pugno, N.; Gong, B.; Wang, D.; Sun, Y.; Ding, Q. Mechanical properties of the hierarchical honeycombs with stochastic Voronoi sub-structures. EPL Europhys. Lett. 2015, 111. [Google Scholar] [CrossRef]
Hooshmand-Ahoor, Z.; Luo, H.; Danas, K. M-Voronoi and other random open and closed-cell elasto-plastic cellular materials: Geometry generation and numerical study at small and large strains. Int. J. Solids Struct. 2024, 290. [Google Scholar] [CrossRef]
Bolshakov, P.; Kharin, N.; Agathonov, A.; Kalinin, E.; Sachenkov, O. Extension of the Voronoi Diagram Algorithm to Orthotropic Space for Material Structural Design. Biomimetics 2024, 9, 185. [Google Scholar] [CrossRef] [PubMed]
Cao, M.; Qiu, T.; Deng, B.; An, Y.; Xing, Y.; Zhao, E. Construction and deformation behavior of metal foam based on a 3D-Voronoi model with real pore structure. Mater. Des. 2024, 238. [Google Scholar] [CrossRef]
Alemayehu, D.B.; Todoh, M.; Huang, S.-J. Advancing 3D Dental Implant Finite Element Analysis: Incorporating Biomimetic Trabecular Bone with Varied Pore Sizes in Voronoi Lattices. J. Funct. Biomater. 2024, 15, 94. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer