Prerpints.org logo
Preprint
Article

CNN-Optimized Electrospun TPE/PVDF Nanofiber Membranes for Enhanced Temperature and Pressure Sensing

Altmetrics

Downloads

97

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.docx (1.44MB )

Submitted:

22 July 2024

Posted:

23 July 2024

You are already at the latest version

Alerts
Abstract
Temperature and pressure sensors currently encounter challenges such as slow response times, large sizes, and insufficient sensitivity. To address these issues, we developed tetraphenylethylene (TPE)-doped polyvinylidene fluoride (PVDF) nanofiber membranes using electrospinning, with process parameters optimized through a convolutional neural network (CNN). We systematically analyzed the effects of PVDF concentration, spinning voltage, tip-to-collector distance, and flow rate on fiber morphology and diameter. The CNN model achieved high predictive accuracy, resulting in uniform and smooth nanofibers under optimal conditions. Incorporating TPE enhanced the hydrophobicity and mechanical properties of the nanofibers. Additionally, the fluorescent properties of the TPE-doped nanofibers remained stable under UV exposure and exhibited significant linear responses to temperature and pressure variations. The nanofibers demonstrated a temperature sensitivity of -0.976 gray value/°C and pressure sensitivity with an increase in fluorescence intensity from 537 a.u. to 649 a.u. under 600 g pressure. These findings highlight the potential of TPE-doped PVDF nanofiber membranes for advanced temperature and pressure sensing applications.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

Temperature and pressure-sensitive materials have become indispensable in various applications such as environmental monitoring, medical diagnostics[1], and industrial process control[2]. These materials play a crucial role in providing accurate real-time environmental data, which is essential for ensuring safety, efficiency, and quality across numerous fields[3]. As the complexity and dynamism of modern technological environments increase, there is a growing demand for high-performance sensors capable of delivering precise measurements quickly and reliably[4].
Polyvinylidene fluoride (PVDF) has been widely used in sensor applications due to its excellent chemical stability, mechanical strength, and piezoelectric properties[5,6]. Its resistance to chemical corrosion and durability in harsh conditions make it a reliable material for sensors operating in extreme environments[7]. Moreover, its mechanical properties allow PVDF-based sensors to maintain performance stability under physical strain and pressure, making them suitable for pressure sensors, mechanical sensors, and accelerometers[8]. For example, research has shown that PVDF nanofibers exhibit outstanding performance in developing flexible pressure sensors and high-sensitivity chemical sensors. On the other hand, tetraphenylethylene (TPE) has attracted significant attention due to its unique aggregation-induced emission (AIE) properties[9]. AIE refers to the phenomenon where certain molecules, non-emissive in solution, become highly luminescent upon aggregation. This property was first introduced by Tang et al[10]. As a classic AIE luminogen, TPE has been extensively studied and applied in various fields due to its remarkable emission efficiency in the aggregated state. Incorporating TPE into PVDF can significantly enhance the sensitivity and selectivity of sensors[11], making them highly responsive to environmental changes. Studies have demonstrated that PVDF nanofibers doped with TPE exhibit enhanced sensitivity and selectivity in temperature and pressure sensing, enabling the provision of accurate real-time data even in complex environments. For instance, Ji et al. utilized glutathione (GSH)-coated copper clusters as precursors to synthesize copper subparticles (Cu-SP), which were then used to construct and modify PVDF-HFP/CeVO4 NP films. Achieved by employing a catalytic hairpin assembly (CHA) strategy was the quantitative detection of miRNA-103a in the range of 100 fM to 100 nM[12]. Similarly, Ma et al. incorporated AIE-active luminogens derived from cyclopentadiene into PVDF polymers, fabricating photoluminescent electrospun nanofibers. Exhibited by these nanofibers were molecular integrity and strong, uniform phosphorescence emission with an average lifetime (τ) of 8.9 microseconds. Paved by this foundation is the way for the digital manufacturing and design of smart textiles[13].
Despite the inherent advantages of PVDF and TPE, traditional temperature and pressure sensors[14] still face significant challenges. These challenges include slow response times, large sizes, and insufficient sensitivity, limiting their effectiveness in applications requiring rapid and precise measurements. Traditional sensors often struggle to operate efficiently in complex and dynamic environments, leading to an urgent need for innovative materials that can overcome these limitations. Additionally, the manufacturing processes of these sensors typically lack the precision required to achieve consistent performance[15].
Electrospinning, as a versatile and cost-effective technique[16], offers the potential to produce nanofibers with controlled diameters[17,18] and uniform morphologies[19,20]. Studies have shown that PVDF-based nanofibers possess excellent mechanical properties and chemical stability[21], making them suitable for various sensing applications[22,23]. PVDF nanofibers have demonstrated superior performance in the development of flexible pressure sensors and high-sensitivity chemical sensors. Bhatta et al. utilized two-dimensional siloxane-polyvinylidene fluoride (S-PVDF) composite nanofiber membranes to develop a high-performance triboelectric nanogenerator (TENG) by optimizing the composition and employing electrospinning techniques. The fabricated membrane exhibited significant improvements in dielectric properties, electronegativity, and compressibility[24]. Furthermore, Xiong et al. successfully fabricated high-performance composite nanofiber membranes composed of PVDF and dopamine (DA) using electrospinning technology. These membranes feature a coherent and uniformly dispersed two-dimensional network topology, and their potential application as flexible wearable sensors for monitoring human motion and subtle physiological signals has been validated [25]. However, optimizing the electrospinning process parameters[26], such as polymer concentration, spinning voltage, tip-to-collector distance, and flow rate, remains complex.
Optimizing the electrospinning process to produce high-quality nanofiber membranes involves multiple challenges. Parameters like PVDF concentration, spinning voltage[27], tip-to-collector distance[28], and flow rate[29] significantly affect fiber morphology and diameter. The complex interactions between these parameters make single-variable optimization insufficient[30,31]. Traditional trial-and-error methods are time-consuming and inefficient, failing to capture the intricate relationships between parameters[32]. These methods typically require extensive experimentation and human resources[33], and the results lack universality[34]. Current models face limitations in accurately predicting fiber diameter and optimizing process parameters[35], failing to reflect the nonlinear effects of various parameters during electrospinning[36], leading to inconsistent fiber quality. For example, although various mathematical models have been used to predict fiber diameter[37,38,39], they often overlook the complex interactions between parameters, resulting in inadequate predictive accuracy[40]. Existing optimization methods usually rely on a large amount of experimental data, which is not only time-consuming but also costly[41].
To address these challenges, this study aims to fabricate high-performance PVDF nanofiber membranes doped with TPE using the electrospinning method. By leveraging the capabilities of convolutional neural networks (CNNs)[42], we aim to create a highly accurate predictive model to optimize electrospinning parameters[43], achieving uniform and high-quality nanofibers[44]. The study will systematically investigate the effects of PVDF concentration, spinning voltage, tip-to-collector distance, and flow rate on fiber morphology and performance[45]. Additionally, we will explore how TPE doping enhances the hydrophobicity, mechanical properties, and fluorescent characteristics of the nanofibers. The ultimate goal is to develop advanced temperature and pressure sensors with higher sensitivity, faster response times, and greater reliability, suitable for various applications. By optimizing these key parameters[46], we hope to improve the manufacturing efficiency and performance consistency of nanofibers, providing new insights and methods for the development of sensor technology[47].

2. Experimental Section

2.1. Materials and Reagents

PVDF was obtained from Jiangsu DeBao Sheng Nylon Co., Ltd. N, N-Dimethylformamide (DMF) was supplied by Tianjin Kermel Chemical Reagent Co., Ltd. TPE was purchased from Shanghai McLean Biochemical Technology Co., Ltd. All reagents were used as received without further purification.

2.2. Fabrication of PVDF Electrospinning Solutions and TPE-Doped PVDF Electrospinning Solutions

PVDF solutions with different mass fractions were prepared by dissolving PVDF powder in DMF. The PVDF concentrations were 15.5 wt%, 16.5 wt%, 17.5 wt%, 18.5 wt%, 19.5 wt%, and 20.5 wt%. The solutions were stirred at 80°C for 8 hours to ensure complete dissolution.
PVDF mass fraction of 17.5 wt% was selected. Using an electronic analytical balance, TPE solid powders were accurately weighed in glass bottles with stoppers, with weights of 0.0051 g, 0.0076 g, 0.0101 g, 0.0126 g, 0.0151 g, 0.0202 g, 0.0303 g, 0.0404 g, and 0.0505 g, respectively. A pipette was then used to add 5 mL of DMF to each glass bottle, preparing TPE spinning solutions with mass fractions of 0.5%, 0.75%, 1%, 1.25%, 1.5%, 2%, 3%, 4%, and 5% (referring to the mass fraction of TPE in the 17.5% PVDF spinning solution). The prepared solutions were placed in an ultrasonic cleaner for 0.5 hours to ensure complete dissolution of TPE in the solvent. Using an electronic balance, 1.0023 g of PVDF solid powder was slowly added to the TPE-containing solutions. A magnetic stirrer bar was placed in each solution, and the solutions were heated at 80°C with a stirring speed of 300 rpm for 8 hours using an intelligent magnetic stirrer. After heating, the solutions were allowed to cool to room temperature and set aside for further use.

2.3. Fabrication of PVDF and TPE-Doped PVDF Nanofiber Membranes

The prepared PVDF electrospinning solution was transferred into a 10 mL syringe, which was connected to a 22-gauge spinning needle through a spinning connector. The syringe was fixed on a syringe pump, and the needle was connected to a high-voltage power supply. The height of the needle was set to be equal to and parallel with the collector. Under the influence of the electrostatic field, the spinning solution was ejected to form nanofibers, which were collected on the receiver after a certain period. The environmental parameters during electrospinning were primarily temperature and humidity, set at 25 ± 5°C and 25% relative humidity, respectively. By adjusting the electrospinning parameters, nanofiber membranes under various conditions can be obtained. The nanofiber membranes were then placed in a drying oven to be dried and stored for future use.

2.4. Characterization

The morphology of the electrospun PVDF nanofibers was characterized using a scanning electron microscope (SEM, Geminutesi SEM500, Germany). The samples were coated with a thin layer of gold before imaging. The fiber diameters were measured using Nano Measure software, and the average diameter was calculated based on the measurements of 100 fibers for each sample.
The viscosity of PVDF spinning solutions with mass fractions of 15.5 wt%, 16.5 wt%, 17.5 wt%, 18.5 wt%, 19.5 wt%, and 20.5 wt% was measured using an NDJ-79 rotational viscometer (Shanghai Changji Geological Instrument Co., Ltd.). After the viscometer stabilized, data were recorded. Each measurement was repeated three times, and the average value was taken. The volume of the spinning solution was 20 mL, and the measurements were performed at room temperature (approximately 20°C) and 15% humidity with a rotation speed of 750 r/min.
The surface tension of the spinning solutions with mass fractions of 15.5 wt%, 16.5 wt%, 17.5 wt%, 18.5 wt%, 19.5 wt%, and 20.5 wt% was measured using a DCAT21 tensiometer. The instrument was calibrated before measuring the surface tension of the spinning solutions. Each measurement was repeated three times, and the average value was taken. The measurements were conducted at a temperature of 20°C and 15% humidity.
The conductivity of the spinning solutions with mass fractions of 15.5 wt%, 16.5 wt%, 17.5 wt%, 18.5 wt%, 19.5 wt%, and 20.5 wt% was measured using a DDS-307A conductivity meter (Shanghai Jiesheng Scientific Instrument Co., Ltd.). Each solution was measured three times, and the average value was taken. The operating conditions were a temperature of 20°C and 15% humidity.
The contact angle of the dried nanofiber membranes was measured using a JC2000DM contact angle measuring instrument. The nanofiber membranes were cut into 50 mm × 20 mm rectangles and attached flatly to glass slides with double-sided tape. The measurements were performed at room temperature (20°C) and 15% humidity, and each sample was measured three times with the average value taken.
The mechanical properties of the PVDF membranes and PVDF membranes containing 1 wt% TPE were analyzed. The membranes were cut into 10 mm × 50 mm rectangles and placed in the jaws of a universal testing machine. The tensile speed was set to 100 mm/min. Each sample was tested three times, and the average value was used to plot the results.
The morphology and structure of the nanofiber membranes were further analyzed using SEM. The dried nanofiber membranes were cut into 10 mm × 10 mm squares, fixed on specimen stubs with conductive tape, and sputter-coated with gold for 2 minutes before imaging.
Fluorescence spectroscopy of the fluorescent nanofiber membranes was performed using a Shimadzu RF6000 fluorescence spectrophotometer. The excitation slit width was set to 5.0 nm, the emission slit width to 3.0 nm, the scan speed to 2000 nm/min, and the sensitivity to High.
Tensile strength is a critical indicator of membrane performance. Uniaxial tensile tests were conducted using an LLY-06E electronic single-fiber testing machine with a loading speed of 5 mm/min. The tensile strength (δ) is defined as the tensile force (F) divided by the cross-sectional area (S) of the test sample, as shown in Equation 1.
δ = F S

2.5. Training of Neural Network for Fiber Diameter Prediction

To predict the diameter of the PVDF nanofibers based on the electrospinning parameters, a conventional neural network (CNN) was developed and trained. The network was trained using the experimental data, which included the PVDF concentration, applied voltage, tip-to-collector distance, and flow rate as input features, and the measured fiber diameters as the output. The PVDF solution concentration ranged from 15.5 wt% to 20.5 wt%, the applied voltage ranged from 9 kV to 15 kV, the tip-to-collector distance ranged from 11 cm to 16 cm, and the flow rate ranged from 0.1 mL/h to 0.5 mL/h. The CNN architecture consisted of 16 convolutional layers and 2 pooling layers. The activation function used was ReLU, and the learning rate was set to 0.01. The training process involved 80 iterations. The performance of model was evaluated using the coefficient of determination (R2) and mean absolute error (MAE).
The PAN spinning process parameters and corresponding nanofiber diameters contained in each data group are shown in Table S2 in the Supporting Information. The PAN spinning parameters involved, including PAN spinning solution concentration, spinning voltage, receiving distance, injection rate, and the resulting PAN nanofiber diameter, have different units, which may affect the prediction results of the CNN model and lead to significant errors. Thus, data normalization preprocessing is necessary. In this study, we employed the logarithmic function normalization method to preprocess the data, enabling all data to have the same impact scale on the model.
In artificial neural networks, all input data is usually divided into three parts: training set, validation set, and test set. The training set is used to train the network model, the validation set is used to check the effectiveness of the network model, and the test set is used to test the final performance of the network model. The partitioning of the dataset plays an essential role in model establishment. When the dataset is improperly partitioned, the model may experience overfitting, where the training data fits the model well, but the test results are not satisfactory. Therefore, it is necessary to partition the dataset reasonably. As the test set does not affect the construction of the network model, after removing unsuitable data groups, the data was divided into three groups using the hold-out method. The 137 sample data sets were randomly divided into three groups with a test set ratio of 0, a training set ratio of 0.8, and a validation set ratio of 0.2.
The network model evaluation indicators include R2 and MAE. R2 ranges from 0 to 1, and the closer R2 is to 1, the better the model's predictive performance. MAE is used to measure the distance between the predicted values and the actual values, and the smaller the value, the better the model's predictive performance. The mathematical expressions are as follows:
R 2 = 1 − ∑ i = 1 n y i − y ^ i 2 ∑ i = 1 n y i − y i ¯ 2
R M S E = 1 n ∑ i = 1 n y i − y i ^ 2
The mathematical expression for the error σ is:
σ = ∆ y i × 100 %
∆ = y ^ i − y i
where y i is the actual value of the sample, y ^ i is the predicted value of the model, y ¯ i is the average value of the actual values of the samples, and n represents the number of input samples.

2.6. Gray Value Method for Thermal Sensitivity Measurement

Photographs taken were input into a pre-written Python program, which processes them through cropping, color-to-gray conversion, and gray value reading, ultimately obtaining the gray value of each image to represent the corresponding fluorescence intensity. The experimental steps are as follows: Fluorescent nanofiber membranes were cut into 2 cm × 2 cm squares and placed on an intelligent temperature-controlled heater. Under a 365 nm UV lamp, photographs of the samples were taken with a mobile phone. The photos were first cropped, then converted to grayscale, and the gray value was read to represent the fluorescence intensity for testing thermal sensitivity. First, the samples were photographed at room temperature, then gradually heated to 100°C using the TM-926U intelligent temperature-controlled heater and photographed. After the temperature dropped back to room temperature, another photograph was taken. This cycle was repeated 12 times.

3. Result and Discussion

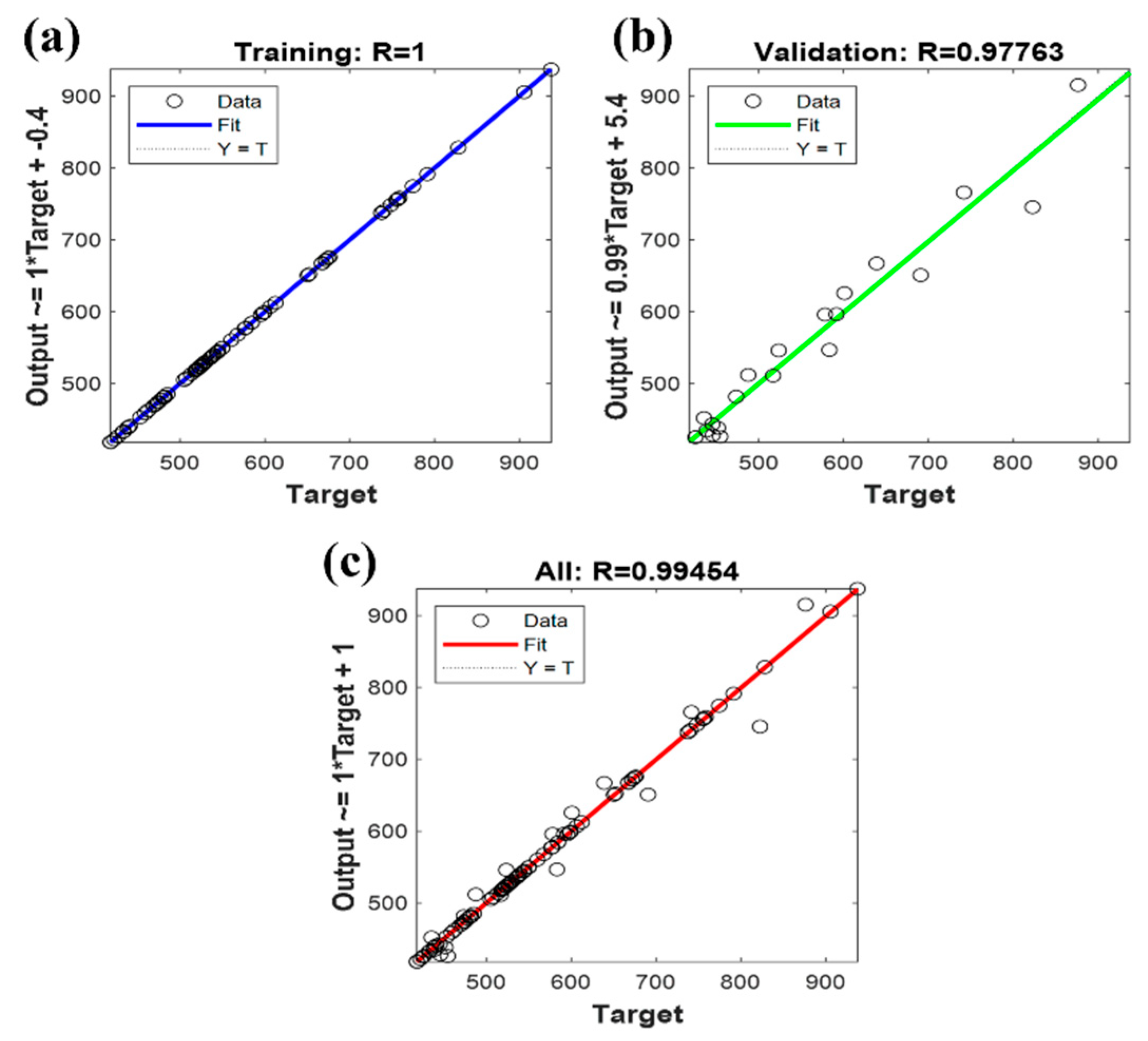
3.1. Comparison of Different Neural Network Prediction Results

From Figure 1, Figures S2 and S3, it is evident that among the five different artificial neural networks evaluated, the Genetic Algorithm-Extreme Learning Machine (GA-ELM) Neural Network demonstrates the closest fit between actual and predicted values, indicating superior predictive performance. The CNN shows solid predictive performance with an R2 value of 0.9776 and an RMSE of 45.4107, though its accuracy is not the highest among the networks tested. The Particle Swarm Optimization BP Neural Network (PSO-BPNN) improves upon the basic CNN, achieving an R2 of 0.9751 and a significantly lower RMSE of 17.3598, suggesting that PSO enhances the weight optimization process, reducing prediction errors. The Radial Basis Function Neural Network (RBFNN) exhibits strong performance with an R2 of 0.9757 and an RMSE of 15.9746, indicating its effectiveness in handling nonlinear relationships. The Extreme Learning Machine (ELM) network, known for its fast-training speed, achieves an R2 of 0.9886 and an RMSE of 31.3541, showing higher accuracy in capturing data variance but still having room for error minimization. The GA-ELM network outperforms all other models with an impressive R2 of 0.9959 and an RMSE of 7.446, showcasing its precision in predicting nanofiber diameters. The genetic algorithm's optimization of the ELM significantly enhances its predictive capability, explaining 99.59% of the variance and minimizing prediction errors. The R2 values of all models being above 0.97 indicate their effectiveness in capturing the relationship between electrospinning parameters and nanofiber diameters, while the RMSE values under 46 highlight their predictive accuracy. The GA-ELM's superior performance, with the highest R2 and lowest RMSE, makes it the most reliable predictor among those tested. This analysis underscores the GA-ELM's robustness and precision, making it an excellent tool for accurate nanofiber diameter predictions based on electrospinning parameters.

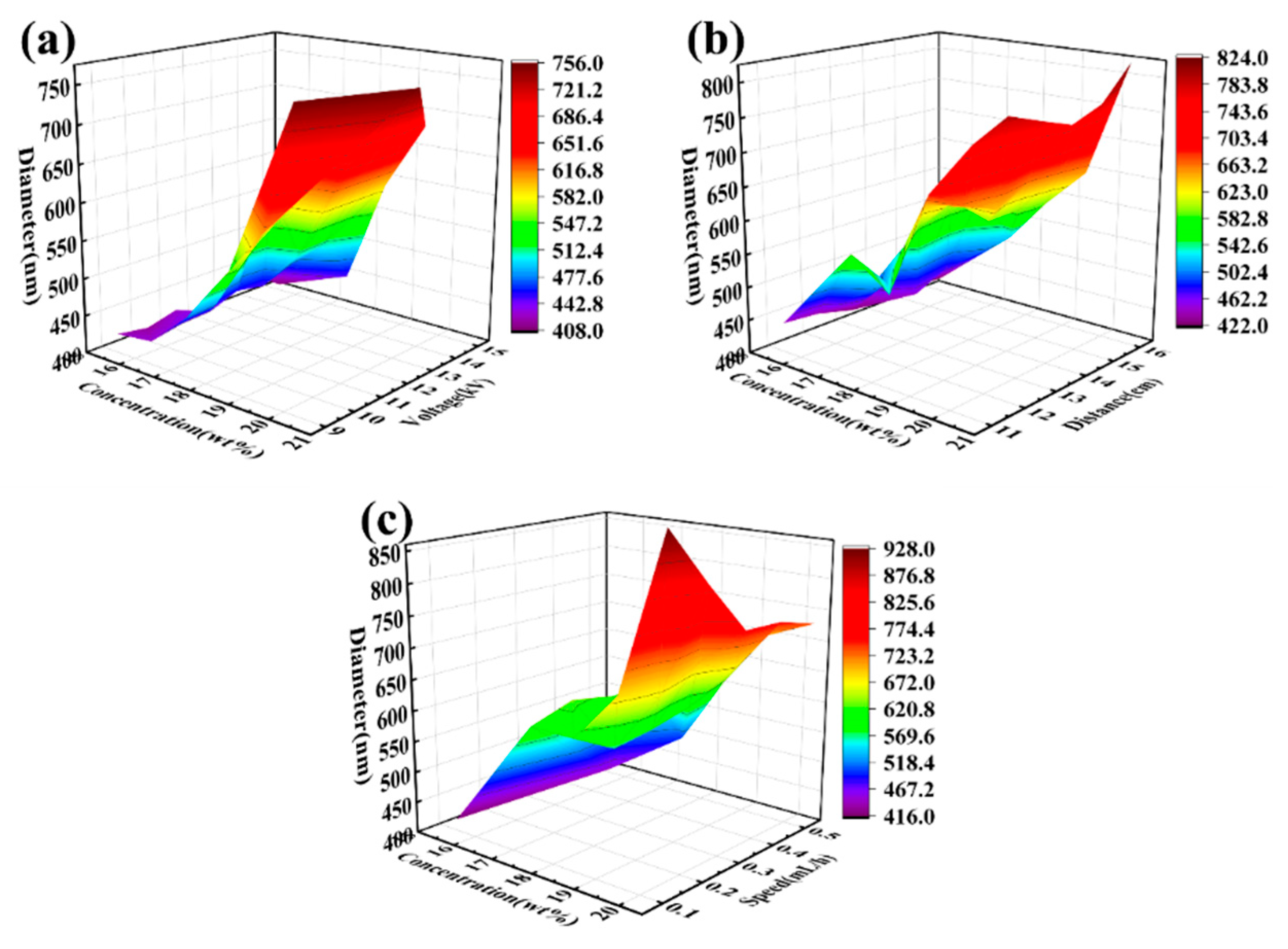
3.2. Interactions among Electrospinning Process Parameters

The primary parameters influencing fiber diameter during the electrospinning process are concentration, flow rate, voltage, and tip-to-collector distance. The effects of these factors on fiber diameter are not simply linear, necessitating an exploration of how each parameter influences the diameter. Trends in fiber diameter as influenced by concentration in conjunction with the other three parameters are discussed below. The combined effects of concentration and voltage on fiber diameter were studied with a fixed tip-to-collector distance of 13 cm and a flow rate of 0.2 mL/h. The PVDF spinning solution concentration ranged from 15.5 wt% to 20.5 wt%, with a step size of 1 wt%, and the voltage ranged from 9 kV to 15 kV, with a step size of 1 kV. As shown in Figure 2(a), results indicate that as the concentration increases, the fiber diameter also increases, regardless of whether the spinning voltage is high or low. This suggests that higher solution concentrations result in thicker fibers under a constant voltage.
The interaction between concentration and tip-to-collector distance was analyzed with a fixed spinning voltage of 13 kV and a flow rate of 0.2 mL/h. The spinning solution concentration ranged from 15.5 wt% to 20.5 wt%, with a step size of 1 wt%, and the distance varied from 11 cm to 16 cm, with a step size of 1 cm. The data, presented in Figure 2(b), show that the fiber diameter increases with increasing concentration when the distance remains constant. However, when the concentration is fixed, the fiber diameter first increases, then decreases, and increases again as the distance increases. This suggests a complex interaction between concentration and tip-to-collector distance, with the overall trend showing an increase in fiber diameter under these combined effects.
The effects of concentration and flow rate on fiber diameter were also examined with a fixed spinning voltage of 13 kV and a tip-to-collector distance of 13 cm. The concentration of the spinning solution ranged from 15.5 wt% to 20.5 wt%, with a step size of 1 wt%, and the flow rate ranged from 0.1 mL/h to 0.5 mL/h, with a step size of 0.1 mL/h. As shown in Figure 2(c), it was observed that at lower concentrations, the fiber diameter increases with increasing flow rate. At higher concentrations, the fiber diameter first increases and then decreases with increasing flow rate. When the concentration is constant, the fiber diameter increases with increasing flow rate. This trend indicates that both concentration and flow rate significantly influence fiber diameter, with a notable interaction between the two parameters.
These analyses highlight the importance of understanding the interactions among electrospinning process parameters to optimize fiber diameter for specific applications. By exploring the combined effects of concentration with voltage, tip-to-collector distance, and flow rate, it becomes possible to fine-tune the electrospinning process to achieve desired fiber characteristics.

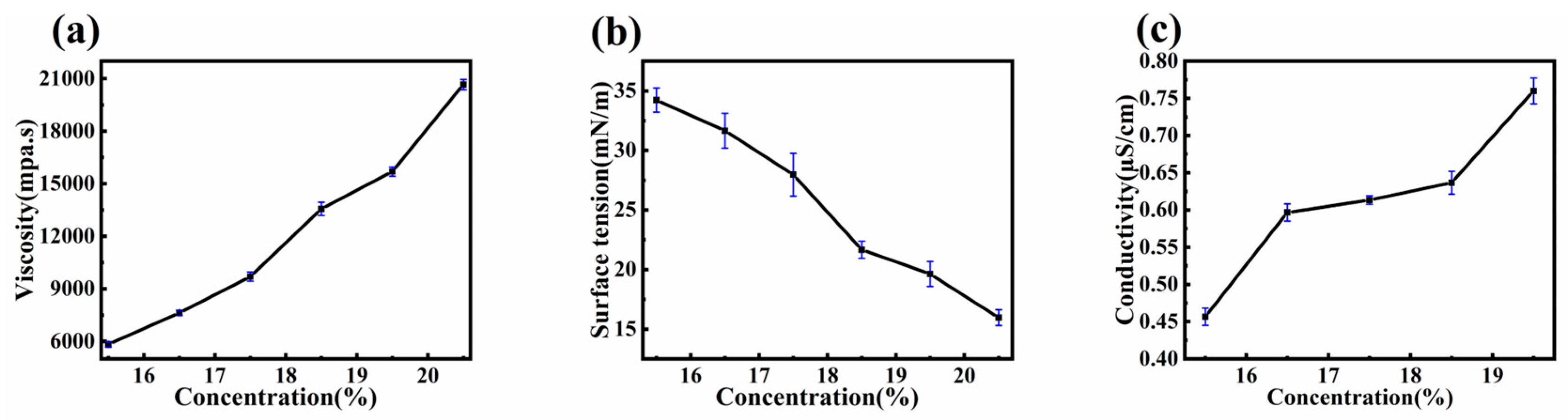
3.3. Effect of PVDF Concentration on Viscosity, Surface Tension, and Conductivity of Spinning Solutions

The primary parameters influencing fiber diameter during the electrospinning process include the viscosity, surface tension, and conductivity of the spinning solution. These properties are significantly affected by the concentration of PVDF in the solution.
Viscosity is a crucial factor in the electrospinning process, as both excessively high and low viscosities can hinder the formation of nanofibers. Generally, the viscosity of a solution is positively correlated with its concentration. As shown in Figure 3(a), the viscosities of PVDF spinning solutions at concentrations of 15.5 wt%, 16.5 wt%, 17.5 wt%, 18.5 wt%, 19.5 wt%, and 20.5 wt% are 5700 mPa•s, 7500 mPa•s, 9600 mPa•s, 13400 mPa•s, 15600 mPa•s, and 20500 mPa•s, respectively. The viscosity of the PVDF spinning solution increases with concentration, more than tripling as the mass fraction increases from 15.5 wt% to 20.5 wt%. This increase is mainly due to the higher probability of polymer chain entanglement in the solution as the polymer concentration increases, forming a network structure that increases flow resistance and thus the viscosity of the PVDF solution.
During the spinning process, the spinning solution pushed out from the syringe initially forms a droplet at the needle tip, known as the Taylor cone. The formation of the Taylor cone is directly related to the surface tension of the solution. When the electrostatic force is less than the surface tension of the droplet, the solution cannot be stretched to form fibers. Conversely, when the electric field strength exceeds the surface tension of the droplet, fibers can form and be collected under the electric field force. Therefore, the surface tension of the solution is critical for the formation and preparation of nanofibers. As shown in Figure 3(b), as the spinning solution concentration increases from 15.5 wt% to 20.5 wt%, the surface tension decreases from 33.5 mN/m, 30.2 mN/m, 26.6 mN/m, 21.3 mN/m, 19.3 mN/m to 15.4 mN/m.
The conductivity of the spinning solution also affects the formation of multiple jets at the needle tip under a high-voltage electric field, influencing the shape of the Taylor cone. As shown in Figure 3(c), the conductivity of PVDF solutions increases with increasing concentrations. When the spinning solution concentration increases from 15.5 wt% to 20.5 wt%, the conductivity increases from 0.43 µS/cm, 0.46 µS/cm, 0.48 µS/cm, 0.54 µS/cm, 0.55 µS/cm to 0.58 µS/cm.

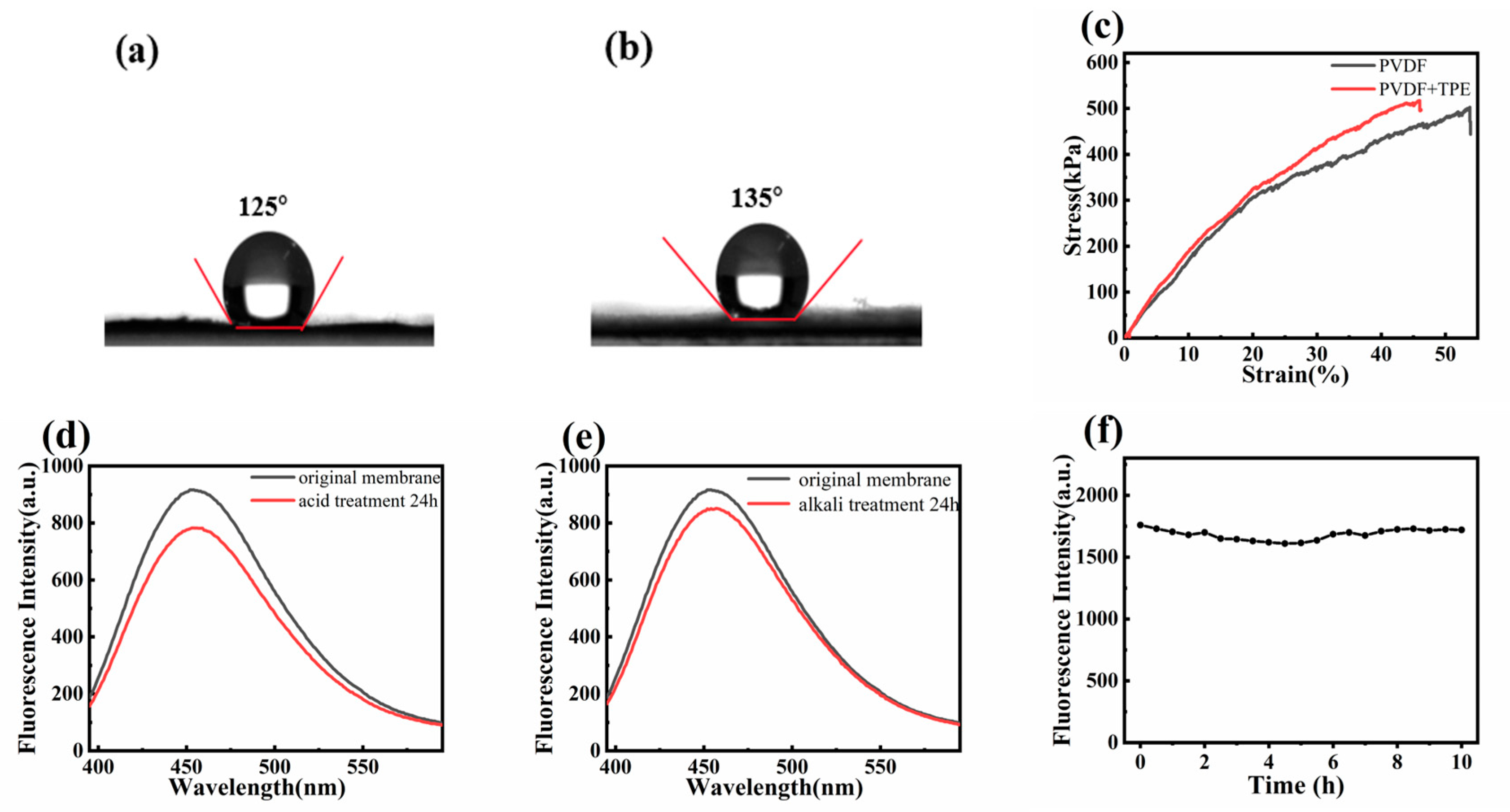
3.4. Surface and Stability Properties of Nanofiber Membranes

PVDF is a hydrophobic polymer due to its fluorine groups (-F), while TPE is also hydrophobic as it does not dissolve in water. Figure 4(a) and (b) show the contact angles of pure PVDF nanofiber membranes and TPE-doped PVDF nanofiber membranes. The contact angle increases from 125° to 135° upon doping with TPE, indicating enhanced hydrophobicity. Figure 4(c) presents the tensile stress-strain curves of pure PVDF membranes and PVDF membranes containing 1 wt% TPE. The pure PVDF membrane exhibits a higher strain of approximately 53.6% but a lower stress of 500 kPa. Upon doping with 1 wt% TPE, the tensile strain decreases to about 45.8%, but the stress increases to 516.5 kPa. Doping PVDF with TPE enhances the mechanical performance of the fiber membranes by increasing their load-bearing capacity. The TPE occupies space within the nanofibers, surrounding and constraining the PVDF, which limits stretching and deformation, resulting in reduced strain but increased stress.
The chemical stability of fluorescent nanofiber membranes was evaluated by immersing them in strong acidic and alkaline solutions. Figure 4(d) and (e) show the fluorescence changes after 24 hours of immersion. In Figure 4(d), the fluorescence intensity of the nanofiber membrane decreases from 917 a.u. to 783 a.u. after immersion in a pH=1 hydrochloric acid solution, representing a reduction of approximately 14%. In Figure 4(e), the fluorescence intensity decreases from 917 a.u. to 852 a.u. after immersion in a pH=12 alkaline solution, representing a reduction of approximately 7%. These results indicate that TPE-doped fluorescent nanofiber membranes exhibit good resistance to strong acids and bases. The UV stability of fluorescent nanofiber membranes was tested by continuous exposure to a UV lamp with a wavelength of 365 nm for 10 hours. The fluorescence intensity at 460 nm was measured every 0.5 hours. As shown in Figure 4(f), the fluorescence intensity slightly decreases after 2 hours of UV exposure but then increases after 2.5 hours. Overall, the fluorescence intensity remains relatively stable over the extended UV exposure period, indicating that the prepared nanofiber membranes maintain their fluorescence properties even after prolonged UV exposure.

3.5. Morphological Analysis of Fluorescent Nanofiber Membranes

PVDF is a hydrophobic polymer due to its fluorine groups (-F), while TPE is also hydrophobic as it does not dissolve in water. The morphology of the fluorescent nanofibers is significantly affected by the spinning voltage. The spinning parameters for 1 wt% TPE spinning solutions at different voltages are listed in Table S3 in the Supporting Information. The tip-to-collector distance was fixed at 13 cm, the flow rate at 0.2 mL/h, and the voltage varied from 9 kV to 13 kV. The PVDF concentration was 17.5 wt%, and the TPE content was 1%. As shown in Figure 5, the nanofibers exhibit uneven distribution and relatively large diameters at 9 kV and 10 kV. This is due to insufficient solvent evaporation in the jet, causing some fibers to stick together. At 11 kV, the solvent evaporates completely, resulting in smooth and uniformly distributed nanofibers, making it the optimal spinning voltage. When the voltage increases to 12 kV and 13 kV, the fiber diameters become uneven, and the morphology deteriorates. This is because higher voltages cause rapid jet ejection and quick solvent evaporation, leading to flattened fibers. Therefore, 11 kV is the most suitable spinning voltage.
The spinning parameters for 1 wt% TPE spinning solutions at different tip-to-collector distances are listed in Table S4 in the Supporting Information. The voltage was set at 11 kV, the flow rate at 0.2 mL/h, and the distance varied from 11 cm to 15 cm. The PVDF concentration was 17.5 wt%. As shown in Figure 6, at distances of 11 cm and 12 cm, the solvent in the jet does not completely evaporate, causing fiber adhesion and a flattened morphology. The fibers are also relatively thick and poorly formed. At a distance of 13 cm, the solvent evaporates fully, resulting in well-formed, smooth, and uniformly distributed fibers. At distances of 14 cm and 15 cm, the reduced electric field strength due to increased distance leads to poorer fiber uniformity. Therefore, 13 cm is the optimal tip-to-collector distance.
The spinning parameters for 1 wt% TPE spinning solutions at different flow rates are listed in Table S5 in the Supporting Information. The voltage was set at 11 kV, the tip-to-collector distance at 13 cm, and the flow rate varied from 0.1 mL/h to 0.5 mL/h. The PVDF concentration was 17.5 wt%. As shown in Figure 7, at a flow rate of 0.1 mL/h, the nanofibers are thin, unevenly distributed, and have a flattened morphology. At a flow rate of 0.2 mL/h, the jet is stable, resulting in uniformly distributed, well-formed nanofibers without adhesion. As the flow rate increases to 0.3 mL/h, 0.4 mL/h, and 0.5 mL/h, the fibers become unevenly distributed with some adhesion. This is due to the increased volume of spinning solution per unit time, which prevents timely solvent evaporation, leading to fiber adhesion. Therefore, a flow rate of 0.2 mL/h is optimal for producing uniformly distributed fibers.

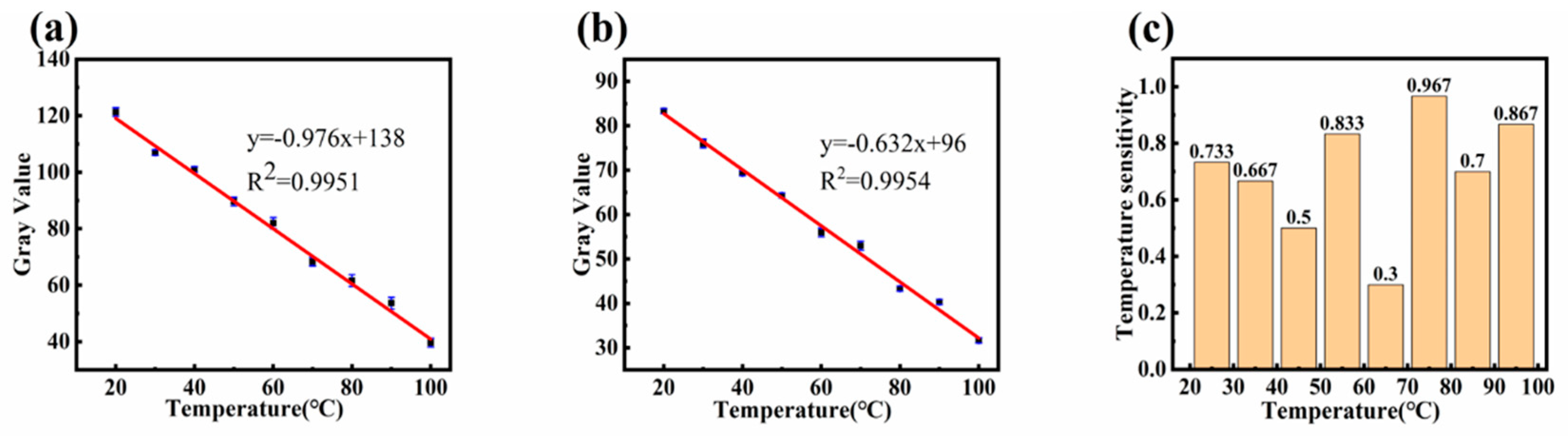
3.6. Thermal Sensitivity Analysis of Fluorescent Nanofiber Membranes

Fluorescent nanofiber membranes with TPE contents of 0.5%, 0.75%, 1%, 1.25%, and 1.5% were cut into suitable shapes and adhered flatly to lead blocks. The lead blocks were placed on a TM-926U intelligent temperature-controlled heater, and the temperature was gradually increased from 20°C to 100°C. At each temperature point, after the temperature stabilized, photographs were taken under a UV lamp. As shown in Figure 8, from top to bottom, the TPE concentrations are 0.5%, 0.75%, 1%, 1.25%, and 1.5%. From left to right, the fluorescence photographs at different temperatures from 20°C to 100°C are displayed. As the temperature increases, the brightness of the fluorescence decreases, with the 1 wt% TPE fluorescent nanofiber membrane showing the most significant change in brightness. Therefore, the 1 wt% TPE fluorescent nanofiber membrane was selected for thermal sensitivity studies.
A fluorescence spectrophotometer was used to test the emission spectra of 1 wt% TPE fluorescent nanofiber membranes as the temperature increased. Figure 9(a) show that as the temperature increases, the fluorescence intensity of the nanofibers decreases due to increased vibration and rotation of TPE fluorescence molecules. The fluorescence intensity at 460 nm was plotted against temperature, and Figure 9(b) show that the fluorescence intensity decreases linearly with increasing temperature, with a fitting coefficient R2=0.9958, indicating a strong linear correlation between fluorescence intensity and temperature. The fluorescent nanofibers were first heated to 100°C, then the heating was turned off, and the fluorescence intensity was measured at different time points. Figure 9(d) show that after 80 minutes of cooling, the fluorescence intensity no longer changes and recovers to 95% of its original.
Figure S8 show that the gray value of the sample before heating was 120, and it decreased to 38 when heated to 100°C. After cooling back to room temperature, the gray value was 100. The second heating to 100°C reduced the gray value to 37, and cooling to room temperature resulted in a gray value of 89. After five heating-cooling cycles, the fluorescent nanofiber membrane's properties stabilized, and the gray value no longer changed. Figure S9 also show that initially, at room temperature, the fluorescence intensity is high, the fluorescence photo is light blue with high brightness, and the converted grayscale photo is lighter. When first heated to 100°C, the fluorescence intensity decreases, the fluorescence photo becomes dark blue with low brightness, and the converted grayscale photo darkens. After cooling to room temperature, the fluorescence intensity decreases, and the colors of both the fluorescence and grayscale photos deepen compared to before heating. With more heating-cooling cycles, the color of the photos at room temperature and 100°C gradually deepens until, after the fifth cycle, the color no longer changes.
Using nanofiber samples that had not been heat-treated and those that had undergone five heating-cooling cycles, the temperature was gradually increased from 20°C to 100°C, and photographs were taken and converted to grayscale every 10°C. Figure 10(a) show the temperature fitting curve for untreated samples as the temperature changes from 20°C to 100°C, and Figure 10(b) show the fitting curve for samples after five heating cycles. Before heating, the fitting coefficient R2 = 0.9951, and the sensitivity is -0.976 gray value/°C. After five heating cycles, the fitting coefficient R2=0.9954, and the sensitivity is -0.632 gray value/°C. This indicates that both untreated and heat-treated samples have a strong linear correlation between gray value and temperature, with reduced sensitivity after heating.
Table 1 compares the temperature sensitivity of the sensor developed in this work with other sensors. As shown in Figure 10(c), the sensitivity is lowest in the 60-70°C range at -0.3 gray value/°C. The highest sensitivity is in the 70-80°C range at -0.967 gray value/°C, while the sensitivity in other temperature ranges is approximately -0.756 gray value/°C. Table 1 demonstrates that the temperature sensitivity of the sensor developed in this work is higher than that of the listed sensors. Additionally, the sensor is smaller in size and covers a temperature range of 20-100°C, making it more suitable for conventional temperature detection.

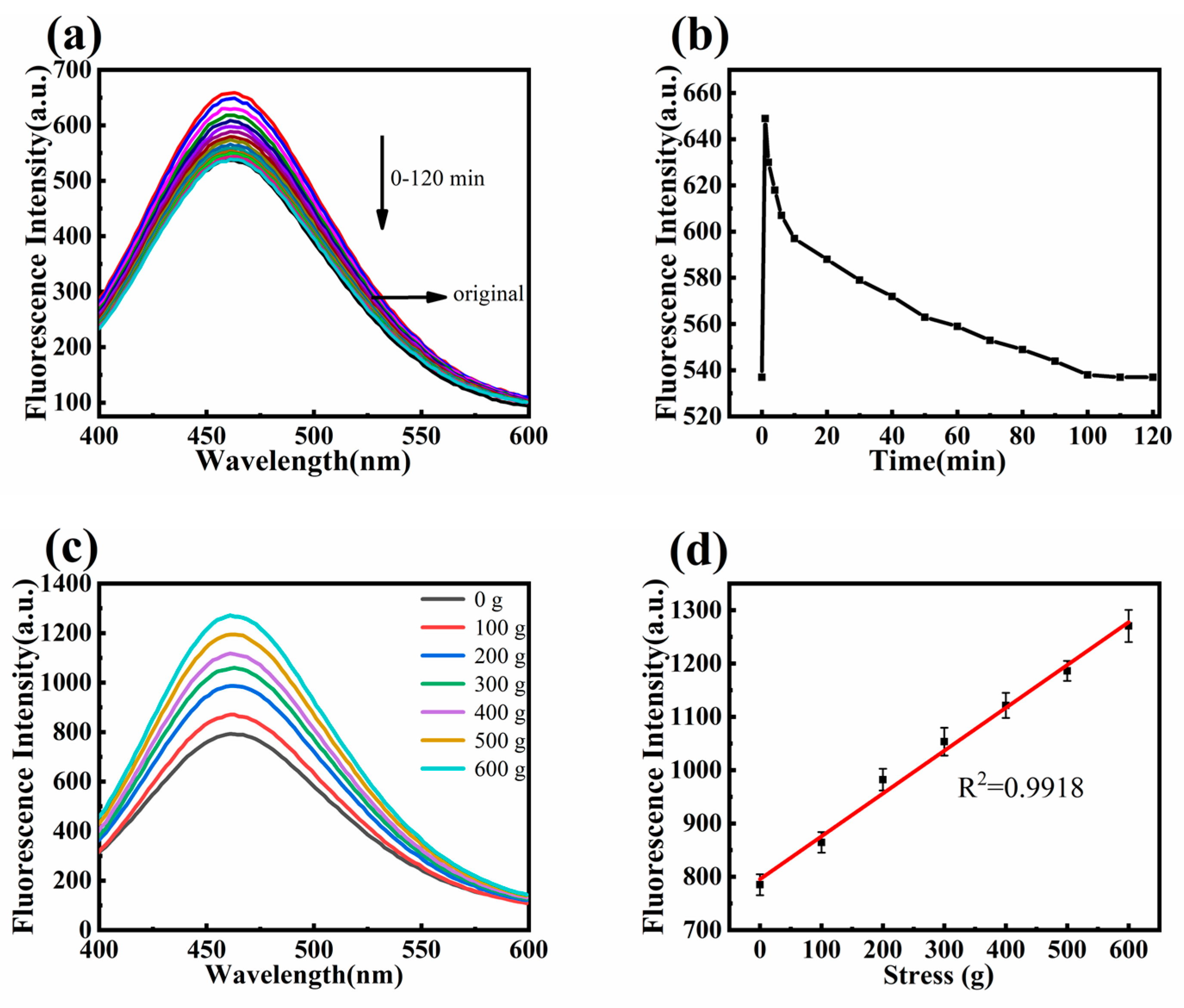
3.7. Pressure Sensitivity Analysis of Fluorescent Nanofiber Membranes

The emission spectra of the original fluorescent nanofiber membranes were measured using a fluorescence spectrophotometer. Then, a 600 g weight was applied for 2 minutes, and the fluorescence intensity was measured at different time intervals. Figure 11(a) show the emission spectra of the fluorescent nanofiber membrane after the removal of 600 g pressure at different times. Figure 11 (b) show the fluorescence intensity at 460 nm over time. Before pressure was applied, the fluorescence intensity was 537 a.u. After applying pressure, the fluorescence intensity increased to 649 a.u. due to restricted intramolecular rotation of TPE, causing most energy to be released as radiation. When the pressure was removed, the restriction on TPE molecular rotation decreased, the intramolecular kinetic energy increased, and the fluorescence intensity decreased. After 100 minutes, the fluorescence intensity no longer changed and recovered to 95% of the initial state.
Fluorescent nanofiber membranes with 1 wt% TPE were cut into rectangular shapes and subjected to pressures of 100 g, 200 g, 300 g, 400 g, 500 g, and 600 g for 2 minutes each. The emission spectra were measured using a fluorescence spectrophotometer, and the fluorescence intensity at 460 nm was plotted against pressure. Figure 11(c) and (d) show that as the pressure increases, the rotation of the TPE molecules in the nanofiber membrane is restricted, causing the energy to be released as radiation, increasing the fluorescence intensity. The fitting coefficient R2 = 0.9958, indicating a good linear correlation between fluorescence intensity and pressure.

4. Conclusion

In this study, we successfully prepared PVDF and TPE-doped PVDF nanofibers using the electrospinning technique and systematically investigated the effects of various parameters on fiber diameter. The GA-ELM neural network exhibited the highest prediction accuracy with an R2 value of 0.9959 and an RMSE of 7.446. Optimal conditions for uniform nanofibers were 17.5 wt% PVDF concentration, 11 kV voltage, 13 cm tip-to-collector distance, and 0.2 mL/h flow rate. TPE doping enhanced hydrophobicity, increasing the contact angle from 125° to 135°, and improved mechanical properties, increasing stress from 500 kPa to 516.5 kPa and reducing strain from 53.6% to 45.8%. The nanofibers exhibited stable fluorescence under UV light, with thermal sensitivity of -0.976 gray value/°C before heating and -0.632 gray value/°C after five cycles. Pressure sensitivity analysis showed a good linear correlation (R2 = 0.9958) between fluorescence intensity and pressure. These results highlight the significant potential of TPE-doped PVDF nanofibers in temperature and pressure sensing applications, suggesting their effective use in advanced sensors for environmental monitoring, medical diagnostics, and industrial process control.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Acknowledgments

The work was funded by the National Natural Science Foundation of China (22108203). We would like to thank the Analytical & Testing Center of Tiangong University for Scanning Electron Micro-scope work.

References

  1. Zhang, M.X.; Song, W.L.; Tang, Y.X.; Xu, X.Z.; Huang, Y.N.; Yu, D.G. Polymer-Based Nanofiber-Nanoparticle Hybrids and Their Medical Applications. Polymers 2022, 14, 27. [Google Scholar] [CrossRef] [PubMed]
  2. Huang, J.T.; Liu, Y.W.; Lin, J.H.; Su, J.T.; Redshaw, C.; Feng, X.; Min, Y.G. Novel pyrene-based aggregation-induced emission luminogen (AIEgen) composite phase change fibers with satisfactory fluorescence anti-counterfeiting, temperature sensing, and high-temperature warning functions for solar-thermal energy storage. Adv. Compos. Hybrid Mater 2023, 6, 15. [Google Scholar] [CrossRef]
  3. Yang, Y.F.; Zhao, C.L.; Chen, X.D.; Yang, S.X.; Zhang, R.M.; Wang, Y.Q.; Wang, K.; Qian, J.; Long, L.L. Development of near-infrared fluorescent sensor and portable measuring device for on-site quantitation of Cys in food samples. Sens. Actuator B-Chem 2024, 414, 7. [Google Scholar] [CrossRef]
  4. Xue, K.; Wang, C.; Wang, J.X.; Lv, S.Y.; Hao, B.Y.; Zhu, C.L.; Tang, B.Z. A Sensitive and Reliable Organic Fluorescent Nanothermometer for Noninvasive Temperature Sensing. J. Am. Chem. Soc 2021, 143, 14147–14157. [Google Scholar] [CrossRef] [PubMed]
  5. Qi, F.X.; Xu, L.; He, Y.; Yan, H.; Liu, H. PVDF-Based Flexible Piezoelectric Tactile Sensors: Review. Cryst. Res. Technol. 2023, 58, 17. [Google Scholar] [CrossRef]
  6. Hujer, J.; Dancova, P.; Korinek, T.; Muller, M. Photolithographically Home-Made PVDF Sensor for Cavitation Impact Load Measurement. Processes 2021. [Google Scholar] [CrossRef]
  7. Hari, M.A.; Karumuthil, S.C.; Rajan, L. Optimization of PVDF nanocomposite based flexible piezoelectric tactile sensors: A comparative investigation. Sens. Actuator A-Phys 2023, 353, 7. [Google Scholar]
  8. Hernández-Rivera, D.; Rodríguez-Roldán, G.; Mora-Martínez, R.; Suaste-Gómez, E. A Capacitive Humidity Sensor Based on an Electrospun PVDF/Graphene Membrane. Sensors 2017, 17, 11. [Google Scholar] [CrossRef] [PubMed]
  9. Ooyama, Y.; Sugino, M.; EnoKi, T.; Yamamoto, K.; Tsunoji, N.; Ohshita, J. Aggregation-induced emission (AIE) characteristic of water-soluble tetraphenylethene (TPE) bearing four sulfonate salts. New J. Chem 2017, 41, 4747–4749. [Google Scholar] [CrossRef]
  10. Yang, Z.Y.; Qin, W.; Leung, N.L.C.; Arseneault, M.; Lam, J.W.Y.; Liang, G.D.; Sung, H.H.Y.; Williams, I.D.; Tang, B.Z. A mechanistic study of AIE processes of TPE luminogens: intramolecular rotation vs configurational isomerization. J. Mater. Chem. C 2016, 4, 99–107. [Google Scholar] [CrossRef]
  11. Wang, N.; Yao, H.; Tao, Q.; Sun, J.; Ma, H.; Wang, Y.; Zhou, C.C.; Fan, H.Y.; Shao, H.X.; Qin, A.J. TPE based aggregation induced emission fluorescent sensors for viscosity of liquid and mechanical properties of hydrogel. Chin. Chem. Lett 2022, 33, 252–256. [Google Scholar] [CrossRef]
  12. Ji, F.Y.; Wang, P.L.; Li, Z.R.; Ji, K.X.; Wang, D.Y.; Ma, Q. Cu superparticle-based aggregation induced enhancement strategy with PVDF-HFP/CeVO4 NP sensing interface for miR-103a detection. Talanta 2024, 276, 9. [Google Scholar] [CrossRef] [PubMed]
  13. Sobhan, M.A.; Lebedev, A.; Chng, L.L.; Anariba, F. Rapid Fabrication of Photoluminescent Electrospun Nanofibers without the Need of Chemical Polymeric Backbone Modifications. J. Nanomater. 2018, 2018, 7. [Google Scholar] [CrossRef]
  14. Peng, X.; Dai, Z.; Zhang, Q.; Gao, S.; Li, N. Intelligent microsphere-gel structures: Pioneering multi-range temperature sensing technology. Appl Mater Today 2024, 38, 102244. [Google Scholar] [CrossRef]
  15. Al-Abduljabbar, A.; Farooq, I. Electrospun Polymer Nanofibers: Processing, Properties, and Applications. Polymers 2022, 15. [Google Scholar] [CrossRef] [PubMed]
  16. Vinh, N.; Kim, H.-M. Electrospinning Fabrication and Performance Evaluation of Polyacrylonitrile Nanofiber for Air Filter Applications. Appl Sci-Basel 2016, 6. [Google Scholar] [CrossRef]
  17. Choi, S.Y.; Han, E.M.; Park, K.H. Porosity Control of Electrospun PAN/PMMA Nanofiber Webs. Mol Cryst Liq Cryst 2019, 688, 68–74. [Google Scholar] [CrossRef]
  18. Zhang, Q.; Zhou, R.; Peng, X.; Li, N.; Dai, Z. Development of Support Layers and Their Impact on the Performance of Thin Film Composite Membranes (TFC) for Water Treatment. Polymers 2023, 15. [Google Scholar] [CrossRef] [PubMed]
  19. Liu, H.; Jiang, W.; Yang, Z.; Chen, X.; Yu, D.-G.; Shao, J. Hybrid Films Prepared from a Combination of Electrospinning and Casting for Offering a Dual-Phase Drug Release. Polymers 2022, 14. [Google Scholar] [CrossRef]
  20. Yu, S.; Milam-Guerrero, J.; Tai, Y.; Yang, S.; Choi, Y.Y.; Nam, J.; Myung, N.V. Maximizing Polyacrylonitrile Nanofiber Piezoelectric Properties through the Optimization of Electrospinning and Post-thermal Treatment Processes. Appl Polym Mater 2021, 4, 635–644. [Google Scholar] [CrossRef]
  21. de Almeida, D.S.; Duarte, E.H.; Hashimoto, E.M.; Turbiani, F.R.B.; Muniz, E.C.; de Souza, P.R.; Gimenes, M.L.; Martins, L.D. Development and characterization of electrospun cellulose acetate nanofibers modified by cationic surfactant. Polymer Testing 2020, 81. [Google Scholar] [CrossRef]
  22. Shi, S.; Si, Y.; Han, Y.; Wu, T.; Iqbal, M.I.; Fei, B.; Li, R.K.Y.; Hu, J.; Qu, J. Recent Progress in Protective Membranes Fabricated via Electrospinning: Advanced Materials, Biomimetic Structures, and Functional Applications. Adv Mater 2022, 34. [Google Scholar] [CrossRef] [PubMed]
  23. Zhu, F.; Zheng, Y.-M.; Zhang, B.-G.; Dai, Y.-R. A critical review on the electrospun nanofibrous membranes for the adsorption of heavy metals in water treatment. J Hazard Mater:2021, 401.
  24. Bhatta, T.; Sharma, S.; Shrestha, K.; Shin, Y.; Seonu, S.; Lee, S.; Kim, D.; Sharifuzzaman, M.; Rana, S.M.S.; Park, J.Y. Siloxene/PVDF Composite Nanofibrous Membrane for High-Performance Triboelectric Nanogenerator and Self-Powered Static and Dynamic Pressure Sensing Applications. Adv. Funct. Mater 2022, 32, 15. [Google Scholar] [CrossRef]
  25. Xiong, J.P.; Wang, L.; Liang, F.H.; Li, M.Y.; Yabuta, Y.; Iqbal, M.A.; Mayakrishnan, G.; Shi, J.; Kim, I.S. Flexible Piezoelectric Sensor Based on Two-Dimensional Topological Network of PVDF/DA Composite Nanofiber Membrane. Adv. Fiber Mater 2024, 17. [Google Scholar] [CrossRef]
  26. Chen, H.; Li, N.; Lin, Y.S.; Dai, Z. Research progress on nanofiber-based support layers in forward/osmosis composite membranes. Fine Chemicals 2023, 10, 1–12. [Google Scholar]
  27. Wang, T.; Kumar, S. Electrospinning of polyacrylonitrile nanofibers. J Appl Polym Sci 2006, 102, 1023–1029. [Google Scholar] [CrossRef]
  28. Du, J.; Shintay, S.; Zhang, X. Diameter control of electrospun polyacrylonitrile/iron acetylacetonate ultrafine nanofibers. J Polym Sci Pol Phys 2008, 46, 1611–1618. [Google Scholar] [CrossRef]
  29. Chang, W.M.; Wang, C.C.; Chen, C.Y. The combination of electrospinning and forcespinning: Effects on a viscoelastic jet and a single nanofiber. Chem Eng J 2014, 244, 540–551. [Google Scholar] [CrossRef]
  30. Papkov, D.; Delpouve, N.; Delbreilh, L.; Araujo, S.; Stockdale, T.; Mamedov, S.; Maleckis, K.; Zou, Y.; Andalib, M.N.; Dargent, E.; et al. Quantifying Polymer Chain Orientation in Strong and Tough Nanofibers with Low Crystallinity: Toward Next Generation Nanostructured Superfibers. ACS Nano 2019, 13, 4893–4927. [Google Scholar] [CrossRef]
  31. Kirecci, A.; Özkoç, Ü.; Içoglu, H.I. Determination of optimal production parameters for polyacrylonitrile nanofibers. J Appl Polym Sci 2012, 124, 4961–4968. [Google Scholar] [CrossRef]
  32. Armaghani, D.J.; Asteris, P.G. A comparative study of ANN and ANFIS models for the prediction of cement-based mortar materials compressive strength. Neural Comput Appl 2020, 33, 4501–4532. [Google Scholar] [CrossRef]
  33. Premasudha, M.; Bhumi Reddy, S.R.; Lee, Y.J.; Panigrahi, B.B.; Cho, K.K.; Nagireddy Gari, S.R. Using artificial neural networks to model and interpret electrospun polysaccharide (Hylon VII starch) nanofiber diameter. J Appl Polym Sci 2020, 138. [Google Scholar] [CrossRef]
  34. Santos, A.F.; Aguado, R.; Corazza, M.L.; Tarrés, Q.; Sanchez-Salvador, J.-L.; Blanco, A.; Negro, C.; Delgado-Aguilar, M. Artificial neural network for aspect ratio prediction of lignocellulosic micro/nanofibers. Cellulose 2022, 29, 5609–5622. [Google Scholar] [CrossRef]
  35. Ahmad, T.; Chen, H.X. A review on machine learning forecasting growth trends and their real-time applications in different energy systems. Sust. Cities Soc 2020, 54, 27. [Google Scholar] [CrossRef]
  36. Lakshmi Narayana, P.; Wang, X.S.; Yeom, J.T.; Maurya, A.K.; Bang, W.S.; Srikanth, O.; Harinatha Reddy, M.; Hong, J.K.; Subba Reddy, N.G. Correlating the 3D melt electrospun polycaprolactone fiber diameter and process parameters using neural networks. J Appl Polym Sci 2021, 138. [Google Scholar] [CrossRef]
  37. Samadian, H.; Zakariaee, S.S.; Faridi-Majidi, R. Evaluation of effective needleless electrospinning parameters controlling polyacrylonitrile nanofibers diameter via modeling artificial neural networks. J. Text. Inst 2019, 110, 477–486. [Google Scholar] [CrossRef]
  38. Khatti, T.; Naderi-Manesh, H.; Kalantar, S.M. Prediction of diameter in blended nanofibers of polycaprolactone-gelatin using ANN and RSM. Fiber Polym 2017, 18, 2368–2378. [Google Scholar] [CrossRef]
  39. Ma, M.; Zhou, H.C.; Gao, S.H.; Li, N.; Guo, W.J.; Dai, Z. Analysis and Prediction of Electrospun Nanofiber Diameter Based on Artificial Neural Network. Polymers 2023, 15. [Google Scholar] [CrossRef] [PubMed]
  40. Wang, F.J.; Elbadawi, M.; Tsilova, S.L.; Gaisford, S.; Basit, A.W.; Parhizkar, M. Machine learning to empower electrohydrodynamic processing. Mater. Sci. Eng. C-Mater. Biol. Appl 2022, 132, 14. [Google Scholar] [CrossRef]
  41. Rubio, J.D. Stability Analysis of the Modified Levenberg-Marquardt Algorithm for the Artificial Neural Network Training. Ieee T Neur Net Lear 2021, 32, 3510–3524. [Google Scholar] [CrossRef]
  42. Sherwani, F.; Ibrahim, B.; Asad, M.M. Hybridized classification algorithms for data classification applications: A review. Egypt. Inform. J 2021, 22, 185–192. [Google Scholar] [CrossRef]
  43. Reddy, B.S.; In, K.H.; Panigrahi, B.B.; Paturi, U.M.R.; Cho, K.K.; Reddy, N.S. Modeling tensile strength and suture retention of polycaprolactone electrospun nanofibrous scaffolds by artificial neural networks. Mater Today Commun 2021, 26. [Google Scholar] [CrossRef]
  44. Malayeri, M.; Nasiri, F.; Haghighat, F.; Lee, C.S. Optimization of photocatalytic oxidation reactor for air purifier design: Application of artificial neural network and genetic algorithm. Chem Eng J 2023, 462, 12. [Google Scholar] [CrossRef]
  45. Narayana, P.L.; Wang, X.S.; Yeom, J.T.; Maurya, A.K.; Bang, W.S.; Srikanth, O.; Reddy, M.H.; Hong, J.K.; Reddy, N.G.S. Correlating the 3D melt electrospun polycaprolactone fiber diameter and process parameters using neural networks. J Appl Polym Sci 2021, 138, 10. [Google Scholar]
  46. Armaghani, D.J.; Asteris, P.G. A comparative study of ANN and ANFIS models for the prediction of cement-based mortar materials compressive strength. Neural Comput. Appl 2021, 33, 4501–4532. [Google Scholar] [CrossRef]
  47. Armaghani, D.J.; Mirzaei, F.; Shariati, M.; Trung, N.T.; Shariati, M.; Trnavac, D. Hybrid ANN-based techniques in predicting cohesion of sandy-soil combined with fiber. Geomech. Eng 2020, 20, 191–205. [Google Scholar]
  48. Han, Y.; Liu, B.; Wu, Y.F.; Mao, Y.Y.; Zhao, L.L.; Nan, T.; Wang, J.; Zhang, Y.L.; Tang, R.; Liu, Y.; et al. High-sensitivity high-temperature sensor based on multi-microspheres improved Michelson interferometer. Opt. Commun 2021, 491, 7. [Google Scholar] [CrossRef]
  49. Wang, K.; He, Q.; Yang, D.R.; Pi, X.D. Erbium-Hyperdoped Silicon Quantum Dots: A Platform of Ratiometric Near-Infrared Fluorescence. Adv. Opt. Mater 2022, 10, 9. [Google Scholar] [CrossRef]
  50. Chen, M.H.; He, Y.C.; Liang, H.H.; Zhou, H.Y.; Wang, X.; Heng, X.B.; Zhang, Z.S.; Gan, J.L.; Yang, Z.M. Stretchable and Strain-Decoupled Fluorescent Optical Fiber Sensor for Body Temperature and Movement Monitoring. ACS Photonics 2022, 9, 1415–1424. [Google Scholar] [CrossRef]
  51. Listewnik, P.; Bechelany, M.; Wierzba, P.; Szczerska, M. Optical-Fiber Microsphere-Based Temperature Sensors with ZnO ALD Coating-Comparative Study. Sensors 2021, 21, 11. [Google Scholar] [CrossRef]
  52. Yang, Y.; Zhang, X.B.; Zhang, Q.; Xie, Y.; Wang, Z.J.; Yu, Y.; Wang, Y.; Dong, Y.H.; Huang, Y.; Wang, T.Y. Packaged Temperature Sensor Based on Fluorescent Microsphere With an Embedded Fiber Microlens. IEEE Photonics Technol. Lett 2023, 35, 398–401. [Google Scholar] [CrossRef]
  53. Yu, J.B.; Lewis, E.; Brambilla, G.; Wang, P.F. Temperature Sensing Performance of Microsphere Resonators. Sensors 2018, 18, 15. [Google Scholar] [CrossRef] [PubMed]
  54. Nguyen, T.V.; Nguyen, T.D.; Mai, H.H.; Pham, N.V.; Ta, V.D.; Nguyen, T.A. Biological miniature temperature sensor based on monodisperse microsphere lasers fabricated by soft microfluidic technology. J. Phys. D-Appl. Phys 2022, 55, 5. [Google Scholar] [CrossRef]
Preprints 112925 g001
Figure 1. Actual values versus predicted values by the CNN.
Figure 1. Actual values versus predicted values by the CNN.
Preprints 112925 g001
Preprints 112925 g002
Figure 2. 3D plots of PVDF nanofiber diameters predicted by GA-ELM model (a) Effect of spinning fluid concentration-voltage. (b) Effect of spinning fluid concentration-acceptance distance. (c) Effect of spinning solution concentration-injection rate.
Figure 2. 3D plots of PVDF nanofiber diameters predicted by GA-ELM model (a) Effect of spinning fluid concentration-voltage. (b) Effect of spinning fluid concentration-acceptance distance. (c) Effect of spinning solution concentration-injection rate.
Preprints 112925 g002
Preprints 112925 g003
Figure 3. Effect of PVDF concentration on (a) viscosity, (b) surface tension, and (c) conductivity of spinning solutions.
Figure 3. Effect of PVDF concentration on (a) viscosity, (b) surface tension, and (c) conductivity of spinning solutions.
Preprints 112925 g003
Preprints 112925 g004
Figure 4. (a) Pure water contact angle of pure PVDF nanofiber membrane; (b) Pure water contact angle of TPE-doped PVDF nanofiber membrane. (c) ensile stress-strain curves of pure PVDF membranes and PVDF membranes containing 1 wt% TPE. (d) Changes in fluorescence intensity of TPE-doped PVDF nanofiber membranes after immersion in acidic solution at pH=1. (e) Changes in fluorescence intensity of TPE-doped PVDF nanofiber membranes after immersion in alkaline solution at pH=12. (f) Changes in fluorescence intensity of nanofiber membranes after 10 hours of continuous irradiation under a UV lamp with a wavelength of 365 nm.
Figure 4. (a) Pure water contact angle of pure PVDF nanofiber membrane; (b) Pure water contact angle of TPE-doped PVDF nanofiber membrane. (c) ensile stress-strain curves of pure PVDF membranes and PVDF membranes containing 1 wt% TPE. (d) Changes in fluorescence intensity of TPE-doped PVDF nanofiber membranes after immersion in acidic solution at pH=1. (e) Changes in fluorescence intensity of TPE-doped PVDF nanofiber membranes after immersion in alkaline solution at pH=12. (f) Changes in fluorescence intensity of nanofiber membranes after 10 hours of continuous irradiation under a UV lamp with a wavelength of 365 nm.
Preprints 112925 g004
Preprints 112925 g005
Figure 5. SEM images of fluorescent nanofibers at different voltages: (a) 9 kV; (b) 10 kV; (c) 11 kV; (d) 12 kV; (e) 13 kV.
Figure 5. SEM images of fluorescent nanofibers at different voltages: (a) 9 kV; (b) 10 kV; (c) 11 kV; (d) 12 kV; (e) 13 kV.
Preprints 112925 g005
Preprints 112925 g006
Figure 6. SEM images of fluorescent nanofibers at different distances: (a) 11 cm; (b) 12 cm; (c) 13 cm; (d) 14 cm; (e) 15 cm.
Figure 6. SEM images of fluorescent nanofibers at different distances: (a) 11 cm; (b) 12 cm; (c) 13 cm; (d) 14 cm; (e) 15 cm.
Preprints 112925 g006
Preprints 112925 g007
Figure 7. SEM images of fluorescent nanofibers at different flow rates: (a) 0.1 mL/h; (b) 0.2 mL/h; (c) 0.3 mL/h; (d) 0.4 mL/h; (e) 0.5 mL/h.
Figure 7. SEM images of fluorescent nanofibers at different flow rates: (a) 0.1 mL/h; (b) 0.2 mL/h; (c) 0.3 mL/h; (d) 0.4 mL/h; (e) 0.5 mL/h.
Preprints 112925 g007
Preprints 112925 g008
Figure 8. UV photographs of fluorescent nanofiber membranes with different TPE contents at different temperatures.
Figure 8. UV photographs of fluorescent nanofiber membranes with different TPE contents at different temperatures.
Preprints 112925 g008
Preprints 112925 g009
Figure 9. (a) Emission spectra of vitamin films at different temperatures; (b) The fitting curve of fluorescence intensity with temperature variation; (c) The fluorescence intensity changes after heating the fiber membrane to 100 ℃ and cooling it; (d) The fluorescence intensity at 460 nm varies over time.
Figure 9. (a) Emission spectra of vitamin films at different temperatures; (b) The fitting curve of fluorescence intensity with temperature variation; (c) The fluorescence intensity changes after heating the fiber membrane to 100 ℃ and cooling it; (d) The fluorescence intensity at 460 nm varies over time.
Preprints 112925 g009
Preprints 112925 g010
Figure 10. (a) Fit curve of grayscale value before heating with temperature change; (b) Fit curve of grayscale value before heating with temperature change; (c) Temperature sensitivity in different temperature ranges.
Figure 10. (a) Fit curve of grayscale value before heating with temperature change; (b) Fit curve of grayscale value before heating with temperature change; (c) Temperature sensitivity in different temperature ranges.
Preprints 112925 g010
Preprints 112925 g011
Figure 11. (a) Fluorescence recovery emission spectrum after removal of 600 g pressure; (b) Changes in fluorescence intensity at 460 nm over time after removal of 600 g pressure; (c) Emission spectra of membranes under different pressures; (d) Fitting curve of fluorescence intensity of fiber membrane with pressure variation.
Figure 11. (a) Fluorescence recovery emission spectrum after removal of 600 g pressure; (b) Changes in fluorescence intensity at 460 nm over time after removal of 600 g pressure; (c) Emission spectra of membranes under different pressures; (d) Fitting curve of fluorescence intensity of fiber membrane with pressure variation.
Preprints 112925 g011
Table 1. Comparison of temperature sensitivity of various sensors.
Table 1. Comparison of temperature sensitivity of various sensors.
Component Materials Structure Average particle size Temperature measurement method Temperature range Sensitivity
SiO2 Arrays 220 µm Ratio of FL 100-800 ℃ 0.15 nm/°C[48]
Er3+- Silica Core-shell 4 µm Emission intensity 4-204 ℃ -0.53/K[49]
Y2O3@Er3+/Yb3+- Silica Core-shell 800 µm Current ratio -10-60 ℃ 1.3 % /℃[50]
ZnO - Silica Shell-core 100 µm Peak position 100-300 ℃ 0.019 nm/℃[51]
Er3--Yb3+@ Tellurite glass Hollow 50 µm Ratio of FL Intensity 30-110 ℃ 1.11×10-2/K[52]
PS Solid 91.7 µm WGM Wavelength shift 20-70 ℃ 0.61796 nm/°C[53]
PDMS Solid 85 µm Laser wavelength 25-50 ℃ 0.47 nm/°C[54]
This work Solid 680 nm Gray value 20-100 ℃ -0.638 gray value/℃
This work Solid 680 nm FL emission value 20-100 ℃ -7.3 a.u./℃
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated